A characterization of Inoue surfaces with $p_g=0$ and $K^2=7$

Abstract

Inoue constructed the first examples of smooth minimal complex surfaces of general type with $p_g=0$ and $K^2=7$. These surfaces are finite Galois covers of the 4-nodal cubic surface with the Galois group, the Klein group $\mathbb {Z}_2\times \mathbb {Z}_2$. For such a surface S, the bicanonical map of S has degree 2 and it is composed with exactly one involution in the Galois group. The divisorial part of the fixed locus of this involution consists of two irreducible components: one is a genus 3 curve with self-intersection number 0 and the other is a genus 2 curve with self-intersection number $-\,1$. Conversely, assume that S is a smooth minimal complex surface of general type with $p_g=0$, $K^2=7$ and having an involution $\sigma$. We show that, if the divisorial part of the fixed locus of $\sigma$ consists of two irreducible components $R_1$ and $R_2$, with $g(R_1)=3, R_1^2=0, g(R_2)=2$ and $R_2^2=-\,1$, then the Klein group $\mathbb {Z}_2\times \mathbb {Z}_2$ acts faithfully on S and S is indeed an Inoue surface.

1 Introduction

In this article we focus on smooth minimal surfaces S of general type with $p_g=0$, $K^2=7$ and nonbirational bicanonical map. By [9] the bicanonical map $\varphi$ has degree 2. Denote by $\sigma$ the involution associated to $\varphi$, called as the bicanonical involution. Despite of the existence of examples, the Inoue surfaces (see [9, Example 4.1], [7] and [1]), and a structure theorem (see [10, Theorem 3.2]), a complete classification of these surfaces is still out of reach. To understand S, one needs to study the quotient surface $\Sigma :=S/\sigma$ and the fixed locus $\mathrm {Fix}(\sigma )$ of $\sigma$. Mendes Lopes and Pardini [10, Propostion 3.1] study $\Sigma$ in detail and show that $\sigma$ has 11 isolated fixed points. However, an explicit description of the divisorial part of $\mathrm {Fix}(\sigma )$ is still missing. In general, for an involution $\sigma$ on a surface of general type with $p_g=0$ and $K^2=7$, denote by $R_\sigma$ the divisorial part of $\mathrm {Fix}(\sigma )$. Lee and the second named author [8, Table in page 3] describe all the possible cases for $R_\sigma$ in terms of the genus and the self-intersection number of each irreducible component of $R_\sigma$, except the case where $\sigma$ is the bicanonical involution. See also [12].

So it is natural to first consider the case where $R_\sigma$ has the same irreducible decomposition as the one of an Inoue surface. For any Inoue surface, $\deg \varphi =2$ (cf. [9, Example 4.1]) and $R_\sigma$ has the irreducible decomposition $R_1+R_2$ with $g(R_1)=3, R_1^2=0, g(R_2)=2$ and $R_2^2=-\,1$ (cf. [8, Section 5]). Conversely, we have the following theorem.

Theorem 1.1

Let S be a smooth minimal surface of general type with $p_g(S)=0$, $K_S^2=7$ and having an involution $\sigma$. Assume that the divisorial part $R_\sigma$ of the fixed locus of $\sigma$ consists of two irreducible components $R_1$ and $R_2$, with $g(R_1)=3, R_1^2=0, g(R_2)=2$ and $R_2^2=-\,1$. Then the automorphism group of S contains a subgroup which is isomorphic to the Klein group $\mathbb {Z}_2 \times \mathbb {Z}_2$ and S is an Inoue surface.

It is not hard to show $\deg \varphi =2$ and that $\sigma$ is the bicanonical involution (see Lemma 2.4). The main claim of the theorem is the existence of involutions on S other than $\sigma$. We briefly mention how to prove the theorem. In Sect. 3, based on the results of [10, Propostion 3.1], we consider the minimal resolution W of the quotient surface $\Sigma =S/\sigma$ and study a rational fibration $\bar{f}:W \rightarrow \mathbb {P}^1$. With the assumption of Theorem 1.1, we not only analyze the singular fibers of $\bar{f}$ in detail (see Proposition 3.4) but also find a fibration of curves of genus 2 on W which induces a hyperelliptic fibration of genus 5 on S (see Propositions 4.1 and 4.2). For these we present several lemmas about curves of genus 2 in Sect. 5. The hyperelliptic fibration of genus 5 implies an involution $\tau$ on S such that $\tau \not =\sigma$. Therefore, we obtain three commuting involutions $\sigma ,\tau ,\sigma \tau$ on S. Then S is an Inoue surface by the result of [3] (see Proposition 2.1).

Notation We mainly consider projective normal surfaces with at worst ordinary double points (nodes) over $\mathbb {C}$ in this article. For such a surface X, we use the following notation:

• $\equiv$: a linear equivalence among divisors on X;

• ${\mathop {\sim }\limits ^{num}}$: a numerical equivalence among divisors on X;

• $\mathrm {Num}(X)$: the quotient of $\mathrm {Pic}(X)$ by ${\mathop {\sim }\limits ^{num}}$;

• $\rho (X)$: the Picard number of X, i.e., the rank of $\mathrm {Num}(X)$;

• $(-\,n)$-curve ($n \in \mathbb {N}$): a smooth irreducible rational curve with the self intersection number $-\,n$;

• a $(-\,2)$-curve is also called a nodal curve.

Throughout this article, we denote by S a smooth minimal surface of general type with $p_g=0$ and $K^2=7$ and by $\varphi :S \dashrightarrow \mathbb {P}^7$ the bicanonical map of S.

2 Inoue surfaces and known results

Now we briefly introduce Inoue surfaces, the first examples of surfaces of general type with $p_g=0$ and $K^2=7$. For explicit construction see [7] and [9, Example 4.1]. Here we just mention that an Inoue surface can be realized as a finite Galois cover of the 4-nodal cubic surface with the Galois group $\mathbb {Z}_2\times \mathbb {Z}_2$, and that its bicanonical map has degree 2 and that its bicanonical involution $\sigma$ belongs to the Galois group (cf. see [9, Example 4.1]). Also $R_\sigma =R_1+R_2$ with $g(R_1)=3, R_1^2=0, g(R_2)=2$ and $R_2^2=-\,1$ (cf. [8, Section 5]). We now state a proposition characterizing Inoue surfaces.

Proposition 2.1

Let S be a smooth minimal surface of general type with $p_g=0$, $K^2=7$ and $\deg \varphi =2$. Assume that there is an involution $\tau$ on S other than the bicanonical involution $\sigma$. Then the subgroup $\langle \sigma , \tau \rangle$ of the automorphism group of S is isomorphic to $\mathbb {Z}_2\times \mathbb {Z}_2$ and S is an Inoue surface.

Proof

By [4, Theorem 1.2], we have $\langle \sigma , \tau \rangle \cong \mathbb {Z}_2 \times \mathbb {Z}_2$. Since $K_SR_\sigma =7$ by Theorem 2.2 (a) below, S is an Inoue surface according to [3, Theorem 1.1]. $\square$

In general, for a minimal surface of general type with $p_g=0$ and $K^2=7$, we know $\deg \varphi =1$ or 2 by [9]. When $\deg \varphi =2$, Mendes Lopes and Pardini prove the following theorem.

Theorem 2.2

(cf. [10]) Assume $\deg \varphi =2$ and let $\sigma$ be the bicanonical involution. Then

• (a) $K_SR_\sigma =7$ and $\sigma$ has 11 isolated fixed points;

• (b) $\Sigma$ is a rational surface with 11 nodes and $K_\Sigma ^2=-\,4$;

• (c) there is a rational fibration $f :\Sigma \rightarrow \mathbb {P}^1$ such that $f\circ \pi$ is a genus 3 hyperelliptic fibration (see the right triangle of the diagram (2.1));

• (d) $K_S$ is ample.

Proof

For (a), see [2, Proposition 3.3(v) and Corollary 3.6(iv)] and [5, Lemma 4.2]. For (b), (c) and (d), see [10, Proposition 3.1 and Theorem 3.3]. $\square$

Remark 2.3

[10, Proposition 3.1(ii) and Theorem 3.2(iv)] describe the singular fibers of f and $f\circ \pi$ explicitly. See also [10, Remark 3.4(i)].

From now on, we keep the assumption and notation of Theorem 1.1.

Lemma 2.4

The bicanonical map $\varphi$ of S has degree 2 and $\sigma$ is the bicanonical involution.

Proof

The adjunction formula gives $K_SR_1=4$ and $K_SR_2=3$, and thus $K_SR_\sigma =7$. Then $\varphi$ is composed with $\sigma$ by [5, Lemma 4.2] and [2, Corollary 3.6(iv)]. Since $\deg \varphi \le 2$ by [9], we conclude $\deg \varphi =2$ and that $\sigma$ is the bicanonical involution. $\square$

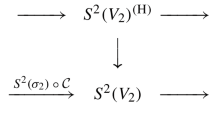
Let $\varepsilon :V \rightarrow S$ be the blow-up of the 11 isolated fixed points of $\sigma$ and denote by $E_j$ ($j=0, 1, \ldots , 10$) the corresponding exceptional divisors. Then $\sigma$ lifts to an involution $\bar{\sigma }$ on V. Denote by W the quotient of V by $\bar{\sigma }$, by $\overline{\pi }:V \rightarrow W$ the quotient map and by $C_j$ the image of $E_j$ under $\overline{\pi }$ for $j=0, \ldots , 10$. Then W is a smooth surface and the curves $C_j$ are nodal curves. The middle square of the diagram (2.1) commutes

(2.1)

where $\eta$ is the minimal resolution of $\Sigma$. In particular, $K_W\equiv \eta ^*K_\Sigma$ and W is a smooth rational surface with $K_W^2=-\,4$ by Theorem 2.2(b).

Note that $\overline{\pi }$ is a smooth double cover branched along the divisor $B_1+B_2+\sum _{j=0}^{10}C_j$, where $B_i=\overline{\pi }(\varepsilon ^*R_i)$ for $i=1,2$. Note that $B_i$ is isomorphic to $R_i$ for $i=1, 2$ and thus smooth. Also $B_1$ and $B_2$ are disjoint, and they are disjoint from the nodal curves $C_0, C_1, \ldots , C_{10}$. There is an invertible sheaf $\mathcal {L}\in \mathrm {Pic}(W)$ such that

$$\begin{aligned} 2\mathcal {L}\equiv B_1+B_2+C_0+C_1+\cdots +C_{10}. \end{aligned}$$

(2.2)

According to Theorem 2.2(b), $\bar{f}:=f\circ \eta :W \rightarrow \mathbb {P}^1$ is a rational fibration. Denote by F the general fiber of $\bar{f}$. We will frequently refer to the following intersection numbers $B_1^2=0,\ K_WB_1=4,\ B_2^2=-\,2$ and $K_WB_2=4$.

Lemma 2.5

Let $D :=2K_W+B_1+B_2$. Then

• (a) $\overline{\pi }^*D \equiv \varepsilon ^*(2K_S)$, $D^2=14,\ DK_W=0$ and D is nef and big;

• (b) $DB_1=8, DB_2=6$ and $DF=4$;

• (c) If $DC=0$ for an irreducible curve C, then C is one of the 11 nodal curves $C_0, C_1, \ldots , C_{10}$.

Proof

For (a), see [2, Proposition 3.1(i), (ii)]. And (b) follows from a direct calculation and Theorem 2.2(c). Now for (c) we use $K_S$ is ample (see Theorem 2.2(d)) and $\epsilon$ contracts exactly the curves $E_0,E_1,\ldots ,E_{10}$. $\square$

3 The branch divisors and the singular fibers of the rational fibration

This section and the next are devoted to the proof of Theorem 1.1. So we stick to the assumption in Theorem 1.1 throughout these two sections. In this section we focus on the description of the divisor class of $B_i$ in $\mathrm {Pic}(X)$ and the singular fibers of $\bar{f}$.

Proposition 3.1

After possibly renumbering the 11 nodal curves $C_0, C_1, \ldots , C_{10}$, we have

$$\begin{aligned} B_1 \equiv -2K_W+2F\ \text {and}\ B_2 \equiv -2K_W+F+2G+C_0, \end{aligned}$$

where G is a $(-\,1)$-curve such that $FG=0$ and $GC_0=1$. Moreover, $B_1G=2$ and $B_2G=1$.

Proof

Note that $(2K_W+B_1)^2=0$ and $K_W(2K_W+B_1)=-\,4$. Then we have $h^0(W, \mathcal {O}_W(2K_W+B_1)) \ge 3$ by the Riemann–Roch theorem. Since F is nef, $F(2K_W+B_1) \ge 0$ and thus $FB_1 \ge -\,2FK_W=4$.

Similarly, we have $h^0(W, \mathcal {O}_W(2K_W+B_2)) \ge 2$ and $FB_2 \ge -2FK_W=4$. By Lemma 2.5(b), $DF=4$ and thus $F(B_1+B_2)=F(D-2K_W)=8$. So $FB_1=FB_2=4$.

Then $F(2K_W+B_1)=0$. Since $(2K_W+B_1)^2=0$, the Zariski lemma implies $2K_W+B_1{\mathop {\sim }\limits ^{num}}aF$ ($a\in \mathbb {N}$) and then $aFK_W=(2K_W+B_1)K_W$, i.e. $-\,2a=-\,4$. So $a=2$ and $B_1 \equiv -\,2K_W+2F$ since a numerical equivalence is the same as a linear equivalence on any smooth rational surface.

We have seen $\dim |2K_W+B_2| \ge 1$ and $F(2K_W+B_2)=0$. It follows that the moving part of $|2K_W+B_2|$ is composed with |F|, namely $2K_W+B_2\equiv bF+\Psi$, where $b \in \mathbb {N}$ and $\Psi$ is the fixed part of $|2K_W+B_2|$. Then $D(bF+\Psi )=D(2K_W+B_2)$, i.e. $4b+D\Psi =6$. By Lemma 2.5(a), we have $b=1$ and $\Psi \equiv B_2+2K_W-F$.

By Lemma 2.5(b), we have

$$\begin{aligned} D\Psi =2, F\Psi =0, K_W\Psi =-\,2, \Psi ^2=-\,2, B_1\Psi =4\ \text {and}\ B_2\Psi =2. \end{aligned}$$

Since $F\Psi =0$, every irreducible component of $\Psi$ is a smooth rational curve with negative self-intersection number. Since $K_W\Psi =-\,2$, there is an irreducible component G of $\Psi$ such that $K_WG<0$. It follows that G is a $(-\,1)$-curve by the adjunction formula and then $DG>0$ by Lemma 2.5(a) and (c). We claim that $DG=1$. Otherwise, since $DG \le D\Psi =2$ by Lemma 2.5(a), $DG=2$ and then $D(\Psi -G)=0$. By Lemma 2.5(c), $\mathrm {Supp}(\Psi -G)$ is contained in $C_0 \cup C_1 \ldots \cup C_{10}$. Then $B_i(\Psi -G)=0$ since $B_i$ is disjoint from $C_0, C_1, \ldots , C_{10}$ for $i=1, 2$. So $B_1G=B_1\Psi =4$ and $B_2G=B_2\Psi =2$. Since $D\equiv 2K_W+B_1+B_2$, we have $K_WG=\frac{1}{2}(D-B_1-B_2)G=-\,2$. This contradicts that G is a $(-\,1)$-curve and thus $DG=1$.

Then $G(B_1+B_2)=G(D-2K_W)=3$. Also $GB_1=G(-2K_W+2F)=2$ and thus $GB_2=1$. By (2.2), $G(C_0+C_1+\cdots +C_{10})=2\mathcal {L}G-3 \not =0$. In particular, $GC_j >0$ for some $j \in \{0,1,\ldots ,10\}$. After possibly renumbering the 11 nodal curves $C_0, C_1, \ldots , C_{10}$, we may assume $j=0$ and thus $GC_0>0$. Since $F(G+C_0)=0$, $G+C_0$ is contained in the same singular fiber of $\bar{f}$ and thus $GC_0=1$.

We have shown $FG=0, DG=1, B_1G=2, B_2G=1$ and $GC_0=1$. It remains to show $\Psi =2G+C_0$. Note that $\Psi G=(B_2+2K_W-F)G=-\,1$ and $\Psi C_0=(B_2+2K_W-F)C_0=0$. It follows that $(\Psi -2G-C_0)^2=\Psi ^2-2\Psi (2G+C_0)+(2G+C_0)^2=0$. Since $D(\Psi -2G-C_0)=0$, $\Psi =2G+C_0$ by the algebraic index theorem. $\square$

Corollary 3.2

$2G|_{B_2}\equiv K_{B_2}$.

Proof

By Proposition 3.1, $2(K_W+B_2)\equiv (-2K_W+2F)+4G+2C_0\equiv B_1+4G+2C_0$. Since $B_1\cap B_2=\emptyset$ and $C_0\cap B_2=\emptyset$, we have $2K_{B_2}\equiv 2(K_W+B_2)|_{B_2}\equiv 4G|_{B_2}$. Note that $G \not = B_2$ and $\deg (G|_{B_2})=GB_2=1$. Since $g(B_2)=2$, $2G|_{B_2} \equiv K_{B_2}$ by Lemma 5.2. $\square$

Corollary 3.3

The linear system $|-2K_W+2F|$ is a base point free pencil of curves of genus 3.

Before the proof, we remark that we can not even conclude $|-2K_W+2F| \not =\emptyset$ from the Riemman-Roch theorem: $\chi (\mathcal {O}_W(-2K_W+2F))=-\,1$.

Proof

Recall that $B_1\equiv -2K_W+2F$ (see Proposition 3.1) and $B_1$ is smooth irreducible with $B_1^2=0$ and $g(B_1)=3$. First assume $|-K_W+F| \not = \emptyset$. Then for $\Delta \in |-K_W+F|$, $B_1\Delta =0$ and thus $B_1$ is disjoint from $\Delta$. Therefore $B_1$ and $2\Delta$ generate a base point free pencil of curves of genus 3.

It suffices to prove $|-K_W+F| \not =\emptyset$. We first show $|-K_W+F+G| \not =\emptyset$. Note that $(-K_W+F+G)^2=1$ and $K_W(-K_W+F+G)=1$ (see Proposition 3.1). By Serre duality, $h^2(W, \mathcal {O}_W(-K_W+F+G))=h^0(W, \mathcal {O}_W(2K_W-F-G))=0$. Then $|-K_W+F+G| \not = \emptyset$ by the Riemann-Roch theorem.

Let $\Phi \in |-K_W+F+G|$. It suffices to show $\Phi \ge G$. Since $K_W+B_2\equiv -K_W+F+2G+C_0\equiv \Phi +G+C_0$ and $p_g(W)=0$, we conclude that $\Phi \not \ge B_2$ and thus $\Phi |_{B_2}\ge 0$. We claim $\Phi \ge G$. Otherwise, since $G\Phi =G(-K_W+F+G)=0$, $\Phi$ and G are disjoint. Note that

$$\begin{aligned} K_{B_2}=(K_W+B_2)|_{B_2}\equiv (\Phi +G+C_0)|_{B_2}=\Phi |_{B_2}+G|_{B_2} \end{aligned}$$

since $C_0\cap B_2=\emptyset$. Then $\Phi |_{B_2}\equiv G|_{B_2}$ by Corollary 3.2. Since $\deg \Phi |_{B_2}=\deg G|_{B_2}=1$ and $\Phi$ is disjoint from G, we have $B_2 \cong \mathbb {P}^1$, a contradiction to $g(B_2)=2$. Hence $\Phi \ge G$. $\square$

Proposition 3.4

Denote by $F_0$ the singular fiber of $\bar{f}$ containing $G+C_0$. The rational fibration $\bar{f}$ has exactly 5 singular fibers (possibly renumbering the 10 nodal curves $C_1, \ldots , C_{10}$):

• (a) $F_0=2G+2C_0+2Z+C_{9}+C_{10}$, where Z is a $(-\,2)$-curve such that $ZG=0$ and $ZC_0=ZC_{9}=ZC_{10}=1$;

• (b) the other 4 fibers are $C_{2i-1}+2\Gamma _i+C_{2i}$, where $\Gamma _i$ is a $(-\,1)$-curve such that $\Gamma _iC_{2i-1}=\Gamma _iC_{2i}=1$ for $i=1, \ldots , 4$.

Proof

We have the following observations.

• (i) The $(-\,1)$-curve G is disjoint from the 10 nodal curves $C_1, \ldots , C_{10}$.

  Since $2G \equiv 2K_W+B_2-F-C_0$ by Proposition 3.1, we have $GC_i=0$ for $i=1, \ldots , 10$.

• (ii) $F_0 \ge 2G+C_0$.

  Actually, since $(-2K_W+2F)B_2=B_1B_2=0$ by Proposition 3.1 and $B_2$ is irreducible, $B_2$ is contained in some member of $|-2K_W+2F|$ (see Corollary 3.3). Then $|-2K_W+2F-B_2| \not =\emptyset$. Since $(-2K_W+2F)-B_2 \equiv F-2G-C_0$, we have $F_0 \ge 2G+C_0$.

• (iii) Every irreducible component of a singular fiber of $\bar{f}$ is either a $(-\,1)$-curve or a nodal curve.

  It suffices to show that $-K_W$ is $\bar{f}$-nef, which follows from Corollary 3.3.

Blowing down G and then blowing down the image of $C_0$, we obtain a birational morphism $\mu :W \rightarrow W'$, where $W'$ is a smooth rational surface with $K_{W'}^2=-2$ and $\rho (W')=\rho (W)-2=12$.

Denote by $p'$ the point $\mu (G+C_0)$ on $W'$. Note that there is a fibration $f':W' \rightarrow \mathbb {P}^1$ such that $\bar{f}=f'\circ \mu$. Set $F_0':=\mu (F_0)$. Then $F_0'$ is a fiber of $f'$ and $p' \in F_0'$.

Set $C_j':=\mu (C_j)$ for $j=1, \ldots , 10$. Since both G and $C_0$ are disjoint from the 10 nodal curves $C_1, \ldots , C_{10}$, we see that $C_j'$ is a nodal curve and $p' \not \in C_j'$ for $j=1, \ldots , 10$. So $W'$ contains 10 pairwise disjoint nodal curves. Applying [5, Theorem 3.3] and possibly renumbering the nodal curves $C_1', \ldots , C_{10}'$, we conclude that $f'$ has exactly 5 singular fibers: $C_{2i-1}'+2\Gamma _i'+C_{2i}'$, where $\Gamma _i'$ is a $(-\,1)$-curve such that $\Gamma _i'C_{2i-1}'=\Gamma _i'C_{2i}=1$ for $i=1, \ldots , 5$. We distinguish two cases.

Case 1: $F_0'$ is a smooth fiber of $f'$. Since $p'\in F_0'$, according to (ii), we have $F_0=\mu ^*F_0'=Z+2G+C_0$, where Z is the strict transform of $F_0'$ and Z is a nodal curve with $ZG=1$ and $ZC_0=0$. Besides $F_0$, $\bar{f}$ has 5 singular fibers $C_{2i-1}+2\Gamma _i+C_{2i}$, i.e., the pullback of the singular fibers of $f'$, where $\Gamma _i:=\mu ^*(\Gamma _i')$ is a $(-\,1)$-curve for $i=1, \ldots , 5$.

Denote by $\gamma :B_2 \rightarrow \mathbb {P}^1$ the restriction of $\bar{f}:W \rightarrow \mathbb {P}^1$ to $B_2$ and denote by $\mathcal {R}_{\gamma }$ the ramification divisor of $\gamma$. Then $\deg \gamma =FB_2=4$ and then $\deg \mathcal {R}_\gamma =10$ by the Riemann–Hurwitz theorem.

Since $\Gamma _i$ ($i=1,\ldots , 5$) appears with multiplicity 2 in a singular fiber of $\bar{f}$, $\mathcal {R}_\gamma \ge \Gamma _i|_{B_2}$ for $i=1,\ldots , 5$. Similarly, $\mathcal {R}_\gamma \ge G|_{B_2}$. Note that $\deg \Gamma _i|_{B_2}=\Gamma _iB_2=\frac{1}{2}(F-C_{2i-1}-C_{2i})B_2=2$ for $i=1, \ldots , 5$ and $\deg G|_{B_2}=GB_2=1$. We have $10=\deg \mathcal {R}_\gamma \ge 2\times 5+1=11$, a contradiction. So Case 1 does not occur.

Case 2: $F_0'$ is one of the singular fiber of $f'$. Without loss of generality, assume $F_0'=C_9'+2\Gamma _5'+C_{10}'$. We have seen $p'\in F_0'$ and $p' \not \in C_9' \cup C_{10}'$. So $p' \in \Gamma _5'$. By (ii) and (iii), $F_0=\mu ^*F_0'=2G+2C_0+2Z+C_{9}+C_{10}$, where Z is the strict transform of $\Gamma _5'$ and Z is a nodal curve such that $ZG=0$ and $ZC_0=ZC_{9}=ZC_{10}=1$. The pullbacks of the other 4 singular fibers of $f'$ are as described in (b) of the proposition since $p'$ does not belong to these 4 fibers. $\square$

Corollary 3.5

We have

$$\begin{aligned} F|_{B_2}\equiv 2K_{B_2},\ \ K_W|_{B_2}\equiv 2K_{B_2},\ \ B_2|_{B_2}\equiv -K_{B_2}. \end{aligned}$$

Proof

Denote by $\gamma :B_2 \rightarrow \mathbb {P}^1$ the restriction of $\bar{f}:W \rightarrow \mathbb {P}^1$ to $B_2$. Then $\deg \gamma =FB_2=4$. The restriction of singular fibers of $\bar{f}$ (see Proposition 3.4) to $B_2$ gives 5 double fibers of $\gamma$, namely, $2\Gamma _i|_{B_2}$ ($i=1, 2, 3, 4$) and $2(G+Z)|_{B_2}$. Then Lemma 5.4 yields $F|_{B_2}\equiv 2K_{B_2}$.

By the adjunction formula, Proposition 3.1, Corollary 3.2 and $C_0 \cap B_2=\emptyset$, we have

$$\begin{aligned} K_{B_2}=(K_W+B_2)|_{B_2}\equiv (-K_W+F+2G+C_0)|_{B_2}\equiv -K_W|_{B_2}+3K_{B_2}. \end{aligned}$$

Hence $K_W|_{B_2}\equiv 2K_{B_2}$. Then $B_2|_{B_2}\equiv K_{B_2}-K_W|_{B_2}\equiv -K_{B_2}$. $\square$

4 The proof of the main theorem

We provide the complete proof of Theorem 1.1. Recall that $G, \Gamma _i$ ($i=1,2,3,4$) and Z are contained in the singular fibers of $\bar{f}$ (see Proposition 3.4).

Proposition 4.1

Let $H:=B_2+2G+C_0$.

• (a) The linear system |H| is a base point free pencil of curves of genus 2.

• (b) For a general smooth $H \in |H|$, $F|_H \equiv 2K_H$ and $(\sum _{i=1}^4\Gamma _i|_H+Z|_H)\equiv 5K_H$.

Proof

By Proposition 3.1, we have $HK_W=2, HB_2=0, HG=0, HF=4$ and $HC_j=0$ for $j=0, \ldots , 10$. It follows that $H^2=H(B_2+2G+C_0)=0$ and $p_a(H)=2$ by the adjunction formula.

Since $C_0\cap B_2=\emptyset$, we have $H|_{B_2}\equiv \mathcal {O}_{B_2}$ by Corollary 3.2 and Corollary 3.5. Tensoring the exact sequence $0 \rightarrow \mathcal {O}_W(-B_2) \rightarrow \mathcal {O}_W \rightarrow \mathcal {O}_{B_2} \rightarrow 0$ by $\mathcal {O}_W(H)$, we obtain

$$\begin{aligned} 0 \rightarrow \mathcal {O}_W(2G+C_0) \rightarrow \mathcal {O}_W(H) \rightarrow \mathcal {O}_{B_2} \rightarrow 0. \end{aligned}$$

It is clear that $\dim H^0(W, \mathcal {O}_W(2G+C_0))=1$ and then $H^1(W, \mathcal {O}_W(2G+C_0))=0$ by the Riemann+-Roch theorem. The long exact sequence of cohomology groups yields $\dim |H|=1$.

To prove (a), it remains to show that |H| is base point free. Since $H^2=0$, it suffices to show that H is nef. If $HC<0$ for an irreducible curve C, since $B_2+2G+C_0 \in |H|$, $C=B_2, G$ or $C_0$. But we have seen $HB_2=HG=HC_0=0$, a contradiction. So H is nef.

For a general H, the same reasoning as the proof of Corollary 3.5 yields that the restriction of $\bar{f}$ to H has degree 4 and that it has 5 double fibers $2Z|_H$ and $2\Gamma _i|_H$ ($i=1, \ldots , 4$). Then Lemma 5.4 yields $F|_H\equiv 2K_H$ and $(\sum _{i=1}^4\Gamma _i+Z)|_H\equiv 5K_H$. $\square$

Proposition 4.2

For a general $H \in |H|$, $\overline{\pi }^*H$ is a hyperelliptic curve of genus 5.

Proof

The double cover $\overline{\pi }^*H \rightarrow H$ is determined by the data $(B_1+B_2+\sum _{j=0}^{10}C_j)|_H$ and $\mathcal {L}|_H$ (see (2.2)). By (2.2), Propositions 3.1 and 3.4, we have

$$\begin{aligned} 2\mathcal {L}&\equiv (-2K_W+2F)+(-2K_W+F+2G+C_0)+(C_0+C_9+C_{10})+\sum _{j=1}^8C_j\\&=-4K_W+3F+(2G+2C_0+C_9+C_{10})+\sum _{i=1}^4(C_{2i-1}+C_{2i})\\&\equiv -4K_W+3F+(F-2Z)+\sum _{i=1}^4(F-2\Gamma _i)=-4K_W+8F-2\left( Z+\sum _{i=1}^4\Gamma _i\right) . \end{aligned}$$

Since W is a smooth rational surface, $\mathrm {Pic}(W)$ is torsion free and thus

$$\begin{aligned} \mathcal {L}\equiv -2K_W+4F-\left( \sum _{i=1}^4\Gamma _i+Z\right) . \end{aligned}$$

Since $H|_H=\mathcal {O}_H$ by Proposition 4.1(a), $K_W|_H=K_H$ by the adjunction formula. Then $\mathcal {L}|_H\equiv (-2K_W+4F-(\sum _{i=1}^4\Gamma _i+Z))|_H \equiv K_H$ by Proposition 4.1(b).

Note that a general H is disjoint from $B_2+\sum _{j=0}^{10}C_j$. So $(B_1+B_2+\sum _{j=0}^{10}C_j)|_H=B_1|_H$. Since a general H intersects $B_1$ transversely and $\deg B_1|_H=B_1H=B_1(B_2+2G+C_0)=4$, we conclude that $\overline{\pi }^*H$ is irreducible and smooth.

We have shown that the double cover $\overline{\pi }^*H \rightarrow H$ and its covering data $B_1|_H$ and $\mathcal {L}|_H$ satisfy the assumption of Lemma 5.5 and hence $\overline{\pi }^*H$ is a hyperelliptic curve of genus 5. $\square$

Recall the commutativity of the square in the diagram (2.1). Denote by $\bar{h} :W\rightarrow \mathbb {P}^1$ the genus 2 fibration defined by |H|. Since $HC_j=0$, $C_j$ is contained in the fibers of $\bar{h}$ for $j=0, \ldots , 10$. By Proposition 4.2, $\bar{h}\circ \overline{\pi }:V \rightarrow \mathbb {P}^1$ is a hyperelliptic fibration of genus 5 (see the left triangle of the diagram (2.1)). Since $\pi ^*C_j=2E_j$, we see that $E_j$ is contained in the singular fibers of $\bar{h} \circ \overline{\pi }$. Therefore $\bar{h} \circ \overline{\pi }$ induces a hyperelliptic fibration of genus 5 on S. The hyperelliptic involutions on smooth fibers of this fibration induce an involution $\tau$ on S since S is minimal. It is clear that $\tau$ is different from $\sigma$. Then Theorem 1.1 follows by Proposition 2.1.

5 Lemmas on genus two curves

Throughout this section, we denote by C a smooth projective curve of genus 2. We omit the proofs of Lemmas 5.1 and 5.2.

Lemma 5.1

Let L be an invertible sheaf on C with $\deg L=2$. Then $h^0(C, L) \ge 1$ and $h^0(C, L) \ge 2$ if and only if $L \equiv K_C$.

Recall that a point p on C is a Weierstrass point if $2p \equiv K_C$.

Lemma 5.2

• (a) If p is a point of C such that $4p \equiv 2K_C$, then $2p \equiv K_C$.

• (b) The sum of the Weierstrass points of C is linearly equivalent to $3K_C$.

Lemma 5.3

Assume that the automorphism group of C contains a subgroup $G \cong \mathbb {Z}_2\times \mathbb {Z}_2$. Denote by $q :C \rightarrow C/G$ the quotient map. Then $C/G \cong \mathbb {P}^1$ and $q^*\mathcal {O}_{\mathbb {P}^1}(1)\equiv 2K_C$.

Proof

From [6, p. 267, V.1.10.], one see that G contains the hyperelliptic involution of C. Then we obtain the conclusion. $\square$

Lemma 5.4

Let $\gamma :C \rightarrow \mathbb {P}^1$ be a morphism of degree 4. Assume that $t_1,\ldots ,t_4$ and $t_5$ are 5 distinct points of $\mathbb {P}^1$ such that $\gamma ^*(t_i)=2x_i+2y_i$ for $i=1,\ldots ,5$. Then $\gamma ^*\mathcal {O}_{\mathbb {P}^1}(1)\equiv 2K_C$ and $\sum _{i=1}^{5}(x_i+y_i) \equiv 5K_C$.

Proof

It follows from Riemann-Hurwitz theorem that $\sum _{i=1}^5(x_i+y_i)$ is the ramification divisor of $\gamma$ and $x_i\not = y_i$ for $i=1,\dots ,5$. Set $X:=\mathbb {P}^1\setminus \{t_1, t_2, t_3, t_4, t_5\}$ and $Y:=\gamma ^{-1}(X)$. Then Y with $\gamma |_Y :Y \rightarrow X$ is a topological covering space of X. Fix $t_0 \in X$ and take a simple loop $l_i$ in X based at $t_0$ and going around $t_i$ for $i=1, \ldots , 5$. Denote by $[l_i]$ the class of $l_i$ in $\pi _1(X, t_0)$. Then $\pi _1(X, t_0)$ is generated by $[l_1],\ldots , [l_5]$ with the relation $[l_1][l_2][l_3][l_4][l_5]=1$.

Identify the permutation group of $\gamma ^{-1}(t_0)$ with the symmetric group $\mathrm {S}_4$ with 4 letters. The group $\pi _1(X,t_0)$ acts on $\gamma ^{-1}(t_0)$ (from the right) and corresponds to an anti-group homomorphism $\alpha :\pi _1(X, t_0) \rightarrow \mathrm {S}_4$. Also the group $\mathrm {D}$ of Deck transformations of the covering $Y \rightarrow X$ acts on $\gamma ^{-1}(t_0)$ (from the left) and corresponds to a group homomorphism $\beta :\mathrm {D} \rightarrow \mathrm {S}_4$. It is well known that $\beta$ is injective and $\mathrm {Im}(\beta )$ is the centralizer of $\mathrm {Im}(\alpha )$ in $\mathrm {S}_4$.

For $i=1,\ldots , 5$, since $\gamma ^*(t_i)=2x_i+2y_i$ and $x_i \not =y_i$, we conclude that $\alpha ([l_i]) \not =1$ and $\alpha ([l_i]) \in \mathrm {V}_4$, where $\mathrm {V}_4:=\{1, (12)(34), (13)(24), (14)(23)\}.$ Since any two nontrivial elements of $\mathrm {V}_4$ generate $\mathrm {V}_4$ and $\alpha ([l_5]) \dots \alpha ([l_1])=\alpha ([l_1] \dots [l_5])=1$, we have $\mathrm {Im}(\alpha )=\mathrm {V}_4$. Since the centralizer of $\mathrm {V}_4$ in $\mathrm {S}_4$ is itself, $\mathrm {D} \cong \mathrm {Im}(\beta ) =\mathrm {V}_4 \cong \mathbb {Z}_2\times \mathbb {Z}_2$.

Note that $\mathrm {D}$ is indeed isomorphic to the Galois group of $\gamma$. So $\gamma ^*\mathcal {O}_{\mathbb {P}^1}(1) \equiv 2K_C$ by Lemma 5.3. Since $K_C =\gamma ^*K_{\mathbb {P}^1}+\sum _{i=1}^5(x_i+y_i)$, we have $\sum _{i=1}^5(x_i+y_i)\equiv 5K_C$. $\square$

Lemma 5.5

Let $\pi :E \rightarrow C$ be a double cover between smooth projective curves. Assume that the branch locus of $\pi$ consists of 4 points $x_1, x_2, x_3, x_4$ such that $x_1+x_2+x_3+x_4 \equiv 2K_C$ and $\pi _*\mathcal {O}_E \cong \mathcal {O}_C\oplus \mathcal {O}_C(-K_C)$. Then E is a hyperelliptic curve of genus 5.

Proof

The Riemann–Hurwitz theorem yields $g(E)=5$. It suffices to show that the canonical image of E is a rational curve in $\mathbb {P}^4$.

Note that $|2K_C|$ is composed with the hyperelliptic pencil $|K_C|$. We may assume $x_1+x_2, x_3+x_4 \in |K_C|$. Choose $s_1, s_2 \in H^0(C, \mathcal {O}_C(K_C))$ such that $(s_1)_0=x_1+x_2, (s_2)_0=x_3+x_4.$ Then $s_1, s_2$ is a basis of $H^0(C, \mathcal {O}_C(K_C))$ and thus $s_1^2, s_1s_2, s_2^2$ is a basis of $H^0(C, \mathcal {O}_C(2K_C))$.

Set $s_j:=\pi ^*s_j'$ for $j=1, 2$ and $y_i:=\pi ^{-1}(x_i)$ for $i=1, 2, 3, 4$. Let $s' \in H^0(E, \mathcal {O}_E(y_1+y_2+y_3+y_4))$ such that $(s')_0=y_1+y_2+y_3+y_4$. Since $2y_1+2y_2+2y_3+2y_4=\pi ^*(x_1+x_2+x_3+x_4)$, we may choose $s'$ such that $s'^2=s_1's_2'$.

Since $\pi _*\mathcal {O}_E\cong \mathcal {O}_C\oplus \mathcal {O}_C(-K_C)$, we have

$$\begin{aligned} H^0(E, \mathcal {O}_E(K_E))\cong s'\pi ^*H^0(C, \mathcal {O}_C(K_C)) \oplus \pi ^*H^0(C, \mathcal {O}_C(2K_C)) \end{aligned}$$

(cf. [11, Proposition 4.1]). It follows that $s's_1', s's_2'$ and $s_1'^2, s_1's_2', s_2'^2$ together form a basis of $H^0(E, \mathcal {O}_E(K_E))$. Since $s'^2=s_1's_2'$, one sees that the image of E under the canonical map defined by this basis a rational normal curve. $\square$