Introduction

Detection of spatial disease clusters, or hot spots, has generated considerable interest among public health researchers and policymakers over several decades (Besag and Newell 1991; Maheswaran and Craglia 2004; Lawson 2006). Defined as a geographic area with significant elevated risk of a particular disease (Lawson 2006), spatial disease clusters may be resulted from the communicability of some diseases, adverse effects from physical, socioeconomic, or psychosocial environment, certain kinds of lifestyles which are commonly considered harmful to health, such as smoking, and poor accessibility to healthcare (Maheswaran and Craglia 2004). Detecting spatial disease clusters not only aids the analysis of disease aetiology, but also enables public health authorities to improve their disease surveillance, more effectively distribute resources, and better control possible disease outbreaks.

Over the past decades, a large body of cluster detection methods have been proposed by geographers and statisticians to reflect different interests and application contexts. A good review on the recent developments in this field was made by McLafferty (2015). Among the existing methods, Kulldorff’s spatial scan statistic (Kulldorff 1997) may be the most used one for cluster detection among spatial units.Footnote 1 This approach moves a circular scan window with varying radii over the study region and identifies the cluster (i.e., the local set of spatial units) with the maximum likelihood ratio. Due to the use of a circular window, this method tends to identify clusters with a compact circular shape, which may mask the actual spatial morphology of disease clusters (e.g., a linear waterborne disease cluster along a river) and can impede statistical inference about the relationship between disease clusters and their contributing factors (Murray et al. 2014). To address these issues, an area of research has been evolved recently focusing on finding clusters in irregular shapes. Their methods usually modify or extend Kulldorff’s spatial scan statistic. Our research is also along this line.

To support irregularly shaped cluster detection, the clustering likelihood ideally needs to be examined for each combination of the spatial units in a study area. However, such exhaustive search could be computationally unmanageable for study areas with a large number of spatial units. In addition, the set of spatial units in a cluster are often assumed to be connected. To address these issues, a sophisticated search process is desired so that the whole search space (i.e., all spatial unit combinations) can be reduced to a subset for clustering testing. An ideal subset usually has three criteria:

  1. 1.

    Each element in the subset should be a zone consisting of a connected spatial unit set;

  2. 2.

    The size of the subset should be computationally manageable;

  3. 3.

    The optimal or suboptimal solution (i.e., the maximum likelihood cluster) should be included in the subset.

To obtain an ideal subset, a range of spatial search strategies have been proposed, including the upper level set scan (Patil and Taillie 2004), simulated annealing (Duczmal and Assunção 2004), exhaustive localized search (Tango and Takahashi 2005), genetic algorithm (Duarte et al. 2010), fast subset scan (Neill 2012), and multi-objective dynamic programming (Moreira et al. 2015). However, these methods either cannot guarantee the connectivity of the identified clusters, or will obtain a too small reduced subset where the optimal or suboptimal solution may not be included, or could easily become computationally unmanageable, or incorporate many tune-up parameters that are difficult to interpret and determine.

In addition to the above spatial search problems, the identified maximum likelihood clusters usually end up with an unrealistic, highly irregular shape (e.g., tree-shaped) spreading over the whole study region, which cannot add new information with regard to its special geographic significance (Duczmal et al. 2006). To avoid this problem, some methods combine a shape penalty parameter into the maximum likelihood ratio function to explicitly penalize the cluster candidates that have a highly irregular shape, such as the non-compactness penalty proposed by Duczmal et al. (2006) and the non-connectivity penalty and the depth limit proposed by Yiannakoulias et al. (2007). Multi-objective frameworks have also been proposed to control the occurrence of highly irregularly shaped clusters, such as the method proposed by Duarte et al. (2010) which simultaneously maximizes the spatial scan likelihood ratio, the cohesion function, and the geometric function. These geometric penalty parameters, however, only use the structure information of the spatial unit tessellations without considering the disease/population data in each spatial unit.

In this paper, we are proposing a fast, hybrid method to detect irregularly shaped clusters, which combines Assunção et al.’s (2006) dynamic Minimum Spanning Tree (dMST) method as the search strategy and Tango’s (2008) restricted likelihood ratio as the test statistic. The dMST method is a simple and fast search strategy that can obtain a computationally manageable subset of connected spatial unit combinations where the optimal or suboptimal solution is very likely to be included. The restricted likelihood ratio excludes individual spatial units with low disease risk from cluster candidates, which, in turn, limits the extreme irregularity of cluster shapes. Although both the dMST method and the restricted likelihood ratio are not newly developed, their combination is expected to be a promising method based on the advantages of each component. To our best knowledge, however, there is no work in the current literature discussing their combination and testing its performance. To fill the gap, our research aims to implement this hybrid method, compare its performance with other well-known cluster detection methods, and demonstrate its use in real-world problems.

This paper is organized as follows. “Related work” section briefly reviews related work, including Kulldorff’s spatial scan statistic, the dMST search process, and the restricted likelihood ratio function. “The hybrid method” section describes the implementation of the hybrid method and discusses its conceptual relationship with other three well-known methods. “Performance evaluation” section uses simulated data to test the performance of the hybrid method, which is followed by an application in “Application: Georgia lung cancer incidence, 1998–2005” section using all of the four methods to detect lung cancer incidence cluster in Georgia from 1998 to 2005. “Conclusions” section concludes the paper.

Related work

Kulldorff’s spatial scan statistic

Following Naus’ pioneering work on scan statistics (Naus 1965), Kulldorff (1997) developed one of the most used spatial cluster detection methods where a circular scan window with various radii is moved over the space of the study area to detect the maximum likelihood cluster. The software program for this method, SaTScan™, can be easily accessed over the Internet (Martin Kulldorff and Information Management Services Inc. 2015).

Consider a study area composed of m spatial units (e.g., counties) with total population N and total number of disease cases C. If n i and c i represent the population and the number of disease cases in spatial unit i, respectively, we can then observe that \(N = \sum\nolimits_{i = 1}^{m} {n_{i} }\) and \(C = \sum\nolimits_{i = 1}^{m} {c_{i} }\). Let us denote a zone as a subset of the spatial units within a circular scan window and Z represents the zone set including all possible zones in the study area. Then the number of observed disease cases in the zone z is \(c_{z} = \sum\nolimits_{i \in z} {c_{i} }\). Under the null hypothesis that there are no clusters in the study area and the number of cases in each zone is Poisson distributed proportionally to its population, the expected number of disease cases in the zone z would be \(\mu_{z} = \left( {\frac{C}{N}} \right)\sum\nolimits_{i \in z} {n_{i} }\).

Define L 0 as the likelihood function under the null hypothesis and L(z) as the likelihood function under the alternative hypothesis that the zone z is a cluster where the occurrence probability of a disease case is higher than that outside. For the zone z, the logarithm of the likelihood ratio, LLR(z) = (L(z)/L 0), can be simplified as below (Martin Kulldorff 1997):

$$LLR\left( z \right) = \left\{ {\begin{array}{*{20}l} {c_{z} \ln \left( {\frac{{c_{z} }}{{\mu_{z} }}} \right) + \left( {C - c_{z} } \right)\ln \left( {\frac{{C - c_{z} }}{{C - \mu_{z} }}} \right), } \hfill & { if \;\left( {\frac{{c_{z} }}{{\mu_{z} }}} \right) > \left( {\frac{{C - c_{z} }}{{C - \mu_{z} }}} \right)} \hfill \\ {0,} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(1)

Assuming the zone z* has the maximum LLR over the whole zone set Z, LLR(z*) is then defined as the scan statistic and the corresponding zone z* is regarded as the most likely cluster. To test the statistical significance of the most likely cluster, the Monte Carlo simulation (Dwass 1957) is used where the scan statistic is computed for a large number of simulations under the null hypothesis (e.g., 999 or 9999 simulations), and their distribution is compared to the scan statistic of the observed most likely cluster, which produces its p value.

The dMST search strategy

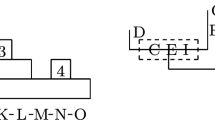
To support irregularly shaped cluster detection, Assunção et al.’s (2006) proposed a dMST search method used to replace the circular scan window in Kulldorff’s spatial scan statistic method. The dMST method is based on the popular minimum spanning tree algorithm. As shown in Fig. 1, this method represents a study region map as a graph G (V, E) where each spatial unit is a vertex in the vertex set V and each pair of adjacent spatial units (i.e., sharing a boundary or a point) are connected by an edge in the edge set E.

Fig. 1
figure 1

The graph-based representation of a study area map

Full size image

In the graph theory, a path is a sequence of vertices connected by edges and a circuit is a special path with the first and the final vertices coinciding. A tree is defined as a connected graph with no circuits. When constructing a tree from a graph with circuits, the first chosen vertex for the tree is defined as the root, and other vertices in the graph are added into the tree orderly under the constraint that each vertex added should be a neighbor of (i.e., be connected to) the existing part of the tree. Each time when a vertex is added into the tree, the current set of the vertices in the tree constitute a zone for clustering testing.

Usually, for the same root, different trees could be built from a graph with circuits. To improve the chance that the maximum likelihood cluster is included in the constructed trees of the study area, the dMST method uses each vertex as the root to construct a tree. At each step of the tree construction, the neighboring vertex added will be the one that can maximize the likelihood ratio of the existing part of the tree. To mathematically express the dMST method, we define T i (V i , E i ) and T i+1 (V i+1 , E i+1) as the constructed tree at steps i and i + 1 respectively. N i is the neighboring vertex set of T i . Then,

$$V_{i + 1} = \left\{ {V_{i} \cup \mathop {\text{arg max}}\nolimits_{{u \in N_{i} }} LLR\left( {V_{i} \cup u} \right)} \right\}$$
(2)

In order to reduce calculation intensity, a search radius K could be set so that at most K − 1 nearest neighboring vertices will be involved when building the tree for each vertex.

The dMST method uses a graph-based representation to make sure all zones explored are connected. The algorithm is very efficient and can greatly reduce the search space while having a high chance to include the optimal or suboptimal solution. Moreover, the dMST method is essentially a simple greedy algorithm without any tune-up parameters to determine subjectively.

The restricted likelihood ratio

When using Kulldorff’s spatial scan statistic (Eq. 1), the detected clusters usually include some individual low-risk spatial units. Such clusters are not very reasonable. In addition, when using a graph-based search process, such as the aforementioned dMST method, these low-risk spatial units are usually found connecting multiple subsets of spatial units, making the detected clusters highly irregular-shaped and much larger than the true clusters (Assunção et al. 2006). Such kind of clusters provides us little information regarding geographic significance and could impede our understanding of the underlying dynamics of disease clusters. To address these problems, Tango (2008) proposed a restricted likelihood ratio as the test statistic, which will not test the cluster candidates with individual low-risk spatial units inside. Denote LLR(z) as the logarithm of Kulldorff’s likelihood ratio (Eq. 1), the logarithm of the restricted likelihood ratio RLLR(z) can be expressed as:

$$RLLR\left( z \right) = \left\{ {\begin{array}{*{20}l} {LLR\left( z \right),} \hfill & {if \mathop \prod \limits_{i \in z} I\left( {p_{i} < \alpha_{1} } \right) = 1} \hfill \\ { - \infty ,} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(3)

where I(·) is an indicator function with a value of 1 when the condition is met and 0 otherwise. In the product of indicator functions: \(\prod\nolimits_{i \in z} {I\left( {p_{i} < \alpha_{1} } \right)}\), α 1, ranging from 0 to 1, is a screening level specified by users for the risk of any individual spatial unit, and p i is the one-tailed mid-p value of spatial unit i under the null hypothesis that its risk is an average of the whole study area. A small p i value indicates that the likelihood of disease risk in spatial unit i is unusually high. The one-tailed mid-p value is defined as below (Tango 2008):

$$p_{i} = \Pr \{ N_{i} \ge c_{i} + 1|N_{i} \,\sim\,Pois\left( {\mu_{i} } \right)\} + \frac{1}{2}\Pr \{ N_{i} = c_{i} |N_{i} \,\sim\,Pois\left( {\mu_{i} } \right)\}$$
(4)

where c i and µ i denote the observed and expected numbers of cases in region i respectively. N i is a Poisson random variable with a mean of µ i , It should be noted that Kulldorff’s likelihood ratio is the special case of the restricted likelihood ratio when the screening level α 1 = 1.

In the restricted likelihood ratio function (Eq. 3), the screening level α 1 represents user’s belief on the minimum disease risk of individual spatial unit in a cluster. The spatial unit with risk less than the screening level α 1 (i.e., p i  ≥ α 1) will be excluded from all cluster candidates. This idea is easy to understand and can efficiently limit the extreme irregularity of cluster shapes due to the decreased connectivity among the spatial units used to construct cluster candidates. However, the choice of the screening level α 1 is totally up to users. Tango (2008) recommended α 1 = 0.2 as a default value when using a circular scan window.

The hybrid method

The scan-based cluster detection methods typically consist of two components: a search strategy and a test statistic. In this paper, we are proposing a hybrid method combining Assunção et al.’s (2006) dMST method as the search strategy and Tango’s (2008) restricted likelihood ratio as the test statistic. This combination is a natural choice when considering the underlying dynamics of epidemiological clustering and manageability of computational intensity. Disease clusters emerge due to different mechanisms and are related to geography, environment, population, and social processes. As a result, the shape and size of disease clusters vary in different contexts and are unknown before we understand their forming mechanisms. The dMST method is an efficient and flexible search strategy that allows irregular-shaped clusters to be identified with manageable computational intensity. In addition, it is reasonable that clusters should not include spatial units with very low disease risk. The restricted likelihood ratio naturally filters out those low-risk spatial units from clustering testing. Furthermore, excluding low-risk spatial units can decrease the connectivity among the spatial units and, in turn, reduce the amount of cluster candidates for testing, which, as side effects, decreases the computational intensity and prevents the detected clusters being unreasonably large and of extremely irregular shape. Therefore, by taking the advantages of the two components, this hybrid method is expected to support fast detection of irregular-shaped clusters while addressing the issues identified in other methods.

Figure 2 shows the two components in the four spatial scan methods, including our hybrid method, Tango’s method (2008), Assunção et al.’s method (2006), and Kulldorff’s circular spatial scan method (1997) (denoted as the CSScan method below). Essentially, these methods are the four combinations of two search strategy (circular scan window vs. the dMST method) and two test statistics (Kulldorff’s likelihood ratio vs. the restricted likelihood ratio).

Fig. 2
figure 2

The test statistics and search strategies of the selected four spatial scan methods

Full size image

It is worth noting that our hybrid method is not the first time combining the restricted likelihood ratio with a search strategy that allows irregular-shaped clusters to be identified. Tango and Takahashi (2012) used the restricted likelihood ratio to replace Kulldorff’s likelihood ratio in their original flexible spatial scan statistic (Tango and Takahashi 2005). The major difference between our hybrid method and their method exists in the search strategy each adopted. Tango and Takahashi’s flexible spatial scan statistic uses an exhaustive search which tests all possible cluster candidates (i.e., a group of connected spatial units) within the search radius of each spatial unit, easily making the method computationally unmanageable. Using the restricted likelihood ratio in their method can mitigate this problem to some degree because excluding low-risk spatial units could reduce the amount of cluster candidates. However, its computational intensity still could exponentially increase as the screening level α 1 or the search radius increases. On the contrary, our dMST method uses a heuristic process trying to identify a good and relatively small subset of cluster candidates for each spatial unit to test. Combining the side effect of the restricted likelihood ratio, our hybrid method is expected to have a better control on the computational intensity.

Since the search strategy and the test statistic interrelate with each other in the scan-based cluster detection methods, the algorithms of the method implementation need to be carefully designed to achieve good efficiency. Table 1 describes the algorithm of our hybrid method. Its Visual Basic source code with sample data will be provided when requested.

Table 1 The algorithm of the hybrid method
Full size table

Tango (2008) designed four simple cluster models to test the statistical power of the restricted likelihood ratio with circular scan windows. However, the performance of the scan statistic under other situations has not been studied, such as different levels of disease incidence in the study area or various true cluster shapes. In addition, it is needed to examine the performance of the restricted likelihood ratio with varying screening levels when using the dMST search strategy. The result is expected to provide a guide on the choice of the parameter when using our hybrid method in the real-world applications.

Performance evaluation

Experimental design

To evaluate the performance of the hybrid method, we simulated disease data in the State of Georgia (GA), which includes 159 counties with a total population of 9,210,790 in year 2000 (Fig. 3). For each set of the simulated data, county populations are fixed to the census 2000, and only the number of disease cases in each county is simulated based on the total number of cases and the true cluster’s location. Specifically, the location and shape of the true cluster was first determined, and then a relative risk r > 1 was assigned to the counties within the cluster and r = 1 to the counties outside. Given the total number of disease cases in the study area, the number of cases in the county i follows a multinomial distribution with the probability of \(r_{i} p_{i} /\sum\nolimits_{{{\text{j}} = 1}}^{m} {r_{j} p_{j} }\) where r i and p i are the relative risk and population at risk in the county i respectively, and m is the total number of counties in the study area. Following the criterion used by Kulldorff et al. (2003), the relative risk for the counties within the cluster is determined using a one-sided binomial test with a significance level of 0.05 such that the null hypothesis is rejected with probability of 0.999 when the alternative is a cluster with a known location. This choice of the relative risk provides an upper limit of 0.999 for the statistical power attainable by any test.

Fig. 3
figure 3

Georgia population in 2000 by counties

Full size image

Following the procedure described above, we design three types of cluster shapes (round, line and trifurcate shape) and two levels of disease incidence (low: 500 cases and high: 5000 cases). Combining the two levels of disease incidence and the three cluster shapes, we have a total of six cluster models, which are labeled in a code format as ‘X_Shape’ where ‘X’ indicates the level of disease incidence with “L” for low and “H” for high. Figure 4 shows the locations of the simulated clusters and the detailed information of the six cluster models is listed in Table 2.

Fig. 4
figure 4

The simulated clusters: a circular shape, b linear shape, c trifurcate shape

Full size image
Table 2 Descriptions of the six cluster models
Full size table

For each cluster model, 500 replications are simulated. The statistical significance of the scan statistic in each replication is tested using the Monte Carlo method (Dwass 1957) with 999 repetitions. In order to explore the effect of the screening level α 1 in the restricted likelihood ratio function, five different values: 0.05, 0.1, 0.2, 0.3 and 0.4 are set, respectively.

We compare the performance of our hybrid method to Tango’s method, Assunção et al.’s method, and Kulldorff’s CSScan method. All of the four methods are implemented using Visual Basic programming and run in a single thread on a personal computer with an i7-6700 CPU (3.4 GHz) and 16 GB ROM. 20 percent of population in the study region was set as the upper limit of clusters in the CSScan method, and the search radius K in other three methods are correspondingly set to 30 counties.

Experimental results

Statistical power analysis

The statistical power indicates how effective the method is in identifying the presence of statistically noteworthy clusters (Kulldorff et al. 2003; Assunção et al. 2006; Tango and Takahashi 2005; Tango 2008). For each cluster model, the power is defined as the proportion of the replications where a statistically significant cluster is detected (p < 0.05) regardless of the geographical matchness between the detected cluster and the true cluster. Table 3 shows the results of the power analysis. The highest value for each cluster model is highlighted with bold type. The test statistic used in both Assunção et al.’s method and CSScan method is regarded as the restricted likelihood ratio with α 1 = 1.

Table 3 Estimated power of the four methods (significance level = 0.05)
Full size table

The results indicate that Assunção et al.’s method has the highest statistical power among the four methods for all of the six cluster models (the average power is 0.876). Our hybrid method outperforms Tango’s method in all models when taking the same value of α 1. When α 1 is 0.4 and 0.2, the hybrid method has the second and third highest average power (0.835 and 0.812) among the four methods with all of the tested α 1. The CSScan method has a relatively low average power (0.789), and Tango’s method has the lowest power whatever the value of α 1 is.

In addition, all of the four methods generally have higher power with a lower level of disease incidence. Their power also varies among the three shapes. When α 1 increases from 0.05 to 0.4, the best power of our hybrid method shifts from the linear clusters to the round clusters and then to the trifurcate clusters. Assunção et al.’s method and CSScan method both have higher power to detect trifurcate clusters than the other two methods with all tested α 1.

Geographic accuracy analysis

In order to understand how well these methods can identify the correct boundaries of a cluster, Kappa Index of Agreement (KIA) is chosen to evaluate the agreement between the identified most likely clusters and the true clusters. One advantage of KIA is that it excludes the probability that the clustering units (e.g., counties in the experiments) are identified merely by chance. Given the study area size (S), the true cluster size (T), the identified cluster size (D), and the size of the intersection between the identified cluster and the true cluster (I), Table 4 is the contingency table.

Table 4 Contingency table of the identified cluster and the true cluster
Full size table

Based on Table 4, the KIA equation for this study can be derived as follows:

$$KIA = \frac{O - E}{1 - E}$$
(5)
$$O = \frac{{I + \left( {S - T - D + I} \right)}}{S},\quad E = \frac{{D \times T + \left( {S - D} \right) \times \left( {S - T} \right)}}{{S^{2} }}$$

where O is the observed proportion of matching values (i.e., the diagonal elements in the contingency table) and E is the expected proportion of matches when the true cluster is assumed independent with the identified cluster. KIA ranges from 0 to 1, and 1 means a perfect agreement.

Table 5 shows the results of the geographic accuracy analysis and the highest KIA value for each cluster model is highlighted with bold type. It is found that our hybrid method generally has a better geographic accuracy of the identified clusters than the other three methods across the six cluster models. Especially when α 1 is 0.2, our hybrid method reaches the highest average geographic accuracy (0.614). In most of the cases, Tango’s method has a lower geographic accuracy than our hybrid method when taking the same value of α 1. It has the highest average accuracy (0.473) when α 1 is 0.4, which is similar to the average accuracy of the CSScan method (0.475). Assunção et al.’s method has a relatively low accuracy (0.435).

Table 5 KIAs between the most likely clusters and the true clusters for the four methods
Full size table

From the above results, we also find that all methods generally have a higher geographic accuracy with a lower level of disease incidence. They also have a varying accuracy among the three types of shapes. Compared to the linear and round shapes, the boundaries of the trifurcate clusters are more difficult to be correctly identified by both our hybrid method and Tango’s method. Assunção et al.’s method is better for the trifurcate shape than the other two shapes, and the CSScan method is better for the round clusters.

Computational intensity analysis

Given a search radius of K, both the dMST method and a circular scan window will lead to up to K cluster candidates for each spatial unit in the study area. The amount of cluster candidates will be further reduced by using the restricted likelihood ratio. Therefore, our hybrid method, in theory, is faster than those methods which need to test more cluster candidates due to the use of complex search strategies, such as simulated annealing (Duczmal and Assunção 2004), exhaustive localized search (Tango and Takahashi 2005), and genetic algorithm (Duarte et al. 2010). To understand the computational intensity of the four methods compared in this paper, we calculate the average computing time taken by each method in the experiment and plot them in Fig. 5.

Fig. 5
figure 5

Average computing time taken by each method in the experiment

Full size image

The result shows that, when the screening level α 1 < 0.4, both our hybrid method and Tango’s method took the least time (4–8 s). However, the time taken by our hybrid method increases faster than Tango’s method does as the screening level α 1 increases. Assunção et al.’s method takes the longest time (98 s).

Application: Georgia lung cancer incidence, 1998–2005

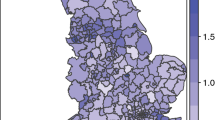
The above experimental results indicate that our hybrid method with the screening level α 1 = 0.2 has the third highest average statistical power and the best average geographic accuracy among the four methods with all of the tested α 1. To demonstrate its application in the real-world problems, we use it to detect the lung cancer incidence cluster in GA from 1998 to 2005. The other three methods are also applied for comparative purpose. The data from the Georgia Comprehensive Cancer Registry shows that there were a total of 42,521 lung cancer cases in GA during that time period, where 25,615 cases were males and 16,906 cases were females. The expected number of cases in each county is calculated based on GA population in year 2000 (Fig. 2) and adjusted by both age and gender.

The screening level α 1 = 0.2 is used in our hybrid method and Tango’s method. The search radius (i.e. maximal cluster size) is set to 30 counties for all methods. To reflect lung cancer relative risk in each county, we also calculate its standardized incidence ratio (SIR), which is a ratio of the observed number of cancer cases over the expected number of cases. A county with an SIR value of one has the average risk of the entire state. Figure 6 shows both the SIR by county and the lung cancer cluster (significance level = 0.05) detected by each method. We can see that all methods find a significant cluster in northwestern GA. However, these clusters vary in size and shape. Influenced by the search strategies, our hybrid method and Assunção et al.’s method find a cluster with a relatively irregular shape, while the clusters found by the other two methods are more compact. By excluding individual counties with low risk from cluster testing, the clusters detected by our hybrid method and Tango’s method are smaller than those detected by the methods using the same search strategy but considering all counties for testing no matter how their individual risk is. Therefore, our method shows a good balance in both the shape and size of the detected cluster.

Fig. 6
figure 6

Lung cancer incidence clusters in GA, 1998–2005, detected by the four methods (significance level = 0.05). a Hybrid method (α 1 = 0.2), b Assunão’s method, c Tango’s method (α 1 = 0.2) and d CSScan

Full size image

To explain the occurrence of the cluster, we need to take a further look at this area and examine its environmental, occupational, behavioral, and social risk factors related to lung cancer. Smoking is a well-known main factor contributing to lung cancer. Among the 18 health districts in GA, the northwest district including most of the counties in the cluster had the highest prevalence of cigarettes smoking among adults from 2000 to 2004 (29% vs. state average of 22.6%) (GDPH 2004). This may partially contribute to the emergence of the cluster. In addition, this cluster is located in Appalachia where increased lung cancer incidence and mortality have been documented in the previous research and considered related to the heavy coal mining activities in the region (Hendryx et al. 2008). Although no coal has been mined in GA since the mi-1980’s, the proximity of the cluster area to the active coal mining sites in the neighboring states, such as Alabama and Tennessee, and the fact that 4 out of the 12 coal plants in GA concentrated within this cluster area (EPA 2000) may increase the residents’ exposure to air pollution and contribute to lung cancer. However, all of these assumptions need further validation with more comprehensive data and analysis, which is beyond the scope of this paper.

Conclusions

Spatial disease cluster detection has been widely used to identify questionable areas for a further investigation and explore spatial or spatio-temporal disease risk patterns. To support fast detection of irregularly shaped clusters, we are proposing a hybrid method combining Assunção et al.’s dMST method as the search strategy and Tango’s restricted likelihood ratio as the test statistic. Although both of the two components are not new, their combination and the associated performance have not been discussed and explored. In this study, we discuss the advantages and the implementation of the hybrid method, and systematically compare its performance with other three well-known scan-based cluster detection methods, including Tango’s method, Assunção et al.’s method, and Kulldorff’s CSScan method. The experimental results show that the four methods all have a varying performance for different disease incidence levels and true cluster shapes. This finding corresponds well with the power analysis conducted by Waller and Gotway (2004) where most cluster detection tests show spatially heterogeneous power. Therefore, when applying these cluster detection methods in the real-word problems, we need to be very careful to interpret the results and acknowledge the associated uncertainty. Among the four methods with all of the parameters we have compared, our hybrid method with the screening level α 1 = 0.2 has the third highest average statistical power and the best average geographic accuracy. Finally, the four methods are applied to the lung cancer incidence in GA between 1998 and 2005, and all find a significant cluster in northwestern GA but varying in shape and size.