1 Introduction

Environmental sensing using crowdsourcing is a promising direction due to the wide-spread availability of mobile devices with positioning capabilities and a broad array of sensing features, e.g., audio and video capture, temperature, velocity, acceleration, etc. In addition, mobile devices can easily interface with external sensors and upload readings for many other environmental parameters (e.g., CO2, water pollution levels, atmospheric pressure). The growing trend towards crowdsourcing environmental sensing is beneficial for a wide range of applications, such as pollution levels monitoring or emergency response. In such settings, authorities can quickly and inexpensively acquire data about forest fires, environmental accidents or dangerous weather events – and the mobile users are crucial entities for generating relevant data.

One particular task that is relevant to many application domains is the detection of anomalous phenomena. Such cases often require to determine a heatmap capturing the distribution of a certain sensed parameter (e.g., temperature, CO2 level) over a geospatial region of interest. Typically, when the value of the parameter of interest in a certain region reaches a predefined threshold, an alarm needs to be triggered, signaling the occurrence of an anomaly. An important issue is that the alarm should identify with good accuracy the region where the dangerous event occurred, so that counter-measures can be activated and deployed.

At the heart of the motivation for this work is the observation that there are important privacy concerns related to crowdsourced sensing. Contributed data may reveal sensitive private details about an individual’s health, lifestyle choices, and may even impact the physical safety of a person. To protect against such disclosure, the state-of-the-art model of differential privacy (DP) adds noise to data in a way that prevents an adversary from learning whether the contribution of an individual is present in a dataset or not. Several DP-compliant techniques for protecting location data have been proposed in [1,2,3]. However, the applicability of the existing approaches is limited, in the sense that they only consider simple, general-purpose count queries, and rely on simplifying assumptions that make them unsuitable for our considered problem of anomalous phenomenon detection with spatial awareness.

Consider an example scenario of a forest fire, where mobile users report air temperature in various regions. To model the fire spread, one needs to plot the temperature distribution, which depends on the values reported by individual users, and the users’ reported locations. With existing techniques, one could partition the dataspace according to a regular grid and split the available privacy budget between two aggregate query types, one counting user locations in each grid cell, and the other summing reported values. Next, a temperature heatmap is obtained by averaging the temperature for each cell. As demonstrated in our experimental evaluation, this approach yields rather useless data, due to the high amount of noise injected. This is the result of a more fundamental limitation of existing approaches that are designed only for general-purpose queries, and do not take into account correlations that are specific to more complex data processing algorithms.

In this paper, we propose an accurate technique for privacy-preserving detection of anomalous phenomena in crowdsourced sensing. We also adopt the powerful semantic model of differential privacy, but we devise a tailored solution, specifically designed for privacy-preserving heatmap construction. Our technique builds a flexible data indexing structure that can provide query results at arbitrary levels of granularity. Furthermore, the sanitization process fuses together distinct types of information (e.g., user count, placement and reported value scale) to obtain an effective privacy-preserving data representation that can help decide with high accuracy whether the sensed value in a certain geographical region exceeds the threshold or not. To the best of our knowledge, this is the first work that addresses the problem of value heatmap construction within the differential privacy framework. Our specific contributions are:

  1. 1.

    We introduce a hierarchical differentially-private structure for representing sensed data collected by mobile users. The structure is customized to address the specific requirements of value heatmap construction, and accurately supports queries at variable levels of granularity.

  2. 2.

    We examine the impact of structure parameters and privacy budget allocation on data accuracy, and devise algorithms for parameter selection and tuning.

  3. 3.

    We derive an analytical model for characterization of errors resulting from noise injection in the heatmap construction process. Based on this model, we propose a flexible mechanism that uses concentration inequalities to compute for each cell voting weights that improve the accuracy of privately deciding whether an anomalous phenomenon occurred or not. To the best of our knowledge, this is the first work that supports fine-grained, cell-level weight assignment.

  4. 4.

    We perform an extensive experimental evaluation which shows that the proposed techniques accurately detect anomalous phenomena, and clearly outperform existing general-purpose sanitization methods that fare poorly when applied to the studied problem.

The paper is organized as follows: Section 2 provides background information on differential privacy. In Section 3, we introduce the system model, and the metrics used to characterize anomalous phenomenon detection accuracy. Section 4 presents the proposed privacy-preserving data indexing structure and analytical models for characterizing query accuracy. We introduce strategies for anomaly detection in Section 5. In Section 6, we introduce a mechanism for determining flexible voting weights based on sensed value error bounds for each cell of the index structure. We present the results of our extensive experimental evaluation in Section 7. We survey related work in Section 8, and conclude with directions for future work in Section 9.

2 Background

In this section, we introduce the basic concepts and notations used in building our proposed solution for privacy-preserving detection of anomalous phenomena.

2.1 Differential privacy

Differential privacy (DP) [4, 5] addresses the limitation of syntactic privacy models (e.g., k-anonymity [6], ℓ-diversity [7], t-closeness [8]) which are vulnerable against background knowledge attacks. DP is a semantic model which argues that one should minimize the risk of disclosure that arises from an individual’s participation in a dataset.

Two datasets \(\mathcal {D}\) and \(\mathcal {D}^{\prime }\) are said to be siblings if they differ in a single record r, i.e., \(\mathcal {D}^{\prime } = \mathcal {D} \cup \{r\}\) or \(\mathcal {D}^{\prime } = \mathcal {D} \diagdown \{r\}\) . An algorithm \(\mathcal {A}\) is said to satisfy differential privacy with parameter ε (called privacy budget) if the following condition is satisfied [4]:

Definition 1 (ε-indistinguishability)

Consider algorithm \(\mathcal {A}\) that produces output \(\mathcal {O}\) and let 𝜖 > 0 be an arbitrarily-small real constant. Algorithm \(\mathcal {A}\) satisfies ε -indistinguishability if for every pair of sibling datasets \(\mathcal {D}, \mathcal {D}^{\prime }\) it holds that

$$ \left| \ln \frac {Pr[\mathcal{A}(\mathcal{D})=\mathcal{O}]} {Pr[\mathcal{A}(\mathcal{D}^{\prime})=\mathcal{O}]} \right| \le \varepsilon $$
(1)

In other words, an attacker is not able to learn, with significant probability, whether output \(\mathcal {O}\) was obtained by executing \(\mathcal {A}\) on input \(\mathcal {D}\) or \(\mathcal {D}^{\prime }\). To date, two prominent techniques have been proposed to achieve ε-indistinguishability [5, 9]: the Laplace mechanism (and the closely related geometric mechanism for integer-valued data) and the exponential mechanism. Both mechanisms are closely related to the concept of sensitivity:

Definition 2 (L 1-sensitivity 5)

Given any two sibling datasets \(\mathcal {D}\), \(\mathcal {D}^{\prime }\) and a set of real-valued functions \(\mathcal {F}=\{f_{1}, \ldots , f_{m}\}\), the L 1 -sensitivity of \(\mathcal {F}\) is measured as \({\Delta }_{\mathcal {F}} = \max _{\forall \mathcal {D}, \mathcal {D}^{\prime }} \displaystyle \sum \limits _{i=1}^{m} |f_{i}(\mathcal {D}) - f_{i}(\mathcal {D}^{\prime })|\).

The Laplace mechanism is used to publish the results to a set of statistical queries. A statistical query set \(\mathcal {Q}=\{Q_{1}, \ldots , Q_{m}\}\) is the equivalent of a set of real-valued functions, hence the sensitivity definition immediately extends to such queries. According to [5], to achieve DP with parameter ε it is sufficient to add to each query result random noise generated according to a Laplace distribution with mean \({\Delta }_{{\mathcal {Q}}}/\varepsilon \). For COUNT queries that do not overlap in the data domain (e.g., finding the counts of users enclosed in disjoint grid cells), the sensitivity is 1.

An important property of differentially-private algorithms is sequential composability [9]. Specifically, if two algorithms \(\mathcal {A}_{1}\) and \(\mathcal {A}_{2}\) executing in isolation on dataset \(\mathcal {D}\) achieve DP with privacy parameters ε 1 and ε 2 respectively, then executing both \(\mathcal {A}_{1}\) and \(\mathcal {A}_{2}\) on \(\mathcal {D}\) in sequence achieves DP with parameter (ε 1 + ε 2). In contrast, parallel composability specifies that executing \(\mathcal {A}_{1}\) and \(\mathcal {A}_{2}\) on disjoint partitions of the dataset achieves DP with parameter max(ε 1,ε 2).

2.2 Private spatial decompositions (PSD)

The work in [1] introduced the concept of Private Spatial Decompositions (PSD) to release spatial datasets in a DP-compliant manner. A PSD is a spatial index transformed according to DP, where each index node is obtained by releasing a noisy count of the data points enclosed within that node’s extent. Various index types such as grids, quadtrees or k-d trees [10] can be used as a basis for PSD.

The accuracy of a given PSD is heavily influenced by the type of PSD structure and its parameters (e.g., height, fan-out). With space-based partitioning PSD, the split position for a node does not depend on data point locations. This category includes flat structures such as grids, or hierarchical ones such as BSP-trees (Binary Space Partitioning) and quadtrees [10]. The privacy budget ε needs to be consumed only when counting the users in each index node. Typically, all nodes at same index level have non-overlapping extents, which yields a constant and low sensitivity of 1 per level (i.e., adding/removing a single location in the data may affect at most one partition in a level). The budget ε is best distributed across levels according to the geometric allocation [1], where leaf nodes receive more budget than higher levels. The sequential composition theorem applies across nodes on the same root-to-leaf path, whereas parallel composition applies to disjoint paths in the hierarchy. Space-based PSD are simple to construct, but can become unbalanced.

Object-based structures such as k-d trees and R-trees [1] perform splits of nodes based on the placement of data points. To ensure privacy, split decisions must also be done according to DP, and significant budget may be used in the process. Typically, the exponential mechanism [1] is used to assign a merit score to each candidate split point according to some cost function (e.g., distance from median in case of k-d trees), and one value is randomly picked based on its noisy score. The budget must be split between protecting node counts and building the index structure. Object-based PSD are more balanced in theory, but they are not very robust, in the sense that accuracy can decrease abruptly with only slight changes of the PSD parameters, or for certain input dataset distributions.

The recent work in [2] compares tree-based methods with multi-level grids, and shows that two-level grids tend to perform better than recursive partitioning counterparts. The paper also proposes an Adaptive Grid (AG) approach, where the granularity of the second-level grid is chosen based on the noisy counts obtained in the first-level (sequential composition is applied). AG is a hybrid method which inherits the simplicity and robustness of space-based PSD, but still uses a small amount of data-dependent information in choosing the granularity for the second level.

All these methods assume general-purpose and homogeneous queries (i.e., find counts of users in various regions of the dataspace) and, as we show later in this paper, are not suitable for the problem of anomalous phenomenon detection. We compare against state-of-the-art PSD techniques in our experimental evaluation (cf. Section 7).

3 System model and evaluation metrics

We consider a two-dimensional geographical region and a phenomenon characterized by a scalar value (e.g., temperature, CO2 concentration) within domain [0,M]. A number of N mobile users measure and report phenomenon values recorded at their location. If a regular grid is super-imposed on top of the data domain, then the histogram obtained by averaging the values reported within each grid cell provides a heatmap of the observed phenomenon. Since our focus is on detecting anomalous phenomena, the actual value in each grid cell is not important; instead, what we are concerned with is whether a cell value is above or below a given threshold T, 0 < T < M.

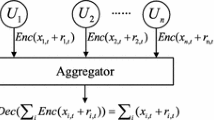
Mobile users report sensed values to a trusted data collector, as illustrated in Fig. 1. The collector sanitizes the set of reported values according to differential privacy with parameter ε, and outputs as result a data structure representing a noisy index of the data domain (i.e., a PSD). This PSD is then released to data recipients (i.e., general public) for processing. Based on the PSD, data recipients are able to answer queries with arbitrary granularity that is suitable for their specific data uses. Furthermore, each data recipient has flexibility to choose a different threshold value T in their analysis. In practice, the trusted collector role can be fulfilled by cell phone companies, which already know the locations of mobile users, and may be bound by contractual obligations to protect users’ location privacy. The collector may charge a small fee to run the sanitization process, or can perform this service free of charge, and benefit from a tax break, e.g., for supporting environmental causes.

Fig. 1
figure 1

System Model

Full size image

According to differential privacy, the goal of the protection mechanism is to hide whether a certain individual contributed to the set of sensed values or not. To achieve protection, noise is added to the values of individual value reports. Inherently, protection decreases data accuracy.

To measure the accuracy of sanitization, we need to quantify the extent to which the outcome for certain regions changes from above the threshold to below, or vice-versa. Given an arbitrary-granularity regular grid, we define the following metrics:

ϕ b o t h :

: number of grid cells above the threshold according to both actual and sanitized readings

ϕ e i t h e r :

: number of grid cells above the threshold according to either actual or sanitized readings

ϕ f l i p :

: number of grid cells above the threshold in one dataset and below in the other

ϕ a l l :

: total number of grid cells

It results immediately from the metric definitions that ϕ e i t h e r = ϕ f l i p + ϕ b o t h . Hence, we can define two additional metrics with domain [0,1] and ideal value of 1 (i.e., perfect accuracy). F lipRatio (FR) quantifies the proportion of cells that change their outcome due to sanitization:

$$FR = 1 - \frac{\phi_{flip}}{\phi_{all}} $$

The Jaccard (J) metric, derived from the Jaccard similarity coefficient [4], measures the dissimilarity between the real and sanitized datasets:

$$J = \frac{\phi_{both}}{\phi_{either}} $$

The FR and J metrics have the advantage of being less dependent on the grid granularity, i.e., the ϕ a l l values, so they maintain their relevance across a broad range of query granularities. However, only the J metric captures the local impact of the sanitization method. Interchanging the state of two random cells will not change the values of any other metrics than J, so they are not sufficient to determine the accuracy of the heatmap. Therefore, in the rest of the paper, we focus on the J metric. Formally, our problem statement can now be specified as follows:

Problem 1

Given N users moving within a two-dimensional space, a phenomenon characterized by a scalar value with domain range [0,M], an anomaly threshold T, 0 < T < M and privacy budget ε, determine an ε-differentially-private release such that the Jaccard metric between the real and sanitized dataset is maximized.

4 PSD for anomalous phenomenon detection

Constructing an appropriate PSD is an essential step, since the accuracy of the entire solution depends on the structure properties. We observe that due to the specific requirements of our problem, general-purpose PSDs such as the ones optimized for count queries ([1,2,3]) are not suitable.

The anomalous phenomenon detection may be performed with respect to a regular grid of arbitrarily fine-grained granularity. On the other hand, creating a PSD that is too fine-grained is not a suitable approach. According to the Laplace mechanism, each cell’s query result is added with random noise of magnitude independent of the actual value. Therefore, PSDs with small cells and PSDs that do not adapt to data density are not appropriate, as the resulting inaccuracy is high. Instead, we construct a flexible structure, based on which the threshold condition can be answered for arbitrary regular grids, as illustrated on the right side of Fig. 1.

The PSD must keep track of two measures necessary to determine phenomena heatmaps: sensor countsFootnote 1 and phenomenon value sums, which together provide average values for each cell. We denote the actual values for sensor count and value sum in a cell by n and s, respectively (we use subscript indices to distinguish the n and s values across cells). We denote the noisy counts and sums by n ∗ and s ∗. The sensitivity of n is 1, whereas the sensitivity of s is M (adding a new sensor in a cell can increase n by 1 and s by M). Hence, if n is answered using privacy budget ε n and s is answered using privacy budget ε s , the variance of n ∗ is \(\frac {2}{{\varepsilon _{n}^{2}}}\), whereas the variance of s ∗ is \(\frac {2M^{2}}{{\varepsilon _{s}^{2}}}\).

To simplify presentation, we introduce our PSD in incremental fashion: first, we outline the main concepts and parameters for a single-level regular grid. Next, we extend our findings to a two-level structure, and then generalize to a multiple-level structure. Table 1 summarizes the notations used.

Table 1 Symbols and notations used in the paper
Full size table

Single-level Grid

Assume a regular grid of N 0 × N 0 cells spanning over a data domain of size w × w. Similar to other work on PSD [2, 11], we assume that a negligible fraction of the privacy budget is spent to estimate \(n_{0}^{*}\), the total number of sensors, and \(s_{0}^{*}\), the sum of all sensed values. Granularity N 0 must be chosen to minimize the expected error over all rectangular queries (since any query can be decomposed into non-overlapping rectangular regions). The error has two sources:

  • Laplace error within a single cell due to noise addition by the Laplace mechanism. These errors are added for all cells covered by the query.

  • Non-uniformity error caused by non-uniformity of sensor distribution within a grid cell. These errors occur only for cells which are partially covered by the query rectangle. In such a case, we output a value proportional to the fraction of the cell that overlaps the query.

Furthermore, errors occur for both sensor counts and sensed values. Since the threshold T is expected to be proportional to scale M, we normalize the error for sensed values to account for the skew introduced by M. The error expression subject to minimization becomes the sum of all count errors plus \(\frac {1}{M}\) of the sum of all value sum errors.

Consider an arbitrary rectangle query of size r w 2, r ∈ (0,1). The query will cover approximately \(r{N_{0}^{2}}\) cells. The total variance of the query result is \(\frac {2r{N_{0}^{2}}}{{\varepsilon _{n}^{2}}}\) for n and \(\frac {2M^{2}r{N_{0}^{2}}}{{\varepsilon _{s}^{2}}}\) for s. Hence, the count error is expressed as \(\sqrt {2r}\frac {N_{0}}{\varepsilon _{n}}\), and the sum error as \(\sqrt {2r}\frac {MN_{0}}{\varepsilon _{s}}\). The total Laplace error is \(\sqrt {2r}N_{0}\left (\frac {1}{\varepsilon _{n}} + \frac {1}{\varepsilon _{s}}\right )\).

The query rectangle might partially cover some cells. The number of such cells is of the order \(\mathcal {O}(\sqrt {r}N_{0})\) (determined by the perimeter of the query rectangle). Hence, we can assume that the number of points in partially covered cells is of the order \(\mathcal {O}(\sqrt {r}N_{0}\frac {n_{0}^{*}}{{N_{0}^{2}}}) = K\sqrt {r}\frac {n_{0}^{*}}{N_{0}}\) , where K is a constant. Assuming uniform sensor density, the error for value sum in partially covered cells is \(K\sqrt {r}\frac {s_{0}^{*}}{N_{0}}\). Hence, the non-uniformity error is \(K\frac {\sqrt {r}}{N_{0}}\left (n_{0}^{*} + \frac {s_{0}^{*}}{M}\right )\).

Thus, we must minimize the expression:

$$ \sqrt{2r}N_{0}\left( \frac{1}{\varepsilon_{n}} + \frac{1}{\varepsilon_{s}}\right) + K\frac{\sqrt{r}}{N_{0}}\left( n_{0}^{*} + \frac{s_{0}^{*}}{M}\right) $$
(2)

According to the sequential composition property (Section 2), the available privacy budget ε must be split between ε n and ε s . We capture this split with parameter β ∈ (0,1), defined as the fraction used by the count sanitization: ε n = β ε and ε s = (1 − β)ε. Minimizing Eq. (2) with respect to N 0, we obtain the optimal single-level granularity

$$ N_{0} = \sqrt{\varepsilon \times \frac{K}{\sqrt{2}} \times \beta(1-\beta)\left( n_{0}^{*} + \frac{s_{0}^{*}}{M}\right)} $$
(3)

Two-level Grid

Starting with the optimal single-level N 0 setting, we further divide each cell according to its noisy n ∗ and s ∗. The privacy budget must be split between the two levels according to sequential composition. We model this split with parameter α ∈ (0,1), which quantifies the budget fraction allocated to the level 1 grid. Levels 1 and 2 receive respectively budgets ε 1 = α ε and ε 2 = (1 − α)ε. Each level budget is further divided between counts and sums using parameter β ∈ (0,1):

$$ \varepsilon_{n1} = \beta\varepsilon_{1}, \varepsilon_{s1} = (1-\beta)\varepsilon_{1}, \varepsilon_{n2} = \beta\varepsilon_{2}, \varepsilon_{s2} = (1-\beta)\varepsilon_{2} $$
(4)

Since each level-1 cell is further divided, we define N 0 as a fraction of the value in Eq. (3) (later in this section, Eq. (11) shows how to choose η > 1):

$$ N_{0} = \frac{1}{\eta}\sqrt{\varepsilon \times \frac{K}{\sqrt{2}} \times \beta(1-\beta)\left( n_{0}^{*} + \frac{s_{0}^{*}}{M}\right)} $$
(5)

For each cell u in the first level we use budgets ε n1 and ε s1 to determine \(n_{u1}^{*}\) and, respectively, \(s_{u1}^{*}\). Based on these values, we split cell u into \({N_{u}^{2}}\) cells. For each cell v ∈ c h i l d(u), we use ε n2 and ε s2 to determine \(n_{v2}^{*}\) and, respectively, \(s_{v2}^{*}\) (the subscript indicates the level of the grid where the value is computed).

Since the actual sensor count in a cell at level 1 is the same as the sum of the sensor counts in all of its children at level 2 (and the same holds for the sums), we perform a constrained inference procedure with the purpose of improving accuracy. Based on the values \(n_{u1}^{*}\), \(s_{u1}^{*}\), \(n_{v2}^{*}\), \(s_{v2}^{*}\) we determine \(\overline {n_{u1}}\), \(\overline {s_{u1}}\), \(\overline {n_{v2}}\) and \(\overline {s_{v2}}\) such that

$$\begin{array}{@{}rcl@{}} \overline{n_{u1}} &=& \sum\limits_{v \in child(u)}{\overline{n_{v2}}} \\ \overline{s_{u1}} &=& \sum\limits_{v \in child(u)}{\overline{s_{v2}}} \end{array} $$

and ∀u, the variances of \(\overline {n_{u1}}\) and \(\overline {s_{u1}}\) are minimized. Note that, since all input values are already sanitized, no budget is consumed in the constrained inference step, and differential privacy is still enforced.

We determine these values in two steps:

  1. 1.

    We determine the weighted average estimators \(n_{u1}^{\prime }\) and \(s_{u1}^{\prime }\) with minimal variance. We average the values of \(n_{u1}^{*}\) and \({\sum }_{v\in child(u)}{n_{v2}^{*}}\) to determine \(n_{u1}^{\prime }\) and the corresponding ones for \(s_{u1}^{\prime }\). To do so, we are using the fact that the variance of the weighted average of two random variables X and Y with variances V a r(X) and V a r(Y ) is minimized by the value

    $$ \frac{Var(Y)}{Var(X) + Var(Y)}\times X+ \frac{Var(X)}{Var(X) + Var(Y)} \times Y $$
    (6)

    In our case, X is \(n_{u1}^{\prime }\) (\(s_{u1}^{\prime }\)) and Y is \({\sum }_{v\in child(u)}{n_{v2}^{*}}\) (respectively \({\sum }_{v\in child(u)}{s_{v2}^{*}}\)).

  2. 2.

    We update the values to ensure mean consistency according to:

    $$\begin{array}{@{}rcl@{}} \overline{n_{u1}} = n_{u1}^{\prime}, && \overline{n_{v2}} = n_{v2}^{\prime} + \frac{1}{{N_{u}^{2}}}\left( \overline{n_{u1}} - \sum\limits_{v \in child(u)}{{n^{\prime}_{v2}}}\right) \end{array} $$
    (7)
    $$\begin{array}{@{}rcl@{}} \overline{s_{u1}} = s_{u1}^{\prime}, && \overline{s_{v2}} = s_{v2}^{\prime} + \frac{1}{{N_{u}^{2}}}\left( \overline{s_{u1}} - \sum\limits_{v \in child(u)}{{s^{\prime}_{v2}}}\right) \end{array} $$
    (8)

The effects of the constrained inference so far concern only queries which partially cover level-1 cells. Suppose that a query covers i × j sub-cells of cell u, where i,j ∈{1,2,…N u }. Then, the effect of the constrained inference is that \(\min (i \times j, {N_{u}^{2}}-i \times j)\) level-2 cells will be used to answer the query. On average, the number of level-2 cells required to answer a query is:

$$\frac{1}{{N_{u}^{2}}-1}\sum\limits_{i=1}^{N_{u}}\sum\limits_{j=1}^{N_{u}}\min(i \times j, {N_{u}^{2}}-i \times j) \approx \frac{{N_{u}^{2}}}{5} + \mathcal{O}(N_{u}) $$

Hence, the total variances are \(\frac {2{N_{u}^{2}}}{5\varepsilon _{n2}^{2}}\) and \(\frac {2M^{2}{N_{u}^{2}}}{5\varepsilon _{s2}^{2}}\), and the resulting total Laplace error is \(\frac {\sqrt {10}N_{u}}{5}\left (\frac {1}{\varepsilon _{n2}} + \frac {1}{\varepsilon _{s2}}\right )\).

For non-uniformity errors, assume r is the ratio between the area used to answer the query and the total area of the cell. We know from the single-level case that the non-uniformity errors are \(K \sqrt {r}\frac {n_{u}^{*}}{N_{u}}\) and \(K\sqrt {r}\frac {s_{u}^{*}}{N_{u}}\). To eliminate the \(\sqrt {r}\) factor, we integrate over its domain ((0, 0.5]) and compute the expected value of the total non-uniformity error. Since \(\frac {{\int }_{0}^{0.5}{\sqrt {r}dr}}{{\int }_{0}^{0.5}{dr}} = \frac {\sqrt {2}}{3}\) we get that the total non-uniformity error is \(\frac {\sqrt {2}K}{3N_{u}}\left (n_{u}^{*}+\frac {s_{u}^{*}}{M}\right )\).

Thus, we must minimize the expression

$$\frac{\sqrt{10}N_{u}}{5}\left( \frac{1}{\varepsilon_{n2}} + \frac{1}{\varepsilon_{s2}}\right) + \frac{\sqrt{2}K}{3N_{u}}\left( n_{u}^{*} + \frac{s_{u}^{*}}{M}\right) $$

and we obtain

$$ N_{u} = \sqrt{\frac{\sqrt{5}}{3}\varepsilon K\beta(1-\beta)(1-\alpha)\left( n_{u}^{*} + \frac{s_{u}^{*}}{M}\right)} $$
(9)

where we can approximate \(\frac {\sqrt {10}}{3}\) by 1. This also provides a value for η (Eq. (5)), such that:

$$\begin{array}{@{}rcl@{}} N_{0} &=& \sqrt{\varepsilon \times \frac{K}{\sqrt{2}} \times \beta(1-\beta)\alpha\left( n_{0}^{*} + \frac{s_{0}^{*}}{M}\right)} \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} N_{u} &=& \sqrt{\varepsilon \times \frac{K}{\sqrt{2}} \times \beta(1-\beta)(1-\alpha)\left( n_{u}^{*} + \frac{s_{u}^{*}}{M}\right)} \end{array} $$
(11)

Generalization to Multiple Levels

The analysis used for the case of two levels can be readily extended to a multiple-level structure, where the privacy budget is split across levels (keeping α ε for the current level and dividing privacy budget between count and sum using β, as before), and the granularity for each new level is determined based on the sanitized data and variance analysis at the previous level. However, we must carefully decide when to end the recursion, as having too many levels will decrease the budget per level, and consequently decrease accuracy. Because of this, we implement two stopping mechanisms: first, we introduce a maximum depth of the PSD, m a x_d e p t h, to prevent excessive reduction of per-level privacy budget. Second, we introduce a threshold, N t such that a cell u is divided only if its estimated sensor count satisfies inequality \(n_{u}^{*} > N_{t}\).

The number N u of children nodes of u is given by:

$$ N_{u} = \sqrt{\varepsilon_{u}\times\frac{K}{\sqrt{2}}\times\beta(1-\beta)(1-\alpha)\left( n_{u}^{*} + \frac{s_{u}^{*}}{M}\right)} $$
(12)

We illustrate the proposed multiple-level PSD approach with a running example, in parallel with the description of the pseudocode provided in Algorithm 1. The PSD is built in three phases. First, the PSD structure is determined (i.e., the spatial extent of each index node), by splitting cells according to Eq. (12), and noisy values are computed for sensor counts and value sums. This is the only step in which the real dataset of readings is accessed, and hence the only step that consumes privacy budget. The recursive function buildPSD (Algorithm 1) summarizes this process.

figure e

Figure 2 illustrates PSD construction with α = 0.2, β = 0.5 and ε = 1.6. The root node will receive a budget of ε n,r o o t = 0.5 × 0.2 × 16 = 0.16 (lines 2-8 of algorithm 1). Line 9 computes the real values for the count and sum of sensor values inside the cell (the sensor counts for the running example are presented in Fig. 2d). Lines 10-11 add Laplace noise, resulting in a value of \(n^{*}_{root}=14\). The split granularity for next level is determined as in Eq. (12). Assume we obtain N u = 4, larger than the threshold N t = 2. The root is split into four cells, and the procedure is recursively applied to each of them with ε 1 = (1 − α)ε = 0.8 × 1.6 = 1.28.

Fig. 2
figure 2

Representation of PSD Construction, including weighted averaging and mean consistency

Full size image

The budget for level 1 is further split between the sum and count values, to obtain ε n,1 = 0.128 (lines 2-8). Adding the corresponding Laplace noise to the real values of 2, 1, 2 and 3 (Fig. 2d) (lines 10-11), results in noisy counts 9, 2, 6 and, respectively, − 2 (Fig. 2a).

The cells with values 9, 2 and 6 are further split, while the one with \(n^{*}_{1}=-2\) is not, due to the value of N t . In case no further splits are performed, the remaining budget is used by running lines 13-20 of Algorithm 1, which compute new noisy estimates which are averaged to determine n ′ and, respectively, s ′.

Since the remaining cells are at the maximal depth allowed by the method, the remaining privacy budget of ε n,2 = 0.512 is used to compute the remaining noisy values. The result of the algorithm is shown in Fig. 2a.

The second phase of the index building method is weighted averaging. We average for each internal node the two estimates and compute n ′ and s ′ according to Eq. (6). For each node, we keep track of the variance of the noisy variables and the averaged values, since they will be needed in the higher levels of the tree. The resulting tree at the end of this phase is shown in Fig. 2b.

Finally, the last phase performs mean consistency, which ensures that the estimate from one node is the same as the sum of the estimates from its children. We use Eq. (7)–(8) in a top-down traversal of the tree, the result of which is shown in Fig. 2c.

5 PSD processing and heatmap construction

As illustrated in Fig. 1 (Section 3), after the PSD is finalized at the trusted collector, it is distributed to data recipients who process it according to their own granularity and threshold requirements. The objective of the data recipient is to obtain a binary heatmap that captures areas with anomalous phenomena, i.e., regions of the geographical domain where the measured values are above the recipient-specified threshold.

We assume that the recipient is interested in building a heatmap according to a recipient resolution grid (rrg). Recall that our solution is designed to be flexible with respect to recipient requirements, and each recipient may have its own rrg of arbitrary granularity. In this section, we show how a recipient is able to accurately determine a phenomenon heatmap given as input the PSD, the recipient-defined rrg and threshold T. The objective of heatmap construction is to determine for each rrg cell a binary outcome: positive if the value derived for the cell is above T, and negative otherwise.

Figure 3 shows an example of rrg superimposed on the PSD index. The PSD has four levels, out of which only three are shown (the root is split into four cells, and it is omitted from the diagram due to space considerations). The bottom layer in the diagram represents the rrg. The shaded cell in the rrg layer represents the cell for which we are currently determining the outcome. In this example, we illustrated a high-resolution rrg, so most rrg cells are completely enclosed within a PSD cell at each index level. However, in general, there may be cases when a rrg cell overlaps with several PSD cells. We consider both cases below.

Fig. 3
figure 3

Construction of Heatmap at the Data Recipient Site

Full size image

Since the recipient has no other information other than the PSD, we assume that the count and sum values inside a PSD cell are uniformly distributed over the cell’s extent. Hence, for each rrg cell we compute n and s in proportion to the overlap between the rrg and PSD cells, normalized by the PSD cell area. If one rrg cell overlaps two or more PSD cells, the values for n and s are determined as the weighted sum of the values corresponding to each PSD cell, where the weight is represented by the overlap amount.

Note that, even if the above procedure may result in values for n and s for each rrg cell which are not too far apart from the actual values, there is another important source of inaccuracy due to the fact that the outcome for an rrg cell is obtained by dividing the noisy s and n values. The ratio can be significantly affected even if the noise is not very high. Furthermore, even though the leaf cells of the PSD are likely to be closer in resolution to the rrg grid, considering solely leaf nodes in the outcome evaluation may have undesirable effects, due to the fact that the noise added to leaf nodes is more significant compared to their actual values compared to PSD nodes that are higher in the hierarchy (i.e., relative errors are higher closer to the leaf level).

In our solution, we account for these factors. Instead of naïvely dividing estimates for n and s in each rrg grid cell (which may have low accuracy), we evaluate individually the outcome based on information at each PSD level, and then combine the outcomes through a voting process in order to determine the outcome for each individual rrg cell. Returning to the example in Fig. 3, assume that threshold T = 80. We determine the outcome of the gray cell at the rrg layer by using the outcomes for all the marked PSD cells on the three levels shown (cells are marked using a small black square). Specifically, the Level 1 PSD cell containing the shaded grid cell has \(\overline {n} = 30\) and \(\overline {s} = 1050\), resulting in a phenomenon value \(\overline {\rho } = \frac {\overline {s}}{\overline {n}} = 35\), below the threshold T = 80. Hence, the root cell’s vote would be negative, meaning that with the information from that layer, the grayed grid cell does not present an anomalous reading.

However, at Level 2 of the PSD, we have \(\overline {n} = 20\) and \(\overline {s} = 1700\), resulting in a value of 85, greater than the threshold. Hence, this layer will contribute a positive vote. Similarly, at Level 3, \(\overline {n} = 8\) and \(\overline {s} = 800\) which also results in a positive vote.

The resulting outcome for any rrg cell depends on the distribution of the votes it has received. We could use the difference between positive and negative votes, but this will report a biased result for grid cells overlapping multiple PSD cells at the same level. A better solution is to use the ratio of positive votes to the total votes. In our example, the grayed cell got two positive votes and a single negative one, hence it would be marked as anomalous.

An alternative approach is to use only the number of positive votes that have been received. For instance, a rrg cell would receive a positive outcome if at least two PSD cells vote positively. This approach has two advantages: first, it captures locality better than the previous strategy. If the region where the phenomenon has an anomalous value is small, majority voting would tend to flatten the heatmap at higher levels, and the sharp spike may be missed. The two-vote strategy, however, may correctly identify the spike if both the leaf level PSD and another level above vote positively. Second, the two-vote strategy may prevent false alarms, caused by small PSD cells that may receive a high amount of random noise. By having a second level confirm the reading, many of the false negatives are eliminated, as it is unlikely that two PSD cells at different levels that overlap each other both receive very high noise due to the Laplace mechanism.

6 Fine-grained vote weighting at cell level

In the previous section, we investigated how accuracy of anomalous phenomenon detection can be improved by taking into account information from multiple levels of the index structure. Specifically, we employed voting, whereby the reading of each PSD cell overlapping a particular rrg cell at a distinct index level contributes equally when determining the outcome for the rrg cell. However, despite improvements, this is a coarse-grained approach to voting, since cells at different levels of the PSD may have different levels of noise-induced errors, due to cell extent and varying density of readings inside the cell. In fact, there may be significant error differences due to density variation even among distinct index cells in the same level that overlap a given rrg cell.

In this section, we propose a flexible, fine-grained mechanism that assigns a voting weight to each PSD cell based on a careful analysis of the error likelihood for each cell. We employ an analytical statistical model to determine weight values, based on the expected error induced by differentially-private noise. To the best of our knowledge, this is the first work that supports individual weights for each particular cell in the PSD structure.

In summary, the proposed fine-grained vote weight computation approach works as follows: after the PSD is constructed, for each cell u we assign a weight w u . The specific value w u for each cell is determined in two steps: first we compute the mean and variance of the average phenomenon value \(\overline {\rho _{u}}\); second, we employ the use of concentration inequalities to bound the probability that the vote given by cell u is inaccurate, and thus we derive the formula for the weight w u .

In Section 6.1, we derive an analytical model for the mean and variance of noise density in the proposed PSD. Based on this model, in Section 6.2, we compute the probability that a specific cell passes the anomalous phenomenon threshold T. Finally, in Section 6.3 we derive the formula for the voting weight that must be assigned to each cell.

6.1 Mean and variance of noisy density

Since the vote of a cell u is given by the value \(\overline {\rho _{u}} = \frac {\overline {s_{u}}}{\overline {n_{u}}}\) we need to investigate the statistical properties (mean and variance) of \(\overline {\rho _{u}}\), considered as a random variable.

Consider the general case of determining the mean and variance of the ratio of two random variables: \(\frac {X}{Y}\) where we assume that Y has no mass at 0 to prevent division by 0 – to achieve this, in the PSD consistency phase we set all negative noisy counts to 0 and we don’t allow cells with a noisy count of 0 to vote. We emphasize that, removing such cells is not a violation of privacy, since the decision is taken entirely based on noisy counts, which are safe to disclose. This removal is a typical step of post-processing, commonly employed in differentially private techniques.

Consider any function f(X,Y ) of two random variables X and Y. The Taylor expansion around \((\mathbb {E}(X), \mathbb {E}(Y))\) is

$$\begin{array}{@{}rcl@{}} f(X, Y) &\approx& f(\mathbb{E}(X), \mathbb{E}(Y))\\ && + f_{X}^{\prime}(\mathbb{E}(X), \mathbb{E}(Y))(X - \mathbb{E}(X)) + f_{Y}^{\prime}(\mathbb{E}(X), \mathbb{E}(Y))(Y - \mathbb{E}(Y)) \\ && + \frac{1}{2}\{f_{XX}^{\prime\prime}(\mathbb{E}(X), \mathbb{E}(Y))(X - \mathbb{E}(X))^{2}\\ &&+ 2f_{XY}^{\prime\prime}(\mathbb{E}(X), \mathbb{E}(Y))(X - \mathbb{E}(X))(Y - \mathbb{E}(Y))\\ &&+ f_{YY}^{\prime\prime}(\mathbb{E}(X), \mathbb{E}(Y))(Y - \mathbb{E}(Y))^{2}\} \end{array} $$

Computing the expected value of f(X,Y ) we have:

$$\begin{array}{@{}rcl@{}} \mathbb{E}(f(X, Y)) &\approx& f(\mathbb{E}(X), \mathbb{E}(Y)) \\ &&+ \frac{1}{2}\{f_{XX}^{\prime\prime}(\mathbb{E}(X), \mathbb{E}(Y))Var(X) + 2f_{XY}^{\prime\prime}(\mathbb{E}(X), \mathbb{E}(Y))Cov(X, Y)\\ &&+ f_{YY}^{\prime\prime}(\mathbb{E}(X), \mathbb{E}(Y))Var(Y)\} \end{array} $$

Furthermore, by computing the derivatives for \(f(X, Y) = \frac {X}{Y}\), we obtain:

$$\begin{array}{@{}rcl@{}} \mathbb{E}(\frac{X}{Y}) &\approx& \frac{\mathbb{E}(X)}{\mathbb{E}(Y)} - \frac{Cov(X, Y)}{(\mathbb{E}(Y))^{2}} + \frac{\mathbb{E}(X)Var(Y)}{(\mathbb{E}(Y))^{3}} \end{array} $$

For the variance \(Var(f(X, Y)) = \mathbb {E}\left [\left (f(X, Y) - \mathbb {E}(f(X, Y))\right )^{2}\right ]\), we consider as an approximation only the first order Taylor expansion, and we obtain:

$$\begin{array}{@{}rcl@{}} \mathbb{E}(f(X, Y)) &\approx& f(\mathbb{E}(X), \mathbb{E}(Y))\\ Var(f(X, Y)) &\approx& \mathbb{E}\left[\left( f(X, Y) -f(\mathbb{E}(X), \mathbb{E}(Y))\right)^{2}\right]\\ &=& \mathbb{E}\left[(f_{X}^{\prime}(\mathbb{E}(X), \mathbb{E}(Y))(X - \mathbb{E}(X)) + f_{Y}^{\prime}(\mathbb{E}(X), \mathbb{E}(Y))(Y - \mathbb{E}(Y)))^{2}\right]\\ &=&f_{X}^{\prime}(\mathbb{E}(X), \mathbb{E}(Y))Var(X) + 2f_{X}^{\prime}(\mathbb{E}(X), \mathbb{E}(Y))f_{Y}^{\prime}(\mathbb{E}(X),\\ && \mathbb{E}(Y))Cov(X,Y) + f_{Y}^{\prime}(\mathbb{E}(X), \mathbb{E}(Y))Var(Y) \end{array} $$

Next, we expand the expressions of the derivatives in the equation above, and we obtain:

$$\begin{array}{@{}rcl@{}} Var(\frac{X}{Y}) &\approx& \left( \frac{\mathbb{E}(X)}{\mathbb{E}(Y)}\right)^{2}\left[\frac{Var(X)}{(\mathbb{E}(X))^{2}} - 2\frac{Cov(X, Y)}{\mathbb{E}(X)\mathbb{E}(Y)} + \frac{Var(Y)}{(\mathbb{E}(Y))^{2}}\right] \end{array} $$

Returning to our specific case, where X = s u and Y = n u , and using the expectations \(\mathbb {E}(\overline {n_{u}}) = n_{u}\) and \(\mathbb {E}(\overline {s_{u}}) = s_{u}\), as well as the fact that random variables \(\overline {n_{u}}\) and \(\overline {s_{u}}\) are independent, we obtain:

$$\begin{array}{@{}rcl@{}} \mathbb{E}(\overline{\rho_{u}}) &=& \rho_{u} \left( 1 + \frac{Var(\overline{n_{u}})}{{n_{u}^{2}}}\right) \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} Var(\overline{\rho_{u}}) &=& {\rho_{u}^{2}} \left( \frac{Var(\overline{s_{u}})}{{s_{u}^{2}}} + \frac{Var(\overline{n_{u}})}{{n_{u}^{2}}}\right) \end{array} $$
(14)

where the values \(\overline {s_{u}}, \overline {n_{u}}\) and their respective variances are obtained from the PSD construction step. In order to estimate the value of the real phenomenon value, we will use the noisy \(\overline {\rho _{u}}\), \(\overline {n_{u}}\) and \(\overline {s_{u}}\) expressions to obtain the noisy estimates:

$$\begin{array}{@{}rcl@{}} \mathbb{E^{*}}(\overline{\rho_{u}}) &=& \overline{\rho_{u}} \left( 1 + \frac{Var(\overline{n_{u}})}{\overline{n_{u}}^{2}}\right) \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} Var^{*}(\overline{\rho_{u}}) &=& \overline{\rho_{u}}^{2} \left( \frac{Var(\overline{s_{u}})}{\overline{s_{u}}^{2}} + \frac{Var(\overline{n_{u}})}{\overline{n_{u}}^{2}}\right) \end{array} $$
(16)

We also observe that the expected value of the noisy density is higher than the real density. This fact will become important in the following section, when we estimate the probability of passing the threshold T for a noisy sensed value.

6.2 Probability of passing threshold T

For each cell u, the value \(\overline {\rho _{u}}\) is a sample of the random variable representing the real phenomenon value ρ. However, due to addition of random noise according to differential privacy, we might have cases where the sampled \(\overline {\rho _{u}}\) is below the threshold T, even though ρ > T. To correct this problem, we add custom weights for each cell during the voting process. The weights are computed based on the probability of the vote corresponding to a cell being wrong.

Formally, we consider the probability \(Pr\{\overline {\rho _{u}} \ge T\}\). Since we have the mean and variance of \(\overline {\rho _{u}}\) given by Eqs. (13)–(14), we will use the Paley-Zygmund inequality [12]. For any positive random variable Z,

$$Pr\{Z \ge \alpha\mathbb{E}(Z)\} \ge 1 - \frac{Var(Z)}{(1-\alpha)^{2}(\mathbb{E}(Z))^{2} + Var(Z)} $$

where α ∈ (0,1) is a parameter to scale the threshold relative to the expected value.

To use this inequality in our case, after substituting ρ for X, we observe that \(T = \frac {T}{\mathbb {E}(\overline {\rho })} \times \mathbb {E}(\overline {\rho })\) where the right-hand side has the same shape as the right-hand side in the inequality inside the probability above. That is, we can use the Payley-Zygmund inequality for \(\alpha = \frac {T}{\mathbb {E}(\overline {\rho })}\). Note, however, that we don’t know the true value of \(\mathbb {E}(\overline {\rho })\), but we can use instead the noisy version, \(\mathbb {E}^{*}(\overline {\rho })\). Finally, note that the inequality is valid only for α ∈ (0,1), hence the noisy estimate must be above the threshold.

However, if the noisy mean is below the threshold T, since the noisy mean is always above the real value (as given by Eq. (13)) we immediately get that the phenomenon value is below the threshold. In this case, the cell will vote negatively with high confidence.

On the other hand, if the noisy mean is above the threshold T, we can apply the inequality to obtain:

$$ Pr\{\overline{\rho_{u}} \ge T\} \ge 1 - \frac{Var^{*}(\overline{\rho_{u}})}{(1-\alpha)^{2}(\mathbb{E^{*}}(\overline{\rho_{u}}))^{2} + Var^{*}(\overline{\rho_{u}})} $$
(17)

which is a lower bound on the probability that the phenomenon value is above the threshold T. Hence, we will use this bound as the confidence level of the positive vote of the cell.

Replacing α, we obtain

$$ Pr\{\overline{\rho_{u}} \ge T\} \ge 1 - \frac{Var^{*}(\overline{\rho_{u}})}{(\mathbb{E^{*}}(\overline{\rho_{u}}) - T)^{2} + Var^{*}(\overline{\rho_{u}})} $$
(18)

6.3 Weighted voting

This section describes the method to compute the specific voting weight w u for each cell u. After computing the values \(\overline {s_{u}}, \overline {n_{u}}, Var(\overline {s_{u}})\) and \(Var(\overline {n_{u}})\) from the PSD construction phase, we determine noisy estimates for the mean and variance of the noisy density, using Eqs. (15)–(16). Then, we determine if the threshold T is above \(\mathbb {E^{*}}(\overline {\rho _{u}})\) and assign the weight as follows:

$$ w_{u} = \left\{\begin{array}{ll} \quad\quad\quad 0 & \quad T > \mathbb{E}(\overline{\rho_{u}})\\ 1 - \frac{Var^{*}(\overline{\rho_{u}})}{(\mathbb{E^{*}}(\overline{\rho_{u}}) - T)^{2} + Var^{*}(\overline{\rho_{u}})} & \quad\text{otherwise} \end{array}\right. $$
(19)

In order to understand the intuition behind the weights, we can analyse the positive case to obtain the following equivalent formulation:

$$ w_{u} = 1 - \frac{1}{1 + \frac{(\mathbb{E^{*}}(\overline{\rho_{u}}) - T)^{2}}{Var^{*}(\overline{\rho_{u}})}} $$
(20)

If we denote by ξ the second term of the denominator (i.e., ratio of the distance between the mean and the threshold to the density variance) we obtain:

$$ w_{u} = 1 - \frac{1}{1 + \xi} $$
(21)

where ξ ∈ [0,∞). Hence, w u ∈ [0,1), that is, no cell will vote with a weight above 1.

This asymptotic formulation allows us to express analytically the intuition behind the weight formulation: if the distance between the noisy estimate of the expected value and the threshold is large compared to the variance, then ξ →∞ and the weight tends to 1. This corresponds to the intuitive interpretation that if the distance is large, then the real phenomenon value is far above the threshold. On the other hand, if the distance is small, due to the addition of noise, the phenomenon value can be below the threshold T even though the estimate provides a value above T. This uncertainty is captured by a weight w u which is close to 0.

The plot of the weight w u as a function of ξ is shown in Fig. 4. As the value of ξ grows, the weight asymptotically tends towards the 1 value. In the experimental evaluation of Section 7, we measure empirically the accuracy gain brought by the proposed fine-grained vote weight assignment mechanism.

Fig. 4
figure 4

Weight as function of ratio ξ

Full size image

7 Experiments

We evaluate experimentally the proposed technique for privacy-preserving detection of anomalous phenomena. We implemented a C prototype, and we ran our experiments on an Intel Core i7-3770 3.4 GHz CPU machine with 8 GB of RAM running Linux OS. We first provide a description of the experimental settings used in Section 7.1. Next, in Section 7.2, we evaluate the accuracy of our technique in comparison with benchmarks. In Section 7.3, we investigate the performance of our technique, including coarse-grained voting decisions, when varying fundamental system parameters. Finally, in Section 7.4 we evaluate the effect of the proposed fine-grained cell-level vote weighting mechanism.

7.1 Experimental settings

We evaluate our proposed approach on two datasets: a synthetic one and a real one. As synthetic dataset, we consider a square two-dimensional location space with size 100 × 100, and a phenomenon with range M = 100 and threshold T = 80. We consider between 10,000 and 50,000 mobile users (i.e., sensors), uniformly distributed over the location domain. The average non-anomalous phenomenon value is 20, and to simulate an anomaly we generate a Gaussian distribution of values with scale parameter 20, centered at a random focus point within the location domain.

For the real dataset, we consider the crowd_temperatureFootnote 2 dataset from Crawdad. This is the Rome taxi dataset coupled with a simulated trace of temperature attached to each taxi position. The details of the temperature distribution are selected from actual weather data at the time the taxi trajectories were produced. For our scenario, we consider that the entire dataset captures a single time snapshot of the phenomenon. Hence, we only considered the latitude, longitude and temperature columns of the dataset. We construct a square bounding box around the locations where the length of the square’s side is 2 latitude/longitude degrees. Then, we run our algorithms on the projected data, assuming as threshold for anomaly a temperature of 10 ∘C, which is approximately the median of the dataset. Furthermore, we consider that the maximum sensor value is M = 25 ∘C, slightly larger than the maximum value on the temperature column.

We consider two benchmark techniques for comparison. The first method, denoted as Uniform Grid (U), considers a single-level fixed-granularity regular grid. The parameters of the grid are chosen according to the calculations presented in the first part of Section 4. The second method, Adaptive Grid (AG), implements the state-of-the-art technique for PSDs as introduced in [2]. Specifically, it uses a two-level grid, where the first grid granularity is chosen according to a fixed split as indicated in [2], whereas the second-level granularity is determined based on the data density in the first level.

7.2 Comparison with competitor methods

We measure the accuracy in detecting anomalous phenomena for the proposed tree-based technique (denoted as t) and the benchmarks U and AG when varying privacy budget ε. In this experiment, we focus on the synthetic dataset. For fairness, we consider the 1-vote decision variant, which is supported by all methods. Figure 5a shows that our technique (presented with two distinct depth settings) clearly outperforms both benchmarks with respect to the Jaccard metric. The U and AG method are only able to achieve values around 0.1 or less. Furthermore, they are not able to make proper use of the available privacy budget, and sometimes accuracy decreases when ε increases. The reason for this behavior is that the procedure for grid granularity estimation proposed in [2] has some built-in constants that are only appropriate for specific datasets and query types. In our problem setting, the granularity of these choices increases when ε increases, and the noise injected offsets the useful information in each cell.

Fig. 5
figure 5

Accuracy Evaluation in Comparison with U and AG Benchmarks

Full size image

To validate the superiority of the proposed technique beyond the J metric, Fig. 5b and c provide visualization of the heatmap obtained for the U method and our technique, respectively (the heatmap obtained for AG is similar to that of U). The anomalous phenomenon in the real data is shown using the circle area (i.e., points inside the circle are above the threshold). The heatmap produced by the U method is dominated by noise, and indicates that there are small regions with above-the-threshold values randomly scattered over the data domain. In contrast, our technique accurately identifies a compact region that overlaps almost completely with the actual anomalous region. Furthermore, for the t technique we consider two distinct maximum depth settings, d = 3 and d = 4. We observe that, although both variants outperform the benchmarks, as the height of the structure increases, a potentially negative effect occurs due to the fact that the privacy budget per level decreases. Hence, it is not advisable to increase too much the PSD depth.

Both the UG and the AG method are unable to maintain data accuracy, and return virtually unusable data, without the ability to detect the occurrence of anomalous phenomena. In the rest of the experiments, we no longer consider competitor methods, and we focus on the effect of varying system parameters on the accuracy of the proposed technique. We also note that our method incurs low performance overhead, similar to that of the U method (between 2 and 4 seconds to sanitize and process the entire dataset). The AG method requires slightly longer, in the range of 15 − 20 seconds.

7.3 Effect of varying system parameters

We perform experiments to measure the accuracy of the proposed technique when varying fundamental system parameters, such as budget split parameters α,β and sensor count N. Figures 6, 7 and 8 show the results obtained for the synthetic dataset, whereas Fig. 9 focuses on the real dataset used.

Fig. 6
figure 6

Impact of cross-level privacy budget split parameter α, d = 3

Full size image
Fig. 7
figure 7

Impact of “count vs sum” privacy budget split parameter β, d = 3

Full size image
Fig. 8
figure 8

Impact of number of mobile users N, β = 0.5, d = 3

Full size image
Fig. 9
figure 9

Effect of α and β parameters on accuracy in Rome Taxi Dataset

Full size image

Figure 6 shows the accuracy of our method when varying α, the budget split fraction across levels. Each graph illustrates several distinct combinations of budget ε and count-sum budget split β. For smaller α values, a smaller fraction of the budget is kept for the current level, with the rest being transferred for the children cells. Since the root node and the high levels of the tree have large spans, a smaller budget does not have a significant effect on accuracy, so it is best when a larger fraction is used in the lower-levels. For α = 0.2, the proposed method reaches close to perfect J metric value.

We also illustrate the effect of the various decision variants based on coarse-grained voting (fine-grained, cell-level weighted voting results are presented in Section 7.4). Comparing Fig. 6a and b, we can see that the accuracy increases slightly for the 2-vote scenario. This confirms that the 2-vote approach is able to filter out cases where some large outlier noise in one of the lower-level cells creates a false positive. The accuracy of the majority-voting strategy from Fig. 6c is slightly better than the 1-vote approach, and virtually the same as the 2-vote case. For the majority voting case, there is the effect of a potentially high false negative rate. Even if some of the levels signal an alarm, it is possible that a large amount of noise on several levels flips the outcome to “below the threshold”. Therefore, there is no sensible gain compared to the 2-vote strategy.

Figure 7 shows the effect of varying parameter β, which decides the privacy budget split between the counts and sums in the PSD. The results show that an equal split between counts and sums yields good results. As long as the β split is not severely skewed, the parameter does not significantly influence accuracy. However, when β is excessively low or high, one of the sum or count components gets very little budget, which causes large errors. In fact, this is one of the main reasons why competitor techniques fail to obtain good accuracy, as they do not consider the correlation between sum and count errors.

Finally, we consider the effect of varying number of sensors N. Figure 8 shows that the accuracy of the method increases slightly with N. This is expected, as a higher data density due to more reporting sensors benefits differential privacy, as the signal-to-noise ratio increases. In this case, we also notice that the majority voting and 2-vote strategies obtain virtually identical accuracy, which is better than the 1-vote case.

Next, we measure the effect of system parameters on the real dataset. Results are summarized in Fig. 9. Similar to the synthetic dataset, we observe from Fig. 9a that a low-to-moderate value of α obtains best results. The trend is also similarly decreasing, with the exception of two data points at α = 0.3 when accuracy is slightly higher than at α = 0.2. However, the difference is small. A slightly more interesting case occurs for the variable β case, illustrated in Fig. 9b. In this case, the best results are obtained for lower values of β. For this particular dataset, the range of temperatures is relatively tight, and the user distribution is not uniform. As a consequence, among the two sanitized measures of sum and count, the sum is significantly less variable than the count. For that reason, allocating a slightly larger budget to the count yields better accuracy. However, the difference between lower β values and the equal split β = 0.5 case are not significant. One can safely set the β value to 0.5 and obtain good results.

Discussion

Based on our experimental results on both synthetic and real datasets, we are able to outline a strategy for the choice of parameters α and β. For the α value, which controls the budget split across levels, it is advisable to always allocate more budget to the lower levels. This is an intuitive find, since in any hierarchical structure it is expected that the actual values are lower when descending in the tree, hence to preserve accuracy, it is important to reduce the noise towards the leaf nodes. Of course, the value should not be too small, so the higher levels also get a reasonable amount of budget. Our results show that a low-to-moderate value of 0.2 − 0.25 should be appropriate for most cases.

With respect to the β parameter, one needs to take into account some characteristics of the actual problem setting. Specifically, a pronounced skew in either the distribution of sensed values, or in the distribution of user placement, can influence accuracy. If the two distributions are expected to be equally skewed, then an equal split (β = 0.5) is appropriate. Otherwise, a larger amount of budget should be allocated to the component (i.e., either count or sum) with the more pronounced skew.

7.4 Evaluation of fine-grained cell-level vote weighting

In this section, we evaluate experimentally the behavior of the fine-grained cell-level voting mechanism introduced in Section 6. Recall that the proposed technique derives the weight for each cell based on the expected error given the density of readings in that cell. As illustrated in Section 6.2, voting weights are assigned at each level in the PSD based on a desired probability for the sensed value to exceed threshold T. The private heatmap of the phenomenon is obtained by adding together all the w u values from applying Eq. (19) to all cells u of the PSD which cover the current rrg cell. As a result, we obtain a value which is higher when more cells of the PSD cover a rrg cell corresponding to an anomalous region. Hence, we will reconstruct the heatmap by comparing \(\displaystyle \sum \limits _{\forall u \in G_{crt}}{w_{u}}\) with a threshold, where G c r t is the set of all PSD cells covering the current rrg cell. This threshold, denoted in the rest of the section as P, is an essential parameter of the weighted voting approach, and may significantly influence accuracy.

First, we evaluate the accuracy of the weighting approach in comparison with the voting approaches without weights, namely: absolute 1-vote count decision (A v1), absolute 2-vote count decision (A v2) and majority decision, or relative 50%-vote (R v50). For the weighted approach, we consider three distinct values of parameter P: 0.25, 0.5 and 0.75. Figure 10a shows the obtained accuracy when varying privacy budget ε for the synthetic dataset. The weighted approach outperforms clearly the absolute and relative votes counterparts (to improve readability, all weighted approaches are represented with full points, whereas the non-weighted methods are represented with empty points). The superiority of the weighted approach is more clear when the privacy budget is more scarce (for high values of ε, all approaches obtain perfect accuracy). Figure 10b illustrates similar trends obtained for the real Rome taxi dataset. The weighted voting techniques clearly outperform the non-weighted approaches. In addition, the absolute values obtained for weighted voting accuracy in the case of the real dataset are better, due to higher density of readings. For the remainder of this section, we keep as benchmark only the R v50 method, which performs best among non-weighted approaches.

Fig. 10
figure 10

Accuracy Evaluation of Weighted Voting Compared to Non-Weighted Approaches

Full size image

In Fig. 11, we measure the impact on accuracy of parameter α, i.e., the budget allocation split across levels, for two different privacy settings: ε = 0.4 and ε = 0.6 (for brevity, we only include synthetic dataset results). As observed earlier in Section 7.3 for non-weighted approaches, an increase in α leads to a decrease in accuracy. However, the weighted approaches always outperform R v50 by a significant margin.

Fig. 11
figure 11

Impact of cross-level privacy budget split parameter α (β = 0.5)

Full size image

Next, we evaluate the impact on accuracy of parameter β, i.e., the budget allocation split between count and sum values. As shown in Fig. 12, the balanced split where counts and sums get equal privacy budgets performs best in this case as well, similar in trend to the approaches that do not use weights. However, the weighted approaches outperform significantly their non-weighted counterparts across the board. Another interesting observation is that the weighted approaches are more robust to changes in the value of β, in particular for the P = 0.5 setting. This shows that the weighted approach also has the benefit of adapting better to changes in parameters.

Fig. 12
figure 12

Impact of “count vs sum” privacy budget split parameter β (α = 0.3)

Full size image

Figure 13 illustrates the behavior of the weighted voting approach when varying number of users N. The accuracy of the weighted approaches increases sharply with the user density, and quickly reaches maximum accuracy J = 1.0 for N = 20,000. In contrast, the non-weighted approach needs a much higher density to obtain perfect accuracy.

Fig. 13
figure 13

Impact of number of mobile users N (α = 0.3,β = 0.5)

Full size image

In addition to number of users N, we also evaluate the effect of data space size, which in combination with N influences the density of users per cell. Figure 14 shows the results, with data space extent ranging from 100 × 100 to 1000 × 1000. For this experiment, we fix N = 20,000, α = 0.4 and β = 0.5. We observe that as the extent grows initially, there is an increase in accuracy, due to the fact that the anomalous phenomenon is more focused relative to the entire space extent. However, after the extent reaches a certain level, the accuracy stabilizes. This is a favorable result for our method, as we are able to provide stable accuracy for a relatively large range of data space extents. Furthermore, even for the smallest setting 100 × 100, the absolute value for the accuracy metric is 0.88, which is quite high.

Fig. 14
figure 14

Impact of Data Space Size (N = 20,000, α = 0.4 and β = 0.5)

Full size image

Finally, we evaluate the behavior of the weighted voting mechanism (label W) when varying parameter P. Figure 15 shows the results for the synthetic dataset. We observe that a moderate value of P (e.g., 0.3 − 0.7) is best for accuracy. Setting a P value that is too low results in false negatives, where the noise is large enough that the sensed value can change from above threshold T to below T. Conversely, a P value that is too high tends to give false positives. In the graph, we also represent the non-weighted approach (the relative 50% vote) for two values of privacy budget ε (since the non-weighted approach does not depend on P, there are two horizontal lines, one for each 𝜖 value). Note that, except for one single setting of P that is excessive (0.9), the weighted approach always outperforms the non-weighted voting method. Often, weighting can improve accuracy such that the counterpart non-weighted method is outperformed even when the latter gets significantly more budget (i.e., in the interval P = 0.3 − 0.7, the weighted approach with ε = 0.3 outperforms the non-weighted method with ε = 0.5).

Fig. 15
figure 15

Impact of weighting parameter P

Full size image

Figure 15b illustrates the results for the same experiment, but this time on the real dataset. For this case, the accuracy obtained is even better, due again to the higher density of readings. For most of the P value range, 100% accuracy is obtained. In addition, the accuracy does not begin its downward slope even for the higher range of values considered. Instead, the deterioration occurs only for higher P values, outside the considered interval. We conclude that the weighted approach performs very well on both synthetic and real datasets, and it is robust to a wide range of parameter P value settings.

8 Related work

Collaborative sensing enables information extraction from a large number of wireless devices, spanning from smart phones to motes in a WSN. We focus on personal devices which are carried by users and may be used in sensing applications – from tracking to shapes-detection – in settings in which there are no WSNs available [13, 14]. Such settings occur in many real-life applications in which the deployment of a WSN is either not possible or the WSN approach is not sustainable. We note that collaborative sensing is, in some sense, a broader paradigm than participatory sensing and opportunistic sensing, and when it comes to issues related to privacy protection, it subsumes the ones from the latter two paradigms in the risk of leaking personal/sensitive information [15]. While privacy-preserving computation has its history in domains such as cryptography and data mining, the existing methodologies cannot be straightforwardly mapped into the collaborative sensing applications.

There are works that have addressed different aspects of the problem of detecting and representing spatial features of a particular monitored phenomenon [16,17,18]. Spatial summaries (e.g., isocontours [16]) may be constructed for energy-efficient querying in wireless sensor networks. A natural trade-off in such settings is the precision of the aggregated representation vs. the energy efficiency.

Location privacy has been studied extensively. Some techniques make use of cryptographic protocols such as private information retrieval [19]. Another category of methods focuses on location cloaking, e.g., using spatial k-anonymity [20,21,22,23], where a user hides among k other users. As discussed in Section 2, such techniques have serious security drawbacks. Another protection model proposed in works such as [24, 25], aims to hide exact user coordinates, and to prevent association with sensitive locations. In the PROBE system [24] for instance, users define their own privacy profiles, by specifying maximum thresholds of association with sensitive feature types.

The recently-proposed concept of geo-indistinguishability [26, 27] provides a mechanism to randomly perturb locations, and quantifies the probability of an adversary to recover the real location from a reported one. The concept is inspired from the powerful semantic model of differential privacy (DP) [4], which in recent years became the de-facto standard for privacy-preserving data publishing. However, while borrowing some of the syntactic transformations of differential privacy, the work in [26, 27] does not also inherit the powerful protection semantics of DP, which only permits access to data through a statistical query interface, and prevents an adversary from learning whether a particular data item is included in a dataset or not.

Closest to our work are the PSD construction techniques in [1,2,3]. An approach based on differentially-private grids for matching workers to tasks has been proposed in [28]. However, the focus there is on search around a single task location, whereas in our case, we focus on the heatmap publication for the entire data space. Recently, a more flexible private index structure has been proposed in [29]. However, as discussed in Section 4, all these techniques are general-purpose, and our experimental evaluation shows that they are not suitable for anomalous phenomenon detection.

Our current work is an extended version of the conference paper in [30]. As additional contribution, we include an analytical model for characterization of value density error in crowdsourced environmental sensing. Based on that, we propose a flexible, fine-grained mechanism for weighted voting that provides accurate means of privately deciding whether the sensed value is above the threshold or not. We also include evaluation on real datasets, compared to [30] where only synthetic ones are considered.

9 Conclusions and future work

We proposed an accurate differentially-private technique for detection of anomalous phenomena in crowdsourced environmental sensing. Our solution consists of a PSD specifically-tailored to the requirements of phenomenon heatmap data, and strategies for flexible processing of sanitized datasets with values collected from mobile users. Experimental results show that the proposed technique is accurate, and clearly outperforms existing state-of-the-art in private spatial decompositions. In the future, we plan to extend our solution to continuous monitoring of phenomena, where multiple rounds of reporting are performed. This scenario is more challenging, as an adversary may correlate readings from multiple rounds to breach individual privacy.