1 Introduction

Spatial data is ubiquitous. Most data contain contain some form of spatial component, whether that be the address of a transaction, a political boundary indicating ownership of some item, or the proximity of a communication to a point of interest. The widespread of adoption of mobile devices coupled with reliable and accurate global position systems allowed a leap the nature and the quality of spatial data available. Instead of focusing on purely spatial aspects of data, spatiotemporal data and its corresponding analysis are increasingly important. Instead of analyzing the position of a taxi at the time of a transaction, one now has the ability to generate accurate trajectories of the taxi both at transaction times and in between them. Thus, spatiotemporal analysis has grown from instant analysis, in which spatial analysis focuses at particular instants in time or at data aggregated and projected out of time, to trajectory analysis, in which spatiotemporal analysis naturally incorporates the motion of data items over time. The result is a much richer form of analysis for many applications. Furthermore, the idea of trajectory analysis is applicable to data streams that record the position and extent of spatial data as it changes over time.

Trajectory analysis of points is conceptually intuitive. For example, a vehicle represented as point that moves over time generates a trajectory. That trajectory can be represented in a variety of ways, for example, as a function over time or as a line in three dimensional space in which the first two dimensions are the spatial dimensions and the third dimension represents time. In any case, the idea of representing a point’s trajectory as a line is natural. Things are less intuitive when one considers spatial data in the form of a region that changes over time. For example, an area affected by drought may be represented as a region on a map. As time progresses, the area may grow, shrink, or develop holes where rain falls in the middle of the region. Again, this can be represented in a variety of ways, but these representations become less intuitive; for example, we may say the region is represented as a function over time, but without specific knowledge of the implementation model of the region, this is quite a vague statement. We can say the region is represented as a volume in three dimensional space but the complexity of the region may make cognitive visualization, or actual visualization, rather tricky. For example, a region containing many holes is tough to visualize, whereas a point forming a line in 3D is less difficult. The complexity of trajectory analysis of regions carries over from the cognitive realm to the practical realm: implementations of trajectory analysis of regions that move are rare and are difficult to achieve.

Spatial data objects that change in shape and/or position over time are a type of spatiotemporal data known as moving objects. Specifically, models exist that extend the traditional spatial types of points, lines, and regions into the moving object realm, resulting in moving points, moving lines, and moving regions. Because these objects move and change shape over time, they imply the existence of trajectories in time. Thus, trajectory analysis opportunities exist for each of the types. From a practical perspective, trajectory analysis of regions, especially complex regions has proven difficult. A complex region may contain multiple, disconnected faces, each of which may contain holes; Italy, for example, contains multiple faces representing the mainland and its islands, and hole that does not belong to Italy where Vatican City sits. There is much work in the literature that explores the mathematic foundations of moving regions, and some work that discusses discrete concepts regarding them, but little work exploring techniques for effectively implementing operations over them.

In this paper, we present implementation techniques to compute set operations over moving regions using the Component Moving Region (CMR) Model. The CMR Model is a mathematical model of complex moving regions that was developed with the goal of allowing straightforward derivation of implementation models. The abstract model itself provides data types and semantic descriptions of operations. Translating the types into implementation models is relatively straightforward, requiring a discretization of region boundaries as polygonal curves. The semantic descriptions of operations, however, leave much flexibility in implementation schemes. One goal of the CMR Model is to allow for easier implementations of operations as opposed to existing moving region models. Effectively, existing proposals for set operation implementations for moving regions are based on 3-dimensional algorithms (space forming the first two dimensions, and time the third), resulting in rather complex algorithms. In this paper, we present implementation techniques for moving region operations that center largely around 2-dimensional algorithms in addition to requiring only simple, and well known, algorithms over 3-dimensional triangles. Therefore, the contributions of this paper include: i) creating an algorithmic framework in which all set operations are efficiently computed for CMR regions, ii) describing the specific mechanisms required for implementation, and iii) discussing an implementation of the algorithm, and depicting results from its execution.

The paper is structured as follows. Section 2 reviews related literature to the work presented in this paper. Section 3 reviews the pertinent concepts of the CMR region model upon which this paper builds. The operational foundation for implementing set operations under the CMR model is discussed in Section 4. In Section 5, the set operations for CMR regions are developed. Mechanisms to build the geometric result of set operations are provided in Section 6. An implementation of the proposed operation for intersecting CMR regions is briefly discussed in Section 8. Finally, we draw some conclusions in Section 9.

2 Related work

This paper provides implementation techniques for operations over moving regions as defined by the CMR model of moving regions [11]. The CMR model is a data model defining types and operations over moving regions. Research into moving objects and the databases that support them have their origins in spatial information management. Spatial information management, and spatial databases, are built upon spatial data type systems. Modeling of spatial types began with the development of the simple spatial objects: simple point, simple line, and simple region (Fig. 1). Simple points represent a single point in space, simple lines are connected structures, and simple regions contain a single face and no holes in the face. The simple spatial types suffered from inability to represent many aspects of geographic reality, and could not ensure type closure under operations.

Fig. 1
figure 1

Example of a simple point (a), line (b) and region (c)

Full size image

Definitions of the complex spatial types emerged as a solution to the problems associated with the simple types. The complex spatial types consist of complex points, complex lines, and complex regions (Fig. 2). A complex point contains many individual points, a complex line represents possibly disconnected networks, and a complex region can contain multiple faces, each containing zero or more holes. Formal definitions for complex types, based on point set theory, are provided in [14].

Fig. 2
figure 2

Example of a complex point (a), line (b) and region (c)

Full size image

To represent spatial data that changes in shape or position over time, spatiotemporal data models were developed [2, 5, 8, 16, 18]. The term moving objects describes spatiotemporal types corresponding to simple and complex spatial types that move or change shape over time. A data model, along with implementation techniques is presented in a series of work that results in a implementation-oriented model of moving types known as the slice model [5]. Essentially, moving objects are represented mathematically by associating complex objects with time instants; thus, a moving region is a mapping from time instants to instances of regions over a continuous time range. In terms of implementation, the slice model introduces time slices such that the movement of a spatial object between two time instants is represented as the motion of individual line segments defining the boundary of a complex spatial object as they travel from a starting position to an ending position over the time interval defined by the slice. In this manner, a moving object is composed of many slices. The slice model defines a complete algebra of types and operations, but suffers from two practical problems: i) data for the model is difficult to generate by hand and algorithms to generate data from real world sources have severe limitations [12, 17], and ii) the algorithms to implement operations over moving regions, in particular, are complex and difficult to implement.

The CMR model was developed to address the practical limitations of the slice model. The goals of the CMR include i) the ability model complex moving regions as components defined as simple spatial objects, ii) to make data generation easier by generating motion between simple components automatic, and iii) make operations easier to implement by defining operations based on well known algorithms and techniques then composing those to create operations. The first two goals have been addressed [11–13]. This paper addresses the third goal. A description of the relevant definitions of the CMR model are included in Section 3. An early version of this work appears in [10]

3 Data model: component moving regions

The complete definition of the CMR Model is presented in [11]. Here we provide a description of the relevant definitions. For the purposes of this paper, we frame the definitions in terms of discrete structures; thus, cycles and lines are defined using polygonal curves. We begin by defining the primitive structures and build up to moving regions under the CMR model.

A simple region is a polygonal curve that defines a single, simple, minimal cycle in 2-dimensional space. A line, for the purposes of this paper, is a polygonal curve in 2-dimensional space that is connected, acyclic, and may contain branches. This definition of a line departs slightly from definitions of simple lines that do not allow branches. Finally, a simple point is a single point in 2-dimensional space.

A triangle is 3-tuple of points in 3-dimensional space. As discussed previously, the CMR model focuses on region representations at individual time instants; therefore, we require that triangles contain a single edge that is planar in the x, y dimensions. Furthermore, the end points of that edge are always the first two points listed in a triangle. A triangle, in this sense, is meant to represent a straight line segment as it travels with constant velocity across a time interval and contracts to, or expands from, a point over that interval. Thus:

Definition 1

A triangle, tri, is a 3-tuple of points such that:

$$tri =((x1,y1,z1),(x2,y2,z2),(x3,y3,z3)) | z1 == z2 \wedge z1 != z3 $$

Structural regions are composed of the geometric primitives simple point, line, and simple region. Structural regions define geometric structures that conform to the definition of complex regions, but represent them as a composition of the geometric primitives. Thus, structural regions separate the structural representation of a complex region from the interpretation of that structure. For example, a complex region representing a face containing a hole will be represented as two separate geometric primitives in a structural region: a simple region defining the face, and simple region defining the hole. The complex region implied by the structural region is computed as the union of all faces minus the union of all holes. Although this is a simplistic representation, we take advantage of it in order to more easily represent moving regions.

We add one additional constraint to the definition of structural regions in addition to those defined in [11]: we require the existince of a mapping, denoted the face-to-hole (F2H) mapping, that indicates which holes affect a particular face. Thus, the interpretation of a structural region is the union of all faces such that the holes associated with each face (according to the F2H mapping) are removed from their respective faces. Let the notation [α] indicate the set of all valid instances of the type α. A structural region is a set of faces, a set of holes, a set of lines, a set of points, and a F2H mapping:

Definition 2

A structural region is a set of faces F, a set of holes H, a set of lines L, a set of simple points P, and a face-to-hole mapping where:

$$\begin{array}{@{}rcl@{}} F &\in& 2^{[simple regions]}\\ H &\in& 2^{[simple regions]}\\ L &\in& 2^{[lines]}\\ P &\in& 2^{[points]}\\ F2H&:& F \rightarrow 2^{H} \end{array} $$

and the complex region r defined by the structural region s is:

$$\begin{array}{@{}rcl@{}} r &=& \bigcup_{f^{\prime} \in F^{\prime} }f^{\prime}\; \text{where}\\ F^{\prime} &=& \{ f - \bigcup_{h \in F2H(f)} h | f \in F \} \end{array} $$

The points, lines, and regions making up a structural region are called components of the structural region. For a structural region S, we use a dot notation to refer to the sets containing the components and the mapping.; i.e., S.F is the set of faces and S.F2H(f) is the set of holes mapped to by face f.

Structural regions are static in time, they contain only 2-dimensional structures and no temporal information. In order to lift structural regions into the spatiotemporal realm, we define component interval regions (CIRs) to describe the motion of a structural region across a fixed time interval. Thus, a CIR contains two time instants: a source time and a destination time. A structural region is then associated with each time interval, resulting in a source region and a destination region. The source region defines the complex region as it exists at the beginning of the time interval, and the destination region defines the complex region as it exists at the end of the time interval. The CIR also contains a component mapping M that associates a component in the source region with a component in the destination region. This association indicates the configuration of that component at the beginning and end of the time interval. CIRs do not explicitly store information to reflect the actual movement of a component across a time interval, rather it relies on a motion function, such as the one in [12, 13] to generate triangles, as defined previously, to represent the motion of components over the time interval.

Definition 3

A component interval region consists of a source time, a source structural region, a destination time, a destination structural region, and a mapping of structures from the source structural region to the destination structural region:

$$\begin{array}{@{}rcl@{}} t_{s} &\in& \mathbb{R}\\ t_{d} &\in& \mathbb{R}\\ s &\in& [structural~region]\\ d &\in& [structural~region]\\ M&:& s_{F} \cup s_{H} \cup s_{L} \cup s_{P} \rightarrow 2^{d_{F} \cup d_{H} \cup d_{L} \cup d_{P}} \end{array} $$

One important point to note about the CIR definition is that the mapping is intentionally free of constraints. A geometric structure in the source region can map to multiple structures in the destination region. Furthermore, a face in the source region can map to a hole in the destination region, and vice versa. Points and lines typically map to faces and holes, allowing faces and holes to come into (or fade out of) existence by growing from a point or line structure.

The fact that the mapping in a CIR is unconstrained allows complex motion patterns to be easily represented. For example, a hole that begins outside of a face, and traverses the face over a time interval can be represented by simply creating cycles representing the hole and face at either end of the time interval, and then using the mapping to indicate the relevant motion. A direct consequence of this is that during the lifetime of a CIR, hole structures may exist outside of a face or faces, faces may overlap with faces, and holes may overlap with holes. Such situations necessitate the requirement for structural regions to be interpreted as complex regions, since their raw representation violates the type constraints of complex regions. We require a method to extract the structural region defined by a CIR at any time instant. The extraction is straightforward: the motion function is applied to all pairs of structures that exist in the CIR’s mapping to generate motion triangles across the time interval. Because motion triangles use constant velocity, the line segment represented by a motion triangle at any time instant is simply interpolated.

Definition 4

The e x t r a c t S R function produces the structural region (SR) defined by a CIR at a specific time instant:

$$extractSR: [component~interval~region] \times \mathbb{R} \rightarrow[structural~region] $$

4 Foundations for set operations

One driving design factor of the CMR Model is that operations should be able to be implemented using well-known 2-dimensional and 3-dimensional operational primitives. The strength of such a design lies in the fact that such algorithms are well studied, optimization techniques for such algorithms are known, and many implementations of such algorithms exist. This design goal was achieved in the semantic description of the intersection operation between two CIRs in [11]. In this section, we discuss a framework of operational primitives upon which the intersection, union, and difference operations between pairs of CIRs, will be implemented. The advantage of this approach is that a single, parameterized framework provides the necessary functionality to compute all three operations.

We assume that all operations operate over a pair of aligned CIRs. Two CIRs are aligned if they have identical source and destination times, and the topological relationship between any pair of components from either of the CIRs do not change in the interior of the time interval. This requirement does not diminish the generality of the operations since two CIRs that are not aligned can be aligned given an extraction function as defined previously. To align two CIRs, one simply uses the motion function to produce motion triangles, and then computes the time instants at which any two motion triangles intersect; such instants are where the boundary of one component intersects the boundary of another component (for example, a face crossing into another face as they move). CIRs are then created using the e x t r a c t S R function to compute the source and destination structural regions for CIRs at adjacent time instants.

The alignment process clearly uses a three-dimensional, triangle/triangle intersection algorithm to discover the time instants when topological change occurs between components of input CIRs. Once aligned, the computation of a set operation is achieved using only two-dimensional operations that operate on the source and destination structural regions in a pair of aligned CIRs. We will continue our explanation assuming that an intersection operation is being computed since both union and difference operations can be expresses in terms of intersection (a fact we take advantage of in later sections).

Intuitively, the intersection of two complex regions consists of the area covered by both input complex regions. Because structural regions use a set of faces to indicate the possible area covered by the region, and a set of holes that remove some of that area, the intersection between two structural regions must 1) find the area covered by faces of both regions, and then 2) remove any of that area covered by a hole from either region. Item 1 is achieved by finding the intersection of pairs of intersecting faces, one face from each respective input region. Item 2 is achieved by finding the portions of any hole from either input structural region that covers an intersection from item 1.

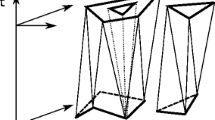
To extend the intersection of structural regions to CIRs, we simply make use of the component mapping in a CIR. If two faces, one from each source region, intersect resulting in a face x, we use the component mapping in the CIR from which they came to find their corresponding faces in the destination region. The intersection, y, of those faces in the destination region is then computed. In the result CIR, the component mapping is updated to reflect the fact that x travels across the time interval as it morphs into y. Holes are handled similarly: the intersection of two faces and a hole from the source will map the intersection of the corresponding structures (with regards to the component mapping) in the destination structural region. Figure 3 depicts an example: the CIR on the left is lightly shaded and the CIR on the right is darkly shaded in Fig. 3a. The lighter CIR contains a hole. The darker CIR has only a single face and overlaps the lighter CIR and its hole at both ends of the interval. The dotted lines indicate the mapping. Figure 3b shows the intersecting faces and their mapping. Figure 3c shows the parts of the holes that intersect intersecting faces, and their mapping. The resulting structures are shown overlaid in Fig. 3d.

Fig. 3
figure 3

Two CIRs (a), one is lighter shaded the other is darker shaded. The intersection of faces (b). The intersection of holes with intersecting faces (c). The result of the intersection (d)

Full size image

Using this procedure results in a set operation being performed using 3D triangle/triangle intersection as the only three-dimensional operation to find times for alignment, followed by two-dimensional extraction and intersection operations over the structural regions. The framework is as follows:

  • Discover time instants of topological change between the input regions.

  • Align the input CIRs according to those time instants.

  • Compute all non-empty intersections between pairs of faces from the respective regions.

  • Compute all non-empty intersections between a hole structure and a non-empty intersection from the previous step.

  • Maintain mappings to build a resulting CIR.

4.1 Operational framework

There are multiple ways to implement the framework presented above. Here, we discuss computational time complexity considerations of one implementation scheme.

Under the framework for set operations, the first step is use a motion function to generate motion triangles over the time intervals covered by two input CIRs. Motion functions exist to achieve this in O(nlgn) time for input of n line segments. The second step is to find intersections between motion triangles for alignment.

A naive approach to computing the intersections between two sets containing n triangles requires O(n 2) time, but index structures exist to lower this to O(nlgn) time (for example, [7]).

The intersections between motion triangles correspond to instants at which the topological relationships between components of the input CIRs change. The extraction function is used to extract structural regions at each time instant. Those structural regions and time instants are then grouped to form aligned CIRs. The component mapping from the original CIRs are used to create the mappings for the aligned CIRs.

At this point in the algorithm, all pairs of faces (where a pair contains one face from each input CIR) with a non-empty intersection must be computed. A naive computation tests all pairs of faces in O(n 2) time for n line segments defining those faces. Similarly, the faces resulting from that step must be intersected with all holes, again resulting quadratic time if implemented naively. Furthermore, the algorithm as described is specific to the intersection operation, and must be modified to accommodate other set operations and topological relationship computations. It will be shown that the proposed framework is achievable using a map overlay algorithm, which is a achievable in linearithimic time bounds, resulting in an overall O(nlgn) time bound for the algorithm. In the following, we propose a generalized method of computing structures that is generic in the sense that the same framework is used to compute all set operations between CIRs.

4.2 A generic approach using map overlay

Given a collection of regions, a map overlay of those regions, for our purposes, overlays all regions into the same scene and such the area covered by the input regions is preserved; furthermore, each input region is assigned a label and a region in the overlay carries the labels of all input regions that cover it [1, 3, 4, 6, 15]. For example, Fig. 4 depicts map overlays that show that an overlay is essentially a labeled partition of the embedding space. More specifically, the model of spatial partitions [3] provides a type system for the concept of a map overlay data type. Because spatial partitions carry labeling information pertaining to the input used for its creation, it is possible to construct a spatial partition based on two input structural regions such that the labeling in the resulting partition allows the selection of relevant structures within the partition that pertain to the result of a desired operation. In other words, a spatial partition created from the components in two input structural regions, if labeled correctly, provides all necessary information to compute the intersection, union, or difference of the input structural regions simply by examining the labels of the resulting partition and extracting structures from the partition based on those labels. Thus, we require a labeling scheme to support such a procedure.

Fig. 4
figure 4

Two structural regions labeled as they would be in a spatial partition (a and b. The first region contains two faces and one hole. The second region contains one face and one hole. c shows the spatial partition constructed by overlaying a and b

Full size image

This section discusses a framework for computing set operations over structural regions. Extending the methods to apply to CIRs is trivial since CIRs are made up of structural regions and a component mapping. The component mapping of a result of a set operation is easy to compute based on the input CIRs to the set operation.

In order to construct an intersection, for example, of two structural regions, r and s, based on a spatial partition constructed from both regions, we must be able to identify if an area in the partition is covered by a face from r, a hole from r, a face from s, a hole from s, or some combination of those. Therefore, we assign component identifiers to the components of r and s as follows:

Definition 5

The scheme for assigning component identifiers to the structures in two structural regions, r and s, that will be used to compute a spatial partition for use in computing set operations between r and s is as follows:

  1. i.

    faces in r are assigned a negative, even integer

  2. ii.

    holes in r are assigned a negative, odd integer

  3. iii.

    faces in s are assigned a positive, even integer

  4. iv.

    holes in s are assigned a positive, odd integer

Therefore, to construct a spatial partition from two input structural regions, we simply take each structure from an input region and assign it a relevant component identifier. The result is a set of simple regions, each with a corresponding component identifier. Computing spatial partitions essentially requires the building of a map overlay, this can be done with a plane sweep style algorithm, among other approaches, with time complexity O(nlgn + k) for n input line segments with k intersections. Such a spatial partition is equivalent to computing a map overlay which maintains the areal coverage of all input geometries. Because the term map overlay has multiple definitions in the literature, we will refer to a spatial partition built as described as a combination partition. Once a combination partition is computed, it contains all information needed to compute a set operation between input structural regions. Figure 4 depicts an example of two input structural regions with component with component identifiers and their resulting combination partition.

5 Building the desired operation

Constructing the intersection of two structural regions encoded in a combination partition is achieved through extracting relevant geometries from the combination partition and storing them in the appropriate set (i.e., the set of faces, holes, lines, or points) in a result structural region. We must extract the relevant portions with two goals, in particular, in mind:

  1. 1.

    The interpretation of the structural region resulting from a spatial operation over two input structural regions must be equivalent to the result of the same operation over the interpretation of the input regions, but must be represented in terms of simple geometries and expressed in terms of CIRs.

  2. 2.

    Spatial operations over structural regions are meant to support spatial operations over CIRs; thus, the result of a spatial operation over structural regions must contain the appropriate geometries to satisfy a motion function in a CIR and must contain information to construct a mapping of geometries from the resulting source region to the resulting destination regions.

The two goals listed above have two direct consequences on the design of the spatial operations over structural regions. First, the geometry of the result of a spatial operation over two complex regions is obvious in a combination partition built from the regions. What is less obvious is how to represent them in terms of simple geometries that form structural regions. For example, the intersection of the complex regions in Fig. 4 is visible in the combination partition as the portions of the input regions that overlap but that are not covered by holes. Because structural regions represent hole and face geometries separately and as simple geometries, we cannot build a structural region by simply extracting only portions of the combination partition that correspond to overlapping faces since such a geometry may be itself a complex region containing holes (a geometry in the face set of a structural region must be a simple region). Thus, we must ensure that only simple geometries are extracted. Consequently, if two faces from respective structural regions overlap in a combination partition, we must extract the entire overlapping portions of the faces (in the case of an intersection operation), regardless of the presence of holes, in order to ensure simple geometries are extracted. Therefore, if we are computing an intersection using the combination partition in Fig. 4, one geometry will be extracted to represent the entire intersecting portion of the simple regions defining face {2} and face {−2}, and one geometry will be extracted to represent the entire intersecting portion of the simple regions defining face {−4} and {2}. Separate hole geometries will be extracted to remove the portions of those face intersections that are covered by holes in the input, rather than directly representing the faces as containing holes.

Note that when extracting hole geometries to form the intersection of the structural regions in Fig. 4, we have some choices. Face {2} and {−2} intersect in the simple region covering all areas whose label’s contain the subset {−2, 2}, and hole geometries then intersect that simple region and are labeled with a superset of {−2, 2}. The geometries with a label that is a superset of {−2, 2} are labeled {−2,−3, 2}, {−2, 2, 3}, and {−2, −3, 2, 3}. The question that arises is then: “What combination of these geometries must be stored in the result structural region to satisfy the two goals listed above?”. Obviously, storing all three of them satisfies goal 1 in this case, but goal 2 forces more care in this situation. The label {−2,−3,2,3} is a superset of both of the other hole labels. Because holes are defined by simple regions, it follows that the hole {−2, −3, 2, 3} is completely contained by both of the other holes. It may be that we only need to keep the holes with labels {−2, −3, 2} and {−2, 2, 3}, but it may also be the case that we need all three. We will clarify this point when the details of the intersection operation are provided in the next section. At this point, it is important to note that all relevant geometries can be identified in the combination partition.

With the goals of building a result structural region for a spatial operation in mind, we must make some final remarks on expected implementation. The general approach to building an operation is to examine the labels in a spatial partition constructed from structural regions that are labeled with the scheme in Definition 5. We assume that the components of structural regions are implemented as polygonal curves. Furthermore, the labels associated with each region in the spatial partition are stored as integers associated with the line segments that define those polygonal curves. Each line segment consists of 2 end points and two labels: LA contains the component identifiers of all components in the input structural region whose interior lies immediately above (or to the left in case of a vertical) of the segment, and LB contains the component identifiers of all components in the input structural region whose interiors lie below (or to the right) of the segment. Note that labels may contain multiple component identifiers; thus, LA and LB are sets:

Definition 6

A line segment consists of two points and two labels:

$$(x_{1},y_{1}),(x_{2},y_{2}),LA, LB | x_{1},y_{1},x_{2},y_{2} \in \mathbb{R} \wedge LA,LB \in 2^{\mathbb{Z}}$$

We use the notation l L A and l L B to refer to the labels of line segment l. A combination partition is represented as a set of line segments for implementation purposes.

We develop the specification of set operations in two steps: i) identify the labels of structures we wish to extract from a combination partition, then ii) specify the method to extract those structures. The first step is operation specific, and is specified independently for the intersection, union, and difference operations. The second step is general, and is specified at the end. In the following, we use the notation that structural regions R and S are used to build a combination partition π R S to compute some operation, the result of which will be structural region Q. Let R F be the set of labels of faces from r, R H be the set of labels of holes from r, S F be the set of labels of faces from s, and S H be the set of labels of holes from s. For example, If R is the spatial partition in Fig. 4a, then:

$$R_{F} = \{ \{-2\},\{-4\} \} $$
$$R_{H} = \{ \{-3\} \} $$

For the remainder of this paper, the term label will always refer to a set of integers.

5.1 Intersection

Intuitively, the intersection of two regions consists of all the area that is covered by the interiors of both input regions, and none of the area covered by exactly 1 of the input regions or none of the input regions. Because structural regions represent holes and faces as separate structures, we must identify the portions of face structures that must be in the result and the portions of hole structures that must be in the result. Again, since faces and holes in structural regions are simple objects, we handle them separately.

To build the structural region Q that is the intersection of S and R from π R S , we first need to identify face structures for Q. Any area covered by a pair of faces, one face from each respective region, must be added as a face structure to Q. We identify such areas based on the labels of line segments in π R S . Let L be a label associated with a line segment k in π R S . If the interior of two faces, one from S and one from R, lie on the side of k to which L corresponds, then L will contain the component identifiers of both of those faces. Thus, for any label L on line segment k, pairs of intersecting faces are discovered by finding all pairs of component identifiers where one label is in the set R F and the other is in the set S F .

Definition 7

F I (L) is the set of sets of component identifiers contained in a label L on a line segment in combination partition π R S that identify faces that must be in the structural region Q that results from computing the intersection of structural regions R and S.

Let L be a label on a line segment in π R S :

$$F_{I}(L) = \{\{l_{1}, l_{2}\} | l_{1},l_{2} \in L \wedge l_{1} \in R_{F} \wedge l_{2} \in S_{F} \} $$

Because holes in a structural region are represented as simple regions enclosing exterior space, the holes relevant to the intersection of R and S are only those that interact with the intersection of two faces, one from each respective input region. Therefore, the label of a hole structure relevant to the intersection of R and S in a label L on a line segment in π R S contains a hole component identifier from either R or S and a label in an element of F I :

Definition 8

H I (L) is the set of sets of component identifers contained in a label L on a line segment in combination partition π R S that identify holes that must be in the structural region Q that results from computing the intersection of structural regions R and S.

Let L be a label on a line segment in π R S :

$$\begin{array}{@{}rcl@{}} H_{I}(L) &=& \{\{l_{1},l_{2},l_{3}\} | \{l_{1},l_{2},l_{3}\} \in L \wedge \{l_{1},l_{2}\} \subseteq F_{I}(L) \wedge l_{3} \in R_{H} \cup S_{H} \\&&\wedge (l_{3} \in R.F2H(l_{1}) \vee l_{3} \in S.F2H(l_{2})) \} \end{array} $$

For example, the labels of the structures corresponding to the intersection of the structural regions encoded in Fig. 4c are the face labels {−2, 2} and {−4, 2} and the hole labels {−2, −3, 2} and {−2, 2, 3}. The final step is to create the F2H mapping of the result region. Because holes are only applied to faces to which they are mapped in their F2H mapping, the labels of the result region reflect the mappings from the input regions. Therefore, in the result, a hole label l h identifies a hole structure in a face structure with label l f iff l f ⊆ l h and the hole component identifier in l h is associated with either face identifier in the respective input F2H mapping . This follows directly from the fact that face and hole structures are simple regions; thus, a label containing a hole ID in conjunction with a face ID indicates a hole within that face. The face to hole mapping for the result of the intersection operation used in our example is then: {−2, 2} → {{−2, −3, 2}, {−2, 2, 3}}; {−4, 2} → ∅.

5.2 Difference

The difference of two regions consists of all area covered by the interior of exactly 1 region. We define difference as the non-symmetric difference operation. One is tempted to define schemes for identifying labels of structures in a combination partition that are unique to the difference operation; however, we cannot do this because structural regions must contain simple geometries. The label identification scheme for the intersection operation is inclusive, in the sense that it only identifies labels to put into the F I and H I set. The consequence is that since no structures that go into the combination partition contain holes (they are all defined as simple regions), any are covered by a single label will not have holes. The temptation for difference is, for example, to collect face labels from a label L on a line segment if that label contains a face component identifier from one input structural region, and does not contain a face identifier from the other input. If a face from one input structural region contains a face from the other input structural region, we will have identified a complex (as opposed to a simple) geometry since it contains a hole. Complex schemes may be able to handle this situation, but our contribution is to create a generic solution for all set operations that does not rely on special cases. Thus, we use De Morgan’s laws to compute difference and union operations using the definitions defined for intersection.

The difference between two sets, A and B, according to De Morgan’s laws, is equivalent to the intersection of the first set and the complement of the second set:

$$A-B = A \cap B^{C}$$

where B C is the complement of B. Because structural regions utilize labels to indicate faces and holes, computing the complement of a structural region S within a combination partition is simply a matter of altering labels: faces are relabeled to reflect hole labels and holes are relabeled to effect face labels. Complementing a structural region does require that the entire exterior of the region being complemented become a face as well. The notion of complementing the exterior seems to indicate a special case in that the exterior is treated differently than face and hole portions of a structural region; however, the definition of structural regions supports an implicit face covering the universe as well as an implicit hole that covers the universe that applies only to the face covering the universe according to the F2H mapping. We denote these structures the external face and external hole, and assume they are present in all structural regions. Because the external hole is equivalent to the external face, they have no practical effect for a structural region, but their presence simplifies operations under complement.

figure d

Algorithm 1 lists the steps to compute the complement of structural region S encoded in a combination partition π R S built from structural regions R and S. The algorithm proceeds by examining each label for each line segment in combination partition π R S . If a label contains face labels for S, they are all converted to hole labels, and mapping M F of face labels to hole labels records the conversion (Lines 6-8). If a label contains hole labels from S, those labels are converted to face labels and the mapping M H of hole labels to face labels records the conversion (lines 9-11). The face to hole mapping for the complement is computed by using S’s F2H mapping and the conversion mappings M F and M H in lines 12-14. Lines 15-18 add the external face and hole labels.

Because structural regions have a defined interpretation, the creation of a complement of a structural region requires a complemented interpretation. Recall that the region represented by a structural region is defined as the union of all face structures minus the union of all hole structures; in effect, faces impose positive space on an embedding space and holes represent negative space which is removed from the positive space. The complement of this definition implies that hole structures are positive space and face structures are negative space; furthermore, instead of negative space removing area from positive space, positive space adds relevant area to negative space under complement. The effect is that faces in a complement are only relevant if they overlap a hole to which they map in the face to hole mapping \(M_{F\rightarrow H}^{c}\), meaning that a face label under a complement will always be paired with a mapped hole label if it is relevant to an operation. For example, Fig. 4b shows a structural region in a combination partition. Under traditional interpretation, the hole (negative space) is removed from the face (positive space). Under the complement of the region, the original face becomes a hole and the original hole becomes a face; clearly, the hole in the complement contains the face complement such that if the hole area is removed from the face area, an empty region is the result. Thus, the differing interpretation under complement is required.

Figure 5 depicts an example in which the combination partition in Fig. 4 is shown after labels have been altered to complement the region with positive labels. The label x f is used for the external face under the complement and the label x h is used for the external hole under complement. The external structures permeate the entire space, since all faces and holes are required to be simple regions. Let R be the region with negative labels, and S be the original region with positive labels. R − S = R∩S C. Thus, we simply compute the intersection based on the labels in Fig. 5. There is one caveate when computing the intersection with a complement: as discussed previously, a face in a complemented region affects the result only if it overlaps a hole to which it maps in the face to hole mapping. Thus, any face label required in the intersection formulas corresponding to a face in the complement region is only applicable if the label contains a hole to which it maps. With this one caveat, face labels in Fig. 5 with respect to the intersection definition are: {−2, x f , x h }, {−4, x f , x h }, {−2, 6, 7}, and the hole labels are: {−2, −3, x f , x h }, {−2, −3, 6, 7}, {−2,7, x f , x h }, {−4, 7, x f , x h }. Once the labels are computed, they can be converted back to their original labels so structures may be identified in the original combination partition. To convert labels, one simply reverses the effects of Algorithm 1; the external face and hole labels are ignored and the remaining complemented labels are un-complemented. The result is the face labels {−2}, {−4}, {−2, 2, 3} and hole labels {−2, −3}, {−2, −3, 2, 3}, {−2, 2}, {−4, 2}. Figure 6 depicts the components identified by those labels.

The face to hole mapping for the result of the difference operation used in our example is computed identically to the intersection operation, with the result: {−2}→{{−2,−3},{−2,−3,2,3}}; {−4}→{{−4,2}}; {−2,2,3}→{{−2,−3,2,3}}. Thus, the result of the R − S operation is shown in Fig. 6.

Fig. 5
figure 5

The combination partition from Fig. 4 where region R is Fig. 4a, region S is Fig. 4b, and with labels reflecting the complement of S. Under the complement, S F ={{6},{x f }} and S H ={{7},{x h }}

Full size image
Fig. 6
figure 6

The components of the combination partition identified by the labels collected during the difference operation using the complemented region in Fig. 5. The labels are converted back to their non-complemented state as they appear in Fig. 4. The final, shaded region depicts the interpretation of the result of the difference operation (union of faces minus union of holes)

Full size image

5.3 Union

As with the difference operator, the union may be represented in terms of intersection and complement operations according to De Morgan’s laws. The union of two sets A and B is equivalent to the following:

$$A \cup B = (A^{C} \cap B^{C})^{C} $$

There is only one additional complexity in the union computation: the final step is to take the complement of the result of the intersection operation that identifies sets of labels corresponding to structures in the combination partition. Those sets are F I and H I , and represent structures that are holes and faces, respectively. The complement algorithm applies to the labels in the combination partition, but not the sets F I and H I as a whole, thus the complement of the result of the intersection must also switch the sets F I and H I (i.e., faces become holes and holes become faces in the complement.

For example, the complement of both input structural regions from Fig. 4 is shown in Fig. 7. Taking the intersection, with the caveat that faces are only applicable if they exist with a hole to which they are mapped (as with the difference operation) results in

$$\begin{array}{@{}rcl@{}} F_{I}&=&\{ \{x_{f},x_{h},y_{f},y_{h}\}, \{-8,-9,x_{f},x_{h}\}, \{6,7,y_{f},y_{h}\},\{\-8,-9,6,7\}\}\\ H_{I}&=&\{ \{x_{f},x_{h},y_{f},y_{h},-9\},\{x_{f},x_{h},y_{f},y_{h},-11\},\{x_{f},x_{h},y_{f},y_{h},7\},\\ &&\{-8,-9,x_{f},x_{h},7\},\{6,7,y_{f},y_{h},-9\}\} \end{array} $$
Fig. 7
figure 7

The combination partition from Fig. 4 with labels reflecting the complement of both regions. x f and x h are the exterior face and hole labels for the region with positive labels, y f and y h are the exterior face and hole labels for the region with negative labels

Full size image

We apply the complement algorithm to those labels and the combination partition, and switch the F I and H I sets to verify the final result. We will assume for clarity that structure identifiers will return to their original values:

$$\begin{array}{@{}rcl@{}} H_{I}&=&\{ \{-3,-2\},\{2,3\},\{-3,-2,2,3\}\}\\ F_{I}&=&\{\{-2\},\{-4\},\{2\},\{-3,-2,2\}\{2,3,-2\}\} \end{array} $$

The face to hole mapping is constructed identically to the other operations. An image of the final result is shown in Fig. 8.

Fig. 8
figure 8

The components of the combination partition identified by the labels collected during the union operation using the complemented regions as shown in Fig. 7. The labels in this figure are converted back to their non-complemented state as they appear in Fig. 4. The final, shaded region depicts the interpretation of the result of the union operation

Full size image

6 Extracting the desired structures

Section 5.1 through Section 5.3 describe a mechanism to identify the structures in a combination partition that pertain to the result of an operation. The final step is to extract the faces, holes, lines, and points that make up those structures in order to build the result structural regions. Recall that combination partitions are defined by segments carrying labels. Each label indicates the component identifiers of all components of the input structural region whose interiors lie on the side of the line segment to which the label corresponds (i.e., above or below). The result of the procedures described in Section 5.1 through Section 5.3 is a set of labels indicating structures in the combination partition that must be extracted in order to create the structural region corresponding to the result of the desired operation. Because all operations are defined in terms of the intersection operation, we are able to define the procedures to extract structures from a combination partition that represent the result of a set operation using Definitions 7 and 8. The following sections describe how to extract the desired structures (Fig. 8).

6.1 Extracting faces and holes

Extracting the faces and holes corresponding to the result of an operation over a combination partition is straightforward. In order to extract the simple region corresponding to a label, one must collect line segments from the combination partition that carry the desired label as a subset of the LA set or LB set, but not both. This follows directly from the fact that a line segment must separate the interior of a simple region from its exterior. A line segment with the desired label as a subset of both LA and LB will lie in the interior of the desired simple region. This procedure allows one to extract both face and hole structures. For example, the result of the union operation in Section 5.3 is depicted in Fig. 8. One can verify the process by looking at the line segments involved with the face label {−3, −2, 2}.

Algorithm 2 defines a procedure to extract the relevant simple regions from a combination partition that define the result of an operation. The algorithm takes a set of labels that represent the desired simple regions to extract as input. The algorithm proceeds by visiting each line segment in the combination partition; each line segment is checked to see if it bounds a region with a desired label, and recorded in a hash table along with its appropriate label for each region it bounds. One important note is that the extracted regions will not have holes, since the desired labels are computed based on the intersection operation, but a region corresponding to a label may have multiple faces. A final post-processing step is required to identify the individual faces of each extracted region. For an input of n line segments and m labels of regions to extract, the time complexity is clearly O(n m) due to the nested loop structure. However, m tends to be very small in practice, and the algorithm is easily parallelizable in the case of larger m.

Figure 9 depicts an example scene. Algorithm 2 results in a hash table that maps the label {−6,2} to the set of 3 line segments defining the triangle surrounding the label {−6,2}. The previous example scenes show more complex interactions of faces and holes.

figure e
Fig. 9
figure 9

A combination partition where faces intersect at point structures, line structures, and face structures. The solid lined geometry is one structural region and the dotted line geometry is a second structural region. Both regions’ structures are labeled

Full size image

6.2 Extracting lines

It is possible that two faces from opposing structural regions meet along a line. In many formulations of spatial set operations, such lines are ignored; however, in our application we are using the results of these set operations to create interval regions so we must identify such lines. Over a time interval, two simple regions may begin such that they meet along a line, but do not have overlapping interiors. Over the course of the interval, they could then move over each other such that they have overlapping interiors. The intersection of two such interval regions will begin with a line from which the intersection emerges over the time interval. Again, since all operations are composed as intersection operations, we only need to handle the identification of such lines under intersection. We denote these lines intersection line segments.

The algorithm to find intersection line segments, shown in Algorithm 3, is similar in structure to Algorithm 2. The algorithm takes a combination partition as input. Because each set operation makes use of the intersection operation, we construct the algorithm around computing the F I and H I sets of labels on line segments. Each line segment is examined individually. For each line segment, the LA and LB labels are merged under a union operation into set X to reveal all labels interacting with the line segment (lines 2-3). If the line segment is an intersection line segment between two simple regions, it will contain a label L in the set F I (X) indicating an intersection of both of those regions (line 4). If the segment truly separates those two regions, the label L will not exist in either LA or LB for that segment, since the interiors of the corresponding region lie respectively on one side of s (recall the labels in F I (X) will all contain two component identifiers) (line 5). Intersection line segments involving holes are computed similarly (lines 7-9), except that holes must interact with a face. Any intersection line segments are added to the the hash table h s which maps the face or hole label to the set of segments to which it corresponds. The time complexity is identical to Algorithm 2 for the same reasoning.

Figure 9 includes a configuration where two faces meet along a line. The identification of face labels on the set L A∪L B corresponding to the line where the area labeled $2$ and the area labeled {−4} meet will result in the label {2,−4} that resides in neither the LA or LB set individually. Therefore, the hash table h l will map the label {2,−4} to that line segment.

figure f

6.3 Extracting points

Finally, the result of a set operation over two structural regions may result in a pair of faces or a pair of holes intersecting at a point. Again, this represents the case when two simple regions, representing either a pair of faces or holes, each from a respective input structural regions, alter their topological configuration over a time interval from meeting at a point to overlapping (or from overlapping to meeting at a point). We denote such points as intersection points. Discovering intersection points is more complex than discovering intersection line segments because an intersection line segment may be identified by examining a single segment. Because a combination partition does not contain line segments that intersect within segment interiors, intersection points will always be line segment end points. The algorithm to find intersection points is shown in Algorithm 4. The first step is to create a mapping of segment end points to a label containing the union of all LA and LB labels of all segments containing the point (lines 3-4). We use a hash table h p2L to implement the mapping. We then iterate over every point. For each point p, we calculate the face labels in the set F I (h p2L [p]) to find the possible faces that may intersect at that point (line 6). p is then an intersection point only if p is not an endpoint in an intersection line for the same face label and it is not an endpoint in a line segment in a face with the same label (lines 7-10). The same process is repeated for holes (lines 11-16), but again, a hole must interact with a face (line 14).

figure g

Figure 9 depicts a scene where a face of one structural region meets the face of another structural region at a point. The face with the label {−2} meets the face with the label {2} at point p. The algorithm will first create the entry in the h p2L hash table to map p to the labels of all segments that include p, which results in the label {−2, 2}. {−2, 2} forms a face label under intersection, and p is not an endpoint of any line segment forming a face, hole, or intersection line segment in the intersection of the two structural regions; therefore, it is an intersection point.

7 Applying the operations to interval regions

The details of the algorithms presented up to this point deal with structural regions; the final step in computing set operations over component moving regions is to connect the results of operations over structural regions across a time interval to form an interval region. Recall that the input to a set operation will be an interval region that is aligned, meaning that the topological relationship between any two structures in the input interval regions will not change except at the beginning and ending instant of the time interval. For example, Fig. 10 depicts a scene where a combination partitions have been created from two input CIRs. The combination partition at the earlier time is identical to Fig. 9. In this section, we walk through the building of a result CIR by computing the intersection of the CIRs in Fig. 10.

Fig. 10
figure 10

The combination partitions formed by two CIRs, one with a solid boundary and one with a dotted boundary. In this example, the input regions contain only faces

Full size image

For the purposes of notation, we will refer to face and hole structures by their labeling in Fig. 10. Let p s the point at which the faces with labels {−2} and {2} meet in the source regions, and let s be the line segment where the faces with labels {−4} and {2} meet in the source regions. Let p d be the point at which the faces {−6} and {2} meet in the destination regions. Therefore, the first input CIR across the time interval 1 − 2 is:

$$\begin{array}{ll} t_{s} =& 1\\ t_{d} = &2 \\ s = & (F = \{\{2\}\}\\ &H = \emptyset \\ &L = \emptyset \\ &P = \emptyset \\ &F2H = \emptyset ) \\ d = &(F = \{\{2\}\}\\ &H = \emptyset \\ &L = \emptyset \\ &P = \emptyset \\ &F2H = \emptyset ) \\ M =& (\{2\} \rightarrow \{2\})\\ \end{array} $$

The second input CIR is:

$$\begin{array}{ll} t_{s} =& 1\\ t_{d} = &2 \\ s = & (F = \{\{-2\},\{-4\},\{-6\}\}\\ &H = \emptyset \\ &L = \emptyset \\ &P = \emptyset \\ &F2H = \emptyset ) \\ d = &(F = \{\{-2\},\{-4\},\{-6\}\}\\ &H = \emptyset \\ &L = \emptyset \\ &P = \emptyset \\ &F2H = \emptyset ) \\ M =& (\{-2\} \rightarrow \{-2\}),(\{-4\} \rightarrow \{-4\})(\{-6\} \rightarrow \{-6\})\\ \end{array} $$

In this example, identical component identifiers are used across the time interval; however, this is not necessary since the mapping M associates the source and destination structures across the interval. Extracting the structures for the result of an intersection operation results in the identification of p s , s, and the face with the label {−6, 2} in the source region and and p d and the face with the label {−4, 2} in the destination region; Fig. 11 depicts those structures. The final step is to create the mapping M in the result CIR. This step is where the fact that we have aligned the input CIRs such that no structures change their respective topological relationships with each other during the interior of a time interval becomes very useful. It follows from the fact that the input is aligned that if two structures intersect at the earlier time instant in an interval, they will also intersect at the later time instant, unless they are disjoint across the time interval. Therefore, if a structure with a label indicating the intersection of two input structures must exist on both ends of the resulting time interval, or that structure simply does not exist in the interior of the time interval. For example, the line segment we have denoted s in Fig. 11 is identified as an intersection of face {2} and face {−4}. A structure at the end of the interval also is an intersection of the faces that those faces in the source region map to. Thus, the mapping M, is constructed simply by mapping structures to their associated structures across the time interval based on the labelling scheme. In this case, the structures were identically labeled across the interval, but that is not necessary since the association between structures is stored in the mapping. Because the point p s does not map to anything on the other side of the time interval, it does not exist within the interval. Therefore, the result CIR is:

$$\begin{array}{ll} t_{s} =& 1\\ t_{d} = &2 \\ s = & (F = \{\{-6,2\}\}\\ &H = \emptyset \\ &L = \{s\} \\ &P = \emptyset \\ &F2H = \emptyset ) \\ d = &(F = \{\{-4,2\}\}\\ &H = \emptyset \\ &L = \emptyset \\ &P = \{p_{d}\} \\ &F2H = \emptyset ) \\ M =& (\{-6,2\} \rightarrow p_{d}),(s \rightarrow \{-4,2\})\\ \end{array} $$
Fig. 11
figure 11

The geometries identified when computing the intersection operation on the input in Fig. 10

Full size image

The interpolated movement of the resulting CIR is shown in Fig. 12.

Fig. 12
figure 12

The result of the intersection operation for the input in Fig. 10. The movement of geometries across the interval is depicted

Full size image

The final step is to construct the mapping of structures across a time interval. The construction of the mapping is trivial since the mappings from the input interval regions are known and the structure identifiers used in labels in the combination partitions come from the structure identifiers used in mappings of the input interval regions.

8 Implementation

We have implemented a prototype of the algorithms presented in this paper as a proof of concept and included them in the the Pyspatiotemporalgeom library available at [9]. The library currently implements the intersection algorithm for two CIRs. The intersection algorithm between CIRs is chosen since the other set operations are based on the intersection operation, and the complexity of the algorithm lies in handling CIRs. The library is a pure python library and is written as reference implementation; as such, it is not optimized for speed. Figure 13a depicts the source and destination structural regions of two CIRs: one is red and the other is green. The red region does not move over the time interval, but the green region moves and deforms as it travels. The triangles representing the motion of the individual line segments are shown in Fig. 13b. Figure 13c depicts the structural regions at the boundaries of the interval regions defining the intersection of the input. Note that the intersection begins at a single point at the earliest time instant and grows into a region. A simplistic example is chosen since even simple examples can result in output that is difficult to read clearly in a static image. Furthermore, the triangles indicating the motion of the individual line segments in the result are omitted since their inclusion causes the image to be so cluttered that its usefulness is limited.

Fig. 13
figure 13

A red and green CIR used as input to an intersection operation (a), the same regions with the motion of the lines drawn (b), the structural regions at the interval region boundaries of the result of the intersection operation

Full size image

9 Conclusion

In this paper, we have developed a mechanism to implement set operations between CIRs. At each time interval, the algorithm takes O(nlgn + k) time for two CIRs with n line segments and k intersections among line segments to compute combination partitions. Once combination partitions are known, the labels on line segments must be examined using a variety of algorithms, all with time complexity O(n m) where n is the number of line segments in a combination partition and m is the number labels of structures that must be extracted. In practice, in geographic data sets in particular, m is small. We have also implemented the algorithms and shown their behavior on sample input. This work affirms the claim of the CMR model of moving regions that operations over moving regions in the model are relatively easy to implement and use well known algorithmic primitives with known, and efficient, time complexities. This work paves the way for spatiotemporal analysis systems that can fully make use of moving region data. Future work includes extending the reference implementation to compute all the set operations and other operations and predicates over CMR regions. High performance implementations of the algorithms should be investigated, as well as a web-accessible interface to the algebra, data sets, and tutorials.