New plane-sweep algorithms for distance-based join queries in spatial databases

Abstract

Efficient and effective processing of the distance-based join query (DJQ) is of great importance in spatial databases due to the wide area of applications that may address such queries (mapping, urban planning, transportation planning, resource management, etc.). The most representative and studied DJQs are the K Closest Pairs Query (KCPQ) and εDistance Join Query (εDJQ). These spatial queries involve two spatial data sets and a distance function to measure the degree of closeness, along with a given number of pairs in the final result (K) or a distance threshold (ε). In this paper, we propose four new plane-sweep-based algorithms for KCPQs and their extensions for εDJQs in the context of spatial databases, without the use of an index for any of the two disk-resident data sets (since, building and using indexes is not always in favor of processing performance). They employ a combination of plane-sweep algorithms and space partitioning techniques to join the data sets. Finally, we present results of an extensive experimental study, that compares the efficiency and effectiveness of the proposed algorithms for KCPQs and εDJQs. This performance study, conducted on medium and big spatial data sets (real and synthetic) validates that the proposed plane-sweep-based algorithms are very promising in terms of both efficient and effective measures, when neither inputs are indexed. Moreover, the best of the new algorithms is experimentally compared to the best algorithm that is based on the R-tree (a widely accepted access method), for KCPQs and εDJQs, using the same data sets. This comparison shows that the new algorithms outperform R-tree based algorithms, in most cases.

1 Introduction

A Spatial Database is a database system that offers spatial data types in its data model and query language, and it supports spatial data types in its implementation, providing at least spatial indexing and efficient spatial query processing [2]. In a computer system, these spatial data are represented by points, line-segments, regions, polygons, volumes and other kinds of 2-d/3-d geometric entities and are usually referred to as spatial objects. For example, a spatial database may contain polygons that represent building footprints from a satellite image, or points that represent the positions of cities, or line segments that represent roads. Spatial databases include specialized systems like Geographical databases, CAD databases, Multimedia databases, Image databases, etc. Recently, the role of spatial databases is continuously increasing in many modern applications; e.g. mapping, urban planning, transportation planning, resource management, geomarketing, environmental modeling are just some of these applications.

The most basic use of such a system is for answering spatial queries related to the spatial properties of the data. Some typical spatial queries are: point query, range query, spatial join, and nearest neighbor query [3]. One of the most frequent spatial queries in spatial database systems is the spatial join, which finds all pairs of spatial objects from two spatial data sets that satisfy a spatial predicate, 𝜃. Some examples of the spatial predicate 𝜃 are: intersects, contains, is_enclosed_by, distance, adjacent, meets, etc. [4]; and when 𝜃 is a distance, we have distance-based join queries (DJQ). The most representative and studied DJQ in the spatial database field are the K Closest Pairs Query (KCPQ) and εDistance Join Query (εDJQ). The KCPQ combines join and nearest neighbor queries: like a join query, all pairs of objects are candidates for the final result, and like a nearest neighbor query, the K Nearest Neighbor property is the basis for the final ordering [5, 6]. The ε DJQ, also known as Range Distance Join, also involves two spatial data sets and a distance threshold ε, and it reports a set pairs of objects, one from each input set, that are within distance ε of each other. DJQ are very useful in many applications that use spatial data for decision making and other demanding data handling operations. For example, we can use two spatial data sets that represent the cultural landmarks and the most populated places of the United States of America. A KCPQ (K = 10) can discover the 10 closest pairs of cities and cultural landmarks providing an increasing order based on their distances. On the other hand, a εDJQ (ε = 10) will return all possible pairs (populated place, cultural landmark) that are within 10 kilometers of each other.

The distance functions are typically based on a distance metric (satisfying the non-negative, identity, symmetry and Δ-inequality properties) defined on points in the data space. A general distance metric is called L _t -distance or Minkowski distance between two points, in the d-dimensional data space, D^d. For t = 2 we have the Euclidean distance, for t = 1 the Manhattan distance and for $t = \infty$ the Maximum distance. They are the most known L _t -distances. Often, the Euclidean distance is used as the distance function but, depending on the application, other distance functions may be more appropriate. The d-dimensional Euclidean space, E^d, is the pair $(\mathrm {D}^{d}, \mathrm {L}_{2})$. That is, E^d is D^d with the Euclidean distance L ₂. In the following we will use dist instead of L ₂ as the Euclidean distance between two points in E^d and this will be the basis for DJQs studied on this paper.

One of the most important techniques in the computational geometry field is the plane-sweep algorithm which is a type of algorithm that uses a conceptual sweepline to solve various problems in the Euclidean plane, E², [7]. The name of plane-sweep is derived from the idea of sweeping the plane from left to right with a vertical line (front) stopping at every transaction point of a geometric configuration to update the front. All processing is carried out with respect to this moving front, without any backtracking, with a look-ahead on only one point each time [8]. The plane-sweep technique has been successfully applied in spatial query processing, mainly for intersection joins, regardless whether both spatial data sets are indexed or not [9]. In the context of DJQ the plane-sweep technique has been used to restrict all possible combinations of pairs of points from the two data sets. That is, using this technique instead of the brute-force nested loop algorithm, the reduction of the number of Euclidean distances computations has been proven [6, 10], and thus the reduction of execution time of the query processing.

It is generally accepted that indexing is crucial for efficient processing of spatial queries. Even more, it is well-known that a spatial join is generally fastest if both data sets are indexed. However, there are many situations where indexing does not necessarily pay off. In particular, the time needed to build the index before the execution of the spatial query plays an important role in the global performance of the spatial database systems. For instance, if the output of a spatial query serves as input to another spatial query, and such an output is not reused several times for subsequent spatial queries, then it may not be worthwhile to spend the time for building a new index. This is especially emphasized for spatial intersection joins that make use of indexes which need a long time to be built (e.g. R*-tree [11]) [12]. For the previous reasons, the time necessary to build the indexes is an important constraint, especially if the input data sets are not used often for spatial query processing. Thus the main motivation of this article is to propose new algorithms for DJQs (the KCPQ and εDJQ) on disk resident data, when none inputs are indexed, and to study their behavior in the context of spatial databases. Our proposal is also motivated by the work of [13, 14] for spatial intersection joins.

Nowadays, the unnecessity of indexes for query processing is not infrequent in practical applications, when the data sets change at a very rapid rate, or the data sets are not reusable for subsequent queries and the use of indexes can be omitted. Moreover, disk-based solutions are necessary, since main memory of a computing system is, in many cases, shared among applications, and it is usually not enough to hold big data (although, main memory increases in size and decreases in cost, acquired data increase at higher rates than main memory, for example, scientific data). As a possible application scenario, consider cadastre, or urban planning very big data sets with spatial and non-spatial characteristics. Big subsets of the data sets may be formed by considering certain (mainly non-spatial) characteristics of the stored properties, or buildings (like, properties owned by the state, buildings higher than 50 meters, constructions older than 50 years, or built under an obsolete anti-seismic construction standard, non build-up large areas, etc). These (big and non-storable in main memory) subsets are dynamic, or non-reusable, in the sense that an engineer, or an official may create them by setting conditions for certain characteristics, use them to answer a query, modify these conditions (and the created subsets), answer again this query, and so on. In the process of conducting a study, like an emergency planning study, the DJQ of interest might be to find pairs of buildings vulnerable by an earthquake and earthquake-safe public buildings that could temporarily host people, at a limited distance.

This paper substantially extends our previous work [1] and its contributions are summarized as follows:

• 1. We present theorems (the proofs of these theorems are included in [15]) regarding the correctness of both algorithms for KCPQ, that is, Classic Circle Plane-Sweep (CCPS) and Reverse Run Circle Plane-Sweep (RCPS) algorithms. They are the basis of the following algorithms for DJQ, when neither inputs are indexed and the data are stored on disk.

• 2. There are many contributions in the context of spatial intersection joins when both, one, or neither inputs are indexed. For DJQs most of the contributions have been proposed when both inputs are indexed (mainly using R-trees for KCPQ). For this reason, in this article we propose four algorithms (FCCPS, SCCPS, FRCPS and SRCPS) for KCPQs and their extensions for εDJQs for performing DJQs, without the use of an index on any of the two disk-resident data sets. These algorithms employ a combination of the plane-sweep algorithms (CCPS) and (RCPS) and space partitioning techniques (uniform splitting and uniform filling) to join the disk-resident data sets.

• 3. We present results of an extensive experimental study, that compares the performance (in terms of efficiency and effectiveness) of the proposed algorithms.

• 4. We also compare the performance (efficiency) of the best of the new algorithms to the best algorithm that is based on the R-tree (a widely accepted access method).

The rest of this paper is organized as follows. Section 2 defines the KCPQ and εDJQ, which are the queries studied on this paper, in the context of spatial databases. Moreover a classification of spatial join and distance-based join queries taking into account whether both, one, or neither inputs are indexed is presented. The Classic Plane-Sweep algorithm for DJQs is described in Section 3, as well as two improvements to reduce the number of distance computations. In Section 4, the new plane-sweep algorithm (Reverse Run Plane-Sweep, RRPS) for KCPQ is presented. In Section 5, we present and analyse the new plane-sweep-based algorithms for the KCPQ and εDJQ. Section 6 exposes the results of an extensive experimental study, taking into account different parameters for comparison. Moreover, Section 6 exposes the results of an extensive experimental comparison between the best of the new algorithms and the best R-tree based algorithm. Section 7 contains some concluding remarks and makes suggestions for future research.

2 Preliminaries and related work

Given two spatial data sets and a distance function to measure the degree of closeness, DJQs between pairs of spatial objects are important joins queries that have been studied actively in the last years. Section 2.1 defines the KCPQ and εDJQ, which are the kernel of this paper. Section 2.2 describes a classification of spatial join and distance-based join queries taking into account whether both, one, or neither inputs are indexed, along with the review of other recent contributions related to these DJQs.

2.1 K closest pairs query and εdistance join query

In spatial database applications, the nearness or farness of spatial objects is examined by performing distance-based queries (DBQs). The most known DBQs in the spatial database framework when just a spatial data set is involved are the range query (RQ) and the K Nearest Neighbors query (KNNQ). When we have two spatial data sets the most representative DBQ are the K Closest Pairs Query (KCPQ) and the εDistance Join Query (εDJQ). They are considered DJQs, because they involve two different spatial data sets and use distance functions to measure the degree of nearness between spatial objects. The former reports only the top K pairs, and the latter, also known as Range Distance Join, finds all the possible pairs of spatial objects, having a distance between ε ₁ and ε ₂ of each other (ε ₁ ≤ ε ₂). Their formal definitions for point data sets (the extension of these definitions to other complex spatial objects is straightforward) are the following:

Definition 1

(K Closest Pairs Query, K CPQ) Let P = {p ₀, p ₁,⋯ , p _n−1} and Q = {q ₀, q ₁,⋯ , q _m−1} be two set of points in E^d, and a natural number K ($K \in \mathbb {N}, K > 0$). The K Closest Pairs Query (K CPQ)) of P and Q ($KCPQ(P, Q, K) \subseteq P \times Q$) is a set of K different ordered pairs K C P Q(P, Q, K) = {(p _Z1, q _L1),(p _Z2, q _L2),⋯ ,(p _{Z K} , q _{L K} )}, with (p _{Z i} , q _{L i} ) ≠ (p _{Z j} , q _{L j} ), Z i≠Z j ∧ L i≠L j, such that for any (p, q)∈P×Q−{(p _Z1, q _L1),(p _Z2, q _L2),⋯ ,(p _{Z K} , q _{L K} )} we have d i s t(p _Z1, q _L1) ≤ d i s t(p _Z2, q _L2) ≤ ⋯≤d i s t(p _{Z K} , q _{L K} ) ≤ d i s t(p, q).

Definition 2

(ε Distance Join Query, ε DJQ) Let P = {p ₀, p ₁,⋯ , p _n−1} and Q = {q ₀, q ₁,⋯ , q _m−1} be two set of points in E^d, and a range of distances defined by [ε ₁, ε ₂] such that $\varepsilon _{1}, \varepsilon _{2} \in \mathbb {R}^{+}$ and ε ₁ ≤ ε ₂. The εDistance Join Query (ε DJQ) of P and Q ($\varepsilon \textit {DJQ}(P, Q, \varepsilon _{1}, \varepsilon _{2}) \subseteq P \times Q$) is a set which contains all the possible pairs of points (p _i , q _j ) that can be formed by choosing one point p _i ∈P and one point of q _j ∈Q, having a distance between ε ₁ and ε ₂ for each other: ε DJQ(P, Q, ε ₁, ε ₂) = {(p _i , q _j )∈P×Q:ε ₁ ≤ d i s t(p _i , q _j ) ≤ ε ₂}.

These two DJQs have been actively studied in the context of R-trees [5, 6, 10, 16]. However, when the data sets are not indexed they have attracted similar attention.

2.2 Related work

This section presents a classification of the spatial join and distance-based join queries depending on one, both or neither inputs are indexed. Moreover, other related DJQ are also revised in the recent literature, in order to show the importance of this type of query in the context of spatial databases.

2.2.1 Spatial join

Spatial data processing is well-known to be both data and computing intensive. The spatial join is one of the most studied spatial query, where given two datasets of spatial objects in Euclidean space, it finds all pairs of spatial objects satisfying a given spatial predicate, such as intersects, contains, etc [4]. Various techniques, such as minimizing disk I/O overheads in spatial indexing and the two phase filter-refinement strategy in spatial joins have been proposed in [9]. During the past decades many algorithms for spatial joins where the datasets reside on disk have been proposed in the literature [9, 17, 18] and recently, several contributions in the context of in-memory spatial join have been proposed. In [19], the authors have developed TOUCH, a novel in-memory spatial join algorithm, inspired with previous works on disk-based approaches and the requirements of the computational neuroscientists. It combines hierarchical data-oriented partitioning, batch processing and filtering concepts, with the target to decrease the number of comparisons, execution time and memory footprint of a spatial join process. In [20], a thorough experimental performance study of several (ten) spatial join techniques in main memory is reported. The techniques are first optimized for in-memory performance and then studied in the same framework. This study suggests that specialized join strategies over simple index structures, such as Synchronous Traversal over R-trees, should be the methods of choice for the considered cases. In [21], the authors re-implement the worst performing technique presented in [20] without changing the underlying high-level algorithm and the conclusion is that the resulting re-implementation is capable of outperforming all the other techniques. It means substantial performance gains can be achieved by means of careful implementation. Finally, in [22] a thorough review of a wide range of in-memory data management and processing proposals and systems is presented, including both data storage systems and data processing frameworks. The authors give a comprehensive presentation of important technology in memory management, and some key factors that need to be considered in order to achieve efficient in-memory data management and processing. In this paper, we are going to focus on disk-resident data, new algorithms for in-memory DJQs is a task for further research.

The spatial join is one of the most related and influential spatial queries with respect to DJQs in spatial databases and GIS. Depending on the existence of indexes or not, different spatial join algorithms have been proposed [23]. If both inputs are indexed, several contributions have been proposed, but the most influential one is the R-tree join algorithm (RJ) [24], due to its efficiency and the popularity of R-trees [11, 25]. RJ synchronously traverses both trees in a Depth-First order. Two optimization techniques were also proposed, search space restriction and plane-sweep, to improve the CPU speed and to reduce the cost of computing overlapping pairs between the nodes to be joined, respectively.

Most research after RJ, focused on spatial join processing when one or both inputs are non-indexed. In this category, the paper that is most closely related to our work is [14], where several spatial joins strategies when only one input data set is indexed are investigated. The main contribution is a method that modifies the plane-sweep algorithm. This approach reads the data pages from the index in a one-dimensional sorted order and inserts entire data pages into the sweep structure (i.e. in this case, one sweep structure will contain objects, while another sweep structure will contain data pages).

Directly related to this paper, when both data sets are non-indexed, are methods that involve sorting and external memory plane-sweep [12, 13], or spatial hash join algorithms [26], like partition based spatial merge join [27]. In [13] the Scalable Sweeping-Based Spatial Join, SSSJ, was proposed, that employs a combination of plane-sweep and space partitioning to join the data sets, and it works under the assumption that in most cases the limit of the sweepline will fit in main memory. In [27] a hash-join algorithm was presented, so called Partition Based Spatial Merge Join, that regularly partitions the space, using a rectangular grid, and hashes both inputs data sets into the partitions. It then joins groups of partitions that cover the same area using plane-sweep to produce the join results. Some objects from both sets may be assigned in more than one partitions, so the algorithm needs to sort the results in order to remove the duplicate pairs. Finally, [12] extends the SSSJ of [13] to process data sets of any size by using external memory, proposing a new join algorithm referred as iterative spatial join.

2.2.2 KCPQ and εDJQ

The problem of closest pairs has received significant research attention by the computational geometry community (see [28] for an exhaustive survey), when all data are stored into the main memory. However, when the amount of data is too large (e.g. when we are working with spatial databases) it is not possible to maintain these data structures in main memory, and it is necessary to store the data on disk. Here, we are going to review the KCPQ and εDJQ, focusing on whether the input data sets are indexed or not. We must emphasize that most of the contributions that have been published until now are focused on the case when both data sets are indexed on R-trees.

Remind that given two spatial data sets P and Q, the KCPQ asks for the K closest pairs of spatial objects in P×Q. If both P and Q are indexed by R-trees, the concept of synchronous tree traversal and Depth-First (DF) or Best-First (BF) traversal order can be combined for the query processing [5, 6, 16]. For a more detailed explanation of the processing of KCPQ-DF and KCPQ-BF algorithms on two R*-trees from the non-incremental point of view, see [6, 15]. In [16], incremental and non-recursive algorithms based on Best-First traversal using R-trees and additional priority queues for DJQs were presented. In [10], additional techniques as sorting and application of plane-sweep during the expansion of node pairs, and the use of the estimation of the distance of the K-th closest pair to suspend unnecessary computations of MBR distances are included to improve [16]. A Recursive Best-First Search (RBF) algorithm for DBQ between spatial objects indexed in R-trees was presented in [29], with an exhaustive experimental study that compares DF, BF and RBF for several distance-based queries (Range Distance, K-Nearest Neighbors, K-Closest Pairs and Range Distance Join). Recently, in [30], an extensive experimental study comparing the R*-tree and Quadtree-like index structures for K-Nearest Neighbors and K-Distance Join queries together with index construction methods (dynamic insertion and bulk-loading algorithm) is presented. It was shown that when data are static the R*-tree shows the best performance. However, when data are dynamic, a bucket Quadtree begins to outperform the R*-tree. This is due to, once the dynamic R*-tree algorithm is used, the overlap among MBRs increases with increasing data set sizes, and the R*-tree performance degrades.

In the case where just only one data set is indexed, recently in [31] a new algorithm has been proposed for KCPQs. The main idea is to partition the space occupied by the data set without an index into several cells or subspaces (according to the VA-File structure [32]) and to make use of the properties of a set of distance functions defined between two MBRs [6].

To the best og the authors knowledge, there are no papers in the literature of spatial databases that have addressed the problem of DJQs if both data sets are non-indexed, and for this reason this is the main motivation of this research work.

εDJQ, also known as Range Distance Join, is a generalization of the Buffer Query, which is characterized by two spatial data sets and a distance threshold ε, which permits search pairs of spatial objects from the two input data sets that are within distance ε from each other. In our case, the distance threshold is a range of distances defined by an interval of distance values [ε ₁, ε ₂] (e.g. if ε ₁ = 0 and ε ₂ > 0, then we have the definition of Buffer Query and if ε ₁ = ε ₂ = 0, then we have the spatial intersection join, which retrieves all different intersecting spatial object pairs from two distinct spatial data sets [9]). This query is also related to the similarity join in multidimensional databases [33], where the problem of deciding if two objects are similar is reduced to the problem of determining if two multidimensional points are within a certain distance of each other. In [34], the Buffer Query is solved for non-point (lines and regions) spatial data sets using R-trees, where efficient algorithms for computing the minimum distance for lines and regions, pruning techniques for filtering in a Depth-First search algorithm (performance comparisons with other search algorithms are not included), and extensive experimental results are presented. We must emphasize that there are no contributions in the literature of spatial databases for εDJQ when one or both inputs are non-indexed.

2.2.3 Other related distance-based join queries

Several DJQs have been studied in the literature which are related to KCPQ and εDJQ. In [35] a new index structure, called b R d n n−T r e e, to solve different distance-based join queries is proposed. Other variants of KCPQ have also been studied in the context of spatial databases. More specifically, approximate K closest pairs in high dimensional data [36, 37] and constrained K closest pairs [38] have been presented. In [39] the exclusive closest pairs problem is introduced (which is a spatial assignment problem) and several solutions that solve it in main memory are proposed, exploiting the space partitioning. In [40] a unified approach that supports a broad class of top-K pairs queries (i.e. K-closest pairs queries, K-furthest pairs queries, etc.) is presented. And recently, in In [41] an external-memory algorithm, called ExactMaxRS, for the maximizing range sum (MaxRS) problem is proposed. The basic processing scheme of ExactMaxRS follows the distribution sweep paradigm, which was introduced as an external version of the plane-sweep algorithm. Moreover, other related problem, the maximizing circular range sum (MaxCRS), is also studied and an approximation algorithm is presented, which uses the ExactMaxRS algorithm.

Other complex DJQs using R-trees have been studied in the literature of spatial databases, as Iceberg Distance Join [42], K Nearest Neighbors Join [43] queries, and closely related to DJQ processing is the All-Nearest-Neighbor (ANN) query [44]. For a more detailed review of this classification, see [15].

3 Plane-sweep in distance-based join queries

An important improvement for join queries is the use of the plane-sweep technique, which is a common technique for computing intersections [7]. The plane-sweep technique is applied in [8] to find the closest pair in a set of points which resides in main memory. The basic idea, in the context of spatial databases, is to move a line, the so-called sweepline, perpendicular to one of the axes, e.g. X-axis, from left to right, and processing objects (points or MBRs) as they are reached by such sweepline. We can apply this technique for restricting all possible combinations of pairs of objects from the two data sets. If we do not use this technique, then we must check all possible combinations of pairs of objects from the two data sets and process them. That is, using the plane-sweep technique instead of the brute-force nested loop algorithm, the reduction of CPU cost is proven (e.g. for intersection joins [12, 13, 24] and KCPQ [6, 10]).

3.1 Classic plane-sweep algorithm

In general, let’s assume that the spatial objects are points. The data sets are $\mathcal {P}$ and $\mathcal {Q}$ and they can be organized as arrays. Let’s also consider a distance threshold δ, which is the distance of the K-th pair found so far for the KCPQ (the initial value of δ is $\infty$), or the constant given maximum distance for the εDJQ. The Classic Plane-Sweep (CPS) algorithm consists of the following steps [1, 15]:

• 1. It sorts the entries of the two arrays of points, based on the coordinates of one of the axes in (e.g. X-axis) in increasing order.

• 2. After that, two pointers p and q are maintained initially pointing to the first entry for processing of each sorted array of points. Let the reference point be the point with the smallest X-value pointed by one of these two pointers, e.g. $\mathcal {P}$, then as reference point will be defined the p.

• 3. Afterwards, the reference point must be paired up with the points stored in the other sorted array of points (called comparison points, $q \in \mathcal {Q}$) from left to right, satisfying d x≡q.x−p.x < δ, processing all comparison points as candidate pairs where the reference point is fixed. After all possible pairs of entries that contain the reference point have been paired up (i.e. the forward lookup stops when d x≡q.x−p.x ≥ δ is verified), the pointer of the reference array is increased to the next entry, the reference point is updated with the point of the next smallest X-value pointed by one of the two pointers, and the process is repeated until one of the sorted array of points is completely processed.

Highlight that Classic Plane-Sweep algorithm applies the distance function over the sweeping axis (in this case, the X-axis, dx) because in the plane-sweep technique, the sweep is only over one axis. Moreover, the search is only restricted to the closest points with respect to the reference point according to the current distance threshold (δ). No duplicated pairs are obtained, since the points are always checked over sorted arrays.

Clearly, the application of this technique can be viewed as a sliding vertical area on the sweeping axis with a width equal to the δ value starting from the reference point (i.e. [0, δ] in the X-axis), where we only choose all possible pairs of points that can be formed using the reference point and the comparison points that fall into the current vertical area (see Fig. 1). This figure shows the points of the data set $\mathcal {P}$ marked with filled circles and the points of the data set $\mathcal {Q}$ marked with empty circles. Their coordinates are shown in, Tables 1 and 2. Note that the ticks on axes are put every two units of length for both dimensions.

Fig. 1

Classic Plane-Sweep Algorithm using sliding vertical area, window and semi-circle

Table 1 The data set $\mathcal {P}$ with 16 points in X-sorted order

Table 2 The data set $\mathcal {Q}$ with 12 points in X-sorted order

In the particular instance on Fig. 1, a reference point is shown, p = {1,(4,15)}, and it is marked by the horizontal arrow with solid line. All points of both sets on the left of p are already processed as reference points. The points Q ₁, Q ₂ on the right of the reference point according to the CPS (step 2) satisfy the requirement d x≡q.x−p.x < δ (step 3) and they are combined with p to create candidate pairs: the two empty circles located within the gray area which has a width equal to threshold δ. The first point of $\mathcal {Q}$ to the right of p which has dx-distance from p larger than δ, q = {3,(15,27)}, is marked by the arrow with dashed line. Once the algorithm reaches this point and calculates the dx-distance it will stop creating pairs with p and continues with the next iteration, setting as reference point q = {1,(7,16)}.

3.2 Improving the classic plane-sweep algorithm

The basic idea to reduce even more the CPU cost is to restrict as much as possible the search space near the reference point in order to avoid unnecessary distance computations (that involve square roots) which are the most expensive operations for DJQs. The proposed approach makes use of the plane-sweep technique and restricting of the search space.

The Classic Plane-Sweep algorithm applies the distance function only over the sweeping axis (X-axis) and for this reason some distances have to be computed even when the points of the other data set are faraway from the reference, since those points are included in the sliding vertical area with width δ. Here we will propose two improvements of the Classic Plane-Sweep algorithm over two data sets to reduce the number of Euclidean distance computations on KCPQ algorithms.

• 1. An intuitive way to save distance computations is to bound the other axis (not only the sweeping axis) by δ as is illustrated in Fig. 1. In this case, the search space is now restricted to the closest points inside the window with width δ and a height 2∗δ (i.e. [0, δ] in the X-axis and [−δ, δ] in the Y-axis, from the reference point). Clearly, the application of this technique can be viewed as a sliding window on the sweeping axis with a width equal to δ (starting from the reference point) and height equal to 2∗δ. And we only choose all possible pairs of points that can be formed using the reference point and the comparison points that fall into the current window. For example in Fig. 1 it is shown the point q = {2,(11,4)} is outside this window and will not be paired with the reference point p.

• 2. If we try to reduce even more the search space, we can only select those points inside the semi-circle centered at the reference point with radius δ (remember that the equation of all points t = (t.x, t.y)∈E² that fall completely inside the circle, centered at the reference point $reference = (reference.x, reference.y) \in \mathcal {P}$ with radius δ is c i r c l e(r e f e r e n c e, t, δ)≡(r e f e r e n c e.x−t.x)²+(r e f e r e n c e.y−t.y)² < δ ²). See Algorithm 1 at lines 11 and 23. For this reason we call this variant Classic Circle Plane-Sweep algorithm, CCPS for short. And the application of this new improvement can be viewed as a sliding semi-circle with radius δ along the sweeping axis and centered on the reference point, choosing only the comparison points that fall inside that semi-circle. See in Algorithm 1 how this improvement works on two X-sorted arrays of points $PS.P \in \mathcal {P}$ and $QS.P \in \mathcal {Q}$, considering the sweeping axis the X-axis. When a new pair of points (p, q) is chosen, we have to determine whether it will be inserted in the M a x K H e a p or not. If the M a x K H e a p is not full, we calculate the distance between (p, q) and insert (d i s t, p, q) unconditionally (lines 6,7 or 18,19). If the M a x K H e a p is full, we check the following condition d x≡q.x−p.x ≥ δ. If it is true, the process will stop and the new reference point must be defined next (lines 9,10 or 21,22). If not, we check the placement of q. If q is inside the circle (p, δ) the pair is inserted into the heap. The insertion process (lines 11-13 or 23-25) consists of (1) removing the pair with the maximum distance (k e y d i s t o f M a x K H e a p r o o t≡δ), (2) adding the newPair and reorganizing the data structure to restore the (binary) max-heap property based on dist and (3) updating the value of δ with the new k e y d i s t o f M a x K H e a p r o o t. See in Fig. 1, the semi-circle, in light grey color, centered at the reference point p. This point p will be paired only with the point q = {1,(7,16)}. As a conclusion of this improvement is that the smaller the δ value the greater the power of discarding unnecessary comparison points to pair up with the reference point for computing the DJQ.

The PS and QS structures contain the information needed for processing the $\mathcal {P}$ and $\mathcal {Q}$ data sets in strips, respectively. P S = {f i r s t, s t a r t, e n d, P[0..n−1]} and Q S = {f i r s t, s t a r t, e n d, P[0..m−1]}, where P[⋯ ] is a sorted (according to the sweeping axis) array of the maximum number of points per strip, that is, of n and m points of the $\mathcal {P}$ and $\mathcal {Q}$ sets, respectively. We note that n and m values depend on the size of page which may be different for the two sets. The array P[⋯ ] may hold one or more pages of points read from the secondary memory; first is the absolute (in relation to the respective data set) index of the first point of this array (used in the algorithms of Section 5); start and end specify the part of this array that forms the current strip of the respective data set on which a plane sweep algorithm is applied.

In [15], we provide a proof of the correctness of the Classic Circle Plane-Sweep algorithm for KCPQ (CCPS) algorithm (Algorithm 1) through the Theorem 1.

Theorem 1

(Correctness) Let PS.P[PS.start ⋯ PS.end] and QS.P[QS.start ⋯ QS.end] be two arrays of points in E² , sorted in ascending order of X-coordinate values (i.e. X-axis is the sweeping axis), the sweeping direction is from left to right, and MaxKHeap is an initially empty binary max-heap storing K pairs of points, where K is a natural number ($K \in \mathbb {N}, 0 < K \leq |PS.P| \times |QS.P|$). The CCPS Algorithm outputs K closest pairs of points from PS.P and QS.P correctly and without any repetition.

Moreover, as we know from [24], the plane-sweep algorithm for intersection of MBRs from two sets R and S of MBRs can be performed in O(|R|+|S| + k _X ), where |R| and |S| are the numbers of MBRs of both sets, and k _X denotes the numbers of pairs of intersecting intervals creating by projecting the MBRs of R and S onto the X-axis. Following the same idea, CCPS can be performed in O(|P S.P|+|Q S.P| + k _{S A} ), where k _{S A} denotes the number of candidate closest pairs generated by the reference points from P S.P and Q S.P on the sweeping axis (e.g. X-axis).

3.3 Extension to εdistance join query

The adaptation of the CCPS algorithm from KCPQs to εDJQs is not so difficult, and we get the Classic Circle Plane-Sweep algorithm for εDJQ (ε C C P S). If we have two sorted sets of points, we only select the pairs of points in the range of distances [ε ₁, ε ₂] for the final result (lines 11 and 23: if (d i s t ≥ ε ₁ and d i s t≤ε ₂)). This means the result of this query must not be ordered and the M a x K H e a p is unnecessary (lines 5, 6, 7 and 8; and lines 17, 18, 19, and 20), since in the case of εDJQ we do not know beforehand the exact number of pairs of points that belong to the result. And now, the distance threshold will be ε ₂ instead of key dist of M a x K H e a p root (line 9: if (t.x−p.x ≥ ε ₂), line 21: if (t.x−q.x ≥ ε ₂), line 11: if ((p.x−t.x)²+(p.y−t.y)² < (ε ₂)²) and line 23: if ((t.x−q.x)²+(t.y−q.y)² < (ε ₂)²)). Therefore, the data structure that holds the result set will be a file of records (resultFile), with three fields (d i s t, p, q). The modifications of this storing are in lines 13 and 25, where we have to replace them by r e s u l t F i l e.w r i t e(n e w P a i r). To accelerate storing on the resultFile we maintain a buffer on main memory (B _{r e s u l t F i l e} ), and when it is full, its content is flushed to disk. If the distance threshold for the query (ε ₂) is large enough, the compact representation of the join result can be applied [45]. It consists of reporting groups of nearby pairs of points instead of every join link separately. This phenomenon is known as output explosion [45] and it can appear when data density of the sets of points is locally very large compared to the range of distances (distance threshold, ε ₂), and the output of the distance-based joins becomes unwieldy. In fact, the output can become quadratic rather than linear in the total number of data points. Finally, the proof of the correctness of ε C C P S algorithm is similar to the proof of Theorem 1 for the CCPS algorithm (KCPQ).

4 Reverse run plane-sweep algorithm for distance join queries

An interesting improvement of the Classic Plane-Sweep algorithm is the Reverse Run Plane-Sweep algorithm, RRPS for short [1]. The main characteristics of this new algorithm are the use of the concept of run and, as long as the reference points are considered in an order (e.g. ascending order), processing of the comparison points in reverse order (e.g. descending order) until a left limit is reached, in order to generate candidate pairs for the required result.

4.1 Reverse run plane-sweep algorithm for KCPQs

The Reverse Run Plane-Sweep (RRPS) algorithm [1] is based on two concepts, illustrated in Fig. 2. First, every point that is used as a reference point forms a run with other subsequent points of the same set. A run is a continuous sequence of points of the same set that doesn’t contain any point from the other set. For each set, we keep a left limit, which is updated (moved to the right) every time that the algorithm concludes that it is only necessary to compare with points of this set that reside on the right of this limit. Each point of the active run (reference point) is compared with each point of the other set (current comparison point) that is on the left of the first point of the active run, until the left limit of the other set is reached. Second, the reference points (and their runs) are processed in ascending X-order (the sets are X-sorted before the application of the RRPS algorithm). Each point of the active run is compared with the points of the other set (current comparison points) in the opposite or reverse order (descending X-order). Figure 2 depicts a particular instance of the algorithm. We see the data sets $\mathcal {P, Q}$ with the points of Tables 1 and 2. The current reference point is q = {6,(21,24)}, and it is marked by an arrow with solid line. All points of both sets on the left of q have already been processed as reference points. The points P ₅, P ₄ and P ₃ on the left of the reference point according to the RRPS satisfy the requirement d x≡q.x−p.x < δ and they are combined with q to create candidate pairs: the three full circles located within the gray area which has a width equal to threshold δ. The first point of $\mathcal {P}$ to the left of q which has dx-distance from q larger than δ, p = {2,(10,21)}, is marked by the arrow with dashed line. Once the algorithm reaches this point and calculates the dx-distance it will stop creating pairs with q also it will update the l e f t l i m i t of the data set $\mathcal {P}$ with the point p = {2,(10,21)}. The algorithm will continue with the next iteration, setting as reference point p = {6,(22,21)}.

Fig. 2

Reverse Run Plane-Sweep algorithm using sliding strip, window and semi-circle

The Reverse Run Circle Plane-Sweep algorithm for the KCPQ (RCPS) is depicted in Algorithm 2: this is the RRPS algorithm with the sliding semi-circle improvement. Again, a binary max-heap (keyed by pair distances, dist), M a x K H e a p, that keeps the K closest point pairs found so far is used. For each point of the active run (reference point) being compared with a point of the other set (current comparison point) there are 2 cases.

Case 1::

If the pair of points (reference point, comparison point) is inside the circle centered at the reference point with radius δ, then this pair with its distance dist is inserted in the M a x K H e a p (rule 1). The insertion process (lines 23-25 or 39-41) consists of (1) removing the pair with the maximum distance (k e y d i s t o f M a x K H e a p r o o t≡δ), (2) adding the newPair and reorganizing the data structure to restore the (binary) max-heap property based on dist and (3) updating the value of δ with the new k e y d i s t o f M a x K H e a p r o o t. In case the heap is not full (it contains less than K pairs), the pair will be inserted in the heap, regardless of the pair distance, dist.

Case 2::

If the distance between this pair of points in the sweeping axis (e.g. X-axis) dx is larger than or equal to δ, then there is no need to calculate the distance dist of the pair (rule 2). The left limit of the comparison set must be updated at the point being compared (a comparison with a previous point of the the updated left limit will have X-distance larger than dx and is unnecessary).

Moreover, if the rightmost current comparison point is equal to the left limit of its set, then all the points of the active run will have larger dx from all the current comparison points of the other set and the relevant pairs need not participate in calculations, i.e. the algorithm advances to the start of the next run (rule 3).

The RCPS algorithm (Algorithm 2) is an enhanced version of Algorithm 1 of [1]. Since the present paper focuses on disk resident data that are gradually transferred and processed in RAM, the RCPS algorithm is applied on strips (sorted subarrays) of data and not on the whole arrays of data, like Algorithm 1 of [1]. In Algorithm 2, p, q are pointers to the current points, and leftp and leftq hold the left limits of the two strips, respectively (in the algorithms of Section 5, gleftp and gleftq are analogous variables that hold the left limits of the whole two data sets, respectively); s t o p_r u n stores the end-limit of the X-coordinates of the current run of the PS, or QS strip. r u n_s e t P is set to false when p.x < q.x (then the current active run will get reference points from the Q S.P, starting from q, and the comparison points will come from the P S.P, starting from the previous point of p). Analogously, r u n_s e t P is set to true when q.x≤p.x (then the current active run will get reference points from the P S.P, starting from p, and the comparison points will come from the Q S.P, starting from the previous point of q). Note that, since active runs always alternate between the data sets, in Algorithm 2, there is no need for an Else block to follow the If block of lines 11-26 (the execution of code in lines 11-26 should be followed by execution of code in lines 27-42).

In [15], we provide a proof of the correctness of the Reverse Run Circle Plane-Sweep algorithm for KCPQ (RCPS) algorithm (Algorithm 2) through the Theorem 2.

Theorem 2

(Correctness) Let PS.P[PS.start ⋯ PS.end] and QS.P[QS.start ⋯ QS.end] be two arrays of points in E ² , sorted in ascending order of X-coordinate values (i.e. X-axis is the sweeping axis), the sweeping direction is from left to right, and MaxKHeap is an initially empty binary max-heap storing K pairs of points, where K is a natural number ( $K \in \mathbb {N}, 0 < K \leq |PS.P| \times |QS.P|$ ). The RCPS Algorithm outputs K closest pairs of points from PS.P and QS.P correctly and without any repetition.

In [15], an example illustrating the operation of the RCPS algorithm is included (not included here, to limit the size of the present article). Note that, the CCPS algorithm always processes pairs from left to right, even when the distance of the reference point to its closest point of the other array is large (this is likely, since, runs of the two arrays can be in general interleaved). On the contrary, RCPS processes pairs of points in opposite X-orders, starting from pairs consisting of points that are the closest possible, avoiding further processing of pairs that is guaranteed not to be part of the result and substituting distance calculations by simpler dx calculations, when possible. This way, δ is expected to be updated more fastly and the processing cost of RCPS to be lower. This is verified in the specific example appearing in [15].

4.2 Extension to εdistance join query

Like adapting CCPS to εDJQs (ε C C P S), the adaptation of the RCPS algorithm from KCPQs to εDJQs (ε R C P S) is quite straightforward. If we have two sorted arrays of points, we only select the pairs of points in the range of distances [ε ₁, ε ₂] for the final result (lines 23 and 39: if (d i s t ≥ ε ₁ and d i s t≤ε ₂)). Since, the result of this query need not be ordered, M a x K H e a p is unnecessary (lines 16, 17, 18 and 19; and lines 32, 33, 34, and 35 can be omitted). Now the distance threshold will be ε ₂ instead of key dist of M a x K H e a p root (lines 20, 36, 23 and 39). Like ε C C P S, the data structure that holds the result set will be a file of records (resultFile), with three fields (d i s t, P S.P[i], Q S.P[j]) and lines 25 and 41 should be replaced by r e s u l t F i l e.w r i t e(n e w P a i r). Finally, the proof of the correctness of ε R C P S algorithm is similar to the proof of Theorem 2 for the RCPS algorithm.

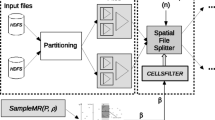
5 External sweeping-based distance join algorithms

Firstly, we present in this section four new algorithms to solve the problem of finding the KCPQ when neither of the inputs are indexed, following similar ideas proposed in [13, 14] for spatial intersection join. We combine plane-sweep and space partitioning to join the data sets and report the required result. These new algorithms extend the CCPS and RRPS algorithms to solve the KCPQ where the two set of points are stored on separate data files on disk. Moreover, we will also extend them to solve the εDistance Join Query (εDJQ).

5.1 The external sweeping-based KCPQ algorithms

In general, the External Sweeping-Based KCPQ algorithms sort the data files containing the sets of points, then perform the Plane-Sweep-Based KCPQ algorithm on the two sorted disk-resident data files and, finally, return the K closest pairs of points in m a x K H e a p data structure.

Sorting each data file by the values of the sweeping axis can be done with the classical external sort/merge algorithm [46]. For instance, to sort $\mathcal {P}$ on the X-axis, first $\mathcal {P}$ is partitioned in $\lceil \mathcal {P} / B \rceil$ runs (where B is the size of a buffer in main memory); each run is sorted in main memory; and finally the runs are recursively merged in larger runs, obtaining the sorted file $\mathcal {P}$.

The External Sweeping-Based KCPQ algorithms start with the two sorted data files ($\mathcal {P}$ and $\mathcal {Q}$) and then, as in the Scalable Sweeping-Based Spatial Join [13, 14], divide the sweeping axis on a set of strips. As is defined Section 3.2, we maintain two strips, PS and QS, one for each file, in main memory, for applying the Plane-Sweep-Based KCPQ algorithm (CCPS or RRPS) and return the K closest pairs of points from $\mathcal {P}$ and $\mathcal {Q}$ on the m a x K H e a p data structure. While strips are filled with data reading the pre-defined number of pages of points from secondary memory into P S.P and Q S.P arrays, the External Sweeping-Based KCPQ algorithms call repetitively CCPS / RCPS with a possibly non empty heap and with, in general, different PS.start / PS.end and QS.start / QS.end limits and different P S.P and Q S.P arrays. At the end of all such calls, the heap will host K closest pairs formed from the two data sets.

Once the data sets are sorted, one can think about: (i) partitioning policies on the sweeping axis and (ii) the appropriate number of strips (n u m O f S t r i p s). We could consider two basic strategies for partitioning the sweeping axis:

• 1. Uniform Filling. A strip hosts a number of points that fit in one or more disk-pages. Using the disk-page size, we calculate the number of points that fit in each strip and divide the data of each set into equally populated numOfStrips (= data file size / strip size) strips (with a possibly underfilled last strip). Thus, numOfStrips is different for each set.

• 2. Uniform Splitting. We partition the sweeping axis to a number of strips (or intervals) covering, every time, the same interval on the sweeping axis for both data sets. To accomplish this, we use a part of main memory as a buffer for P S.P and Q S.P arrays (equal to a pre-defined number of disk pages for each set) and load it with points. Next, a synchronization process takes place. We compare the X coordinates (w.l.o.g. we consider that X is the sweeping axis) of the last points of the two arrays of the sets. The smallest coordinate is set as the right border of the current two strips and the points of the other set (not the one where the point with the smallest X coordinate belongs) that are located after the right border (have greater value of X coordinate) are left to be examined and processed in the future. Thus, the strip for each set contains the points of this set up to the right border. In this way, after the first iteration, the data examined are located in an X interval with specified limits. Subsequently, we process the points residing in the two strips. Next, we load from secondary to main memory data points from any of the sets which does not have any points left unprocessed and we repeat the synchronization between the points of the two sets that are located in main memory. Of course, null strips could be created in some cases, but only for one of the two data sets at every iteration. This situation is not problematic, however. It helps prune pairs that will not be part of the result.

As we can see in Figs. 3 and 7, for each set, the search space is partitioned to non-overlapping vertical strips, whatever the partition policy. We assign each point of $\mathcal {P}$ and $\mathcal {Q}$ to one (and only one) strip. This is a very important condition for the correctness of the algorithms, because, in this way, the same pair cannot be generated twice.

Fig. 3

Applying the FCCPS algorithm on two data sets partitioned in strips equally full (4 points/strip

5.2 Algorithms using uniform filling

5.2.1 The FCCPS algorithm

Following the Uniform Filling partitioning policy, the two sorted data sets $\mathcal {P}$ and $\mathcal {Q}$ are partitioned in strips equally full. W.l.o.g let’s consider strips and pages that have equal sizes, as we can see in Fig. 3. The first sorted set ($\mathcal {P}$) is partitioned in four strips (P S ₀, P S ₁, P S ₂, and P S ₃). The second sorted set ($\mathcal {Q}$) is partitioned in three strips (Q S ₀, Q S ₁, and Q S ₂).

The FCCPS algorithm, see Algorithm 3, requires every time two strips, one from each data set, to be present in the main memory. Starting the first iteration of the algorithm we load one page from each set, $\mathcal {P}$ and $\mathcal {Q}$. Since every strip corresponds to a page, we have the two strips P S ₀ and Q S ₀ in main memory. These two strips are the current strips. One of the current strips will be set as the reference strip, that is, the strip with the leftmost first point; and the other one as a comparison strip.

The process is starting by loading the first two strips P S ₀ and Q S ₀. In the first step we set the leftmost strip (P S ₀) as the reference strip, the other strip (Q S ₀) as a comparison strip (as it is shown in Fig. 3; lines 6 and 20 of Algorithm 3). Next we examine the K closest pairs in these strips by using the C l a s s i c P l a n e S w e e p (CCPS) algorithm at lines 8 and 22, during the first iteration of while-loop at lines 7 and 21, respectively, of Algorithm 3.

In the second step we must examine the points near the border (i.e. the coordinate on the sweeping axis of the last point of the current comparison strip) with the next comparison strip. If m a x K H e a p is not full, all the points of the reference strip (P S ₀) must be joined with the next comparison strip (Q S ₁). If m a x K H e a p is full, we must check the points of the reference strip which have dx distance from the border smaller than the key dist of m a x K H e a p root. In Fig. 3 we can see the border after the join between P S ₀ and Q S ₀, and the points of the reference strip (the two last points) which are near the border in the dark gray area. Then we load in main memory the next comparison strip (Q S ₁) to continue searching the K closest pairs between the P S ₀ and Q S ₁. After the join between the reference strip (P S ₀) and the comparison strip (Q S ₁) we update the border with a new value, because of a new last point of the current comparison strip. The process will continue by loading a new comparison strip (Q S ₂) as long as we have strips in the comparison set ($\mathcal {Q}$) and the m a x K H e a p is not full or there is at least one point of the reference strip near the border. This step is implemented by lines 7-17 and 21-31 in the Algorithm 3.

In the third step, we will load in main memory the next page which corresponds to the next strip P S ₁ of the reference set $\mathcal {P}$ as one of the current strips. The pair of current strips in the new iteration will consist of P S ₁ and Q S ₀ and the process will be restarted (from the first step) by examining which of the two current strips of the sets is the left most one. This step is implemented at lines 18 and 32 in the Algorithm 3.

We must also highlight that in Algorithm 3, TS is a temporary strip which sometimes is loaded with points of the $\mathcal {P}$ set and other times of the $\mathcal {Q}$ set. We use this strip to read the sequence of the next (for the CCPS algorithm) or the previous (for the RRPS algorithm) points of the current strip which must give us comparison points. Moreover, the function c h e c k_n e a r_b o r d e r(b o r d e r, r e f e r e n c e_s t r i p) discovers the first point of the r e f e r e n c e_s t r i p which has dx smaller than δ from the (right) border, for a more detailed algorithmic presentation see [15].

5.2.2 The FRCPS algorithm

For the FRCPS algorithm, see Algorithm 4, we scan the strips in a different order to the previous algorithm (FCCPS). The reference strips are scanned in the same order in which the points of the data sets are sorted (i.e. in ascending order in X-axis), but the comparison strips are scanned in the opposite order (i.e. in descending order in X-axis). In this way, we continue to apply the basic concept of the RRPS algorithm. If A is a reference point from the one data set and B, C (with B.x > C.x) are comparison points from the other data set and moreover: (i) A.x > B.x, that is the reference points are always on the right of the comparison points (ii) The points B and C are adjacent to the X-axis (no other item of the same set lies between them), then we first calculate the distance of the pair (A, B) and next the distance of the pair (A, C). Unlike the previous algorithm (FCCSP), now we have every time in main memory four strips, two from each data set. The leftmost strip of each data set will be defined as current and the other as next (of the current strip). So we have two pairs of strips, the current pair and the next pair.

As it shown in Fig. 4, during the execution of the algorithm, we can have as current pair the strips P S ₁ and Q S ₁ and next pair the strips P S ₂ and Q S ₂ (denoted by n P S and n Q S, respectively, in Algorithm 4).

Fig. 4

Applying the FRCPS algorithm on two data sets partitioned in strips equally full (4 points/strip)

In the first step of this iteration, we join the strips of the current pair (P S ₁ and Q S ₁). From the current pair, we will set as reference strip, the strip which has the rightmost first point (P S ₁) and the other strip will be set as comparison strip (Q S ₁). This step is implemented by lines 13-18 and 25-30 of Algorithm 4.

In the second step, while the left limit is outside of the comparison strip, we will load the previous strip (Q S ₀) of the current comparison strip and we make the join between the strips P S ₁ and Q S ₀. This loop will continue until the left limit will be reached inside the comparison strip. This step is implemented by lines 19-23 and 31-35 of Algorithm 4.

The third step is to prepare the new pair of the current strips. One of the strips of the current pair will be replaced by one strip of the next pair. The leftmost of the strips of the next pair will moved from the next pair to the current pair, and this strip will be replaced by a new strip which will be loaded from secondary memory. This step is implemented by lines 36-47 of the Algorithm 4.

We must also highlight that in Algorithm 4, gleftp and gleftq are variables that hold global left limits for the sorted sets $\mathcal {P}$ and $\mathcal {Q}$. leftlim is local variable that saves the old values of gleftp and gleftq (previous strips). n P S and n Q S are the next strips of (the current strips) PS and QS. For a more detailed presentation of Algorithm 4, see [15].

Now, we are going to show a step-by-step example of the application of the FRCPS algorithm to find the K(=3) closest pair of the data sets $\mathcal {P}$ and $\mathcal {Q}$ having 16 and 12 points, respectively. We also consider that the maximum number of points per strip is 4 and every page from disk can host the same number of points (4). The data sets and the separation into strips are shown in Tables 1 and 2 and in Fig. 3.

The FRCPS algorithm firstly reads the strips: P S ₀{f i r s t = 0, s t a r t = 0, e n d = 3, P[0,1,2,3]}, Q S ₀{f i r s t = 0, s t a r t = 0, e n d = 3, P[0,1,2,3]} as current strips and P S ₁{f i r s t = 4, s t a r t = 0, e n d = 3, P[4,5,6,7]}, Q S ₁{f i r s t = 4, s t a r t = 0, e n d = 3, P[4,5,6,7]} as next strips (see Fig. 5). Both left limits (leftp and leftq) are initialized to non existing point on the left of two sets: l e f t p = l e f p q = {−1,(−1,0)}.

Fig. 5

Join of strips P S ₀ and Q S ₀ using the FRCPS algorithm

The function using the algorithm RCPS executes the K(=3)CPQ for the strips P S ₀ and Q S ₀. Finishing this join the m a x K H e a p has the pairs {(d i s t(P ₂, Q ₁) = 5.831),(d i s t(P ₁, Q ₀) = 5.385),(d i s t(P ₁, Q ₁) = 3.162)}, where d i s t(P _i , Q _j ) is the distance dist between the points (P[i] and Q[j]) from sets $\mathcal {P}$ and $\mathcal {Q}$, having absolute indexes in their sets i and j respectively (regardless of the strip in which they are located), and values for left limits l e f t p = P ₁, l e f t q = Q ₂.

In this first iteration there are no strips on the left of the current strips, so we skip the second step and we are going to execute the third step of the algorithm. In order to prepare the next cycle, the algorithm compares the X-coordinates of the first points of the next strips P S ₁.P[4].x = 19 and Q S ₁.P[4].x = 18.5. Since the point Q S ₁.P[4] is on the left, the strip Q S ₂ is read.

For the second iteration, we have that P S ₀{f i r s t = 0, s t a r t = 2, e n d = 3, P[0,1, 2,3]}, Q S ₁{f i r s t = 4, s t a r t = 0, e n d = 3, P[4,5,6,7]} are the current strips, and P S ₁{f i r s t = 4, s t a r t = 0, e n d = 3, P[4,5,6,7]}, Q S ₂{f i r s t = 8, s t a r t = 0, e n d = 3, P[8,9,10,11]} are the next strips.

The RCPS executes the K(=3)CPQ for the current strips. Note that the current strip P S ₀ is starting from the point P S ₀.P[2] because of the l e f t p = P ₁ value from the previous iteration. Exiting from RCPS function, no new pair is inserted into m a x K H e a p, but the left limits are updated to l e f t p = P ₃, l e f t q = Q ₂. In order to prepare the next cycle, the algorithm compares the first points of the next strips, P S ₁.P[4].x = 19 and Q S ₂.P[8].x = 30. Since the point P S ₁.P[4] is on the left, the strip P S ₂ is read.

For the third iteration, we have that P S ₁{f i r s t = 4, s t a r t = 0, e n d = 3, P[4,5,6,7]}, Q S ₁{f i r s t = 4, s t a r t = 0, e n d = 3, P[4,5,6,7]} are the current strips, and P S ₂{f i r s t = 8, s t a r t = 0, e n d = 3, P[8,9,10,11]}, Q S ₂{f i r s t = 8, s t a r t = 0, e n d = 3, P[8,9,10,11]} are the next strips (see Fig. 6).

Fig. 6

Join of strips P S ₁ and Q S ₁ using the FRCPS algorithm

The RCPS executes the K(=3)CPQ for the current strips. Exiting from RCPS function, the m a x K H e a p has now the pairs {(d i s t(P ₄, Q ₅) = 4.123),(d i s t(P ₅, Q ₆) = 3.162),(d i s t(P ₁, Q ₁) = 3.162)} and l e f t p = P ₄, l e f t q = Q ₄. Since the dx distance between points P S ₁.P[4] and Q S ₁.P[4] is d x(P ₄, Q ₄) = 19−18.5=0.5<4.123, the algorithm continues checking the points near the left border. The RCPS is called to join the strips P S ₁ and Q S ₀. No new pair is inserted into m a x K H e a p. Since the point P S ₂.P[8] is on the left of the point Q S ₂.P[8], the strip P S ₃ is read.

For the forth iteration, we have that P S ₂{f i r s t = 8, s t a r t = 0, e n d = 3, P[8,9,10,11]}, Q S ₁{f i r s t = 4, s t a r t = 0, e n d = 3, P[4,5,6,7]} are the current strips, and P S ₃{f i r s t = 12, s t a r t = 0, e n d = 3, P[12,13,14,15]}, Q S ₂{f i r s t = 8, s t a r t = 0, e n d = 3, P[8,9,10,11]} are the next strips.

The RCPS executes the K(=3)CPQ for the current strips. Exiting from RCPS function, the m a x K H e a p has no changes, but the left limit of the $\mathcal {Q}$ set is updated to l e f t q = Q ₆. Since the dx distance between the (first) points P S ₂.P ₈ and Q S ₁.P ₄ is d x(P ₈, Q ₄) = 23−18.5=4.5>4.123, the algorithm has no need to continues checking the points near the left border.

Now, the data set $\mathcal {P}$ has no next strip (it is finished) and, then the status for the fifth cycle is as follow: P S ₂{f i r s t = 12, s t a r t = 0, e n d = 3, P[12,13,14,15]}, Q S ₁{f i r s t = 4, s t a r t = 3, e n d = 3, P[4,5,6, 7]} are the current strips and only Q S ₂{f i r s t = 8, s t a r t = 0, e n d = 3, P[8,9,10,11]} is the next strip.

The RCPS executes the K(=3)CPQ for the current strips. Exiting from RCPS function, the m a x K H e a p has no changes, but the left limit of the $\mathcal {Q}$ set is updated to l e f t q = Q ₇. The data set $\mathcal {P}$ has no next strip (it is finished), then the status for the sixth cycle is as follows: P S ₂{f i r s t = 12, s t a r t = 0, e n d = 3, P[12,13,14,15]}, Q S ₂{f i r s t = 8, s t a r t = 0, e n d = 3, P[8,9,10,11]} are the current strips and there is not any next strip.

Finally, the RCPS executes the K(=3)CPQ for the current strips. Exiting from RCPS function, the m a x K H e a p has new pairs {(d i s t(P ₁₂, Q ₈) = 1.000),(d i s t(P ₁₃, Q ₈) = 1.000),(d i s t(P ₁₃, Q ₉) = 2.000)} and the left limits are updated to l e f t p = P ₁₅ and l e f t q = Q ₉. Since the dx distance between points P S ₃.P ₁₂ and Q S ₂.P ₈ is d x(P ₁₂, Q ₈) = |29−30|=1<2.0, the algorithm will continue by checking the points near the left border between the strips P S ₂ and Q S ₂. But, no new pair is found and the algorithm is finished.

As a summary, the pages which are read from disk were 9, the pairs involved in calculations were 57, the dx calculations were 89 and the complete dist-calculations were 10.

5.3 Algorithms using uniform splitting

5.3.1 The SCCPS algorithm

Following the Uniform Splitting partitioning policy, the first sorted set ($\mathcal {P}$) is partitioned in five strips (P S ₀, P S ₁, P S ₂, P S ₃ and P S ₄). The second sorted set ($\mathcal {Q}$) is partitioned in seven strips (Q S ₀, Q S ₁, Q S ₂, Q S ₃, Q S ₄ and Q S ₅).

The SCCPS algorithm, see Algorithm 5, requires two strips, one of each data set, to be present in main memory. We define the width of a strip as the distance between the leftmost (first) and rightmost (last) points of the strip on the sweeping axis. After loading a buffer of disk pages from secondary memory with points from the two data sets into strip arrays $\mathcal {P}$, we have to execute a synchronization process (through s y n c_q u e u e s function). This process determines the points in the two arrays that form the respective two strips. Note that every point between the leftmost and rightmost points of both strips has been read from secondary memory. The coordinate of the rightmost point of the strips is defined as border.

We examine the coordinates on the sweeping axis (i.e. X-axis) of the last points of the current arrays P S.P and Q S.P. As it is shown in Fig. 7 the strip P S ₀ has the 77array of points with indexes P = [0,1,2,3] which are depicted with filled circles. The strip Q S ₀ has the array of points with indexes P = [0,1,2,3] which are depicted with empty circles. The last point Q S ₀.P[3] is on the left of the last point P S ₀.P[3] (Q S ₀.P[Q S ₀.e n d].x < P S ₀.P[P S ₀.e n d]). Since, it is not known if the first point of the $\mathcal {Q}$ set next to the last point of the Q S ₀ strip (the point Q S ₁.P[4]) is on the left or on the right of the last point of the current P S ₀ page, we set as right border the coordinate on the sweeping axis of the last point of the QS page (Q S ₀.P[3].x). In this way, at least one strip (Q S ₀) will have the maximum number of points per strip while the other strip (P S ₀) will have points from zero to the maximum number of points per strip (as we can see in Fig. 7 the P S ₀ strip has three points).

Fig. 7

Applying the SCCPS algorithm on two data sets partitioned in strips of variable width

The process starts loading pages of points into P S ₀.P and Q S ₀.P. After the synchronization process we have two strips and the value of the border = border1. If both strips have some points (are not empty) we examine the K closest pairs of points inside these strips by using the Classic Plane Sweep (CCPS). This first step is implemented by lines 5-6 of Algorithm 5.

The second step is to examine in any not empty strip, first PS and next QS the points near the border. If the m a x K H e a p is full only the points that reside near the border, having dx-distance from the border smaller than the key dist of m a x K H e a p root, will be selected for joins. If the m a x K H e a p is not full all the points of the current strips will be eligible for joins. First, we must join the points of the PS strip near the border with the points of the QS strip that have not been joined with the points of the PS strip in the previous first step. Then we must update the value of the border with the coordinate of the last point of the Q S ₀ strip, find the eligible points of the P S ₀ strip taking into account the new value of the border. If there are some points left, we must continue by loading the next page of the $\mathcal {Q}$ set (Q S ₁). The process will continue as long as we have a strip in the comparison set ($\mathcal {Q}$) and there is at least one point of the reference strip (P S ₀) near the current value of the border. This second step will be executed setting as reference strip the Q S ₀ and comparison strips the rest of the points of P S ₀, P S ₁, ⋯. This step is implemented by lines 7-39 of Algorithm 5.

The third step is to prepare the next pair of strips (P S ₁ and Q S ₁) by loading pages of points from secondary memory into arrays $\mathcal {P}$, synchronizing them and continuing from the first step as long as we have points for both strips. This step is implemented by lines 40-44 of Algorithm 5.

We must also highlight that in Algorithm 5, the function s y n c_q u e u e s(P S, Q S) finds which of the last points of the two strips is the leftmost one. Then it sets the value of the right border equal to the X-coordinate of this point. Finally, it returns the value of the right border. border is a variable that holds the right border of the current strips. c u r_b o r d e r is a local variable of the if-structure in lines 7-23 that holds the updated value of the current border of the current comparison strip. For the other if-structure in lines 24-39 the variable border holds the updated value of the current border. For a more detailed presentation of Algorithm 5, see [15].

5.3.2 The SRCPS algorithm

The SRCPS algorithm, see Algorithm 6, requires two strips, one of each data set, to be present in main memory. Before the main process of this algorithm and for the leftmost set we reach either the first strip which has overlap with the first strip of the other set, or the last strip (which has no overlap with the first strip of the other set); lines 5-12 of Algorithm 6.

The first step is to synchronize the current strips (if both are not empty) and afterwards the RRPS algorithm is called to join the points between them. This step is implemented by lines 14-15 and 16-19 of Algorithm 6.

The second step consists of two parts. In the first part, we examine three conditions: (1) if the strip of the first set $\mathcal {P}$ has at least one point in the area on left of the right border (see Section 5.3.1), (2) if the current strip of the other set $\mathcal {Q}$ has points on the left of its starting point (in the same strip or in previous strips), and (3) if the m a x K H e a p is not full or if the first point of the P S _i strip has a distance on the sweeping axis (dx) from the left border (the coordinate of the last point of the previous strip of Q S _j ) less than the key dist of maxKHeap root (line 16 of Algorithm 6). If all conditions are true then we call the subroutine s r c p s_o n_b o r d e r (Algorithm is presented in [15]). In this subroutine we join the points of the strip PS and all points of the set $\mathcal {Q}$ which are on the left of the starting point of the current QS strip. This process continues while the m a x K H e a p is not full or the points have dx distance from the left border smaller than the key dist of maxKHeap root. For each set, we keep a left limit (leftp, leftq), which is updated (moved to the right) every time that the algorithm concludes that it is only necessary to compare with points of this set that reside on the right of this limit. In Fig. 8 we can see the dx distance of the first point of the P S ₁ strip from the lborderq which is smaller than the key dist of m a x K H e a p root. In the second part, we swap the roles between PS and QS and we execute the same process as in the first part. This step is implemented by lines 24-27 of Algorithm 6.

Fig. 8

Applying the SRCPS algorithm on two data sets partitioned in strips of variable width

The third step is to prepare the next iteration from the beginning by updating the values of the borders and loading the next of the current strips of both sets. This step is implemented by lines 30-47 of Algorithm 6. We must also highlight that in Algorithm 6, lborderp and lborderq are variables that store the current left borders of the sorted sets $\mathcal {P}$ and $\mathcal {Q}$. For a more detailed presentation of Algorithm 6, see [15].

Next, we are going to show a step-by-step example for the SRCPS algorithm, using the same input data sets as in the previous example (for FRCPS). The query is also the same, that is, we are looking for the K(=3) closest pairs in the data sets $\mathcal {P}$ and $\mathcal {Q}$. As in the previous example,we define that disk-page and array $\mathcal {P}$ in the strip have the same size, enough to fit four points. The data sets and the separation into strips, having variable width, are shown in the Fig. 8.

The algorithm SRCPS firstly reads the pages with the points [0,1,2,3] of the $\mathcal {P}$ set and $\mathcal {P}$[0,1,2,3] of the $\mathcal {Q}$ set. After the synchronization process the current strips are P S ₀{f i r s t = 0, s t a r t = 0, e n d = 2, P[0,1,2,3]} and Q S ₀{f i r s t = 0, s t a r t = 0, e n d = 3, P[0,1,2,3]} (see Fig. 9). Both left limits (leftp and leftq) are initialized to non existing point on the left of two sets: l e f t p = l e f p q = {−1,(−1,0)}. In the first step, the algorithm RCPS executes the K(=3)CPQ for the strips P S ₀ and Q S ₀. Finishing this task the m a x K H e a p has the pairs {(d i s t(P ₂, Q ₁) = 5.831),(d i s t(P ₁, Q ₀) = 5.385),(d i s t(P ₁, Q ₁) = 3.162)} and the values for left limits are l e f t p = P ₁, l e f t q = Q ₀. Since there are no strips on the left of the current strips, we must skip the second step and continue with the third one, in which the algorithm must prepare the next iteration. Therefore, the array P S ₀.P will remain in main memory. Setting the values of the indexes start and end to the value 3, P S ₁{f i r s t = 0, s t a r t = 3, e n d = 3, P[0,1,2, 3]} will be created and the next page, containing points [4,5,6,7], will be read from disk into array Q S ₁.P.

Fig. 9

Join of strips P S ₀ and Q S ₀ using the SRCPS algorithm

For the second iteration and after the synchronization process, the current strips are P S ₁{f i r s t = 0, s t a r t = 3, e n d = 3, P[0,1,2, 3]} and Q S ₁{f i r s t = 4, s t a r t = 0, e n d = −1, P[4,5,6,7]} (see Fig. 10). The value of Q S ₁.e n d is smaller than Q S ₁.s t a r t and the first step (join between current strips P S ₁ and Q S ₁) will be omitted (line 16 of the Algorithm 6). The current strip P S ₁ has the point P S ₁.P[3] which is at the right border (P S ₁.s t a r t = P S ₁.e n d), the starting point of the current strip Q S ₁ is not the first point of the set $\mathcal {Q}$. The task will continue with the second step by comparing the dx distance between the starting point of the current P S ₁ strip (P S ₁.P[3].x = 17) and the value of lborderq which is equal to the value of the last point of the previous strip Q S ₀ (Q S ₀.P[3].x = 15). Thus it is possible to find closest pairs comparing the point P S ₁.P[3] with the points of the strip Q S ₀. The second part of the second step will not be executed since the current strip Q S ₁ is empty (Q S ₁.s t a r t > Q S ₁.e n d). Finishing this step, the m a x K H e a p has not been updated with new pairs, but the left limit l e f t q = Q ₂. In the third step, the algorithm must prepare the current strips for the next iteration. Therefore, the page of $\mathcal {P}$ points [4,5,6,7] is read and the array Q S ₁.P is kept in main memory for the next iteration.

Fig. 10

Join of strips P S ₁ and Q S ₁ using the SRCPS algorithm

For the third iteration and after the synchronization process, the current strips are P S ₂{f i r s t = 4, s t a r t = 0, e n d = 3, P[4,5,6,7]} and Q S ₁{f i r s t = 4, s t a r t = 0, e n d = 2, P[4,5,6,7]} (see Fig. 10). In the first step, the RCPS executes the K(=3)CPQ for the current strips. Exiting from the RCPS function, m a x K H e a p has new values {(d i s t(P ₄, Q ₅) = 4.123),(d i s t(P ₅, Q ₆) = 3.162),(d i s t(P ₁, Q ₁) = 3.162)}, and the left limits have values l e f t p = P ₁, l e f t q = Q ₄. The current strip P S ₂ has points (all points) at, or on the left of, the right border, the starting point of the current strip Q S ₁ is not the first point of the set $\mathcal {Q}$ and the difference P S ₂.P[4].x−l b o r d e r q = 19−15=4<4.123. Therefore, the second step will continue by checking the strips P S ₂ and Q S ₀ (previous strip of the current strip Q S ₁). The current strip Q S ₁ has (three) points at, or on the left of, the right border, the starting point of the current strip P S ₂ is not the first point of the set $\mathcal {P}$ and the difference Q S ₁.P[4].x−l b o r d e r p = 18.5−17=1.5<4.123. Therefore, the second step will continue by checking the strips Q S ₁ and P S ₁ (previous strip of the current strip P S ₂). The m a x K H e a p is not updated with new pairs, but the left limits of the sets are updated to the new values l e f t p = P ₂ and l e f t q = Q ₄. In the third step, the algorithm must prepare the current strips for the next iteration. Therefore, the page of $\mathcal {P}$ points [8,9,10,11] is read and the array Q S ₁.P remains in main memory for next iteration.

For the forth iteration and after the synchronization process, the current strips are P S ₃{f i r s t = 8, s t a r t = 0, e n d = 0, P[8,9,10,11]} and Q S ₂{f i r s t = 4, s t a r t = 3, e n d = 3, P[4,5,6, 7]}. In the first step, the RCPS executes the K(=3)CPQ for the current strips. Exiting from the RCPS function, the m a x K H e a p has not been updated with new values, and the left limits keep the same values l e f t p = P ₂, l e f t q = Q ₄. The current strip P S ₃ has (one) point at or on the left of the right border, the starting point of the current strip Q S ₂ is not the first point of the set $\mathcal {Q}$ and the difference P S ₃.P[8].x−l b o r d e r q = 23−21=2<4.123. Therefore, the second step will continue by checking the strips P S ₃ and Q S ₁ (previous points of the starting point of the current strip Q S ₂). The current strip Q S ₂ has (one) point at, or on the left of, the right border, the starting point of the current strip P S ₃ is not the first point of the set $\mathcal {P}$ and the difference Q S ₂.P[7].x−l b o r d e r p = 24−23=2<4.123. Therefore, the second step will continue by checking the strips Q S ₂ and P S ₂ (previous strip of the current strip P S ₃). The m a x K H e a p is not updated with new pairs, but the left limits of the sets are updated to the new value l e f t p = P ₄. In the third step, the algorithm must prepare the current strips for the next iteration. Therefore, the array P S ₂.P is kept and the page of $\mathcal {Q}$ points [8,9,10,11] is read from the disk for next iteration.

For the fifth iteration and after the synchronization process, the current strips are P S ₄{f i r s t = 8, s t a r t = 1, e n d = 3, P[8, 9,10,11]} and Q S ₃{f i r s t = 8, s t a r t = 0, e n d = −1, P[8,9,10,11]}. The value of index Q S ₃.e n d is smaller than the index Q S ₃.s t a r t and the first step (join between current strips P S ₄ and Q S ₃) will be omitted (lines 16-19 of the Algorithm 6). The current strip P S ₄ has three points at, or on the left of, the right border, the starting point of the current strip Q S ₃ is not the first point of the set $\mathcal {Q}$ and the difference P S ₄.P[9].x−l b o r d e r q = 25−24=1<4.123. Therefore, the second step will continue by checking the strips P S ₄ and Q S ₂ (previous points of the starting point of the current strip Q S ₃). The second part of the second step will not be executed since the current strip Q S ₃ has no points at, or on the left of, the right border (Q S ₃.e n d < Q S ₃.s t a r t). The m a x K H e a p is not updated with new pairs, but the left limit of the set $\mathcal {Q}$ updated to the new value l e f t q = Q ₆. In the third step, the algorithm must prepare the current strips for the next iteration. Therefore, the page of $\mathcal {P}$ points [12,13,14,15] is read and the array Q S ₂.P is kept in main memory for the next iteration.

For the sixth iteration and after the synchronization process, the current strips are P S ₅{f i r s t = 12, s t a r t = 0, e n d = 3, P[12,13,14,15]} and Q S ₃{f i r s t = 8, s t a r t = 0, e n d = 2, P[8,9,10,11]}. In the first step, the RCPS executes the K(=3)CPQ for the current strips. Exiting from RCPS function, the m a x K H e a p has new values {(d i s t(P ₁₃, Q ₉) = 2),(d i s t(P ₁₃, Q ₈) = 1),(d i s t(P ₁₂, Q ₈) = 1)}, and the left limits have values l e f t p = P ₁₄, l e f t q = Q ₉. The current strip P S ₅ has all its four points at, or on the left of, the right border, the starting point of the current strip Q S ₃ is not the first point of the set $\mathcal {Q}$ but the difference P S ₅.P[12].x−l b o r d e r q = 29−24=5>2. Therefore, the first part of the second step will be skipped. The current strip Q S ₃ has three points at, or on the left of, the right border, the starting point of the current strip P S ₅ is not the first point of the set $\mathcal {P}$ but the difference Q S ₃.P[8].x−l b o r d e r p = 30−27=3>2. Therefore, the second part of the second step will be skipped. In the third step, the algorithm must prepare the current strips for the next iteration. Therefore, the strip P S ₅ is finished and will be updated to the following values P S ₅{f i r s t = 12, s t a r t = 4, e n d = −2, P[12,13,14,15]} and the array Q S ₂.P is kept in main memory for the next iteration.

In the last iteration (seventh), the first step and the first part of the second step are skipped because the set $\mathcal {P}$ is finished (P S ₅.e n d = −2<0). The current strip Q S ₄ has only one point that resides at the right border, the starting point of the current strip P S ₅ is not the first point of the set $\mathcal {P}$ but the difference Q S ₄.P[11].x−l b o r d e r p = 40−37=3>2. Therefore, the second part of the second step will be skipped. In the third part, the algorithm must prepare the current strips for the next iteration. For this, the strips PS and QS do not need any update because they have finished their points from the two sets and the algorithm is terminated.

As a summary, the pages which are read from the disk were 12, the pairs involved for calculations were 52, the dx calculations were 84 and the complete dist-calculations were 10.

5.4 Analysis

The proofs of the correctness of the External Sweeping-Based KCPQ algorithms (FCCPS, FRCPS, SCCPS and SRCPS) are similar to the proofs of CCPS and RRPS given by the Theorems 1 and 2, respectively. Since the latter are the kernel for the query processing of the former. To extend that proof we must take into account the split of the sweeping axis into strips and the processing strategy of those strips. To see that External Sweeping-Based KCPQ algorithms report the K closest pairs correctly and without any repetition, one key property is that each point (from $\mathcal {P}$ or $\mathcal {Q}$) is assigned to one and only one strip, hence a same pair of points cannot be generated twice. And taking into account the treatment on the borders of the strips, the External Sweeping-Based KCPQ algorithms guarantee that all possible candidate pairs of points are considered and no duplicates are generated.

The I/O cost of the External Sweeping-Based KCPQ algorithms can be estimated, following a similar reasoning as in [14]:

• 1. The cost of sorting each data set can be expressed as $2m \times \mathcal {P}$, where m represents the number of merge levels and is logarithmic in $|\mathcal {P}|$ [47], and the constant factor 2 accounts for reading and writing $\mathcal {P}$ at each merge level.

• 2. The cost of the External Sweeping-Based KCPQ algorithms depends of the number of strips that must be read from disk (sr). Let M R _{m a x} the maximum value of MR (memory requirements) during the execution of a plane-sweep-based algorithm, the sr can be estimated by: $sr \backsimeq numOfStrips \times \lceil \max \{(MR_{max} / M), 0\} \rceil$, where M is the available main memory size. Each point belonging to one of the strips must be read just once. Therefore, the I/O cost of the External Sweeping-Based KCPQ algorithms can be estimated as $(|\mathcal {P}| + |\mathcal {Q}|) \times sr/numOfStrips$.

In summary, the I/O cost of the External Sweeping-Based KCPQ algorithms can be estimated as:

$$2m \times (\mathcal{P}</p><p class="noindent">+ \mathcal{Q}) + (\mathcal{P} + \mathcal{Q}) \times sr/numOfStrips$$

In the best case (M > M R _{m a x} ), s r = n u m O f S t r i p s and the cost is $2m \times (\mathcal {P} + \mathcal {Q}) + (\mathcal {P} + \mathcal {Q})$. In the worst case (M≤M R _{m a x} ), additional readings are necessary to complete the processing for each strip as we have mentioned above.

5.5 Extension to εdistance join query

The adaptation of the External Sweeping-Based KCPQ algorithms from KCPQ to εDJQ is not difficult. As we know, for εDJQ, we have two sets of points $\mathcal {P}$ and $\mathcal {Q}$ as input, and the pairs of points in the range of distances [ε ₁, ε ₂] are selected for the final result and stored in a file of records (resultFile) with three fields (d i s t, P[i], Q[j]), where 0≤i≤N−1 and 0≤j≤M−1. The M a x H K e a p data structure is not needed. The modifications are related to the file operations on resultFile and instead of calling to CCPS or RCPS, the algorithms should call to ε C C P S or ε R C P S, respectively. Moreover, instead of calling c h e c k_n e a r_b o r d e r(b o r d e r, r e f e r e n c e_s t r i p), the algorithm will call the function ε c h e c k_n e a r_b o r d e r(b o r d e r, r e f e r e n c e_s t r i p), which will do the same functionality, discovering the first point of the r e f e r e n c e_s t r i p which has dx smaller than ε ₂ from the (right) border. More specifically, from FCCPS to get ε F C C P S we should call ε C C P S instead of CCPS at lines 8 and 22, and ε c h e c k_n e a r_b o r d e r(b o r d e r, r e f e r e n c e_s t r i p) should be called at lines 11 and 25.

From SCCPS to get ε S C C P S we should call ε C C P S instead of CCPS at lines 6, 14 and 30, and ε c h e c k_n e a r_b o r d e r(b o r d e r, r e f e r e n c e_s t r i p) should be called at lines 9, 17, 25 and 33.

From FRCPS to get ε F R C P S we should call ε R C P S instead of RCPS at lines 16, 22, 28 and 34. Line 20 should be replaced by while(dx-distance b/t first points of Q S.P, T S.P≤ε ₂) and line 32 bywhile(dx-distance b/t first points of P S.P, T S.P≤ε ₂).

And from SRCPS to get ε S R C P S we should call ε R C P S instead of RCPS at line 18. Line 20 should be replaced by if (the strip PS is not emptyandthe strip QS is not the first oneand(dx-distance b/t first point of PS and l b o r d e r q≤ε ₂)) and line 24 by if (the strip QS is not emptyandthe strip PS is not the first oneand(dx-distance b/t first point of QS and l b o r d e r p≤ε ₂)). Finally, we have to replace RCPS by ε R C P S in line 18, m a x K H e a p is not used at all, ε s r c p s_o n_b o r d e r is called in lines 21 and 25.

6 Performance evaluation

This section provides the results of an extensive experimental study a) aiming at measuring and evaluating the efficiency of the new algorithms proposed in Section 5 (Sections 6.2–6.6) and effectiveness of these algorithms (Section 6.7), and b) the comparison of the new algorithms proposed in Section 5 and four algorithms that process the same queries on R-trees (Section 6.8). Section 6.1 presents the experimental setup that is common for parts (a) and (b).

6.1 Experimental setup

In order to evaluate the behavior of the proposed algorithms, we have used four real spatial data sets of North America, representing cultural landmarks (NAcl) consisting of 9203 points and populated places (NApp) consisting of 24491 points, roads (NArd) consisting of 569082 line-segments, and railroads (NArr) consisting of 191558 line-segments. To create sets of points, we have transformed the MBRs of line-segments from NArd and NArr into points by taking the center of each MBR. Moreover, in order to get the double amount of points from NArr and NArd we choose the two points (min, max) of the MBR of each line-segment. The data of these 6 files were normalized in the range [0,1]². We have also created 6 combinations of input sets (N A p p N×N A r r N, N A p p N×N A r d N, N A r r N×N A r d N, N A r r N×N A r d N D, N A r r N D×N A r d N and N A r r N D×N A r d N D) for query processing. We have also used big real spatial data (retrieved from http://spatialhadoop.cs.umn.edu/datasets.html) to justify the use of spatial query algorithms on disk-resident data instead of using them in-memory. They represent water resources (Water) consisting of 5836360 line-segments, parks or green areas (Park) consisting of 11504035 polygons and world buildings (Build) consisting of 114736611 polygons. To create sets of points, we have transformed the MBRs of line-segments from Water into points by taking the center of each MBR and we have considered the centroid of polygons from Park and Build. We have also created 3 combinations of input sets (W a t e r×P a r k, W a t e r×B u i l d, P a r k×B u i l d) for query processing.

We have also created synthetic clustered data sets of 125000, 250000, 500000 and 1000000 points, with 125 clusters in each data set (uniformly distributed in the range [0,1]²), where for a set having N points, N/125 points were gathered around the center of each cluster, according to Gaussian distribution. We made 4 combinations of synthetic data sets by combining two separate instances of data sets, for each of the above 4 cardinalities (i.e. 125K C1N×125K C2N, 250K C1N×250K C2N, 500K C1N×500K C2N, and 1000K C1N×1000K C2N) and 1 combination of synthetic data sets by combining two data sets of different cardinalities (500K C2N×1000K C1N).

All experiments were performed on a PC with Intel Core 2 Duo, 2.2 GHz CPU with 4 GB of RAM and 2TBs of secondary storage, with Ubuntu Linux v. 14.04 LTS (Linux OS), using the GNU C/C++ compiler (gcc).

In our previous paper [1], it is shown that the semi-circle variant of both Classic Plane-Sweep and Reverse Run Plane-Sweep algorithms has the highest execution-time efficiency, for the KCPQ. Therefore, all experiments were executed using CCPS and RCPS. For the KCPQ and for all (4) algorithms we study how the value of K, disk page size, size of the strips and size of the LRU buffer affects efficiency, by executing experiments for the previous 14 combinations of data sets. As efficiency measures we used:

• 1. The overall execution time (i.e. response time); this measurement is reported in milliseconds (ms) and represents the overall CPU time consumed, as well as the I/O time needed by each algorithm.

• 2. The number of X-axis distance calculations (dx).

• 3. The number of disk accesses (disk-pages read).

To measure the effectiveness of the new algorithms, we can use the selection ratio, which is defined as the fraction of pairs considered by the algorithms for processing over the total number of possible pairs. This is just the opposite to the pruning ratio, and a pair selection occurs when a candidate pair from two strips is considered for processing according to its dx distance.

6.2 The effect of the number of pairs (K)

In order to examine the effect of the number of pairs (K) on the new algorithms, K is set equal to 1, 10, 100, 1000 and 10000; the size of disk page equals to 4 KBytes; the size of strip is 16 KBytes; and there is no LRU buffer (its size is 0).

6.2.1 The execution time

The results for execution time are similar for all input data sets. Table 3 shows the execution time in ms when KCPQ is processed by the FCCPS, SCCPS, FRCPS and SRCPS algorithms on the N A r r N×N A r d N D data sets (in Tables 3–21, a value in bold is the best value of its line). As the value of K increases, the execution time increases, but the rate of the increment gets higher as K increases. For example, using the FCCPS algorithm, from K = 1 to K = 10 the time increased by 0 %, from K = 10 to K = 10² by 3 %, from K = 10² to K = 10³ by 16 % and from K = 10³ to K = 10⁴ by 29 %.

Table 3 Execution time in ms for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on N A r r N×N A r d N D, in relation to K

Considering all experiments and all data sets, we find that SCCPS overcomes FCCPS 58-12 times and FRCPS overcomes SRCPS 36-34 times. Comparing the best result among FCCPS and SCCPS (variants of Classic Plane-Sweep algorithm) and the best result among FRCPS and SRCPS (variants of Reverse Run Plane-Sweep algorithm) for every combination of data sets, we conclude that Reverse Run algorithms are faster in all cases (70-0).

Figure 11 shows the execution time of each algorithm for KCPQ as a fraction of the total time consumed by all algorithms(represented by the respective bar). It is shown that the SRCPS (line with down facing triangles as markers) was the fastest for K = 1,10,100, while FRCPS (line with up facing triangles as markers) was the fastest for K = 1000,10000. This situation is dominating in most data set combinations.

Fig. 11

Fractions of execution time for KCPQ, using FCCPS, SCCPS, FRCPS and SRCPS on N A r r N×N A r d N D, in relation to K

6.2.2 The number of the dx distance calculations

The results with respect to the number of dx distance calculations are similar for all input data sets. Table 4 shows the values of this metric when KCPQ is processed by the FCCPS, SCCPS, FRCPS and SRCPS algorithms on the N A r r N×N A r d N D data sets. As the value of K increases, the number of dx distance calculations also increases. However, while the number of K increases geometrically with a ratio of 10, the number of dx distance calculations increases with a ratio ranging between 1.83 and 2.66. For example, using the SRCPS algorithm from K = 1 to K = 10 the number of dx distance calculations increased by 266 %, from K = 10 to K = 10² by 183 %, from K = 10² to K = 10³ by 207 % and from K = 10³ to K = 10⁴ 213 %.

Table 4 Number of dx distance calculations is millions (×10⁶) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on N A r r N×N A r d N D, in relation to K

Considering all experiments and all data sets, we find that SCCPS overcomes FCCPS 49-21 times and SRCPS overcomes FRCPS 61-9 times. Comparing the best result among FCCPS and SCCPS and the best result among (the almost identical results of) FRCPS and SRCPS for every combination of data sets, we conclude that Reverse Run algorithms need fewer dx distance calculations in all cases (70-0).

Figure 12 shows the number of dx distance calculations of each algorithm for KCPQ as a fraction of the total number of dx distance calculations performed by all algorithms (represented by the respective bar). It is shown that the SRCPS (line with down-facing triangles as markers) took from 13.7 % up to 24.7 % of the total number of dx distance calculations needed to execute the queries. The FRCPS algorithm has almost equal number of dx distance calculations so its line (with up-facing triangles as markers) is overwritten from the line of the SRCPS (note that overlapping down-facing and up-facing triangles appear as stars). RR algorithms need fewer dx distance calculations in all cases.

Fig. 12

Fractions of the number of dx distance calculations for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on N A r r N×N A r d N D, in relation to K

6.2.3 The number of the disk accesses (pages read)

The results for number of disk accesses are similar for all input data sets and this performance measure proved to be the most important factor that shaped the results. Table 5 shows the values of this metric when KCPQ is processed by the FCCPS, SCCPS, FRCPS and SRCPS algorithms on the N A r r N×N A r d N D data sets. As the value of K increases, the number of disk accesses increases slightly, or marginally. While K increases geometrically with a ratio of 10, the number of pages read increases, for example, in the FRCPS algorithm, by 0.051 %, 0.358 %, 1.069 %, and 3.678 %.

Table 5 Number of disk accesses for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on N A r r N×N A r d N D, in relation to K

Considering all experiments and all data sets, we find that FCCPS overcomes SCCPS 68-2 times and FRCPS overcomes SRCPS 70-0 times. Comparing the best result among FCCPS and SCCPS and the best result among FRCPS and SRCPS for every combination of data sets, we conclude that Reverse Run algorithms need fewer disk accesses in all cases (70-0).

Figure 13 shows the number of disk accesses of each algorithm for KCPQ as a fraction of the total number of disk accesses needed by all algorithms (represented by the respective bar).

Fig. 13

Fractions of number of disk accesses for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on N A r r N×N A r d N D, in relation to K

Summarizing the results of experiments on the effect of K, we note that: (1) The exponential growth of K causes (non geometrical) increase in the execution time. (2) The exponential growth of K causes increase in the number of dx-distance calculations with a lower ratio (up to 3 for most datasets and up to 7 for the biggest data set combination). (3) The number of disk accesses required by FCCPS and FRCPS algorithms increases marginally with the growth of K, unlike SCCPS and SRCPS where the increment is more pronounced. Moreover, (4) the fastest algorithm proved to be the SRCPS for small values of K, while FRCPS is the fastest for large values of K. Finally, (5) SRCPS was slightly the most economical algorithm in terms of dx distance calculations.

6.3 The effect of the disk page size (pg)

In order to examine the effect of the disk page size (pg) on the new algorithms, the size of disk pages (pg) is set equal to 1, 2, 4, 8 and 16 KBytes; K = 1000; the size of strips is 16 KBytes; and there is no LRU buffer (its size is 0).

6.3.1 The execution time

The results for execution time are similar for all input data sets. Table 6 shows the execution time in ms when KCPQ is executed by the algorithms FCCPS, SCCPS, FRCPS and SRCPS on the 1000K C1N×1000K C2N data sets. As the page size increases the execution time is reduced, but the rate of decrement continuously decreases. For example, using SRCPS algorithm from p g = 1K B to p g = 2K B the time decreased by 12 %, from p g = 2K B to p g = 4K B by 7.3 %, from p g = 4K B to p g = 8K B by 4 % and from p g = 8K B to p g = 16K B by 0.15 %.

Table 6 Execution times in ms for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on 1000K C1N×1000K C2N, in relation to pg

Figure 14 shows the execution time of each algorithm values as a fraction of the total execution time consumed by all algorithms (represented by the respective bar). Considering all experiments and all data sets, we find that SCCPS overcomes FCCPS 54-16 times and FRCPS overcomes SRCPS 51-19 times. Comparing the best result among FCCPS and SCCPS and the best result among FRCPS and SRCPS, for every combination of data sets, we conclude that Reverse Run algorithms are the fastest in all cases. In Fig. 14, it is shown that the increment of the disk page size for sizes larger than 8 KB, does not give any advantage in query execution for any algorithm. Experiments with page sizes larger than 32 KB show that the execution becomes slightly slower.

Fig. 14

Fractions of execution time for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on 1000K C1N×1000K C2N, in relation to pg

6.3.2 The number of dx distance calculations

The results of the number of dx distance calculations are similar for all input data sets. In Table 7, we can see the values of this metric when KCPQ is executed by the algorithms FCCPS, SCCPS, FRCPS and SRCPS on the 1000K C1N×1000K C2N data sets. As the value of disk page size increases, the number of dx distance calculations stays almost constant.

Table 7 Number of dx distance calculations in millions (×10⁶) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on 1000K C1N×1000K C2N, in relation to pg

Considering all experiments and all data sets, we find that SCCPS overcomes FCCPS 45-25 times and SRCPS overcomes FRCPS 58-12 times. Comparing the best result among FCCPS and SCCPS and the best result among FRCPS and SRCPS, for every combination of data sets, we conclude that Reverse Run algorithms need fewer dx calculations in all cases (70-0).

Figure 15 shows the number of dx distance calculations of each algorithm as a fraction of the total number of dx distance calculations needed by all algorithms (represented by the respective bar). SRCPS (line with down-facing triangles as markers) needed 20.63 % up to 20.64 % of the total number of dx distance calculations needed to execute the queries. FRCPS has almost equal numbers of dx distance calculations, so its line (with up-facing triangles as markers) is overwritten by the line of the SRCPS. The Reverse Run algorithms need fewer dx distance calculations in all cases.

Fig. 15

Fractions of number of dx distance calculations for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on 1000K C1N×1000K C2N, in relation to pg

6.3.3 The number of the disk accesses (pages read)

The results for the number of disk accesses (pages read) are similar for all input data sets and this performance measure proved to be the most important factor that shaped the results. Table 8 shows the values of this metric when KCPQ is executed by the FCCPS, SCCPS, FRCPS and SRCPS algorithms on the 1000K C1N×1000K C2N data sets. As the disk page size (pg) increases, the number of disk accesses decreases. The rate of this decrement is quite stable. While the disk page size increases geometrically with a ratio of 2, the number of pages read decreases smoothly, for example, in the FRCPS algorithm steps by 50.74 %, 50.00 %, 49.78 %, 49.99 %.

Table 8 Number of disk accesses (pages read) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on 1000K C1N×1000K C2N, in relation to pg

Considering all experiments and all data sets, we find that FCCPS overcomes SCCPS 64-6 times and FRCPS overcomes SRCPS 70-0 times. Comparing the best result among FCCPS and SCCPS and the best result among FRCPS and SRCPS for every combination of data sets, we conclude that FRCPS needs fewer disk accesses in all cases (70-0). Figure 16 shows the values of the number of disk accesses of each algorithm as a fraction of the total number of disk accesses needed by all algorithms (represented by the respective bar).

Fig. 16

Fractions of number of disk accesses (pages read) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on 1000K C1N×1000K C2N, in relation to pg

Summarizing the results of experiments on the effect of disk page size, pg, we note that: (1) Doubling the size of pg causes decrease in execution time not larger than 20 % on real and synthetic data sets and not larger than 30 % on the big real data sets. (2) As pg increases, the number of disk accesses required by the FCCPS and FRCPS algorithms decreases significantly, but for the SCCPS and SRCPS algorithms this decrease is limited. (3) The number of dx distance calculations remains quite stable (not affected by pg). Moreover, (4) the fastest algorithm proves to be FRCPS, while SRCPS proves to be quite economical in terms of dx distance calculations.

6.4 The effect of the size of strips (ss)

In order to examine the effect of the size of the strips (ss) in terms of performance of the new algorithms, we set the value of K = 1000; p g = s s (size of disk page = size of strip), the size of strip (ss) = 2, 4, 8, 16 and 32 KBytes; and there is no LRU buffer (its size is 0). In the previous Section 6.3.1 it was proved that the page size, having constant the size of strip (but larger than the disk page size), affects the execution time up to 20 % in some cases. In order to neutralize this effect of page size with respect to the execution time, we set equal size for pg and ss.

6.4.1 The execution time

The results for execution time are similar for all input data sets. Table 9 shows the execution time in ms when KCPQ is executed by the FCCPS, SCCPS, FRCPS and SRCPS algorithms on the W a t e r×P a r k data sets. As the strip size increases, the execution time is reduced, with a decreasing rate. For example, using SCCPS, from s s = 2K B to s s = 4K B the time decreased by 15.5 %, from s s = 4K B to s s = 8K B by 7 %, from s s = 8K B to s s = 16K B by 1 % and from s s = 16K B to s s = 32K B by 1 %. The Reverse Run algorithms are shown to be faster than the Classic ones.

Table 9 Execution time in ms for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on W a t e r×P a r k, in relation to ss

Figure 17 shows the execution time of each algorithm as a fraction of the total execution time consumed by all algorithms (represented by the respective bar). Considering all experiments and all data sets, we find that SCCPS overcomes FCCPS 54-16 times and FRCPS overcomes SRCPS 52-18 times. Comparing the best result among FCCPS and SCCPS and the best result among FRCPS and SRCPS for every combination of data sets, we conclude that Reverse Run algorithms are the fastest in most cases (68-2). In Fig. 17, it is shown that the increment of the strip size, for sizes larger than 32 KB does not give advantage in query execution time for any algorithm. Experiments with strip sizes larger than 32 KB show that execution becomes slower. The Reverse Run algorithms are faster and the best strip size is 8 or 16 KB for all types of data sets, which, in all cases, is larger than the physical I/O unit.

Fig. 17

Fractions of execution time for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on W a t e r×P a r k, in relation to ss

6.4.2 The number of dx distance calculations

The results for the number of dx distance calculations are similar for all input data sets. Table 10 shows the values of this metric when KCPQ is executed by the FCCPS, SCCPS, FRCPS and SRCPS algorithms on the W a t e r×P a r k data sets. As the value of strip size increases the number of dx distance calculations remains almost constant.

Table 10 Number of dx distance calculations in millions (×10⁶) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on W a t e r×P a r k, in relation to ss

Considering all experiments and all data sets, we find that SCCPS overcomes FCCPS 45-25 times and SRCPS overcomes FRCPS 49-21 times. Comparing the best result among FCCPS and SCCPS and the best result among FRCPS and SRCPS for every combination of data sets, we conclude that the Reverse Run algorithms need fewer dx calculations in all cases (70-0).

Figure 18 shows the number of dx distance calculations of each algorithm as a fraction of the total number of dx distance calculations of all algorithms (represented by the respective bar). It is shown that FRCPS (line with up-facing triangles as markers) needed from 24.48 % up to 24.63 % of the total number of dx distance calculations. The SRCPS algorithm has almost equal number of dx distance calculations so its line (with down-facing triangles as markers) is overwritten from the line of the FRCPS. The Reverse Run algorithms need fewer dx distance calculations in all cases.

Fig. 18

Fractions of number of dx distance calculations for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on W a t e r×P a r k, in relation to ss

6.4.3 The number of the disk accesses (pages read)

The results for the number of disk accesses (pages read) are similar for all input data sets and this performance measure proved to be the most important factor that shaped the results. Table 11 shows the values of this metric when KCPQ is executed by the FCCPS, SCCPS, FRCPS and SRCPS algorithms on the W a t e r×P a r k data sets. As the strip size (ss) increases the number of disk accesses decreases. The rate of this decrement is quite stable. While the strip size increases geometrically with a ratio of 2, the number of pages read decreases, for example, in the SRCPS algorithm, by 54.13 %, 51.47 %, 50.69 % and 50.36 %.

Table 11 Number of disk accesses (pages read) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on W a t e r×P a r k, in relation to ss.

Considering all experiments and all data sets, we find that FCCPS overcomes SCCPS 62-8 times and FRCPS overcomes SRCPS 70-0 times. Comparing the best result among FCCPS and SCCPS and the best result among FRCPS and SRCPS for every combination of data sets, we conclude that FRCPS needs fewer disk accesses in all cases (70-0). Figure 19 shows the number of disk accesses of each algorithm as a fraction of the total number of disk accesses needed by all algorithms (represented by the respective bar).

Fig. 19

Fractions of number of disk accesses (pages read) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on W a t e r×P a r k, in relation to ss

Summarizing the results of experiments on the effect of strip size, ss, we note that: (1) The exponential growth of ss causes decrease in the execution time not larger than 15 % for all, real and synthetic data sets. (2) As ss increases, the number of disk accesses needed by each of the algorithms decreases notably, but the best behaviour for this performance measure is for FRCPS. (3) The number of dx distance calculations remains quite stable (not affected by ss). Moreover, (4) the fastest algorithm proves to be FRCPS, while SRCPS proves to be quite economical in terms of dx distance calculations.

6.5 The effect of the LRU buffer

In order to examine the effect of the size of the LRU buffer on the performance of the new algorithms, we examined several LRU buffer sizes. Although, one might expect that, as a result of finding in RAM (and not reading from disk) some of the strips needed for processing, the execution time would be possibly reduced, in fact, the cost for the management of the LRU-buffer proved to overcome any such reduction and the execution time increased when the LRU buffer size increased. For all LRU buffer sizes, FRCPS proved to be faster than the SRCPS algorithm in double the cases (47-23), and the one with the smallest number of strips found in the buffer (the fastest execution of FRCPS was the one without any buffering). Moreover, the LRU-buffer does not have any effect on the number of dx distance calculations, since this performance measure is not affected whether the data are in RAM or in disk.

6.6 Experimental results for εDJQ

In this section, we study the effect of the increment of the distance threshold (ε) on the εDJQ. In order to examine the effect of ε on the εDJQ algorithms, ε ₁ is set equal to 0 and ε ₂ = ε. ε = 0,1.25×10⁻⁵,2.5×10⁻⁵,5×10⁻⁵ and 10×10⁻⁵ for medium real and synthetic data, and ε = 0,1.25×10⁻³,2.5×10⁻³,5×10⁻³ and 10×10⁻³ for big real data. p g = 4 KBytes, s s = 16 KBytes and there is no LRU buffer (its size is 0).

6.6.1 The execution time

The results for execution time are similar for all input data sets. Table 12 shows the execution time in s when the εDJQ is processed by the εFCCPS, εSCCPS, εFRCPS and εSRCPS algorithms on P a r k×B u i l d data sets. As the value of ε increases the execution time grows, and the rate of the increment continuously grows (after the first non zero value of the maximum distance ε). The εFRCPS algorithm is shown to be faster in the most cases.

Table 12 Execution time in s for εDJQ using εFCCPS, εSCCPS, εFRCPS and εSRCPS on P a r k×B u i l d, in relation to ε

Considering all experiments and all data sets, we find that εFCCPS overcomes εSCCPS 52-18 times and εFRCPS overcomes εSRCPS 50-20 times. Comparing the best result among εFCCPS and εSCCPS and the best result among εFRCPS and εSRCPS for every combination of data sets, we conclude that ε Reverse Run algorithms are faster in the most cases (67-3).

Table 13 shows the values of the execution time of each algorithm as a fraction of the total time consumed by all algorithms on P a r k×B u i l d data sets. It is shown that the εFRCPS needed from 20.43 % up to 23.82 % of the total time to execute the queries and it is the fastest algorithm for all values of ε > 0. For, ε = 0 the εSRCPS algorithm was faster, since its fraction of time was 17.37 %.

Table 13 Fractions of execution time of each algorithm over the total execution time for εDJQ using εFCCPS, εSCCPS, εFRCPS and εSRCPS on P a r k×B u i l d, in relation to ε

6.6.2 The number of dx distance calculations

The results for the number of dx distance calculations are similar for all input data sets. Table 14 shows the values of this metric when εDJQ is processed by the εFCCPS, εSCCPS, εFRCPS and εSRCPS algorithms on P a r k×B u i l d data sets. As the value of ε increases the number of dx distance calculations also increases. However, while the value of ε increases geometrically with a ratio of 2, the number of dx distance calculations increases to a same ratio near to 2.

Table 14 Number of dx distance calculations in billions (×10⁹) for εDJQ using εFCCPS, εSCCPS, εFRCPS and εSRCPS on P a r k×B u i l d, in relation to ε

Considering all experiments and all data sets, we find that εSCCPS overcomes εFCCPS 70-0 times and εFRCPS overcomes εSRCPS 35-29 times. Comparing the best result among εFCCPS and εSCCPS and the best result among εFRCPS and εSRCPS for every combination of data sets, we conclude that Reverse Run algorithms need fewer dx distance calculations in all cases (70-0).

Table 15 shows the number of dx distance calculations of each algorithm as a fraction of the total number of dx distance calculations needed by all algorithms on P a r k×B u i l d data sets. It is shown that the εFRCPS needed 4.63 % for the case of ε = 0 and for the other cases from 24.21 % up to 24.91 % of the total number of dx distance calculations. The εSRCPS algorithm has a little fewer dx distance calculations than εFRCPS only in the case ε = 0 and in all other cases the number of dx distance calculations is almost equal. The Reverse Run algorithms need fewer dx calculations in all cases.

Table 15 Fraction of number of dx distance calculations of each algorithm over the total number of dx distance calculations for εDJQ using εFCCPS, εSCCPS, εFRCPS and εSRCPS on P a r k×B u i l d, in relation to ε

6.6.3 The number of the disk accesses (pages read)

The results for the number of disk accesses (pages read) are similar for all input data sets and this performance measure proved to be the most important factor that shaped the results. Table 16 shows the values of this metric when εDJQ is executed by the εFCCPS, εSCCPS, εFRCPS and εSRCPS algorithms on P a r k×B u i l d data sets. As the value of ε increases, the number of disk accesses increases. But the rate of this increment is too small for the Reverse Run algorithms and bigger for the Classic ones. While ε increases geometrically with a ratio of 2, the number of pages read increases with a lower ratio, for example, the number of pages read for the εFRCPS algorithm increases by 1.57 %, 1.51 %, 3.00 % and 5.80 %.

Table 16 Number of disk accesses (pages read) in thousands (×10³) for εDJQ using εFCCPS, εSCCPS, εFRCPS and εSRCPS on P a r k×B u i l d, in relation to ε

Considering all experiments and all data sets, we find that εFCCPS overcomes 63-7 times εSCCPS and εFRCPS overcomes 57-0 times εSRCPS (there are 13 cases of tie). Comparing the best result between εFCCPS and εSCCPS and the best result between εFRCPS and εSRCPS for every combination of data sets, we can conclude that ε Reverse Run algorithms need fewer disk accesses in all cases (70-0). Table 17 shows the values of the number of disk accesses of each algorithm as a fraction of the total number of disk accesses needed by all algorithms.

Table 17 Fraction of number of disk accesses of each algorithm on the total number of disk accesses for εDJQ using εFCCPS, εSCCPS, εFRCPS and εSRCPS on P a r k×B u i l d, in relation to ε

Summarizing the results of experiments on the effect of ε, note that: (1) the geometrical growth of ε causes a non-geometrical increase of execution time. (2) the exponential growth of ε causes an increase in the number of dx distance calculations with a lower ratio (ranging very close to 2). (3) The number of disk accesses required by εFCCPS and εFRCPS algorithms increases marginally with the growth of ε, unlike εSCCPS and εSRCPS, where the increment is more pronounced. Moreover, (4) faster algorithm proves to be the εFRCPS than εSRCPS (50-20), while εFRCPS proves to be more economical in terms of dx distance calculations than εFRCPS (35-29).

The experiments were continued in the same manner as in Sections 6.3, 6.4 and 6.5 for KCPQ, in order to study the effect of the disk page size, the strip size and the size of the LRU-buffer. In general, the results are similar between KCPQ and εDJQ. The fastest in execution time and reading fewer pages from the disk proved to be the εFRCPS algorithm. We note only that, for the case of ε = 0, SRCPS is slightly better than FRCPS. For the cases where ε > 0, the results for εFRCPS are not as good as the ones of FRCPS. This is explained, since the most important factors that improve the performance of an algorithm for the KCPQ are (1) how quickly pairs with very small distances will enter the m a x K H e a p, and (2) how efficiently the algorithm will manage the largest distance of these pairs. In contrast to KCPQ, εDJQ does not need the fast finding of pairs with small distance, since the maximum acceptable distance is consistently defined by the user beforehand (ε). Only the smart and economical management of the given distance affects the final performance of an algorithm.

6.7 Effectiveness study

To study the effectiveness of the proposed algorithms we will use the selection ratio, that is, the fraction of pairs considered by the new algorithms for processing over the total number of possible pairs (a pair is selected for processing if its dx distance is smaller than the distance of the K-th closest pair found so far). This effectiveness measure is the opposite to the pruning ratio, and therefore the smaller the selection ratio, the higher the power of pruning of the algorithm.

We are going to focus on the increment of K. Tables 18 and 19 report the effect of K on the selection ratio for real and synthetic data, respectively. In order to extract conclusions from the tables, we have to take into account that for the specific combination of real data there are 191,558×1,134,164= 217,258,187,512 possible pairs (2.17×10¹¹) and for the specific synthetic data there are 10¹² possible pairs. We can observe that an increasing K makes the selection ratio of the proposed algorithms to increase continuously. Therefore, the effectiveness of our algorithms degrades as K turns to be too large, due to the increase of the distance of the K-th closest pair. And, the larger the K value, the smaller the difference between Reverse Run algorithms and Classic plane-sweep algorithms (we mainly observe this fact on real data) in terms of selection ratio. From these tables, we observe that SRCPS is the winner in most of the cases, but FRCPS is very close to it (being the winner in the remaining cases). This means that FRCPS sacrifices slightly effectiveness for efficiency, in the use of the partitioning technique. An interesting conclusion from this effectiveness measure is that the best algorithms in pruning are the Reverse Run ones and this conclusion is in accordance to efficiency. Moreover, since the selection ratio depends on the dx distance, it is the most representative measure for pruning and for effectiveness.

Table 18 Fraction of pairs (×10⁻⁶) processed over the total number of possible pairs (selection ratio) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on N A r r N×N A r d N D

Table 19 Fraction of pairs (×10⁻⁶) processed over the total number of possible pairs (selection ratio) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS on 1000K C1N×1000K C2N

We note that the average performance in pruning, for all combinations of real and synthetic data, follows the same trend. This behaviour is shown in Tables 20 and 21, where SRCPS is the winner in most of the cases, but FRCPS is very close to it.

Table 20 Average fraction of pairs (×10⁻⁶) processed over the total number of possible pairs (selection ratio) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS for all real data sets

Table 21 Average fraction of pairs (×10⁻⁶) processed over the total number of possible pairs (selection ratio) for KCPQ using FCCPS, SCCPS, FRCPS and SRCPS for all synthetic data sets

6.8 Performance comparison to R-trees

In order to examine the performance of the new algorithms in comparison to a widely accepted access method, like R-trees, we have performed experiments for measuring:

• The creation time of the sorted files needed for the new algorithms and the creation time of the R-tree structure. In the case of the new algorithms, we used external merge sort with 16 buffers of 16KB and in the case of the R-tree, we used advanced bulk loading [48] (using code available form http://libspatialindex.org), to reduce the time needed for tree construction.

• The execution time and number of disk accesses for processing the KCPQ and εDJQ.

The experiments were run for the following data set combinations: N A r r N×N A r d N, N A r r N D×N A r d N D, 500K C1N×500K C2N, 500K C2N×1000K C1N, 1000K C1N×1000K C2N, W a t e r×P a r k, W a t e r×B u i l d and P a r k×B u i l d.

6.8.1 Experimental results for KCPQ

Table 22 shows the name and the number of objects for each data set in ascending order of size. It also shows the sizes and creation times of the R-tree structure and sorted data files used by the new algorithms. It is obvious that the size of the files used by the new algorithms is approximately 3.7 times smaller than the size of the R-tree structure. The time for the creation of files for the new algorithms ranges from 3.9 up to 8.6 times smaller than the time for the R-tree structure.

Table 22 Creation time of R-tree structures and sorted data files used by the new algorithms, for several data sets

The 8 combinations of data sets were chosen in order to take measurements between small and big data sets and also between real and synthetic data sets. We have chosen the fastest algorithm executing the KCPQ with R-trees, the CCPS-BF. It is the algorithm which scans the nodes of the R-tree in Best First manner (using one global minimum heap to sort the pairs of the nodes reached so far with minmin distance) and when a pair of leafs is reached, the pairs of points are processed using the classic plain sweep algorithm. On the other hand we have chosen to compare to the FRCPS algorithm executing the same KCPQs because it is faster than SRCPS algorithm in more cases (36-34) of all combinations and all K values. The smaller number of total pairs was for the combination N A r r N×N A r d N having a total number of pairs equal to 191,558×569,082, while the biggest number of total pairs was for the combination P a r k×B u i l d data sets having a total number of pairs equal to 11,504,035×114,736,611. Observing the values of the metrics of experiments on real and synthetic data for the first 5 combinations we see that the FRCPS was the absolute winner for all values of K and for all metrics. Table 23 shows both the values of query time and total time (creation + query) needed by the CCPS-BF and FRCPS algorithms to execute the KCPQ on N A r d N×N A r d N D data sets. As the value of K increases, the relative difference of execution time between the two algorithms is slightly reduced (gain by 93.16 %, 93.16 %, 92.88 %, 91.03 % and 88.70 %). The total time, creation and query execution time showcased similar behavior with an even smaller reduction. FRCPS needs less total time by gain by 83.61 %.

Table 23 Query execution time(ms) and total time(s) (creation+execution) of CCPS-BF and FRCPS for N A r d N×N A r d N D data sets

In Table 24 (second and third columns) we can see the number of disk accesses when the KCPQ is executed by the CCPS-BF and FRCPS algorithms on N A r d N×N A r d N D data sets. The increment of K didn’t significantly affect the number of needed disk accesses for both algorithms. FRCPS again proved to be more efficient than CCPS-BF by an average gain of 88.73 %.

Table 24 Number of disk accesses of CCPS-BF and FRCPS algorithms for N A r d N×N A r d N D and W a t e r×B u i l d data sets

Table 25 shows the values of query time and total time (creation + query) when the KCPQ is executed by the CCPS-BF and FRCPS algorithms on the combination of big data sets W a t e r×B u i l d. As the value of K increases, the relative difference of execution time between the two algorithms didn’t showcase a clear pattern. The FRCPS remained faster for all K values smaller than 10.000 while CCPS-BF was faster for the last value of K. The relative differences (gain) are as follows: 8.99 %, 54.35 %, 49.14 %, 35.93 % and −39.13 %. For positive (negative) values the FRCPS is faster (slower). FRCPS was also faster for all K values of the total time, creation and query execution time. FRCPS needs less total time by 88.09 %. In Table 24 (forth and fifth columns) we can see the number of disk accesses in relation to K values for the same data sets combination. The increment of K didn’t significantly affect the number of needed disk accesses for both algorithms. FRCPS again proved to be more efficient than CCPS-BF by an average gain of 12.58 %.

Table 25 Query execution time(s) and total time(s) (creation+execution) of CCPS-BF and FRCPS for W a t e r×B u i l d data sets

Considering all experiments and all data sets, we find that FRCPS overcomes CCPS-BF 38-2 times for query execution time, 40-0 for total time and 38-2 times for disk accesses.

6.8.2 Experimental results for εDJQ

The same 8 combinations of data sets were used in order to take measurements while executing the εDJQs with ε = 0,1.25×10⁻⁵,2.5×10⁻⁵,5×10⁻⁵ and 10×10⁻⁵ for the first 5 combinations (medium real and synthetic data), and with ε = 0,1.25×10⁻³,2.5×10⁻³,5×10⁻³ and 10×10⁻³ between the last 3 combinations (big real data). We have chosen the fastest algorithm for executing εDJQ with R-trees: the εCCPS-BF. On the other hand we have chosen to compare to the εFRCPS algorithm executing the same εDJQs because it is faster than εSRCPS algorithm in more cases (50-20) of all combinations and all ε values. Observing the values of the metrics of experiments on real and synthetic data, small or big data sets for all the 8 combinations we see that the εFRCPS was the absolute winner for all values of ε and for all metrics. Table 26 shows both the values of query time and total time (creation + query) needed by the εCCPS-BF and εFRCPS algorithms to execute the εDJQ on the biggest combination, P a r k×B u i l d data sets. As the value of ε increases, the relative difference of execution time between the two algorithms was slightly reduced (gain by 98.62 %, 96.76 %, 94.88 %, 91.16 % and 83.95 %). The total time, creation and query execution time showcased similar behavior with an even smaller reduction. εFRCPS needs less total time gain of 88.80 %.

Table 26 Query execution time(s) and total time(s) (creation+execution) of εCCPS-BF and εFRCPS for P a r k×B u i l d data sets

In Table 27 we can see the number of disk accesses when εDJQ is executed by the εCCPS-BF and εFRCPS algorithms on P a r k×B u i l d data sets. The increment of ε didn’t significantly affect the number of needed disk accesses for both algorithms. εFRCPS again proved to be more efficient than εCCPS-BF by an average gain of 89.46 %.

Table 27 Number of disk accesses of εCCPS-BF and εFRCPS algorithms for P a r k×B u i l d data sets

Considering all experiments and all data sets, we find that εFRCPS overcomes εCCPS-BF in all cases of ε values and for all data sets in all performance metrics.

6.9 Conclusions from the experiments

In our previous work [1], it was shown that the Reverse Run PS algorithms are faster than the Classic ones for the KCPQ, when the data is stored and processed in main memory. Classic PS algorithms always process data sets from left to right and the runs of the two sets are generally interleaved. On the other hand, RR PS algorithms process pairs of points in opposite sweeping order, starting from pairs of points that are the closest possible to each other, avoiding further processing of pairs that is guaranteed not to be part of the final result and restricting the search space by using dx distance values on the sweeping axis. Due to these, the pruning distance (key dist of MaxKHeap root) is expected to be updated more quickly and the query processing cost of RR PS algorithms is expected to be smaller.

From the experiments presented previously, when the data are stored on disk, we conclude that the main factors that determine the execution time are: (1) The number of operations and comparisons; (2) The number of pages that are transferred from disk to main memory; (3) The volume of memory required and its management; and (4) How quickly m a x K H e a p is filled up with pairs having small distances and how fast the pruning distance is reduced (it is important for the KCPQ, unlike the εDJQ), because the lower its value is, the greater the power of pruning. Each of these factors affects differently the final result. FRCPS is faster in more cases, considering different values of K, disk page size (pg), size of strips (ss) and size of LRU buffer (bs), although SRCPS requires less memory in comparison to FRCPS.

With respect to the number of dx distance calculations, the SRCPS algorithm seems to be better (lower number of calculations) in most cases, although FRCPS is quite close (i.e. the difference compared to SRCPS in total calculations is rather small). This is due to the fact that for the RR PS algorithms, if we ignore the non-sweeping dimension, the number of calculations can be proved to be optimal, since we always start with the closest pair of points.

With respect to the number of disk accesses, FRCPS needs the least disk accesses in all experiments (considering different values of K, pg and ss). This is due to the combination of RR PS processing and the uniform filling technique, since, for uniform filling, the number of strips is predefined beforehand and it is smaller than for uniform splitting (higher non-uniformity of data leads to larger difference between the two techniques). This means that the number of strips read from disk, or the number of disk accesses, is smaller. In addition, the number of disk accesses seems to be the most influential factor governing an algorithm’s efficiency in execution time, and the difference between SRCPS and FRCPS becomes significant for this performance measure: FRCPS is totally dominating, and thus, faster.

In conclusion, FRCPS is the best algorithm for all performance or efficiency measures for the following reasons:

• 1. a smaller number of strips partition the space,

• 2. a smaller number of strips are read from disk,

• 3. a more consistent application of RR PS processing is applied in the management of strips.

Moreover, this work emphasizes on the effective use of dx distance for pruning, considering the selection ratio as the effectiveness measure. The main conclusion in this context is that RR PS algorithms are the most effective ones for pruning, highlighting that SRCPS is slightly better than FRCPS.

Finally, from this extensive experimental study of the new algorithms, we conclude that RR PS algorithms are the most efficient and effective ones for the KCPQ and εDJQ, and the FRCPS variant is the best one.

Regarding the comparison of the new algorithms to the widely accepted R-tree based methods, the file needed by the new algorithms is created in extremely smaller time than the R-tree structure. The best new algorithm (FRCPS) answers the KCPQ in significantly smaller time than the best R-tree based algorithm (CCPS-BF), in most cases. It is slower in only 2 cases out of the 40 cases studied. An analogous situation (in 2 out of the 40 cases the new algorithm looses) arises for the number of disk pages read by the algorithms. This can be attributed to the data distribution of these cases that favors the algorithms that work on a tree structure. Nevertheless, even in these 2 cases, the total (creation + query) time of the new algorithm for answering the KCPQ is significantly smaller. The best new algorithm (εFRCPS) answers the εDJQ in significantly smaller time and with significantly less pages read from disk than the best R-tree based algorithm (εCCPS-BF), in all cases. The fact that the εDJQ requires finding of all (not only K) pairs within a specified distance forces the R-tree algorithms to search within the whole tree, and thus the new algorithm is faster even in the above 2 cases.

Overall, even when the data sets do not change at a very rapid rate, or are reusable for subsequent queries, the best new algorithm is a better choice than the best R-tree based algorithm for the KCPQ and the εDJQ.

7 Conclusions and future work

This paper has presented several efficient and effective algorithms (FCCPS, SCCPS, FRCPS and SRCPS) for the KCPQ and εDJQ, when neither inputs are indexed. First of all, we have enhanced the classic plane-sweep algorithm for DJQs with two improvements: sliding window and sliding semi-circle. Next, we proposed a new algorithm called Reverse Run Plane-Sweep, that improves the processing of the classic plane-sweep algorithm for DJQs, minimizing the Euclidean and sweeping axis distance calculations. Then, as the main contribution of this work, four algorithms (FCCPS, SCCPS, FRCPS and SRCPS) for KCPQ and εDJQ are proposed, without the use of indexes on both disk-resident data sets. These four algorithms employ a combination of plane-sweep and space partitioning techniques to join the data sets. We also presented results of an extensive experimental study, where efficiency and effectiveness measures are explored for the proposed algorithms. From this performance study, that was conducted on medium and big spatial (real and synthetic) data sets, when neither input is indexed, we conclude that RR PS algorithms are the most efficient and effective for the KCPQ and εDJQ, and that FRCPS is the best variant, which combines RR PS processing with uniform filling partitioning technique. Finally, the best of the new algorithms was experimentally compared to the best algorithm that is based on the R-tree (a widely accepted access method), for KCPQs and εDJQs and it was shown that the new algorithms outperform R-tree based algorithms, in most cases. For future work, we plan to further investigate the adaptation of the new plane-sweep-based algorithms, when neither input is indexed, to other DJQs (as Iceberg Distance Join Query [42] and K Nearest Neighbour Join query [43]). Moreover, it would be interesting to study approximate implementations of the proposed algorithms by using the distance-based approximate techniques presented in [37] and to implement new in-memory DJQ algorithms inspired in the disk-based approaches.