A Pseudo-dynamic Approach for Seismic Stability Analysis of Rock Slopes in Hoek–Brown Media

Abstract

Earthquake is a major trigger for failure of rock slope in seismically active regions. This study presents a novel pseudo-dynamic approach for predicting the seismic stability of slopes in Hoek–Brown rock masses, in which the earthquake effect is characterized by a sinusoidal seismic wave with a motion amplification behavior. The discretization kinematic analysis combined with generalized tangent technique is also used to construct the failure mechanism of the rotation sliding of seismic slopes. The methodology was validated through comparison with published results and numerical simulation. The effect of temporal and spatial varying of seismic waves on slope stability was investigated. The results indicate that the pseudo-static approach may over or underestimate the stability of rock slopes. The pseudo-dynamic analysis is recommended to provide a more meaningful solution of safety factors. A parametric study was also carried out to explore the effect of rock strength, slope geometry, and earthquake parameters.

1 Introduction

Earthquake-induced landslides often cause heavy casualties and property loss due to their great suddenness and destructiveness. The prediction of seismic stability is of great significance in slope engineering such as dam filling, open pit excavation, and highway construction.

Characterization of earthquake effect is a procedure of great importance in seismic slope analysis, as it is directly associated with the accuracy of stability prediction. In general, seismic signals can be characterized as displacement, velocity, or acceleration in the time domain. For slope stability problems, peak acceleration characterization is more often used (Li et al. 2009).

A common peak acceleration characterization-based approach is the conventional pseudo-static (PS) method, in which the seismic acceleration is assumed constant with space and time, and can be regarded as static forces in horizontal and/or vertical directions. Pseudo-static method has been widely employed in theoretical works (Li et al. 2009; Jiang et al. 2016), however, it completely ignores the dynamic nature of seismic input.

Another strategy to represent the earthquake effect is taking the actual acceleration time history measured in situ. The time-history (Zhou et al. 2013) method is more reliable than pseudo-static method because it makes full use of the ground vibration information. However, this method needs enormous computational cost, which hinders the use in scenarios where require high computational efficiencies are required, such as reliability analysis and rapid assessment.

A sound compromise between PS and time history methods is pseudo-dynamic (PD) method (Choudhury and Nimbalkar 2007; Pain et al. 2017). PD method employs a sinusoidal function to characterize the seismic acceleration because a specific signal can be expressed as a weighted sum of sinusoidal signals by the Fourier transform. This assumption makes that dynamic properties of seismic acceleration can be expressed by a relatively simple theoretical derivation in PD method.

The pseudo-dynamic approach was originally proposed for the earth pressure problem of a retaining wall (Choudhury and Nimbalkar 2007; Ghosh 2007), and was later extended to the field of slope stability analysis. Qin and Chian (2018a) used the pseudo-dynamic method to analyze the seismic stability of soil slopes with non-uniformly distributed friction angles. Hou et al. (2019) carried out a pseudo-dynamic analysis on heterogeneous soil slope with a crack. However, the pseudo-dynamic analysis is currently limited to soil slopes, which is inconsistent with the fact that many seismic geological hazards are caused by the failure of rock slopes.

The strength properties of soils and rocks are significantly different. Soils broadly obey linear strength properties, but most types of rock, which contain discontinuities, including joints, fractures, and bedding planes, exhibit significant nonlinearity in a shear failure behavior.

Therefore, the linear criterion suitable for soils is inapplicable to describe the shear strength of rock masses. To address this problem, some nonlinear strength criteria are proposed, among which the Hoek–Brown criterion is the most widely used one. This criterion is summarized from a large number of triaxial test results and covers a wide range of rock types from intact rock to highly fractured rock masses.

Many theoretical efforts have been contributed to seismic stability assessment of slopes in Hoek–Brown media (Li and Yang 2018; Xu and Yang 2018). But to our knowledge, only the pseudo-static strategy has been used. However, performing a pseudo-dynamic analysis in nonlinear Hoek–Brown rock still poses a challenge. Notice that the commonly used limit equilibrium method cannot well handle this nonlinear problem (Deng et al. 2017; Lin et al. 2014). This paper uses the kinematic analysis method to conduct the PD analysis for Hoek–Brown slope, as this method has the rigor of plastic mechanics (He et al. 2011; Michalowski 2010).

In particular, the present study uses a novel discretization technique to construct the failure mechanism in kinematic analysis (Qin and Chian 2018a, b, 2019). This technique decomposes the velocity discontinuity surface into numbers of infinitesimal components, so it is especially suitable for taking the spatial varying seismic acceleration into account.

This article is organized as follows: Firstly, the fundamental methodology of this paper is briefly introduced, and then the derivation process, calculation formula, and optimization strategy of the proposed pseudo-dynamic method are introduced in detail. The verification of the present method was conducted from both theoretical calculations and numerical simulations. A comparison of pseudo-static/dynamic solutions was presented to highlight the superiority of the pseudo-dynamic analysis for rock slopes. Finally, a parametric analysis provides the impact of rock strength, slope geometry, and earthquake effect on slope stability.

In addition, two other points of this paper need to be stressed: (1) The safety factor is adopted as the slope stability index with a corresponding calculation procedure proposed. Most relevant studies used the limit state indicators such as stability number and critical reinforcement strength, which are of less significance in practice engineering. (2) A numerical validation with FLAC^3D is carried out through a stress-extract technique, compensating the shortage that all previous validations of pseudo-dynamic analysis are theoretical.

2 Methodology

2.1 Hoek–Brown Failure Criterion and Generalized Tangential Technique

As mentioned above, a nonlinear criterion is more appropriate for rocks (Hoek and Brown 1980, 1988). Through an extensive review of triaxial test results, Hoek and Brown proposed the widely accepted Hoek–Brown criterion as follows (Hoek and Brown 1997; Hoek et al. 1992, 2002):

$$\sigma_{{1}} - \sigma_{3} = \sigma_{{\text{c}}} \left( {\frac{{m\sigma_{3} }}{{\sigma_{{\text{c}}} }} + s} \right)^{n}$$

(1)

where $\sigma_{1}$ and $\sigma_{3}$ are the maximum and minimum principal stresses respectively, $\sigma_{c}$ is the uniaxial compressive stress of the rock mass. $m$, $s$ and $n$ are dimensionless parameters to represent the fracturing degree of rock masses.

These three parameters can be derived from the following equations:

$$m = m_{{\text{i}}} \exp \left( {\frac{GSI - 100}{{28 - 14D_{0} }}} \right)$$

(2)

$$s = {\text{exp}}\left( {\frac{GSI - 100}{{9 - 3D_{0} }}} \right)$$

(3)

$$n = \frac{1}{2} + \frac{1}{6}\left[ {\exp \left( { - \frac{GSI}{{15}}} \right) - \exp \left( { - \frac{20}{3}} \right)} \right]$$

(4)

The geological strength index $GSI$ quantifies the degree of weathering and structure of rock mass, which can overcome the limitations of the RMR system (Bieniawski 1979) and Q-system (Barton 2002). $GSI$ values 5 (for extremely poor rock masses) to 100 (for intact rock). $D_{0}$ represents the degree of rock disturbance, where $D_{0} = 0$ indicates that the rock mass is undisturbed and $D_{0} = 1$ indicates that the rock mass has been severely disturbed. $m_{{\text{i}}}$ denotes the hardness of the rock mass. Its value is determined by uniaxial tests, and the suggested value by Hoek (1990) can be used when test data are not available.

Although Hoek–Brown criterion gives a more reasonable description of the rock strength, its nonlinearity hinders its direct utilization in theoretical reasoning.

To solve the problem, the Hoek–Brown parameters are converted to equivalent Mohr–Coulomb parameters using a generalized tangent technique in this paper (Yang et al. 2004; Yang and Yin 2004). As shown in Fig. 1, the intercept of the tangent line of the Hoek–Brown envelope with the $\tau$-axis is the cohesion value, and the arctangent of its slope is the frication angle value.

Fig. 1

Tangential line to the Hoek–Brown criterion

The tangential line can be expressed as follows:

$$\tau = c_{t} + \sigma_{n} \tan \varphi_{t}$$

(5)

where $c_{t}$ and $\varphi_{t}$ are instantaneous cohesion and friction angle, respectively.

Equation (5) is a reasonable linear alternative of Hoek–Brown failure criterion, as the yield surface that completely covers the actual yield surface yields an upper bound solution of limit load. In addition, it is worth noting that the tangential technique is only applicable to the convex failure criterion.

The equivalent cohesion and friction angle can be expressed (Yang et al. 2004):

$$\frac{{c_{t} }}{{\sigma_{c} }} = \frac{{\cos \varphi_{t} }}{2}\left[ {\frac{{mn\left( {1 - \sin \varphi_{t} } \right)}}{{2\sin \varphi_{t} }}} \right]^{{\frac{n}{1 - n}}} - \frac{{\tan \varphi_{t} }}{m}\left( {1 + \frac{{\sin \varphi_{t} }}{n}} \right)\left[ {\frac{{mn\left( {1 - \sin \varphi_{t} } \right)}}{{2\sin \varphi_{t} }}} \right]^{{\frac{1}{1 - n}}} + \frac{s}{m}\tan \varphi_{t}$$

(6)

2.2 Pseudo-dynamic method

Generally, the main drawbacks of the pseudo-static analysis can be summarized in two points.

• (1) The pseudo-static method assumes that wave velocity of soil/rock is infinite, not consistent with the fact that the real velocity of soils or rocks ranges from several hundred to thousands meters per second. Therefore the phase change in the wave propagation process cannot be considered in pseudo-static analysis.

• (2) Field study (Zhang et al. 2018) shows that peak acceleration in the top zone of slope can be significantly larger than the input base acceleration, due to the slope geometry. But this acceleration amplification is not considered by pseudo-static method.

The pseudo-dynamic method was proposed to overcome the two shortcomings above. This method postulates that seismic waves propagate at a finite velocity within the geotechnical medium, and the incident seismic waves are assumed in the vertical direction. The primary wave velocity $V_{{\text{p}}}$ and shear wave velocity $V_{{\text{s}}}$ can be determined from experimental data or equations based on elastic mechanics: $V_{{\text{p}}} = \sqrt {{{2G\left( {1 - v} \right)} \mathord{\left/ {\vphantom {{2G\left( {1 - v} \right)} {\rho \left( {1 - 2v} \right)}}} \right. \kern-\nulldelimiterspace} {\rho \left( {1 - 2v} \right)}}}$ and $V_{{\text{s}}} = \sqrt {{G \mathord{\left/ {\vphantom {G \rho }} \right. \kern-\nulldelimiterspace} \rho }}$ (Choudhury and Nimbalkar 2007), where $v$ is the Poisson ratio, $\rho$ is density, and $G$ is the shear modulus. Thus, the phase differences in primary and shear waves between any two points with height distance h within the slope are $V_{{\text{p}}} /h$ and $V_{{\text{s}}} /h$.

To encompass more scenarios, the pseudo-dynamic analysis assumed that seismic wave amplitude increases linearly with height in a slope and introduces the amplification factor $f$ to quantify the acceleration amplification. $f$ is the ratio of the amplified acceleration of the ground surface to the base acceleration at the slope bottom.

Combined the presumptions of finite wave velocity and motion acceleration, the seismic wave acceleration varies with height $y$ and time $t$ as follows:

$$\left\{ \begin{aligned} a_{{\text{h}}} = & \left[ {1 + \frac{y}{H}\left( {f - 1} \right)} \right]k_{{\text{h}}} g\sin 2\pi \left( {\frac{t}{T} - \frac{y}{{\lambda_{{\text{s}}} }}} \right) \\ a_{{\text{v}}} = & \left[ {1 + \frac{y}{H}\left( {f - 1} \right)} \right]k_{{\text{v}}} g\sin 2\pi \left( {\frac{t}{T} - \frac{y}{{\lambda_{{\text{p}}} }} + \frac{{t_{0} }}{T}} \right) \\ \end{aligned} \right.$$

(7)

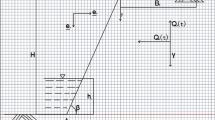
where the $k_{{\text{h}}}$ and $k_{{\text{v}}}$ are horizontal and vertical seismic coefficients related to earthquakes, respectively. $T$ is the period of seismic propagation, $\lambda_{{\text{s}}} = TV_{{\text{s}}}$ and $\lambda_{{\text{p}}} = TV_{{\text{p}}}$ are the wavelengths of shear wave and primary wave, $g$ is the gravitational acceleration, $t_{0}$ is the initial phase difference between shear and primary waves at the slope base, $H$ is the slope height, as sketched in Fig. 2.

Fig. 2

Discrete failure mechanism of slope

It is noteworthy that a modified pseudo-dynamic approach was proposed to strictly satisfy the boundary condition (Bellezza 2014; Pain et al. 2017). However, this simplified pseudo-dynamic approach was used in this study because it gives a sufficiently reasonable description of seismic waves and pseudo-dynamic analysis of rock slope is limited at this juncture.

2.3 Failure Mechanism and Computation Procedure

2.3.1 Generation of Failure Mechanism

A kinematically admissible mechanism is required in kinematic analysis. Commonly a log-spiral mechanism is used to characterize velocity fields of a slope under normal circumstances. But this mechanism is not suitable in the scenario of pseudo-dynamic since it will face complex integral calculation when taking spatially variation of seismic acceleration into account.

Thus, a recently proposed discretization technique is adopted in this paper. This technique designs a ‘point-to-point’ principle to generate the sliding surface, the points of which are systematically deduced from the previous known point. Its discrete characteristic provides avenues to consider more complications that cannot be readily resolved in the conventional approach.

A discretization failure mechanism is graphically illustrated in Fig. 2. The rotation center O is determined by two independent variables $\theta_{0}$ and $r_{0}$, where $r_{0}$ is the initial radius line OC, and $\theta_{0}$ is the initial angle of radius OC.

The key to mechanism generation is to locate the infinitesimal segment $P_{i} P_{i + 1}$ that is enclosed by two adjacent radial lines. The generation procedure starts from point C, processing towards the slope crest BA. The location of any point $P_{i + 1}$ can be derived from the previous known point $P_{i}$, which is due to the adoption of the associated flow rule (Mollon et al. 2011; Hou et al. 2019). The coordinate $P_{i + 1} \left( {x_{i + 1} ,y_{{i{ + }1}} } \right)$ can be expressed as follows in the established coordinate system with the origin at point C.

$$\left\{ \begin{aligned} x_{i + 1} = & x_{i} + \frac{{\sqrt {\left( {x_{i} - x_{{\text{o}}} } \right)^{2} + \left( {y_{i} - y_{{\text{o}}} } \right)^{2} } \times \sin {\updelta }\theta }}{{\sin \left( {\pi /2 + \varphi - {\updelta }\theta } \right)}} \times \cos \left( {\theta_{i} - \pi /2 + \varphi } \right) \\ y_{i + 1} = & y_{i} + \frac{{\sqrt {\left( {x_{i} - x_{{\text{o}}} } \right)^{2} + \left( {y_{i} - y_{{\text{o}}} } \right)^{2} } \times \sin {\updelta }\theta }}{{\sin \left( {\pi /2 + \varphi - {\updelta }\theta } \right)}} \times \sin \left( {\theta_{i} - \pi /2 + \varphi } \right) \\ \end{aligned} \right.$$

(8)

where $\left( {x_{i} ,y_{i} } \right)$ and $\left( {x_{{\text{o}}} ,y_{{\text{o}}} } \right)$ are the coordinates of points $P_{i}$ and O, respectively, ${\updelta }\theta$ is the angle between two adjacent radii $OP_{i}$ and $OP_{i + 1}$. $\theta_{i}$ is the angle between the negative x-axis and radius $OP_{i}$.

The point generation is performed repeatedly until the slip surface exceeds the ground surface. Then, a linear interpolation is conducted to make the endpoint exactly located on the top surface. The value of ${\updelta }\theta$ is set to 0.1° to achieve a good balance between accuracy and efficiency.

2.3.2 Rates of External Work and Internal Dissipation

In establishing the energy balance equation, the external work rate and the internal energy dissipation need to be determined. For the present mechanism, the external working rate is provided by rock gravity and seismic forces, and the energy dissipation only occurs on the slip surface.

The total value of external work rates is calculated through the summation of that of every element ${\text{C}}_{i}$ (Fig. 3). In triangular and trapezoidal element methods, the work rate of soil gravity is both caused by the weight of soil mass of sliding block. The selection of triangular or trapezoidal method determines the discretization of sliding block in gravity work rate calculation but has no impact on the obtained total work rate. The trapezoidal element is used as a fundamental element as it is more suitable to account for the seismic effect which is invariant with height.

Fig. 3

a Triangular element, b Trapezoidal element

As shown in Fig. 3b, $j$ trapezoidal elements are obtained when the sliding surface consists of a total of $j + 1$ points. The gravity work rate can be expressed as:

$$W_{{\text{G}}} { = }\sum\limits_{j} {\gamma S_{i} \omega \left( {x_{{C_{i} }} - x_{{\text{o}}} } \right)}$$

(9)

It is worth noting that, the use of the moment of inertia is more rigid for a rotational mechanism. However, here we use the moment of force instead of the moment of inertia because we assume the failure mechanism rotates at a slight virtual angular velocity. Here, we also assume that seismic forces are constant in a trapezoidal element. The assumption is to avoid more complicated computation, and in fact, does not cause significant errors.

As with the work rate of gravity, the work rate of horizontal and vertical seismic force can be calculated as follows:

$$\left\{ \begin{aligned} W_{{{\text{seismic}} - {\text{h}}}} = & \sum {\gamma S_{i} \omega \left( {y_{{\text{o}}} - y_{{C_{i} }} } \right) \times \left[ {1 + \frac{{y_{i} }}{H}\left( {f - 1} \right)} \right]k_{{\text{h}}} \sin 2\pi \left( {\frac{t}{T} - \frac{{y_{i} }}{{\lambda_{{\text{s}}} }}} \right)} \\ W_{{\text{seismic - v}}} = & \sum {\gamma S_{i} \omega \left( {x_{{C_{i} }} - x_{{\text{o}}} } \right) \times \left[ {1 + \frac{{y_{i} }}{H}\left( {f - 1} \right)} \right]k_{{\text{v}}} \sin 2\pi \left( {\frac{t}{T} - \frac{{y_{i} }}{{\lambda_{{\text{p}}} }} + \frac{{t_{0} }}{T}} \right)} \\ \end{aligned} \right.$$

(10)

where $\gamma$ is the unit weight of rock masses, $S_{i}$ is trapezoidal element area, $\left( {x_{{C_{i} }} ,y_{{C_{i} }} } \right)$ is coordinate of the centroid of trapezoidal element i. The expressions of $S_{i}$ and $\left( {x_{{C_{i} }} ,y_{{C_{i} }} } \right)$ are as follows:

$$S_{i} = \frac{1}{2}\left( {x_{i} - y_{i} \cot \beta + x_{i + 1} - y_{i + 1} \cot \beta } \right)\left( {y_{i + 1} - y_{i} } \right)$$

(11)

$$\left\{ \begin{aligned} x_{{C_{i} }} = & \frac{{\left( {y_{i} + y_{i + 1} } \right)\cot \beta + x_{i} + x_{i + 1} }}{4} \\ y_{{C_{i} }} = & \frac{{y_{i} + y_{i + 1} }}{2} \\ \end{aligned} \right.$$

(12)

The total rate of external work is then derived as:

$$W = W_{{\text{G}}} + W_{{{\text{seismic}} - {\text{h}}}} + W_{{{\text{seismic}} - {\text{v}}}}$$

(13)

The rate of energy dissipation on the failure surface is obtained through the summation of the elementary rates of $P_{i} P_{i + 1}$:

$$D = \omega \sum\limits_{j} {c_{i} L_{i} R_{i} } \cos \varphi_{i}$$

(14)

where $L_{i}$ is the length of $P_{i} P_{i + 1}$, and $R_{i}$ is the length of $OP_{i}$, $c_{i}$, and $\varphi_{i}$ are the cohesion and internal friction angle at the point $P_{i}$, respectively.

2.3.3 Calculation Flow of Safety Factor

The safety factor ($F_{S}$) is the reduction factor of strength parameters to render a limit state of slope stability. In kinematic analysis, the upper bound solution of safety factor is obtained through equating the external work rate and the energy dissipation, where cohesion and friction angle is replaced by ${c \mathord{\left/ {\vphantom {c {F_{S} }}} \right. \kern-\nulldelimiterspace} {F_{S} }}$ and $\varphi { = }\arctan \left( {{{\tan \varphi } \mathord{\left/ {\vphantom {{\tan \varphi } {F_{S} }}} \right. \kern-\nulldelimiterspace} {F_{S} }}} \right)_{{}}$.

The critical safety factor can be obtained by solving the implicit function, and a dichotomy method is used with the following procedure (Fig. 4).

• Step 1 Set the search range of the safety factor $\left( {F_{S1} ,F_{S2} } \right)$ and optimized variables. There are four variables in the optimization process: Two are geometry variables $\theta_{0}$ and $r_{0}$, the other two are time t and instantaneous friction angle $\varphi_{t}$. The initial phase difference between the shear and primary wave is set to zero for convenience.

• Step 2 Make $F_{S} = {{\left( {F_{S1} + F_{S2} } \right)} \mathord{\left/ {\vphantom {{\left( {F_{S1} + F_{S2} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}$ and search the minimum absolute difference between $W$ and $D$.

• Step 3 Determine if $\min \left| {W - D} \right|$ equals to 0. Make $F_{S1} = F_{S}$ if $\min \left| {W - D} \right| = 0$, otherwise make $F_{S2} = F_{S}$. Note that inherent error of the searching algorithm causes the value of $\min \left| {W - D} \right|$ to always be identically zero, even if its value is theoretically zero. A threshold value $\varepsilon$ is introduced to perform the judgment. To our experiences, the value of $\varepsilon$ is relate to ${\updelta }\theta$. $\varepsilon$ can be set to 5 when ${\updelta }\theta = 0.1^\circ$.

• Step 4 Repeat step 3 until the difference between $F_{S1}$ and $F_{S2}$ less than a prescribed value ${\updelta }F_{S} = 0.01$.

Fig. 4

Flow chart of safety factor solution

3 Comparison

The validation of the present pseudo-dynamic method and the programmed code are verified in this section.

3.1 Comparison with Pseudo-static Analysis

The pseudo-dynamic analysis degenerates to the pseudo-static one when $f = 1$ and $V_{{\text{s}}} \to \infty$. The comparison between the pseudo-static solutions and degenerated pseudo-dynamic results will give conclusive evidence of the reasonableness of the discretization technique.

Zhao (2009) evaluated the safety factor of Hoek–Brown slope using the pseudo-static analysis and log-spiral mechanism, and the evaluation results were used to validate the solution of this method. Table 1 lists the solutions obtained by Zhao and the present method, where the collective parameters are $H = {20}$ m, $\beta = {60}^\circ$, $\gamma = 28{\text{kN}}/{\text{m}}^{3}$, $\sigma_{{\text{c}}} = 40{\text{MPa}}$, $D = 0$, $m_{{\text{i}}} = 10$, and the parameters specially for pseudo-dynamic analysis are: $f = 1$, $V_{{\text{s}}} = 1 \times 10^{10} {\text{m/s}}$, ${t \mathord{\left/ {\vphantom {t T}} \right. \kern-\nulldelimiterspace} T} = 0.25$, $k_{{\text{v}}} = 0$. The comparison shows that the maximum error of two solutions does not exceed 6%, while the discrepancy may be attributed to the optimization process and discretization error. The good agreement demonstrates the reliability of the present method.

Table 1 Comparison the results of pseudo-dynamic and pseudo-static

3.2 Comparison with Numerical Simulation

Further literature review shows that there is no numerical validation published for pseudo-dynamic analysis. To fill the gap, this study conducts a verification with commercial software FLAC^3D.

The example is shown in Fig. 5, where the slope has a height of 200 m and a slope inclination of 45°. The model is sized sufficiently large to ensure that the boundaries do not affect stability analysis and is properly fixed at the low horizontal and two vertical boundaries. The rock mass was assigned an elastic-perfectly plastic model of Hoek–Brown criterion with $\gamma = 28$ kN/m³, $\sigma_{c} = 30$ MPa, $GSI = 40$, $m_{{\text{i}}} = 10$, $D = 0$.

Fig. 5

Diagram of slope numerical model

To speed up the convergence, a large value of Young’s modulus E can usually be used in static analysis. However, Young’s modulus should be assigned a ‘real’ value in dynamic analysis because its value determines the wave velocity and thus affects the acceleration distribution within the structure. Thus, this model determines the value E = 3 × 10³ MPa according to an empirical relationship between Young’s modulus and uniaxial compressive strength $E(GPa) = \sqrt {\sigma_{c} /100} \times 10^{(GSI - 10)/40}$ (Pain et al. 2017). And the other elastic parameter Poisson’s ratio $v$ is set to 0.3.

The seismic input is a sinusoidal shear wave with a normal incidence on base surface, where the horizontal seismic coefficients is $k_{{\text{h}}} = 0.3$ and the period is $T = 0.3$ s. The damping of the model is the Rayleigh damping with a center frequency of 4 and a fractional critical damping ratio of 1%. The dynamic boundary condition is the free-field condition, to ensure the plane waves propagating upward suffer no distortion close to the boundary.

FLAC^3D provides the command ‘model safety factor’ to compute the safety factor under static circumstances. However, this command is unavailable in dynamic analysis where the value of safety factor varies with time. Thus, this paper uses a stress-extraction technique to help access the seismic safety factor (Fig. 6). This technique extracts the earthquake-induced stress from dynamic analysis and assigns them to corresponding nodes of a static model, then uses this command ‘model safety factor’ to access the safety factor. The stress-extraction technique is feasible because a failure of material is only associated with the change of stress state under Hoek–Brown criterion. The procedure of this technique is detailed below.

• Step 1 Create a numerical model with dynamic mode turned on, the initial condition is the gravity loading. Set the static and dynamic boundary conditions and input the parameters as described above.

• Step 2 Perform a dynamic analysis of the present model. Extract the acceleration data into a text file every 0.1 s using a FISH code. These date represent the earthquake-induced stresses of the rock slope during an earthquake. Terminate the dynamic analysis when the computation time exceeds 3 times periods.

• Step 3 Rebuilt the same model as in step 1, but only with static mode turned on. Apply the earthquake forces to every node of the static model, with a value equal to the extracted acceleration data multiplied by the gravity acceleration. Compute the safety factor using the ‘safety factor model’ command.

• Step 4 Repeat step 3 using the stress data extracted at each time step. the minimum of all safety factors obtained can be identified as the final solution.

Fig. 6

Extraction and reapply of stress

Using this procedure, it is found that the seismic safety factor of rock slope is 1.09, at the 0.4 s after the occurrence of the earthquake. Then the safety factor was computed using the pseudo-dynamic method using the same parameters and two additional parameters: amplification factor and the shear wave velocity. The assigned values of $f = 2.27$ and $V_{{\text{s}}} = \left( {{E \mathord{\left/ {\vphantom {E {2\rho \left( {1 + v} \right)}}} \right. \kern-\nulldelimiterspace} {2\rho \left( {1 + v} \right)}}} \right)^{0.5} {\text{ = 2030m}}/{\text{s}}$ is taken from the numerical analysis results. The results show that the theoretical analysis yields a safety factor equal to 1.11, which is quite close to the value of 1.09 given by the numerical simulation. The slight discrepancy indicates the feasibility and accuracy of the proposed method.

4 Discussion

The pseudo-dynamic approach can readily account for the dynamic nature and amplitude amplification of seismic waves. This section illustrates the effects of the two factors on the seismic stability of rock slope by comparing the pseudo-static and pseudo-dynamic solutions.

4.1 Effect of Phase Change

The existence of phase change is inherent since the rigidity of geomaterials cannot be ideally infinite. The influence of phase change can be studied by comparing the pseudo-static solutions with the present pseudo-dynamic results excluding acceleration amplification. The results were graphically provided in Fig. 7 for two slope heights H = 100 m and 200 m. The other input parameters are: $k_{{\text{h}}} = 0.1$ to 0.7, $\beta = 50^\circ$, $\gamma = 28$ kN/m³, $\sigma_{c} = 100$ MPa, $m_{{\text{i}}} = 10$, $GSI = 40$, $D = 0$, $T = 0.25$ s, $V_{{\text{s}}} = 2055$ m/s, $V_{{\text{p}}} = 3695$ m/s and $\lambda = 0.5$, where $\lambda$ is the ratio of vertical and horizontal accelerations. These parameters are referenced from previous literature (Zhao 2009; Pain et al. 2017; Xu and Yang 2018).

Fig. 7

Influence of horizontal seismic coefficient $k_{{\text{h}}}$ on slope stability with $f = 1$

The primary concern in Fig. 7 is that the pseudo-dynamic analysis ($f = 1$) always provides a larger solution of the safety factor, which indicates that phase change certainly results in an increase of slope stability. The impact of phase change grows with horizontal accelerations coefficient and slope height. For instance, phase change increases the safety factor by 1.03% ($k_{{\text{h}}} = 0.1$) to 4.1% ($k_{{\text{h}}} = 0.7$) when $H = 100$ m, while such an increase grows to 5.84% ($k_{{\text{h}}} = 0.1$) and 12.94% ($k_{{\text{h}}} = 0.7$) at the slope height $H = 200$ m. The pseudo-static analysis produces conservative solutions when the phase change is not considered, especially at a large slope height.

4.2 Effect of Acceleration Amplification

Topography such as slope and valley can significantly aggravate strong seismic motions, thus the effect of acceleration amplification should also be considered in seismic analysis. The pseudo-dynamic solutions with the amplification factor $f = 1.6$ and the corresponding pseudo-static solutions were shown in Fig. 8, where the other parameters are the same as in Fig. 7. One can observe that the pseudo-static approach overestimates the seismic safety factor of rock slope, which is completely different from the observation in Fig. 7. As the pseudo-dynamic solutions in Fig. 8 additionally include the effect of acceleration amplification, it is understood that phase change and acceleration amplification have opposite impacts. The former one is conducive to slope stability while the latter renders the instability of slope, and the influence of amplification factor outweighs the contrary impact of phase change for the given parameters. At this point, the pseudo-static analysis produces unstable results and further increases the potential risk of practical engineering. In addition, the differences between pseudo-static/dynamic solutions decrease with the increasing slope height. For instance, for 100 m slope height the maximum discrepancy is 0.257, and this value decreases to 0.12 when the slope height is 200 m.

Fig. 8

Influence of horizontal seismic coefficient $k_{{\text{h}}}$ on slope stability with $f = 1.6$

Obviously, the amplification factor determines the impact of acceleration amplification. Figure 9 depicts the variation of safety factor with the amplification factor. The results show that the slope safety factor decreases linearly with the increase of amplification factor, and its variation rate is related to the slope height and horizontal seismic coefficient. It is interesting to note that the combined effect of phase changes and acceleration amplification varies with the value of amplification factor. The phase change plays a separate role at the starting point of $f = 1$, where the pseudo-dynamic analysis yields a larger (although slightly) solution. Then the effect of phase change gradually offset with the increase of the amplification factor, and the pseudo-dynamic solution trends significantly downward. Soon the effect of phase change is completely offset by acceleration amplification at the "offset" point (intersection of the curves) when the pseudo-dynamic/static methods provide the equivalent solutions. When the amplification factor crosses the "offset" point, the acceleration amplification plays a more important role than the phase change, and the pseudo-dynamic analysis also provides a smaller solution of safety factor.

Fig. 9

Influence of amplification factors $f$ on slope stability

4.3 Seismic Acceleration Distribution

The effects of phase change and acceleration amplification mentioned above can be explained by the distribution of seismic acceleration within a slope. Figure 10 shows the acceleration distributions under pseudo-static/dynamic assumption, where $k_{{\text{h}}} = 0.1$, $T = 0.25$ s, $f = 1$ and 1.6.

Fig. 10

Seismic wave propagation diagrams at different heights

In the pseudo-static case, the seismic accelerations within a slope are uniformly distributed with the value of $k_{{\text{h}}} g$. In the pseudo-dynamic scenario where only phase change is considered, the seismic acceleration is sinusoidally distributed, with the peak $k_{{\text{h}}} g$ occurring only at the crest of waves. This means that the pseudo-dynamic force is always smaller than the pseudo-static one except for a few points, which is also the reason why the pseudo-dynamic analysis shown in Fig. 7 gives a larger safety factor solution. In the scenario of simultaneous consideration of phase change and acceleration amplification, the seismic acceleration increases significantly compared to the other two cases. The seismic acceleration exceeds the value of $k_{{\text{h}}} g$ in most portions of the slope except for zones at the bottom and top regions. Thus, this pseudo-dynamic force produces worse stability of slope than the pseudo-static force. Another point worth noting is that the proportion of the range where $a_{{\text{h}}}$ is greater than $k_{{\text{h}}} g$ decreases when slope height grows from 100 to 200 m. This is the explanation that the difference between pseudo-dynamic/static solution in Fig. 8 decreases with increasing slope height.

The discussion above indicates that the pseudo-static analysis may over/underestimate slope stability compared to the pseudo-dynamic method, especially in the cases of severe earthquakes and significant motion amplification. To give more realistic safety factor solutions, pseudo-dynamic method is recommended in seismic stability assessment of rock slopes.

5 Parametric Analysis

The section conducts the parametric analysis using pseudo-dynamic analysis method, to investigate the impact of various parameters on seismic stability of rock slope. The parameters analyzed include rock strength (geological strength index $GSI$ and Hoek–Brown constant $m_{{\text{i}}}$), slope geometry, (slope height $H$, slope inclination $\beta$), and seismic effect (earthquake period $T$). The basic parameter inputs are as follows: $GSI = 40$, $m_{{\text{i}}} = 15$, $\sigma_{c} = 30$ MPa, $D = 0$, $H = 50$ m, $\beta = 50^\circ$, $\gamma = 22$ kN/m³, $f = 1.3$, $T = 0.25$ s, $k_{{\text{h}}} = 0\sim 0.4$, $\lambda = 0$.

The influence of rock strength was given by Figs. 11 and 12, where two slope examples with different geometric features are considered. The low steep slope is 40 m high with an inclination of 60°, and the high gentle slope is 100 m high with an inclination of 40°.

Fig. 11

Influence of the strength parameter $GSI$ on safety factors

Fig. 12

Influence of the strength parameter $m_{{\text{i}}}$ on safety factors

Figure 11 presents the variation of safety factor with the geological strength index $GSI$. These curves clearly show that the safety factor increases with the increase of $GSI$. This is because the greater the rock strength, the more difficult it is to fail the rock slope. The variation rule of $F_{s}$ in these two examples are different. For the low-steep slope, the value of safety factor increases linearly when $GSI$ is less than 30, with a gradual acceleration the range of 30 < $GSI$ < 50. For high-gentle slope, this variation is roughly linear within the given range of $GSI$. Figure 12 demonstrates the effect of strength parameter $m_{{\text{i}}}$. The safety factor increases with the increasing $m_{{\text{i}}}$, while its changing rate has a slowing downtrend.

Comparing Figs. 11 and 12, it can be found that $m_{{\text{i}}}$ has less effects on slope stability than $GSI$. For example, the maximum increment of $F_{s}$ brought by $m_{{\text{i}}}$ is 0.849, while the corresponding increment with $GSI$ is 2.165.

The effects of slope height and slope inclination were demonstrated in Figs. 13 and 14. Two different rock qualities are considered here, where the good rock has a $GSI$ value of 40, while the poor rock’s $GSI$ reaches only 20. Figure 13 clearly shows that the safety factors steadily decrease with the increase of slope height. The descending trend is rather evident when slope height is small, but gradually becomes gentler with the increasing $H$. For instance, when $GSI = 20$ and $k_{{\text{h}}} = 0.4$, the safety factor decreases by 0.169 as slope height changes from 50 to 100 m, whereas the safety factor only changes by 0.054 when slope height grows from 100 to 250 m. Figure 14 shows that the safety factors decrease sharply with increasing slope inclination. The maximum reduction of safety factor can reach 1.344. Figure 14 also indicates that the variation law of $F_{s}$ also varies with the horizontal seismic coefficients. The descending rate of $F_{s}$ witnesses a decrease when $k_{{\text{h}}} = 0,0.1$ but exhibits an increase for a high value of $k_{{\text{h}}}$, resulting in concave and convex curves respectively. Comparing Figs. 13 and 14, it is found that slope inclination has a greater impact on seismic stability than slope height.

Fig. 13

Influence of slope height $H$ on safety factors

Fig. 14

Influence of slope inclination $\beta$ on safety factors

The influence of period $T$ is discussed in Fig. 15 with two slope examples. Example 1 has a slope height $H = 40{\text{m}}$, slope inclination $\beta = 60^\circ$ and $GSI = 20$, while $H = 100{\text{m}}$, $\beta = 40^\circ$ and $GSI = 40$ for example 2. The value of $F_{s}$ decreases as period increases, however, the various rules have some differences in Fig. 15a, b. The effect of periods $T$ in example 1 is not significant, even ignorable, while in example 2 the decline of $F_{s}$ is quite significant when $T$ less than 0.2. Overall, the influence of the period $T$ on slope stability is relatively small, especially compared with the other parameters discussed above.

Fig. 15

Influence of seismic wave period $T$ on safety factors

6 Conclusion

Considering that the conventional pseudo-static method cannot account for the nonlinear dynamic behavior and intensity-frequency characteristics of seismic effect, this paper proposed a pseudo-dynamic method for seismic stability prediction of rock slope in Hoek–Brown media. This approach combinates the discretization-based kinematic analysis and generalized tangential technique, to address the nonlinear problem of Hoek–Brown criterion.

The proposed method is verified by the published theoretical and numerical simulation solutions (FLAC^3D) employing stress extraction techniques. The comparison of the pseudo-dynamic and static solutions shows that pseudo-static analysis may overestimate or underestimate the safety factor, depending on whether phase change or acceleration amplification plays a dominant role.

The parametric analysis reveals the influence of the main properties of seismic rock slopes on the safety factor solutions. Among the strength parameters, the variation of $GSI$ has a greater effect, while the effect of $m_{{\text{i}}}$ is relatively modest; Regarding the slope geometry parameters, both slope height and slope inclination have a significant effect, although the effect of the former is non-linear while the latter is linear; For the earthquake parameters, the impact of the period is the least, while the other two (acceleration factor and seismic coefficient) have stronger influences.

The pseudo-dynamic analysis can better consider the actual seismic wave characteristics than the pseudo-static method and provides a rapid theoretical approach for seismic stability assessment of rock slope.