1 Introduction

Slope stability analysis is a very important research topic of rock mechanics, and its research field involves many engineering fields, such as mining engineering, water conservancy and hydropower engineering, highway engineering and so on. So it has attracted the attention of many scholars and researchers (Ignacio et al. 2019; Xia et al. 2019; Luis and Edwin 2019). With the continuous improvement of mining technology and mining equipment, more and more open pit mines are put into production in cold regions (Li et al. 2018). The main characteristics of the slope in high altitude and cold regions are that the slope stability is greatly affected by freeze–thaw cycle, the rock mass joints are developed, and the climate environment of the slope is changeable and complex. Due to the serious weathering of rock mass, the strength is greatly reduced. The blasting and excavation will further cause rock fragmentation and crack development on the slope surface, thus reducing the slope stability (Luo et al. 2020; Jiang et al. 2015). The slope stability in high altitude and cold regions plays an important role in the feasibility, safety and economy of the whole project construction (Azarfar et al. 2019). Therefore, it is of great practical significance to study it. At present, there are many methods to study the slope stability in the normal area, but the research on the slope stability in the high altitude and cold regions is less and not perfect.

The research method of slope stability is developing from experience to theory, from single qualitative or quantitative method to qualitative and quantitative multi-level method, from traditional theory to new theory. Especially for the special complex regions, there are complex factors affecting the slope stability, which have the uncertainty characteristics (Qu et al. 2020; Dotta et al. 2017). Moreover, it is difficult to establish a reasonable mathematical model and mechanical model to measure the rock slope stability in high altitude and cold regions. With the development of the research, more and more attention has been paid to the influence of uncertain factors on slope stability (Zhang et al. 2018). Li (1997) applied the fuzzy comprehensive evaluation method to study the open-pit mine slope stability. Liu et al. (2014) used the ideal point evaluation function to evaluate the slope stability grade, and verified the practicability of this method by engineering examples. Li and Liu (2013) used rough set theory to reduce the prediction indicator, and used the catastrophe series method to predict the slope stability, and verified the feasibility of the method applied to engineering examples. However, the uncertainty and complexity bring great challenges to the research methods. It is necessary to improve the accuracy of slope state judgment by using simple methods.

Extension theory introduces the concept of distance into the correlation function, and changes the evaluation index from a single definite value to an interval value, so as to evaluate the object more comprehensively. In view of the shortcomings of the traditional entropy weight method, the improved entropy weight method is used to determine the entropy weight of the index, so as to minimize the interference of subjective factors. Based on the characteristics of slope in high altitude and cold regions, the extension theory and improved entropy weight method are applied to analyze the slope stability. The improved entropy weight method is used to determine the weight coefficient of evaluation index, and the matter element extension evaluation of slope is carried out by extension theory, and a new method suitable for slope stability evaluation in cold regions is formed.

2 Methodology Overview

2.1 Extension Theory

The quantitative analysis of the significance of each evaluation index can be realized by extension theory. The core content of extension theory mainly includes two parts, one is matter element theory, the other is extension set theory. Matter element theory is used to study matter element and its transformation. Its core is to analyze the extension, transformation and related properties of matter element, and describe the complexity and variability of research object in formal language, so as to realize its operation and ratiocination. Extension set theory realizes the quantitative analysis of research object through the determination of correlation function and the calculation of correlation degree (Bao et al. 2020; Zhao et al. 2015).

2.1.1 Matter element Theory

The extension theory introduces matter element as the basic element of describing research object. The so-called matter element refers to that the name of the research object is N, its quantity value about characteristic c` is v. The ordered triple is taken as the basic element to describe research object and the name N, characteristic c and quantity v are called the three elements of matter element R. It can be expressed as follows:

$$R = \left( {N,c,v} \right)$$

when research object has more than one characteristic, that is to say, N are described by n characteristics c1, c2,…,cn and the corresponding values are v1,v2,…,vn, then it can be expressed as follows:

$$R{ = }\left[ {\begin{array}{*{20}c} N & {c_{1} } & {v_{1} } \\ {} & {c_{2} } & {v_{2} } \\ {} & \vdots & \vdots \\ {} & {c_{n} } & {v_{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{1} } \\ {R_{2} } \\ \vdots \\ {R_{n} } \\ \end{array} } \right]$$
(1)

where R is the n-dimensional matter element and Ri = (N,ci,vi) is the component element of R.

2.1.2 Extension Set Theory

Suppose U is a universe, if there is a number K (u) corresponding to any element u in U, then A is called an extension set on the universe U. A can be expressed as follows:

$$A = \left\{ {\left( {u,y} \right)|u \in U,y = K\left( u \right) \in \left( { - \infty , + \infty } \right)} \right\}$$

where y = K (u) is the correlation function of A and K (u) is the correlation degree of u with respect to A. When K (u) > 0, it is the positive domain of A; when K (u) < 0, it is the negative domain of A; when K (u) = 0, it is the zero bound of A.

Using extension set to study the relationship between research object and quantity, and extension set is described by correlation function. Therefore, it is necessary to establish correlation function to analyze the research object quantitatively. The correlation function expresses the correlation degree of a certain characteristic of the research object.

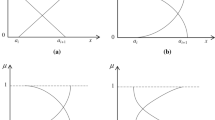
When calculating the correlation degree between point M ∈ X and interval X = [a,b], K(x) is the correlation function of x with respect to interval X and point M. The simple correlation function is used, and the calculation formula is:

$$K\left( x \right) = \left\{ {\begin{array}{*{20}c} {\frac{x - a}{{M - a}},x \le M} \\ {\frac{b - x}{{b - M}},x \ge M} \\ \end{array} } \right.$$
(2)

when calculating the correlation degree of an index in two intervals, the primary correlation function is used. Suppose that X0 = [a,b], X = [c,d], X0 ∈ X and there is no common point, the calculation formula is:

$$K\left( x \right) = \frac{{\rho \left( {x,X_{0} } \right)}}{{D\left( {x,X_{0} ,X} \right)}} = \left\{ {\begin{array}{*{20}c} {\frac{{\rho \left( {x,X_{0} } \right)}}{{\rho \left( {x,X} \right) - \rho \left( {x,X_{0} } \right)}},x \notin X_{0} } \\ { - \rho \left( {x,X_{0} } \right) - 1,x \in X_{0} } \\ \end{array} } \right.$$
(3)

where ρ(x,x0) is the distance between point x and interval X0.

$$\rho \left( {x,X_{0} } \right) = \left| {x - \frac{a + b}{2}} \right| - \frac{1}{2}\left( {b - a} \right)$$
(4)

2.2 Improved Entropy Weight Method

Entropy is a parameter used to represent the state of matter in the classical thermodynamics of physics. It is a measure of system uncertainty. Later, Shennong introduced the concept of entropy into information theory, and called the uncertainty of information source signal as information entropy (Tao et al. 2020; Li et al. 2019). Therefore, if the entropy of a certain index is smaller, the more information it contains and the less uncertainty of the system state will be. This means that the index is more important in the decision-making process at the later stage, so it has a higher weight. The entropy method can effectively avoid the subjective influence of weight decision-making and make the results more objective.

When using extension theory to evaluate slope stability, weight plays an important role in evaluation and decision-making. It reflects the status of each factor in the evaluation and directly affects the final evaluation results. Because the traditional extension evaluation method uses simple correlation function method to determine the weight of evaluation index, it can not objectively reflect the importance difference of evaluation index in evaluating object, so we propose to introduce entropy weight method into extension theory to determine the weight.

However, there are two shortcomings in the traditional entropy weight method. First, if the entropy value of the index is close to 1, the small change between them may cause the great change of the entropy weight of different indexes. Second, when the proportion of the difference coefficient of the evaluation index is the same, the calculation results of different factor weights are the same regardless of the difference degree between entropy values. In view of the shortcomings of the traditional entropy weight method, this paper uses the improved entropy weight method to determine the weight.

3 Calculation Steps

In this paper, the entropy weight method is used to improve the extension theory, and then the slope stability in cold regions is evaluated.

3.1 Matter Element Method for Determining Slope Stability in Cold Regions

The evaluation index system of slope stability in cold region is determined, and the indexes are pretreated. If there are n indexes affecting slope stability, the slope in cold region can be described by the following n-dimensional matter-element.

$$R{ = }\left( {N,C,V} \right) = \left[ {\begin{array}{*{20}c} {N_{i} } & {c_{1} } & {v_{i1} } \\ {} & {c_{2} } & {v_{i2} } \\ {} & \vdots & \vdots \\ {} & {c_{n} } & {v_{in} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{1} } \\ {R_{2} } \\ \vdots \\ {R_{n} } \\ \end{array} } \right]$$
(5)

where R is the matter element of n-dimensional slope stability evaluation. ck(k = 1,2,…, n) is the kth index affecting slope stability. vik is the value of influence index k corresponding to the slope.

3.2 Determine the Classical Domain R 0, Node Domain R p and Matter Element R m

According to the standard of slope stability grade, the slope stability is divided into y grade, and the classical matter element R0j = (N0j,C,V0j) of the research object in matter-element system can be obtained.

$$R_{0j} = \left[ {\begin{array}{*{20}c} {N_{0j} } & {c_{1} } & {v_{0j1} } \\ {} & {c_{2} } & {v_{0j2} } \\ {} & \vdots & \vdots \\ {} & {c_{n} } & {v_{0jn} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {N_{0j} } & {c_{1} } & {\left\langle {a_{0j1} ,b_{0j1} } \right\rangle } \\ {} & {c_{2} } & {\left\langle {a_{0j2} ,b_{0j2} } \right\rangle } \\ {} & \vdots & \vdots \\ {} & {c_{n}^{{}} } & {\left\langle {a_{0jn} ,b_{0jn} } \right\rangle } \\ \end{array} } \right]$$
(6)

where Nj0 is the j (j = 1,2,…, y) category of the slope matter-element system. v0jk is the normalized value range of the kth index of j category.

All values corresponding to each index range from the minimum value to the maximum value, that is, the nodal matter-element Rp of slope stability. Np is the whole of slope stability grade in matter-element system, Vpk is the value range of characteristic ck, that is, the node domain of Np.

$$R_{p} = \left[ {\begin{array}{*{20}c} {N_{p} } & {c_{1} } & {v_{p1} } \\ {} & {c_{2} } & {v_{p2} } \\ {} & \vdots & \vdots \\ {} & {c_{n} } & {v_{pn} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {N_{p} } & {c_{1} } & {\left\langle {a_{p1} ,b_{p`} } \right\rangle } \\ {} & {c_{2} } & {\left\langle {a_{p2} ,b_{p2} } \right\rangle } \\ {} & \vdots & \vdots \\ {} & {c_{n} } & {\left\langle {a_{pn} ,b_{pn} } \right\rangle } \\ \end{array} } \right]$$
(7)

The evaluation information collected by class m slope to be evaluated is represented by matter-element, that is, matter element Rm.

$$R_{m} = \left[ {\begin{array}{*{20}c} {N_{m} } & {c_{1} } & {v_{m1} } \\ {} & {c_{2} } & {v_{m2} } \\ {} & \vdots & \vdots \\ {} & {c_{n} } & {v_{mn} } \\ \end{array} } \right]$$
(8)

where Nm is the class m slope to be evaluated, ck is the kth index affecting slope stability (k = 1,2,…, n), vmk is the value of the kth index corresponding to the class m slope to be evaluated.

3.3 Dimensionless Treatment of Evaluation Indexes

The range transformation is used to transform the different dimensions of each index into a common dimensionless value for the convenience of comprehensive quantitative calculation. The evaluation indexes selected in this paper are divided into positive index and reverse index. Positive index, that is, the larger the better, such as cohesion, internal friction angle, and bulk density. The formula (9) is used for dimensionless processing of such evaluation index. Reverse index, that is, the smaller the better, such as slope height, slope angle, and freeze–thaw cycle. The formula (10) is used for dimensionless processing of such evaluation index.

$$x_{i} = \frac{{x_{i} - x_{\min } }}{{x_{\max } - x_{\min } }}$$
(9)
$$x_{i} = \frac{{x_{\max } - x_{i} }}{{x_{\max } - x_{\min } }}$$
(10)

In the formula, xi represents the actual data of an evaluation index about i, and xmax, xmin represent the maximum and minimum values of the measured data of an evaluation index.

3.4 Calculation the Correlation Function of Slope Evaluation Index

Firstly, according to the classical domain and the element to be evaluated, the simple correlation degree is calculated as follows.

$$K_{j} \left( {v_{0i} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{{2\left( {v_{0i} - a_{ji} } \right)}}{{b_{ji} - a_{ji} }},\quad v_{0i} < \frac{{b_{ji} + a_{ji} }}{2}} \\ {\frac{{2\left( {b_{ji} - v_{0i} } \right)}}{{b_{ji} - a_{ji} }},\quad v_{0i} > \frac{{b_{ji} + a_{ji} }}{2}} \\ \end{array} } \right.$$
(11)

Then the primary correlation function of each evaluation index is calculated according to Eq. (15), so as to determine the influence degree of each evaluation index on the slope stability.

$$K_{j} \left( {v_{0i} } \right) = \left\{ {\begin{array}{*{20}c} {\frac{{\rho \left( {v_{0i} ,v_{ji} } \right)}}{{\rho \left( {v_{0i} ,v_{pi} } \right) - \rho \left( {v_{0i} ,v_{ji} } \right)}},\rho \left( {v_{0i} ,v_{pi} } \right) - \rho \left( {v_{0i} ,v_{ji} } \right) \ne 0} \\ { - \rho \left( {v_{0i} ,v_{ji} } \right) - 1,\rho \left( {v_{0i} ,v_{pi} } \right) - \rho \left( {v_{0i} ,v_{ji} } \right) = 0} \\ \end{array} } \right.$$
(12)

where ρ(v0i,vji) is the distance between v0i and interval vji.

$$\rho \left( {v_{0i} ,v_{ji} } \right) = \left| {v_{0i} - \frac{{b_{ji} + a_{ji} }}{2}} \right| - \frac{{b_{ji} - a_{ji} }}{2} = \left\{ {\begin{array}{*{20}c} {a_{ji} - v_{0i} ,v_{0i} \le \frac{{b_{ji} + a_{ji} }}{2}} \\ {v_{0i} - b_{ji} ,v_{0i} > \frac{{b_{ji} + a_{ji} }}{2}} \\ \end{array} } \right.$$
(13)

where ρ(v0i,vpi) is the distance between v0i and interval vpi.

$$\rho \left( {v_{0i} ,v_{pi} } \right) = \left| {v_{0i} - \frac{{b_{pi} + a_{pi} }}{2}} \right| - \frac{{b_{pi} - a_{pi} }}{2} = \left\{ {\begin{array}{*{20}c} {a_{pi} - v_{0i} ,v_{0i} \le \frac{{b_{pi} + a_{pi} }}{2}} \\ {v_{0i} - b_{pi} ,v_{0i} > \frac{{b_{pi} + a_{pi} }}{2}} \\ \end{array} } \right.$$
(14)

3.5 Determination of WEIGHT Coefficient by Entropy Weight Method

  1. ①

    Assuming that the stability grade of the evaluated slope is divided into y grade and n evaluation indexes, the judgment matrix R is constructed, which is the correlation degree matrix determined in the previous step (Liu et al. 2020; Wang et al. 2018).

    $$R{ = }\left[ {K_{j} \left( {v_{0i} } \right)} \right]\quad \left( {i = {1},{2}, \ldots ,\;y;\;j = {1},{2}, \ldots ,n} \right)$$
    (15)
  2. ②

    The judgment matrix R is normalized to get the normalized matrix.

  3. ③

    According to the traditional entropy concept, the entropy of each evaluation index can be defined as follows:

    $$H_{j} = \frac{ - 1}{{\ln y}}\sum\limits_{i = 1}^{y} {f_{ij} } \ln f_{ij} \, \left( {i = 1,2,...,y;j = 1,2,...,n} \right)$$
    (16)
    $$f_{ij} = {{\left[ {1 + K_{j} \left( {v_{0i} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {1 + K_{j} \left( {v_{0i} } \right)} \right]} {\sum\limits_{i = 1}^{y} {\left[ {1 + K_{j} \left( {v_{0i} } \right)} \right]} }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{i = 1}^{y} {\left[ {1 + K_{j} \left( {v_{0i} } \right)} \right]} }}$$
    (17)
  4. ④

    Using the improved weight formula to calculate the entropy weight of each index.

    $$w = \frac{{\exp \left( {\sum\nolimits_{k = 1}^{n} {H_{k} + 1 - H_{j} } } \right) - \exp \left( {H_{j} } \right)}}{{\sum\nolimits_{j = 1}^{n} {\left[ {\exp \left( {\sum\nolimits_{k = 1}^{n} {H_{k} + 1 - H_{j} } } \right) - \exp \left( {H_{j} } \right)} \right]} }}$$
    (18)

3.6 Determining the Correlation Degree of Slope Stability Grade

The correlation degree of the matter element Ni of the slope to be evaluated with respect to the grade t is as follows.

$$K_{it} \left( {N_{i} } \right){ = }\sum {w_{j} } K_{jt} \left( {v_{0i} } \right)$$
(19)

According to formula (14), the slope stability grade of matter element Ni is t0.

The extension theory is used to quantitatively analyze the influence degree of each evaluation index on rock slope stability, and the specific implementation steps are shown in Fig. 1.

Fig. 1
figure 1

Steps of significance analysis of evaluation indexes

Full size image

4 Calculation and Application of Engineering Examples

Beizhan iron mine is located in the northwest of Hejing county, Xinjiang, with a straight line of about 130 km. The trend of the mountain is nearly east–west, the overall terrain is high in the south and low in the north, with an altitude of 3160–575 m and a height of 700–00 m. The minimum temperature in this area reaches − 25 °C, and the temperature difference between day and night can reach 30 °C. Therefore, the Beizhan open pit mine slope is under the action of freeze–thaw cycle for a long time, and its stability is of great significance for the safety construction of the project. The general terrain slope is 25°–5°, and the ditch is deep and steep, which belongs to deep mountain landform. The ore body is located at an altitude of 3450–723 m, forming a complex high and steep slope.

There are many factors influencing slope stability. In this paper, the slope stability indicator is divided into two categories: environmental hydrological conditions and engineering geological conditions. Based on the existing achievements and engineering experience, nine evaluation indicators are selected, including internal friction angle c1, cohesion c2, bulk density c3, slope angle c4, slope height c5, freeze–thaw cycle c6, temperature difference between day and night c7, rainfall intensity c8 and earthquake intensity c9. The evaluation indicator system of slope instability is shown in Fig. 2.

Fig. 2
figure 2

Evaluation indicators system of slope instability

Full size image

According to the field survey and the actual engineering data of the mine, the representative line 1–6# slopes are selected as the object of stability analysis. The extension theory of improved entropy weight is used to evaluate the stability of the six slopes. Combined with the engineering geological and environmental hydrological conditions of the slope and the measurement of relevant experiments, the characteristic parameters are determined as shown in Table 1.

Table 1 Characteristic parameters of slope to be evaluated
Full size table

4.1 Establishing Standard Matter Element Model

According to the specific test analysis, combined with the research results of relevant experts and scholars and the current specification requirements, the standard matter-element model of evaluation index is established, as shown in the Tables 2 and 3.

Table 2 Standard matter element model of engineering geological index
Full size table
Table 3 Standard matter element model of environmental hydrology index
Full size table

Since the units of each evaluation index in Tables 2 and 3 are not unified, the dimensionless treatment is carried out. The formula (9) is used for dimensionless processing of positive evaluation index. The formula (10) is used for dimensionless processing of reverse index evaluation index. The dimensionless treatment results of each evaluation index are shown in Tables 4 and 5.

Table 4 Dimensionless standard matter element model of engineering geological index
Full size table
Table 5 Dimensionless standard matter element model of environmental hydrology index
Full size table

4.2 Determine Classical Domain

The classical domain represents the value range of each evaluation index for each stability grade of rock slope. For this slope, the classical domain is:

$$\begin{aligned} R_{{1}} & { = }\left[ {\begin{array}{*{20}c} {P_{1} } & {c_{1} } & {\left\langle {0.00,0.30} \right\rangle } \\ {} & {c_{2} } & {\left\langle {0.00,0.03} \right\rangle } \\ {} & {c_{3} } & {\left\langle {0.00,0.45} \right\rangle } \\ {} & {c_{4} } & {\left\langle {0.00,0.56} \right\rangle } \\ {} & {c_{5} } & {\left\langle {0.00,0.05} \right\rangle } \\ {} & {c_{6} } & {\left\langle {0.00,0.08} \right\rangle } \\ {} & {c_{7} } & {\left\langle {0.0,0.3} \right\rangle } \\ {} & {c_{8} } & {\left\langle {0.0,0.2} \right\rangle } \\ {} & {c_{9} } & {\left\langle {0.00,0.42} \right\rangle } \\ \end{array} } \right]\quad R_{{2}} { = }\left[ {\begin{array}{*{20}c} {P_{{2}} } & {c_{1} } & {\left\langle {0.{3}0,0.{44}} \right\rangle } \\ {} & {c_{2} } & {\left\langle {0.0{3},0.0{9}} \right\rangle } \\ {} & {c_{3} } & {\left\langle {0.{45},0.{5}5} \right\rangle } \\ {} & {c_{4} } & {\left\langle {0.{56},0.{67}} \right\rangle } \\ {} & {c_{5} } & {\left\langle {0.0{5},0.{10}} \right\rangle } \\ {} & {c_{6} } & {\left\langle {0.0{8},0.{21}} \right\rangle } \\ {} & {c_{7} } & {\left\langle {0.{3},0.{4}} \right\rangle } \\ {} & {c_{8} } & {\left\langle {0.{2},0.{4}} \right\rangle } \\ {} & {c_{9} } & {\left\langle {0.{42},0.{50}} \right\rangle } \\ \end{array} } \right]\quad R_{{3}} { = }\left[ {\begin{array}{*{20}c} {P_{{3}} } & {c_{1} } & {\left\langle {0.{44},0.{56}} \right\rangle } \\ {} & {c_{2} } & {\left\langle {0.0{9},0.{19}} \right\rangle } \\ {} & {c_{3} } & {\left\langle {0.{55},0.{65}} \right\rangle } \\ {} & {c_{4} } & {\left\langle {0.{67},0.{78}} \right\rangle } \\ {} & {c_{5} } & {\left\langle {0.{10},0.{1}5} \right\rangle } \\ {} & {c_{6} } & {\left\langle {0.{21},0.{30}} \right\rangle } \\ {} & {c_{7} } & {\left\langle {0.{4},0.{5}} \right\rangle } \\ {} & {c_{8} } & {\left\langle {0.{4},0.{6}} \right\rangle } \\ {} & {c_{9} } & {\left\langle {0.{5}0,0.{58}} \right\rangle } \\ \end{array} } \right] \\ R_{{4}} & { = }\left[ {\begin{array}{*{20}c} {P_{{4}} } & {c_{1} } & {\left\langle {0.{56},0.{67}} \right\rangle } \\ {} & {c_{2} } & {\left\langle {0.{19},0.{27}} \right\rangle } \\ {} & {c_{3} } & {\left\langle {0.{65},0.{80}} \right\rangle } \\ {} & {c_{4} } & {\left\langle {0.{78},0.{89}} \right\rangle } \\ {} & {c_{5} } & {\left\langle {0.{15},0.{20}} \right\rangle } \\ {} & {c_{6} } & {\left\langle {0.{30},0.{42}} \right\rangle } \\ {} & {c_{7} } & {\left\langle {0.{5},0.{7}} \right\rangle } \\ {} & {c_{8} } & {\left\langle {0.{6},0.{8}} \right\rangle } \\ {} & {c_{9} } & {\left\langle {0.{58},0.{67}} \right\rangle } \\ \end{array} } \right]\quad R_{{5}} { = }\left[ {\begin{array}{*{20}c} {P_{{5}} } & {c_{1} } & {\left\langle {0.{67},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{2} } & {\left\langle {0.{27},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{3} } & {\left\langle {0.{80},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{4} } & {\left\langle {0.{89},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{5} } & {\left\langle {0.{20},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{6} } & {\left\langle {0.{42},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{7} } & {\left\langle {0.{7},{1}{\text{.0}}} \right\rangle } \\ {} & {c_{8} } & {\left\langle {0.{8},{1}{\text{.0}}} \right\rangle } \\ {} & {c_{9} } & {\left\langle {0.{67},{1}{\text{.00}}} \right\rangle } \\ \end{array} } \right] \\ \end{aligned}$$

4.3 Determine Node Domain

According to the value range of each evaluation index in the whole evaluation system, the node domain is established. For this slope, the node domain is:

$$R_{{\text{p}}} { = }\left[ {\begin{array}{*{20}c} {P_{{5}} } & {c_{1} } & {\left\langle {0.00,{1}{\text{.00}}} \right\rangle } \\ {} & {c_{2} } & {\left\langle {0.{00},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{3} } & {\left\langle {0.0{0},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{4} } & {\left\langle {0.00,{1}{\text{.00}}} \right\rangle } \\ {} & {c_{5} } & {\left\langle {0.0{0},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{6} } & {\left\langle {0.{00},{1}{\text{.00}}} \right\rangle } \\ {} & {c_{7} } & {\left\langle {0.{0},{1}{\text{.0}}} \right\rangle } \\ {} & {c_{8} } & {\left\langle {0.0,{1}{\text{.0}}} \right\rangle } \\ {} & {c_{9} } & {\left\langle {0.{00},{1}{\text{.00}}} \right\rangle } \\ \end{array} } \right]$$

4.4 Establish the Element Model to Be Evaluated

In this paper, 4# slope is selected as an example to analyze the slope stability based on the extension theory and improved entropy weight. The matter element of the slope to be evaluated is established according to the specific values of 9 evaluation indexes. The characteristic parameters of the slope are also dimensionless. The results are shown in Table 6.

Table 6 Characteristic parameters of dimensionless treatment of slope to be evaluated
Full size table

Therefore, the matter element model to be evaluated is as follows:

$$R_{{0}} { = }\left[ {\begin{array}{*{20}c} {P_{{0}} } & {c_{1} } & {{0}{\text{.34}}} \\ {} & {c_{2} } & {{0}{\text{.65}}} \\ {} & {c_{3} } & {{0}{\text{.78}}} \\ {} & {c_{4} } & {{0}{\text{.41}}} \\ {} & {c_{5} } & {{0}{\text{.93}}} \\ {} & {c_{6} } & {{0}{\text{.83}}} \\ {} & {c_{7} } & {{0}{\text{.60}}} \\ {} & {c_{8} } & {{0}{\text{.37}}} \\ {} & {c_{9} } & {{0}{\text{.58}}} \\ \end{array} } \right]$$

4.5 Calculate Correlation Function

According to the classical domain and matter element to be evaluated, the simple correlation degree is calculated by formula (11). The simple correlation degree of the slope is shown in Table 7.

Table 7 Simple correlation degree of each evaluation index
Full size table

According to formula (12), the primary correlation function of each evaluation index is calculated to determine the influence degree of each matter element to the slope stability. The primary correlation function of each evaluation index are shown in Table 8 and Fig. 3.

Table 8 The primary correlation function of each evaluation index
Full size table
Fig. 3
figure 3

Evaluation indicators system of slope instability

Full size image

By calculating the correlation degree between each index and the slope stability grade, the maximum correlation degree of each evaluation index and its related index are determined, so as to determine the significance of each evaluation index. The maximum correlation degree of each evaluation index is shown in Fig. 4.

Fig. 4
figure 4

The maximum correlation degree of each evaluation index

Full size image

Because the rock slope stability grade is V > IV > III > II > I, that is, grade I rock slope is the most unstable and grade V rock slope is the most stable. Therefore, the evaluation index associated with grade I has the greatest influence on the rock slope stability, followed by grade II, and so on. It can be found from Fig. 3 that the influence degree of each evaluation index on the rock slope stability in cold region is: cohesion > freeze–thaw cycle > slope height > internal friction angle > slope angle > temperature difference between day and night > earthquake intensity > bulk density > rainfall intensity. Therefore, the significant evaluation indexes of rock slope stability in cold region are cohesion and freeze–thaw cycle.

4.6 Determination of Index Weight by Improved Entropy Weight Method

According to formula (15), the judgment matrix R of the slope can be constructed, and the normalized judgment matrix can be obtained, as shown in the Table 9.

Table 9 Normalized judgment matrix of each evaluation to five evaluation grade
Full size table

Through calculation, the entropy weight of each index can be obtained as shown in Table 10.

Table 10 Entropy weight of each evaluation index
Full size table

The extension correlation degree of each evaluation grade is obtained by calculation, as shown in Table 11.

Table 11 Extension correlation degree of evaluation grade
Full size table

Using the same method, the extension correlation degree of 1–6# slopes can be obtained. The grade of slope stability can be calculated by calculating the correlation degree and entropy weight, as shown in Table 12 and Fig. 5.

Table 12 Extension correlation degree of 1–6# slope
Full size table
Fig. 5
figure 5

Stability grade of 1–6# rock slope

Full size image

According to the evaluation method mentioned above, we can clearly judge the stability grade of 1–6# slope through Table 12 and Fig. 4, which are grade IV, grade I, grade II, grade I, grade V and grade III respectively.

According to the profile of line 1–6, the current pit bottom is located at an elevation of about 3320 m. The slope height of the current area is 400 ~ 700 m, and the slope angle is 46°–48°, which is a high and steep slope. The occurrence conditions of ore body are mainly skarn. The rock mass quality is medium and the integrity degree is medium. The strata are mainly quaternary weathered gravel and skarn. The fracture structure is well developed in the slope, and the joints on the rock mass surface are developed. According to the field design data and slope monitoring results, 2#, 3# and 4# slopes are the west side slopes, and the 1, 5 and 6 slopes are the east side slopes. There are too many landslides on the west side slopes, as shown in Fig. 6. Through analysis, it can be concluded that the evaluation results of slope stability analysis in cold regions based on extension theory and improved entropy weight method are consistent with the actual engineering situation, which verifies that the evaluation model proposed in this paper has a good application effect in slope stability analysis.

Fig. 6
figure 6

Actual situation of Beizhan iron mine slope (a east slope of Beizhan iron mine; b West slope of Beizhan iron mine)

Full size image

5 Conclusions

  1. 1.

    The slope stability is affected by many factors. In this paper, nine evaluation indexes are selected to evaluate the matter element of rock slope in cold regions by using extension theory and improved entropy weight method. The results show that the influence degree of each evaluation index on rock slope stability is cohesion > freeze–thaw cycles > slope height > internal friction angle > slope angle > temperature difference between day and night > earthquake intensity > bulk density > rainfall intensity. Therefore, the significant evaluation indexes of rock slope stability in cold regions are cohesion and freeze–thaw cycles.

  2. 2.

    Because the standard extension evaluation method uses simple correlation function method to determine the weight of evaluation index, it can not objectively reflect the importance of evaluation index. In this paper, the improved entropy weight method is used to determine the entropy weight of the index, which can effectively avoid the subjective influence when determining the index weight, and make the research results more objective.

  3. 3.

    Slope evaluation has nonlinear and uncertain characteristics. The extension theory evaluation model based on the improved entropy weight method is verified in the case study of rock slope in cold regions, and it has good applicability and accuracy. The analysis method can be applied to the stability evaluation in cold regions.