A Mathematical Model Based on Artificial Neural Networks to Predict the Stability of Rock Slopes Using the Generalized Hoek–Brown Failure Criterion

Abstract

Stability of rock slopes is a critical issue in many mining and civil engineering projects. The current state of practice for slope stability analysis is based on obtaining the factor of safety (FOS). Stability charts are widely used by engineers to obtain a FOS for a quick assessment of the initial stability of slopes. The stability of rock slopes with vertical walls in urban areas adjacent to existing structures is another important issue in this regard. However, the stability of earth or rock slopes are usually analyzed ignoring surcharge loads. The effect of adjacent structures (as surcharge load) on slope stability (considering these loads) can be very useful in slope stability analyses in urban or even non-urban areas. In the present study, it is tried to investigate the effect of surcharge load on the stability of rock slopes based on the generalized Hoek–Brown failure criterion using a finite element numerical software and the related charts are presented. Since there is a stability chart for each slope angle, a comprehensive mathematical model utilizing artificial neural networks is proposed to predict the stability factor of rock slopes. The independent variables in this study were slope angles, slope height, the intensity of surcharge load, Geological Strength Index (GSI), and unconfined compressive strength of the intact rock. Sensitivity analysis showed that the changes in GSI, effect of surcharge and unconfined compressive strength of rock have the highest effect on the slope stability assurance coefficient.

1 Introduction

Stability analysis of rock slopes in geotechnical engineering is a well-known issue that plays an important role in the safe design of excavation walls in open pit mine trenches, railway bridges, dams, and tunnels. In this regard, studying the conditions of the equilibrium of natural slopes is of great importance (Fleurisson and Cojean 2014). Although knowledge related to stability analysis and monitoring of slope movements such as stabilization methods has improved significantly in recent years, failures of rock slopes may cause heavy social, economic, and environmental damages in mountainous regions. One of the fast methods for examining the stability of slopes is the use of charts and nomograms produced based on simple analytical methods (Radoslaw 2002). In almost all of the proposed methods for the analysis of the stability of rock slopes by previous researches, the effect of surcharge load has not been taken into account, despite presence of a considerable surcharge load in urban areas in the immediate vicinity of the excavations. The stability of the excavated walls also may jeopardize the safety of nearby structures in addition to the safe working environment at the bottom of the excavation. Due to the incidents occurred in a number of urban projects such as failure of excavation walls and destruction of the surrounding structures, identification and analysis of methods and factors that can be resolved to overcome these problems is of great necessity. In this study, it is tried to analyze the effect of the surcharge load on the wall slope stability based on the generalized Hoek–Brown failure criterion. Also, using the results of finite element analysis, a mathematical model based on artificial neural networks (ANNs) is proposed in order to analyze the sensitivity of stability factor to the input parameters. Accordingly, the objective of this research is to prepare suitable charts for the design of rock excavations with different slope angles and depths considering the effect of proximity on the side structures as surcharge loads and the development of a mathematical model based on artificial neural networks for direct use to determine slope stability in general conditions.

2 Literature Research

Soil slope stability charts were initially first produced by Taylor (1937). Later, the development of slope stability charts as a design tool was considered by many researchers. The stability of the rock slopes has attracted much attention for several decades. Hoek and Bray (1981) presented some charts to analyze the stability of rock and rockfill slopes. Siad (2003) presented a set of stability charts based on the upper bound approach for stability analysis of fractured rock slopes under seismic conditions. Zanbak (1983) proposed a set of design charts for rock slopes susceptible to toppling based on the original analytical solution. All these charts have been developed based on the behavioral model of the Mohr–Coulomb, which is applied to extract the equivalent friction angle (ϕ) and the cohesion (c) of the rock mass according to this model. Sonmez et al. (1998) utilized back analysis of slope failures to obtain shear strength parameters mobilized in slope cuts in closely jointed rock masses and provided a practical procedure using the classification of the rock mass to estimate the mobilized shear strength according to the Hoek–Brown failure criteria. Hack et al. (2003) proposed a probabilistic classification method to analyze the stability of rock slopes in which there is no need for c and ϕ as input. Li et al. (2008) presented stability charts based on the Hoek–Brown failure criterion using the upper and lower bound limit method. Yang et al. (2004a, b) and Yang and Zou (2006) used the upper bound analysis to determine the optimum slope height. In this study, the Hoek–Brown failure criterion and the shear strength parameters (c and ϕ) were used. Shen et al. (2013) proposed a set of rock slope stability charts for stability analysis of rock mass slopes based on Generalized Hoek–Brown criterion. Sun et al. (2016) presented stability charts for estimating the stability of rock mass slopes based on the generalized Hoek–Brown criterion using the nonlinear strength reduction technique. The proposed charts in this research can be used to calculate the factory of safety (FOS) of a slope directly from the Hoek–Brown parameters, slope geometry and rock mass properties (Sun et al. 2016).

Jiang et al. (2016) evaluated the rock slope stability based on the limit equivalent method using the pseudo-static method and proposed a new chart-based technique for analyzing seismic stability of rock slope. The FOS of slopes is calculated directly based on the parameters of the Hoek–Brown criterion (GSI and mi), slope geometry (H and β), rock mass properties (σ_ci and γ) and seismic effect (k_h). Qian et al. (2017) used a finite element upper bound and lower bound limit analysis methods to estimate rock slope stability for inhomogeneous rock masses based on the Hoek–Brown failure criterion.

According to the progress of various computational methods, the ability to assess the sustainability of the rock slopes and accurate interpretation of the failure mechanisms have increased recently. In the previous studies, a wide range of numerical methods including continuum methods (e.g., finite element and finite difference methods), the discontinuum methods (e.g., distinct element and discontinuous deformation analysis), and probabilistic analytical method are used to analyze the stability of rock slopes (Hoek et al. 2000; Wang et al. 2003; Eberhardt et al. 2004; Stead et al. 2006). ANNs can also be useful tools to predict the stability of the rock slopes. These networks are capable of learning highly complex relationships through a mass of data and information because of their sophisticated structure that resembles human brain. This unique capability has caused ANNs to be used in sciences such as geotechnics. Qi and Tang (2018) studied the stability of the soil slopes using integrated metaheuristic and machine learning approaches. They proposed and compared six integrated artificial intelligence approaches including logistic regression, decision tree, random forest, gradient boosting machine, support vector machine (SVM), and multilayer perceptron (MLP) neural network for slope stability prediction.

The problems relating to the analysis of the stability of soil or rock slopes are usually associated with the existence of a surcharge load, which has been ignored by previous researchers or considered as an equivalent rock layer. In the present study, we tried to investigate the effect of surcharge load on the stability of rock slopes based on the Hoek–Brown failure criterion with the finite elemental software PHASE² and to provide stability charts. Also, using the results obtained from the finite element analysis, a mathematical model based on artificial neural networks is developed to predict the stability factor of rock slopes under the influence of surcharge load.

3 The Generalized Hoek–Brown Failure Criterion

Hoek (1994), Hoek and Brown (1997,2018) and Hoek et al. (2002) presented the following empirical failure criteria for continuous and jointed rocks by fitting the curve from the results of the triaxial test results:

$${\upsigma }_{1}^{^{\prime}} = {\upsigma }_{3}^{^{\prime}} + {\upsigma }_{{{\text{ci}}}} \left( {{\text{m}}_{{\text{b}}} \frac{{{\upsigma }_{3}^{^{\prime}} }}{{{\upsigma }_{{{\text{ci}}}} }} + {\text{s}}} \right)^{{\text{a}}}$$

(1)

where ${\upsigma }_{1}^{^{\prime}}$ and ${\upsigma }_{3}^{^{\prime}} { }$ are respectively the effective maximum and minimum principal stresses, ${\upsigma }_{{{\text{ci}}}}$ is the uniaxial compressive strength (UCS) of the intact rock material,${\text{ m}}_{{\text{b}}}$ is a reduced value (for the rock mass) of the material constant ${\text{m}}_{{\text{i}}}$ (for the intact rock), ${\text{s }}$ and ${\text{a}}$ are constants, which depend upon the characteristics of the rock mass. According to the latest research, the parameters of the generalized Hoek–Brown criterion (Hoek 1994; Hoek and Brown 1997,2018; Hoek et al. 2002) are given by the following equations:

$${\text{m}}_{{\text{b}}} = {\text{m}}_{{\text{i}}} {\text{ exp}}^{{\left[ {\left( {{\text{GSI}} - 100} \right)/\left( {28 - 14{\text{D}}} \right)} \right]}}$$

(2)

$${\text{s}} = {\rm exp}^{{\left( {\left( {{\text{GSI}} - 100} \right)/\left( {9 - 3{\text{D}}} \right)} \right)}}$$

(3)

$${\text{a}} = \frac{1}{2} + \frac{1}{6}\left[ {{\exp}^{{ - {\text{GSI}}/15}} - {\exp}^{ - 20/3} } \right]$$

(4)

where The Geological Strength Index (GSI) is a simple classification system based on geological observation introduced by Hook and Brown for both hard and weak rock masses. The GSI varies from 10 for extremely poor rock masses to 100 for intact rock. In this study, the GSI values of 25, 50, and 75 were considered.

The parameter D (disturbance factor) depends upon the degree of disturbance due to blast damage and/or stress relaxation and varies from 0 for undisturbed in situ rock masses to 1 for very disturbed rock masses.

In this study, it was assumed that the environment is continuous and the rock mass is intact; and so the parameter D is considered 0 for all models. The quantity of ${\text{m}}_{{\text{i}}} { }$ is the constant related to rock material, obtained using triaxial tests on the core of the rock and changes from 0.007 to 25. In this work, the quantity of ${\text{m}}_{{\text{i}}} { }$ was assumed to be 10 in average.

4 Model Validation

Although three-dimensional analysis software are widely available, the two-dimensional analyses are still broadly used today because of the relative ease of model construction and the relatively fast model run times. Certainly, the literature mainly shows that 2D analyses are more conservative than 3D analyses (Cheng et al. 2005; Nian et al. 2012; Leong and Rahardjo 2012), particularly in stability analysis of rock slopes (Shen 2013; Sun 2016; Jiang 2016; Qian 2017). Accordingly, in the present investigation, a two-dimensional analysis was used to investigate the stability of rock slopes. In this section, a failed rock slope presented by Leong and Rahardjo (2012) and Sonmez and Ulusay (1999) is examined for model calibration.

4.1 Slope Failure in Closely Jointed Rock Mass in Barite Open Pit Mine

The first real case, extracted from Sonmez and Ulusay (1999), was located at Baskoyak barite open pit mine, in western Anatolia. Due to the heavily jointed nature of the schist, the rock mass was assumed as homogeneous and isotropic. The mean unit weight (γ) and uniaxial compressive strength (σ_ci) of the heavily broken part of the schist are 22.2 kN/m3 and 5.2 MPa, respectively (Sun 2016; Sonmez and Ulusay 1999). Other parameters required can be obtained from Sonmez and Ulusay (1999) and Sonmez et al. (2003), where mi = 7 and GSI = 16. They indicated that if the overburden material and ore were removed by an excavator without any blasting, the disturbance factor was suggested to be D = 0.7. The parameters for calculating the FOS for a real case rock slope are summarized and listed in Table 1.

Table 1 Result for real case of rock slope

Figure 1 also provides the slip surface obtained from the present study. The FOS and plastic zone obtained from the present strength reduction analysis are in reasonably good agreement with the FOS and the slip surface from Sonmez and Ulusay (1999).

Fig. 1

Critical slip surface (Screenshot of Phase2 software)

5 Research Method

In this study, 756 rock slopes were modeled numerically using finite element method (FEM) to study various physical and geometric factors on the FOS of rock slopes. The model variables included geometric variables (e.g., height and slope angle), geomechanical parameters of rocks (e.g., Geological Strength Index (GSI) and unconfined compressive strength of the rock $\left( {{\upsigma }_{{{\text{ci}}}} } \right)),$ and intensity of surcharge load. Range of changes of each of the above variables is shown in Table 2. According to Table 2, the models were simulated for heights 20, 30, and 40 m and slope angles of 30°, 45°, 60°, and 75°. Also, the GSI values of 25, 50, and 75 and unconfined compressive strength values of 20, 40, and 60 MPa were considered. The intensity of the surcharge load was considered to be 0.162, 0.324, 0.675, 1.35, 2.7 and 5.4 MPa. In all mentioned models, the unit weight of the rock mass was considered to be 0.027 MPa.

Table 2 Numerical model variables

One of the most popular techniques for performing FEM slope analysis is the shear strength reduction (SSR) approach (Hammah et al. 2005). This method has many potentialities for studying the stability of the slopes in complicated conditions. In this method, the shear strength parameters of soil are reduced so that the slope is on the verge of instability; hence, the FOS is defined as the ratio between the initial shear strength parameter and the final shear strength parameter.

In this study, the finite element method (FEM) with the SSR technique was used for the stability analysis of rock slopes. For this purpose, the technique was implemented in the FEM Phase 2 program. The geometric dimensions of the models are shown in Fig. 2.

Fig. 2

The geometrical dimension of the rock slope model

The model was assumed to have a plane strain and so the two-dimensional analysis was used to determine the FOS. The models are named as ${\text{Sx}}_{1} {\text{x}}_{2} {\text{x}}_{3} {\text{x}}_{4} {\text{x}}_{5}$, where ${\text{x}}_{{\text{i}}} { }\left( {{\text{i}} = 1,\,2,\,3,\,4} \right)$ is a two-digit integer that represents the angle of slope, height of slope, unconfined compressive strength of rock, GSI, respectively and ${\text{ x}}_{5}$ represents the surcharge load intensity,. The failure mechanism and the maximum shear strain for the S3020204045 model are shown in Fig. 3. In this figure, the SSR area is clearly visible. The FOS for this model is 3.41. After simulating all models, the obtained results were used for the preparation of stability charts and training of the artificial neural network.

Fig. 3

Typical contours of the maximum shear strain and shear strength reduction area

6 Results of Analysis

As mentioned for each of the slopes, a stability chart was prepared to calculate the FOS. Since a large number of variables exist in the model, for each model, a dimensionless parameter was defined as:

$$N_{s} = c_{d} \cdot \frac{{\sigma_{c} }}{\gamma H + P}$$

(5)

where $N_{s}$ is dimensionless parametr, $\sigma_{c}$ is unconfined compressive strength of rock,$\gamma$ is unit weight of the rock mass,$H$ is slope height, $P$ is intensity of surcharge load and $c_{d}$ is reduction coefficient of surcharge load which is defined as follows:

$$c_{d} = 1 - \left( {\frac{P}{{\sigma_{c} }}} \right)^{\beta }$$

(6)

where, $\beta , t$ he non-dimensional coefficient, is obtained by fitting the best curve passing through the data and by the least squares error method.

So, the number of variables was reduced using this dimensionless parameter. Then, in Fig. 4, the stability charts are shown for different slopes as FOS versus Ns.

Fig. 4

Stability chart of the rock slope a α = 30, b α = 45, c α = 60, d α = 75

The best-fit relationship was calculated for each of the stability curves using the method of least squares. In all models, the best relationship for fitting the FOS and the dimensionless parameter (Ns) is the following power relationship:

$$Fs = A \cdot \left( {N_{s} } \right)^{n}$$

(6)

where, A and n are non-dimensional coefficients, which are functions of GSI.

Figure 5 presents the variation of the coefficient A in Eq. (6) versus the GSI index for different slopes. Also, the variation of the coefficient n versus the GSI index for various slopes is shown in Fig. 6.

Fig. 5

Curve of non-dimensional coefficient (A) for different slopes

Fig. 6

Curve of non-dimensional coefficient (n) for different slopes

7 Artificial Neural Networks (ANNs)

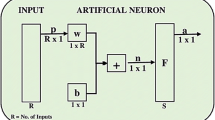
As cited, ANNs have been used by researchers as a tool for the development of predictive models on various geotechnical problems. ANNs are digitized models of a human brain and required designed through computer programs to simulate the way human brain processes information. ANNs learn through experience with appropriate learning exemplars just as people do, not from programming. ANNs receive and transfer information through some elements called “neurons”. Some inputs to the neuron may have greater importance than the others. This difference is modeled by weighting the input of the neurons (Fig. 7) (Haykin 1999).

Fig. 7

Adapted from Haykin (1999)

Neuron model with weighted inputs and embedded transfer function

A neuron can be a nonlinear mathematical function. As a result, a neural network formed by the community of these neurons can also be a complex and nonlinear system. The following equation is required for calculated the output of the neuron.

$${\text{y}}_{{\text{j}}} = {{\upvarphi }}\left( {\mathop \sum \limits_{{{\text{i}} = 0}}^{{\text{m}}} {\text{w}}_{{{\text{ji}}}} {\text{x}}_{{\text{i}}} + {\text{b}}_{{\text{j}}} } \right)$$

(7)

where ${\text{w}}_{{{\text{ji}}}}$: connection weight between nodes j and i, ${\text{x}}_{{\text{i}}}$: input from node 1, i = 0,1,…m, ${{\upvarphi }}$: activation function, ${\text{b}}_{{\text{j}}}$: bias value or threshold for node j, ${\mathbf{y}}_{{\mathbf{j}}}$: the target output node j.

The activation function determines the output of the neuron and can be linear or nonlinear. There are several activation functions to transform the output of the neuron. An activation function is selected based on the particular requirement to solve a problem. In this study, the back propagation (BP) neural network algorithm is used. The only requirement for this algorithm is that activation functions are differentiable everywhere because the derivative of activation function is used in this algorithm. The BP algorithm is one of the most widely applied ANNs in which training is based on the error BP algorithm.

The BP ANN is a conventional method of optimization, which can be described as follows (Li et al. 2012):

Feedforward (FF) The input data are multiplied by the weight and then accumulated with constant bias values and the network output is calculated using the activate functions, which is probably different from the actual output. At this stage, the difference between the real output and expected output of the network is defined as the error signal.

Backpropagation (BP) of error BP distributes the error signal back through the layers, by modifying the weights at each node.

In a BP ANN, sigmoid or hyperbolic tangent sigmoid transfer functions are often used. If the absolute value of the input to the sigmoid function is > 6 and the absolute value of the input to the Hyperbolic tangent sigmoid function is > 3, then the derivation of these functions tends to 0. Since the derivative of the activation functions is used as a multiple in weight change equations, in this case, the entered weights of that neuron will not be trained. To avoid this problem, the input values of the learning pairs are mapped to the range of [0.1 1] in the mode of using the sigmoid function and in the mode of using the Hyperbolic tangent sigmoid hyperbolic function to the interval [−1 1].

Multi-layer perceptron (MLP) networks with an intermediate layer of neurons and the sigmoid function as activation function are capable to model each level of response through an adequate number of neurons in the hidden layer. If a mapping is available, the MLP network could be found it with a hidden layer. This issue was first proved by Cybenko (1989) and then by Hornik (1991).

In the present research, only a hidden layer with different activation functions was used in the intermediate and output layer. In general, this study consisted of six main types of models for network training, with their characteristics shown in Table 3. The number of hidden neurons is the fundamental question that is generally discussed, especially when using neural networks to solve technical-engineering problems. In general, the real and accurate analysis of this issue is very complex. The reason for this complexity includes the MLP network itself and the random and uncertain nature of learning processes. Therefore, the hidden layer size is generally obtained experimentally through the trial and error (Nian et al. 2012). In this work, each model was investigated for 2, 3, 4, and 5 neurons in the hidden layer and finally the best model was selected. The number of neurons in the hidden layer is as an index after the model name. For example, LP5 represents a model whose activation function in hidden and the output layer is log sigmoid and linear respectively and has 5 neurons in the hidden layer.

Table 3 The structure of the neural network models used in this research

8 The Mathematical Model Based on Artificial Neural Networks

In this study, the slope angle $\left( \alpha \right)$, the dimensionless parameter $\left( {N_{S} } \right)$, Geological Strength Index (GSI) and coefficient of surcharge load effect $\left( {CSL = 1 - \frac{P}{{\sigma_{c} }}} \right)$ were considered as the input variables and the FOS was considered as the output variable. The mean squared error (MSE) was as network performance function. To batch the network data, 70% of them were selected as training data, 15% for validation, and 15% data for network testing. The BP algorithm of the MLP architecture was implemented in Matlab Software. The inappropriate selection of validation values leads to a lack of generalizability of the network. Since these values are also selected as a percentage of instructional data, the program’s response is sometimes not generalized. So, to determine the best response to the performances, we repeated the model runs. In appropriate selection of validation values leads to a poor generalization of the model. Besides, because these values are selected as a percentage of training data, sometimes the response of the program is not generalized and thus we have to execute the best responses to determine the best response. In selecting the optimal model, in addition to the mean of squared errors and correlation coefficient between the actual results and network outputs, the structure simplicity was also considered. Accordingly, the best response was obtained for the TP5 model with five neurons in the hidden layer, which the activation function of the hidden and output layers is hyperbolic tangent sigmoid and linear function, respectively. The weights and biases of the final network are presented in Table 5. The weights and biases can be utilized for sensitivity analysis and framing an ANN model in equation form. The same will be discussed in the following sections.

The basic mathematical equation according to the ANN can be written as:

$$FOS = \left[ {\begin{array}{*{20}c} { - 11.27} \\ { - 2.26} \\ { - 42.03} \\ {0.403} \\ {53.96} \\ \end{array} } \right]^{T} .tansig\left( {\left[ {\begin{array}{*{20}c} {0.0188} & { - 0.1044} & { - 0.0021} & { - 43.294} \\ {0.0175} & { - 0.0189} & { - 0.0098} & { - 2.264} \\ {0.0118} & { - 0.0321} & {0.0045} & { - 26.893} \\ { - 0.0013} & {0.1801} & {0.0495} & {4.274} \\ {0.0119} & { - 0.0338} & {0.0068} & { - 28.172} \\ \end{array} } \right].\left[ {\begin{array}{*{20}c} \alpha \\ {N_{s} } \\ {GSI} \\ {CSL} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {50.32} \\ {2.82} \\ {28.43} \\ { - 17.39} \\ {29.93} \\ \end{array} } \right]} \right) + 2.2561$$

(8)

9 The Network Interpretation Diagram (NID)

Ozmesmi and Ozmesmi (1999) proposed the use of network interpretation diagram (NID) to interpret the weights attached to each neuron. In the NID, the lines that connect the inputs to the hidden layer neurons, as well as the hidden layer neurons to the output layer, represent the magnitude of the weights. Positive coefficients are denoted by black lines and negative coefficients with gray lines, and the thickness of these lines is proportional to the magnitude of the weight coefficients. If the hidden layer input and the hidden layer are both positive and negative, then the input variable has a positive effect on the output; otherwise, it has a negative effect. The variables with the positive effect with a gray background and the negative effect with a white background are presented. for the model with the weights as obtained and shown in Table 4, a NID is presented as shown in Fig. 8.

Table 4 Connection weights and biases of neural network model

Fig. 8

The NID showing axons representing connection weights and effects of inputs on safety factor

It can be seen from Fig. 11 that the (GSI), $\left( {{\text{N}}_{{\text{s}}} } \right)$ and (CSL) have a positive contribution to the FOS and slope angle $\left( {{\upalpha }} \right)$ has negative effects on the FOS. Thus it inferred that (GSI), $\left( {{\text{N}}_{{\text{s}}} } \right)$ and (CSL) are directly and $\left( {{\upalpha }} \right)$ is indirectly proportional to FOS value. So, it can be seen that NID is an effective method in indicating the physical relationship between inputs with the output.

10 Comparison of Stability Charts and ANNs

Statistical analysis can be a good indicator for the classification of methods proposed for predicting the stability FOS of the rock slope. The use of statistical analyses alone, however, may lead to misjudgment of the audience. Therefore, it is necessary to use the statistical analyses and the ratio of the predicted values to the measured values synchronous (Haykin 1999).

Theoretically, the ratio of the predicted stability factor to the measured values (depending on the method used to predict) changes from 0 to an uncertain value, with the optimal value being 1. In a precise and accurate modeling, the mean of this ratio is 1 and the standard deviation is 0.

The more the average and standard deviation of this ratio are closer to 1 and 0, respectively, the more accurate the model is. A mean value greater than 1 represents overprediction and underprediction otherwise.

Another criterion that can be used to measure the performance of different prediction methods is the relative error between the predetermined value and the actual value. In this study, the minimum and maximum relative errors, mean relative error, the standard deviation of relative errors, the ratio of a predicted FOS $\left( {{\text{F}}_{{{\text{S}},{\text{P}}}} } \right),{ }$ to the existing value $\left( {{\text{F}}_{{{\text{S}},{\text{m}}}} } \right),$, and the mean square error (MSE) were used as the performance criteria (Table 5).

Table 5 Comparison of different methods of predicting the safety factor of rock slope

According to Table 5, both methods show a good performance in predicting the FOS, except that in the ANN model the independent variables such as slope angle (α) and GSI are directly imported to the equations. However, in the chart stability, there may be a need for interpolation.

The correlation coefficient (R) was used as another criterion for comparing different methods. In Figs. 9 and 10, the R values are measured and predicted by both the stability charts and the ANNs. The results show that in both methods, there is a high correlation between the measured and predicted stability factors.

Fig. 9

Correlation coefficient of measured and predicted stability factors through stability charts

Fig. 10

Correlation coefficient of measured and predicted stability factors through neural network model

It will be desirable to have certain other statistical measures to test the effectiveness of the developed models in terms of their predictability criteria.

Abu-Farsakh (2004) suggested the use of cumulative probability as an additional criterion for evaluating different prediction methods. For different methods, the ratio of a predicted FOS to the obtained FOS is arranged as per their values and the cumulative probability is calculated from the following:

$${\text{p}} = \frac{{\text{i}}}{{{\text{n}} + 1}}$$

(9)

where i is the order number given to the ${\text{F}}_{{{\text{S}},{\text{P}}}} /{\text{F}}_{{{\text{S}},{\text{m}}}} { }$ ratio and n is the number of data points.

If the computed value of 50% cumulative probability (P₅₀) is less than 1, underprediction is implied while values greater than 1 means overprediction. The ‘best’ model is corresponding to the P₅₀ value close to 1. The 90% cumulative probability (P₉₀) reflects the variation in the ratio of ${\text{F}}_{{{\text{S}},{\text{P}}}} /{\text{F}}_{{{\text{S}},{\text{m}}}} { }$ for the total observations. The model with ${\text{F}}_{{{\text{S}},{\text{P}}}} /{\text{F}}_{{{\text{S}},{\text{m}}}} { }$ close to 1.0 is the better one.

Figure 11 shows the variation of ${\text{F}}_{{{\text{S}},{\text{P}}}} /{\text{F}}_{{{\text{S}},{\text{m}}}} { }$ with cumulative probability (%) for the ANN model and stability charts methods. As can be seen, model based on neural network have the more proper distribution.

Fig. 11

Predicted over measured safety factor ratio against cumulative porosity for ANN and safety chart models

11 Sensitivity Analysis

Sensitivity analysis is the study of how the variation in the output of a mathematical model can be attributed to variations of its input factors. Different approaches have been proposed for determining the important input variables and ranking the input variables in terms of the impact on the network output. Goh (1994) and Shahin et al. (2002) used the Garson’s algorithm (1991) to choose important input variables. In this method, the input-hidden and hidden-output weights of the trained ANN model are partitioned and the absolute values of the weights are taken to select the important input variables.

Garrison’s algorithm process can be described as follows:

• 1. For each neuron j of the hidden layer, the absolute of the ith input weight multiplies the absolute value of the output weights of the neuron and the product of their multiplication is combined. This will get the S_ij.

• 2. For each input variable i, P_i is calculated from the sum of Sij obtained from the previous step $({\text{P}}_{{\text{i}}} = \sum {\text{S}}_{{{\text{ij}}}} )$.

• 3. The relative importance of each variable i from the input layer is obtained by dividing Pi by the sum of Pi ${ }({\text{rank}}_{{\text{i}}} = \frac{{{\text{P}}_{{\text{i}}} }}{{\mathop \sum \nolimits_{{\text{i}}} {\text{P}}_{{\text{i}}} }})$

Olden et al. (2004) presented a method of connection weights in which the actual values of weight coefficients are considered. This method calculates the product of the raw input-hidden and hidden-output connection weights between each input neuron and output neuron and sums the products across all hidden neurons.

Connection weights process can be described as follows (Olden et al. 2004):

• 1. For each neuron j of the hidden layer, the ith input weight multiplies the value of the output weights of the neuron and the product of their multiplication is combined. This will get the S_ij.

• 2. For each input variable i, P_i is calculated from the sum of S_ij obtained from the previous step $({\text{P}}_{{\text{i}}} = \sum {\text{S}}_{{{\text{ij}}}} )$.

• 3. The relative importance of each input variable i is proportional to the absolute value of ${\text{P}}_{{\text{i}}}$.

The sensitivity analysis for the model as per Garson’s method and Olden et al. connection weight approach to find out important input parameters is presented in Table 6.

Table 6 Relative importance of different inputs as per Garson’s algorithm and connection weight approach

According to Garson’s method, the coefficient of surcharge load effect (CSL) has the highest effect and the slope angle has the least effect on the FOS. The noteworthy point in the Garson algorithm is that due to the use of absolute weight coefficients, this method does not show that the desired variable is direct with network output or indirect ratio.

Based on the method of communication weights, the dimensionless parameter (${\text{GSI}}$) has the highest effect and the slope angle has the least effect on the slope stability factor. Also, GSI, coefficient of surcharge load effect (CSL) and the dimensionless parameter (${\text{N}}_{{\text{s}}}$) have a positive contribution to the FOS and slope angle $\left( {{\upalpha }} \right)$ has negative effects on the FOS it should be noted that the mentioned methods for sensitivity analysis show the relative importance of the input variables of the ANN model, since the variables of surcharge load intensity (p), the unconfined compressive strength of rock $\left( {{\upsigma }_{{{\text{ci}}}} } \right)$, and height of slope (H) in the dimensionless parameter (Ns) are incorporated. Therefore, these methods do not independently examine the effect of each of these parameters on the network output. Two other methods were used to determine the sensitivity of slope stability to all parameters.

One of these methods is the Pearson correlation coefficient, which is used to rank the appropriate inputs for the network. According to this method, the correlation coefficient between the actual output and each input variable indicates the relative importance of each variable. Table 7 presents the correlation coefficient between the input variables and the output value.

Table 7 The correlation coefficient between the input variables and the actual output variables

Based on Pearson’s correlation coefficient method, the GSI is the most important input parameter and the height of slope is less important than other input parameters. Also, the negative values of correlation coefficient indicate the inverse effect of the input parameter on the FOS. Therefore, by increasing the slope angle, the intensity of the surcharge load and height of slope of the FOS decreases.

A parametric study was carried out through a basic approach to sensitivity analysis by fixing all but one input variable to their mean values and varying the remaining one within the range of its maximum and minimum values. The sensitivity analysis was repeated for every contributing parameter with the aim of providing a better understanding of the contribution of individual parameters to predictions of the proposed ANN. Figures 12, 13, 14, 15 and 16 represent the results of the sensitivity analysis for the slope angle, the height of the slope, the intensity of the surcharge load, the unconfined compressive strength of rock, and GSI, respectively.

Figure 12 represents the sensitivity analysis of the FOS with the slope angle variations. It is observed that the change of FOS is linear and have an inverse relationship with the slope angle. On average, when the angle of slope is increased by 10%, the FOS decreases by 8.85%.

Fig. 12

Sensitivity analysis of the neural network model (effect of angle of slope)

Figure 13 shows the sensitivity analysis of the FOS with respect to the height of slope variations. It is observed that the changes of FOS are nonlinear (quadratic function) and have an inverse relationship with the height of the angle. On average, when the height of the slope is increased by 10%, FOS decreases by 0.5%

Fig. 13

Sensitivity analysis of the neural network model (effect of height of slope)

Figure 14 presents the sensitivity analysis of the FOS against the surcharge load intensity variations. It is observed that the changes of FOS are nonlinear and have an inverse relationship with surcharge intensity. In the lower values of the surcharge load intensity, the FOS is very sensitive to surcharge load intensity variations, but at high values that is almost constant. On average, when the surcharge load intensity is increased by 10%, FOS decreases by 2.4%

Fig. 14

Sensitivity analysis of the neural network model (effect of surcharge load intensity)

Figure 15 shows the sensitivity analysis of the FOS versus the unconfined compressive strength of rock variations. It is observed that the changes of FOS are almost linear and have a direct relationship with the unconfined compressive strength of the rock. On average, when the unconfined compressive strength of rock is increased by 10%, FOS increases by 6.01%

Fig. 15

Sensitivity analysis of the neural network model (effect of unconfined compressive strength of rock)

Figure 16 illustrates the sensitivity analysis of the FOS with GSI variations. It is observed that the changes of FOS are nonlinear and have a direct relationship with the GSI. On average, when the GSI by 10%, the FOS increased by 14.17%.

Fig. 16

Sensitivity analysis of the neural network model (effect of ground strength index)

12 Slope Cases Application

The following six examples with a wide range of rock properties and slope geometry were used to compare efficiency of the rock slope stability charts proposed in this paper and rock slope stability charts proposed by Li et al. (2008), Shen et al. (2013), Sun et al. (2016), and ANN. The results are shown in Table 8.

Table 8 Six slope examples analyzed using the proposed stability charts and neural networks

The ratio of the predicted FOS to the measured FOS is shown in Table 9. As can be seen, the stability charts provided by Li et al., on average, predict a stability factor of 9.1 times greater than the real value. It seems the ratio of the predicted stability factor (F_S,P) to the measured value (F_S,M) by stability charts provided by Li et al. (2008) is reduced by increasing the dimensionless parameter (Ns) or decreasing the GSI.

Table 9 Ratio of the predicted stability factor to the measured value

For a state that the unconfined compressive strength is very low, the rock slope stability charts proposed in predict FOS much less and more than the real value, respectively. It is also observed that ANNs yield more reliable FOS than the stability chart curves.

13 Summary and Conclusions

In this study, the effect of various physical and geometric factors on the stability of rock slope stability is investigated using the finite element method (FEM) and the shear strength reduction (SSR) method. Independent variables in this research included geometric variables (e.g., height and slope angle), geomechanical parameters of rock (e.g., GSI and the unconfined compressive strength of the rock ${ }\left( {{\upsigma }_{{{\text{ci}}}} } \right)$, and surcharge load intensity. A stability chart was developed for each slope using nonlinear regression and FEM analysis results. In order to reduce the independent variables, a dimensionless parameter is defined as: ${\text{N}}_{{\text{s}}} = \left( {{\text{CSL}}} \right)\frac{{{\upsigma }_{{\text{c}}} }}{{\upgamma{\text{ H}} + {\text{P}}}}$. A mathematical model based on ANNs was developed using FEM analysis results and the following conclusions can be drawn:

• 1. The results showed that in all stability charts, the best relation for fitting the FOS and the dimensionless parameter (Ns) is a power relation as ${\text{FS}} = {\text{A}}.\left( {{\text{N}}_{{\text{s}}} } \right)^{{\text{n}}}$, where A and n are dimensionless parameters, which are functions of GSI.

• 2. Effect of surcharge using a decreasing coefficient $\left( {CSL = 1 - \left( {\frac{P}{{\sigma_{c} }}} \right)^{0.3} } \right)$ was considered. As the surcharge increased, it reduced the dimensionless parameter (Ns) and, consequently, reduced the factor of safety.

• 3. Using the back propagation (BP) neural network algorithm, a mathematical model was developed to predict the FOS of rock slopes and an equation was presented based on the trained weights of the ANN.

• 4. The performance of stability charts and ANN was compared and observed that both methods have a good agreement in predicting the FOS. However, in the ANN model, unlike the stability charts, independent variables of the angle of slope and GSI are directly introduced in the model equations and need not be interpolated.

• 5. Analysis of statistical mean and standard deviation, along with cumulative probability function, were also utilized to investigate the quality of predictions made by the proposed models. The results showed that ANN model have the better proper distribution.

• 6. The sensitivity analysis was carried out based on different approaches. In general, the GSI, effect of surcharge (CSL) and then the dimensionless parameter (Ns) have the highest effect on the stability factor of slopes. The slope angle, slope height, and intensity of the surcharge load have an inverse relation and other parameters have a direct relation with the FOS of rock slope stability. Among all independent variables, surcharge load intensity has the smallest effect on slope stability

• 7. It is observed that ANN yields more reliable stability factor than stability charts curves.