1 Introduction

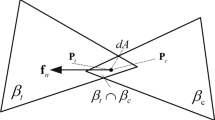
The porous medium and the fissure medium is the main storing positions of oil in fractured-vuggy reservoirs. As the main oil storage space, the porous medium and the fissure medium can make a difference to the oil production if their mechanical properties change (Kang 2008; Huang et al. 2013; Li et al. 2014; Zhao et al. 2012). The porous medium usually composes of two parts. The one is the solid skeleton which plays a part as the acceptor of force. The other is the porous medium which plays a part as the flow channel for the fluid. The mechanical properties of the solid skeleton shall be influenced by the fluid flow. At the same time, the fluid flowing shall be influenced by the deformation of the solid skeleton. And that’s just how the coupled mechanical behaviors emerge in the porous medium. However, for the porous medium with large cracks, they usually maintain more complex mechanical properties (See Fig. 1). The whole seepage field and the stress field will be influenced as the fluid exchanges between the fractures and the pores, which will then lead to the closure and propagation of the cracks. As the crack closure and propagation can influence the mechanical properties of the porous medium, vice versa. Therefore, the mechanical property study of porous medium with cracks is a more complex one and agrees with actual situations better.

Fig. 1
figure 1

Flow characteristics in a fractured deforming porous medium and boundary conditions

Full size image

Terzaghi (1943) was the first one doing research on the porous medium, and he put forward the consolidation theory of one-dimensional fluid saturated viscoelastic porous medium and the famous effective stress equation. And up till now, this equation is still the basic formula to study the interactions between the rock mass and the fluid. Biot (1941) and Boit and Willis (1957) then promoted Terzaghi’s theory to the linear elastic porous medium three-dimensional consolidation theory. Later some scholars (Morland 1972; Wu and Forsyth 2001; Stelzer and Hofstetter 2005; Abdul et al. 2011; Bitao et al. 2012; Alexandre 2013) continuously developed the Blot’s three-dimensional consolidation theory into the theoretical model of coupled effect involving the multiple-phase saturated flow and the porous medium.

Large cracks in fractured-vuggy reservoirs are not only reservoir spaces but also seepage channels. As the existence of cracks has a great difference in the rock permeability, it is necessary to consider the influence on the seepage field and stress field brought by the fluid exchange between pores and cracks as well as on the crack propagation and closure. In petroleum domain, the former research mainly focuses on hydraulic fracturing. Benoit and Sylvie (2012) used cohesive zone model to simulate the propagation of hydraulic fracturing in the porous medium. Magnus (2012) adopted the finite element method (FEM) to establish the modeling approach for the anisotropic rock hydraulic fracturing in a macro-scale. Chen (2012) developed the pore pressure cohesive finite elements to simulate the hydraulic fracturing propagation in the porous medium. Cuo et al. (2015) used the FEM to study the mutual influence regularities between the hydraulic fractures and the natural fractures. Olaga et al. (2013) and Wen (2015) developed the UFM to simulate the propagation of pre-existing cracks in the complicated geological mass. Wang et al. (2014) studied the influence to the hydraulic fracturing propagation by the injection parameter. Farzin and Ali (2014) developed the numerical simulation method of the three-dimensional hydraulic fracturing propagation. Wang et al. (2013) studied the influence to the crack propagation in the anisotropic rock mass by the pore pressure based on the FEM.

The finite element method has been successfully applied to various engineering simulations and has a great advantage in dealing with continuous problems (Sarris and Papanastasious 2012; Birk and Behnke 2012; Erasmo et al. 2013; Zhang et al. 2017a, b). However, when it involves the discontinuous problems of cracked rock masses, FEM betrays huge limitation and deficiency. During the simulation of the crack propagation, the mesh must be re-divided. This increases computational cost and makes the whole simulation process a more complex one. To solve this problem many numerical methods are developed at the right moment. The extended finite element method (XFEM) is one of them. It is a new, improved numerical solution method on the base of FEM. Compared to FEM, XFEM contains an advantage in effectively solving the discontinuous problems and it can exist separately from grid. Therefore, the redividing process can be avoided. Mousavi and Sukumar (2010) put forward a new Gauss integration scheme under the extended finite element framework, which improved the computation efficiency. Motamedi and Mohammadi (2010) studied the dynamic crack propagation regularities in the transversely anisotropic rock mass with the XFEM. (Gupta and Duarte 2014) did research on the three-dimensional crack extension process. Giner et al. (2008) and Shi et al. (2010) realized the secondary development for XFEM function on the ABAQUS platform. Elizaveta and Anthony (2013) adopted the level set to simulate the hydraulic fracture propagation. With the assistance of the cohesive extended finite element method, Mohammadnejad and Khoei (2013a, b) carried out studies on simple cracks with known propagation directions.

In this thesis, the coupled stress and fluid flow control equations of the porous medium and the fissure medium are established. And the weak form of the equations are also obtained with the help of divergence theorem. Based on this, the spatial dispersion of the control equation is carried out through the XFEM; and the time discretization through Newton’s method. With the assistance of the above spatial dispersion as well as time discretization, the numerical solution of the porous media-crack model is finally obtained. After this, the secondary development of the finite element analysis software-ABAQUS is carried out, which implements the full coupling of the hydraulic fractures’ propagation in the porous medium. Besides, the crack propagation regularities under the condition of fluid–solid coupling are analyzed through calculating examples.

2 Governing Equation

Just as shown in Fig. 1, inside the porous medium are the solid skeleton and the pore medium. It is a mutual coupling process of the solid skeleton and the porous medium while the former one shows a force–deformation and the latter shows a deformation caused by fluid flow. So in this section, the equation of the solid–liquid coupling is established in the porous medium. And the fluid flow satisfy the two-dimensional Darcy’s law in the porous medium. Besides, there is still a fluid exchange process between the fractured fluid and the porous medium fluid. Thus, in this thesis, the fractured fluid and the surrounding leakage flux of the porous medium are regarded as the mass delivery channel for the coupled porous medium as well as the fissured medium. Through the above procedure, the solid–liquid coupling model of the crack fluid and the solid porous medium can be established.

2.1 Governing Equation of the Porous Medium

  1. 1.

    Stress field equation

The effective stress principle was put forward by Terzaghi in 1923 when he studied the mutual effect on the water-filled saturated soils. And this principle has been further developed as a significant one of the poroelastic theory. Many other theories studying the percolating-mechanic interactions like the one-dimensional consolidation theory of Terzaghi, the consolidation theory of Biot and so on was all based on this effective stress principle. However, with the deepening of the research, this equation is found to be insufficient in describing some deformation characteristics in terms of certain porous mediums such as the concrete and the rock mass. Therefore, a universal effective stress principle is developed and expressed as follows:

$$\varvec{\sigma^{\prime}} = {\varvec{\upsigma}} - \alpha {\mathbf{m}}p$$
(1)

where \(\varvec{\sigma^{\prime}}\) is the effective stress; \(\varvec{\sigma}\) is the total stress; \(p\) is the pore pressure; \(\alpha\) is the Biot coefficient; m refers to the constant vector whose evaluation is \(\left[ {\begin{array}{*{20}c} 1 & 1 & 0 \\ \end{array} } \right]^{\text{T}}\) under the condition of two-dimension.

The solid skeleton displacement is regulated as \(u_{i} \left( {x,t} \right)\) and the relative displacement of the crack fluid to the solid skeleton is regulated as \(v_{i} \left( {x,t} \right)\). As for the static problems, the acceleration velocity shall be negligible. Therefore, the momentum balance equation of the solid–liquid mixture can be written as:

$$\nabla \cdot {\varvec{\upsigma}} + \rho {\mathbf{b}} = 0$$
(2)

where \({\mathbf{b}}\) is the body force vector; \(\rho\) is the average density of the porous medium, which is defined as \(\rho = n\rho_{w} + \left( {1 - n} \right)\rho_{s}\), where n is the porosity, \(\rho_{w}\) is the density of fluid phase and \(\rho_{s}\) is the density of solid grains.

The constitutive equation of the solid skeleton can be written as

$$d{\mathbf{\sigma^{\prime}}} = {\mathbf{D}}d{\varvec{\upvarepsilon}}$$
(3)

In which \({\varvec{\upvarepsilon}}\) represents the strain tensor of the skeleton, which is obtained through its geometric equation.

$${\varvec{\upvarepsilon}} = \frac{1}{2}\left( {\nabla {\mathbf{u}} + \left( {\nabla {\mathbf{u}}} \right)^{\varvec{T}} } \right)$$
(4)

In Eq. (3) \({\mathbf{D}}\) represents the fourth-order tangential stiffness matrix, and for the isotropic elastic plane strain problem, \({\mathbf{D}}\) can be written as follows:

$${\mathbf{D}} = \frac{E}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[ {\begin{array}{*{20}c} {1 - \nu } & \nu & 0 \\ \nu & {1 - \nu } & 0 \\ 0 & 0 & {\frac{1 - 2\nu }{2}} \\ \end{array} } \right]$$
(5)

where E is the elastic modulus, v is the Poisson’s ratio. Therefore, Eqs. (1) to Eq. (5) constitute the stress field equation of the porous medium.

  1. 2.

    Seepage field equation

According to the momentum conservation of the fluid in the porous medium, the generalized Darcy’s law is given by

$$- \nabla p - {\mathbf{R}} + \rho_{f} {\mathbf{b}} = 0$$
(6)

where \(\rho_{f}\) is the fluid density; \({\mathbf{R}}\) is the fluid viscous resistance, which can be written according to Darcy’s law as

$${\mathbf{R}} = \frac{{{\dot{\mathbf{V}}}}}{{\varvec{k}_{f} }}$$
(7)

where \({\dot{\text{V}}}\) is the crack fluid velocity; \(k_{f}\) is the permeability coefficient matrix. Combining Eqs. (6) and (7), the expression of the crack fluid velocity can be written as

$${\dot{\mathbf{V}}} = \varvec{k}_{f} \left( { - \nabla p + \rho_{f} {\mathbf{b}}} \right)$$
(8)

In the saturated porous medium, the continuity equation of the seepage can be expressed as:

$$\nabla \cdot {\dot{\mathbf{V}}} + \alpha \nabla \cdot {\dot{\mathbf{u}}} + K\dot{p} = 0$$
(9)

where \(K\) is the compression coefficient, which can be expressed as

$$K = \frac{\alpha - n}{{K_{s} }} + \frac{n}{{K_{f} }}$$
(10)

where \(K_{s}\) denotes the solid bulk modulus; \(K_{f}\) denotes the fluid modulus; n is the porosity, \(\alpha\) is the Biot coefficient. The continuity seepage equation of the saturated porous medium can be written by combining Eqs. (8) and (9) as:

$$\nabla \cdot \left( {\varvec{k}_{f} \left( { - \nabla \dot{p} + \rho_{f} {\mathbf{b}}} \right)} \right) + \alpha \nabla \cdot {\dot{\mathbf{u}}} + K\dot{p} = 0$$
(11)

Stress field Eqs. (1)–(5) and Seepage field Eq. (11) are the fluid–solid coupled governing equations in a porous medium.

  1. 3.

    Boundary conditions

As shown in Fig. 1, the boundary conditions of the displacement field include stress boundary condition and displacement boundary condition. The stress boundary condition is \({\mathbf{t}} = {\varvec{\upsigma}} \cdot {\mathbf{n}}_{{\varGamma_{t} }} = {\bar{\mathbf{t}}}\). On \(\varGamma_{t}\). Where \({\mathbf{n}}_{{\varGamma_{t} }}\) is the unit outward normal vector to the external boundary \(\varGamma\). \({\bar{\mathbf{t}}}\) denoting the known surface force on the boundary \(\varGamma_{t}\). The displacement boundary condition can be interpreted as follows: it must meet the condition that \({\mathbf{u}} = {\bar{\mathbf{u}}}\) on the boundary \(\varGamma_{u}\). \({\bar{\text{u}}}\) is the known displacement on this boundary. \(\varGamma\) is the whole external boundary. Besides, it must meet the equation \(\varGamma = \varGamma_{t} \cup \varGamma_{u}\).

The boundary conditions of the seepage field include constant hydraulic pressure boundary condition and constant flow boundary condition. The constant hydraulic pressure boundary condition can be expressed as: it must meet the condition that \({\mathbf{p}} = {\bar{\mathbf{p}}}\) on boundary \(\varGamma_{p}\), in which \({\bar{\mathbf{p}}}\) is the known pore-fluid pressure on this boundary. The constant flow boundary condition can be explained as \({\mathbf{v}} \cdot {\mathbf{n}}_{{\dot{\varGamma }_{w} }} = \bar{q}\) on the boundary \(\varGamma_{w}\) and the \({\bar{\text{q}}}\) is the fluid outflow rate exerted on it. Besides, it must meet the equation, \(\varGamma = \varGamma_{p} \cup \varGamma_{w}\).

Because of the existence of the large cracks as well as the quality exchanges between the cracks and the porous medium, the boundary conditions on the cracks meet the following equations: \({\varvec{\upsigma}} \cdot {\mathbf{n}}_{{\varGamma_{d} }} = - p{\mathbf{n}}_{{\varGamma_{d} }}\); \(\left[\kern-0.15em\left[ {{\dot{\mathbf{v}}}} \right]\kern-0.15em\right] \cdot {\mathbf{n}}_{{\varGamma_{d} }} = \bar{q}_{d}\). In which, \(\varGamma_{d}\) denoting the crack boundary, \(\bar{q}_{d}\) is the leakage flux of the crack fluid and the surrounding porous and it is also the mass transfer channel of the coupled porous medium as well as the fissured medium.

  1. 4.

    The weak form of the governing equation

The derivation of the weak form of the governing equation in this section is mainly to meet the calculated requirements in simulating the strong discontinuity based on XFEM so that the testing function can be applied to the weak form of the governing equation and the discrete system can also be obtained. In order to get the weak form of the balanced equation in the porous medium, u(x, t) and p(x, t) are defined as testing functions satisfying all boundary conditions. Using the divergence theorem for Eqs. (2) and (11) leads to the following weak form of governing equations as:

$$\mathop \int \limits_{\varOmega }^{{}} \nabla \delta {\mathbf{u}} \cdot {\varvec{\upsigma}}d\varOmega + \mathop \int \limits_{{\varGamma_{d} }}^{{}} \left[\kern-0.15em\left[ {\delta {\mathbf{u}}} \right]\kern-0.15em\right]{\varvec{\upsigma}} \cdot {\mathbf{n}}_{{\varGamma_{d} }} d\varGamma - \mathop \int \limits_{\varOmega }^{{}} \nabla \delta {\mathbf{u}} \cdot \rho \,{\mathbf{b}}d\varOmega - \mathop \int \limits_{{\varGamma_{t} }}^{{}} \delta {\mathbf{u}} \cdot {\bar{\mathbf{t}}}\,d\varGamma = 0$$
(12)
$$\begin{aligned} & \mathop \int \limits_{\varOmega }^{{}} \nabla \delta p\varvec{k}_{\varvec{f}} \nabla pd\varOmega + \mathop \int \limits_{{\varGamma_{d} }}^{{}} \delta p\left[\kern-0.15em\left[ {{\dot{\mathbf{v}}}} \right]\kern-0.15em\right] \cdot {\mathbf{n}}_{{\varGamma_{d} }} d\varGamma \\ & \quad - \mathop \int \limits_{\varOmega }^{{}} \delta p\alpha \nabla \cdot {\dot{\mathbf{u}}}d\varOmega - \mathop \int \limits_{\varOmega }^{{}} \delta pK\dot{p}d\varOmega \\ & \quad - \mathop \int \limits_{\varOmega }^{{}} \nabla \delta p\varvec{k}_{f} \cdot \rho_{f} {\mathbf{b}}d\varOmega + \mathop \int \limits_{{\varGamma_{w} }}^{{}} \delta p\left( {{\dot{\mathbf{v}}} \cdot {\mathbf{n}}_{\varGamma } } \right)d\varGamma = 0 \\ \end{aligned}$$
(13)

2.2 Governing Equation of the Fluid Flow in Cracks

In order to derive the motion equation of the fluid flow in cracks, an analytical model as shown in Fig. 1 and a local Cartesian coordinate system are established.

  1. 1.

    Strong form equation

In order to simulate the flow of fluid in the fracture, the continuity equation of the fluid flow in the fracture can be written as

$$\nabla \cdot {\dot{\mathbf{v}}} + \alpha \nabla \cdot {\dot{\mathbf{u}}} + \frac{1}{{K_{f} }}\dot{p} = 0$$
(14)

where \(K_{f}\) is the bulk modulus of the solid particles in the porous medium, \({\dot{\mathbf{v}}}\) is the relative velocity vector of the crack fluid with respect to the porous medium and is defined as

$${\dot{\mathbf{v}}} = k_{fd} \left( { - \nabla p + \rho_{f} {\mathbf{b}}} \right)$$
(15)

where \(k_{fd}\) is the permeability coefficient of the cracks which can be written based on the classical cubic law as:

$$k_{fd} = \frac{1}{\kappa }\frac{{w^{2} }}{{12u_{f} }}$$
(16)

where \(w\) refers to the width of the cracks. \(\kappa\) is the influencing variable of the angle deviation between cracks and the level surface. \(u_{f}\) is the fluid viscosity in cracks.

  1. 2.

    Weak form equations

The fluid inside the cracks is usually regarded as non-compressible. Therefore the continuity equation weak form of the crack fluid can be obtained through the following procedures. Firstly, let Eq. (14) multiply the testing equation \(\delta p\left( {x,t} \right)\). Secondly, in the fissure fluid region \(\varOmega^{\prime }\) using the divergence theorem. Lastly, plug Eq. (15) into the above calculations. Then the continuity equation weak form of the crack fluid can be written as

$$\mathop \int \limits_{{\varOmega^{\prime}}}^{{}} \delta p\left( {\nabla \cdot \left[ {k_{fd} \left( { - \nabla p + \rho_{f} b} \right)} \right] + \alpha \nabla \cdot {\dot{\mathbf{u}}} + \frac{1}{{K_{f} }}{\dot{\text{p}}}} \right)d\varOmega$$
(17)

Applying the divergence theorem to Eq. (17) and the continuity equation weak form can be written as:

$$\begin{aligned} & \mathop \int \limits_{{\varOmega^{\prime } }}^{{}} \nabla \delta pk_{fd} \nabla pd\varOmega + \mathop \int \limits_{{\varGamma_{d} }}^{{}} \delta p\left[\kern-0.15em\left[ {{\dot{\mathbf{v}}}} \right]\kern-0.15em\right] \cdot {\mathbf{n}}_{{\varGamma_{d} }} d\varGamma \\ & \quad - \mathop \int \limits_{{\varOmega^{\prime } }}^{{}} \delta p\alpha \nabla \cdot {\dot{\mathbf{u}}}d\varOmega - \mathop \int \limits_{{\varOmega^{\prime } }}^{{}} \delta p\frac{1}{{K_{f} }}\dot{p}d\varOmega \\ \end{aligned}$$
(18)

In order to compute the coupling term of the mass transmission, the cracked shall be calculated under the topical Cartesian coordinates system \(\left( {x^{\prime},y^{\prime}} \right)\). The directions of \(x^{\prime}\) and \(y^{\prime}\) are in line with the directions of crack unit tangential vector \({\mathbf{t}}_{{\varGamma_{\text{d}} }}\) and unit normal vector \({\mathbf{n}}_{{\varGamma_{\text{d}} }}\). Because the length of the cracks is much larger than width, the fluid pressure are distributed evenly over the cracks’ transverse section. Therefore, the weak equation form of the coupling mass in cracks can be written based on Eq. (18) as:

$$\begin{aligned} \mathop \int \limits_{{\varGamma_{d} }}^{{}} \delta p\left[\kern-0.15em\left[ {{\dot{\mathbf{v}}}} \right]\kern-0.15em\right] \cdot {\mathbf{n}}_{{\varGamma_{d} }} d\varGamma & = - \mathop \int \limits_{{\varGamma_{d} }}^{{}} k_{fd} \rho_{f} \left( {2h} \right)\frac{\partial \delta p}{{\partial x^{\prime}}}\frac{\partial p}{{\partial x^{\prime}}}d\varGamma \\ & \quad + \mathop \int \limits_{{\varGamma_{d} }}^{{}} \delta p\alpha \rho_{f} \left( {2h} \right)\left\langle {\frac{{\partial \dot{u}_{{x^{\prime}}} }}{{x^{\prime}}}} \right\rangle d\varGamma + \mathop \int \limits_{{\varGamma_{d} }}^{{}} \delta p\alpha \left[\kern-0.15em\left[ {\dot{u}_{{y^{\prime}}} } \right]\kern-0.15em\right]d\varGamma \\ & \quad + \mathop \int \limits_{{\varGamma_{\text{d}} }}^{{}} k_{fd} \rho_{f} \left( {2h} \right)\frac{\partial \delta p}{{\partial x^{\prime}}}b_{{x^{\prime}}} {\text{d}}\varGamma \\ \end{aligned}$$
(19)

3 Discretization of Governing Based on XFEM

3.1 Spatial Discretization

In this section, the spatial discretization of the weak forms of the porous media balance equation, as well as the fluid continuity equation, are carried out through XFEM. In order to describe the discontinuous crack displacement field, the jump function Heaviside and the crack-tip progressive function is introduced in. Their expressions can be given by

$${\text{H}}\left( {\varphi \left( {\text{x}} \right)} \right) = \left\{ {\begin{array}{*{20}c} { + 1 \varphi \left( {\text{x}} \right) \ge 0 } \\ { - 1 \varphi \left( {\text{x}} \right) < 0 } \\ \end{array} } \right.$$
(20)
$$\upbeta\left( {\gamma ,\theta } \right) = \left\{ {\sqrt \gamma \sin \frac{\theta }{2},\sqrt \gamma \cos \frac{\theta }{2},\sqrt \gamma \sin \frac{\theta }{2}\sin \theta ,\cos \frac{\theta }{2}\sin \theta } \right\}$$
(21)

The displacement field \(u\left( {\varvec{x},t} \right)\) can be written based on the XFEM as:

$$\begin{aligned} u\left( {x,t} \right) & = \mathop \sum \limits_{{I \in {\mathcal{N}}}} N_{uI} \left( x \right)\bar{u}_{I} \left( t \right) + \mathop \sum \limits_{{J \in {\mathcal{N}}^{dis} }} N_{uJ} \left( x \right)H\left( {\varphi \left( x \right)} \right)\bar{a}_{J} \left( t \right) \\ & \quad + \mathop \sum \limits_{{K \in {\mathcal{N}}^{tip} }} N_{uK} \left( x \right)\beta \left( {\gamma ,\theta } \right)\bar{b}_{K} \left( t \right) \\ \end{aligned}$$
(22)

The pressure field is a discontinuous one because of the existence of the cracks. And in order to describe this kind of discontinuity the level set function is introduced, which is written as:

$$\psi \left( \varvec{x} \right) = \mathop \sum \limits_{{I \in {\mathcal{N}}^{dis} }} N_{pJ} \left( \varvec{x} \right)\left| {\varphi_{I} } \right| - \left| {\mathop \sum \limits_{{I \in {\mathcal{N}}^{dis} }} N_{pJ} \left( \varvec{x} \right)\varphi_{I} } \right|$$
(23)

Therefore the expression of the pressure field \(p\left( {\varvec{x},t} \right)\) can be written based on the XFEM as:

$$p\left( {\varvec{x},t} \right) = \mathop \sum \limits_{{I \in {\mathcal{N}}}} N_{pI} \left( \varvec{x} \right)\bar{p}I\left( t \right) + \mathop \sum \limits_{{J \in {\mathcal{N}}^{dis} }} N_{pJ} \left( \varvec{x} \right)\psi \left( x \right)\bar{c}_{J} \left( t \right)$$
(24)

where \({\mathcal{N}}\) denotes the collection of nodes; the \({\mathcal{N}}^{dis}\) denotes the collection of nodes in crack-penetrating; \({\mathcal{N}}^{tip}\) denotes the collection of crack-tip nodes. The specific unit node information is shown in Fig. 2.

Fig. 2
figure 2

Element and node representation in XFEM

Full size image

The final XFEM equation of displacement and pressure field can be written as:

$$\begin{aligned} \varvec{u}^{h} \left( {\varvec{x},t} \right) & = \varvec{ N}_{u}^{std} \left( \varvec{x} \right)\bar{\varvec{u}}\left( t \right) + \varvec{N}_{u}^{Hev} \left( \varvec{x} \right)\bar{\varvec{a}}(t) + \varvec{N}_{u}^{tip} \left( \varvec{x} \right)\bar{\varvec{b}}\left( t \right) \\ p^{h} \left( {\varvec{x},t} \right) & = \varvec{N}_{p}^{std} \left( \varvec{x} \right)\bar{\varvec{p}}\left( t \right) + \varvec{N}_{p}^{abs} \left( \varvec{x} \right)\bar{\varvec{c}}(t) \\ \end{aligned}$$
(25)

where \(\varvec{ N}_{u}^{std} \left( \varvec{x} \right)\) is the displacement shape function matrix of standard notes. \(\varvec{N}_{u}^{Hev} \left( \varvec{x} \right)\) is the shape function matrix of the enriched penetrating nodes \(\varvec{N}_{u}^{tip} \left( \varvec{x} \right)\) is the shape function matrix of the crack-tip penetrating nodes. \(\varvec{N}_{p}^{std} \left( \varvec{x} \right)\) is the shape function matrix of the pressure. \(\varvec{N}_{p}^{abs} \left( \varvec{x} \right)\) refers to the shape function matrix of the enriched nodes. \(\bar{\varvec{u}}\left( t \right)\), \(\bar{\varvec{a}}(t)\), \(\bar{\varvec{b}}\left( t \right)\), \(\bar{\varvec{p}}\left( t \right)\) and \(\bar{\varvec{c}}(t)\) respectively refer to the vector of degrees of freedom (DOF) of their correspondent node.

Discretizing the Eqs. (12) and (13) by using the Bubnov–Galerkin method, we can obtain the XFEM discretization equations as:

$$\left( {\begin{array}{*{20}c} {K_{uu } } \\ {K_{au } } \\ {K_{bu } } \\ \end{array} \begin{array}{*{20}c} {K_{ua } } \\ {K_{aa } } \\ {K_{ba } } \\ \end{array} \begin{array}{*{20}c} {K_{ub } } \\ {K_{ab } } \\ {K_{bb } } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\bar{u}} \\ {\bar{a}} \\ {\bar{b}} \\ \end{array} } \right\} - \left( {\begin{array}{*{20}c} {Q_{up } } \\ {Q_{ap } } \\ {Q_{bp } } \\ \end{array} \begin{array}{*{20}c} {Q_{uc } } \\ {Q_{ac } } \\ {Q_{bc } } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\bar{p}} \\ {\bar{c}} \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {f_{u}^{int} } \\ {f_{a}^{int} } \\ {f_{b}^{int} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {f_{u}^{ext} } \\ {f_{a}^{ext} } \\ {f_{b}^{ext} } \\ \end{array} } \right\} = 0$$
(26)
$$\left( {\begin{array}{*{20}c} {Q_{up}^{T} } \\ {Q_{uc}^{T} } \\ \end{array} \begin{array}{*{20}c} {Q_{ap}^{T} } \\ {Q_{ac}^{T} } \\ \end{array} \begin{array}{*{20}c} {Q_{bp}^{T} } \\ {Q_{bc}^{T} } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\dot{\bar{u}}} \\ {\dot{\bar{a}}} \\ {\dot{\bar{b}}} \\ \end{array} } \right\} + \left( {\begin{array}{*{20}c} {H_{pp } } \\ {H_{cp } } \\ \end{array} \begin{array}{*{20}c} {H_{pc } } \\ {H_{cc } } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\bar{p}} \\ {\bar{c}} \\ \end{array} } \right\} + \left( {\begin{array}{*{20}c} {S_{pp } } \\ {S_{cp } } \\ \end{array} \begin{array}{*{20}c} {S_{pc } } \\ {S_{cc } } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\dot{\bar{p}}} \\ {\dot{\bar{c}}} \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {q_{p}^{int} } \\ {q_{c}^{int} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {q_{p}^{ext} } \\ {q_{c}^{ext} } \\ \end{array} } \right\} = 0$$
(27)

In which K is the stiffness matrix. Q is the coupled element matrix. H is the penetration coefficient matrix. S is the compression coefficient matrix. \(f_{\alpha }^{ext}\) and \(q_{\delta }^{ext}\) are external forces vector quantities. \(f_{\alpha }^{int}\) is the interfacial forces vector quantities produced by the fluid pressure on the crack face. \(q_{\delta }^{int}\) is the flow vector quantities produced by the fluid exchange between the porous medium and the crack face. They are defined as

$$\begin{aligned} {\mathbf{K}}_{\alpha \beta } & = \mathop \int \limits_{\varOmega }^{{}} \left( {{\mathbf{B}}_{u}^{\alpha } } \right)^{T} \varvec{D}{\mathbf{B}}_{u}^{\beta } d\varOmega \\ {\mathbf{Q}}_{\alpha \gamma } & = \mathop \int \limits_{\varOmega }^{{}} \left( {{\mathbf{B}}_{u}^{\alpha } } \right)^{T} \alpha {\mathbf{mN}}_{\rho }^{\gamma } d\varOmega \\ {\mathbf{H}}_{\delta \gamma } & = \mathop \int \limits_{\varOmega }^{{}} \left( {\nabla {\mathbf{N}}_{p}^{\delta } } \right)^{T} \varvec{k}_{\varvec{f}} \left( {\nabla {\mathbf{N}}_{p}^{\gamma } } \right)d\varOmega \\ {\mathbf{S}}_{\delta \gamma } & = \mathop \int \limits_{\varOmega }^{{}} \left( {{\mathbf{N}}_{p}^{\delta } } \right)^{T} \frac{1}{Q}{\mathbf{N}}_{\rho }^{\gamma } d\varOmega \\ \end{aligned}$$
(28)
$$\begin{aligned} {\mathbf{f}}_{\alpha }^{ext} & = \mathop \int \limits_{\varOmega }^{{}} \left( {{\mathbf{N}}_{u}^{\alpha } } \right)^{T} \rho \varvec{b}d\varOmega + \mathop \int \limits_{{\varGamma_{t} }}^{{}} \left( {{\mathbf{N}}_{u}^{\alpha } } \right)^{T} \bar{t}d\varGamma \\ {\mathbf{q}}_{\delta }^{\text{ext}} & = \mathop \int \limits_{\varOmega }^{{}} \left( {\nabla {\mathbf{N}}_{p}^{\delta } } \right)^{T} \varvec{k}_{\varvec{f}} \cdot \rho_{f} {\mathbf{b}}d\varOmega - \mathop \int \limits_{{\varGamma_{\varpi } }}^{{}} \left( {{\mathbf{N}}_{p}^{\delta } } \right)^{T} \bar{q}d\varGamma \\ \varvec{f}_{\alpha }^{ext} & = \mathop \int \limits_{{\varGamma_{d} }}^{{}} \left[\kern-0.15em\left[ {\varvec{N}_{u}^{\alpha } } \right]\kern-0.15em\right]^{T} {\varvec{\upsigma}} \cdot \varvec{n}_{{\varGamma_{d} }} d\varGamma = - \mathop \int \limits_{{\varGamma_{d} }}^{{}} \left[\kern-0.15em\left[ {\varvec{N}_{u}^{\alpha } } \right]\kern-0.15em\right]^{T} p \cdot \varvec{n}_{{\varGamma_{d} }} d\varGamma \\ {\mathbf{q}}_{\delta }^{\text{int}} & = \mathop \int \limits_{{\varGamma_{d} }}^{{}} \left( {{\mathbf{N}}_{p}^{\delta } } \right)^{T} \left[\kern-0.15em\left[ {{\dot{\mathbf{v}}}} \right]\kern-0.15em\right]\varvec{n}_{{\varGamma_{d} }} d\varGamma = \mathop \int \limits_{{\varGamma_{d} }}^{{}} \left( {{\mathbf{N}}_{p}^{\delta } } \right)^{T} \bar{q}_{d} d\varGamma \\ \end{aligned}$$

where B is the strain matrix and the XFEM discretization equation can be written as

$$\begin{aligned} & {\mathbf{K}}{\bar{\mathbb{U}}} - {\mathbf{Q}}{\bar{\mathbb{P}}} + {\mathbf{f}}_{{\mathbb{U}}}^{int} - {\mathbf{f}}_{{\mathbb{U}}}^{ext} = 0 \\ & {\mathbf{Q}}^{\varvec{T}} {\dot{\bar{\mathbb{U}}}} + {\mathbf{H}}{\bar{\mathbb{P}}} + {\mathbf{S}}{\dot{\bar{\mathbb{P}}}} - {\mathbf{q}}_{{\mathbb{P}}}^{int} - {\mathbf{q}}_{{\mathbb{P}}}^{ext} = 0 \\ \end{aligned}$$
(29)

In which \({\mathbb{U}} = \left\langle {{\bar{\text{u}}},{\bar{\text{a}}},{\bar{\text{b}}},} \right\rangle\) and \({\mathbb{P}} = \left\langle {{\bar{\text{p}}},{\bar{\text{c}}}} \right\rangle\) respectively refer to the standard freedom and enriched freedom of the displacement as well as the pressure field.

3.2 Time Domain Discretization

In order to get the numerical solution, the temporal discretization is carried out based on the method of backward-difference in this section, just as follows

$$\begin{aligned} \frac{{\partial {\mathbf{u}}}}{{\partial {\text{t}}}} & = \frac{{\Delta {\mathbf{u}}}}{\Delta t} = \frac{{{\mathbf{u}}^{n} - {\mathbf{u}}^{n - 1} }}{\Delta t} \\ \frac{\partial p}{{\partial {\text{t}}}} & = \frac{\Delta p}{\Delta t} = \frac{{p^{n} - p^{n - 1} }}{\Delta t} \\ \end{aligned}$$
(30)

where \(\Delta t\) refers to the time step; the superscript n refers to the nth time step. So the equation set can be obtained by substituting Eqs. (30) into (29) as

$$\begin{aligned} {\varvec{\Psi}}_{{{\mathbb{U}}_{n + 1} }} & = + {\mathbf{K}}{\bar{\mathbb{U}}}_{n + 1} - {\mathbf{Q}}{\bar{\mathbb{P}}}_{n + 1} + {\mathbf{f}}_{{{\mathbb{U}}_{{\varvec{n} + 1}} }}^{int} - {\mathbf{f}}_{{{\mathbb{U}}_{{\varvec{n} + 1}} }}^{ext} \\ {\varvec{\Psi}}_{{{\mathbb{P}}_{n + 1} }} & = \frac{1}{\Delta t}{\mathbf{Q}}^{\text{T}} {\bar{\mathbb{U}}}_{n + 1} + {\mathbf{H}}{\bar{\mathbb{P}}}_{n + 1} + \frac{1}{\Delta t}{\mathbf{S}}{\bar{\mathbb{P}}}_{n + 1} - {\mathbf{q}}_{{{\mathbb{P}}_{{\varvec{n} + 1}} }}^{int} - {\mathbf{q}}_{{{\mathbb{P}}_{{\varvec{n} + 1}} }} = 0 \\ \end{aligned}$$
(31)

In terms of this kind of non-linear equation set, Newton’s method is a good way to get the numerical solution. And with the assistance of the one-order truncation Taylor’s formula to expand the Eq. (31), the linear equation set can be written as

$$\left\{ {\begin{array}{*{20}c} {{\varvec{\Psi}}_{{{\mathbb{U}}_{n + 1} }}^{{\varvec{i} + 1}} } \\ {{\varvec{\Psi}}_{{{\mathbb{P}}_{n + 1} }}^{{\varvec{i} + 1}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{\varvec{\Psi}}_{{{\mathbb{U}}_{n + 1} }}^{i} } \\ {{\varvec{\Psi}}_{{{\mathbb{P}}_{n + 1} }}^{i} } \\ \end{array} } \right\}{\mathbf{ + J}}_{\varvec{n}}^{\varvec{i}} \left\{ {\begin{array}{*{20}c} {d{\bar{\mathbb{U}}}_{n + 1}^{i} } \\ {d{\bar{\mathbb{P}}}_{n + 1}^{i} } \\ \end{array} } \right\} = 0$$
(32)

where J denotes the Jacobian matrix. It shall be analyzed under each iteration with a time step of \(\Delta t\) so that whether the linear equation set reaches convergence or not can be figured out. And then the next time step shall be calculated. Given that it is a non-symmetric matrix and to simplify the calculation, it is necessary to carry out the corresponding simplification process. The symmetric Jacobian matrix after the simplification can be written as

$$\begin{aligned} {\mathbf{J}} & = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\varvec{\Psi}}_{{\mathbb{U}}} }}{{\partial {\bar{\mathbb{U}}}}}} \\ {\frac{{\partial {\varvec{\Psi}}_{{\mathbb{P}}} }}{{\partial {\bar{\mathbb{U}}}}}} \\ \end{array} \begin{array}{*{20}c} { \frac{{\partial {\varvec{\Psi}}_{{\mathbb{U}}} }}{{\partial {\bar{\mathbb{P}}}}}} \\ { \frac{{\partial {\varvec{\Psi}}_{{\mathbb{P}}} }}{{\partial {\bar{\mathbb{P}}}}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {K + \frac{{\partial {\mathbf{f}}_{{\mathbb{U}}}^{int} }}{{\partial {\bar{\mathbb{U}}}}}} \\ {\frac{1}{\Delta t}{\mathbf{Q}}^{\varvec{T}} - \frac{{\partial {\mathbf{q}}_{{\mathbb{P}}}^{int} }}{{\partial {\bar{\mathbb{U}}}}}} \\ \end{array} \varvec{ }\begin{array}{*{20}c} { - Q + \frac{{\partial {\mathbf{f}}_{{\mathbb{U}}}^{int} }}{{\partial {\bar{\mathbb{P}}}}}} \\ {H + \frac{1}{\Delta t}S - \frac{{\partial {\mathbf{q}}_{{\mathbb{P}}}^{int} }}{{\partial {\bar{\mathbb{P}}}}}} \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{uu }}} } & { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{ua }}} } & { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{ub }}} } & { \frac{1}{\Delta t}{\mathbf{Q}}_{up} } & {\frac{1}{\Delta t}{\mathbf{Q}}_{uc} } \\ { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{au }}} } & { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{aa }}} } & { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{ab }}} } & {\frac{1}{\Delta t}\left( {{\mathbf{Q}}_{ap} - \frac{{\partial {\mathbf{f}}_{a}^{int} }}{{\partial {\bar{\mathbf{p}}}}}} \right)} & {\frac{1}{\Delta t}\left( {{\mathbf{Q}}_{ac} - \frac{{\partial {\mathbf{f}}_{a}^{int} }}{{\partial {\bar{\mathbf{c}}}}}} \right)} \\ { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{bu }}} } & { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{ba }}} } & { - \frac{1}{\Delta t}{\mathbf{K}}_{{\varvec{bb }}} } & {\frac{1}{\Delta t}\left( {{\mathbf{Q}}_{bp} - \frac{{\partial {\mathbf{f}}_{b}^{int} }}{{\partial {\bar{\mathbf{p}}}}}} \right)} & {\frac{1}{\Delta t}\left( {{\mathbf{Q}}_{bc} - \frac{{\partial {\mathbf{f}}_{b}^{int} }}{{\partial {\bar{\mathbf{c}}}}}} \right)} \\ {\frac{1}{\Delta t}{\mathbf{Q}}_{pu}^{\text{T}} } & { \frac{1}{\Delta t}\left( {{\mathbf{Q}}_{pa}^{T} - \frac{{\partial {\mathbf{f}}_{a}^{int} }}{{\partial {\bar{\mathbf{p}}}}}} \right)^{\text{T}} } & { \frac{1}{\Delta t}\left( {{\mathbf{Q}}_{pb}^{\text{T}} - \frac{{\partial {\mathbf{f}}_{b}^{int} }}{{\partial {\bar{\mathbf{p}}}}}} \right)^{\text{T}} } & {{\mathbf{H}}_{{\varvec{pp}}} + \frac{1}{\Delta t}{\mathbf{S}}_{{\varvec{pp}}} - \frac{{\partial {\mathbf{q}}_{p}^{int} }}{{\partial {\bar{\mathbf{p}}}}}} & {{\mathbf{H}}_{{\varvec{pc}}} + \frac{1}{\Delta t}{\mathbf{S}}_{{\varvec{pc}}} - \frac{{\partial {\mathbf{q}}_{p}^{int} }}{{\partial {\bar{\mathbf{c}}}}}} \\ {\frac{1}{\Delta t}{\mathbf{Q}}_{cu}^{\text{T}} } & { \frac{1}{\Delta t}\left( {{\mathbf{Q}}_{ca}^{\text{T}} - \frac{{\partial {\mathbf{f}}_{a}^{int} }}{{\partial {\bar{\mathbf{c}}}}}} \right)^{\text{T}} } & { \frac{1}{\Delta t}\left( {{\mathbf{Q}}_{cb}^{\text{T}} - \frac{{\partial {\mathbf{f}}_{b}^{int} }}{{\partial {\bar{\mathbf{c}}}}}} \right)^{\text{T}} } & {{\mathbf{H}}_{{\varvec{pp}}} + \frac{1}{\Delta t}{\mathbf{S}}_{{\varvec{pp}}} - \left( {\frac{{\partial {\mathbf{q}}_{p}^{int} }}{{\partial {\bar{\mathbf{p}}}}}} \right)^{\text{T}} } & {{\mathbf{H}}_{{\varvec{cc}}} + \frac{1}{\Delta t}{\mathbf{S}}_{{\varvec{cc}}} - \frac{{\partial {\mathbf{q}}_{c}^{int} }}{{\partial {\bar{\mathbf{c}}}}}} \\ \end{array} } \right] \\ \end{aligned}$$
(33)

3.3 Crack Propagation Criterion

The rock fracturing mechanics mainly include three criteria: the maximum tensile circumferential stress theory, the maximum energy release rate theory and the minimum strain–energy–density theory. Among all these three theories, the maximum tensile circumferential stress theory is the universal one. According to this theory, when the circle tensile stress of the crack tip reaches the critical value, cracks will emerge from the tip and then propagate along the direction of the maximum circle tensile stress.

The maximum tensile circumferential stress theory contains two basic assumptions: (1) Cracks propagate along the direction of the maximum circle tensile stress. (2) When the maximum tensile circumferential stress reaches the critical value, crack propagation starts to appear.

According to the first basic assumption of the maximum tensile circumferential stress theory, the crack initiation angle can be obtained. According to the second assumption, the critical stress conditions can be determined.

In terms of the cracks of type I–II, the stress components of the crack-tip polar coordinates can be written by superimposing their tip stress components as:

$$\left\{ {\begin{array}{*{20}l} {\sigma_{\rho } = \frac{1}{{2\sqrt {2\pi \rho } }}\left[ {K_{I} \left( {3 - cos\frac{\theta }{2}} \right) + K_{II} \left( {3cos\theta - 1} \right)sin\frac{\theta }{2}} \right]} \hfill \\ {\sigma_{\theta } = \frac{1}{{2\sqrt {2\pi \rho } }}cos\frac{\theta }{2}\left[ {K_{I} cos^{2} \frac{\theta }{2} - \frac{3}{2}K_{II} sin\theta } \right]} \hfill \\ {\tau_{\rho \theta } = \frac{1}{{2\sqrt {2\pi \rho } }}cos\frac{\theta }{2}\left[ {K_{I} sin\theta + K_{II} \left( {3cos\theta - 1} \right)} \right]} \hfill \\ \end{array} } \right.$$
(34)

The incipient crack angle \(\uptheta_{0}\) is obtained by taking the extreme value of the axial stress \(\sigma_{\theta }\):

$$\frac{{\partial \sigma_{\theta } }}{\partial \theta } = 0$$
(35)

Then solve the equation and acquire the crack growth angle \(\uptheta_{0}\)

$$\uptheta_{0} = 2{ \arctan }\left( {\frac{{K_{I} }}{{4K_{II} }} \pm \frac{1}{4}\sqrt {\left( {\frac{{K_{I} }}{{K_{II} }}} \right)^{2} + 8} } \right)$$
(36)

By substituting Eqs. (36) into (34) the maximum circumferential stress can be acquired and written as

$$\sigma_{\theta max} = \frac{1}{{2\sqrt {2\pi \rho_{0} } }}cos\frac{{\theta_{0} }}{2}\left[ {K_{I} \left( {1 + cos\theta_{0} } \right) - 3K_{II} sin\theta_{0} } \right]$$
(37)

According to the second basic assumption of the maximum tensile circumferential stress theory, the equation of the crack propagation criterion can be written as:

$$\sigma_{\theta max} = \sigma_{\theta c} = \frac{{K_{IC} }}{{\sqrt {2\pi \rho } }}$$
(38)

where \(\sigma_{\theta c}\) is to the critical stress value; \(K_{IC}\) is the fracture toughness which can be written by substituting Eqs. (37) into (38) as

$$K_{IC} = \frac{1}{2}cos\frac{{\theta_{0} }}{2}\left[ {K_{I} cos^{2} \frac{\theta }{2} - \frac{3}{2}K_{II} sin\theta } \right]$$
(39)

4 Numerical Calculation

In this thesis, by inserting XFEM into the traditional finite element software ABAQUS, the development of the crack propagation analysis program is realized under the condition of fluid–solid coupled interaction in the porous medium. Several modules including model creation, crack initialization, level-set renovation, crack propagation parameters calculation in fluid–solid coupling and so on are successfully developed, which makes a dynamic display of the crack propagation process come true. Figure 3 is the flow chart of numerical simulation.

Fig. 3
figure 3

Flow chart of numerical simulation

Full size image

Using the calculation method established in this thesis and through three calculating examples in this section, the propagation rules of the fractured-vuggy reservoir are analyzed to verify the effectiveness and validity of the crack propagation analysis program.

4.1 Effects on Crack Propagation by the Water Flow Action

Figure 4 is the Calculation model of porous medium with an inclined crack. The model is 10 m in length and 5 m in width. The displacement constraint is added along directions of x and y on the bottom surface. The normal liquid added on the top surface is defined as q. The bottom surface is the free draining profile of which the pore pressure is 0. The left and right surfaces are impervious surfaces. Cracks are in the central part of the model with a length of 0.5 m and an angle of 45°. Calculating parameters are shown in Table 1. In this calculating example, the crack propagation rules are analyzed under different top flow q. So that effects on crack propagation by the water flow action can be studied.

Fig. 4
figure 4

Calculation model of porous medium with an inclined crack

Full size image
Table 1 Parameters of the model with an inclined crack
Full size table

Calculating the model based on the parameters in Table 1. The Displacement nephogram, the stress nephogram and the pore pressure diagram under the condition of different flow q are shown in Fig. 5.

Fig. 5
figure 5

The displacement nephogram, the stress nephogram and the pore pressure diagram under the condition of different fluid flux q

Full size image

As shown in Fig. 5, the pore pressure inside the porous medium and the cracks increases because of the water injection pressure, which leads to the crack propagation and the structure deformation correspondingly. The crack propagation shows a good symmetric form. Its width reaches the maximum at the crack mouth and gradually decreases inside Finally, crack propagation shows wedge fracture morphology. It can be known by comparing the displacement nephogram and the stress nephogram under different fluid flux that the crack propagation changes obviously with different water pressures. When q = 1e−4 m/s, the crack has a larger propagation length and the surrounding displacement value is bigger. Besides, the stress concentration at the crack-tip is more obvious under the water pressure.

The crack propagation angle also varies greatly under different fluid flux. When the fluid flux are small, the crack propagation angle is small, too. As the fluid flux increases, the crack propagation angle is becoming larger and eventually it turns to the same direction as the water injection. There are apparent differences found in the pore pressure diagram as the fluid flux changes. This is mainly because there is water exchange between the crack and the porous medium. As the crack propagates, the exchange process keeps going on. However, the water flows much slower in the porous medium than in the fissured medium. When the crack increases the water shall be discharged more from it. That means the water will make a greater difference to the crack propagation. Therefore, the more the fluid flux are, the bigger the crack opening is; the greater the effects to the seepage field will be.

Figure 6a is the variation curves of crack propagation length with different fluid flux. It can be obviously seen that with the increasing fluid flux, the propagation length also increases continuously. When the fluid flux increases from 4e−5 to 2.6e−4 m/s the crack propagation length increases from 0.4 to 1.6 m in accordance, 300 percent more than before. Figure 6b is variation curve of crack width with different fluid flux. It can be obviously seen that with the increasing fluid flux, the propagation width also increases continuously. When the fluid flux increases from 4e−5 to 2.6e−4 m/s the crack propagation width increases from 0.123 to 0.202 m in accordance, 64% more than before.

Fig. 6
figure 6

Crack propagation rules under different fluid flux

Full size image

It follows that the variation of the fluid flux will influence the length and width of the crack propagation. Compared with the length changes, the crack propagation width changes less obviously under different fluid flux.

4.2 Influence of Crack Angle and Crack Length on Crack Propagation

Figure 7 is the calculation model of porous medium with a crack in different lengths and different inclinations. The length and width of the model is both 20 m. Applying a displacement constraint in the x and y directions at the bottom. Applying the x-direction displacement constraint on the left and right sides. The top surface have a free drain surface with a pore pressure of 0. The hydrostatic pressure of left and right surfaces is \(\gamma_{w} h\), where \(\gamma_{w}\) is liquid bulk density, \(h\) is model depth. The concentrated load added to the top surface is 10 Mpa, cracks are in the central part of the model with a length of \(\upbeta\) and an angle of \(\upalpha\). By analyzing the different crack propagation situations under consolidation, the author studies the effects of the crack propagation caused by the dip angle as well as the crack length.

Fig. 7
figure 7

Calculation model of porous medium with a crack in different lengths and different inclinations

Full size image

Figures 8 and 9 show the stress nephogram and the displacement nephogram with different dip angles and crack lengths. Compare Fig. 8a with Fig. 8b, it can be seen that under the condition of the same crack length, the crack propagation length becomes larger as the dip angle rises. Besides, the deflection angle of the crack propagation also becomes larger. Compare Fig. 8c with Fig. 8d, it can be seen that under the condition of the same crack dip angle, the longer the crack length are, the longer the crack propagation length will be.

Fig. 8
figure 8

Stress nephogram of crack propagation with different length and different dip angle

Full size image
Fig. 9
figure 9

Displacement nephogram of crack propagation with different length and different dip angle

Full size image

Figure 9 shows that there are obvious differences between the displacement nephogram after crack propagation with different lengths and angles. On one hand, the displacement nephogram continuity decreases after the crack propagation if the crack is a longer one. Besides, there is an obvious discontinuity of the displacement nephogram with the increase of the crack length. On the other hand, as the crack length increases, the displacement value is becoming larger and larger. That is mainly because a longer crack can carry out a more influential effect of rock mass stiffness so that the rock failure and deformation became more severer.

Figures 10 and 11 are the curves of fracture propagation length and vertex displacement versus time under different fracture length and dip angle. The results show: (1) With the increase of time, the crack length and the vertex displacement is increasing constantly. The crack length and the vertex displacement is changed rapidly, and then gradually converge to a steady state value, and finally, reach equilibrium. (2) The larger the dip angle is, the longer the crack propagation will be, which indicates that the crack propagation happens much more easily if the crack dip angle is a larger one. The longer the original crack is, the larger the crack propagation length will be, which indicates that the crack propagation happen much more easily if the original crack is a longer one. (3) The larger the dip angle as well as the crack length are, the larger the top displacement value will be. It indicates that the whole stability will be influenced more severely if the crack length and the dip angle are both very large. (4) The dip angle increased from 15° to 60°. During this process, the crack propagation length increased from 2.3 to 3.41 m correspondingly, 48% more than before; the top displacement value increased from 0.035 to 0.055 m, 57% more than before. The crack length increased from 2 to 8 m during this process, the crack propagation length increased from 1.69 to 3.81 m correspondingly, 125% more than before; the top displacement value increased from 0.035 to 0.06 m, 80% more than before. Thus, it can be inferred that compared with dip angle, the crack length have a more sensitive influence to the crack propagation.

Fig. 10
figure 10

Curves of fracture length versus time

Full size image
Fig. 11
figure 11

The change curve of vertex displacement with time

Full size image

4.3 Propagation Rules of Multiple Cracks

Figure 12 shows the porous medium and the uniform pressure are distributed both on the top surface, as well as the side faces, a normal flow defined as q is applied to the top surface; the bottom surface is defined as free; both left and right sides are impervious boundaries; the normal displacement of the bottom surface is 0. The length and width of the model is both 2 m. Two cracks are in the central part of the model with a length of 0.6 m and an angle of 45°. The vertical distance between two cracks are defined as \({\text{S}}_{1}\) while the horizontal distance is \({\text{S}}_{2}\). The calculation parameters are shown in Table 2 and the time step is 1 s, and a total of 100 s is calculated.

Fig. 12
figure 12

Double cracks calculation model

Full size image
Table 2 Parameters of the model with a crack in different lengths and different inclinations
Full size table

It can be seen from Fig. 13 that both cracks have appeared in varying degrees of expansion, the expansion angle is roughly the same, but the degree of crack expansion is different. The crack propagation at the bottom surface are less than that of the top surface. That is because when the fluid passes through the crack it does not directly flow out of the medium. Instead, there is a process of temporary storage. Therefore, there exists a delayed phenomenon during the crack propagation. The crack propagation influence on seepage field and stress field under the condition of different crack distributions can be analyzed through the ratio of the outflow volume qout to the inflow volume q.

Fig. 13
figure 13

Displacement nephogram and stress nephogram of two cracks

Full size image

Figure 14a shows the change law of qout/q with time under different S1. The result shows that the smaller S1 is, the less obvious the delay phenomenon will be during the crack propagation. When S1 is 0, which indicates that there is only one crack, the delay phenomenon is the least obvious at this moment. So it can be known that the larger the vertical distance are, the more huge the crack propagation influence to the seepage field will be. This also explains why the larger the vertical distance are, the longer crack propagation length will be.

Fig. 14
figure 14

Propagation rules of cracks with different intervals

Full size image

Figure 14b shows the change law of qout/q with time under different S2. The result shows that the bigger S2 is, the more obvious the delay phenomenon will be during the crack propagation. That indicates the larger the horizontal distance are, the more huge the crack propagation the influence to the seepage field will be. As the crack propagation is accomplished under the coupling of seepage field and stress field, it causes the instability to the whole fluid field as well as stress field. Therefore, the larger the horizontal distance are, the easier the fracture is to expand.

5 Conclusion

  1. 1.

    Fully coupled governing equations are developed for hydro-mechanical analysis of deforming porous medium with fractures based on the stress balance equation, the seepage continuity equation and the effective stress principle. The final nonlinear fully coupled equations reflect not only the coupling effect of the physical quantity within the porous medium but also the coupling between the medium and the fracture.

  2. 2.

    In this thesis, a numerical calculation system is established. During the spatial discretization of coupled equations, two kinds of additional displacement functions are introduced in the displacement model of the fracture area based on XFEM to reflect the strong discontinuity and the crack tip stress singularity of the fracture surface. The pore pressure enhancement function is also applied to represent the weak discontinuous features of the normal pore pressure. During the time domain discretization, the XFEM calculation format of the fully coupled governing equations for deforming porous medium with fractures is derived in detail based on the method of backward difference.

  3. 3.

    The validity and efficiency of this model and calculation are verified through three calculating examples: (1) The larger the water flow rate is, the longer the crack propagation length is, and the larger the propagation width is. (2) The larger the dip angle as well as the crack length are, the much more easily crack propagation will happen. Besides, compared with dip angle, the crack length have a more sensitive influence to the crack propagation. (3) When multiple cracks exist, the larger the fracture spacing is, the easier the crack will expand. The crack propagation rules acquired in this thesis can well guide the fractured-vuggy reservoir exploitation.