1 Introduction

The Hoek–Brown (HB) failure criterion has been widely used in engineering practice to predict the rock strength (Hoek and Brown, 1980, 1988, 1997; Hoek 1983, 1990,1994; Hoek et al. 1995, 2002; Marinos and Hoek 2001). A major criticism of this criterion is that it cannot account for the influence of the intermediate principal stress σ 2, and numerous experimental tests suggest that σ 2 has a profound effect on the rock strength (Mogi 1971; Wang and Kemeny 1995; Chang and Haimson 2000; Colmenares and Zoback 2002; Al-Ajmi and Zimmerman 2005). There have been a number of attempts at generalizing the HB criterion in three dimensions (3D) to account for the effect of σ 2, including Pan and Hudson (1988); Priest (2005); Zhang (2007, 2008); Melkoumian et al. (2009); Jiang et al. (2011). Among them, the studies by Pan and Hudson (1988) and Priest (2005) employed circular sections in the deviatoric stress plane for their 3D failure criteria, which may tend to overestimate or underestimate the failure strength of rocks in polyaxial compression (Priest 2012). The 3D failure criteria presented by Zhang (2007, 2008) and Jiang et al. (2011) used non-circular and non-convex sections in the deviatoric stress plane, which may cause difficulties in obtaining the failure strength σ 1 in some special stress paths and issues may be encountered when plastic flow rule was considered. Priest (2012) compared five 3D failure criteria and recommended that further research and rock testing was required before any of the 3D Hoek–Brown failure criteria can be applied with confidence. With this background, there is indeed a practical need for a new 3D failure criterion to be developed which can overcome the above-mentioned drawbacks and offer improved yet convenient predictions on the rock strength in engineering applications.

We hereby propose a simple 3D failure criterion with a convex failure surface. Based on a similar expression for the classical HB criterion, the mathematical derivation of the new failure function is presented, and its smoothness and convexity are discussed. To calibrate the proposed failure criterion, we use triaxial compression tests data of rocks to evaluate the best pair of values, m i (m b  = m i ) and σ ci, and then predict the results of the other loading conditions using this best pair m i and σ ci. In addition, comparison of the new 3D failure criterion and two typical existing ones is also made.

2 Relevant Definitions

2.1 Stress Invariants

A failure criterion is normally expressed in terms of either the principal stresses f(σ 1, σ 2, σ 3), or the stress invariants f(I 1, J 2, θ), f(I 1, J 2, J 3) or f(I 1, I 2, I 3), and the following relationships between the principal stresses and the stress invariants are given as

$$\sigma_{1} = \frac{{I_{1} }}{3} + \frac{2}{\sqrt 3 }\sqrt {J_{2} } \cos \theta$$
(1)
$$\sigma_{3} = \frac{{I_{1} }}{3} + \frac{2}{\sqrt 3 }\sqrt {J_{2} } \cos \left( {\frac{2\pi }{3} + \theta } \right)$$
(2)
$$I_{1} = 3\sigma_{m} = \sigma_{1} + \sigma_{2} + \sigma_{3}$$
(3)
$$J_{2} = \frac{1}{2}trS^{2} = \frac{1}{6}\left[ {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{1} - \sigma_{3} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} } \right]$$
(4)
$$\theta = ar\cos \frac{{2\sigma_{1} - \sigma_{2} - \sigma_{3} }}{{2\sqrt 3 \sqrt {J_{2} } }}$$
(5)

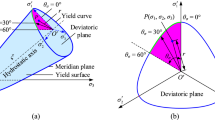
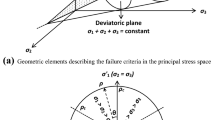
where θ(0 ≤ θ ≤ π/3) is the similarity angle given in Eq. (5). The deviatoric stress tensor S is related to the stress tensor σ by S = σ−trσI/3. There is another set of widely used invariants (ξ, ρ, θ) based on the cylindrical coordinate system (also called the Haigh–Westergaard coordinates), which has a direct physical interpretation (Ottosen 1977). A geometrical interpretation of this coordinate system is shown in Fig. 1, where ξ is a unit vector on the hydrostatic axis, ρ is the radial distance from the failure point P to the hydrostatic axis N and θ is the measure of a rotation from axis σ ′1 . They are defined as follows:

Fig. 1
figure 1

Haigh–Westergaard space and principal stress space

Full size image
$$\xi = \left| {\overrightarrow {\text{ON}} } \right| = I_{1} /\sqrt 3 = \left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)/\sqrt 3$$
(6)
$$\rho = \left| {\overrightarrow {\text{NP}} } \right| = \sqrt {2J_{2} } = \frac{1}{\sqrt 3 }\sqrt {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{1} - \sigma_{3} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} }$$
(7)

where the ξ−ρ plane is also called the Rendulic plane.

2.2 Smoothness and Convexity of the Failure Surface

A smooth failure surface requires that the gradients of the failure surface exist everywhere. However, due to the threefold symmetry of the failure surface for isotropic materials, a single value of θ corresponds to six different points in the deviatoric plane (Lin and Bazant 1986). In this case, the gradients on the symmetry axis should be zero (Piccolroaz and Bigoni 2009).

$$\rho^{\prime}\left( 0 \right) = \rho^{\prime}\left( {\pi /3} \right) = 0$$
(8)

A convex failure envelope surface requires that the surfaces in both the meridian and deviatoric planes should be convex. In the meridian plane, the convexity can be proven according to the meridian functions. In the deviatoric plane, the convexity is proven as follows.

Considering the failure function ρ = ρ(θ) in the polar coordinate system (ρ, θ), the convexity of ρ in the deviatoric plane is satisfied when the curvature

$$k = \frac{{\rho^{2} + 2\rho^{'2} - \rho \rho^{\prime\prime}}}{{\left( {\rho^{2} + \rho^{'2} } \right)^{3/2} }} \ge 0$$
(9)

which requires (Jiang and Pietruszczak 1988)

$$\rho^{2} + 2\rho^{'2} - \rho \rho^{\prime\prime} \ge 0$$
(10)

Substituting g = c/ρ(c is a constant) into inequality (10), after some algebraic manipulation, gives an equivalent expression of the above inequality

$$c^{2} \frac{{g + g^{\prime\prime}}}{{g^{3} }} \ge 0,{\text {which\, requires }}g + g^{\prime\prime} \ge 0.$$
(11)

2.3 The Classic Hoek–Brown Failure Criterion

The HB failure criterion is empirical, based on the curve-fitting of triaxial test data, in which the generalized form is defined as follows (Hoek et al. 2002)

$$\sigma^{\prime}_{1} = \sigma^{\prime}_{3} + \sigma_{\text{ci}} \left( {m_{b} \frac{{\sigma^{\prime}_{3} }}{{\sigma_{\text{ci}} }} + s} \right)^{a}$$
(12)

where σ 1′ and σ 3′ are the major and minor effective principal stresses (denoted by primes as opposed to the total stresses) with compression taken as positive. σ ci is the uniaxial compression strength of the intact rock with material constant m i . The empirical constants m b , s and a can be estimated from the geological strength index (GSI) for a rock mass with the following expressions:

$$m_{b} = m_{i} \exp \left( {\frac{{{\text{GSI}} - 100}}{28 - 14D}} \right),s = \exp \left( {\frac{{{\text{GSI}} - 100}}{9 - 3D}} \right),\;{\text{and }}a = \frac{1}{2} + \frac{1}{6}\left[ {\exp \left( {\frac{{ - {\text{GSI}}}}{15}} \right) - \exp \left( {\frac{ - 20}{3}} \right)} \right]$$

where D is the disturbance of a rock mass (0 ≤ D ≤ 1).

Rearranging Eq. (12), another expression of the HB criterion is given as

$$\frac{{\sigma^{\prime}_{1} - \sigma^{\prime}_{3} }}{{\sigma_{\text{ci}} }} = \left( {m_{b} \frac{{\sigma^{\prime}_{3} }}{{\sigma_{\text{ci}} }} + s} \right)^{a}$$
(13)

Substituting Eqs. (1) and (2) into Eqs. (12) or (13), one obtains the following invariant representation of the failure envelope surface

$$\frac{1}{{m_{b} \sigma_{\text{ci}}^{{1/a\text{ - }1}} }}\left[ {2\sin \left( {\pi /3 + \theta } \right)\sqrt {J^{\prime}_{2} } } \right] \, ^{{^{1/a} }} + \frac{{2\cos \left( {\pi /3 - \theta } \right)}}{\sqrt 3 }\sqrt {J^{\prime}_{2} } - \frac{{s\sigma_{\text{ci}} }}{{m_{b} }} - \frac{{I_{1}^{'} }}{3} = 0$$
(14)

Setting θ = 0 in Eq. (14), the compressive meridian for the triaxial compression condition (σ ′2  = σ ′3  < σ ′1 ) is obtained as follows

$$\frac{1}{{m_{b} \sigma_{\text{ci}}^{1/a - 1} }}\left( {\sqrt {3J^{\prime}_{2} } } \right)^{1/a} + \frac{1}{\sqrt 3 }\sqrt {J^{\prime}_{2} } - \frac{{s\sigma_{\text{ci}} }}{{m_{b} }} - \frac{{I_{1}^{'} }}{3} = 0$$
(15)

When θ = π/3, Eq. (14) leads to the tensile meridian for the triaxial extension condition (σ ′2  = σ ′1  > σ ′3 )

$$\frac{1}{{m_{b} \sigma_{ci}^{1/a - 1} }}\left( {\sqrt {3J^{\prime}_{2} } } \right)^{1/a} + \frac{2}{\sqrt 3 }\sqrt {J^{\prime}_{2} } - \frac{{s\sigma_{ci} }}{{m_{b} }} - \frac{{I_{1}^{'} }}{3} = 0$$
(16)

Noting that the only difference between Eqs. (15) and (16) is the coefficient of \(\sqrt {J^{\prime}_{2} }\) in the second term.

2.4 Three-Dimensional Failure Criteria Based on the Hoek–Brown Criterion

The International Society of Rock Mechanics (ISRM) (Priest 2012) summarizes typical 3D failure criteria based on the HB criterion. A thorough comparison among these criteria is absent, and the comparison is now provided in this section, based on which a unified expression is also proposed.

Pan and Hudson (1988) developed a 3D criterion with circular shapes in the deviatoric plane, where the failure function is written as

$$\frac{1}{{m_{b} \sigma_{\text{ci}}^{1/a - 1} }}\left( {\sqrt {3J^{\prime}_{2} } } \right)^{1/a} + \frac{1.5}{\sqrt 3 }\sqrt {J^{\prime}_{2} } - \frac{{s\sigma_{\text{ci}} }}{{m_{b} }} - \frac{{I_{1}^{'} }}{3} = 0$$
(17)

Priest (2005) proposed a 3D criterion, whose failure envelope surface is an outer bounded cone matching the irregular hexagonal cone of the HB criterion at θ = 0. The failure function of his proposed criterion is shown in Eq. (15).

Zhang and Zhu (2007, 2008) extended the HB criterion to a 3D one from the ideal of the Mogi criterion, where the failure function is expressed as

$$\frac{1}{{\sigma_{\text{ci}}^{1/a - 1} }}\left( {\frac{3}{\sqrt 2 }\tau_{\text{oct}} } \right)^{1/a} + \frac{{m_{b} }}{2}\left( {\frac{3}{\sqrt 2 }\tau_{\text{oct}} } \right) - s\sigma_{\text{ci}} - m_{b} \sigma^{\prime}_{m,2} = 0$$
(18)

where \(\sigma^{\prime}_{m,2} = \frac{{\sigma^{\prime}_{1} + \sigma^{\prime}_{3} }}{2}\).

An alternative expression can be written as

$$\frac{1}{{m_{b} \sigma_{\text{ci}}^{1/a - 1} }}\left( {\sqrt {3J^{\prime}_{2} } } \right)^{1/a} + \frac{1}{\sqrt 3 }\frac{{3 - 2\cos \left( {\pi /3 + \theta } \right)}}{2}\sqrt {J^{\prime}_{2} } - \frac{{s\sigma_{\text{ci}} }}{{m_{b} }} - \frac{{I_{1}^{'} }}{3} = 0$$
(19)

Jiang et al. (2011) proposed three 3D criteria by referring to the failure function of the Hsieh–Ting–Chen criterion for concrete. Criterion C with a smooth cross section was considered the most reasonable criterion, with the failure function given by

$$\frac{1}{{m_{b} \sigma_{\text{ci}}^{1/a - 1} }}\left( {\sqrt {3J^{\prime}_{2} } } \right)^{1/a} + \frac{1}{\sqrt 3 }\frac{3 - \cos 3\theta }{2}\sqrt {J^{\prime}_{2} } - \frac{{s\sigma_{\text{ci}} }}{{m_{b} }} - \frac{{I_{1}^{'} }}{3} = 0$$
(20)

In view of Eqs. (15)–(20), a unified expression that includes all the criteria can be written as

$$\frac{1}{{m_{b} \sigma_{\text{ci}}^{1/a - 1} }}\left( {\sqrt {3J^{\prime}_{2} } } \right)^{1/a} + \frac{1}{\sqrt 3 }A\left( \theta \right)\sqrt {J^{\prime}_{2} } - \frac{{s\sigma_{\text{ci}} }}{{m_{b} }} - \frac{{I_{1}^{'} }}{3} = 0$$
(21)

The term A(θ) varies, depending on the criterion adopted:

  • A(θ) = 1 corresponds to the compressive meridian of the HB criterion or the Priest 3D failure criterion;

  • A(θ) = 2 corresponds to the tensile meridian of the HB criterion;

  • A(θ) = 1.5 corresponds to the Pan–Hudson 3D failure criterion;

  • \(A\left( \theta \right) = \frac{{3 - 2\cos \left( {\pi /3 + \theta } \right)}}{2}\) corresponds to the Zhang–Zhu 3D failure criterion;

  • \(A\left( \theta \right) = \frac{3 - \cos 3\theta }{2}\) corresponds to the Jiang 3D failure criterion;

3 A Simple Three-Dimensional Failure Criterion

3.1 Mathematical Expression of the New 3D HB Criterion

To develop a 3D failure criterion that shares the same compressive and tensile meridians with those of the HB criterion, the failure function needs to be reduced to Eqs. (15) and (16) when θ = 0 and θ = π/3. A feasible method is to introduce the Lode dependence R 3(θ) into the deviatoric plane, based on the ratio of the tensile and compressive meridian radii ρ t /ρ c . Typical Lode dependences include those forms proposed by Willam and Warnke dependence (1975); Argyris et al. (1974); Lade and Duncan, Matsuoka and Nakai (LMN) (Bardet 1990) and Rubin (1991). However, the failure criteria generated using the Lode dependency are generally complicated. In this section, a simple method is proposed based on the principal representation of the HB criterion, as shown in Eq. (13). A natural extension to the 3D case can be obtained by replacing (σ ′1 −σ ′3 )/σ ci on the left side of Eq. (13) with \(\sqrt {\left( {\sigma^{\prime}_{1} - \sigma^{\prime}_{2} } \right)^{2} + \left( {\sigma^{\prime}_{1} - \sigma^{\prime}_{3} } \right)^{2} + \left( {\sigma^{\prime}_{2} - \sigma^{\prime}_{3} } \right)^{2} } /\sqrt 2 \sigma_{\text{ci}}\), giving

$$\frac{1}{{\sqrt 2 \sigma_{\text{ci}} }}\sqrt {\left( {\sigma^{\prime}_{1} - \sigma^{\prime}_{2} } \right)^{2} + \left( {\sigma^{\prime}_{1} - \sigma^{\prime}_{3} } \right)^{2} + \left( {\sigma^{\prime}_{2} - \sigma^{\prime}_{3} } \right)^{2} } = \frac{{\sqrt {3J^{\prime}_{2} } }}{{\sigma_{\text{ci}} }} = \left( {\frac{{\sigma^{\prime}_{3} }}{{\sigma_{ci} }}m_{b} + s} \right)^{a}$$
(22)

When σ ′2  = σ ′3 or σ ′2  = σ ′1 , Eq. (22) is reduced to Eq. (13). Unlike Eq. (13), the influence of σ ′2 is explicitly considered here. The expression indicated in Eq. (22) is mathematically rather straightforward, but has not been found in previously published research.

The invariant representation of Eq. (22) is

$$\frac{1}{{m_{b} \sigma_{\text{ci}}^{{1/a\text{ - }1}} }}\left[ {\sqrt {3J^{\prime}_{2} } } \right] ^{{^{1/a} }} + \frac{A\left( \theta \right)}{\sqrt 3 }\sqrt {J^{\prime}_{2} } - \frac{{s\sigma_{\text{ci}} }}{{m_{b} }} - \frac{{I_{1}^{'} }}{3} = 0$$
(23)

with A(θ) = 2 cos (π/3−θ). Hence, the proposed 3D failure criterion can be also represented by the unified expression shown in Eq. (21).

Figure 2 plots A(θ) for five 3D failure criteria: the former three curves increase from 1 (corresponding to triaxial compression) to 2 (corresponding to triaxial extension), and A(θ) of the new 3D failure criterion is clearly different from that of the existing ones.

Fig. 2
figure 2

A versus θ (0 ≤ θ ≤ π/3) for five 3D failure criteria

Full size image

For intact rocks with a = 0.5, Eq. (23) can be simplified to

$$\frac{3}{{m_{b} }}\frac{{J^{\prime}_{2} }}{{\sigma_{\text{ci}}^{2} }} + \frac{2}{\sqrt 3 }\cos \left( {\pi /3 - \theta } \right)\frac{{\sqrt {J^{\prime}_{2} } }}{{\sigma_{\text{ci}} }} - \frac{s}{{m_{b} }} = \frac{{\sigma^{\prime}_{m} }}{{\sigma_{\text{ci}} }}$$
(24)

Using the expression for σ 3 given in Eq. (2), an alternative expression for this new 3D criterion is

$$\frac{3}{{m_{b} }}\frac{{J^{\prime}_{2} }}{{\sigma_{\text{ci}}^{2} }} - \frac{s}{{m_{b} }} = \frac{{\sigma^{\prime}_{3} }}{{\sigma_{\text{ci}} }}$$
(25)
$$ Or \, \frac{{\sqrt {3J^{\prime}_{2} } }}{{\sigma_{\text{ci}} }} = \sqrt {m_{b} \frac{{\sigma^{\prime}_{3} }}{{\sigma_{\text{ci}} }} + s} $$
(26)

Likewise, a simple expression for the new 3D failure criterion in terms of the principal stress is

$$\frac{1}{{\sqrt 2 \sigma_{\text{ci}} }}\sqrt {\left( {\sigma^{\prime}_{1} - \sigma^{\prime}_{2} } \right)^{2} + \left( {\sigma^{\prime}_{1} - \sigma^{\prime}_{3} } \right)^{2} + \left( {\sigma^{\prime}_{2} - \sigma^{\prime}_{3} } \right)^{2} } = \sqrt {m_{b} \frac{{\sigma^{\prime}_{3} }}{{\sigma_{\text{ci}} }} + s}$$
(27)

Figure 3 presents a comparison of the new 3D failure criterion with the classical HB criterion in the deviatoric plane for a rock with σ ′ m  = 8σ ci, m b  = 23.6, s = 1 and a = 0.5 (these values are used for illustration purpose). The radius (\(\sqrt {J^{\prime}_{2} }\)) of the new 3D failure case decreases from 6.001 to 4.6176 as θ increases from 0 to π/3, whereas the classical HB criterion changes its radius from 6.001 to a minimum value 4.428 and then gradually increases to 4.6176 again. The prediction of strength by the new 3D failure criterion is greater than that of the classical one over the whole range of θ due to the consideration of the influence of σ 2 on rock failure. Figure 4 further shows the failure envelope surfaces of the new 3D criterion. Notably, the surface of the new 3D criterion circumscribes that of the classical HB criterion, and is nearly triangular for σ ′ m  = 0 (the loci of two criteria almost coincide with each other) but becomes more circular for increasing σ ′ m .

Fig. 3
figure 3

\(\sqrt {J^{\prime}_{2} }\) versus θ (0 ≤ θ ≤ π/3) for two failure criteria with σ ′ m  = 8 mb = 23.6, s = 1, and a = 0.5

Full size image
Fig. 4
figure 4

Failure criteria on the deviatoric plane with mb = 23.6, s = 1, and a = 0.5

Full size image

3.2 Examination of the smoothness and convexity

Based on Eq. (24), an explicit expression of \(\sqrt {J^{\prime}_{2} }\) can be obtained as

$$\frac{{\sqrt {J^{\prime}_{2} } }}{{\sigma_{\text{ci}} }} = - \frac{\sqrt 3 }{9}\cos \left( {\pi /3 - \theta } \right)m_{b} + \sqrt {\frac{1}{27}\cos^{2} \left( {\pi /3 - \theta } \right)m_{b}^{2} + \frac{1}{3}\left( {s + \frac{{\sigma^{\prime}_{m} m_{b} }}{{\sigma_{\text{ci}} }}} \right)}$$
(28)
$$Or \, \rho = \sqrt 2 \sigma_{\text{ci}} m_{b} \left[ { - \frac{\sqrt 3 }{9}\cos \left( {\frac{\pi }{3} - \theta } \right) + \sqrt {\frac{1}{27}\cos^{2} \left( {\frac{\pi }{3} - \theta } \right) + \frac{1}{3}\left( {\frac{s}{{m_{b}^{2} }} + \frac{\xi }{{\sqrt 3 \sigma_{\text{ci}} m_{b} }}} \right)} } \right] \,$$
(29)

Equation (29) is used to determine the two material parameters m b and σ ci via the best fitting method described in the next section.

The derivative of ρ (θ) with respect to θ is

$$\rho^{\prime} = \sqrt 2 m_{b} \sigma_{\text{ci}} \left[ { - \frac{\sqrt 3 }{9}\sin \left( {\frac{\pi }{3} - \theta } \right) + \frac{1}{54}\frac{{\sin 2\left( {\frac{\pi }{3} - \theta } \right)}}{{\sqrt {\frac{1}{27}\cos^{2} \left( {\frac{\pi }{3} - \theta } \right) + \frac{1}{3}\left( {\frac{s}{{m_{b}^{2} }} + \frac{\xi }{{\sqrt 3 m_{b} \sigma_{\text{ci}} }}} \right)} }}} \right]$$
(30)

For θ = 0,

$$\rho^{\prime}_{\theta = 0} = \sqrt 2 \sigma_{\text{ci}} \left[ { - \frac{{m_{b} }}{6} + \frac{{m_{b} }}{6}\frac{1}{{\sqrt {1 + 36\left( {s/m_{b}^{2} + \xi /\sqrt 3 m_{b} \sigma_{\text{ci}} } \right)} }}} \right]$$
(31)

For θ = π/3,

$$\rho^{\prime}_{\theta = \pi /3} = 0$$
(32)

Note that \(\rho^{\prime}_{\theta = 0} = 0\) in Eq. (31) only occurs when \(\xi = - \sqrt 3 s\sigma_{\text{ci}} /m_{b}\), which happens to be the apex of the failure surface as seen from Eq. (24). Otherwise Eq. (31) has a negative value. Evidently, the failure surface is not smooth in the triaxial compression case but is smooth in all the other loading conditions. The singularity induced by the nonsmooth intersection of the failure surface in triaxial compression can be dealt using the methods summarized by Karaoulanis (2013).

The convexity of the new 3D criterion can be verified by examining the derivative of g, where g is defined as follows:

$$g = c/\rho = \left[ {\cos \left( {\pi /3 - \theta } \right)m_{b} + \sqrt {\cos^{2} \left( {\pi /3 - \theta } \right)m_{b}^{2} + b} } \right]$$
(33)

where \(c = \sqrt 6 bm_{b} \sigma_{\text{ci}} /9\), and \(b = 9\left( {s/m_{b}^{2} + \xi /\sqrt 3 \sigma_{\text{ci}} m_{b} } \right) \ge 0\). Its derivative with respect to θ is

$$g^{\prime} = \sin \left( {\frac{\pi }{3} - \theta } \right) + \frac{{\sin 2\left( {\frac{\pi }{3} - \theta } \right)}}{{2\sqrt {\cos^{2} \left( {\frac{\pi }{3} - \theta } \right) + b} }}$$
(34)

The second derivative of g is

$$g^{\prime\prime} = - \cos \left( {\frac{\pi }{3} - \theta } \right) - \frac{{\left[ {\cos 2\left( {\frac{\pi }{3} - \theta } \right) + 1} \right]^{2} + 4b\cos 2\left( {\frac{\pi }{3} - \theta } \right)}}{{4\left[ {\cos^{2} \left( {\frac{\pi }{3} - \theta } \right) + b} \right]^{1.5} }}$$
(35)

Summarizing Eqs. (34) and (35) gives

$$g + g^{\prime\prime} = \frac{{b\left( {1 + b} \right)}}{{\left[ {\cos^{2} \left( {\frac{\pi }{3} - \theta } \right) + b} \right]^{1.5} }} \ge 0$$
(36)

where “=” in Eq. (36) is valid only at the apex of the failure surface. According to the convexity requirements introduced in Sect. 2.2, the new 3D criterion satisfies the convexity requirements at all stresses.

4 Calibration and Validation

4.1 Calibration of the Failure Criterion

In practice, only experimental data under axi-symmetrical conditions are commonly available. We hence only used triaxial compression test data of rocks to evaluate the best pair of values m i (m b  = m i ) and σ ci, and then predicted the results of the other loading conditions using the best pair m i and σ ci.

We selected eight different rock types for which both triaxial compression (σ ′2  = σ ′3  < σ ′1 )and polyaxial (σ ′1  ≠ σ ′2  ≠ σ ′3 ) (also called ‘‘true triaxial’’) compression strength data exist. Testing data on Manazuru andesite, Mizuho trachyte, Dunham dolomite, and Solnhofen limestone were taken from Mogi (1971, 2007), data on Shirahama sandstone, KTB amphibolite and Yuubari shale were taken from Colmenares and Zoback (2002), while the data of westerly granite were acquired from Al-Ajmi and Zimmerman (2005). Because all the tests were conducted on intact rock under drained conditions, we set the parameter GSI to 100, which lead to s = 1, and a = 0.5 according to the definitions in Sect. 2.3.

The residual of the prediction using the failure criterion is defined as follows:

$$r_{i} = \rho_{i}^{\text{calc}} - \rho_{i}^{\text{test}} ,\,\;i = 1,\;2 \ldots ,\;n$$
(37)

where n is the number of test series for a specific rock, ρ test i is the i-th tested data, and ρ calc i is the i-th calculated value according to Eq. (29).

To measure the misfits between the predicted strength and the test data, the object function is defined by

$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {r_{i}^{2} } }$$
(38)

and is also called the root-mean-square error.

The best fitting pair of unknown parameters is obtained by minimizing RMSE, using non-linear least squares methods. It is worth noting that ρ is considered as a dependent variable, while ξ is an independent variable and θ = 0 in Eq. (29) for triaxial compression. In addition, the Coefficient of Determination DC, a scalar indicator, is used to assess the reliability of prediction by the proposed failure criterion

$${\text{DC}} = 1 - \frac{{\sum\limits_{i = 1}^{n} {\left( {\rho_{i}^{\text{calc}} - \rho_{i}^{\text{test}} } \right)^{2} } }}{{\sum\limits_{i = 1}^{n} {\left( {\rho_{i}^{\text{test}} - \bar{\rho }_{\text{test}} } \right)^{2} } }}$$
(39)

Where \(\bar{\rho }_{\text{test}}\) is the mean value of the test sample which is defined by

$$\bar{\rho }_{\text{test}} = \sum\limits_{i = 1}^{n} {\rho_{\text{i}}^{\text{test}} /n}$$
(40)

While it is desirable to have a higher DC, the ideal case is where the test data agrees with the predicted data with zero misfit (e.g., DC = 1).

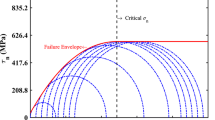
Figure 5 shows the calibration result of the failure criterion in triaxial compression tests on eight rock types, where the solid red lines represent the best fitting curve according to Eq. (29). The best pair of values m i and σ ci together with the DC is also shown in the figures. The best fitting m i strictly falls into the suggested range of m i (Hoek and Brown 1997; Marinos and Hoek 2001) for six rocks. It is slightly larger than the upper range for Yuubari shale, and a little less than the lower range for Solnhofen limestone. DC is in the range 0.931–0.999 for the eight rock types, indicating that the failure criterion describes rock failure in triaxial compression very well. These fitting results are also summarized in Table 1.

Fig. 5
figure 5

Calibration of the proposed 3D failure criterion in triaxial compression for eight rock types

Full size image
Table 1 Calibration results using the triaxial compression tests for eight rock types
Full size table

4.2 Validation of the Failure Criterion

To validate the proposed failure criterion for non-symmetrical loading conditions, the predictions for rock failure under polyaxial compression (σ ′1  ≠ σ ′2  ≠ σ ′3 ) using the best fitting parameters obtained in triaxial compression is compared with the test data. DC, defined by Eq. (39), is also used to assess the prediction reliability for polyaxial compression by the proposed failure criterion. ρ calc i is obtained by substituting the best pair of values m i and σ ci into Eq. (29), and two independent variables ξ and θ are calculated according to the polyaxial compression data. To compare the predicted strength with the experimental data for each set of tests, the predicted error ɛ i for the i-th test is defined by

$$\varepsilon_{i} = \left( {\rho_{\text{i}}^{\text{calc}} - \rho_{\text{i}}^{\text{test}} } \right)/\rho_{\text{i}}^{\text{test}} \times 100\%$$
(41)

Table 1 presents DC for the polyaxial compression (non-symmetrical) of eight rock types: the match is very good for five of the rocks with DC > 0.939, and is not as good for the other three rock types (i.e., Mizuho trachyte, Solnhofen limestone and Dunham dolomite) with 0.722 < DC < 0.853. However, for Mizuho trachyte and Solnhofen limestone, most of the results for ρ test i are close to ρ calc i , with a misfit |ɛ i | less than 8 % as seen in the distribution of ɛ i in Fig. 6b, d. The distribution of ɛ i for other rocks in polyaxial compression is also shown in Fig. 6, and most of the fitting errors |ɛ i | in the polyaxial compression tests are less than 6 % for the five rocks with high values of DC.

Fig. 6
figure 6

Distribution of the prediction errors ɛ i in polyaxial compression for eight rock types

Full size image

Figure 7 shows a comparison of the test data and the calibrated models in the σ ′1 −σ ′2 plane, for various of σ ′3 . In the figure, the symbols represent the actual polyaxial test data, where the black solid lines represent the predicted strength according to Eq. (27) using the best fitting parameters listed in Table 1, and the two red solid lines show the values from the conventional triaxial test. Compared to the HB criterion marked with blue dash lines, the predictions by the proposed 3D failure criterion clearly show that σ ′2 has a significant influence on rock failure. The predictions fit the test data reasonably well for Shirahama sandstone and Yuubari shale, and agree very well for Manazu andesite, Mizuho trachyte, Solnhofen limestone at high σ ′3 . It is worth noting that the predictions for polyaxial compression using the best pair of values m i and σ ci obtained from triaxial compression tend to be less accurate than the optimization procedure used for all test data reported by Zhang (2007, 2008); Jiang et al. (2011); Priest (2012). Therefore, failure under polyaxial stresses can be predicted from triaxial test data using the proposed 3D failure criterion.

Fig. 7
figure 7figure 7

Comparisons of the proposed 3D failure criterion with polyaxial test data on the σ ′1 −σ ′2 plane

Full size image

5 Comparison of the Proposed Model with Two Existing 3D Criteria

To compare the proposed 3D failure criterion with existing ones in the case of non-circular cross sections, we further derive the following invariant representation for a unified expression of the 3D failure criterion (see Eqs. (43)–(46) in Appendix)

$$\rho = \frac{{\sqrt 2 \sigma_{\text{ci}} m_{b} }}{6}\left[ { - \frac{A\left( \theta \right)}{\sqrt 3 } + \sqrt {\frac{{A^{2} \left( \theta \right)}}{3} + 12\left( {\frac{\xi }{{\sqrt 3 m_{b} \sigma_{\text{ci}} }} + \frac{s}{{m_{b}^{2} }}} \right)} } \right]$$
(42)

When \(A\left( \theta \right) = \frac{{3 - 2\cos \left( {\pi /3 + \theta } \right)}}{2},\) Eq. (42) represents the Zhang–Zhu failure criterion;

And when \(A\left( \theta \right) = \frac{3 - \cos 3\theta }{2},\) Eq. (42) represents the Jiang failure criterion. Parameters m i and σ ci in Eq. (42) are the same as those obtained from triaxial compression using the proposed failure criterion. When A(θ) = 2cos(π/3−θ)in Eqs. (42), (29) can be obtained (see Eqs. (47), (48) in Appendix).

A comparison of DC obtained using three 3D criteria for polyaxial compression testing of eight rocks is presented in Fig. 8. It shows that the proposed criterion has the highest value of DC for five of the rocks, while the Zhang–Zhu criterion best fits the other three rocks. However, the shape of the two existing 3D criteria in the deviatoric plane is not convex, which violates Drucker’s stability postulation and cannot be used to obtain σ ′1 in certain special stress paths. Moreover, the failure functions of two criteria mentioned above are not as general as the principal stress expression shown in Eq. (22).

Fig. 8
figure 8

Comparisons of DC obtained from three 3D failure criteria

Full size image

6 Summary and Conclusions

A simple 3D failure criterion has been proposed in this paper wherein the influence of σ ′2 on rock failure is explicitly considered, with all the features of the classic HB criterion being retained. The failure envelope surface of the proposed criterion has non-circular convex loci in the deviatoric stress plane for all stress conditions and is smooth everywhere, except in the triaxial compression condition.

The parameters involved in the proposed failure criterion can be estimated from conventional triaxial test data. The performance of the proposed failure criterion has been further validated by polyaxial test data using the estimated parameters. This polyaxial failure criterion can be applied, even in the absence of polyaxial (true triaxial) data. This offers a great advantage, as the most widely available testing means in practice is by the traditional triaxial compression tests. A comparison of the proposed criterion with existing ones shows that the new 3D criterion generally performs better in predicting the strength of rocks.