The effect of superimposed hydrostatic pressure on shear decohesion in round bar tensile specimens

Abstract

The modified Gurson–Tvergaard–Needleman model, that considers shear decohesion as an increment in the total void volume fraction, is used to investigate the effect of superimposed hydrostatic pressure on the ductility of a round bar specimen. Experiments indicate that the fracture mode is not uniform across the cross section of a round bar specimen–no shear damage exists at the center while it is pronounced at the edge. The damage mechanisms of shear decohesion and void growth are delayed by applying superimposed hydrostatic pressure, which leads to an increase in the fracture strain and ductility. However, the effect of pressure on ductility depends on the location within the cross section. Void growth at both the center and the edge becomes increasingly delayed with increasing pressure, but this effect is more significant at the edge because of the existence of shear stress. Shear decohesion at the edge becomes the dominant damage mechanism, rather than void growth, when pressure is increased. The numerical results presented herein are used to explain and discuss this phenomenon in depth.

1 Introduction

Applying superimposed hydrostatic pressure is known to increase the ductility of metals (Bridgman 1952). It is generally accepted that this is a result of the delaying or complete elimination of void nucleation and growth (Ashby et al. 1985; Kao et al. 1989; French and Weinrich 1975; French et al. 1973; Brownrigg et al. 1983; Korbel et al. 1984). However, applying hydrostatic pressure also allows more damage to accumulate at the edge of a round bar specimen by the shear mechanism, or so-called matrix decohesion, which becomes the primary damage mechanism (Kao et al. 1990). This study aims to investigate this phenomenon numerically using the modified Gurson–Tvergaard–Needleman (GTN) (Gurson 1977) model that includes the effect of the shear decohesion. To the best of the author’s knowledge this matter has not been reported numerically elsewhere, as previous numerical studies used the conventional GTN model to investigate the effect of superimposed hydrostatic pressure on ductility.

Various types of fracture modes exist, such as brittle, fully plastic, ductile, and shear decohesion (Ashby et al. 1985). A material that exhibits no appreciable plastic deformation prior to fracture is said to have a low fracture toughness, and to undergo brittle fracture. The presence of impurities is an example of a condition that may lead to a low value of fracture toughness. For brittle fracture to occur, a crack must first initiate. This occurs either within a grain or along the grain boundary, typically at inclusions or second phase particles due to slip. Next, sufficient stress causes the crack to rapidly propagate to fracture. Since pressure works against the opening of cracks, it strongly inhibits brittle fracture (Ashby et al. 1985). When all other fracture mechanisms are suppressed, a material undergoes fully plastic failure. It will fail in simple tension, or in tension with superimposed pressure by plastic failure. A ductile material yields during plastic deformation and as the material is strained to higher values, volume is conserved by a reduction in cross sectional area that balances the increase in length. Inhomogeneity in the material leads to strain localization, or necking, and the progression of this neck culminates in the reduction of the cross-sectional area to a point or so-called chisel-edge of zero area. This mechanism, unlike brittle fracture, is only weakly influenced by pressure because there is no change in volume associated with the fracture process (Ashby et al. 1985). In the ductile fracture process, voids nucleate at initiators, grow, and eventually coalesce, which causes the fracture. As stated by Ashby et al. (1985), the load-bearing area of the band drops drastically due to the voids that nucleate in slip bands under certain conditions. Separation happens in the plane of the band with increasing the voids area due to further shear. The extended void in the shear band does not grow in volume, so these are much less dependent on pressure compared to voids which do extend in volume.

Kao et al. (1990) showed that, unlike the void growth mechanism, shear decohesion is not suppressed by pressure, causing it to be the only valid mechanism to explain the observed failure under the influence of hydrostatic pressure (Kao et al. 1990). Figure 1 compares fracture surfaces in round bar specimens pulled to fracture (a) in an ambient atmosphere and (b) under superimposed hydrostatic pressure. At the centre of the specimens, no shear stresses exists, and fracture occurs by the mechanism of void nucleation, growth, and coalescence. This figure also shows that the application of pressure reduces the size of the central tearing region and the number of equiaxed dimples within it. Additionally, at the edge of the specimen, applied pressure results in matrix decohesion becoming the main damage mode in the large shear lip that develops.

Fig. 1

Fractured surfaces of round bar specimens: a under ambient pressure, b under 1120 MPa pressure (Kao et al. 1990)

Many researchers who have studied this subject have utilized micromechanical ductile damage models to cover the wide range of stress triaxialities and Lode angle parameters in tension, shear, and/or compression, such as Brünig et al. (2013) and Barsoum and Faleskog (2007). However, particle-induced microvoids are known to localize plastic flow and limit the formability and ductility of sheet metals (Ashby et al. 1985). The GTN model, proposed by Tvergaard and Needleman (1984) considers the influence of these microvoids on formability and fracture, and is therefore considered to be an improvement on the accuracy of the original Gurson model (Gurson 1977). These models treat voids as spherical cavities and capture their effects on material yield following a modification of the von Mises yield criterion (Gurson 1977). Many demonstrations of the utility of these models exist in the literature. For example, forming limit diagrams (FLDs) were predicted in Shahzamanian and Wu (2021) using the GTN model as a yield function for anisotropic materials. Furthermore, Peng et al. (2009), Wu et al. (Wu et al. 2010) and Shahzamanian et al. (2021a, b) employed the conventional GTN model to investigate the effect of superimposed hydrostatic pressure on fracture in round bars, sheet metals under tension, and sheet metals under bending, respectively. It was shown that pressure has a negligible effect on the yield strength of metals since void formation is insignificant prior to necking. Additionally, the local mean stress and stress triaxiality were shown to decrease with an increase in superimposed hydrostatic pressure. Consequently, the extent of void growth decreases, which causes the fracture strain to increase (Peng et al. 2009; Wu et al. 2010; Shahzamanian et al. 2021a, b). Peng et al. (2009) used the GTN model with axisymmetric elements to simulate the influence of superimposed hydrostatic pressure on the fracture of round bar specimens, but the effect of the shear decohesion was not considered. It was found in this study that void growth becomes delayed with an increase in superimposed hydrostatic pressure, which leads to increase in fracture strain.

The GTN model has been extended by Nahshon and Hutchinson (2008) to consider the effect of shear decohesion as an increment in void volume fraction. The shear-modified GTN model has been found to be applicable in literature. Chen et al. (2021) used machine learning to determine the parameters for the shear-modified GTN model for a typical aluminum alloy and simulated the test under various constraints. In addition, Chen and Osovski (2020a) used this model to simulate the shear dominant compression-tension test for the titanium alloy Ti6Al4V. In another study performed by Chen and Osovski (2020b), the shear-modified GTN model was used to investigate the damage evolution around shear loaded intervoid ligaments under plane strain and plane stress conditions. Li et al. (2021) studied the size effect on the damage evolution of the shear-modified GTN model under various stress triaxialities in metals. Yang et al. (2021) used the shear-modified GTN model to predict ductile fracture for additive manufactured Ti6Al4V.

The aim of this paper is to perform a numerical study on the effect of superimposed hydrostatic pressure on shear fracture in round bar specimens under tension and to offer a comprehensive explanation for this phenomenon. All the simulations presented in this study are performed using ABAQUS/Explicit based on the shear-modified GTN model implemented in a VUMAT subroutine. It is shown numerically that the failure mode is non-uniform across the cross section of a specimen, as observed in experiments (Kao et al. 1990). The effect of superimposed hydrostatic pressure on the mechanisms of void growth and shear damage at the center and edge of specimens is determined and explained in detail. Numerical results are found to be in good agreement with experimental observations.

2 Constitutive model

The modified GTN model (Tvergaard and Needleman 1984; Gurson 1977; Chu and Needleman 1980) that is used in this study considers damage growth in metals due to void nucleation, growth, and coalescence as well as shear decohesion. The approximate yield function that is used is:

$$\Phi \left({\varvec{\sigma}},\tilde{\sigma },f\right)=\frac{{\sigma }_{e}^{2}}{{\tilde{\sigma }}^{2}}+2{f}^{\ast}{q}_{1}{\text{cosh}}\left(\frac{3{q}_{2}{\sigma }_{H}}{2\tilde{\sigma }}\right)-\left[1.0+{\left({q}_{2}{f}^{\ast}\right)}^{2}\right]=0$$

(1)

where ${\varvec{\sigma}}$ is the macroscopic Cauchy stress tensor. Bold font is used throughout to distinguish a tensor. ${\sigma }_{e},\;{\sigma }_{H},$ and $\tilde{\sigma }$ are the equivalent stress, hydrostatic stress, and matrix yield stress, respectively. The matrix and the equivalent stresses are undamaged and damaged stresses, respectively. Finally, the quantities ${q}_{1}$ and ${q}_{2}$ are calibrated parameters.

The elastic constitutive is:

$$\widehat{{\varvec{\sigma}}}={{\varvec{\psi}}}^{e}:{{\varvec{D}}}^{e}$$

(2)

where $\widehat{{\varvec{\sigma}}}$ is the Jaumann rate of Cauchy stress tensor, ${{\varvec{D}}}^{e}$ is the elastic strain rate tensor, and ${{\varvec{\psi}}}^{e}$ is the fourth-order elastic modulus tensor:

$${{\varvec{\psi}}}^{e}={\psi }_{ijkl}^{e} {{\varvec{e}}}_{i}\otimes {{\varvec{e}}}_{j}\otimes {{\varvec{e}}}_{k}\otimes {{\varvec{e}}}_{l}$$

(3)

and

$${\psi }_{ijkl}^{e}=\frac{E}{2\left(1+\nu \right)}[{\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}+\frac{2\nu }{1-2\nu }{\delta }_{ij}{\delta }_{kl}]$$

(4)

with E being the Young’s modulus and $\nu$ the Poisson’s ratio.

The uniaxial elastic–plastic undamaged stress–strain curve for the matrix material is provided by the following power-law form:

$$\tilde{\sigma }=\left\{\begin{array}{c} E\overline{\varepsilon }, for \,\tilde{\sigma }\le {\sigma }_{y}\\ K{\overline{\varepsilon }}^{n}, for \,\tilde{\sigma }>{\sigma }_{y}\end{array}\right.,$$

(5)

where ${\sigma }_{y}$ is the yield stress of the material, while $K, \;\mathrm{and}\; n$ are the Power law parameters. Additionally, $\overline{\varepsilon }$ and $\tilde{\sigma }$ are effective strain and stress, respectively.

Void growth ${\left(\dot{f}\right)}_{growth}$ is a function of the plastic strain rate ${{\varvec{D}}}^{P}$:

$${\left(\dot{f}\right)}_{growth}=\left(1-f\right){\varvec{I}}:{{\varvec{D}}}^{P}$$

(6)

Void nucleation is assumed to be strain controlled, and is defined as:

$${\left(\dot{f}\right)}_{nucleation}=\overline{A}{\dot{\overline{\varepsilon }} }^{P}$$

(7)

where ${\dot{\overline{\varepsilon }}}^{P}$ is the effective plastic strain rate, and the parameter $\overline{A }$ is chosen so that nucleation follows a normal distribution as suggested by Chu and Needleman (Chu and Needleman 1980):

$$\overline{A }=\frac{{f}_{N}}{{S}_{N}\sqrt{2\pi }}{\text{exp}}\left[-\frac{1}{2}{\left(\frac{{\overline{\varepsilon }}^{p}-{\varepsilon }_{N}}{{S}_{N}}\right)}^{2}\right],$$

(8)

where ${f}_{N}$ is the volume fraction of void nucleating particles, ${\varepsilon }_{N}$ is the average void nucleating strain, ${S}_{N}$ is the standard deviation of the void nucleating strain, and ${\overline{\varepsilon }}^{p}$ is the accumulated plastic strain.

The shear damage growth proposed by Nahshon and Hutchinson (2008) is as follows:

$${\left(\dot{f}\right)}_{shear}={k}_{w}w\left({\sigma }_{ij}\right)f\frac{{\varvec{\sigma}}:{{\varvec{D}}}^{P}}{{\sigma }_{ef}}$$

(9)

where ${k}_{w}$ is a calibration parameter. The function $w\left({\sigma }_{ij}\right)$ identifies the current state of stress, which is defined as $w\left({\sigma }_{ij}\right)=1.0-{\left(\frac{27{J}_{3}}{2{\sigma }_{eq}^{3}}\right)}^{2}$ where ${J}_{3}$ is the third invariant of the deviatoric stress matrix.

The growth of existing voids and the nucleation of new voids are considered in the evolution of the void volume fraction as follows:

$$\dot{f}={\left(\dot{f}\right)}_{growth}+{\left(\dot{f}\right)}_{nucleation}+{\left(\dot{f}\right)}_{shear damage}$$

(10)

and the function of void volume fraction $\left({f}^{\ast}(f)\right)$ in Eq. (1) is defined to consider coalescence as follows:

$${f}^{\ast}=\left\{\begin{array}{c}f, for f\le {f}_{c}\\ {f}_{c}+\frac{{f}_{u}^{\ast}-{f}_{c}}{{f}_{f}-{f}_{c}}\left(f-{f}_{c}\right), for f{f}_{c}\end{array}\right.$$

(11)

where ${f}_{c}$ is the critical void volume fraction for coalescence and ${f}_{f}$ is the void volume fraction at failure. The parameter ${f}_{u}^{\ast}$ is equal to $\frac{1}{{q}_{1}}.$ It should be mentioned that void nucleation and growth cannot occur under compression; it may only take place in tension. The modified GTN model is implemented using the VUMAT subroutine in the ABAQUS/Explicit.

3 Problem formulation and method of solution

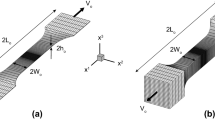
A round bar specimen under superimposed hydrostatic pressure p, with length ${L}_{o}$ and diameter ${D}_{o},$ is considered and shown schematically in Fig. 2. In the schematic, applied pressure is represented by small brown arrows directed into the specimen from all directions. The sequence of tensile strain under superimposed hydrostatic pressure is modeled as two steps. In the first step, the pressure is gradually increased up to a desired level of $p=-\alpha {\sigma }_{y},$ where $\alpha$ defines the value of applied pressure as a fraction of the initial yield stress of the material, without applying any tensile deformation. In the second step, tensile deformation (U) is applied to the specimen while maintaining the constant pressure value $p=-\alpha {\sigma }_{y}.$

Fig. 2

Schematic of a round bar specimen under superimposed hydrostatic pressure; Points A and B indicate respectively the center and edge of the cross-section at the middle/symmetric plane

The elastic–plastic properties of the matrix material are specified as presented in Table 1. These values of mechanical properties are taken from Tvergaard and Needleman (1984) and Tvergaard (1981) except the ${k}_{w}$ parameter. It should be emphasized that the main objective of this study was to investigate the effect of superimposed hydrostatic pressure on shear decohesion across the cross-sectional area of a round bar specimen. Therefore, the overall results and conclusions are not particularly dependent on the material parameters presented in Table 1. Regarding the ${k}_{w}$ value, Shahzamanian et al. (2021c) studied the effect of this parameter on the force as a function of tensile strain under ambient pressure ($\alpha =0.0$) in a wide sheet metal. Shear damage growth increases with ${k}_{w}$ according to Eq. (9), leading to a decrease in the fracture strain. In this study, ${k}_{w}=1.5$ is used to consider the effect of the shear decohesion in the modified GTN model. However, the effect of ${k}_{w}$ on fracture strain will be studied to understand the effect of such a parameter on fracture strain.

Table 1 Material constants

The three-dimensional element C3D8R in ABAQUS/Explicit is used for the round bar specimen having dimensions of ${D}_{o}=10$ mm and ${L}_{o}=60$ mm. Figure 3 shows the finite element (FE) configuration of the specimen with a typical mesh consisting of 276 × 45 elements. The element distribution across the cross-sectional area is the same as along its length. However, the element distribution in the Z-direction is not uniform—it is biased to the middle section of the specimen where fracture is expected to occur. Only half of the length of the specimen is simulated by using the symmetric boundary conditions in the middle section. Symmetry is assumed about the middle-plane of round bar specimens studied by Tvergaard and Needleman (1984) and Peng et al. (2009) as well as where two symmetrical conical fracture surfaces were predicted. However, it must be emphasized that cup-cone fracture is observed experimentally in round bar specimens when one of the cracks in the two symmetrical conical fracture surfaces dominates where symmetry does not exist (Besson et al. 2001).

Fig. 3

FE configuration of a round bar specimen under tension

Mesh sensitivity is inevitable in FEA particularly when fracture is investigated. Thus, the effect of mesh sensitivity on localized deformation as well as fracture for a round bar specimen is investigated in this study. Figure 4 shows the normalized stress (${S}^{\ast})$ as a function of the tensile strain (ε) for round bar specimens with two different numbers of elements. The normalized stress is defined as ${S}^{\ast}=\frac{4}{\pi {D}_{o}^{2}}\frac{F}{{\sigma }_{y}}$ and $\varepsilon =\mathrm{ln}(1.0+\frac{\Delta l}{{l}_{o}}).$ In this study, the force–displacement curve is insignificantly affected by mesh parameters. However, the significant effect of mesh parameters on fracture strain is reported frequently in other studies (Tvergaard and Needleman 1984; Gurson 1977; Shahzamanian and Wu 2021; Peng et al. 2009; Wu et al. 2010; Shahzamanian et al. 2021a, b; Shahzamanian and Wu 2021; Nahshon and Hutchinson 2008; Chen et al. 2010, 2021; Chen and Osovski 2020a, b; Li et al. 2021; Yang et al. 2021; Abaqus/CAE User’s Manual 2014; Chu and Needleman 1980; Tvergaard 1981; Besson et al. 2001).

Fig. 4

Effect of mesh sensitivity on normalized stress–tensile strain

ABAQUS/Explicit is used even though the tensile test is a static analysis. The method of mass scaling was used with a sufficiently low target time increment to minimize dynamic effects on the sample.

4 Results and discussions

4.1 α Sensitivity

Superimposed hydrostatic pressure delays or completely eliminates void nucleation, growth, and coalescence during tensile deformation of metals (Peng et al. 2009; Shahzamanian et al. 2021a). The effect of pressure on ductility and bendability is investigated in Peng et al. (2009) and Shahzamanian et al. (2021a) using the conventional GTN model without considering the effect of the shear decohesion. In this study, the effect of superimposed hydrostatic pressure on fracture in a round bar specimen under tension is determined by using the modified GTN model that accounts for the effect of the shear decohesion. Figure 5 shows the effect of α on the normalized stress–tensile strain curve, and it is observed that as the value of α increases, the fracture strain increases while the tensile strength remains unaffected. It must be emphasized that the normalized stress presented is based on tensile strain, which is applied in step 2 while the specimen is under pressure. Therefore, it starts from zero for all values of α.

Fig. 5

Effect of superimposed hydrostatic pressure on normalized stress–tensile strain curves

As shown in Peng et al. (2009), Wu et al. (2010) and Shahzamanian et al. (2021a), increasing the superimposed hydrostatic pressure leads to a decrease in the local mean stress and stress triaxiality, which explains the delay of void growth and the corresponding increase in fracture strain. Stress-triaxiality has a significant effect on fracture strain. Figure 6 presents the local mean stress ${\sigma }_{H}=\left(1/3\right)\left({\sigma }_{xx}+{\sigma }_{yy}+{\sigma }_{zz}\right)$ at the center and the edge of the specimen (Points A and B, respectively, as shown in Fig. 2) as a function of tensile strain under various superimposed hydrostatic pressures. Local mean stress is equivalent to the mean stress at a specific point and on the contrary, the superimposed hydrostatic pressure is applied on the surfaces of a specimen.

Fig. 6

The effect of superimposed hydrostatic pressure on local mean stress a at the center and b at the edge of round bar specimens

At ambient pressure $(p=0.0),$ local mean stress develops in a way that assists void growth as tensile strain is applied. On the contrary, under a superimposed hydrostatic pressure $p=-\alpha {\sigma }_{y},$ the local mean stress value is initially compressive. This delays void growth until an adequately large component of tensile stress is generated. As shown in Fig. 6, increasing the superimposed hydrostatic pressure causes the maximum value of local mean stress at fracture to decrease at every location in the specimen. However, it decreases more at the edge than at the center.

The local mean stress at the center and the edge of a specimen is compared for $\alpha =0.0\; \mathrm{and}\; 0.5,$ as shown in Fig. 7. It is clearly observed that the local mean stress before necking is independent of location throughout the specimen, but as tensile strain increases past the onset of necking, it is concentrated in the center. This causes the development of a significantly higher volumetric strain at the centre than at the edge, as shown in Fig. 8 for $\alpha =0.0\; \mathrm{and} \;0.5.$ It is also interesting to note that the volumetric strain is almost zero before necking. Because stress triaxiality is equivalent to the ratio of hydrostatic pressure to equivalent stress, higher values of local mean stress result in an increase in stress triaxiality as well as volumetric strain since hydrostatic stress accumulates plastic strain. Stress triaxiality has a significant effect on fracture strain as well as the yield function based on Eq. (1). The rate of void growth volume fraction is proportional to plastic volumetric strain rate according to Eq. (6), which will be discussed in further detail in this study.

Fig. 7

Comparison of local mean stress at the center and the edge for a $\alpha =0.0$ and b $\alpha =0.5$

Fig. 8

Comparison of volumetric strain at the center and the edge for a $\alpha =0.0$ and b $\alpha =0.5$

As mentioned previously, the highest and lowest values of local mean stress can be found at the center and edge of the specimen, respectively. On the contrary, the edge has the highest value of the shear stress while none exists at the center. One component of shear stress at the center and the edge was calculated under various superimposed hydrostatic pressures and is shown in Fig. 9. It must be noted that the values of the shear stress components $({\tau }_{ij})$ around the edge are not uniform and depend on the location at the edge. However, Fig. 9b represents the shear stress, ${\tau }_{13},$ at point B (see Fig. 2). Superimposed hydrostatic pressure causes a delay in the growth of ${\tau }_{13}$ at the edge but an increase in the amount that develops before fracture. This contrasts with the effect on the local mean stress, as was shown in Fig. 6. The ductility increases with an increase of superimposed hydrostatic pressure and the shear stress grows.

Fig. 9

The effect of superimposed hydrostatic pressure on shear stress a at the center and b at the edge of round bar specimens

Figures 10 and 11 show the effect of superimposed hydrostatic pressure on void growth, void nucleating volume fraction, shear decohesion, and total void volume fraction at the center and the edge of a specimen. As shown in Fig. 10c, the shear damage at the center is zero for every value of superimposed hydrostatic pressure since the shear stress at the center is zero (Fig. 9a). Figure 10a demonstrates that the final value of nucleated void volume fraction is unchanged by the application of superimposed hydrostatic pressure as the strained void nucleating GTN model is used in this study. As discussed by Shahzamanian et al. (2021a), the void nucleation volume fraction in the strain-controlled void nucleating GTN model is not a function of superimposed hydrostatic pressure, but it is considered when using the stress-controlled void nucleating GTN model. However, superimposed hydrostatic pressure clearly delays void growth at the center as shown in Fig. 10b. The inverse relationship between superimposed hydrostatic pressure and void growth has been reported in other studies for round bar specimens under tension (Peng et al. 2009) and sheet metals under bending (Shahzamanian et al. 2021a). Finally, Fig. 10d plots the total void volume fraction as a function of tensile strain under various superimposed hydrostatic pressures. The evolution of total void volume fraction is shown to be delayed by pressure, and it will be shown that this causes the fracture strain to increase.

Fig. 10

Effect of superimposed hydrostatic pressure on a, e void nucleation volume fraction, b, f void growth volume fraction, c, g shear void growth volume fraction and d, h total void volume at the center (left sub-figures) and the edge (right sub-figures)

Fig. 11

Contours of void volume fractions of the deformed shapes right before fracture initiation; a $\alpha =0$, “left subfigures” and b $\alpha =0.5$, “right subfigures”

Figure 10e shows the effect of superimposed hydrostatic pressure on void nucleation at the edge. Again, it is demonstrated that the final value of nucleated void volume fraction is not a function of superimposed hydrostatic pressure as the GTN model used in this study assumes that the nucleation is strain controlled. As shown in Fig. 9b, shear stress exists at the edge of a round bar specimen, and it is more pronounced under superimposed hydrostatic pressure. Upon comparison of Fig. 10g to f, it is clear that shear becomes the dominant deformation mechanism at higher values of superimposed hydrostatic pressure. As mentioned previously, the void growth mechanism is excluded by imposing hydrostatic pressure which causes shear decohesion to be the dominant failure mechanism (Kao et al. 1990). Although the shear void growth volume fraction becomes greater in response to an increase in pressure, the damage due to both shear and void growth calculated using the modified GTN model does not begin to accumulate until greater values of tensile strain. Finally, Fig. 10h shows the total void volume fraction under various values of superimposed hydrostatic pressures at the edge. It is seen that applying more hydrostatic pressure has no influence on the maximum value of total void volume fraction, since the final volume fraction at failure (${f}_{f})$ is constant for every case. However, an increase in applied pressure increases the tensile strain at which total void volume fraction reaches its maximum value, as well as the fracture strain.

The contours for the void nucleation, void growth, shear void growth, and total void volume fraction of the deformed cross-section of the round bar specimens immediately before fracture in ABAQUS are shown in Fig. 11. Void nucleation is distributed uniformly throughout the cross-section of the specimen for both $\alpha =0.0$ and $\alpha =0.5$. The applied tensile strains for $\alpha =0.0$ and $\alpha =0.5$ are 0.125 and 0.1688, respectively. Void growth is concentrated at the center and diminishes towards the edge. Void growth due to shear decohesion is distributed in the opposite manner–it is zero at the centre and pronounced at the edge of the specimens. It is also observed that the total void volume fraction is greatest at the centre, which is where fracture begins in a specimen. Finally, Fig. 11 also demonstrates that the area in the centre of the specimen where total void volume fraction is concentrated becomes smaller as superimposed hydrostatic pressure is increased.

Figure 12 shows profile views of deformed round bar specimens at fracture under various levels of superimposed hydrostatic pressure. It is clearly seen that the minimum cross-sectional area at fracture decreases with superimposed pressure. By definition, this increases the fracture strain according to the following equation:

Fig. 12

Deformed shapes of round bar specimens at fracture under various levels of superimposed hydrostatic pressure

$${\varepsilon }_{f}=\mathrm{ln}\frac{{A}_{o}}{{A}_{min}},$$

(9)

where ${A}_{min}$ and ${A}_{o}$ are the minimum and undeformed cross-sectional area in a round bar specimen, respectively. The fracture strains calculated as a function of superimposed hydrostatic pressure are shown in Fig. 13. This clearly demonstrates that with an increase of superimposed hydrostatic pressure, the specimen can deform more before fracture, which leads to an increase in the ductility and fracture strain.

Fig. 13

Effect of superimposed hydrostatic pressure on fracture strain

4.2 Transition in void volume fractions

The amount of damage due to void growth and shear void growth under ambient ($\alpha =0.0$) and superimposed hydrostatic pressure ($\alpha =0.5$) was calculated along the radius of a specimen, as displayed in Fig. 14. It is observed that as the modeled element under consideration becomes further away from the centre of the specimen, the extent of void growth diminishes along with an increase in shear damage. Additionally, it is observed that the magnitude of these changes in void growth and shear void growth volume fraction is similar between each element under ambient pressure, but not under applied pressure. When hydrostatic pressure is applied, there are large jumps in shear void growth and void growth volume fractions as the edge of a specimen is approached. This modeling demonstrates the increase in dominance of the void shear mechanism at the edge of a round bar specimen under pressure, as shown in Fig. 11.

Fig. 14

Shear void growth and void growth volume fractions changes along the radius on the fractured cross-section of the specimens b, c under ambient ($\alpha =0.0)$ and d, e superimposed hydrostatic pressure ($\alpha =0.5)$; element numbers are shown in (a)

4.3 ${k}_{w}$ Sensitivity

The effect of ${k}_{w}$ on void volume fraction has been investigated under different pressures at the edge (Point B on Fig. 2) and is presented in Fig. 15. As expected, void nucleating void volume fraction is not dependent on ${k}_{w}$ and it is unchanged for both $\alpha =0.0, \mathrm{and} 0.5$ (Fig. 15a and e). As shown in Fig. 15b and f, the final values of void growth volume fraction are constant at ambient pressure and applied pressure when ${k}_{w}=0.0.$ The shear void growth is zero when ${k}_{w}=0.0$ and the void nucleation volume fraction is unchanged. Therefore, the ultimate value of the void growth volume fraction is unaffected when ${k}_{w}=0.0.$ However, void growth volume fraction is delayed with increasing pressure. By comparison of Fig. 15b and c as well as f and g, it can be seen that the void growth volume fraction decreases with increasing ${k}_{w}$ as the shear damage volume fraction is increased. Overall, the total void volume fraction is delayed with increasing pressure as shown in Fig. 15d and f. Additionally, it is observed that ${k}_{w}$ has an insignificant effect on the total void volume fraction and it only affects the shear decohesion as well as the void growth volume fraction.

Figures 15

Effect of ${k}_{w}$ on a, e void nucleation volume fraction, b, f void growth volume fraction, c, g shear void growth volume fraction and d, h total void volume with $\alpha =0.0$ (left sub-figures) and $\alpha =0.5$ (right sub-figures)

5 Conclusion

In this study, round bar specimens were simulated and an FEA was performed to understand the effect of superimposed hydrostatic pressure on ductility and fracture strain. The modified GTN model was employed to enable the consideration of the effect of the shear decohesion as an increment in the total void volume fraction. The dominant fracture mode across the cross section of a round bar specimen was found to transition from a void growth mechanism at the centre to a shear decohesion at the edge.

Up to the onset of necking, stress is uniformly distributed throughout the cross-sectional area. However, once a neck develops, mean stress becomes localized to the center of the specimen. Therefore, void growth volume fraction is higher in the center than at the edge. It is shown that shear stress is present at the specimen edge but not at the center; therefore, shear decohesion only occurs at the edge of the specimen.

The numerical results show that the development of microvoids as well as damage due to the shear decohesion are delayed by the application of superimposed hydrostatic pressure. The final values of void growth at the center are independent of pressure while the ultimate value of void growth at the edge drops. An increase in superimposed hydrostatic pressure increases the shear void volume fraction at the specimen edge before failure. However, it also causes the development of this damage to be delayed until higher values of strain are reached.

Overall, the numerical results show that by increasing the superimposed hydrostatic pressure, the ductility of a specimen is increased. Additionally, the application of pressure causes shear decohesion to become the dominant fracture mode at the specimen edge. These phenomena have been confirmed experimentally in the existing literature.