1 Introduction

The scope of the present paper is to highlight the effects of micro-inertia when porous materials containing parallel cylindrical voids are submitted to dynamic loading. The void geometry may be representative of honeycomb structures or materials containing drilled holes. The development of additive manufacturing could also help provide more dedicated and controlled pores distributions following, for instance, a specific geometry such as a cylindrical shape. This study aims to bring new insights in the response of such porous structures under dynamic loading.

The response of porous materials has been largely studied in the context of low strain rate loadings, where inertia effects may be disregarded. The pioneering works of McClintock (1968) and Rice and Tracey (1969), where the void was assumed embedded in an infinite rigid plastic matrix, have revealed the exponential influence of the stress triaxiality on the damage growth. The strain rate sensitivity has also been introduced in various approaches. For instance Budiansky et al. (1982), have considered a power law constitutive relationship for the matrix behavior, to identify the complex influence of the stress triaxiality on the porosity growth. Since micro-inertia effects were not accounted for, these approaches may thus find some limitations in cases of very high loading rates encountered in various applications (e.g. high speed forming processes, ballistic impacts, design of shock wave mitigation devices, planetary science, \(\ldots \)).

Under dynamic conditions, local acceleration fields are developed in the vicinity of voids which will modulate the overall response. Glennie (1972) has extended the variational approach of Rice and Tracey (1969) for spherical voids and shown that micro-inertia effects tend to delay the porosity growth. In fact, the inertial contribution is found scaled by the square of the void radius and the mass matrix density. Note that the inertial term arising from this approach in solid mechanics is similar to the one present in the equation of motion of a cavitation bubble in fluid mechanics, see Rayleigh (1917), Plesset (1949). At this stage, most of the works dedicated to micro-inertia effects have been done considering a spherical shape for the voids. Within this context, Klöcker (1991) has introduced the coupling of linear viscous rate dependence with micro-inertia to reveal that neglecting micro-inertia would lead to an infinite growth rate of void, confirming the stabilizing effect of the dynamic contribution developed at the local scale. Ortiz and Molinari (1992) have also considered a combination of viscous and micro-inertia effects, adding the strain hardening contribution. The authors have characterized the interplay between viscous and inertia effects by means of a dimensionless parameter and at the same time have given more insights into the role of each contribution in the dynamic void growth process: the early stage is governed by viscous effects, while the late stage is dominated by micro-inertia, see also Wu et al. (2003). In previous cited works, the void is assumed to be surrounded by an infinite medium. The case of spherical voids embedded in a finite matrix, as considered in various static and dynamic approaches, accounts for some interactions between voids by introducing the effect of the porosity on the overall response. Considering the classical hollow sphere model as representative of the porous medium, Carroll and Holt (1972) have proposed an analytical void collapse law including micro-inertia effects. The case of a pure hydrostatic loading was considered and the external pressure was found to be the sum of two contributions: a quasistatic part and an inertia-dependent part still scaled by the square of the void radius and the mass matrix density. Founded on this approach, numerous authors have proposed some adjustments and applied the modeling to study spall fracture in ductile materials (see for instance Johnson 1981; Eftis and Nemes 1992).

Wang (1994, 1997) and Molinari and Mercier (2001) have proposed a dynamic homogenization approach based on the principle of virtual power and have defined the macrostress as the sum of two terms: static and micro-inertia contributions. Nevertheless, the definition proposed by Wang (1994, 1997) or Molinari and Mercier (2001) are different. These authors applied the dynamic homogenization to the case of porous materials containing spherical voids. From the hollow sphere model and the trial velocity field of Gurson (1977), Molinari and Mercier (2001) obtained an explicit constitutive behavior accounting for micro-inertia and viscoplasticity for general states of stress, not only restricted to specific loading configurations like pure hydrostatic path or shearing, as it was the case in Wang (1994, 1997). The modeling of Molinari and Mercier (2001) has been used in Czarnota et al. (2006, 2008); Jacques et al. (2010); Versino and Bronkhorst (2018) to describe spall fracture in a high purity grade tantalum, or in Czarnota et al. (2017) for shock wave propagation in elastic viscoplastic porous materials.

Void shape may have an important influence on the behavior of porous solids. Sartori et al. (2015) accounted for void shape effects on the dynamic response. In this last work, the representative volume element is spheroidal. The trial velocity field of Gologanu et al. (1993) was used to derive the micro-inertia contribution which appears to be scaled by the mass matrix density and two internal length parameters (semi-axis of the spheroidal void). Indeed, this type of geometry is characterized by two length parameters (or equivalently by the length of one of the semi-axes and the void aspect ratio) whereas for spherical voids, the geometry is solely defined by the radius. Cylindrical voids are also defined by two length parameters, the radius and the length of the void which are expected to play a role in the dynamic response. This has been revealed in the work of Molinari et al. (2015), focusing on the coalescence stage in presence of micro-inertia. In this study, the representative volume element consists of a cylindrical unit cell embedding a cylindrical void at its central part, representing the void ligament, with two rigid domains placed above and below the void. The kinematics considered in this study correspond to that of uniaxial strain. The case of a porous material with cylindrical void under dynamic loading has also been considered by Leblond and Roy (2000). The authors have proposed a model accounting for micro-inertia and viscous rate dependence of the matrix material (power law) considering spherical and cylindrical cavities. For the latter cell geometry, the velocity field of Gurson (1977) was used to derive the dynamic response under generalized plain strain conditions. Upon integration of the radial equation of motion, the macroscopic stress components were shown to be the sum of a static term and a dynamic one scaled by the mass matrix density and the void radius. Most importantly, the component of the acceleration field in the axial direction was neglected, so that the axial stress remains unaffected by the length of the cylinder. Therefore, the modeling cannot restitute the influence of the second internal length which is the void length.

The aim here is to consider a cylindrical shell, representative of porous media like thick wall honeycombs, submitted to dynamic loading and to reveal the main influence of micro-inertia effects through the radius and the length of the void. The theory is developed for general homogeneous kinematic boundary conditions, keeping, however, that the velocity field adopted here supposes that the section of the void keeps a circular shape. Results shown in the paper are analytically derived by combining the dynamic homogenization procedure of Molinari and Mercier (2001) with the approximate velocity inherited from Gurson (1977) for cylindrical shells.

The paper is organized as follows. The main steps of the dynamic homogenization procedure for porous viscoplastic materials are recalled in Sect. 2 where the trial velocity for the adopted cylindrical unit cell is also presented. The dynamic stress tensor, which includes micro-inertia effects, is derived in Sect. 3 with detailed calculations provided in Appendix A. In Sect. 4, a series of results obtained from the analytical modeling is presented, assuming that the matrix material is perfectly plastic (no strain hardening and no rate dependence of the matrix material) so that rate effects are only inherited from micro-inertia. We restrict the attention to axisymmetric loadings and present the results. The micro-inertia effects are exemplified considering various loading configurations. All results obtained in this paper are verified against finite element calculations and some validation cases are provided in Appendix B.

2 Modeling

2.1 Dynamic homogenization

The dynamic homogenization procedure proposed in Molinari and Mercier (2001) for porous viscoplastic materials is summarized in this section. A Representative Volume Element (RVE) of porous material is subjected to high strain rate loading. The matrix material is assumed incompressible and rigid-viscoplastic (elastic deformation neglected). The viscoplastic response of the matrix is defined from a stress potential:

$$\begin{aligned} \varvec{\sigma }=\frac{\partial \varPhi ({\varvec{x}},\mathbf{d})}{\partial \mathbf{d}}\, \end{aligned}$$
(1)

where \(\varvec{\sigma }\) is the local Cauchy stress tensor, taken at a material particle of the RVE, and \(\varvec{x}\) the position vector expressed in a rectangular frame with origin at the center of mass of the RVE. \(\mathbf{d}=\dfrac{1}{2}\left( {\mathbf{grad}}\,{\mathbf{v}}+\,^\text {t}{\mathbf{grad}}\,{\mathbf{v}}\right) \) is the local strain rate tensor, with \(\mathbf{v}\) the velocity vector of a particle inside the RVE, \(\mathbf{grad}\) and \(^\text {t}(\cdot )\) standing for the gradient operator and the transpose of \((\cdot )\) respectively.

Homogeneous boundary conditions of the following type are assumed:

$$\begin{aligned} {\mathbf{v}}=\mathbf{D}\cdot {\varvec{x}} \quad \text {on} \quad \partial V\,, \end{aligned}$$
(2)

where “\(\cdot \)” represents the simple contracted product and \(\partial V\) the boundary of the RVE. \(\mathbf{D}\) is supposed to be uniform on \(\partial V\) and represents the macroscopic strain rate tensor.

Let us denote \(\varvec{\varSigma }\) the macroscopic stress tensor prevailing at the RVE scale when kinematic boundary conditions (2) are applied. From the principle of virtual work:

$$\begin{aligned} \varvec{\varSigma }:\mathbf{D}={\langle \varvec{\sigma }:\mathbf{d}\rangle }+\frac{1}{2}\left\langle \rho \frac{\text {d}{{|\mathbf{v}|}^2}}{\text {d}{t}}\right\rangle \,, \end{aligned}$$
(3)

where “ : ” stands as the double contracted product. Molinari and Mercier (2001) have shown that \(\varvec{\varSigma }\) and \(\mathbf{D}\) are work conjugated with the proposed definition:

$$\begin{aligned} \mathbf{D}=\langle \mathbf{d}\rangle ,\quad {\varvec{\varSigma }}=\langle {\varvec{\sigma }}\rangle +\langle \rho {\varvec{\gamma }}\otimes {\varvec{x}}\rangle \end{aligned}$$
(4)

where \(\rho \) is the mass matrix density (assumed incompressible), \({\varvec{\gamma }}=\dfrac{\text {d}{\mathbf{v}}}{\text {d} t}\) is the acceleration of a particle in the RVE and \(\otimes \) stands for the tensor product. The symbol \(\langle \bullet \rangle =\frac{1}{|V|}\int _{V} \bullet \ \text {d}V\) represents volume averaging over the RVE, |V| being the volume of the domain.

It should be noted that the local (microscopic) velocity field, at a position \(\varvec{x}\) inside the RVE, cannot be precisely known, except for some particular cases. As a matter of fact, it is generally not possible to obtain, for general loading conditions, the exact solution of the local (microscopic) stress field \(\varvec{\sigma }\), and consequently the macrostress defined by Eq. (4) cannot be reached exactly as well. An alternative was then proposed by Molinari and Mercier (2001) to derive an approximate solution from the use of a variational approach and by considering isochoric virtual velocity fields of the following form:

$$\begin{aligned} \bar{\mathbf{v}}=\bar{\mathbf{v}}({\varvec{x}},\mathbf{D})\, \end{aligned}$$
(5)

satisfying the boundary condition Eq. (2). By applying the principle of virtual power to an increment \(\delta \mathbf{D}\) of the macroscopic strain rate, the following approximation (\(\bar{\mathbf{v}}\) is not the exact solution) is found by Molinari and Mercier (2001):

$$\begin{aligned} {\varvec{\varSigma }}:\delta \mathbf{D}{\simeq }\langle {{\bar{\varvec{\sigma }}}}:\delta \bar{\mathbf{d}}\rangle +\langle \rho {\bar{\varvec{\gamma }}}\cdot \delta \bar{\mathbf{v}}\rangle \end{aligned}$$
(6)

where the acceleration field \(\bar{\varvec{\gamma }}\), the plastic strain rate tensor \(\bar{\mathbf{d}}\), and the Cauchy stress tensor \({\bar{\varvec{\sigma }}}\) are all associated with the virtual velocity field \(\bar{\mathbf{v}}\) given by Eq. (5):

$$\begin{aligned} \bar{\varvec{\gamma }}= & {} \frac{{\text {d}}{\bar{\mathbf{v}}({\varvec{x}},\mathbf{D})}}{{\text {d}}t},\nonumber \\ {\bar{\mathbf{d}}}= & {} \bar{\mathbf{d}}({\varvec{x}},\mathbf{D}),\ \bar{\varvec{\sigma }}({\varvec{x}},\mathbf{D}){\mathop {=}\limits ^{ {\text {Eq.}~(1)}}}\frac{\partial \varPhi ({\varvec{x}},\bar{\mathbf{d}}({\varvec{x}},\mathbf{D}))}{\partial \bar{\mathbf{d}}({\varvec{x}},\mathbf{D})}\,, \end{aligned}$$
(7)

From Eqs. (5, 7), one gets in addition:

$$\begin{aligned} \delta \bar{\mathbf{v}}= & {} \frac{\partial \bar{\mathbf{v}}}{\partial \mathbf{D}}:\delta \mathbf{D}=\mathbf{K}:\delta \mathbf{D}, \nonumber \\ \langle \bar{\varvec{\sigma }}:\delta \bar{\mathbf{d}}\rangle= & {} \frac{\partial \langle {\hat{\varPhi }}({\varvec{x}},\mathbf{D})\rangle }{\partial \mathbf{D}}:\delta \mathbf{D}\,, \end{aligned}$$
(8)

where \(\mathbf{K}=\frac{\partial \bar{\mathbf{v}}}{\partial \mathbf{D}}\) is a third order tensor and \({\hat{\varPhi }}({\varvec{x}},\mathbf{D})\ \ = \varPhi ({\varvec{x}},\bar{\mathbf{d}}({\varvec{x}},\mathbf{D}))\). After substitution of Eq. (8) into Eq. (6), it follows that:

$$\begin{aligned} {\varvec{\varSigma }}:\delta \mathbf{D}=\frac{\partial \langle {\hat{\varPhi }}\rangle }{\partial \mathbf{D}}:\delta \mathbf{D}+\langle \rho {\bar{\varvec{\gamma }}}\cdot \mathbf{K}\rangle :\delta \mathbf{D} \end{aligned}$$
(9)

where the dependencies of quantities with respect to \({\varvec{x}}\) and \(\mathbf{D}\) have been omitted for ease of reading. This last relationship is valid for any virtual increment \(\delta \mathbf{D}\) so that the symmetric part of the macroscopic stress, in presence of micro-inertia, is found to be the sum of two contributions:

$$\begin{aligned} \varvec{\varSigma }^\text {s}={\varvec{\varSigma }}^\text {static}+({\varvec{\varSigma }}^\text {dyn})^{\text {s}} \end{aligned}$$
(10)

where \({\varvec{\varSigma }}^\text {static}\) represents the micro-inertia independent term given by:

$$\begin{aligned} {\varvec{\varSigma }}^\text {static}=\frac{\partial \langle {\hat{\varPhi }}\rangle }{\partial \mathbf{D}} \end{aligned}$$
(11)

and \(({\varvec{\varSigma }}^\text {dyn})^\text {s}\) is the inertial dependent term, expressed as:

$$\begin{aligned} ({\varvec{\varSigma }}^\text {dyn})^\text {s}=\langle \rho {\bar{\varvec{\gamma }}}\cdot \mathbf{K}\rangle ^\text {s}\,. \end{aligned}$$
(12)

\((\cdot )^\text {s}\) represents the symmetric part of the second order tensor \((\cdot )\). Note that at this stage, only the symmetric part of \({\varvec{\varSigma }}^\text {dyn}\) is obtained. By considering more general kinematic boundary condition of the form \(\bar{\mathbf{v}}={\mathbf{L}}\cdot {\varvec{x}}\) on \(\partial V\) instead of Eq. (2), one can obtain the antisymmetric part of \({\varvec{\varSigma }}^\text {dyn}\). This is addressed in Appendix A for the case of cylindrical voids.

Note also that \({\varvec{\varSigma }}^\text {static}\) represents the inertia independent response and can be evaluated from any viscoplastic potential or flow surface developed for porous material. It may thus include viscous rate dependency. Finally, from Eq. (5), the trial velocity field used in the dynamic problem is originated from the corresponding static problem. From this comment, the velocity field proposed by Gurson (1977) for hollow cylinders is used in our approach to derive the static and dynamic stresses.

Fig. 1
figure 1

Schematic representation of the porous material. A cylindrical unit cell (length 2l, void radius a, external radius b) is taken as the representative volume element. A cartesian coordinate system is adopted for the derivation of the model with \(-l<x_3<l\)

Full size image

2.2 Geometry of the RVE and formulation of the velocity field

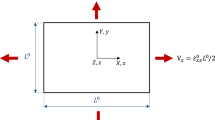
The representative volume element (RVE) of the porous material corresponds to a hollow cylinder (circular cross section) of current internal radius a, external radius b, length 2l, see Fig. 1. The current porosity is defined as:

$$\begin{aligned} f=\frac{a^2}{b^2}\,. \end{aligned}$$
(13)

The matrix surrounding the cylindrical cavity is assumed incompressible and elasticity is neglected. The evolution law for the porosity is classically given by:

$$\begin{aligned} \dot{f}=3\left( 1-f\right) D_\text {m} \end{aligned}$$
(14)

where \(D_\text {m}=\frac{1}{3}\text {tr}(\mathbf{D})\) is the spherical part of the macroscopic strain rate tensor, \(\text {tr}(\bullet )\) representing the trace of the second order tensor \(\bullet \).

An approximate velocity, denoted by \(\mathbf{v}\) (the upper symbol “−” used in the previous section is intentionally omitted), is considered, satisfying the kinematic condition (2) at the boundary \(\partial V\) of the RVE and the incompressibility condition.

The cylinder is loaded under general strain rate condition with \(\mathbf{D}\) written in the orthonormal frame basis (\(\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3\)) as:

$$\begin{aligned} \mathbf{D}= \begin{bmatrix}D_{11} &{} D_{12} &{} D_{13} \\ D_{12} &{} D_{22} &{} D_{23} \\ D_{13} &{} D_{23} &{} D_{33} \end{bmatrix}\,. \end{aligned}$$
(15)

Based on the analysis of Gurson (1977) and assuming uniform shear components of the strain rate tensor within the matrix material (see also Torki et al. 2015, 2017), the admissible velocity field of the following form is adopted:

$$\begin{aligned} {\mathbf{v}}=\left( {\mathbf{D}}^{\text {d}}+{\mathbf{D}}^{\text {s}}+{\mathbf{D}}^{\text {u}}\right) \cdot {\varvec{x}} \end{aligned}$$
(16)

where \({\mathbf{D}}^{\text {s}}\) and \({\mathbf{D}}^{\text {u}}\) are traceless tensors (inducing no dilatation); \({\mathbf{D}}^{\text {s}}\) represents the change of shape of the void (including evolution of the cross section) whereas \({\mathbf{D}}^{\text {u}}\) is describing the stretching or elongation of the void preserving the shape of the cross section (assumed circular) at constant porosity. Both are uniform and only depending on the macroscopic strain rate tensor components:

$$\begin{aligned} {\mathbf{D}^{\text {s}}}= \begin{bmatrix}\frac{D_{11}-D_{22}}{2} &{} D_{12} &{} D_{13} \\ D_{12} &{} \frac{D_{22}-D_{11}}{2} &{} D_{23} \\ D_{13} &{} D_{23} &{} 0 \end{bmatrix} \,, \end{aligned}$$
(17)

and

$$\begin{aligned} {\mathbf{D}^{\text {u}}}= \begin{bmatrix}\frac{-D_{33}}{2} &{} 0 &{} 0 \\ 0 &{} \frac{-D_{33}}{2} &{} 0 \\ 0 &{} 0 &{} D_{33} \end{bmatrix} \,. \end{aligned}$$
(18)

The last contribution to the approximate velocity field of Eq. (16) is expressed as:

$$\begin{aligned} {\mathbf{D}^{\text {d}}}= \begin{bmatrix}\frac{\text {tr}(\mathbf{D})}{2} \left( \frac{b}{r}\right) ^2 &{} 0 &{} 0 \\ 0 &{} \frac{\text {tr}(\mathbf{D})}{2} \left( \frac{b}{r}\right) ^2&{} 0 \\ 0 &{} 0 &{} 0\end{bmatrix} \, \end{aligned}$$
(19)

and is inducing porosity evolution, see Eq. (14). Note that the trial velocity field given by Eqs. (16–19) supposes that the shape of voids remains cylindrical with a circular cross section. Therefore, the tensor \({\mathbf{D}}^{\text {s}}\), related to the shape change, has to be overwhelmed by the other contributions in our applications. Let us remark that various trial velocity fields found in the literature for the dynamic response of porous materials fall within the formulation adopted here. For instance, the velocity field used in Leblond and Roy (2000) is retrieved for \(\mathbf{D}^\text {s}=\mathbf{0}\). This is also the case for the velocity field adopted in Molinari et al. (2015) for the description of the coalescence stage.

From Eqs. (16–19), the trial velocity can also be put in the following condensed form:

$$\begin{aligned} {\mathbf{v}}={\hat{\mathbf{D}}}\cdot {\varvec{x}}+ B {\tilde{\varvec{x}}} \end{aligned}$$
(20)

where \(B=\frac{\text {tr}(\mathbf{D})}{2} \left( \frac{b}{r}\right) ^2-\frac{{D}_{33}}{2}\), \({\hat{\mathbf{D}}}\) is a strain rate tensor expressed in the frame basis (\(\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3\)) as:

$$\begin{aligned} {\hat{\mathbf{D}}}= \begin{bmatrix}\frac{D_{11}-D_{22}}{2} &{} D_{12} &{} D_{13} \\ D_{12} &{} \frac{D_{22}-D_{11}}{2} &{} D_{23} \\ D_{13} &{} D_{23} &{} D_{33} \end{bmatrix} \,, \end{aligned}$$
(21)

and \({\tilde{\varvec{x}}}=x_1{\mathbf{e}_1}+x_2{\mathbf{e}_2}\) represents the projection in the plane \((\mathbf{e}_1,\mathbf{e}_2)\), along \(\mathbf{e}_3\), of the position vector \({\varvec{x}}\). Eq. (20) will be used to calculate the components of the dynamic stress tensor \({\varvec{\varSigma }}^\text {dyn}\), see Appendix A for more details.

3 Macroscopic governing equations in presence of micro-inertia

3.1 Formulation of the micro-inertia dependent term \({\varvec{\varSigma }}^\text {dyn}\)

To evaluate \({\varvec{\varSigma }}^\text {dyn}\), we determine explicitly the integral term \(1/|V|\int _V \rho {{\varvec{\gamma }}}\cdot \delta {\mathbf{v}}\) with use of the boundary condition \({\mathbf{v}}={\mathbf{L}}\cdot {\varvec{x}}\) (where L represents the macroscopic velocity gradient) instead of Eq. (2). Within this context, the antisymmetric part of the dynamic stress tensor is also defined. From expressions provided in Appendix A, the stress tensor is obtained:

$$\begin{aligned} \varvec{\varSigma }={\varvec{\varSigma }}^\text {static}+{\varvec{\varSigma }}^\text {dyn}\, \end{aligned}$$
(22)

In the results section, we restrict our attention to boundary condition Eq. (2). Therefore, the components of the dynamic stress \({\varvec{\varSigma }}^\text {dyn}\) are:

$$\begin{aligned} {\varSigma }^\text {dyn}_{11}= & {} \frac{\rho a^2}{4}\Bigg [\left( f^{-1}-f\right) \left( {\dot{\hat{D}}_{11}}+{\hat{C}_{11}}-{D}_{33}{\hat{D}_{11}}\right) \nonumber \\&-\frac{9}{2}\left( f^{-2}-f^{-1}\right) {D_\text {m}}^2+3f^{-1}\nonumber \\&\ln \left( \frac{1}{f}\right) \left( \dot{D_\text {m}}+3{D_\text {m}}^2-D_\text {m} D_{33}\right) \nonumber \\&+\left( f^{-1}-1\right) \left( \frac{{D_{33}}^2}{2}-\dot{D_{33}}+{C}_{11}\nonumber \right. \\&\left. +{C}_{22}+6{D}_\text {m}{\hat{D}_{11}}\right) \Bigg ] \end{aligned}$$
(23)
$$\begin{aligned} {\varSigma }^\text {dyn}_{22}= & {} \frac{\rho a^2}{4}\Bigg [\left( f^{-1}-f\right) \left( {\dot{\hat{D}}_{22}}+{\hat{C}_{22}}-{D}_{33}{\hat{D}_{22}}\right) \nonumber \\&-\frac{9}{2}\left( f^{-2}-f^{-1}\right) {D_\text {m}}^2+3f^{-1}\nonumber \\&\ln \left( \frac{1}{f}\right) \left( \dot{D_\text {m}}+3{D_\text {m}}^2-D_\text {m} D_{33}\right) \nonumber \\&+\left( f^{-1}-1\right) \left( \frac{{D_{33}}^2}{2}-\dot{D_{33}}+{C}_{11}\nonumber \right. \\&\left. +{C}_{22}+6{D}_\text {m}{\hat{D}_{22}}\right) \Bigg ] \end{aligned}$$
(24)
$$\begin{aligned} {\varSigma }^\text {dyn}_{33}= & {} \frac{\rho a^2}{4}\Bigg [\left( f^{-1}-f\right) \left( \frac{\dot{D}_{33}}{2}-\frac{D_{33}^2}{4}-\frac{C_{11}+C_{22}}{2}\right) \nonumber \\&-\frac{9}{2}\left( f^{-2}-f^{-1}\right) D_\text {m}^2\nonumber \\&+\left( f^{-1}-1\right) \left( C_{11}+C_{22}+3D_\text {m}D_{33}\nonumber \right. \\&\left. +\frac{D_{33}^2}{2}-9D_\text {m}^2-\dot{D}_{33}-3\dot{D}_\text {m}\right) \nonumber \\&+3f^{-1}\ln \left( \frac{1}{f}\right) \left( \dot{D}_\text {m}+\frac{9}{2}D_\text {m}^2-D_\text {m} D_{33}\right) \Bigg ]\nonumber \\&+\frac{\rho l^2}{3}\left( 1-f\right) \left( \dot{D}_{33}+C_{33}\right) \end{aligned}$$
(25)
$$\begin{aligned} {\varSigma }^\text {dyn}_{12}= & {} {\varSigma }^\text {dyn}_{21}= \frac{\rho a^2}{4}\Bigg [\left( f^{-1}-f\right) ({\dot{{D}}_{12}}+{C}_{12}-{D}_{33}{{D}_{12}})\nonumber \\&+6\left( f^{-1}-1\right) {D}_\text {m}{{D}_{12}}\Bigg ] \end{aligned}$$
(26)
$$\begin{aligned} \varSigma ^\text {dyn}_{13}= & {} \frac{\rho l^2}{3}\left[ \left( 1-f\right) \Bigg (\dot{{D}}_{13}+C_{13}-\frac{D_{33}}{2}{{D}}_{13}\right) \nonumber \\&+\frac{3}{2}\ln \left( \frac{1}{f}\right) D_\text {m}{{D}_{13}}\Bigg ] \end{aligned}$$
(27)
$$\begin{aligned} \varSigma ^\text {dyn}_{23}= & {} \frac{\rho l^2}{3}\Bigg [\left( 1-f\right) \left( \dot{{D}}_{23}+C_{23}-\frac{D_{33}}{2}{{D}}_{23}\right) \nonumber \\&+\frac{3}{2}\ln \left( \frac{1}{f}\right) D_\text {m}{{D}_{23}}\Bigg ] \end{aligned}$$
(28)
$$\begin{aligned} \varSigma ^\text {dyn}_{31}= & {} \frac{\rho a^2}{4}\Bigg [\left( f^{-1}-f\right) \left( {\dot{{D}}_{13}}+{C}_{13}-\frac{{D}_{33}}{2}{{D}_{13}}\right) \nonumber \\&+3\left( f^{-1}-1\right) {D}_\text {m}{{D}_{13}}\Bigg ] \end{aligned}$$
(29)
$$\begin{aligned} \varSigma ^\text {dyn}_{32}= & {} \frac{\rho a^2}{4}\Bigg [\left( f^{-1}-f\right) \left( {\dot{{D}}_{23}}+{C}_{23}-\frac{{D}_{33}}{2}{{D}_{23}}\right) \nonumber \\&+3\left( f^{-1}-1\right) {D}_\text {m}{{D}_{23}}\Bigg ] \end{aligned}$$
(30)

where \({\mathbf{C}}=\hat{\mathbf{D}}\cdot \hat{\mathbf{D}}\) and \({\hat{\mathbf{C}}}\) is defined as in Eq. (21) replacing \(\mathbf{D}\) with \(\mathbf{C}\).

The dynamic stress tensor reveals particular aspects that are further commented upon. The influence of quadratic and time derivative terms involving strain rate tensor components are revealed here for the RVE consisting of a hollow cylinder. This illustrates the specific rate dependencies brought by the micro-inertia to the overall response of porous materials. This has already been observed for spherical voids (Molinari and Mercier 2001) and spheroidal voids (Sartori et al. 2015).

As revealed for other geometries, the dynamic response is closely related to the cell size. Here, for cylindrical voids, it appears from Eqs. (23–30) that the dynamic stress tensor is scaled, by the mass matrix density \(\rho \) and by the square of two characteristic lengths of the unit cell: the void radius a and half the void length l.

The macroscopic stress tensor \(\varvec{\varSigma }\) is the sum of the static and the dynamic contributions, see Eq. (22), with \({\varvec{\varSigma }}^\text {static}\) being a symmetric tensor describing the static response of the porous material. As a consequence, from Eqs. (27–30), the macroscopic stress tensor \(\varvec{\varSigma }\) is shown to be nonsymmetric. This is similar to the results obtained by Molinari and Mercier (2001) for porous materials containing spherical voids, where the loss of symmetry was only due to spin effects. Here, however, even when spin effects vanish (i.e. \({\varvec{\varOmega }}=\mathbf{0}\) is imposed), owing to the anisotropy of the cell geometry, the macroscopic stress tensor may remain non symmetric.

3.2 Quasistatic stress tensor \({\varvec{\varSigma }}^\text {static}\)

The quasistatic stress depicts the response of porous materials under static loading, when micro-inertia effects are neglected. The quasistatic stress tensor \({\varvec{\varSigma }}^\text {static}\) is derived here from the yield function proposed by Gurson (1977) expressed for cylindrical voids as:

$$\begin{aligned} \begin{aligned} \varPhi _\text {G}({\varvec{\varSigma }}^\text {static},{\tilde{\sigma }},f)&=C_\text {eqv}\left( \frac{\varSigma ^\text {static}_\text {eq}}{{\tilde{\sigma }}}\right) ^2\\&\quad +2f\cosh \left( \frac{\sqrt{3}}{2}\frac{\varSigma ^\text {static}_{\gamma \gamma }}{{\tilde{\sigma }}}\right) \\&\quad -(1+f^2)=0 \end{aligned} \end{aligned}$$
(31)

where \(C_\text {eqv}\) is a function of f whose expression depends on the loading state and boundary conditions, see Gurson (1977) for details. \(\varSigma ^\text {static}_{\gamma \gamma }\) is the macroscopic transverse stress defined by:

$$\begin{aligned} \varSigma ^\text {static}_{\gamma \gamma }=\varSigma _{11}^\text {static}+\varSigma _{22}^\text {static} \end{aligned}$$
(32)

and \(\varSigma ^\text {static}_\text {eq}\) is the macroscopic equivalent stress expressed as:

$$\begin{aligned} \varSigma ^\text {static}_\text {eq}=\sqrt{\frac{3}{2}{{\varvec{\varSigma }}^\text {static}}':{{\varvec{\varSigma }}^\text {static}}'}\,, \end{aligned}$$
(33)

\((\bullet )'\) being the deviatoric part of the second order tensor \((\bullet )\).

In Eq. (31), \({\tilde{\sigma }}\) is a measure of the effective stress in the matrix. The quasistatic stress \({\varvec{\varSigma }}^\text {static}\) and the macroscopic plastic strain rate \(\mathbf{D}\) are related by the flow law:

$$\begin{aligned} \mathbf{D}={\dot{\kappa }}\frac{\partial \varPhi ({\varvec{\varSigma }}^\text {static},{\tilde{\sigma }},f)}{\partial {\varvec{\varSigma }}^\text {static}}\,, \end{aligned}$$
(34)

where \({\dot{\kappa }}\) is the plastic multiplier subjected to the Kuhn-Tucker complementary conditions: \(\varPhi \le 0\), \({\dot{\kappa }}\ge 0\), \(\varPhi {\dot{\kappa }}=0\) (Simo and Hughes 1998) and is obtained from the equivalence between the plastic work rate of the porous medium and the matrix dissipation rate.

4 Results—axisymmetric loading

In this section, we restrict our attention to axisymmetric loading conditions that have been selected to reveal important effects brought by the micro-inertia contribution. As a consequence, \(C_\text {eqv}=1\) in Eq. (31), as reported in Gurson (1977). In addition, the matrix material is assumed rigid and perfectly plastic: \({\tilde{\sigma }}=\sigma _0\) with \(\sigma _0\) denoting the matrix yield stress. Within this context, the static stress is related to the strain rate tensor by explicit relationships, Gurson (1977); Leblond et al. (1994); Sartori et al. (2019).

All the analytical results shown and discussed in this paper have been verified against finite element calculations conducted with Abaqus/Explicit. Appendix B provides details on the various numerical models developed for the comparative study accompanied by some validation cases. One should note that the finite element results will not be specifically mentioned in the main text, since analytical and numerical results were shown to be coinciding.

The analytical modeling proposed in this paper was developed for general loading conditions. However, keep in mind that the velocity field used to derive the dynamic and static stresses assume that the cross section of voids remain circular, so that the contribution \(\mathbf{D}^\text {s}\) has to be of negligible magnitude, see Eqs. (16–19).

For application purposes, we restrict the attention to axisymmetric loading paths without shear contributions. Thus \(\mathbf{D}^\text {s}\) vanishes. Consequently, \(D_{22}=D_{11}\) and the macroscopic stress tensor \(\varvec{\varSigma }\) satisfies \(\varSigma _{22}=\varSigma _{11}\), \(\varSigma _{ij}=0\) for all \(i\ne j\). The same applies for the static and dynamic contributions, \({\varvec{\varSigma }}^\text {static}\) and \({\varvec{\varSigma }}^\text {dyn}\) respectively.

The dynamic stress tensor for axisymmetric loading still reveals the influence of both \(a^2\) and \(l^2\). Its explicit form, given in Eqs. (23–25) or in Appendix A, can be written in the following condensed way:

$$\begin{aligned} {\varSigma }^\text {dyn}_{11}= & {} {\varSigma }^\text {dyn}_{22}=\rho a^2F,\nonumber \\ {\varSigma }^\text {dyn}_{33}= & {} \rho a^2G+\frac{\rho l^2}{3}\left( 1-f\right) \left( \dot{D}_{33}+D_{33}^2\right) \end{aligned}$$
(35)

where functions F and G, see Eqs. (64–65), depend on the porosity f, quadratic terms in \(D_{11}\) and \(D_{33}\), and linear terms in time derivatives \(\dot{D}_{11}\) and \(\dot{D}_{33}\).

Of particular interest is that it appears from Eq. (35) that the influence of l vanishes when one of the following two conditions is fulfilled:

$$\begin{aligned} l=0 \end{aligned}$$
(36)

or

$$\begin{aligned} \dot{D}_{33}+D_{33}^2=0\, \end{aligned}$$
(37)

which, upon time integration, leads to:

$$\begin{aligned} D_{33}=\frac{D_{33}^0}{1+D_{33}^0t} \end{aligned}$$
(38)

with \(D_{33}^0=D_{33}(t=0)\). Note that since \(v_3=D_{33}x_3\) (see Eqs. 20–21), Eq. (37) also corresponds to a nil acceleration in the longitudinal direction, \(\gamma _3(x_3,t)=0\). It is therefore interesting to notice that prescribing a constant axial velocity \(v_{3}^{0}\) at \(x_3=l\) (a similar condition but of opposite sign is found for the bottom of the cylinder) imposes the fact that Eq. (37) is satisfied and the length of the cylinder is no longer present in Eq. (35). Note that the particular case when \(D_{33}=0\) fulfills the condition also.

In the following the RVE is initially at rest and axisymmetric loading is prescribed by imposing in the plane, the conditions:

$$\begin{aligned} \varSigma _{22}= & {} \varSigma _{11}=\dot{p} t\, , \nonumber \\ \dot{p}= & {} \text {constant}\ge 0\text { (positive in tension)} \end{aligned}$$
(39)

where \(\dot{p}\) denotes the stress rate. Various types of conditions (in stress or in velocity) imposed in the axial direction (\(x_3=\pm l\)) will also be considered. To fix ideas, we will consider the dynamic void expansion for stress rates up to 250 MPa/ns and/or imposed strain rates up to 10\(^6\) s\(^{-1}\). These high levels of strain and stress rates typically fall within ranges of values encountered in plate impact experiments, spall fracture (e.g. Roy 2003) and dynamic crack propagation (e.g. Freund and Hutchinson 1986).

4.1 Plane strain (parametric study)

We first focus on the dynamic expansion of porous materials under plane strain configuration with \(\varSigma _{11}=\varSigma _{22}=\dot{p} t\). In addition we set: \(D_{33}=0\) so the length of the cylinder is fixed. Under axisymmetric plane strain loading conditions, as mentioned by Gurson (1977), the static stress is spherical with the mean static stress under void expansion (i.e. when \(D_\text {m}>0\)) expressed as:

$$\begin{aligned} \varSigma _\text {m}=\varSigma ^\text {static}_\text {m}=\frac{\sigma _0}{\sqrt{3}}\ln \left( \frac{1}{f}\right) \end{aligned}$$
(40)

As a consequence, when micro-inertia is neglected, plane strain with axisymmetric loading condition is akin to the hydrostatic loading path. This situation is no more valid when micro-inertia effects are included since \(\varSigma _{33}^\text {dyn}\) is different from \(\varSigma _{22}^\text {dyn}=\varSigma _{11}^\text {dyn}\), see Eqs. (64–65). Consequently, the macroscopic stress tensor is no more spherical \(\varSigma _{33}\ne \varSigma _{11}\).

A reference porous material is defined where the flow stress of the matrix material is \(\sigma _0\) = 100 MPa and the matrix mass density is representative of aluminum material, \(\rho \) = 2700 kg/m\(^3\). For the reference material, the initial void radius is \(a_0\) = 50 \(\upmu \)m, the external radius is \(b_0\) = 1500 \(\upmu \)m, the initial porosity being \(f_0=a_0^2/b_0^2\) = 0.0011, see Table 1. Recall that under plane strain configuration, the length of the cylinder does not play a role so that no specific value of \(l_0\) is needed in this section to define the material.

Table 1 Reference material parameters, representative for porous aluminum
Full size table
Fig. 2
figure 2

Evolution of the porosity f versus a time and b macroscopic stress \(\varSigma _{11}=\varSigma _{22}={\dot{p}}t\) under plane strain loading. A comparison between dynamic (micro-inertia dependent) and static (micro-inertia independent) analyses is carried out for two stress rates: \(\dot{p}\) = 10 MPa/ns and \(\dot{p}\) = 250 MPa/ns. Material parameters are provided in Table 1. For \(D_{33}\) = 0, results are independent from the void length

Full size image

Figure 2a (resp. Fig. 2b) represents the evolution of the porosity f versus time (resp. macroscopic stress \(\varSigma _{11}=\dot{p}\,t\)) for two values of the loading rate \(\dot{p}\) = 10 and 250 MPa/ns. The porosity is limited to values below 0.3 because it is assumed that fracture occurs by direct impingement when the porosity f reaches this value. The results of the dynamic analysis (micro-inertia included) and the quasistatic approach (micro-inertia disregarded) are provided in Fig. 2. The stabilizing effect of micro-inertia is clearly highlighted, the dynamic void evolution being significantly delayed. This trend is well known from the literature for porous materials with spherical voids, (e.g. Glennie 1972; Ortiz and Molinari 1992; Tong and Ravichandran 1995; Molinari and Mercier 2001; Wu et al. 2003; Czarnota et al. 2006). Note that the static analysis, for perfectly plastic matrix material, predicts an instantaneous void expansion once the yield limit is reached. Remembering that the plane strain and hydrostatic configurations coincide for the static approach, the stress at yield from Eq. (40) is: \(\varSigma _{11}=\frac{\sigma _0}{\sqrt{3}}\ln \left( \frac{1}{f_0}\right) \). With the set of parameters of Table 1, one obtains 0.39 GPa leading to a time around 39 ns (resp. 1.57 ns) when \(\dot{p}\) = 10 MPa/ns (resp. \(\dot{p}\) =  250 MPa/ns). Note that even if the void evolution is triggered earlier when \(\dot{p}\) is larger, the micro-inertia effects are stronger. Indeed, Fig. 2b shows that the porous material sustains a much larger stress when \(\dot{p}\) = 250 MPa/ns. This is attributed to the sole effect of micro-inertia, since the matrix response is perfectly plastic (no viscosity).

Fig. 3
figure 3

Time evolution of the macroscopic stress \(\varSigma _{33}\) under plane strain loading. The macroscopic stress \(\varSigma _{11}=\varSigma _{22}=\dot{p}t\) is imposed with \(\dot{p}\) = 10 MPa/ns. Material parameters are listed in Table 1. The time to fracture (i.e. when f = 0.3 is reached) is strongly influenced by micro-inertia effects (around 1020 ns in the micro-inertia dependent calculation). Under quasistatic approach (micro-inertia being neglected), the porous material sustains very limited stress up to fracture which occurs at a time around 39 ns

Full size image

Figure 3 shows the time evolution of the macroscopic stress components \(\varSigma _{11}=\varSigma _{22}=\dot{p}t\) (prescribed) and \(\varSigma _{33}\) calculated from the theory Eq. (67) when plane strain case is adopted. From Fig. 3, it appears that the stress amplitude needed to maintain the cylinder at a constant length \(2l_0\) happens to decrease at large deformation stages even when the lateral stress is still increasing. This finding, which could not have been adequately anticipated without the proposed analytical approach, clearly highlights the peculiar role of micro-inertia in the dynamic response of porous materials containing cylindrical voids. Note that the work of Leblond and Roy (2000), developed for cylindrical voids under dynamic loading, also includes the micro-inertia effects in the overall response. However, with their approach, the authors state that the total stress tensor (sum of static and dynamic parts) is spherical under plane strain loading. Consequently, the decrease of axial stress with time, revealed by our modeling and confirmed by finite element calculations (see Fig. 16 of Appendix B), could not be replicated with the modeling of Leblond and Roy (2000).

Fig. 4
figure 4

Effects of the mass density, of the initial radius, of the initial porosity and of the flow stress level, on the porosity evolution for dynamic extension under plane strain configuration. The parameters of the reference material are listed in Table 1. The stress rate is \(\dot{p}\) =  10 MPa/ns

Full size image

A parametric study is now conducted under plane strain configuration in order to figure out the effects of micro-inertia and of material properties on the time evolution of porosity. Fig. 4 portrays the influence of various material parameters on the dynamic void evolution. Results are obtained by varying the mass density, the flow stress level, the initial void radius and the initial porosity. Recall that the micro-inertia effects are scaled partially by the mass matrix density. As a consequence, when \(\rho \) is reduced, the stabilizing effect of micro-inertia is less pronounced and the rate of porosity is increased. The case with \(\rho \) = 0.27 kg/m\(^3\) is hardly distinguishable from the static analysis conducted on the reference material. An increase of the flow stress delays the void expansion. This is due to the higher static stress carrying capacity of the porous material (see Eq. 40), and is not entirely attributed to micro-inertia effects. When the initial porosity is increased (from \(f_0\) = 0.0011 to 0.01) or the initial cavity radius is reduced (from \(a_0\) = 50 to 20 \(\upmu \)m), the void expansion is accelerated. The first configuration reflects a porous material containing more voids of initial size \(a_0\). In that case, the static stress is lower and the micro-inertia is reduced, because the void is surrounded by less matrix. The second case is representative of a porous material containing smaller voids for which the micro-inertia effects are also reduced. The results provided in Fig. 4 again confirm previous trends found in the literature for spherical (Wu et al. 2003) and spheroidal voids (Sartori et al. 2015).

4.2 Hydrostatic loading

We now consider hydrostatic loading with:

$$\begin{aligned} {{\varSigma }}_{11}=\varSigma _{22}=\varSigma _{33}=\varSigma _\text {m}=\dot{p}\,t, \quad \dot{p}>0 \end{aligned}$$
(41)

where \(\dot{p}\) coincides here with the mean stress rate \(\varSigma _\text {m}\). Note that since \({\varSigma }^\text {dyn}_{33}\ne {\varSigma }^\text {dyn}_{11}\), see Eq. (35), the dynamic stress tensor is not spherical, and consequently the same applies for the static stress tensor. By contrast with the plane strain configuration, the length now plays a role in the overall response. Its influence will be explored first, then specific attention will be directed to the case of short cylinders where \(l_0\rightarrow 0\).

Figure 5 illustrates the porosity evolution for the reference material with parameters listed in Table 1 considering various values of the initial length \(l_0\) ranging from 1 to 20,000 \(\upmu \)m, initial \(f_0\), \(\rho a_0^{2}\) and stress rate \(\dot{p}\) being fixed. It is shown that an increase in initial length \(l_0\) leads to the delay of the void evolution. This illustrates the stabilizing effect of micro-inertia modulated this time by the additional influence of the length of the cylindrical void. From Fig. 5, it is seen that the porosity evolves between two asymptotic responses. The first one is obtained when the initial length adopts a large value \(l_0\) = 20,000 \(\upmu \)m and depicts the response of elongated cylinders. Within that configuration it is observed that the porosity evolution under spherical loading (\(\varSigma _{11}=\varSigma _{22}=\varSigma _{33}=\dot{p}t\)) coincides with the results of Fig. 2a obtained under plane strain condition (\(\varSigma _{11}=\varSigma _{22}=\dot{p}t\) and \(D_{33}\) = 0). However, it has been shown in Fig. 3 that, due to micro-inertia effects, the axial stress \(\varSigma _{33}\) resulting from plane strain loading is different from \(\dot{p}t\).

The second asymptotic response, revealed with \(l_0\) = 1 \(\upmu \)m, describes the response of short cylinders (\(l_0\rightarrow 0\)) under dynamic loading. This situation can be retrieved from Eq. (36) which also implies that the dynamic stress expressed by Eq. (35) is not depending on \(l_0\). This case of short cylinders under dynamic loading is investigated now more deeply.

Fig. 5
figure 5

Effect of the initial length on the time evolution of the porosity under hydrostatic loading. The material parameters are listed in Table 1 except for \(l_0\) which is varying in the range [1:20,000] \(\upmu \)m. The stress rate is \(\dot{p}\) = 10 MPa/ns. The case where \(l_0\rightarrow \infty \) (resp. \(l_0\rightarrow \)0) depicts the response of long (resp. short) cylinders under dynamic loading

Full size image
Fig. 6
figure 6

Time evolution, under spherical loading, of the external and internal radii for \(l_0\rightarrow \)0, \(l_0\) = 810 and 1000 \(\upmu \)m. Other material parameters, displayed in Table 1, and the stress rate, \(\dot{p}\) = 10 MPa/ns, are those of Fig. 5

Full size image
Fig. 7
figure 7

a, b Time evolution, under spherical loading, of \(D_{11}\) for \(l_0\rightarrow \)0, \(l_0\) = 810 and 1000 \(\upmu \)m. Other material parameters, displayed in Table 1, and the stress rate, \(\dot{p}\) = 10 MPa/ns, are those of Fig. 6. A magnified scale, where the y-axis is reduced, is proposed in b

Full size image

From Fig. 5, we isolate the cases \(l_0\rightarrow \)0 and \(l_0\) = 1000 \(\upmu \)m which are obtained for material parameters listed in Table 1 and \(\dot{p}\) = 10 MPa/ns. Fig. 6 displays the time evolution of the external and internal radii for \(l_0\rightarrow 0\) and \(l_0\) = 1000 \(\upmu \)m. For further insight, the case where \(l_0\) = 810 \(\upmu \)m is also presented. When the initial length is large enough, e.g. \(l_0\) = 1000 \(\upmu \)m, the porosity growth is characterized by the increase of the external and internal void radii. This result is classically expected under quasistatic conditions. Interestingly, when \(l_0\rightarrow \) 0, the evolution of damage is resulting from the reduction of the external radius b, while the internal radius a is still increasing. As a consequence, \(D_{11}=\dot{b}/b\) is negative (after some time) when \(l_0\rightarrow \)0 and positive when \(l_0\) is large, as reflected by Fig. 7 providing the evolution of \(D_{11}\) with time. This observation in configuration evolution, revealed for short cylinders, is counterintuitive and brings new insights in the behavior of porous materials under dynamic loading. This effect is due to micro-inertia and cannot be observed under quasistatic conditions. For intermediate values, it is expected that the strain rate oscillates due to the change of sign of \(\dot{D}_{11}\). This is confirmed in Fig. 7b for \(l_0\) = 810 \(\upmu \)m. For this case, \(D_{11}\) is shown to first increase, then decrease, adopting negative values, and finally increase up to the final stage of the growth process. Note, from Fig. 6, that the late stage of the porosity growth for \(l_0\) = 810 \(\upmu \)m is quite similar to the case where \(l_0\) = 1000 \(\upmu \)m.

In an attempt to identify by analytical means the critical length, denoted by \(l_0^\text {cr, approx.}\), at which the porosity evolution switches from one mechanism (increase of the external radius) to another (decrease of the external radius), an approximate analysis is proposed. Regarding the large stress amplitude developed during the process, we first assume that the static stress components are negligible when compared to the dynamic ones. Under spherical loading, this implies that \(\varSigma _{33}^\text {dyn}=\varSigma _{11}^\text {dyn}=\dot{p}t\). For the approximate analysis, we also assume that the quadratic terms in \(D_{11}\) and \(D_{33}\) are negligible and that only linear terms in \(\dot{D}_{11}\) and \(\dot{D}_{33}\) are held in Eqs. (64–65) of Appendix A. These assumptions lead to the following relationships:

$$\begin{aligned} \dot{p}t= & {} {\varSigma }^\text {dyn}_{11}={\varSigma }^\text {dyn}_{22} =\frac{\rho a^2}{4}\Bigg \{2f^{-1}\ln \left( \frac{1}{f}\right) \dot{D}_{11}\nonumber \\&+\left[ 1-f^{-1}+f^{-1}\ln \left( \frac{1}{f}\right) \right] \dot{D}_{33}\Bigg \} \end{aligned}$$
(42)
$$\begin{aligned} \dot{p}t= & {} {\varSigma }^\text {dyn}_{33}=\frac{\rho a^2}{4}\Bigg \{2\left[ 1+f^{-1}\ln \left( \frac{1}{f}\right) -f^{-1}\right] \dot{D}_{11} \nonumber \\&+\left[ f^{-1}\ln \left( \frac{1}{f}\right) -\frac{1}{2}\left( f^{-1}-1\right) \left( 3-f\right) \right] \dot{D}_{33}\Bigg \}\nonumber \\&+\frac{\rho l^2}{3}\left( 1-f\right) \dot{D}_{33} \end{aligned}$$
(43)

which give after some manipulation:

$$\begin{aligned} \left( \frac{2l^2}{3b^2}-\frac{1-f}{4}\right) \dot{D}_{33}=\dot{D}_{11} \end{aligned}$$
(44)

where relationship \(b=f^{-1/2}a\) has been used. One can substitute \(\dot{D}_{11}\) expressed by Eq. (44) into Eq. (42) to get:

$$\begin{aligned} \dot{D}_{33}=\frac{4\dot{p} t}{\rho b^2}\left[ \left( \frac{l^2}{3b^2}+\frac{1+f}{2}\right) \ln \left( \frac{1}{f}\right) +f-1\right] ^{-1} \nonumber \\ \end{aligned}$$
(45)

It can be seen that \(\dot{D}_{33}\) is strictly positive (i.e. \(D_{33}>0\)) when \(\dot{p}>\)0. Therefore Eq. (44) reveals that \(\dot{D}_{11}<0\) when \(l\rightarrow 0\). The critical length \(l_0^\text {cr, approx.}\) is evaluated from Eq. (44) with the condition \(\dot{D}_{11}\) = 0. Assuming in addition that the porosity and length have slightly evolved, one obtains:

$$\begin{aligned} l_0^\text {cr, approx.}=\sqrt{\frac{3\left( 1-f_0\right) }{8}}b_0 \end{aligned}$$
(46)

Using this last equation with \(f_0\) = 0.0011, \(b_0\) = 1500 \(\upmu \)m gives \(l_0^\text {cr, approx.}\) = 916 \(\upmu \)m which compares well with 810 \(\upmu \)m shown in Fig. 7.

Table 2 Various configurations used to compute the critical length below which \(\dot{D}_{11}<0\)
Full size table

Eq. (46) indicates that the critical length solely involves \(b_0\) and \(f_0\), while being independent from the stress rate \(\dot{p}\) and other material parameters. Various configurations have been considered serving at testing the validity of the analytical approximation. From Table 2, compiling all tested cases, one notes that the critical length \(l_0^\text {cr, approx.}\) obtained from the analytical approximation (46), predicts, relatively well, the value \(l_0^\text {cr} \) obtained from the complete theory. The analytical approximation supposes that the micro-inertia effects are strong enough so that the static stress can be neglected. As a matter of fact, when \(\dot{p}\) is increased, the micro-inertia effects are enhanced and the value of \(l_0^\text {cr, approx.} \) becomes closer to the actual value \(l_0^\text {cr} \). By contrast, when \(\sigma _0\) is increased, one notices from Table 2 that the gap between \(l_0^\text {cr}\) and \(l_0^\text {cr, approx.}\) is getting larger. When \(b_0\) is half the reference value, \(l_0^\text {cr} \) obtained from the complete theory is reduced by a factor of two, thus validating the mathematical dependence on \(b_0\) in the analytical approximation. Finally, \(l_0^\text {cr} \) is also shown to be a little sensitive to a variation in \(f_0\), as predicted by the analytical approximation (46).

4.3 Additional loading cases

In this section we complement the analysis by first considering the following boundary conditions: (i) homogeneous stress different from hydrostatic loading and (ii) imposed axial strain rate and homogeneous pressure on the lateral surface.

Stress boundary conditions of two different types are first explored, see Table 3. Case 1 corresponds to \(\varSigma _{11}=\varSigma _{22}=0\) and \(\varSigma _{33}=\dot{p} t\). Case 2 is obtained for \(\varSigma _{11}=\varSigma _{22}=\dot{p} t\), \(\varSigma _{33}=0\). The stress triaxiality, defined by \(\chi =\frac{\varSigma _\text {m}}{\varSigma _\text {eq}}\), is equal to 1/3 and 2/3 for Case 1 and Case 2, respectively. In Case 1, which corresponds to uniaxial stress loading, the void axis is aligned with the loading direction and \(D_{33}\) is naturally positive under remote extension. For Case 2, the cylinder is stretched in the radial direction (\(D_{33}<0\)). The two cases serve to complement the spherical loading addressed previously. Note that within the adopted study, the macroscopic equivalent stress is \(\dot{p}t\) for both \(\chi =1/3\) (Case 1) and 2/3 (Case 2), while vanishing under spherical loading. A fixed value of the stress rate, \(\dot{p}\) = 10 MPa/ns, is adopted in this section. The reference material parameters listed in Table 1 are first considered.

Table 3 Loading configurations and corresponding triaxialities
Full size table
Fig. 8
figure 8

Time evolution of the porosity for spherical loading and for Case 1 and Case 2 under dynamic condition, see Table 3. The stress amplitude is \(\dot{p} t\) with \(\dot{p}\) = 10 MPa/ns. The initial length is a\(l_0\) = 2000 \(\upmu \)m, b\(l_0\) = 10 \(\upmu \)m. Other material parameters are listed in Table 1

Full size image

Figure 8 shows the time evolution of the porosity for Case 1 and Case 2 when \(l_0\) = 2000 \(\upmu \)m (Fig. 8a) and \(l_0\) = 10 \(\upmu \)m (Fig. 8b). The response under spherical loading is also reported for comparison purpose. The initial porosity is \(f_0\) =  0.001 in all calculations. Since a static analysis provides a time to fracture for the porous material of around 10 ns for both Case 1 and Case 2, Fig. 8 clearly illustrates that micro-inertia effects are important whatever the stress triaxiality. Note the stabilizing effect of the length of the cylinder during uniaxial loading (Case 1), due to an enhancement of global inertia for the large value \(l_0\) = 2000 \(\upmu \)m, see Fig. 8a. It is seen by comparing Figs 8a, b, that the response under spherical loading is slightly sensitive to a reduction in \(l_0\), see also Fig. 5. By contrast, for the two other cases, the porosity evolution is strongly depending on \(l_0\).

Fig. 9
figure 9

Time evolution of a the void radius a and external cylindrical radius b and b the macroscopic strain rate components \(D_{11}\) and \(D_{33}\), for Case 2: \(\varSigma _{11}=\varSigma _{22}=\dot{p} t\) with \(\dot{p}\) = 10 MPa/ns, \(\varSigma _{33}=0\). The initial length is \(l_0\) = 2000 \(\upmu \)m, other material parameters being listed in Table 1

Full size image

Of particular situation, Fig. 8a and b show that the void may collapse under loading Case 2 (\(\chi =2/3\)). To have a better explanation of the situation, Fig. 9a provides the time evolution of a and b and Fig. 9b shows the time evolution of \(D_{11}\) and \(D_{33}\). In fact, when the top and bottom surfaces of the cylinder are traction-free with \(\dot{p}>\)0 imposed in the radial direction, the length of the cylinder is naturally reduced (i.e. \(D_{33}<0\)). At the same time, the external radius is always increased whereas the internal void radius is first increased before void collapse occurs at the final stage. This peculiar behavior results only from the micro-inertia effects. Indeed, in a quasistatic analysis, it can be easily shown from the Gurson model, that when \(\varSigma _{\gamma \gamma }=\varSigma _{11}+\varSigma _{22}\) is positive, then \(D_\text {m}>0\). So the porosity is increasing and no void collapse can occur within a micro-inertia independent approach. In addition, in the quasistatic approach l is decreasing while a and b are both increasing.

Fig. 10
figure 10

Influence of a the mass matrix density when \(l_0\) = 2000\(\upmu \)m and b the initial void length when \(\rho \) = 2700kg/m\(^3\) for Case 2: \(\varSigma _{11}=\varSigma _{22}=\dot{p} t\) with \(\dot{p}\) = 10 MPa/ns, \(\varSigma _{33}=0\). The other material parameters are displayed in Table 1. The response with \(l_0\) = 10,000 \(\upmu \)m provides the plane strain case of Fig. 2

Full size image

Case 2 is investigated more deeply by varying \(\rho \) (\(l_0\) =  2000 \(\upmu \)m being fixed, Fig. 10a) and \(l_0\) (\(\rho \) = 2700 kg/m\(^3\) being fixed, Fig. 10b). When \(\rho \) is reduced (smaller effects of micro-inertia), the porosity growth is triggered for earlier time and develops faster. Note that micro-inertia effects are always included in the complete theory and that void collapse occurs even for low values of \(\rho \). The static response would be obtained with a very low value of \(\rho \) for which, as previously stated, one would observe an instantaneous growth without collapse (at \(t\simeq \)10ns).

The effect of \(l_0\) portrayed in Fig. 10b confirms the important role of the axial length of the cylinder on the dynamic response. As \(l_0\) is reduced, the collapse process is triggered earlier. Remind that the micro-inertia stress is the sum of two terms, the first being scaled by \(\rho a^2\), the second by \(\rho l^2\). Thus, when \(l_0 \rightarrow 0\) micro-inertia is solely dependent upon the void radius. Finally, one notes from Fig. 10b that the response obtained with a large value of \(l_0\), e.g. \(l_0\) = 10,000 \(\upmu \)m, coincides with the plane strain case of Fig. 2, in terms of porosity evolution.

Fig. 11
figure 11

Influence of a the mass matrix density when \(l_0\) = 2000 \(\upmu \)m and b the initial void length when \(\rho \) = 2700 kg/m\(^3\) on the dynamic damage evolution for loading Case 1 (uniaxial stress). The other material parameters are displayed in Table 1. The evolution of the axial stress is given by \(\varSigma _{33}=\dot{p} t\) with \(\dot{p}\) = 10 MPa/ns

Full size image
Fig. 12
figure 12

Time evolution of a the void radius a and external cylindrical radius b and b the macroscopic strain rate components \(D_{11}\) and \(D_{33}\) for loading Case 1 (uniaxial stress with \(\varSigma _{33}=\dot{p} t\), \(\dot{p}\) = 10 MPa/ns). The initial length is \(l_0\) = 2000 \(\upmu \)m, the mass matrix density is \(\rho \) = 270 kg/m\(^3\), other material parameters being listed in Table 1

Full size image

The uniaxial stress loading (Case 1) is next explored by varying the mass matrix density (with fixed \(l_0 =\) 2000 \(\upmu \)m in Fig. 11a) and the initial length of the cylinder (\(\rho \) = 2700 kg/m\(^3\) being fixed in Fig.11b). Again, when \(l_0\) is fixed and \(\rho \) is reduced, the micro-inertia effects are lowered down, and the porosity growth occurs earlier. But, most interestingly, when \(\rho \) is lower than 270 kg/m\(^3\), the critical porosity \(f_c\) = 0.3 (for which fracture is assumed to occur) is not reached during the dynamic process. Instead of continuously increasing up to the ultimate fracture at \(f=f_c\), the porosity is reduced and tends to a stabilized value. This plateau is characterized by the collective decrease of a and b, f being constant. Fig. 12a illustrates the evolution of the internal and external cell radii while Fig. 12b presents the time evolution of \(D_{11}\) and \(D_{33}\). Note from the last figure, that since \(\dot{f}\simeq 0\) at late stage of the process, \(D_{11}\) is close to \(-D_{33}/2\).

Increasing \(l_0\) with fixed \(\rho \) also favors the occurrence of a plateau. Indeed, from Fig. 11b obtained with \(\rho \) = 2700 kg/m\(^3\), it appears that when \(l_0\) = 5000 \(\upmu \)m, the porosity is frozen after some time (\(t>8000\) ns) while the cell internal and external radii are still decreasing. When \(l_0\) is reduced, the porosity growth is faster and the critical porosity is reached prior to any decrease in f. Note that a plateau could have been observed by adopting a larger critical porosity \(f_c\) for lower values of \(l_0\).

The length of the cylinder plays an important role in the dynamic response of cylindrical voids. In the last two examples, the dynamic behavior may be characterized by a saturation in the damage evolution or a collapse process. These effects are solely due to micro-inertia.

Fig. 13
figure 13

Time evolution, under imposed constant strain rate \(D_{33}\) and prescribed \(\varSigma _{11}=\varSigma _{22}=\dot{p}t\) with a\(\dot{p}\) = 10 MPa/ns, b\(\dot{p}\) = 100 MPa/ns. The initial length is \(l_0\) = 100 \(\upmu \)m, other material parameters being listed in Table 1

Full size image

We now consider the loading path where homogeneous pressure is prescribed on the lateral surface, \(\varSigma _{11}=\varSigma _{22}=\dot{p} t\), while a constant strain rate \(D_{33}\) is imposed in the longitudinal direction. In that case the current position of the top surface is given by \(l=l_0\exp (D_{33}t)\). Fig. 13 shows the evolution of the porosity for various values of \(D_{33}\) up to 10\(^6\)s\(^{-1}\) with \(\dot{p}\) = 10 MPa/ns (Fig. 13a) and \(\dot{p}\) = 100 MPa/ns (Fig. 13b). The reference material of Table 1 is adopted with \(l_0\) = 100 \(\upmu \)m. As expected, when the strain rate \(D_{33}\) increases, the porosity growth is accelerated. Most interestingly, when comparing Fig. 13a and b, one notes that when \(D_{33}\) = 10\(^6\) s\(^{-1}\) the evolution of the porosity is almost identical for the two applied pressures considered. In such situation (i.e. under intense imposed constant strain rate), the void evolution appears to be exclusively governed by \(D_{33}\) irrespective of the value of \(\dot{p}\). Naturally, when \(D_{33}\) = 0, the growth process is solely driven by the stress rate \(\dot{p}\). For intermediate values, the evolution of the porosity results from both the influences of \(\dot{p}\) and \(D_{33}\). One has to mention also that if the stress rate \(\dot{p}\) is further increased, it is expected that for the effect of the lateral stress (\(\dot{p} t\)) to be negligible, larger values of the strain rate \(D_{33}\) have to be considered.

In the last example, the in-plane macroscopic stress tensor components are still \(\varSigma _{11}=\varSigma _{22}=\dot{p}t\) while a constant velocity \(v_3=\pm v_3^0\) is prescribed at \(x_3=\pm l\). The corresponding nominal strain rate is \(D_{33}^0=v_3^0/l_0\) and the current position of the top surface is \(l=l_0(1+D_{33}^0t)\). It was demonstrated from the analysis of Eqs. (35) and (38) conducted at the beginning of Sect. 4, that the term related to \(l^2\) in \(\varSigma _{33}^\text {dyn}\) vanishes. This is exemplified in Fig. 14 for the reference material (parameters given in Table 1) considering two lengths \(l_0\) = 1000, 2000 \(\upmu \)m and \(D_{33}^0\) = 10\(^5\) s\(^{-1}\), 10\(^6\) s\(^{-1}\). Note that, as for the configuration of an imposed constant strain rate addressed previously, the growth process is less dependent on \(\dot{p}\) and is largely influenced by the imposed axial strain rate when \(D_{33}^0\) is large, e.g. \(D_{33}^0\) = 10\(^6\) s\(^{-1}\) in Fig. 14.

Fig. 14
figure 14

Time evolution of the porosity under imposed in-plane stress \(\varSigma _{11}=\varSigma _{22}=\dot{p}t\) and constant velocity \(v_3^0\). Calculations are performed for \(D_{33}^0\) = 10\(^5\) s\(^{-1}\) and 10\(^6\) s\(^{-1}\) considering \(l_0\) = 1000 and 2000 \(\upmu \)m which infers various applied constant velocities. Other material parameters are given in Table 1

Full size image

5 Conclusion

The main goal of the present work was to explore the dynamic response of porous materials containing parallel cylindrical voids. An analytical modeling was proposed, that takes into account micro-inertia effects which are absent from conventional quasistatic approaches. In this work, the dynamic homogenization scheme formerly developed by Molinari and Mercier (2001) for spherical voids was adapted to the cylindrical cell geometry (RVE). The macroscopic stress was found to be the sum of a quasistatic part and a micro-inertia dependent contribution. The quasistatic part was evaluated from the Gurson yield function Gurson (1977) while the dynamic part was calculated by adopting the admissible velocity field of Gurson (1977). It was of interest to highlight the respective influences of the two geometrical characteristics of the cylindrical voids (i.e. length and radius) on damage evolution. It is worth noting that the effects of void length and radius can be separated. Indeed, the macroscopic dynamic stress appears as the summation of two terms: the first (resp. second) term is scaled by the matrix mass density and the square of the void radius (resp. void length).

Predictions of the present model have been verified against numerical simulations for various axisymmetric loading paths. A parametric study has been conducted under plane strain configuration, confirming the refraining effect of micro-inertia when modulated by the mass matrix density and the initial void size. In addition, under plane strain, the axial stress component is found to decrease with time at large deformation. This reflects that the stress needed to constrain the length of the cylinder is reduced because of micro-inertia. Since the longitudinal stress cannot be obtained when the axial acceleration of the material particles is neglected, this trend could not be restituted from a 2D analysis.

The influence of the length of the cylindrical void has been revealed. In particular, for spherical stress loading, it has been shown that micro-inertia effects are more important for longer voids. At the same time, it was shown that two asymptotic responses in the time evolution of the porosity are emerging from the spherical loading path: the plane strain case is retrieved when \(l_0\rightarrow \infty \) and the case of short cylinders is obtained from \(l_0\rightarrow 0\).

The case of short cylinders reveals a peculiar damage evolution. In fact, the porosity is found to increase due to a reduction of the external radius and an increase of the void radius. This situation is solely due to micro-inertia effects.

The modeling has been applied to stress states with various triaxialities. Under radial expansion with traction free top and bottom surfaces, the void was found to collapse, at least for the reference set of material parameters. Under uniaxial stress loading, after an initial void growth, the porosity may decrease and reach a plateau. Under such case, the late stage of the deformation process is characterized by a continuous decrease of the internal and external radii.

Our findings can be used in several applications such as thick wall honeycomb structures or additively manufactured materials submitted to dynamic loading.