A comparison between some fracture modelling approaches in 2D LEFM using finite elements

Abstract

The finite element method has been widely used to solve different problems in the field of fracture mechanics. In the last two decades, new methods have been developed to improve the accuracy of the solution in 2D linear elastic fracture mechanics problems, such as the extended finite element method (XFEM) or the phantom node method (PNM). The goal of this work is to quantify the differences between some numerical approaches: standard finite element method (FEM), mechanical property degradation, interelemental crack method with multi-point constraints, XFEM and PNM. We explain the different techniques analysed together with their advantages and disadvantages. We compare these numerical techniques to model fracture using problems of reference with known solutions, evaluating their behaviour in terms of convergence with respect to the element size and accuracy of the stress intensity factor (SIF), stresses ahead the crack tip and crack propagation prediction. Some of the new techniques have shown a better accuracy in SIF calculation or stress fields ahead the crack tip and other lead to high errors in local results estimations. However, all methods reviewed here can predict crack propagation for the problems of reference of this work, showing good accuracy in crack orientation prediction.

1 Introduction

From the 50s to the present day, the finite element method (FEM) has been widely used to solve different problems in engineering. As forefather of FEM, works by Turner et al. (1956) and Argyris and Kelsey (1954) must be mentioned. The name of finite element method was coined by Clough in 1960 (Clough 1960) and since then, a huge number of contributions have been proposed, making the method accurate and efficient.

The FEM has been also applied to the field of computational fracture mechanics, solving different crack geometries and boundary conditions. The results obtained by FEM predict crack-tip stress and strain fields, relevant fracture mechanics parameters such as the stress intensity factors (SIFs) and the critical energy release rate (G) and also crack propagation paths. This is why it has been used in a large number of works to assess the lifetime of a component which is crucial in current damage tolerance design approaches. On the other hand, it is well known that modelling the crack propagation process is a cumbersome task. Cracks usually deviate as they grow, requiring the modification of the mesh topology during its simulation in FEM. To ease the process of crack growth modelling, numerical techniques such as the extended finite element method (XFEM) (Moës et al. 1999) or the phantom node method (PNM) (Hansbo and Hansbo 2004) have been developed during the last two decades. These methods can model crack propagation without remeshing, which is a remarkable advantage when using the FE method.

The computation of characterizing LEFM parameters, such as SIFs and G, has been thoroughly treated in the literature. From the 70’s, there are numerous studies dealing with the calculation of K and G using FEM. The works of (Rice and Tracey 1973; Gallagher 1978; Owen and Fawkes 1983), to name a few, provide a thorough description of several extraction techniques. Other works provide a comparison of different calculation methods of K and G regarding local and global approaches (Banks-Sills and Sherman 1986; Banks-Sills 1991; Banks-Sills and Sherman 1992). For example, (Bittencourt et al. 1992) compares techniques to calculate mixed-mode SIFs, such as the displacement correlation method, the J-integral and the modified crack-closure integral.

More recently, (Qian et al. 2016) analysed 2D and 3D models to calculate $K_{\mathrm {I}}$ in compact tension specimens, curved crack problems and a cracked reactor pressure vessel using XFEM and FEM. They also used different numerical field variable and energy release methods to calculate SIFs, comparing their capabilities (Qian et al. 2016). They claim that XFEM has advantages when modelling multiple cracks but it still presents some difficulties for 3D crack problems regarding oscillations of the solution, so they recommend its use when no other methods are feasible. Thus, their best results with 3D geometries are obtained by means of standard FEM with a refined mesh and domain integrals.

There are many other recent works regarding the analysis of crack initiation and propagation on fracture dynamics. For example, (Song et al. 2008), studied the performance of XFEM, element deletion and interelemental crack method for dynamic fracture propagation. Agwai et al. (2010) compared XFEM, cohesive zone models (CZM) and the peridynamic theory to predict dynamic fracture against experimental observations. An excellent review of finite element techniques for crack analysis in LEFM can be found in the book by Kuna (2013). Other recent approaches have led to the phase-field method (Francfort and Marigo 1998; Bourdin et al. 2000), alleviating some problems related to complex crack topologies that are found in XFEM and, at the same time, predicting crack initiation. The formulation of the phase-field method introduces a smooth transition between the damaged and undamaged domains and involves a diffuse crack description using a phase indicator. These strategies will not be considered in this work. A comparison of phase-field and fracture mechanics stress fields can be found in (Staroselsky et al. 2019).

Table 1 Numerical techniques to model fracture analysed in this work and their main features

All the methods used in computational fracture mechanics have their own advantages and disadvantages. After a conscientious search in the literature, we only found one work explicitly dealing with a comparison of different computational approaches to model fracture (Ingraffea 2004). Ingraffea (2004) makes a thorough review and classification of computational fracture mechanics approaches for representation of cracking processes, depending on how the crack is introduced within the numerical approach. It consists on a conceptual explanation of each method, together with a literature review about early usages of each computational fracture mechanics method. Although it clearly highlights conceptual pros and cons of each procedure, there is a lack of a quantitative comparison of the performance of each method, which we intend to address in the present work. In particular, we focus on crack tip stress field reproduction and SIF estimation when using finite elements, under the assumption of linear elastic fracture mechanics (LEFM). Other enhancements, such as the use of quarter-point isoparametric singular elements or the use of hybrid elements, are not considered in this work. A review on the performance of singular FE elements can be found in (Banks-Sills 1991). In addition, crack propagation models need to consider complex scenarios such as crack branching and coalescence. Intricate crack patterns can be found in brittle fracture of rocks or problems under highly non-proportional fatigue loading (Qian and Wang 1996; Bobet and Einstein 1998). Some of the crack propagation techniques (e.g. smeared crack approaches or phase-field models) exhibit advantages in the implementation, although other methods such as X-FEM require a more in-depth formulation modification. However, we consider these scenarios out of the scope of this study.

In this work, different fracture mechanic problems are compared through numerical models in which the material decohesion and loss of stiffness resulting from fracture process are modelled. As mentioned above, a crack can be simulated through explicit approaches (either with cracks along element faces, extended finite element method or phantom node method) or smeared approaches (modelling the discontinuity by means of a mechanical property degradation). These numerical techniques and their abbreviations used henceforth are: standard FEM (STD-FEM), mechanical property degradation (MPD), interelemental crack method with multi-point constraints (ICM-MPC), extended finite element method (XFEM) and phantom node method (PNM). Therefore, one of the goals of this work is to quantify the differences between the classical approaches (STD-FEM, MPD and ICM-MPC) and the more recent ones (XFEM and PNM). To achieve this objective, 2D problems with known analytical solution are analysed in this work to validate and compare the numerical methods. The problems are the infinite array of collinear cracks [(see e.g. (Kanninen and Popelar 1985)] and the Westergaard’s crack problem [(see e.g. (Gdoutos 1993)]. Furthermore, an experimental fracture test reported in the literature will be numerically assessed in order to compare the predicted crack paths calculated by the approaches reviewed in this work with the experimental crack path.

2 Methods

2.1 Numerical modelling techniques under study

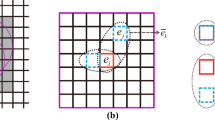
The different techniques under study are summarized in Table 1, together with their main features, advantages and disadvantages. Figure 1 shows a sketch visualizing the essential features of these methods that will be explained in the following sections.

Fig. 1

Schemes of the different numerical modelling techniques analysed in fracture problems. a Standard FEM (STD-FEM). b Mechanical property degradation of the elements (MPD); c Interelemental crack method with MPC (ICM-MPC). d Extended finite element method (XFEM). e Phantom node method (PNM)

2.1.1 Standard FEM (STD-FEM)

In this method, cracks are geometrically modelled as topological discontinuities, i.e. cracks are introduced explicitly during the discretization of the domain, matching the faces of the elements with the crack faces. If the crack path is known ‘a priori’, a fatigue or quasi-static crack propagation can be modelled by the separation of the element faces as the crack grows. This separation is modelled through the deactivation of the connectivity at these nodes, as shown in the scheme of Fig. 1a.

This technique was the first used in fracture modelling by Clough (1962), investigating the effects on the stresses in a concrete dam due to an internal vertical crack. When the crack path is unknown ‘a priori’, remeshing techniques are necessary to model the crack propagation. Saouma and Ingraffea (1981) proposed an automatic remeshing technique coupled with this method.

Under the assumption of small scale yielding (SSY), the stresses can be considered proportional to the inverse square root of the distance to the crack tip. The singular behaviour at the crack tip can be reproduced in STD-FEM through the use of quarter point elements (QPE). The QPE were introduced by Henshell and Shaw in 1975 (Henshell and Shaw 1975). They are quadratic elements in which the midside node is relocated to the L/4-position measured from the crack tip, being L the element side. It is well known that introducing QPEs around the crack tip node improves the accuracy of the FE approximation.

2.1.2 Mechanical property degradation (MPD)

In this method, the crack discontinuity is represented in a diffuse, smeared way (i.e. implicitly) in contrast to methods where crack face location is explicitly defined. The stresses are almost zero in all the elements intersected by the crack by means of the degradation of the mechanical properties, which is similar to element deletion (the scheme of the technique is shown in Fig. 1b). The method simulates the progressive loss of stiffness due to the propagation and coalescence of microcracks, microvoids, and similar defects, see e.g. (Jirásek 2011). This technique was apparently first used by (Rashid 1968) to represent a crack in reinforced concrete. In our work, the smeared crack approach has been implemented by reducing the Young’s modulus of the elements to 0.1% of the initial value. Thus, in this work the region of the elements has not been removed, such as in other works (Song et al. 2008). The principal disadvantage of the method is that the smeared crack approach affects to the whole damaged element, thus the crack is not explicitly defined and the method is mesh-dependent. It becomes necessary to define such a refined mesh that allows the proper representation of the crack. In addition, this implies that the precision of the crack tip in a 2D problem depends on the element size used in the model.

Beyond these cons, the simple implementation of this approach makes it suitable to be applied to geometrically complicated problems in 3D with a high number of DOF, where the accuracy of the local results is not so relevant and a fast solution is required, see e.g. the application to the fracture simulation of a human femoral neck (Marco et al. 2018b).

In our work we intend to reproduce fracture conditions, which is equivalent to a total loss of stiffness through crack faces. Therefore, an abrupt reduction of stiffness approximately reproduces this condition. The authors have performed an analysis on a pure mode I problem, comparing the strain field for the component in the direction normal to the crack plane $\varepsilon _{\mathrm {22}}$. The solutions are compared for an explicit representation of a crack (STD-FEM technique) and the MPD technique with elements of reduced stiffness. Figure 2 shows that the strain field distribution is, in general, very similar for both techniques, even for a not very refined mesh.

Fig. 2

Comparison of the strain component normal to the crack plane obtained using an explicit crack model (STAFEM technique) and a reduced stiffness approach (MPD method) for the elements intersected by the crack

2.1.3 Interelemental crack method with MPC (ICM-MPC)

In this technique the crack is modelled by the separation of the elements that contain the crack, by means of subdividing the elements intersected by the crack and releasing the connectivity of the elements on both sides of the fracture. The scheme of the technique is shown in Fig. 1c, where the connectivity of blue nodes has been unlinked to simulate the crack opening. A master node (red node in Fig. 1c) is necessary to enforce a crack tip location. Multipoint constraints (MPC) are defined to interpolate the displacements of the crack tip node between the displacements of the adjacent nodes (green nodes in Fig. 1c). One of the disadvantages of this technique is that the crack tip is always at an element side, unless the crack tip element is subdivided into triangular elements. Here, the approach proposed by Xu and Needleman (1994) is considered, so that all elements are separated from the beginning of the simulation. This technique reproduces a realistic discontinuity and an explicit representation of the crack.

The analysis of the same problem in pure mode I is shown in Fig. 3, comparing the strain component normal to the crack plane obtained through standard FE (STD-FEM) and the ICM-MPC technique, yielding a similar strain field distribution.

Fig. 3

Comparison of the strain component normal to the crack plane obtained using an explicit crack model (STAFEM technique) and the ICM-MPC method

2.1.4 Extended finite element method (XFEM)

The XFEM method (Moës et al. 1999) enables the introduction of crack surfaces that are independent of the mesh geometry (they do not need to conform to element sides). Therefore, the mesh topology and the connectivity can be maintained throughout the crack propagation process without remeshing. Although XFEM is nowadays available in some commercial FE software, such as Abaqus/Standard (Hibbitt et al. 2004), in this work the implementation developed by Giner et al. (2009) will be used. A user element with multiple DOF per node is programmed in Abaqus using a user element subroutine (UEL) to enable the incorporation of extended finite elements capabilities. The method implies DOF enrichment of the nodes belonging to the elements intersected by the crack. Figure 1d shows a scheme of the method, where different kind of enrichments are described, depending on the relative position of the crack nodes. Elements intersected by the crack are modified by a Heaviside enrichment that introduces the discontinuity across the crack faces $(H(\hbox {x}) = \pm 1)$. In addition, crack tip nodes have a special enrichment that reproduces the asymptotic behaviour of LEFM. In this work, a topological enrichment has been used for crack tip enrichment (Giner et al. 2009), i.e. only a single layer of nodes surrounding the crack tip are enriched. Nodes with eight additional DOFs are enriched in the two Cartesian directions with four crack-tip functions $F_{\alpha }(\hbox {x})$ (Belytschko and Black 1999):

Fig. 4

Comparison of the strain component normal to the crack plane obtained using an explicit crack model (STAFEM technique) and a XFEM model

$$\begin{aligned}&{[F}_{\alpha }\left( r,\theta \right) , \, \alpha =1-4]\nonumber \\&\quad =\left[ \sqrt{r} \sin {\frac{\theta }{2},\sqrt{r} \cos {\frac{\theta }{2},\sqrt{r} \sin {\frac{\theta }{2}\sin \theta ,\sqrt{r} \cos {\frac{\theta }{2}\sin \theta }}}} \right] \nonumber \\ \end{aligned}$$

(1)

where r, $\uptheta$ are local polar co-ordinates defined at the crack tip. The displacement approximation for crack modelling in the extended finite element method takes the form (Moës et al. 1999)

$$\begin{aligned} u_{\mathrm {xfem}}\left( \mathrm {x} \right)= & {} \sum \limits _{i\in g} {\mathrm {N}_{i}(\mathrm {x})\mathrm {u}_{i}} \nonumber \\&+\sum \limits _{i\in h} {\mathrm {N}_{i}\left( \mathrm {x} \right) [H\left( \mathrm {x} \right) -H\left( \mathrm {x}_{i} \right) ]\mathrm {a}_{i}} \nonumber \\&+\sum \limits _{i\in k} \left[ \mathrm {N}_{i}(\mathrm {x})\sum \limits _{\alpha =1}^4 {[F_{\alpha }\left( \mathrm {x} \right) -F_{\alpha }\left( \mathrm {x}_{i} \right) ]\mathrm {b}_{i\alpha }} \right] \nonumber \\ \end{aligned}$$

(2)

where $N_{i}$(x) is the nodal shape function and u$_{i}$ is the standard DOF of node i (u$_{i}$ represents the physical nodal displacement for non-enriched nodes only). g is the set of all nodes in the model, h is the set of nodes of elements intersected by the crack (except the crack tip element) and k contains the nodes enriched with crack-tip functions $F\alpha$ (x). The extra DOFs introduced in the approximation are a$_{i}$ and b$_{i\alpha }$.

The intersected elements have discontinuous displacement fields and therefore, these elements must be subdivided into subdomains in order to carry out the numerical integration in the area of the element. The element is subdivided into two quadrilateral subdomains when it is intersected by the crack at opposite faces, or subdivided into triangular subdomains when contiguous faces are intersected. This subdomain division is detailed in Moës et al. (1999).

The analysis of the same problem is shown in Fig. 4, comparing the strain component normal to the crack plane obtained through an explicit crack representation (STD-FEM technique) and the XFEM technique, obtaining a similar strain field distribution.

2.1.5 Phantom node method (PNM)

The PNM was firstly proposed by Hansbo (Hansbo and Hansbo 2004) and it is based on nodes duplication (named phantom nodes) overlapping real nodes in the numerical model. Thus, the enrichment of the FE model with additional DOF as in XFEM is not necessary. The PNM treats discontinuities explicitly, similarly to XFEM, with straight internal crack segments. When a crack propagates through an element, this element is subdivided into subdomains in order to perform the numerical integration, which can be the same as used in the XFEM. A scheme of several elements intersected by a crack with the PNM topology is shown in Fig. 1e.

In Fig. 1e, the original nodes are represented by circular markers and the phantom nodes by square markers. By using phantom nodes on real nodes, elements can be separated, simulating crack opening, although only one of the subdomains of each of the duplicated elements is integrated and taken into account in the model. At the crack tip element, only connectivity of the nodes of the side that contains the crack tip keeps active (nodes 3 and 4 in Fig. 1e). Therefore, the nodes of the crack tip element are only partially duplicated, and the crack tip will always be at the element side that connects the two non-duplicated nodes (these nodes are not phantom nodes).

The implementation of the PNM has been carried out through a user element (UEL) subroutine in the finite element commercial code Abaqus/Standard. This method was validated and explained in detail in (Marco et al. 2018a).

The analysis of the same reference problem is shown in Fig. 5, where the strain component normal to the crack plane is represented, comparing a standard FE solution and the PNM technique, leading to similar strain distributions.

Fig. 5

Comparison of the strain component normal to the crack plane obtained using an explicit crack model (STAFEM technique) and a PNM model

2.1.6 Relative errors respect to the analytical solution in mode I problem

In this section we show the contour error maps of equivalent strains for each technique for a mode I problem. The equivalent strain and the relative error are computed as follows:

$$\begin{aligned} \varepsilon _{\mathrm {eq}}=\frac{2}{3}\sqrt{\frac{3(\epsilon _{xx}^{2}+\epsilon _{yy}^{2})}{2}+\frac{3(\gamma _{xy}^{2})}{4}} \end{aligned}$$

(3.1)

where:

$$\begin{aligned} \epsilon _{xx}&=\frac{2}{3}\varepsilon _{xx}-\frac{1}{3}\varepsilon _{yy} \end{aligned}$$

(3.2)

$$\begin{aligned} \epsilon _{yy}&= -\frac{1}{3}\varepsilon _{xx}+\frac{2}{3}\varepsilon _{yy} \end{aligned}$$

(3.3)

$$\begin{aligned} \gamma _{xy}&= 2\varepsilon _{xy} \end{aligned}$$

(3.4)

$$\begin{aligned} {\textit{relative error}}= & {} \frac{\left| \varepsilon _{exact}-\varepsilon _{numerical} \right| }{\left| \varepsilon _{exact} \right| }\cdot 100\% \end{aligned}$$

(4)

Figure 6 shows the relative error (Eq. 4) between analytical results and each numerical technique. As shown in Figs. 2, 3, 4 and 5, the strain field far and ahead the crack tip is similar for each technique, showing a typical strain field in fracture problems under mode I conditions.

Fig. 6

Comparison between FE models and analytical solutions for a mode I problem. Relative error in equivalent strain

Figure 6 shows how XFEM technique is the most accurate solution to this example problem due to the incorporation of crack enrichment functions. In addition, the standard solution STD-FEM and the PNM show a very similar error distribution, since their formulation is essentially equivalent, as the PNM simply includes the crack discontinuity with no crack tip enrichment, as explained above. Finally, the MPD presents large errors near the crack faces due to the abrupt discretization of the crack in this zone.

2.2 Application to reference problems with known solution

Two different analytical problems with known analytical solution from LEFM have been used to compare the capabilities of each numerical modelling technique. The SIFs and the stresses ahead the crack tip will be compared with the analytical solution. The SIFs are calculated through the J-integral (in pure mode I) or through the interaction integral (in plane mixed mode behaviour). A sketch of the problems and their respective numerical models is shown in Fig. 7. In this figure, the shaded area represents the domain of the numerical model. Firstly, an infinite array of collinear cracks under tension in pure mode I is modelled. In addition, a finite element mesh sensitivity analysis has been carried out to analyse the influence of the element size around the crack tip on the solution. Secondly, the Westergaard’s crack problem under mixed mode loading is assessed.

Fig. 7

Problems analysed in this work. a Infinite array of collinear cracks in tension; b$\sigma _{22}$ contour plot for an infinite array of collinear cracks with ICM-MPC method; c Westergaard’s crack problem; d von Mises contour plot in Westergaard’s crack problem with ICM-MPC method

2.2.1 Infinite array of collinear cracks in tension

The exact value of $K_{\mathrm {I}}$ for this problem is given by the expression (Kanninen and Popelar 1985):

$$\begin{aligned} K_{\mathrm {I}}=\sqrt{\frac{2b}{\pi a}tan\left( \frac{\pi a}{2b} \right) } \sigma \sqrt{\pi a} \end{aligned}$$

(5)

where the different variables are defined in the sketch of Fig. 7a. In this problem we consider $a=1$ and $b=2a$, therefore, the model dimensions are 12a in y-axis and 2a in x-axis. $\sigma$ value is defined as $\sigma = 1/2$ (units of pressure), in order to yield $K_{\mathrm {I}} = 1$. The Young’s modulus is $E=10^{\mathrm {4}}$ (units of pressure) and the Poisson’s ratio is $\nu = 0.33$. Plane stress conditions are considered, using quadrilateral finite elements with full integration (code CPS4 in Abaqus). Boundary conditions simulate the periodic symmetry problem so that lateral nodes are constrained in the X-direction, being thus able to model an infinite array with a finite domain. The SIF is calculated using the J-integral, applied to a domain surrounding the crack tip.

A sensitivity analysis has been carried out in order to study the convergence of the results as we refine the mesh and to stablish a proper mesh size to compare the different techniques to model fracture. Four meshes have been used for each technique, with element sizes equal to: a/2, a/4, a/8 and a/16. We define the proper element size as the one that leads to a variation of less than 2% on the relative error in $K_{\mathrm {I}}$ calculation when successive meshes are analysed. In this problem, this condition is reached for an element size equal to a/8. The final mesh used in this problem is shown in Fig. 7b.

2.2.2 Westergaard’s crack problem

Westergaards’s crack problem has been used to compare the accuracy of the different methods under mixed mode loading. The analysed problem is an infinite plate with a crack of finite length. This problem has also been used to validate different numerical approaches, such as XFEM (Giner et al. 2009) or PNM (Marco et al. 2018a). The crack length is 2a, and the domain is biaxially loaded with remote uniform tractions. Antisymmetry conditions are applied along y-axis. Exact solutions for the SIFs in this problem are:

$$\begin{aligned} K_{\mathrm {I,ex}}=\sigma \sqrt{\pi a} \end{aligned}$$

(6)

and

$$\begin{aligned} K_{\mathrm {II,ex}}=\tau \sqrt{\pi a} \end{aligned}$$

(7)

Non-uniform tractions must be applied to the finite boundaries of the numerical model in order to reproduce the behaviour of an infinite plate with remote uniform tractions. To do so, we use the explicit expressions for the stress field in terms of spatial coordinates analytically derived in (Giner et al. 2005). Then, it is possible to compute equivalent nodal forces for the finite portion of the domain. For biaxial loading with remote uniform traction $\sigma$, the stress field at a point (xy) associated with mode I loading is:

$$\begin{aligned} \sigma _{\mathrm {xx}}^{\mathrm {I}}= & {} \frac{\sigma }{\sqrt{\vert t\vert } }\left[ \left( x\cos {\frac{\varPhi }{2}-y\sin \frac{\varPhi }{2}} \right) \right. \nonumber \\&\left. +\,y\frac{a^{2}}{{\vert t\vert }^{2}}\left( m\sin {\frac{\varPhi }{2}-n\cos \frac{\varPhi }{2}} \right) \right] \end{aligned}$$

(8a)

$$\begin{aligned} \sigma _{\mathrm {yy}}^{\mathrm {I}}= & {} \frac{\sigma }{\sqrt{\vert t\vert } }\left[ \left( x\cos {\frac{\varPhi }{2}-y\sin \frac{\varPhi }{2}} \right) \right. \nonumber \\&\left. -\,y\frac{a^{2}}{{\vert t\vert }^{2}}\left( m\sin {\frac{\varPhi }{2}-n\cos \frac{\varPhi }{2}} \right) \right] \end{aligned}$$

(8b)

$$\begin{aligned} \sigma _{\mathrm {xy}}^{\mathrm {I}}= & {} y\frac{a^{2}\sigma }{{\vert t\vert }^{2}\sqrt{\vert t\vert } }\left( m\cos {\frac{\varPhi }{2}+n\sin \frac{\varPhi }{2}} \right) \end{aligned}$$

(8c)

For remote uniform traction $\tau$ (mode II), the stress field at points (x,y) belonging to the half plane $x\ge 0$ are given by:

$$\begin{aligned} \sigma _{\mathrm {xx}}^{\mathrm {II}}= & {} \frac{\tau }{\sqrt{\vert t\vert } }\left[ 2\left( y\cos {\frac{\varPhi }{2}+x\sin \frac{\varPhi }{2}} \right) \right. \nonumber \\&\left. -\,y\frac{a^{2}}{{\vert t\vert }^{2}}\left( m\cos \frac{\varPhi }{2}+n\sin \frac{\varPhi }{2} \right) \right] \end{aligned}$$

(9a)

$$\begin{aligned} \sigma _{\mathrm {yy}}^{\mathrm {II}}= & {} y\frac{a^{2}\tau }{{\vert t\vert }^{2}\sqrt{\vert t\vert } }\left( m\cos \frac{\varPhi }{2}+n\sin \frac{\varPhi }{2} \right) \end{aligned}$$

(9b)

$$\begin{aligned} \sigma _{\mathrm {xy}}^{\mathrm {II}}= & {} \frac{\tau }{\sqrt{\vert t\vert } }\left[ \left( x\cos {\frac{\varPhi }{2}-y\sin \frac{\varPhi }{2}} \right) \right. \nonumber \\&\left. +\,y\frac{a^{2}}{{\vert t\vert }^{2}}\left( m\sin \frac{\varPhi }{2}-n\cos \frac{\varPhi }{2} \right) \right] \end{aligned}$$

(9c)

where m, n, |t| and $\varPhi$ are real-valued functions of x and y coordinates, defined as

$$\begin{aligned} m= & {} \mathrm {Re}t=x^{2}-y^{2}-a^{2} \end{aligned}$$

(10)

$$\begin{aligned} n= & {} \mathrm {Im}t=2xy \end{aligned}$$

(11)

$$\begin{aligned} \left| t \right|= & {} \left| m+\mathrm {i}n \right| =\sqrt{m^{2}+n^{2}} \end{aligned}$$

(12)

$$\begin{aligned} \varPhi= & {} \mathrm {arg}\bar{t}=\mathrm {arg}(m-\mathrm {i}n)\qquad \hbox { with }\varPhi \in [-\uppi , \uppi ] \end{aligned}$$

(13)

In this problem, crack length is $a=$1 and the finite domain dimensions are $b=2a$, $c=a$. Nodal equivalent forces applied to the model are those that yield $K_{\mathrm {I,ex}} = K_{\mathrm {II,ex}} = 1$, so that $\sigma =\tau =1/\sqrt{\pi a}$ . The Young’s modulus is $E=10^{\mathrm {4}}$ (units of pressure), the Poisson’s ratio is $\nu =0.33$ and plane stress conditions are assumed.

The expressions above let us to calculate the exact value of the stress components ahead the crack tip. Therefore, the stress components $\sigma _{\mathrm {xx}}$, $\sigma _{\mathrm {yy}}$ and $\sigma _{\mathrm {xy}}$ estimated numerically will be compared to their exact values for different directions ahead the crack tip ($\varPhi = 0^{\circ }, 45^{\circ }$ and $90^{\circ }$).

A mesh sensitivity analysis has also been performed for the Westergaard’s crack problem, using element sizes equal to: a/4, a/8, a/16 and a/32. $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ calculation has been used to set an appropriate element size. We have considered a sufficiently refined mesh when the relative error between subsequent element sizes is about 2%. As a result, the element size that satisfies this condition is a/32. This final mesh is shown in Fig. 7d.

2.3 Crack propagation for fracture tests

Two crack propagation evolutions of tests have been numerically modelled in order to compare the predicted crack path of each technique. The problem schemes are shown in Fig. 8, with dimensions given in mm. The first problem (Fig. 8a) was studied initially by Bittencourt et al. in (Bittencourt et al. 1996) and has been used in several works to validate crack propagation models with new simulation strategies (Bittencourt et al. 1996) or new mesh methodologies (Ooi et al. 2015). Fig. 8a shows a sketch of the problem with the specimen dimensions. The second problem (Fig. 8b) was developed specifically for this work, to validate the conclusions obtained from this section.

Fig. 8

Crack propagation problems. a A cracked beam with three holes. The red solid line represents the initial crack. The red dashed line is the experimental path obtained by Bittencourt et al. (1996). b Experimental test developed for this work. The red dashed line is the experimental fracture path.

The first problem (Fig. 8a) consists of a cracked beam subjected to three-point bending test. The beam has three holes arranged vertically that have an influence on the trajectory of the initial crack, marked in red in Fig 8a. The load is $P = 4.5\hbox { kN}$ and the beam is made of polymethylacrylate with the following mechanical properties: $E = 29\cdot 10^{\mathrm {3}}$ MPa and $\nu = 0.3$. A plane strain formulation and a linear elastic material behaviour are assumed.

In the second problem (Fig. 8b) an aluminium alloy specimen was axially tested until fracture. The material is the aluminium alloy 7075, with $E=71.7\cdot 10^{\mathrm {3}}\hbox { MPa}$ and $\nu = 0.3$. The stress applied for the numerical models is $P=100\hbox { MPa}$. Plane strain formulation and linear elastic material have been also considered in this problem.

The application of explicit crack modelling techniques in crack propagation problems requires the use of crack tracking algorithms without exception (Jäger et al. 2008). Several strategies can be used for crack tracking: fixed tracking (Jäger et al. 2008), local tracking (Areias and Belytschko 2005), non-local tracking (Moës and Gravouil 2002) and global tracking (Oliver et al. 2002). In our implementations, crack modelling techniques are coupled with level sets based on signed-distance functions to the crack face and crack tip (Stolarska et al. 2001; Duflot 2007) in order to perform the crack tracking. For all the crack modelling techniques, the crack path is defined by linear segments. In each crack propagation, level set functions are calculated in order to perform the node enrichment in X-FEM, the node duplication in PNM or the mechanical property degradation of elements intersected by the crack path in the MPD.

Crack propagations in the numerical models have been performed considering crack increments of about $\varDelta a = 0.25\hbox { mm}$ each. Increments are slightly different for each method, since some of them only simulate the crack advance along the entire element. Specifically, only XFEM and STD-FEM combined with remeshing are capable to model crack tips inside of an element. The crack orientation for each crack growth increment has been predicted according to maximum tangential stress (MTS) criterion (Eq. 14):

$$\begin{aligned} \theta =\mathrm {arccos}\left( \frac{3K_{\mathrm {II}}^{2}+\sqrt{K_{\mathrm {I}}^{4}+8K_{\mathrm {I}}^{2}K_{\mathrm {II}}^{2}} }{K_{\mathrm {I}}^{2}+9K_{\mathrm {II}}^{2}} \right) \end{aligned}$$

(14)

The experimental fracture paths have been digitalized to determine its coordinates and compared with the crack paths predicted through the numerical techniques analysed in this work. Only STD-FEM technique has not been used in this section, since propagation along crack faces of a given mesh cannot suitably reproduce the crack path and it would need of remeshing. Both problems have been modelled using structured and unstructured meshes in order to analyse the influence of the mesh discretization on the predicted crack paths.

3 Results and discussion

3.1 Convergence analysis for an infinite array of collinear cracks

Figure 9 shows the relative error in $K_{\mathrm {I}}$ calculation for different element sizes for each technique analysed in this work. In this section we represent the error with logarithmic axes (Fig. 9a) and also linear vertical axis (Fig. 9b). This is due to the relative errors of MPD technique, which are negative in contrast to the other techniques.

Fig. 9

Convergence analysis for an infinite array of collinear cracks. a Relative error in $K_{\mathrm{I}}$ (in %) with logarithmic axes; b Relative error in $K_{\mathrm{I}}$ (in %) with linear vertical axis

With the exception of MPD, all techniques show a clear convergence with mesh refinement (see Fig. 9a). STD-FEM, ICM-MPC and PNM present very similar error values between them, following an analogous trend. MPD shows the largest relative error and the values are negative for all meshes (i.e., MPD overestimates $K_{\mathrm {I}})$, in contrast to the other techniques. Despite this fact, MPD shows a relatively good behaviour in this problem. Regarding XFEM, it shows the least relative error in $K_{\mathrm {I}}$ for each element size (see Fig. 9a) due to the incorporation of the crack tip enrichment functions in the solution space, and hence it is better suited to the reproduction of the singular behaviour. We have also included the analysis of XFEM without no tip enrichment. This is achieved by simply constraining the extra degrees of freedom for the crack tip elements in our in-house implementation. As a result, it is worth mentioning that the error increases to the level of the rest of methods presented in Fig. 9a when no crack tip enrichment is included.

3.2 ${K}_{\mathrm {I}}$ for an infinite array of collinear cracks

Values of $K_{\mathrm {I}}$ have been computed for each modelling technique and compared with the exact value obtained through Eq. (5). The estimations and relative errors with respect to the analytical solution are shown in Table 2.

Table 2 Relative errors in $K_{\mathrm {I}}$ with different numerical techniques for an infinite array of collinear cracks

Fig. 10

Convergence analysis for Westergaard’s crack problem. a Relative error in $K_{\mathrm {I}}$ (in %) with logarithmic axes. b Relative error in $K_{\mathrm {I}}$ (in %) with linear vertical axis. c Relative error in $K_{\mathrm {II}}$ (in %) with logarithmic axes; d Relative error in $K_{\mathrm {II}}$ (in %) with linear vertical axis

Results presented in Table 2 show that all modelling techniques lead to relative errors less than 2% for the estimation of $K_{\mathrm {I}}$. As expected, due to the smeared crack approach, MPD technique shows the highest relative error in $K_{\mathrm {I}}$ calculation. Therefore, if high accuracy is required, the MPD technique should be avoided. On the other hand, its simplicity regarding implementation makes it suitable to be used in geometrically complicated problems, with a high number of DOFs or to model diffuse damage, representing the initiation of micro cracks prior to complete fracture.

STD-FEM, ICM-MPC, PNM show a fairly good accuracy in $K_{\mathrm {I}}$ estimation. ICM-MPC and PNM have similar errors, since both techniques are based on element subdivision. In the ICM-MPC technique the element is explicitly subdivided, while in PNM the element subdivision is carried out through integration of the corresponding areas of the elements. In the standard FE (STD-FEM) crack faces are modelled explicitly, yielding an error slightly less than for ICM-MPC and PNM.

Finally, XFEM shows the highest accuracy in this problem, with a relative error equal to 0.4% with respect to the analytical solution. This is because of the crack-tip functions implemented in enriched elements surrounding the crack tip, which allow reproducing the singularity in terms of the asymptotic behaviour in the crack tip vicinity. When crack tip functions are not included in the approximation space, the results are similar to STD-FEM, ICM-MPC or PNM.

3.3 Convergence analysis for Westergaard’s crack problem

Figure 10 shows the relative error in $K_{\mathrm {I}}$ (Fig. 10a, b) and $K_{\mathrm {II}}$ (Fig. 10c, d) calculation for all the techniques analysed in this work using different element sizes. The error is both represented with logarithmic scale (Fig. 10a, c) and linear scale for the vertical axis (Fig. 10b, d). This is caused by the negative and positive relative errors of the MPD technique, unlike the other methods. Again, we also include the XFEM technique without crack tip enrichment.

Table 3 Relative errors in $K_{\mathrm{I}}$, $K_{\mathrm{II}}$ and propagation angle for the Westergaard’s problem solved with each numerical technique

All techniques have shown a clear convergence with mesh refinement except MPD, which changes from negative to positive errors when decreasing the mesh size. STD-FEM, ICM-MPC and PNM present very similar error values between them, with approximately the same convergence rate. Again, XFEM shows the smallest relative error in $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ for each element size due to the crack tip enrichment functions.

3.4 $K_{\mathrm{I}}, K_{\mathrm{II}}$ for Westergaard’s crack problem

In this section the different numerical techniques have been applied to solve the Westergaard’s crack problem. Values of the SIFs $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ in plane mixed mode have been estimated using each technique and compared with the exact values obtained through Eqs. (6 and 7). Relative errors with respect to the exact solution are shown in Table 3. Since this is a mixed mode problem, the propagation angle is not zero and the relative error in the propagation angle is also shown in Table 3. The value of reference is given by the MTS criterion, Eq. (14), after substituting the exact SIFs ($\theta _{\mathrm {ex,MTS}} = 53.13^{\circ }$).

Results in Table 3 are in line with those obtained for an infinite array of collinear cracks. There are differences between the MPD technique and the rest of the methods: the MPD technique yields a larger error than the rest of the techniques in $K_{\mathrm {II}}$, and it is higher than the one obtained for $K_{\mathrm {I}}$, contrary to the other methods. STD-FEM, ICM-MPC, XFEM and PNM present always relative errors less than 3%, thus providing good accuracy in the SIFs calculation under mixed mode. XFEM provides again the best accuracy in the SIFs calculation due to the crack tip enrichment functions. The deactivation of the crack tip functions in XFEM leads to results very similar to the ones given by STD-FEM or ICM-MPC.

We note in passing the differences found between the relative errors in $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ regardless the technique used. For all methods except MPD, the relative error in $K_{\mathrm {I}}$ is greater than in $K_{\mathrm {II}}$, being even more than twice for STD-FEM, ICM-MPC, XFEM and PNM. These variations in the error in $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ were also observed by Giner et al. (2009) and deserve further study.

Regarding the angle estimation, it is very interesting to note that the relative errors are minimal, because the angle estimation depends on the ratio $K_{\mathrm {II}}$/$K_{\mathrm {I}}$ and the errors in $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ tend to compensate. For the predicted angle, all techniques show a relative error less than 1%, except for the MPD technique, which presents a greater error, about 3%. Note that even MPD yields an acceptable error, especially taking into account the simplicity of the method, due to the mentioned error compensation between $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$.

3.5 Stresses ahead the crack tip $(\sigma _{\mathrm{xx}}, \sigma _{\mathrm{yy}}$ and $\tau _{\mathrm{xy}})$

The stresses $\sigma _{\mathrm {xx}}$, $\sigma _{\mathrm {yy}}$ and $\tau _{\mathrm {xy}}$ ahead the crack tip for each modelling technique have been analysed for the Westergaard’s problem, since the exact analytical stress field is available (Eqs. 8 and 9). Stresses have been plotted for different angles ahead the crack tip ($\varPhi = 0^{\circ }, 45^{\circ }$ and $90^{\circ }$), although in this section only values for $\varPhi = 0^{\circ }$ are shown in Fig. 11, where d is the distance to the crack tip. Values of stresses are normalized with respect to the applied remote stress. Results for $\varPhi = 45^{\circ }$ and $90^{\circ }$ are plotted in Fig. 13. In addition, colour error maps are shown for each technique in Fig. 12. In these figures, the von Mises stress is compared with the analytical solution.

Fig. 11

Comparison of stress components for Westergaard’s crack problem ahead the crack tip with different techniques for $\varPhi = 0^{\circ }$. a$\sigma _{\mathrm {xx}}$; b$\sigma _{\mathrm {yy}}$; c$\tau _{\mathrm {xx}}$

Fig. 12

Contour map of relative errors in von Mises stress respect the analytical solution in Westergaard’s crack problem. White dashed line shows the location of the crack

Results show a good accuracy in stresses ahead the crack tip for methods based on an explicit crack representation, especially at a distance greater than 10% of the half crack size a. As expected, MPD technique is less accurate, especially for the $\tau _{\mathrm {xy}}$ stress component.

The singular asymptotic behaviour for $\sigma _{\mathrm {yy}}$ and $\varPhi = 0^{\circ }$ is well reproduced with all the methods. For this stress component, numerical methods show a good accuracy even for distances very close to the crack tip.

For the $\sigma _{\mathrm {xx}}$ component, the ICM-MPC technique yields the best asymptotic behaviour. STD-FEM shows also good accuracy for distances close to the crack tip, even better than XFEM, despite crack tip asymptotic functions of the method. Predictions for $\tau _{\mathrm {xy}}$ present similar error between the different techniques. The MPD shows the highest error, probably due to significant variations in the first elements ahead the crack tip due to the smeared crack representation.

Error maps (Fig. 12) reinforce the conclusions obtained from the stress components analysis. MPD technique is the less accurate method with large errors surrounding the crack tip and XFEM shows the lowest relative error in the area around the crack tip due to the crack tip enrichment functions.

Results along radiuses $\varPhi = 45^{\circ }$, $90^{\circ }$ are shown in Fig. 13 and follow similar trends as for the case $\varPhi = 0^{\circ }$. In general, the predictions are reasonably good and tend to give better results for cases where stress intensity is higher, e.g. $\tau _{\mathrm {xy}}$ for the case $\varPhi = 45^{\circ }$. Again, the MPD technique is the least accurate.

Fig. 13

Comparison of $\sigma _{\mathrm{xx}}, \sigma _{\mathrm{yy}}, \sigma _{\mathrm{xy}}$ ahead the crack tip for Westergaard’s crack problem with different techniques. $\varPhi = 45^{\circ }, 90^{\circ }$

3.6 Crack propagation in real experiments

Figure 14 shows the structured and unstructured meshes and the numerical crack paths predicted by each numerical technique. The numerical path predictions are compared to the one obtained experimentally reported in (Bittencourt et al. 1996). As mentioned previously, the STD-FEM technique is not used in this section, since it would involve continuous remeshing at each crack increment.

Fig. 14

Crack path numerical predictions for a fracture test reported in (Bittencourt et al. 1996) and comparison with the experimental crack path. a Structured mesh used in the model. b Results obtained with the structured mesh. c Unstructured mesh used in the model. d Results obtained with the unstructured mesh

Numerical predictions are in good agreement with the experimental path (Bittencourt et al. 1996) for all techniques, since crack orientation using the MTS criterion depends on the ratio $K_{\mathrm {II}}$/$K_{\mathrm {I}}$ and the errors in $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ tend to compensate for each method. XFEM shows the best accuracy, with a path prediction very similar to the experimental crack path. The rest of techniques MPD, ICM-MPC and PNM show in general good accuracy, and the path prediction can be regarded as sufficiently good for practical purposes, even for the least accurate method MPD.

Figure 15 shows the structured and unstructured meshes and the numerical predictions for an experimental problem developed by the authors. Again, ICM-MPC, PNM and XFEM show in general good accuracy in crack path prediction, even for unstructured meshes. In this problem, MPD shows larger differences between its crack path prediction and the experimental one, although the first increments are realistic.

Fig. 15

Crack path numerical predictions for a fracture test developed for this work and comparison with the experimental crack path. a Structured mesh used in the model. b Results obtained with the structured mesh. c Unstructured mesh used in the model. d Results obtained with the unstructured mesh

The use of unstructured meshes affects mainly to the MPD technique. In the problem of Fig. 14, the MPD approach is the only one that slightly varies the trajectory of the path when an unstructured mesh is used. However, crack path predictions by the rest of techniques are not significantly influenced by the mesh pattern. Similarly, in Fig. 15 the trajectory is slightly influenced by the unstructured mesh, increasing its error respect experimental results. It is important to remark that a small element size is used in these crack propagation problems, providing good crack path predictions with all the techniques with the exception of the MPD approach.

4 Conclusions

In this work, a comparison between different numerical crack modelling techniques has been performed, analysing their behaviour for two bidimensional problems of the LEFM with known solution. Pros and cons of each technique as well as their main features have been reviewed in the document. Problems have been modelled using the commercial code Abaqus and user’s subrourtines, assessing the performance of these techniques in terms of mesh sensitivity, SIF calculation, stresses ahead the crack tip and crack path prediction.

The convergence of the solution when the element size is reduced has been analysed for a pure mode I problem, leading to good convergences for all techniques. The XFEM method has proven to be the most accurate, because of the crack tip enrichment functions of its formulation.

The convergence of the methods under mixed mode loading has been analysed using the Westergaard’s crack problem, leading to similar results to those obtained for pure mode I. For this problem, relative errors in the computation of $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ are slightly high for some of the methods, especially the MPD technique. However, these errors are less evident in terms of the crack propagation angle. This is due to the angle dependence on the ratio $K_{\mathrm {II}}$/$K_{\mathrm {I}}$, with errors in $K_{\mathrm {I}}$ and $K_{\mathrm {II}}$ that tend to compensate for each method.

The in-plane components of stresses ahead the crack tip have been compared with analytical solutions for three different angular directions (radiuses from the crack tip). In addition, error maps have been included for von Mises stress, comparing the methods presented in this work with analytical results. In general, most methods show results similar to the analytical solution of reference. The XFEM yields the best results thanks to the enrichment functions, being MPD the least accurate.

Despite the very different approaches and formulations of each method, all of them can predict crack propagation paths with a reasonable accuracy for practical purposes. This has been verified comparing the predicted paths with an experimental path reported in the literature and an experiment developed in our laboratory for this work. Indeed, even the least accurate method MPD leads to reasonable good crack path estimations for the first of the problems because the ratio $K_{\mathrm {II}}$/$K_{\mathrm {I}}$ used for computing the orientation angle is still preserved. The use of structured and unstructured meshes has been checked, concluding that if a small enough element size is used the crack path is not affected by this fact, except for the MPD technique.

Therefore, simple techniques such as MPD can be used to estimate crack propagation paths in complex geometries, branching or coalescence, since its implementation is direct and does not need remeshing, nodal enrichment or topological variations. However, when accurate values of SIFs or local stresses are sought, XFEM is especially useful thanks to the enrichment functions of its formulation, which allow to reproduce the asymptotic LEFM fields close to the crack tip.