Local and non-local modeling aspects of three-dimensional cracks growth initiation

Abstract

Three-dimensional crack growth initiation is examined under the assumption that the crack front remains smooth. Two important modeling issues, specific to three-dimensional rather than two-dimensional cracks, are addressed. First, it is established that, at each point along the crack front, the velocity and configurational force are two-dimensional vectors, lying in the local normal plane. This allows one to generalize any two-dimensional crack growth criterion to three dimensions. Second, a simple mesoscopic model to account for along-the-front non-locality is proposed. This model eliminates pathological growth patterns ubiquitous to basic models applied to three-dimensional cracks. Further, the model is straightforward to use as it relies on standard fracture properties only.

1 Introduction

The most basic setting of linear elastic fracture mechanics involves a crack under pure Mode I loading conditions. Such a crack initiates its growth once the stress intensity factor $K_{I}$ reaches the fracture toughness $K_{IC}$. This setting has been used as the blueprint for extending fracture mechanics to cracks under mixed-mode loading conditions. The most studied extension involves a crack under combined Mode I and II plane strain loading conditions; see Mahajan and Ravichandar (1989), Xu et al. (1994) and Gurtin and Podio-Guidugli (1996) for references. Under such conditions, one is concerned with crack kinking and curving, both modeled using variances of the growth initiation criterion $K_I = K_{IC}$, although the former is associated with microcrack nucleation and the latter with main crack growth (Hull 1999). The situation becomes significantly more complicated in the presence of anti-plane shear, as the setting becomes essentially three-dimensional. Furthermore, since the pioneering experiments of Sommer (1969) and Knauss (1970), it has been accepted that, under loading conditions involving anti-plane shear, the crack front may fragment; see Lin et al. (2010) for references. The fragmentation is a result of nucleation of microcracks along the main crack front, which subsequently may grow or generate the next generation of microcracks.

Fig. 1

Pathological pattern of crack growth: a circular crack subjected to a non-uniform $K_I$ distribution; b local pathological growth pattern; c non-local smooth growth pattern

This paper is concerned with growth initiation of three-dimensional cracks under general mixed-mode loading conditions. The essential restriction adopted here is that the crack front is a smooth curve, and it remains smooth as the crack grows. This restriction rules out not only cracks with fragmented fronts and other nucleation events, but also surface-breaking cracks, for which the smoothness breaks down at the surface. The smoothness restriction is essential for three-dimensional cracks, as it is the underlying assumption of asymptotic analysis leading to the K-fields (Rice 1984).

Existing criteria for growth initiation of three-dimensional cracks are not entirely satisfactory. For example, consider the criterion based on extending the two-dimensional version of the local symmetry principle (Goldstein and Salganik 1974) to three dimensions (Xu et al. 1994; Movchan et al. 1998). In the standard notation, this criterion states that growth is initiated when the energy release rate

$$\begin{aligned} G = \frac{1-\nu ^2}{E} K_{I}^2 + \frac{1+\nu }{E} K_{III}^2 =G_c \left( \frac{K_{III}}{K_{I}}\right) , \end{aligned}$$

(1)

where $G_c$ is the critical energy release rate, dependent on the $K_{III}/K_{I}$ ratio. While the logic behind this equation is transparent, it is unclear how assumptions adopted in Xu et al. (1994) and Movchan et al. (1998) for semi-infinite cracks can be extended to other three-dimensional cracks. Further, the $K_{III}/K_{I}$ ratio must be somehow restricted to eliminate nucleation/fragmentation events.

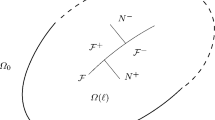
Another problematic aspect of (1) can be exposed by considering a circular crack subjected to pure Mode I loading conditions with varying$K_I$ along the front (Fig. 1a). If the load is such that $K_I < K_{IC}$ everywhere except for one point, where $K_I = K_{IC}$, then, according to (1), the crack must advance only at that point and nowhere else. This results in a pathological crack front shape involving a needle (Fig. 1b). To remedy this pathology, one should insist that the condition $K_I = K_{IC}$ should be non-local, so that it results in growth in a neighborhood of the critical point (Fig. 1c). This issue has been addressed in Hodgdon and Sethna (1993), but the model there involves an additional non-standard fracture parameter and a kinematics assumption that precludes curving.

In this paper, we rely on the vector-valued configurational force ${\mathbf{J}}$ (Eshelby 1951; Knowles and Sternberg 1972) rather than the stress intensity factors. To this end, we establish that, at each point along the crack front, ${\mathbf{J}}$ is confined to the plane normal to the crack front at that point. This result allows us to generalize any of the many crack growth criteria for mixed-mode plane strain conditions to three dimensions.

The proposed model of along-the-front non-locality combines elements of configurational mechanics, direct theory of rods, and differential geometry. The configurational mechanics component is influenced by Gurtin’s vision 2000, in which configurational forces are regarded as primitive quantities. However, our approach is very different from that in Gurtin (2000) and Gurtin and Podio-Guidugli (1996), as we regard the crack front as a configurational rod subjected to an external distributed force ${\mathbf{J}}$. Accordingly, the proposed model is based on introducing appropriate rates of deformation, conjugate internal forces, and constitutive equations, similar to the way its done in direct theory of rods (Antman 2005). Thus, in our approach, the significance of Eshelby’s stress is reduced to calculating ${\mathbf{J}}$, whereas in Gurtin (2000) and Gurtin and Podio-Guidugli (1996) Eshelby’s stress plays a central role. Our development relies significantly on elementary differential geometry, and we refer to Pressley (2007) as an excellent source for background material.

The remainder of this paper is structured as follows. In Sect. 2, we consider the classical local setting, and establish that at any point along the crack front both ${\mathbf{v}}$ and ${\mathbf{J}}$ can be confined to the local plane normal to the crack front. Then we exploit this result for extending two-dimensional crack growth initiation criteria to three dimensions. In Sect. 3, we develop a model for quantifying along-the-front non-locality for circular cracks. In Sect. 4, we show how this model can be extended to general three-dimensional cracks. In Sect. 5, we discuss key results of our work and possible extensions.

2 Local analysis

In this section, we focus on classical local relationships between the crack front velocity ${\mathbf{v}}$ and configurational force $\mathbf{J}$. We demonstrate that, locally, both vectors are two-dimensional, as they can be confined to the local normal plane. This result allows us to generalize any two-dimensional crack growth criterion to three dimensions.

2.1 Velocities and forces as local two-dimensional vectors

Consider a three-dimensional linear elastic isotropic body containing an internal crack modeled as an open discontinuity surface $\Sigma$ with the boundary (crack front) $\Gamma$ (Fig. 2a). We assume that $\Gamma$ is a smooth closed non-self-intersecting curve with a continuously varying tangent. This means that the points along $\Gamma$ can be parameterized by a continuously differentiable function of the arc length: ${\mathbf{x}} = {{\varvec{\gamma }}}(S)$. For this parametrization, the unit tangent vector is calculated as

$$\begin{aligned} {\mathbf{t}} (S) = \frac{{\mathrm{d }} {{\varvec{\gamma }}}(S) }{{\mathrm{d }}S} = {{\varvec{\gamma }}}^\prime (S). \end{aligned}$$

(2)

The plane containing ${\mathbf{x}} = {{\varvec{\gamma }}}(S)$ and perpendicular to ${\mathbf{t}} (S)$ is denoted by ${{\mathcal {N}}}(S)$ and referred to as the normal plane.

Fig. 2

Three-dimensional crack and it attributes: a the discontinuity surface $\Sigma$, crack front $\Gamma$, and the tangent t at ${\mathbf{x}} = {{\varvec{\gamma }}}(S)$. b Attributes within the normal plane ${{\mathcal {N}}}(S)$ at ${\mathbf{x}} = {{\varvec{\gamma }}}(S)$; the vector ${\mathbf{t}} = -{\mathbf{e}}_3$, perpendicular to the plane, is not shown

In this paper, we are interested in basic crack growth, and therefore assume that $\Sigma$ evolves solely due to the motion of $\Gamma$, which remains smooth closed and non-self-intersecting. Thus crack growth over an infinitesimal time interval $\Delta \Theta$ between times $\Theta$ and $\Theta + \Delta \Theta$ can be expressed in terms of the instantaneous velocity field $\mathbf{v}(S)$:

$$\begin{aligned} {\mathbf{x}}_{\Theta + \Delta \Theta } = {\mathbf{x}}_\Theta +{\mathbf{v}} (S) \Delta \Theta . \end{aligned}$$

(3)

The key feature of this relation is that one can restrict $\mathbf{v}(S)$ to the normal plane, as the tangential velocity component merely changes the parameterization of the crack front but it does not change its shape. This assertion parallels that for evolving surfaces, whose instantaneous motion can be prescribed without specifying the tangential velocity components.

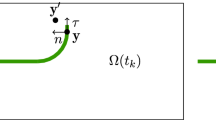
Let us demonstrate that ${\mathbf{J}}$ is also confined to the normal plane. To this end, we introduce a local coordinate system $(\xi _1, \xi _2, \xi _3)$ with the origin at ${\mathbf{x}}={{\varvec{\gamma }}}(S)$, and the unit basis vector ${\mathbf{e}}_3(S)=-{\mathbf{t}}(S)$. Thus ${{\mathcal {N}}} (S)$ is spanned by the basis unit vectors $\mathbf{e}_1(S)$ and ${\mathbf{e}}_2(S)$. Let us define the local crack curve ${{\mathcal {C}}}(S)$ as the intersection between ${{\mathcal {N}}}(S)$ and $\Sigma$. Then the vector ${\mathbf{e}}_1(S)$ is defined as the tangent vector of ${{\mathcal {C}}}(S)$ at $\mathbf{x}={{\varvec{\gamma }}}(S)$; this vector points in the direction of crack growth as opposed to healing. Finally, the vector ${\mathbf{e}}_2(S)$ is defined so that the local basis vectors are orthonormal: $\mathbf{e}_2(S)={\mathbf{e}}_3(S)\times {\mathbf{e}}_1(S)$ (Fig. 2b). In this coordinate system, the distributed configurational force is calculated via (configurational) Eshelby’s stress tensor

$$\begin{aligned} E_{ij} = W \delta _{ij} - \sigma _{jk}u_{k,i}. \end{aligned}$$

(4)

here we regard the deformation as infinitesimal, and denote the strain energy density by W, the stress tensor by $\sigma _{jk}$, and the displacement vector by $u_k$. The configurational traction vector is naturally defined as

$$\begin{aligned} T_i = E_{ij}n_j, \end{aligned}$$

so that now the force distributed along the crack front can be expressed as (Shih et al. 1986)

$$\begin{aligned} J_i (S)= \int _{\omega \left( S \right) }T_i {\mathrm{d}}l=\int _{\omega \left( S \right) } \left( n_i W - n_j \sigma _{jk} u_{k,i} \right) {{\mathrm{d}}}l,\nonumber \\ \end{aligned}$$

(5)

where $\omega (S) \in {{\mathcal {N}}}(S)$ is an infinitesimal circular contour centered at ${\mathbf{x}}={{\varvec{\gamma }}}(S)$, and the unit normal $n_i$ is defined with respect to this contour. Here we do not emphasize path-independence of the integral (Rice 1968; Cherepanov 1967; Knowles and Sternberg 1972), as it is neither necessary not useful for our purposes.

Let us calculate ${\mathbf{J}}(S)$ using the K-fields:

$$\begin{aligned} J_1 (S)= & {} \frac{1-\nu ^2}{E} \left[ K_{I}^2 (S) + K_{II}^2(S) \right] + \frac{1+\nu }{E} K_{III}^2 (S) \nonumber \\\end{aligned}$$

(6)

$$\begin{aligned} J_2 (S)= & {} -2\frac{1-\nu ^2}{E} K_{I}(S) K_{II}(S), \end{aligned}$$

(7)

$$\begin{aligned} J_3 (S)= & {} 0. \end{aligned}$$

(8)

The first equation here is the well-known Irwin’s formula. The second expression is not widely known, but it is not new (Eshelby 1975; Hakim and Karma 2009). The third expression is the most important here as it implies that ${\mathbf{J}}$ is confined to the local normal plane.

2.2 Generalization of two-dimensional criteria

Typically, growth of two-dimensional cracks is modeled as a sequence of initiation events, each followed by incremental crack growth by an amount $\Delta a$. For example, for the local symmetry principle (Goldstein and Salganik 1974), $\Delta a$ is chosen at an angle $\Delta \beta$ so that $K_{II}=0$ at the new tip. This process has been quantified using asymptotic analysis (Cotterell and Rice 1980), which provides the relationship

$$\begin{aligned} \Delta \beta = \Psi \left( \phi \right) , \end{aligned}$$

(9)

where $\Psi$ is a dimensionless function and

$$\begin{aligned} \phi := -\tan ^{-1} \left( \frac{K_{II}}{K_{I}}\right) . \end{aligned}$$

(10)

In general, the function $\Psi$ is criterion specific, but the functional form in (9) always holds.

Equation (9) can be extended to three dimensions by retaining $\Psi$ and redefining $\Delta \beta$ and $\phi$. Since ${\mathbf{v}}$ can be confined to the local normal plane, $\Delta \beta$ is simply interpreted as the angle within the normal plane. Next, we observe that if $K_{III}=0$, (6) and (7) imply that the mode-mixity angle can be defined as

$$\begin{aligned} \phi = \frac{1}{2} \sin ^{-1} \frac{J_2}{J_1}. \end{aligned}$$

(11)

Now we assume that (11) holds for $K_{III}\ne 0$, and thus extend (9) to three dimensions.

3 Non-local analysis

In this section, we develop a non-local model for crack growth initiation by considering a circular crack of radius a loaded such that $K_I(S)$ varies along the front, whereas $K_{II}(S)=K_{III}(S)=0$ (Fig. 1a). According to (6) and (7), for such a loading, the only non-zero configurational force is

$$\begin{aligned} J_1 (S) = \frac{1-\nu ^2}{E} K_{I}^2 (S). \end{aligned}$$

In the absence of $J_2$, the crack remains planar, so that $v_2(S)=0$, and the only non-trivial velocity field is $v_1(S)$. To simplify the notation, in this section, we refer to $J_1$ and $v_1$ as J and v, respectively.

The essential aspect of the proposed model is that the crack front is treated as a configurational mechanical object rather than just a geometrical one, as we did in the previous section. This difference is manifested in endowing the crack front with deformation rates, conjugate internal configurational forces, and constitutive equations. This allows us to treat the crack front as a configurational rod subjected to external distributed force J(S). In this setting, non-locality arises naturally, as it does in conventional mechanical rods, in which a force applied at a point results in displacements in the entire rod. A significant aspect of the model is that it is necessary only in a small neighborhood where the crack advances. Thus, on the one hand, the model is non-local, and, on the other hand, the non-locality is restricted to domains much smaller than the crack radius, which we regard as the macroscopic length scale. Accordingly, we refer to the model and its attributes as mesoscopic.

3.1 Rates of deformation

The key difference between purely geometric and configurational-mechanical descriptions of the crack front is that the latter endows the crack front with deformation rates, conjugate internal configurational forces, and constitutive equations. In this subsection, we focus on the deformation rates. This development requires us to introduce two basic concepts from differential geometry of planar curves. The curvature of ${{\varvec{\gamma }}}(S)$ and the normal unit vector are defined as

$$\begin{aligned} \kappa (S) := \left| {{\varvec{\gamma }}}^\prime (S) \times {{\varvec{\gamma }}}^{\prime \prime } (S)\right| \end{aligned}$$

(12)

and

$$\begin{aligned} {\mathbf{n}} (S) := \frac{1}{\kappa (S)}{{\varvec{\gamma }}}^{\prime \prime } (S), \end{aligned}$$

(13)

respectively. For the circular crack under considertaion, the growth direction ${\mathbf{e}}_1(S)$ is radial,

$$\begin{aligned} \kappa (S) = \frac{1}{a}, \quad {\mathrm{and}} \quad {\mathbf{n}}(S) = - {\mathbf{e}}_1(S). \end{aligned}$$

A fundamental theorem of differential geometry of planar curves states that two curves with the same signed curvature function $\kappa _s (S)$ are congruent. That is, the deformation of a curve can be related to changes between the signed curvature function evaluated at instances $\Theta$ and $\Theta +\Delta \Theta$. For the circular crack, $\kappa _s (S) = \kappa (S)$, and small changes in the front geometry due to growth do not affect this relationship. Therefore from now on we retain $\kappa (S)$ rather than $\kappa _s (S)$ as the fundamental curve descriptor.

For the circular crack, (3) can be simplified as

$$\begin{aligned} {{\varvec{\gamma }}}_{\Theta +\Delta \Theta }({\hat{S}}) ={{\varvec{\gamma }}}_{\Theta }(S) - v (S){\mathbf{n}} (S)\Delta \Theta . \end{aligned}$$

(14)

here we use the argument ${\hat{S}}$ rather than S for the function ${{\varvec{\gamma }}}_{\Theta +\Delta \Theta }$ to emphasize that the motion may change the crack front length, and therefore the natural parameterization of the front at time $\Theta +\Delta \Theta$ is in terms of its own arc length ${\hat{S}}$. Thus the deformation can be associated with the differences between the functions $\kappa _{\Theta } (S)$ and $\kappa _{\Theta +\Delta \Theta }({\hat{S}})$. To this end, we define the stretch

$$\begin{aligned} \lambda :=\frac{{{\mathrm{d}}}{\hat{S}}}{{{\mathrm{d}}}S}, \end{aligned}$$

(15)

and the rates

$$\begin{aligned} {\dot{\lambda }} (S):= \lim _{\Delta \Theta \rightarrow 0} \frac{\lambda _{\Theta +\Delta \Theta } -\lambda _{\Theta }}{\Delta \Theta } \end{aligned}$$

and

$$\begin{aligned} {\dot{\kappa }} (S):= \lim _{\Delta \Theta \rightarrow 0} \frac{\kappa _{\Theta +\Delta \Theta } -\kappa _{\Theta }}{\Delta \Theta }. \end{aligned}$$

Of course for our purposes it is sufficient to set $\lambda _{\Theta }=1$ and $\kappa _{\Theta } = 1/a$.

The calculations for ${\dot{\lambda }} (S)$ and ${\dot{\kappa }} (S)$ are somewhat tedious but straightforward. Let us outline the steps leading to ${\dot{\lambda }} (S)$. First, we observe that

$$\begin{aligned}&\left| \frac{{{\mathrm{d}}}{{\varvec{\gamma }}}_{\Theta }(S)}{{\mathrm{d }}S}\cdot \frac{{\mathrm{d}}{{\varvec{\gamma }}}_{\Theta }(S)}{{\mathrm{d }}S}\right| \\&\quad = \left| \frac{{\mathrm{d}}{{\varvec{\gamma }}}_{\Theta +\Delta \Theta }({\hat{S}})}{\mathrm{d }{\hat{S}}}\cdot \frac{{\mathrm{d}}{{\varvec{\gamma }}}_{\Theta +\Delta \Theta }({\hat{S}})}{{\mathrm{d }}{\hat{S}}}\right| = 1. \end{aligned}$$

Therefore the stretch can be calculated as

$$\begin{aligned} \lambda = \left| \frac{{\mathrm{d}}{{\varvec{\gamma }}}_{\Theta +\Delta \Theta }({\hat{S}})}{{\mathrm{d }}S}\cdot \frac{{\mathrm{d}}{{\varvec{\gamma }}}_{\Theta +\Delta \Theta }({\hat{S}})}{\mathrm{d }S}\right| ^{-1/2}. \end{aligned}$$

Next we calculate

$$\begin{aligned}&\frac{{{\mathrm{d}}}{{\varvec{\gamma }}}_{\Theta +\Delta \Theta }({\hat{S}})}{{{\mathrm{d}}}S} \\&\quad = \left[ {{\varvec{\gamma }}}_{\Theta }(S)- v (S){\mathbf{n}} (S) \Delta \Theta \right] ^\prime \\&\quad = \left[ 1+v (S)\kappa (S)\Delta \Theta \right] \mathbf{t}(S)-v^\prime (S)\Delta \Theta {\mathbf{n}}(S), \end{aligned}$$

so that

$$\begin{aligned} \lambda = 1 +\kappa (S)v(S)\Delta \Theta + {{\mathcal {O}}}\left( \Delta \Theta ^2\right) . \end{aligned}$$

In deriving these relationships, we exploited the Frenet–Serret formulae for differentiating the vectors ${\mathbf{t}}$ and ${\mathbf{n}}$. Now the rate of stretch is calculated as

$$\begin{aligned} {\dot{\lambda }} (S)= \kappa (S) v(S) = \frac{v(S)}{a}. \end{aligned}$$

(16)

Similar calculations result in the rate of curvature:

$$\begin{aligned} {\dot{\kappa }}(S) = - v^{\prime \prime }(S) -\kappa ^2(S) v(S)=- v^{\prime \prime }(S)-\frac{v(S)}{a^2}.\nonumber \\ \end{aligned}$$

(17)

This expression involves two terms. The first one is familiar from elementary theory of bending. The second term reflects the fact that even self-similar growth, which does not involve bending, reduces the curvature. Thus, for mechanical modeling, it is useful to introduce the rate of bending curvature

$$\begin{aligned} {\dot{\mu }}(S): = {\dot{\kappa }}(S) + {\kappa }(S) {\dot{\lambda }} (S)= - v^{\prime \prime } (S), \end{aligned}$$

(18)

which together with ${{\dot{\lambda }}} (S)$, we adopt as the strain rates. This choice will be further justified in the next subsection.

3.2 Principle of virtual power

In classical mechanics, the principle of virtual power is introduced as a weak form of equilibrium. It defines the internal forces implicitly, as the conjugates to the chosen strain rates, and yields the equilibrium equations for those forces. In our case, the power generated by J is equated to the power dissipated on deforming the crack front and moving the entire crack as a rigid body:

$$\begin{aligned} \oint _\Gamma J(S) v(S) {{\mathrm{d}}}S= & {} \oint _\Gamma [F(S){\dot{\lambda }}(S)+M(S){\dot{\mu }}(S)] {{\mathrm{d}}}S \nonumber \\&+ \, \mathbf{R\cdot V}+ {\mathbf{T}}\cdot {{\varvec{\Omega }}}. \end{aligned}$$

(19)

here the line tension F and bending moment M are introduced simply as the internal configurational forces conjugate to the rates of deformation ${{\dot{\lambda }}}$ and ${{\dot{\mu }}}$, respectively. The force ${\mathbf{R}}$ and torque ${\mathbf{T}}$ are the resultants of the distributed force J(S), and ${\mathbf{V}}$ and ${{{\varvec{\Omega }}}}$ are the rigid body translational and angular velocities, respectively. Of course, for planar cracks, many components of these vectors are equal to zero.

The integral on the right-hand side of (19) can be integrated by parts using (16) and (18):

$$\begin{aligned}&\oint _\Gamma [F(S){\dot{\lambda }}(S)+M(S){\dot{\mu }}(S)]{\mathrm{d}}S \nonumber \\&\quad =\oint _\Gamma [F(S){\kappa }(S)+M^{\prime \prime }(S)]v(S){\mathrm{d}}S. \end{aligned}$$

(20)

If J is self-equilibrated, so that ${\mathbf{R}}={\mathbf{T}}=0$, then (20) yields the strong form of equilibrium

$$\begin{aligned} \kappa (S) F (S)+ M^{\prime \prime }(S) = J (S), \end{aligned}$$

(21)

which involves the familiar membrane and bending components. Since the internal forces F and M were introduced as the conjugate quantities to the rates ${\dot{\lambda }}$ and ${\dot{\mu }}$, the fact that we arrived at the familiar equilibrium equation (21) lends further support to the choice of ${\dot{\lambda }}$ and ${\dot{\mu }}$ as the strain rates.

3.3 Constitutive equations

The rates of deformation and internal forces reveal that the crack front behaves as a configurational rod subjected to tension and bending. Therefore it is appropriate to consider constitutive equations in the form

$$\begin{aligned} F= & {} \eta ^*A^*{\dot{\lambda }},\nonumber \\ M= & {} \eta ^*I^*{\dot{\mu }}. \end{aligned}$$

(22)

here $\eta ^*$ is a configurational viscosity, $A^*$ is a cross-sectional area, and $I^*$ is a moment of inertia of the configurational rod. The asterisk sign is used to declare that (22) merely mimics the well-established constitutive equations of elementary beam theory. Nevertheless the constitutive equations in (22) warrant two observations. First, they provide proper dimensional groups, and therefore can be rewritten in the form

$$\begin{aligned} T= & {} \eta ^*\pi \rho ^2 {\dot{\lambda }}\nonumber \\ M= & {} \eta ^*\frac{\pi }{4} \rho ^4 {\dot{\mu }}, \end{aligned}$$

(23)

where $\rho$ is a cross-sectional radius. Second, in the context of linear elastic fracture mechanics, modulo a multiplier, the only sensible choice for $\rho$ is the process zone size at initiation. For small-scale yielding conditions, the process zone is governed by plasticity, and the zone size can be estimated as

$$\begin{aligned} r_y = \frac{1}{2\pi } \left( \frac{K_{IC}}{\sigma _y}\right) ^2, \end{aligned}$$

where $\sigma _y$ is the yield stress (Broek 1986).

One must also specify constitutive equations for the rigid body motion modes. But the macroscopic rigid body motion modes are expected to be much slower in comparison to the mesoscopic growth modes, and therefore we assume that the last two terms in (20) are negligible. As a result we can adopt (21) as the statement of equilibrium.

3.4 Asymptotic analysis

Once we combine (16), (18), (21), and (23), we obtain the differential equation

$$\begin{aligned} \eta ^*\frac{\pi }{4} \rho ^4 v^\mathrm{IV} (S) + \eta ^*\pi \left( \frac{\rho }{a}\right) ^2 v (S) =J (S). \end{aligned}$$

(24)

In classical mechanics, this equation represents a viscous beam with a bending viscosity $\pi \eta ^*\rho ^4 /4$ resting on a continuous viscous foundation with the viscosity $\pi \eta ^*(\rho /a)^2$. Since we are interested in constructing an approximate solution in a mesoscopic neighborhood of a reference point $\mathbf{x}_0 = {{\varvec{\gamma }}}(S_0)$, specifying the boundary conditions is neither necessary nor useful. To this end, (24) can be approximated, and rewritten as

$$\begin{aligned} \frac{{{\mathrm{d}}}^{4}v (\xi )}{{{\mathrm{d}}}\xi ^{4}}+ 4 v (\xi ) =4{\hat{v}}_0, \end{aligned}$$

(25)

where

$$\begin{aligned} {l}= & {} \sqrt{\rho a }, \end{aligned}$$

(26)

$$\begin{aligned} \xi= & {} \frac{S-S_0}{l}, \end{aligned}$$

(27)

and

$$\begin{aligned} {\hat{v}}_0 = \frac{J (S_0) l^4 }{\pi \eta ^*\rho ^4 }. \end{aligned}$$

(28)

Since $\rho \ll a$, l is the mesoscopic scale because $\rho \ll l \ll a$. Also note that the left-hand side of (25) implies that over the mesoscopic scale, the bending and membrane contributions have the same order of magnitude.

In the absence of boundary conditions, we construct an asymptotic solution of (25) by regarding $v_0 = v(S_0)$ as given. Further we want the solution $v (\xi )$ to be even, decay for large $|\xi |$, and twice continuously differentiable. In this setting $v_0$ can be treated as an unknown constant, or determined from macroscopic considerations. This is similar to the way the stress intensity factors are treated in fracture mechanics. The desired solution is

$$\begin{aligned} v (\xi )= & {} v_0 e^{ -\left| \xi \right| }\left( \sin \left| \xi \right| +\cos \xi \right) \nonumber \\&-{\hat{v}}_0 \left[ 1-e^{ -\left| \xi \right| }\left( \sin \left| \xi \right| +\cos \xi \right) \right] . \end{aligned}$$

(29)

The obvious drawback of (29) is its dependence on ${\hat{v}}_0$ and ultimately on $\eta ^*$, which makes it unappealing for most practical purposes. Therefore we seek an approximation to (29) which does not involve $\eta ^*$. To this end, we observe that if the bending viscosity were negligible then the solution would be simply

$$\begin{aligned} v(\xi )={\hat{v}}_0. \end{aligned}$$

Therefore, in the presence of bending viscosity, on the one hand,

$$\begin{aligned} v_0<{\hat{v}}_0, \end{aligned}$$

because the bending viscosity makes the entire system more viscous. On the other hand, $v_0$ and ${\hat{v}}_0$ must have the same order of magnitude because the bending and membrane contributions are of the same order over lengths ${{\mathcal {O}}}(l)$. Since in (29) the term proportional to $v_0$ is ${{\mathcal {O}}}(1)$ and the term proportional to ${\hat{v}}_0$ is ${{\mathcal {O}}}(\xi ^2)$, one can approximate it with the expression

$$\begin{aligned} v(\xi )\approx v_0 e^{ -\left| \xi \right| }\left( \sin \left| \xi \right| +\cos \xi \right) , \end{aligned}$$

(30)

which does not depend on $\eta ^*$.

While (30) is easy to use, it is not compactly supported, and therefore may introduce spurious velocities along the front. To avoid this, we seek an approximation of (30) with the following properties:

• Compactly supported on the interval $-1<\xi < 1$.

• Differ from (30) by no more than ${{\mathcal {O}}}(\xi ^2)$.

• Twice continuously differentiable.

• Even.

A function that satisfies these conditions is

$$\begin{aligned} v(\xi )= {\left\{ \begin{array}{ll} v_0 e^{ -\left| \xi \right| }\left( 1-\left| \xi \right| \right) ^3\left( 1+4\left| \xi \right| \right) \quad {\mathrm{if}}\quad \left| \xi \right| \le 1\\ 0 \quad {\mathrm{if}}\quad \left| \xi \right| >1. \end{array}\right. }.\nonumber \\ \end{aligned}$$

(31)

We adopt this function as the mesoscopic model, and plot it in Fig. 3.

Fig. 3

The normalized non-local velocity field $v/v_0$ as a function of the normalized distance $\xi$

4 General cracks

For planar non-circular cracks, the model is straightforward to extend because, to the second order, near ${\mathbf{x}}_0 ={{\varvec{\gamma }}}(S_0)$, any curve can be approximated as a circle with the radius $1/\kappa (S_0)$. Thus one can generalize the mesoscopic model to non-circular cracks by replacing a with $1/\kappa (S_0)$.

For non-planar cracks, the geometric complexity increases significantly. Nevertheless, as far as the mesoscopic model is concerned, we only have to focus on identifying the mesoscopic length l. Since for non-planar cracks, the cross-sectional radius $\rho$ is expected to enter the expression for l the same way it does in (26), our focus is on replacing the local curvature $\kappa (S_0)$ with a quantity that represents both $\Gamma$ and $\Sigma$. Our proposal is very simple to state: $\kappa (S_0)$ must be replaced with $\left| \kappa _g (S_0)\right|$, the absolute value of the geodesic curvature. Thus (26) takes the form

$$\begin{aligned} l = \sqrt{\frac{\rho }{\left| k_g (S_0)\right| }}. \end{aligned}$$

(32)

In what follows, we arrive at (32) in an inductive manner using simple examples and heuristic arguments, but the replacement of $\kappa (S_0)$ with $\left| \kappa _g (S_0)\right|$ is intuitive, as the geodesic curvature is a measure of how the curve curves with respect to the imbedding surface.

By definition

$$\begin{aligned} k_g (S): = {{\varvec{\gamma }}}^{\prime \prime }(S) \cdot \left[ \mathbf{N}\times {{\varvec{\gamma }}}^{\prime }(S)\right] , \end{aligned}$$

(33)

where ${\mathbf{N}}$ is the unit normal with respect to $\Sigma$. To calculate this normal, we suppose that $\Sigma$ is parametrized as ${\mathbf{x}} = {{\varvec{\sigma }}}(p , q)$, where p and q are local surface coordinates. Then

$$\begin{aligned} {\mathbf{N}} = \frac{\frac{\partial {{\varvec{\sigma }}}}{\partial p } \times \frac{\partial {{\varvec{\sigma }}}}{\partial q }}{\left| \frac{\partial {{\varvec{\sigma }}}}{\partial p } \times \frac{\partial {{\varvec{\sigma }}}}{\partial q }\right| }. \end{aligned}$$

As a first example, let us compare a circular crack of radius a with a semi-infinite circular cylindrical crack of radius a (Fig. 4a, b). The fronts for these two cracks are identical, but ${\mathbf{e}}_1 = {\mathbf{e}}_r$ for the circular crack and ${\mathbf{e}}_1 ={\mathbf{e}}_z$ for the cylindrical crack; here ${\mathbf{e}}_r$ and ${\mathbf{e}}_z$ as the basis vectors of the standard cylindrical coordinates. If both cracks grow uniformly along ${\mathbf{e}}_1$, then $\Gamma$ of the circular crack undergoes self-similar expansion, whereas $\Gamma$ of the cylindrical crack undergoes rigid body translation along the z-axis. The latter growth mode does not fit the framework adopted in Sect. 3, as the front does not deform. With this example, we are not concerned about generality of results developed in Sect. 3, as we regard a non-deforming crack front merely as an interesting counter-example rather than a case of practical significance. Rather we seek a length parameter capable of discriminating between the two circular fronts, and the geodesic curvature senses the difference, as $\kappa _g = 1/a$ for the circular crack and $\kappa _g = 0$ for the cylindrical crack.

Fig. 4

Three cracks and their attributes: a circular, b circular cylindrical, c truncated spherical

Our next example involves a truncated spherical crack formed by cutting a sphere of radius R with a plane located at a distance h from the center (Fig. 4c). In this case $\Gamma$ is a circle of radius $a=\sqrt{R^2-h^2}$. It is convenient to parameterize the cut with the azimuth angle $\theta$, so that $h=R\cos {\theta }$ and $a=R\sin {\theta }$. The expressions for the curvatures are

$$\begin{aligned} \kappa = \frac{1}{R\sin {\theta }}\quad {\mathrm{and}}\quad \kappa _g = \frac{1}{R\tan {\theta }}. \end{aligned}$$

Note that $\kappa _g<0$ for $\theta > \pi /2$, which justifies the use of $\left| \kappa _g\right|$ rather than just $\kappa _g$ in (32).

If $\theta = \pi /2$ then $\kappa _g = 0$ and the crack is hemi-spherical. In this particular case, ${\mathbf{e}}_1$ is perpendicular to the equator, and uniform growth along ${\mathbf{e}}_1$ involves rigid body motion. Thus, the fronts of the hemi-spherical and cylindrical cracks have the same growth modes and geodesic curvatures. In general, ${\mathbf{e}}_1$ is along the negative meridional direction,

$$\begin{aligned} {\mathbf{e}}_1 = -{\mathbf{e}}_\theta =- {\mathbf{e}}_r \cos {\theta } + {\mathbf{e}}_z \sin {\theta }, \end{aligned}$$

where ${\mathbf{e}}_r$ is along the radial direction of the standard cylindrical coordinates attached to $\Gamma$ (Fig.  4c). A uniform crack growth increment along ${\mathbf{e}}_1$ with velocity v, shrinks the crack front from a to $a-v \cos {\theta }\Delta \Theta$, so that the corresponding rate of stretch is

$$\begin{aligned} {{\dot{\lambda }}} = -\frac{v \cos {\theta }}{a}= -\frac{v }{R\tan {\theta }}=-v \kappa _g. \end{aligned}$$

Upon comparison of this equation with (16), one can conclude that $\kappa _g$ should be a good candidate for replacing $\kappa$. Note that there is no minus sign in (16) because $\kappa \ge 0$ and growth along ${\mathbf{e}}_1$ results in expansion of $\Gamma$. This is a moot point since $\kappa$ is replaced with $\left| \kappa _g\right|$ rather than $\kappa _g$.

5 Discussion

In this paper, we examined three-dimensional crack growth initiation under the assumption that the crack front remains smooth. We addressed two important modeling issues. First, we established that, at each point along the front, the velocity and configurational force can be confined to the local normal plane. This allows us to generalize any two-dimensional criterion to three dimensions. Second, we developed a simple mesoscopic model for along-the-front non-locality to eliminate pathological growth patterns like the one shown in Fig. 1.

While the replacement of three stress intensity factors with two configurational forces, adopted in Sect. 2, is entirely rigorous, it limits ones modeling capabilities. In particular, for local symmetry principle, $K_{II} (S)=0$ (7) implies that there is only one non-zero configurational force component,

$$\begin{aligned} J_1 (S) = \frac{1-\nu ^2}{E} K_{I}^2 (S)+ \frac{1+\nu }{E} K_{III}^2 (S). \end{aligned}$$

It is clear that any prescribed $J_1 (S)$ can be realized by infinitely many combinations of $K_{I} (S)$ and $K_{III} (S)$, ranging from pure Mode I to pure Mode III. For small values of the ratio $K_{III}/K_{I}$, the crack grows smoothly, similar to pure Mode I cracks. In contrast, for large values of the ratio, the crack front fragments by forming secondary cracks, and this behavior must be associated with nucleation/fragmentation rather than growth. This dependence on the ratio $K_{III}/K_{I}$ is reflected in the right-hand side of (1). Of course this limitation does not invalidate our work, but rather demonstrates its limitations, and suggests that a more general approach is required for modeling both growth and nucleation/fragmentation. Such an approach must overcome major conceptual obstacles, as dominant K-fields require smooth fronts whose characteristic along-the-front length scale must significantly exceed the process zone size. This requirement may be difficult to satisfy in the presence of nucleated micro-cracks.

The second issue was resolved by regarding the crack front as a configurational rod, and developing a basic mechanical model to describe its behavior. A proposed approximate solution, given by (27), (31), and (32), is a twice differentiable function, compactly supported over a neighborhood of the crack front (Fig. 3). Further, it does not involve any non-standard fracture parameters, but it involves $v_0$ as a free parameter. Its determination is particularly instructive for hydraulic fracturing problems (Rungamornrat et al. 2005; Castonguay et al. 2013; Detournay 2016), where $v_0$ is dictated by the balance between the volume created by crack growth vis-a-vis the volume of injection fluid.

The proposed mesoscopic model was developed by significantly extending the scope of configurational mechanics, by introducing appropriate rates of deformation, conjugate configurational internal forces, and constitutive equations. While the geometric and equilibrium equations have a solid footing, the constitutive equations were constructed using nothing more than dimensional analysis. Nevertheless, we are comfortable with the key constitutive assumption that the characteristic cross-sectional radius $\rho$ is the process zone size. The structure of governing equations echoes numerous connections between configurational and structural mechanics (Bigoni et al. 2015). Furthermore, recent developments in interpreting configurational forces in the Newtonian (as opposed to Lagrangian) context of continuum mechanics (Ballarini and Royer-Carfagni 2016) lend more support to the approach presented in Sect. 3.

Differential geometry of planar curves was central to introducing the strain rates and relating them to the crack front velocity. To accomplish this, it was essential to replace $\kappa _s$, fundamental to identifying the curve shape, with $\kappa$, natural for carrying out calculations. For the circular crack, the distinction between $\kappa _s$ and $\kappa$ is immaterial, but in general one must require that $\kappa _s$ does not change its sign in the mesoscopic neighborhood of ${\varvec{x}}_0$.

Formally, our approach easily extends to three-dimensional curves, and it results in the equations

$$\begin{aligned} {{\dot{\lambda }}}= & {} - \kappa v_n, \\ {{\dot{\kappa }}}= & {} (\kappa ^2 - \tau ^2)v_n - v^{\prime \prime }_n - \tau ^\prime v_b - 2 \tau v_b^\prime , \\ {{\dot{\tau }}}= & {} \frac{ \kappa \tau ''-\kappa ' \tau ' +2 \kappa ^3 \tau }{\kappa ^2} v_n + \frac{3 \kappa \tau ' -2 \tau \kappa ' }{\kappa ^2}v_n^\prime + \frac{2 \tau }{\kappa }v_n^{\prime \prime } \\&- \frac{\tau \left( 2 \kappa \tau '-\tau \kappa ' \right) }{\kappa ^2} v_b + \frac{\kappa ^2 -\tau ^2}{\kappa } v_b^\prime -\frac{\kappa '}{\kappa ^2} v_b^{\prime \prime }+ \frac{1}{\kappa } v_b^{\prime \prime \prime }. \end{aligned}$$

In these equations, the subscript b refers to the bi-normal direction, and $\tau$ is the torsion. For three-dimensional curves, the shape is fully prescribed by the functions $\kappa (S)$ and $\tau (S)$, so there is no need to negotiate between $\kappa _s$ and $\kappa$. However, this is true only for $\kappa (S)>0$, and one can easily establish that by eliminating points with zero curvature, one effectively eliminates the difference between $\kappa$ and $\kappa _s$.

Using the principle of virtual power, we introduced the internal forces conjugate to the rates of deformation. For planar curves, those included line tension and line bending. The former is an established concept in mechanics of dislocations, while the latter is critical to non-locality. That is, if line bending is neglected, the proposed model becomes local. In three dimensions, ${{\dot{\tau }}}$ induces the line twisting T. Further, the principle of virtual power yields two equilibrium equations relating the F, M, and T to $J_n$ and $J_b$. However those equations are extremely complicated and their usefulness is unclear.