1 Introduction

Nuclear reactor pressure vessel (RPV) is one of the most important equipments for nuclear power plants. It is very important to ensure the structural integrity of the RPV under pressurized thermal shock (PTS) for the operation safety of nuclear power plant. PTS is characterized by a rapid cooling of the internal surface of pressure vessel. Under the PTS loads, the cooling injection water is pumped into the downcomer through inlet nozzles (Siegele et al. 1999; González-Albuixech et al. 2015). During the cooling transient, the difference of temperature along the RPV wall generates a high tensile stress. Together with the internal repressurization, the safety of RPV could undergo a great challenge. Moreover, the interior of RPV is irradiated by an intensive neutron (Marini et al. 2015; Kim et al. 2000), which causes a decrease in the fracture toughness of the RPV steel. If the operation temperature and pressure exceed the limit, the defect in the inner surface of the vessel could propagate rapidly, even through the wall thickness. So it is necessary to carry out the research on the integrity of RPV during the PTS transient, and fully analyze the various factors that affect the failure of the structure.

The purpose of the PTS analysis and assessment is to provide technical support for the safe operation of RPV. By deterministic fracture mechanics (DFM) analysis, the structural integrity during the PTS transient can be analyzed. Traditionally, linear elastic fracture mechanics was mostly used to study the threat of brittle fracture of material to RPV security (Keim et al. 2001; Chen et al. 2014; Jhung et al. 2009; Chou and Huang 2014). Nevertheless, the RPV materials have certain ductility when the operating temperature is higher than the ductile–brittle transition (DBT) temperature. In this case, the thermo-mechanical analysis is relevant with multiple nonlinear factors, and the DFM analysis can easily cause over conservatism.

In recent years, the problems of elastic–plastic fracture of RPV have gradually aroused concern. Through the tensile and elastic–plastic fracture tests of a low-alloy RPV steel in hydrogenated high-temperature water (HTW), the fracture and deformation mechanism were evaluated in detail (Roychowdhury et al. 2016). Under core meltdown scenario, failure analysis of plane axisymmetric RPV model was carried out with consideration of creep and plasticity (Mao et al. 2016, 2017). The elastic and elastic–plastic fracture analysis of a RPV subjected to PTS was performed by considering the crack tip constraint effect (Qian et al. 2014). Then, the elastic–plastic constitutive model was adopted for ductile crack propagation analysis under the PTS loads. Combined with the specified damage criterion, the ultimate bearing capacity of the cracked nozzle region of the RPV with fixed wall thickness was evaluated (Sun et al. 2017). On the basis of the previous work, an integrated RPV model (including the downcomer, nozzles, hemispherical caps, etc.) is first established in this study. The XFEM (Belytschko and Gracie 2007) is used to obtain the allowable crack sizes for different base wall thicknesses at the critical time of the PTS transient. Furthermore, the effects of the crack position and crack tip shape on the ultimate bearing capacity of the RPV structure are fully analyzed. Through comparison and verification, the results of this study can accurately simulate the plastic failure behavior of the RPV structure under PTS, and provide a guarantee for the safe operation and management of the nuclear power plant.

2 Methodology

2.1 Elastic–plastic constitutive relation

When the plastic deformation occurs, the stress level for the isotropic material is determined by the Von-Mises yield criterion. The strain after the initial yield can be assumed to be the sum of the elastic and plastic strains

$$\begin{aligned} d\varepsilon _{{ij}} =d\varepsilon _{{ij}}^e +d\varepsilon _{{ij}}^p \end{aligned}$$
(1)

The elastic strain increment is divisible into the deviator stress and hydrostatic stress components

$$\begin{aligned} {d\varepsilon _{{ij}}^e} =\frac{d{\sigma }_{{ij}}^{'} }{2G}+\frac{\left( {1-2\nu } \right) }{E}\delta _{{ij}} d\sigma _{{kk}} \end{aligned}$$
(2)

where G is the shear modulus, \({\sigma }_{{ij}}^{'} \) is the deviator stress, and \(\sigma _{{kk}} \) represents the hydrostatic stress.

The plastic strain increment is proportional to the stress gradient of the plastic potential function

$$\begin{aligned} d\varepsilon _{{ij}}^p =d\lambda \frac{\partial Q}{\partial \sigma _{{ij}} } \end{aligned}$$
(3)

where \(d\lambda \) is the plastic multiplier. According to plastic flow rule (Bland 1957), the potential function and yield function are identical, i.e. \(Q\equiv f\). Hence, Eq. (1) can be written as

$$\begin{aligned} d\varepsilon _{{ij}} =\frac{d{\sigma }'_{{ij}} }{2G}+\frac{\left( {1-2\nu } \right) }{E}\delta _{{ij}} d\sigma _{{kk}} +d\lambda \frac{\partial f}{\partial \sigma _{{ij}} } \end{aligned}$$
(4)

The Von-Mises yield function is expressed as

$$\begin{aligned} f\left( {\varvec{\upsigma }} \right) =K\left( \kappa \right) \end{aligned}$$
(5)

where \(\kappa \) is the plastic work in the plastic deformation process. Then Eq. (5) takes the form

$$\begin{aligned} F\left( {{\varvec{\upsigma }},\kappa } \right) =f\left( {\varvec{\upsigma }} \right) -K\left( \kappa \right) =0 \end{aligned}$$
(6)

After resolution, the following equations are given by

$$\begin{aligned} \mathbf{a}^{\mathrm{T}}d{\varvec{\upsigma }}-Ad\lambda =0 \end{aligned}$$
(7)

with

$$\begin{aligned} \mathbf{a}^{\mathrm{T}}= & {} \left\{ {\frac{\partial F}{\partial {\varvec{\upsigma }}}} \right\} ^{\mathrm{T}}\nonumber \\= & {} \left[ {\frac{\partial F}{\partial \sigma _{{xx}} },\frac{\partial F}{\partial \sigma _{{yy}} },\frac{\partial F}{\partial \sigma _{{zz}} },\frac{\partial F}{\partial \sigma _{{yz}} },\frac{\partial F}{\partial \sigma _{{zx}} },\frac{\partial F}{\partial \sigma _{{xy}} }} \right] , \nonumber \\ A= & {} -\frac{1}{d\lambda }\frac{\partial F}{\partial \kappa }d\kappa \end{aligned}$$
(8)

Then, Eq. (3) can be rewritten as

$$\begin{aligned} d{\varvec{\upvarepsilon }}=\left[ \mathbf{D} \right] ^{-1}d{\varvec{\upsigma }}+d\lambda \frac{\partial Q}{\partial {\varvec{\upsigma }}} \end{aligned}$$
(9)

where \(\left[ \mathbf{D} \right] \) is elastic constitutive matrix. After mathematical calculation, the plastic multiplier can be obtained as

$$\begin{aligned} d\lambda =\frac{\mathbf{a}^{\mathrm{T}}\left[ \mathbf{D} \right] \;d{\varvec{\upvarepsilon }}}{\mathbf{a}^{\mathrm{T}}\left[ \mathbf{D} \right] \;\mathbf{a}+A} \end{aligned}$$
(10)

Finally, the relation of stress and strain increments can be expressed as

$$\begin{aligned} d{\varvec{\upsigma }}= & {} \left[ \mathbf{D} \right] _{{ep}} d{\varvec{\upvarepsilon }}=\left( {\left[ \mathbf{D} \right] -\left[ \mathbf{D} \right] _p } \right) d{\varvec{\upvarepsilon }} \end{aligned}$$
(11)
$$\begin{aligned} \left[ \mathbf{D} \right] _p= & {} \frac{\left[ \mathbf{D} \right] \mathbf{aa}^{\mathrm{T}}\left[ \mathbf{D} \right] }{\mathbf{a}^{\mathrm{T}}\left[ \mathbf{D} \right] \mathbf{a}+A} \end{aligned}$$
(12)

As mentioned above, the yield and potential functions are identical in accordance with the plastic flow rule. In this way, the elastoplastic constitutive matrix \(\left[ \mathbf{D} \right] _{{ep}}\) is symmetric.

2.2 XFEM displacement approximation and discretized equations

Compared with the traditional finite element method, the XFEM is used to deal with the problem of crack propagation. The stress singularity near the crack tip is expressed by the asymptotic function, and the displacement jump at the crack surface is described by the discontinuous function. The integral displacement function is defined as (Singh et al. 2012)

$$\begin{aligned} \hbox {u}\left( x \right)= & {} \!\sum _{i=1}^{n_c } {N_i } \left( x \right) u_i \!+\!\sum _{j=1}^{n_s } {N_j } \left( x \right) \left[ {H\left( x \right) \!-\!H\left( {x_j } \right) } \right] a_j\nonumber \\&+\sum _{k=1}^{n_t } {N_k } \left( x \right) \left[ {\beta _\alpha \left( x \right) -\beta _\alpha \left( {x_k } \right) } \right] b_k \end{aligned}$$
(13)

where, \(n_c\), \(n_s\) and \(n_t\) respectively represent the number of regular nodes, the number of reinforced nodes and the number of crack-tip nodes; \(N_i \left( x \right) \), \(N_j \left( x \right) \), and \(N_k \left( x \right) \) is the node shape function; \(u_i\) is the node displacement vector; \(\hbox {a}_j\) and \(\hbox {b}_k\) is the nodal enriched variables; \(H\left( x \right) \) is the Heaviside function across the crack surface; \(\beta _\alpha \left( x \right) \) the asymptotic function at crack tip.

The discontinuous jump function \(H\left( x \right) \) is expressed as

$$\begin{aligned} H\left( x \right) =\left\{ {\begin{array}{ll} 1&{}\quad \hbox {if }(\hbox {x}-\hbox {x}^*)\cdot n\ge 0 \\ -\,1&{}\quad {otherwise} \\ \end{array}} \right. \end{aligned}$$
(14)

where x is the sample point, \(x^{{*}}\) is the closest point to x, and n is the unit outward normal vector.

In the discrete system of equilibrium equations, the elemental stiffness matrix and external force vector are defined as

$$\begin{aligned} \mathbf{K}_{{ij}}^e= & {} \left[ {\begin{array}{l} \mathbf{K}_{{ij}}^{{uu}} \quad \mathbf{K}_{{ij}}^{{ua}} \quad \mathbf{K}_{{ij}}^{{ub}} \\ \mathbf{K}_{{ij}}^{{au}}\quad \mathbf{K}_{{ij}}^{{aa}} \quad \mathbf{K}_{{ij}}^{{ab}} \\ \mathbf{K}_{{ij}}^{{bu}} \quad \mathbf{K}_{{ij}}^{{ ba}} \quad \mathbf{K}_{{ij}}^{{bb}} \\ \end{array}} \right] \end{aligned}$$
(15)
$$\begin{aligned} \mathbf{f}^{e}= & {} \left\{ {\mathbf{f}_i^u \;\;\;\mathbf{f}_i^a \;\;\;\mathbf{f}_i^{b1} \;\;\;\mathbf{f}_i^{b2} \;\;\;\mathbf{f}_i^{b3} \;\;\;\mathbf{f}_i^{b4} } \right\} ^{T} \end{aligned}$$
(16)

For finite strain, the sub-matrices of Eq. (15) can be written as

$$\begin{aligned} \mathbf{K}_{{ij}}^{{rs}} =\int _{\Omega ^{e}} {\left( {\mathbf{B}_i^r } \right) { }^T\mathbf{D}_{\mathrm{eq}} \left( {\mathbf{B}_j^s } \right) \;h\;d\Omega \;\;\;\;\left( {r,s=u,a,b} \right) } \end{aligned}$$
(17)

The sub-vectors of Eq. (16) are expressed as follows

$$\begin{aligned} \mathbf{f}_i^u= & {} \int _{\Omega ^{e}} {N_i \;\mathbf{b}\;d\Omega } +\int _{\Gamma _t } {N_i \;{\bar{\mathbf{t}}}\;d\Gamma } \end{aligned}$$
(18)
$$\begin{aligned} \mathbf{f}_i^a= & {} \int _{\Omega ^{e}} {N_i \left( {H\left( \mathbf{x} \right) -H\left( {\mathbf{x}_i } \right) } \right) \;\mathbf{b}\;d\Omega }\nonumber \\&+\int _{\Gamma _t } {N_i \left( {H\left( \mathbf{x} \right) -H\left( {\mathbf{x}_i } \right) } \right) \;{\bar{\mathbf{t}}}\;d\Gamma } \end{aligned}$$
(19)
$$\begin{aligned} \mathbf{f}_i^{b\alpha }= & {} \int _{\Omega ^{e}} {N_i \left( {\beta _\alpha \left( \mathbf{x} \right) -\beta _\alpha \left( {\mathbf{x}_i } \right) } \right) \;\mathbf{b}\;d\Omega } \nonumber \\&+\int _{\Gamma _t } {N_i \left( {\beta _\alpha \left( \mathbf{x} \right) -\beta _\alpha \left( {\mathbf{x}_i } \right) } \right) \;{\bar{\mathbf{t}}}\;d\Gamma } \end{aligned}$$
(20)

where \(\Gamma _t\) is traction boundary. The derivative matrices of shape function are given by

$$\begin{aligned} \mathbf{B}_i^u= & {} \left[ {\begin{array}{ll} N_{i,x} &{} \hbox {0} \\ \hbox {0}&{} N_{i,y} \\ N_{i,y} &{} N_{i,x} \\ \end{array}} \right] \end{aligned}$$
(21)
$$\begin{aligned} \mathbf{B}_i^a= & {} \left[ {\begin{array}{cc} \left( {N_i \left( {H\left( \mathbf{x} \right) -H\left( {\mathbf{x}_i } \right) } \right) } \right) _{,x}&{} \hbox {0} \\ \hbox {0}&{} \left( {N_i \left( {H\left( \mathbf{x} \right) -H\left( {\mathbf{x}_i } \right) } \right) } \right) _{,y} \\ \left( {N_i \left( {H\left( \mathbf{x} \right) -H\left( {\mathbf{x}_i } \right) } \right) } \right) _{,y} &{}\left( {N_i \left( {H\left( \mathbf{x} \right) -H\left( {\mathbf{x}_i } \right) } \right) } \right) _{,x} \\ \end{array}} \right] \nonumber \\ \end{aligned}$$
(22)
$$\begin{aligned} \mathbf{B}_i^{b\alpha }= & {} \left[ {\begin{array}{cc} \left( {N_i \left( {\beta _\alpha \left( \mathbf{x} \right) -\beta _\alpha \left( {\mathbf{x}_i } \right) } \right) } \right) _{,x} &{} \hbox {0} \\ \hbox {0}&{}\left( {N_i \left( {\beta _\alpha \left( \mathbf{x} \right) -\beta _\alpha \left( {\mathbf{x}_i } \right) } \right) } \right) _{,y} \\ \left( {N_i \left( {\beta _\alpha \left( \mathbf{x} \right) -\beta _\alpha \left( {\mathbf{x}_i } \right) } \right) } \right) _{,y} &{}\left( {N_i \left( {\beta _\alpha \left( \mathbf{x} \right) -\beta _\alpha \left( {\mathbf{x}_i } \right) } \right) } \right) _{,x} \\ \end{array}} \right] \nonumber \\ \end{aligned}$$
(23)

According to the above XFEM equations, the displacements and stresses in the domain can be obtained. Then the XFEM will be combined with the following damage criterion to simulate ductile crack propagation.

2.3 Damage criterion

In the damage model, the materials will show certain ductility characteristics as long as the temperature is above the nil-ductility reference temperature (Woods et al. 2001). Before fracture, local yield occurs at the crack tips, and then the cohesive crack begins to expand (Barani et al. 2011; Fagerström and Larsson 2008; Yuan and Li 2014; Su et al. 2010).

Here, the crack initiation criterion is the maximum principal tensile stress criterion. The maximum principal stress is taken as the tensile strength of material. After the initiation of damage, damage evolution is based on energy dissipated during the damage process. The damage model specifies that the fracture energy per unit area is equal to the critical energy release rate. The critical energy release rate is given by

$$\begin{aligned} G_C =\int _{\bar{{\varepsilon }}_0^{{pl}} }^{\bar{{\varepsilon }}_f^{{pl}} } {L\sigma _y } d\bar{{\varepsilon }}^{{pl}}=\int _0^{\bar{{u}}_f^{{pl}} } {\sigma _y } d\bar{{u}}^{{pl}} \end{aligned}$$
(24)

where L is the characteristic length associated with the integration points. \(\bar{{\varepsilon }}^{{pl}}\), \(\bar{{u}}^{{pl}}\) are the equivalent plastic strain and equivalent plastic displacement, respectively.

The evolution in the damage is specified in exponential form

$$\begin{aligned} D=\int _{\delta _m^o }^{\delta _m^f } {\frac{T_{\mathrm{eff}} d\delta }{G_C -G_o }} \end{aligned}$$
(25)

where \(T_{\mathrm{eff}}\) and \(\delta \) are the effective traction and displacement, respectively. \(G_o\) is the elastic energy at damage initiation. It is ensured that the energy dissipated during the damage evolution process is equal to \(G_C\), which can be obtained from Benzeggagh–Kenane law (Benzeggagh and Kenane 1996). The degradation of the mechanical properties is realized by reducing the stiffness of damage elements. The material is completely damaged if the overall damage variable reaches \(D=1\) at all integration points of an element.

3 Analysis model

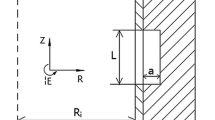
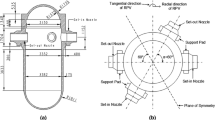
In the numerical analysis, the selected physical model of a real RPV with an inner surface crack is shown in Fig. 1. The inner radius of the RPV is 1994 mm, the thickness of the cladding is 8 mm, and the initial thickness of the base metal wall is 200 mm. Through the thickness of the vessel wall, there are two symmetric inlet nozzles opened, and the diameter is 800 mm. The inner crack is located on one of the nozzles. The 3-D model for thermal and stress analyses is created using the finite element analysis software ABAQUS v 6.13 (2013). Figure 2 shows the finite element model for the RPV containing an inner surface crack. The bottom of the vessel are constrained to restrict the movement of the rigid body. In this way, the upper part can move along the axial direction, so it is basically in accordance with the actual situation.

Fig. 1
figure 1

The physical model containing the characteristic properties

Full size image
Fig. 2
figure 2

Finite element mesh containing an inner crack on one of the nozzles

Full size image

During the cooling process, the inner sides of the downcomer and water inlet pipes are assumed to be subjected to a thermal shock caused by the emergency cooling water. Eight-node linear heat transfer brick elements (DC3D8) are adopted for heat conduction. The heat flux in the wall of the vessel is determined by the thermal conductivity and temperature gradient, and the heat flux through the inner surface of the vessel wall mainly depends on the heat transfer coefficient (Heming et al. 2003) and cooling water temperature. Since the parameters related to the convective heat transfer in the transient information are clearly given in Sect. 4.1, the cooling plume effect is not considered in the numerical modeling. The initial stress-free temperature applied in the whole model is set to \(295\,^{\circ }\hbox {C}\) to ensure no residual temperature stress is generated. The initial temperature of the injected water is consistent with that temperature. The numerical model also assumes that the distributions of heat transfer coefficient and temperature are uniform along the inner surface of the vessel. The transient temperature field is obtained and is used for fracture mechanics analysis. Correspondingly, Eight-node linear brick reduced integration elements (C3D8R) are used for high computational efficiency.

4 Reference transient and material properties

4.1 Reference transient information

During the PTS transient, the emergency cooling water is injected into the downcomer of the RPV through the inlet nozzles, and then the inner surface of the downcomer is considered to be subjected to a thermal shock. In the cooling down process, the heat flux density in the convective heat transfer from fluid to solid is the product of the heat transfer coefficient and the temperature difference between the wall temperature and water temperature. The heat transfer coefficient is a nonlinear function of the surface temperature and a large heat transfer coefficient can obviously increase the cooling rate of the wall of the vessel. Whereas the radial temperature difference of the wall is reduced with the decrease of the heat transfer coefficient. Figure 3 shows the heat transfer coefficient between the cooling water and the inner surface of the vessel for the analyzed transient. The reference transient is selected from the IAEA CRP9 (2010). According to the reference transient, the distributions of the transient internal pressure and water temperature are shown in Fig. 4. It should be noted that the pressure value suddenly reaches 16.8 MPa at 7185 s and then has a very small fluctuation, so it is theoretically the critical time of the PTS transient.

Fig. 3
figure 3

The history of heat transfer coefficient between the cooling water and the inner surface of the downcomer

Full size image
Fig. 4
figure 4

Internal pressure and cooling water temperature histories

Full size image

4.2 Material properties and fracture parameters

The base material is A508 Class 3 steel (Wu et al. 2014; Lu et al. 2017; Tanguy et al. 2005) and the cladding is made of austenitic stainless steel (Yuan et al. 1995; Hu and Cocks 2016). The thermal and mechanical parameters of the materials are introduced from previous studies (Qian and Niffenegger 2013) and listed in Table 1. In the unsteady heat conduction process, the heat exchange causes the wall temperature to change with time. In addition to the surface heat transfer coefficient introduced above, the heat flux in the wall is proportional to the thermal conductivity and temperature gradient. Thermal diffusivity \(\alpha \) are related to the thermal conductivity \(\lambda \) and specific heat capacity \(C_p\) by \(\alpha =\lambda /\rho C_p \).

Table 1 Material properties of the base metal and cladding
Full size table
Fig. 5
figure 5

Test setup

Full size image
Fig. 6
figure 6

Schematic diagram of the sample

Full size image

To study the mechanical properties of materials in the post yield state, tensile tests are carried out by using a Zwick universal testing machine, as shown in Fig. 5. The operable temperature range is 20–350 \(^{\circ }\hbox {C}\). The tests are performed under the displacement control at 0.03 mm/s for the 9 mm diameter specimens of the selected cladding and base materials. Figure 6 shows the geometry of the tensile test specimens. The test procedures meet the requirements defined by EN ISO 6892-1 (2009). The forces are measured with a load cell of 100 kN capacity and the strains with an optical system for data acquisition and analysis. The tension sensor can accurately measure the tensile forces of the specimens, and the grating ruler is used to measure the tensile deformation of the specimens during the tensile test. The accuracy of the machine is up to 1 N in force and \(1\,\upmu \hbox {m}\) in displacement. After the test data are processed by computer, the stress–strain values including tensile strength and peak strain can be obtained.

Based on the experimental data, Fig. 7 shows the relevant stress–strain curves for the base metal and cladding. The nonlinear material behavior is described by generalized Ramberg–Osgood model (Elguedj et al. 2006)

$$\begin{aligned} \frac{\varepsilon E}{\sigma _0 }=\frac{\sigma }{\sigma _0 }+\alpha \left( {\frac{\sigma }{\sigma _0 }} \right) ^{n} \end{aligned}$$
(26)

where \(\sigma _0\) and E are the yield strength and Young’s modulus, respectively. \(\alpha \) is the material constant and n is the hardening exponent. In Fig. 7a, the fitting dimensionless parameters \(\alpha =2.372\), \(n=7\) for the base metal and \(\alpha =2.912\), \(n=11\) for the cladding. In Fig. 7b, \(\alpha =0.998\), \(n=9\) for the base metal and \(\alpha =2.809\), \(n=12\) for the cladding.

Fig. 7
figure 7

Stress strain curves of base metal and cladding at different temperatures for a \(20\,^{\circ }{\hbox {C}}\) and for b \(300\,^{\circ }{\hbox {C}}\)

Full size image

In the life of reactor, the interior of RPV is irradiated by the intensive neutron. According to ASME Code Sec. XI (2010) and 10 CFR 50.61 (1996), the fracture toughness and nil-ductility reference temperature are written as

$$\begin{aligned}&\left\{ {\begin{array}{l} K_{\mathrm{IC}} =36.5+3.1\exp \left[ {0.036\;\left( {T\hbox {-}RT_{\mathrm{NDT}} +55.5} \right) } \right] \\ K_{\mathrm{IC}} \le 220\;\mathrm{MPa}\sqrt{m} \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(27)
$$\begin{aligned}&RT_{\mathrm{NDT}} =RT_{\mathrm{NDT (U)}} +M+\Delta RT_{\mathrm{NDT}} \end{aligned}$$
(28)

where, \(K_{\mathrm{IC}}\) is the crack growth fracture toughness, \(K_{\mathrm{Ia}}\) is the crack arrest fracture toughness, \(RT_{\mathrm{NDT (U)}}\) is the initial reference temperature, M is the average safety margin, and \(\Delta RT_{\mathrm{NDT}}\) is the correction value of reference temperature.

Table 2 shows the distributions of the main random parameters of the base material. It is conservatively considered that the inner wall of the RPV is subjected to a fast neutron fluence of \(5\times 10^{19}\,\hbox {n}/\hbox {cm}^{2}\) at the end of the reactor’s life. From Eq. (28), the nil-ductility reference temperature is calculated as

$$\begin{aligned} RT_{\mathrm{NDT}}= & {} RT_{\mathrm{NDT(U)}} +\Delta RT_{\mathrm{NDT}} +M\\= & {} RT_{\mathrm{NDT(U)}} +C_F \times f^{(0.28-0.1\log f)}\\&+2\sqrt{\sigma _I^2 +\sigma _\Delta ^2 }\\= & {} -\,4+20.0\times 1.4\\&+\,2\sqrt{(9.0\times 1.8)^{2}+(9.4\times 1.8)^{2}}\\= & {} 70.8\,\mathrm{F}=21.6\;^{\circ }\hbox {C} \end{aligned}$$

Then, bringing it into Eq. (27) leads to the following equations as

$$\begin{aligned} \left\{ {\begin{array}{l} K_{\mathrm{IC}} =36.5+10.5\mathrm{e}^{0.036\;T} \\ K_{\mathrm{IC}} \le 220\;\mathrm{MPa}\sqrt{m} \\ \end{array}} \right. \end{aligned}$$
(29)

For the elastic–plastic fracture problem, the critical energy release rate includes not only the surface energy but also the plastic dissipation energy. However, the latter changes with the way of loading. To deal with this complex problem, the critical energy release rate could be calculated by the above obtained fracture toughness based on the conservative principle. The relation between them for plane-strain condition is given by

$$\begin{aligned} G_{\mathrm{I}C} =\frac{1-\upsilon ^{2}}{E}K_{\mathrm{I}C}^2 \end{aligned}$$
(30)

According to Eqs. (29) and (30), the calculated critical energy release rates for the base metal are listed in Table 3.

Table 2 Main random variables of A508 Cl3 steel
Full size table
Table 3 Critical energy release rates at different temperatures
Full size table

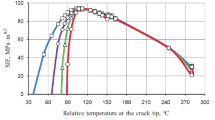
Next, the fracture test is used to assess the feasibility of the above numerical calculation. Taking into account the risk of the actual loading of the RPV, Fig. 8 shows the standard SENT specimen used for the fracture test. The specimen is directly cut from TA2 sheet, and is manually grinded and polished by using sandpaper. The main test equipment contains a MTS809 universal testing machine and a TestStarII control system. According to ASTM E1820-05a (2016), fatigue precracking is performed on the specimen. The initial crack length is obtained by flexibility method, and a MTS632.02F-20 extensometer is used to measure the crack tip opening displacement of the specimen. According to the relevant parameters obtained from the experimental results, the critical energy release rates can be calculated by Eq. (24). It shows that the critical energy release rate obtained in the environment of 50 \({^{\circ }}\)C is close to the corresponding numerical result in Table 3. Note that this temperature is close to the temperature of the crack tip region obtained from the following thermal analysis at the critical time of the PTS transient (see Fig. 4). In this way, the data in Table 3 is considered to be applied to the analysis of crack propagation.

Fig. 8
figure 8

Configuration and dimensions of the SENT specimen

Full size image

5 Numerical result and discussion

5.1 Thermal analysis and thermo-mechanical coupling analysis

In thermal analysis, the whole vessel is given a uniform initial temperature \(295\,^{\circ }\hbox {C}\). Due to the rotationally symmetry of the downcomer, the heat conduction can only produce a one-dimensional transient temperature distribution. For the structure with defects, the direction of crack is generally consistent with the heat conduction direction.

According to the history of the cooling water temperature, the 8-node linear heat transfer brick elements are used for thermal analysis. The distributions of temperature and heat flux along the wall thickness of the vessel during the PTS transient are shown in Figs. 9 and 10, respectively. From Fig. 9, the temperatures along the vessel wall show a downward trend from outside to inside. With the time extension, the temperature gradients in the base wall gradually decline. Nevertheless, the temperature gradients in the cladding continue to be very high. According to the heat flux distributions in Fig. 10, the relatively high heat fluxes are generated close to the inner wall, which shows a strong thermal shock effect. Due to the different thermal properties of the cladding and base metal, a discontinuity of heat flux exists in the interface between the base metal and cladding. The lower thermal conductivity of the cladding reduces the heat fluxes through the base metal wall. This heat insulation effect of the cladding is obvious, especially in the early stage of the thermal shock.

In the high stress area near the nozzle, Fig. 11 shows the circumferential stress curves along the wall thickness of the vessel at different transient times. It can be found that the presence of the cladding does not improve the carrying capacity of the base material. In the unloading process of the internal pressure, the total stress values change little due to the continuous increase of thermal stress. Later, as the internal pressure increases sharply, the stress generated by it plays a major role in the thermo-mechanical coupling field. Consequently, most of the base material close to the inner wall has yielded. Since the strength of cladding is relatively low, the values of the stresses in it almost remain unchanged.

Fig. 9
figure 9

Temperature distributions along the wall thickness of the vessel at different transient times

Full size image
Fig. 10
figure 10

Heat flux distributions along the wall thickness of the vessel at different transient times

Full size image
Fig. 11
figure 11

Distributions of the circumferential stresses along the wall thickness direction on one inlet nozzle of the RPV with free defect during the PTS transient

Full size image

5.2 Ductile fracture and failure analysis for different base wall thicknesses

Firstly, it is assumed that a surface crack appears on one nozzle. The purpose is to evaluate the form of crack propagation and obtain the critical crack sizes under the PTS. Since the overall temperature is much higher than the calculated reference temperature, the materials show good ductility characteristics. The damage process is simulated using the XFEM. When \(a=40\) mm and \(L=80\) mm (refer to Fig. 1), the severe PTS loads can cause crack propagation, and then the ultimate load bearing state is reached. Figure 12 shows the Mises stress distributions and propagation path of the inner crack with the above sizes from 7125 to 7185 s. As the internal pressure load sharply increases from 2.5 to 16.8 MPa, the crack is extended along the radial direction. Figure 13 shows the corresponding crack propagation path obtained by the mesh refinement. In the same thermo-mechanical coupling field, the paths and the sizes of the extended crack in Figs. 12 and 13 are basically consistent. From Fig. 13, the damage evolution characterized by the STATUSXFEM indicates that a part of the cohesive cracks forms real cracks, and the other part requires additional energy to be opened. Although the extended crack has not been fully opened, the unsteady crack propagation is about to occur.

Fig. 12
figure 12

Crack path and Von Mises stress fields for the base wall thickness \(t=200\) mm, \(a=40\) mm and \(L=80\) mm (the water inlet pipe is not displayed)

Full size image
Fig. 13
figure 13

Crack path obtained by different element sizes \((10\,\hbox {mm}\,\times \,10\,\hbox {mm})\) on the crack surface for the base wall thickness \(t=200\) mm, \(a=40\) mm and \(L=80\) mm

Full size image

In fact, most of the cracks found in RPVs are surface cracks (Bass et al. 2001; Beardsmore et al. 2003; Dickson et al. 2000; Moinereau et al. 2001). Then different cracks with a / t ratio of 0.1, 0.2 and 0.3 are created for fracture mechanics analysis. Figure 14a shows the effect of crack size on ultimate bearing capacity of the structure in the transient temperature field at 7185 s. When the base wall thickness is reduced to 160 mm, the ultimate pressure curves are plotted in Fig. 14b. Compared with the results in Fig. 14a, the allowable crack lengths are reduced under the peak internal pressure of 16.8 MPa during the PTS transient for relatively deep cracks. For the shallow surface crack (\(a=20\) mm), the crack length does not pose a challenge to the strength of the RPV structure.

Fig. 14
figure 14

Ultimate internal pressure versus crack size for different base wall thicknesses at the critical time a \(t=200\) mm, b \(t=160\) mm

Full size image
Fig. 15
figure 15

Crack path and Von Mises stress fields for the base wall thickness \(t=120\) mm, \(a=20\) mm and \(L=60\) mm

Full size image

When \(t \le 120\) mm, the allowable crack sizes are confined to \(a=20\) mm and \(L=60\) mm during the PTS transient. The crack path and Mises stress fields are shown in Fig. 15. It can be found that the crack only expands the dimension of one element along the radial direction and then the ultimate bearing state would be reached. Since the surface crack is close to the inner wall of the vessel, the thermal shock significantly reduces the toughness of the base material and contributes to the unstable crack propagation. Correspondingly, Fig. 16 plots the circumferential stress curves along the thickness of the base wall in longitudinal symmetrical section (including the crack surface). l in the label denotes the distance from the inlet nozzle along the axial direction. Since the cladding is not the main bearing part of the structure, the stress distributions within it are not shown. At 7185 s, the stress level of the whole base wall is greatly improved. Combined with Figs. 15 and 16, the stress concentration area is located at the radial extended crack tips with \(l=0\)–0 mm, 40 mm away from the base interface, where most of the stresses nearly reach the tensile strength of the base material in the transient temperature field. Due to the decrease of the base wall thickness, the low stress area on the ligament does not exist. The maximum value of the equivalent plastic strain at the critical time is 0.0153, which satisfies the requirement of stiffness.

Fig. 16
figure 16

Circumferential stress distributions along the base wall with \(t=120\) mm at different transient times a 7125 s, b 7185 s

Full size image

5.3 The effect of crack position on the ultimate bearing capacity

For a certain wall thickness of the RPV, the allowable crack sizes increase as the distance from the nozzle increases. Figure 17 shows the allowable crack length curves corresponding to the distance from the nozzle in the limit bearing state. The non-extended parts in the curves indicate that the change of crack length doesn’t affect the ultimate bearing capacity of the structure. For \(t=200\) mm and \(t=160\) mm, the length of the shallow surface crack with a \(=\) 20 mm also could not pose a threat to the bearing capacity of the structure.

From Fig. 17, relatively short cracks are allowed to appear on the nozzle for different base wall thicknesses. The corresponding allowable crack sizes are obtained from the results in Sect. 5.3. When the distance from the nozzle reaches 80 mm, the allowable crack length is doubled. Figures 18 and 19 shows the transient Von Mises stress fields and crack paths for \(t=200\) mm and \(t=120\) mm, respectively. As the internal pressure rises to 16.8 MPa at 7185 s, they both reach the ultimate bearing state. At the critical time, the stress level in the crack zone is generally high. Especially when the thickness of the base wall reaches 120 mm, most of the base material near the nozzle region bears extremely high stress, and the overall failure of the structure is about to occur.

Fig. 17
figure 17

Allowable crack length vs. crack position during the PTS transient

Full size image

5.4 The effect of crack tip shape on the ultimate bearing capacity

Fig. 18
figure 18

Crack path and Von Mises stress fields for the base wall thickness \(t=200\) mm. The distance from the axial crack tips to the nozzle is 80 mm

Full size image
Fig. 19
figure 19

Crack path and Von Mises stress fields for the base wall thickness \(t=120\) mm. The distance from the axial crack tips to the nozzle is 80 mm

Full size image

In order to make a complete analysis of the fracture properties of the RPV, the effect of the crack tip shape on the bearing capacity of the structure should be taken into account. For comparison, the rectangular and 1/4 circumferential (or elliptical) cracks with equal depth and length are considered respectively on the nozzle. Through the ductile fracture analysis, the aim is to find out the law of the crack propagation and check whether the shape of the crack tips has a influence on the ultimate bearing capacity of the structure.

First, the depth and length of the selected cracks are set to be 20 mm, i.e. \(a/t=L/t=0.1\). The Mises stress fields and the crack propagation paths for different base wall thicknesses before and after the mutation of internal pressure are shown in Figs. 20 and 21 respectively. At 7185 s, the limit internal pressure values corresponding to the two shapes of cracks are consistent in the same transient temperature field. This means that the crack tip shape has no influence on the ultimate bearing capacity of the structure. Compared with the actual PTS peak pressure of 16.8 MPa, the limit internal pressure values of the critical time increase sharply. Figure 22 shows the damage degrees and propagation paths of the two shapes of cracks for different base wall thicknesses. The red part represents the preset, fully opened crack. In the limit bearing state, both of the two kinds of cracks propagate along the radial and axial directions for the thick base wall. With the decrease of the base wall thickness, the circumferential crack propagates just along the radial direction before the unstable crack propagation in the thermo-mechanical coupling field.

Fig. 20
figure 20

Crack paths and Von Mises stress fields before and after the sudden change of internal pressure for \(t=200\) mm, \(a=20\) mm and \(L=20\) mm

Full size image
Fig. 21
figure 21

Crack paths and Von Mises stress fields before and after the sudden change of internal pressure for \(t=120\) mm, \(a=20\) mm and \(L=20\) mm

Full size image

Next, the fracture failure behavior caused by the rectangular and elliptical cracks with the depth length ratio of 1/2 is then analyzed. The results show that the cracks with two different shapes both tend to propagate along the radial direction, and the ultimate bearing capacity of the RPV model with the elliptical crack is slightly lower than that with the rectangular crack. Compared with the crack depth of 20 mm, the doubling of the crack length causes the value of the limit internal pressure to drop by more than 5 MPa. As a result, the utilization ratio of the strength of the base material is obviously decreased. From Fig. 23, it can be seen that the extension direction of the cracks with the two shapes is basically consistent, and the extension degree of the rectangular cracks in the steady state is equal. When \(t=200\) mm, the expansion of the elliptical crack is sufficient, and some of the extended cracks are fully opened. With the decrease of the base wall thickness, the degree of steady expansion of the elliptical crack declines.

Fig. 22
figure 22

Comparison of crack propagation paths and damage degrees for the cracks with two different shapes

Full size image
Fig. 23
figure 23

Comparison of crack propagation paths and damage degrees for the two shapes of cracks with the depth length ratio of 1/2

Full size image

6 Conclusions

The finite element method is used to obtain the transient temperature field and the elastic–plastic stress strain field of the RPV model. Combined with the specified damage criterion, the propagation of the ductile crack is simulated with XFEM. The indirect coupling method is used to deal with the complex thermal-mechanical coupling problems. Under the severe PTS loads, the allowable crack sizes for different base wall thicknesses are obtained. The effects of the crack position and the crack tip shape on the ultimate bearing capacity of the RPV structure are emphatically analyzed. From the numerical results of the plastic failure analysis, the following conclusions can be drawn:

  • When the internal pressure value reaches 16.8 MPa, i.e.the critical time of the PTS transient, the inner surface crack on the nozzle tends to propagate along the radial direction. Due to the decrease of the toughness of the base material caused by the thermal shock, the steady crack propagation under the critical load condition is not sufficient.

  • Under the severe PTS, the thickness effect of the base wall is obvious. When the base wall thickness \(t\ge 160\) mm, the length of the shallow surface crack could not pose a threat to the bearing capacity of the RPV structure. When the base wall thickness is reduced to 120 mm, the allowable depth and length of the surface crack on the nozzle are confined to 20 mm and 60 mm, respectively.

  • When \(t=120\) mm, the effect of the crack length on the structure bearing capacity can be avoided only if the shallow surface crack is more than 80 mm away from the nozzle. The stress field in the cladding is maintained at a lower level for its relatively low material strength.

  • For the shallow surface crack with a short length on the nozzle, the crack tip shape does not affect the ultimate bearing capacity of the structure. For the shallow surface crack with the depth length ratio of 1/2, the ultimate bearing capacity of the RPV with the elliptical crack is slightly lower than that with the rectangular crack. As the crack length continues to increase, the effect of the crack tip shape on the ultimate bearing capacity of the structure can be ignored.