1 Introduction

As a smart material, hygrothermopiezoelectric material can couple mechanical, electric and hygrothermal characteristics and has been widely used in transportation, aerospace and automotive industries (Varadan et al. 2006). The multi-physical behaviors of hygrothermopiezoelectric material can be influenced by complex environment including mechanical, electrical, moisture and temperature fields, and these fields can affect each other (Smittakorn and Heyliger 2000). Furthermore, it is reported that the combined effect of moisture and temperature, the so-called hygrothermal effect, has a significant influence on the structural behavior of hygrothermopiezoelectric composites (Whitney and Ashton 1971; Sih et al. 1986; Hyer 1998).

Due to the significant importance in engineering application, a lot of literature was published analyzing the behavior of hygrothermopiezoelectric media in multi-field environments, analytically and numerically. In terms of the analytical solution, Smittakorn and Heyliger (2001) studied both steady-state and transient behavior of laminated hygrothermopiezoelectric plate under the coupled multi-field environment and presented the fundamental equations of linear hygrothermopiezoelectricity in a differential form. Wang et al. (2005) presented an analytical method to analyze the histories and distribution of dynamic interlaminar stresses in rectangular laminated plates with layered piezoelectric actuators and simply supported edges in hygrothermal environments. Altay and Dokmeci (2007) reviewed the variational principles for fundamental equations of hygrothermopiezoelectric materials. Akbarzadeh and Chen (2013) presented an analytical solution for hygrothermal stresses in 1D functionally graded, piezoelectric media. Zenkour (2014) obtained an analytical solution for hygrothermal responses in inhomogeneous piezoelectric hollow cylinders under mechanical and electric loadings. Altay and Dokmeci (2014) listed the fundamental equations for hygrothermopiezoelectricity in both differential and variational forms, and proposed the generalized, variational principle for the interaction of two different hygrothermopiezoelectric materials. Dini and Abolbashari (2016) presented the general theoretical analysis of a thick-walled cylinder made of functionally graded, piezoelectric materials subjected to a non-axisymmetric hygro-thermo-electro-mechanical loading.

In terms of numerical simulation, Yi et al. (1999) developed a finite element algorithm to efficiently deal with the problems in the design of smart structures. Yang et al. (2006) studied the coupling effect of moisture and temperature on the transient hygrothermal stresses of an infinite long, circular cylinder. Raja et al. (2004a, b, c) utilized a finite element method involving coupled piezoelectric field with hygrothermal strain.

The first order shear deformation theory was implemented in a nine-noded Lagrangian plate or shell element to study the dynamic behavior of smart composite thin plates and shells. Mahato and Maiti (2010) investigated the flutter control of smart composite plates under subsonic airflow in an hygrothermal environment and presented numerical examples of isotropic and laminated composite plates with and without hygrothermal effect based on finite element model. Chiba and Sugano (2011) numerically analyzed the transient heat and moisture diffusion in a multi-layer plate and the resulting hygrothermal stresses. Saadatfar and Aghaie-Khafri (2015) presented a numerical solution for deformation of a functionally graded hollow cylindrical shell with the inner and the outer surface imperfectly bonded functionally graded piezoelectric layers subjected to hygrothermo-electro-mechanical loads. Dai et al. (2017) numerically obtained the distributions of the temperature, moisture, displacement and stress of a functionally graded, piezoelectric circular disk under a coupled hygrothermal field.

General solutions or Green’s functions can be employed as the fundamental building blocks to construct the solution for many complicated boundary value problems such as cracks, inclusions, dislocations, punch and indentation in hygrothermopiezoelectric media. For example, Dang et al. (2018) used the general solution for hygrothermoelastic media to study crack problems, and Wu et al. (2013) solved the indentation problem of one-dimensional hexagonal quasicrystals based on the corresponding general solution. However, to the best of the authors’ knowledge, no general solutions have been reported in the literature for hygrothermopiezoelectricity. Therefore, it is critical to get the general solutions for hygrothermopiezoelectricity and lay the foundation for further studies of cracks, defects, inclusions and other boundary value problems in hygrothermopiezoelectric media. Chen (1993) used the complex variable function technique to derive the 2D Green’s functions for bimaterials. Ding et al. (1996) used it to get the general solution for piezoelectric material; Michelitsch and Levin (2000) used the potential method to obtain the Green’s function for displacements of the 2D infinite medium with orthotropic symmetry in terms of elementary functions; and Hou et al. (2009a, b) obtained the general solutions for magnetoelectrotermoelastic and piezothermoelastic materials, respectively. Considering the effect of moisture, Zhao et al. (2018a) used the potential theory method to obtain the general solution for three-dimensional hygrothermoelastic media in terms of potential functions. Compared with other methods, the potential theory method exhibits superior advantages in giving the complete form of general solution for coupled fields, particularly suitable for 2D or 3D multi-field materials. This general solution can be flexibly applied in different kinds of problems such as crack, punch, inclusion, etc. For a specific problem, one can construct the potential functions in a certain harmonic form by virtue of the trial-and-error method. After substituting them into the boundary conditions, one can obtain the coefficients of the harmonic functions, thus the whole fields can be determined. Motivated by this, the present paper intends to utilize the potential function method proposed by Fabrikant (1989, 1991) to derive the complete general solution for the three-dimensional, transversely isotropic, hygrothermopiezoelectric material. The paper is organized as follows: In Sect. 2, the constitutive equations as well as the governing equations are listed in the Cartesian coordinate system. The differential operator theory and superposition principle are used to construct the complete general solution in Sect. 3. As an application of the general solutions, the fundamental solution for a steady point moisture source combined with a steady point heat source in the interior of an infinite, hygrothermopiezoelectric body is derived in Sect. 4. To show the wide application of the fundamental solution, a flat crack in an arbitrary shape subjected to combined mechanical, electric, moisture and temperature loads is investigated in Sect. 5 via the generalized, potential theory method, and the exact solution for a penny-shaped crack under uniform loads is presented in terms of elementary functions. As last, conclusions and perspectives are presented in Sect. 6.

2 Basic equations

The linear theory for a transversely isotropic, hygrothermopiezoelectric medium can be referred to Smittakorn and Heyliger (2000), Akbarzadeh and Chen (2013), and Altay and Dokmeci (2008, 2014). In the Cartesian coordinates (x,y,z), the plane xoy is supposed to be parallel to the plane of isotropy such that the materials constants will remain the same in any direction within the plane, while the z-axis coincides with the axis of polarization direction. The 3D, constitutive equations for the transversely isotropic, hygrothermopiezoelectric medium can then be expressed as follows:

$$\begin{aligned} \sigma _x&=c_{11} \frac{\partial u}{\partial x}+c_{12} \frac{\partial v}{\partial y}+c_{13} \frac{\partial w}{\partial z} \nonumber \\&\quad +e_{31} \frac{\partial \varphi }{\partial z}-\xi _{11} m-\beta _{11} \theta , \nonumber \\ \sigma _y&= c_{12} \frac{\partial u}{\partial x}+c_{11} \frac{\partial v}{\partial y}+c_{13} \frac{\partial w}{\partial z} \nonumber \\&\quad +e_{31} \frac{\partial \varphi }{\partial z}-\xi _{11} m-\beta _{11} \theta , \nonumber \\ \sigma _z&= c_{13} \left( {\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}} \right) +c_{33} \frac{\partial w}{\partial z} \nonumber \\&\quad +e_{33} \frac{\partial \varphi }{\partial z}-\xi _{33} m-\beta _{33} \theta , \nonumber \\ \sigma _{xy}&= c_{66} \left( {\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}} \right) , \nonumber \\ \sigma _{yz}&=c_{44} \left( {\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}} \right) +e_{15} \frac{\partial \varphi }{\partial y}, \nonumber \\ \sigma _{zx}&=c_{44} \left( {\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}} \right) +e_{15} \frac{\partial \varphi }{\partial x}, \nonumber \\ D_x&= e_{15} \left( {\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}} \right) -\varepsilon _{11} \frac{\partial \varphi }{\partial x}+\chi _1 m+\gamma _1 \theta , \nonumber \\ D_y&= e_{15} \left( {\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}} \right) -\varepsilon _{11} \frac{\partial \varphi }{\partial y}+\chi _1 m+\gamma _1 \theta , \nonumber \\ D_z&= e_{31} \left( {\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}} \right) +e_{33} \frac{\partial w}{\partial z} \nonumber \\&\quad -\varepsilon _{33} \frac{\partial \varphi }{\partial z}+\chi _3 m+\gamma _3 \theta , \nonumber \\&\left\{ \begin{array}{l} {\begin{array}{l} q_x \\ q_y \\ \end{array}} \\ {q_z} \\ \end{array} \right\} =-\left[ \begin{array}{ccc} {\kappa _{11} }&{} 0&{} 0 \\ 0&{} {\kappa _{11} }&{} 0 \\ 0&{} 0&{} {\kappa _{33} } \\ \end{array} \right] \left\{ \begin{array}{l} {m_{,x} } \\ {m_{,y} } \\ {m_{,z} } \\ \end{array} \right\} , \nonumber \\&\left\{ {\begin{array}{l} h_x \\ h_y \\ h_z \\ \end{array}} \right\} =-\left[ \begin{array}{ccc} {\lambda _{11} }&{} 0&{} 0 \\ 0&{} {\lambda _{11} }&{} 0 \\ 0&{} 0&{} {\lambda _{33} } \\ \end{array} \right] \left\{ \begin{array}{l} {\theta _{,x} } \\ {\theta _{,y} } \\ {\theta _{,z} } \\ \end{array} \right\} , \end{aligned}$$
(1)

where u, v, and w are the elastic displacements, and \(\sigma _{ij}\) are the stresses; \(D_{i}\) are the electric displacements, and \(\varphi \) is the electric potential; m and \(\theta \) are changes of moisture concentration and temperature, respectively; \(m=0\) and \(\theta = 0\) correspond to the free stress state; \(q_{i}\) and \(h_{i}\) are the respective moisture flux and heat flux; \(c_{ij}\), \(e_{ij}\), \(\varepsilon _{ij}\), \(\beta _{ij}\), \(\gamma _{i}\), \(\xi _{ij}\), and \(\chi _{i}\) are the elastic, piezoelectric, dielectric, thermal stress, pyroelectric, hygroscopic stress, and hygroelectric coefficients, respectively; and \(\kappa _{ij}\), and \(\lambda _{ii}\) are the respective conduction coefficients of moisture content and heat. Note that \(c_{12} =c_{11} -2c_{66}\).

In addition, the thermal stress and hygroscopic stress coefficients are related with the elastic coefficient, thermal expansion coefficient \(\alpha _{kl}^T\), and moisture expansion coefficient \(\beta _{kl}^C\) as follows:

$$\begin{aligned} \beta _{ij} =c_{ijkl} \alpha _{kl}^T ,\qquad \xi _{ij} =c_{ijkl} \beta _{kl}^C . \end{aligned}$$
(2)

The moisture flux and heat flux follow the Fickian equation and Fourier law, respectively:

$$\begin{aligned} \begin{aligned}&\left( {\kappa _{11} \frac{\partial ^{2}}{\partial x^{2}}+\kappa _{11} \frac{\partial ^{2}}{\partial y^{2}}+\kappa _{33} \frac{\partial ^{2}}{\partial z^{2}}} \right) m=0, \\&\left( {\lambda _{11} \frac{\partial ^{2}}{\partial x^{2}}+\lambda _{11} \frac{\partial ^{2}}{\partial y^{2}}+\lambda _{33} \frac{\partial ^{2}}{\partial z^{2}}} \right) \theta =0. \end{aligned} \end{aligned}$$
(3)

In the absence of body forces and free charges, the mechanical and electrical equilibrium equations in Cartesian coordinate system (x,y,z) are given as:

$$\begin{aligned}&\frac{\partial \sigma _x }{\partial x}+\frac{\partial \sigma _{xy} }{\partial y}+\frac{\partial \sigma _{xz} }{\partial z}=0, \nonumber \\&\frac{\partial \sigma _{yx} }{\partial x}+\frac{\partial \sigma _y }{\partial y}+\frac{\partial \sigma _{yz} }{\partial z}=0,\nonumber \\&\frac{\partial \sigma _{zx} }{\partial x}+\frac{\partial \sigma _{zy} }{\partial y}+\frac{\partial \sigma _z }{\partial z}=0, \nonumber \\&\frac{\partial D_x }{\partial x}+\frac{\partial D_y }{\partial y}+\frac{\partial D_z }{\partial z}=0. \end{aligned}$$
(4)

The governing equations are defined point-wisely in the solid volume \(\Omega _0\) for the initial-boundary-value problem. Appropriate boundary and initial conditions should be specified to guarantee the uniqueness and existence of solutions to the problem. The boundary conditions of the mechanical, electrical, moisture and temperature fields are specified on the bounding surface \(\Gamma _0\) of the solid body at time \(t\ge 0\) as follows:

$$\begin{aligned}&({u,v,w} )=( {\bar{{u}}( {x,y,z,t} ),\bar{{v}}( {x,y,z,t} ),\bar{{w}}( {x,y,z,t} )} ), \nonumber \\&\quad \hbox { on } \quad \Gamma _1^{( {u,v,w})} \nonumber \\&( {\varphi ,m,\theta } )= ( {\bar{{\varphi }}( {x,y,z,t} ),\bar{{m}}( {x,y,z,t} ),\bar{{\theta }} ( {x,y,z,t} )} ), \nonumber \\&\quad \hbox { on } \quad \Gamma _1^{( {\varphi ,m,\theta } )} \nonumber \\&\sigma _{ij} n_j = \bar{{f}}_j ( {x,y,z,t} ), \quad \hbox { on } \quad \Gamma _2^{( {u,v,w} )} \nonumber \\&( {D_i n_i ,q_i n_i ,h_i n_i}) = ( {\bar{{D}}_n ( {x,y,z,t}),\bar{{q}}_n ( {x,y,z,t} ),} \nonumber \\&\quad {\bar{{h}}_n ( {x,y,z,t} )} ), \hbox { on } \quad \Gamma _2^{( {\varphi ,m,\theta } )} \end{aligned}$$
(5)

where the superscripts denote specified values of the functions. \(\Gamma _1^\alpha \) and \(\Gamma _2^\alpha \) are parts of the boundary for variable \(\alpha \), and they two constitute the entire solid boundary \(\Gamma _0\) (namely \(\Gamma _1^\alpha +\Gamma _2^\alpha = \Gamma _0\)). Specifically, the boundary condition on \(\Gamma _1\) are the essential boundary conditions, which are the Dirichlet conditions, while the boundary condition on \(\Gamma _2\) are the natural boundary conditions, which are the Neumann conditions. In the present study, the special case of steady-state problem is considered.

Inserting Eq. (1) into the equilibrium equations in Eq. (4), one can easily get the equations for transversely isotropic, hygrothermopiezoelectricity in terms of the mechanical displacement, electric potential, temperature increment and moisture increment as follows (in the absence of body forces and free charges):

$$\begin{aligned} \begin{aligned}&\left( {c_{11} \frac{\partial ^{2}}{\partial x^{2}}+c_{66} \frac{\partial ^{2}}{\partial y^{2}}+c_{44} \frac{\partial ^{2}}{\partial z^{2}}} \right) u \\&\quad + ({c_{12} +c_{66}})\frac{\partial ^{2}v}{\partial x\partial y} + ({c_{13} + c_{44}}) \frac{\partial ^{2}w}{\partial x\partial z} \\&\quad + ({e_{15} + e_{31}}) \frac{\partial ^{2}\varphi }{\partial x\partial z}-\xi _{11} \frac{\partial m}{\partial x}-\beta _{11} \frac{\partial \theta }{\partial x}=0, \\&\left( {c_{66} \frac{\partial ^{2}}{\partial x^{2}}+c_{11} \frac{\partial ^{2}}{\partial y^{2}}+c_{44} \frac{\partial ^{2}}{\partial z^{2}}} \right) v \\&\quad + ({c_{12} +c_{66}}) \frac{\partial ^{2}u}{\partial x \partial y} + ({c_{13} +c_{44}}) \frac{\partial ^{2}w}{\partial y\partial z} \\&\quad + ({e_{15} + e_{31}}) \frac{\partial ^{2}\varphi }{\partial y\partial z}-\xi _{11} \frac{\partial m}{\partial y}-\beta _{11} \frac{\partial \theta }{\partial y}=0, \\&({c_{13} + c_{44}})\frac{\partial }{\partial z}\left( {\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}} \right) +\left( {c_{44} \Delta +c_{33} \frac{\partial ^{2}}{\partial z^{2}}} \right) w \\&\quad +\left( {e_{15} \Delta +e_{33} \frac{\partial ^{2}}{\partial z^{2}}} \right) \varphi -\xi _{33} \frac{\partial m}{\partial z}-\beta _{33} \frac{\partial \theta }{\partial z}=0, \\&({e_{15} + e_{31}})\frac{\partial }{\partial z}\left( {\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}} \right) +\left( {e_{15} \Delta +e_{33} \frac{\partial ^{2}}{\partial z^{2}}} \right) w \\&\quad -\left( {\varepsilon _{11} \Delta +\varepsilon _{33} \frac{\partial ^{2}}{\partial z^{2}}} \right) \varphi +\chi _1 \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) m \\&\quad +\chi _3 \frac{\partial m}{\partial z}+\gamma _1 \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \theta +\gamma _3 \frac{\partial \theta }{\partial z}=0, \end{aligned} \end{aligned}$$
(6)

where \(\Delta \) is the Laplace operator.

3 General solution

Introducing two displacement functions G and \(\Psi _{0}\), the components of displacement, u and v, are expressed as follows

$$\begin{aligned} u=\frac{\partial \Psi _0 }{\partial y}-\frac{\partial G}{\partial x}, \qquad v=-\frac{\partial \Psi _0 }{\partial x}-\frac{\partial G}{\partial y}, \end{aligned}$$
(7)

with which, Eqs. (3) and (6) can be transformed to

$$\begin{aligned} \left( {c_{66} \Delta +c_{44} \frac{\partial ^{2}}{\partial z^{2}}} \right) \Psi _0= & {} 0, \end{aligned}$$
(8a)
$$\begin{aligned} \mathbf{M}\left\{ \begin{array}{l} G \\ w \\ \varphi \\ m \\ \theta \\ \end{array} \right\} = \left\{ \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right\} , \end{aligned}$$
(8b)

where M is the following differential operator matrix

$$\begin{aligned} \mathbf{M}=\left[ \begin{array}{lllll} {-({c_{11} \Delta +c_{44} \frac{\partial ^{2}}{\partial z^{2}}})} &{} {({c_{13} + c_{44}}) \frac{\partial }{\partial z}} &{} {({e_{31} +e_{15}}) \frac{\partial }{\partial z}}&{} {-\xi _{11} }&{} {-\beta _{11} } \\ {-({c_{11} +c_{44}})\Delta \frac{\partial }{\partial z}}&{} {c_{44} \Delta +c_{33} \frac{\partial ^{2}}{\partial z^{2}}}&{} {e_{15} \Delta +e_{33} \frac{\partial ^{2}}{\partial z^{2}}}&{} {-\xi _{33} \frac{\partial }{\partial z}}&{} {-\beta _{33} \frac{\partial }{\partial z}} \\ {- ({e_{15} +e_{31}}) \Delta \frac{\partial }{\partial z}}&{} {e_{15} \Delta +e_{33} \frac{\partial ^{2}}{\partial z^{2}}} &{} {- \left( {\varepsilon _{11} \Delta +\varepsilon _{33} \frac{\partial ^{2}}{\partial z^{2}}}\right) } &{} {\chi _1 \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) +\chi _3 \frac{\partial }{\partial z}}&{} {\gamma _1 \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) +\gamma _3 \frac{\partial }{\partial z}} \\ 0 &{} 0 &{} 0 &{} {\kappa _{11} \Delta +\kappa _{33} \frac{\partial ^{2}}{\partial z^{2}}}&{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {\lambda _{11} \Delta +\lambda _{33} \frac{\partial ^{2}}{\partial z^{2}}} \\ \end{array} \right] \end{aligned}$$
(9a)

of which the determinant can be calculated as

$$\begin{aligned} |\mathbf{M}|= & {} \left( {a_0 \frac{\partial ^{6}}{\partial z^{6}}+b_0 \Delta \frac{\partial ^{4}}{\partial z^{4}}+c_0 \Delta ^{2}\frac{\partial ^{2}}{\partial z^{2}}+d_0 \Delta ^{3}} \right) \nonumber \\&\times \, \left( {\kappa _{11} \Delta +\kappa _{33} \frac{\partial ^{2}}{\partial z^{2}}} \right) \left( {\lambda _{11} \Delta +\lambda _{33} \frac{\partial ^{2}}{\partial z^{2}}} \right) .\nonumber \\ \end{aligned}$$
(9b)

Therefore, the completely coupled, partial differential equations are now transformed into partially coupled, partial differential equations. The above derivation procedure is analogous to Li et al. (2010) and Chen et al. (2004), where the equations of moisture concentration and heat conduction are combined with the other three equations governing the displacement and electric potential. It can be observed that the displacement function \(\Psi _{0}\) can be solved from Eq. (8a) independently. While Eq. (8b) is a set of homogeneous differential equations of G, w, \(\varphi \), m and \(\theta \). Unlike the traditional treatment that the heat conduction equation is solved independently (Ashida et al. 1993), the equations for moisture concentration and heat conduction are combined with the other three differential equations in the present paper. Hence, the general solution can be obtained routinely by virtue of the operator theory as

$$\begin{aligned}&G=A_{i1} F, \quad w=A_{i2} F, \quad \varphi =A_{i3} F, \nonumber \\&m=A_{i4} F, \quad \theta =A_{i5} F, \end{aligned}$$
(10)

where \(A_{ij}\) are the algebraic cofactors of the matrix M, and F satisfies

$$\begin{aligned} |\mathbf{M}|F=0, \end{aligned}$$
(11)

Combining Eqs. (10) and (11) with Eq. (8a), we have

$$\begin{aligned}&\left( {\Delta +\frac{\partial ^{2}}{\partial z_0^2 }} \right) \Psi _0 =0, \nonumber \\&\left( {\Delta +\frac{\partial ^{2}}{\partial z_1^2 }} \right) \left( {\Delta +\frac{\partial ^{2}}{\partial z_2^2 }} \right) \left( {\Delta +\frac{\partial ^{2}}{\partial z_3^2 }} \right) \nonumber \\&\left( {\Delta +\frac{\partial ^{2}}{\partial z_4^2 }} \right) \left( {\Delta +\frac{\partial ^{2}}{\partial z_5^2 }} \right) F=0, \end{aligned}$$
(12)

where \(z_{i}=s_{i} z\), \(s_0 =\sqrt{c_{66} /c_{44}}\), \(s_4 =\sqrt{\kappa _{11} /\kappa _{33}}\), \(s_5 =\sqrt{\lambda _{11}/ \lambda _{33}}\), and \(s_{j}\) (\(j=1,2,3\)) are the characteristic roots with positive real part of the following algebraic equation

$$\begin{aligned} a_0 s^{6}-b_0 s^{4}+c_0 s^{2}-d_0 =0, \end{aligned}$$
(13)

in which \(a_{0}\), \(b_{0}\), \(c_{0}\) and \(d_{0}\) are given in “Appendix A”.

It can be easily seen that if we take \(i=1,2,3\) in Eq. (10), one can get two sets of general solutions with \(m = 0\) and \(\theta = 0\), which are actually the solution to the pure piezoelectricity; the solution for \(i = 4\) corresponds to the general solution \({\mathbf{X}}_{1}\) with \(\theta = 0\), which should be identical to that for hygropiezoelasticity; the solution for \(i = 5\) corresponds to the general solution \({\mathbf{X}}_{2}\) with \(m = 0\), which is identical to the thermopiezoelasticity.

Due to the linearity of hygrothermopiezoelectric theory, superposing \({\mathbf{X}}_{1}\) and \({\mathbf{X}}_{2}\) leads to

$$\begin{aligned}&G=\left( {A_{41} +A_{51} } \right) F, \quad w=\left( {A_{42} +A_{52}} \right) F, \nonumber \\&\varphi =\left( {A_{43} +A_{53} } \right) F, \quad m=A_{44} F, \quad \theta =A_{55} F,\nonumber \\ \end{aligned}$$
(14)

namely

$$\begin{aligned} G= & {} \left[ a_1 \frac{\partial ^{6}}{\partial z^{6}}+b_1 \frac{\partial ^{5}}{\partial z^{5}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) +c_1 \frac{\partial ^{4}}{\partial z^{4}}\Delta \right. \nonumber \\&+\,d_1 \frac{\partial ^{3}}{\partial z^{3}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta +f_1 \frac{\partial ^{2}}{\partial z^{2}}\Delta ^{2} \nonumber \\&\left. +\,g_1 \frac{\partial }{\partial z}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta ^{2}+h_1 \Delta ^{3} \right] F, \end{aligned}$$
(15a)
$$\begin{aligned} w= & {} \left[ a_2 \frac{\partial ^{7}}{\partial z^{7}}+b_2 \frac{\partial ^{6}}{\partial z^{6}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) +c_2 \frac{\partial ^{5}}{\partial z^{5}}\Delta \right. \nonumber \\&+\,d_2 \frac{\partial ^{4}}{\partial z^{4}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta +f_2 \frac{\partial ^{3}}{\partial z^{3}}\Delta ^{2} \nonumber \\&+\,g_2 \frac{\partial ^{2}}{\partial z^{2}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta ^{2}+h_2 \frac{\partial }{\partial z}\Delta ^{3} \nonumber \\&\left. +\,j_2 \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta ^{3} \right] F,\end{aligned}$$
(15b)
$$\begin{aligned} \varphi= & {} \left[ a_3 \frac{\partial ^{7}}{\partial z^{7}}+b_3 \frac{\partial ^{6}}{\partial z^{6}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) +c_3 \frac{\partial ^{5}}{\partial z^{5}}\Delta \right. \nonumber \\&+\,d_3 \frac{\partial ^{4}}{\partial z^{4}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta +f_3 \frac{\partial ^{3}}{\partial z^{3}}\Delta ^{2} \nonumber \\&+\,g_3 \frac{\partial ^{2}}{\partial z^{2}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta ^{2}+h_3 \frac{\partial }{\partial z}\Delta ^{3} \nonumber \\&\left. +\,j_3 \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta ^{3} \right] F, \end{aligned}$$
(15c)
$$\begin{aligned} m= & {} \left( a_4 \frac{\partial ^{8}}{\partial z^{8}}+b_4 \frac{\partial ^{6}}{\partial z^{6}}\Delta +c_4 \frac{\partial ^{4}}{\partial z^{4}}\Delta ^{2} \right. \nonumber \\&\left. +\,d_4 \frac{\partial ^{2}}{\partial z^{2}}\Delta ^{3}+f_4 \Delta ^{4} \right) F,\end{aligned}$$
(15d)
$$\begin{aligned} \theta= & {} \left( a_5 \frac{\partial ^{8}}{\partial z^{8}}+b_5 \frac{\partial ^{6}}{\partial z^{6}}\Delta +c_5 \frac{\partial ^{4}}{\partial z^{4}}\Delta ^{2} \right. \nonumber \\&\left. +\,d_5 \frac{\partial ^{2}}{\partial z^{2}}\Delta ^{3}+f_5 \Delta ^{4} \right) F, \end{aligned}$$
(15e)

and the displacements in the x- and y-directions are obtained as well

$$\begin{aligned} u= & {} -\left[ a_1 \frac{\partial ^{6}}{\partial z^{6}}+b_1 \frac{\partial ^{5}}{\partial z^{5}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) +c_1 \frac{\partial ^{4}}{\partial z^{4}}\Delta \right. \nonumber \\&\quad +\,d_1 \frac{\partial ^{3}}{\partial z^{3}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta +f_1 \frac{\partial ^{2}}{\partial z^{2}}\Delta ^{2} \nonumber \\&\quad \left. +\,g_1 \frac{\partial }{\partial z}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta ^{2}+h_1 \Delta ^{3} \right] \frac{\partial F}{\partial x} \nonumber \\&+\,\frac{\partial \Psi _0 }{\partial y}, \end{aligned}$$
(15f)
$$\begin{aligned} v= & {} -\left[ a_1 \frac{\partial ^{6}}{\partial z^{6}}+b_1 \frac{\partial ^{5}}{\partial z^{5}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) +c_1 \frac{\partial ^{4}}{\partial z^{4}}\Delta \right. \nonumber \\&\quad +\,d_1 \frac{\partial ^{3}}{\partial z^{3}}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta +f_1 \frac{\partial ^{2}}{\partial z^{2}}\Delta ^{2} \nonumber \\&\quad \left. +\,g_1 \frac{\partial }{\partial z}\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \Delta ^{2}+h_1 \Delta ^{3} \right] \frac{\partial F}{\partial y} \nonumber \\&-\,\frac{\partial \Psi _0 }{\partial x}, \end{aligned}$$
(15g)

where the involved coefficients are given in “Appendix A”.

By virtue of the generalized Almansi theorem (Ding et al. 1996), F can be expressed by five quasi-harmonic functions

$$\begin{aligned} F=\left\{ {\begin{array}{l} F_1 +F_2 +F_3 +F_4 +F_5 \quad \quad \quad \;\hbox {for}\;\hbox {distinct}\;s_i ,\quad \hbox {Case}\;1, \\ F_1 +F_2 +F_3 +F_4 +zF_5 \quad \quad \;\;\;\hbox {for}\;s_1 \ne s_2 \ne s_3 \ne s_4 =s_5 ,\quad \hbox {Case}\;2, \\ F_1 +F_2 +F_3 +zF_4 +z^{2}F_5 \quad \quad \hbox {for}\;s_1 \ne s_2 \ne s_3 =s_4 =s_5 \ne s_1 ,\quad \hbox {Case}\;3, \\ F_1 +F_2 +zF_3 +z^{2}F_4 +z^{3}F_5 \quad \;\hbox {for}\;s_1 \ne s_2 =s_3 =s_4 =s_5 ,\quad \hbox {Case}\;4, \\ F_1 +zF_2 +z^{2}F_3 +z^{3}F_4 +z^{4}F_5 \;\;\hbox {for}\;s_1 =s_2 =s_3 =s_4 =s_5 ,\quad \hbox {Case}\;5, \end{array}} \right. \end{aligned}$$
(16)

where \(F_{j}\) satisfy

$$\begin{aligned} \left( {\Delta +\frac{\partial ^{2}}{\partial z_j^2 }} \right) F_j =0,\quad \quad ({j=1,2,3,4,5}). \end{aligned}$$
(17)

In this paper, the distinct eigenvalues for Case 1 is discussed briefly. When equal eigenvalues appear, the derivation is similar to Case 1. It is also noted that the general solution for Case 1 is the most complicated, whilst the solutions for other cases can be treated as a simplified version of Case 1. For Case 1, the general solution in Eq. (15) can be rewritten with the Almansi theorem as:

$$\begin{aligned} u= & {} \frac{\partial \Psi _0 }{\partial y}-\sum _{i=1}^5 \left[ \eta _{11i} \frac{\partial ^{7}F_i }{\partial x\partial z_i^6} \right. \nonumber \\&\quad \left. +\,\eta _{12i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{6}F_i }{\partial x\partial z_i^5} \right] , \nonumber \\ v= & {} -\frac{\partial \Psi _0 }{\partial x}-\sum _{i=1}^5 \left[ \eta _{11i} \frac{\partial ^{7}F_i }{\partial y\partial z_i^6} \right. \nonumber \\&\quad \left. +\,\eta _{12i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{6}F_i }{\partial y\partial z_i^5} \right] , \nonumber \\ w= & {} \sum _{i=1}^5 \left[ {\eta _{21i} \frac{\partial ^{7}F_i }{\partial z_i^7 }+\eta _{22i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{6}F_i }{\partial z_i^6 }} \right] , \nonumber \\ \varphi= & {} \sum _{i=1}^5 \left[ {\eta _{31i} \frac{\partial ^{7}F_i }{\partial z_i^7 }+\eta _{32i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{6}F_i }{\partial z_i^6 }} \right] , \nonumber \\ m= & {} \eta _{44} \frac{\partial ^{8}F_4 }{\partial z_4^8 }, \quad \theta =\eta _{55} \frac{\partial ^{8}F_5 }{\partial z_5^8 }, \end{aligned}$$
(18)

where

$$\begin{aligned}&\eta _{11i} =\left( {a_1 -c_1 +f_1 -h_1 } \right) s_i^6 , \nonumber \\&\eta _{12i} =\left( {b_1 -d_1 +g_1 } \right) s_i^5 , \nonumber \\&\eta _{21i} =\left( {a_2 -c_2 +f_2 -h_2 } \right) s_i^7, \nonumber \\&\eta _{22i} =\left( {b_2 -d_2 +g_2 -j_2 } \right) s_i^6 , \\&\eta _{31i} =\left( {a_3 -c_3 +f_3 -h_3 } \right) s_i^7 , \nonumber \\&\eta _{32i} =\left( {b_3 -d_3 +g_3 -j_3 } \right) s_i^6 , \nonumber \\&\eta _{44} =\left( {\lambda _{33} s_4^2 -\lambda _{11} } \right) \left( {a_0 s_4^6 -b_0 s_4^4 +c_0 s_4^2 -d_0 } \right) , \nonumber \\&\eta _{55} =\left( {\kappa _{33} s_5^2 -\kappa _{11} } \right) \left( {a_0 s_5^6 -b_0 s_5^4 +c_0 s_5^2 -d_0 } \right) .\nonumber \end{aligned}$$
(19)

Letting

$$\begin{aligned} \eta _{11i} \frac{\partial ^{5}F_i }{\partial z_i^5 }=\Psi _i, \quad ({i=1,2,3,4,5}), \end{aligned}$$
(20)

Equation (18) can be simplified as:

$$\begin{aligned} u= & {} \frac{\partial \Psi _0 }{\partial y}-\sum _{i=1}^5 {\left[ {\frac{\partial ^{2}\Psi _i }{\partial x\partial z_i }+\mu _{1i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial \Psi _i }{\partial x}} \right] }, \nonumber \\ v= & {} -\frac{\partial \Psi _0 }{\partial x}-\sum _{i=1}^5 {\left[ {\frac{\partial ^{2}\Psi _i }{\partial y\partial z_i }+\mu _{1i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial \Psi _i }{\partial y}} \right] }, \nonumber \\ w= & {} \sum _{i=1}^5 {\left[ {\mu _{2i} \frac{\partial ^{2}\Psi _i }{\partial z_i^2 }+\mu _{3i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial \Psi _i }{\partial z_i }} \right] }, \nonumber \\ m= & {} \mu _6 \frac{\partial ^{3}\Psi _4 }{\partial z_4^3}, \nonumber \\ \varphi= & {} \sum _{i=1}^5 {\left[ {\mu _{4i} \frac{\partial ^{2}\Psi _i }{\partial z_i^2 }+\mu _{5i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial \Psi _i }{\partial z_i }} \right] }, \nonumber \\ \theta= & {} \mu _7 \frac{\partial ^{3}\Psi _5 }{\partial z_5^3 }, \end{aligned}$$
(21)

where

$$\begin{aligned}&\mu _{1i} =\frac{\eta _{12i} }{\eta _{11i} }, \quad \mu _{2i} =\frac{\eta _{21i} }{\eta _{11i} }, \quad \mu _{3i} =\frac{\eta _{22i} }{\eta _{11i} }, \nonumber \\&\mu _{4i} =\frac{\eta _{31i} }{\eta _{11i}}, \quad \mu _{5i} =\frac{\eta _{32i} }{\eta _{11i} }, \quad \mu _6 =\frac{\eta _{44} }{\eta _{114} }, \nonumber \\&\mu _7 =\frac{\eta _{55} }{\eta _{115} }, \quad \hbox {for} \quad i=1,2,3,4,5, \end{aligned}$$
(22)

It is easy to conclude that the new functions, \(\Psi _{i}\), are also quasi-harmonic:

$$\begin{aligned} \left( {\Delta +\frac{\partial ^{2}}{\partial z_j^2 }} \right) \Psi _j=0, \quad ({j=0,1,2,3,4,5}). \end{aligned}$$
(23)

Inserting Eq. (21) into Eq. (1), one can get the expressions for the components of stress, electric displacement, moisture flux, and heat flux in terms of functions \(\Psi _{i}\) in the Cartesian coordinate system (x, y, z)

$$\begin{aligned} \sigma _x= & {} \left( {c_{11} -c_{12} } \right) \frac{\partial \Psi _0 }{\partial x\partial y} \\&-\,c_{11} \sum _{i=1}^5 {\left[ {\frac{\partial ^{3}\Psi _i }{\partial x^{2}\partial z_i }+\mu _{1i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial x^{2}}} \right] } \\&-\,c_{12} \sum _{i=1}^5 {\left[ {\frac{\partial ^{3}\Psi _i }{\partial y^{2}\partial z_i }+\mu _{1i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial y^{2}}} \right] } \\&+\,\sum _{i=1}^5 s_i \left[ \left( {c_{13} \mu _{2i} +e_{31} \mu _{4i} } \right) \frac{\partial ^{3}\Psi _i }{\partial z_i^3} \right. \\&\left. +\,\left( {c_{13} \mu _{3i} +e_{31} \mu _{5i} } \right) \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}}\right) \frac{\partial ^{2}\Psi _i}{\partial z_i^2} \right] \\&-\,\xi _{11} \mu _6 \frac{\partial ^{3}\Psi _4 }{\partial z_4^3 }-\beta _{11} \mu _7 \frac{\partial ^{3}\Psi _5 }{\partial z_5^3}, \\ \sigma _y= & {} ({c_{12} -c_{11}}) \frac{\partial \Psi _0 }{\partial x\partial y} \\&-\,c_{12} \sum _{i=1}^5 {\left[ {\frac{\partial ^{3}\Psi _i }{\partial x^{2}\partial z_i }+\mu _{1i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial x^{2}}} \right] } \\&-\,c_{11} \sum _{i=1}^5 {\left[ {\frac{\partial ^{3}\Psi _i }{\partial y^{2}\partial z_i }+\mu _{1i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial y^{2}}} \right] } \\&+\,\sum _{i=1}^5 s_i \left[ \left( {c_{13} \mu _{2i} +e_{31} \mu _{4i} } \right) \frac{\partial ^{3}\Psi _i }{\partial z_i^3} \right. \\&\left. +\, ({c_{13} \mu _{3i} +e_{31} \mu _{5i} }) \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial z_i^2 } \right] \\&-\,\xi _{11} \mu _6 \frac{\partial ^{3}\Psi _4 }{\partial z_4^3} -\beta _{11} \mu _7 \frac{\partial ^{3}\Psi _5 }{\partial z_5^3 }, \\ \sigma _z= & {} c_{13} \left\{ {\sum _{i=1}^5 {\left[ {\frac{\partial ^{3}\Psi _i }{\partial z_i^3 }+\mu _{1i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial z_i^2 }} \right] } } \right\} \\&+\,\sum _{i=1}^5 s_i \left[ \left( {c_{33} \mu _{2i} +e_{33} \mu _{4i} } \right) \frac{\partial ^{3}\Psi _i }{\partial z_i^3} \right. \\&\left. +\,({c_{33} \mu _{3i} +e_{33} \mu _{5i} }) \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial z_i^2 } \right] \\&-\,\xi _{33} \mu _6 \frac{\partial ^{3}\Psi _4 }{\partial z_4^3 }-\beta _{33} \mu _7 \frac{\partial ^{3}\Psi _5 }{\partial z_5^3 }, \\ \sigma _{xy}= & {} c_{66} \left\{ \left( {\frac{\partial ^{2}}{\partial y^{2}} -\frac{\partial ^{2}}{\partial x^{2}}} \right) \Psi _0 \right. \\&\left. -\,2\sum _{i=1}^5 {\left[ {\frac{\partial ^{3}\Psi _i }{\partial x\partial y\partial z_i }+\mu _{1i} \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial x\partial y}} \right] } \right\} , \\ \sigma _{yz}= & {} -c_{44} s_0 \frac{\partial ^{2}\Psi _0 }{\partial x\partial z_0} \\&+\,\sum _{i=1}^5 \left\{ {\left[ {c_{44} \left( {\mu _{2i} -s_i } \right) +e_{15} \mu _{4i} } \right] \frac{\partial ^{3}\Psi _i }{\partial y\partial z_i^2 }} \right. \\&+\,\left[ {c_{44} \left( {\mu _{3i} -\mu _{1i} s_i } \right) +e_{15} \mu _{5i} } \right] \\&\left. \times \,\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i}{\partial y\partial z_i } \right\} , \\ \sigma _{zx}= & {} -c_{44} s_0 \frac{\partial ^{2}\Psi _0 }{\partial y\partial z_0} \\&+\,\sum _{i=1}^5 \left\{ {\left[ {c_{44} \left( {\mu _{2i} -s_i } \right) +e_{15} \mu _{4i} } \right] \frac{\partial ^{3}\Psi _i }{\partial x\partial z_i^2 }} \right. \\&+\,\left[ {c_{44} \left( {\mu _{3i} -\mu _{1i} s_i } \right) +e_{15} \mu _{5i} } \right] \\&\left. \times \,\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial x\partial z_i } \right\} , \\ \end{aligned}$$
$$\begin{aligned} D_x= & {} e_{15} s_0 \frac{\partial ^{2}\Psi _0 }{\partial y\partial z_0} \nonumber \\&+\,\sum _{i=1}^5 \left\{ {\left[ {e_{15} \left( {\mu _{2i} -s_i } \right) -\varepsilon _{11} \mu _{4i} } \right] \frac{\partial ^{3}\Psi _i }{\partial x\partial z_i^2 }} \right. \nonumber \\&+\left[ {e_{15} \left( {\mu _{3i} -\mu _{1i} s_i } \right) -\varepsilon _{11} \mu _{5i} } \right] \nonumber \\&\left. \times \, \left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}}\right) \frac{\partial ^{2}\Psi _i }{\partial x\partial z_i } \right\} \nonumber \\&+\,\chi _1 \mu _6 \frac{\partial ^{3}\Psi _4 }{\partial z_4^3 }+\gamma _1 \mu _7 \frac{\partial ^{3}\Psi _5 }{\partial z_5^3}, \nonumber \\ D_y= & {} e_{15} s_0 \frac{\partial ^{2}\Psi _0 }{\partial x\partial z_0} \nonumber \\&+\,\sum _{i=1}^5 \left\{ \left[ {e_{15} \left( {\mu _{2i} -s_i } \right) -\varepsilon _{11} \mu _{4i} } \right] \frac{\partial ^{3}\Psi _i }{\partial y\partial z_i^2}\right. \nonumber \\&+\, \left[ {e_{15} \left( {\mu _{3i} -\mu _{1i} s_i } \right) -\varepsilon _{11} \mu _{5i} } \right] \nonumber \\&\left. \times \,\left( {\frac{\partial }{\partial x} +\frac{\partial }{\partial y}}\right) \frac{\partial ^{2}\Psi _i }{\partial y\partial z_i} \right\} \nonumber \\&+\,\chi _1 \mu _6 \frac{\partial ^{3}\Psi _4 }{\partial z_4^3 }+\gamma _1 \mu _7 \frac{\partial ^{3}\Psi _5 }{\partial z_5^3}, \nonumber \\ D_z= & {} \sum _{i=1}^5 \left\{ {\left[ {e_{31} +\left( {e_{33} \mu _{2i} -\varepsilon _{33} \mu _{4i} } \right) s_i } \right] \frac{\partial ^{3}\Psi _i }{\partial z_i^3 }} \right. \nonumber \\&+\,\left[ {e_{31} \mu _{1i} +\left( {e_{33} \mu _{3i} -\varepsilon _{33} \mu _{5i} } \right) s_i } \right] \nonumber \\&\left. \times \,\left( {\frac{\partial }{\partial x}+\frac{\partial }{\partial y}} \right) \frac{\partial ^{2}\Psi _i }{\partial z_i^2} \right\} \nonumber \\&+\,\chi _3 \mu _6 \frac{\partial ^{3}\Psi _4 }{\partial z_4^3 }+\gamma _3 \mu _7 \frac{\partial ^{3}\Psi _5 }{\partial z_5^3}, \nonumber \\ q_x= & {} -\kappa _{11} \mu _6 \frac{\partial ^{4}\Psi _4 }{\partial x\partial z_4^3 }, \quad q_y =-\kappa _{11} \mu _6 \frac{\partial ^{4}\Psi _4 }{\partial y\partial z_4^3 }, \nonumber \\ q_z= & {} -\kappa _{11} \mu _6 s_4 \frac{\partial ^{4}\Psi _4 }{\partial z_4^4}, \quad h_x =-\lambda _{11} \mu _7 \frac{\partial ^{4}\Psi _5 }{\partial x\partial z_5^3 }, \nonumber \\ h_y= & {} -\lambda _{11} \mu _7 \frac{\partial ^{4}\Psi _5 }{\partial y\partial z_5^3 }, \quad h_z =-\lambda _{11} \mu _7 s_5 \frac{\partial ^{4}\Psi _5 }{\partial z_5^4}. \end{aligned}$$
(24)

The general solution in the cylindrical coordinate system can be readily obtained through transformation of coordinates. The harmonic functions, \(\Psi _{i}\) (\(i=0,1,2,3,4,5\)), are the so-called potential functions. Once the potential functions are determined, the mechanical, electric, moisture and temperature fields can be readily obtained. The domain of definition for the general solution is suitable for the whole three-dimensional space of hygrothermopiezoelectric medium, and one can apply it to obtain the solution at any point in the medium.

4 Fundamental solution for a point moisture source and heat source in the infinite body

Consider an infinite, transversely isotropic, hygrothermopiezoelectric body whose isotropic plane is perpendicular to the z-axis. A point moisture source M and a heat source H are applied at the origin of the cylindrical coordinate (r, \(\phi \), z) or Cartesian coordinate (x, y, z), as shown in Fig. 1. The hygro-thermo-electro-elastic fields are derived with the aid of the obtained general solution.

Fig. 1
figure 1

An infinite hygrothermopiezoelectric body subjected to a point moisture source, M, and a point heat source, H, in the origin

Full size image

Considering the boundary condition, one can conclude that this is a non-torsional axisymmetric problem. By virtue of the trial-and-error method, the harmonic functions in the general solutions are assumed to take the following specific forms

$$\begin{aligned} \begin{aligned}&\Psi _0 =0, \\&\Psi _j =\frac{\zeta _j }{4}[ {( {R_j^2 -3z_j^2 }) \ln R_j^*-3sign( z )z_j R_j}], \\&\quad ({j=1,2,3,4,5}), \end{aligned} \end{aligned}$$
(25)

where \(\zeta _j \, (j=1,2,3,4,5)\) are constants to be determined; sign(\(\zeta \)) is the signum function of \(\zeta \), and

$$\begin{aligned} R_j = \sqrt{x^{2}+y^{2}+z_j^2}, \quad R_j^*=R_j +sign (z) z_j. \end{aligned}$$
(26)

Once the constants \(\zeta _j\) are determined, the general solution can be obtained, and the problem is thus solved, which shows the advantage of the present method. Substituting Eq. (25) into the general solution (24), one can obtain the variables in Cartesian coordinate as

$$\begin{aligned}&u = \sum _{j=1}^5 {\zeta _j \frac{x}{R_j^*}} , \quad v=\sum _{j=1}^5 {\zeta _j \frac{y}{R_j^*}} , \nonumber \\&w=\sum _{j=1}^5 {\mu _{2j} \zeta _j sign (z)\ln R_j^*}, \nonumber \\&\varphi =\sum _{j=1}^5 {\mu _{4j} \zeta _j sign (z)\ln R_j^*} , \quad m=\mu _6 \zeta _4 \frac{1}{R_4 }, \nonumber \\&\theta =\mu _7 \zeta _5 \frac{1}{R_5 }, \nonumber \\&\sigma _{zx} =-\sum _{j=1}^5 {\left[ {c_{44} \left( {\mu _{2j} -s_j } \right) +e_{15} \mu _{4j} } \right] \zeta _j \frac{sign (z) x}{R_j R_j^*}}, \nonumber \\&\sigma _{yz} =-\sum _{j=1}^5 {\left[ {c_{44} \left( {\mu _{2j} -s_j } \right) +e_{15} \mu _{4j} } \right] \zeta _j \frac{sign\left( z \right) y}{R_j R_j^*}}, \nonumber \\&\sigma _z= \sum _{j=1}^5 {\left( {c_{13} +c_{33} \mu _{2j} s_j +e_{33} \mu _{\mathrm {4}j} s_j } \right) \zeta _j \frac{1}{R_j }} \nonumber \\&\qquad -\,\xi _{33} \mu _6 \zeta _4 \frac{1}{R_4 }-\beta _{33} \mu _7 \zeta _5 \frac{1}{R_5 }, \nonumber \\&D_z = \sum _{j=1}^5 {\left( {e_{31} +e_{33} \mu _{2j} s_j -\varepsilon _{33} \mu _{\mathrm {4}j} s_j } \right) \zeta _j \frac{1}{R_j }} \nonumber \\&\qquad \quad +\,\chi _3 \mu _6 \zeta _4 \frac{1}{R_4 }+\gamma _3 \mu _7 \zeta _5 \frac{1}{R_5}, \nonumber \\&D_x = -\sum _{j=1}^5 {\left[ {e_{15} \left( {\mu _{2j} -s_j } \right) -\varepsilon _{11} \mu _{4j} } \right] \zeta _j \frac{sign\left( z \right) x}{R_j R_j^*}} \nonumber \\&\qquad \quad +\,\chi _1 \mu _6 \zeta _4 \frac{1}{R_4 }+\gamma _1 \mu _7 \zeta _5 \frac{1}{R_5 }, \nonumber \\&D_y = -\sum _{j=1}^5 {\left[ {e_{15} \left( {\mu _{2j} -s_j } \right) -\varepsilon _{11} \mu _{4j} } \right] \zeta _j \frac{sign\left( z \right) y}{R_j R_j^*}} \nonumber \\&\qquad +\,\chi _1 \mu _6 \zeta _4 \frac{1}{R_4} + \gamma _1 \mu _7 \zeta _5 \frac{1}{R_5}, \end{aligned}$$
(27a)

and the expressions for \(\sigma _{zr}\) and \(D_{r}\) by adopting the transformation of coordinates

$$\begin{aligned} \sigma _{zr}= & {} -\sum _{j=1}^5 {[ {c_{44} ( {\mu _{2j} -s_j} )+e_{15} \mu _{4j} } ]\zeta _j \frac{sign( z)r}{R_j R_j^*}}, \nonumber \\ D_r= & {} -\sum _{j=1}^5 {[ {e_{15} ( {\mu _{2j} -s_j } )-\varepsilon _{11} \mu _{4j} } ]\zeta _j \frac{sign( z )r}{R_j R_j^*}} \nonumber \\&+\,\chi _1 \mu _6 \zeta _4 \frac{1}{R_4 }+\gamma _1 \mu _7 \zeta _5 \frac{1}{R_5}, \end{aligned}$$
(27b)

Considering the continuity of w, \(\varphi \), \(\sigma _{zr}\) and \(D_{r}\) in plane \(z = 0\), whose expressions in Eq. (27) contain sign(z), we have

$$\begin{aligned}&\sum _{j=1}^5 {\mu _{2j} \zeta _j } =0, \nonumber \\&\sum _{j=1}^5 {\left[ {c_{44} \left( {\mu _{2j} -s_j } \right) +e_{15} \mu _{4j} } \right] \zeta _j } =0, \nonumber \\&\sum _{j=1}^5 {\mu _{4j} \zeta _j } =0, \nonumber \\&\sum _{j=1}^5 {\left[ {e_{15} \left( {\mu _{2j} -s_j } \right) -\varepsilon _{11} \mu _{4j} } \right] \zeta _j } =0. \end{aligned}$$
(28)

Substituting the expressions of \(\mu _{2j}\) and \(\mu _{4j}\) into Eq. (28), we have

$$\begin{aligned}&\frac{a_2 -c_2 +f_2 -h_2 }{a_1 -c_1 +f_1 -h_1 }\sum _{j=1}^5 {s_j \zeta _j } =0, \nonumber \\&\frac{a_3 -c_3 +f_3 -h_3 }{a_1 -c_1 +f_1 -h_1 }\sum _{j=1}^5 {s_j \zeta _j } =0, \nonumber \\&\left[ c_{44} \left( {\frac{a_2 -c_2 +f_2 -h_2 }{a_1 -c_1 +f_1 -h_1 }-1} \right) \right. \nonumber \\&\quad \left. +\,e_{15} \frac{a_3 -c_3 +f_3 -h_3 }{a_1 -c_1 +f_1 -h_1 } \right] \sum _{j=1}^5 {s_j \zeta _j} =0, \nonumber \\&\left[ e_{15} \left( {\frac{a_2 -c_2 +f_2 -h_2 }{a_1 -c_1 +f_1 -h_1 }-1} \right) \right. \nonumber \\&\quad \left. -\,\varepsilon _{11} \frac{a_3 -c_3 +f_3 -h_3 }{a_1 -c_1 +f_1 -h_1 } \right] \sum _{j=1}^5 {s_j \zeta _j } =0, \end{aligned}$$
(29)

and it is easy to simplify Eq. (29) as

$$\begin{aligned} \sum _{j=1}^5 {s_j \zeta _j } =0. \end{aligned}$$
(30)

When the mechanical, electrical, moisture and thermal equilibrium for a cylinder of \(h_1 \le z\le h_2 \quad ({h_1<0<h_2})\) and \(0\le r\le R\) are considered (Fig. 1), four additional equations can be obtained

$$\begin{aligned}&\int _0^{2\pi } {\int _0^R {\left[ {\sigma _z \left( {r,\phi ,h_2 } \right) -\sigma _z \left( {r,\phi ,h_1 } \right) } \right] rdrd\phi }} \nonumber \\&\quad +\,R\int _0^{2\pi } {\int _{h_1 }^{h_2 } {\sigma _{zr} \left( {R,\phi ,z} \right) dzd\phi } } =0, \nonumber \\&\int _0^{2\pi } {\int _0^R {\left[ {D_z \left( {r,\phi ,h_2 } \right) -D_z \left( {r,\phi ,h_1 } \right) } \right] rdrd\phi } } \nonumber \\&\quad +R\int _0^{2\pi } {\int _{h_1 }^{h_2 } {D_z \left( {R,\phi , z} \right) dzd\phi } } =0, \nonumber \\&\qquad -\kappa _{33} \int _0^{2\pi } {\int _0^R {\left[ {\frac{\partial m}{\partial z}\left( {r,\phi ,h_2 } \right) -\frac{\partial m}{\partial z}\left( {r,\phi ,h_1 } \right) } \right] rdrd\phi }} \nonumber \\&\qquad -\,R\kappa _{11} \int _0^{2\pi } {\int _{h_1 }^{h_2 } {\frac{\partial m}{\partial r}\left( {R,\phi ,z} \right) dzd\phi } } =\mathrm{M}, \nonumber \\&\qquad -\lambda _{33} \int _0^{2\pi } {\int _0^R {\left[ {\frac{\partial \theta }{\partial z}\left( {r,\phi ,h_2 } \right) -\frac{\partial \theta }{\partial z}\left( {r,\phi ,h_1 } \right) } \right] rdrd\phi }} \nonumber \\&\qquad -\,R\lambda _{11} \int _0^{2\pi } {\int _{h_1 }^{h_2 } {\frac{\partial \theta }{\partial r}\left( {R,\phi ,z} \right) dzd\phi } } =\mathrm{H}. \end{aligned}$$
(31)

Using the useful integrals given in Hou et al. (2009a), one can obtain the expressions of the coefficients

$$\begin{aligned} \zeta _4 =\frac{\mathrm{M}}{4\pi \mu _6 \sqrt{\kappa _{11} \kappa _{33} }}, \quad \zeta _5 =\frac{\mathrm{H}}{4\pi \mu _7 \sqrt{\lambda _{11} \lambda _{33} }}, \end{aligned}$$
(32)

With the obtained \(\zeta _4\) and \(\zeta _5\), one can get the other three coefficients by inserting Eq. (32) into (28) and (30)

$$\begin{aligned} \left\{ \begin{array}{l} {\zeta _1 } \\ {\zeta _2 } \\ {\zeta _3 } \\ \end{array} \right\} = \left[ \begin{array}{ccc} {\mu _{21} }&{} {\mu _{22} }&{} {\mu _{23} } \\ {\mu _{41} }&{} {\mu _{42} }&{} {\mu _{43} } \\ {s_1 }&{} {s_2 }&{} {s_3 } \\ \end{array} \right] ^{-1}\left\{ \begin{array}{l} {-\mu _{24} \zeta _4 -\mu _{25} \zeta _5 } \\ {-\mu _{44} \zeta _4 -\mu _{45} \zeta _5 } \\ {-\zeta _4 -\zeta _5 } \\ \end{array} \right\} . \end{aligned}$$
(33)

At this point, all the coefficients are determined. Substituting the coefficients into Eq. (27), one can obtain the complete, hygrothermopiezoeletroealstic response induced by the point moisture source M and heat source H. When the moisture field is omitted, the fundamental solution can be reduced to the solution for transversely isotropic, piezothermoelastic materials, which can be validated by Hou et al. (2009b).

5 Application for a flat crack under combined loads

The obtained general solution can be easily utilized to investigate the mixed boundary value problems associated with cracks or punches (Fabrikant 1989, 1991). In this section, to show the practical application of the general solution, a flat crack under combined loads is studied as an example.

Fig. 2
figure 2

A flat crack, S, contained in an infinite transversely isotropic hygrothermopiezoelectric medium subjected to mechanical, electric, moisture and temperature loads in the Cartesian coordinate system

Full size image

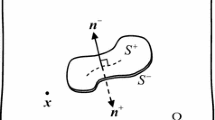
Assume a planar crack S is contained in an infinite, transversely isotropic, hygrothermopiezoelectric medium, and located in the plane \(z=0\). It is assumed that arbitrary normal distributed mechanical force, \(\Xi _1 ({x,y})\), electric displacement, \(\Xi _2 ({x,y})\), moisture load, \(\Xi _3 ({x,y})\), and temperature load, \(\Xi _4 ({x,y})\), are symmetrically applied on the upper and lower crack faces, with the same magnitude but opposite in direction, as is illustrated in Fig. 2. The problem can be converted into a mixed, boundary value problem of the half-space, \(z\ge 0\), with the boundary conditions prescribed on the plane, \(z=0\), as follows:

$$\begin{aligned}&\sigma _z =\Xi _1 \left( {x,y} \right) , \quad D_z =\Xi _2 \left( {x,y} \right) , \quad m=\Xi _3 \left( {x,y} \right) , \nonumber \\&\theta =\Xi _4 \left( {x,y} \right) , \quad \hbox {for} \quad \left( {x,y} \right) \in S, \end{aligned}$$
(34a)
$$\begin{aligned}&w=0, \quad \varphi =0, \quad q_z =0, \nonumber \\&h_z =0, \quad \hbox {for} \quad ({x,y})\notin S, \end{aligned}$$
(34b)
$$\begin{aligned}&\sigma _{zx} =0, \quad \sigma _{zy} =0, \quad \hbox {for} \quad -\infty< ({x,y}) <\infty .\nonumber \\ \end{aligned}$$
(34c)

To extend the potential theory method (Fabrikant 1989) to hygrothermopiezoelectricity, we assume that

$$\begin{aligned} \Psi _0 =0, \quad \Psi _i =\sum _{j=1}^4 {h_{ij} H_j ({z_i})} ,\quad ({i=1,2,3,4,5}), \nonumber \\ \end{aligned}$$
(35)

where \(h_{ij}\) are constants to be determined, and

$$\begin{aligned} H_1 ({x,y,z})= & {} \iint _S {\frac{w ({N_0})}{R ({M,N_0})}dS}, \end{aligned}$$
(36a)
$$\begin{aligned} H_2 ({x,y,z})= & {} \iint _S {\frac{\varphi ({N_0})}{R ({M,N_0})}dS}, \end{aligned}$$
(36b)
$$\begin{aligned} H_3 ({x,y,z})= & {} -\frac{1}{\kappa _{33} }\iint _S q_z ({N_0}) \nonumber \\&\times \,\left\{ z\ln [{R ({M,N_0}) +z}] - R ({M,N_0})\right\} dS, \nonumber \\ \end{aligned}$$
(36c)
$$\begin{aligned} H_4 ({x,y,z})= & {} -\frac{1}{\lambda _{33} }\iint _S h_z ({N_0}) \nonumber \\&\times \,\left\{ z\ln [{R ({M, N_0})+z}] - R ({M,N_0})\right\} dS,\nonumber \\ \end{aligned}$$
(36d)

where \(R(M, N_{0})\) denotes the distance between points M(x, y, z) and \(N_{0}(x_{0}, y_{0}, 0)\); \(u_z ({N_0})\), \(\varphi ({N_0})\), \(q_z ({N_0})\), and \(h_z ({N_0})\) denote the elastic displacement in z-direction, electric potential, moisture flux, and heat flux on the upper crack surface, respectively; and the integration is taken over the crack face S. To meet the zero-shear stress condition in Eq. (34c), one can have

$$\begin{aligned} \sum _{i=1}^5 {\gamma _{1i} h_{ij} =0} ,\quad \quad ({j=1,2,3,4}), \end{aligned}$$
(37)

in which \(\gamma _{1i} =c_{44} ({\mu _{2i} -s_i}) +e_{15} \mu _{4i}\).

According to the well-known property of a simple layer potential, one can get

$$\begin{aligned}&\frac{\partial H_1}{\partial z} \big |_{z=0} = \left\{ \begin{array}{ll} -2\pi w( {x,y,0} ) &{} ( {x,y} )\in S, \\ 0 &{} ( {x,y} )\notin S, \\ \end{array} \right. \nonumber \\&\frac{\partial H_2 }{\partial z} \big |_{z=0} = \left\{ \begin{array}{ll} -2\pi \varphi ( {x,y,0} ) &{} ( {x,y} )\in S, \\ 0 &{} ( {x,y} )\notin S, \\ \end{array} \right. \nonumber \\&\frac{\partial ^{3}H_3}{\partial z^{3}}\big |_{z=0} = \left\{ \begin{array}{ll} 2\pi q_z ( {x,y,0} )/\kappa _{33} &{} ( {x,y} )\in S, \\ 0 &{} ( {x,y} )\notin S, \\ \end{array} \right. \nonumber \\&\frac{\partial ^{3}H_4}{\partial z^{3}}\big |_{z=0} = \left\{ \begin{array}{ll} 2\pi h_z ( {x,y,0} )/\lambda _{33} &{} ( {x,y} )\in S, \\ 0 &{} ( {x,y} )\notin S. \\ \end{array} \right. \end{aligned}$$
(38)

Combining Eqs. (36b) and (40) and the general solutions, one can have

$$\begin{aligned}&\sum _{i=1}^5 {\mu _{2i} h_{ij} =-\frac{\delta _{1j} }{2\pi }}, \quad \sum _{i=1}^5 {\mu _{4i} h_{ij} =-\frac{\delta _{2j} }{2\pi }}, \nonumber \\&\mu _6 s_4 h_{4j} =-\frac{\delta _{3j} }{2\pi }, \quad \mu _7 s_5 h_{5j} =-\frac{\delta _{4j} }{2\pi }, \end{aligned}$$
(39)

where \(\delta _{ij}\) is the Kronecker delta. Combining Eqs. (37) and (39), one can obtain \(h_{ij}\) from following equation

$$\begin{aligned}&\left\{ {\begin{array}{l} h_{1j} \\ h_{2j} \\ h_{3j} \\ h_{4j} \\ h_{5j} \\ \end{array}} \right\} =\frac{-1}{2\pi }\left[ {{\begin{array}{ccccc} {\gamma _{11} } &{} {\gamma _{12} } &{} {\gamma _{13} } &{} {\gamma _{14} } &{} {\gamma _{15} } \\ {\mu _{21} } &{} {\mu _{22} } &{} {\mu _{23} } &{} {\mu _{24} } &{} {\mu _{25} } \\ {\mu _{41} } &{} {\mu _{42} } &{} {\mu _{43} } &{} {\mu _{44} } &{} {\mu _{45} } \\ 0 &{} 0 &{} 0 &{} {\mu _6 s_4 } &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {\mu _7 s_5 } \\ \end{array} }} \right] ^{-1}\left\{ {\begin{array}{l} 0 \\ \delta _{1j} \\ \delta _{2j} \\ \delta _{3j} \\ \delta _{4j} \\ \end{array}} \right\} , \nonumber \\&\quad ({j=1,2,3,4}). \end{aligned}$$
(40)

To satisfy the condition in Eq. (34a), one can arrive at the following equations

$$\begin{aligned}&m_{11} \Delta \int \int _S {\frac{w( {N_0 } )}{R( {N,N_0 } )}dS} +m_{12} \Delta \int \int _S {\frac{\varphi ({N_0 } )}{R( {N,N_0 })}dS} \nonumber \\&\quad +\frac{m_{13} }{\kappa _{33} }\int \int _S {\frac{q_z ( {N_0 } )}{R( {N,N_0 } )}dS} \nonumber \\&\quad +\frac{m_{14} }{\lambda _{33} }\int \int _S {\frac{h_z ( {N_0 } )}{R( {N,N_0} )}dS} =-2\pi \Xi _1 ( N ), \end{aligned}$$
(41a)
$$\begin{aligned}&m_{21} \Delta \int \int _S {\frac{w\left( {N_0 } \right) }{R\left( {N,N_0 } \right) }dS} +m_{22} \Delta \int \int _S {\frac{\varphi \left( {N_0 } \right) }{R\left( {N,N_0 } \right) }dS} \nonumber \\&\quad +\frac{m_{23} }{\kappa _{33} }\int \int _S {\frac{q_z \left( {N_0 } \right) }{R\left( {N,N_0 } \right) }dS} \nonumber \\&\quad +\frac{m_{24} }{\lambda _{33} }\int \int _S {\frac{h_z \left( {N_0 } \right) }{R\left( {N,N_0 } \right) }dS} =-2\pi \Xi _2 \left( N \right) , \end{aligned}$$
(41b)
$$\begin{aligned}&\int \int _S {\frac{q_z \left( {N_0 } \right) }{R\left( {N,N_0 } \right) }dS} =2\pi \kappa _{33} s_4 \Xi _3 \left( N \right) , \end{aligned}$$
(41c)
$$\begin{aligned}&\int \int _S {\frac{h_z \left( {N_0 } \right) }{R\left( {N,N_0 } \right) }dS} =2\pi \lambda _{33} s_5 \Xi _4 \left( N \right) , \end{aligned}$$
(41d)

where \(R(N_{0}, N)\) is the distance between two points, \(N_{0}(x_{0}, y_{0}, 0)\) and N(x, y, 0) both of which lie on the crack S, and \(m_{ij}\) can be obtained as follows

$$\begin{aligned}&m_{1j} =\sum _{i=1}^5 {\gamma _{2i} h_{ij} } ,\quad m_{2j} =\sum _{i=1}^5 {\gamma _{3i} h_{ij}}, \nonumber \\&\quad j=1,2,3,4, \end{aligned}$$
(42)

in which

$$\begin{aligned} \gamma _{2i}= & {} c_{13} +c_{33} \mu _{2i} s_i +e_{33} \mu _{4i} s_i -\xi _{33} \mu _6 -\beta _{33} \mu _7, \\ \gamma _{3i}= & {} e_{31} +e_{33} \mu _{2i} s_i -\varepsilon _{33} \mu _{4i} s_i +\chi _3 \mu _6 +\gamma _3 \mu _7 . \end{aligned}$$

Substituting Eqs. (41c) and (41d) into (41a) and (41b) leads to

$$\begin{aligned}&\Delta \int \int _S {\frac{w\left( {N_0 } \right) }{R\left( {N,N_0 } \right) }dS} =-2\pi \overline{\Xi _1 \left( N \right) } , \nonumber \\&\Delta \int \int _S {\frac{\varphi \left( {N_0 } \right) }{R\left( {N,N_0 } \right) }dS} =-2\pi \overline{\Xi _2 \left( N \right) } , \end{aligned}$$
(43)

where

$$\begin{aligned} \overline{\Xi _1 (N)}= & {} \frac{1}{m_{11} m_{22} -m_{21} m_{12}} \nonumber \\&\times \,[{m_{22} \Xi _1 (N)-m_{12} \Xi _2 (N)} \nonumber \\&-\,( {m_{12} m_{23} -m_{13} m_{22} } )s_4 \Xi _3 ( N ) \nonumber \\&-\,( {m_{12} m_{24} -m_{14} m_{22} } )s_5 \Xi _4( N )], \nonumber \\ \overline{\Xi _2 ( N )}= & {} \frac{1}{m_{12} m_{21} -m_{11} m_{22}} \nonumber \\&\times \,[{m_{21} \Xi _1 ( N )-m_{11} \Xi _2 ( N)} \nonumber \\&-\,( {m_{11} m_{23} -m_{13} m_{21} } )s_4 \Xi _3 ( N ) \nonumber \\&-\,( {m_{11} m_{24} -m_{14} m_{21} } )s_5 \Xi _4 ( N ) ]. \end{aligned}$$
(44)

It is observed that, the moisture and thermal loads can affect the elastic and electric fields (see Eq. 43), whilst the mechanical and electric loads cannot influence the moisture or temperature field. Furthermore, no mutual influences exist between the moisture and temperature fields, which is due to the adoption of the uncoupled theory.

In addition, Eqs. (41c) and (41d) share a similar form as those of crack problems in elasticity (Fabrikant 1989), while the integro-differential equations in Eq. (43) are similar to that of contact problems in elasticity (Fabrikant 1989). Due to this similarity, we can directly adopt the results given by (Fabrikant 1989, 1991) to construct the solutions to the governing equations in some particular cases. For cracks with irregular geometries and that are subjected to arbitrary loads, the boundary element method may be utilized for numerical simulation, and the detailed application can be found in Zhao et al. (2018b).

Specifically, when the crack is penny-shaped under uniform mechanical, electric, moisture as well as temperature loads, the exact, closed-form solution can be obtained. Consider the crack \(S= \{(x=r\cos \phi , y=r\sin \phi ,0): r=\sqrt{x^{2}+y^{2}}\le a,0\le \phi \le 2\pi \}\) i.e. for a penny-shaped crack of radiusa with its center located at the origin of the cylindrical coordinate system (\(r, \phi , z\)). The uniform mechanical load, \(\Xi _1^0\), electric displacement, \(\Xi _2^0\), moisture load, \(\Xi _3^0\) and heat load, \(\Xi _4^0\), are applied on the crack faces. In this case, it is possible to obtain a complete solution in elementary functions due to an analogy with the corresponding problem in Fabrikant (1991), the exact solutions for Eqs. (41) and (43) can be obtained as:

$$\begin{aligned}&w( {\rho ,\phi } )=\frac{2\overline{\Xi _1^0 } \sqrt{a^{2}-\rho ^{2}}}{\pi }, \nonumber \\&\varphi ( {\rho ,\phi })=\frac{2\overline{\Xi _2^0 } \sqrt{a^{2}-\rho ^{2}}}{\pi }, \nonumber \\&q_z ( {\rho ,\phi } )=\frac{\kappa _{33} s_4 }{\pi } \frac{\Xi _3^0 }{\sqrt{a^{2}-\rho ^{2}}}, \nonumber \\&h_z ( {\rho ,\phi }) =\frac{\lambda _{33} s_5 }{\pi }\frac{\Xi _4^0}{\sqrt{a^{2}-\rho ^{2}}}. \end{aligned}$$
(45)

Because of the axisymmetry of the problem, the right hand terms of Eq. (45) are independent of the angular coordinate \(\phi \). Inserting Eqs. (45) into (36) yields

$$\begin{aligned} H_1 ({r,\phi ,z})= & {} \overline{\Xi _1^0} \left[ {({2a^{2}+2z^{2}-r^{2}}) \sin ^{-1}\left( {\frac{a}{l_2 }} \right) } \right. \nonumber \\&\left. -\frac{2a^{2}-3l_1^2 }{a}\sqrt{l_2^2 -a^{2}} \right] , \nonumber \\ H_2 ({r, \phi ,z})= & {} \overline{\Xi _2^0 } \left[ \left( {2a^{2}+2z^{2}-r^{2}} \right) \sin ^{-1}\left( {\frac{a}{l_2 }} \right) \right. \nonumber \\&\left. -\frac{2a^{2}-3l_1^2 }{a}\sqrt{l_2^2 -a^{2}} \right] , \nonumber \\ H_3 ({r,\phi ,z})= & {} -2s_4 \Xi _3^0 \left[ {\left( {a^{2}+z^{2}-\frac{r^{2}}{2}} \right) \sin ^{-1}\left( {\frac{a}{l_2 }} \right) } \right. \nonumber \\&-\frac{2a^{2}-3l_1^2 }{a}\sqrt{l_2^2 -a^{2}} \nonumber \\&\left. +2az\ln \left( {l_2 +\sqrt{l_2^2 -a^{2}}} \right) \right] , \nonumber \\ H_4 ({r, \phi ,z})= & {} -2s_5 \Xi _4^0 \left[ {\left( {a^{2}+z^{2}-\frac{r^{2}}{2}} \right) \sin ^{-1}\left( {\frac{a}{l_2 }} \right) } \right. \nonumber \\&-\frac{2a^{2}-3l_1^2 }{a}\sqrt{l_2^2 -a^{2}} \nonumber \\&\left. +2az\ln \left( {l_2 +\sqrt{l_2^2 -a^{2}}} \right) \right] , \end{aligned}$$
(46)

where

$$\begin{aligned} l_1= & {} l_1 ( {r,a,z} ) \nonumber \\= & {} \frac{1}{2}[ {\sqrt{( {r+a})^{2}+z^{2}}-\sqrt{( {r-a} )^{2}+z^{2}}}], \nonumber \\ l_2= & {} l_2 ( {r,a,z} ) \nonumber \\= & {} \frac{1}{2}[ {\sqrt{( {r+a})^{2}+z^{2}}+\sqrt{( {r-a})^{2}+z^{2}}} ]. \end{aligned}$$
(47)

At this stage, the whole hygrothermopiezoelectric field can be obtained by simply differentiating \(H_{i}\). The complete expressions are given as

$$\begin{aligned}&u+\hbox {i}v = 2re^{\mathrm {i}\phi }\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 h_{jk} \nonumber \\&\quad \qquad \quad \times \left[ {\sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\frac{a\sqrt{l_{2j}^2 -a^{2}}}{l_{2j}^2 }} \right] \nonumber \\&\qquad \qquad -\,4\frac{e^{\mathrm {i}\phi }}{r}\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 h_{jk} \nonumber \\&\qquad \qquad \times \left[ \sqrt{l_{2j}^2 -a^{2}}\left( {a-\frac{l_{1j}^2 }{2a}} \right) -az_j \right. \nonumber \\&\qquad \qquad \left. +\,\frac{r^{2}}{2}\sin ^{-1}\left( {\frac{a}{l_{2j}}} \right) \phantom {\sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\frac{a\sqrt{l_{2j}^2 -a^{2}}}{l_{2j}^2 }}\right] , \nonumber \\&w = 4\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 \mu _{2j} h_{jk} \nonumber \\&\qquad \times \left[ {z_j \sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\sqrt{a^{2}-l_{1j}^2 }} \right] \nonumber \\&\qquad -\,4\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 \mu _{2j} h_{jk} \nonumber \\&\qquad \times \left[ z_j \sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\sqrt{a^{2}-l_{1j}^2} \right. \nonumber \\&\qquad \quad \left. +\,a\ln \left( {l_{2j} +\sqrt{l_{2j}^2 -r^{2}}} \right) \phantom {\left( {\frac{a}{l_{2j} }} \right) }\right] , \nonumber \\&\varphi = 4\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 \mu _{4j} h_{jk} \nonumber \\&\qquad \times \left[ {z_j \sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\sqrt{a^{2}-l_{1j}^2 }} \right] \nonumber \\&\quad -\,4\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 \mu _{4j} h_{jk} \nonumber \\&\quad \times \Bigg [ z_j \sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\sqrt{a^{2}-l_{1j}^2} \nonumber \\&\qquad \quad +\,a\ln \left( {l_{2j} +\sqrt{l_{2j}^2 -r^{2}}} \right) \Bigg ], \nonumber \\&\sigma _z = 4\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 \gamma _{2j} h_{jk} \nonumber \\&\qquad \times \left[ {\sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\frac{a\sqrt{l_{2j}^2 -a^{2}}}{l_{2j}^2 -l_{1j}^2 }} \right] \nonumber \\&\qquad -\,4\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 {\gamma _{2j} h_{jk} \sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) } , \nonumber \end{aligned}$$
$$\begin{aligned}&D_z = 4\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 \gamma _{3j} h_{jk} \nonumber \\&\qquad \times \left[ {\sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\frac{a\sqrt{l_{2j}^2 -a^{2}}}{l_{2j}^2 -l_{1j}^2 }} \right] \nonumber \\&\qquad -\,4\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 {\gamma _{3j} h_{jk} \sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) }, \nonumber \\&\sigma _x +\sigma _y = 4\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 \gamma _{4j} h_{jk} \nonumber \\&\quad \times \left[ {\sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) -\frac{a\sqrt{l_{2j}^2 -a^{2}}}{l_{2j}^2 -l_{1j}^2 }} \right] \nonumber \\&\quad -\,4\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 {\gamma _{4j} h_{jk} \sin ^{-1}\left( {\frac{a}{l_{2j} }} \right) } , \nonumber \\&\sigma _x -\sigma _y +2\hbox {i}\sigma _{xy} \nonumber \\&\quad = -8c_{66} ae^{2\hbox {i}\phi }\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 {\frac{h_{jk} l_{1j}^2 \sqrt{l_{2j}^2 -a^{2}}}{l_{2j}^2 \left( {l_{2j}^2 -l_{1j}^2 } \right) }} \nonumber \\&\qquad +\,4c_{66} \frac{e^{2\hbox {i}\phi }}{r^{2}}\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 h_{jk} \nonumber \\&\qquad \times \,\left( {a\sqrt{l_{2j}^2 -a^{2}}+z_j \sqrt{a^{2}-l_{1j}^2 }-2az_j } \right) , \nonumber \\&\sigma _{zx} +\hbox {i}\sigma _{yz} = 4a^{2}re^{\mathrm {i}\phi }\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 {\frac{\gamma _{1j} h_{jk} \sqrt{a^{2}-l_{1j}^2 }}{l_{2j}^2 \left( {l_{2j}^2 -l_{1j}^2 } \right) }} \nonumber \\&\quad +\,4\frac{e^{\mathrm {i}\phi }}{r}\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 {\gamma _{1j} h_{jk} \left( {\sqrt{a^{2}-l_{1j}^2 }-a} \right) } , \nonumber \\&D_x +\hbox {i}D_y = 4a^{2}re^{\mathrm {i}\phi }\sum _{k=1}^2 {\overline{\Xi _k^0 } } \sum _{j=1}^5 {\frac{\gamma _{5j} h_{jk} \sqrt{a^{2}-l_{1j}^2 }}{l_{2j}^2 \left( {l_{2j}^2 -l_{1j}^2 } \right) }} \nonumber \\&\quad +\,4\frac{e^{\mathrm {i}\phi }}{r}\sum _{k=3}^4 {s_{k+1} \Xi _k^0 } \sum _{j=1}^5 {\gamma _{5j} h_{jk} \left( {\sqrt{a^{2}-l_{1j}^2 }-a} \right) }, \nonumber \\&m = \frac{2}{\pi }\Xi _3^0 \sin ^{-1}\left( {\frac{a}{l_{24} }} \right) , \nonumber \\&\theta =\frac{2}{\pi }\Xi _4^0 \sin ^{-1}\left( {\frac{a}{l_{25}}} \right) , \end{aligned}$$
(48)

wherein

$$\begin{aligned} \gamma _{4i}= & {} 2 [c_{11} -c_{66} +c_{13} \mu _{2i} s_i +e_{31} \mu _{4i} s_i \nonumber \\&-\xi _{11} \mu _6 -\beta _{11} \mu _7], \nonumber \\ \gamma _{5i}= & {} e_{15} \left( {\mu _{2i} -s_i } \right) -\varepsilon _{11} \mu _{4i} +\chi _1 \mu _6 s_4 +\gamma _1 \mu _7 s_5, \nonumber \\ l_{1i}= & {} \frac{1}{2}\left[ {\sqrt{\left( {r+a} \right) ^{2}+z_i^2 }-\sqrt{\left( {r-a} \right) ^{2}+z_i^2 }} \right] , \nonumber \\ l_{2i}= & {} \frac{1}{2}\left[ {\sqrt{\left( {r+a} \right) ^{2}+z_i^2 }+\sqrt{\left( {r-a} \right) ^{2}+z_i^2 }} \right] . \end{aligned}$$
(49)

Making use of the following properties (Li et al. 2010)

$$\begin{aligned}&l_1 \big |_{z=0} =l_1 ({r,a,0}) = \min ({a,r}), \nonumber \\&l_2 \big |_{z=0} =l_2 ({r,a,0}) = \max ({a,r}), \end{aligned}$$
(50)

one can obtain from Eq. () that

$$\begin{aligned} \sigma _z \left( {r,\phi ,0} \right)= & {} \left\{ \begin{array}{ll} \frac{2}{\pi }\Xi _1^0 \left[ {\sin ^{-1}\left( {\frac{a}{r}} \right) -\frac{a}{\sqrt{r^{2}-a^{2}}}} \right] +\frac{4a}{m_{22} \sqrt{r^{2}-a^{2}}} &{} \\ \left[ {\left( {m_{11} m_{22} -m_{21} m_{12} } \right) s_4 \Xi _3^0 +\left( {m_{12} m_{24} -m_{14} m_{22} } \right) s_5 \Xi _4^0 } \right] , &{} \left( {r,\phi } \right) \notin S, \\ \Xi _1^0 , &{} \left( {r,\phi } \right) \in S, \\ \end{array} \right. \nonumber \\ D_z \left( {r,\phi ,0} \right)= & {} \left\{ \begin{array}{ll} \frac{2}{\pi }\Xi _2^0 \left[ {\sin ^{-1}\left( {\frac{a}{r}} \right) -\frac{a}{\sqrt{r^{2}-a^{2}}}} \right] -\frac{4a}{m_{11} \sqrt{r^{2}-a^{2}}} &{} \\ \left[ {\left( {m_{11} m_{23} -m_{13} m_{21} } \right) s_4 \Xi _3^0 +\left( {m_{11} m_{24} -m_{14} m_{21} } \right) s_5 \Xi _4^0 } \right] , &{} \left( {r,\phi } \right) \notin S, \\ \Xi _1^0, &{} \left( {r,\phi } \right) \in S, \\ \end{array} \right. \nonumber \\ m\left( {r,\phi ,0} \right)= & {} \left\{ \begin{array}{ll} \frac{2}{\pi }\Xi _3^0 \sin ^{-1}\left( {\frac{a}{r}} \right) , &{} \left( {r,\phi } \right) \notin S, \\ \Xi _3^0, &{} \left( {r,\phi } \right) \in S, \\ \end{array} \right. \nonumber \\ \theta \left( {r,\phi ,0} \right)= & {} \left\{ \begin{array}{ll} \frac{2}{\pi }\Xi _4^0 \sin ^{-1}\left( {\frac{a}{r}} \right) , &{} \left( {r,\phi } \right) \notin S, \\ \Xi _4^0, &{} \left( {r,\phi } \right) \in S. \\ \end{array} \right. \end{aligned}$$
(51)

It can be easily proven that the boundary conditions at the crack surface are satisfied. It is also interesting to note that the normal stress, \(\sigma _{z,}\) and electric displacement, \(D_{z,}\) on the \(z = 0\) plane outside the crack domain are both the sum of two terms which are the respective singular and non-singular parts at the crack tip.

Defining the following stress and electric displacement intensity factors:

$$\begin{aligned} K_I= & {} \mathop {\lim }\limits _{r\rightarrow a} \sqrt{2\pi \left( {r-a} \right) }\sigma _z \big |_{z=0} , \nonumber \\ K_D= & {} \mathop {\lim }\limits _{r\rightarrow a} \sqrt{2\pi \left( {r-a} \right) }D_z \big |_{z=0} , \end{aligned}$$
(52)

one can obtain their expressions from Eq. (51) as

$$\begin{aligned} K_I= & {} -\frac{2}{\pi }\Xi _1^0 \sqrt{\pi a} \nonumber \\&+\frac{4}{m_{22} }\left[ \left( {m_{11} m_{22} -m_{21} m_{12} } \right) s_4 \Xi _3^0 \right. \nonumber \\&\quad \qquad \left. +\left( {m_{12} m_{24} -m_{14} m_{22} } \right) s_5 \Xi _4^0 \right] \sqrt{\pi a}, \nonumber \\ K_D= & {} \frac{2}{\pi }\Xi _2^0 \sqrt{\pi a} \nonumber \\&-\frac{4}{m_{11}} \left[ \left( {m_{11} m_{23} -m_{13} m_{21} } \right) s_4 \Xi _3^0 \right. \nonumber \\&\quad \qquad \left. +\left( {m_{11} m_{24} -m_{14} m_{21} } \right) s_5 \Xi _4^0 \right] \sqrt{\pi a}.\nonumber \\ \end{aligned}$$
(53)

It can be concluded from Eq. (53) that the stress and electric displacement intensity factors are independent of the material constants, and only related to the load of the corresponding fields. When the moisture and temperature loads are removed, they reduce to the expressions for the piezoelectric materials (Chen and Shioya 2000). In addition, the above analysis can be readily extended to study the problem of when the uniform mechanical, electric, moisture as well as temperature loads are applied at infinity with impermeable conditions at the crack faces. In this case, the complete solution includes two parts. One part is the solution presented in this section, and the other is a uniform one that can be easily expressed according to Chen and Shioya (2000).

6 Conclusions and perspectives

With the aid of differential operator theory, superposition principle, and the generalized Almansi theorem, two displacement functions were introduced to simplify the fundamental equations of transversely isotropic, hygrothermopiezoelectric material, and the general solution in terms of six quasi-harmonic functions was derived. Some of its applications in fracture were presented. No particular solutions associated with the moisture and temperature fields appear in the general solution, making it possible to extend the potential theory method to hygrothermopiezoelectricity.

The general solution or Green’s function for hygrothermopiezoelectricity was provided for the first time in the present work. The obtained general solution is expressed in terms of harmonic functions, which makes it conveniently applicable for mixed, boundary value problems such as crack and punch problems in hygrothermopiezoelectricity. It should be pointed out that the hygrothermopiezoelectric field was only presented for the materials with distinct characteristic roots. The potential theory method can also be employed for other hygrothermopiezoelectric materials if appropriate potential functions are determined. Nevertheless, as pointed out by Fabrikant (1989), the corresponding solutions in the case of multiple roots can be derived directly from the solutions with the aid of the L’Hospital rule. The application of the general solution was illustrated through a crack problem in hygrothermoelectroelasticity. Specifically, for the problem of a penny-shaped crack under uniformly distributed loads, the exact, 3D hygro-thermo-electro-elastic field in the entire space was expressed in terms of elementary functions. The stress and electric displacement intensity factors were obtained in a concise form.