3D model of transversal fracture propagation from a cavity caused by Herschel–Bulkley fluid injection

Abstract

The paper presents an extension of authors’ previous model for a 3D hydraulic fracture with Newtonian fluid, which aims to account for the Herschel–Bulkley fluid rheology and to study the associated effects. This fluid rheology model is the most suitable for description of modern complex fracturing fluids, in particular, for description of foamed fluids that have been successfully utilized recently as fracturing fluids in tight and ultra-tight unconventional formations with high clay contents. Another advantage of using Herschel–Bulkley rheological law in the hydraulic fracture model consists in its generality as its particular cases allow describing the behavior of the majority of non-Newtonian fluids employed in hydraulic fracturing. Except the Herschel–Bulkley fluid flow model the considered model of hydraulic fracturing includes the model of the rock stress state. It is based on the elastic equilibrium equations that are solved by the dual boundary element method. Also the hydraulic fracturing model contains the new mixed mode propagation criterion, which states that the fracture should propagate in the direction in which mode ${{\mathrm{\mathrm {II}}}}$ and mode ${{\mathrm{\mathrm {III}}}}$ stress intensity factors both vanish. Since it is not possible to make both modes zero simultaneously the criterion proposes a functional that depends on both modes and is minimized along the fracture front in order to obtain the direction of propagation. Solution for Herschel–Bulkley fluid flow in a channel is presented in detail, and the numerical algorithm is described. The developed model has been verified against some reference solutions and sensitivity of fracture geometry to rheological fluid parameters has been studied to some extent.

1 Introduction

Fig. 1

The parametric spaces for penny-shaped fracture: early time solution with fluid lag in impermeable rock O–M–K (Bunger and Detournay 2007) (left) and developed fracture with leak-off M–K–${\tilde{M}}$–${\tilde{K}}$ (Dontsov and Kresse 2018) (right)

The hydraulic fracturing process for classical reservoirs and developed cracks has been investigated by many researches. For classical models, such as radial and KGD, along with numerical models, analytical solutions describing crack propagation are also obtained. They describe fracture propagation caused by dominant influence of one of the physical processes or parameters (Detournay 2016): hydraulic fluid viscosity (viscosity dominated regime M), rock fracture toughness (toughness dominated regime K) (Savitski and Detournay 2002; Detournay 2004), fluid leak-off in the surrounding rock (leak-off regimes ${\tilde{M}}$, $\tilde{K}$) (Adachi and Detournay 2008; Bunger et al. 2005) or overburden stress in the fluid lag region (fluid lag regime O) (Garagash and Detournay 2000; Garagash 2006; Bunger and Detournay 2007).

At the same time, the development of unconventional reservoirs causes the development of new fracturing fluids and additives to them (flocks, fibers, etc.), which significantly change their rheology. Growing interest in tight and ultra-tight unconventional formations with high clay contents had resulted in developing special fluid systems with large fractions of gas and small water fractions or so called foamed fluids (Barati and Liang 2014). Most foamed fluids reportedly show Herschel–Bulkley (HB) rheological behaviours (Herschel and Bulkley 1926). This rheological model has been successfully used to model the flow of other types of fracturing fluids within porous media as well (Barati et al. 2009). The advantage of Herschel–Bulkley rheological law is that as its particular cases it includes simpler rheological models: from Newtonian and pseudoplastic fluids to the ones governed by the Bingham law. The latter two rheological models are often used in hydraulic fracturing simulators, in particular, while modeling proppant transport and settling.

Investigation of fractures propagating caused by non-Newtonian fluids injection is much more complicated than Newtonian. Nevertheless, for power law fluid, a few analytical solutions were proposed for the case of plane fracture (Adachi and Detournay 2002; Dontsov and Kresse 2018) and penny shaped fracture (Linkov 2015). It should be noted that the case of Bingham fluid has been studied much less. The present paper is intended to fill this gap by investigating the effect of non-Newtonian fluid rheology parameters on the fracture propagation at the initial stage. The research is based on numerical modeling of the fracture propagation in three-dimensional formulation. There is no enough experience of the solution of three-dimensional problems of fracture propagation caused by injection of fluid with Herschel–Bulkley rheology.

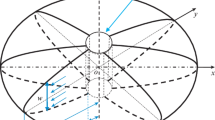
To describe the penny-shaped fracture behavior in transient regimes the solutions for regimes K–${\tilde{K}}$ and K–M have been proposed in Detournay (2016) and Bunger et al. (2005), respectively and in Dontsov (2016) the solutions for the whole parametric K–M–${\tilde{M}}$–${\tilde{K}}$ space has been proposed. The parametric spaces for penny-shaped fracture is shown in Fig. 1. Solutions map are presented for the case of impermeable rock and with fluid lag taken into account [O–M–K triangle space (Bunger and Detournay 2007)] and for the developed fracture in permeable rock K–M–${\tilde{M}}$–${\tilde{K}}$ (Dontsov and Kresse 2018). the definition and the values of the parameters are described in Bunger and Detournay (2007) and Dontsov and Kresse (2018). As can be seen in the figure, analytical or numerical analytical solutions are proposed for all regimes in the parametric space of a developed penny-shaper fracture.

For plane KGD fracture solutions have been proposed for the M–${\tilde{M}}$ transition regime (Adachi and Detournay 2008) and for M–K regime (Garagash and Detournay 2000). However, for the initial stage of penny-shaped fracture propagation, during the transition from the regime with dominant fluid lag to the viscous regime (O–M regime), no analytical solution has been proposed. On the one hand, the duration of this regime is limited to a few seconds (Bunger and Detournay 2007), and in impermeable rock, the penny-shaped fracture propagates most of the time in the regime with the dominant viscosity (Savitski and Detournay 2002). On the other hand, at the initial stage, the fracture trajectory is formed. And the fracture trajectory affects the entire fracturing process (Aud and Wright 1994; Cleary et al. 1993). For example if the fracture is curved then width is decreased in the wellbore vicinity (Cherny et al. 2009). It generates a near-wellbore pressure loss and creates a risk of wellbore screenout due to proppant bridging (Economides and Nolte 2000).

To describe the initial stage in Shokin et al. (2015) and Cherny et al. (2016), a new fully three-dimensional numerical model of fracture propagation caused by Newtonian fluid pumping is constructed and justified. A feature of this model is a direct account of the wellbore influence on the development of the fracture and the pressure variation along the fracture surface. In the current paper this three-dimensional model is improved by the model of non-Newtonian fluid with Herschel–Bulkley rheology. It allows to describe the propagation of three-dimensional curvilinear fractures and to study the effect of the rheology parameters on the wellbore pressure, the fracture trajectory and the fracture width.

Implementation and application of the Herschel–Bulkley model are complicated due to its nonlinearity. It would be good to know if the Newtonian model can be used to describe the fracture propagation caused by the injection of a non-Newtonian fluid. This question is investigated for various regimes of fracture propagation. For the case of a developed fracture, the analytical solutions (Adachi and Detournay 2002; Dontsov and Kresse 2018; Linkov 2015), obtained for power law fluid, explicitly contain the power law index, so in general case this replacement is impossible without loss of accuracy. The present work is aimed at studying the initial regime (O–M) of fracture propagation, when the fracture trajectory is formed. Therefore, this question was investigated under the assumption that time is small. The possibility of using Newtonian rheology for modeling the propagation of fracture caused by the injection of complex fluid is considered in Sect. 3 using dimensionless analysis, and in Sect. 4 using numerical modeling. The numerical simulation is performed within the framework of three-dimensional formulation, taking into account the effect of the wellbore, the anisotropy of in-situ stresses and the lag of the fluid from the fracture front.

2 Model description

In the model which is described in the current paper we use the geometrical concept presented in Fig. 2. There is a penny-shaped initial fracture of radius R in a plane inclined to axis Oz at an angle $\alpha$. The initial crack adjoins a wellbore of radius $R_{w}$ and is perpendicular to this wellbore. The surrounding medium is loaded at the infinity by compressing principal stresses $\sigma _x^\infty$, $\sigma _y^\infty$, $\sigma _z^\infty$, that have negative values. The principal components $\sigma _x^\infty$, $\sigma _y^\infty$ and $\sigma _z^\infty$ of stress tensor ${{\mathrm{\varvec{\sigma }}}}^\infty$ are applied in the directions of axis x, y and z respectively and are revealed as the in-situ stress. The wellbore and the initial fracture are loaded from the inside by Herschel–Bulkley fluid flow.

Fracturing fluid is injected into the wellbore and then from the wellbore to the fracture through the boundary $\Gamma ^q$ under the pressure that is sufficient to cause the rock breakdown at the fracture edge followed by the fracture propagation. The fluid front $\Gamma ^p$ lags the fracture front $\Gamma ^f$. In the general case the wellbore is not aligned with the directions of principal in-situ stresses compressing the rock at infinity. Therefore, the propagating fracture will deviate from its initial plane turning toward the so-called preferred fracture plane (PFP), which is perpendicular to the minimum principal in-situ stress as shown in Fig. 2. This figure corresponds to the case when $\sigma _z^\infty < \sigma _x^\infty$ and $\sigma _z^\infty < \sigma _y^\infty$ and, therefore, the PFP is perpendicular to z axis.

Fig. 2

The transversal fracture propagation from the inclined wellbore

To model the process of hydraulic fracture propagation one needs to consider its three inseparable parts: changes of the stress-strained state of the rock, the fluid flow inside the fracture and the processes of crack growth and crack front deflection.

2.1 Determination of rock stress-strained state

The stress-strain state of an isotropic homogeneous medium near the cavity and the fracture at each step of fracture propagation is described by the elastic equilibrium equations. The equations are solved in an infinite domain. At the infinity the stress tensor ${{\mathrm{\varvec{\sigma }}}}^\infty$ with principal components $\sigma _x^\infty$, $\sigma _y^\infty$, $\sigma _z^\infty$ applied in the directions of axis x, y, z respectively and the condition of zero displacements are set up. The principal components are revealed as an in-situ stress. On the cavity and the fracture surface the tractions

$$\begin{aligned} t_i = - p n_i - \sigma _{ij}^\infty n_j \end{aligned}$$

(1)

are set up. In (1) $\sigma _{ij}^\infty$ are the components of tensor ${{\mathrm{\varvec{\sigma }}}}^\infty$, $n_i$ are the components of the surface outer unit normal, p is the pressure in the cavity or the fracture. In the region of the fracture between the fluid front and the fracture front the pore pressure is applied.

For the solution of elasticity sub-problem the Boundary Element Method (BEM) is used in the most papers that concern 3D initiation and evolution of hydraulic fractures. The conventional BEM was used for it in Cherny et al. (2016). To overcome the difficulty concerning the singular system of algebraic equations on the crack surfaces the real fracture is replaced by a fictitious notch of the finite width. The artificial width parameter is chosen in a way to minimize the error caused by such modification. The collocation nodes of the opposite sides of the notch are positioned far enough to make the algebraic equations well-conditioned and close enough to keep the errors of the calculation of crack width and stress intensity factors (SIFs) minimal.

However the most suitable method for the solution of the elasticity problem in 3D model of fracture propagation from the arbitrary cavity is the Dual Boundary Element Method (DBEM) (Hong and Chen 1988; Chen and Hong 1999). Mi and Aliabadi (1992, 1994) have developed the DBEM for solving the 3D problems of elasticity.

In Kuranakov et al. (2016) the authors proposed a modification of the DBEM, which implies solving the traction boundary integral equation relative to the displacement discontinuities at one of the fracture sides for the specified tractions, which gives the fracture width. Similar to the original DBEM, the displacement boundary integral equation should be solved on the regular boundary as well. However, no equations for the other fracture side are needed for the final hydraulic fracture model. The proposed modification significantly reduces the amount of computations, since the numerical approximation of the only fracture side is required. The modified 3D DBEM is employed in the current paper for the determination of the rock stress-strained state.

The detailed review of the other methods for solution of the elasticity problem in 3D model of fracture propagation is presented in Cherny et al. (2016).

2.2 Crack growth model

As in Cherny et al. (2016) the basis of the crack growth model consists in the fundamental postulate of linear elastic fracture mechanics: the behaviour of cracks is determined solely by the value of SIFs. In the present paper the displacement extrapolation method for evaluating SIFs is employed (Aliabadi 2002; Cherny et al. 2016).

The maximum energy release rate criterion is used to describe the magnitude of the crack front advance at each crack front vertex (Nuismer 1975; Cherny et al. 2016). In accordance with this criterion the fracture propagates when the energy release rate in the direction of crack propagation $\theta ^*$ reaches the critical energy release rate of the material

$$\begin{aligned}&(1-\nu ) \left( K_I^2 (\theta ^*, t + \Delta t) + K_{{{\mathrm{\mathrm {II}}}}}^2 (\theta ^*, t + \Delta t) \right) \nonumber \\&\quad +\, K_{{{\mathrm{\mathrm {III}}}}}^2(\theta ^*, t + \Delta t) =(1-\nu ) K_{{{\mathrm{\mathrm I}}}c}^2, \end{aligned}$$

(2)

where t is the time moment before the crack front advance, $\Delta t$ is time increment for the transition to the next crack front position, $\theta ^*$ is the kinking angle.

For realistic determination of the crack front deflection in arbitrary 3D problems of real structures in Cooke and Pollard (1996), Pereira (2010) and Cherny et al. (2016) the three-dimensional mixed-mode criteria are applied. In Cherny et al. (2016) the new crack front kinking and twisting model for three-dimensional mixed mode case is suggested. To define the kinking and twisting angles it uses conditions

$$\begin{aligned} K_{{{\mathrm{\mathrm {II}}}}} (\theta (l)) = 0, \quad K_{{{\mathrm{\mathrm {III}}}}}(\psi (l)) = 0, \end{aligned}$$

(3)

where the kinking angle $\theta$ and the twisting angle $\psi$ define the direction of crack front propagation at each front point l. In Cherny et al. (2016) the dependence of the twisting angle on the derivative of kinking angle with respect to the coordinate l along the crack front is obtained. The third mode is written as a function of the kinking angle

$$\begin{aligned} K_{{{\mathrm{\mathrm {III}}}}}(\psi (l)) = {\overline{K}}_{{{\mathrm{\mathrm {III}}}}}(\theta (l)). \end{aligned}$$

(4)

It allows to rewrite the conditions (3) only for this angle $\theta$

$$\begin{aligned} K_{{{\mathrm{\mathrm {II}}}}}(\theta (l)) = 0, \quad {\overline{K}}_{{{\mathrm{\mathrm {III}}}}}(\theta (l)) = 0. \end{aligned}$$

(5)

It is impossible to fulfill the second condition in (5) at each point of the crack front separately from the adjacent points because the ${\overline{K}}_{{{\mathrm{\mathrm {III}}}}}$ depends on the kinking angle $\theta$ derivative with respect to the l. Therefore, we have combined both modes $K_{{{\mathrm{\mathrm {II}}}}}$ and $K_{{{\mathrm{\mathrm {III}}}}}$ with weight $\beta$ into a single function and have considered this function as the integral along the whole crack front at new time step $t + \Delta t$

$$\begin{aligned} F(t+\Delta t, \theta (l))= & {} \int \limits _{\text {Crack front}} (1-\beta ) K_{{{\mathrm{\mathrm {II}}}}}^2(t+\Delta t, \theta (l))\nonumber \\&+ \beta {\overline{K}}_{{{\mathrm{\mathrm {III}}}}}^2(t+\Delta t, \theta (l))dl. \end{aligned}$$

(6)

The crack front deflection in a 3D mixed mode criterion is determined by the distribution of $\theta ^*(l)$ giving minimum F

$$\begin{aligned} F(t+\Delta t, \theta ^*(l)) = \min \limits _{\theta (l)} F(t+\Delta t, \theta (l)). \end{aligned}$$

(7)

In Cherny et al. (2016) an original method of functional (6) minimization is proposed to find the fracture propagation direction $\theta ^*(l)$ at each point l.

2.3 Herschel–Bulkley fluid flow in a fracture

The current paper employs the general concept of the model of Newtonian fluid flow in a three-dimensional fracture presented in Shokin et al. (2015) and Cherny et al. (2016). In Cherny and Lapin (2016) the first steps have been made to extend this concept to the case of Herschel–Bulkley fluid rheology: the formula for the apparent fluid viscosity has been proposed and its applicability for curvilinear fracture simulation has been demonstrated. In the given paper the justification (see “Appendix”) and the comprehensive investigation (see Sect. 4) of the Herschel–Bulkley fluid model and numerical algorithm are performed. The new expression for the apparent viscosity as a function of the fluid flux is proposed. Also sensitivity analysis carried out in Sect. 5 shows that the statement of the paper (Cherny and Lapin 2016) about the applicability of the Newtonian model for the Herschel–Bulkley fluid flow simulation is true only for the early stage of the fracture propagation. If the Newtonian model is applied for case of low shear rate that is typical for the developed hydraulic fractures then pressure distribution will be predicted with high error. Only accurate Herschel–Bulkley fluid model should be used in this case.

2.3.1 Equations for 2D HB fluid flow in 3D fracture

Two-dimensional model of the Herschel–Bulkley fluid flow between two plates is used to calculate the fluid pressure distribution inside the fracture. The model is based on two equations: the continuity equation

$$\begin{aligned} \frac{\partial W}{\partial t} + \nabla \cdot {\mathbf {q}} = 0 \end{aligned}$$

(8)

and the formula for fluid flux ${\mathbf {q}}=(q_1,q_2)$ derived from 3D Navier–Stokes equations

$$\begin{aligned} {\mathbf {q}} = - \frac{W^3}{12\eta _p} \nabla p. \end{aligned}$$

(9)

Here for simplicity the fluid flux (9) is written in the form that is used for Newtonian fluid with variable viscosity $\eta _p$ and the operator $\nabla$ is written in two-dimension coordinate system used on the fracture surface. In contrast with Newtonian fluid the viscosity here depends on flow parameters and should been written as a function of fluid flux ${\mathbf {q}}$ or pressure p. In the current paper the last option has been chosen

$$\begin{aligned} \eta _p(\nabla p)= & {} \frac{(2K)^{1/n}(2n+1)}{6n} (W |\nabla p|)^{(n-1)/n} \nonumber \\&+ \frac{(4n+2)2^{1/n} \tau _0}{3 n (W |\nabla p|)^{1/n} }. \end{aligned}$$

(10)

It can be seen that the expression (10) degenerates when $| \nabla p | \rightarrow 0$, since the yield stress $\tau _0$ is divided by this value. Indeed, the equations of fluid flow that are written in the form (8)–(10) are satisfied only in the region where the fluid moves (unyielded region). In this region the shear stress produced by the pressure gradient, exceeds the yield stress $\tau _0$ (for more details see “Appendix”). This restriction is not essential here. In Sect. 5.3 it is shown that while the fracture propagates, the stopping the fluid flow (the arrest state) is impossible, and so the pressure gradient $| \nabla p |$ is bounded from zero. Therefore, the expression (10) does not degenerate in the model.

The substitution of the expression for the fluxes (9) into continuity Eq. (8) gives the following equation for the fluid pressure distribution

$$\begin{aligned} \nabla \cdot \left( \frac{W^{3}}{12 \eta _{a}} \nabla p \right) = \frac{\partial W}{\partial t}. \end{aligned}$$

(11)

2.3.2 Boundary conditions for 2D HB fluid flow equations

To solve the Eq. (11) boundary conditions should be added on inflow and outflow boundaries. Let’s consider the scheme of the fracture surface without wellbore that is shown in Fig. 3. The fracturing fluid is injected from the wellbore to the fracture through the boundary $\Gamma ^q$. This line is the intersection of the wellbore and fracture surfaces. The unit vector ${{\mathrm{\mathbf n}}}_q$ normal to the boundary $\Gamma ^q$ is located on the fracture surface and directed from the wellbore to the fracture. The unit vector ${{\mathrm{\mathbf n}}}_p$ normal to the fluid front $\Gamma ^p$ is located on the fracture surface and directed outward the fluid. The following conditions are set at the fluid front $\Gamma ^p$ and at the inflow boundary $\Gamma ^q$

$$\begin{aligned} p \mid _{\Gamma ^{p}} = p_{pore}, \ \ {\mathbf {q}} \mid _{\Gamma ^{q}} = q_{in} \cdot {\mathbf {n}}_q, \end{aligned}$$

(12)

where $p_{pore}$ is the pressure of the porous fluid, $q_{in} = Q_{in}/L_{q}$ is the average inflow rate that is calculated using the given inflow rate $Q_{in}$ and the length $L_{q}$ of the inflow boundary $\Gamma ^q$. Taking into account Eq. (9) the second condition (12) is rewritten in terms of pressure as

$$\begin{aligned} \frac{\partial p}{\partial n} =- \frac{12 \mu q_{in} }{W^3} {\mathbf {n}}_q. \end{aligned}$$

(13)

At the fluid front $\Gamma ^p$ an additional Stefan’s condition is set

$$\begin{aligned} {{\mathbf {v}}_f} \Big |_{\Gamma ^p} = {{\mathrm{\mathbf n}}}_p \frac{\mathbf {|q|}}{W} \Big |_{\Gamma ^p} \ , \end{aligned}$$

(14)

where ${{\mathrm{\mathbf v}}}_f$ is the velocity of the fluid front $\Gamma ^p$ that is orthogonal to $\Gamma ^p(t)$. This condition is not necessary to solve the Eq. (11) but it is used to calculate the position of the fluid front ${\Gamma ^p}$.

Fig. 3

Curved fracture surface in 3D space and its piecewise planar representation

2.3.3 Numerical method for 2D HB fluid flow equations

Equation (11) is solved by the finite element method that was applied in Shokin et al. (2015) and Cherny et al. (2016) for the case of Newtonian fluid. This method transforms the differential problem (11)-(13) into a system of linear algebraic equations. First of all the Eq. (11) is rewritten in the weak formulation as

$$\begin{aligned} \int \limits _{S_n} \nabla (a \nabla p) \omega dS = \int \limits _{S_n} f \omega dS, \end{aligned}$$

(15)

where $\omega$ is a test function, $a = {W^3}/{12 \eta _{p}}$, $f = {\partial W}/{\partial t}$. After that the computational domain is covered by the finite element mesh as it is shown in Fig. 3 and inside each element the pressure is represented as the sum of shape functions $\phi _i(\xi _1, \xi _2)$ that are written in local coordinate system of the element $(\xi _1, \xi _2)$:

$$\begin{aligned} p(\xi _1, \xi _2) = \sum _{i=1}^M p_i \phi _i(\xi _1, \xi _2), \end{aligned}$$

(16)

where coefficient $p_i$ is the value of the fluid pressure at i-th ($i=1,\ldots ,M$) node of the element, M is the number of nodes in the element. For each element, one can put the expression (16) into (15) and derive the following system of equations:

$$\begin{aligned} K_{ij} p_i = Q_j + F_j, \end{aligned}$$

(17)

where

$$\begin{aligned} K_{ij}= & {} \iint \limits _{S_n} a \nabla \phi _i \cdot \nabla \phi _j |J| d\xi _1 d\xi _2, \ \ \ Q_j = \int \limits _{\partial S_n} a \frac{\partial p}{\partial n} \phi _i dG, \nonumber \\ F_j= & {} -\iint \limits _{S_n} f \phi _i |J| d \xi _1 d\xi _2. \end{aligned}$$

(18)

Finally, the united system of linear equations is obtained by assembling the system for each element (17)

$$\begin{aligned} \mathbf {Kp = Q + F}, \end{aligned}$$

(19)

where ${\mathbf {p}} = (p_1,\ldots p_N)$ is the vector of the fluid pressure values at the all nodes of all the elements, ${\mathbf {K}}$ is a $N \times N$ matrix, $\mathbf {Q, F}$ are vectors of order N. When the system of equations (19) is solved it is simple to find the pressure distribution at each point of the fracture surface.

It should be noted that in the case of non-Newtonian fracturing fluid, the coefficients of the matrix ${\mathbf {K}}$ include the apparent viscosity $\eta _{p}$ and, thus, depend on the solution ${\mathbf {p}}$. Consequently, the system of equations (19) is nonlinear. The iterative relaxation method is used for solving it. The steps of the algorithm are the following.

• 1. $s=0:$ The pressure from the previous n-th time step of the fracture propagation is taken as the initial solution ${\mathbf {p}}^0 = {\mathbf {p}}^n$.

• 2. At each iteration s the apparent viscosity $\eta _p^s$ is calculated at each point using (10). It gives coefficients of ${\mathbf {K}}({\mathbf {p}}^s)$ and ${\mathbf {Q}}({\mathbf {p}}^s)$ for (19).

• 3. The interim pressure $\widetilde{{\mathbf {p}}}$ is calculated by solving (19) with ${\mathbf {K}}({\mathbf {p}}^s)$, ${\mathbf {Q}}({\mathbf {p}}^s)$.

• 4. The pressure distribution at the next $(s+1)$-th iteration is calculated by using the relaxation procedure

  $$\begin{aligned} {\mathbf {p}}^{s+1}= & {} \widetilde{{\mathbf {p}}}(r) + {\mathbf {p}}^s (1-r), \ \ \mathrm {where} \nonumber \\ r(s)= & {} r_{max} \frac{||{\mathbf {p}}^s||}{||{\mathbf {p}}^s-\widetilde{{\mathbf {p}}}||}. \end{aligned}$$

  (20)

• 5. $s=s+1$. The iterations 2–4 are repeated until the condition $\frac{||{\mathbf {p}}^s-\widetilde{{\mathbf {p}}}||}{||{\mathbf {p}}^s||}<\varepsilon _c$ is fulfilled.

The values of parameters and $r_{max}=0.1$ , and $\varepsilon _c = 10^{-4}$ are taken to provide the highest speed of convergence of this iteration process, norm $||\cdot ||$ used here is the uniform norm. Usually it takes about 5-10 iterations to obtain the solution with the given accuracy.

2.4 Coupling of the submodels

To simulate the fracture propagation it is necessary to unite the equations, initial and boundary conditions and criteria described in the previous sections into the one system of nonlinear equations and solve them simultaneously at each step of the fracture propagation. Each component of the system provides one or more components of the solution that should be obtained at each time step: fracture width W, fluid pressure p, fluid flux ${\mathbf {q}}$, positions of fluid front $\Gamma ^p$ and fracture front $\Gamma ^f$. The following stages of coupling solution method for the submodels are developed.

• Elasticity equations with boundary conditions (1) are solved in 3D infinite domain with a cavity and a fracture. These equations gives the distribution of fracture width $W=W(p,\Gamma ^f)$ as function of the fluid pressure in the fracture p and the fracture geometry specified by the fracture front position $\Gamma ^f$ (see Fig. 2) at the current and previous steps.

• Conditions (2) and (3) for fracture front increment and the crack front deflection give the fracture front position $\Gamma ^f$ as function of stress field.

• Equations (9)–(11) with boundary conditions (12) and (13) are used to calculate distributions of the fluid pressure p and the fluid flux ${\mathbf {q}}$ with known fracture width W.

• Stefan condition (14) gives the fluid front position $\Gamma ^p$ as function of fluid fluxes ${\mathbf {q}}$.

The numerical algorithm for the described system is proposed and verified in Shokin et al. (2015), Kuranakov et al. (2016) and Cherny et al. (2016) for the case of Newtonian fluid. At each step of the fracture propagation two non-linear problems are solved iteratively. The two iteration cycles are the following.

• 1. External cycle to calculate the positions of the fracture $\Gamma _f$ and the fluid $\Gamma _p$ fronts.

• 2. Internal cycle to obtain the pressure p and width W distributions using the given positions of the fracture $\Gamma _f$ and the fluid $\Gamma _p$ fronts at each iteration of the cycle 1.

Due to the non-linearity of the used fluid rheology model an additional iteration cycle is required to calculate the apparent viscosity and the fluid pressure as it described in Sect. 2.3.3. This complication of the algorithm results in the convergence deceleration and in the computational time increase as compared to the Newtonian fluid case.

3 Dimensional analysis of the investigated problem

3.1 Regimes of fracture propagation

Dimensional analysis will be carried out on the one-dimensional model of penny-shaped fracture. This assumption simplifies the discussion in comparison with the three-dimensional statement. Such fracture corresponds to the formulation of the problem described in Sect. 2, for the case of the transverse fracture that propagates from the wellbore not inclined against with the axis z ($\alpha = 0$ in Fig. 2). At the same time, even in the one-dimensional formulation, the dimensional analysis gives representation of the effect of various physical processes on the propagation of cracks, such as energy losses on viscous friction and fracture toughness, fluid lag etc.

Dimensional analysis of the early stage of the development of a penny-shaped fracture in an impenetrable rock for the case of a Newtonian fluid with fluid lag taken into account is given in Bunger and Detournay (2007) and Detournay (2016). The equations of a penny-shaped fracture propagation are written in accordance with the notation adopted in these works. Unlike Bunger and Detournay (2007) and Detournay (2016), we assume that the fluid is described by the Herschel–Bulkley model, and the pore pressure in the rock is zero. Then the equations and the boundary conditions look as follows

$$\begin{aligned}&\frac{\partial W}{\partial t} = \frac{1}{{\mu ^\prime }^{1/n} r} \frac{\partial }{\partial r} \left[ r W^{(2+1)/n} \left( \frac{\partial p}{\partial r} - \frac{\tau _0}{W} \right) ^{1/n} \right] , \end{aligned}$$

(21)

$$\begin{aligned}&W = \frac{8 R}{\pi E^\prime } \left[ \int _0^{\gamma _f} G\left( \frac{r}{R}, \zeta \right) p_{net}(\zeta ) \zeta d \zeta \right. \nonumber \\&\qquad \quad \left. - \int _{\gamma _f}^1 G\left( \frac{r}{R}, \zeta \right) \sigma _z^{\infty } \zeta d \zeta \right] , \end{aligned}$$

(22)

$$\begin{aligned}&\frac{2^{7/2}}{\pi R^{1/2}} \left[ \int _0^{R_f} \frac{p_{net}}{(R^2-r^2)} r dr - \sigma _z^\infty \sqrt{R^2-R_f^2} \right] = K^\prime _{Ic}, \end{aligned}$$

(23)

$$\begin{aligned}&Q_{in} \cdot t = 2 \pi \int _0^{R_f} W(r,t) r dr, \end{aligned}$$

(24)

$$\begin{aligned}&r=R_f: \ \frac{d R_f}{d t } = -\frac{w^2}{\mu ^\prime } \frac{\partial p}{\partial r}. \end{aligned}$$

(25)

Here R and $R_f$ are fracture and fluid front radii, $\gamma _f = R_f/R$ is dimensionless radius of the fluid front, $p_{net} = p - \sigma _z^\infty$ is net pressure. In addition, the following notations are used: $E^\prime = E/(1-\nu ^2)$, $K^\prime _{Ic} = 4 (2/\pi )^{1/2} K_{Ic}$ (Bunger and Detournay 2007; Detournay 2016), and $\mu ^\prime = 2 K ((4n+2)/n)^n$ (Linkov 2015). The kernel G in (22) is given in terms of the incomplete elliptic integral of the first kind F

$$\begin{aligned} G(\xi ,\xi ^\prime ) = {\left\{ \begin{array}{ll} \frac{1}{\xi } F \left( \arcsin \sqrt{\frac{1-\xi ^2}{1-{\xi ^\prime }^2}}, \frac{{\xi ^\prime }^2}{\xi ^2} \right) \\ \frac{1}{\xi ^\prime } F \left( \arcsin \sqrt{\frac{1-{\xi ^\prime }^2}{1-\xi ^2}}, \frac{\xi ^2}{{\xi ^\prime }^2} \right) \end{array}\right. }. \end{aligned}$$

(26)

The difference of the system of Eqs. (21)–(26) from the system proposed in Bunger and Detournay (2007) and Detournay (2016) is a generalization (21) to the case of Herschel–Bulkley fluid. The remaining equations completely the same. Therefore, we will use the classification of propagation regimes proposed in Bunger and Detournay (2007) and Detournay (2016).

In impermeable rock, the behavior of the penny-shaped fracture is characterized by two timescales

$$\begin{aligned} t_o = \frac{{E^\prime }^2 \mu ^\prime }{(\sigma _z^\infty )^3}, \ \ t_m = \left( \frac{{\mu ^\prime }^5 Q_{in}^3 {E^\prime }^{13} }{{K^\prime }^{18} } \right) ^{1/2}, \end{aligned}$$

(27)

These timescales can each be associated with a physical transition the fracture makes in its lifetime. The timescale $t_o$ is the measure of the time for which the fluid pressure in the fracture balances the overburden stress in the significant lag between the fluid and fracture fronts. The timescale $t_m$ gives a measure of how long it takes for the fracture to transit from viscosity dominated regime to toughness dominated one.

The triangular parametric space proposed in Bunger and Detournay (2007), Detournay (2016) and shown in Fig. 1 gives a useful way of visualizing this evolution. The vertex O corresponds to the initial propagation regime mode for $t \ll t_o < t_m$. In this regime, a large fluid lag is observed. Since the fluid occupies a small part of the fracture, its viscosity has little effect on the process of fracture propagation. The main role is played by the balance between the fluid pressure and the compressive stresses in the area between fluid and fracture front. The vertex M corresponds to the viscous propagation regime, which is observed for $t_o \ll t \ll t_m$. Most of the energy in this regime is spent on overcoming the viscous friction in the fluid. The vertex K corresponds to the toughness regime, which is reached at $t \gg t_m> t_o$.

The evolution of a radial fracture, begins in regime mode O and ends with K (Bunger and Detournay 2007). The transition between them and the corresponding trajectory in O–M–K space (Fig. 1) is determined by the ratio $t_o / t_m$. For $t_o / t_m \sim 1$ the trajectory is far from the vertex M, and the fracture passes from regime O to regime K directly. For $t_o / t_m \ll 1$, the trajectory passes near the vertex M, and the crack propagates most of the time in viscous regime.

The three-dimensional model of fracture propagation (Cherny et al. 2016) used here is designed to calculate the evolution of a fracture only in the vicinity of the O, M and transition O–M regimes. This does not limit the applicability of the model, since, according to Savitski and Detournay (2002), K regime is not reached for typical parameters of hydraulic fracturing. In addition, the fracture path is formed in the initial period of time when the fracture propagates in the O, M regimes. Therefore, the three-dimensional model (Cherny et al. 2016) is used in Sect. 5 to investigate the influence of fluid parameters on the fracture trajectory.

Here for simplicity, the analysis of the influence of each Herschel–Bulkley fluid parameters $\tau _0$ and n is carried out independently for the cases of Bingham ($\tau _0> 0, n = 1$) and power law ($\tau _0 = 0, n <1$) fluids.

3.2 Yield stress influence

For the case of a Bingham fluid, we use the dimensionless analyses performed in Savitski and Detournay (2002) and Detournay (2004) for the M regime. It gives equations for dimensionless radius of the fracture $\gamma ({\mathbf {P}}(t))$ and the distributions of the dimensionless width $\Omega (\rho , {\mathbf {P}}(t))$ and the pressure $\Pi (\rho , {\mathbf {P}}(t))$ along the dimensionless radius $\rho = r / R$. Dimensionless variables depend only on the set of parameters of the regime ${\mathbf {P}}(t)$ and are related to physical variables by formulas

$$\begin{aligned} W (r, t)= & {} \varepsilon (t) L(t) \Omega (\rho , {\mathbf {P}}(t)), \ \end{aligned}$$

(28)

$$\begin{aligned} p(r,t)= & {} \varepsilon (t) E^\prime \Pi (\rho , {\mathbf {P}}(t)), \ \end{aligned}$$

(29)

$$\begin{aligned} R(t)= & {} L(t) \gamma ({\mathbf {P}}) \end{aligned}$$

(30)

with the scaling factors

$$\begin{aligned} \varepsilon (t) = \left( \frac{\mu ^\prime }{E^\prime t} \right) ^{1/3}, \ L(t) = \left( \frac{E^\prime Q_{in}^3 t^4}{\mu ^\prime } \right) ^{1/9}. \end{aligned}$$

(31)

Dimensionless analog of Eq. (21) is written as

$$\begin{aligned}&\left( \frac{\partial \varepsilon }{\partial t } \frac{t}{\varepsilon } + \frac{\partial L }{\partial t } \frac{t}{L} \right) \Omega - \frac{\partial L }{\partial t } \frac{t}{L} \rho \frac{\partial \Omega }{\partial \rho } \nonumber \\&\quad + \frac{\partial {\mathbf {P}} }{\partial t } t \left( \frac{\partial \Omega }{\partial {\mathbf {P}} } - \frac{\rho }{\gamma } \frac{\partial \gamma }{\partial {\mathbf {P}}} \frac{\partial \Omega }{\partial \rho } \right) \nonumber \\&\qquad =\frac{1}{{\mathbf {M}} \gamma ^2 } \frac{\partial }{\partial \rho } \left[ \Omega ^3 \left( \frac{\partial \Pi }{\partial \rho } - {\mathbf {M}}_\tau \frac{\gamma }{\Omega } \right) \right] . \end{aligned}$$

(32)

Here two dimensionless complexes or as regime parameters ${\mathbf {P}}(t)$ are introduced. They are dimensionless viscosity (Savitski and Detournay 2002; Detournay 2004)

$$\begin{aligned} {\mathbf {M}} = \mu ^\prime \left( \frac{Q_{in}^3 {E^\prime }^{13}}{ t^{2} {K^\prime }^{18} } \right) ^{1/5} \ \ \end{aligned}$$

(33)

and dimensionless yield stress

$$\begin{aligned} {\mathbf {M}}_\tau = \tau _0 \left( \frac{ t^{2}}{{\mu ^\prime }^2 E^\prime } \right) ^{1/3}. \end{aligned}$$

(34)

It can be seen that ${\mathbf {M}} _\tau$ (34) is a monotonically increasing function of t. Therefore, the influence of the yield stress at the initial moment will be insignificant, and then it will grow. Consequently, the use of the Newtonian fluid model to describe the Bingham fluid is possible only for ${\mathbf {M}}_\tau \ll 1$, that is, when

$$\begin{aligned} t \ll t_\tau = \left( \frac{{\mu ^\prime }^2 E^\prime }{\tau _0^3} \right) ^{1/2}. \end{aligned}$$

(35)

Let us estimate the values of timescales $t_\tau$ in (35) and $t_o$, $t_m$ in (27) for the typical values of the parameters given in Savitski and Detournay (2002): $E = 7 \div 40~\hbox {GPa}$, $\nu = 0.15 \div 0.4$, $\mu = 0.1 \div 0.5~\hbox {Pa}\,\hbox {s}$, $Q_{in} = 0.03 \div 0.08~\hbox {m}^3/\hbox {s}$ and the values of the yield stress $\tau _0 = 100 \div 500~\hbox {Pa}$. The values of the time scales will vary in the intervals $t_\tau = 10 \div 1000 \hbox {s}$, $t_o = 0.1 \div 1000 \hbox {s}$ and $t_m \gg 100 \mathrm { h}$. Since $t_\tau \sim t_o$, for the developed fracture that propagates in the regime M $t_o \ll t \ll t_m$, it is necessary to take yield stress into account $\tau _0$.

To estimate the influence of the yield stress $\tau _0$ at the stage when the fracture trajectory is formed, let us also estimate the time of the fracture reorientation to the preferred fracture plane $t_{path}$. According to Abass et al. (1994) and Cherny and Lapin (2016) the fracture becomes almost flat before it’s length reaches several (up to 10) wellbore diameters. For the regime M the expression (31) for L(t) and the inequality $L (t) <10 \cdot 2 \cdot R_w = 2.5 \hbox {m}$ give

$$\begin{aligned} t_{path} < \left( \frac{\mu ^\prime L^9}{E^\prime Q_{in}^3} \right) ^{1/4} = 0.1 \div 0.6 \hbox {s}. \end{aligned}$$

(36)

For the regime O the following expression for the characteristic length (Bunger and Detournay 2007)

$$\begin{aligned} L(t) = \left( \frac{ {E^\prime }^{16} \ {\mu ^\prime }^2 \ Q_{in}^{12} \ t^{10} }{{K^\prime }^{18}} \right) ^{1/27}, \end{aligned}$$

(37)

should be used instead of (31). It gives the following interval

$$\begin{aligned} t_{path} = \left( \frac{ L^{27} {K^\prime }^{18} }{ {E^\prime }^{16} {\mu ^\prime }^2 Q_{in}^{12} } \right) ^{1/10} = 0.001 \div 0.5\hbox {s}. \end{aligned}$$

(38)

The above estimates show that for different values of the parameters, the fracture trajectory is formed when the fracture propagates in the regime O ($t_ {path} \ll t_o$) or in transient regime from the O–M ($t_{path} \sim t_o$ ). On the one hand it is necessary to take the fluid lag into account, on the other hand it is not always possible to use the asymptotic solution obtained for the regime O in Bunger and Detournay (2007). At the same time when the fracture trajectory is formed then $t_ {path} \ll t_\tau$. So the influence of yield stress is insignificant and this parameter can be neglected while the fracture trajectory is calculated.

3.3 Power law index influence

While the yield stress $\tau _0$ can be neglected in the simulation of the initial stage of the fracture propagation, the power law index should be taken into account for the entire period of fracture propagation. Such a conclusion can be made on the basis of the work (Linkov 2015), where the scaling of the penny shaped fracture propagation equations is made for the case of power law fluid and self similar solution is obtained for the regime M.

In this work, in order to obtain a self-similar solution, the modified formulation of hydraulic fracture problem by employing the particle velocity is used in contrast to the formulation (21)–(25). Therefore, the dimensionless equations are not identical to those used in Bunger and Detournay (2007), Savitski and Detournay (2002) and Detournay (2004), where pressure and the fracture width are independent variables. Let us repeat the analyses provided in Linkov (2015) using the notations of Bunger and Detournay (2007) and Detournay (2016). Using for $\varepsilon (t)$ the modified expression

$$\begin{aligned} \varepsilon (t) = \left( \frac{\mu ^\prime }{E^\prime t^n} \right) ^{\frac{1}{n+2}}, \end{aligned}$$

(39)

instead of (31) the following equation is obtained instead of (32)

$$\begin{aligned}&\left( \frac{\partial \varepsilon }{\partial t } \frac{t}{\varepsilon } + \frac{\partial L }{\partial t } \frac{t}{L} \right) \Omega - \frac{\partial L }{\partial t } \frac{t}{L} \rho \frac{\partial \Omega }{\partial \rho } \nonumber \\&\quad + \frac{\partial {\mathbf {P}} }{\partial t } t \left( \frac{\partial \Omega }{\partial {\mathbf {P}} } - \frac{\rho }{\gamma } \frac{\partial \gamma }{\partial {\mathbf {P}}} \frac{\partial \Omega }{\partial \rho } \right) \nonumber \\&\qquad =\frac{1}{{\mathbf {M}} \gamma ^2 } \frac{\partial }{\partial \rho } \left[ \Omega ^{\frac{2n+1}{n}} \left( \frac{\partial \Pi }{\partial \rho } \right) ^{1/n} \right] . \end{aligned}$$

(40)

Here, in contrast with (32), the terms with power law index n can not be allocated to a separate group with a new dimension parameter of the regime. Therefore, it is not possible to conclude that the influence of the power law index is significant or not like it has been done in Sect. 3.2 for the yield stress.

The following formula derived in Linkov (2015) provides an opportunity to assign an apparent viscosity $\mu _a$ when simulating the action of a thinning fluid consistency factor K and power law index n by replacing it with an equivalent Newtonian fluid.

$$\begin{aligned} \mu _a = C_\xi \frac{\theta _n^{\frac{3}{n+2}}}{12} \frac{t^{\frac{2-2n}{n+2}}}{{E^\prime }^{\frac{1-n}{n+2}}} K^{\frac{3}{n+2}}. \end{aligned}$$

(41)

Here $\theta _n = 2 \left( \frac{4n+2}{n} \right) ^n$, $C_\xi$ is the coefficient calculated in Linkov (2015). It’s value varies from 0.65 to 0.88 while n increases from 0.2 to 0.8. Note that it is assumed in Linkov (2015) that the fluids equivalent when under the same pumping rate $Q_{in}$ they produce fractures of the same size R for a typical reference time t of a treatment. As can be seen from (41), the power law index decreasing has the same effect as the viscosity (or consistency factor) decreasing.

Since the equivalent viscosity of a Newtonian fluid depends on time, it is impossible to replace the power-law fluid model with the Newtonian fluid model in general case. This is also confirmed by the calculations made in 4.2. Nevertheless, we estimate the possibility of such a replacement at the stage of fracture trajectory formation.

The equivalent viscosity of a Newtonian fluid calculated with typical parameters of the hydraulic fracturing (Savitski and Detournay 2002) and power law fluid parameters $n = 0.8$, $K = 1~\hbox {Pa}\, \hbox {s}^n$ increases two times while time varies in the interval $0.006 \hbox {s}= 0.01 \cdot t_{path}<t <t_{path} = 0.6 \hbox {s}$. If the average value of equivalent viscosity $\mu _a = 0.1~\hbox {Pa}\, \hbox {s}$ was taken when simulating the action of a thinning fluid by replacing it with an equivalent Newtonian fluid the error in viscosity setting would be less than 40 %.

It is shown in Sect. 5.1.1 that a variation of the viscosity by a factor of 10 significantly changes the fracture trajectory. But it can be expected that an error of $40 \%$ when specifying the viscosity during the fracture propagation modeling in the first second of the process will have a little effect on the fracture trajectory. A similar conclusion is made in Cherny and Lapin (2016), where it is shown that the fractures trajectories caused by power fluid injection and the injection of the Newtonian fluid with equivalent viscosity practically coincide. Thus, a model of a Newtonian fluid with a correctly chosen viscosity can be used to calculate the fracture trajectory at the initial propagation stage in place of the Herschel–Bulkley model. It can be expected that this simplification provides just small error.

4 Verification of Herschel–Bulkley fluid flow solution algorithm

The algorithm for solving the equations of HB fluid flow has been verified against the results obtained in the frameworks of the plane radial flows in channels of constant and variable width and the penny-shaped fracture propagation.

4.1 Radial flow of HB fluid in the channel of constant width at constant pumping rate

Let us consider a radial flow between two parallel disks located at the distance of $W = 0.001~\hbox {m}$ from each other. The radius of the cylindrical inlet section is equal to $R_{{{\mathrm{\mathrm {in}}}}}=0.1~\hbox {m}$ and the radius of the cylindrical outlet section is equal to $R_{{{\mathrm{\mathrm {out}}}}}=1~\hbox {m}$. At the outlet boundary, constant pressure $P_{{{\mathrm{\mathrm {out}}}}}=0$ is maintained. Herschel–Bulkley fluid with the rheological parameters $K=100~\hbox {Pa}\,\hbox {s}^n$, $n=0.5$, $\tau _0=900$ Pa is injected through the inflow boundary with the rate of $Q_{{{\mathrm{\mathrm {in}}}}} = 0.5 \times 10^{-6}~\hbox {m}^3/\hbox {s}$.

Figure 4 shows the pressure distribution along the radial coordinate calculated by the proposed 2D model of HB fluid flow on a mesh with $N_r$=20 elements in the radial coordinate and $N_c$=12 elements in the circumferential direction. The pressure distribution obtained by the analytical formula given in Kauzlarich and Greenwood (1972) is shown in Fig. 4 as well. One can see that the difference between the solutions is very small (less than 1.2%). It should be noted that further mesh refinement does not lead to any noticeable change of the numerical solution.

Fig. 4

Pressure distribution along the radial coordinate for radial flow of HB fluid in the channel of constant width at constant pumping rate: solid line—exact solution; circle—2D model

4.2 Radial flow of Bingham fluid in the channel of constant width at constant pumping pressure

A radial flow between two parallel disks is considered. The distance between the disks is equal to $W = 0.001~\hbox {m}$ and the radius of the cylindrical inlet boundary is $R_{{{\mathrm{\mathrm {in}}}}}=0.1~\hbox {m}$. Bingham fluid is injected through the inflow boundary under constant pressure $p_{{{\mathrm{\mathrm {in}}}}}=1~\hbox {MPa}$. The consistency factor of the fluid is equal to $K=0.3~\hbox {Pa}\, \hbox {s}$ and its yield stress varies in the range from $\tau _0 = 0$–$100~\hbox {Pa}$. The area occupied by the fluid represents a circle with its outer boundary denoted as $R_{{{\mathrm{\mathrm {out}}}}}$. Zero pressure condition is set at the fluid front: $P_{{{\mathrm{\mathrm {out}}}}}=0$.

Fig. 5

Injection rate versus the fluid front radius for radial flow of Bingham fluid in the channel of constant width at constant injection pressure at different values of fluid yield stress $\tau _0$: 1—$\tau _0=0~\hbox {Pa}$; 2—$\tau _0=50~\hbox {Pa}$; 3—$\tau _0=100~\hbox {Pa}$

With the extension of the area occupied by the fluid, the flow friction related to the fluid yield stress rises and, consequently, the fluid injection rate Q decreases. The outer fluid boundary propagates until the inlet pressure is enough to overcome the flow resistance. Then the flow stops and the fluid becomes arrested. Figure 5 shows the dependence of the fluid injection rate on the fluid front radius calculated by the proposed 2D model of HB fluid flow for different values of fluid yield stress $\tau _0$. The intersection of each curve with the horizontal axis in Fig. 5 gives the corresponding maximum distance that can be reached by the fluid. As expected, the increase of the fluid yield stress leads to the reduction of the maximum area occupied by the fluid. For comparison, the curve corresponding to Newtonian fluid (curve 1) is presented in Fig. 5. It approaches the horizontal axis asymptotically but never crosses it.

4.3 Penny-shaped fracture propagation driven by HB fluid flow

Two cases of penny-shaped fracture propagation have been examined. In the first case, Newtonian fluid with the viscosity of $\mu =1000~\hbox {Pa}\, \hbox {s}$ is injected into the fracture with the rate of $Q_{{{\mathrm{\mathrm {in}}}}}=32 \times 10^{-6}~\hbox {m}^3/\hbox {s}$ and, in the second one, Herschel–Bulkley fluid with the rheological parameters $K=1000~\hbox {Pa}\, \hbox {s}^n$, $n=0.5$, $\tau _0 = 400~\hbox {Pa}$ is pumped with the same fluid rate. The wellbore is vertical ($\alpha =0$) and its radius is equal to $R_w=0.5~\hbox {m}$. The radius of an initial fracture is $R_{{{\mathrm{\mathrm {in}}}}}=1~\hbox {m}$. The rock with the mechanical properties $E=20~\hbox {GPa}$, $\nu =0.2$, $K_{Ic}=3~\hbox {MPa}\sqrt{\hbox {m}}$ is compressed at infinity by the following stresses: $\sigma _{x}^\infty =\sigma _{y}^\infty =4~\hbox {MPa}$, $\sigma _{z}^\infty =3~\hbox {MPa}$. The computations were performed with the 3D hydraulic fracture model presented in the current paper and with the 1D model of penny-shaped fracture propagation described in Esipov et al. (2014). A mesh with $N_c=32$ elements in the circumferential direction was used for the 3D model. For the 1D model, the mesh was extremely fine.

The results of the wellbore pressure and the fracture radius calculations are shown in Figs. 6 and 7 correspondingly. One can see that the error magnitude of the fracture radius computation with the 3D hydraulic fracture model is quite small and is approximately the same for both the Herschel–Bulkley fluid and the Newtonian one. The error of the wellbore pressure determination with the 3D model is insignificant for both considered fluids. Figure 8 demonstrates that mesh refinement leads to the convergence of the 3D model numerical solution to the solution of the 1D model obtained with high accuracy.

Fig. 6

Wellbore pressure versus time for penny-shaped fracture propagation driven by Newtonian (left) and HB fluids (right): solid line—1D model; circle—2D model, $N_c$ = 32

Fig. 7

Fracture radius versus time for penny-shaped fracture propagation driven by Newtonian (left) and HB fluids (right): solid line—1D model; circle—2D model, $N_c$ = 32

Fig. 8

Wellbore pressure versus time for penny-shaped fracture propagation driven by HB fluids for different mesh sizes: solid line—1D model, circle—$N_c=32$, square—$N_c=16$; triangle—$N_c=8$

5 Results

As mentioned above, the model developed in the given paper has an advantage over the other existing three-dimensional models because it directly takes into account both the influence of borehole and the effect of variable loading along the fracture sides related to the flow of the fluid with a complex rheology. This makes it attractive for modeling the early stage of hydraulic fracture propagation and, in particular, for the study of the near wellbore fracture tortuosity. Let us start the review of the results obtained with the present model from the study of the sensitivity of the fracture behavior in the near wellbore zone to the variations of the input problem parameters and, first of all, to the rheological parameters of the fracturing fluid.

For this purpose, the series of computations have been performed with the following base values of input parameters. The wellbore of the radius $R_w =0.12~\hbox {m}$ is rotated around the x axis by an angle $\alpha$ (wellbore inclination angle) as shown in Fig. 2. The $y'z'$ plane of the rotated coordinate system coincides with the yz plane of the original coordinate system. At the wellbore, there is a planar transversal initial fracture of the external radius $R_{{{\mathrm{\mathrm {in}}}}}=0.25~\hbox {m}$ perpendicular to the wellbore axis. The in-situ remote compressive stresses in the rock are $\sigma _x^\infty =\sigma _y^\infty =16~\hbox {MPa}$, $\sigma _z^\infty =12~\hbox {MPa}$. The mechanical properties of the surrounding rock are described by the following parameters: Young’s modulus $E=20~\hbox {GPa}$, Poisson’s ratio $\nu =0.2$, fracture toughness $K_{Ic}=3~\hbox {MPa}\sqrt{\hbox {m}}$. A non-Newtonian fracturing fluid is pumped into the wellbore at the rate of $Q_{{{\mathrm{\mathrm {in}}}}} = 0.1 \hbox {m}^3 / \hbox {s}$. The fluid is characterized by the following rheological parameters: the consistency factor K, the power law index n and the yield stress $\tau _0$. The general case of non-zero values of K and $\tau _0$ and $n \ne 1$ corresponds to Herschel–Bulkley rheology law.

In Cherny and Lapin (2016) the propagation of the transversal fracture inclined on an angle $\alpha$ varied form $0^\circ$ to $60^\circ$ has been simulated to show the influence of the angle on the fracture trajectory. In the all considered cases the shape of the growing fracture was similar to the one can be seen in Fig. 2—the fracture to reorients in PFP-direction. The main conclusion was that the greater the wellbore inclination angle is, the larger distance is required for that. But the particular distance of fracture reorientation and the curvature of the fracture surface are difficult to predict without simulation. The simulations performed in Cherny and Lapin (2016) show that the reorientation is quite fast. Thus the fracture started from $60^\circ$ inclined wellbore became almost flat (i.e. inclined less than on $5^\circ$ from PFP) before it propagates on the distance of 10 wellbore diameters. Table 1 contains the fracture sizes corresponded to the moment when the fracture became almost flat for the other wellbore inclination angles. For generality the sizes are measured in borehole diameters. It should be noted that the fracture never became exactly plane, so the sizes of the fracture correspond to the moments when the fracture is inclined less than on $10^\circ$ or $5^\circ$ from PFP.

Table 1 Influence of wellbore inclination angle $\alpha$ on the size of the curved near-wellbore part of hydraulic fracture

5.1 Sensitivity of fracture behavior to rheology parameters of fracturing fluid

Let us consider how the rheological parameters of the fracturing fluid influence the fracture behavior in the near wellbore zone. We will fix two of three rheological parameters K, n, $\tau _0$ and vary the third one in quite a wide range. Of course, a large parametric space of rheology parameters can not be covered by a few points, but main dependencies can be clarified. The 3D code is computationally expensive but it has been chosen because it demonstrates the fracture trajectory variation and the consequences of such variation, such as fracture width narrowing, increasing of wellbore pressure, etc.

Fig. 9

Fracture shape for $\alpha =60^\circ$ and analyzed fracture cross-sections

The sensitivity study is performed for the wellbore inclination angle equal to $\alpha =60^\circ$. With such an inclination the shape of the resulting fracture is essentially three-dimensional, and to enhance the visibility of the calculated variables, the distributions of these variables are shown below for several selected radial fracture cross-sections. Due to the chosen orientation of the wellbore relative to the principal remote stresses the fracture is symmetric with respect to the yz($y'z'$) plane as well as to the rotation axis Ox (Fig. 2). Therefore, it is enough to consider some radial cross-sections in only one quadrant. Further, we will consider three cross-sections (Fig. 9) corresponding to the following values of an angle $\varphi$: $\varphi =0^\circ$ (yz plane), $\varphi =45^\circ$, and $\varphi =90^\circ$ (xz plane). Here, the angle $\varphi$ determines the rotation of the yz plane around the Oz axis in a clockwise direction when viewed against the direction of Oz.

5.1.1 Effect of fluid consistency factor

Let us fix the values of behavior index $n=1$ and yield stress $\tau _0=0~\hbox {Pa}$ and consider three different values of the consistency factor $K = 0.03, 0.3, 3~\hbox {Pa}\,\hbox {s}$. Such values of parameters correspond to the rheology of Newtonian fluid. In Fig. 10 the calculated fracture trajectories in the radial cross-section yz ($\varphi =0^\circ$) are shown. Here, the rectangle denotes the position of the wellbore, and the PFP-direction coincides with the direction of the axis Oy. One can see that with the increase of the consistency factor the fracture trajectory becomes flatter and it takes longer for it to align with the PFP-direction. The same general conclusion have been made in Cherny et al. (2016) and Cherny and Lapin (2016) but below these results are presented in more details.

Fig. 10

Fracture trajectories in yz plane for Newtonian fluid and wellbore inclination angle $\alpha =60^\circ$: 1—$K = 0.03~\hbox {Pa}\,\hbox {s}$; 2—$K = 0.3~\hbox {Pa}\,\hbox {s}$; 3—$K = 3~\hbox {Pa}\,\hbox {s}$

Fig. 11

Fracture width versus radial coordinate for $\alpha =60^\circ$ and Newtonian fluid with viscosity $K = 0.03~\hbox {Pa}\,\hbox {s}$ (left) and $K = 3~\hbox {Pa}\,\hbox {s}$ (right): 1—$\varphi =0^\circ$; 2—$\varphi =45^\circ$; 3—$\varphi =90^\circ$

The distributions of the fracture width and the fluid pressure for the selected radial cross-sections at the same time moment are shown in Figs. 11 and 12, correspondingly, for low and high values of the consistency factor: $K = 0.03~\hbox {Pa}\,\hbox {s}$ (on the left) and $K=3~\hbox {Pa}\,\hbox {s}$ (on the right). In these figures, the variable r is the radial coordinate of the corresponding fracture point in the cylindrical coordinate system connected with the vertical axis Oz (Fig. 9) and with the origin at the center of the initial fracture. One can see that in the case of low fluid viscosity for $\varphi =0^\circ$ and $\varphi =45^\circ$ there is an inconsiderable fracture width narrowing: not more than 10 to 15% of its maximum width. However, comparing these fracture width profiles with the one at the cross-section $\varphi =90^\circ$, one can conclude that there is not a narrowing but rather the fracture widening in the near wellbore zone of several borehole diameters in size. In the case of highly viscous fluid, the fracture width behavior is similar to the planar fracture case: the width reaches its maximum at the borehole and then monotonically decreases with the distance from the wellbore.

In the case of low fluid viscosity the pressure profile is more convex than for the case of highly viscous fluid as presented in Fig. 12: the pressure is almost constant at the most part of the fracture and falls abruptly near the fluid front. Moreover the higher viscosity produces the higher length of the fluid lag that can be seen in the figure as an interval of zero pressure near the fracture front. Despite some fracture widening in the cross-sections for $\varphi =0^\circ$ and $\varphi =45^\circ$ (as shown in Fig. 11, left), the pressure distributions are almost the same in all the considered cross-sections. In the case of high fluid viscosity, the fluid pressure is more sensitive to the curvature of the trajectory. It decreases considerably faster in the most curved cross-section ($\varphi =90^\circ$). And this leads to the significant difference in penetration of the fracture into the rock in different directions.

In Fig. 11 one can see that the fracture penetration in the direction of the xz plane ($\varphi =90^\circ$) is by almost 40% larger than in the direction of the yz plane ($\varphi =0^\circ$). In the case of low viscosity fluid, this difference is about 8% only.

Fig. 12

Fluid pressure versus radial coordinate for $\alpha =60^\circ$ and Newtonian fluid with viscosity $K = 0.03~\hbox {Pa}\,\hbox {s}$ (left) and $K = 3~\hbox {Pa}\,\hbox {s}$ (right): 1—$\varphi =0^\circ$; 2—$\varphi =45^\circ$; 3—$\varphi =90^\circ$

5.1.2 Effect of fluid yield stress

To demonstrate the effect of the fluid yield stress, let us fix the values of the behavior index $n=1$ and the consistency factor $K = 0.03~\hbox {Pa}\,\hbox {s}$ and consider two different values of the yield stress $\tau _0 = 0~\hbox {Pa}$ and $\tau _0 = 1000~\hbox {Pa}$. The latter value is chosen as the upper limit of the yield stress for practically used fluids. With non-zero value of $\tau _0$ such a combination of the rheology parameters corresponds to the rheology of Bingham fluid. In Fig. 13 the calculated fracture trajectories in the radial cross-section yz are shown. One can see that in the chosen wide range, the fracture trajectory is almost insensitive to the fluid yield stress. This is related to the fact that at the early stage of the transversal fracture development the fluid shear rates in the fracture are very high, because of the radial flow spreading. In Cherny and Lapin (2016) it has been shown that values of fluid shear rate at the early stage of transversal fracture propagation are about 3 orders greater than values that is typical for long fractures. Hence, the contribution of the yield stress into the fluid shear stress becomes negligible. For example it can be seen from the apparent viscosity formula written in terms of fluid flux $|{\mathbf {q}}|$ (10) in “Appendix” for the case of high values of the fluid flux. Due to that the influence of yield stress is negligible, and Bingham fluid model ($n=1, \tau \ne 0$) can be replaced by the Newtonian one.

Fig. 13

Fracture trajectories in yz plane for wellbore inclination angle $\alpha =60^\circ$ and Bingham fluid with $K=0.03~\hbox {Pa}\,\hbox {s}$: 1—$\tau _0 = 0$; 2—$\tau _0 = 1000~\hbox {Pa}$

Fig. 14

Fracture trajectories in yz plane for wellbore inclination angle $\alpha =60^\circ$ and Power-law fluid with $K=0.66~\hbox {Pa}\,\hbox {s}$: 1–$n=1$; 2—$n=0.9$; 3—$n=0.8$

5.1.3 Effect of fluid behavior index

Fig. 15

Fracture width versus radial coordinate for $\alpha =60^\circ$ and power-law fluid with parameters $K=0.66~\hbox {Pa}\,\hbox {s}$, $n=0.8$ (left) and $K=0.66~\hbox {Pa}\,\hbox {s}$,$n=1$ (right): 1—$\varphi =0^\circ$; 2—$\varphi =45^\circ$; 3—$\varphi =90^\circ$

Fig. 16

Fluid pressure versus radial coordinate for $\alpha =60^\circ$ and power-law fluid with parameters $K=0.66~\hbox {Pa}\,\hbox {s}$, $n=0.8$ (left) and $K=0.66~\hbox {Pa}\,\hbox {s}$,$n=1$ (right): 1—$\varphi =0^\circ$; 2—$\varphi =45^\circ$; 3— $\varphi =90^\circ$

In this subsection, let us study how the fracture behavior depends on the fracturing fluid behavior index. Three fluids with the same values of the consistency factor $K=0.66~\hbox {Pa}\,\hbox {s}$ and yield stress $\tau _0=0$ and different values of the behavior index $n=1; 0.9; 0.8$ will be considered. With $n \ne 1$ such a combination of the rheological parameters corresponds to the model of power-law fluid. Figure 14 presents the calculated fracture trajectories in the radial cross-section yz. The distributions of the fracture width and the fluid pressure in the selected radial cross-sections at the same time moment are shown in Figs. 15 and 16, correspondingly, for two different values of the behavior index: $n=0.8$ (on the left) and $n=1$ (on the right). Comparing the curves presented in Figs. 10, 11 and 12 with the ones shown in Figs. 14, 15 and 16, one can conclude that, on the whole, the increase of the fluid behavior index has the same effect on the fracture behavior as the fluid consistency factor increase. The higher the behavior index value is, the slower the fracture reorientation in the PFP-direction. The fracture width grows with the increase of the behavior index. There is practically no fracture width narrowing near the wellbore. With the increase of the behavior index, the non-uniformity of the fracture propagation in different radial directions becomes more pronounced.

The analysis conducted in the current section shows that due to the peculiarities of transversal fractures geometry they are not prone to the fracture width narrowing near the wellbore, which is known as “pinching” in the oil and gas industry. The fracture curvature (turning and twisting) influences only the degree of its penetration into the rock in different radial directions. In the considered case of the fracture orientation relative to the remote stresses, the least penetration is observed in the cross-section containing the deviated wellbore axis as compared to other directions. However, one should not extend these conclusions directly to the other types of the fracture geometry, for example, to band-type fractures (PKN-like geometry), which require a separate study. The analysis conducted by the authors in Cherny et al. (2009) within the KGD type fracture geometry has demonstrated that for fractures under plane deformation conditions the pinching can lead to a considerable narrowing of the fracture width at the wellbore.

5.2 Sensitivity of fracture behavior to fracturing fluid rheology in the case of “low shear rates”

In previous sections it has been shown that both the consistency factor and the behavior index affect the fracture trajectory in a similar way. Variation of any of these parameters leads to variation of the apparent viscosity (10). The question arises if a variation of any parameters has the same effect as a variation of viscosity has, will it be enough to set one parameter—the viscosity only? In Cherny and Lapin (2016) for the case of high shear rate ${\dot{\gamma }}={\partial v_1} / {\partial x_3}$ it has been shown that it is really possible and Herschel–Bulkley model may be replaced by Newtonian one. But the value of apparent viscosity should be chosen carefully. The apparent viscosity strongly depends on the shear rate value, this fact is easy to demonstrate for example using its expression for 1D fluid flow

$$\begin{aligned} \eta _{p}=( K {\dot{\gamma }}^n + \tau _0 ) / {\dot{\gamma }}, \end{aligned}$$

(42)

So the shear rate value that is used to calculate the apparent viscosity should be chosen accurately and should be close to the value that is observed in the fracture at the proper stage of the propagation. Then Newtonian fluid model can be used both for pseudoplastic ($n \le 1, \tau =0$) and Bingham ($n=1, \tau \ne 0$) fluid flow simulation.

It also has been shown in Cherny and Lapin (2016) that both the wellbore pressure and the fracture width are sensitive to fluid rheology. But if the apparent viscosity is constant then the variation of all other fluid parameters almost has no effect on the fracture trajectory. These conclusions in Cherny and Lapin (2016) have been made only for the case of very high shear rates, which is typical for the early stage of transverse fracture propagation.

In this section another case of fluid flow is considered—case of “low shear rates” to estimate the influence of apparent viscosity and other fluid rheology parameters separately. The term “low shear rates” means that under such shear rates the summands in formula (42) provide comparable effect on the value of the apparent viscosity. To study the effect of the fracturing fluid rheology on the hydraulic fracture behavior for this case, the following set of input parameters has been chosen. The radius of the borehole shown in Fig. 2 is equal to $R_w=0.5~\hbox {m}$ and the wellbore is not deviated: $\alpha =0$. The outer radius of the initial transversal fracture is equal to $R_{{{\mathrm{\mathrm {in}}}}}=1~\hbox {m}$. The remote compressive in-situ stresses in the rock are $\sigma _x^\infty =\sigma _y^\infty =4~\hbox {MPa}$, $\sigma _z^\infty =3~\hbox {MPa}$. The mechanical properties of the surrounding rock are described by the following parameters: Young’s modulus $E=20~\hbox {GPa}$, Poisson’s ratio $\nu =0.2$, fracture toughness $K_{Ic}=3~\hbox {MPa}\sqrt{\hbox {m}}$. The fracturing fluid is injected with the rate of $Q_{{{\mathrm{\mathrm {in}}}}} = 32\times 10^{-3}~\hbox {m}^3/\hbox {s}$. The base value of the consistency factor is $K=1000~\hbox {Pa}\,\hbox {s}^n$. The values of the fluid behavior index n and the fluid yield stress $\tau _0$ can vary from fluid to fluid. Four cases of the fluid rheology have been considered:

• 1. Newtonian fluid: $K=1000~\hbox {Pa}\,\hbox {s}^n$, $n=1$, $\tau _0=0~\hbox {Pa}$;

• 2. Bingham fluid: $K=1000~\hbox {Pa}\,\hbox {s}^n$, $n=1$, $\tau _0=400~\hbox {Pa}$;

• 3. Power-law fluid: $K=1000~\hbox {Pa}\,\hbox {s}^n$, $n=0.5$, $\tau _0=0~\hbox {Pa}$;

• 4. Herschel–Bulkley fluid: $K=1000~\hbox {Pa}\,\hbox {s}^n$, $n=0.5$, $\tau _0=400~\hbox {Pa}$.

Fig. 17

Wellbore pressure versus time in logarithmic scale for $\alpha =0$: 1—Newtonian fluid; 2—Bingham fluid; 3—Power-law fluid; 4—Herschel–Bulkley fluid

Fig. 18

Wellbore pressure versus time in logarithmic scale for $\alpha =0$ and for Newtonian fluid with viscosity: 1—$K = 500~\hbox {Pa}\,\hbox {s}$; 2—$K = 1000~\hbox {Pa}\,\hbox {s}$; 3—$K = 2000~\hbox {Pa}\,\hbox {s}$

In Fig. 17, the dependences of the wellbore pressure on time are shown in logarithmic scale for the rheological models of the fracturing fluids listed above. One can see that the slopes of all four curves relative to the abscissa axis differ from each other. The increase of the yield stress and the decrease of the power law index lead to the reduction of the inclination angle of the corresponding pressure curve. In the first case, this happens due to the increase of the wellbore pressure required by the fracture development for late times, and in the second case—due to its decrease for early times. One can see also that on the considered time interval the wellbore pressure curve for Newtonian fluid cannot serve as a good approximation for any of the cases of non-Newtonian fluid injection in Fig. 17. It should be noted that in contrast to the “high shear rates” case this mismatch cannot be corrected by the proper choice of the Newtonian fluid viscosity only. The variation of Newtonian fluid viscosity does not result in the variation of the pressure curve slope but just changes the distance between the curve and the abscissa axis. This can be observed in Fig. 18, where the dependences of the wellbore pressure on time are presented for a wide range of variation of the Newtonian fracturing fluid viscosity.

Fig. 19

Distribution of fluid velocity modulus for $\alpha =60^\circ$ and Herschel–Bulkley fluid with parameters: $K = 1000~\hbox {Pa}\,\hbox {s}$, $n=0.5$, $\tau _0 = 400~\hbox {Pa}$

It should be noted that an inaccurate determination of the fluid pressure causes errors in the fracture width estimation. In practice, this may lead to incorrect conclusions about the necessary volume of clean gel injected into the wellbore before proppant slurry pumping, to errors in the calculation of the propped fracture profile and, ultimately, to an incorrect prediction of the well productivity after hydraulic fracturing.

5.3 Probability of the arrested state of the hydraulic fracture driven by HB fluid

Overview of the results will complete the answer to the question whether the hydraulic fracture driven by HB fluid can stop? This is quite an appropriate question. Herschel–Bulkley rheology law includes non-zero yield stress. This rheology feature causes HB fluid flow stop in a number of practical cases of its application. Examples include the pumping through a pipe, a flow between two planes (see Sect. 4.2), spreading on a plane, etc. It would be natural to expect that the use of the HB fluid as a fracturing fluid under certain conditions will also lead to the arrested state of the hydraulic fracture when the wellbore pressure that pushes the fluid into the fracture is not enough to overcome the friction forces at the fracture sides. However, for the growing transversal hydraulic fracture this is a misleading idea. The calculations of the penny-shaped fracture propagation at constant injection rate have shown that with the fracture growth the wellbore pressure does not increase but it falls (see curve 4 in Fig. 17, for example). However, despite the wellbore pressure decrement the force pushing the fluid into the fracture grows proportionally to the increase of the fracture width at the wellbore.

Fig. 20

Fluid velocity modulus versus radial coordinate for $\alpha =60^\circ$ and Herschel–Bulkley fluid with parameters: $K = 1000~\hbox {Pa}\,\hbox {s}$, $n=0.5$, $\tau _0 = 400~\hbox {Pa}$: 1—$\varphi =0^\circ$; 2—$\varphi =45^\circ$; 3—$\varphi =90^\circ$

As an illustration of the statement made above, Fig. 19 shows the 3D picture of fluid velocity inside the fracture for $\alpha =60^\circ$ for Herschel–Bulkley fluid with the following parameters: $K = 1000~\hbox {Pa}\,\hbox {s}$, $n=0.5$, $\tau _0 = 400~\hbox {Pa}$. The velocity profiles for the selected radial cross-sections $\varphi =0^\circ$; $45^\circ$; $90^\circ$ (as indicated in Fig. 9) are presented in Fig. 20. One can see that the fluid velocity becomes zero only at the fluid front and in the fluid lag where fluid doesn’t flow. This means there is no zones inside the fracture where the fluid is arrested.

The statement about the impossibility of an arrested state is valid not only for the penny-shaped fracture but also for any other geometrical fracture model that does not include any artificial limitations for the fracture width growth at the wellbore such as, for instance, the KGD model geometry. The stress barrier preventing the fracture propagation along the borehole can serve as an example of such limitations. The geometry of the fracture developing under high stress barrier restriction is described well within the PKN model, which, in fact, is very similar to the model of the fluid flow in a pipe of a variable length. For the PKN model, the arrest of the fluid flow in the fracture and the subsequent stop of its propagation seem quite probable, for example, in the case of maintaining a constant injection pressure in the wellbore.

6 Conclusion

The 3D model of transversal hydraulic fracture propagation from a cavity developed by the authors earlier has been extended to the case of Herschel–Bulkley fluid injection. It should be noted that the new model takes into account the following specifics: the presence of borehole, the variable fluid pressure gradient along the fracture, and the lag between the fluid front and the fracture front during its propagation. Such features make the model very suitable for simulating the early stage of hydraulic fracture development and, in particular, for studying the near wellbore fracture tortuosity. Due to the additional non-linearity of the problem introduced by Herschel–Bulkley fluid rheology, the model algorithm is slower and more prone to the issues with convergence in comparison with the original 3D model of hydraulic fracture driven by Newtonian fluid.

The analysis of the fracture behavior sensitivity to the parameters of Herschel–Bulkley fracturing fluid has been performed. Based on the obtained results one can conclude that the transverse hydraulic fracture is not prone to the so-called “pinching” effect and there is no zones inside the propagating fracture where the fracturing fluid is in an arrested state even with high values of the fluid yield stress.

It was shown that while simulating the early stage of transverse hydraulic fracture development one can neglect the yield stress of Bingham fracturing fluid without loss of accuracy. The influence of yield stress on the main parameters of the fracture trajectory, width, wellbore pressure is neglible and the variation of the behavior index affects the main fracture parameters in the same way as the variation of the fluid viscosity or consistency factor does. Therefore Herschel–Bulkley fluid model can be replaced by Newtonian one if the hydraulic fracture simulation results provided that the parameter of the linear rheological law (apparent viscosity) is measured for the expected shear rates interval. This is only valid for the early stage of the fracture growth modeling (small scale fracture). For large scale fractures, it is impossible to obtain the low error of approximation at each moment of the considered time interval while approximating the actual rheological curve of the fracturing fluid with just a constant apparent viscosity.

The obtained results have demonstrated once again that one should be careful while interpreting the results of any laboratory experiments with hydraulic fracturing (lab scale) and using them for designing a full-scale hydraulic fracturing job (field scale).

Appendix

1.1 A.1 Herschel–Bulkley fluid model

Let us consider the most general form of the equations of incompressible HB-fluid flow in the 3D case. It includes the continuity equation

$$\begin{aligned} \nabla \cdot {{\mathrm{\mathbf v}}}= 0 \end{aligned}$$

(43)

and the momentum equation

$$\begin{aligned} \rho \frac{D {{\mathrm{\mathbf v}}}}{D t} = \nabla \cdot {\mathbb {P}}. \end{aligned}$$

(44)

In (43), (44) ${{\mathrm{\mathbf v}}}= \{ v_i \}$ is the fluid velocity vector and ${\mathbb {P}} = \{ p_{ij} \}$ is the total stress tensor divided into two parts

$$\begin{aligned} {\mathbb {P}} = -p {\mathbb {E}} + {\mathbb {T}}, \end{aligned}$$

(45)

where p is the scalar called the hydrodynamic pressure, ${\mathbb {T}} = \{ \tau _{ij} \}$ is the viscous stress tensor, and ${\mathbb {E}} = diag(1,1,1)$ is the unit (or identity) tensor. The viscous stress tensor ${\mathbb {T}}$ is connected with the strain rate tensor ${\mathbb {D}}=\{ D_{ij} \}$ by the constitutive relations

$$\begin{aligned} {\mathbb {T}}= & {} \eta {\mathbb {D}}, \quad \text {for} \ T \geqslant \tau _0, \end{aligned}$$

(46)

$$\begin{aligned} {\mathbb {D}}= & {} 0, \quad \text {for} \ T < \tau _0. \end{aligned}$$

(47)

In (46), (47) the components of the tensor ${\mathbb {D}}$ are

$$\begin{aligned} D_{ij} = \frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} \end{aligned}$$

(48)

and $\eta$ is the viscosity function given by the Herschel–Bulkley rheology model

$$\begin{aligned} \eta (D) = K D^{n-1} + \frac{\tau _0}{D}. \end{aligned}$$

(49)

Here, K is the flow consistency factor; n is the flow behavior index that governs the degree of shear thinning or thickening; $\tau _0$ is the yield stress. T and D denote the second invariants of the respective tensors given by the following formulas

$$\begin{aligned} T = \sqrt{\frac{1}{2} \tau _{ij} \tau _{ij}} \quad \text {and} \quad D = \sqrt{\frac{1}{2} D_{ij} D_{ij}}. \end{aligned}$$

(50)

The index form of Eqs. (43) and (44) is the following:

$$\begin{aligned}&\frac{\partial v_i}{\partial x_i} = 0, \end{aligned}$$

(51)

$$\begin{aligned}&\rho \left[ \frac{\partial v_i}{\partial t} + \frac{\partial (v_i v_j)}{\partial x_j} \right] = - \frac{\partial p}{\partial x_i} \nonumber \\&\quad + \frac{\partial }{\partial x_j} \left[ \eta (D) \left( \frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i} \right) \right] . \end{aligned}$$

(52)

1.2 A.2 Equations for 2D HB fluid flow in 3D fracture

The fracture width W is much smaller than its longitudinal size. Therefore, the flow inside the fracture can be considered locally as the flow in a thin channel between two parallel plates. Without loss of generality let’s assume that the axis $x_1, x_2$ of the local coordinate system lie in the tangent plane to the fracture surface and the axis $x_3$ is orthogonal to the fracture surface. Then the transversal fluid velocity component can be assumed small ($v_3 \approx 0$) as compared to its longitudinal components. Also the derivatives of the fluid velocity components in the longitudinal directions ${\partial }/ {\partial x_1}$, ${\partial }/{\partial x_2}$ are small in comparison with their derivatives in the transverse direction ${\partial }/{\partial x_3}$. The fluid pressure and its consistency factor are considered constant in the transverse direction. The time derivatives in Eq. (52) are disregarded. The non-stationarity of the fracture propagation model is conditioned by the continuity Eq. (51) through the relationship between the fracture width W and the transversal fluid velocity $v_3$

$$\begin{aligned} \frac{\partial W}{\partial t} = v_3. \end{aligned}$$

(53)

Under the assumptions made above, Eqs. (51) and (52) can be simplified. Omitting small terms in Eq. (52), one can obtain for $i=1,2$

$$\begin{aligned} \frac{\partial p}{\partial x_1} = \frac{\partial }{\partial x_3}\left[ \eta (D) \frac{\partial v_1}{\partial x_3} \right] ,\frac{\partial p}{\partial x_2} = \frac{\partial }{\partial x_3}\left[ \eta (D) \frac{\partial v_2}{\partial x_3} \right] . \nonumber \\ \end{aligned}$$

(54)

Equation (52) for $i=3$ degenerates under the stated assumptions. The integration of Eq. (54) over $x_3$ gives

$$\begin{aligned} \eta (D) \frac{\partial v_i}{\partial x_3} = \frac{\partial p}{\partial x_i} + A_i, \ \ \end{aligned}$$

(55)

where $A_i$ are some constant values.

Further, the cases of Newtonian and Herschel–Bulkley fluids are discussed separately. For Newtonian fluid, we have $\eta (D) = \mu = const$, $\tau _0=0$ and then from Eq. (55) it follows that

$$\begin{aligned} v_i = \frac{x_3^2}{2\mu } \frac{\partial p}{\partial x_i} + A_i \frac{x_3}{2\mu } + B_i. \ \ \end{aligned}$$

(56)

Taking into account the boundary conditions at $x_3=0$ and $x_3=W$

$$\begin{aligned} v_i=0, i=1,2 \end{aligned}$$

(57)

one can obtain

$$\begin{aligned} v_i = -x_3 \frac{W-x_3}{2\mu } \frac{\partial p}{\partial x_i}. \end{aligned}$$

(58)

From the expressions for fluid fluxes

$$\begin{aligned} q_i = \int _{0}^{W} v_i d x_3, \ \ i = 1,2 \end{aligned}$$

(59)

and Eq. (58) we can get the equations connecting the derivatives of the fluid pressure with the fluxes

$$\begin{aligned} q_i = - \frac{W^3}{12\mu } \frac{\partial p}{\partial x_i}, \end{aligned}$$

(60)

Equations (60) coincide with the ones used in Shokin et al. (2015) and Cherny et al. (2016).

Using the Equations (58) and (60) one can obtain shear rate value

$$\begin{aligned} {\dot{\gamma }}= \frac{\partial v_1}{\partial x_3} = \frac{6q_i}{W^2}. \end{aligned}$$

(61)

For HB-fluid, the viscosity function $\eta (D)$ depends on the velocity components that are functions of $x_3$. For integrating Equations (55), let us move to a coordinate system, in which the direction of $x_1$-axis coincides with the direction of the velocity vector ${\mathbf {u}}$. In this coordinate system, we have

$$\begin{aligned} \eta (D) = K \left( \frac{\partial v_1}{\partial x_3} \right) ^{n-1} + \tau _0 \left( \frac{\partial v_1}{\partial x_3} \right) ^{-1} . \end{aligned}$$

(62)

Integrating Equation (55) and taking into account the boundary conditions (57) and the expressions for the viscosity function (62), one can obtain

$$\begin{aligned} v_1= & {} -\frac{n K^{-1/n}}{ (n+1)} \left( \frac{\partial p}{\partial x_1} \right) ^{1/n}\nonumber \\&\left( (0.5W-z_{\tau })^{1+1/n}-v_{d}(x_3)^{1+1/n}\right) , \end{aligned}$$

(63)

where

$$\begin{aligned} v_d(x_3) = {\left\{ \begin{array}{ll} 0.5W- x_3 - z_{\tau }, &{} x_3<0.5W-z_{\tau } \\ 0, &{} 0.5W-z_{\tau } \le x_3 \le 0.5W+z_{\tau } \\ x_3 - 0.5W - z_{\tau }, &{} x_3>0.5W+z_{\tau } \end{array}\right. }, \ z_{\tau } = \tau _0 \left| \frac{\partial p}{\partial x_1}\right| ^{-1} . \end{aligned}$$

The latter formula for $v_d(x_3)$ takes into account the typical velocity profile of the HB fluid flow between two parallel plates as shown in Fig. 21. This formula is correct if the pressure gradient is enough to overcome the yield stress

$$\begin{aligned} \left| \frac{\partial p}{\partial x_1}\right| > \frac{2 \tau _0}{W}. \end{aligned}$$

(64)

Otherwise the fluid is motionless. Similarly, one can obtain the expression for the second velocity component $v_2$. Now the expressions for the fluid fluxes can be written in the following form:

$$\begin{aligned} q_i= & {} - \frac{n}{(4n+2) (2K)^{1/n}} W^{2+1/n} \left( \frac{\partial p}{\partial x_i} \right) ^{1/n}\nonumber \\&\left( 1-\frac{2z_{\tau }}{W} \right) ^{1+1/n} \left( 1+\frac{2z_{\tau }}{W}\frac{n}{n+1} \right) . \end{aligned}$$

(65)

Fig. 21

Typical velocity profile of HB fluid flow between two parallel plates

Extracting the first degree of the pressure derivatives ${\partial p}/{\partial x_i}$ in the right-hand side of Equation (65) gives

$$\begin{aligned} q_i = - \frac{W^3}{12\eta _a} \frac{\partial p}{\partial x_i}, \end{aligned}$$

(66)

where $\eta _{a}$ is an apparent viscosity. It can be expressed in terms of the pressure derivatives ${\partial p}/{\partial x_i}$ as well as in terms of the fluxes.

The expression of the apparent viscosity through the pressure derivatives can be obtained from the Equation (63)

$$\begin{aligned} \eta _{a}= & {} \eta _{p} = \frac{(2K)^{1/n}(2n+1)}{6n} \left| \frac{\partial p}{\partial x_1}\right| ^{(n-1)/n}\nonumber \\&W^{(n-1)/n} + \frac{(4n+2)2^{1/n} \tau _0}{3 n \left| \frac{\partial p}{\partial x_1}\right| ^{1/n} W^{1/n}}. \end{aligned}$$

(67)

Rewriting Equation (67) in another coordinate system results in the substitution of the pressure derivative ${\partial p}/{\partial x_i}$ by the pressure gradient $\nabla p$, which is invariant relative to coordinate transformations

$$\begin{aligned} \eta _a= & {} \eta _p(\nabla p) = \frac{(2K)^{1/n}(2n+1)}{6n} (W |\nabla p|)^{(n-1)/n}\nonumber \\&+ \frac{(4n+2)2^{1/n} \tau _0}{3 n (W |\nabla p|)^{1/n} }, \end{aligned}$$

(68)

where

$$\begin{aligned} |\nabla p| = \left( \left( \frac{\partial p}{\partial x_1}\right) ^2 + \left( \frac{\partial p}{\partial x_2}\right) ^2 \right) ^{1/2}. \end{aligned}$$

To get the formula for the apparent viscosity in terms of the fluid fluxes, let us sum the squares of the right-hand sides of Equation (65) for $q_1$ and $q_2$ and express the pressure gradient $|\nabla p|$ in terms of the fluid flow vector module $|\mathbf{q}| = (q_1^2 + q_2^2)^{1/2}$, which is invariant relative to coordinate transformations similar to $|\nabla p|$. Then we obtain

$$\begin{aligned} \eta _{q} = \frac{K}{6} \left( \frac{4n+2}{n}\right) ^n \left( \frac{W^2}{|\mathbf{q}|} \right) ^{1-n} + \frac{2n+1}{3(n+1)}\frac{\tau _0 W^2}{|\mathbf{q}|} . \nonumber \\ \end{aligned}$$

(69)

Formula (69) is a 2D generalization to the case of Herschel–Bulkley rheology of the expressions obtained earlier by other researchers for a Power-law fluid. For the case of the Power-law fluid ($\tau _0 \equiv 0$) the Equation (66) with the apparent viscosity expressed by formula (69) has been used in Sousa et al. (1993), Garagash (2006), and the expression (68) has been employed in Ouyang et al. (1997) and Rungamornrat et al. (2005). Here as well as in Cherny and Lapin (2016) formula (68) is chosen because then there is no need to calculate the fluid flux while the fluid flow equations are solving.

Note that like in case of Newtonian fluid one can obtain the value of shear rate using the Equations (63), (66) (69), but the calculations are quite more complicated

$$\begin{aligned} {\dot{\gamma }}= \frac{\partial v_1}{\partial x_3} = \frac{1}{K^{1/n}} \left[ K \left( \frac{4n+2}{n}\right) ^n \left( \frac{|{\mathbf {q}}|}{W^2} \right) ^n + \frac{3n+1}{n+1} \tau _0 \right] ^{1/n}. \nonumber \\ \end{aligned}$$

(70)

Integrating equation (51) over $x_3$ and taking into account relationships (53) and (59), one can obtain the equation for the fracture width W

$$\begin{aligned} \frac{\partial W}{\partial t} + \frac{\partial q_1}{\partial x_1} + \frac{\partial q_2}{\partial x_2} = 0. \end{aligned}$$

(71)

The substitution of the expression for the fluxes (66) into Equation (71) gives the equation for the fluid pressure

$$\begin{aligned} \frac{\partial }{\partial x_1} \left( \frac{W^{3}}{12 \eta _{a}} \frac{\partial p}{\partial x_1} \right) + \frac{\partial }{\partial x_2} \left( \frac{W^{3}}{12 \eta _{a}} \frac{\partial p}{\partial x_2} \right) = \frac{\partial W}{\partial t}. \end{aligned}$$

(72)

One should note that one of the major difficulties while modeling the fluid flows with non-zero yield stress (such as Bingham of Herschel–Bulkley fluids) is the necessity to trace the boundary between the region of non-zero strain rate (46), where the Eqs. (49), (52), (62), (65)–(66), (67), (68), (69), (72) are applied and the region (47) where the fluid flow should be treated as the rigid body motion ($D_{ij}=0$). For the modeling of the regions with the zero and non-zero strain rate tensor (yielded and unyielded regions) within the framework of the same equations various modifications of the expression for the viscosity (49), are used, and they prevent its degeneration when $D\rightarrow 0$ (Mitsoulis 2007).

In the problems of fluid flow in the hydraulic fracture the search for the boundary of the unyielded region is easier than in the problems of fluid flow in the regions with the given boundaries. The unyielded region appears in each point of the fracture ($x_1, x_2$) in the middle of its cross-section (between the fracture sides $0<x_3<W$). The boundaries of the region are calculated explicitly, while solving the problem of fluid flow between two parallel plates (65). This solutions is used to obtain equation (72) As it can be concluded from (64) the pressure gradient is bounded from zero. The area where strain rate tensor is zero can fill the whole cross section, then fluid at this crack point ($x_1, x_2$) stops, and equation (72) is not valid. But the calculations made in Sect. 5.3, show that such a situation can not be realized in the simulation of the fractures considered. This means that at all points of the fracture the fluid flows, and the pressure gradient always exceeds $\frac{2 \tau _0}{W}$. This allows us to use equation (72) with the expression for viscosity (68) without additional modifications.