Locking-free triangular plate element using polynomial incompatible approximation for analysis of cracked thick–thin plates

Abstract

In this paper, a simple locking-free triangular plate element, referred to here as the Mindlin triangular plate element with full integration (MTPF), is presented for the analysis of cracked thick–thin plates. The element employs a new specially designed incompatible meshless approximation, independent of the nodes and triangle shape, in order to define displacements for the purpose of avoiding the use of reduced/selected integration to make the MTPF locking-free and valid for the thin plate. The current MTPF is also extended for the analysis of cracked thick–thin plates, and the virtual crack closure technique is applied in order to compute the crack tip stress intensity factors of the cracked thick–thin plates, where the formula derivation and numerical implementation are very simple and convenient for the present MTPF. Several representative numerical examples demonstrate that the MTPF is a robust and high-performance element for cracked thick–thin plates.

1 Introduction

Plate (and shell) structures play an important role and offer wide applications in civil, mechanical, and aerospace engineering. The existence of defects and cracks in such structures may lead to a substantial decrease in load capacity, structural safety, and even structural collapse, and therefore, accurate evaluation of the fracture mechanics parameters of the cracked plates is an important topic in structural engineering practice.

Generally, elastic plate analysis can be performed by means of three-dimensional elasticity, Kirchhoff plate formulation, or Reissner–Mindlin plate theory (Bayesteh and Mohammadi 2011). Among these theories, Reissner–Mindlin plate theory may be the most widely used in engineering applications, because it requires only $C_{0}$ continuity for the displacement fields, avoids the $C_{1}$ continuity requirement difficulties in the Kirchhoff-type theory, and has a relatively very low computational cost compared to the three-dimensional theory. Unfortunately, the Reissner–Mindlin plate elements suffer from the shear locking phenomenon and yield poor results in a thin plate limit (Ayad et al. 1998; Cen and Shang 2015). Techniques including the assumed shear strain approach, discrete Kirchhoff/Reissner–Mindlin representation, mixed/hybrid formulation, and reduced/selected integration have been employed in order to develop the locking-free triangular thick–thin plate elements, such as the element DST-BL by Batoz and Lardeur (1989), the element DST-BK by Batoz and Katili (1992), the element MITC by Bathe and Dvorkin (1985), the element MiSP by Ayad et al. (1998), the element DKMT by Katili (1993), the element RDKTM by Chen and Cheung (2001), and the element TIP3 by Brasile (2008). Many of these elements exhibit high accuracy, demonstrate effective performance for thick and thin plates, and are applicable to a wide range of practical engineering problems. However, these popular elements always involve very complex formulations to include the transverse shear effects, and are seldom used in the fracture analysis of cracked plates, because of their more complex mathematical patterns around the crack tip.

In recent years, several alternative computational methods or techniques have been proposed in order to solve cracked bending problems, including the three-dimensional FE method (Agnihotri and Parameswaran 2016), extended finite element method (Yu et al. 2014; Nasirmanesh and Mohammadi 2015), dual boundary element method (Dirgantara and Aliabadi 2000, 2002), phantom-node method (Chau-Dinh et al. 2012), strip yield model (Chang and Kotousov 2012), singular finite elements (Lim 2011), extended isogeometric analysis method (Bhardwaj et al. 2015, 2016), reproducing kernel meshless approach (Mohammad et al. 2011; Wang and Peng 2013; Tanaka et al. 2015), and discrete shear gap method (Nguyen-Thoi et al. 2012, 2014, 2015; Liu et al. 2015; Nguyen-Xuan et al. 2009; Phung-Van et al. 2013a, b). The majority of these methods are free of shear-locking, avoid remeshing of finite elements, exhibit high accuracy, demonstrate great potential and promising application for cracked plate modeling, and are undergoing rapid development.

In the work of Cai and Zhu (2017a, b), a simple MTP9 (Mindlin-type triangular plate element with nine degrees of freedom) was proposed for thick–thin plate analysis. The element MTP9 avoids shear locking, and exhibits an effective convergence rate as well as high accuracy; however, reduced/selected integration must still be applied to the shear energy term to make the element MTP9 valid for the thin plate. In this study, several specifically designed meshless approximations are employed for the construction of a new type of locking-free MTPF without the use of reduced/selected integration, which is necessary in the element MTP9. Moreover, the present MTPF is extended for the analysis of cracked thick–thin plates, and the virtual crack closure technique (VCCT) is employed in order to compute the crack tip stress intensity factors (SIFs) of the cracked thick–thin plates, in which the formula derivation and numerical implementation are very simple and convenient. Numerical evaluation demonstrates that the element MTPF is highly useful and applicable to practical engineering.

Fig. 1

Linear elastic bending plate

2 Basic theory of element MTPF

2.1 Meshless approximation at triangular element

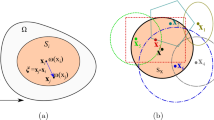
We consider a linear elastic plate containing a through-thickness crack and undergoing infinitesimal deformation, as shown in Fig. 1. The length, width, and height of the plate are a, b,  and h respectively. The plate mid plane is taken as the $x-y$ plane. The z-axis is perpendicular to the mid plane, which is divided into arbitrary triangular elements, as illustrated in Fig. 2.

Fig. 2

Triangular mesh for mid-surface of plate

According to the Reissner–Mindlin plate theory, a meshless approximation in each triangular element $e_i$ is assumed as

$$\begin{aligned} \mathbf{u}=\mathbf{N}^{e}{} \mathbf{a}^{e} \end{aligned}$$

(1)

where $\mathbf{u}=\left\{ {{\begin{array}{lll} u&{} v&{} w \\ \end{array} }} \right\} ^{{\mathrm{T}}}$ is the displacement approach of $e_i$ along the x, y, and z axes; $\mathbf{a}^{e}=\left[ {{\begin{array}{llll} {a_1 }&{} {a_2 }&{} \cdots &{} {a_m } \\ \end{array} }} \right] ^{{\mathrm{T}}}$ is the interpolation degrees of freedom (d.o.f.) of $e_i$; $\mathbf{N}^{e}$ is the shape function of $e_i$, where

$$\begin{aligned} \mathbf{N}^{e}=\left[ {{\begin{array}{lll} {z\mathbf{P}^{\mathrm {T}}\left( \mathbf{x} \right) }&{} 0&{} 0 \\ 0&{} {z\mathbf{P}^{\mathrm {T}}\left( \mathbf{x} \right) }&{} 0 \\ 0&{} 0&{} {\mathbf{P}^{\mathrm {T}}\left( \mathbf{x} \right) } \\ \end{array} }} \right] \end{aligned}$$

(2)

are employed in this work. Here, $x_0 =x-x_i$, $y_0 =y-y_i$, $\left( {x_i ,y_i } \right)$ are the coordinates of the central point of element $e_i$, and the linear shape function is taken as

$$\begin{aligned} \mathbf{P}^{{\mathrm{T}}}\left( \mathbf{x} \right) =\left[ {{\begin{array}{lll} 1&{} {x_0 }&{} {y_0 } \\ \end{array} }} \right] . \end{aligned}$$

(3)

The quadratic shape function is taken as

$$\begin{aligned} \mathbf{P}^{{\mathrm{T}}}\left( \mathbf{x} \right) =\left[ {{\begin{array}{llllll} 1&{} {x_0 }&{} {y_0 }&{} {x_0^2 }&{} {x_0 y_0 }&{} {y_0^2 } \\ \end{array} }} \right] \end{aligned}$$

(4)

and the cubic shape function is taken as

$$\begin{aligned} \mathbf{P}^{{\mathrm{T}}}\left( \mathbf{x} \right) =\left[ {{\begin{array}{llllllllll} 1&{} {x_0 }&{} {y_0 }&{} {x_0^2 }&{} {x_0 y_0 }&{} {y_0^2 }&{} {x_0^3 }&{} {x_0^2 y_0 }&{} {y_0^2 x_0 }&{} {y_0^3 } \\ \end{array} }} \right] \end{aligned}$$

(5)

The displacement approximation in Eq. (1) is a meshless interpolation, which is defined at the central point of element $e_i$ and is independent of the nodes and element shape. Moreover, $\left( {x_i {,}y_i } \right)$ are the central point coordinates of element $e_i$. Because the displacement approximation in Eq. (1) is independent of the nodes and element shape, an arbitrary displacement approximation order, as required by the solving accuracy, can be constructed with no difficulty in the current plate element.

Substituting Eq. (1) into the following strain–displacement relations of the linear elastic problem,

$$\begin{aligned} \varepsilon _x= & {} \frac{\partial u}{\partial x},\;\varepsilon _y =\frac{\partial v}{\partial y},\;\varepsilon _z =\frac{\partial w}{\partial z}\approx 0,\nonumber \\ \gamma _{xy}= & {} \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}, \; \gamma _{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z},\;\gamma _{xz} =\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\nonumber \\ \end{aligned}$$

(6)

we obtain

$$\begin{aligned} {\varvec{\varepsilon }}=\mathbf{Lu}=\mathbf{LN}^{e}{} \mathbf{a}^{e}=\mathbf{Ba}^{e} \end{aligned}$$

(7)

where ${{\varvec{\varepsilon }} }=\left\{ {\varepsilon _x ,\varepsilon _y ,\gamma _{xy} ,\gamma _{yz} ,\gamma _{xz} } \right\} ^{\mathrm {T}}$ is the strain vector and $\mathbf{B}$ is the strain matrix. Furthermore,

$$\begin{aligned} \mathbf{B}= & {} \mathbf{LN}^{e} \end{aligned}$$

(8)

$$\begin{aligned} \mathbf{L}= & {} \left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\frac{\partial }{\partial x}}&{} 0&{} 0 \\ 0&{} {\frac{\partial }{\partial y}}&{} 0 \\ {\frac{\partial }{\partial y}}&{} {\frac{\partial }{\partial x}}&{} 0 \\ 0&{} {\frac{\partial }{\partial z}}&{} {\frac{\partial }{\partial y}} \\ {\frac{\partial }{\partial z}}&{} 0&{} {\frac{\partial }{\partial x}} \\ \end{array} }} \right] \end{aligned}$$

(9)

For an isotropic linear elastic material, we can express the stress–strain relations in element $e_i$ as

$$\begin{aligned} {{\varvec{\sigma }} }=\mathbf{DBa}^{e} \end{aligned}$$

(10)

where the elasticity matrix

$$\begin{aligned} \mathbf{D}=D_0 \left[ {{\begin{array}{lllll} 1&{} \quad v&{} \quad 0&{}\quad 0&{}\quad 0 \\ v&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {\frac{1-v}{2}}&{} \quad 0&{}\quad 0 \\ 0&{} \quad 0&{} \quad 0&{}\quad {\frac{1-v}{2k}}&{} 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {\frac{1-v}{2k}} \\ \end{array} }} \right] \end{aligned}$$

(11)

Here $D_0 =\frac{E}{1-v^{2}}$, E is the elastic modulus,v is the Poisson ratio, and $k=1.2$ is the shear correction factor of the section. Because $\sigma _z \ll \sigma _x$ and $\sigma _z \ll \sigma _y$ in the Reissner–Mindlin plate theory, $\sigma _z$ and its influence on deformation are neglected in Eqs. (7) and (10).

Thus, the strain energy of element $e_i$ can be expressed as

$$\begin{aligned} {{\varvec{\Pi }} }^{e}=\frac{1}{2}\left( {\hbox {a}^{e}} \right) ^{\mathrm {T}}\mathop \int \nolimits _{-h/2}^{h/2} \left( {\mathop \int \int \nolimits _{{\Delta e_i }^ {\mathrm{B}}}{^{{\mathrm{T}}}}{} \mathbf{DB}dxdy} \right) dz\mathbf{a}^{e} \end{aligned}$$

(12)

With the definition of the meshless approximation in Eq. (1), the adjacent elements $e_i$ and $e_j$ in Fig. 2 have their own d.o.f. and independent deformation, which means that these elements are totally discontinuous. However, the displacement and deformation over the share boundary of non-overlapping elements $e_i$ and $e_j$ should actually be continuous. A fictitious thin layer $e_l$ may be introduced, with length l, width $\delta$, and height h, where $\delta \ll l$ and $\delta \ll h$, in order to enforce the continuous conditions over the share boundary of the elements, as shown in Fig. 3.

Because $\delta \ll l$ and $\delta \ll h$, points $p_1$ and $p_2$ in Fig. 3 can be regarded approximately as the same point p, having local coordinates $\left( {s,n,z} \right)$ and global coordinates $\left( {x_p ,y_p ,z_p } \right)$, and the strain–displacement relations in thin layer $e_l$ are simplified as

$$\begin{aligned} \gamma _{ns} \approx \frac{{\bar{u}}^{p_2 }- {\bar{u}}^{p_1 }}{\delta },\varepsilon _n \approx \frac{ {\bar{v}}^{p_2 }-{\bar{v}} ^{p_1 }}{\delta },\gamma _{nz} \approx \frac{{\bar{w}} ^{p_2 }-{\bar{w}} ^{p_1 }}{\delta } \end{aligned}$$

(13)

where ${\bar{\mathbf{u}}}^{p_1 }$ and ${\bar{\mathbf{u}}}^{p_2 }$ can be computed using Eq. (1), as follows:

$$\begin{aligned} {\bar{\mathbf{u}}}^{p_1 }= & {} {{\varvec{\lambda }} }^{l}{} \mathbf{N}^{e_i }\left( {x_p ,y_p ,z_p } \right) \mathbf{a}^{e_i } \end{aligned}$$

(14)

$$\begin{aligned} {\bar{\mathbf{u}}}^{p_2 }= & {} {{\varvec{\lambda }} }^{l}{} \mathbf{N}^{e_j }\left( {x_p ,y_p ,z_p } \right) \mathbf{a}^{e_j } \end{aligned}$$

(15)

Here, $\mathbf{N}^{e_i }\left( {x_p ,y_p ,z_p } \right)$ is the shape function of point p in element $e_i$, $\mathbf{N}^{e_j }\left( {x_p ,y_p ,z_p } \right)$ is the shape function of point p in element $e_j$, $\mathbf{a}^{e_i }$ is the d.o.f. of element $e_i$, $\hbox {a}^{e_j }$ is the d.o.f. of element $e_j$, and ${{\varvec{\lambda }} }^{l}$ is the transformation matrix from the global coordinates $\left( {x,y,z} \right)$ to local coordinates $\left( {s,n,z} \right)$, where

$$\begin{aligned} {{\varvec{\lambda }} }^{l}=\left[ {{\begin{array}{lll} {\cos \theta }&{} {\sin \theta }&{} 0 \\ {-\sin \theta }&{} {\cos \theta }&{} 0 \\ 0&{} 0&{} 1 \\ \end{array} }} \right] \end{aligned}$$

(16)

Fig. 3

Fictitious thin layer over share boundary

The detailed derivation process of Eq. (13) can be found in the work of Cai and Zhu (2017a). Substituting Eqs. (14) and (15) into Eq. (13) results in

$$\begin{aligned} {{\varvec{\varepsilon }} }^{l}=\frac{1}{\delta }{} \mathbf{N}^{l}{} \mathbf{a}^{l} \end{aligned}$$

(17)

where

$$\begin{aligned} {{\varvec{\varepsilon }} }^{l}= & {} \left[ {{\begin{array}{lll} {\gamma _{ns} }&{} {\varepsilon _n }&{} {\gamma _{nz} } \\ \end{array} }} \right] ^{{\mathrm{T}}} \end{aligned}$$

(18)

$$\begin{aligned} \mathbf{N}^{l}= & {} {\mathbf{\lambda } }^{l}\left[ {{\begin{array}{ll} {{-\mathbf{N}}^{e_i }}&{} {\mathbf{N}}^{e_j } \\ \end{array} }} \right] \end{aligned}$$

(19)

$$\begin{aligned} \mathbf{a}^{l}= & {} \left[ {{\begin{array}{l} {\mathbf{a}}^{e_i } \\ {{\mathbf{a}}^{e_j }} \\ \end{array} }} \right] \end{aligned}$$

(20)

The stress–strain relations in thin layer $e_l$ are then expressed as

$$\begin{aligned} {{\varvec{\sigma }}}^{l}=\mathbf{D}^{l}{{\varvec{\varepsilon }} }^{l} \end{aligned}$$

(21)

where

$$\begin{aligned} {{\varvec{\sigma }} }^{l}= & {} \left[ {{\begin{array}{lll} {\tau _{ns} }&{} {\sigma _n }&{} {\tau _{nz} } \\ \end{array} }} \right] ^{{\mathrm{T}}} \end{aligned}$$

(22)

$$\begin{aligned} \hbox {D}^{l}= & {} \left[ {{\begin{array}{lll} {G_0 }&{} 0&{} 0 \\ 0&{} {E_0 }&{} 0 \\ 0&{} 0&{} {G_0 /k} \\ \end{array} }} \right] \end{aligned}$$

(23)

in which $G_0 =\frac{E}{2\left( {1+v} \right) }$, $E_0 =\frac{E}{1-v^{2}}$, and $k=1.2$. The material constants in Eq. (23) are taken as those of the average of elements $e_i$ and $e_j$. The width $\delta$ of the fictitious thin layer $e_l$ is an important artificial parameter for the MTPF, but it is easy to select a reasonable $\delta$ to satisfy $\delta \ll l$ and$\delta \ll h$ in the current formulation. Numerical studies indicate that the variation of $\delta$ in a relatively large range has little effect on the accuracy of the calculation results for the analyses of thick–thin plates in practical engineering. In this paper, the width $\delta$ is taken as $\delta =0.0001l$.

It can be seen that, if the fictitious thin layer $e_l$ is replaced by contact springs $k_s$, $k_n$, and $k_z$ between adjacent elements, the current formulation becomes a discontinuous deformation analysis (DDA, Shi 1993) type of method for plate analysis, which is also a special case of the numerical manifold method (NMM, Shi 1991).

Fig. 4

Minor adjustment at crack tip for implementation of VCCT

Therefore, the strain energy of thin layer $e_l$ can be expressed as

$$\begin{aligned} {{\varvec{\Pi }} }^{l}=\frac{1}{2\delta }\left( {\hbox {a}^{l}} \right) ^{{\mathrm{T}}}\mathop \int \nolimits _{-h/2}^{h/2} \left( {\mathop \int \nolimits _{-l/2}^{l/2} \left( {{\mathbf{N}}^{l}} \right) ^{{\mathrm{T}}}{\mathbf{D}}^{l}{\mathbf{N}}^{l}ds} \right) dz{\mathbf{a}}^{l} \end{aligned}$$

(24)

The enforcement of the displacement and load boundary conditions can be derived in a similar manner (Cai and Zhu 2017a) as in Eq. (24). Please refer to Cai and Zhu (2017a) for the detailed derivation of the equilibrium equation for the plate

$$\begin{aligned} {\mathbf{K}} \cdot {\mathbf{U}}={\mathbf{F}} \end{aligned}$$

(25)

where K is the global stiffness matrix, F is the force vector, and U is the d.o.f. vector to be solved.

It is well established that the general Reissner–Mindlin triangular plate element sharing degrees of freedom at the nodes exhibits the serious problem of shear-locking for the thin plate, even if reduced/selected integration is applied for the element. However, the difficulty of constructing a simple and locking-free triangular plate element is effectively solved in the current MTPF by means of the definition of the new incompatible approximation in Eq. (1), which is independent of the nodes and triangular element shape. Furthermore, it is noted that regular full integration can be applied to make the element MTPF valid for the thin plate for the computation of Eq. (25), which differs from the work of Cai and Zhu (2017a) and others using reduced/selected integration for the shear term. The following numerical examples indicate that the current MTPF exhibits a highly effective convergence rate for both thick and thin plates.

3 Crack tip analysis

For the convenience of implementing the VCCT, as shown in Fig. 4b, point $q_2$, which is the nearest node along the extended line direction of $q_1 -q$, is temporarily moved to $q_3$ to cause $q_1 -q$ and $q-q_3$ to have an equal distance. The movement of $q_2$–$q_3$ does not affect interpolation accuracy, because the approximation in Eq. (1) is meshless and independent of the element shape.

In the local coordinates $\left( {s,n,z} \right)$ of Fig. 5, the relative displacements $\left[ {\Delta {\bar{u}} \left( {s,z} \right) ,\Delta {\bar{v}}\left( {s,z} \right) ,\Delta {\bar{w}} \left( {s,z} \right) } \right]$ of $\left( {-\,r_0 ,0} \right)$ to $\left( {0,0} \right)$ in front of crack tip q and the stresses $\left[ {\tau _{ns} \left( {s,z} \right) ,\sigma _n \left( {s,z} \right) ,\tau _{nz} \left( {s,z} \right) } \right]$ of $\left( {0,0} \right)$ to $\left( {r_0 ,0} \right)$ behind crack tip q can easily be calculated using Eqs. (17) and (21) for the thin layer. According to the VCCT (Rybicki and Kanninen 1977; Valvo 2015), the energy release rate at crack tip q can be approximately calculated by

$$\begin{aligned} \left\{ {{\begin{array}{l} {G_{\mathrm{I}} \cong \frac{1}{2hr_0 }\displaystyle \mathop \int \nolimits _{-h/2}^{h/2}\displaystyle \mathop \int \limits _0^{r_0 } \sigma _n \left( {s,z} \right) \Delta {\bar{v}} \left( {s-r_0 ,z} \right) \hbox {dsdz}} \\ {G_{{\mathrm{II}}} \cong \frac{1}{2hr_0 }\displaystyle \mathop \int \nolimits _{-h/2}^{h/2} \displaystyle \mathop \int \limits _0^{r_0 } \tau _{ns} \left( {s,z} \right) \Delta {\bar{u}}\left( {s-r_0 ,z} \right) \hbox {dsdz}} \\ {G_{{\mathrm{III}}} \cong \frac{1}{2hr_0 }\displaystyle \mathop \int \nolimits _{-h/2}^{h/2}\displaystyle \mathop \int \limits _0^{r_0 } \tau _{nz} \left( {s,z} \right) \Delta {\bar{w}} \left( {s-r_0 ,z} \right) \hbox {dsdz}} \\ \end{array} }} \right. \end{aligned}$$

(26)

where $G_{\mathrm{I}}$ is the energy release rate of crack mode $\hbox {I}$, $G_{{\mathrm{II}}}$ that of crack mode $\hbox {II}$, and $G_{{\mathrm{III}}}$ is that of crack mode $\hbox {III}$.

Fig. 5

Calculation of SIFs by VCCT

The SIFs for the Reissner–Mindlin plate are defined as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {K_1 =\mathop {\lim }\nolimits _{r\rightarrow 0} \sqrt{2\pi r}\sigma _\theta \left( {r,0,h/2} \right) } \\ {K_2 =\mathop {\lim }\nolimits _{r\rightarrow 0} \sqrt{2\pi r}\tau _{r\theta } \left( {r,0,h/2} \right) } \\ {K_3 =\mathop {\lim }\nolimits _{r\rightarrow 0} \sqrt{2\pi r}\tau _{\theta z} \left( {r,0,0} \right) } \\ \end{array} }} \right. \end{aligned}$$

(27)

where $r,\theta$ are the local polar coordinates around crack tip q. The SIFs can be computed by means of the relations between the energy release rate and SIFs for the Reissner–Mindlin plate theory,for example, $K_1 =\sqrt{3EG_{\mathrm{I}} }$ (Dirgantara and Aliabadi 2000).

It is observed that the proposed method contains a very simple formula that avoids using of singular integrations due to the local enrichment basis capturing the stress singularity around the crack tip, and prevents the relatively complicated J-integral for the crack modeling of plate bending problems in the previous popular methods. To the best of our knowledge, the proposed MTPF should be the simplest element for calculating the SIFs of the cracked thick–thin plates at this stage.

4 Numerical examples

In this section, several problems are solved in order to demonstrate the performance of the current element MTPF for the thick-to-thin plates.

4.1 Simply supported square plate under uniform load

A simply supported square plate under uniform load q is considered for linear elastic analysis. The plate side length and thickness are L and h, respectively. A quarter of the plate is modeled based on symmetry, as shown in Fig. 6. The $n\times n$ regular mesh in Fig. 7 and irregular mesh in Fig. 8 are employed for the convergence studies. This example is also solved by the MTP9 with the linear shape function and reduced/selected integration in Cai and Zhu (2017a), but here it is used for the purpose of testing the performance of the current MTPF without using reduced integration for the shear energy term.

In the following numerical examples, seven quadrature points for each triangular element (Cowper 1973) and three Gauss quadrature points for each fictitious layer are used for the MTPF integration using the quadratic shape function in Eq. (3). Furthermore, 12 quadrature points for each triangular element (Cowper 1973) and four Gauss quadrature points for each fictitious layer are used for the MTPF integration using the cubic shape function in Eq. (4).

Fig. 6

Model of square plate

Fig. 7

Typical regular mesh ($16\times 16$) for square plate

Fig. 8

Irregular mesh with 460 elements for square plate

Table 1 Central deflection for simply supported square plate with quadratic shape function

Table 2 Central deflection for simply supported square plate with cubic shape function

Tables 1 and 2 list the results of the dimensionless central displacement $w_0$ ($\times qL^{4}/100D_0 )$ for the simply supported plate with the quadratic and the cubic shape functions, respectively. The results listed in Tables 1 and 2 indicate that the current MTPF with the quadratic shape function is free from shear locking with an aspect ratio of $h/L\ge 0.005$, while the MTPF with the cubic shape function is locking-free to the thin limit of $h/L=0.0001$. In general, from a practical viewpoint, the current MTPF with different shape function orders, which is locking-free at least for $h/L\ge 0.005$, is sufficient for the analyses of various thick–thin plate types in practical engineering. Tables 1 and 2 also illustrate that the present MTPF exhibits satisfactory results for the thick-to-thin plates, and is insensitive to element distortions of the irregular mesh in Fig. 8.

Table 3 Number of quadrature points for reduced/selected integration of plate element

Table 4 Central deflection for simply supported square plate using reduced/selected integration

Table 5 Convergence of central deflection for simply supported square plate with different width-to-length ratios

Similar to the MTP9 in Cai and Zhu (2017a), reduced/selected integration can be used to solve the problem of shear locking in the current plate element exploiting the higher-order displacement functions. Table 3 lists the number of quadrature points for reduced/selected integration of the plate element. Table 4 provides the central deflection of the simply supported square plate using reduced/selected integration and the regular mesh of 16 $\times$ 16. It can be seen that, although it is not necessary for practical engineering, the current plate element with reduced/selected integration exhibits effective performance for thick-to-thin plates (locking-free to the thin limit of $h/L=0.0001\hbox {}$for both the quadratic and cubic shape functions).

Because the element MTPF with the cubic shape function exhibits an improved convergence rate and overall superior performance to that of the quadratic shape function, only the cubic shape function is studied in the following numerical examples.

In order to test the effect of the width-to-length ratio $\delta /l$ of the fictitious thin layer, the convergence of the simply supported square plate central deflection with different values of $\delta /l$ and an aspect ratio of $h/L=0.01$ is shown in Table 5, and the results indicate that the ratio $\delta /l$ has little effect on the MTPF accuracy when $\delta /l\le 0.001$.

4.2 Rectangular plate with center crack

A rectangular plate with a center crack is analyzed, as illustrated in Fig. 9. The width and length of the plate are $2b=1\hbox {m}$ and $2c=2\hbox {m}$, respectively, while the material properties are $E=1.0\hbox {E}6\,\hbox {MPa}$ and $v=0.3$. The crack size is 2a, and the plate thickness is h. The two edges parallel to the crack are simply supported, and moment M is applied to these, while the other two edges are free. Divisions of 2728 and 7338 triangular elements are employed for the computation of the rectangular plate SIFs. Figure 10 illustrates a discrete model of the rectangular plate with 1421 triangular elements. The numerical results for different a / h are presented in Table 6, along with reference solutions for comparison (Tanaka et al. 2015; Boduroglu and Erdogan 1983), where the SIF is normalized by $F_1 =\frac{h^{2}K_1 }{6M\sqrt{\pi a}}$. It is observed that high-accuracy SIF solutions are obtained for the current element MTPF.

Fig. 9

Analysis model of center crack plate

Fig. 10

Discrete model of center crack plate with 2728 triangular elements

Table 6 Normalized SIFs $F_1$ for center crack plate

4.3 Rectangular plate with symmetric edge cracks

As illustrated in Fig. 11, symmetric edge cracks in a rectangular plate are analyzed. The boundary conditions, geometry dimensions, and material properties are the same as those of the center crack problem described in Sect. 4.2. The crack size is a and the plate thickness is h. The discrete model with 2728 triangular elements shown in Fig. 10 is also employed for this problem. The numerical results for different d / b values are presented in Tables 7 and 8 for $b/h=2.0$ and 10.0. As expected, the results obtained using the current method coincide with the reference solutions (Tanaka et al. 2015; Boduroglu and Erdogan 1983) in all cases.

Fig. 11

Analysis model of symmetric edge cracks in square plate

Table 7 Normalized SIFs $F_1$ for symmetric edge crack problem ($b/h=2.0$)

Table 8 Normalized SIFs $F_1$ for symmetric edge crack problem ($b/h=10.0$)

Fig. 12

Analysis model for a single crack emanating from a hole

4.4 Single crack emanating from hole

A single crack emanating from a hole in a finite rectangular plate is analyzed, as shown in Fig. 12. The width and length of the plate are $2b=1\hbox {m}$ and $2c=2\hbox {m}$, respectively. The hole radius is $r=0.05\hbox {m}$, the crack size is a, and the plate thickness is h, while the material properties are $E=1.0\hbox {E}6\,\hbox {MPa}$ and $v=0.3$. The two edges parallel to the crack are simply supported, and moment M is applied to these, while the other two edges are free. Different ratios of a / b = 0.3–0.8 are analyzed, and a division of 3076 triangular elements is employed for the SIFs computation of the plate, as shown in Fig. 13. The numerical results for different b / h values are presented in Fig. 14, along with reference solutions for comparison (Dirgantara and Aliabadi 2002). It can be seen that the current results closely match the reference solutions.

Fig. 13

Discrete model for a single crack emanating from a hole

Fig. 14

Normalized SIFs for a single crack emanating from a hole

5 Conclusions

In this work, a new locking-free element MTPF is developed for the analysis of cracked thick–thin plates. The proposed MTPF has the following characteristics:

• (1) Without any numerical expediencies, such as reduced/selected integration, the use of assumed strain/stress, or the need for stabilization of the attendant zero energy modes, shear locking is completely eliminated to the thin limit of $h/L=0.0001$ for the MTPF with a cubic shape function, which is very useful and applicable for the analyses of various hick-thin plate types in practical engineering.

• (2) The MTPF has a very simple formulation as well as numerical implementation for including the transverse shear effects for thick plates. Furthermore, it exhibits an effective convergence rate, is insensitive to element distortions, and provides stable solutions for thick and thin plates.

• (3) The element MTPF can conveniently compute the crack tip SIFs by using the VCCT, which has a very simple formula derivation and numerical implementation. Numerical examples indicate that the element MTPF maintains high accuracy in the calculation of crack tip SIFs for cracked thick–thin plates.

• (4) The element MTPF uses a meshless approach and is independent of the nodes and triangle shape. Thus, similar to other meshless methods, the MTPF is easy and ready for automatic simulation of the failure process of a cracked plate along arbitrary directions by introducing an appropriate crack propagation criterion for the plates, and this will be the next work offered by the author.