1 Introduction

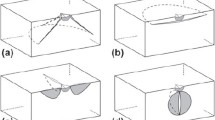
Since the early experimental work by H. Hertz at the end of the nineteenth century (and later named after him; see, e.g., Fischer-Cripps 2007; Lawn 1993) fracture caused by the compression of a hard indenter on the surface of a brittle solid has been subject to intense and ongoing experimental and theoretical studies. Besides of their beauty, the perfectly cone-shaped cracks produced in case of axisymmetric indenters (spherical or flat punch) have been of interest, for instance, as a means for determining the fracture toughness of brittle materials, particularly in the ceramics and glass community, e.g. Lawn (1998) and Kocer (2003). The evolution of these cracks proceeds essentially in two stages (Fig. 1):

  • the spontaneous formation of a ring crack (somewhat outside the contact region) which extends over a short length almost perpendicular from the surface towards the interior of the solid and

  • its subsequent stable propagation (i.e. with increasing load) as a cone-shaped crack of almost constant angle.

Both stages have been subject of numerous experimental and theoretical studies, and the propagation stage (with the angle of the evolving cone-crack being a major point of interest, e.g. Kocer and Collins 1998) meanwhile appears to be rather well understood. For instance, the experimentally observed dependence of the cone angle on Poisson’s ratio could be well reproduced using, e.g., finite element (Lawn et al. 1974), boundary element (Selvadurai 2000), weight function (Fett et al. 2004) and phase field (Strobl et al. 2016) methods. It also could be shown by means of numerical simulations—correcting earlier semi-analytical approaches solely based on the pre-fracture indentation stress field, e.g. Frank and Lawn (1967)—that it is necessary for properly computing the angle of crack propagation to account for changes of the stress field induced by the presence of the crack, e.g. Lawn et al. (1974).

Fig. 1
figure 1

Axisymmetric boundary value problem of isotropic half-space subjected to indentation by rigid cylindrical punch

Full size image

Less well understood, still to date, appears to be the initiation stage, i.e. the sudden formation of the cylindrical ring crack at some critical load. From a fracture mechanics point of view this is not surprising since, while the propagation of an existing crack in an isotropic brittle solid can reliably be predicted by established criteria (e.g. maximum energy release rate), crack formation lies beyond the scope of classical fracture hypotheses. Previous studies have tackled this shortcoming of classical fracture mechanics in the initiation phase of indentation fracture by two different ways of thought. It was either assumed the pre-existence of a statistical distribution of surface flaws of a certain size, e.g. Fischer-Cripps (1997), or the axial extension of the spontaneously formed ring crack was taken as a free parameter in an analysis involving crack propagation stability arguments, e.g. Mouginot and Maugis (1985) and Wang et al. (2008). A detailed discussion of these approaches is not aimed in the present work and may be found, for instance, in the review article (Kocer 2003). Yet, it should be mentioned that various researchers have conjectured a likelihood of the formation of shorter cracks closer to the contact region from the strong variation of the indentation stress field with distance from the indenter and depth from the free surface, e.g. Lawn et al. (1974), Mouginot and Maugis (1985) and Fischer-Cripps (1997). It was also emphasized the prerequisite of a sufficiently strong tensile loading acting on flaws of a certain size in order to cause fracture; a sound criterion, however, remained lacking.

The quest for the size of the crack (“critical flaw”) initially created in the course of indentation fracture can be solved by the concept of finite fracture mechanics (FFM). In the formulation by Leguillon (2002) it is based on a hybrid (two-part) fracture criterion that consists of an energetic and a stress statement and involves two well-defined material properties, i.e. strength and (fracture) toughness, e.g. Weissgraeber et al. (2016). Applied to indentation fracture initiation (in the present work apparently for the first time) FFM provides a unique determination of the size (axial length) and location (radius) of the spontaneously formed ring crack as well as the critical load. The dependence of these quantities on the indenter radius includes a size effect commonly referred to as Auerbach’s law in the literature on indentation fracture, e.g. Fischer-Cripps (2007), which is shown to be also captured by FFM.

The paper is organized as follows. Section 2 is devoted to the problem description, including the stress field in an isotropic linear elastic half-space caused by indentation loading as well as the formulation of the hybrid criterion of FFM in general. In Sect. 3 the application of this criterion to the present problem is discussed in detail; this involves a comparison of different (i.e. semi-analytical vs. numerical) ways of its evaluation. A quantitative analysis with a comparison to experimental results from the literature is subject of Sect. 4. Conclusions on the suggested and analyzed approach to indentation fracture initiation are finally discussed in Sect. 5.

2 Problem formulation

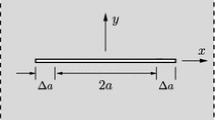
The problem investigated here is that of an isotropic linear elastic half-space with Young’s modulus E and Poisson’s ratio \(\nu \), subjected to indentation (normal) loading by a rigid cylindrical punch of radius a (Fig. 1). The contact between punch and half-space is assumed frictionless, and axisymmetry of the boundary value problem is exploited in the following. Loading is specified in terms of indenter force F or displacement d. With increasing load we consider—in accord with experimental observation—the formation of a ring-shaped cylindrical crack of some radius \(r_0 \ge a\) and length \(z_0\) (Fig. 1). The question to be analyzed here is when (i.e. at which critical load) and where (\(r_0\)) this spontaneous crack formation (of likewise unknown length \(z_0\)) takes place, while the subsequent cone crack growth is outside the scope of this study.

2.1 Indentation stress field

Analogous to previous work on the above problem, e.g. Fischer-Cripps (1997), Frank and Lawn (1967) and Mouginot and Maugis (1985), the stress field in an uncracked half-space under indentation loading plays a key role in the following analysis. While the complete axisymmetric stress and displacement field may be found, e.g., in the textbooks (Fischer-Cripps 2007; Kachanov et al. 2003) only those components relevant for the present work are briefly recapitulated here. For instance, the force F on the flat punch and its displacement d are related by

$$\begin{aligned} F = \frac{2Eda}{1-\nu ^2} . \end{aligned}$$
(1)

Due to linearity of the boundary value problem the radial stress can in a cylindrical coordinate system (Fig. 1) be written as

$$\begin{aligned} \sigma _r (r, z) = E \, \frac{d}{a} \, \psi \left( \frac{r}{a}, \frac{z}{a}, \nu \right) \end{aligned}$$
(2)

where \(\psi (...)\) is a dimensionless function. In particular, at the free surface \(z=0\) outside the contact area \(r > a\) the radial stress reads

$$\begin{aligned} \sigma _r (r, z=0) = \frac{E}{\pi } \, \frac{d}{a}\left( \frac{1-2\nu }{1-\nu ^2}\right) \left( \frac{a}{r} \right) ^2 . \end{aligned}$$
(3)

Note, that the variation of \( \sigma _r\) with the coordinates r and z as well as its dependence on the indenter displacement d in (2) and (3) scales with the indenter radius a which is prior to fracture the only characteristic length in the boundary value problem. According to (3) the radial stress at the free surface is positive (for \(\nu < 0.5\)) and thus understood to be responsible for the formation of the ring crack observed in experiments. Some details of the axisymmetric radial stress distribution outside the contact region (\(r \ge a\)) where crack initiation is expected are presented in Fig. 2 in terms of the dimensionless function \(\psi \) introduced in (2). Figure 2a shows the radial variation of the radial stress at the free surface (\(z=0\)) and at a small distance below (inside the half-space). It can be seen that, except for \(z=0\), a local stress maximum exists and that the stress level strongly depends on Poisson’s ratio with \(\sigma _r (r, z=0) = 0\) for \(\nu \rightarrow 0.5\) according to (3). The rapid decay of the radial stress with distance z from the free surface, especially close to the contact radius \(r=a\), is depicted in Fig. 2b. It should be noted that \(\sigma _r\) (\({\sim }\psi \)) decreases almost linearly with increasing z in the range where \(\sigma _r\) is positive; this fact will be exploited below (Sect. 3.2.1) in the semi-analytical calculation of the energy release rate.

Fig. 2
figure 2

Normalized radial stress: a versus r / a for different z / a,   b versus z / a for different r / a and \(\nu = 0.22\)

Full size image

2.2 Hybrid fracture initiation criterion

Indentation fracture initiation from a defect-free surface solely due to the presence of a stress concentration belongs to a class of problems not accessible to classical fracture mechanics which requires the pre-existence of a well established crack. Other examples from this class are crack initiation from holes or from sharp notches with finite opening angle; see, e.g., Gross and Seelig (2011). As a remedy and an alternative to the classical idea of infinitesimal crack growth controlled by a stress intensity factor or (equivalently) by the energy release rate, several researchers have suggested to instead consider the spontaneous formation of a crack of small, yet finite, length; e.g. Hashin (1996), Leguillon (2002), Taylor et al. (2005) and Weissgraeber et al. (2016). Bringing this approach, which is sometimes referred to as finite fracture mechanics (FFM), into a rigorous form Leguillon (2002) proposed a two-part fracture initiation criterion that involves two well-defined material parameters, the (tensile) strength \(\sigma _c\) and the specific (i.e. per area) fracture energy \(G_c\) (toughness). This hybrid criterion states that over the prospective finite crack increment a certain stress measure, typically the maximum principal stress \(\sigma _1\), as well as the released energy must exceed critical values. As a consequence, the criterion encompasses the two limiting cases of crack initiation at a well-defined pre-crack and crack formation in a uniform stress field (Gross and Seelig 2011). While a thorough discussion and various applications may be found in the recent review article (Weissgraeber et al. 2016), it is noteworthy with regard to the present work that the hybrid fracture criterion is also capable to predict size effects; see, e.g., Leguillon et al. (2007). In the context of indentation fracture, one such size effect manifests itself in the so-called Auerbach law (Sect. 4).

Following Leguillon (2002) we here assume that

$$\begin{aligned}&\sigma _1 \ge \sigma _c \quad \text {on entire crack} \; \varDelta A_c \nonumber \\&{and} \\&\bar{G} := - \frac{\varDelta \Pi }{\varDelta A_c} \ge G_c \nonumber \end{aligned}$$
(4)

must hold for a finite crack of area \(\varDelta A_c\) to form. That means that the maximum principal stress must exceed the tensile strength at every point of the hypothetical finite crack surface as well as the released energy per area of this crack must exceed the fracture toughness. The quantity \(\bar{G}\) in (4)\(_2\) is referred to as the average energy release rate in the following, and \(\Pi \) is the total potential energy. In an alternative version (see, e.g., Weissgraeber et al. 2016) the stress criterion may be satisfied only in the mean, i.e.

$$\begin{aligned} \bar{\sigma }_1 \ge \sigma _c \qquad \text {where} \qquad \bar{\sigma }_1 := \frac{1}{\varDelta A_c} \int \limits _0^{\varDelta A_c} \sigma _1 \, \mathrm{d} A. \end{aligned}$$
(5)

Fulfillment of both parts of the criterion generally determines the critical load for fracture initiation and—at the same time—the size, position and orientation of the finite crack increment.

3 Analysis of indentation fracture initiation

In applying the above hybrid criterion to the indentation problem (Fig. 1) in the following, we look for the minimum load in terms of indenter displacement d which satisfies both (i.e. stress and energy) parts for the same radius \(r_0\) and length \(z_0\) of the ring crack. This determines these geometric entities of spontaneous crack formation as well as the critical load at which it takes place. Based on experimental observations, the crack orientation thereby is assumed normal to the free surface (cylindrical crack), though this is a principal stress direction only at the free surface. In the following, both parts of the criterion are at first analyzed separately before they are combined in Sect. 3.3.

3.1 Stress criterion

In the stress criterion (4)\(_1\) or (5) we replace \(\sigma _1\) by the radial stress \(\sigma _r\) which at the free surface is indeed the maximum principal stress. From Fig. 2b it can be seen that \(\sigma _r\) decreases monotonically with increasing z at fixed r in the range where \(\sigma _r\) is positive. It is hence sufficient for satisfying the stress criterion (4)\(_1\) at some radius \(r=r_0\) that \(\sigma _r (r_0, z_0) \ge \sigma _c\) where \(z_0\) denotes the length of the fictitious ring crack measured from the free surface (\(z=0\)). Using the representation (2), the stress criterion (4)\(_1\) can be written as

$$\begin{aligned}&E \, \frac{d}{a} \, \psi \left( \frac{r_0}{a}, \frac{z_0}{a}, \nu \right) \, \ge \, \sigma _c \nonumber \\&\qquad \text {or}\\&\frac{d}{a} \, \ge \, \frac{\sigma _c}{\displaystyle E \, \psi \left( \frac{r_0}{a}, \frac{z_0}{a}, \nu \right) }.\nonumber \end{aligned}$$
(6)

Equality in (6)\(_2\) determines the load (indenter displacement) \(d_{\sigma } (r_0, z_0)\) necessary to form a cylindrical crack of length \(z_0\) at radius \(r_0\) according to the stress criterion. The dependence of \(d_{\sigma } \) on the radius \(r_0\) and the length \(z_0\) of the crack is shown in terms of the dimensionless quantity

$$\begin{aligned} d_{\sigma }^{*} := \frac{d_{\sigma } E}{a \, \sigma _c} = \psi ^{-1} \end{aligned}$$
(7)

in Fig. 3a. The analogous evaluation using \( \bar{\psi }^{-1} (\bar{\sigma }_1) \) based on the average stress criterion (5) is shown in Fig. 3b for the same set of crack lengths (\(z_0 /a\)). Both versions of the stress criterion yield qualitatively similar results and indicate that the critical load to cause fracture according to the stress criterion increases with increasing length of the fictitious crack. It should also be noted that the critical load as a function of crack radius \(r_0\) displays local minima well outside the contact region \(r=a\). The value of Poisson’s ratio \(\nu = 0.22\) is chosen here already in correspondence to real material data for borosilicate glass considered in Sect. 4. In the evaluation of the hybrid fracture criterion in Sect.’s 3.3 and 4 the stress criterion in the version (4)\(_1\) with results depicted in Fig. 3a will be used while the effect of utilizing the average stress criterion (5) is discussed in “Appendix 1”.

Fig. 3
figure 3

Dimensionless functions \( \psi ^{-1}\) (a) and \(\bar{\psi }^{-1}\) (b) for \(\nu = 0.22\)

Full size image

It should be mentioned that the idea of a critical tensile stress acting over the entire length of some (fictitious) flaw being necessary for initial ring crack formation was already suggested in Mouginot and Maugis (1985) as an explanation for the observation that the ring crack forms at some distance (\(r_0 > a\)) outside the contact region where the stress gradient (see, e.g., Fig. 2) is less severe.

3.2 Energy release criterion

In applying the energy criterion (4)\(_2\) to the present problem of indentation fracture we analyze two different approaches. Firstly (Sect. 3.2.1), we compute the energy release semi-analytically by imposing the fictitious ring crack to the pre-existing stress field (Sect. 2.1) in the uncracked half-space. Secondly (Sect. 3.2.2), in order to overcome (and study) the simplifying assumptions made in the semi-analytical approach, we perform detailed finite element analyses of the boundary value problem of the half-space including the ring crack (Fig. 1) and compute the energy release numerically.

3.2.1 Semi-analytical evaluation

Similar to earlier approaches, e.g. Frank and Lawn (1967), Mouginot and Maugis (1985) and Fischer-Cripps (1997), the calculation of the energy released by the formation of the ring crack is here based on the key assumption that the stress field prevailing in the uncracked half-space (Sect. 2.1) can be considered as an imposed external loading and is not altered by the presence of the crack. This allows to compute the mode I stress intensity factor approximately from the relation

$$\begin{aligned} K_I (z) = 2 \sqrt{\frac{z}{\pi }} \int \limits _0^z \frac{\sigma _r (\bar{z})}{\sqrt{z^2 - {\bar{z}}^2}} \, f(\bar{z}) \, \mathrm{d} \bar{z} \end{aligned}$$
(8)

where \(f(\bar{z}) \approx 1 + 0.3 (1 - \bar{z} / z)\) for a crack of length z emanating from a free surface and subjected to a spatially varying normal load \(\sigma _r (\bar{z})\), e.g. Tada et al. (2000). In earlier approaches (mentioned above) the factor \(f(\bar{z})\) is taken equal to 1 which corresponds to half an internal crack of length 2z, thus neglecting the effect of the free surface.

The average energy release rate for a crack of length \(z_0\) according to (4)\(_2\) is then computed as

$$\begin{aligned} \bar{G} (z_0) = \frac{1}{\varDelta A_c} \int \limits _0^{\varDelta A_c} G \, \mathrm{d} A = \frac{1-\nu ^2}{E} \, \frac{1}{z_0} \int \limits _0^{\displaystyle z_0} K_I^2 (z) \, \mathrm{d} z\nonumber \\ \end{aligned}$$
(9)

where \( G = - \, \mathrm{d} \Pi / \mathrm{d} A = K_I^2 (1-\nu ^2)/E \) is the standard energy release rate and \(\mathrm{d} A = 2 \pi r_0 \mathrm{d} z\) and \(\varDelta A_c = 2 \pi r_0 z_0\) are the increment of cylindrical crack area at radius \(r_0\) and the total crack area, respectively.

As depicted in Fig. 2b the radial stress decreases almost linearly with z from the surface value given by (3) to \(\sigma _r (z=z^{*}) =0\) at some depth \(z^{*} (r_0)\) which depends on the radial position \(r_0\). Exploiting this by approximating \(\sigma _r (z)\) by a linear function allows to evaluate the integrals in (8) and (9) in closed form and the average energy release rate can be written as

$$\begin{aligned} \bar{G} = E \, a \left( \frac{d}{a} \right) ^2 \phi _{ana} \left( \frac{r_0}{a}, \frac{z_0}{a}, \nu \right) \end{aligned}$$
(10)

where \(\phi _{ana} (...)\) is a dimensionless function. Only \(z^{*} (r_0)\) needs to be determined numerically. Results are shown in Fig. 5 along with those obtained from finite element analyses discussed in the following.

3.2.2 Numerical evaluation

The average energy release rate due to formation of the cylindrical ring crack (Fig. 1) can alternatively be calculated from the change of the total potential energy \(\Pi \) between the uncracked and the cracked configuration at the same load. With the latter specified in terms of prescribed indenter displacement d and due to linearity of the boundary value problem we have

$$\begin{aligned} \varDelta \Pi = \frac{d}{2} \, \varDelta F = \frac{d}{2} \, ( F_{crack} - F_0 ) \end{aligned}$$
(11)

where \(F_{crack}\) is the indentation force on the cracked half-space and \(F_0\) that on the uncracked half-space according to (1). In both (linear elastic) configurations the force is proportional to \(E, \, a\) and d so that \(F_{crack} = E \,a\, d\, \tilde{F}_{crack} (r_0/a, z_0/a, \nu ) \) and \( F_0 = E\, a \,d \,\tilde{F}_0 (\nu ) \) where \( \tilde{F}_{crack} (...) \) and \(\tilde{F}_0 (...)\) are dimensionless functions. The average energy release rate according to (4)\(_2\) can thus be written as

$$\begin{aligned} \bar{G}= & {} - \frac{\varDelta \Pi }{\varDelta A_c} \\= & {} \frac{E\,a}{4 \pi } \left( \frac{d}{a} \right) ^2 \frac{a^2}{r_0 \,z_0} \Bigg [ \tilde{F}_0 (\nu ) - \tilde{F}_{crack} \left( \frac{r_0}{a}, \frac{z_0}{a} , \nu \right) \Bigg ] \nonumber \end{aligned}$$
(12)

or in compact form analogous to (10) as

$$\begin{aligned} \bar{G} = E \, a \left( \frac{d}{a} \right) ^2 \phi _{num} \left( \frac{r_0}{a}, \frac{z_0}{a}, \nu \right) \end{aligned}$$
(13)

where \(\phi _{num} (...) \) is a dimensionless function to be determined numerically (e.g. by finite element analyses) from the force difference \(\varDelta F\) on the cracked and the uncracked half-space.

Fig. 4
figure 4

Axisymmetric finite element model with magnification of contact region

Full size image

For the numerical evaluation of the axisymmetric boundary value problem including the ring crack (Fig. 1), the finite element package ABAQUS 6.13 (ABAQUS 2013) was used and the half-space was approximated by a finite domain of height H and radius R. Some aspects of the model consisting of about \(10^5\) four-node linear displacement elements [type CAX4R (ABAQUS 2013)] are shown in Fig. 4. The discretization was highly refined in the region comprising the contact edge (\(r=a\)) and the ring crack (\(r=r_0 \ge a\)). There, a regular mesh was used (see Fig. 4 bottom) in order to accurately represent the crack by introducing double nodes over a length \(z_0\) extending perpendicular to the free surface. Generation of the variety of finite element meshes containing a thus modeled crack with a wide range of radii \(r_0\) and lengths \(z_0\) as well as the computations were automatized using Python scripting (Puri 2011). Frictionless loading by the indenter displacement d was modeled by prescribing constant vertical displacements to nodes inside the contact region (\(r \le a, z=0\)). Convergence studies were performed to ensure that numerical results were not affected by the finite domain size and a dimension of \(H = R = 100\,a\) was finally used in the simulations. Nevertheless, for consistency the indenter force \(F_0\) on the uncracked domain was—instead of using the analytical relation (1)—also computed numerically (using the same discretization as for the cracked domain, yet without double nodes).

Numerical results for the average energy release rate along with those from the semi-analytical approach (Sect. 3.2.1) are collectively shown in Fig. 5 in terms of the dimensionless functions \(\phi _{num}\) and \(\phi _{ana}\) introduced in (13) and (10), respectively. For clarity, results are depicted only for a small number of crack lengths (\(z_0/a\)) given in the figure caption. Obviously, the deviations between \(\phi _{num}\) and \( \phi _{ana}\) are rather small which indicates that the assumption made in the semi-analytical approach, that the presence of the ring crack does not much affect the pre-fracture indentation stress field, is not very severe. As expected, however, the deviations become larger for larger crack lengths. In this case the semi-analytical approach (employing the stress field unaffected by the crack) leads to a small overestimation of the energy release (see maxima of curves in Fig. 5). The local maxima in the energy release rate with respect to crack radius \(r_0\)—present for all crack lengths \(z_0\), yet at different \(r_0\)—indicates a propensity to crack formation at the respective radii.

Fig. 5
figure 5

Dimensionless measure \(\phi \) of average energy release rate computed from finite element analyses (num) and from semi-analytical approach (ana) for crack lengths \(z_0/a = \{0.005, 0.015, 0.035, 0.055, 0.075, 0.095, 0.115 \}\) and \(\nu = 0.22\)

Full size image

3.2.3 Critical load from energy criterion

With the average energy release rate given by (10) or (13) the energetic criterion \( \bar{G} \ge G_c \) in (4)\(_2\) can be written as

$$\begin{aligned} \frac{d}{a} \, \ge \, \sqrt{\displaystyle \frac{G_c}{\displaystyle E a \phi \left( \frac{r_0}{a}, \frac{z_0}{a}, \nu \right) } } . \end{aligned}$$
(14)

Equality in (14) determines the load (indenter displacement) \(d_{\pi } (r_0, z_0)\) necessary to form a cylindrical crack of length \(z_0\) at radius \(r_0\) according to the energy criterion. Analogous to (7) this critical load can be represented in dimensionless form as

$$\begin{aligned} d_{\pi }^{*} := \frac{d_{\pi } E}{a \, \sigma _c} = \sqrt{\frac{G_c \,E}{a \, \sigma _c^2}} \, \frac{1}{\sqrt{\phi }} . \end{aligned}$$
(15)

The dependence of this critical load on the radius \(r_0\) and the length \(z_0\) of the crack is shown in terms of the dimensionless quantity \(1/\sqrt{\phi }\) in Fig. 6. Note, that in view of the small difference between the semi-analytical and the numerical evaluation of the average energy release rate (Fig. 5) these are taken equal \(\phi _{ana} \approx \phi _{num}\) and \(\phi = \phi _{ana}\) is used in the following. From Fig. 6 it can be seen that the critical load to cause fracture according to energy criterion decreases with increasing length \(z_0\) of the fictitious crack (contrary to the effect of the stress criterion, Fig. 3) and that local minima of this critical load exist with respect to the crack radius \(r_0\).

Fig. 6
figure 6

Dimensionless function \(\phi ^{-1/2}\) for \(\nu = 0.22\)

Full size image

For typical values of the material parameters \(E, G_c\) and \(\sigma _c\) (see Sect. 4) and an indenter radius of \(a=1\) mm the pre-factor of \(1/\sqrt{\phi }\) in (15) is approximately \( \sqrt{G_c \,E / a \, \sigma _c^2}\, \approx 0.3 \). Considering this in conjunction with Fig. 6 and comparison with Fig. 3 indicates that the critical loads (indenter displacements normalized in the same way) according to the stress criterion and the energy criterion are of similar magnitude; a quantitative evaluation is subject of Sect. 4.

3.3 Combined (hybrid) criterion

The hybrid fracture initiation criterion (4) formulated by means of the critical indenter displacements \(d_{\sigma }\) and \(d_{\pi }\) satisfying the stress and the energy criterion, respectively, can be expressed as

$$\begin{aligned}&d_c \, = \, \min _{\{r_0,z_0\}} \; \max \,\left\{ \, d_{\sigma } (r_0, z_0), \,d_{\pi } (r_0, z_0)\right\} \end{aligned}$$
(16)

where \(d_c\) is the indenter displacement that actually causes fracture. By taking the maximum of \(d_{\sigma }\) and \(d_{\pi }\) in (16) it is guaranteed that both criteria are fulfilled, while minimizing over the whole range of \(r_0\) and \(z_0\) determines the critical load as well as the radius and the length of the crack.

Prior to a quantitative evaluation of the criterion for real material data and a comparison with experiments in Sect. 4, it appears worthwhile to look at the mode of operation of the hybrid criterion in principle when applied to the present situation of indentation fracture. Therefore, we write (16) in dimensionless form [analogous to (7) and (15)]

$$\begin{aligned}&d_c^{*} := \frac{d_c E}{a \, \sigma _c} \, = \, \min _{\{r_0,z_0\}} \; \max \left\{ \frac{1}{\psi }, \underbrace{\sqrt{\frac{G_c \,E}{a \, \sigma _c^2}}}_{\displaystyle \sqrt{l_c / a\, \varepsilon _c}} \; \frac{1}{\sqrt{\phi }} \right\} \nonumber \\ \end{aligned}$$
(17)

where \(\psi \) and \(\phi \) depend only on \(r_0/a , \,z_0/a\) and \(\nu \). The characteristic length \(l_c := G_c / \sigma _c\) introduced in (17) can be taken as a measure of toughness while \(\varepsilon _c := \sigma _c/E\) is a measure of strength, so that the dimensionless parameter \(\sqrt{l_c / a\, \varepsilon _c}\) can be interpreted as the ratio of toughness to strength for a certain indenter radius a. The normalized critical load \(d_c^{*}\) hence depends on material properties and indenter geometry only through the parameter \(\sqrt{l_c / a\, \varepsilon _c}\).

It also seems instructive to look at the ratio of critical loads according to the energy and stress criteria

$$\begin{aligned} \frac{d_{\pi }}{d_{\sigma }} = \sqrt{\frac{l_c}{a\, \varepsilon _c}} \; \frac{\psi }{\sqrt{\phi }} \left( \frac{r_0}{a}, \frac{z_0}{a}, \nu \right) \end{aligned}$$
(18)

which determines the range in which either of the two criteria controls crack initiation. For \(d_{\pi }/d_{\sigma } > 1\) the energy criterion is dominant (and vice versa) so that relation (18) predicts for larger values of \(\sqrt{l_c / a\, \varepsilon _c}\) (toughness/strength) a stronger influence of the energy criterion—as expected. In addition, for fixed material properties the energy criterion is favored by smaller indenter radii a. The ratio \(d_{\pi } / d_{\sigma }\) of critical loads vs. crack radius \(r_0/a\) shown in Fig. 7 for various crack lengths \(z_0/a\) indicates that at a fixed crack radius the formation of short cracks is more prone to be controlled by the energy criterion (\(d_{\pi }/d_{\sigma } > 1\)) whereas longer cracks are likely to be controlled by the stress criterion (\(d_{\pi }/d_{\sigma } < 1\)).

Fig. 7
figure 7

Ratio of critical loads \(d_{\pi }/d_{\sigma }\) from energy and stress criterion for \(\sqrt{l_c / a\, \varepsilon _c} = 0.3\) and \(\nu = 0.22\)

Full size image

The application of the hybrid fracture criterion in principle is illustrated in the following by considering for clarity a limited set of only three different crack lengths \(z_0/a = \{0.02, 0.05, 0.08\}\), whereas its exact evaluation in Sect. 4 involves a continuous variation of \(z_0/a\) over a wide range. Figure 8 shows the normalized critical loads (indenter displacements) according to the stress criterion (dashed lines) and the energy criterion (solid lines) separately for values of \(\sqrt{l_c / a\, \varepsilon _c} = 0.3\) (Fig. 8a) and \(\sqrt{l_c / a\, \varepsilon _c} = 0.6\) (Fig. 8b). Points A (\(z_0/a=0.02)\), B (\(z_0/a=0.05)\) and C (\(z_0/a=0.08)\) in Fig. 8a indicate the minimum load by which both criteria are satisfied for each of the crack lengths considered here. They also determine the corresponding radius \(r_0/a\) of the ring crack. Among the three crack lengths considered in Fig. 8a the lowest critical load is found for \(z_0/a = 0.05\) (point B). That means that according to the hybrid fracture criterion, crack initiation would take place by the formation of a crack of length \(z_0 = 0.05\,a\) and radius \(r_0 \approx 1.3\,a\), i.e. well outside the punch contact zone (\(r=a\)) which is in qualitative agreement with experimental observations (as mentioned in the Introduction, see Fig. 1). Note, that in case of the two longer cracks (\(z_0/a = 0.05, \, 0.08\)) considered in Fig. 8a the critical loads (points B and C) are found at intersection points of the \(d_{\sigma }^{*}\)- and \(d_{\pi }^{*}\)-curves (there having slopes of different sign) whereas the critical load in case of the shorter crack (\(z_0/a = 0.02\)) is found at a local minimum of the \(d_{\pi }^{*}\)-curve (point A). At this latter point the stress criterion is clearly over-satisfied and crack initiation hence would be controlled solely by the energy criterion, while intersection of the \(d_{\sigma }^{*}\)- and \(d_{\pi }^{*}\)-curves means that both criteria are active.

Fig. 8
figure 8

Normalized critical loads (indenter displacements) from stress (dashed lines) and energy (solid lines) criterion for a \(\sqrt{l_c / a\, \varepsilon _c} = 0.3\) and b \(\sqrt{l_c / a\, \varepsilon _c} = 0.6 \);   (\(\nu = 0.22\))

Full size image

Increasing the parameter \(\sqrt{l_c / a\, \varepsilon _c} \) from 0.3 to 0.6 leads to the situation depicted in Fig. 8b where now the minimum critical load (indicated by the arrow) is found for the largest of the three considered crack lengths (again at the intersection point of the \(d_{\sigma }^{*}\)- and \(d_{\pi }^{*}\)-curves). Comparison of Fig. 8a, b shows that increasing the parameter \(\sqrt{l_c / a\, \varepsilon _c} \) leads to ring crack formation with a larger (normalized) radius \(r_0/a\) and length \(z_0/a\) at higher critical loads.

4 Comparison with experiments

For a quantitative evaluation of the hybrid fracture initiation criterion we adopt material data for borosilicate glass from Mouginot and Maugis (1985) where indentation fracture tests are reported for a wide range of indenter radii. The provided material data are \(E=80\) GPa, \(\nu =0.22\) and \(G_c \approx 9\) J/m\(^2\). The fracture strength \(\sigma _c\) of glass is not considered in Mouginot and Maugis (1985) and is generally known to be rather unclear. For that reason the range of \(\sigma _c\) values between 50 and 150 MPa (Lawn 1993) is considered in the following.

The critical load in terms of normalized indenter displacement \(d_c / a\) thus computed from the criterion (16) is depicted in Fig. 9 as a function of indenter radius a. Obviously, the fracture strength \(\sigma _c\) becomes irrelevant for small indenter radii (\(a \le 0.5\) mm), i.e. in the range where solely the energetic criterion controls fracture initiation as discussed above. This can also be anticipated from (17) resolved for \(d_c/a\) where \(\sigma _c\) cancels out when the energy criterion (\(\phi ^{-1/2}\)-term) is dominant.

Fig. 9
figure 9

Variation of normalized critical indenter displacement \(d_c\) with indenter radius a

Full size image

In Fig. 10 the normalized radius \(r_0/a\) and length \(z_0/a\) of the ring crack predicted from (16) are shown as functions of the indenter radius a. Both quantities decrease with increasing indenter radius. This means that indenters with a larger radius give rise to the formation of (relatively) shorter cracks closer to the contact edge (\(r=a\)) which is in qualitative agreement with experimental observations, e.g. Mouginot and Maugis (1985) and Chai (2006). For a quantitative comparison, experimental data from Mouginot and Maugis (1985) are included in Fig. 10a. Deviations between those and the predicted values have to be seen in the light of various idealizations made in the present analysis as well as the scatter in the experimental data (Fig. 19 in Mouginot and Maugis 1985). Rather striking, however, is the predicted “saturation” value of \(r_0/a \approx 1.35\) for very small indenter radii which underestimates the experimental data in Mouginot and Maugis (1985) where \(r_0/a \) is found to increase monotonically with decreasing indenter radii.

Fig. 10
figure 10

Variation of a normalized crack radius \(r_0/a\) and b normalized crack length \(z_0/a\) with indenter radius a. Experimental findings from Mouginot and Maugis (1985) are indicated by symbols (filled circle)

Full size image

This saturation regime for small indenter radii—also seen in Fig. 10b in terms of the relative crack length \(z_0/a\) and even more pronounced when the average stress criterion (5) is employed as depicted in Fig. 13 of “Appendix 1”—appears to be an artifact of the hybrid fracture criterion applied here. It corresponds to the range where crack initiation is solely controlled by the energy criterion (with the stress criterion oversatisfied), while otherwise both criteria are active. The critical load, when solely determined by the energy criterion, displays a local minimum with respect to the relative crack radius and length (local maximum of \(\phi (r_0/a, z_0/a, \nu )\), Fig. 5) at \(r_0/a \approx 1.35\) and \(z_0/a \approx 0.08\) (also discussed in conjunction with Fig. 8). These are the saturation values seen in Fig. 10 which depend only on Poisson’s ratio \(\nu \). A change of the indenter radius a or of material parameters (except \(\nu \)) in this regime only affects the critical load \(d_c\) but not the “optimal” values of \(r_0/a\) and \(z_0/a \).

Fig. 11
figure 11

Variation of apparent critical load \(F_c / a^{3/2}\) with indenter radius a. Experimental findings from Mouginot and Maugis (1985) are indicated by symbols (filled circle)

Full size image

A measure for comparison of critical loads obtained from theoretical and experimental analyses is suggested by the experimental findings of F. Auerbach (see, e.g., Fischer-Cripps 2007) who shortly after Hertz stated that the critical force to initiate indentation fracture is approximately proportional to the radius \(\rho \) of the (at that time used) spherical indenter, i.e. \(F_c \sim \rho \). As calculated by Hertz (see, e.g., Fischer-Cripps 2007) the contact radius a in case of a spherical indenter scales with the radius \(\rho \) of the latter and the indentation force according to \( a \sim (F \rho / E)^{1/3}\). Thus the critical load in Auerbach’s experiments scales with the contact radius as \( F_c \sim a^{3/2}\). In the (experimental) literature hence the range of indenter radii where \(F_c / a^{3/2} \approx const.\) is referred to as the Auerbach range, e.g. Fischer-Cripps (2007). Using this measure of apparent critical load, results obtained from the hybrid fracture criterion (16) are depicted in Fig. 11 as a function of indenter radius a. Note, that in case of the cylindrical flat punch considered here (Fig. 1) the indenter radius is identical to the contact radius in the above considerations, and that the stress fields outside the contact zone due to spherical or flat indentation are very similar, e.g. Fischer-Cripps (2007). Also included in Fig. 11 are experimental data from Mouginot and Maugis (1985) which (see Fig. 21 in the original paper) display some amount of scatter. The stationary value of about 70 MN/m\(^{3/2}\) in Fig. 11 predicted for small indenter radii is in reasonable quantitative agreement with the experimental findings. This range of constant \(F_c / a^{3/2}\) which here extends up to 0.5 or 1 mm (depending on the fracture strength \(\sigma _c\)) corresponds to the above mentioned Auerbach range. Also well predicted according to Fig. 11 is the increase of the apparent critical load to about 100 MN/m\(^{3/2}\) and above for larger indenter radii up to \(a=2.5\) mm. With regard to experimentally observed critical loads causing indentation fracture it should be noted that some amount of uncertainty also arises from the load increase between the onset of fracture and its complete encirclement of the contact area as reported in Chai (2006).

5 Conclusions

The present study illustrates that the concept of finite fracture mechanics (in the format suggested by Leguillon 2002) is a reasonable tool for analyzing the problem of Hertzian indentation fracture initiation. Using a hybrid fracture criterion comprising a strength (stress) and a toughness (energy) condition it is hence possible to reproduce experimental findings without any assumptions beyond the material properties “stiffness” (\(E, \nu \)), “strength” (\(\sigma _c\)) and “fracture toughness” (\(G_c\)). In particular, the experimentally observed dependence of the critical load as well as the crack location (radius) on the indenter radius could be qualitatively and—to some extent—also quantitatively be reproduced. This comprises the size effect commonly referred to as Auerbach’s law. Quantitative deviations from experimental findings have to be seen in the light of various assumptions made in the theoretical analysis. For instance, indentation was idealized as frictionless with a rigid and perfectly sharp-edged punch; effects of rounded indenter edges and friction on the indentation stress field have been examined, e.g., in Ciavarella et al. (1998). Interestingly, it has turned out that application of the hybrid (two-part) criterion of finite fracture mechanics to indentation fracture gives rise to two regimes: one in which both the stress and the energy criterion are active, and a second regime where only the energy criterion is active while the stress criterion is oversatisfied. The existence of two regimes with respect to the dependence of the critical load on the indenter radius has experimentally been shown already by Tillett (1956). However, its relation to the two regimes predicted by the present theoretical analysis is not yet fully understood.

The comparison of the semi-analytical determination of the average energy release rate with its numerical computation from detailed finite element simulations has shown (see Fig. 5, \(\phi _{num} \approx \phi _{ana}\)) that the simplification of using the pre-fracture indentation stress field for analyzing the initial ring crack formation (similarly made also in earlier analyses, e.g. Mouginot and Maugis 1985; Fischer-Cripps 1997) is not very severe. However, during subsequent cone crack propagation the alteration of the initial indentation stress field by the presence of the crack is known to much stronger and needs to be accounted for, e.g. Lawn et al. (1974).

With regard to the application of the concept of finite fracture mechanics in general, it appears noteworthy that the assumption of finite crack formation (or extension) yields results which depend on the “type” of loading, i.e. prescribed force or displacement. While in case of (“classical”) infinitesimal crack advance the type of loading enters only in the analysis of crack propagation stability, this issue is anticipated in FFM by the assumed finite crack extension. This effect has tacitly been neglected in the evaluation of the average energy release rate \(\bar{G}\) in the present work by utilizing the pre-fracture stress field in the semi-analytical approach and by considering only the case of prescribed indenter displacement in the numerical analysis. As briefly worked out in “Appendix 2” the average energy release rate of FFM is generally larger when a prescribed force is considered than in case of a prescribed displacement.