Virtual crack closure technique for an interface crack between two transversely isotropic materials

Abstract

The virtual crack closure technique makes use of the forces ahead of the crack tip and the displacement jumps on the crack faces directly behind the crack tip to obtain the energy release rates ${{\mathcal {G}}}_I$ and ${\mathcal {G}}_{II}$. The method was initially developed for cracks in linear elastic, homogeneous and isotropic material and for four noded elements. The method was extended to eight noded and quarter-point elements, as well as bimaterial cracks. For bimaterial cracks, it was shown that ${\mathcal {G}}_I$ and ${\mathcal {G}}_{II}$ depend upon the virtual crack extension $\varDelta a$. Recently, equations were redeveloped for a crack along an interface between two dissimilar linear elastic, homogeneous and isotropic materials. The stress intensity factors were shown to be independent of $\varDelta a$. For a better approximation of the Irwin crack closure integral, use of many small elements as part of the virtual crack extension was suggested. In this investigation, the equations for an interface crack between two dissimilar linear elastic, homogeneous and transversely isotropic materials are derived. Auxiliary parameters are used to prescribe an optimal number of elements to be included in the virtual crack extension. In addition, in previous papers, use of elements smaller than the interpenetration zone were rejected. In this study, it is shown that these elements may, indeed, be used.

1 Introduction

Initial assumptions for the Virtual Crack Closure Technique were made by Rybicki and Kanninen (1977). Using those assumptions, Raju (1987) presented a mathematical derivation for this method. While Rybicki and Kanninen (1977) proposed the method for four noded elements, Raju (1987) developed it for higher order elements, including eight noded and quarter-point elements. For the mathematical derivation, Raju (1987) used the Irwin (1958) crack closure integral which is given as

$$\begin{aligned} {\mathcal {G}}= & {} \displaystyle \lim _{\varDelta a \rightarrow 0} \frac{1}{\varDelta a} \int _0^{\varDelta a} \left[ \sigma _{yy}(\varDelta a - r) u_y(r) \right. \nonumber \\&\left. +\, \sigma _{yx}(\varDelta a - r)u_x(r) \right] dr \end{aligned}$$

(1)

Fig. 1

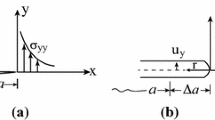
a Crack of length a and b crack of length $a + \varDelta a$ (from Banks-Sills and Farkash 2016)

Fig. 2

The forces and displacement jumps used for calculating ${\mathcal {G}}_{I}$ with an eight noded element

in two dimensions. In Eq. (1), $\sigma _{yy}$ and $\sigma _{yx}$ are the tensile and shear stresses, respectively, ahead of the crack tip. The tensile stress $\sigma _{yy}$ is shown in Fig. 1a. The sliding and opening displacements are denoted as $u_{x}$ and $u_{y}$, respectively; $u_{y}$ is shown in Fig. 1b. Note that r is the radial coordinate emanating from the crack tip whose length is $a + \varDelta a$, as shown in Fig. 1b. The first and second integrals in Eq. (1) are, respectively, the modes I and II energy release rates, ${\mathcal {G}}_{I}$ and ${\mathcal {G}}_{II}$. Raju (1987) derived the VCCT equations using expression for the traction ahead of the crack tip and for the crack face displacements, that depend upon element type. These were substituted into the Irwin crack closure integral in Eq. (1). While Rybicki and Kanninen (1977) suggested carrying out one finite element analysis for a crack of length $a+\varDelta {a}$, Raju (1987) suggested carrying out one analysis using a crack of length a. The equation for the mode I energy release rate, using a finite element formulation with an eight noded element, is given by

$$\begin{aligned} {\mathcal {G}}_{I} = \frac{1}{2\varDelta a} \sum _{m = 1}^{2} F_{ym} \varDelta u_{ym'}. \end{aligned}$$

(2)

In Eq.( 2), the virtual crack extension $\varDelta a$ is defined as the length of the element ahead of the crack tip, as shown in Fig. 2. It may be noted that the length of the element behind the crack tip must be identical for this formulation. The forces $F_{y1}$ and $F_{y2}$, are the nodal forces in the y-direction at nodes 1 and 2, respectively, as shown in Fig. 2; $\varDelta u_{y1'}$ and $\varDelta u_{y2'}$ are the crack opening displacements at nodes $1'$ and $2'$, respectively, also shown in Fig. 2. To calculate ${\mathcal {G}}_{II}$, y is replaced with x in Eq. (2).

The VCCT was first extended to interface cracks between two dissimilar isotropic media by Sun and Jih (1987). A literature survey on this subject was presented in Banks-Sills and Farkash (2016). For completeness, it may be noted that the energy release rates ${\mathcal {G}}_I$ and ${\mathcal {G}}_{II}$ have been shown to oscillate as the virtual crack extension $\varDelta a$ is varied. Since this investigation deals with an interface crack between two dissimilar anisotropic media, a few words will be devoted to these studies. Raju et al. (1988) investigated an edge crack along an interface in a laminate composed of two dissimilar monoclinic materials. The energy release rates were shown to depend upon $\varepsilon$ and $\varDelta a$ as $e^{ \pm 2i\varepsilon ln \varDelta a}$. Sun and Manoharan (1989) presented the same dependency for interface cracks between two orthotropic materials. Other anisotropic material pairs were considered by Chow and Atluri (1995), Beuth (1996) and Hemanth et al. (2005).

Banks-Sills and Farkash (2016) derived new and simpler equations for an interface crack between two dissimilar isotropic materials. Two pairs of stress intensity factors were determined. To obtain a unique solution, it was postulated that the crack faces are open. The suggestion of Beuth (1996) and Oneida et al. (2015) to use a virtual crack extension consisting of many elements was adopted. Choice of an optimal number of elements was determined by means of two auxiliary parameters. This paper is an extension of the investigation presented by Banks-Sills and Farkash (2016). Here, an interface crack is located between two dissimilar transversely isotropic materials.

In Sect. 2, the basic concepts related to an interface crack between two transversely isotropic materials are presented. The basic equations for this interface crack are presented in Sect. 2.1. In Sect. 2.2, an expression for calculating the length of the interpenetration zone is derived. This phenomenon was also considered in Toya (1992), Sun and Qian (1997), Hemanth et al. (2005) and Agrawal and Karlsson (2006). In Toya (1992) and Sun and Qian (1997), it was pointed out that $\varDelta a$ should be larger than the interpenetration zone. In this study, this proposal is questioned. In Sect. 3, expressions for calculating the stress intensity factors for two transversely isotropic materials, by means of the VCCT are rederived following Banks-Sills and Farkash (2016). One problem is described for three different sets of applied tractions in Sect. 4. Numerical results are presented there, as well. In Sect. 5, a discussion and conclusions will be presented.

Fig. 3

Interface crack between two dissimilar linear elastic, transversely isotropic and homogeneous materials

2 Interface crack

The basic concepts for an interface crack between two dissimilar transversely isotropic materials as shown in Fig. 3, are presented in this section. The upper material is a unidirectional composite with fibers in the x-direction; therefore, $x=0$ is a symmetry plane. The lower material is a unidirectional composite with fibers in the z-direction; therefore, $z=0$ is a symmetry plane. Moreover, for the derivation, conditions of plane deformation were assumed. Each of these materials is transversely isotropic and, hence, described by five independent effective elastic constants. For the upper material, the constants are $E_A$ and $E_T$, the Young’s moduli in the axial and transverse directions, respectively; $\nu _A$ and $\nu _T$ are the Poisson’s ratios in the axial and transverse directions, respectively; and the axial shear modulus is $G_A$. The transverse shear modulus is given by

$$\begin{aligned} G_T = \frac{E_T}{2 (1+\nu _T)}. \end{aligned}$$

(3)

The upper and lower material are the same; the lower material is rotated by $90^\circ$ with respect to the y-axis shown in Fig. 3.

2.1 Equations for an interface crack between two dissimilar transversely isotropic media

In this section, the analytical development follows Banks-Sills and Boniface (2000) which relies on the Stroh (1958) and Lekhnitskii (1950,1963) formalisms. The in-plane stresses in the neighborhood of the crack tip for an interface between two orthotropic materials are given by

$$\begin{aligned} _k\sigma _{\alpha \beta }= & {} \frac{1}{\sqrt{2 \pi r}} \left[ \mathfrak {R}\left( K r^{i \varepsilon }\right) {}_{k}{\!\mathrm {\Sigma }}_{\alpha \beta }^{(1)} (\theta )\right. \nonumber \\&\left. +\,\mathfrak {I}\left( K r^{i \varepsilon }\right) {}_{k}{\!\mathrm {\Sigma }}_{\alpha \beta }^{(2)} (\theta )\right] \end{aligned}$$

(4)

where $k=1,2$ denotes the upper and the lower materials, respectively, as shown in Fig. 3; $\alpha ,\beta =1,2$ represent polar or Cartesian coordinates; $\mathfrak {R}$ and $\mathfrak {I}$ represent the real and imaginary parts of the expression in parentheses, respectively; K is the complex stress intensity factor and is given by

$$\begin{aligned} K = K_1 + i K_2 \end{aligned}$$

(5)

In Eq. (5), $i = \sqrt{-1}$ and $K_1$ and $K_2$ are the real and imaginary parts of K. The stress functions $_k\mathrm {\Sigma }_{\alpha \beta }^{(1)}(\theta )$ and $_k\mathrm {\Sigma }_{\alpha \beta }^{(2)}(\theta )$ are known functions of $\theta$ and the mechanical properties which are referred to $\mathfrak {R}\left( K r^{i \varepsilon }\right)$ and $\mathfrak {I}\left( K r^{i \varepsilon }\right)$, respectively. The oscillatory parameter is given by

$$\begin{aligned} \varepsilon = \frac{1}{2\pi } \ln \left( \frac{1+\beta }{1-\beta }\right) \end{aligned}$$

(6)

where

$$\begin{aligned} \beta = \left[ -\frac{1}{2}tr\left( \breve{\mathbf {S}}\right) ^2\right] ^{1/2}. \end{aligned}$$

(7)

In Eq. (7), the matrix $\breve{\mathbf {S}}$ is given by

$$\begin{aligned}&\breve{\mathbf {S}} = \mathbf {D}^{-1}\mathbf {W}, \end{aligned}$$

(8)

$$\begin{aligned}&\mathbf {D} = \mathbf {L}^{-1}_1+\mathbf {L}^{-1}_2, \end{aligned}$$

(9)

$$\begin{aligned}&\mathbf {W} = \mathbf {S}_1\mathbf {L}^{-1}_1- \mathbf {S}_2\mathbf {L}^{-1}_2. \end{aligned}$$

(10)

For two orthotropic materials $\mathbf {D}$ and $\mathbf {W}$ will be different from those presented here for two transversely isotropic materials. In Eqs. (9) and  (10), the subscripts 1 and 2 represents the upper and the lower material, respectively. The second rank tensors $\mathbf {S}_k$ and $\mathbf {L}_k$, are real, and may be calculated using four $3\times 3$ matrices $\mathbf {A}_k$ and $\mathbf {B}_k$, where $k=1,2$. For the upper material, explicit expressions for $\mathbf {A}_1$ and $\mathbf {B}_1$ may be found in Appendix 1 of Banks-Sills and Boniface (2000). Using the relation

$$\begin{aligned} -\mathbf {A}_k \mathbf {B}^{-1}_k= \mathbf {S}_k\mathbf {L}^{-1}_k+i\mathbf {L}^{-1}_k \end{aligned}$$

(11)

for $k=1$, one may determine $\mathbf {S}_1\mathbf {L}^{-1}_1$ and $\mathbf {L}^{-1}_1$, since the left hand side of Eq. (11) is known. Note that in Eq. (11), there is no sum on k. The lower material is mathematically degenerate. In order to obtain $\mathbf {A}_2 \mathbf {B}^{-1}_2$, for the lower material, further development was required, since the matrix $\mathbf {B}^{-1}_2$ is singular. In this case, one may define two new matrices $\mathbf {A}_2'$ and $\mathbf {B}'^{-1}_2$ such that

$$\begin{aligned} \mathbf {A}_2 \mathbf {B}^{-1}_2= \mathbf {A}_2' \mathbf {B}'^{-1}_2. \end{aligned}$$

(12)

The matrices $\mathbf {A}_2'$ and $\mathbf {B}'^{-1}_2$ may be found in Appendix 1 of Banks-Sills and Boniface (2000). By means of Eqs. (11) and (12), explicit expression for $\mathbf {S}_2 \mathbf {L}^{-1}_2$ and $\mathbf {L}^{-1}_2$ are obtained. These expressions are substituted into Eqs. (9) and (10) to determine $\mathbf {W}$, $\mathbf {D}$ and $\breve{\mathbf {S}}$ in Eq. (8).

For plane deformation, the tractions along the interface ahead of the crack tip are given by

$$\begin{aligned} \left. \left( \sqrt{\frac{D_{11}}{{D_{22}}}}\sigma _{yy} + i \sigma _{yx}\right) \right| _{\theta = 0} = \frac{K x^{i \varepsilon }}{\sqrt{2 \pi x}}. \end{aligned}$$

(13)

In Eq. (13), K is given in Eq. (5) and the x-coordinate is shown in Fig. 3. The crack face displacement jumps in the neighborhood of the crack tip are given by

$$\begin{aligned} \sqrt{\frac{D_{11}}{{D_{22}}}}\varDelta u_y + i \varDelta u_x= & {} \frac{2 D_{11}}{(1 + 2i\varepsilon ) \cosh \pi \varepsilon }\nonumber \\&\times \,\sqrt{\frac{\varDelta a - x}{2 \pi }} \, (\varDelta a - x)^{i\varepsilon } K .\nonumber \\ \end{aligned}$$

(14)

In Eqs. (13) and (14), the parameters $D_{11}$ and $D_{22}$ are components of the matrix $\mathbf {D}$ in Eq.( 9) and are given by

$$\begin{aligned} D_{11}= & {} \frac{\beta _1+\beta _2}{E_A}\left( 1-\nu ^2_A \frac{E_T}{E_A}\right) +\frac{1+2\kappa }{4 G_T} \,, \end{aligned}$$

(15)

$$\begin{aligned} D_{22}= & {} \frac{\beta _1 \beta _2(\beta _1+\beta _2)}{E_A}\left( 1-\nu ^2_A \frac{E_T}{E_A}\right) +\frac{1+2\kappa }{4 G_T} .\nonumber \\ \end{aligned}$$

(16)

The complex eigenvalues of the compatibility equations $p_j$ of the upper material are given by

$$\begin{aligned} p_j=i\beta _j \quad \quad \quad (j=1,2,3) \end{aligned}$$

(17)

(see Banks-Sills and Boniface 2000); so that the real parameters $\beta _j$ in Eqs. (15) and (16) are known. The parameter $\kappa$ is given by

$$\begin{aligned} \kappa = \frac{3-\nu _T-\nu ^2_A E_T/E_A}{2(1+\nu _T)} \,. \end{aligned}$$

(18)

The interface energy release rate ${\mathcal {G}}_i$ is related to the the stress intensity factors by

$$\begin{aligned} {\mathcal {G}}_i = \frac{1}{H_1}\left( K_1^2 + K_2^2\right) \end{aligned}$$

(19)

where the subscript i represents interface and

$$\begin{aligned} \frac{1}{H_1} = \frac{D_{11}}{4 \cosh ^2\pi \varepsilon }. \end{aligned}$$

(20)

The energy release rate for an interface crack may be calculated from Irwin’s crack closure integral in Eq. (1). The interface energy release rate is also the sum of the energy release rates from modes I and II, namely

$$\begin{aligned} {\mathcal {G}}_i = {\mathcal {G}}_{I} + {\mathcal {G}}_{II} \;. \end{aligned}$$

(21)

A mode mixity or phase angle may be defined as

$$\begin{aligned} \psi \equiv \tan ^{-1} \left( \frac{K_2}{K_1}\right) \;. \end{aligned}$$

(22)

A normalized stress intensity factor may be written as

$$\begin{aligned} \hat{K} = K\hat{L}^{i\varepsilon } \end{aligned}$$

(23)

where $\hat{L}$ is an arbitrary length scale. Thus,

$$\begin{aligned} \hat{K}=|K|e^{i\hat{\psi }} \end{aligned}$$

(24)

where it is possible to define another phase angle

$$\begin{aligned} \hat{\psi } = \tan ^{-1} \left[ \frac{\mathfrak {I}(K \hat{L}^{i\varepsilon })}{\mathfrak {R}(K \hat{L}^{i\varepsilon })}\right] . \end{aligned}$$

(25)

2.2 Interpenetration zone

Using the method presented in Rice (1988), one may derive an expression for the length of the interpenetration zone for an interface crack between two transversely isotropic materials. Taking the real part of Eq. (14), one may write

$$\begin{aligned} \varDelta u_y = \tilde{C} \sqrt{r}\mathfrak {R}\left[ \frac{K}{1 + 2i\varepsilon }r^{i\varepsilon }\right] \end{aligned}$$

(26)

where $\tilde{C}$ is a constant and r has been substituted for $\varDelta a-x$ in Eq. (14). Solving Eq. (23) for K and substituting Eq. (24) into it, leads to

$$\begin{aligned} K=|K|\hat{L}^{-i\varepsilon }e^{i\hat{\psi }}. \end{aligned}$$

(27)

Use of Eq. (27) in (26) yields

$$\begin{aligned} \mathfrak {R}\left[ \frac{K}{1 + 2i\varepsilon }r^{i\varepsilon }\right]= & {} \frac{|K|}{1 + 4\varepsilon ^2} \cos \left[ \hat{\psi }+\varepsilon \ln \left( \frac{r}{\hat{L}}\right) \right. \nonumber \\&\left. -\tan ^{-1}2\varepsilon \right] \;. \end{aligned}$$

(28)

In order to determine $r_c$, the length of the interpenetration zone, one may require $\varDelta u_y=0$; thus,

$$\begin{aligned} \cos \left[ \hat{\psi }+\varepsilon \ln \left( \frac{r_c}{\hat{L}}\right) -\tan ^{-1}2\varepsilon \right] =0. \end{aligned}$$

(29)

For $\varepsilon < 0$, Eq. (29) implies that

$$\begin{aligned} \left[ \hat{\psi }+\varepsilon \ln \left( \frac{r_c}{\hat{L}}\right) -\tan ^{-1}2\varepsilon \right] =\frac{\pi }{2}. \end{aligned}$$

(30)

Therefore

$$\begin{aligned} r_c=\hat{L}\exp \left\{ \frac{1}{\varepsilon }\left[ \left( \frac{\pi }{2} -\hat{\psi }\right) +\tan ^{-1}2\varepsilon \right] \right\} . \end{aligned}$$

(31)

Equation (31) depends explicitly on $\hat{L}$ and implicity on this quantity through $\hat{\psi }$. However, it may be shown that $r_c$ does not depend on $\hat{L}$.

3 Stress intensity factors

In this section, equations are derived using those in Sect. 2.1, in order to determine expressions for the stress intensity factors related to ${\mathcal {G}}_{I}$ and ${\mathcal {G}}_{II}$. Separating ${\mathcal {G}}_i$ for modes I and II, using Eq. (1), one may obtain the expressions

$$\begin{aligned}&{\mathcal {G}}_{I} = \lim _{\varDelta a \rightarrow 0} \frac{1}{2 \varDelta a} \int _{0}^{\varDelta a} \sigma _{yy}(x) \varDelta u_y(\varDelta a - x) \, dx \nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned}&{\mathcal {G}}_{II} = \lim _{\varDelta a \rightarrow 0} \frac{1}{2 \varDelta a} \int _{0}^{\varDelta a} \sigma _{yx}(x) \varDelta u_x(\varDelta a - x) \, dx .\nonumber \\ \end{aligned}$$

(33)

In Eqs. (32) and (33), $\varDelta a$ is the virtual crack extension shown in Fig. 1b; the tensile and shear stresses ahead of the crack tip are $\sigma _{yy}$ and $\sigma _{xy}$, respectively. The tension stress $\sigma _{yy}$, as well as the x-coordinate emanating from the original crack tip are shown in Fig. 1a. The displacement jumps in the x and y-directions are, respectively, $\varDelta u_x$ and $\varDelta u_y$. Note, that in Eqs. (32) and (33) use was made of $\varDelta u_x$ and $\varDelta u_y$ rather than $u_x$ and $u_y$ as in Eq. (1). Thus, the former equations are multiplied by 1 / 2.

In order to determine the relations between the complex stress intensity factor components and ${\mathcal {G}}_{I}$ and ${\mathcal {G}}_{II}$, two auxiliary integrals are presented

$$\begin{aligned}&A_T = \frac{1}{2 \varDelta a} \int _{0}^{\varDelta a} \left[ \sqrt{\frac{D_{22}}{{D_{11}}}}\sigma _{yy}(x) + i \sigma _{yx}(x) \right] \nonumber \\&\quad \times \,\left[ \sqrt{\frac{D_{11}}{{D_{22}}}}\varDelta u_y(\varDelta a - x) - i \varDelta u_x(\varDelta a - x) \right] \, dx. \nonumber \\ \end{aligned}$$

(34)

$$\begin{aligned}&D_T = \frac{1}{2 \varDelta a} \int _{0}^{\varDelta a} \left[ \sqrt{\frac{D_{22}}{{D_{11}}}}\sigma _{yy}(x) + i \sigma _{yx}(x) \right] \nonumber \\&\quad \times \,\left[ \sqrt{\frac{D_{11}}{{D_{22}}}}\varDelta u_y(\varDelta a - x) + i \varDelta u_x(\varDelta a - x) \right] \, dx .\nonumber \\ \end{aligned}$$

(35)

To denote that the material is transversely isotropic, a subscript T is used in Eqs. (34) and (35). Using Eqs. (32)–(35), it is possible to show that the energy release rates for modes I and II are given by

$$\begin{aligned}&{\mathcal {G}}_{I} = \frac{1}{2} \lim _{\varDelta a \rightarrow 0} \Big [\mathfrak {R}(A_T) + \mathfrak {R}(D_T) \Big ] \end{aligned}$$

(36)

$$\begin{aligned}&{\mathcal {G}}_{II} = \frac{1}{2} \lim _{\varDelta a \rightarrow 0} \Big [\mathfrak {R}(A_T) - \mathfrak {R}(D_T) \Big ] \end{aligned}$$

(37)

Substitution of Eqs. (36) and (37) into Eq. (21) results in

$$\begin{aligned} {\mathcal {G}}_i =\displaystyle \lim _{\varDelta a \rightarrow 0} \mathfrak {R}(A_T). \end{aligned}$$

(38)

By substituting Eqs. (13) and (14) into Eq. (34) leads to

$$\begin{aligned} A_T = \frac{D_{11}}{8\pi \varDelta a (1 - 2i\varepsilon )\cosh \pi \varepsilon } \,\left( K_1^2+K_2^2\right) I_1 \end{aligned}$$

(39)

where

$$\begin{aligned} I_1 = \int _0^{\varDelta a} \left( \frac{\varDelta a - x}{x} \right) ^{\frac{1}{2} - i\varepsilon } dx. \end{aligned}$$

(40)

In Banks-Sills and Farkash (2016), the integral in Eq. (40) was shown to be

$$\begin{aligned} I_1 = \varDelta a \frac{(1 - 2i\varepsilon ) \pi }{2 \cosh \pi \varepsilon } \;. \end{aligned}$$

(41)

Substituting Eq. (41) into Eq. (39) results in

$$\begin{aligned} A_T = \frac{D_{11}}{4 \cosh ^2\pi \varepsilon } \,\left( K_1^2+K_2^2\right) . \end{aligned}$$

(42)

Use of Eq. (42), in Eq. (38) leads to the relation in Eq. (19).

Considering the imaginary components in Eq. (34), one may define

$$\begin{aligned} \mathcal {I}_{I}^{(T)}= & {} \frac{1}{2\varDelta a}\sqrt{\frac{D_{22}}{{D_{11}}}} \int _{0}^{\varDelta a} \sigma _{yy}(x) \varDelta u_x(\varDelta a - x) dx \end{aligned}$$

(43)

$$\begin{aligned} \mathcal {I}_{II}^{(T)}= & {} \frac{1}{2\varDelta a}\sqrt{\frac{D_{11}}{{D_{22}}}} \int _{0}^{\varDelta a} \sigma _{yx}(x) \varDelta u_y(\varDelta a - x) dx.\nonumber \\ \end{aligned}$$

(44)

As mentioned before, $A_T$ is real, so that $\mathfrak {I}(A_T) = 0$; using this and Eqs. (34), (43) and (44), it is possible to show that

$$\begin{aligned} \mathcal {I}_{I}^{(T)} =\mathcal {I}_{II}^{(T)}. \end{aligned}$$

(45)

Next, calculation of the integral in Eq. (35) is carried out. Substitution of Eqs. (13) and (14) into Eq. (35) leads to

$$\begin{aligned} D_T = \frac{D_{11}}{4\pi \varDelta a (\frac{1}{2} + i\varepsilon ) \cosh \pi \varepsilon } \,K^2 I_2 \end{aligned}$$

(46)

where

$$\begin{aligned} I_2 = \int _0^{\varDelta a} x^{-\frac{1}{2} + i\varepsilon }(\varDelta a - x)^{\frac{1}{2} + i\varepsilon } dx. \end{aligned}$$

(47)

In Banks-Sills and Farkash (2016), it was shown that $I_2$ may be written as

$$\begin{aligned} I_2 = \varDelta a^{1 + 2i\varepsilon } \Big (\textstyle \frac{1}{2} + i \varepsilon \Big ) \, P \end{aligned}$$

(48)

where

$$\begin{aligned} P = \frac{\varGamma \Big (\textstyle \frac{1}{2} + i \varepsilon \Big ) \varGamma \Big (\textstyle \frac{1}{2} + i \varepsilon \Big )}{\varGamma \Big (2 + 2i \varepsilon \Big )} \;. \end{aligned}$$

(49)

Note, $\varGamma (a+ib)$ is the Gamma function. By using Maple (2014), the real and imaginary parts of P are obtained. Substituting Eq. (48) into (46) leads to

$$\begin{aligned} D_T = \frac{D_{11}}{4\pi \cosh \pi \varepsilon } P K^2 \varDelta a^{2i\varepsilon } \;. \end{aligned}$$

(50)

One may separate $D_T$ into real and imaginary parts as

$$\begin{aligned} \mathfrak {R}(D_T)= & {} \frac{1}{H_1} (K_1^2 + K_2^2) \, C \cos \chi \end{aligned}$$

(51)

$$\begin{aligned} \mathfrak {I}(D_T)= & {} \frac{1}{H_1} (K_1^2 + K_2^2) \, C \sin \chi \end{aligned}$$

(52)

where

$$\begin{aligned}&C = \frac{\cosh \pi \varepsilon }{\pi } \sqrt{P_R^2 + P_I^2} \end{aligned}$$

(53)

$$\begin{aligned}&\chi = 2\tan ^{-1} \left( \frac{K_2}{K_1}\right) + \psi _P + 2 \varepsilon \ln \varDelta a \end{aligned}$$

(54)

$$\begin{aligned}&\psi _P = \tan ^{-1} \left( \frac{P_I}{P_R} \right) . \end{aligned}$$

(55)

In Eqs. (53) and (55), P given in Eq. (49) is separated into its real and imaginary parts, respectively, $P_R$ and $P_I$. It should be noted that in Eq. (54), the same length units should be used for the stress intensity factors and for $\varDelta a$. In Eqs. (51) and (52), only $\chi$ is a function of $\varDelta a$.

Following Banks-Sills and Farkash (2016), the ratio between the energy release rates for modes II and I is defined as

$$\begin{aligned} g \equiv \frac{{\mathcal {G}}_{II}}{{\mathcal {G}}_{I}}. \end{aligned}$$

(56)

Substituting Eqs. (42) and (51) into (36) and (37) with Eq. (20) while omitting the limit, results in

$$\begin{aligned} \chi =\cos ^{-1} \frac{1}{C} \frac{1 - g}{1 + g} \;. \end{aligned}$$

(57)

Solving for the first term in Eq. (54), the phase angle $\psi$ in Eq. (22), and substituting Eq. (57) into it leads to

$$\begin{aligned} \psi = \frac{1}{2} \cos ^{-1}\left( \frac{1}{C} \frac{1 - g}{1 + g}\right) - \frac{1}{2} \psi _P - \varepsilon \ln \varDelta a. \end{aligned}$$

(58)

On the other hand, use of Eqs. (19) and (22) yields

$$\begin{aligned} K_1 = \pm \sqrt{H_1 {\mathcal {G}}_i} \cos \psi \;. \end{aligned}$$

(59)

Note that two solutions are obtained for $K_1$. Solving Eq. (22) for $K_2$ leads to

$$\begin{aligned} K_2 = K_1 \tan \psi \;. \end{aligned}$$

(60)

Note that two pairs of solutions are found. Using the analytical condition suggested in Banks-Sills and Farkash (2016), requiring the crack faces to be open, Eq. (14) leads to

$$\begin{aligned} -\frac{\pi }{2}< \tan ^{-1} \left( \frac{K_2}{K_1}\right) - \tan ^{-1} 2 \varepsilon + \varepsilon \ln r < \frac{\pi }{2}. \end{aligned}$$

(61)

In Eq. (61), r, the distance from the crack tip, is chosen to be approximatly a / 100. By using this condition, the invalid pair of stress intensity factors is eliminated.

Fig. 4

Example of the elements that are used for the calculation of the energy release rates when N, the number of the nodes ahead of the crack tip, is equal to 4 (adapted from Banks-Sills and Farkash 2016)

Following Banks-Sills and Farkash (2016), the energy release rates ${\mathcal {G}}_{I}$ and ${\mathcal {G}}_{II}$, are calculated from the finite element results as

$$\begin{aligned} {\mathcal {G}}_{I}= & {} \frac{1}{2\varDelta a} \sum _{m = 1}^{N} F_{ym} \varDelta u_{ym'} \end{aligned}$$

(62)

$$\begin{aligned} {\mathcal {G}}_{II}= & {} \frac{1}{2\varDelta a} \sum _{m = 1}^{N} F_{xm} \varDelta u_{xm'}. \end{aligned}$$

(63)

In Eqs. (62) and (63), $\varDelta a = N \ell /2$ where N is the number of nodes ahead of the crack tip used for the calculation and $\ell$ is the length of the elements that participant in the calculation, as shown in Fig. 4 for $N=4$. The forces $F_{ym}$ and $F_{xm}$ are, respectively, the nodal point forces in the y and x-directions at node m. The jump in the crack opening and sliding displacements at node $m'$ are, respectively, $\varDelta u_{ym'}$ and $\varDelta u_{xm'}$. A larger number of elements may be taken in the calculation. By means of the same method, Eqs. (43) and (44) are calculated as

$$\begin{aligned} \mathcal {I}_{I}^{(T)}= & {} \frac{1}{2\varDelta a} \sqrt{\frac{D_{22}}{{D_{11}}}}\sum _{m = 1}^{N} F_{ym} \varDelta u_{xm'}\end{aligned}$$

(64)

$$\begin{aligned} \mathcal {I}_{II}^{(T)}= & {} \frac{1}{2\varDelta a} \sqrt{\frac{D_{11}}{{D_{22}}}}\sum _{m = 1}^{N} F_{xm} \varDelta u_{ym'}\;. \end{aligned}$$

(65)

Note that the last two expressions are related to the left and right hand sides of Eq. (45), respectively, and analytically they are equal. When calculated numerically, the parameters will not, in general, be equal; but for a certain number of elements used for the virtual crack extension $\varDelta a$, their values approach one another. The difference between $\mathcal {I}_{I}^{(T)}$ and $\mathcal {I}_{II}^{(T)}$ may be used as a measure of accuracy of the solution by considering the parameter

$$\begin{aligned} \mathcal {I}_{T}=\frac{\mathcal {I}_{I}^{(T)}-\mathcal {I}_{II}^{(T)}}{\mathcal {I}_{I}^{(T)}}\times 100\;. \end{aligned}$$

(66)

4 Numerical results

In this section, the problem of an infinite body containing a finite crack of length 2a, with $a=1$ mm, along an interface between two dissimilar linear elastic, transversely isotropic and homogeneous materials is considered, as shown in Fig. 5. Three different cases of applied tractions are examined. In order to approximate an infinite body, the dimensions of the body are taken to be $w/a = 40$ and $h/w = 1$; 2h and 2w are, respectively, the height and width of the body. The material that is used in this problem is a fiber reinforced composite made of graphite/epoxy AS4/3501-6. The effective mechanical properties were taken from Banks-Sills and Boniface (2000), and are shown in Table 1. For the upper material, the fibers are in the x-direction, and for the lower material, they are in the z-direction (see Fig. 3).

Fig. 5

Finite length interface crack between two transversely isotropic materials, with applied tractions of tension $\sigma$ and shear $\tau$. In the finite element analysis, the infinite body is approximated as a square with height and width 2h and 2w, respectively (adapted from Banks-Sills and Farkash 2016)

Table 1 Effective mechanical properties of graphite/epoxy AS4/3501-6 (Banks-Sills and Boniface 2000)

Table 2 Parameters used to calculate the stress intensity factors

Table 3 Applied tractions and the analytic solutions for the cases investigated in this study

In order to maintain displacement continuity along the interface, stresses $\sigma _{xx}^{(1)}$ and $\sigma _{xx}^{(2)}$, as shown in Fig. 5, are applied parallel to the crack. The stress $\sigma _{xx}^{(1)}$ in the upper material was chosen to be the same as the tensile stress. The expression for the stress $\sigma _{xx}^{(2)}$ is found in Boniface and Banks-Sills (2002), using the principles from Rice and Sih (1965), and is given for plane strain by

$$\begin{aligned} \sigma _{xx}^{(2)} \!= \!\frac{E_T}{E_A}\sigma _{xx}^{(1)} \!+\! \left[ \frac{E_A \nu _T \!+\! E_T (\nu _A^2-\nu _A-\nu _A \nu _T)}{E_A\!-\!\nu _A^2 E_T} \right] \sigma \end{aligned}$$

(67)

where $\sigma$ is the far field tensile stress. The analytical solution for this problem is given by Boniface and Banks-Sills (2002) as

$$\begin{aligned} K = \left( \sqrt{\frac{D_{22}}{D_{11}}}\sigma + i \tau \right) (1 + 2i\varepsilon )\sqrt{\pi a}(2a)^{-i\varepsilon } \end{aligned}$$

(68)

where $D_{11}$ and $D_{22}$ are found in Eqs. (15) and (16), respectively and $\tau$ is the far field shear stress. The values of $D_{11}$, $D_{22}$ and $\varepsilon$, P, C and $\psi _P$ from Eqs. (49), (53) and (55), respectively, are given in Table 2. Three cases of applied tractions have been examined in this study. The applied tractions and the analytic solution for the stress intensity factors are presented in Table 3.

Three meshes were constructed using Abaqus/CAE (2014) with eight noded isoparametric elements (CPE8). In each case, the entire body was modeled. The size of the elements near the crack tip, $\ell$, and number of elements and nodes, for each mesh, are presented in Table 4.

Table 4 The size $\ell$ of the elements near the crack tip and the number of elements and nodes for each mesh

Fig. 6

Schematic view of part of mesh A presented in Table 4. This mesh contains 1,037,444 eight noded isoparametric elements and 3,117,284 nodal points

Fig. 7

Schematic view of the a crack region and b the crack tip region of meshes B and C presented in Table 4

A schematic figure of part of mesh A is shown in Fig. 6. The parts of the mesh that are far from the crack, at the corners of the body, contain uniform elements whose dimensions are about $2\times 2~mm ^2$. Note that the crack length 2a is 2 mm. There is a uniform mesh of elements each $5\times 5~\upmu \hbox {m}^2$ surrounding the crack tip. Therefore, $\ell =5~\upmu \hbox {m}$. Above, below and on the sides of the crack, there are transition zones between the two regions with elements which have a large aspect ratio, the largest being 400. The stress gradients are low in those regions; so that these elements should not adversely affect the accuracy of the results. In addition, meshes B and C presented in Table 4 with smaller values of $\ell$ were constructed. For those two meshes, a focused region around the crack tip was utilized as shown schematically in Fig. 7. For the elements in the vicinity of the crack tip, $\ell = 0.05~\upmu \hbox {m}$ and $\ell = 0.5~\upmu \hbox {m}$, respectively, for meshes B and C. A uniform mesh with an element size of $\ell \times \ell$, was constructed only in the crack tip region, as shown schematically in Fig. 7b. An enlargement of the region surrounded by a dotted red line in Fig. 7a is illustrated in Fig. 7b.

For Mesh B, the size of the uniform mesh in the crack tip region, is $10\times 10~\upmu \hbox {m}^2$, and there are $200\times 200$ elements with $\ell =0.05~\upmu \hbox {m}$. Note that there are 100 such elements in front of the crack tip and 100 elements on each crack face behind the crack tip. To allow for this small element size, the mesh is focused towards the crack tip, as shown in Fig. 7a. In the focused zone there are 70 square rings, each one smaller and thinner than the outer one. Three inner rings are shown in Fig. 7b. In the outer region, a uniform coarse mesh was constructed, similar to that in Fig. 6. The elements in that region are $1\times 1~\hbox {mm}^2$. The largest aspect ratio of the transition elements is 100.

For mesh C, the size of the uniform mesh in the crack tip region, is $25\times 25~\upmu \hbox {m}^2$; there are $50\times 50$ elements with $\ell =0.5~\upmu \hbox {m}$, instead of $200\times 200$ elements with $\ell =0.05~\upmu$m in mesh B. Note that there are 25 elements in front of the crack and 25 elements on each crack face behind the crack tip. In the focused zone, there are 25 square rings instead of 70 square rings as in mesh B. In the outer region, elements are $1\times 1~\hbox {mm}^2$, with no change compared to mesh B. The largest aspect ratio of the transition elements is 25. It may be noted that for meshes B and C, there are no stress gradients in the transition regions. One of the aims of this study is to determine accurate stress intensity factors values for meshes which are as coarse as possible. Hence, elements in the transition region have high aspect ratios.

Using the finite element results, the values of the energy release rates ${\mathcal {G}}_I$ and ${\mathcal {G}}_{II}$ are calculated by means of Eqs. (62) and (63), respectively. In order to compute the stress intensity factors, ${\mathcal {G}}_I$ and ${\mathcal {G}}_{II}$ are substituted into Eqs. (21) and (56) to obtain the interface energy release rate ${\mathcal {G}}_i$ and the ratio g, respectively. Using the value of the oscillatory parameter $\varepsilon$ given in Eq. (6) and Table 2, the constants P, C and $\psi _p$ in Eqs. (49), (53) and (55), respectively, are calculated; their values may be found in Table 2. By substituting C, $\psi _p$, g and $\varDelta a$ into Eq. (58), the phase angle $\psi$, defined in Eq. (22), is obtained. Two pairs of stress intensity factors are determined by substituting ${\mathcal {G}}_i$ and $\psi$ into Eqs. (59) and (60). Using the condition in Eq. (61), the valid solution is found. By means of Eqs. (64), (65) and (66) the parameters $\mathcal {I}_{I}^{(T)}$, $\mathcal {I}_{II}^{(T)}$ and $\mathcal {I}_{T}$, respectively, are also computed. These are used to indicate a best solution.

Table 5 Data for case 1 in Table 3, solved with mesh A ($\ell =5~\upmu \hbox {m}$)

Table 6 Data for case 1 in Table 3, solved with mesh B ($\ell =0.05~\upmu \hbox {m}$)

Table 7 Data for case 1 in Table 3, solved with mesh C ($\ell =0.5~\upmu \hbox {m}$)

Table 8 Data for case 2 in Table 3, solved with mesh A ($\ell =5~\upmu \hbox {m}$)

Table 9 Data for case 2 in Table 3, solved with mesh B ($\ell =0.05~\upmu \hbox {m}$)

Table 10 Data for case 2 in Table 3, solved with mesh C ($\ell =0.5~\upmu \hbox {m}$)

Table 11 Data for case 3 in Table 3, solved with mesh B ($\ell =0.05~\upmu \hbox {m}$)

The first two cases in Table 3 were considered for all three meshes described above. The results for the first and second cases are shown in Tables 5, 6, 7, 8, 9 and 10, respectively. The third case in Table 3 was carried out only with mesh B presented in Table 4. The results for this case are shown in Table 11. In Tables 5, 6, 7, 8, 9, 10 and 11, the first column represents the number of elements used for $\varDelta a$, the virtual crack extension, which is given in the second column. Since $\varDelta a$ consists of N nodes and eight noded elements are used in the analyses, the number of elements is N / 2. In the next two columns, errors in the stress intensity factors $K_1$ and $K_2$ appear. The percentage $\mathcal {I}_T$ in Eq. (66) is shown in column 5. Recall that $\mathcal {I}_T$ should be zero.

In Table 5, the results are shown for case 1 in Table 3, using mesh A. Since there is a difference of two orders of magnitude between the two stress intensity factors, as shown in Table 3, it is difficult to obtain an accurate solution. For $K_1$, the percent error is less than 0.06% for $\varDelta a = 5~\upmu \hbox {m}$ to $155~\upmu \hbox {m}$. For $\varDelta a = 35~\upmu \hbox {m}$ to $125~\upmu \hbox {m}$, the percent error for $K_2$ is 0.27%. The lowest value of $\mathcal {I}_T$ is obtained for $\varDelta a = 95~\upmu \hbox {m}$. For this value of $\varDelta a$, $K_1$ has no error to 3 significant figures and $K_2$ has an error of 0.27%. Note, that by using one element for $\varDelta a$, the error for $K_2$ is $-15.5$%.

Mesh A consists of over 1,000,000 elements making this method impractical for extension to three dimensions. Hence, the focused mesh B was used to reduce the required computer memory and CPU time in the finite element analyses. By using a focused mesh, a smaller value of $\ell$ was also achieved. In Table 6, the results are shown for case 1 in Table 3 using mesh B in Table 4 and shown schematically in Fig. 7. For $\varDelta a \ge 0.3~\upmu \hbox {m}$, the percent error converges to 0.06% for $K_1$ and 0.27% for $K_2$. The value of $\mathcal {I}_T$ decreases as $\varDelta a$ increases. For the greatest value of $\varDelta a$ used in the calculation, the value of $\mathcal {I}_T$ is $-0.24$%. Note that the largest value of $\varDelta a$ in Mesh B is the smallest one in mesh A. As a result of the stress singularity, using only the elements that are in the vicinity of the crack tip leads to poor results for $K_2$. For example, in Table 5, for $\varDelta a = 15~\upmu \hbox {m}$ and comprising the first 3 elements, the percent error for $K_2$ is larger than 1.3%. This behavior was also observed for other methods such as the M-integral and displacement extrapolation (see: Freed and Banks-Sills 2005). For the M-integral, use of the first volume of elements surrounding the crack front produced poor results. For displacement extrapolation, good results were obtained from elements that are at least two or more elements distant from the crack tip. On the other hand, as one may see in Eq. (1), $\varDelta a$ should be small. Therefore, there is a range of values for $\varDelta a$ which produce good results. The lowest value of $\mathcal {I}_T$ is a good indicator for the choice of $\varDelta a$ and, hence, the values for $K_1$ and $K_2$.

A further step to reduce the number of elements was made with mesh C. Recall that the number of elements in the uniform mesh surrounding the crack tip and the number of rings used for mesh C is less than those of mesh B. As presented in Table 4, the number of elements in mesh C is about 30,000, a decrease of about one-eighth as compared to mesh B. In Table 7, the results are shown for case 1 in Table 3 using mesh C. For $\varDelta a \ge 3~\upmu \hbox {m}$, the percent error converges to 0.06% for $K_1$ and 0.27% for $K_2$. The value of $\mathcal {I}_T$ decreases as $\varDelta a$ increases. For the greatest value of $\varDelta a$ used in the calculation, the value of $\mathcal {I}_T$ is $-1.9$%. The values obtained for $K_1$ and $K_2$ using meshes B and C, as a function of the number of elements are very similar. Note that for both meshes B and C, by using one element for $\varDelta a$ the error for $K_2$ is quite large. It may be noted that the lowest values of $\mathcal {I}_T$ are obtained with use of mesh B. This mesh is quite fine. Hence, mesh C which is much coarser than mesh B was used (see Table 4). It may be observed in Table 7 that values of $\mathcal {I}_T$ are not as small as those presented in Table 6 for mesh B. But convergence is obtained with small errors in the stress intensity factors.

In Tables 8 through 10, the results are presented for case 2 from Table 3 using meshes A, B and C. In this case, a shear stress is applied at the outer boundary of the body as shown in Fig. 5, which is the same magnitude as the tensile stress, $\sigma$. Since the stress intensity factors are the same order of magnitude for this problem, it should be easier to obtain accurate results. In Table 8, the results are shown for case 2 in Table 3, using mesh A. The absolute values of the percent errors are less than 0.06% for both $K_1$ and $K_2$, when $\varDelta a = 15~\upmu \hbox {m}$ to $165~\upmu \hbox {m}$ for the former and $\varDelta a = 15~\upmu \hbox {m}$ to $90~\upmu \hbox {m}$ for the latter. The lowest value of $\mathcal {I}_T$ is obtained for $\varDelta a = 150~\upmu$m. For this value of $\varDelta a$, $K_1$ has an error of $-0.04$% and $K_2$ has an error of $-0.11$%. Note that by using one element for $\varDelta a$, the errors are less than 1% for both stress intensity factors.

In Table 9, the results are presented for case 2 in Table 3, using mesh B. For $\varDelta a \ge 0.25~\upmu \hbox {m}$, the percent error converges to 0.07% for $K_1$ and 0.02% for $K_2$. For the greatest value of $\varDelta a$ used in the calculation, the value of $\mathcal {I}_T$ is -0.14%.

In Table 10, the results are presented for case 2 in Table 3, using mesh C. For $\varDelta a \ge 3.5~\upmu \hbox {m}$, the percent error converges to 0.06% for $K_1$ and 0.02% for $K_2$. For the greatest value of $\varDelta a$ used in the calculation, the value of $\mathcal {I}_T$ is -0.72%. Also here, by using one element for $\varDelta a$ the errors are less than 1% for both stress intensity factors. It is shown that a mesh consisting of less elements in the vicinity of the crack tip and less square rings, compared to mesh B, leads to excellent results.

In case 3 presented in Table 3, the applied shear stress is increased to 4 MPa. Using Eq. (31) for this case, $r_c=0.076~\upmu \hbox {m}$. Hence, the interpenetration zone occurs for a distance $r \le 0.076~\upmu \hbox {m}$ from the crack tip. Only mesh B presented in Table 4 was used for this calculation. Since the size of one element is $\ell =0.05~\upmu \hbox {m}$, the first two elements behind the crack tip are in the interpenetration zone. It is expected that interpenetration should occur between the third and the fourth nodes from the crack tip. In Fig. 8, the deformed configuration of the crack faces in the vicinity of the crack tip are plotted. As may be observed, the first two elements penetrate each other. Indeed, the interpenetration ends between the third and fourth nodes from the crack tip. For cases 1 and 2 in Table 3, there will be an interpenetration zone; but it will be smaller than the smallest distance between the nodes in the vicinity of the crack tip in mesh B.

Fig. 8

For case 3 in Table 3 using mesh B, a schematic view of the deformed configuration of the crack faces using data obtained from the finite element analysis

In Table 11, the results are shown for case 3 from Table 3 obtained using mesh B. Since interpenetration occurs for $\varDelta a < 0.1~\upmu \hbox {m}$, results for $\varDelta a = 0.05~\upmu \hbox {m}$ and $0.1~\upmu \hbox {m}$, are not presented. For $\varDelta a \ge 0.85~\upmu \hbox {m}$, the percent error converges to 0.09% for $K_1$ and 0.02% for $K_2$. For the greatest value of $\varDelta a$ used in the calculation, the value of $\mathcal {I}_T$ is 0.09%. The percent error of $-2.33$% for $K_1$ when $\varDelta a = 0.15~\upmu \hbox {m}$ and values of more than 25% for $\mathcal {I}_T$ when $\varDelta a = 0.15\text {--}0.20~\upmu \hbox {m}$ are higher than the corresponding values for cases 1 and 2. These high values appear to be a result of crack face interpenetration. Using the elements that are in the interpenetration zone for the calculation does not cause the results to deteriorate. On the contrary, in order to obtain accurate results, those elements should be used in the calculation.

5 Summary and conclusions

The virtual crack closure technique presented in Banks-Sills and Farkash (2016) has been extended to an interface crack between two dissimilar transversely isotropic materials. New equations for calculating the stress intensity factors $K_1$ and $K_2$ have been developed. Two pairs of solutions are produced. An analytic condition to determine the valid solution is presented. As shown in Banks-Sills and Farkash (2016), in some cases in order to obtain accurate results, the virtual crack extension $\varDelta a$ should contain many small elements. A low value of $\mathcal {I}_T$ in Eq. (66), indicates an optimal number of elements to be used for $\varDelta a$. In all of the load cases considered with meshes B and C, $\mathcal {I}_T$ converged towards zero as the number of elements in the virtual crack extension increased. For the coarse mesh A, values of $\mathcal {I}_T$ decreased as the number of elements used in the virtual crack extension increased; but then increased. The lowest value of $\mathcal {I}_T$ was used to determine the stress intensity factor values. It may be pointed out that a virtual crack extension containing only one element may be used when the stress intensity factors are of the same order of magnitude.

In addition, an expression for the size of the interpenetration zone was presented. In previous papers (Toya 1992; Sun and Qian 1997), use of elements larger than the interpenetration zone was recommended. For cases in which the virtual crack extension contains many small elements, excellent results are achieved even if the elements are smaller than the interpenetration zone. This conclusion also applies to an interface crack between two dissimilar isotropic materials.

Three cases for different applied tractions with three meshes have been considered for an interface crack between two transversely isotropic materials in an infinite body. Using one element as the virtual crack extension $\varDelta a$ leads to errors in the stress intensity factors ranging in absolute value from 0.02 to 16%. Low errors are obtained for the stress intensity factors when the values of $K_1$ and $K_2$ are the same order of magnitude. When they differ substantially, more than one element is required in the calculation. In this study, it was suggested to choose the number of elements for $\varDelta a$ for which the lowest value of $\mathcal {I}_T$ was obtained. According to this suggestion, the errors for the stress intensity factors ranged in absolute value from 0.02 to 0.27%. The method presented here may be extended to other anisotropic material pairs and to three dimensions.