Scaling of the fracture process zone in rock

Abstract

The zone of microcracks surrounding a notch tip—the process zone—is a phenomenon observed in fracture of quasi-brittle materials, and the characterization of the process zone is the topic of the paper. Specimens of different sizes with a center notch fabricated from a granite of large grain (Rockville granite, average grain size of 10 mm), were tested in three-point bending. Acoustic emissions were recorded and locations of microcracks were determined up to peak load. The results show that both the length and width of the process zone increase with the increase of the specimen size. Furthermore, the suitability of a proposed theoretical relationship between the length and width of the process zone and specimen size was studied experimentally and numerically. The discrete element method with a tension softening contact bond model was used to investigate the development of the process zone with the specimen size. A synthetic rock composed of rigid circular particles that interact through normal and shear springs was tested in the numerical simulations. It was shown that the limiting specimen size, beyond which no further noticeable increase in the length of the process zone is observed, is significantly larger than the limiting specimen size beyond which the width of the process zone shows no size effect.

1 Introduction

The zone of microcracking that is formed at peak load in a structure composed of a quasi-brittle material is referred to as the process zone, and this region is associated with energy dissipation due to crack growth (Evans 1976; Hillerborg et al. 1976). Furthermore, it is well known that the fracture energy must be finite and for linear fracture mechanics, this parameter is a material constant (Knott 1973). Therefore, to ensure the condition of constant fracture energy, the size of the process zone must eventually reach a limiting value (Bazant and Pfeiffer 1987; Bazant and Kazemi 1990). However, some experiments show that a limiting size is often not observed (e.g. Otsuka and Date 2000), while other experiments report a constant process zone size (e.g. Le et al. 2014). Indeed, the specimen size itself is an important factor in evaluating the process zone.

Studies on the process zone have been of considerable interest to many researchers (Jankowski and Stys 1990; Cattaneo and Biolzi 2010; Biolzi et al. 2011; Lin et al. 2014). Different parameters such as microstructure (Barton 1982; Brooks et al. 2012; Tarokh and Fakhimi 2014), notch length (Zhang and Wu 1999; Ohno et al. 2014), and loading rate (Bazant et al. 1993; Backers et al. 2005) have been reported to have an impact on process zone size.

The objective of this work is to investigate experimentally and numerically the size effect on the width and length of the process zone in rock. Scaled specimens of Rockville granite, with an average grain size of 10 mm, were tested in three-point bending. Acoustic emission (AE) monitoring was used to find the dimensions of the process zone. AE is one of the most common methods to study fracture, with the advantage that the entire volume of the specimen is sampled (Mihashi et al. 1991; Zang et al. 2000). Speckle interferometry (Wang et al. 1990; Haggerty et al. 2010) and digital image correlation (Lin et al. 2014) are examples of other techniques that provide higher resolution of measurement, but these are limited to surface observations. Numerical methods, where features of the fracture process (e.g. critical opening displacement) are found through a comparison with experiments and fitting parameters such as load-deflection or load-crack mouth opening displacement curves (de Borst 2003), can also provide an insight. To demonstrate the ability of the bonded particle model to simulate rock fracture, numerical beams of Rockville granite were tested. Experimental and numerical results are compared and the limiting specimen sizes for both width and length of the fracture process zone are found and discussed.

2 Theoretical model

Consider two geometrically similar beams in two dimensions under three-point bending (Fig. 1), with the process zone developed at the peak load around the notch tip in both specimens. Linear fracture mechanics shows that the extent of the K-dominant zone, where stresses and displacements are well predicted by the one-term solution, scales with the specimen size: by increasing the beam dimensions, the extent of K-dominant zone increases proportionally. If the process zone size is assumed to be a material constant, a small beam size can be chosen in which the size of the process zone is larger than the K-dominant zone (Fig. 1a). On the other hand, for a much larger beam, the process zone can be completely confined within the K-dominant zone. This suggests that in the vicinity of the notch tip in these beams, two different stress regimes can exist, which is not consistent with the assumption that the size of the process zone is invariant. Therefore, the process zone must change as the specimen size is modified, although from an energy argument, a constant process zone size will be eventually reached.

Fig. 1

Two geometrically similar beams of the same material in three point bending: a small beam in which the K-dominant zone (in black) falls within the process zone (in red) and b large beam in which the process zone (in red) lies within the K-dominant zone

The concept adopted in this paper is a process zone of a two dimensional rectangular shape with length l and width W. Three different scenarios can be considered for the size-dependency of the process zone. In the first scenario, the beam height (D) is smaller than a certain value $(D<D_{W})$ and, with increase in the beam size, both the length and width of the process zone increase. In the second scenario, with beam size in the range of $D_{W}< D < D_{l}$, the width of the process zone becomes approximately constant, but its length can continue to increase with the specimen size. Eventually, in the third scenario, for beam size larger than $D_{l}$ $(D > D_{l})$, both the length and the width of the process zone do not change with specimen size. The limiting sizes of $D_{W}$ and $D_{l}$ are postulated to be dependent on material characteristics (e.g. grain size). Furthermore, the limiting sizes of $D_{W}$ and $D_{l}$ in some rock types (e.g. Berea sandstone with 0.2 mm grains) is small enough such that with typical laboratory sizes (tens of mm), a constant process zone size is observed (Le et al. 2014). However, in other rock types (e.g. Rockville granite), the minimum specimen size ($D_{l})$ after which both the length and the width of the process zone are approximately constant is significantly large (>1 m) and difficult to test in a laboratory. As a consequence, depending on the specimen size and material, different conclusions regarding the size of process zone have been reported in the literature (Zietlow and Labuz 1998; Otsuka and Date 2000).

Based on Bazant’s size effect law, Fakhimi and Tarokh (2013) proposed the following equation for the evolution of the process zone with specimen size:

$$\begin{aligned} W=\frac{W_\infty D}{D_{0w} \left( {1+\frac{D}{D_{0w}}} \right) } \end{aligned}$$

(1)

where W is the width of the process zone, D is a characteristic dimension (here it is equal to the beam height), $D_{0w}$ is a constant with the dimension of length, and $W_{\infty }$ is the width of the process zone for very large specimens. Furthermore, the following formula for the length of the process zone was proposed, which is similar to that suggested by Bazant and Kazemi (1990):

$$\begin{aligned} \ell =\frac{\ell _\infty D}{D_{0l} \left( {1+\frac{D}{D_{0l}}}\right) } \end{aligned}$$

(2)

where l is the length of the process zone, $D_{0l}$ is a constant with the dimension of length, and $l_{\infty }$ is the length of the process zone for very large specimens. Figure 2 schematically illustrates the variation of width and length of the process zone from Eqs. (1) and (2), where $D_{0l} = 3 D_{0w}$ and $l_{\infty } = 3W_{\infty }$. An approach that can be used to obtain the four constants $W_{\infty }$, $D_{0w}$, $l_{\infty }$ and $D_{0l}$ will be discussed in the subsequent sections.

Fig. 2

Schematic view of the effect of specimen size on the dimensions of the process zone

3 Experimental procedure

3.1 Rock properties

A series of three-point bending tests with a center notch were performed on Rockville granite. This rock, quarried in Cold Spring, Minnesota, is a porphyritic, microcline quartz monzonite. The average grain size for this rock is 10 mm (largest grain size is about 20 mm) with the density of $2.7 \hbox { g}/\hbox {cm}^{3}$. The matrix is medium to coarse grained, and is primarily composed of gray quartz and white plagioclase with some biotite. An average P wave velocity is 3.2 km/s. Young’s modulus and Poisson’s ratio obtained from uniaxial compression tests are E = 25–30 GPa and $\nu$ = 0.15–0.20. The uniaxial compressive strength UCS = 106 MPa and the indirect tensile strength $\sigma _{t}= 8.1$ MPa.

3.2 Testing apparatus

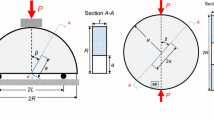
Four different beam sizes (height $\times$ span) of $50.8 \times 127$, $101.6 \times 254$, $203.2 \times 508$ and $406.4 \times 1016$ mm (each size increases by a factor of 2) were tested with the same thickness of approximately 30 mm (Fig. 3). For each beam size, the tests were duplicated. The height to span ratio was kept constant and equal to 0.4. All beams were machined with a sawn notch (1.2 mm wide) in the center position. The ratio of notch length to the specimen height ($a_{o}/D)$ was constant and equal to 0.2. The rock beams were loaded in three-point bending and as a result, the process zone developed at the center notch; the sensors for monitoring the AE activity were positioned around the notch tip (Fig. 4).

The three-point bending tests were conducted in a closed-loop, servo-hydraulic load frame with the feedback signal taken as the crack mouth opening displacement (CMOD) across the sawn notch at a gage length of 15 mm. A strain gage based transducer monitored the CMOD and was programmed to increase at a rate of $0.05\,\upmu \mathrm{{m}}$/s. The applied load was recorded with a load cell with the capacity of 22.2 kN. The mechanical behavior of the beams is represented in Fig. 5.

Fig. 3

Beams of Rockville granite scaled with a factor of 2

Fig. 4

Experimental set up for the three-point bending test with the crack mouth opening displacement (CMOD) gage and AE sensors

Fig. 5

Force-crack mouth opening displacement (CMOD) behavior for specimens of different sizes

3.3 Acoustic emission

Failure in quasi-brittle materials is associated with microcracking, where elastic waves called acoustic emission (AE) are emitted. These transient elastic waves have diminutive amplitudes and high frequency components. By recording the time histories and finding the arrival time of the P wave, it is possible to locate the AE event with an error of a few millimeters using the following assumptions: (i) the microcrack is a point-source of displacement discontinuity, (ii) propagation of the elastic wave is through a homogeneous and isotropic medium, and (iii) the transducers are considered to be a point. Since the initiation of the AE source time ($t_{0})$ is unknown, the back-analysis requires at least five sensors to solve for the four unknowns ($x_{0}$, $y_{0}$, $z_{0}$, spatial coordinates of the event and $t_{0})$; the need for a fifth sensor is due to the quadratic form of the distance equation. Considering an error associated with arrival time detection and with the P wave velocity measurements, the number of sensors should be increased so that finding the event location becomes an optimization problem. Eight sensors were used with four sensors on each face of the beam. Details on the event location algorithm are reported by Labuz et al. (1996).

Eight AE sensors (Physical Acoustics model S9225) with an operating frequency range of 300–1800 kHz, diameter of 3.6 mm and height of 2.4 mm, were attached with cyanoacrylate glue to the surface of the beams. AE signals were preamplified (Physical Acoustics model S1220C) with a 40 dB gain and a 0.1–1.2 MHz band-pass filter. Typical noise level at the output of the preamplifiers was around ±2 mV. The high speed data acquisition (National Instrument model NI-5112 digitizer) of 8-bit ADC resolution that has four two-channel modular transient recorders was used. The sampling rate was set at 20 MHz, with 0.2 ms for the time length of each acquisition and 0.1 ms pretrigger. The recording system was triggered when the signal amplitude from a selected channel exceeded a preset threshold of ±25 mV. The threshold of amplitude must be set so that background noise does not trigger the system, but not too high avoiding excluding low-amplitude signals. The whole process is controlled by an in-house program written in LabView and the data recording is continuous without interruption. Finally, AE locations with an error less than 3 mm were considered.

4 Experimental results

4.1 Size effect analysis

The nominal strength of geometrically similar structures can be defined as:

$$\begin{aligned} \sigma _N =c_N \frac{P_{\max } }{bD} \end{aligned}$$

(3)

where $c_{N}$ is a dimensionless constant, $P_{max}$ is the peak load, b is the structure width, and D is the structure size (e.g. beam height). In the three-point bending test, this nominal strength can be determined from engineering beam theory (elastic beam without a notch) as:

$$\begin{aligned} \sigma _N =\frac{3S}{2D}\frac{P_{\max } }{bD}=\frac{3SP_{\max } }{2bD^{2}} \end{aligned}$$

(4)

where S is the beam span. Based on a strength of materials (critical stress) approach, the nominal strength of a structure is independent of the structural size (i.e. $\sigma _{N} \propto D^{0})$. On the other hand, when linear elastic fracture mechanics (LEFM) is applied to geometrically similar structures that are perfectly brittle and have geometrically similar cracks, the nominal strength is a function of $D^{-1/2 }$ (i.e. $\sigma _{N} \propto D^{-1/2})$. These size-effect relationships can be considered as a type of power-law scaling. However, for quasi-brittle materials, due to the existence of the process zone, power-law scaling does not capture the transition from the two limiting cases, i.e. strength and fracture toughness (LEFM).

For quasi-brittle materials such as rock, the process zone could contain a large volume of the structure and hence its effect should not be ignored. A size effect law was proposed by Bazant (1984):

$$\begin{aligned} \sigma _N =\frac{B\sigma _t }{\sqrt{1+\frac{D}{D_0 }}} \end{aligned}$$

(5)

where $\sigma _{t }$ is the tensile strength, B is a dimensionless parameter characterizing the geometry, and $D_{0}$ is the transitional structure size. This scaling law has an energetic (i.e. non-statistical) basis and covers the two limiting cases (strength and toughness), together with the transitional situation.

To find the size effect parameters, Bazant’s law can be rearranged as a linear expression $Y = {AX}+ C$ by assuming $X=D$ and $Y=1/\sigma _{N}^{2}$. With this rearrangement, the size effect parameters are found using the slope A and the y-intercept C:

$$\begin{aligned} B\sigma _t =\frac{1}{\sqrt{C}} \quad ,\quad D_0 =\frac{C}{A} \end{aligned}$$

(6)

The parameters, obtained by implementing this linear regression method to the experimental data with Rockville granite and considering the average values of $\sigma _{N}$ for different beam sizes, are $B = 2.1$ and $D_{0 }= 21.5$ mm. Based on the size effect parameters, the normalized nominal strength versus specimen size relationship can be plotted (Fig. 6). It is evident from the laboratory test results that the laboratory scale beam sizes are in the transition zone between the two asymptotic behaviors shown with the dashed lines in Fig. 6. For extremely small specimens (i.e. $D<< D_{0})$, the size of the fracture process zone is large compared to the size of the structure. On the other hand, for extremely large specimens (i.e. $D>> D_{0})$, LEFM governs failure and the nominal strength $(\sigma _{N})$ is proportional to $D^{-1/2}$. In this case, the volume of fracture process zone is small compared to the volume of the entire structure. Figure 6 shows that linear elastic fracture mechanics starts dominating with increasing the beam size.

Fig. 6

Size effect on the dimensionless nominal strength based on the Bazant’s size effect law

To investigate the fracture properties of the rock, the apparent fracture toughness $K_{ICA}$ was obtained using the following equation (Bazant and Planas 1998), valid for the three-point bending geometry:

$$\begin{aligned} K_{ICA} =\sigma _N \sqrt{D}\frac{\sqrt{\alpha }}{(1+2\alpha )(1-\alpha )^{1.5}}\mathrm{P}_{S/D} (\alpha ) \end{aligned}$$

(7)

where $\sigma _{N}$ is the nominal strength, S is the beam span, $\alpha$ is the ratio of notch length to beam height $(a_{0}/D)$, and $P_{S/D }(\alpha )$ is a shape factor. The equation for $P_{S/D } (\alpha )$ is (Pastor et al. 1995):

$$\begin{aligned} \mathrm{P}_{S/D} (\alpha )=\mathrm{P}_\infty (\alpha )+4\left( \frac{D}{S}\right) (\mathrm{P}_4 (\alpha )-\mathrm{P}_\infty (\alpha )) \end{aligned}$$

(8)

in which the expressions for $\hbox {P}_{4 }(\alpha )$ and $\hbox {P}_{\infty }(\alpha )$ are:

$$\begin{aligned} \mathrm{P}_4 (\alpha )= & {} 1.900-\alpha [-0.089+0.603(1-\alpha )\nonumber \\&-\,0.441(1-\alpha )^{2}+1.223(1-\alpha )^{3}] \end{aligned}$$

(9)

$$\begin{aligned} \mathrm{P}_\infty (\alpha )= & {} 1.989-\alpha (1-\alpha )[0.448-0.458(1-\alpha )\nonumber \\&+\,1.226(1-\alpha )^{2}] \end{aligned}$$

(10)

Table 1 summarizes the nominal strength and apparent fracture toughness values obtained for the rock beams with average values from the tests. It is observed that the apparent fracture toughness increases and the nominal strength decreases with the increase in the specimen size.

Table 1 Nominal strength and apparent fracture toughness average values from two tests at each beam size

4.2 Width and length of the process zone

The locations of AE events up to the peak load were used to find the dimensions of the process zone. The standard deviation of the X-coordinates $(S_X )$ and Y-coordinates $(S_Y )$ of the events were obtained and the width (W) and length (l) of the process zone were defined by three standard deviation:

$$\begin{aligned}&W=3S_X \end{aligned}$$

(11a)

$$\begin{aligned}&l=3S_Y \end{aligned}$$

(11b)

Figure 7 shows the distribution of the AE events in the X and Y directions for one of the beams, $406.4 \times 1016$ mm in size. Out of 201 events located prior to the peak load, 86.1% (173 events) were in the defined region $(3S_{X})$ across the width. Also 85.6% (172 events) were located in the defined region $(3S_{Y})$ across the length. Assuming a normal distribution and the three times standard deviation across the width and length directions, 86.6% of data should be contained in each direction. It appears that normal distribution is a fairly good approximation for the statistical distribution of the events, especially along the width direction. To include most of the events (not all, as some are outliers) three standard deviation were selected. The choice of “three” is not critical, as “two” would give similar results: the width and length of the process zone are size dependent but reach a constant value at sufficiently large specimen size.

Fig. 7

Distribution of the AE events in the direction of a beam span and b beam height for beam size of $406.4 \times 1016$ (depth $\times$ span) mm

Typical scatter of the AE events around the notch up to the peak load for the largest beam of Rockville granite is presented in Fig. 8. The process zone is shown with a rectangular region in this figure using equation 11. The dimensions of the process zones for different beam sizes (two tests for each beam size) are summarized in Table 2. It can be noticed that both the width and length of the process zone change with the increase in beam size.

Fig. 8

Locations of acoustic emission events in the largest beam up to the peak load in a $X{-}Y$ plane and b $Z{-}X$ plane. The bottom side of the rectangular region to define the domain of the process zone is assumed to coincide with the notch tip

4.3 Fitting approach for process zone data

In Sect. 2, it was suggested that the variation of width and length of the process zone with specimen size can be captured by Eqs. 1 and 2 and the four material constants (i.e. $W_{\infty }$, $D_{0w}$, $l_{\infty }$ and $D_{0l})$ in the equations must be obtained. The equations are rewritten in a linear form:

$$\begin{aligned}&\frac{1}{W}=\left( \frac{D_{0W} }{W_\infty }\right) \frac{1}{D}+\frac{1}{W_\infty } \end{aligned}$$

(12a)

$$\begin{aligned}&\frac{1}{l}=\left( \frac{D_{0l} }{l_\infty }\right) \frac{1}{D}+\frac{1}{l_\infty } \end{aligned}$$

(12b)

By plotting 1 / W and 1 / l versus 1 / D and finding the slopes and Y-intercepts, the four material constants for Rockville granite are obtained directly: $W_{\infty }$ = 10.0 mm, $D_{0W} = 43.7$ mm, $l_{\infty } = 100.0$ mm, $D_{0l} = 538.0$ mm. Note that the fitted curves in Fig. 9 are predictions of the theoretical Eqs. (1, 2) based on the input of experimental data; the parameters of the Eqs. 1 and 2 were obtained based on the experimental data using linear regression (Eqs. 12a,  12b).

Using these material constants, the variations of the width and length of the process zone with the beam size, along with the theoretical predictions (Eqs. 1,  2), are shown in Fig. 9. The predictions are in good agreement with the experimental data, suggesting that the proposed equations can provide reasonable estimates of the evolution of the process zone width and length as the beam size is changed.

Table 2 Width and length of the process zones obtained from two tests at each beam size

Fig. 9

Variation of process zone size with specimen size in terms of a width and b length

Figure 9 demonstrates that the specimen size at which the width of the process zone $(D_{0W})$ can be considered as a material property is significantly smaller than that for the length of the process zone $(D_{0l})$. In other words, a larger minimum beam size is required at which the length of the process zone is a size independent parameter. Consequently, in most beam sizes tested in the lab, the length of the process zone can change with size while this may not be case for the width. This may explain the controversy in the literature (Otsuka and Date 2000; Le et al. 2014) regarding the variation of the process zone size with the specimen size.

To reach to a conclusion, we consider the dimensions of the process zone as a material property for specimens in which the width and length of the process zone are equal or greater than 95% of $W_{\infty }$ and $l_{\infty }$, respectively. By rearranging Eqs. 1 and 2, we obtain:

$$\begin{aligned} W= & {} \frac{W_\infty D}{D_{0W} \left( {1+\frac{D}{D_{0W} }} \right) }=\frac{W_\infty \left( { \frac{D}{D_{0W} }} \right) }{\left( {1+\frac{D}{D_{0 W} }} \right) }\nonumber \\= & {} \frac{W_\infty \beta }{1+\beta }\rightarrow \frac{W}{W_\infty }=\frac{\beta }{1+\beta } \end{aligned}$$

(13)

$$\begin{aligned} \ell= & {} \frac{\ell _\infty D}{D_{0l} \left( {1+\frac{D}{D_{0l} }} \right) }=\frac{\ell _\infty \left( { \frac{D}{D_{0l}}} \right) }{\left( {1+\frac{D}{D_{0l} }} \right) }\nonumber \\= & {} \frac{\ell _\infty \beta ^{\prime }}{1+\beta ^{\prime }}\rightarrow \frac{\ell }{\ell _\infty }=\frac{\beta ^{\prime }}{1+\beta ^{\prime }} \end{aligned}$$

(14)

in which $\beta ={D/D}_{0W}$ and $\beta '=D/D_{0l}$ are the brittleness numbers.

A brittleness number can be defined as the ratio of stored elastic energy to dissipated fracture energy, with size effect as the consequence from the competition between stored energy per volume and dissipated energy per area (Palmer and Rice 1973; Bazant 1976). Other definitions of brittleness have been proposed for specific loading conditions (Papanastasiou and Atkinson 2015; Holt et al. 2015; Tarokh et al. 2016). Brittleness defined as $\beta = D/D_{o}$, introduced by Bazant (1987), embodies the influence of material, geometry, and shape of the structure. The brittleness numbers $\beta ={D/D}_{0W}$ and $\beta '=D/D_{0l }$ defined in this paper include the effect of the material and the size of the structure; whether these brittleness numbers are sensitive to the applied boundary conditions needs further study.

For $W/W_{\infty }= 0.95$ and $l/l_{\infty }= 0.95$ in Eqs. 13 and 14, the brittleness number is 19. Since the $D_{0W}$ value for Rockville granite is 43.7 mm, the size needed to obtain a brittleness number of 19 is $D_{w }= 19 \times 43.7 = 830$ mm. This implies that a beam with a minimum height of 0.83 m is required, beyond which the width of the process zone is a size independent parameter. Applying the same procedure for the length of the process zone reveals that a Rockville granite beam with a minimum height of $D_{l}= 19 \times 538 = 10,200$ mm (10.2 m) is needed, which is an unrealistic size for laboratory testing.

4.4 Effect of specimen size on the shape of the process zone

Inspecting the variation of width and length of process zone shows that specimen size not only influences the size of the process zone, but it also has a direct impact on its shape, defined by the ratio of length to width (l / W). From Fig. 10, it can be seen that l / W increases with specimen size and eventually it reaches its ultimate value of $l_{\infty }/ W_{\infty }$, which is 10 for Rockville granite. The influence of specimen size on shape of the process zone has also been reported by Vesely and Frantik (2014) and Galouei and Fakhimi (2015).

Fig. 10

Shape ratio (l / W) versus brittleness number $(\beta = D/D_{0})$. The $D_{0}$ value was obtained from Eq. 6.

4.5 Process zone and characteristic size

Bazant and Planas (1998) showed that the size of the process zone for a very large structure may be proportional to the characteristic size $(l_{ch})$:

$$\begin{aligned}&W_\infty =\eta \ell _{ch} =\eta \left( {\frac{K_{IC} }{\sigma _t }} \right) ^{2} \end{aligned}$$

(15)

$$\begin{aligned}&\ell _\infty ={\eta }'\ell _{ch} ={\eta }'\left( {\frac{K_{IC} }{\sigma _t }} \right) ^{2} \end{aligned}$$

(16)

where $\eta$ and $\eta ^{\prime }$ are dimensionless constants. To find these constants, the fracture toughness $K_{IC}$ for a very large beam (size independent) was found by combining Eqs. 5 and 7 to obtain:

$$\begin{aligned} K_{ICA}= & {} \sigma _N \sqrt{D}\frac{\sqrt{\alpha }}{(1+2\alpha )(1-\alpha )^{1.5}}\mathrm{P}_{S/D} (\alpha )\nonumber \\= & {} \frac{B\sigma _t }{\sqrt{1+\frac{D}{D_0 }}}\sqrt{D}f(\alpha ) \end{aligned}$$

(17)

Equation 17 is cast in a linear form Y = aX + b by assuming $X = 1/D$ and $Y = (1/K_{ICA})^{2}$. For very large beams, 1 / D will approach zero. Therefore, the Y-intercept will be equal to the inverse of $K_{IC}$ squared. Hence, the fracture toughness for a very large beam ($K_{IC})$ is predicted to be $1.89 \hbox { MPa}\, \hbox {m}^{0.5}$ for Rockville granite. Using $K_{IC} = 1.89 \hbox { MPa}\, \hbox {m}^{0.5}$, $l_{\infty }= 100.0 \hbox { mm}$, $W_{\infty }=10.0 \hbox { mm}$ and $\sigma _{t }= 8.1$ MPa, constants $\eta$ and $\eta ^\prime$ are found to be equal to 0.18 and 1.84, respectively. The constant $\eta ^\prime$ is reported to be between 2 and 5 for concrete (Bazant and Planas 1998).

5 Discrete element modeling

Discrete element modeling (DEM) is a numerical approach that has been proposed for simulating the mechanical behavior of granular materials (Cundall and Strack 1979). In DEM, the domain (e.g. rock) is discretized into an assembly of particles that can interact at the contact points. In this study, the CA2 software (Fakhimi 2004; Fakhimi and Villegas 2007), a hybrid discrete-finite element program for two-dimensional analysis of geomaterials, was used. The discrete particles are assumed to be rigid and circular in shape and can interact through normal and shear springs to simulate elasticity. In order to withstand tensile and deviatoric stresses, the rigid circular particles (disks) are bonded together at the contact points. The bonded-particle system has been used extensively for simulating rock failure (Potyondy 2007; Schopfer and Childs 2013). This model has proven its capabilities in simulating the mechanical response of granular media that are comparable to many experimental observations (Hazzard et al. 2002; Scholtes et al. 2011). The micromechanical parameters are $K_{n }$(normal stiffness), $K_{s }$ (shear stiffness), $n_{b}$ (normal bond), $s_{b}$ (shear bond), and $\mu$ (friction coefficient). In addition, the radius of the particles (R) must be specified. The genesis pressure $(\sigma _{0})$, which is the confining pressure during sample preparation ($\sigma _{0}$ determines the small amount of initial overlap of contacting particles) can affect the material behavior too. The significance of these parameters has been discussed in a previous study (Fakhimi and Villegas 2007).

Since quasi-brittle materials such as rock typically exhibit softening in mode I fracturing (Chong et al. 1989), a tension softening contact bond feature was implemented in the discrete element model. In this tension softening model, the normal bond at a contact point is assumed to reduce linearly after the peak tensile contact load (Fig. 11a). Therefore, a new microscopic parameter, the slope in the post peak region of the normal force-normal displacement relation between two particles in contact $(K_{np})$ is introduced. The relation between shear force and relative shear displacement of a contact $(F_{s }-U_{s})$ is linear with a slope of $K_{s }$ until reaching the contact shear strength $(s_{b})$. Following the peak point P in Fig. 11b, the shear force is assumed to drop abruptly and follow Coulomb frictional behavior under a compressive normal contact force. Softening in shear is only relevant for loading under confined conditions (mean stress greater than $1/3 \times$ UCS). This is not the case in the three point bending tests conducted in this study; no shear bonds fail in the simulation. The loading and unloading paths for both normal and shear contact forces are shown with arrows in Fig 11.

Fig. 11

Tensile softening contact bond model a Normal force and normal displacement. b Shear force and shear displacement. The post-peak slope $K_{np}$ is the parameter to control the softening (Fakhimi and Tarokh 2013)

The assumption of a linear softening behavior in Fig. 11a is a simplification and a contact point may follow a nonlinear path in the post-peak regime. This simple linear softening behavior facilitates the calibration procedure of the discrete element model. Further, the numerical results are comparable to the physical experiments with regard to process zone dimensions.

After sample preparation (i.e. creating densely packed particles), the discrete element model was calibrated for Young’s modulus, Poisson’s ratio, flexural strength, and uniaxial compressive strength of Rockville granite. For uniaxial compression tests, a $40 \times 80 \hbox { mm}$ rectangular sample was used. For the bending test, a beam with no notch, 50.8 mm in height and 127 mm in span, was numerically tested to obtain the flexural strength. The model was also calibrated for both the length and the width of the process zone at the peak load for the notched beam with 50.8 mm in height and 127 mm in span. The ratio of $K_{n}/K_{np}=22$ reproduced approximately the process zone sizes observed using the acoustic emission technique. Details on sample preparation and calibration procedure of a bonded particle model can be found in the work of Fakhimi and Villegas (2007). Following the calibration, numerical uniaxial compressive tests on a $40 \times 80$ mm rectangular sample and three-point bending tests were performed to verify the accuracy of the model. The following numerical mechanical properties were obtained for the simulated Rockville granite: $E = 26.2$ GPa, $\nu = 0.18$, UCS = 106 MPa, and $\sigma _{N} = 8.8$ MPa (flexural strength for a $50.8 \times 127$ mm beam), that are in close agreement with the properties obtained in the experiments. The micro-mechanical parameters that were found from the calibration procedure are $K_{n} = 42.4$ GPa, $K_{s} = 10.6$ GPa, $n_{b} = 7.5$ kN/m, $s_{b} = 40$ kN/m, $\mu = 0.5$, $\sigma _{0} = 4.2$ GPa (genesis pressure), and $K_{np} = 1.93$ GPa. The circular particles radii (R) were assumed to have a uniform random distribution with a range of 0.54–0.66 mm ($R_{ave }= 0.6 \hbox { mm}$).

The choice of particle size is an important decision in DEM simulations. The particle size can affect the nominal strength and process zone dimensions. In a previous study (Tarokh and Fakhimi 2014), it was shown that the process zone size is a linear function of particle size if normal contact strength $(\sigma _{n}=n_{b} /2R)$ and shear contact strength $(\sigma _{s}=s_{b} /2R)$ are kept constant. The particle size can affect the fracture toughness of the simulated material too (Huang 1999). Note that the AE locations in Fig. 8 and the small width of the process zone suggest that the AE activity is not only occurring at the contact points of the grains but within the individual grains. Because the DEM grains are not deformable, they must be smaller than the physical grain size to be able to mimic AE.

For Rockville white granite, four different beam sizes $(\hbox {height} \times \hbox {span})$ of $50.8 \times 127$, $101.6 \times 254$, $203.2 \times 508$ and $406.4 \times 1016 \hbox { mm}$ were tested. In the discrete element simulation, the random distribution of particles can have some effects on the overall mechanical properties, as well as on the size of the process zone. Therefore, for each beam size, five different random distributions for the initial locations of particles were used. The applied vertical velocity at the beam center line (at the top surface) was 2.5$\times$10$^{-10}$ m/cycle to obtain a quasi-static solution. All specimens had a 1.2 mm wide notch at their center. The ratio of notch length ($a_{0})$ to beam height (D) was kept constant at $a_{0}$/D= 0.2 for all sizes in the three-point bending tests.

6 Numerical results and discussion

6.1 Fracture toughness

The nominal tensile strength and apparent fracture toughness values were calculated using Eqs. 4 and 7 and are summarized in Table 3. The numerical values are in close agreement (less than 10% difference) with those obtained from experiments. Fig. 12 shows the fitting procedure to obtain the fracture toughness: both experimental and numerical data are shown to highlight the differences and similarities of the results. Note that the numerical results are the average values for the five different realizations on each beam size. The fracture toughness value for the simulated Rockville granite is $1.92\;\hbox {MPa}\; \hbox {m}^{0.5}$ which is in a good agreement with the experiments $(1.89\;\hbox {MPa}\;\hbox {m}^{0.5})$.

Table 3 Numerical nominal strength and apparent fracture toughness values. Average values from five realizations are shown

Fig. 12

Experimental and numerical data plotted with the linear regression of Eq. 17 to obtain $K_{IC}$

6.2 Size of the process zone

The process zone in the numerical model is defined by the contact points between circular particles that are in the post peak regime (e.g. point D in Fig 11a). On the other hand, the macroscopic crack is defined by failed contacts that have no contact bond strength, point F in Fig. 11a. The width and the length of the process zone were determined by performing statistical analyses similar to that for the physical samples; the process zone width and length were defined as three times the standard deviation of X and Y values of the induced damaged contacts, respectively. Figure 13 shows the histograms of the damage points in the numerical model. Since no damage contact occurs below the notch tip, the damaged contacts across the width and length have been divided into 8 and 10 bins, respectively, all above the notch tip. The width and length of the process zone at the peak load are reported in Table 4. Note that the reported widths and lengths of process zones are the average values for the five different realizations (random distribution of particles) for each beam size; the averages ±1 SD are reported. Considering the complexity of the rock behavior and the simplification of the numerical model, relatively good agreement between the physical and numerical results is observed (less than 20% difference with experiments).

Fig. 13

Histograms of numerical damaged contacts for beam size $406.4 \times 1016\,\hbox {mm}$ a across the width of the process zone and b across the length of the process zone

Table 4 Numerical widths and lengths of the process zones along with the standard deviations (using five different realizations)

To study the variation of the length and width of the process zone, linear fitting using Eqs. 12a and 12b was implemented for the numerical results. The four material constants obtained for the numerical data were: $W_{\infty }$ = 11.1 mm, $D_{0W}$ = 72.8 mm, $l_{\infty }$ = 100.0 mm, $D_{0l}$ = 670 mm. The variation of the length and width of the process zone with beam size (numerical and experimental) along with the prediction of the theoretical equations for each set of data are presented in Fig 14. The prediction of the theoretical (Eqs. 1, 2) is in a good agreement (less than 10% difference) with the numerical data.

Fig. 14

Variation of the average process zone dimensions with the beam height: a width of the process zone and b length of the process zone. The experimental data (averages) are included in the figure for comparison

While discrepancy in some aspects of the physical and numerical results is undeniable, there are many similarities between them that are worth mentioning. Both numerical and experimental data suggest the increase in the length and width of the process zone as the specimen size increases. It appears also that the theoretical Eqs. 1 and 2 are able of capturing the growth of the process zone size with the specimen size. Furthermore, both the physical and numerical test results suggest different $D_{0 }$ values for the width and length of the process zone. This confirms that the shape of the process zone is changed as the specimen size is increased, and that, while a specimen might be large enough for the width of the process zone to appear as a material property and independent of the specimen size, the length of the process may show size dependency until extremely large specimens are used. Thus representative elemental volumes corresponding to width and length of the process zone are different.

7 Conclusions

Acoustic emission was used to investigate the size dependency of the mode I process zone in Rockville granite. It was shown that both width and length of the process zone increase with specimen size. The variations of the width and length with specimen size were characterized using analytical equations. To demonstrate the ability of a simple bonded particle model to simulate the experiments, numerical beams of Rockville granite were generated and also demonstrated the size dependency of the process zone. The input parameters of the model were chosen so that the global model response in the form of uniaxial compressive strength, rupture strength, elastic properties, as well as the size of the process zone for the small size specimen, were in close agreement with the those obtained in the experiments. The results indicate that the shape of the process zone is changed as the specimen size is modified, and that the specimen size at which no further noticeable increase in the length of process zone is observed should be significantly larger than that for the width of the process zone for the studied rock.