Dugdale model for a dynamically expanding crack in an orthotropic solid

Abstract

The Dugdale model has been extended to a dynamically expanding crack in an orthotropic material. The stresses in the plastic zone as functions of applied stress, plastic zone tip speed and crack speed are derived. Expression for the energy release rate is obtained. The effects of plastic anisotropy and elastic anisotropy on ductile crack propagation are studied using a quadratic yield criterion and an admissible condition for self-similar crack expansion.

1 Introduction

Rapid unstable crack growth in which dynamic effects are significant is a research topic of practical importance in preventing catastrophic failure. To gain insight into the mechanical aspect of dynamic crack propagation, several analytic solutions have been obtained. The first dynamic solution was given by Yoffe (1951) who considered a crack of constant length propagating with constant speed in an isotropic medium. The first solution to a more realistic problem of an expanding crack was provided by Broberg (1960) and Craggs (1963) for isotropic materials. The expanding crack solution for orthotropic materials was obtained by Atkinson (1965) and for general anisotropic materials by Wu (2000).

In all of the aforementioned works the materials were assumed to be purely elastic and the stress field is singular at the crack tips. The Dugdale model (Dugdale 1960) is a simplified model commonly used to remove the stress singularity with crack-tip plasticity. In the Dugdale model, yielding is assumed to take place only in a line plastic zone along the crack edge. This line plastic zone is then treated as an extended part of the physical crack with the closure stress $\sigma _{22}=Y$ acting on the extended crack faces. The line plastic zone and the physical crack form the effective mathematical crack. With the Dugdale model, the elastic-plastic crack problem is reduced to an elastic one with finite stresses at the effective crack tip, which is actually the end of the plastic zone.

The Dugdale model was first developed for a stationary mode I crack in an isotropic material. The model was subsequently extended to a propagating semi-infinite crack by Goodier and Field (1963), a moving crack of castanet length by Kanninen (1968), and an expanding crack by Atkinson (1968), Embley and Sih (1972) for mode I and Wu and Huang (2013) for mode II and III cracks. An extension to a stationary mode I crack in orthotropic materials was provided by Stormont et al. (1972). However, the Dugdale model has not been applied to an expanding mode I crack in an orthotropic medium yet. The objective of this paper is thus to generalize the Dugdale model so that the inertial and anisotropic effects are both included for mode I cracks.

In the original Dugdale model, Tresca yield criterion is implicitly assumed and $Y$ is simply taken as the uniaxial yield stress of the material. This is true for static or slowly moving cracks in isotropic materials where the normal stress parallel to the crack line $\sigma _{11}=T<Y$. However, anisotropy as well as inertia effects may significantly increase $T$ (Stormont et al. 1972; Wu and Ru 2014) so that the influence of $T$ cannot be ignored. Here a more general yield criterion $F\left( T,Y\right) =0$ is considered. Moreover, a limiting crack speed with the elastic and plastic anisotropy taken into account will be determined using a yield criterion.

2 Moving dislocation solution

Consider an infinite orthotropic elastic medium at rest and stress-free at $t=0$ with the $x_{1}$ and $x_{2}$ axes as the material symmetry axes. A straight infinitely-long dislocation with relative displacement $\Delta u_{2},$ aligned parallel to the $x_{3}$-axis, appears at $t=0^{+}$and moves on the plane $x_{2}=0$ thereafter with constant subsonic speed $v$ along the $x_{1}$-axis. The corresponding $\sigma _{11}$ and $\sigma _{22}$ are given by (Wu 2002)

$$\begin{aligned} \sigma _{22}(x_{1},t)= & {} \frac{\text{ Re }\left[ L_{22}\left( y_{1}\right) \right] }{2\pi t\left( y_{1}-v\right) }{\Delta {u}_{2}}, \end{aligned}$$

(1)

$$\begin{aligned} \sigma _{11}(x_{1},t)= & {} -\frac{\text{ Re }\left[ S_{12}(y_{1})\right] }{2\pi t\left( y_{1}-v\right) s_{11}}\Delta u_{2}-\frac{s_{12}}{s_{11}}\sigma _{22}(x_{1},t),\nonumber \\ \end{aligned}$$

(2)

where $y_{1}=x_{1}/t, s_{ij}$ is the contracted notation for the elastic compliance, Re denotes the real part and

$$\begin{aligned} L_{22}(y_{1})&=\frac{X(y_{1})}{\sqrt{\hat{C}_{11}C_{66}Y(y_{1})}}, \end{aligned}$$

(3)

$$\begin{aligned} S_{12}(y_{1})&=-\frac{Z(y_{1})}{\sqrt{\hat{C}_{11}C_{66}Y(y_{1})}}. \end{aligned}$$

(4)

Here

$$\begin{aligned} X(y_{1})&=\left( \hat{C}_{11}C_{22}-C_{12}^{2}\right) \sqrt{\hat{C} _{66}C_{66}}-\rho y_{1}^{2}C_{66}\sqrt{\hat{C}_{11}C_{22}}, \\ Y(y_{1})&=\left( \sqrt{\hat{C}_{11}C_{22}}+\sqrt{\hat{C}_{66}C_{66}}\right) ^{2}-(C_{12}+C_{66})^{2}, \\ Z(y_{1})&=\left( \sqrt{\hat{C}_{11}C_{22}}C_{66}-C_{12}\sqrt{\hat{C} _{66}C_{66}}\right) , \end{aligned}$$

$\hat{C}_{ij}=C_{ij}-\rho y_{1}^{2}, C_{ij}$ is the contracted notation for the elastic constants and $\rho$ is the density. The values of $S_{12}\left( y_{1}\right)$ and $L_{22}\left( y_{1}\right)$ are real if $y_{1}<c_{2}=\sqrt{C_{66}/\rho }$. They are purely imaginary if $y_{1}>c_{1}= \sqrt{C_{11}/\rho }$. The Rayleigh surface wave speed $c_{R}$ is determined by $L_{22}\left( c_{R}\right) =0$ (Ting 1996). The expressions shown above are for plane strain $\left( \varepsilon _{33}=0\right)$ deformation. For plane stress deformation $(\sigma _{33}=0)$ considered in this paper the elastic constant $C_{pq}$ should be replaced with the reduced elastic constant $C_{pq}^{\prime }$ defined as (Ting 1996)

$$\begin{aligned} C_{pq}^{\prime }=C_{pq}-\frac{C_{p3}C_{3q}}{C_{33}}. \end{aligned}$$

3 Dugdale model

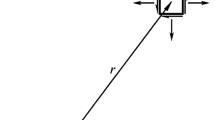
A crack is assumed to be initiated at the origin at $t=0$, and subsequently expands at constant speed $U$ along the $x_{1}$ axis under an applied uniform stress $\sigma _{22}=P$. Plastic yielding is assumed to occur in the region $Ut\le \left| x_{1}\right| \le Vt,$ or $U\le \left| y_{1}\right| \le V,$ where $V <c_{R}$ is the plastic zone tip speed. The stress is required to be finite in the entire body. The configuration of the problem is shown in Fig. 1. In the yielding zone, it is assumed that $\sigma _{11}=T$ and $\sigma _{22}=Y,$ where $T$ and $Y$ are constants. The constant stress $Y$ on the plastic-zone boundary is related to the yield properties of the material through a yield criterion. In the original Dugdale model, Tresca yield criterion is implicitly assumed so that $Y$ is simply the uniaxial tensile yield stress of the material. In this paper the stresses $T$ and $Y$ are assumed to satisfy a criterion $F\left( T,Y\right) =0$.

Fig. 1

An expanding line crack with Dugdale plastic zone

The problem may also be formulated as the problem of a crack of length $2Vt$ with the following stress on the crack faces:

$$\begin{aligned} \sigma _{22}(y_{1})= & {} \left[ 1+H\left( y_{1}-U\right) \right. \nonumber \\&\left. -\,H\left( y_{1}+U\right) \right] Y-P, \quad \left| y_{1}\right| <V, \end{aligned}$$

(5)

or

$$\begin{aligned} \sigma _{22}^{\prime }(y_{1})=\left[ \delta \left( y_{1}-U\right) -\delta \left( y_{1}+U\right) \right] Y, \quad \left| y_{1}\right| <V, \end{aligned}$$

(6)

where $\sigma _{22}^{\prime }(y_{1})$ denotes the derivative of $\sigma _{22}(y_{1})$ with respect to $y_{1}, \delta$ the Dirac delta function and $H$ the unit step function. The crack can be simulated by a distribution of dislocations moving at a constant speed $v, -V\le v \le V$ along the $x_{1}$ axis. However, the applied stress is a homogeneous function of degree $0$, while the stress given by (1) for the moving dislocation is homogeneous function of degree $-1,$ thus time rate of $\sigma _{22},$ instead of $\sigma _{22},$ is represented by (Wu and Huang 2013)

$$\begin{aligned} \sigma _{22}^{\prime }(y_{1})=\frac{1}{2\pi y_{1}}\text{ Re }\left[ L_{22}\left( y_{1}\right) \right] \int _{-V}^{V}\frac{1}{v-y_{1}}g\left( v\right) dv\mathbf {,} \end{aligned}$$

(7)

where $L_{22}\left( y_{1}\right)$ is given by Eq. (3), $g\left( y_{1}\right)$ is related to the relative crack face displacement $\Delta u_{2}$ by

$$\begin{aligned} g\left( y_{1}\right) =-\frac{\partial }{\partial y_{1}}\left( \frac{\partial \Delta u_{2}}{\partial t}\right) . \end{aligned}$$

(8)

The crack closure conditions lead to

$$\begin{aligned} \int _{-V}^{V}\left( \int _{0}^{y_{1}}\frac{g\left( \eta \right) }{\eta }d\eta \right) dy_{1}=0. \end{aligned}$$

(9)

The general solution of $g\left( y_{1}\right)$ satisfying Eqs. (7 ) and (9) is given by

$$\begin{aligned} g\left( y_{1}\right) =-\frac{2}{\pi }\frac{1}{\sqrt{V^{2}-y_{1}^{2}}} \,\int _{-V}^{V}\frac{\eta \sqrt{V^{2}-\eta ^{2}}}{\eta -y_{1}}\frac{\sigma _{22}^{\prime }(\eta )}{L_{22}\left( \eta \right) }d\eta , \end{aligned}$$

(10)

where the finite stress requirement has been taken into account. With (6), (10) yields

$$\begin{aligned} \sigma _{22}^{\prime }(y_{1})= & {} \frac{2U\left( V^{2}-U^{2}\right) ^{1/2}}{\pi }\nonumber \\&\times \, \text{ Re }\left[ \frac{1}{\left( y_{1}^{2}-V^{2}\right) ^{1/2}\left( U^{2}-y_{1}^{2}\right) }\right] \nonumber \\&\times \,\frac{\text{ Re }\left[ L_{22}\left( y_{1}\right) \right] }{L_{22}\left( U\right) }P. \end{aligned}$$

(11)

Integrating Eq. (11) leads to

$$\begin{aligned}&\sigma _{22}(y_{1})=\frac{2U\sqrt{\left( V^{2}-U^{2}\right) }}{\pi }\nonumber \\&\quad \times \,\text{ Re } \left[ \int _{\infty +i0}^{y_{1}+i0}\frac{L_{22}\left( z\right) }{\sqrt{ z^{2}-V^{2}}\left( U^{2}-z^{2}\right) }dz\right] \frac{Y}{L_{22}\left( U\right) }.\nonumber \\ \end{aligned}$$

(12)

A link between the remote applied stress $P$ and the stress $Y$ can be established by setting $y_{1}=0$ in Eq. (12) as

$$\begin{aligned} P=\lambda (U,V)Y, \end{aligned}$$

(13)

where

$$\begin{aligned}&\lambda (U,V) =\frac{2\sqrt{1-\left( \frac{U}{V}\right) ^{2}}}{ \pi }\frac{\tilde{L}_{22}(U,V)}{L_{22}\left( U\right) }, \end{aligned}$$

(14)

$$\begin{aligned}&\tilde{L}_{22}(U,V) =UV\text{ Re }\left[ \int _{i0}^{\infty +i0}\frac{ L_{22}\left( z\right) }{\sqrt{z^{2}-V^{2}}\left( U^{2}-z^{2}\right) }dz \right] .\nonumber \\ \end{aligned}$$

(15)

Note that the integrand for $\tilde{L}_{22}$ of (15) contains a simple pole at $z=U$ and a branch point at $z=V$. In view of the fact that $\text{ Re } \left[ L_{22}\left( y_{1}\right) \right] =0$ if $y_{1}>c_{1}$, Eq. (15 ) may also be rewritten as

$$\begin{aligned} \tilde{L}_{22}(U,V)=\frac{\pi }{2\sqrt{1-\left( \frac{U}{V}\right) ^{2}}} L_{22}\left( U\right) +\hat{L}_{22}\left( U,V\right) , \end{aligned}$$

(16)

where

$$\begin{aligned} \hat{L}_{22}\left( U,V\right) =UV\text{ Re }\left[ \! \int _{V}^{c_{1}}\!\!\frac{ L_{22}\left( z\right) }{\sqrt{z^{2}-V^{2}}\left( U^{2}-z^{2}\right) }dz \!\right] . \end{aligned}$$

(17)

With Eq. (16), Eq. (14) may be expressed as

$$\begin{aligned} \lambda (U,V)=1\mathbf {+}\frac{2\sqrt{1-\left( \frac{U}{V}\right) ^{2}}}{\pi }\frac{\hat{L}_{22}\left( U,V\right) }{L_{22}\left( U\right) }. \end{aligned}$$

(18)

The stress $\sigma _{11}(y_{1})$ can be derived by the same procedure as that for $\sigma _{22}(y_{1}).$ The result is

$$\begin{aligned} \sigma _{11}(y_{1})= & {} \frac{1}{s_{11}}\text{ Re }\left[ UV\int _{\infty +i0}^{y_{1}+i0}\frac{S_{12}\left( z\right) }{\sqrt{z^{2}-V^{2}}\left( U^{2}-z^{2}\right) }dz\right] \nonumber \\&\quad \times \,\frac{Y-P}{\hat{L}_{22}\left( U,V\right) } -\frac{s_{12}}{s_{11}}\sigma _{22}(y_{1}), \end{aligned}$$

(19)

where Eqs. (12), (13) and (18) have been incorporated. In particular, at $y_{1}=V,$ Eq. (19) yields

$$\begin{aligned} \frac{T}{Y}=\frac{1}{s_{11}}\!\left[ \! \frac{2\sqrt{1-\left( \frac{U}{V}\right) ^{2}}\hat{S}_{12}\left( U,V\right) }{\pi L_{22}\left( U\right) } +s_{12}\left( \lambda (U,V)-1\right) \!\right] \!, \end{aligned}$$

(20)

where

$$\begin{aligned}&\hat{S}_{12}\left( U,V\right) \nonumber \\&\quad =\text{ Re }\left[ UV\int _{V}^{c_{1}} \frac{1}{\sqrt{z^{2}-V^{2}}\left( U^{2}-z^{2}\right) }S_{12}\left( z\right) dz\right] .\nonumber \\ \end{aligned}$$

(21)

As the crack propagates energy is dissipated by the plastic flow in the yield zone. The rate of the plastic energy dissipation at the right crack tip is given by

$$\begin{aligned} \dot{W}_{p}= & {} \sigma _{22}^{\left( 0\right) }\!\int _{Ut}^{Vt}\Delta \dot{u} _{2}\left( y_{1},t\right) dx_{1} \nonumber \\= & {} \!\frac{4}{\pi }U^{2}t\,\left( \log \left( \!\frac{U}{V}\right) +\sqrt{\left( \!\frac{V}{U}\right) ^{2}-1}\!\cos ^{-1}\left( \frac{U}{V}\right) \right) \nonumber \\&\times \,\frac{Y^{2}}{L_{22}\left( U\right) }. \end{aligned}$$

(22)

Equation (22) is a generalization of the result obtained by Embley and Sih (1972) for isotropic material. The energy release rate per unit crack extension, $G,$ may be defined as

$$\begin{aligned} G= & {} \frac{\dot{W}_{p}}{U}=\frac{4}{\pi }Ut\left( \log \left( \frac{U}{V} \right) +\sqrt{\left( \frac{V}{U}\right) ^{2}-1}\cos ^{-1}\left( \frac{U}{V} \right) \right) \nonumber \\&\times \,\frac{Y^{2}}{L_{22}\left( U\right) }. \end{aligned}$$

(23)

From Eq. (13), Eq. (23) may also be expressed as

$$\begin{aligned} G= & {} \pi Ut\nonumber \\&\times \,\frac{\log \left( \frac{U}{V}\right) {+}\sqrt{\left( \frac{V}{U} \right) ^{2}{-}1}\cos ^{-1}\left( \frac{U}{V}\right) }{1{-}\left( \frac{U}{V} \right) ^{2}}\frac{P^{2}L_{22}\left( U\right) }{\left[ \tilde{L}_{22}(U,V) \right] ^{2}}.\nonumber \\ \end{aligned}$$

(24)

For small scale yielding, $U\rightarrow V$, and Eq. (24) becomes

$$\begin{aligned} G=\frac{\pi Vt}{2}\frac{P^{2}L_{22}\left( V\right) }{\left[ \tilde{L} _{22}(V,V)\right] ^{2}}. \end{aligned}$$

(25)

Equation (25) is identical with the energy release rate for a crack expanding with the constant speed $V$ under the applied stress $P$ in a purely elastic solid (Wu 2000).

For stationary cracks, $U \rightarrow 0$, the limiting form of either $\hat{L}_{22}(U,V)$ or $\hat{S}_{12}(U,V)$ is given by

$$\begin{aligned}&\left[ \hat{L}_{22}(U,V),\hat{S}_{12}(U,V)\right] \nonumber \\&\quad =-\frac{\sin ^{-1}\left( \frac{U}{V}\right) }{\sqrt{1-\left( \frac{U}{V}\right) ^{2}}}\left[ L_{22}\left( 0\right) ,S_{12}\left( 0\right) \right] . \end{aligned}$$

(26)

With Eq. (26), Eq. (14) becomes

$$\begin{aligned} \lambda =\frac{2}{\pi }\cos ^{-1}\left( \frac{a}{b}\right) , \end{aligned}$$

(27)

with $a=Ut$ and $b=Vt$ representing the half crack length and the half plastic zone length, respectively. Equation (27) shows that for stationary cracks the proportionality factor $\lambda$ is independent of the elastic constants. Equation (20) is simplified as (Ting 1996)

$$\begin{aligned} \frac{T}{Y}=\sqrt{\frac{s_{22}}{s_{11}}}\left( 1-\frac{P}{Y}\right) . \end{aligned}$$

(28)

Equation (28) agrees with the result obtained by Stormont et al. (1972). Equation (24) becomes

$$\begin{aligned} G=\pi a\frac{\log \left( \frac{a}{b}\right) +\sqrt{\left( \frac{b}{a}\right) ^{2}-1}\cos ^{-1}\left( \frac{a}{b}\right) }{\left( \cos ^{-1}\left( \frac{a }{b}\right) \right) ^{2}}\frac{P^{2}}{L_{22}\left( 0\right) }. \end{aligned}$$

(29)

For small scale yielding, $a\rightarrow b$, Eq. (29) yields the energy release rate for a stationary crack of half length $a$ under the applied stress $P$ in a purely elastic material:

$$\begin{aligned} G_{0}=\frac{\pi a}{2}\frac{P^{2}}{L_{22}\left( 0\right) }. \end{aligned}$$

(30)

4 Yield criterion and limiting crack speed

The results derived in the previous section depend only on the elastic properties of the material and are valid regardless of the form of the yield criterion. To proceed further, the following quadratic Mises–Hill yield criterion (Kaminskii and Bogdanova 1996) is used:

$$\begin{aligned} \frac{T^{2}}{Y_{1}^{2}}-\frac{TY}{Y_{1}Y_{2}}+\frac{Y^{2}}{Y_{2}^{2}}=1, \end{aligned}$$

(31)

where $Y_{1}$ and $Y_{2}$ are, respectively, the tensile yield stresses in the $x_{1}$ and $x_{2}$ directions. From Eq. (31), the ratio $\phi =Y/Y_{2}$ can be expressed as

$$\begin{aligned} \phi \left( U,V\right) =\left[ \left( \frac{BT}{Y}\right) ^{2}-\frac{BT}{Y}+1 \right] ^{-1/2}, \end{aligned}$$

(32)

where $B=Y_{2}/Y_{1}$ and $T/Y$ as a function of $U$ and $V$ is given by Eq. (20). A normalized applied stress may be introduced as

$$\begin{aligned} \frac{P}{Y_{2}}=\lambda \left( U,V\right) \phi \left( U,V\right) , \end{aligned}$$

(33)

where $\lambda$ is given by Eq. (18).

As will be shown in the next section that anisotropy as well as inertia effects may significantly increase the normal stress parallel to the crack line, $T$. The presence of large $T$ may cause yielding to spread out in a direction normal to the crack line and the crack to turn from the original straight path. These cicumstances would invalidate the use of the Dugdale model. Let $U_{\max }$ be the limiting crack speed defined as the maximum speed below which the crack propagates along the original crack line. It is postulated here that at a fixed applied stress $P,$ a crack can expand at speed $U$ only if

$$\begin{aligned} \frac{T}{Y}\le \frac{1}{B}. \end{aligned}$$

(34)

The limiting speed $U_{\max }$ is determined as the speed for which equality sign in Eq. (34) holds. The condition is a generalization of the one proposed by Kanninen (1968) for isotropic materials $(B=1)$. From Eqs. (32), (34) implies that for $U\le U_{\max }, 1\le \phi \le 2/\sqrt{3}\approx 1.154$ with $\phi =1$ at $U_{\max }.$ Moreover as $P\rightarrow 0$, Eqs. (28) and (34) yield

$$\begin{aligned} B\le \sqrt{A}, \end{aligned}$$

(35)

where $A=s_{11}/s_{22}=C_{22}^{\prime }/C_{11}^{\prime }.$ Equation (35 ) is a necessary condition for the Dugdale model to be applicable.

5 Numerical results and discussions

Consider a class of orthotropic materials characterized by the following reduced elastic constants for plane stress condition

$$\begin{aligned} C_{11}^{\prime }/C_{66}^{\prime }=2.5,C_{12}^{\prime }/C_{66}^{\prime }=0.5, \ C_{22}^{\prime }/C_{66}^{\prime }=2.5A. \end{aligned}$$

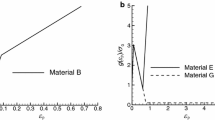
For $A=1$ the material is isotropic with the Poisson ratio $\nu =0.2.$ Using the preceding equations, the relative plastic zone size $(V-U)/U$ [Eq. (13)] and the normalized energy release rate $G/G_{0}$ [Eqs. (24) and (30)], the stress ratio $T/Y$ [Eq. (20)] are plotted as a function of $\lambda =P/Y$ [Eq. (18)] for $U=0.5c_{2}$ in Figs. 2, 3, and 4, respectively, for $A=0.5,1,5$. The results were obtained by varying $V$ from $U$ to $c_{R}$. The Rayleigh surface wave speed, $c_{R}/c_{2}$, is $0.84,0.90,0.98$ for $A=0.5,1,5,$ respectively. For comparison purposes, the corresponding results [Eqs. (27), (29) and (28) ] for stationary cracks are also given in those plots. Figures 2 and 3 show that the variations of $(V-U)/U$ and $G/G_{0}$ with $\lambda$ share the same feature. For a fixed value of $A,$ the quantities increase with $\lambda$ at a given $U$ but decrease with $U$ at a given $\lambda$. Moreover, the reductions of the quantities due to $U$ are inversely proportional to $A$. Figure 4 reveals that, similar to the case of stationary cracks, $T$ decreases almost linearly with $\lambda$ for $U=0.5c_{2}$ regardless of the value of $A;$ however, the values of $T$ are significantly larger than those for stationary cracks.

Fig. 2

The relative plastic zone size $(V-U)/U$ as a function of $\lambda =P/Y$ for $U=0.5c_{2}$ and $U\rightarrow 0$

Fig. 3

The normalized energy release rate $G/G_{0}$ as a function of $\lambda =P/Y$ for $U=0.5c_{2}$ and $U\rightarrow 0$

Fig. 4

The stress ratio $T/Y$ as a function of $\lambda =P/Y$ for $U=0.5c_{2}$ and $U\rightarrow 0$

Equation (35) shows that for a given $A, B$ can only vary from $0$ to $\sqrt{A}$.The results displayed Figs. 2 and 3 may be regarded as those for the materials with the lower bound $B=0$ such that $Y=Y_{2}$ as assumed in the original Dugdale model. For $B=0,$ Eq. (34) is satisfied identically and the crack speed is only limited by the elastic Rayleigh surface wave speed. To study the influence of the plastic anisotropy characterized by $B$, the limiting crack speed, $U_{\max },$ as a function of $P/Y_{2}$ is plotted in Fig. 5 for $A=0.5,1,5$ with the upper bound $B= \sqrt{A}.$ It may be inferred from Fig. 5 that at a fixed $P,$ the limiting crack speed increases with decreasing $B$ for a given $A$ but with increasing $A$ for a given $B.$ Figure 5 also implies that there is a minimum applied stress for a crack to propagate at a certain speed. For example for $U=0.5c_{2}$ the minimum value of $P/Y_{2}= 0.55,0.47,0.37$, respectively, for $A=0.5,1,5$ and $B=\sqrt{A}$. The plots of $(V-U)/U$ and $G/G_{0}$ with $P/Y_{2}$ for $B=\sqrt{A}$ can be obtained, respectively, from Fig. 2, and 3 for $B=0$ by adjusing the horizontal axis according to Eq. (33). As an example, $G/G_{0}$ with $P/Y_{2}$ for $A=0.5,1,5$ and $B= \sqrt{A}$ at $U=0.5c_{2}$ is shown in Fig. 6. For comparison purposes, the corresponding results in Fig. 3 for $B=0$ are also plotted. It is clearly seen that at a fixed $P,$ the energy release rate decreases as $B$ increases for a given $A$ but increases as $A$ increases for a given $B.$

Fig. 5

The limiting crack speed $U_{\max }$ as a function of $P/Y_{2}$ for $A=0.5,1,5$ and $B=\sqrt{A}$

Fig. 6

The normalized energy release rate $G/G_{0}$ as a function of $P/Y_{2}$ for $A=0.5,1,5$ and $B=0,\sqrt{A}$ at $U=0.5c_{2}$