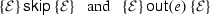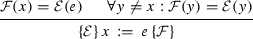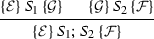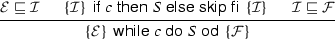Securing a compiler transformation

Abstract

A compiler optimization may be correct and yet be insecure. This work focuses on the common optimization that removes dead (i.e., useless) store instructions from a program. This operation may introduce new information leaks, weakening security while preserving functional equivalence. This work presents a polynomial-time algorithm for securely removing dead stores. The algorithm is necessarily approximate, as it is shown that determining whether new leaks have been introduced by dead store removal is undecidable in general. The algorithm uses taint and control-flow information to determine whether a dead store may be removed without introducing a new information leak. A notion of secure refinement is used to establish the security preservation properties of other compiler transformations. The important static single assignment optimization is, however, shown to be inherently insecure.

1 Introduction

An optimizing compiler translates programs expressed in high-level programming languages into executable machine code. This is typically done through a series of program transformations, many of which are aimed at improving performance. It is essential that each transformation preserve functional behavior, so that the resulting executable has the same input–output functionality as the original program. It is difficult to formally establish the preservation property, given the complexity and the size of a typical compiler; this is a long-standing verification research challenge.

Along with functional preservation, one would like to ensure the preservation of security properties. I.e., the final executable should be at least as secure against attack as the original program. At first glance, it may seem that a functionally correct compiler should also be secure, but this is not so. A well-known example is dead store elimination [10, 13]. Consider the program on the left hand side of Fig. 1. A secret password is read into a local variable and used. After the use, the memory containing password data is erased, so that the password does not remain in the clear any longer than is necessary. To a compiler, however, the erasure instruction appears useless, as the new value is not subsequently used. The dead-store elimination optimization targets such useless instructions, as removing them speeds up execution. Applied to this program, the optimization removes the instruction erasing x. The input–output behavior of the two programs is identical, hence the transformation is correct. In the resulting program, however, the password may remain in the clear in the stack memory beyond the local procedure scope, as a procedure return is typically implemented by moving the stack pointer to point to a new frame, without erasing the current one. As a consequence, an attack that gains access to the program stack in the untrusted procedure may be able to read the password from the stack memory, as might attacks that gain access after the procedure foo has terminated.

Fig. 1

C programs illustrating the insecurity of dead-store elimination

There are workarounds for this problem, but those are specific to a language and a compiler. For instance, if x is declared volatile in C, the compiler will not remove any assignments to x. Compiler-specific pragmas could also be applied to force the compiler to retain the assignment to x. But such workarounds are unsatisfactory, in many respects. First, a workaround can be applied only when a programmer is aware of the potential problem, which may not be the case. Next, a programmer must understand enough of the compiler’s internal workings to implement the correct fix, which need not be the case either—compilation is a complex, opaque process. Furthermore, the solution need not be portable, as studied in [21]. Finally, the fix may be too severe: for instance, marking x as volatile blocks the removal of any dead assignments to x, although an assignment x := 5 immediately following x := 0 can be removed safely, without leaking information. Inserting instructions to clear potentially tainted data before untrusted calls is also inefficient; as taint analysis is approximate, such instructions may do more work than is necessary. For these reasons, we believe it is necessary to find a fundamental solution to this problem.

One possible solution is to develop an analysis which, given an instance of a correct transformation, checks whether it is secure. This would constitute a Translation Validation mechanism for security, similar to those developed for correctness in e.g., [15, 18, 22]. We show, however, that translation validation for security of dead store elimination is undecidable for general programs and PSPACE-hard for finite-state programs. On the other hand, translation validation for the correctness of dead store elimination is easily decided in polynomial time.

Faced with this difficulty, we turn to provably secure dead-store removal methods. Our algorithm takes as input a program P and a list of dead assignments. It prunes that list to those assignments whose removal does not introduce a new information leak, and removes them from P, obtaining the result program Q. The analysis of each assignment relies on taint and control-flow information from P. We formalize a notion of secure transformation and establish that this algorithm is secure. Although the algorithm relies on taint information, it is independent of the specific analysis method used to obtain this information, as it relies only on the results of such a method, presented as a taint proof outline for P.

Three important points should be noted. First, the algorithm is necessarily sub-optimal given the hardness results; it may retain more stores than is strictly necessary. Second, the algorithm enforces relative rather than absolute security. I.e., it does not eliminate information leaks from P, it only ensures that no new leaks are introduced in the transformation from P to Q. Finally, the guarantee is for information leakage, which is but one aspect of program security. Other aspects, such as protection against side-channel attacks, must be checked separately.

The difference between correctness and security is fundamentally due to the fact that correctness can be defined by considering individual executions, while the definition of information flow requires the consideration of pairs of executions. The standard proof methodology, based on refinement relations, that is used to show the correctness of transformations, does not, therefore, always preserve security properties. We develop a stronger notion of refinement which preserves information flow, and use it to show that several common compiler optimizations do preserve information flow properties. Unfortunately, an optimization that is key to modern compilers, the SSA (static single assignment) transformation, does not satisfy this stronger notion and will, in fact, leak information. In follow-up work [7], we present a method to restore the security level of a program after a series of SSA-dependent transformations.

To summarize, the main contributions of this work are a formulation of the security of a transformation; results showing that a posteriori verification of the security of dead store elimination is undecidable in general and difficult for finite-state programs; a new dead-store elimination procedure which is provably correct and secure; and a general proof method, secure refinement, which helps establish security preservation for several standard compiler transformations. These are first steps towards the construction of a fully secure compiler.

2 Preliminaries

We formulate the correctness and security of program transformations for a basic programming language. The language is deliberately kept simple to clearly illustrate the issues and the proof arguments.

2.1 Program syntax

Programs are structured While programs with syntax given below. (Illustrative examples are, however, written in C.) All variables have Integer type. Variables are partitioned into input and state variables and, on a different axis, into sets H (high security) and L (low security). All state variables are low security while input variables may be of either level.

A program can be represented by its control flow graph (CFG). (We omit a description of the conversion process, which is standard.) Each node of the CFG represents a program location, and each edge is labeled with a guarded command, of the form “$g \,\rightarrow \,x \,:=\,e$” or “$g \,\rightarrow \,\mathsf {skip}$” or “$g \,\rightarrow \,\mathsf {out}(e)$”, where g is a Boolean predicate and e is an expression over the program variables. A special node, $\mathsf {entry}$, with no incoming edges, defines the initial program location, while a special node, $\mathsf {exit}$, defines the final program location. Values for input variables are specified at the beginning of the program and remain constant throughout execution.

2.2 Program semantics

The semantics of a program is defined in the standard manner. A program state s is a pair (m, p), where m is a CFG node (referred to as the location of s) and p is a function mapping each variable to a value from its type. The function p can be extended to evaluate an expression in the standard way (omitted). We suppose that a program has a fixed initial valuation for its state variables. An initial state is one located at the $\mathsf {entry}$ node, where the state variables have this fixed valuation. The transition relation is defined as follows: a pair of states, $(s=(m,p),t=(n,q))$ is in the relation if there is an edge $f=(m,n)$ of the CFG which connects the locations associated with s and t, and for the guarded command on that edge, either i) the command is of the form $g \,\rightarrow \,x \,:=\,e$, the guard g evaluates to $true$ at p, and the function q(y) is identical to p(y) for all variables y other than x, while q(x) equals p(e); ii) the command is of the form $g \,\rightarrow \,\mathsf {skip}$ or $g \,\rightarrow \,\mathsf {out}(e)$, the guard g evaluates to $true$ at p, and q is identical to p. The predicates guarding the outgoing edges of a node partition the state space, so that a program is deterministic and deadlock-free. A execution trace of the program (referred to in short as a trace) from state s is a sequence of states $s_0=s,s_1,\ldots$ such that adjacent states are connected by the transition relation. A computation is a trace from the initial state. A computation is terminating if it is finite and the last state has the $\mathsf {exit}$ node as its location.

2.3 Post-domination in CFG

A set of nodes N post-dominates a node m if each path in the CFG from m to $\mathsf {exit}$ passes through at least one node from N.

2.4 Information leakage

Information leakage is defined in a standard manner [3, 9]. A program P is said to leak information if there is a pair of H-input values $\{a,b\}$, with $a \ne b$, and an L-input c such that the computations of P on inputs $(H=a,L=c)$ and $(H=b,L=c)$ either (a) differ in the sequence of output values produced by the $\mathsf {out}$ actions, or (b) both terminate but differ in the value of one of the L-variables at their final states. We call (a, b, c) a leaky triple for program P.

2.5 Correct transformation

Program transformations are assumed not to alter the set of input variables. A transformation from program P to program Q may alter the code of P or the set of state variables. The transformation is correct if, for every input value a, the sequence of output values for executions of P and Q from a is identical.

2.6 Secure transformation

A correct transformation supplies the relative correctness guarantee that Q is at least as correct as P; it does not assure the correctness of either program with respect to a specification. Similarly, a secure transformation ensures relative security, i.e., that Q is not more leaky than P; it does not ensure the absolute security of either P or Q. We define a transformation from P to Q to be secure if the set of leaky triples for Q is a subset of the leaky triples for P.

Suppose that the transformation from P to Q is correct. Consider a leaky triple (a, b, c) for Q. If the computations of Q from inputs $(H=a,L=c)$ and $(H=b,L=c)$ differ in their output, from correctness, this difference must also appear in the corresponding computations in P. Hence, the only way in which Q can be less secure than P is if both computations terminate in Q with different values for low-variables, while the corresponding computations in P terminate with identical values for low-variables.

2.7 Quantifying leakage

This definition of a secure transformation does not distinguish between the amount of information that is leaked by the two programs. Consider, for instance, a program P which leaks the last four digits of a credit card number, and a (hypothetical) transformation of P to a program Q where the entire card number is made visible. This transformation would be considered secure by the formulation above, as both programs leak information about the credit card number. From a practical standpoint, though, one might consider Q to have a more serious leak than P, as the last four digits are commonly printed on credit card statements and can be considered to be non-secret data. For this example, it is possible to make the required distinction by partitioning the credit card number into a secure portion and a “don’t care” final four digits. More generally, a formulation of secure transformation should take the “amount of leaked information” into account; however, there is as yet no standard definition of this intuitive concept, cf. [19] for a survey. We conjecture, however, that the secure dead-store elimination procedure presented here does not allow a greater amount of information leakage than the original program. A justification for this claim is presented in Sect. 5.

3 The hardness of secure translation validation

The Translation Validation approach to correctness [15, 18, 22] determines, given input program P, output program Q, and (possibly) additional hints from the compiler, whether the functional behavior of P is preserved in Q. We show, however, that translation validation for secure information flow is substantially more difficult than validation for correctness. The precise setting is as follows. The input to the checker is a triple (P, Q, D), where P is an input program, Q is the output program produced after dead store elimination, and D is a list of store instructions, known to be dead (i.e., useless) through a standard, imprecise liveness analysis on P. The question is to determine whether Q is at most as leaky as P. To begin with, we establish that correctness can be checked in polynomial time. We then establish that checking security is undecidable in general. It is also hard for programs with finite-state domains: PSPACE-complete for general finite-state programs, and co-NP-complete for loop-free, finite-state programs (proofs in the Appendix).

Theorem 1

The correctness of a dead store elimination instance (P, Q, D) can be checked in PTIME.

Proof

The check proceeds as follows. First, check that every store in D is dead in P, by re-doing the liveness analysis on P. Then check that P and Q are identical programs, except at the location of stores in D, which are replaced with $\mathsf {skip}$. These checks are in polynomial time in the size of the programs. $\square$

Theorem 2

Checking the security of a dead store elimination given as a triple (P, Q, D) is undecidable for general programs.

Proof

We use a simple reduction from the Halting problem. Consider a program Y with no input and no output. Let h be a fresh High security input variable, and let l be a fresh Low security state variable. Define program P(h) as $Y; \, l \,:=\,h; \, l \,:=\,0$, program Q(h) as $Y; \, l \,:=\,h$, and let $D=\{``l \,:=\,0''\}$.

If Y terminates, then P has no leaks, while Q leaks the value of h. If Y does not terminate, then by the definition of leakage, neither P nor Q have an information leak. Thus, the transformation is insecure if, and only if, Y terminates. $\square$

4 A taint proof system

Taint analysis is a static program analysis method aimed at tracking the influence of input variables on program state. The taint proof system introduced here records the results of such an analysis. It is similar to the proof systems of [9, 20] but explicitly considers per-variable, per-location taints. It is inspired by the taint proof system of [4], which is the basis of the STAC taint analysis plugin of the Frama-C compiler. There are small differences in the treatment of IF-statements with a tainted condition: in that system, every variable assigned in the scope of the condition must be tainted; in ours, the taint may be delayed to a point immediately after the statement.

The Appendix includes a proof of soundness for this system. Although the focus here is on structured programs, the properties of the taint system and the overall results carry over to arbitrary CFGs.

4.1 Preliminaries

A taint environment is a function $\mathcal {E}: { Variables} \rightarrow \mathsf {Bool}$ which maps each program variable to a Boolean value. For a taint environment $\mathcal {E}$, we say that x is tainted if $\mathcal {E}(x)$ is true, and untainted otherwise. The taint environment $\mathcal {E}$ can be formally extended to apply to terms as follows:

• $\mathcal {\tilde{E}}(c)$ is false, if c is a constant

• $\mathcal {\tilde{E}}(x)$ is $\mathcal {E}(x)$, if x is a variable

• $\mathcal {\tilde{E}}(f(t_1,\ldots , t_N))$ is true if, and only if, $\mathcal {\tilde{E}}(t_i)$ is true for some i

To simplify notation, in the rest of the paper, we silently extend $\mathcal {E}$ to terms without using the formally correct notation $\mathcal {\tilde{E}}$. A pair of states $(s=(m,p), t=(n,q))$ satisfies a taint environment $\mathcal {E}$, denoted by $(s,t) \models \mathcal {E}$, if $m=n$ and for every variable x, if $\mathcal {E}(x)$ is false, then $s(x)=t(x)$. I.e., (s, t) satisfy $\mathcal {E}$ if s and t are at the same program location, and s and t have identical values for every variable x that is not tainted in $\mathcal {E}$.

Taint environments are ordered by component-wise implication: $\mathcal {E} \sqsubseteq \mathcal {F}$ (read as “$\mathcal {E}$ better than $\mathcal {F}$”) is defined as $(\forall x: \mathcal {E}(x) \Rightarrow \mathcal {F}(x))$. If $\mathcal {E}$ is better than $\mathcal {F}$, then $\mathcal {F}$ taints all variables tainted by $\mathcal {E}$ and maybe more. These definitions induce some basic properties, shown below.

Proposition 1

(Monotonicity) If $(s, t) \models \mathcal {E}$ and $\mathcal {E} \sqsubseteq \mathcal {F}$, then $(s, t) \models \mathcal {F}$.

For a statement S and states $s=(m, p)$ and $s'=(n, q)$, we write ${s}\xrightarrow []{S}{s'}$ (read as $s'$ is the successor of s after S) to mean that there is an execution trace from s to $s'$ such that m denotes the program location immediately before S and n denotes the program location immediately after S.

In addition, for taint environments $\mathcal {E}$ and $\mathcal {F}$, we write $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$ to mean that for any pair of states satisfying $\mathcal {E}$, their successors after S satisfy $\mathcal {F}$. Formally, $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$ holds if for all s, t such that $(s, t) \models \mathcal {E}$, ${s}\xrightarrow []{S}{s'}$, and ${t}\xrightarrow []{S}{t'}$, it is the case that $(s', t') \models \mathcal {F}$.

Proposition 2

If $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$, $\mathcal {E'} \sqsubseteq \mathcal {E}$ and $\mathcal {F} \sqsubseteq \mathcal {F'}$, then $\{\mathcal {E'}\}\, {S}\, \{\mathcal {F'}\}$.

4.2 Proof system

We present a taint proof system for inferring $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$ for a structured program S. The soundness proof, given in the Appendix, is by induction on program structure, following the pattern of the proof in [20].

Conditional: For a statement S, we use Assign(S) to represent a set of variables which over-approximates those variables assigned to in S. There are two cases, based on whether the condition is tainted in $\mathcal {E}$:

Theorem 3

(Soundness) Consider a structured program P with a proof of $\{\mathcal {E}\}\, {P}\, \{\mathcal {F}\}$. For all initial states (s, t) such that $(s,t) \models \mathcal {E}$: if ${s}\xrightarrow []{P}{s'}$ and ${t}\xrightarrow []{P}{t'}$, then $(s',t') \models \mathcal {F}$.

The proof system can be turned into an algorithm for calculating taints. The proof rule for each statement other than the while loop can be read as a monotone forward environment transformer. For while loops, the proof rule requires the construction of an inductive environment, I. This can be done through a straightforward least fixpoint calculation for I based on the transformer for the body of the loop. Let $I^{k}$ denote the value at the k-th stage. The fixpoint step from $I^{n}$ to $I^{n+1}$ must change the taint status of least one variable from untainted in $I^{n}$ to tainted in $I^{n+1}$, while leaving all tainted variables in $I^{n}$ tainted in $I^{n+1}$. Thus, the fixpoint is reached in a number of stages that is bounded by the number of variables. The entire process is thus in polynomial time.

5 A secure dead store elimination transformation

The results of Sect. 3 show that translation validation for security is computationally difficult. The alternative is to build security into each program transformation. In this section, we describe a dead store elimination procedure built around taint analysis, and prove that it is secure.

Fig. 2

Secure Dead Store Elimination Algorithm

The algorithm is shown in Fig. 2. It obtains the set of dead assignments and processes them using taint and control-flow information to determine which ones are secure to remove. The program is in structured form, with taint information represented as in the proof system of the previous section. The control-flow graph is assumed to be in a normalized form where each edge either has a guarded command with a skip action, or a trivial guard with an assignment or output. I.e., $g \,\rightarrow \,\mathsf {skip}$, $true \,\rightarrow \,x \,:=\,e$, or $true \,\rightarrow \,\mathsf {out}(e)$. The “removal” of dead stores is done by replacing the store with a $\mathsf {skip}$, so the CFG structure is unchanged.

Removal of dead stores can cause previously live stores to become dead, so the algorithm should be repeated until no dead store can be removed. In Case 1 of the algorithm, removal could cause the taint proof to change, so the taint analysis is repeated. For cases 2 and 3, we establish and use the fact that removal does not alter the taint proof.

As the algorithm removes a subset of the known dead stores, the transformation is correct. In the following, we prove that it is also secure. We separately discuss each of the (independent) cases in the algorithm. For each case, we give an illustrative example followed by a proof that the store removal is secure.

Fig. 3

C programs illustrating Case 1 of the algorithm

5.1 Post-domination (case 1)

The example in Fig. 3 illustrates this case. In the program on the left, the two dead assignments to x are redundant from the viewpoint of correctness. Every path to the exit from the first assignment, x = 0, passes through the second assignment to x. This is a simple example of the situation to which Case 1 applies. The algorithm will remove the first dead assignment, resulting in the program to the right. The result is secure as the remaining assignment blocks the password from being leaked outside the function. The correctness of this approach in general is proved in the following lemmas.

Lemma 1

(Trace Correspondence) Suppose that T is obtained from S by eliminating a dead store, $x \,:=\,e$. For any starting state $s=(H=a,L=c)$, there is a trace in T from s if, and only if, there is a trace in S from s. The corresponding traces have identical control flow and, at corresponding points, have identical values for all variables other than x, and identical values for x if the last assignment to x is not removed.

Proof

(Sketch) This follows from the correctness of dead store elimination, which can be established by showing that the following relation is a bisimulation. To set up the relation, it is easier to suppose that dead store $x \,:=\,e$ is removed by replacing it with $x \,:=\,\bot$, where $\bot$ is an “undefined” value, rather than by replacement with $\mathsf {skip}$. The $\bot$ value serves to record that the value of x is not important. Note that the CFG is unaltered in the transformation. The relation connects states (m, s) of the source and (n, t) of the target if (1) $m=n$ (i.e., same CFG nodes); (2) $s(y)=t(y)$ for all y other than x; and (3) $s(x)=t(x)$ if $t(x) \ne \bot$. This is a bisimulation (cf. [14], where a slightly weaker relation is shown to be a bisimulation). The fact that corresponding traces have identical control-flow follows immediately, and the data relations follow from conditions (2) and (3) of the bisimulation. $\square$

Lemma 2

If $\alpha$ is a dead assignment to variable x in program S that is post-dominated by other assignments to x, it is secure to remove it from S.

Proof

Let T be the program obtained from S by removing $\alpha$. We show that any leaky triple for the transformed program T is already present in the source program S. Let (a, b, c) be a leaky triple for T. Let $\tau _a$ (resp. $\sigma _a$) be the trace in T (resp. S) from the initial state $(H=a,L=c)$. Similarly, let $\tau _b$ (resp. $\sigma _b$) be the trace in T (resp. S) from $(H=b,L=c)$. By trace correspondence (Lemma 1), $\sigma _a$ and $\sigma _b$ must also reach the exit point and are therefore terminating.

By the hypothesis, the last assignment to x before the exit point in $\sigma _a$ and $\sigma _b$ is not removed. By Lemma 1, $\tau _a$ and $\sigma _a$ agree on the value of all variables at the exit point; thus, they agree on the value of x. Similarly, $\tau _b$ and $\sigma _b$ agree on the values of all variables at the exit point. As (a, b, c) is a leaky triple for T, the L-values are different at the final states of $\tau _a$ and $\tau _b$. It follows that the L-values are different at the final states for $\sigma _a$ and $\sigma _b$, hence (a, b, c) is a leaky triple for S. $\square$

5.2 Stable untainted assignment (case 2)

An example of this case is given by the programs in Fig. 4. Assume that the user identity is public and the password is private, hence read_password returns an H-input value while read_user_id returns an L-input value. There are two dead assignments to x in the program on the left, and the algorithm will remove the first one, as x is untainted before that assignment and untainted at the final location as well. This is secure as in the program on the right x remains untainted at the final location; hence, it does not leak information about the password. The general correctness proof is given below.

Fig. 4

C programs illustrating Case 2 of the algorithm

Lemma 3

Let $x \,:=\,e$ be a dead store in program S. Suppose that there is a taint proof for S where x is untainted at the location immediately before the dead store. The taint assertions form a valid taint proof for the program T obtained by replacing the store with $\mathsf {skip}$.

Proof

The proof outline for S is also valid for the program T obtained by replacing the dead store “$x\,:=\,e$ with “$\mathsf {skip}$”. Let $\{\mathcal {E}\}\, {x\,:=\,e}\, \{\mathcal {F}\}$ be the annotation for the dead store in the proof outline. By the inference rule of assignment, we know that $\mathcal {F}(x)=\mathcal {E}(e)$ and that, for all other variables y, $\mathcal {F}(y)=\mathcal {E}(y)$.

Now we show that $\mathcal {E}\sqsubseteq \mathcal {F}$ is true. Consider any variable z. If z differs from x, then $\mathcal {E}(z) \Rightarrow \mathcal {F}(z)$, as $\mathcal {E}(z) = \mathcal {F}(z)$. If z is x then, by hypothesis (2), $\mathcal {E}(z) \Rightarrow \mathcal {F}(z)$ is trivially true, as $\mathcal {E}(z)=\mathcal {E}(x)$ is false.

The annotation $\{\mathcal {E}\}\, {\mathsf {skip}}\, \{\mathcal {E}\}$ is valid by definition, therefore $\{\mathcal {E}\}\, {\mathsf {skip}}\, \{\mathcal {F}\}$ is also valid by $\mathcal {E}\sqsubseteq \mathcal {F}$ and Proposition 2. Hence, the replacement of an assignment by $\mathsf {skip}$ does not invalidate the local proof assertions. The only other aspect of the proof which may depend on the eliminated assignment is the proof rule for a conditional statement: Case B depends on the set of assigned variables within the scope of the condition, and the elimination of the assignment to x may remove it from that set. However, the proof assertions will remain valid, as the considered set of assigned variables can be an over-approximation of the actual set of assigned variables. $\square$

Lemma 4

Let $x \,:=\,e$ be a dead store in program S. Suppose that there is a taint proof for S where (1) x is untainted at the final location and (2) x is untainted at the location immediately before the dead store. It is then secure to eliminate the dead store.

Proof

By Lemma 3, the taint proof for S remains valid for T. By hypothesis (1), as x is untainted at the final location in S, it is also untainted at the final location in T. By the soundness of taint analysis, there is no leak in T from variable x. Hence, any leak in T must come from variable y different from x. By trace correspondence (Lemma 1), the values of variables other than x are preserved by corresponding traces; therefore, so is any leak. $\square$

5.3 Final assignment (case 3)

The example in Fig. 5 illustrates this case. Assume the credit card number to be private, so that credit_card_no returns an H-input value. In the program on the left, there are two dead assignments to x. The first one is post-dominated by the second one, while the second one is always the final assignment to x in every terminating computation, and x is untainted before it. By Case 1, the algorithm would remove the first one and keep the second one. Such a transformation is secure, as the source program and result program leaks same private information. But Case 3 of the algorithm would do a better job: it will remove the second dead assignment instead, resulting in the program on the right. We show that the result program is at least as secure as the source program (in this very example, it is actually more secure than the source program), as x becomes untainted at the final location and no private information can be leaked outside the function via x. The following lemma proves the correctness of this approach.

Fig. 5

C programs illustrating Case 3 of the algorithm

Lemma 5

Let $x \,:=\,e$ be a dead store in program S. Suppose that there is a taint proof for S where (1) x is untainted at the location immediately before a dead store, (2) no other assignment to x is reachable from the dead store, and (3) the store post-dominates the entry node. It is then secure to eliminate the dead store.

Proof

By Lemma 3, the taint proof for S is also valid for T. By hypothesis (1), x is still untainted at the same location in T.

By hypothesis (3), the dead store “$x\,:=\,e$” is a top-level statement; thus, the dead store (resp. the corresponding $\mathsf {skip}$) occurs only once in every terminating computation of S (resp. T). Let $t_a, \ldots , t_a', \ldots , t_a''$ be the terminating trace in T from the initial state $(H=a, L=c)$, and $t_b, \ldots , t_b', \ldots , t_b''$ be the terminating trace in T from the initial state $(H=b, L=c)$ where $t_a'$ and $t_b'$ are at the location immediately before the eliminated assignment. By the soundness of taint analysis, x must have identical values in $t_a'$ and $t_b'$.

By hypothesis (2), the value of x is not modified in the trace between $t_a'$ and $t_a''$ (or between $t_b'$ and $t_b''$). Thus, the values of x in $t_a''$ and $t_b''$ are identical, and there is no leak in T from x. Hence, any leak in T must come from a variable y different from x. By trace correspondence (Lemma 1), the values of variables other than x are preserved in corresponding traces; therefore, so is any leak. $\square$

Theorem 4

The algorithm for dead store elimination is secure.

Proof

The claim follows immediately from the secure transformation properties shown in Lemmas 2, 4 and 5. $\square$

Although the dead store elimination algorithm is secure, it is sub-optimal in that it may retain more dead stores than necessary. Consider the program

The second store to x is dead and could be securely removed, but it will be retained by our heuristic procedure.

The case discussed at the end of Sect. 2, in which the transformed program reveals the entire credit card number, cannot happen with dead store elimination. More generally, we conjecture that this algorithm preserves the amount of leaked information. Although there is not a single accepted definition of quantitative leakage, it appears natural to suppose that if two programs have identical computations with identical leaked values (if any) then the leakage amount should also be identical. This is the case in our procedure. By Lemma 1, all variables other than x have identical values at the final location in the corresponding traces of S and T. From the proofs of Theorem 4, we know that at the final location of T, variable x has either the same value as in S (Case 1) or an untainted value (Cases 2 and 3) that leaks no information, thus T cannot leak more information than S.

6 Discussion

In this section, we discuss variations on the program and security model and consider the security of other compiler transformations.

6.1 Unstructured while programs

If the while program model is extended with goto statements, programs are no longer block-structured and the control-flow graph may be arbitrary. The secure algorithm works with CFGs and is therefore unchanged. An algorithm for taint analysis of arbitrary CFGs appears in [8, 9]. This propagates taint from tainted conditionals to blocks that are solely under the influence of that conditional; such blocks can be determined using a graph dominator-based analysis. The Appendix contains a taint proof system for CFGs that is based on these ideas. It retains the key properties of the simpler system given here; hence, the algorithms and their correctness proofs apply unchanged to arbitrary CFGs.

6.2 Procedural programs

An orthogonal direction is to enhance the programming model with procedures. This requires an extension of the taint proof system to procedures, but that is relatively straightforward: the effect of a procedure is summarized on a generic taint environment for the formal parameters and the summary is applied at each call site. A taint analysis algorithm which provides such a proof must perform a whole-program analysis.

6.3 Other attack models

The attack model in this paper is one where the attacker knows the program code, can observe outputs, and inspect the values of local variables at termination.

An extension is to consider an attacker that can observe the local variables at intermediate program points, such as calls to procedures. This would model situations such as those shown in Fig. 1, where a leak may occur inside an untrusted procedure. The location of an untrusted procedure call can be considered as a leakage point, in addition to the leakage point at the end of the current procedure (foo in the example). One may also insert other leakage points as desired. The analysis and algorithms developed here are easily adapted to handle multiple leakage points.

As discussed previously, the security guarantee is only with respect to information flow. It does not guarantee that side-channel attacks, such as those based on timing, will not be successful; ensuring that requires different forms of analysis, cf. [2].

7 The security of other compiler transformations

A natural question that arises is that of the security of other compiler optimizations. In the following, we present a general proof technique to show that an optimization is secure. The technique is a strengthening of the standard refinement notion used to establish correctness. Using this technique, we show that some common optimizations are secure. On the other hand, we show that the important SSA optimization is insecure.

The correctness of a transformation from program S to program T is shown using a refinement relation, R. For the discussion below, the exact form of the refinement relation (i.e., whether it relates single steps, or allows stuttering) is not important. We only require the property that if T is related by refinement to S, then any computation of T has a corresponding computation in S with identical output.

However, to fix a particular notion, we present the definition of a single step refinement R from T to S. This is a relation from the state-space of T to the state-space of S, such that

• For every initial state t of T, there is an initial state s of S such that R(t, s), and

• If R(t, s) holds and $t'$ is a T-successor of t, there is an S-successor $s'$ of s such that $R(t',s')$ and the output (if any) is identical on the transitions $(t,t')$ and $(s,s')$

An easy induction shows the desired property that every computation of T has an R-related computation in S, with identical outputs.

For states u, v of a program P, define $u \equiv _{P} v$ (u and v are “low-equivalent in P”) to mean that u and v agree on the values of all Low-variables in program P.

We say that R is a secure refinement if R is a refinement relation from T to S and satisfies the additional conditions below. (This was referred to as a ‘strict’ refinement in [6]).

• (a) A final state of T is related by R only to a final state of S, and

• (b1) If $R(t_0,s_0)$ and $R(t_1,s_1)$ hold, $t_0$ and $t_1$ are initial states of T, and $t_0 \equiv _{T} t_1$ holds, then $s_0 \equiv _{S} s_1$ holds as well, and

• (b2) If $R(t_0,s_0)$ and $R(t_1,s_1)$ hold, $t_0$ and $t_1$ are final states, and $t_0 \equiv _{T} t_1$ does not hold, then $s_0 \equiv _{S} s_1$ does not hold.

Theorem 5

Consider a transformation from program S to program T which does not change the set of high variables and has an associated secure refinement relation R. Such a transformation is both correct and secure.

Proof

Correctness follows from R being a refinement relation. We now establish security.

Consider a leaky triple (a, b, c) for T. As the transformation is correct, one needs to consider only the case of a leak through the low variables at the final states of the computations $\tau _a$ (from $(H=a,L_T=c)$) and $\tau _b$ (from $(H=b,L_T=c)$). Let $t_a,t_b$ be the final states of $\tau _a,\tau _b$, respectively. As the triple is leaky, $t_a \equiv _{T} t_b$ is false. We show that there is a corresponding leak in S.

Let $\sigma _a$ be the computation of S which corresponds to $\tau _a$ through R, such a computation exists as R is a refinement relation. Similarly let $\sigma _b$ correspond to $\tau _b$ through R. By condition (a) of secure refinement, the state of $\sigma _a$ ($\sigma _b$) that is related to the final state of $\tau _a$ ($\tau _b$) must be final for S, hence, $\sigma _a$ and $\sigma _b$ are terminating computations. Apply condition (b1) to the initial states of the corresponding computations $(\tau _a,\sigma _a)$ and $(\tau _b,\sigma _b)$. As the initial $\tau$-states are low-equivalent in T, condition (b1) implies that the initial $\sigma$-states are low-equivalent in S. Apply condition (b2) to the final states of the corresponding computations. As $t_a \equiv _{T} t_b$ does not hold, the final $\sigma$-states are also not low-equivalent. Hence, (a, b, c) is a leaky triple for S, witnessed by the computations $\sigma _a$ and $\sigma _b$. $\square$

For several transformations, the refinement relation associated with the transformation has a simple functional nature. We show that any such relation has properties (b1) and (b2). Precisely, we say that a refinement relation R is functional if:

• (a) Every low state variable x of S has an associated 1–1 function $f_{x}(Y_{x})$, where $Y_{x}=(y_1,\ldots ,y_k)$ is a vector of low state variables of T. We say that each $y_i$ in $Y_{x}$ influences x.

• (b) Every low state variable of T influences some low-state variable of S

• (c) For every pair of states (t, s) related by R, s(x) equals $f_{x}(t(y_1),\ldots ,t(y_k))$

Lemma 6

A functional refinement relation satisfies conditions (b1) and (b2) of secure refinement.

Proof

Suppose that $R(t_0,s_0)$ and $R(t_1,s_1)$ hold. By conditions (a) and (c) of the functionality assumption, for every low state variable x of S, $s_0(x)$ equals $f_{x}(t_0(Y_{x}))$ and $s_1(x)$ equals $f_{x}(t_1(Y_{x}))$.

First, suppose that $t_0 \equiv _{T} t_1$. As $t_0$ and $t_1$ agree on the values of all low variables in $Y_{x}$, $s_0(x)$ and $s_1(x)$ are equal. This holds for all x, so that $s_0 \equiv _{S} s_1$. Next, suppose that $t_0 \equiv _{T} t_1$ does not hold. Hence, $t_0(y) \ne t_1(y)$ for some low state variable y of T. By condition (b) of the assumption, y influences some low-state variable of S, say x. I.e., y is a component of the vector $Y_{x}$ in the function $f_{x}(Y_{x})$. Hence, $t_0(Y_{x})$ and $t_1(Y_{x})$ are unequal vectors. Since $f_{x}$ is 1–1, it follows that $s_0(x)=f_{x}(t_0(Y_{x}))$ and $s_1(x)=f_{x}(t_1(Y_{x}))$ differ, so that $s_0 \equiv _{S} s_1$ does not hold.

This establishes that $t_0 \equiv _{T} t_1$ if, and only if, $s_0 \equiv _{S} s_1$ at all related states, regardless of whether the states are initial or final, ensuring (b1) and (b2). $\square$

The standard constant propagation and folding transformation does not alter the set of program variables. The refinement relation used to show correctness equates the values of each variable x in corresponding states of S and T. Hence, the relation meets the conditions of Lemma 6 and, therefore, conditions (b1–b2) of secure refinement. These relations also satisfy condition (a), as the transformations do not change the termination behavior of the source program. Certain control-flow simplifications, such as the merge of successive basic blocks into one, or the removal of an unsatisfiable branch of a conditional statement, can be similarly shown to be secure. The refinement relations for loop peeling and loop unrolling are also secure, as the relations imply that the value of each variable is identical in states related by the refinement relation.

7.1 Insecurity of SSA

An important transformation whose refinement relation is not secure is the static single assignment (SSA) transformation. Indeed, the transformation leaks information, as shown by the example in Fig. 6. In the program on the right-hand side, the assignments to x have been replaced with single assignments to x1 and to x2. The value of the password is leaked via x2.

Fig. 6

C programs illustrating the insecurity of SSA transformation

Modern compilers make extensive use of the SSA format, relying on it to simplify the implementation of optimizations. Thus, the possibility of leakage via conversion to SSA form is particularly troubling. The question of securing SSA was left open in the initial version of this paper [6]. Recent work [7] designs a mechanism to track and block the leaks introduced by a SSA transformation.

8 Related work and conclusions

The fact that correctness preservation is not the same as security preservation has long been known. Formally, the issue is that refinement in the standard sense, as applied for correctness, does not preserve security properties. Specifically, a low-level machine model may break security guarantees that are proved on a higher-level language model. Full abstraction has been proposed as a mechanism for preserving security guarantees across machine models in [1]. A transformation $\tau$ is fully abstract if programs P and Q are observationally indistinguishable (to an attacker context) if and only if the transformed programs $P'=\tau (P)$ and $Q'=\tau (Q)$ are indistinguishable. Recent work on this topic [5, 11, 17] considers various mechanisms for ensuring full abstraction. In our context, the observables are the values of variables at the exit point—an attacker can observe the values of local variables on termination. For this attack model, the standard DSE transformation is not fully abstract. For example, the original program in Fig. 1 is observationally equivalent to program Q given by int x=0; where x is initialized to 0, while the transformed programs $P'=\mathsf {DSE}(P)$ (the right-hand program in Fig. 1) and $Q'=\mathsf {DSE}(Q)$, which equals Q, are observationally distinguishable. The proofs of the new secure transform, which we may denote $\mathsf {SDSE}$, establish that programs P and $\mathsf {SDSE}(P)$ are observationally equivalent, for all P; it follows immediately that the transformation $\mathsf {SDSE}$ is fully abstract.

The earliest explicit reference to the insecurity of dead store elimination that we are aware of is [13]; however, the issue has possibly been known for a longer period of time. Nevertheless, we are not aware of other constructions of a secure dead store elimination transformation. The complexity results in this paper on the difficulty of translation validation for security, in particular for the apparently simple case of dead store elimination are also new, to the best of our knowledge.

Theorem 5 in Sect. 6 on secure refinement relations is related to Theorem 10.5 in [5] which has a similar conclusion, in a different formal setting. The application of Theorem 5 to establish the security of common compiler transformations appears to be new.

A recent paper [10] has an extensive study of possible ways in which compiler transformations can create information leaks. The authors point out that the “correctness-security gap” (their term) can be understood in terms of observables: establishing security requires more information about internal program state than that needed to establish correctness. (This is related to the full abstraction property discussed above.) They describe several potential approaches to detecting security violations. The inherent difficulty of security checking has implications for translation validation and testing, two of the approaches considered in [10]. Our secure dead code elimination algorithm removes an important source of insecurity, while Theorem 5 is used to establish the security of several other transformations. The insecurity of SSA is tackled in our follow-on paper [7], which presents a method that restores the security level of a program to its original level, after the program has been converted to SSA form and transformed by SSA-dependent optimizations.

There is a considerable literature on type systems, static analyses and other methods for establishing (or testing) the security of a single program, which we will not attempt to survey here. In contrast, this paper treats the relative security question: is the program resulting from a transformation at least as secure as the original? This has been less studied, and it has proved to be an unexpectedly challenging question. Several new directions arise from these results. An important question is to fully understand the security of other compiler optimizations and register allocation methods. A witnessing structure for security, analogous to the one for correctness in [14], might be a practical way to formally prove the security of compiler implementations. A different direction is to consider transformations that enhance security, rather than just preserve it; one such transformation is described in [12]. The ultimate goal is a compilation process that is both correct and secure.

Appendices

Appendix

1.1 Hardness of security checking for finite-state programs

Theorem 6

Checking the security of a dead store elimination given as a triple (P, Q, D) is PSPACE-complete for finite-state programs.

Proof

Consider the complement problem of checking whether a transformation from P to Q is insecure. By definition, this is so if there exists a triple (a, b, c) which is leaky for Q but not for P. Determining whether (a, b, c) is leaky can be done in deterministic polynomial space, by simulating the program on the input pairs (a, c) and (b, c). Non-termination is detected in a standard way by adding an n-bit counter, where $2^{n}$ is an upper bound on the size of the search space: the number n is linear in the number of program variables. A non-deterministic machine can guess the triple (a, b, c), then check that the triple is leaky for Q but not leaky for P. Thus, checking insecurity is in non-deterministic PSPACE, which is in PSPACE by Savitch’s theorem.

To show hardness, consider the problem of deciding whether a finite-state program with no inputs or outputs terminates, which is PSPACE-complete by a simple reduction from the IN-PLACE-ACCEPTANCE problem [16]. Given such a program R, let h be a fresh high security input variable and l a fresh low-security state variable, both Boolean, with l initialized to $false$. Define program P as: “$R ;\,l \,:=\,h;\,l \,:=\, false$”, and program Q as: “$R;\,l \,:=\,h$”. As the final assignment to l in P is dead, Q is a correct result of dead store elimination on P. Consider the triple $(h= true ,h= false ,\_)$. If R terminates, then Q has distinct final values for l for the two executions arising from inputs $(h= true ,\_)$ and $(h= false ,\_)$, while P does not, so the transformation is insecure. If R does not terminate, there are no terminating executions for Q, so Q has no leaky triples and the transformation is trivially secure. Hence, R is non-terminating if, and only if, the transformation from P to Q is secure. $\square$

1.2 Hardness of security checking for loop-free finite-state programs

We consider the triple (P, Q, D) which defines a dead store elimination, and ask whether Q is at least as secure as P. We show this is hard, even for the very simple program structure where all variables are Boolean, and assignments are limited to the basic forms $x \,:=\,y$ or $x \,:=\,c$, where x, y are variables and c is a Boolean constant. Some of the variables will be designated as high-security, depending on context.

To simplify exposition, we will use a general assignment of the form $x \,:=\,e$ where e is a Boolean formula. This can be turned into a simple loop-free program of size O(|e|) by introducing fresh variables for each sub-tree of e and turning Boolean operators into if-then-else constructs. (E.g., $x \,:=\,((y\;\vee \;w) \;\wedge \;z)$ is first turned into $t_1 \,:=\,y \;\vee \;w;\, t_2 \,:=\,z;\, x \,:=\,t_1 \;\wedge \;t_2$, then the Boolean operators are expanded out, e.g., the first assignment becomes $\;\mathsf {if}\;y \;\mathsf {then}\;t_1 \,:=\, true \;\mathsf {else}\;t_1 \,:=\,w \;\mathsf {fi}\;$).

Theorem 7

Checking the security of a dead store elimination given as a triple (P, Q, D) is co-NP-complete for loop-free programs.

Proof

Consider the complement problem of checking whether a transformation from P to Q is insecure. Note that P and Q have the same set of low-security variables.

We first show that this problem is in NP. By definition, an insecurity exists if and only if there is a leaky triple (a, b, c) for Q which is not leaky for P. Given a triple (a, b, c) and a program, say P, a machine can deterministically test whether the triple is leaky for P by simulating the pair of executions from (a, c) and (b, c), keeping track of the current low-security state and the last output value for each execution. This simulation takes time polynomial in the program length, as the program is loop-free. A non-deterministic machine can guess a triple (a, b, c) in polynomial time (these are assignments of values to variables), then use the simulation to check first that the triple is not leaky for P and then that it is leaky for Q, and accept if both statements are true. Thus, checking insecurity is in NP.

To show NP-hardness, let $\phi$ be a propositional formula over N variables $x_1,\ldots ,x_N$. Let y be a fresh Boolean variable. Let the x-variables be the low-security inputs, and let y be a high security input. Let z be a low-security variable, which starts at $false$. Define Q(x, y) as the program $z := (\phi \;\wedge \;y)$, and let P(x, y) be the program $Q;\, z := false$. As the final assignment in P is dead, Q is a correct outcome of dead store elimination applied to P. (Note: the programs P and Q may be turned into the simpler form by expanding out the assignment to y as illustrated above, marking all freshly introduced variables as low-security.

Suppose $\phi$ is satisfiable. Let $\overline{m}$ be a satisfying assignment for $\overline{x}$. Define the inputs $(\overline{x}=\overline{m},y= true )$ and $(\overline{x}=\overline{m},y= false )$. In Q, the final value of z from those inputs is $true$ or $false$ depending on value of y, so the triple $t = (y= true ,y= false ,\overline{x}=\overline{m})$ is leaky for Q. However, in P, the final value of z is always $false$, regardless of y, and t is not leaky for P. Hence, the elimination of dead store from P is insecure. If $\phi$ is unsatisfiable then, in Q, the final value of z is always $false$ regardless of y, so the transformation is secure. I.e., the transformation is insecure if, and only if, $\phi$ is satisfiable, which shows NP-hardness. $\square$

1.3 Soundness of the taint proof system

Proposition 2

If $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$ and $\mathcal {E'} \sqsubseteq \mathcal {E}$ and $\mathcal {F} \sqsubseteq \mathcal {F'}$, then $\{\mathcal {E'}\}\, {S}\, \{\mathcal {F'}\}$.

Proof

Consider s, t such that $(s, t) \models \mathcal {E'}$ and ${s}\xrightarrow []{S}{s'}$ and ${t}\xrightarrow []{S}{t'}$.

$\square$

Lemma 7

If $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$, variable x is tainted in $\mathcal {E}$ and S does not modify x, then x is tainted in $\mathcal {F}$.

Proof

(Sketch) Here we prove that $\mathcal {E}(x)$ implies $\mathcal {F}(x)$ by induction on the structure of S. If S is an assignment, this is clearly true by the assignment rule. For a sequence $S_1; S_2$ such that $\{\mathcal {E}\}\, {S_1}\, \{\mathcal {G}\}$ and $\{\mathcal {G}\}\, {S_2}\, \{\mathcal {F}\}$, this is true by the induction hypothesis: $\mathcal {E}(x)$ implies $\mathcal {G}(x)$ which implies $\mathcal {F}(x)$. For a loop, by the inference rule, the loop invariant environment $\mathcal {I}$ must be such that $\mathcal {E}\sqsubseteq \mathcal {I}$, so $\mathcal {I}(x)$ holds. As $\mathcal {I}\sqsubseteq \mathcal {F}$, $\mathcal {F}(x)$ holds. For a conditional, as $\mathcal {E}(x)$ holds by assumption and $\{\mathcal {E}\}\, {S_1}\, \{\mathcal {F}\}$ and $\{\mathcal {E}\}\, {S_2}\, \{\mathcal {F}\}$ hold, by the induction hypothesis, $\mathcal {F}(x)$ holds. $\square$

Theorem 3

Consider a structured program P with a proof of $\{\mathcal {E}\}\, {P}\, \{\mathcal {F}\}$. For all initial states (s, t) such that $(s,t) \models \mathcal {E}$: if ${s}\xrightarrow []{P}{s'}$ and ${t}\xrightarrow []{P}{t'}$, then $(s',t') \models \mathcal {F}$.

Proof

• (0) S is $\mathsf {skip}$ or $\mathsf {out}(e)$:

  

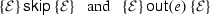
Consider states $s=(m, p)$, $t=(n, q)$, $s'=(m', p')$ and $t'=(n', q')$ such that ${s}\xrightarrow []{S}{s'}$ and ${t}\xrightarrow []{S}{t'}$ hold. By the semantics of $\mathsf {skip}$ and $\mathsf {out}(e)$, $s'=s$ and $t'=t$. Thus, if $(s, t)\models \mathcal {E}$, then $(s', t')\models \mathcal {E}$.

• (1) S is an assignment $x \,:=\,e$:

  

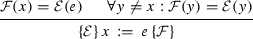
Consider states $s=(m, p)$, $t=(n, q)$, $s'=(m', p')$ and $t'=(n', q')$ such that ${s}\xrightarrow []{S}{s'}$ and ${t}\xrightarrow []{S}{t'}$ hold. By the semantics of assignment, it is clear that $p'=p[x\leftarrow p(e)]$, $q'=q[x\leftarrow q(e)]$, and $m'=n'$ denotes the program location immediately after the assignment. Assume $(s, t)\models \mathcal {E}$, we want to prove $(s', t')\models \mathcal {F}$, or more precisely, $\forall v: \lnot \mathcal {F}(v) \Rightarrow p'(v)=q'(v)$.

Consider variable y different from x. If $\mathcal {F}(y)$ is false, so is $\mathcal {E}(y)$, hence $p(y)=q(y)$ since $(s, t)\models \mathcal {E}$. As $p'(y)=p(y)$ and $q'(y)=q(y)$, we get $p'(y)=q'(y)$ as desired.

Consider variable x. If $\mathcal {F}(x)$ is false, so is $\mathcal {E}(e)$, hence only untainted variables in $\mathcal {E}$ appear in e. As $(s, t)\models \mathcal {E}$, those variables must have equal values in s and t, thus $p(e)=q(e)$. Since $p'=p[x\leftarrow p(e)]$, $q'=q[x\leftarrow q(e)]$, we know $p'(x)=q'(x)$.

• (2) Sequence:

  

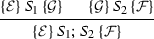
Consider states s and t such that ${s}\xrightarrow []{S_1; S_2}{s'}$ and ${t}\xrightarrow []{S_1; S_2}{t'}$. There must exist intermediate states $s''$ and $t''$ such that ${s}\xrightarrow []{S_1}{s''}$, ${t}\xrightarrow []{S_1}{t''}$, ${s''}\xrightarrow []{S_2}{s'}$ and ${t''}\xrightarrow []{S_2}{t'}$. Now suppose $(s, t)\models \mathcal {E}$, we have:

• (3) Conditional: For a statement S, we use Assign(S) to represent the set of variables assigned in S. The following two cases are used to infer $\{\mathcal {E}\}\, {S}\, \{\mathcal {F}\}$ for a conditional:

  

Let S = $\;\mathsf {if}\;c\;\mathsf {then}\;S_1\;\mathsf {else}\;S_2\;\mathsf {fi}\;$, states $s=(m, p), t=(n, q), s'=(m', p'), t'=(n', q')$. Suppose $(s, t) \models \mathcal {E}$, ${s}\xrightarrow []{S}{s'}$, ${t}\xrightarrow []{S}{t'}$.

Case A: $\mathcal {E}(c)=\text {false}$, hence by definition of $(s, t) \models \mathcal {E}$, we know $p(c) = q(c)$. Thus, both successors $s'$ and $t'$ result from the same branch, say $S_1$. By the hypothesis that $\{\mathcal {E}\}\, {S_1}\, \{\mathcal {F}\}$ and $(s, t) \models \mathcal {E}$, we have $(s', t') \models \mathcal {F}$.

Case B: $\mathcal {E}(c)=\text {true}$, hence $s'$ and $t'$ may result from different branches of S. To show that $(s', t') \models \mathcal {F'}$, let x be a variable untainted in $\mathcal {F'}$. By the definition of $\mathcal {F'}$, there must be no assignment to x in either $S_1$ or $S_2$. Hence, $p'(x)=p(x)$ and $q'(x)=q(x)$.

If $p(x)=q(x)$, then $p'(x)=q'(x)$. Otherwise, consider $p(x)\ne q(x)$, and we show that this cannot be the case. As $(s, t) \models \mathcal {E}$, x must be tainted in $\mathcal {E}$. As x is not modified in $S_1$ and $\{\mathcal {E}\}\, {S_1}\, \{\mathcal {F}\}$ holds, by Lemma 7 (below), x is tainted in $\mathcal {F}$. Since $\mathcal {F}\sqsubseteq \mathcal {F'}$, x is tainted in $\mathcal {F'}$, which is a contradiction. Hence, we show that $p'(x)=q'(x)$ for any variable x untainted in $\mathcal {F'}$. Clearly, $m'=n'$, thus $(s', t') \models \mathcal {F'}$.

• (4) While Loop:

  

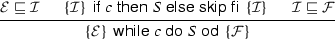
Let states s, t be such that $(s, t) \models \mathcal {E}$, and $s', t'$ be the states reached from s, t at the end of the while loop. By $\mathcal {E}\sqsubseteq \mathcal {I}$, $(s, t) \models \mathcal {I}$. We want to prove that $(s', t') \models \mathcal {I}$, so that by $\mathcal {I}\sqsubseteq \mathcal {F}$, we can have $(s', t') \models \mathcal {F}$.

Let the trace from s to $s'$ be $s=s_0, s_1, \ldots , s_n=s'$ where $s_i$ are states at the start of successive loop iterations. Similarly, let the trace from t to $t'$ be $t=t_0, t_1, \ldots , t_m=t'$. Without loss of generality, assume that $n > m$, then we can pad the t-trace with sufficiently many $\mathsf {skip}$ actions (i.e., the same as “$\;\mathsf {if}\;c\;\mathsf {then}\;S\;\mathsf {else}\;\mathsf {skip}\;\mathsf {fi}\;$” where the evaluation of c is false) to make the two traces of the same length. The final state of padded t-trace is still $t'$. For the rest of proof, we assume that $n = m$ and prove by induction on n that $(s_i, t_i) \models \mathcal {I}$.

The induction basis $(s_0=s, t_0=t) \models \mathcal {I}$ holds. Then, assume the claim that for $k\ge 0$, $(s_k, t_k) \models \mathcal {I}$. From the hypothesis “$\{\mathcal {I}\}\, {\;\mathsf {if}\;c\;\mathsf {then}\;S\;\mathsf {else}\;\mathsf {skip}\;\mathsf {fi}\;}\, \{\mathcal {I}\}$” of the inference rule, we get $(s_{k+1}, t_{k+1}) \models \mathcal {I}$ as well. Hence, $(s'=s_n, t'=t_m) \models \mathcal {I}$ holds. $\square$

Taint analysis for control-flow graphs

In this section, we describe how to adjust the taint proof system to apply to control-flow graphs (CFGs). We assume that a control-flow graph has a single entry node and a single exit node. A program is defined by its control flow graph, which is a graph where each node is a basic block and edges represent control flow. A basic block is a sequence of assignments to program variables.

The entry and exit nodes are special. All other nodes fall into one of three classes. The partitioning makes it easier to account for taint values and propagation.

• A merge node has multiple incoming edges and a $\phi$ function $x \leftarrow \!\phi \!((x_1,e_1), \ldots , (x_n,e_n))$ for every variable x, which (simultaneously over all variables) assigns x the value of $x_1$ if control is transferred through edge $e_1$, the value of $x_2$ if control is transferred through edge $e_2$ and so forth,

• A basic node, which is a single assignment statement, and

• A branch node, which is either an unconditional branch to the following node, or a conditional branch on condition c, through edge $e_t$ if c is true, and through edge $e_f$ if c is false.

The edge relations are special. The entry node has a single merge node as a successor and no incoming edge. The exit node has itself as the single successor, and behaves like a $\mathsf {skip}$. Every merge node has a single successor, which is a basic node. Every basic node has a single successor, which is either a basic or a branch node. Every successor of a branch node is either a merge node or the exit node.

A taint annotation for a control-flow graph is an assignment of environments to every CFG edge. An annotation is valid if the following conditions hold:

• The assignment to the outgoing edge from the entry node has high-security input variables set to H ($true$) and all other variables set to L ($false$),

• For a merge node with assignments $x \leftarrow \phi ((x_1,e_1), \ldots , (x_n,e_n))$, incoming edges annotated with $\mathcal {E}_1,\ldots ,\mathcal {E}_n$ and outgoing edge annotated with $\mathcal {F}$, for all i: $\{{\mathcal {E}_i}\} {x \leftarrow x_i} \{{F}\}$ holds. Note that here all $\phi$ assignments are gathered into one to keep the notation simple,

• For a basic node with assignment statement S, incoming edge annotated with $\mathcal {E}$ and outgoing edge annotated with $\mathcal {F}$, the assertion $\{{\mathcal {E}}\} {S} \{{\mathcal {F}}\}$ holds,

• For an unconditional branch node with incoming edge annotated with $\mathcal {E}$ and outgoing edge annotated with $\mathcal {F}$, $\{{\mathcal {E}}\} {\mathsf {skip}} \{{\mathcal {F}}\}$ holds, and

• For an conditional branch node $\;\mathsf {if}\;c\;\mathsf {then}\;e_t \;\mathsf {else}\;e_f \;\mathsf {fi}\;$, with incoming edge annotated with $\mathcal {E}$ and outgoing edges annotated with $\mathcal {F}_t$ and $\mathcal {F}_f$, respectively:

  • $\{{\mathcal {E}}\} {\mathsf {skip}} \{{\mathcal {F}_t}\}$ and $\{{\mathcal {E}}\} {\mathsf {skip}} \{{\mathcal {F}_f}\}$ hold, and

  • If $\mathcal {E}(c)$ is true (i.e., c is tainted in $\mathcal {E}$), then let d be the the immediate post-dominator for this branch node. Node d must be a merge node, say with incoming edges $f_1,\ldots ,f_k$. Let $\mathcal {F}_1,\ldots ,\mathcal {F}_k$ be the environments assigned, respectively, to those edges. Let $\mathsf {Assign}(n,d)$ be an over-approximation of the set of variables assigned to on all paths from the current branch node n to d. Then, for all $x \in \mathsf {Assign}(n,d)$, and for all i: it must be the case that $\mathcal {F}_i(x)= true$.

A structured program turns into a control flow graph with a special (reducible) structure. It is straightforward to check that a valid structured proof annotation turns into a valid CFG annotation for the graph obtained from the structured program.

1.1 Soundness

We have the following soundness theorem. Informally, the theorem states that if (the node from) edge f post-dominates (the node from) edge e, then computations starting from states consistent with e’s annotation to f result in states which are consistent with f’s annotation. It follows that terminating computations starting from states consistent with the entry edge annotation result in states consistent with the exit edge annotation. We write ${(s,e)} {\mathop {\longrightarrow }\limits ^{p}} {(s',f)}$ to indicate that there is a path (a sequence of edges $e_0=e,e_1,\ldots ,e_k=f$ such that the target of $e_{i}$ is the source of $e_{i+1}$, for all i) from e to f, and that $s'$ at edge f is obtained from state s at edge e by the actions along that path.

Theorem 8

For a given CFG: let e be an edge incident on node n, and let f be an outgoing edge from node m which post-dominates n. Let $\mathcal {E}, \mathcal {F}$ be the annotations for edges e and f, respectively. For states s, t such that $(s,t) \models \mathcal {E}$ and states u, v and paths p, q such that ${(s,e)} {\mathop {\longrightarrow }\limits ^{p}} {(u,f)}$ and ${(t,e)} {\mathop {\longrightarrow }\limits ^{q}} {(v,f)}$, it is the case that $(u,v) \models \mathcal {F}$.

Proof

The proof is by induction on the sum of the lengths of paths p and q, where the length is the number of edges on the path.

The base case is when the sum is 2. Then $m=n$, and f is an outgoing edge of node n. The validity conditions ensure that $\{{\mathcal {E}}\} {S} \{{\mathcal {F}}\}$ hold, where S is the statement associated with n. It follows that $(u,v) \models \mathcal {F}$.

Assume inductively that the claim holds when the sum is at most k, for $k \ge 0$. Now suppose the sum is $k+1$. The argument goes by cases on the type of node n.

• (1) n is a merge node, a basic node, or an unconditional branch node. Then it has a single successor node, say $n'$, via some edge $e'$. Let $\mathcal {E'}$ be the annotation on $e'$. By the conditions on a valid annotation, $\{{\mathcal {E}}\} {S} \{{\mathcal {E'}}\}$ holds, where S is the statement associated with n. Thus, for the immediate successors $s',t'$ of s, t along the paths p, q (respectively), $(s',t') \models \mathcal {E'}$. As $n'$ is the immediate post-dominator of n and all post-dominators of n are linearly ordered, m is a post-dominator of $n'$. The suffixes $p',q'$ of the paths p, q starting at $e'$ have smaller total length. By the induction hypothesis, as $(s',t') \models \mathcal {E'}$, it follows that $(u,v) \models \mathcal {F}$.

• (2) n is a conditional branch node with condition c and successor edges $e_t,e_f$ leading to successor nodes $n_t,n_f$. There are two cases to consider.

• (2a) The branch condition is tainted, i.e., $\mathcal {E}(c)= true$. Let $n'$ be the immediate post-dominator of n. This must be a merge node by the canonical structure of the CFG, with a single outgoing edge, say $g'$. By the constraints on valid annotation, if $\mathcal {G}$ is the annotation on $g'$, then $\mathcal {G}(x)= true$ if variable x is assigned to on a path from n to $n'$. Hence, if $\mathcal {G}(x)= false$, then x has no assignment on such a path, in particular, it has no assignment on the segments $p'$ of p and $q'$ of q from n to the first occurrence of $n'$. Let $s',t'$ be the states after execution of $p'$ and $q'$ (resp.). Then, $s'(x)=s(x)$ and $t'(x)=t(x)$. By the contrapositive of Lemma 7, $\mathcal {E}(x)= false$. As $(s,t) \models \mathcal {E}$, it follows that $s(x)=t(x)$ and, therefore, $s'(x)=t'(x)$. This shows that $(s',t') \models \mathcal {G}$. As the suffixes $p'',q''$ of the paths p, q after $n'$ have smaller total length, and m is a post-dominator of $n'$ (recall that all post-dominators of n are linearly ordered and $n'$ is the first), from the induction hypothesis, it follows that $(u,v) \models \mathcal {F}$.

• (2b) The branch condition is untainted, i.e., $\mathcal {E}(c)= false$. Thus, $s(c)=t(c)$, so the paths p, q have a common successor, say $n_t$, through edge $e_t$. The validity conditions imply that $\{{\mathcal {E}}\} {\mathsf {skip}} \{{\mathcal {E}_t}\}$ hold, where $\mathcal {E}_t$ is the annotation for edge $e_t$. Hence, $(s,t) \models \mathcal {E}_t$. As m is a post-dominator of n, it is also a post-dominator of $n_t$. The suffixes $p',q'$ of p, q from $n_t$ have smaller total length; hence, by the induction hypothesis, $(u,v) \models \mathcal {F}$.$\square$