Relating Bell’s Local Causality to the Causal Markov Condition

Abstract

The aim of the paper is to relate Bell’s notion of local causality to the Causal Markov Condition. To this end, first a framework, called local physical theory, will be introduced integrating spatiotemporal and probabilistic entities and the notions of local causality and Markovity will be defined. Then, illustrated in a simple stochastic model, it will be shown how a discrete local physical theory transforms into a Bayesian network and how the Causal Markov Condition arises as a special case of Bell’s local causality and Markovity.

1 Introduction

Local causality is a concept introduced by John Stewart Bell into the foundations of quantum theory. A physical theory is said to be locally causal if, fixing its past, any event happening in a given spacetime region will be probabilistically independent of any other event localized in a spatially separated region.

Causal Markov Condition is the central notion of the theory of Bayesian networks. Here events are represented both as random variables in a probability space and also as vertices in a causal graph. A set of events is said to satisfy the Causal Markov Condition relative to the graph, if, conditioned on its causal parents, any event will be probabilistically independent of any of its causal non-descendants.

The similarity between the logical schema of both principles is conspicuous even at first blush: if events are localized in the spacetime/causal graph in a certain way, then they are to satisfy certain probabilistic independencies. In this paper I will argue that this intuition is correct: Bell’s local causality, read in an appropriate way, is a Causal Markov Condition. Causal Markov Condition relates random variables to causal structures, local causality relates them to a net of spacetime regions. We will show that the causal graph generated by the net structure of a local physical theory transforms the theory into a Bayesian network and yields the Causal Markov Condition as a kind of composition of Bell’s local causality plus a similar screening-off condition, called Markovity.

To treat physical events both as probabilistic and also as spatiotemporal/causal entities in a unified framework and to be able to infer from spatiotemporal/causal relations to probabilistic independencies one needs to have a common conceptual schema integrating both spatiotemporal/causal and probabilistic concepts. This formalism is thoroughly worked out in the theory of Bayesian networks. Here Causal Markov Condition is functioning as a ’bridge law’ connecting the causal and the probabilistic side of the theory. In the foundations of quantum physics, however, local causality is used in a much more intuitive way. Here one simply “reads off” probabilistic independencies from the spatiotemporal localization of the events in question. Hence our first task is to introduce a mathematically well-defined and physically well-motivated framework which treats probabilistic and spatiotemporal entities in a common mathematical formalism. We will call such a theory a local phys ical theory. We will borrow a lot from the most elaborate physical theory offering such a general framework, namely algebraic quantum field theory (AQFT). Having such a framework integrating spatiotemporal and probabilistic aspects, we will be able to provide a clear-cut formulation of Bell’s notion of local causality.

To relate Bell’s local causality to the Causal Markov Condition, we will introduce a simple stochastic local classical theory on a discretized two dimensional spacetime. This toy theory will display all the features previously defined in an abstract way, and provide us a useful tool to study the properties of local causality in a more manageable way, and to trace its connections to the Causal Markov Condition.

In the paper we will proceed as follows. In Sect. 2 we make a historical detour and take a closer look at Bell’s different definitions of local causality. In Sect. 3 we introduce the concept of a local physical theory and give a precise mathematical definition of Bell’s notion of local causality together with Markovity within this framework. In Sect. 4 our stochastic local classical theory will be introduced. In Sect. 5 we define the Causal Markov Condition and show how a local physical theory gives rise to a Bayesian network and how local causality plus Markovity go over to the Causal Markov Condition. We will conclude in Sect. 6.

There is a huge literature available relating the Causal Markov Condition to the EPR scenario and to the Bell inequalities. The standard way to derive the Bell inequalities is to start with Reichenbach’s Common Cause Principle together with some locality conditions. Since Reichenbach’s Common Cause Principle is a special case of the Causal Markov Condition, many authors start the derivation directly from this latter. [2] shows that the EPR case has no causal explanation compatible with the Causal Markov Condition. [15] systematically apply the Causal Markov Condition to the EPR scenario and make a connection to the robustness condition, a probabilistic causality condition thoroughly discussed in the early 1990s. On the other hand, [5] argue that the Causal Markov Condition is inapplicable to the EPR scenario since the non-separability of the quantum state renders interventions, a necessary criterion for applicability, unavailable. As a reply to their claim see [16]. Hofer-Szabó and co-workers [7] connect the Causal Markov Condition both to the so-called common-common-causal and also to the separate-common-causal explanation of the EPR case. They show that hidden locality, an assumption of the standard derivation of the Bell inequalities, can be justified by the Causal Markov Condition only in case of common common causes but not in case of separate common causes.

Despite the rich literature on the topic I am unaware of any work relating the Causal Markov Condition directly to Bell’s notion of local causality. This paper intends to fill this gap.

2 Bell’s Three Definitions of Local Causality

Local causality is the idea that causal processes propagate though space continuously and with velocity less than the speed of light. John Stewart Bell formulates this intuition in a 1988 interview as follows:

[Local causality] is the idea that what you do has consequences only nearby, and that any consequences at a distant place will be weaker and will arrive there only after the time permitted by the velocity of light. Locality is the idea that consequences propagate continuously, that they don’t leap over distances. [11]

Bell has returned to this intuitive idea of local causality from time to time and provided a more and more elaborate formulation of it. First he addressed the notion of local causality in his “The theory of local beables” delivered at the Sixth GIFT Seminar in 1975; later in a footnote added to his 1986 paper “EPR correlations and EPW distributions” intending to clean up the first version; and finally in the most elaborate form in his “La nouvelle cuisine” posthumously published in 1990. Below I will overview the different versions briefly commenting on each of them.

Version 1 Bell’s first definition of local causality reads as follows:

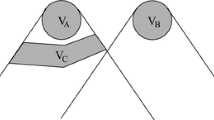
Consider a theory in which the assignment of values to some beables $\Lambda$ implies, not necessarily a particular value, but a probability distribution, for another beable $A$. Let $p(A\vert \Lambda )$ denote¹ the probability of a particular value $A$ given particular values $\Lambda$. Let $A$ be localized in a space-time region A. Let $B$ be a second beable localized in a second region B separated from A in a spacelike way. (Fig. 1). Now my intuitive notion of local causality is that events in B should not be ‘causes’ of events in A, and vice versa. But this does not mean that the two sets of events should be uncorrelated, for they could have common causes in the overlap of their backward light cones. It is perfectly intelligible then that if $\Lambda$ in (1) does not contain a complete record of events in that overlap, it can be usefully supplemented by information from region B. So in general it is expected that

$$\begin{aligned} p(A\vert \Lambda ,B ) \ne p(A\vert \Lambda ) \end{aligned}$$

(1)

However, in the particular case that $\Lambda$ contains already a complete specification of beables in the overlap of the light cones, supplementary information from region B could reasonably be expected to be redundant.

Fig. 1

Bell’s first figure illustrating local causality (1975)

Let $C_2$ denote a specification of all beables, of some theory, belonging to the overlap of the backward light cones of spacelike regions A and B. Let $C_1$ be a specification of some beables from the remainder of the backward light cone of A, and $B$ of some beables in the region B. (See Fig. 2.) Then in a locally causal theory

$$\begin{aligned} p(A\vert C_1, C_2, B) = p(A\vert C_1, C_2) \end{aligned}$$

(2)

whenever both probabilities are given by the theory. (Bell 1975/2004 [1, p. 54])

Fig. 2

Bell’s second figure illustrating local causality (1975)

First, let us comment briefly on the terminology Bell is using in his first version of local causality.

The term “beable” has been introduced into the literature by Bell himself. It is intended to be opposed to the term ”observable” used in quantum theory and to refer to something that ”really” exists. “The word ’beable’ will also be used to carry another distinction already in classical theory between ’physical’ and ’non-physical’ quantities. In Maxwell’s electromagnetic theory, for example, the fields $\mathbf{E}$ and $\mathbf{H}$ are physical (beables, we will say) but potentials $\mathbf{A}$ and $\phi$ are non-physical.” (Bell 1975/2004 [1, p. 52]) Without the clarification of what the “beables” of a given theory really are, one cannot even formulate local theory.

”Beables” are to be local. “We will be particularly concerned with local beables, those which (unlike for example the total energy) can be assigned to some bounded space-time region. For example, in Maxwell’s theory the beables local to a given region are just the fields $\mathbf{E}$ and $\mathbf{H}$, in that region, and all functionals thereof.” (Bell 1975/2004 [1, p. 53])

Finally, the beables localized in the region $C_1$ are to provide a ”completely specification” of the region in question. We will come back to this point later on.

Although the beables are to be local, in his screening-off condition (2) Bell takes into account the whole causal past of the events in question. He does not assume some kind of Markovity rendering superfluous the remote past regions below a certain Cauchy surface. The second version of his formulation of local causality can be regarded as a step towards this Markovian direction.

Version 2

The notion of local causality presented in this reference [namely in (Bell 1975/2004) [1]] involves complete specification of the beables in an infinite space-time region. The following conception is more attractive in this respect: In a locally-causal theory, probabilities attached to values of local beables in one space-time region, when values are specified for all local beables in a second space-time region fully obstructing the backward light cone of the first, are unaltered by specification of values of local beables in a third region with spacelike separation from the first two. (Bell 1986/2004 [1, p. 200])

Bell’s second version is in a footnote; it is very succinct and contains no figure. The new element is the phrasing “space-time region fully obstructing the backward light cone of the first”. This idea gets a more precise exposition in Bell’s third, final version of local causality.

Version 3

A theory will be said to be locally causal if the probabilities attached to values of local beables in a space-time region A are unaltered by specification of values of local beables in a space-like separated region B, when what happens in the backward light cone of A is already sufficiently specified, for example by a full specification of local beables in a space-time region C (Fig. 3). (Bell 1990/2004 [1, pp. 239–240])

Fig. 3

Bell’s figure illustrating local causality (1990)

The localization of region $C$ is of crucial importance. It is not enough that $C$ completely cuts across the causal past of region $A$; it also has to ”obstruct the backward lightcone of the first”. Bell explicitly stresses this point: “It is important that region $C$ completely shields off from $A$ the overlap of the backward light cones of $A$ and $B$.” (Bell, 1990/2004 [1, p. 240]) This requirement will play a central role in our investigation on the relation of local causality to the Causal Markov Condition. We will come back to that having defined local causality in the next section.

3 Local Causality in Local Physical Theories

The framework integrating probabilistic and spatiotemporal entities can be defined as follows. (For the details and motivations of the definition see [8, 9].)

Definition 1

A ${\mathcal {P}}_{\mathcal{K}}$-covariant local physical theory is a net $\{\mathcal{A}(V),V\in \mathcal{K}\}$ associating algebras of events to spacetime regions which satisfies isotony, microcausality and covariance defined as follows [4]:

• Isotony Let $\mathcal{M}$ be a globally hyperbolic spacetime and let $\mathcal{K}$ be a covering collection of bounded, globally hyperbolic subspacetime regions of $\mathcal{M}$ such that $(\mathcal{K},\subseteq )$ is a directed poset under inclusion $\subseteq$. The net of local observables is given by the isotone map $\mathcal{K}\ni V\mapsto \mathcal{A}(V)$ to unital $C^*$-algebras, that is $V_1 \subseteq V_2$ implies that $\mathcal{A}(V_1)$ is a unital $C^*$-subalgebra of $\mathcal{A}(V_2)$. The quasilocal algebra $\mathcal{A}$ is defined to be the inductive limit $C^*$-algebra of the net $\{\mathcal{A}(V),V\in \mathcal{K}\}$ of local $C^*$-algebras.

• Microcausality (also called as Einstein causality) is the requirement that $\mathcal{A}(V')'\cap \mathcal{A}\supseteq \mathcal{A}(V),V\in \mathcal{K}$, where primes denote spacelike complement and algebra commutant, respectively.

• Spacetime Covariance Let $\mathcal {P}_\mathcal{K}$ be the subgroup of the group $\mathcal {P}$ of geometric symmetries of $\mathcal{M}$ leaving the collection $\mathcal{K}$ invariant. A group homomorphism $\alpha :\mathcal {P}_\mathcal{K}\rightarrow \mathrm Aut \,\mathcal{A}$ is given such that the automorphisms $\alpha _g,g\in \mathcal {P}_\mathcal{K}$ of $\mathcal{A}$ act covariantly on the observable net: $\alpha _g(\mathcal{A}(V))=\mathcal{A}(g\cdot V), V\in \mathcal{K}$.

If the quasilocal algebra $\mathcal{A}$ of the local physical theory is commutative, we speak about a local classical theory; if it is noncommutative, we speak about a local quantum theory. For local classical theories microcausality fulfills trivially.

A state $\phi$ in a local physical theory is defined as a normalized positive linear functional on the quasilocal observable algebra $\mathcal{A}$. The corresponding GNS representation $\pi _{\phi }:\mathcal{A}\rightarrow \mathcal {B}(\mathcal {H}_\phi )$ converts the net of $C^*$-algebras into a net of $C^*$-subalgebras of $\mathcal {B}(\mathcal {H}_\phi )$. Closing these subalgebras in the weak topology one arrives at a net of local von Neumann observable algebras: $\mathcal{N}(V):=\pi _{\phi }(\mathcal{A}(V))'', V\in \mathcal{K}$. Von Neumann algebras are generated by their projections representing quantum events. The net $\{\mathcal{N}(V),V\in \mathcal{K}\}$ of local von Neumann algebras also obeys isotony, microcausality, and $\mathcal {P}_\mathcal{K}$-covariance, hence one can also refer to a net $\{\mathcal{N}(V),V\in \mathcal{K}\}$ of local von Neumann algebras as a local physical theory.

Why von Neumann algebras?

Classical field theories are characterized by their sets of field configurations. Taking the equivalence classes of those field configurations which have the same field values on a given spacetime region one can generate local (cylindrical) $\sigma$-algebras. One can translate $\sigma$-algebras into the language of abelian von Neumann algebras and then generalize this framework also for non-abelian von Neumann algebras. We come back to the details of this procedure in the next section when we introduce our stochastic local classical theory. Thus, we translate Bell’s term “local beables” into the language of local physical theories simply as “elements of a local von Neumann algebra”. Now, how to translate the term “a complete specification of beables”? We are of the opinion that the natural translation of this term is simply “an atomic event of a local von Neumann algebra” [6]. Here it is assumed that the local algebras of the net are atomic, which is not t he case, for example, in Poincaré covariant algebraic quantum field theory. (For a more general definition of local causality see [8].) With these notions in hand now one can formulate Bell’s notion of local causality in a local physical theory as follows:

Definition 2

A local physical theory represented by a net $\{\mathcal{N}(V),V\in \mathcal{K}\}$ of von Neumann algebras is called locally causal, if for any pair $A \in {\mathcal {\mathcal{N}}}(V_A)$ and $B\in {\mathcal {\mathcal{N}}}(V_B)$ of projections supported in spacelike separated regions $V_A, V_B\in \mathcal{K}$ and for every locally normal and faithful state $\phi$ establishing a correlation $\phi (AB)\ne \phi (A)\phi (B)$ between $A$ and $B$, and for any spacetime region $V_C$ such that

• (i) $V_C \subset J_-(V_A)$,

• (ii) $V_A \subset V''_C$,

• (iii) $J_-(V_A) \cap J_-(V_B) \cap \big (J_+(V_C) \setminus V_C\big )= \emptyset$,

(see Fig. 4) and for any atomic event $C_k$ of $\mathcal{A}(V_C)$ ($k\in K$), the following holds:

$$\begin{aligned} \frac{\phi (C_k ABC_k)}{\phi (C_k)} = \frac{\phi ( C_k AC_k)}{\phi (C_k)}\frac{\phi (C_kBC_k)}{\phi (C_k)} \end{aligned}$$

(3)

Fig. 4

A region $V_C$ satisfying Requirements (i)–(iii)

In case of local classical theories a locally faithful state $\phi$ determines uniquely a locally nonzero probability measure $p$ by $p(A):=\phi (A), A\in \mathcal{P}(\mathcal{N}(V))$. By means of this (3) can be written both in the symmetric form

$$\begin{aligned} p(AB\vert C_k) = p(A\vert C_k)p(B\vert C_k) \end{aligned}$$

(4)

and also in the equivalent asymmetric form

$$\begin{aligned} p(A\vert BC_k) = p(A\vert C_k) \end{aligned}$$

(5)

featuring in Bell’s first version of local causality.

Now, the localization of region $V_C$ by Requirements (i)–(iii) is a bit more liberal than that required in Bell’s second version. Although $V_C$ ”completely shields off” region $V_A$ from the common past of $V_A$ and $V_B$, it is not spacelike separated from $V_B$ (as is, for example, region $V_C$ in Fig. 3). But why not to be more liberal? Why Requirement (iii) is needed at all? Why does a region $V_C$ such as the one depicted in Fig. 5 not suffice? The brief answer to this question is that the region above $V_C$ (lighter shaded in Fig. 5) can contain stochastic events which, though completely specified by the region $V_C$, still, being stochastic, could establish a correlation between $A$ and $B$ in a classical stochastic theory [10, 12, 14]. Indeed, exactly this will be the case in our model introduced in the next section.

Fig. 5

A region $V_C$ for which Requirement (iii) does not hold

In order to relate Bell’s local causality to the Causal Markov Condition we need to introduce a screening-off condition similar to local causality, namely Markovity:

Definition 3

A local physical theory represented by a net $\{\mathcal{N}(V),V\in \mathcal{K}\}$ of von Neumann algebras is called Markov, if for any pair $A \in {\mathcal {\mathcal{N}}}(V_A)$ and $B\in {\mathcal {\mathcal{N}}}(V_B)$ of projections supported in regions $V_A, V_B\in \mathcal{K}$ with $V_B \subset I_-(V_A)$ and for every locally normal and locally faithful state $\phi$ establishing a correlation $\phi (AB)\ne \phi (A)\phi (B)$ between $A$ and $B$, and for any spacetime region $V_C$ such that

• (i) $V_C \subset J_-(V_A)$,

• (ii) $V_A \subset V''_C$,

• (iii’) $V_B \subset J_-(V_C)$,

(see Fig. 6) and for any atomic event $C_k$ of $\mathcal{A}(V_C)$ ($k\in K$) (3) holds.

Fig. 6

A region $V_C$ satisfying Requirements (i)–(iii’) of Markovity

The relation between local causality and Markovity is straightforward. In both cases events localized in region $V_A$ and $V_B$, respectively are screened-off by the atomic events in region $V_C$. If $V_A$ and $V_B$ are spacelike separated and $V_C$ is localized according to Requirements (i)–(iii), then (3) expresses local causality. If $V_A$ and $V_B$ are timelike separated and $V_C$ is localized according to Requirements (i)–(iii’), then (3) expresses Markovity. As we will see later Causal Markov Condition will be a special case of the composition of local causality and Markovity.

4 A Simple Stochastic Local Classical Theory

In this section we will develop a simple stochastic local classical theory. Before introducing it in a full-fledged form, let us sketch it in brief. The spacetime of the theory will be a 1+1 dimensional discretized Minkowski spacetime covered by minimal double cones. (See Fig. 7.) The field configurations of the theory are given by mappings assigning a $+$ or a $-$ to each minimal double cone. The dynamics of the theory is generated by the following transition probabilities: The value $+$ or $-$ in a given minimal double cone is probabilistically fixed by the product of the values in the three minimal double cones adjacent to it from below, irrespectively of the value in other minimal double cones, like earlier or spatially separated ones. The probabilistic dependence is this: If the product of the values in the three adjacent minimal double cones is +, then the value in the upper minimal double cone will be + with probability $p$ and $-$ with probability $1-p$; if the product is $-$, the value will be $-$ with probability $p$ and + with probability $1-p$. The process is deterministic, if $p \in \{0,1\}$ and stochastic, if $p \in (0,1)$. Now, let us see the theory in a more detailed way.

Fig. 7

A simple stochastic local classical theory

Consider a discretized version of the two dimensional Minkowski spacetime $\mathcal M^2$ which is composed of minimal double cones $V^m(t,i)$ of unit diameter with their center in $(t,i)$ for $t,i\in \mathbb {Z}$ or $t,i\in \mathbb {Z}+1/2$. The set $\{V^m(t,i), i\in {\frac{1}{2}}\mathbb {Z}\}$ of such minimal double cones with $t=0, -1/2$ defines a ‘thickened’ Cauchy surface in this spacetime, denoted by $\mathcal{S}_0$. For double cones sitting on $\mathcal{S}_0$ we will drop the time coordinate and simply write $V^m_i$. (See Fig. 8.)

Fig. 8

Two dimensional discrete Minkowski spacetime with a ‘thickened’ Cauchy surface

A double cone $V(t,i;s,j)$ is defined to be the smallest double cone containing both $V^m(t,i)$ and $V^m(s,j)$, that is generated by them: $V(t,i;s,j):=V^m(t,i)\vee V^m(s,j)$. The directed poset of such double cones is denoted by $\mathcal{K}^m$ and the directed poset of double cones generated by minimal double cones sticked to the Cauchy surface $\mathcal{S}_0$ is denoted by $\mathcal{K}^m_0$. Obviously, $\mathcal{K}^m_0$ will be left invariant by integer space translations and $\mathcal{K}^m$ will be left invariant by integer space and time translations. By shifting the time coordinates of the minimal double cones by $t$ one can similarly define the Cauchy surface $\mathcal{S}_t$ and the net $\mathcal{K}^m_t$.

Let $S^m$ denote the set of minimal double cones of $\mathcal M^2$ and let $\mathbf{Z}_2$ be the multiplicative group of the integers $\{1,-1\}$. Define the set $\mathcal{C}$ of configurations of the theory as: $\mathcal{C}:=\{ c:S^m\rightarrow \mathbf{Z}_2\}$. The maximal $\sigma$-algebra of classical events $(\mathcal{C},\mathcal{P}(\mathcal{C}))$ is given by the power set $\mathcal{P}(\mathcal{C})$ of the set of configurations. But one can also obtain a narrower $\sigma$-algebra in tune with the net structure $\mathcal{K}^m$. This is done by taking the equivalence classes of those configurations which have the same field values on a given region in $\mathcal{K}^m$. The sets $\mathcal{C}_V$ of local equivalence classes (the ‘cylindrical subsets’ of $\mathcal{C}$ concentrated on $V$) are obtained by the equivalence relation: $c\sim _V c'$ if $c_{\vert V}=c'_{\vert V}$. Clearly, $\mathcal{C}_V$ contains $2^{\vert V\vert }$ elements, where $\vert V\vert$ is the number of minimal double cones in $V$. One can get the power set $\mathcal{P}(\mathcal{C}_V)$ of $\mathcal{C}_V$ by definin g the following map $Z_V$ for $V\in \mathcal{K}^m$:

$$\begin{aligned} Z_V:\mathcal{P}(\mathcal{C})\rightarrow \mathcal{P}(\mathcal{C}), \, \, C\mapsto \{ c'\in \mathcal{C}\, | \exists c\in C: c_{\vert V}= c'_{\vert V}\} \end{aligned}$$

(6)

For a given $V\in \mathcal{K}^m$ the image sets of $Z_V$ define a unital $\sigma$-subalgebra $\Sigma (V)$ of $\mathcal{P}(\mathcal{C})$, which is isomorphic to the power set $\mathcal{P}(\mathcal{C}_V)$ of $\mathcal{C}_V$. By ranging over $V\in \mathcal{K}^m$ one obtains an isotone net structure $\{(\mathcal{C},\Sigma (V)), V\in \mathcal{K}^m\}$. The $2^{\vert V\vert }$ dimensional abelian local von Neumann algebra $\mathcal{N}(V)$ corresponding to the local $\sigma$-algebra $\Sigma (V)$ is spanned by the orthogonal set of minimal projections $P^c_V,c\in \mathcal{C}_V$ corresponding to characteristic functions $\chi ^c_V:\mathcal{C}\rightarrow \mathbf{C}$ which are $1$ on the cylindrical subset $c\in \mathcal{C}_V$ of $\mathcal{C}$ and $0$ otherwise. Clearly, $\{\mathcal{N}(V),V\in \mathcal{K}^m\}$ is an isotone net of finite dimensional abelian von Neumann algebras, hence it defines a local classical theory.

The quasilocal $C^*$-algebra $\mathcal{A}$ is given by the inductive limit of the local von Neumann algebras $\mathcal{N}(V), V\in \mathcal{K}^m$, and similarly the unital $C^*$-subalgebras $\mathcal{A}_0$ of $\mathcal{A}$ is given by the inductive limit of the local von Neumann algebras $\mathcal{N}(V), V\in \mathcal{K}^m_0$. Now, a stochastic theory can be regarded as a state extension procedure from the subalgebra $\mathcal{A}_0$ (or from any $\mathcal{A}_t$) to the quasilocal algebra $\mathcal{A}$ by means of so-called transition probabilities. This is done in the following way.

Let $V\left( t+{\frac{1}{2}}\right)$ be a finite set of minimal double cones on the time slice $t+{\frac{1}{2}}$. Define the nearest past of $V\left( t+{\frac{1}{2}}\right)$ as follows: $\mathcal{P}_t\left( V\left( t+{\frac{1}{2}}\right) \right) \equiv \mathcal{S}_t\cap \left( \mathcal{S}_t\setminus J_-\left( V\left( t+{\frac{1}{2}}\right) \right) \right) '$. Specifically, the nearest past $\mathcal{P}_t\left( V^m\left( t+{\frac{1}{2}},i\right) \right)$ of the minimal double cone $V^m\left( t+{\frac{1}{2}},i\right)$ contains the three minimal double cones adjacent to $V^m\left( t+{\frac{1}{2}},i\right)$ from below, namely $V^m\left( t,i-{\frac{1}{2}}\right)$, $V^m\left( t-{\frac{1}{2}},i\right)$ and $V^m\left( t,i+{\frac{1}{2}}\right)$. For a given configuration $c \in \mathcal{C}$ define the generating transition probabilities from the equivalence class $c_{\mathcal{P}_t(V^m(t+{\frac{1}{2}},i))}$ to the equivalence class $c_{V^m(t+{\frac{1}{2}},i)}$ as follows:

$$\begin{aligned}&p\left( c_{V^m(t+{\frac{1}{2}},i)}|c_{\mathcal{P}_t(V^m(t+{\frac{1}{2}},i))}\right) \nonumber \\&\quad := \left\{ \begin{array}{rl} p, &{}\quad \text{ if } \, \, \, c\left( t+{\frac{1}{2}},i\right) = c\left( t,i-{\frac{1}{2}}\right) c\left( t-{\frac{1}{2}},i\right) c\left( t,i+{\frac{1}{2}}\right) \\ 1-p, &{}\quad \text{ if } \, \, \, c\left( t+{\frac{1}{2}},i\right) = - c\left( t,i-{\frac{1}{2}}\right) c\left( t-{\frac{1}{2}},i\right) c\left( t,i+{\frac{1}{2}}\right) \end{array}\right. \end{aligned}$$

(7)

where $c(t,i)$ is short for $c(V^m(t,i))$, the value of the configuration $c$ at the minimal double cone $V^m(t,i)$. Assuming that the generating transition probabilities are independent with respect to spacelike separation, one can define the transition probabilities from the Cauchy surface $\mathcal{S}_t$ to the time slice $t+{\frac{1}{2}}$ as:

$$\begin{aligned} p\left( c_{V(t+{\frac{1}{2}})}|c_{\mathcal{P}_t(V(t+{\frac{1}{2}}))}\right) := \prod _{V^m(t+{\frac{1}{2}},i)\in V(t+{\frac{1}{2}})} p\left( c_{V^m(t+{\frac{1}{2}},i)}|c_{\mathcal{P}_t(V^m(t+{\frac{1}{2}},i))}\right) \end{aligned}$$

(8)

Intuitively, these transition probabilities do the following: The value $+$ or $-$ in a given minimal double cone is probabilistically fixed purely by the product of the values in the three minimal double cones adjacent to it from below. (See again Fig. 7.) Negatively speaking, they do not depend on the value of other minimal double cones, like earlier or spatially separated ones. As we will see, these two independencies are closely connected to Markovity and local causality, respectively. If the product is +, then the value is + with probability $p$ and $-$ with probability $1-p$; if the product is $-$, the value is $-$ with probability $p$ and + with probability $1-p$.

Finally, let $U(t)$ be a finite set of minimal double cones on the Cauchy surface $\mathcal{S}_t$. We define the state on the equivalence class $c_{V(t+{\frac{1}{2}})} \cap c_{U(t)}$ as follows:

$$\begin{aligned} \phi \left( c_{V(t+{\frac{1}{2}})} \cap c_{U(t)}\right) := p\left( c_{V(t+{\frac{1}{2}})}|c_{\mathcal{P}_t(V(t+{\frac{1}{2}}))}\right) \phi \left( c_{\mathcal{P}_t(V(t+{\frac{1}{2}}))} \cap c_{U(t)}\right) \end{aligned}$$

(9)

Thus, starting from $\phi _0$ on $\mathcal{A}_0$ one can recursively define the state $\phi$ on the whole $\mathcal{A}$. (For the Cauchy surfaces below $\mathcal{S}_0$ we use Bayes theorem for the extension.)

To simplify things, introduce the following denotation. Let $i^+$ and $i^-$ denote three different things at the same time: the two cylindrical subsets of $\mathcal{C}_{V^m_i}$ concentrated on the minimal double cone $V^m_i$ on the Cauchy surface $\mathcal{S}_0$; the two corresponding characteristic functions; and also the two corresponding orthogonal projections in $\mathcal{N}(V^m_i)$. If we are not specifying which of the two sets/characteristic functions/projections we are speaking about, we simply write $i$. The $n$th forward and backward space translates of $i$ will be denoted by $(i+n)$ and $(i-n)$, respectively ($n \in {\frac{1}{2}}\mathbb N$); the $t$th forward and backward time translates will be denoted by $i_t$ and $i_{-t}$, respectively ($t \in \mathbb N$).

Let, furthermore,

$$\begin{aligned} i \cdot \left( i+{\frac{1}{2}}\right) \dots \left( j-{\frac{1}{2}}\right) \cdot j \end{aligned}$$

denote the product of a sequence of projections localized on the Cauchy surface $\mathcal{S}_0$ between minimal double cones $V^m_i$ and $V^m_j$, and let $p_{i\dots j}$ denote the probability thereof in state $\phi$. Since we will deal only with projections of abelian von Neumann algebras, from now on instead of $\phi$ we simply write $p$. Finally, we will express the condition

$$\begin{aligned} c\left( t+{\frac{1}{2}},i\right) = c\left( t,i-{\frac{1}{2}}\right) c\left( t-{\frac{1}{2}},i\right) c\left( t,i+{\frac{1}{2}}\right) \end{aligned}$$

in (7) by the Dirac delta symbol

$$\begin{aligned} \delta _{c\left( t+{\frac{1}{2}},i\right) ,c\left( t,i-{\frac{1}{2}}\right) c\left( t-{\frac{1}{2}},i\right) c\left( t,i+{\frac{1}{2}}\right) } \end{aligned}$$

or in the short form

$$\begin{aligned} \delta _{i_1,\left( i-{\frac{1}{2}}\right) i\left( i+{\frac{1}{2}}\right) } \end{aligned}$$

Now, let $A = i_t$ and $B =j_s$ be two projections localized in the minimal double cones $V^m(t,i)$ and $V^m(s,j)$, respectively, with $i<j$. Suppose that $V^m(t,i)$ and $V^m(s,j)$ are spatially separated, that is $|j-i| > |s-t|$. To calculate the probability of $A$, $B$ and $AB$, we need a little geometry. (See Fig. 9.) Consider the minimal double cone $V^m(u,k)$ (striped horizontally) at the ’top of the common past’ of regions $V^m(t,i)$ and $V^m(s,j)$. The coordinates of $V^m(u,k)$ are the following:

$$\begin{aligned} u = {\frac{1}{2}}(t+s+i-j) \quad k = {\frac{1}{2}}(i+j+t-s) \end{aligned}$$

(10)

Fig. 9

A little geometry

Consider now the Cauchy surface $\mathcal{S}_{\lceil u \rceil }$ fitting $V^m(u,k)$, where the ceiling function $\lceil \cdot \rceil$ in the subscript is just to round up the $u$ coordinates if half integers. Let the number of minimal double cones in the causal past of $V^m(t,i)$ above $\mathcal{S}_0$ (including $V^m(t,i)$ but not including double cones on $\mathcal{S}_0$) be denoted by $n$, and the number of minimal double cones in the causal past of $V^m(t,i)$ above $\mathcal{S}_{\lceil u \rceil }$ (again including $V^m(t,i)$ but not including double cones on $\mathcal{S}_{\lceil u \rceil }$) by $n'$. Similarly, the number of minimal double cones in the causal past of $V^m(s,j)$ above $\mathcal{S}_0$ and $\mathcal{S}_{\lceil u \rceil }$ be denoted by $m$ and $m'$, respectively. Finally, denote the number of minimal double cones in the causal past of $V^m(u,k)$ above $\mathcal{S}_0$ by $l$. The numbers $n$, $n'$, $m'$, $m$ and $l$ are the following functions of $i,j,t$ and $s$:

$$\begin{aligned} n&= \left\{ \begin{array}{ll} -t + 4\sum _{x=1}^tx, &{}\quad \text{ if }\ i\in \mathbb N\\ t + 4\sum _{x=1}^t(x-1), &{}\quad \text{ if }\ i\in {\frac{1}{2}}\mathbb N \end{array} \right. \end{aligned}$$

(11)

$$\begin{aligned} n'&= \left\{ \begin{array}{ll} -t + 4\sum _{x=\lceil u \rceil }^tx, &{}\quad \text{ if }\ i\in \mathbb N\\ t + 4\sum _{x=\lceil u \rceil }^t(x-1), &{}\quad \text{ if }\ i\in {\frac{1}{2}}\mathbb N \end{array} \right. \end{aligned}$$

(12)

$$\begin{aligned} m&= \left\{ \begin{array}{ll} -s + 4\sum _{x=1}^sx, &{}\quad \text{ if }\ j\in \mathbb N\\ s + 4\sum _{x=1}^s(x-1), &{}\quad \text{ if }\ j\in {\frac{1}{2}}\mathbb N \end{array} \right. \end{aligned}$$

(13)

$$\begin{aligned} m'&= \left\{ \begin{array}{ll} -s + 4\sum _{x=\lceil u \rceil }^sx, &{}\quad \text{ if }\ j\in \mathbb N\\ s + 4\sum _{x=\lceil u \rceil }^s(x-1), &{}\quad \text{ if }\ j\in {\frac{1}{2}}\mathbb N \end{array} \right. \end{aligned}$$

(14)

$$\begin{aligned} l&= \left\{ \begin{array}{ll} -\lceil u \rceil + 4\sum _{x=1}^{\lceil u \rceil }x, &{}\quad \text{ if }\ k\in \mathbb N\\ \lceil u \rceil + 4\sum _{x=1}^{\lceil u \rceil }(x-1), &{}\quad \text{ if }\ k\in {\frac{1}{2}}\mathbb N \end{array} \right. \end{aligned}$$

(15)

In Fig. 9, for example, $n=m=3$, $n'=m'=21$ and $l=6$. With these numbers one can also calculate the number $r$ of minimal double cones between $\mathcal{S}_{\lceil u \rceil }$ and $\mathcal{S}_0$ (including double cones on $\mathcal{S}_{\lceil u \rceil }$ but not on $\mathcal{S}_0$):

$$\begin{aligned} r&= n-n'+m-m'-l \end{aligned}$$

(16)

which is 30 in Fig. 9. Now, using the above numbers (11)–(16) the probability of $A$, $B$ and $AB$ will be the following:

$$\begin{aligned} p(A)&= \sum _{\left( i-t-\left\{ i+{\frac{1}{2}}\right\} \right) , \dots , \left( i+t+\left\{ i+{\frac{1}{2}}\right\} \right) } \bigg [q_n\delta _{i_t,(i-t+\{i\}) \dots (i+t-\{i\})}\nonumber \\&+\,\,(1-q_n)\delta _{-i_t,(i-t+\{i\}) \dots (i+t-\{i\})}\bigg ]p_{\left( i-t-\left\{ i+{\frac{1}{2}}\right\} \right) \dots \left( i+t+\left\{ i+{\frac{1}{2}}\right\} \right) } \end{aligned}$$

(17)

$$\begin{aligned} p(B)&= \sum _{\left( j-s-\left\{ j+{\frac{1}{2}}\right\} \right) , \dots , \left( j+s+\left\{ j+{\frac{1}{2}}\right\} \right) } \bigg [q_{m}\delta _{j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\nonumber \\&+\,\,(1-q_m)\delta _{-j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\bigg ]p_{(j-s-\{j+{\frac{1}{2}}\}) \dots (j+s+\{j+{\frac{1}{2}}\})} \end{aligned}$$

(18)

$$\begin{aligned} p(AB)&= \sum _{(i-t+\{i\}), \dots , ( j+s-\{j\})} \bigg [q_{n'}q_{m'}q_r \, \delta _{i_t,(i-t+\{i\}) \dots (i+t-\{i\})}\delta _{j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\nonumber \\&+\,\,q_{n'}(1-q_{m'})q_r \, \delta _{i_t,(i-t+\{i\}) \dots (i+t-\{i\})}\delta _{-j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\nonumber \\&+\,\,(1-q_{n'})q_{m'}q_r \, \delta _{-i_t,(i-t+\{i\}) \dots (i+t-\{i\})}\delta _{j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\nonumber \\&+\,\,(1-q_{n'})(1-q_{m'})q_r \, \delta _{-i_t,(i-t+\{i\}) \dots (i+t-\{i\})}\delta _{-j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\bigg ]\nonumber \\&\,\,\times p_{(i-t-\{i+{\frac{1}{2}}\}) \dots (j+s+\{j+{\frac{1}{2}}\})} \end{aligned}$$

(19)

where the fractional part function $\{\cdot \}$ in the subscript is again to treat integer and half integer coordinates together, and $q_x$ ($x=n,n',m,m',r$) is the even part of the binomial expression:

$$\begin{aligned} q_x&:= p^x + {x \atopwithdelims ()2}p^{x-2}(1-p)^2 + {x \atopwithdelims ()4}p^{x-4}(1-p)^4 + \dots \end{aligned}$$

(20)

Obviously, in the general case:

$$\begin{aligned} p(AB)\ne p(A)p(B) \end{aligned}$$

(21)

so there is a superluminal correlation between $A$ and $B$.

Example 1 As an example, let $A= i_1^+$ and $B=j_1^+$, where $j= i+2 \in \mathbb N + {\frac{1}{2}}$. (See Fig. 10.) Let the ’prior’ probabilities $p_{(i-1) \dots (j+1)}$ on $\mathcal{S}_0$ be fixed as follows:

$$\begin{aligned} p_{+++++++++}&= \frac{1}{2} \end{aligned}$$

(22)

$$\begin{aligned} p_{+++++++-+}&= \frac{1}{4} \end{aligned}$$

(23)

$$\begin{aligned} p_{+-+++++++}&= \frac{1}{4} \end{aligned}$$

(24)

and all the other combinations be $0$. Then the probability of $A$, $B$ and $AB$ is the following:

$$\begin{aligned} p(A)&= \sum _{(i-1), \dots , (i+1)} \bigg [p\, \delta _{i_1^+,(i-{\frac{1}{2}}) i (i+{\frac{1}{2}})}+(1-p)\delta _{-i_1^+,(i-{\frac{1}{2}}) i (i+{\frac{1}{2}})}\bigg ]p_{(i-1) \dots (i+1)} \nonumber \\&= \frac{1}{2}\bigg (\frac{1}{2}+p\bigg )\end{aligned}$$

(25)

$$\begin{aligned} p(B)&= \sum _{(j-1), \dots , (j+1)} \bigg [p\, \delta _{j_1^+,(j-{\frac{1}{2}}) j (j+{\frac{1}{2}})}+(1-p)\delta _{-j_1^+,(j-{\frac{1}{2}}) j (j+{\frac{1}{2}})}\bigg ]p_{(j-1) \dots (j+1)}\nonumber \\&= \frac{1}{2}\bigg (\frac{1}{2}+p\bigg )\end{aligned}$$

(26)

$$\begin{aligned} p(AB)&= \sum _{(i-1), \dots , (j+1)} \bigg [p^2\, \delta _{i_1^+,(i-{\frac{1}{2}}) i (i+{\frac{1}{2}})}\delta _{j_1^+,(j-{\frac{1}{2}}) j (j+{\frac{1}{2}})} \nonumber \\&\!\quad +\,(1-p)p\, \delta _{-i_1^+,(i-{\frac{1}{2}}) i (i+{\frac{1}{2}})}\delta _{j_1^+,(j-{\frac{1}{2}}) j (j+{\frac{1}{2}})} \nonumber \\&\!\quad +\,(1-p)^2\delta _{-i_1^+,(i-{\frac{1}{2}}) i (i+{\frac{1}{2}})}\delta _{-j_1^+,(j-{\frac{1}{2}}) j (j+{\frac{1}{2}})}\bigg ]p_{(i-1) \dots (j+1)} = \frac{1}{2} p \end{aligned}$$

(27)

thus $A$ and $B$ are correlating whenever $p\ne \frac{1}{2}$.

Fig. 10

Superluminally correlating events $i_1^+$ and $j_1^+$

Example 2 In the second example, let $A= i_2^+$ and $B=j_2^+$, where again $j= i+2 \in \mathbb N + {\frac{1}{2}}$. (See Fig. 11.) With the ’prior’ probabilities $p_{(i-2) \dots (j+2)}$:

$$\begin{aligned} p_{+++++++++++++}&= \frac{1}{2} \end{aligned}$$

(28)

$$\begin{aligned} p_{+++++++++++-+}&= \frac{1}{4} \end{aligned}$$

(29)

$$\begin{aligned} p_{+-+++++++++++}&= \frac{1}{4} \end{aligned}$$

(30)

(and the rest is 0) one obtains the probability of $A$, $B$ and $AB$ as:

$$\begin{aligned} p(A)&= \sum _{(i-2), \dots , (i+2)} \bigg [q_6\, \delta _{i_2^+,(i-{\frac{3}{2}}) \dots (i+{\frac{3}{2}})}+(1-q_6)\delta _{-i_2^+,(i-{\frac{3}{2}}) \dots (i+{\frac{3}{2}})}\bigg ]p_{(i-2) \dots (i+2)} \nonumber \\&= \frac{1}{2}\bigg (\frac{1}{2}+q_6\bigg )\end{aligned}$$

(31)

$$\begin{aligned} p(B)&= \sum _{(j-2), \dots , (j+2)} \bigg [q_6\, \delta _{j_2^+,(j-{\frac{3}{2}}) \dots (j+{\frac{3}{2}})}\nonumber \\&\quad +\,(1-q_6)\delta _{-j_2^+,(j-{\frac{3}{2}}) \dots (j+{\frac{3}{2}})}\bigg ]p_{(j-2) \dots (j+2)} = \frac{1}{2}\bigg (\frac{1}{2}+q_6\bigg )\end{aligned}$$

(32)

$$\begin{aligned} p(AB)&= \sum _{(i-2), \dots , (j+2)} \bigg [p^2 q_9\, \delta _{i_2^+,(i-{\frac{3}{2}}) \dots (i+{\frac{3}{2}})}\delta _{j_2^+,(j-{\frac{3}{2}}) \dots (j+{\frac{3}{2}})}\nonumber \\&\quad +p\, (1-p)\, q_9\,\delta _{i_2^+,(i-{\frac{3}{2}}) \dots (i+{\frac{3}{2}})}\delta _{-j_2^+,(j-{\frac{3}{2}}) \dots (j+{\frac{3}{2}})}\nonumber \\&\quad +\,(1-p)\, p\, q_9\, \delta _{-i_2^+,(i-{\frac{3}{2}}) \dots (i+{\frac{3}{2}})}\delta _{j_2^+,(j-{\frac{3}{2}}) \dots (j+{\frac{3}{2}})}\nonumber \\&\quad +\,(1-p)^2 q_9\, \delta _{-i_2^+,(i-{\frac{3}{2}}) \dots (i+{\frac{3}{2}})}\delta _{-j_2^+,(j-{\frac{3}{2}}) \dots (j+{\frac{3}{2}})}\bigg ] \nonumber \\&\quad \times \, p_{(i-2) \dots (j+2)} = \frac{1}{2} pq_9 \end{aligned}$$

(33)

thus $A$ and $B$ are correlating whenever $\frac{1}{4}(\frac{1}{2}+q_6)^2 \ne {\frac{1}{2}}pq_9$ which is the typical case.

Fig. 11

Superluminally correlating events $i_2^+$ and $j_2^+$.

The difference between Example 1 and 2 is that in Example 1 there is no minimal double cone above $\mathcal{S}_0$ in the common past of $A$ and $B$, whereas in Example 2 there is such a minimal double cone, namely $V^m(1, i+1)$.² This difference will have crucial consequences concerning local causality to which we turn now.

First, we prove that the above local classical theory is locally causal. Actually, we prove a little less: local causality for a specific choice of $V_A$, $V_B$ and $V_C$. (For a general proof see [8].) Let $V_A=V^m(t,i)$ and $V_B = V^m(s,j)$ be two spatially separated minimal double cones with $i<j$, and let $V_C$ be generated by the intersection of the causal past of $V_A$ and a Cauchy surface ”shielding off” $V_A$ from the common past of $V_A$ and $V_B$. Any Cauchy surface $\mathcal{S}_v$ with $\lceil u \rceil \leqslant v\leqslant t$ will be such a ”shielder-off” Cauchy surface, where $u$ is defined in (10). (For a ”shielder-off” Cauchy surface see Fig. 9.) The region $V_C$ generated by this intersection will obviously satisfy Requirements (i)–(iii) in Definition 2 of local causality.

Now, we prove local causality with respect to these regions.

Proposition 1

The stochastic local classical theory $\{\mathcal{N}(V),V\in \mathcal{K}^m\}$ is locally causal for any three regions $V_A$, $V_B$ and $V_C$ specified above.

Proof

Let $A = i_t$ and $B =j_s$ be two projections localized in $V_A$ and $V_B$, respectively, and correlating in the probability measure $p$. We are to show that for any atomic event

$$\begin{aligned} C=\bigg (i-t+v-\bigg \{i+{\frac{1}{2}}\bigg \}\bigg )_v \dots \bigg (i+t-v+\bigg \{i+{\frac{1}{2}}\bigg \}\bigg )_v \end{aligned}$$

of $V_C$ the following holds:

$$\begin{aligned} p(AB |C) = p(A |C) p( B |C) \end{aligned}$$

(34)

First, for the sake of convenience, shift the Cauchy surface $\mathcal{S}_0$ up to $\mathcal{S}_v$ and denote the new time coordinates by a prime: $t':=t-v$ and $s' := s-v$. Similarly let $q'_n$ and $q'_m$ denote the appropriate number of minimal double cones with respect to the shifted Cauchy surface. With this notation the conditional probabilities are the following:

$$\begin{aligned} p(A|C)&= \bigg [q'_n\delta _{i_{t'},(i-t'+\{i\}) \dots (i+t'-\{i\})}+(1-q'_n)\delta _{-i_{t'},(i-t'+\{i\}) \dots (i+t'-\{i\})}\bigg ] \end{aligned}$$

(35)

$$\begin{aligned} p(B|C)&= \sum _{\big (j-s'-\big \{j+{\frac{1}{2}}\big \}\big ), \dots , \big (j+s'+\big \{j+{\frac{1}{2}}\big \}\big )} \bigg [q'_{m}\delta _{j_{s'},(j-s'+\{j\}) \dots (j+s'-\{j\})}\nonumber \\&\quad +\,(1-q'_m)\delta _{-j_{s'},(j-s'+\{j\}) \dots (j+s'-\{j\})}\bigg ]p_{C\big (j-s'-\big \{j+{\frac{1}{2}}\big \}\big ) \dots \big (j+s'+\big \{j+{\frac{1}{2}}\big \}\big )} \end{aligned}$$

(36)

$$\begin{aligned} p(AB|C)&= \sum _{\big (j-s'-\big \{j+{\frac{1}{2}}\big \}\big ), \dots , \big (j+s'+\big \{j+{\frac{1}{2}}\big \}\big )} \bigg [q'_{n}q'_{m} \, \delta _{i_{t'},(i-t'+\{i\}) \dots (i+t'-\{i\})}\delta _{j_{s'},(j-s'+\{j\}) \dots (j+s'-\{j\})}\nonumber \\&\quad +\,q'_{n}(1-q'_{m}) \, \delta _{i_{t'},(i-t'+\{i\}) \dots (i+t'-\{i\})}\delta _{-j_{s'},(j-s'+\{j\}) \dots (j+s'-\{j\})}\nonumber \\&\quad +\,(1-q'_{n})q'_{m} \, \delta _{-i_{t'},(i-t'+\{i\}) \dots (i+t'-\{i\})}\delta _{j_{s'},(j-s'+\{j\}) \dots (j+s'-\{j\})}\nonumber \\&\quad +\,(1-q'_{n})(1-q'_{m}) \, \delta _{-i_{t'},(i-t'+\{i\}) \dots (i+t'-\{i\})}\delta _{-j_{s'},(j-s'+\{j\}) \dots (j+s'-\{j\})}\bigg ]\nonumber \\&\quad \times \, p_{C\big (j-s'-\big \{j+{\frac{1}{2}}\big \}\big ) \dots \big (j+s'+\big \{j+{\frac{1}{2}}\big \}\big )} \end{aligned}$$

(37)

where $p_{C\big (j-s'-\big \{j+{\frac{1}{2}}\big \}\big ) \dots \big (j+s'+\big \{j+{\frac{1}{2}}\big \}\big )}$ is a short for

$$\begin{aligned} p_{\big (i-t'-\big \{i+{\frac{1}{2}}\big \} \dots \big (i+t'+\big \{i+{\frac{1}{2}}\big \}\big )\big (j-s'-\big \{j+{\frac{1}{2}}\big \}\big ) \dots \big (j+s'+\big \{j+{\frac{1}{2}}\big \}\big )} \end{aligned}$$

From (35)–(37) the screening-off (34) follows immediately. $\square$

One can see from the proof that if $V_C$ is a segment of Cauchy surface satisfying Requirements (i)–(iii) in Definition 2, that is a segment of Cauchy surface located at or above the top of the common causal past of the correlating events $A$ and $B$, then from (19) the $q_r$ terms will drop out leaving no correlation between the conditional probabilities. Note that $V_C$ need not necessarily be above the common past of $A$ and $B$, it can also intersect with the top of it (see again Fig. 5). All is needed is that there is no region above $V_C$ in the common past. Such a region, namely, can contain stochastic events which could establish a correlation between $A$ and $B$. Mathematically this means that from (19) the $q_r$ terms would not drop out and hence the correlation would not be screened off by the atomic events of $V_C$. Requirement (iii) in the definition of local causality is just to exclude this case. The next proposition shows that Requirement (iii) also is a necessary condition in the localization of $V_C$.

Proposition 2

The local classical theory $\{\mathcal{N}(V),V\in \mathcal{K}^m\}$ would not be locally causal if Requirement (iii) was dropped from Definition 2.

Proof

Consider Example 2 of the previous Section that is let $A= i_2^+$ and $B=(i+2)_2^+$ and the prior probabilities those fixed in (28)–(30). Let $C$ be the minimal projection

$$\begin{aligned} (i-2)^+\left( i-{\frac{3}{2}}\right) ^+(i-1)^+\left( i-{\frac{1}{2}}\right) ^+i^+\left( i+{\frac{1}{2}}\right) ^+(i+1)^+\left( i+{\frac{3}{2}}\right) ^+(i+2)^+ \end{aligned}$$

localized in region $V_C$. (See Fig. 12.) For the region $V_C$ Requirement (iii) does not hold since there is a minimal double cone, $V^m(1, i+1)$ (the one with horizontal stripes) above region $V_C$ in the common past of $V_A$ and $V_B$.

Using the identity

$$\begin{aligned} \sum _{\left( i+\frac{5}{2}\right) ,(i+3),\left( i+\frac{7}{2}\right) ,(i+4)} \left( i+\frac{5}{2}\right) (i+3)\left( i+\frac{7}{2}\right) (i+4) = \mathbf {1}\end{aligned}$$

(38)

it is easy to see that $C$ does not screen off the correlation between $A$ and $B$ since

$$\begin{aligned}&p(A |C) = q_6 \end{aligned}$$

(39)

$$\begin{aligned}&p( B |C) \nonumber \\&\quad = \frac{\sum _{(i+\frac{5}{2}),(i+3),(i+\frac{7}{2}),(i+4)} p\big (B\big |C(i{+}\frac{5}{2}),(i{+}3),(i+\frac{7}{2}),(i{+}4)\big )p_{C(i{+}\frac{5}{2}),(i{+}3),(i{+}\frac{7}{2}),(i{+}4)}}{p(C)} \nonumber \\&\quad = \frac{1}{3}(1+q_6)\end{aligned}$$

(40)

$$\begin{aligned}&p(A B |C) \nonumber \\&\quad = \frac{\sum _{(i{+}\frac{5}{2}),(i{+}3),(i{+}\frac{7}{2}),(i{+}4)} p\big (AB\big |C(i{+}\frac{5}{2}),(i+3),(i{+}\frac{7}{2}),(i{+}4)\big )p_{C(i{+}\frac{5}{2}),(i{+}3),(i{+}\frac{7}{2}),(i+4)}}{p(C)} \nonumber \\&\quad = \frac{1}{3}(1+p)pq_9 \end{aligned}$$

(41)

for any $C$ of non-zero measure. But typically

$$\begin{aligned} \frac{1}{3} q_6(1+q_6)&\ne \frac{1}{3}(1+p)pq_9 \end{aligned}$$

(42)

since the left and right hand side are of different ordo in $p$. $\square$

Next we prove that the above local classical theory is also Markov. Again, we prove a little less: local causality for a minimal double cone $V_A=V^m(t,i)$, another minimal double cone $V_B = V^m(s,j)$ lying in the causal past of $V_A$, and a third region $V_C$ generated by the intersection of the causal past of $V_A$ and a Cauchy surface ”shielding off” $V_A$ from $V_B$. (See Fig. 13.) $V_C$ will obviously satisfy Requirements (i)–(iii’) in Definition 3 of Markovity. $\square$

Fig. 12

A region $V_C$ for which Requirement (iii) does not hold.

Fig. 13

The regions $V_A$, $V_B$ and $V_C$ for which Markovity holds

Proposition 3

The stochastic local classical theory $\{\mathcal{N}(V),V\in \mathcal{K}^m\}$ is Markov for any three regions $V_A$, $V_B$ and $V_C$ specified above.

Proof

Let $A = i_t$ and $B =j_s$ be two projections localized in $V_A$ and $V_B$, respectively, and correlating in the probability measure $p$. We are to show that for any atomic event

$$\begin{aligned} C=\bigg (i-t+v-\bigg \{i+{\frac{1}{2}}\bigg \}\bigg )_v \dots \bigg (i+t-v+\bigg \{i+{\frac{1}{2}}\bigg \}\bigg )_v \end{aligned}$$

of $V_C$ with $s<v<t$ the following holds:

$$\begin{aligned} p(A|C) = p(A |CB) \end{aligned}$$

(43)

But it does, since both sides of (43) are simply

$$\begin{aligned} q'_n\delta _{i_{t'},(i-t'+\{i\}) \dots (i+t'-\{i\})}+(1-q'_n)\delta _{-i_{t'},(i-t'+\{i\}) \dots (i+t'-\{i\})} \end{aligned}$$

where again $t':=t-v$ and $q'_n$ denotes the appropriate number of minimal double cones with respect to the shifted Cauchy surface. $\square$

5 Local Causality, Causal Markov Condition and d-Separation

Now, I connect local causality and Markovity to the Causal Markov Condition used in the theory of Bayesian networks (see [13] and Spirtes and co-workers [3]). Consider a directed acyclic graph $\mathcal {G}$ and a set of random variables $\mathcal {V}$ on a classical probability space $(\Sigma ,p)$ such that the elements $X, Y \dots$ of $\mathcal {V}$ are represented by the vertices of $\mathcal {G}$ and the arrows $X\rightarrow Y$ on the graph represent that $X$ is causally relevant for $Y$. For any $X\in \mathcal {V}$ let $Par(X)$, the parents of $X$, be the set of vertices that have directed edges in $X$; let $Anc(X)$, the ancestors of $X$, be the set of vertices from which a directed paths is leading to $X$; and finally let $Des(X)$, the descendants of $X$, be the set of vertices that are endpoints of a directed paths from $X$. The set $\mathcal {V}$ is said to satisfy the Causal Markov Condition Causal Markov Condition relative to the graph $\mathcal {G}$ if for any $X\in \mathcal {V}$ and any $Y\notin Des(X)$ the following is true:

$$\begin{aligned} p(X\vert Par(X) \wedge Y)&= p(X\vert Par(X)) \end{aligned}$$

(44)

In other words, conditioning on its parents the random variable $X$ will be probabilistically independent from any of its non-descendant. Non-descendants of $X$ can be of two types: either ancestors or non-relatives (non-descendants and non-ancestors). As we will see, being independent of ancestors is related to the Markovity, whereas being independent of non-relatives is related to local causality.

We say that the set $\mathcal {V}$ is faithful relative to the graph $\mathcal {G}$ if all probabilistic independencies between the random variables of $\mathcal {V}$ are implied by the Causal Markov Condition. This implication can neatly be depicted graphically by the so-called d-separation criterion. Let $\mathcal {P}$ be a path in $\mathcal {G}$. A variable $C$ on $\mathcal {P}$ is a collider if there are arrows to $C$ from both its neighbors on $\mathcal {P}$. Now, let $\mathcal {X}$, $\mathcal {Y}$ and $\mathcal {Z}$ be three disjoint sets of vertices in $\mathcal {G}$. $\mathcal {X}$ and $\mathcal {Y}$ are said to be d-connected by $\mathcal {Z}$ in $\mathcal {G}$ iff there exists a path $\mathcal {P}$ between some vertex in $\mathcal {X}$ and some vertex in $\mathcal {Y}$ such that for every collider $C$ on $\mathcal {P}$, either $C$ or a descendant of $C$ is in $\mathcal {Z}$, and no non-collider on $\mathcal {P}$ is in $\mathcal {Z}$. $\mathcal {X}$ an d $\mathcal {Y}$ are said to be d-separated by $\mathcal {Z}$ in $\mathcal {G}$ iff they are not d-connected by $\mathcal {Z}$ in $\mathcal {G}$. Specifically, the Causal Markov Condition entails that the variables $X$ and $Y$ are probabilistically independent conditional upon the subset $\mathcal {Z}$ just in case $\mathcal {Z}$ d-separates $X$ and $Y$ in $\mathcal {G}$.

Now, consider the stochastic local classical theory $\{\mathcal{N}(V),V\in \mathcal{K}^m\}$ introduced in the previous Section. A local von Neumann algebra $\mathcal{N}(V)$ of the theory gives rise to a graph $\mathcal {G}(V)$ and a set of random variables $\mathcal {V}(V)$ on a classical probability space $(\Sigma ,p)$ in the following way. Consider a region $V$ in $\mathcal{K}^m$ with the set $\{V^m\}$ of minimal double cones contained in $V$. Let the minimal double cones be the vertices of a causal graph and draw an arrow to every minimal double cone $V^m(t,i)$ from the three minimal double cones adjacent to it from below, that is from $V^m(t-{\frac{1}{2}},i-{\frac{1}{2}})$, $V^m(t-1,i)$ and $V^m(t-{\frac{1}{2}},i+{\frac{1}{2}})$, if all contained in $V$. (See Fig. 14.) The set of vertices and arrows will uniquely determine a causal graph $\mathcal {G}(V)$ associated to $V$.

Fig. 14

The causal graph $\mathcal {G}(V)$ associated to $V$

As for the set of random variables $\mathcal {V}(V)$, to each minimal double cone $V^m(t,i)$ in $V$ assign simply the two cylindrical subsets of $\mathcal{C}_{V(t,i)}$, denoted by $c^+_{V^m(t,i)}$ and $c^-_{V^m(t,i)}$, or equivalently the projections $i^+_t$ and $i^+_t$, respectively. Thus, the parents of a given random variable will be the projections in the three past timelike related adjacent minimal double cones, the descendants of a random variable will be the projections in the future timelike related minimal double cones, etc. The pair $\big (\mathcal {G}(V),\mathcal {V}(V)\big )$ will form a Bayesian network.

The translation manual between the vocabulary of the theory of Bayesian networks and that of the stochastic local classical theory $\{\mathcal{N}(V),V\in \mathcal{K}^m\}$ is shown in the following table:

Theory of Bayesian networks	Stochastic local classical theory
Bayesian network $\big (\mathcal {G}(V),\mathcal {V}(V)\big )$	Associated to every $V\in \mathcal{K}^m$
Causal graph $\mathcal {G}(V)$	Local von Neumann algebra $\mathcal{N}(V)$
	with $V\in \mathcal{K}^m$
Vertices	Minimal double cones in $V$
Arrows	Pointing to future timelike related
	adjacent minimal double cones
Random variables $\mathcal {V}(V)$	Projections localized in the
	minimal double cones contained in $V$
Parents	Projections in past timelike related
	adjacent minimal double cones
Ancestors	Projections in past timelike related
	minimal double cones
Descendants	Projections in future timelike related
	minimal double cones
Causal Markov condition	Bell’s local causality plus Markovity

The last line of the table contains the central point of our discussion, namely:

• 1. The Causal Markov Condition is a consequence of Bell’s local causality and Markovity when applied to the parents of a random variable.

• 2. Bell’s local causality/Markovity are consequences of the Causal Markov Condition, since the set of random variables localized in a region satisfying Requirements (i)–(iii)/(iii’) is d-separating.

We prove the first claim in the following proposition and illustrate the second in the subsequent examples.

Proposition 4

Let $\{\mathcal{N}(V),V\in \mathcal{K}^m\}$ be the stochastic local classical theory introduced above satisfying local causality and Markovity. Then for any pair $\big ({\mathcal {G}}(V),{\mathcal {V}}(V)\big )$ associated to any $V\in \mathcal{K}^m$ the Causal Markov Condition holds.

Proof

First we prove Causal Markov Condition for non-relatives which follows from the theory being locally causal. Let $V\in \mathcal{K}^m$ and let $V^m(t,i)$ and $V^m(s,j)$ be two minimal double cones in $V$ such that $i < j$. Suppose that $V^m(t,i)$ and $V^m(s,j)$ are spatially separated (non-relatives), that is $|j-i| > |s-t|$. Without loss of generality we also can assume that $t={\frac{1}{2}}$ and $s\geqslant t$, as depicted in Fig. 15. We are to show that the Causal Markov Condition (44) holds for $X= i_1$ and $Y= j_s$ in the Bayesian network $\big (\mathcal {G}(V),\mathcal {V}(V)\big )$ associated to $V$.

First, observe the parents of the variable $i_1$ are $(i-{\frac{1}{2}})$, $i$ and $(i+{\frac{1}{2}})$. Thus, the Causal Markov Condition (44) reads as follows:

$$\begin{aligned} p\left( i_1\bigg \vert \bigg (i-{\frac{1}{2}}\bigg ) i \bigg (i+{\frac{1}{2}}\bigg ) \, j_s\right) = p\left( i_1\bigg \vert \bigg (i-{\frac{1}{2}}\bigg ) i \bigg (i+{\frac{1}{2}}\bigg )\right) \end{aligned}$$

(45)

or equivalently

$$\begin{aligned} p\left( i_1 j_s\bigg \vert \bigg (i\!-\!{\frac{1}{2}}\bigg ) i \bigg (i\!+\!{\frac{1}{2}}\bigg )\right) \!=\! p\left( i_1\bigg \vert \bigg (i-{\frac{1}{2}}\bigg ) i \bigg (i\!+\!{\frac{1}{2}}\bigg )\right) p\left( j_s\bigg \vert \bigg (i\!-\!{\frac{1}{2}}\bigg ) i \bigg (i\!+\!{\frac{1}{2}}\bigg )\!\right) \nonumber \\ \end{aligned}$$

(46)

Or in other words, the atomic events $(i-{\frac{1}{2}}) i (i+{\frac{1}{2}})$ screen off the correlation between $i_1$ and $j_s$. But (46) does hold, since from (35)–(37) it follows that

$$\begin{aligned}&p\left( i_1\bigg \vert \bigg (i-{\frac{1}{2}}\bigg ) i \bigg (i+{\frac{1}{2}}\bigg )\right) = \bigg [p\delta _{i_1,(i-{\frac{1}{2}})i(i+{\frac{1}{2}})}+(1-p)\delta _{-i_1,(i-{\frac{1}{2}})i(i+{\frac{1}{2}})}\bigg ] \end{aligned}$$

(47)

$$\begin{aligned}&p\left( j_s\bigg \vert \bigg (i-{\frac{1}{2}}\bigg ) i \bigg (i+{\frac{1}{2}}\bigg )\right) = \sum _{(i-{\frac{1}{2}}), \dots , (j+s+\{j+{\frac{1}{2}}\})} \bigg [q_{m}\delta _{j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\nonumber \\&\quad +\,(1-q_m)\delta _{-j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\bigg ]p_{(i-{\frac{1}{2}})i(i+{\frac{1}{2}}) (j-s+\{j\}) \dots (j+s-\{j\})} \end{aligned}$$

(48)

$$\begin{aligned}&p\left( i_1 j_s\bigg \vert \bigg (i-{\frac{1}{2}}\bigg ) i \bigg (i+{\frac{1}{2}}\bigg )\right) \nonumber \\&= \bigg [p\delta _{i_1,(i-{\frac{1}{2}})i(i+{\frac{1}{2}})}+(1-p)\delta _{-i_1,(i-{\frac{1}{2}})i(i+{\frac{1}{2}})}\bigg ] \nonumber \\&\quad \,\,\times \sum _{(i-{\frac{1}{2}}), \dots , (j+s+\{j+{\frac{1}{2}}\})} \bigg [q_{m}\delta _{j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\nonumber \\&\quad \quad +\,(1-q_m)\delta _{-j_s,(j-s+\{j\}) \dots (j+s-\{j\})}\bigg ]p_{(i-{\frac{1}{2}})i(i+{\frac{1}{2}}) (j-s+\{j\}) \dots (j+s-\{j\})} \end{aligned}$$

(49)

Next we prove Causal Markov Condition for ancestors which follows from the theory being Markov. Let again $V\in \mathcal{K}^m$ and let $V^m(t,i)$ and $V^m(s,j)$ be two minimal double cones in $V$ such that $V^m(s,j)$ is in the causal past (is an ancestor) of $V^m(t,i)$, that is $|j-i| \leqslant |s-t|$. Again, we can assume that $t={\frac{1}{2}}$ and $s\geqslant t$, as depicted in Fig. 16. To prove (45) just observe that both sides equal to

$$\begin{aligned} p\delta _{i_1,(i-{\frac{1}{2}})i(i+{\frac{1}{2}})}+(1-p)\delta _{-i_1,(i-{\frac{1}{2}})i(i+{\frac{1}{2}})} \end{aligned}$$

This completes the proof. $\square$

Fig. 15

Causal Markov Condition follows from Bell’s local causality relative to the parents

Fig. 16

Causal Markov Condition follows from Markovity relative to the parents

Thus, the Causal Markov Condition is a special case of Bell’s local causality and Markovity in the stochastic local classical theory $\{\mathcal{N}(V),V\in \mathcal{K}^m\}$, namely when $V_C$ is a special spacetime region: the union of the three parental minimal double cones, that is minimal double cones adjacent to a given minimal double cone from below. We stress again that Causal Markov Condition is a composition of two screening-off conditions: one for the ancestors and the other for the non-relatives. The first is the consequence of Markovity, the second is the consequence of local causality.

Now, we go over to our inverse claim, namely that Bell’s local causality/Markovity are consequences of the Causal Markov Condition, since the set of random variables localized in a region $V_C$ satisfying Requirements (i)–(iii)/(iii’) is d-separating. Here we do not prove this claim generally, but only illustrate the connection of Requirements (i)–(iii) in the definition of local causality to d-separation on our previous two examples.

Example 1

Consider the smallest region $V \in \mathcal{K}^m$ in our Example 1 (in Sect. 4) containing the superluminally correlating events $i_1^+$ and $j_1^+$ with $j= i+2 \in \mathbb N + {\frac{1}{2}}$ and a region $V_C$ satisfying Requirements (i)–(iii) in the definition of local causality. (See Fig. 17.)

Now, consider the Bayesian network $\big (\mathcal {G}(V),\mathcal {V}(V)\big )$ associated to this $V$. The causal graph of the network is illustrated in Fig. 18. Let the variables be $X=i_1$, $Y=j_1$ and the subset $\mathcal {Z}$ be defined as:

$$\begin{aligned} \mathcal {Z} := \left\{ (i-1), \bigg (i-{\frac{1}{2}}\bigg ), i, \bigg (i+{\frac{1}{2}}\bigg ), (i+1)\right\} \end{aligned}$$

In other words, $\mathcal {Z}$ contains the random variables associated to the minimal double cones of $V_C$.

Now, $\mathcal {Z}$ d-separates $i_1$ and $j_1$ in $\mathcal {G}(V)$, since for every path $\mathcal {P}$ connecting $i_1$ and $j_1$ in $\mathcal {G}(V)$ there is a non-collider in $\mathcal {Z}$, namely, $(i+1)$. Therefore, $i_1$ and $j_1$ are probabilistically independent conditional upon any atomic event

$$\begin{aligned} (i-1)^{\pm } \bigg (i-{\frac{1}{2}}\bigg )^{\pm } i^{\pm } \bigg (i+{\frac{1}{2}}\bigg )^{\pm } (i+1)^{\pm } \end{aligned}$$

Fig. 17

The smallest region containing the scenario of Example 1

Fig. 18

A d-separating scenario

This fact is the Bayesian network analogon of the situation illustrated in Fig. 10 where $V_C$ is such that there is no minimal double cone above $V_C$ in the intersection of the causal past of the correlating events. As said before, this is due to the fact that $V_C$ satisfies Requirement (iii) in the definition of local causality. If Requirement (iii) does not fulfil, region $V_C$ turns into d-connecting, as is shown in the next example.

Example 2

Consider the smallest region $V \in \mathcal{K}^m$ in our Example 2 containing the superluminally correlating events $i_2^+$ and $j_2^+$ with $j= i+2 \in \mathbb N + {\frac{1}{2}}$ and a region $V_C$ still in the causal past of $i_2^+$ but not satisfying Requirement (iii). (See Fig. 19.)

Let the variables be $X=i_2$, $Y=j_2$ and let

$$\begin{aligned} \mathcal {Z} := \left\{ \bigg (i-{\frac{3}{2}}\bigg ), (i-1), \bigg (i-{\frac{1}{2}}\bigg ), i, \bigg (i+{\frac{1}{2}}\bigg ), (i+1), \bigg (i+{\frac{3}{2}}\bigg )= \bigg (j-{\frac{1}{2}}\bigg ) \right\} \end{aligned}$$

again a subset containing the random variables associated to the minimal double cones within $V_C$.

Now, $\mathcal {Z}$ does not d-separate $i_2$ and $j_2$ in $\mathcal {G}$, since the path

$$\begin{aligned} \mathcal {P}:=\left\{ i_2, \bigg (i+{\frac{1}{2}}\bigg )_1, (i+1)_1, \bigg (j-{\frac{1}{2}}\bigg )_1, j_2 \right\} \end{aligned}$$

(denoted by a broken line in Fig. 20) connecting $i_2$ and $j_2$ in $\mathcal {G}(V)$ contains only non-colliders which are outside $\mathcal {Z}$. Therefore, the probabilistic independence of $i_1$ and $j_1$ conditional upon the atomic events

$$\begin{aligned} (i-{\frac{3}{2}})^{\pm } (i-1)^{\pm } \bigg (i-{\frac{1}{2}}\bigg )^{\pm } i^{\pm } \bigg (i+{\frac{1}{2}}\bigg )^{\pm } (i+1)^{\pm } \bigg (i+{\frac{3}{2}}\bigg )^{\pm } \end{aligned}$$

is not ensured by the Causal Markov Condition (and if the graph is faithful, it is even excluded). This fact is the Bayesian network analogon of the situation illustrated in Fig. 11 where $V_C$ does not satisfy Requirement (iii) in the definition of local causality.

Fig. 19

The smallest region containing the scenario of Example 2

The causal graph $\mathcal {G}$ of the network is illustrated in Fig. 20.

Fig. 20

A d-connecting scenario

These examples point in the same direction: the Causal Markov Condition and the d-separation together ensure that Bell’s local causality will hold for the atomic projections localized in a region satisfying Requirements (i)–(iii). Moreover, they also show that Requirements (iii) is a necessary condition.

6 Conclusions

In the paper I was arguing, based on a simple stochastic local classical model, that Bell’s local causality, read in an appropriate way, is a Causal Markov Condition. I have not though provided a general proof. This would amount to solve the following

Open problem Let $\{\mathcal{N}(V),V\in \mathcal{K}\}$ be a discrete local physical theory, discrete in the sense that every $V\in \mathcal{K}$ contains only a finite number of elements of $\mathcal{K}$ and the local von Neumann algebras $\mathcal{N}(V)$ are finite. Construct the Bayesian network $\big (\mathcal {G}(V),\mathcal {V}(V)\big )$ associated to a region $V$ in $\mathcal{K}$. Prove (or falsify) that $\{\mathcal{N}(V),V\in \mathcal{K}\}$ is Markov and locally causal in Bell’s sense iff $\big (\mathcal {G}(V),\mathcal {V}(V)\big )$ fulfils the Causal Markov Condition for every $V\in \mathcal{K}$.