Material flow optimisation of production planning and scheduling problem in flexible manufacturing system by real coded genetic algorithm (RCGA)

Abstract

In a loading problem of flexible manufacturing system (FMS), part type selection and operations allocation are two critical problems. The total completion time of a product for the selected process plan in the system can be minimum for the loading problem. But, in a real time scheduling system, this process plan may not be optimum because of consideration of waiting time of product and machine. So, the total completion time and thereby the material flow of the selected process plan in the FMS may be high. Due to this problem an integrated approach of part type selection and an operation allocation problem i.e. production planning problem and scheduling problem is considered to optimise material flow in FMS. Loading and scheduling problems are NP-hard in nature. So, to solve complex problems like this, real coded genetic algorithm (RCGA) is used which overcomes some limitations of genetic algorithm. It is observed that, the results of optimisation using RCGA outperforms those obtained by earlier researchers.

1 Introduction

Flexible manufacturing system (FMS) consists of an integration of computerized numerical controlled (CNC) machines for manufacturing of different parts and automated material handling system for conveying material from machine to machine and to the storage area with a central computer system for storing data and information and controlling the activities of machines and material handling systems (Tompkins et al. 2003). Customers are more concerned about the product quality and the demand of product is also changing drastically. So, to cater the needs of customers, it is inevitable for the manufacturing industries to enhance the flexibility and efficiency of the manufacturing system (Tanchoco 1994). FMS have two most important flexibilities i.e. machine flexibility and routing flexibility. Machine flexibility means to manufacture different types of products on a machine whereas routing flexibility means the manufacturing of the operations on different machines. FMS is capable of achieving flexibility of low volume production as well as efficiency of high volume mass production (Gamila and Motavalli 2003). Therefore, FMS development is a milestone in manufacturing industries (Sujono and Lashkari 2007). The investment required in FMS is high and a less payback period is desired by the manufacturing industries. This can be achieved by proper planning and execution in the FMS (Kumar et al. 2012).

In the planning phase of FMS, two decisions are involved i.e. pre-release decisions and post release decisions (Stecke 1985). In the pre-release decisions, pre-arrangements of parts and tools is carried out before the beginning of processing of FMS and in post release decisions, scheduling problems which consists of sequencing and routing of parts are addressed. Stecke (1983) had divided the planning problem into six sub problems: part type selection, machine grouping, determination of production ratio, batching of part types, allocation of parts and fixtures and allocation of operations and tools among machines.

A product has alternate process plans which shows that a product can be manufactured by different operations on different machines. Chan et al. (2007) had defined the process plan selection problem as to select exactly one process plan for each part type from a number of accessible and feasible process plans and to provide optimal processing sequence for the manufacturing of part types. When a random process plan is selected, it gives the information about the sequence of operations to be performed on the product on different machines. Thus, if a process plan is selected from available alternate process plans, then it will select the part type to be produced and then these part types will be allocated as per selected process plan on the machines for manufacturing. This selected process plan will give the information about the time elements such as processing time, material handling time and set up time which in a total, is a completion time of a product in the manufacturing system.

Material flow can be defined as the time required from the start of the first operation to the finish of the last operation in the system. For the part type selection and operation allocation problem, material flow consists of processing time, set up time, material movement time. But, in the real time scheduling system, the waiting time of the product or machine is considered. In the queuing system, the waiting cost is proportional to the waiting time. Due to this waiting cost, there may be a loss of profit or loss of future business. There can be a linear, polynomial or exponential relationship between waiting time and cost (Hillier and Lieberman 2001). In a real time scheduling system, if a waiting time is not considered then the completion time for a selected process plan may be less, but the waiting time might be high. This will increase the actual completion time and thereby material flow of the product in the system. So, for the real time scheduling system, the material flow consist of four time elements i.e. processing time, set up time, material movement time and waiting time.

As the flexibility of each machine is different from the other, the processing time and set up time is different for each and every product on each and every machine. Material handling time depends upon the material handling equipment selected. In a real time scheduling system, from a set of alternate process plans, exactly one process plan is selected for each product. The selected process plan can have minimum process time, material handling time, setup time and waiting time and thereby minimum material flow of the system. However, to select an optimal process plan becomes more complex with increasing number of alternate process plan. Thus, the combination of part type selection, operation allocation problem and scheduling problem of a FMS becomes a NP-hard problem (Shanker and Srinivasulu 1989). The complexity of this problem is so immense that even for 8–10 jobs there can be more than 10⁸ possible operation-machine allocation combinations (Prakash et al. 2008).

There are many objectives and constraints considered in this type of problems. The search space to find out optimal solution becomes large and the problem becomes complex to solve by exact methods. Researchers have developed and used many heuristics and metaheuristics to solve the problems like genetic algorithms (GA), particle swarm optimisation (PSO), ant colony optimisation (ACO), tabu search, Simulated Annealing (Tiwari et al. 2006), and Immune Algorithm. Among the above methods, genetic algorithm (GA) have proven to be a powerful method with a large search space. In genetic algorithm (GA), solutions are jumping from one sequence to another randomly and the chance of entrapping of solutions in local optima is avoided. However, simple GA is not able to solve complex problems like integrated part type selection and operation allocation and scheduling problem. Hence, real coded genetic algorithm is used to solve the problem. Mahmudy et al. (2012, 2013b) have proposed real coded genetic algorithm (RCGA) to solve part type selection and machine loading problems and obtained the near optimal solution in reasonable amount of time.

This research work is based on two case studies. First case study is based on problem of an integration of operation allocation and material handling system selection (Paulo et al. 2002). The objectives considered are (a) to minimise the operations cost, material handling cost, machine set ups cost and (b) to maximize the part equipment compatibility. Machine available time was considered as constraint. Second case study is based on integration of material handling selection & operation allocation problem (Mahdavi et al. 2011). The objective functions are (a) to minimise machine operation, material handling and set up cost and (b) maximize machine utilization with machine capacity as a constraint. Both the case studies are based on production planning problem. However, when production planning is integrated with scheduling, the optimum solution of production planning stage remains no more valid. Hence, to deal with this issue of integrated production planning and scheduling, in this work the objective function is reformulated considering the waiting time and then real coded genetic algorithm (RCGA) is applied as a solution methodology.

This work is organized as follows. In Sect. 2, a brief review of the literature based on integrated loading and scheduling problems in FMS and material flow optimisation problems is carried out. In the Sect. 3, issues in flexible manufacturing system, real time scheduling problems in FMS and a brief information of real coded genetic algorithm (RCGA) is presented. In Sect. 4, two case studies based on Paulo et al. (2002) and Mahdavi et al. (2011) have considered with scheduling problem.

2 Literature review

Flexible manufacturing system problems are divided into three types:

• Loading problem,

• Scheduling problem and

• Integrated loading and scheduling problem

In machine loading problems, the parts are selected and allocated to the machines for performing different operations. Some researchers have considered only loading problem for research. Stecke (1983) has formulated machine loading problem as a nonlinear integer programming problem. Stecke and Morin (1985) have considered a flow shop and job shop workload balancing problem and proposed a closed queuing network model to optimise the throughput of the system. Shankar and Tzen (1985) have considered a loading problem of a random FMS and proposed two different algorithms, one for workload balancing and second one for workload balancing and minimizing the number of late jobs. Stecke (1986) has considered a loading problem and suggested a hierarchical approach for solving actual machine grouping and machine loading problems. Mukhopadhyay et al.(1992) have proposed a heuristic which is based on predefined and fixed sequencing rule for a loading problem considered by Shankar and Tzen (1985) and Shanker and Srinivasulu (1989). Tiwari et al. (1997) have considered machine loading problem of Mukhopadhyay et al. (1992). The objectives considered were workload balance, minimise inter machine part movement, routing flexibility, tool investment and machine utilization. They proposed petri net model for the optimisation. Chen and Askin (1990) have considered objectives as workload balance, maximize machine utilization, volume of inter machine part movement, routing flexibility and tool investment. Tiwari and Vidyarthi (2000) have considered a loading problem of random flexible manufacturing system with batch production. The objectives were to minimize the system unbalance and maximization of utilization with the constraints of available machining time and tool slot. Swarnkar and Tiwari (2004) have considered a loading problem and the objectives were to minimise system unbalance and maximise throughput and the constraints were available machine time and tool slots. They have proposed hybrid algorithm based on Tabu Search and Simulated Annealing. Biswas and Mahapatra (2008) have considered the Tiwari and Vidyarthi (2000) problem. A mathematical model was prepared by considering two cases. Abazari et al. (2012) have considered a loading problem of a batch production flexible manufacturing system. Objective was to reduce total cost and constraints were capacity of machines, batch sizes, processing time of operations, machine costs, tool requirements and capacity of tool magazine. A mathematical programming model with continuous and zero one variables was developed to find out system unbalance due to underutilized time and over utilized time. Kumar et al. (2012) have considered a loading problem of random flexible manufacturing system with batch production. The objectives were minimization of system unbalance and maximization of utilization with the constraints of available machining time and tool slot.

In the scheduling problem, parts are assigned to various machines by their sequences. The jobs are assigned in the proper sequence to complete each and every activity in less time and cost. In the scheduling problem, the ‘n’ jobs are scheduled on the ‘m’ machines in the predefined sequence. The objective functions of the scheduling problem is to minimise completion time, inventory reduction, maximizing machine utilization and tardiness, etc. Kurz and Askin (2001) have considered a sequence dependent set up times of parallel machines to optimise makespan. To optimise the makespan, various heuristics were proposed. Jerald et al. (2006) have considered a scheduling optimisation problem to minimise machine idleness and minimise penalty cost. Varadharajan and Rajendran (2005) have considered a scheduling problem of permutation flowshop. Zandieh et al. (2006) have considered a scheduling problem of hybrid flowshop. Saidi-Mehrabad and Fattahi (2007) have considered flexible job shop scheduling problem. Paternina-Arboleda et al. (2008) have considered a sequence dependent flexible flow shop scheduling problem having 7 jobs and 5 stages. Ronconi and Henriques (2009) have considered a flow shop scheduling problem without any buffer. Zeballos (2010) has considered a scheduling problem of FMS. Bagheri and Zandieh (2011) have considered flexible job shop scheduling problem having sequence dependent set up times. Behnamian and Fatemi Ghomi (2011) have considered a scheduling problem of sequence dependent hybrid flowshop. Abyaneh and Zandieh (2012) have considered a scheduling problem of a hybrid flow shop with sequence dependent setup times. Burnwal and Deb (2013) have used a breading behavior of cuckoo to develop a metaheuristic model to solve a scheduling problem. Marichelvam et al.(2014) have considered a hybrid flow shop scheduling problem. Li et al. (2015) have considered rescheduling problem of flow shop with minimization of two objectives, i.e. maximal completion time and instability performance.

In the early stages, some researchers have developed a mathematical model to address the problems of FMS to optimise material flow. Malmborg (1994) has considered material transportation and handling cost with buffer storage to formulate a mathematical model with single objective to minimise vehicle travel minutes and constraints such as to minimise waiting time, minimise output overflow, minimise number of vehicles needed and to minimise average total space required. Herrmann et al. (1994) have proposed a mathematical model for design of material handling flow paths based on single objective as minimizing total material flow times distance and 5 constraints such as continuity of flow path between origin–destination pair, traffic congestion, capacity of material handling system on the arc, vehicle collision avoidance and prohibition of flow through non selected arcs. Herrmann et al. (1999), have considered the same single objective function of Herrmann et al. (1994) with 4 constraints such as waiting times due to congestion or on-line scheduling decisions, each loaded move should have exactly one transporter, continuity on the path consisting of loaded moves performed by each transporter and sub tour elimination. Sinriech and Samakh (1999) have considered a segmented flow based material handling system optimisation problem of pick up/delivery location. They have considered objective function as to minimise the total flow distance. Genetic algorithm was used for optimisation. Ioannou (2007) proposed a mathematical model for integrated plant layout and material handling system with the objective of minimizing the fixed acquisition and the variable operational costs of the material handling system. Having constraints such as continuity of loaded and unloaded moves, traffic congestion, sub tour elimination, no move is performed by inactive transporters, limit for the overall distance traveled by each transporter.

Few researchers have considered material flow optimisation problems in FMS. Fazlollahtabar et al. (2010) have considered material flow optimisation of a flexible flowshop of automated manufacturing systems in which automated guided vehicles (AGVs) were used to carry raw materials, semi-finished and final products in batch sizes. A mathematical model was proposed for the material flow optimisation with the constraints such as completion time, job allocation, cycle time and AGV capability. Ramalingam et al. (2015) have considered the same problem of Fazlollahtabar et al. (2010) and considered objective of minimization of material flow time and completion time. They proposed Genetic Algorithm (GA) to minimise material flow optimisation problem. Bhosale and Pawar (2016) have considered the problem of Fazlollahtabar et al. (2010) and proposed Real Coded Genetic Algorithm to optimise the material flow. The results obtained shows that RCGA is performing better as compared to GA. Alvarado-Iniesta et al. (2013) have considered a manufacturing plant to standardize the time required for a worker to deliver raw material to different production lines from a central warehouse.

In a production planning problems, the parts are selected and allocated to the machines for performing different operations. In sequencing problem, the order of performing operations on the product is determined and in scheduling problems, the starting and finishing time of the product is determined. Some researchers have considered part selection, operation allocation and machine loading problems separately. However, if these problems are solved in an integrated way, then it will give a feasible solution to the problem (Zeballos 2010). So, in this research work an integrated way of production planning and scheduling is considered to optimise the material flow.

Stecke and Kim (1988) have considered the flexible approach in which when the requirement of some part type is over, they replaced with the new part types. They formulated a mathematical model for the selection of part types and selection of part mix ratios while tool magazine capacity was considered as constraint. They also tried different batching approaches to find the optimal part type selection. Lee et al. (1997) have considered multi period order selection and machine loading problem for maximizing system throughput and minimise lateness and earliness of the jobs. Paulo et al. (2002) have considered an integrated problem of operation allocation and material handling system selection. The objectives considered were to minimise the costs of operations, material handling, machine set ups, and to maximize the part equipment compatibility. Machine available time was considered as constraints. The mathematical model was prepared for this system. Sujono and Lashkari (2007) have considered the problem of Paulo et al. (2002). A mathematical model was prepared for this system. The proposed model was solved by the ε-constrained method. Gamila and Motavalli (2003) have considered part loading, tool loading and part scheduling problem of a flexible manufacturing system. The objectives were to minimise the summation of maximum completion time, movement of parts between machines, total processing time considering machine and tool capacities, due dates of parts, cost of processing and setup and precedence relationship. However, the machine tool assignment and operation allocation was done before scheduling.

Chan et al. (2005) have considered machine tool allocation problem. Fuzzy goal programming model was used to solve the problem. Kumar et al. (2006) reviewed part type selection and assignment problem of random FMS. In this paper, an extension of Genetic Algorithm, i.e., CBGA (constraint-based genetic algorithm) was applied to solve machine-loading. Khayat et al. (2006) have considered an integrated production and material handling scheduling problem of a job shop. The objective was to minimise the makespan. Tiwari et al. (2008) have considered a Part-selection and machine-loading problems to minimise system unbalance and maximise throughput with the constraints of availability of machining time and tool slot. They proposed new heuristic which is based on operation allocation and reallocation of part types simultaneously. Prakash et al. (2008) have considered a job selection and machine loading problem. The objectives were maximization of throughput and maximizing load balance and constraints were machining time and tool slots. Zeballos (2010) has presented a constraint programming (CP) model that integrated machine assignment, tool planning and allocation, part routing and task timing decisions in an FMS. The proposed model considered limitation on number of tool copies, tool lifetime and parts’ due dates. Mahdavi et al. (2011) have considered integrated material handling selection & operation allocation problem. The objective functions were to minimise machine operation, material handling and set up cost, and maximize machine utilization and the constraint was machine capacity. Mahmudy et al. (2012, 2013a, b, 2014) have considered two objectives as to maximize the throughput of the system and to minimise the unbalance of the system of a part type selection and loading problem of FMS. Paslar et al. (2014) have considered an integrated machine loading, part routing, sequencing and scheduling decision in flexible manufacturing systems. Novas and Henning (2014) have considered an integrated scheduling problem simultaneously with machine loading, part routing, machine buffer scheduling, tool planning and allocation and AGV scheduling. In Table 1, review based on integrated loading and scheduling problems is presented.

Table 1 Integrated loading and scheduling problems

Researchers have considered integrated loading and scheduling problems. However, in real time scheduling system, the waiting time of the machine or product is to be considered. The optimum process plan selected in the production planning stage may not remain optimum due to addition of waiting time. This waiting time has been addressed by researchers while solving scheduling problems. Pan and Shi (2005)have considered single machine sequencing problem to minimise total weighted time completion whereas constraints were release dates and deadlines. Bauman and Józefowska (2006) have considered single machine scheduling problem to minimise total cost. Li et al. (2007) have considered job scheduling of a single machine to minimise weighted waiting time. Hendel and Sourd (2007) have proposed an earliness-tardiness timing algorithm for a flow shop problem. Amiri et al. (2014) have single machine scheduling to minimise total tardiness and waiting time variance.

From the literature, it is found that researchers have not considered the waiting time for integrated operation allocation and real time scheduling problems. In many situations, though the completion time for the selected process plan is less, waiting time in the system may be high. This will increase the material flow in the system. So, in this paper the objective is considered as material flow optimisation so that the total time required by all the products in the system should be optimum.

3 Issues in flexible manufacturing system

3.1 Production planning in FMS

Hwan and Shogan (1989) have investigated that from the six planning problems (Stecke 1983), there are only two critical problems i.e. part type selection and operation allocation. In the part type selection problem, a subset of part types is selected for manufacturing of parts and in operation allocation problem, operations of the parts to be manufactured on machines are allocated to machine based on the process plan of the product. Hence, part type selection and operation allocation problems are the most important problems in the planning stage. The objectives considered are: maximize throughput, minimise production cost, due date satisfaction, maximize resource utilization, maximize flexibility, maximize resource utilization and balance the workloads. These problems have been formulated as mixed integer programming problems (MIP). FMS are having various flexibilities. So, the search space even for the moderate problems becomes unmanageable and computationally intractable. Researchers have developed heuristic methods. The solution of the planning problem give the set of parts to be manufactured from the alternate process plans, the machine routing of each part, an allocation of tools to machines and assignment of operations to machines.

3.2 Real time scheduling problems in FMS

An optimal solution proposed by the planning system does not remain feasible in the scheduling stage because of the drastic changes in the system such as machine breakdowns, changes in demand, unavailability of material, changeovers etc. So, a FMS should be capable of tackling these changes in a shorter time and find an optimal process plan so that the material flow should be optimum. In a real time scheduling system, a starting and completion times for each operation of each job waiting for manufacturing on machine is determined. An optimal schedule minimizes the material flow in the system. For the determination of a schedule, dispatching rules are used which assigns priority value to a waiting job in sequence of each machine. Different scheduling rules are followed as: FIFO (jobs in queue ranked by arrival into queue), SPT (Jobs ranked by the shortest processing), DDT (Jobs ranked according to their earliest due date), LWKR (Jobs ranked by least work remaining), MWKR (Jobs ranked by most work remaining), MWKR-P (Jobs ranked by MWKR after the present schedulable operation), MWKR/P (Jobs ranked by greatest ratio of total remaining work to processing time of schedulable operation), MOPNR (Jobs ranked according to most operations remaining), SLK/RO (Jobs ranked by the least ratio of slack time remaining to number of operations remaining, at the instance that the machine or resource becomes free), RANDOM (At the instance that the machine or resource is freed, any job already in the queue has equal probability to any other of going on the machine. In this paper, SPT rule is used which is efficient with respect to waiting time related criteria of a scheduling problem. SPT rule is simple to use. When the machine is available, from the available unscheduled operations which are waiting to be manufactured, the operation which is having shortest processing time is chosen to be scheduled next on the machine (Chengbin and Portmann 1993).

Whenever the machines are available then different operations are allocated as per the priority rule. Thus, when the schedule is prepared, it will determine the start time and finish time of the operation on the selected machine from the selected process plan. The objectives considered are: minimise the makespan, minimise maximum tardiness, minimise the total processing time and minimise the total cost. When the operation on the machine is finished then the next operation is processed if the parts are available, otherwise the machine becomes idle. So, it becomes difficult to find optimum process plan that is having minimum material flow. Thus, this problem is known to be NP-hard.

3.3 Proposed approach

In flexible manufacturing system, part selection and operation allocation problems i.e. loading problems and scheduling problems are formulated as mixed integer programming problems (MIP). If these problems are solved individually, the solutions may conflict with each other and may become less efficient. For example in the loading problem, the real time scheduling is not taken into considerations and in the scheduling problems, operation allocation and sometimes waiting time is not considered. This will either overload or underload the machines and solution may not be feasible. Therefore, an integrated approach will be useful to find optimum solution.

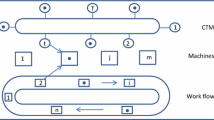
The first operation of the part can be started at time zero if the machine is available for processing the operation. If the machine is not available at time zero then the waiting time is to be found out. Suppose, P₁, P₂, P₃,……P_n parts to be manufactured on M₁, M₂, M₃,……M_n machines having O₁, O₂,…….,O_n is the processing time of the part types as shown in Fig. 1. Operation O_i of part type P_i can be started on machine M_i if operation O_i-1 is completed or machine is available for operation. If operation O_i-1is completed but the machine M_i+1 is not available then the waiting time W_t is to be calculated as

Fig. 1

Gantt chart of scheduling of ‘n’ parts on ‘m’ machines

$$W_{t} = \, C_{i - 1} \left( {M_{i + 1} } \right) - C_{i - 1} \left( {Mi} \right)$$

(1)

S_i and C_i denote the start time and completion time of operation O_i respectively. The completion time of the operation will be C_i= S_i+ O_i. The start time may be zero or it will be equal to C_i-1 +W_t. The next operation will be completed on C_i+1= C_i+ O_i+1.

3.4 Real coded genetic algorithm (RCGA)

Genetic algorithm (GA) is a population based stochastic search algorithm and based on the concept of nature’s law of survival of fittest and natural selection procedure. Evolution of nature is driven by the principle of survival of fittest. Stronger ones live for many years, they reproduce many off-springs by passing on many attributes to their children, while weaker ones die early without reproduction (Godberg 1989).

In binary GA, genes and chromosomes are used to encode the optimisation parameters. Each gene is a binary bit and representing a variable of a problem and the length of chromosomes is kept equal to the solution length of the problem. So, in the case of binary coded Genetic Algorithm, the string length required is large and solution obtained may be redundant and the time required for processing of data is high. So, to avoid these problems, a real coded system is selected which is easy to handle and less time consuming. In real coded system the solution is represented directly with the real numbers and the size of chromosome is kept as same to the vector for which the solution is to be obtained (Herrera et al. 1998).

In binary GA, the solution parameters are first encoded in binary bits and these binary bits are again decoded in solution parameters. So, while encoding and decoding, discretization error occurs and computation time required is large. While in case of Real Coded GA, there is no need of coding and decoding procedure (Chuang et al. 2015, 2016). Deb and Kumar (1995) have also expressed that real coded genetic algorithm performs well or even better as compared to binary coded genetic algorithm in many real world optimisation applications.

In RCGA three fundamental evolutionary operators are used i.e. selection, crossover and mutation to obtain optimal solution. Each operator have specific mechanism so that the solution will approach to optimal solution. The selection operator selects the potential chromosomes from the whole population and these selected solution will undergo subsequent crossover manipulation. The roulette wheel selection method is an imaginary wheel in which each solution presents an area and the size of the area represents the fitness of the solution. When the spinning wheel stops it will show which solution is to be selected to take part in the crossover operation.

The crossover operator creates new offspring by recombination from the selected parent chromosomes. Crossover is the main effective operator because it assists the algorithm to achieve the optimum value by creating some new child solutions. The crossover points are selected randomly, in the traditional method. However, operations to be performed in the process plan on the part are not same. So, if the crossover is taken at random site then the child solution may become infeasible. So, in this work, the whole operations in a process plan on the part is considered as sub-string of the chromosome and then site for crossover is selected randomly.

The mutation operator randomly changes the gene of chromosomes for the prevention of premature convergence so that the solution should not be get trapped in the local minima. In the traditional mutation, random numbers are generated and from that random number, mutation is operated. Similar type of mutation can be applied for two case studies also.

In the penalty function method, the objective value is degraded/increased by the value of constraint violation. In the case of integrated planning and scheduling problems, the variable and constraints are large in numbers. So, a solution generated randomly may be infeasible. Here in this work, a static penalty approach suggested by (Homaifar et al. 1994) is used in which the value of violation of constraint is added to the objective function. By this static penalty function method, infeasible solution will die out due to large objective function value. Kumar and Shanker (2000) have used penalty function to obtain feasible solution from the randomly generated solution in less time and to avoid hamming cliff. In the next section, two case studies based on Paulo et al. (2002) and Mahdavi et al. (2011) are presented.

4 Case studies

In this research work, two case studies based on operation allocation problem and loading problem are described.

4.1 Case study based on operation allocation and material handling system separately

First case study is based on a numerical example of Paulo et al. (2002). Though Paulo et al. (2002) have considered problem of operation allocation and material handling system separately, here in this present paper only a part of operation allocation problem is considered. There are 14 parts to be manufactured. The demand for different part types is as follows: P(1) = 30, P(2) = 50, P(3) = 45, P(4) = 65, P(5) = 25, P(6)  =  40, P(7) = 90, P(8) = 20, P(9) = 15, P(10) = 55, P(11) = 60, P(12) = 35, P(13) = 80 and P(14) = 40. The total manufacturing operation time (Ot) and operation costs (Oc) for these demands is given in Table 2. All the 14 part types have different process plans. Each part can be manufactured by following any one of the process plan. There are maximum four operations and these operations can be performed on 10 machines. The available time in units for machine j = 3 and j = 7 are 480 units and for the remaining machines it is 980 units.

Table 2 Manufacturing operation times (Reproduced with permission from Paulo et al. 2002)

The cost of moving is shown in Table 3. The machine set up cost in $ is as follows: SC(1) = $120, SC(2) = $230, SC(3) = $450, SC(4) = $60, SC(5) = $180, SC(6) = $ 220, SC(2) = $310, SC(8) = $90, SC(9) = $260, SC(10) = $550.

Table 3 Cost of moving parts from machine to machine

The 0–1 integer-programming model is explained below.

There is a set of ‘n’ part types labelled with the indices i = 1,…; n, where the part type I has the known and uniform demand d_i over the planning period. A part type i can be processed under the different process plans p = 1,…;,P(i). For a process plan p ∈ P(i) of a part type i, the manufacturing operations are represented by the indices s = 1,…, S(ip), where for simplicity we use (ip) to indicate part type i under process plan p. There is a set of m machines labelled with the indices j = 1,…, m. The set of machines that can perform manufacturing operation s of part type i under process plan p is given by J_ips.

The operation allocation model involves the assignment of operations of each part type to appropriate machines to minimize the total costs of manufacturing operations, machine set-ups and materials handling. The 0–1 decision variables are denoted by X_sj(ip), where X_sj(ip) = 1 if operation s of (ip) is performed on machine j and zero otherwise.

$$X_{sj} (ip) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {ifoperation{\kern 1pt} \;s\;is\;processed\;on\;machine\;j\;for\;the\;combination\;\left( {ip} \right)} \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

• 1) The operation cost is given by E₁(X_sj(ip)):

$$E_{1} (X_{sj} \left( {ip)} \right) = \sum\limits_{i = 1}^{n} {di\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {\sum\limits_{{j \in J_{ips} }}^{{}} {OC_{sj} (ip)X_{sj} (ip),} } } }$$

(2)

where OC_sj(ip) is the known per-unit cost of operation s of (ip) on machine j. This includes both the manufacturing and the re-fixturing costs.

Index sets are:

• i∈ {1,2,…n} part types,

• p∈ {1,2,….P(i)} process plans for part type i,

• s∈ {1,2,…S(ip)} operations for part type i under process plan p,

• j∈J_ips⊂ {1,2,.m} set of machines that can perform operation s of part type i under process plan p,

• 2) The machine set-up cost is given by E₂(Mj):

$$M_{j} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {ifmachine\;j\;is\;selected} \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

$$E_{2} (M_{j} ) = \sum\limits_{j = 1}^{m} {SC_{j} M_{j,} }$$

(3)

Where, SC_j is the known set-up cost for machine j and the auxiliary variable M_j takes the value of one if machine j is selected and zero otherwise. Only one set-up cost per planning period is assumed. Since these machines are operated under a flexible manufacturing system, it is assumed that the only significant set-up cost is the initial one where the machines must be programmed and equipped with the required tools.

• 3) The materials-handling cost is given by E₃(Xsj(ip)):

$$E_{3} \left( {Xsj(ip)} \right) \, = \sum\limits_{i = 1}^{n} {di\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {\sum\limits_{{j \in J_{ip(s + 1)} }}^{{}} {T_{i(j + 1)j} X_{sj} (ip)X_{(s + 1)(j + 1)} (ip),} } } }$$

(4)

Where, Ti(j + 1)j is the cost of moving a unit of part type i from machine j to machine j + 1 for the next operation.

Since E₃(Xsj(ip))is a non-linear function, the linearization technique given in Taha (2007) is applied. This prescribes replacing · E₃(Xsj(ip)):with:

$$E_{3} (Ls\left( {j + 1)j(ip)} \right) \, = \sum\limits_{i = 1}^{n} {di\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {\sum\limits_{{j \in J_{ip(s + 1)} }}^{{}} {T_{ij(j + 1)} L_{sj(j + 1)} (ip),} } } }$$

(5)

$$L_{sj(j + 1)} (ip) = \left\{ {\begin{array}{*{20}l} 1 \hfill & \begin{aligned} & ifpart\;type\;i\;moves\;to\;moves\;(j + 1)\;to\;perform\;operation\;(s + 1)\;after \\ & {\text{performing}}\;operation\;s\;on\;machine\;j\;for\;the\;{\text{combination}}\;(ip) \\ \end{aligned} \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

The objective function of the model is considered by Paulo et al. (2002), to determine Xsj(ip) and Ls(j + 1)j(ip) that will minimize:

$$E_{1} (Xsj\left( {ip} \right)) \, + \, E_{2} (Mj) \, + E3(Ls\left( {j + 1} \right)j(ip)$$

(6)

Paulo et al. (2002) have considered only operation allocation problem. The mathematical model have not considered the real time scheduling system in which waiting time of machine and product should be considered. So, to accommodate this waiting time, a model of Paulo et al. (2002) is modified.

• 4) The waiting cost Wc is given by:

The waiting time is calculated from Eq. 1. From this waiting time, waiting cost (W_C) is calculated. Here in this problem (Paulo et al. 2002), the data regarding waiting cost of product and machine is not given. Hence, it is assumed that waiting cost of the machines would be significant and there is a linear relationship between operation cost and operation time. From that relation, the waiting cost of individual machine per unit time is calculated as follows: Wc₁ = $1.5, Wc₂ = $1.2, Wc₃ = $1.0, Wc₄ = $2.0, Wc₅ = $1.0, Wc₆ = $1.3, Wc₇ = $0.6, Wc₈ = $1.0, Wc₉ = $1.6 and Wc₁₀ = $1.3.

$$\sum\limits_{i = 1}^{n} {\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {\sum\limits_{{j \in J_{ip(s + 1)} }}^{{}} {W_{Cij} X_{sj} (ip)} } } }$$

(7)

Assembling the above Eqs. 2–3, 5, 7, we get the following complete statement of our 0–1 mathematical programming model of the operation allocation model and scheduling, which is designated as P(OA).

P(OA): minimise cost

$$\sum\limits_{i = 1}^{n} {di\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {\sum\limits_{{j \in J_{ips} }}^{{}} {OC_{sj} (ip)X_{sj} (ip)} } } } + \sum\limits_{j = 1}^{m} {SC_{j} M_{j} } + \sum\limits_{i = 1}^{n} {di\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {\sum\limits_{{j \in J_{ip(s + 1)} }}^{{}} {T_{ij(j + 1)} L_{sj(j + 1)} (ip)} } } } + \sum\limits_{i = 1}^{n} {\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {\sum\limits_{{j \in J_{ip(s + 1)} }}^{{}} {W_{Cij} X_{sj} (ip)} } } }$$

(8)

The constraints are developed next. The first constraint set ensures that each part type is processed under a single process plan, and it is given by:

$$\sum\limits_{p = 1}^{P(i)} {Z(ip) = 1}$$

(9)

Where, Z(ip) = 1 if part type i is processed under process plan p and zero otherwise.

The next set of constraints ensures that once a process plan is selected for a part type, each operation in that plan is processed on only one of the available machines.

It is given by:

$$\sum\limits_{{j \in J_{ips} }} {X_{sj} } (ip) = Z(ip)\quad \forall i, \, p, \, s.$$

(10)

The third set of constraints ensures that a machine j is selected before we assign any operations to it. It is given by:

$$\sum\limits_{i = 1}^{n} {\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {X_{sj} } } } (ip) \ge M_{j} \forall_{j}$$

(11)

The next set of constraints ensures that the total time required by the operations allocated to a machine j, once it is selected, does not exceed the machine’s known capacity. It is given by:

$$\sum\limits_{i = 1}^{n} {\sum\limits_{p = 1}^{P(i)} {\sum\limits_{s = 1}^{S(ip)} {t_{sj} (ip)X_{sj} } } } (ip) \le b_{j} M_{j} \forall_{j}$$

(12)

Where, t_sj (ip) is the time to perform operation s of (ip) on machine j. The two sets of constraints, (10) and (11), ensure consistency between the allocation of operations of the part types to machines and the selection of machines.

The mathematical model considered in Eq. 8 is applied on this numerical problem. The material flow is calculated by considering the mathematical model. For example, in Table 2, for part no. 7, the demand is 90 and there are two different process plans. If we consider the process plan no. 1, the minimum operation time required for the first operation is 90 × 5 = 450 units on machine number 7 and the minimum operation time required for the second operation is 90 × 7 = 630 units on machine number 3. It means that, unless and until the first operation is completed, the second operation cannot be started. So, there is a waiting of 450 units for the second operation. Due to this, the total completion of time of part number 7 under process plan 1 is 450 + 630 = 1080 units. Similarly, if we consider the process plan no.2, the minimum operation time required for the first operation is 90 × 9 = 810 units on machine number 10 and the minimum operation time required for the second operation is 90 × 7 = 630 units on machine number 1. It means that, unless and until the first operation is completed, the second operation cannot be started. So, there is a waiting of 810 units for the second operation. Due to this, the total completion of time of part number 7 under process plan 2 is 810 + 630 = 1440 units. But, the total available time is 980 units. So, it is not possible to complete all the demands by considering this model.

Table 2 shows that, all products have one or more process plan and each process plan have one or more operations. It is assumed that the details regarding number of jobs to be produced, their processing time, number of operations to be performed on each product is already available in advance. In this problem, the flexibility of selecting a process plan and then allocating an operation to a machine is available. In this problem, 14 products with one or more operations are to be manufactured on 10 machines. The flexibility is complex and can be calculated. Let ‘j’ be total number of products having ‘o_j’ operations to be processed on ‘m’ machines. Therefore, the number of possible solutions can be calculated by (Abazari et al., 2012):

$${\text{Number}}\;{\text{of}}\;{\text{Possible}}\;{\text{solutions}} = \prod\limits_{j = 1}^{j} {\left\{ {\left( {\prod\limits_{o = 1}^{{o_{j} }} {m_{{o_{j} }} } } \right) + 1} \right\}}$$

(13)

The illustration for the example given in Table 2, is as follows:

$$\prod\limits_{j = 1}^{14} {\left\{ {\left( {\prod\limits_{o = 1}^{4} {m_{{o_{j} }} } } \right) + 1} \right\}} = \, \left( {\left( {5 \times 4 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {3 \times 5} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {5 \times 4 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 5} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 3 \times 4 \times 5} \right) + 1} \right) \, \times \, \left( {\left( {3 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {5 \times 5 \times 5} \right) + 1} \right) \, \times \, \left( {\left( {3 \times 4 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {3 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {3 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 3 \times 5 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {5 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {3 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 5 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {2 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {5 \times 4 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {3 \times 5} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {5 \times 4 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 3} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 5} \right) + 1} \right) \, \times \, \left( {\left( {4 \times 3 \times 4 \times 5} \right) + 1} \right) \, \times \, \left( {\left( {3 \times 4} \right) + 1} \right) \, \times \, \left( {\left( {5 \times 5 \times 5} \right) + 1} \right) = 3.7 \times 10^{40}$$

Some of the solutions may not be feasible due to constraint of machine availability time. As to determine the optimum solution from all these solutions, it is computationally difficult. Because of these facts, a Real Coded Genetic Algorithm (RCGA) is proposed in this paper for solving problem.

4.2 Working of RCGA

As discussed in Sect. 3, the working of RCGA is explained below:

Step 1 The parameters of real coded Genetic Algorithm used are: Population size: 20, generations = 100, Crossover type: Single point, Crossover probability: 0.7, Mutation probability: 0.1. Population is determined by various experiments. Different sizes from 10 to 30 are checked and it is observed that after population size 20, there is no significant change in solutions and it is also observed that after 100 generation, there is no significant change in results.

Step 2 Initialisation:

There are 14 products and these products are to be manufactured from 10 machines. In the initialization stage, 20 random initial solutions are generated and for these solutions objective function value is calculated from Eq. 8 as the objective function is to minimise the material flow. A single random solution is called as “Chromosome”. In this way, 20 random chromosomes are generated. These random chromosomes are called as “initial population”.

The initial random objective function value is calculated by considering operation cost given in Table 2, set up cost is given in previous section, material handling cost given in Table 3, waiting cost is calculated from Eq. 7 and a static penalty is applied for the violation of available time constraint.

For example, the initial solution, 1(2) {2, 4} as shown in Table 5, indicates that the objective function is to be evaluated for product 1, second process plan is selected with first operation is to be performed on machine 2 and second operation to be performed on machine 4. The operation cost and operation time is calculated from Table 2. The demand of product 1 is 30 (from Sect. 4.1). For process plan 2, first operation to be performed on machine two which has operation time is 6 units (from Table 2) and operation cost is $8 (from Table 2). So, the total operation time and operation cost for the first operation is 180 units (= 30 × 6 units) and $240(= 30 × $8) respectively. Similarly, for the second operation to be performed on machine six which has operation time is 13 units (from Table 2) and operation cost is $26 (from Table 2). So, the total operation time and operation cost for the first operation is 390 units (= 30 × 13 units) and $780 (= 30 × $26) respectively. Thus, total operating cost for product 1 is $240 + $780 = $1020. The cost of moving is calculated from Table 3. After completion of the first operation, the material is moved from machine 2 to 4. So, the cost of moving is $13 (Table 3). Similarly, the operating cost and cost of moving of all 14 products is calculated and shown in Table 4.

Table 4 Operation cost and cost of moving of random solution

The total set up costs (given in Sect. 4.1) of all 14 products for all 10 machines is $2470. Waiting time of machines is calculated by using Eq. 1. For example, the total planned operation time on machine 2 is 905 units and operation completion time for machine 2 is 1495 units. So, waiting time for machine 2 is 1495 − 905 = 590 units. Thus, waiting cost of machine 2 is 590 × $1.2 = $726. Similarly, the waiting cost of all machines calculated and it is equal to $2887. Then by adding operation cost ($14,890), cost of moving ($201), set up cost ($2470), and waiting cost ($2887) of all 14 products, the total cost (objective function value) becomes $25,419 which is shown in Table 5 for solution 1. In similar way, the objective function value is evaluated for all initial 20 solutions. However, for demonstration purpose, four solutions are presented in Table 5.

Table 5 Objective values calculated according to Eq. 8

Step 3 Selection:

From the calculated objective function values, the fitness function value is calculated and shown in Table 6. As this problem is of minimization, the fitness function values will be reciprocal of objective values. From these values cumulative values are calculated. From these cumulative values, roulette wheel values are obtained. The roulette wheel values shows that solution number 3 have more probability to take part in crossover. Then random numbers are generated. From the random number generated, the decision regarding reproduction of the solution is taken. For example, for the first solution, the random number generated is 0.16 which lies between the cumulative ranges of 0–0.255. So, the first solution will be continued for crossover. Similarly, for the second solution, the random number generated is 0.713 which lies between the cumulative ranges of 0.472–0.756. Hence, the second solution will be discarded and it will be replaced by third solution. Thus, using the roulette wheel selection method, the solutions selected for reproduction will undergo crossover (Fig. 2).

Table 6 Fitness function calculation

Fig. 2

Roulette wheel example

Step 4 Crossover:

In crossover procedure two solutions are selected at random and then crossover is done at single point as shown in Fig. 3. In the present case, the maximum process plans can be 1, 2, 3 or 4 and the number of operations in each process plan are not same. Hence, crossover location is set at the end of process plan and not after every operation. There are 14 products are to be manufactured. To perform crossover, two parent strings are selected randomly and a random number is generated between 2 and 14 numbers. For example, if a random number 2 is selected, then crossover is performed as shown in Fig. 3.

Fig. 3

Crossover procedure

Step 5 Mutation:

Mutation is carried out by considering mutation probability of 0.1 i.e. single point mutation. A random site is selected for mutation. Then from the available set of machine numbers, only a random machine number is selected and mutation is carried out. The mutation operation is explained in Fig. 4. In this figure operation 1 of process plan 2 of product 1 will undergo mutation. This operation can only be performed on machine number 2 or 3 or 6 as given in Table 2. So, the number 2 can be flipped with either 3 or 6.

Fig. 4

Mutation procedure

After mutation operation, objective values are calculated. This will complete one iteration. As the objective is to find minimum values, the minimum value of this iteration is noted down. The same procedure is followed for another iterations. The minimum objective value will give optimum solution. If there is no change in solution observed for 50 solutions, then the process is terminated.

After carrying out different iterations the optimum solution is obtained. The optimum solution is given in Table 7. In Table 7, for part 1, process plan 2 is selected and first operation is performed on machine 2 and second operation is performed on machine 1.

Table 7 Optimum solution of the present case study

Paulo et al. (2002) have only considered operation allocation and material handling selection problem. To optimise the material flow of the problem, 20 random solutions are generated as per Eq. 8. There are 14 part types which have different process plans. Each part can be manufactured by following any one of the process plan. There are maximum four operations and these operations can be performed on 10 machines. The available time units for machine j = 3 and j = 7 are 480 units and for the remaining machines it is 980 units.

The part selection and operation allocation problem was solved with real coded genetic algorithm. The optimum solution was obtained and shown in Table 7 and the material flow for the same process plan is explained in Table 8. The part which is having minimum processing time will be processed first and then the part having second minimum processing time will be processed next i.e. shortest processing time (SPT) scheduling priority rule is used. Likewise, according to the processing time of the parts they are selected and processed on different machines. In Table 8, the product 1 is having two operations and first operation having processing time of 180 units will be performed on machine 2 and then second operation having processing time of 120 units will be performed on machine 1. But, as the product 14 is having first operation of 120 units, it will be processed first (as it is minimum one) on machine 2. So, machine 2 will process first operation of product 14 for 120 units and meanwhile operation 1of product 1 will have waiting time of 120 units. When the first operation on machine 2 is over then operation 1 of product 1 will be taken for processing which is having processing time of 180 units. So, the completion time for operation 1 of product 1is 120 + 180 = 300 units. So, product 1 is ready at 300 units for further operation 2. But, as machine 1 is busy in processing another operations and it will be finish operations at 460 units. So, operation 2 of product 1 will have a total waiting of 460 units. It has processing time of 120 units, so, the completion time is 460 + 120 = 580 units. The same is shown in Fig. 5 with the help of Gantt’s chart.

Table 8 Optimum material flow for the first case study

Fig. 5

Gantts chart for the optimum process plan

In Table 8, following notations are used:

• S = start time,

• O = operation or processing time,

• W = waiting time,

• F = finish time.

A Gantts chart for the optimum process plan is shown in Fig. 5. Scheduling is based on shortest processing time (SPT) rule. For product 12 (P12), the first operation will be processed on machine 6 (M6) and after finishing first operation at 105 units, the second operation of product 12 (P12) will be started at 105 units and finished at 315 units on machine 3 (M3). For machine number 3, there are two operations. But, due to waiting, the first operation will start at 105 units and finish at 315 units. Whereas, second operation start at 315 units and finish at 555 units.

In Table 9, the optimum solutions based on the proposed model, Paulo et al. (2002) is presented. The sequence of operations 1(2) {2,1} means for part 1, process plan 2 is selected and sequence of operations to be carried out is on machine 2 and then machine 1. Though the Operation cost and material handling cost is high by the proposed methodology, but waiting cost is less as compared to the optimum solution of Paulo et al. (2002). The total cost is obtained by adding operation cost ($9755), material handling cost ($150), machine set up cost ($2470) and waiting cost ($2664) by using objective function explained in Eq. 8. So, the total cost by the proposed methodology is $15,039, whereas the total cost of Paulo et al. (2002) is $15600.This shows that Paulo et al. (2002) have considered a mathematical model only for operation allocation problem which is not suitable in real time scheduling system.

Table 9 Optimum solutions for the first case study

Figure 6 shows the convergence of RCGA for the present case study.

Fig. 6

Convergence graph for RCGA

4.3 Case study based on integrated operation allocation and material handling equipment selection and scheduling problem

The second case study is based on an operation allocation and material handling equipment selection problem of Mahdavi et al. (2011). In this work, an operation allocation and material handling equipment selection problem of Mahdavi et al. (2011) is considered to optimise material flow under integrated operation allocation, material handling equipment selection problem and scheduling problem. The modified objective function is:

$${\text{Minimise}} = \sum\limits_{i = 1}^{N} {d_{i} } \sum\limits_{p = 1}^{{p_{i} }} {} \sum\limits_{{s_{(ip)} = 1}}^{{S_{(ip)} }} {\sum\limits_{{j \in j_{ips} }} {OC_{{js_{(ip)} }} .X_{{js_{(ip)} }} } } + \sum\limits_{i = 1}^{N} {} \sum\limits_{p = 1}^{{p_{i} }} {} \sum\limits_{{s_{(ip)} = 1}}^{{S_{(ip)} }} {\sum\limits_{j = 1}^{M} {SC_{{js_{(ip).} .X_{{js_{(ip)} }} }} } } + \sum\limits_{i = 1}^{N} {d_{i} } \sum\limits_{p = 1}^{{p_{i} }} {} \sum\limits_{{s_{(ip)} = 1}}^{{S_{(ip)} }} {} \sum\limits_{j = 1}^{M} {\sum\limits_{h = 1}^{H} {\sum\limits_{e = 1}^{E} {(MH_{{hjes_{(ip)} }} } } } + RC_{{js_{(ip)} }} ).(Y_{{jhes_{(ip)} }} ) + \sum\limits_{i = 1}^{N} {} \sum\limits_{p = 1}^{{p_{i} }} {} \sum\limits_{{s_{(ip)} = 1}}^{{S_{(ip)} }} {\sum\limits_{j = 1}^{M} {Wc_{js(ip)} } }$$

(14)

Constraints

• 1) Each part type should be processed just under a particular process plan.

$$\sum\limits_{p = 1}^{{p_{i} }} {w_{(ip)} } = 1\;\;\;\forall i$$

(15)

• 2) Make sure that at most one machine should be selected to perform operation

$$M.k_{j} \le \sum\limits_{{s_{(ip)} = 1}}^{{S_{(ip)} }} {X_{{js_{(ip)} }} } \;\;\forall j$$

(16)

• 3) This constraint guarantees that the operations allocated to any machine cannot exceed the machine’s capacity

$$\sum\limits_{i = 1}^{N} {d_{i} } \sum\limits_{p = 1}^{{p_{i} }} {\sum\limits_{s = 1}^{{s_{(ip)} }} {t_{{js_{(ip)} }} } } .X_{{js_{(ip)} }} \le T_{j} k_{j} C_{j\;} \;\;\forall_{j}$$

(17)

• 4) The remaining time on each machine should be greater or equal to the time required by the next operation s(ip) to be assigned to this machine

$$d_{i} .t_{{js_{(ip)} }} .X_{{js_{(ip)} }} \le \;t_{{js_{(ip)} }}^{r} \;\;\;\forall_{{s_{(ip)} }} ,j$$

(18)

• 5) Each operation s(ip) of the selected process plan is assigned to only one of the available machines

$$\sum\limits_{{j \in j_{{s_{(ip)} }} }} {X_{{js_{(ip)} }} } = w_{(ip)} \;\;\forall_{{s_{(ip)} }}$$

(19)

• 6) The remaining time on any machine after any assignment of operation should be more or equal to zero:

$$t_{{js_{(ip)} }}^{r} \ge 0\;\;\;\forall_{{s_{(ip)} }} ,j$$

(20)

• 7) Once a machine is selected for operation s(ip), then all the material handling operation h corresponding to (sj) have to be performed

$$X_{{js_{(ip)} }} = v_{{jhs_{(ip)} }} \;\;\;\forall_{j} ,h,s_{(ip)}$$

(21)

• 8) This constraint ensures that, once a machine is selected for operation s(ip), then all the material handling operation h corresponding to (sj) have to be performed.

$$\sum\limits_{i = 1}^{N} {\sum\limits_{p = 1}^{{p_{i} }} {\sum\limits_{s = 1}^{{s_{(ip)} }} {\sum\limits_{j = 1}^{M} {\sum\limits_{{e \in E_{js(ip)} }} {X_{{js_{(ip)} }} } } } } } \ge k_{j} \;\;\;\;\;\forall_{j}$$

(22)

• 9) If machine j is selected, then at least one operation has to be allocated to that machine.

$$\sum\limits_{i = 1}^{N} {\sum\limits_{p = 1}^{{p_{i} }} {\sum\limits_{s = 1}^{{s_{(ip)} }} {X_{{js_{(ip)} }} } } } \ge k_{j} \;\;\;\;\forall_{j}$$

(23)

There exist N part types (i = 1,…, N), which can be sequenced in N! ways and set of machines labeled (j = 1,…, M) where the demand di of a given part type i is assumed to be uniform over the planning period. Each part type can be processed under the different process plans (p = 1,…, pi). The operations of a process plan pi are represented by the indices S = 1,…, S(ip). All together M × S(ip) combinations of machine-operation allocation are possible for one of the part type sequence. Hence, for N! part type sequences the total number of possible allocation N!M × S(ip). However some of these allocations are not possible because they are not able to satisfy system constraints.

For example, as shown in Table 10, the first part type has two different process plans (p1 = 2) and (p2 = 2), (p3 = 1), (p4 = 2). There is j = 1, 2,…, 6 machines, each with a capacity of 480 s during the planning period. The capabilities of the machines to perform the operations of the part types are illustrated too. For example, part type i = 1 has p1 = 2 process plans. Under process plan p = 1, this part type has s₍₁₁₎ = 2 operations with the indices s ∈{1,2}, whereas under process plan p = 2, it has s₍₁₁₎ = 3 operations, with indices s∈{1,2,3}. Operation s = 1 of process plan p = 1 for part type 1 can be completed on any of the machines j∈j₁₁₁ = {2,3} while operation s = 2 can be completed on any of the machines j∈j₁₁₂ = {1,4,5,6} and operation s = 1 from process plan 2 of part type 1 can be completed on any of the machines j∈j₁₂₁ = {1,3,4}.

Table 10 Values of demand, operation cost, robot cost, operation time, material handling cost

The mathematical model is based on optimisation of total cost which is based on operation cost, set up cost, material handling cost, robot cost and waiting cost. In Table 10, the values of demand, operation cost, material handling cost, robot cost and operation time are given. The set up cost of machine 1 is $225, machine 2 is $250, machine 3 is $150, machine 4 is $275, machine 5 is $800 and machine 6 is $150.

The revised mathematical model presented in Eq. 14 is used to optimise the material flow of this problem. The optimum material flow obtained by the process plan is given in Table 11. In Table 11, following notations are used: S = start time, P = operation or processing time, W = waiting time, F = finish time

Table 11 Optimum process plan for the second case study

As shown in Table 12, the sequence of operation is given by 1(1) {3, 1} which indicates that for part 1, process plan 1 is selected and first operation is performed on machine 3 and the second one is on machine 1. The optimum process plan obtained by proposed methodology is 1(1){3,1}, 2(1){1,6}, 3(1){3,4}, 4(2){4,6}. The operation cost is $1530, robot cost is $1650, material handling cost is $1046, set up cost is $800 and waiting cost is $375 which is assumed and equal to total waiting time. So, the total cost is $5401 as compared to $10,899 which is given by one of the process plan of Mahdavi et al. (2011). Though the optimum total cost given by Mahdavi et al. (2011) is $7139, which is much higher than optimum total cost obtained by proposed methodology and there is about 24% reduction in the total cost.

Table 12 Optimum solutions for the second case study

5 Conclusions

In this research work, an integrated production planning and scheduling problem is presented. A mathematical model for waiting time of product and machine for the real time scheduling system is proposed. This model is based on SPT scheduling rule. This mathematical model is verified by considering two case studies. In the first case study, Paulo et al. (2002) have considered two mathematical models, one for an operation allocation and second one for material handling system selection. In this case study, the objective function considered is to minimise the total cost i.e. material flow of the system. To optimise the material flow, real coded genetic algorithm (RCGA) is proposed.

In the second case study, a mathematical model of Mahdavi et al. (2011) is considered which considered an integrated approach of an operation allocation and material handling equipment selection problem. But, author have not considered the waiting time in the real time scheduling. The optimum process plan selected by the author does not remain optimum in the real time scheduling.

In this work, real coded genes are used to generate variables of solution for part type selection and operation allocation problem. Only one gene is sufficient to represent each operation. So, the chromosome length required in RCGA is 30–50% less as compared to binary coding. Thus, there is a reduction in computational time and burden to handle large variables.