The theory of static deformation of polymeric systems (melts and solutions of polymers) in the viscoelastic and solid states was presented earlier [1]. More recently [2, 3] the theory was examined as applied to dynamic deformation. The results from experimental verification for the case of dynamic deformation of a polymeric system of the first type with a polymer concentration somewhat below the critical value were presented. For this type of curve in a wide range of variation of cyclic frequency (velocity gradient) a stable deformation regime, characterized by constant complex viscosity, was observed. This makes it possible to compare experimental and theoretical data on the complex viscosity and its viscous and elastic components with each other. Good agreement between them was observed.

The present work gives the results from examination of the more complex process of dynamic deformation of polymeric systems of the second type with a polymer concentration above the critical value in stable and unstable regimes. A characteristic feature of such a deformation regime is intersection of the curves of the viscous component of the tangential force for the first measurement point and the curve for the elastic component of the tangential force for the second measurement point, which corresponds to intersection of the classical curves of the elastic modulus G′(ω1o) and the shear modulus G″(ω1o).

A 14% spinning solution of polyacrylonitrile (PAN) and dimethyl sulfoxide (DMSO) at 298 K was used for the investigation. The viscosity-average molecular mass was calculated by means of the equation [η] = 1,75·10−3 \( {M}_{\upsilon}^{0,66} \) [4] where η is the characteristic viscosity. The molecular mass of the polymer amounted to 290 kDa.

The viscoelastic characteristics of the polymeric systems were investigated on a Haake RheoStress-1 rheometer (Germany) with a cone and plate measurement system in dynamic deformation mode. The diameter of the cone was 30 mm, and the cone angle was 2°. The rotational frequency was defined by the equation [2] ω1 = ω1osin ωt, where ω1o is the amplitude of the rotational frequency of the cone (the inner cylinder), ω is the rotational frequency, and t is time.

The experimental data were determined at sin ωt = 1, when the rotational frequency ω1 = ω1o can be regarded as the angular velocity, just like the velocity gradient. The investigations were conducted in a rotational frequency range of ω1o = 0.628–628 s-1.

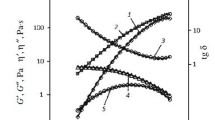
We will change the designation of the indirectly measured tangential stress τ1v(ω1o = G″(ω) at the first measurement point, relating to the surface of the cone (the inner cylinder), and the elastic component of the tangential stress τ1u(ω1o) = G′(ω) at the second measurement point, relating to the working surface of the “retarded” outer cylinder (plate). It was assumed that identical results are obtained on the cone–plate and cylinder–cylinder viscosimeters. Previously examined relationships [2] were used to assign and determine the remaining components of the tangential stress at the first and second measurement points. All the tangential stresses for the first measurement point are presented in Fig. 1 by the relationships for the viscous component of the tangential stress τ1v(ω1o) (curve 1), the elastic component τ1u(ω1o) (curve 2), and their total value – the tangential stress τ2c(ω1o) (curve 3). The analogous relationships for the second measurement point are represented by curves for the viscous component τ2v(ω1o) (curve 4), the elastic component τ2u(ω1o) (curve 5), and their total value – the complex tangential stress τ2c(ω1o) (curve 6). Since the curves for paths 1 and 6 coincide they are represented in Fig. 1 by one curve with dual notation 1.6.

Fig. 1
figure 1

Dependence of the tangential stresses on the rotational frequency. Polymeric system: 14% spinning solution of PAN in DMSO. Temperature 298 K, M = 300 kDa. First measurement point: 1) t1v; 2) t1u; 3) t1c. Second measurement point: 4) t2v; 5) t2u; 6) t2c.

Full size image

Before going on to analyze the behavior of the presented curves let us briefly examine features of the behavior of the polymeric systems during deformation. In the initial state we will treat the polymeric system as a network consisting of separate bent macromolecules in contact with each other. We will treat their points of contact as nodes that can be both viscous and elastic. At deformation rates with low gradients the macromolecules at the nodes can move in relation to each other subject only to frictional resistance. We will define such nodes as viscous. If the velocity gradient is increased not all of the macromolecules can move freely at the nodes. They only move within the elasticity limits of the nodes, forming a spatial network of entanglements consisting of viscous and elastic nodes.

The deformation methods (longitudinal deformation or shear) have a significant effect on the strength characteristics of the fibers [6]. These deformations differ greatly in the direction of their action. Whereas the velocity gradient during longitudinal deformation coincides with the direction of flow (extension deformation) during shear it is normal to this direction. Differences in the direction of deformation cannot affect the behavior of the initial structure of the polymeric system or its properties. This shows up particularly strongly at the initial moment of application of the deformation (the velocity gradient) and with the appearance of obstacles to flow at the entry sections [6]. Since it is difficult to observe the deformation process of a polymeric system in a continuously operating viscosimeter we will make certain assumptions that will subsequently be examined in detail during static deformation of the system as it is moves through the capillary.

We will suppose that the initial structure of the polymeric system is a network and the initial deformation is longitudinal deformation. We will consider them first. We are only concerned with longitudinal deformation at the initial moment of deformation. The deformation process terminates with this on the attainment of the most highly oriented polymer system and, in particular, a high-strength fiber.

Secondly we will consider the shear deformation and the structural changes that arise here in the polymeric system. Under the secondary manifestations of the structure of the polymeric system we also include the appearance of known structures of the shish–kebab type, an amorphous structure with complex chains [6], a bicomponent structure [7], a two-phase structure [6], etc. We will discuss them later.

We pass on directly to dynamic deformation of the polymeric systems. It was not expected that the complex stresses and their elastic components could have negative values. For their presentation, therefore, in addition to the system of coordinates in double logarithmic axes (Fig. 1) we also used a semilogarithmic system of coordinates (Fig. 2) that made it possible to analyze data with a negative sign. The rotational frequencies in logarithmic form were plotted on the abscissa axis, and the tangential stresses in natural form were plotted on the ordinate axis. Such relationships, which also make it possible to include their negative values, give a more complete picture of the variation of their stresses. During analysis of the experimental data we will use both methods of representation simultaneously.

Fig. 2
figure 2

Dependence of the tangential stresses on the rotational frequency. Polymeric system, the same as in Fig. 1. First measurement point: 1) τ1v; 2) τ1u; 3) τ1c. Second measurement point: 4) τ2v; 5) τ2u; 6) τ2c; 7) τ1co.

Full size image

Right away we see that the curves presented in Fig. 2 for the second type of flow differ significantly from the curves for the first type [3]. This applies above all to the presence of a point of intersection (point d1) of the initial τ1v(ω1o) (curve 1) and τ2u(ω1o) (curve 5) relationships obtained for the different measurement points. It is also necessary to mention the complicated nature of the behavior of the complex tangential stress τ1c(ω1o) (curve 3) and its elastic component τ1u(ω1o) (curve 2).

As for the first type of flow curves [3], we will break the whole range of variation of the complex tangential stress down into three sections. The first section of deformation of the polymeric system abcd (Fig. 2) we will allocate to shear deformation, and the section de to the destruction of secondary network nodes accompanied by an abrupt transition to negative values for the tangential stresses. The third section ef (Fig. 1) we assign to longitudinal deformation and formation of an oriented new structure for the polymeric system.

We will consider these sections in greater detail. We divide the first section in Fig. 1 into two sections abc and cd. The abc section is characterized by stable deformation with linear increase of the complex tangential stress. The viscous and elastic components of the stresses vary within the limits of the values for the complex tangential stress. On this section at ω1o = ω1oR there is a point for the equilibrium state O1, for which we have τ1vR = τ1uR =GR/2. As shown earlier [3], from this point it is possible to obtain the principal rheological characteristics of the employed polymeric system, i.e., the equilibrium shear modulus τ1ocR = GR and the equilibrium relaxation time \( {\uptheta}_R={\upomega}_{\mathrm{l} oR}^{-1} \). The values for the spinning solution of PAN in DMSO amounted to GR = 2τvR = 1.058 and \( {\uptheta}_R={\upomega}_{\mathrm{l} oR}^{-1} \) = 0.0343 s-1.

We allocate the cd section to hardening of the polymeric system in the state of a three-dimensional network on the surface of the cone (or the inner cylinder), at which the complex tangential stress and its elastic component increase more energetically, reaching a maximum value at point d.

The second section cd in Fig. 1 we allocate to destruction of only the secondary structure of the polymeric system that appears during shear. The macromolecules themselves retain their integrity. As a result of such destruction the complex tangential stress and its elastic component decrease sharply, cross the zero mark, and pass into the negative region, reaching minimum values at point e. On this section the complex tangential stress is mainly determined by the elastic component τ1u(ω1o) (Fig. 1, curve 2). The moment of transition from the maximum to the minimum values of the tangential stresses can be related to the circular frequency ω1v = ω1omax, corresponding to intersection of the curves for the tangential stresses τ1v(ω1o) and τ2u(ω1o) at the intersection point d1. These flow curves are characterized by different equations of state τ1v = α1vτ1c (the first measurement point) and τ2v = α1vα1uτ1c (the second measurement point). Here α1v and α1u are the coefficients of viscosity and elasticity. According to the equations, the equality of the named tangential stresses can only be fulfilled on the condition that α-1v = 0 and α1u = 1, i.e., when the polymeric system reaches a completely elastic state on the surface of the cone (the inner cylinder) and on the surface of the plate (the outer cylinder).

During analysis of the dynamic deformation the second measurement point becomes very significant since on this section the complex tangential stress τ2c = G″ and its elastic component τ2v = G′ are measured indirectly while the viscous component is determined from their difference: τ2v = G″ − G′ [3]. In Fig. 2 they are represented by the curves for τ2v(ω1o) (curve 4), τ2u(ω1o) (curve 5), and τ2c(ω1o) (curve 6). This means that the system also reaches an elastic state on the surface of the stationary cylinder. It is natural to suppose that the elastic state of the polymeric system is reached over the whole working gap, after which the structure of the polymeric system begins to be destroyed. The point of intersection d1 we attribute to the end of transition of the polymeric system to the elastic state and beginning of destruction of the structure. Section de will only apply to destruction of this secondary structure, which is superimposed on the initial structure in the shear process. We turn our attention to the fact that with circular velocity ω1o = ω1omax the viscous component of the tangential component of the stress changes its sign to negative, which we attribute to elastic shrinkage of the polymeric system. This means that counter motion of the polymeric system appears in the working gap.

We pay special attention to the fact that only the τ2u(ω1o) (Fig. 2, curve 5) and τ2c(ω1o) (curve 6) relationships keep positive values. This indicates that the unpacking of the secondary structure takes place under control of the elastic component of the tangential stress at the second measurement point. We will discuss this aspect of the destruction of the secondary structure later.

The third section ef in Fig. 1. After reaching the minimum value at point e the elastic component starts increasing again. The complex tangential stress also increases. We assign this section to the beginning of the formation and strengthening of the initial structure. Figure 1 shows only the initial part of this section, which makes it impossible to present a full picture of the deformation of the polymeric systems at high values of the circular frequency (velocity gradients).

Earlier, in the theoretical part [2], it was shown that the dynamic deformation process can be regarded as flow of a viscoelastic liquid, as in the deformation of polymeric systems in the solid state. In this communication the dynamic deformation process in polymeric systems will be regarded as the flow of a viscoelastic fluid.

For this purpose we will consider what forms of viscosity are displayed by the polymeric system during deformation. To start with we will consider the first measurement point. In order to define complex viscosity and its viscous and elastic components we use the equations η1v = τ1v/ω1o, η1u = τ1u/ω1o, and η1c = τ1c/ω1o, which have been confirmed as true [2, 3]. The obtained data in the form of the relationships η1v(ω1o) (curve 1), η1u(ω1o) (curve 2), and η1c (ω1o) (curve 3) for the first measurement point are presented in Fig. 3 in semilogarithmic coordinates and in Fig. 4 in double logarithmic coordinates. For comparison the η1co(ω1o) relationship in Newtonian flow is presented in Fig. 4 in the form of straight line 7. As for the flow curves of the first type, we divide the region of variation of the complex viscosity into three characteristic sections. At this stage we disregard the viscosity of the solvent on account of its smallness.

Fig. 3
figure 3

Dependence of the complex viscosity and its viscous and elastic components on the circular velocity. Polymeric system, the same as in Fig. 1.

Full size image
Fig. 4
figure 4

Dependence of the complex viscosity and its viscous and elastic components on the circular frequency. Polymeric system, the same as in Fig. 1.

Full size image

On the first section (ab) the complex viscosity retains its constancy. Decrease of the viscous and increase of the elastic components of the complex viscosity are observed for values in the range of η1v + η1u = η1c = η1oc. Equality of the viscous and elastic components is reached at the point of the equilibrium state O1 with ω1o = ω1oR. Since the behavior of the investigated flow curves of the second type on the section of stable deformation is analogous with the behavior of the curves of the first type [3] they are not considered here in detail. We note only that the relationships obtained for the first type of flow curves are retained for those of the second type. Thus, for the equilibrium state at the first measurement point we have η1c + η1cR = 2η1vR = 2η1uR. According to the data for the first measurement point η1o = η1oR =35.6 Pa.s.

On the bcd section, the hardening section, the elastic component of the viscosity first increases slowly and then increases quite quickly, and at point d it almost reaches the limiting state of complex viscosity: η1c = η1c max = 249.4 Pa.s and η1u = η1u max = 243.7 Pa.s.

The second section de is the section for active destruction of the primary structure of the polymeric system. Here the complex viscosity and its elastic component fall sharply to minimal values at point e, acquiring a negative value.

The negative viscosity of a liquid is known from the literature [5]. It is also observed during the flow of a gas. It is considered that negative viscosity appears as a result of the inverse state of the medium. In the presence case the inverse state arises as a result of destruction of the secondary structure of the polymeric system and its transition into the initial state and by the nonuniformity of this destruction in the section of the working gap.

It is difficult to imagine the existence of negative viscosity as applied to the rheology of polymers. If the flow of a polymeric liquid is regarded as deformation of a solid-phase body and negative values of the normal and tangential stresses are accordingly related to the negative values for the deformation and compression this is no longer a problem.

The third section ef corresponds to the beginning of the formation of an oriented structure for the polymeric system. On this section the negative values remain both for the complex viscosity and its elastic component at the first measurement point and for the viscous component at the second measurement point on the surface of the stationary cylinder. The viscosity begins to increase, and it can be assumed that it will increase up to the values of the complex viscosity, known as the lowest Newtonian viscosity. This is demonstrated by the behavior of the previously investigated first type flow curves [3].

We will now look at the characteristics of expression of the viscous elastic properties of the polymeric system at the second measurement point. The apparent complex viscosity ηkc = τ2c/ω1o, the viscous component ηkv = τ2v/ω1o, and the elastic component ηku = τ2u/ω1o were determined from the obtained τ2v, τ2u, and τ2c values. They were called apparent [21] for the reason that the stresses obtained for the second measurement point were used for their determination while the circular frequency was used for the first measurement point.

The obtained data are presented in Figs. 3 and 4 in the form of ηkv(ω1o) (curve 4), ηku(ω1o) (curve 5), and ηkc(ω1o) (curve 6). A feature of the method of expressing the deformation characteristics in such a form for the second measurement point is that the very apparent complex viscosity changes with change of the reduced circular frequency together with change of the viscous and elastic components. Earlier it was mentioned that the nature of variation of this viscosity is determined by change of the viscous component at the first measurement point and that the viscous and elastic components change within the limits of change in the complex apparent viscosity, determined by the equation ηkc = ηkv + ηku = η1v.

As already mentioned above, the flow curves η1v(ω1o) (curve 1) and ηkc(ω1o) (curve 6) coincide. In Fig. 3, therefore, they are represented by one common curve 1.6. Since the behavior of these curves follows the traditional behavior of the effective viscosity they will not be examined in detail. We note only that the behavior of the relationship of the viscous component ηkv(ω1o) is similar in nature to the η1v(ω1o) curve, differing only in the value of the viscosity

We note also that three components of the examined six retain their positive value and, what is particularly important, the elastic component at the second measurement point retains a positive value.

As for the flow curves of the first type [3], we see extremal character in the behavior of the elastic component of the apparent viscosity ηku(ω1o) (curve 5). The elastic component of the polymeric system increases with increase of the circular frequency, at ω1o = ω1oR at the O2 equilibrium state it reaches its maximum value ηkuR = ηkvRmax = ηkR/2 = η1oR/4 [3], and it then decreases, intersecting the η1v(ω1o) (curve 5) at point d1. The equilibrium value of the viscous component reaches the same value ηkvR = ηkR/2 = η1oR/4.

It follows from this that the true complex viscosity at the point of the equilibrium state amounts to η1ocR = 4ηkvRmax. For the given polymeric system it amounted to 36.3 Pa.s. As already mentioned, the value obtained from the data of the first measurement point was 35.6 Pa.s. The deviation of the presented values for the complex viscosity amounts to 2%. It can thus be considered that the complex viscosity determined from the maximum value of the apparent elastic component at the second measurement point coincides with the complex viscosity calculated from the elastic component at the first measurement point.

The obtained data confirm that the maximum apparent complex viscosity at the second measurement point can be used as a quick analysis for determining the complex (Newtonian) viscosity at the first measurement point: η1oc = η1cR = 4ηkvRmax. This conclusion is very important in the examination of dynamic deformation, when the flow (deformation) curves η1v(ω1o) and η1u(ω1o) have a common point for the equilibrium state but do not have an initial Newtonian section.

With further increase of the circular frequency ω1o > ω1oR the elastic component of the complex viscosity begins to decrease, approaching the ηkv(ω1o) curve, intersects it at point d1, and then lies above it. Since this intersection point corresponds to transition of the polymeric system to the elastic state it must be concluded that the polymeric system at this point in the inner and outer surfaces of the working parts of the viscosimeter reach the elastic state. It can be considered that the polymeric system in such an elastic state is situated in the working gap between these surfaces. Such an elastic state in a polymeric system is called a “bottleneck” [6]. The polymeric system in the bottleneck state becomes transparent, which indicates fairly high orientation of the macromolecules and their close positioning. The macromolecules of the polymeric system in this state are elongated and compacted [6]. As a result of this the solvent starts to be forced out of the polymeric system, acting as a lubricant, and this leads to equalization of the velocity profile. Tensile stresses then come into operation. The polymeric system (a network of entanglements) reaches a limiting state and starts to break down.

We will now consider the experimental data on the complex viscosity and its viscous and elastic components in reduced form. We will use the method of reducing the complex viscosity and its components in relation to the initial complex viscosity η1c = η1o, which at low values of the circular frequency coincides in value with Newtonian viscosity. For this we divide the components of the viscosity balance for both measurement points by η1o. We obtain reduced coefficients of complex viscosity α1oc = η1oc/η1o, viscosity α1ov = η1ov /η1o, and elasticity α1ou = η1ou/η1o for the first measurement point and reduced coefficients of complex viscosity αkoc = η2c/η1o, viscosity αkov = ηkv/η1o, and elasticity αkou = ηku/η1o for the second measurement point. The obtained coefficients are related to each other by the equations α1oc = α1ov + α1ou and αkov = αkov + αkou.

Since the coefficients of viscosity and elasticity are expressed in relation to the constant initial complex viscosity the generalized flow curves vary in the same way as the initial flow curves. The reduced coefficients in the form of the α1ov(s1o) (curve 1), α1ou(s1o) (curve 2), and α1oc(s1o) (curve 3) relationships are presented in Fig. 5 by the scale on the left. We will treat the expression S1o = ω1o/ω1oR = θ1Rω1o as the reduced circular frequency [2].

Fig. 5
figure 5

Dependence of the coefficient of complex viscosity and its viscous and elastic components on the equilibrium strain deformation. Polymeric system, the same as in Fig. 1. Experimental data. First measurement point: 1) α1ov; 2) α1ou; 3) α1oc. Second measurement point: 4) αko5; 5) αkou; 6) αkoc. Calculated data. First measurement point: 12) α1ov; 22) α1ou; 32) α1oc. Second measurement point: 42) αkov; 52) αkou; 62) αkoc.

Full size image

We will compare the obtained deformation curves with the calculated relationships for the stable deformation regime. For their calculation we use the previously obtained equations [2] α1oc = 1, α1o𝜐 = \( {\left(1+{s}_{\mathrm{l}o}^m\right)}^{-1} \) and α1ou = \( {s}_{\mathrm{l}o}^m{\left(1+{s}_{\mathrm{l}o}^m\right)}^{-1} \) for the second measurement point αko𝜐 = \( {\left(1+{s}_{\mathrm{l}o}^m\right)}^{-2} \) , αkou = \( {s}_{\mathrm{l}o}^m{\left(1+{s}_{\mathrm{l}o}^m\right)}^{-2} \) , αkoc = \( {\left(1+{s}_{\mathrm{l}o}^m\right)}^{-1} \). The reduced (deformation) flow curves, including the sections with the initial complex (Newtonian) viscosity, were calculated. The parameters θR = 0.0343 s and m = 0.7 were used for the calculations. The calculated curves are presented in Fig. 6 with the scale on the right without symbols.

Fig. 6
figure 6

Dependence of the reduced coefficient of complex viscosity and its viscous and elastic components on the equilibrium shear deformation. Polymeric system, the same as in Fig. 1. First measurement point: 1) α1pv; 2) α1pu; 3) α1pc; 4) m = 0.7; 6) m = 1.

Full size image

It follows from analysis of the deformation curves that the degree of correspondence between theory and experiment for the first and second measurement points differs. We will begin the analysis from the second measurement point. It can be seen that good agreement between theory and experiment is observed over the whole range of variation of the shear deformation. In particular, the agreement of the experimental and calculated elasticity coefficients, which have extremal values at the O2 point of equilibrium with s1o = s1oR, should be noted.

For the first measurement point good agreement between theory and experiment is only observed on the stable deformation section ab. Some increase is observed on the bc section, while on the cd section there is a fairly sharp increase of the elastic and complex components to a maximum (point d) followed by a sharp decrease to a minimum (point e) and repeated growth. The viscosity coefficient αkov decreases to approximately the same value.

Let us reexamine the method previously presented in the theoretical part [1] to represent the rheological characteristics in relation to the viscous component of the complex tangential stress τ1v. It is possible similarly to use the viscous component of the complex viscosity η1v. For the first measurement point we obtain the reduced viscosity coefficient α1pv = τ1v/τ1v = η1v/η1v = 1, the reduced elasticity coefficient α1pu = τ1u/τ1v = η1u/η1v(θRω1o)m = \( {s}_{\mathrm{l}o}^m \) , and the reduced complex viscosity coefficient α1pc = τ1c/τ1v = η1c/η1v = 1 + \( {s}_{\mathrm{l}o}^m \) which are related to each other by the equation α1pc = α1pv + α1pu. The reduced elasticity coefficient α1pu = τ1u/τ1v = (θRω1o)m = \( {s}_{\mathrm{l}o}^m \) is known as “hyperelastic strain” [1].

For the second measurement point the coefficients of complex viscosity and its viscous and elastic components amount to αkpc = τ2c/τ1v = ηkc/η1v, αkpv = τ2v/τ1v = ηkv/η1v, and αkpu = τ2u/τ1v = ηku/η1v. In accordance with the name of the initial apparent viscosity and its components we will also call the reduced coefficients apparent. In Fig. 6 the coefficients are only represented by the relationships α1pv(s1o) (line 1), α1pu(s1o) (line 2), and α1pc(s1o) (curve 3) for the first measurement point.

When this method is used the deformation relationships α1pv(s1o) and αkpc(s1o) coincide since α1pv = 1 and αkpc = α1pv = 1 appear in the form of the superimposed straight lines 1 and 6. Above these lines there are deformation curves α1pu(s1o) (curve 2) and α1pc(s1o) (curve 3) for the first measurement point, and below there are curves α2pv(s1o) (curve 4) and α2pu(S1o) (curve 5) for the second measurement point. Of particular interest for the presented curves is the relationship (curve 2) the slope of which against logarithmic coordinates is determined by the exponential parameter m closely related to the density of the polymeric system during deformation [8].

The behavior of the other curves is clearly seen from Fig. 6, and we will not therefore dwell on their examination. We note only that the complex viscosity and its elastic component increase with increase of the strain deformation, reaching maximum values after which they simultaneously decrease sharply.

We will examine the α1pu(s1o) curve (curve 2) in greater detail. As before, we will divide the range of variation of the equilibrium strain into three sections according to the type of variation. The first section abcd is the section of stable deformation of the polymeric system in the state of a network of entanglements, and the second is a section of unstable deformation de within the limits of which the network structure is destroyed with a sharp transition to negative values for the tangential stresses and viscosities. We attribute the third section ef to the formation of a new structure in the polymeric system.

This figure also shows the calculated α1pu(s1o) curves obtained for the exponential parameters m = 0.7 (line 4) and m = 1 (line 5). We trace the variation of the experimental α1pu(s1o) curve in relation to these calculated curves. As seen from Fig. 6, on the section of steady deformation ab, which as shown above corresponds to constant complex viscosity, the α1pu(s1o) relationship against double logarithmic coordinates is represented by the straight line ab, the slope of which is determined by the exponential parameter m = 0.7. As shown in [8], the exponential parameter corresponds to a specific coefficient of packing for the macromolecules in the polymer. It decreases somewhat with increase of the shear deformation. However, on account of the insignificant change of slope it can be assumed that it is constant. At the equilibrium point (point O) the exponential parameter increases quite sharply to m = 1 and then remains constant over a certain range of variation of the equilibrium shear deformation (section bc). With variation of the equilibrium shear deformation the experimental and calculated data for the exponential parameter at m = 1 coincide. Such a state in the polymeric system is characteristic of a solid. For shear we will consider it as limiting. Increase of the equilibrium shear deformation at this section leads to complete transition of the polymeric system from the viscous state to the limiting elastic state over the whole working gap. The complex viscosity begins to be determined entirely by the elasticity. Further increase of the deformation only becomes possible as a result of rearrangement of the rate and stress profile. There is a transition from shear deformation with a transverse velocity gradient to extension deformation with a longitudinal velocity gradient accompanied by increase of the exponential parameter to approximately 1.6-1.8. We allocate this transition to section cd on the s1pu (s1o) curve (Fig. 6, curve 2). On the attainment of the limiting strength (elasticity) the initial structure of the polymeric system is finally disrupted and changes to a new qualitative state.

It was not possible to obtain a second section of stable deformation in the full volume for the given polymeric system. According to the numerous data there is such a section of deformation in polymeric systems with high circular frequencies (velocity gradients). Examination of the section of unstable deformation therefore becomes extremely important with regard to the aim of finding methods of overcoming the unstable flow and the transition to the second section of stable deformation (flow). It is important to understand what happens here. A more detailed mechanism of the transition of the polymeric system across the section of unstable deformation will be examined in future communications.