The swelling pressure is of fundamental importance for estimating the thermodynamic affinity between a polymer (PM) and a low molecular weight substance (LMW, the solvent) [1, 2], which is determined by the structure of the polymer (chemical and supermolecular) and the nature of the LMW, and is the driving force for the change in volume of the solid solution of the LMW in the PM. The theory and practice for swelling of a polymer in a liquid LMW has been intensely developed for network polymers, especially ion-exchange gels [3,4,5,6,7,8,9,10,11,12,13,14,15,16 and others]. This is connected with the widespread application of gels as superabsorbents in ion-exchange technology, as sanitary materials, in agriculture to improve soil quality and in hydroponics, in construction, and in other areas [14]. Significantly less attention has been focused on the theory of swelling for fibrous partially crystalline polymers, which are increasingly widely used within composite materials. In this case, the “guest” and the “host”, besides having adhesion properties, should also have comparable swelling characteristics, since the forces due to swelling pressure can break down adhesion contacts.

Accordingly, the aim of this work is thermodynamic analysis of the general principles and details of swelling in amorphous/crystalline polymers, which first of all can be considered as network polymers with network nodes in the form of crystallites and other physical units, and secondly amorphous regions of such polymers, when water is dissolved in them, undergo a transition to a rubbery (high elasticity) state.

Usually the swelling pressure (Π) is calculated in systems undergoing limited swelling; for polymer solutions, the osmotic pressure (Πos) is measured. Π and Πos are calculated starting from one thermodynamic equation [5, 17] which is not connected to the mechanism for the process:

$$ \varPi \overline{V_1}=- RT\ln {\overline{a}}_1+ RT\ln {a}_1, $$
(1)

where a1 and \( {\overline{a}}_1 \)are the activities of the solvent in the external phase and the polymer phase respectively; \( \overline{V_1} \)is the partial molar volume of the solvent in the solid or liquid solution phase.

In Eq. (1), in absorption of the LMW by the swelling polymer from the gas phase, we assume that a1 = p/p0, while from the liquid phase, when considering osmosis when considering osmosis of the pure solvent (a1 = 1) through the membrane into the polymer solution, for maximally dilute solutions [1, 5] Eq. (1) goes to the van’t Hoff equation:

$$ {\varPi}_{\mathrm{os}}= CRT, $$
(2)

where C is the polymer concentration in the dilute solution, mol/m3.

In a number of cases, the swelling pressure is called the osmotic pressure, but these two phenomena are quite different in nature. This is clearly demonstrated by the Gregor model [4, 5,6,7], schematically shown in Fig. 1.

Fig. 1
figure 1

Schematic drawing of a polymer PM (1, 2) and osmosis of a low molecular weight substance LMW through the membrane (3, dashed line).

Full size image

In the initial state (Position 1), the polymer retains its shape and volume (V0) as a result of intermolecular forces and the forces due to surface pressure. Absorption of the LMW from the vapor or liquid phase (Position 2) occurs as a result of the potential difference between the LMW in the polymer phase and the external phase. At equilibrium, the chemical potentials of the LMW in both phases become identical, and Eq. (1) corresponds to this case. At the same time “elastic deformation of the polymer network as a result of its stretching by the sorbed solvent” occurs [3, 11]. These elastic deformations are modeled by springs, the volume of the polymer changes, and excess pressure arises: Πel. In contrast to the above, osmotic processes require the presence of a semipermeable barrier (Fig. 1, Position 3) and do not depend on the nature of the dissolved substance (the polymer PM), and like other colligative phenomena, are determined only by the number of particles (macromolecules) in solution [18].

Here, let us consider only the equilibrium swelling of polymers, in which the state of both the polymer and the solvent change. The state function is the internal energy (U) and its derivative is the internal pressure (l) [18]. The internal energy is

$$ U=f\left(V,T\right), $$
(3)
$$ dU={\left(\partial U/\partial V\right)}_{\mathrm{T}} dV+{\left(\partial U/\partial T\right)}_{\mathrm{V}} dT. $$
(4)

In swelling of a polymer, in the system only the work of expansion is important and there is no electrical work, gravitational work, work due to surface forces, etc. Then

$$ \updelta Q= dU+ PdV, $$
(5)
$$ \updelta Q={\left(\partial U/\partial V\right)}_{\mathrm{T}} dV+{\left(\partial U/\partial T\right)}_{\mathrm{v}}+ PdV, $$
(6)
$$ \updelta Q=\left[{\left(\partial U/\partial V\right)}_{\mathrm{T}}+P\right] dV+{\left(\partial U/\partial T\right)}_{\mathrm{v}}+ dT, $$
(7)
$$ \updelta Q=l\partial V+{C}_{\mathrm{v}} dT, $$
(8)

where (δQ/dV)T = l = (dU/dV)T + P; (δQ/dT)v =  = (dU/dT)v = Cv.

The first derivative (the heat of isothermal expansion of the body, it has the same dimensions as pressure and is a combination of the external pressure P and the derivative (∂U/∂V)T, reflecting the mutual attraction of the molecules) is the internal pressure [18]. This term is small for real gases, and is very large for liquids and solids, i.e., l >> P and l = (∂U/∂V)T. For liquids and solids, the internal pressure can be calculated [18] as

$$ l=\Delta {U}_{\mathrm{vap}}/{\upsilon}^0, $$
(9)

where ΔUvap is the increment in internal energy on expansion of the liquid to the volume of the saturated vapor (a process equivalent to vaporization); v0 is the specific volume of the liquid. For low molecular weight liquids and melts, l is calculated from handbook data. For polymers, this quantity is called the cohesive energy density

$$ {\updelta}^2=\Delta {E}_0/V, $$
(10)

which can be calculated by the additivity method [19]

$$ \updelta =\Delta E/N\cdot \Delta V, $$
(11)

where \( \Delta {E}_{\mathrm{i}}^{\ast } \)is the contribution of the atoms and the types of intermolecular interactions to the internal energy; NA is Avogadro’s number; the ΔVi are the increments in the intrinsic volumes of the atoms. The results of the calculations for a number of solvents and polymers are presented in Table 1.

Table 1. Internal Pressure of Solvents and Polymers (d = density)
Full size table

In fact, the values of the internal pressure, proportional to the intermolecular interaction energy, are greater than the values for liquids and polymers and increase as the polarity of the substance increases, especially in the presence of hydrogen bonds. With polymer – solvent interaction, the internal pressure of the system will vary within these limits.

The internal pressure is a thermodynamic characteristic of the liquid and the polymer, and is used in theories of solutions typically as a solubility parameter.

$$ {\updelta}^2=\Delta {E}_0/V, $$
(12)

For example, in Hildebrand’s theory of regular solutions [20], the equation for the energy of mixing for the components is

$$ \Delta {U}_{mix}={V}_x{\upvarphi}_1{\upvarphi}_2{\left[\left({E}_1^{0.5}/{V}_1\right)-\left({E}_2^{0.5}/{V}_2\right)\right]}^2, $$
(13)

or

$$ \Delta {U}_{mix}={V}_x{\upvarphi}_1{\upvarphi}_2{\left[{l}_1^{0.5}-{l}_2^{0.5}\right]}^2, $$
(14)

where φ1, φ 2 are the volume fractions of the components.

In the Flory – Huggins theory of athermal solutions, the solubility parameter is proportional to the difference between the internal pressures of the components:

$$ {\upchi}_1=\frac{\left({\updelta}_1-{\updelta}_2\right){V}_1}{RT}-\frac{{\left({l}_1^{0.5}-{l}_2^{0.5}\right)}^2{V}_1}{}. $$
(15)

It is interesting to note that in the Hildebrand theory, equal internal pressures of the components l1 = l2 corresponds to an ideal solution.

In swelling of polymers, the internal energy of the system changes and hence the internal pressure changes, and a consequence of this is the swelling pressure in nonideal systems. For analysis of this phenomenon, let us consider an open thermodynamic system [21], consisting of a solid polymer capable of exchanging energy with the surrounding medium and a low molecular weight substance (the sorbate). The gas (or liquid) phase found in thermodynamic equilibrium with it is considered as the medium and is not included in the system. For such a system, the fundamental Gibbs equation for the change in the internal energy under the influence of the low molecular weight substance has the form

$$ d\Delta U= Td\Delta S+\sum {Y}_{\mathrm{i}}d{y}_i+\sum {\Delta \upmu}_{\mathrm{i}}d{m}_{\mathrm{i}}, $$
(16)

where S is the entropy of the system; Yi, yi are the generalized forces and coordinates characterizing the work done by the system; μi, mi are the specific chemical potentials and masses of the component.

Let us assume that the work done by the system is positive while the work done on the system is negative. The equilibrium pressure of the LMW substance P should be considered as an external mechanical action hydrostatically compressing the polymer, i.e., PdV. Let us express the internal stresses, also including surface tension, as in the Gregor model by a single term ledV, where le is the hydrostatic pressure created by the springs in the Gregor model (see Fig. 1). Let us refer all the quantities in Eq. (16) to the mass of the polymer (m2), i.e. dm2 = 0. Then

$$ \sum {\Delta \upmu}_id{m}_i=\Delta {\overline{\upmu}}_1d{m}_1+\Delta {\overline{\upmu}}_2d{m}_2=\Delta {\overline{\upmu}}_1d{m}_1= RT\ln {\overline{a}}_1d{m}_1 $$

The change in entropy of the system is usually [4-6, 12, 22 and others] connected with two processes: mixing of the components in forming a solution, and the change in conformation of the macromolecules in their interaction with the solvent. Tager [1] deals with these changes in entropy as combinatorial entropy of mixing (Sc), which is always positive, and noncombinatorial entropy of mixing Snc. The total entropy of mixing is the sum of the two contributions:

$$ \Delta S=\Delta {S}_{\mathrm{c}}+\Delta {S}_{\mathrm{nc}} $$
(17)

and can be both positive and negative.

Let us express the entropy in terms of the internal pressure l. Under equilibrium conditions

$$ dS=\left(\updelta Q/T\right);\updelta Q= TdS. $$
(18)

Let us substitute l into Eq. (8) for T = const, then

$$ dS/d{V}_{\mathrm{T}}\Big)=l/T. $$
(19)

Let us use the relations obtained for transformation of Eq. (16):

$$ d\Delta U= Td\left(\Delta {S}_{\mathrm{c}}+\Delta {S}_{\mathrm{nc}}\right)- pdV-{l}_e dV+ RT\ln {a}_1d{m}_1, $$
(20)

let us divide all terms in the equation by dV:

$$ {\displaystyle \begin{array}{l}d\left(\Delta U\right)/ dV= Td\left(\Delta {S}_{\mathrm{c}}+\Delta {S}_{\mathrm{nc}}\right)/ dV-P-{l}_e+ RT\ln {\overline{a}}_1\left(d{m}_1/ dV\right),\\ {}\kern5em {\left( dS/ dV\right)}_T=l/T;{\left( dV/d{m}_1\right)}_{T.{m}_2}=\overline{V_1};\\ {}\kern8em \left( RT\ln {\overline{a}}_1\right)/{\overline{V}}_1=-{\prod}^{\hbox{'}},\end{array}} $$

then

$$ \Delta l=l-{l}_0={l}_{\mathrm{c}}+{l}_{\mathrm{nc}}-P-{l}_{\mathrm{c}}-{\varPi}^{\hbox{'}}. $$
(21)

Thus the change in the internal pressure, which should be called the swelling pressure of the polymer, is connected with the particular details of the change in conformation of the chains, if we neglect P << l, and Eq. (1) in sorption from the LMW phase (a1= 1) reflects only part of this phenomenon. In special cases of linear uncrosslinked amorphous polymers undergoing unlimited swelling in the solvent as a1 → 1 (dilute solution), the swelling pressure Π → 0 in accordance with Eq. (1): ( lc + lnc – le = 0).

For chemically and physically (crystallites and other units) crosslinked polymers undergoing limited swelling, the terms in Eq. (21) lc, lnc, le can have a substantial effect on the swelling pressure both in the vapor phase and in the liquid phase of the LMW. Considerable attention has been focused on the swelling pressure of a polymer in solutions of the LMW in neutral gels [9, 13] and polyelectrolyte gels [5-8, 14-16 and others], in this case in Eq. (21) we need to introduce an ionic component. Then the swelling pressure is defined as

$$ \varPi ={\varPi}_{\mathrm{os}}+{\varPi}_{\mathrm{el}}+{\varPi}_{\mathrm{i}} $$
(22)

where Πos, the osmotic component (the name used in the theory of polyelectrolyte hydrogels), reflects the polymer –solvent interaction, and is usually determined using the Flory – Rehner or Flory – Huggins equation; Πel is the plastic component, connected with deformation of the chains in the network and their conformational properties; Πi, the ionic component due to the different concentrations of ions in solution and in the polymer phase, is usually calculated from the van’t Hoff equation. Πel is calculated using different equations [3, 4, 15, 16 and others]. We should point out that the measurements and calculations in the papers cited above on ion exchange were done in solutions and for a very high degree of swelling of gels [4]. Thus for a degree of swelling of the polymer equal to tens and hundreds of mL H2O/mL polymer, all three components of Eq. (22) have comparable values [11, 15].

Glassy polymer materials are also used in both the liquid and the vapor phase, and also in the form of composites, where the “guest” and “host” should have close swelling pressures to avoid failure of the composite. Many polymers typically have a transition from the initial glassy state under the influence of the medium during absorption to a rubbery state [22,23,24]. In this case, the conformations of the macromolecules and le change according to laws far from those for gels strongly swelling in solutions [3]. Comparing Eqs. (21) and (22), we see that in the absence of ion exchange

$$ {\prod}_{\mathrm{e}\mathrm{l}}={l}_{\mathrm{c}}+{l}_{\mathrm{nc}}-{l}_{\mathrm{e}};{\prod}^{\hbox{'}}={\prod}_{\mathrm{os}};\Delta l={\prod}_{\mathrm{e}\mathrm{l}}+{\prod}_{\mathrm{os}}, $$
(23)

where Πos is usually calculated from Eq. (1); Πel can changes its sign depending on the contributions of the entropic internal pressures and the pressure due to internal stresses in the polymer during swelling .

The limitations of Eq. (1) for crosslinked polymers (Π = 0 for relative water vapor pressure h = P/P0 = 1) forced us to look for a way to estimate the swelling pressure in such systems. Gregor and Glueckauf proposed a clear and wellsubstantiated solution [25, 26]. The method we developed can be called a comparison method, where as the reference object for a real crosslinked polymer we selected a polymer of identical nature and identical composition, but with a minimum number of crosslinks, the swelling pressure in which can be assumed to be close to zero for all values of the equilibrium relative pressure in the vapor phase of the absorbent water. Experimental data are given in [5] as absorption isotherms for absorption of water vapor by network sulfonated polystyrene (H+ form) with different numbers of crosslinks created by divinylbenzene (DVB), ranging from 0.25% to 24% DVB. In fact, it is difficult to assume that these polymer samples, when transferred into liquid water (h = 1), according to Eq. (1) (a1 = 1) should have identical swelling pressure Π → 0. In this case, the crosslinks play the role of powerful springs (see Fig. 1) [the component Πel in Eq. (23)] which limit the increase in water content (W) in the polymer.

The Gregor and Glueckauf method has been discussed in detail in [5, 6]. For two ion exchanger samples, Gregor and Glueckauf write the equilibrium conditions as

$$ {\varPi}_x\overline{V_1}= RT\ln {h}_x- RT\ln {\overline{a}}_x; $$
(24)
$$ {\varPi}_0{\overline{V}}_1= RT\ln {h}_0- RT\ln {\overline{a}}_0, $$
(25)

where the subscript x refers to the sample under study, while the subscript 0 refers to the reference sample; \( {\overline{a}}_1 \) ,\( {\overline{a}}_0 \) is the activity of water in the polymer for relative humidity of the medium respectively equal to hx = Px/P and h0 = P0/P, P is the saturated vapor pressure, or the standard pressure P = 1 atm.

Assuming a partial molar volume of water \( \overline{V_1} \)not depending on the activity of water in the polymer and equal to the molar volume of water \( {V}_1^0 \), and a swelling pressure in the reference sample (0.25% DVB) equal to Π0 = 0, the authors obtained:

$$ {\varPi}_x=\frac{RT\ln {h}_x/{h}_0}{V_1^0}. $$
(26)

The calculation results for crosslinked polymers showed that the swelling pressure in the liquid phase is approximately proportional to the degree of crosslinking of the macromolecules, and is hundreds of atmospheres.

However, the initial convex parts of the water vapor absorption isotherms for all the samples coincided, i.e., the swelling pressure in this region does not depend on the degree of crosslinking of the chains. In this region, the polymer is found in the glassy state, and interaction of water molecules occurs with active groups of the macromolecules within the free volume of the polymer, which cannot increase the entropy of the process but rather decreases it, since it is accompanied by formation of additional bonds between the macromolecules [22, 27] and ordering of the polymer structure. But according to Eq. (26), in this region hx = h0 and Π′ = 0, but Πos, calculated according to Eq. (1), for example for h = 0.6, is equal to Πos = 690 atm. Probably the considered method reflects only the term Πel in the swelling pressure (23) and only in the region of the rubbery state for the polymer. The advantages and a critique of the Gregor and Glueckauf method are given in [5,6,7].

From a thermodynamic and practical standpoint, in the analyzed model there is “arbitrariness” in selection of the reference object: first of all, a sample cannot be synthesized for all crosslinked polymers that has minimal degree of crosslinking of the chains; and secondly, even such an object, if it retains its physical shape, then has a swelling pressure different from zero. Therefore the values obtained for Πx to a significant extent are qualitative in nature, even though they are very important and a meaningful estimate for swelling phenomena.

We can somewhat improve this method by using the conventional comparison method in thermodynamics. As a characteristic of nonideal systems, typically we use a comparison system with a thermodynamically ideal system, for example the method of excess quantities [28]. Thus for the excess internal energy UE, this is the difference between the internal energy of mixing for the components UM for the real solution and the value of this function for an ideal solution:

$$ {U}^E={U}^M-{U}^{M, id}, $$
(27)
$$ {U}^M={U}^E+{U}^{M, id}, $$
(28)

Let us differentiate this function with respect to volume for T = const. Then, taking into account Eq. (8), we obtain:

$$ {p}^M={p}^E+{p}^{M, id}. $$
(29)

Thus the change in the internal pressure during formation of the solution (this is essentially the swelling pressure) is a combination of the excess pressure PE and the obligatory ideal mixing of the components PM, id. To a rough approximation, let us assume that PE is equal to Πel, while

$$ {p}^{M, id}={\varPi}_{\mathrm{os}}=\left(- RT\ln h\right)/{V}_i^0, $$
(30)

In order to determine Πel, let us represent a solid solution of the LMW in the polymer as an ideal solution, i.e., following Raoult’s law

$$ {p}_1^{id}={p}_1^0{x}_1{h}^{id}={x}_1 $$
(31)

ssure equal to zero. Then, using the Gregor and Glueckauf method, we obtain:

$$ {\varPi}_{el}=\left(- RT\ln {h}_x/{h}^{id}\right)/{V}_i^0, $$
(32)

where the determinations are made for constant mole fraction of the LMW (below, this is water), for the calculation of which we replace the molecular weight of the polymer (here and below) with the molecular weight of a unit of the polymer. Fig. 2 shows the swelling isotherms in h(xi) coordinates; the diagonal corresponds to Raoult’s law.

Fig. 2
figure 2

Isotherms (T = 298 K) for swelling of the amorphous regions in cellulose (1), poly(para-amide) (2), and polyamide (5) fibers, sulfonated polystyrene (PS) with 0.25% (3) and 16% (4) DVB crosslinks. Dashed line: Raoult’s law.

Full size image

As we see from Fig. 2, the absorption isotherm for absorption of H2O by a sample of polystyrene (PS) with 0.25% DVB is found practically entirely in the negative region relative to Raoult’s law; 16% crosslinks take the final part of the isotherm into the positive region. Accordingly, in the initial region of the isotherms, the “springs” prevent swelling of the polymer, while in the final region, when the polymer goes to a rubbery state, the springs so to speak “try” to increase os and swelling of the polymer. The results of the calculations are given in Table 2, where

Table 2. Components of the Swelling Pressure Π(atm) (osmotic Πos, elastic Πel) for Relative Pressure h for Polystyrene Polymers (PS) and Cellulose Materials (C)
Full size table
$$ \varPi ={\varPi}_{\mathrm{os}}+{\varPi}_{\mathrm{el}} $$
(33)

The calculations using Eq. (33) repeat the behavior found by Gregor and Glueckauf, but are found at a somewhat lower level. Of course, the two numbers are arbitrary, but the latter method does not require looking for a sample of a “freely” swelling polymer analogous to the sample under study.

Partially crystalline polymers can also be considered as “crosslinked”, where the “units” of the network are crystallites, including some of the tie chains [22]. However ,they have a number of peculiarities. Thus the absorption of water (Wam) by the analog of the polymer (relative to chemical structure) with degree of crystallinity xc = 0 can be calculated by the van Krevelen method [29], or approximately calculated using the equation

$$ {W}_{\mathrm{am}}=W/\left(1-{x}_{\mathrm{c}}\right), $$
(34)

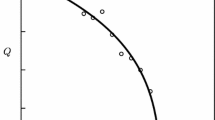
since absorption of water in partially crystalline polymers (W) occurs only in amorphous regions of the polymer. For example, in Figs. 3 and 4, we give the absorption isotherms for absorption of water by cellulose materials with degree of crystallinity 70% and 42% and by the amorphous analog starch (xc = 0), and also calculated by the van Krevelen method and using Eq. (34).

Fig. 3
figure 3

Isotherms for sorption of water (a) by starch (1), by cotton cellulose for xC = 70% (2), viscose rayon fiber for xC = 42% (3), calculated for cellulose by the van Krevelen method (4). Sorption of water in amorphous regions of a second (5) and third (6) polymer respectively. Change in volume of viscose rayon cord fiber (b) [22].

Full size image
Fig. 4
figure 4

Isotherms for sorption of water (303 K) by poly(para-amide) fibers: 1) freshly spun; 2) heat-treated and thermally drawn; 3) recalculated for the amorphous part of the latter.

Full size image

As we can see, in starch on absorption of water the “physical units” are preserved and the isotherm is found somewhat below the isotherm calculated from Eq. (34) for the amorphous analog. The latter practically agreed with calculations by the van Krevelen method and from Eq. (34) for samples with degree of crystallinity 70% and 42%. Similar results are shown in Fig. 4 for poly(para-aramid) fibers [30], and also are characteristic for linear polyamide fibers [31]. That is, the amorphous regions of such polymers to some extent retain their supermolecular structure, regardless of the degree of crystallinity.

Thus the swelling pressure in the amorphous regions of the polymer does not depend on the degree of crystallinity xc and can be determined from the absorption isotherm of the amorphous analog. Fig. 2 shows the recalculated absorption isotherms for water (W, g/g) in amorphous regions of the polymer vs. mole fractions of water. As we see, as for network polystyrene, the initial absorption region (in which the polymer is found in the glassy state) corresponds to negative deviations from Raoult’s law. Here the “spring force” is enhanced, since “water molecules at a temperature below the glass transition temperature act as very short cross bridges, damping even local forms of molecular motion in amorphous regions” [32]. For a linear polyamide, this region is significantly smaller than for cellulose and stiff para-aramid chains, since Capron and Anid begin transition to the rubbery state for very low moisture content in the fiber [33]. The calculation results for the swelling pressure for cellulose materials (for poly(paraaramids, the results are similar) are presented in Table 2. The elastic component is negative until h = 0.7, which corresponds to the convex part of the absorption isotherm and the glassy state of the polymer. This should lead not to an increase in the volume of the polymer, but rather to its compression, which is supported by the data shown in Fig. 3b. From [22]: “the increase in the polymer density as water vapor is absorbed is due to the increase in the degree of ordering of the molecular chains,” which was noted a little above relative to water in linear polyamides [32]. For a moisture content in the polymer above the inflection region of the absorption isotherm, its transition begins to the rubbery state, and Πel increases the swell pressure compared with Πos = –(RTlnh)V10. For relative humidity h = 1 and transfer of the polymer to the liquid absorbate Πos = 0, but according to Eq. (33), for hx = 1, hid < 1 (for xi = const) and Πel is tens and hundreds of atmospheres (see Table 2).

Thus the conventional thermodynamic relation in the form of Eq. (1) reflects only part of the complex swelling process, especially for glassy, partially crystalline polymers. The second part of the phenomenon is connected with the state of the macromolecules and their noncombinatorial interaction with solvent molecules, especially with polar water molecules providing hydrogen bonds. The method proposed here for analysis of the components of the swelling pressure lets us explain the mechanism for interaction of partially crystalline polar polymers with water and to roughly calculate the actual swelling pressure.