The ABC mechanism: an incentive compatible payoff mechanism for elicitation of outcome and probability transformations

Abstract

When it comes to experiments with multiple-round decisions under risk, the current payoff mechanisms are incentive compatible with either outcome weighting theories or probability weighting theories, but not both. In this paper, I introduce a new payoff mechanism, the Accumulative Best Choice (“ABC”) mechanism that is incentive compatible for all rational risk preferences. I also identify three necessary and sufficient conditions for a payoff mechanism to be incentive compatible for all models of decision under risk with complete and transitive preferences. I show that ABC is the unique incentive compatible mechanism for rational risk preferences in a multiple-task setting. In addition, I test empirical validity of the ABC mechanism in the lab. The results from both a choice pattern experiment and a preference (structural) estimation experiment show that individual choices under the ABC mechanism are statistically not different from those observed with the one-round task experimental design. The ABC mechanism supports unbiased elicitation of both outcome and probability transformations as well as testing alternative decision models that do or do not include the independence axiom.

1 Introduction

Archer is recruited as a human subject to participate in an economic experiment. His job is to make choices in a series of tasks. His primary concern is how much he gets paid. If Archer is told he will earn $20 flat, he might go through the tasks as fast as possible without even reading the options. If Archer is told he will get paid for all his choices combined, he may construct a portfolio with all the decisions and optimize as he progresses. However, those are not what experimentalists want. We want subjects to reveal their preferences truthfully in every task. Archer’s “single-task preference” between options A and B refers to Archer’s ranking of the options revealed by his choice in a single-task setting; this has been called “true preference” in earlier literature (Starmer and Sugden 1991; Cubitt et al. 1998). How can we ensure Archer’s choices in a many-decisions setting are consistent with his “single-task preference” in each decision (also known as incentive compatibility)? We must find an incentive compatible payoff mechanism. Let us focus on experiments involving decision making under risk for now.

A universal solution is the one-round task design. That is, if we would like to know Archer’s “single-task preference” between A and B, we ask Archer to pick one from A and B and pay him his choice. It is the only known incentive compatible payoff mechanism (ICPM) for all risk theories. Therefore, choices under the one-round task design have served as the gold standard to test empirically the incentive compatibility of other mechanisms–whether choices under a certain mechanism are significantly different from those under the one task only. However, the drawback of one-round task design is that we only get one data point from each subject, which would be insufficient if we want to test, say, the Allais Paradox. Another solution in practice is to randomly select one choice to pay each subject (also well-known as Random Lottery Incentive System, RLIS)¹. The rationale is that since any round could count as payment, Archer should treat every round seriously. However, with RLIS, we must assume that Archer’s preference satisfies independence axiom, as first discussed in Holt (1986) and Karni and Safra (1987). What if it does not?

There is no known ICPM with the multiple-round task setting when preferences are from rational domain (complete and transitive, otherwise unrestricted). That is the gap this paper addresses. An ICPM, Accumulative Best Choice (ABC) mechanism is proposed for all risk models representing complete and transitive preferences. Three necessary and sufficient conditions for the family of ICPM are identified through two propositions and the main theorem: ABC is the unique ICPM when no assumptions restrict subjects’ anticipation about the future. The validity of ABC–individual choices or the estimates of their risk attitude parameters under the one-round task design are statistically the same as under the ABC mechanism–is tested via lab experiments: The results from two experiments fail to reject such hypothesis at 5% significance level.

Risk theories representing rational preferences include expected utility theory (EUT) [initially proposed by Bernoulli, and axiomatized by von Neumann and Morgenstern (1944)], dual expected utility theory (DT) (Yaari 1987), rank dependent utility theory (RDU) (Quiggin 1982) and cumulative prospect theory (CPT) (Tversky and Kahneman 1992)². Models allowing violation of transitivity are beyond the scope of this work, such as prospect theory with endogenous reference point (Schmidt et al. 2008) or reference-dependent utility theory (Kőszegi and Rabin 2006), regret theory (Bell 1982; Loomes and Sugden 1982) and disappointment aversion (Bell 1985; Gul 1991)³.

2 Accumulative best choice (ABC) mechanism

ABC operates in (0) an n-round sequential choice task where the set of options is fixed and predetermined, with the following conditions:

• (1) Every subject gets paid the realized outcome of their last choice;

• (2) For each but the last round, subject’s current choice carries over to become one accessible option in the next round;

• (3) Each subject does not know the new options they will face in future rounds.

At the beginning of the experiments, subjects are informed of (0)(1)(2)(3).

The following elaborates the ABC mechanism with minimal notations: The experiment is an n-round individual decision task. Suppose there is a general lottery set ${\mathscr {L}}$. For Round $i (i=1,\ldots ,n)$, decision task consists of choosing from some subset $D_i$ of ${\mathscr {L}}$. The set of lotteries subject encounters in the whole experiment, ${\mathscr {L}}_0=\{l:l\in \cup _{i=1,\ldots ,n}D_i\}$, is fixed and predetermined. Let $c_i$ denote individual choice in Round i, that is, $c_i\in D_i$.

ABC works as follows with Archer as our example subject:

Round 1: Decision 1 ($D_1$): Archer makes a choice, $c_1$, from set $D_1=T_1$, where $T_1\in {\mathscr {L}}$ is determined by the experimenter. Archer only knows lotteries in $D_1$;

Round 2: Decision 2 ($D_2$): Archer makes a choice, $c_2$, from set $D_2=T_2\cup \{c_1\}$, where $T_2\in {\mathscr {L}}$ is determined by the experimenter. Archer only knows lotteries in $D_1, D_2$;

...

Round i: Decision i ($D_{i}$): Archer makes a choice, $c_{i}$, from set $D_{i}=T_{i}\cup \{c_{i-1}\}$, where $T_{i}\in {\mathscr {L}}$ is determined by the experimenter and $c_{i-1}$ is Archer’s choice in Round $i-1$. Archer only knows lotteries in $D_1, D_2, \ldots , D_{i}$;

...

Round n: Decision n ($D_n$): Archer makes a choice, $c_n$, from set $D_n=T_n\cup \{c_{n-1}\}$, with $T_n$ being chosen by the experimenter.

Payment: Archer gets paid the realized outcome of $c_n$.

Before making any decisions, Archer is informed of: n (the number of rounds of decisions); that the set of lotteries in the whole experiment, ${\mathscr {L}}_0=\{l:l\in \cup _{i=1,\ldots ,n} T_i\}$, is fixed and predetermined but not what the specific lotteries are; the carry-over task structure (his preceding decision carries over to the next round to become one of the options in the task); that he will get paid the realized outcome of the last choice $c_n$.

At every round, ABC incentivizes Archer to reveal his single-task preference. Suppose at some arbitrary round, Archer prefers lottery A to lottery B, but contemplates choosing B instead of A (not stating the single-task preference). Since he does not know the lottery options he has not met, two possible situations await him : (i) the best lottery in the future is weakly better than A; (ii) the best lottery in the future is worse than A. For (i), as long as Archer picks the best lottery and keeps it to the end, he will get paid that lottery. In this scenario, choosing A or B, sticking to or deviating from truthful revelation, makes no difference for Archer. For (ii), if all the lotteries in the future are worse than A, then no matter how Archer chooses, he will end up with some lottery less favorable than A. However, if he chooses A, he can keep and get paid A. In scenario (ii), Archer is worse off by deviating from the always truthfully revealing strategy. In all, with ABC as the payoff mechanism, always stating single-task preference in every round is Archer’s only weakly dominant strategy. The following example illustrates such an idea:

Example 1

Let ${\mathscr {L}}_0=\{A,B,E\}$ where $A,B,E\in {\mathscr {L}}$. Suppose there is a 2-round decision task with ABC: $T_1=\{A,B\}$ and $T_2=\{E\}$. Before making any choices, Archer knows: $n=2$; ${\mathscr {L}}_0=\{l:l\in T_1\cup T_2\}$ is fixed and predetermined but does not know A, B, E specifically; the carry-over task structure, $c_1\in D_2$; he will be paid the realized outcome of $c_2$. Suppose that the Archer’s preference is: $A\succ B\succ E$. Let’s consider two scenarios:

(1) Truthful revelation⁴:

Choice set $D_1=T_1=\{A, B\}$, Archer chooses A, $c_1=A$;

Choice set $D_2=T_2\cup \{c_1\}=\{E,A\}$, Archer chooses A, $c_2=A$.

Archer gets paid according to A.

(2) Misrepresentation:

Choice set $D_1=T_1=\{A, B\}$, Archer chooses B, $c_1=B$;

Choice set $D_2=T_2\cup \{c_1\}=\{E, B\}$, Archer chooses B, $c_2=B$.

Archer gets paid according to B, which is worse than the result with truthful revelation.

Besides the theoretical incentive compatibility, ABC has another appealing feature on the practical side: It is easy to explain. The intuition with ABC is some form of a tournament: Individuals eliminate the loser options, carry on their current champion option, and eventually get paid their final champion option. It is easy for subjects to understand the procedure as well as why truthful revelation is their best strategy.

3 Recent related literature

Holt (1986) and Karni and Safra (1987) are the first to discuss the incentive compatibility issue with payoff mechanisms, more specifically, RLIS. Another wave of discussion has arisen recently. There are four closely related research streams that provide theoretical and empirical bases for this research: Cox et al. (2015), Harrison and Swarthout (2014), and Azrieli et al. (2018, 2020). The following explores each.

In Cox et al. (2015), the authors examine RLIS and several other payoff mechanisms commonly used in experiments. They use five binary lottery decisions to compare subjects’ choices (proportion of choosing safer/riskier lotteries) under different mechanisms. The lottery pairs are also for detecting violations of independence axiom and its dual axiom by directly checking choice patterns in certain pairs of those five binary lotteries.

Their findings indicate that individual behavior is significantly affected by payoff mechanisms (Table 4 in Cox et al. 2015). By comparing the choices with the gold standard, the one-round task design, they show that both theoretically and behaviorally, the payoff mechanism issue does not exist with only RLIS, but does with almost all the popular payoff mechanisms. They left a remaining important question unaddressed: Other than the one-round task design, what payoff mechanism is incentive compatible for multiple popular theories which do or do not involve the independence axiom? The present paper addresses this question for a class of experimental designs.

Cox et al. (2015) distinguish between two different implementations of RLIS: With or without prior information. “With no prior information” implementation subjects are only informed of the lotteries in the past and the current rounds, whereas “with prior information” implementation subjects know all lotteries in the experiment before they make any decisions. This paper demonstrates the information property is crucial in constructing an incentive compatible payoff mechanism (for example, see (3) in the ABC mechanism described above). For replicability, the Cox et al. (2015) experiment using the ABC mechanism is conducted.

Rather than a choice-pattern experiment, Harrison and Swarthout (2014) conduct a risk preference estimation experiment–relying on econometric technique to estimate the risk preference parameters and treatment dummies. They report that estimates in the RLIS treatment differ from those in the one-round task treatment when RDU is assumed. The current paper “replicates” the (Harrison and Swarthout 2014) experiment with the same lottery set as well as the same analysis technique to compare the choices under ABC with those under the one-round task design.

Azrieli et al. (2018) provide a general theoretical framework for the analysis of payoff mechanisms. They conclude that, in a multiple-round experiment, RLIS (or RPS, in their terms) is the only ICPM with the assumption of a weaker version of independence, which they call “monotonicity” in the paper.⁵ In a follow-up article, Azrieli et al. (2020) focus more on the objective lotteries as the choice objects. The authors show that ICPMs can be extended beyond RLIS when all tasks are exogenously given and subjects’ preferences satisfy: (a) monotonicity or compound independence, as in Azrieli et al. (2018), (b) first-order stochastic dominance; (c) not transforming the objective probabilities associated with the random device that determines the payment objects.

Unlike Azrieli et al. (2018, 2020), none of the above assumptions restricts the preferences domain in the theoretical framework in the current paper. Preferences are limited to rationality (completeness and transitivity) only. On the other hand, instead of fixing all options in every round, in this paper only the set of options subjects see in the whole experiment is fixed. Next section argues that forgoing the full exogenous task order and connecting the tasks through individual choices (for example, as (2) in the ABC mechanism) is one necessary condition for ICPM with all rational preferences. In summary, comparing the settings, Azrieli et al. (2018, 2020) impose more assumptions on the preferences while this paper relinquishes exogenous control of the task structure. Restricting on the exogenously fixed order of decision tasks, the only ICPM with all rational preferences is the one-round task design. The existence of ICPM with multiple tasks requires additional assumptions on preferences, such as “monotonicity” or “compound independence” [See Proposition 0 and 1 in Azrieli et al. (2018)]. Such restriction on the full exogenous task order precludes the possibility of the existence of the mechanism developed in this paper.

4 Necessary and sufficient conditions for incentive compatible payoff mechanisms

Section 2 explained why ABC is incentive compatible under a multiple-round decision task. It is natural to ask: In an individual experiment where subjects are required to make more than one decision, is ABC the unique ICPM? If not, what are the necessary and sufficient conditions for ICPMs? This section provides answers to those questions.

4.1 Theoretical framework

The formal theoretical framework is set up as the following:

The experiment is an n-round individual decision making task. Suppose there is a general lottery set ${\mathscr {L}}$ including all the simple and compound lotteries and for Round $i (i=1,\ldots ,n)$, decision task is $D_i$, where $D_i\subset {\mathscr {L}}$. ${\mathscr {L}}_0=\{l:l\in \cup _{i=1,\ldots ,n}D_i\}$ is fixed and predetermined.

Choices Individual decisions are recorded as ${\mathbf {c}}=(c_1,\ldots ,c_n)$ where $c_i\in D_i,\forall i=1,\ldots ,n$.

Task structure Denote $D=(D_1,\ldots ,D_n)$ as the n-round task structure. If $D_i (i=1,\ldots ,n)$ are completely exogenously determined by the experimenter, it is our conventional n-round decision task under risk as in the literature. I relax the assumption by allowing $D_i (i>1)$ to be dependent on subject’s previous choices $c_1,\cdots ,c_{i-1}$.

Rational risk preference (relation) Each individual has a rational preference relation $\succeq$ over ${\mathscr {L}}$ if $\succeq$ is complete and transitive: (1) Completeness: $\forall X, Y\in {\mathscr {L}}$, $X\succeq Y$ or $Y\succeq X$ or both; (2) Transitivity: $\forall X, Y, Z\in {\mathscr {L}}$, if $X\succeq Y, Y\succeq Z$, then $X\succeq Z$. $\{\succeq \}$ is the set including all rational preferences.

General risk theories Denote $U_{\succeq }(\cdot ): {\mathscr {L}}\rightarrow {\mathbb {R}}$ as a utility representation for the complete and transitive risk preference $\succeq$ over the domain of ${\mathscr {L}}$. That is, $\forall X,Y\in {\mathscr {L}}, X\succeq Y$ if and only if $U_{\succeq }(X)\ge U_{\succeq }(Y)$. General risk theories refer to $\{U_{\succeq }(\cdot )\}$, the set of all possible utility representations for all rational preferences.

Information (over the lottery options) At Round i, individual information set of the known lotteries is denoted as $I_i$. $\{l: \forall l\in D_k, k=1,\ldots ,i\}\subset I_i\subset {\mathscr {L}}_0, i=1,\ldots ,n$ and $I_n={\mathscr {L}}_0$ since each subject knows the lotteries they met in earlier and current rounds. Denote $I=(I_1,\ldots ,I_n)$ as the information structure of the experiment.

Payoff rule and Payoff prospect A payoff rule specifies the rule to select the paying round(s). Denote ${\mathscr {N}}=\{1,\ldots ,n\}$, and we use the power set $2^{\mathscr {N}}$ to represent all the possible paying events: $\forall X\in 2^{\mathscr {N}}$, if $i\in X$, then we can interpret it as Round i or $c_i$ is paid; if $i\notin X$, Round i or $c_i$ is not paid. A payoff rule is a probability measure ${\mathbb {P}}$ over the sample space of $2^{\mathscr {N}}$.⁶ In experiments, such probability measure or payoff rule is chosen by the experimenter.

Payoff prospect, $P(c_1,\ldots ,c_n)$, refers to the grand lottery describing subject’s payment, indicated by the payoff rule ${\mathbb {P}}$ and subject’s choices ${\mathbf {c}}$.

Here are some examples with Archer, our representative subject, that show the relationship between some commonly used payoff rules ${\mathbb {P}}$ and the payoff prospects $P(c_1,\ldots ,c_n)$ that identify subject’s payments.

Example 2

• (1) Flat-payment scheme: if the experimenter informs Archer before he makes any decisions that he will get paid $10 in total regardless of what he chooses ($10 with certainty as a lottery itself may not appear in the decision problems at all), then we could treat such scheme as a payment to none of Archer’s choices. Such payoff rule, the probability measure over $2^{\mathscr {N}}$ is represented as: ${\mathbb {P}}(\emptyset )=1, {\mathbb {P}}_{X\in 2^{\mathscr {N}}\backslash \emptyset }(X)=0$, resulting in $P(c_1,\ldots ,c_n)=\$10$.

• (2) Pay all scheme: If Archer gets paid all of his choices, then ${\mathbb {P}}(\{1,\ldots ,n\})=1,{\mathbb {P}}_{X\in 2^{\mathscr {N}}\backslash \{1,\ldots ,n\}}(X)=0$, and $P(c_1,\ldots ,c_n)=c_1+\cdots +c_n$.

• (3) Pay one round scheme: (i) Pay Round i with certainty. If the experimenter pays Archer only his choice in Round i, that is, ${\mathbb {P}}(\{i\})=1, {\mathbb {P}}_{X\in 2^{\mathscr {N}}\backslash \{i\}}(X)=0$, then $P(c_1,\ldots ,c_n)=c_i$. (ii) Pay one random round. RLIS is ${\mathbb {P}}(\{1\})=\cdots ={\mathbb {P}}(\{n\})=1/n, {\mathbb {P}}(X)=0,\forall X\in 2^{\mathscr {N}}\backslash \{1\}\{2\}\ldots \{n\}$. Then, $P(c_1,\ldots ,c_n)=(c_1,1/n;\ldots ;c_n,1/n)$. That is, only the realized outcome of one random choice lottery from all rounds is paid.

• (4) Pay multiple random rounds scheme: One example of a more complicated payoff rule is to randomly select multiple rounds to pay (Charness and Rabin 2002). Take randomly selecting 3 rounds to pay as an example: It can be represented as ${\mathbb {P}}(\{i,j,k\})=1/(^n_3), {\mathbb {P}}_{X\in 2^{\mathscr {N}}\backslash \{i,j,k\}}(X)=0, \forall i\ne j\ne k$, thus, $P(c_1,\ldots ,c_n)=(c_i+c_j+c_k, 1/(^n_3))(i\ne j\ne k)$ where $(^n_3)$ is the 3-combinations from an n-element set, to represent the payoff prospect.

Payoff mechanism A payoff mechanism is defined as $(D,I,{\mathbb {P}})$ or $(D, I, P({\mathbf {c}}))$.⁷

Experiment A general n-round individual decision experiment is defined as $({\mathscr {L}}_0, D, I, {\mathbb {P}})$ (or (${\mathscr {L}}_0, D,I, P({\mathbf {c}})$)). For an experiment, each subject is informed of the payoff mechanism $(D, I,{\mathbb {P}})$⁸ as well as ${\mathscr {L}}_0$ being fixed and predetermined.

Subject’s optimization problem Given $D, I,{\mathbb {P}}$, by choosing ${\mathbf {c}}$, the subject tries to optimize the payoff prospect $P(c_1,\ldots ,c_n)$. That is, the subject chooses $(c^*_1,\ldots ,c^*_n)$ where $c_i^*\in D_i$, such that $P(c_1^*,\ldots ,c_n^*)\succeq P(c'_1,\ldots ,c'_n),\forall c'_i\in D_i, i=1,\ldots ,n$. Such optimization is constrained on D, I.

Note that there are no further assumptions on how individuals evaluate the payoff prospect $P(c_1,\ldots ,c_n)$ other than following completeness and transitivity. It is because we want to keep the domain of preferences unrestricted. However, there is an implicit assumption made here: realization of the random events and revelation of the results to subjects happen at the same time. It is not an issue for the experiments of decision tasks under risk, but matters for those under uncertainty (Baillon et al. 2014).

Now, we can define ABC formally.

Definition 1

(Accumulative Best Choice (ABC) mechanism) With an n-round decision making experiment $({\mathscr {L}}_0, D, I, {\mathbb {P}})$, ${\mathscr {L}}_0=\{l:l\in \cup _{i=1,\ldots ,n}D_i\}$ is fixed and predetermined for each subject, a payoff mechanism $(D,I,{\mathbb {P}})$ is called Accumulative Best Choice mechanism if it satisfies:

• 1. ${\mathbb {P}}(\{n\})=1,{\mathbb {P}}_{X\in 2^{\mathscr {N}}\backslash \{n\}}(X)=0$, that is, $P(c_1,\ldots ,c_n)=c_n$;

• 2. For every Round $i (i=1,\ldots ,n-1)$, $c_i\in D_{i+1}$;

• 3. For every Round $i (i=1,\ldots ,n)$, $I_i=\{l: \forall l\in D_k, k=1,\ldots ,i\}$.

Each subject is informed of all the above information about ABC before making any decisions.

Incentive compatibility and incentive compatible payoff mechanism can be defined as the following:

Definition 2

(Incentive Compatible (IC) and Incentive Compatible Payoff Mechanism (ICPM)) An experiment is $({\mathscr {L}}_0, D, I, {\mathbb {P}})$. A payoff mechanism $(D,I,{\mathbb {P}})$ is incentive compatible (IC) if, for any rational preference $\succeq$, for any $(c_1,\ldots , c_n)$ with $c_1 \in D_1, \ldots , c_n \in D_n$, we have $[P(c_1, \ldots , c_n)\succeq P(c'_1, \ldots , c'_n), \forall c'_i \in D_i, i=1,\ldots ,n] \Leftrightarrow [c_i\succeq c'_i, \forall c'_i\in D_i, i=1, \ldots ,n]$. We named such $(D,I,{\mathbb {P}})$ an incentive compatible payoff mechanism (ICPM).⁹

In words, IC means that optimal choices for the whole experiment are identical to optimal choices for the individual rounds separately. That is, truthful revelation in each round is the only weakly dominant strategy for the whole experiment.

Let us denote $S(A)=\{x:x\succeq y, \forall y\in A\}$ as the set of the most preferred option(s) of set A, and s(A) refers to an element, $s(A)\in S(A)$. We use $s^*_i$ to represent any arbitrary element in $S(D_i) (i=1,\ldots ,n)$. In Round i, choosing $s^*_i$ indicates subject truthfully reveals their single-task preference.

4.2 Main theoretical results

In this part, we identify three necessary and sufficient conditions for the family of ICPM via two propositions and the main theorem. Propositions 1 and 2 can be viewed as stepping stones to the main theorem: ABC is the unique ICPM. Please see appendices for formal proof. In this section, only informal arguments are provided.

Proposition 1

$(D,I,{\mathbb {P}})$ is an ICPM for general risk theories, if and only if it has the following three properties:

• 1. ${\mathbb {P}}(\{n\})=1,{\mathbb {P}}_{X\in 2^{\mathscr {N}}\backslash \{n\}}(X)=0$, that is, $P(c_1,\ldots ,c_n)=c_n$;

  [The realized outcome of the last choice is paid with certainty, and no other decision is paid.]

• 2. If $n>1$, $\forall i=1,\ldots ,n-1$, there exists a unique $k_i (i<k_i\le n)$, such that $c_i\in D_{k_i}$ ;

  [For every round before the last round, the current choice carries over as a selectable option in a later round.]

• 3. If $n>1$, $\forall i=1,\ldots ,n-1$, with subject’s previous choices are $s_1^*,\ldots ,s^*_{i-1}$, $\forall x\in I_i\backslash D_i$, and $x\in D_j (i<j\le n)$, then we need to have $s^*_i\succ x$ for all rational preferences.

  [Assume subject keeps truthfully revealing their single-task preference. If subject is ever aware of another option that will show up in a later round, that option needs to be strictly worse than their most preferred option from the current round.]

First, let us check the sufficiency side: if a payoff mechanism satisfies Properties 1, 2, and 3, then it is an ICPM.

Sufficiency: The following is to explain why truthful revelation in every round is the only weakly dominant strategy under such a payoff mechanism that satisfies Properties 1, 2, and 3. Let us still take Archer as our example subject. First, from Properties 1 and 2, since the whole experiment is a chained sequence, if Archer always declares his favorite option in every round, eventually he gets paid the most preferred option in the whole experiment lottery set ${\mathscr {L}}_0$. Thus, truthful revelation weakly dominates all other strategies. Then, let us see what happens if Archer deviates from truthful revelation. Suppose Archer first misreports at Round k and his favorite lottery in Round k is, say, lottery Z. Since he truthfully reports in all previous rounds, if there is any other future lottery Archer has known, from Property 3, lottery Z is strictly better than that. Consider the possible scenario that all the lotteries Archer meets in the future are worse than Z. From Properties 1 and 2, Archer eventually gets paid his last choice, which is worse than Z. He could have obtained Z by choosing Z in Round k and kept it to the end. Therefore, Archer may regret it if deviating from truthful revelation.

Let us now turn to the necessity of ICPM. Each property is explored separately below.

Necessity: Property 1: The realized outcome of the last choice is paid with certainty, and no other decision is paid.

Incentive compatibility for the last round is required if incentive compatibility for every round is desired. The former demands payment of the subject’s last choice. It is evident that if we tell Archer his last choice is paid, he will state his single-task preference in the last round. On the other hand, if we pay anything other than the realized outcome of the last choice, without further assumptions about Archer’s preference and accessible lotteries, the weighting over outcomes or probabilities (or both) may ruin IC.

Moreover, we can directly get the following corollary:

Corollary 1

When $n=1$, the only ICPM $(D,I,{\mathbb {P}})$ is ${\mathbb {P}}(\{1\})=1$ (or $P(c_1)=c_1), c_1\in D_1$.

The one-round task design is IC for general risk theories.

Necessity: Property 2: For every round before the last round, the current choice carries over as a selectable option in a later round.

This condition states that the whole experiment is a connected sequence. From Property 1, Archer knows only his last choice is paid, then how can we incentivize him to take earlier rounds seriously? A chained sequence of tasks provides such an incentive. If Archer knows his choices from the previous rounds can affect the paying round, then he should treat those nonpaying rounds carefully. Suppose there is some round that is not connected with later rounds. Archer then knows that no matter what he chooses in that round, the lottery options in the paying round will not be affected; he could pick randomly in that round. That ruins incentive compatibility.

What if a choice lottery is connected with multiple later rounds? Then again, it may lead to incentive incompatibility. Suppose in some earlier round, Archer’s choice is lottery X. Now it is the round where Archer first sees X carried over. If he knows X will appear again in the future even if he does not choose it now, picking another option rather than keeping X in the current round does not reduce his payout. If lottery X happens to be Archer’s most preferred option in the current round, then he is not incentivized to reveal truthfully. (Also see example in the appendices.)

What if a choice lottery “maybe” carries over to some later round? That possibility can create a new layer of risk and compound with the risks in the lottery options. In that case, either IC is compromised or we need more assumptions on the preferences. The following numerical example illustrates the point.

Example 3

There is a 2-round experiment with ${\mathscr {L}}_0=\{A_1,B_1,A_2\}$. $A_1=\$15, B_1=(\$49,0.5;\$0,0.5), A_2=\$14$. $D_1=\{A_1,B_1\}$, $D_2=\{A_2, {\text {50\% of }} c_1\}$ (whether $c_1\in D_2$ is determined by a random device after subject chooses $c_1$). That is, 50% chance $D_2=\{A_2\}$, and 50% chance $D_2=\{A_2, c_1\}$. ${\mathbb {P}}(\{2\})=1$ or $P(c_1,c_2)=c_2$. Subjects are informed of: the task structure, last choice being paid as well as ${\mathscr {L}}_0$ being fixed and predetermined.

Suppose Archer’s preference fits Rank Dependent Utility theory with $u(x)=\sqrt{x}$ and $w(p)=p^{0.9}$ and satisfies reduction of compound lottery axiom. Therefore, to Archer, $A_1\succ B_1\succ A_2$.

Two possible information structures:

• (1) Archer knows $A_2$ at Round 1: He will think ahead what he would face at Round 2: If he chooses $A_1$, 50% chance he will have $D_2=\{A_2, A_1\}$ and 50% chance he will have $D_2=\{A_2\}$. If the former, Archer will choose $A_1$ in Round 2 since $A_1\succ A_2$ and $P(c_1, c_2)=c_2$; if the latter, Archer will be paid the singleton $A_2$ without any choice need to be made in Round 2. So by choosing $A_1$ in Round 1, Archer faces a lottery of $(A_1, 0.5; A_2, 0.5)=(\$15, 0.5; \$14, 0.5)$ in terms of his final payment. Similarly, by choosing $B_1$ in Round 1, Archer constructs a lottery of $(B_1, 0.5; A_2, 0.5)=((\$49,0.5;\$0,0.5),0.5; \$14,0.5)=(\$49, 0.25; \$14, 0.5;\$0, 0.25)$ by applying reduction axiom. We can verify that $RDU(B_1, 0.5; A_2, 0.5)>RDU(A_1,0.5;A_2,0.5)$. That is, Archer will choose $B_1$ in Round 1 despite of $A_1\succ B_1$, which violates IC.

• (2) Archer does not know $A_2$ at Round 1: Notice that we do not have any restrictions on subject’s anticipation of the unknown future options. At Round 1, Archer may guess $A_2$ say, $(\$14,1)$, that can lead him to choose $B_1$ instead of $A_1$.

Remark 1

From the example above, readers may argue that the chance would be slim that Archer guesses the future correctly, which is a valid argument. However, the key is that in the current framework, there are no assumptions on individual beliefs about future options: they can guess as they want. Belief is hard to control in practice, and that is why we start with leaving it unrestricted in theory now. Regardless of how subjects speculate about the future, carry-over with certainty removes the possibility to construct a compound lottery from anticipation. If we assume that subjects do not guess the future options, as pointed out by one referee of this paper, we cannot pin down the carry-over probability to be 1.

The connected sequence feature also leads to a further conclusion that an ICPM should allow subject to choose their most preferred option in the whole experiment if they truthfully reveal their single-task preference in every round:

Corollary 2

If $(D, I,{\mathbb {P}})$ is an ICPM, then, for all rational preferences, with the strategy $s^*=(s^*_1,\ldots ,s^*_n)$, there must be $s^*_n\in S(\cup _{i=1,\ldots ,n}D_i)=S({\mathscr {L}}_0)$.

Necessity: Property 3: Assume subject keeps truthfully revealing their single-task preference. If subject is ever aware of another option that will show up in a later round, that option needs to be strictly worse than their most preferred option from the current round.

If this does not hold, IC cannot be guaranteed. For instance, at some round, suppose there is a future lottery Y that Archer has known. Y is not shown now, and it is weakly better than his favorite lottery in the current round. From Properties 1 and 2, Archer knows that he can carry and keep Y, and eventually get paid Y. That is, Archer can secure Y as his worst paid lottery. Given Y is weakly better than all the lotteries at present, Archer’s choice now does not matter to his final payment. Thus, he has no incentive to reveal his single-task preference in the current round.

From Property 3, we can get the following corollary:

Corollary 3

If a payoff mechanism $(D,I,{\mathbb {P}})$ has an information structure I with $I_1=\cdots =I_n={\mathscr {L}}_0$, with $n>1$, there is no existence of ICPM for general risk theories.

Hitherto, we see the condition stated in Proposition 1 from both necessary and sufficient sides for an ICPM. Without more restrictions on the preferences, we can get the following proposition:

Proposition 2

$(D,I,{\mathbb {P}})$ is an ICPM, if and only if it has the following four properties:

• 1. ${\mathbb {P}}(\{n\})=1,{\mathbb {P}}_{X\in 2^{\mathscr {N}}\backslash \{n\}}(X)=0$, that is, $P(c_1,\ldots ,c_n)=c_n$;

• 2. If $n>1$, for all $i=1,\ldots ,n-1$, there exists a unique $k_i(i<k_i\le n)$, such that $c_i\in D_{k_i}$;

• 3. For all $i=1,\ldots ,n$, $I_i=\{l:\forall l\in D_k, k=1,\ldots ,i\}$;

  [Each subject is only informed of the options in the past and the current rounds.]

• 4. For all $i=1,\ldots ,n$, if the subject’s previous choices are $s^*_1,\ldots ,s^*_{i-1}$, then $s^*_i\succeq s^*_{i-1}\succeq \ldots \succeq s^*_1$ for all rational preferences.

  [For each round, if the subject keeps revealing truthfully, their favorite lottery in a later round needs to be always weakly better than any lottery in any earlier round.]

Properties 1 and 2 are the same in Proposition 2 as in Proposition 1. Given those two properties, the formal proof of equivalence between Property 3 in Proposition 1 and Properties 3 and 4 in Proposition 2 is provided in the appendices. From Proposition 2, we can pin down the uniqueness of the ABC mechanism:

Theorem

(Uniqueness of ABC) With no more assumptions on the preferences or beliefs about future options, the ABC mechanism is the only ICPM for all general risk theories with rational preferences.

First, ABC meets all four properties in Proposition 2. Therefore, ABC is an ICPM. On the other hand, suppose there exists some Round k, $c_k\notin D_{k+1}$. With no restrictions on the rational preferences domain, we can pick an arbitrary complete and transitive preference that has $s^*_k\succ s^*_{k+1}$, then Property 4 in Proposition 2 is violated. Therefore, $c_i\in D_{i+1}$ is the only way of chaining to satisfy Property 4 in Proposition 2.

Remark 2

It should be noted that with more assumptions over preferences, Propositions 1 and 2 are not always equivalent, and the uniqueness of ABC may not hold. Here is an example that shows why the specific ABC way of sequencing is not necessary in some cases with rational preferences having first-order stochastic dominance.¹⁰

Example 4

There is a 4-round experiment. Lotteries are ${\mathscr {L}}_0=\{A_1, B_1, A_2, B_2, A_3, B_3, E\}$ and there is strict first-order stochastic dominance relations between them: $A_3, B_3$ strictly dominate $A_2, B_2$, and $A_2, B_2$ strictly dominate $A_1, B_1$, and $A_1, B_1, A_2, B_2, A_3, B_3$ strictly dominate E. Use $c_i, i=1,2,3,4$ to record subjects’ choices. An ICPM $(D,I,{\mathbb {P}})$ that is not ABC is: (1) ${\mathbb {P}}(\{4\})=1,{\mathbb {P}}_{X\in 2^{\mathscr {N}}\backslash \{4\}}(X)=0$ or $P(c_1,\ldots ,c_4)=c_4$; (2) $D_i=\{A_i, B_i\}$ for $i=1,2,3$, and $D_4=\{c_1,c_2,c_3, E\}$; (3) At Round $i=1,2,3,4$, $I_i=\{l: \forall l\in D_k, k=1,\ldots ,i\}$.

Since we assume preferences sastisfy FOSD, we know that $A_3, B_3$ are strictly better than $A_2, B_2$, and $A_2, B_2$ are strictly better than $A_1, B_1$, and E is the least preferred among all. Then, the mechanism above is an ICPM since it fulfills all the properties in Propositions 1 and 2 when preferences are rational and satisfy first-order stochastic dominance.¹¹ However, when the dominance relations break down in the above example, such a payoff mechanism can be problematic. If $A_1$ is Archer’s most preferred lottery and appears in Round 1, then he can choose $A_1$ in Round 1, then randomly chooses in Rounds 2 and 3, and chooses $A_1$ in Round 4 again and gets paid according to $A_1$. Alternatively, if we remove the first-order stochastic dominance assumption, the payoff mechanism above cannot guarantee incentive compatibility.

Also, the uniqueness of ABC fails to hold if we assume subjects do not guess the future unknown options, as discussed in Remark 1.

Remark 3

In both Proposition 2 and ABC, the feature of $I_i=\{l:\forall l\in D_k,k=1,\ldots ,i\}, i=1,\ldots ,n$ is mentioned. That is, subjects are only informed of the lotteries in the past and the current rounds. As mentioned earlier, it is called “with no prior information” protocol in the literature (Cox et al. 2015). One example experiment with risk tasks with no prior information is Hey and Orme (1994). On the contrary, multiple price list experiments (for example, Holt and Laury 2002) are usually conducted “with prior information” (each subject is fully informed of all the lotteries in the whole experiment before making any decisions, that is, $I_1=\ldots =I_n={\mathscr {L}}_0$).

However, without prior information, it may generate uncertainty for subjects: Archer may think the future options he sees are affected by his previous and current decisions. Thus, Archer may make choices strategically based on his subjective belief and uncertainty preference. Epstein and Halevy (2017) discuss that one’s uncertainty attitude about how different tasks are related could affect his choices under risk. That is why we keep ${\mathscr {L}}_0$ fixed and predetermined: Let the subjects know that their choices do not affect the lotteries they see in the whole experiment, even though the lottery order may depend on their choices. Thus, we only deal with risk preferences here.

Remark 4

Another possibility is that Archer may have degenerate or optimistic belief: he is sure about the options he will meet, or the options will only get better in later rounds. For example, Archer is facing lottery $X, Y (X\succ Y)$ in the current round, and he is sure that a lottery strictly better than X will appear later. Therefore, he may randomly pick X or Y now. If he guesses correctly, this will not matter in the end. However, since Archer is not informed of later options, he may never meet any option that is better than X. In this case, such random picking will make him worse off eventually. Even though Archer is sure subjectively, there is no guarantee that his subjective belief turns out to be true.

From the implementation side, however, such concern needs to be addressed with more caution. If possible, experimenters should try to prevent or dispel the belief that options will be monotonically improving for subjects. Two things can be done. One is to control the number of rounds to keep the experiment short. Random picking is more likely to happen when subjects are tired or bored. The other is to break down the monotonic pattern by varying the order of appearance of “good” and “bad” lotteries. Sophisticated and deliberate design may be required depending on the research question and the lotteries.

Remark 5

Experimenters sometimes prefer the comparison between designated pairwise lotteries. However, in ABC, only one option carries over to the next round. In this case, we can use the payoff mechanism in Example 4 to preserve the pairwise comparisons by taking advantage of dominance relations. Most of the popular risk models satisfy first-order stochastic dominance. If the lotteries in later rounds always dominate those in earlier rounds, then Property 3 in Proposition 1 can be satisfied, as illustrated in Example 4. Alternatively, we can apply ABC by inserting “ladder” rounds: use the lotteries with dominance relation to moving subjects from one pair to another by climbing up those ladders. The “ladder trick” is implemented in Experiment I in the next section. Ultimately, it seems that we have to compromise to some extent in order to ensure IC for general risk models. If we insist on having particular lotteries paired-up, we need to have some lotteries with dominance relations; otherwise, we drop the full exogenous control of all lotteries in each round of task.

5 Empirical properties of the ABC mechanism

Harrison and Swarthout (2014) argue that studying choice patterns and the preference estimation approach are complementary to each other. Cox et al. (2015) use the choice pattern design, preferred in testing for violations of certain properties such as Common Consequence Effect, Common Ratio Effect (violations of the independence axiom), as they focus on choice behavior in certain lottery pairs. Harrison and Swarthout (2014) adopt the approach in Hey and Orme (1994): No specific choice pattern can be observed directly to reject the hypothesis or assumptions; they mainly rely on econometric techniques (specifically conditional maximum likelihood) to infer the preferences. In addition, both (Cox et al. 2015) and (Harrison and Swarthout 2014) have found the differences in choices or estimates in the RLIS treatment from the one-round task treatment.

For thoroughly examining the ABC mechanism, both methodologies are adopted from Cox et al. (2015) and Harrison and Swarthout (2014) (same lotteries, same ways of lottery representations, same show-up fees) with the ABC mechanism procedure. Both papers have one-round task data, which will be used for comparison with ABC data. In both experiments, the null hypothesis is: The choices or the estimates under the ABC mechanism are the same as those under the one-round task design. If ABC works, then such a null hypothesis should not be rejected.

The applications of ABC for these two types of experiments are a little different. In a Hey and Orme (1994) or Harrison and Swarthout (2014) type experiment, there are no restrictions that each lottery must have its counterpart. Therefore, to apply ABC, we can randomize the order of the lotteries beforehand, and carry a subject’s most recent choice over to the next round. However, to implement ABC on the (Cox et al. 2015) lottery pairs (choice pattern type of experiment) is a little tricky. Each lottery has its counterpart, and only comparisons within some certain lottery pairs are meaningful for detecting paradoxical risk preferences. However, in the ABC mechanism, current choice carries over to the next round. Then the question is, how can we get subjects’ choices for certain pairs of lotteries if we do not know their preferences beforehand? For this, the additional assumption is that a lottery that is first-order stochastically dominated is not chosen. Details on how to use first-order stochastic dominance relations as ladders in a choice pattern experiment are provided below.

5.1 Experiment I: choice pattern experiment (non-structural)

5.1.1 Lottery pairs

Cox et al. (2015) five lottery pairs allow us to directly observe the Common Ratio Effect (CRE), Common Consequence Effect (CCE), Dual CRE, and Dual CCE that are violations of the independence axiom or the dual independence axiom. They use the same lottery pairs with different payoff mechanisms. One of their treatments uses the one-round task design: each subject is randomly assigned one of the five pairs, makes one choice, and gets paid that choice. This treatment is their baseline, the gold standard among all payoff mechanisms.

Table 1 Lottery pairs in experiment I

Another attribute of their lottery pairs is that between S (Safer) lotteries and between R (Riskier) lotteries in different pairs. There are lotteries that are strictly first-order stochastic dominance related ($S_5>^{FOSD} S_4>^{FOSD} S_2>^{FOSD} S_3>^{FOSD} S_1$, and $R_5>^{FOSD} R_4>^{FOSD} R_2>^{FOSD} R_3>^{FOSD} R_1$). Such first-order stochastic dominance is the crucial feature to get the paired-up lottery choices ($S_1$ vs. $R_1$, ... , $S_5$ vs. $R_5$) through the ABC mechanism procedure.

5.1.2 The ABC mechanism experiment procedure

The needed comparisons are between $S_i$ and $R_i$ as shown in Table 1. Recall that ABC carries over only the chosen lottery in each round. Therefore $S_i$ and $R_i$ might not be feasible in the same task, which is not appealing. The key to solving the problem is first-order stochastic dominance: with the design, an individual whose risk preferences reflect first-order stochastic dominance will encounter every lottery pair $S_i$ and $R_i$ $i=1,\ldots ,5$ in the experiment. Since there are five S lotteries and five R lotteries, there are ten lotteries in total, and the ABC mechanism needs nine rounds.

For easier description, let us swap the orders of lotteries in Pair 2 and Pair 3 in Cox et al. (2015). That is, define $S_2'=S_3, R_2'=R_3, S_3'=S_2, R_3'=R_2$, and $S_i'=S_i, R_i'=R_i$ for $i=1,4,5$. Then we have $S_5'>^{FOSD}S_4'>^{FOSD}S_3'>^{FOSD}S_2'>^{FOSD}S_1'$, and $R_5'>^{FOSD}R_4'>^{FOSD}R_3'>^{FOSD}R_2'>^{FOSD}R_1'$. The procedure goes like this for Archer, our example subject:

• Step 1 Round 1: Archer faces $\{R_1', S_1'\}$, and makes his choice $c_1\in \{R_1', S_1'\}$;

• Step 2 Round 2: if Archer chooses $c_1=R_1'$ in Round 1, then he will face $\{R_1', R_2'\}$ ($R_1'$ carries over from Round 1, and $R_2'$ is the new added option); if Archer chooses $c_1=S_1'$ in Round 1, then he will face $\{S_1', S_2'\}$ ($S_1'$ carries over from Round 1, and $S_2'$ is the new added option). It is shown in Fig. 1 as the procedures between Round 1 and Round 2. Option on each arrow refers to a subject’s choice of that round. Given that $R_2'>^{FOSD} R_1', S_2'>^{FOSD} S_1'$ and Archer follows first-order stochastic dominance, at Round 2, Archer will choose $c_2=S_2'$ if he faces $\{S_1', S_2'\}$, and $c_2=R_2'$ if he faces $\{R_1', R_2'\}$. It is shown in Fig. 1 as the solid arrows between Round 2 and Round 3.

• Step 3 Round 3: if Archer chooses $c_2=R_2'$, then he will face $\{R_2', S_2'\}$ ($R_2'$ carries over from Round 2 and $S_2'$ is the new added option); if Archer chooses $c_2=S_2'$, then he will face $\{S_2', R_2'\}$ ($S_2'$ carries over from Round 2 and $R_2'$ is the new added option), too. Therefore, no matter what Archer chooses in Round 1, $S_1'$ or $R_1'$, as long as he follows first-order stochastic dominance in Round 2, he faces $\{S_2', R_2'\}$ in Round 3.

• Step 4 Round 4: subjects are divided into two paths again based on their choices in Round 3, either $S_2'$ or $R_2'$. If $c_3=S_2'$ for Archer, then he will face $\{S_2', S_3'\}$; if $c_3=R_2'$, he will face $\{R_2', R_3'\}$, as shown in the procedures between Round 3 and Round 4 in Fig. 1. And so on and so forth...

Fig. 1

Complete path of experiment I with the ABC mechanism

If individuals always follow first-order stochastic dominance, their behavior can be represented by the solid-line paths in Fig. 1. At even rounds, they make choices between two lotteries that are ordered according to first-order stochastic dominance; in odd rounds, they make choices between $S_i$ and $R_i (i=1,2,3,4,5)$. If they do not follow first-order stochastic dominance, they still will meet all the same ten lotteries through nine rounds of the ABC mechanism (see the dashed arrow paths in Fig. 1, as well as the mathematical expressions in the appendices).

The experiment was run in the laboratory of the Experimental Economics Center (ExCEN) at Georgia State University in June 2015. The subjects were all undergraduates. I recruited 49 subjects from the same population and conducted the ABC mechanism using the same lotteries and the same representation of the lotteries as Cox et al. (2015). There were nine rounds of individual decision tasks for ten lotteries with the ABC mechanism. Subjects were informed that the choice they made in the previous round would be carried over to the next round, and they would be paid the realized outcome of their last choice. It was also explained why choosing one’s preferred lottery in every round is the dominant (best) strategy (see subject instructions in the appendices for detail). As in Cox et al. (2015), no show-up fee was offered. Instead, after subjects finished all their choices, I announced that I would like to pay them $5 (the same amount as in Cox et al. (2015)) for completing a demographic survey. The experiment was conducted with ZTREE software (Fischbacher 2007).

5.1.3 Data results

We can examine behavioral compliance with first-order stochastic dominance as a byproduct of this design. The data shows that only 3 (out of 49) subjects made choices violating the dominance assumption. Such violations led them to miss some of the paired-up lottery comparisons (that is, $S_i$ vs. $R_i, i=1,\ldots ,5$). Therefore their choices are excluded in the following analysis. The choices in five $\{S_i, R_i\}$ lottery pairs, completed by the 46 subjects who never chose dominated lotteries are reported.

The null hypothesis is:

Hypothesis 1

The choices come from the same population under the one-round task design and the ABC mechanism.

Table 2 Proportions of subjects choosing riskier lottery in experiment I

If ABC works, we expect not to reject such hypothesis. The results are displayed in Table 2 and Tables D.1 and D.2 in the appendices. (The data of one-round and RLIS are from Cox et al. (2015), including undergraduate students only.) In Table 2, the proportions of risky (R) lottery choices in all pairs (overall risk tolerance) and within each pair are reported. Table 2 shows that in the sense of being close to the baseline, except for Pair 1, ABC outperforms both versions of RLIS (with and without prior information). We can see that for two-tailed Tests of Proportions, the p-value of Pair 1 is significant at 10% level but not at 5% level, and all other p-values are not significant.¹²

Table D.1 in the appendices reports more thorough comparisons within demographic subgroups. ABC displays more insignificant results than both versions of RLIS compared with the one-round task baseline in general. From Table D.2, all four Probit regression models show that the choices under ABC are not significantly different from those with the one-round task, while both versions of RLIS have significant differences.

By and large, the null hypothesis cannot be rejected at 5% significance level. In other words, the ABC mechanism works empirically for this choice pattern experiment. ABC outperforms both versions of RLIS.

5.2 Experiment II: preference estimation experiment (structural)

5.2.1 Lotteries and ABC mechanism experiment procedure

In the setting of Harrison and Swarthout (2014), there are 69 lottery pairs. Those pairs consist of 38 different lotteries (see appendices for the detailed lottery list). The ABC mechanism is conducted as follows: 21 lotteries out of 38 are randomly selected for each subject, and the orders of lotteries are independently randomized for each subject beforehand. In each round, each subject faces two lotteries and is required to pick one. Individual choice in the previous round carries over to the following round, and eventually, one gets paid the realized outcome of their last chosen lottery. There are 20 rounds in the experiment. Subjects are informed of the above information.

The experiment was run in July 2015 and April 2016, and all 51 subjects were students from Georgia State University. To get better comparisons with Harrison and Swarthout (2014), I adopted their $7.50 show-up fee and used pie representations of lotteries as they did. The experiment was conducted with ZTREE software (Fischbacher 2007).

5.2.2 Data results

Among those 38 lotteries, some are first-order stochastically dominated by others. Subjects may see such dominance pairings in some rounds. Even though first-order stochastic dominance is not required when we analyze the data, it can be used to check whether subjects understand the ABC procedure. For example, one subject kept the same option for all 20 rounds and violated first-order stochastic dominance 6 times. I treat this subject as not understanding the procedure and exclude the data from this subject in the analysis. I also exclude the data of three subjects who were graduate students since all subjects from Harrison and Swarthout (2014) were Georgia State undergraduates. Each of the remaining 47 subjects violated first-order stochastic dominance no more than 3 times.¹³

There are no dominance lottery pairs within 69 tasks in Harrison and Swarthout (2014) . However, given the sequence of choices in ABC and the randomization of the lottery orders, there can be dominance pairs in the ABC treatment. For example, a subject may face the lotteries $(\$5, 0.75; \$20, 0.25)$ (Lottery No. 3 in Table E.1 in the appendices, which lists all the lotteries in Harrison and Swarthout (2014)) and $(\$10, 1)$ (Lottery No. 4) at Round $k-1$. According to ABC, at Round k, the task consists of their choice in Round $k-1$ and the new added option, which is, say, $(\$20, 1)$ (Lottery No. 14). Then, with this example, in Round k, the subject will make choices between a pair of lotteries where one dominates the other regardless of their choice in Round $k-1$. Choices from dominance lottery pairs usually inform little about testing competing models or estimating parameters. Choosing the dominant one fits most risk theories, including EUT and RDU. Therefore, we focus on the choices from non-dominance pairs only (219 observations). Results from all pairs (940 observations) are also reported as robustness check.

The data set consists of the ABC data with one-round task data (75 observations) from Harrison and Swarthout (2014). Following their non-parametric estimation approach (as well as Hey and Orme 1994 and Wilcox 2010), in the EUT model, we assume

$$\begin{aligned} U(\$5)=0, U(\$10)=u_{10}, U(\$20)=u_{20}, U(\$35)=u_{35}, U(\$70)=1 \end{aligned}$$

and in RDU model, we assume more probability weighting parameters:

$$\begin{aligned} \omega (0)=0,\omega (1/4)=\varphi _{1/4},\omega (1/2)=\varphi _{1/2},\omega (3/4)=\varphi _{3/4},\omega (1)=1 \end{aligned}$$

Please see Harrison and Rutstrom (2008) or the appendices for details on the estimation methods.

The focus in the regression is the coefficient for the binary treatment dummy variable “pay1” (to keep the same variable name as in the original paper). The “pay1” dummy equals 1 for the one-round task treatment and 0 for ABC. Such a treatment dummy is added to each estimate of outcome or probability weighting mentioned above. The hypothesis is:

Hypothesis 2

The estimated coefficients for the variable “pay1” are not significantly different from 0.

The results from Table H.1 in the appendices show that “pay1” coefficients are not significant, under either EUT or RDU model, for both “ABC non-dominance pairs only” and “all ABC observations”. The insignificant coefficients are not only for individual parameter estimates, but also from testing the joint effect across all utility or weighted probability parameters or both. Appendices also provide robustness checks allowing heterogeneity in gender or race or both.

In summary, all estimates of coefficients for the “pay1” dummy variables are insignificant. Hypothesis 2 cannot be rejected.

5.3 Summary: implementation and robustness of the ABC mechanism

Experiments I and II are two implementations of the ABC mechanism in conventional individual decision making under risk. In Experiment I, lotteries are paired-up, and first-order stochastic dominance exists between lottery pairs. When subjects never choose dominated lotteries, the implementation with ABC includes all the tasks consisting of the desired lottery pairs (in this case, $\{S_i, R_i\} (i=1,...,5)$) along with transition tasks consisting of the dominance lottery pairs. Compared with the conventional n-round pairwise lottery comparison with other payoff methods, to ensure incentive compatibility, the ABC mechanism with binary comparison needs additional n-1 rounds.¹⁴ In the ABC treatment, each subject met the same ten lotteries in the experiment. However, the orders may be different for individuals depending on their previous choices. Thus, individual decisions affect the order in which lottery pairs are encountered but not the lottery set, which is fixed for all subjects. Note that as long as the preference relation is complete and transitive, the order should not affect choices in the original five lottery pairs. In a general choice-pattern experiment, in order to let subjects meet all the desired pairs, experimenters can use dominance pairs and control the intermediate steps to make subjects transition from one pair to another by climbing up such “ladders”. To summarize, choice-pattern experiments with the ABC mechanism cannot be completely “path-free”.

In Experiment II, where researchers mainly rely on econometric estimates rather than focusing on possible paradoxes from the choice pattern, no two specific lotteries must pair-up. In this case, the lottery set can be randomly and independently predetermined for each subject. The lottery set for two individuals may not be the same, but it is fixed during the experiment and independent of their choices. Also, in this case, there are no transition steps. Every choice might reveal some information about individual risk preferences. However, in this experiment, information revealed with ABC is not as effective and efficient as the conventional decision tasks where both lotteries are exogenously given. In the ABC treatment, subjects had more comparisons between lotteries has dominance relations since they determined one of the options in each round. If one met their favorite option at early rounds, then they would carry it over in later rounds and to the end. In a general preference estimate experiment, the efficiency of ABC could be improved by selecting the lottery set to reduce comparisons between dominance pairs.

With the data analysis, the same methods as those in the original studies with other payoff mechanisms were applied. Statistical tests and Probit models are implemented with Experiment I data, similar to Cox et al. (2015); error noise is allowed in Experiment II data, matching Harrison and Swarthout (2014). In the aspect of robustness, the ABC mechanism is neither better nor worse compared with the traditional decision-making tasks.

In terms of subject payments, with everything else similar, ABC is expected to cost more than RLIS and less than paying all choices since each subject gets paid for their one favorite lottery among all options.

In conclusion, the purpose of the ABC mechanism is to provide incentive compatibility in multiple-task experiments with general risk theories. Trade-offs include the increased number of rounds, reduced information effectiveness from each round, and maybe also higher experiment expense.

6 Conclusion and discussion

This paper addressed the question “other than the one-round task design, is it possible to find an incentive compatible payoff mechanism for general risk theories?” The answer is the Accumulative Best Choice (ABC) mechanism proposed here: in an experiment with a fixed and predetermined lottery set, subjects are not informed of the lotteries they will face in future rounds; the preceding choice carries over to the following round as one selectable lottery option in the task; and eventually subject gets paid the realized outcome of their choice in the last round. I prove that ABC is the unique incentive compatible payoff mechanism (ICPM) under the assumptions of complete and transitive risk preferences and no restrictions on how a subject might anticipate their unknown upcoming options.

The intuition behind these conditions rests on avoiding wealth effect and portfolio effect, thus requiring that experimenters pay the choice of one certain round. It is hard to engage subjects after the paying round. Thus, the one certain paying round has to be the last. On the other hand, one must find a way to incentivize subjects for the nonpaying decisions, resulting in the need for bridges to connect earlier choices to the final paying round. Therefore, all the tasks must be a chained sequence. When facing any nonpaying round, Archer knows his current nonpaying choice can affect the options he sees at the paying round. That is the incentive for him to take it seriously. In other words, any ICPM requires that the decision tasks cannot be entirely exogenous even though the lottery set is exogenous and fixed.

ABC is also empirically tested in the lab. The data from both the choice pattern experiment (Experiment I) and the preference estimation experiment (Experiment II) show that there are no significant differences between the choices under the one-round task design and the ABC mechanism.

How applicable is the ABC mechanism for experimenting with decision tasks under risk? From Experiment I, we see ABC can be applied in experiments that test the classic paradoxes of decision theory if different lottery pairs have first-order stochastic dominance between each other. It is “path-dependent” in the sense that subjects may face different orders of the lotteries due to their choices. Nevertheless, in the end, each subject has encountered tasks with every required lottery pair if their behavior follows first-order stochastic dominance. From Experiment II, we see ABC supports econometric estimation of general risk preferences when no specific lotteries need to be paired. In this scenario, to apply ABC, we can predetermine a random order of (a subset of) the lotteries, and a subject’s current choice will not affect the order of the lotteries they see in the future.

ABC can also be used to elicit certainty equivalents of risky options. For example, if we are interested in individual’s certainty equivalent of lottery X, we can add a series of degenerate lotteries $A_i=(a_i, 1)$ (prize $a_i$ with 100%)$(i=1,\ldots ,k)$ , where $a_1<a_2<...<a_k$ where $a_1$ and $a_k$ are the smallest and the largest prizes in lottery X. Then, apply ABC by comparing X from $A_1$ to $A_k$: without informing subjects the options, Round 1: $\{X, A_1\}$, denote the choice as $c_1$; Round 2: $\{c_1, A_2\}$, denote the choice as $c_2$, and so forth. If we observe the subject switching from lottery X to a sure amount at Round j, that is $X\succeq A_{j-1}$ and $A_j\succeq X$, then we can infer their certainty equivalent for lottery X is between $a_{j-1}$ and $a_j$. As discussed in Remark 2, when implementing ABC, experimenters may mix the orders of small outcomes to make the series not monotonic. It is to dispel the belief subjects may form that the prize amounts will only get larger, which may lead them to random picking until the final round.

Now that we have an ICPM for general risk theories, it opens the door to explore other questions. For example, to research ICPM for general uncertainty models or to test some fundamental assumptions of preferences such as the independence axiom, the reduction axiom, or transitivity.

Notice that ABC is not just incentive compatible when the set of options contains lotteries but could have more general applications, such as intertemporal options and commodity goods. While general applicability of ABC is beyond the scope of this paper, two examples below illustrate how one can apply ABC to generate useful data that are not contaminated by the payoff protocol.

6.1 Application 1: ABC with multiple price lists in time preference elicitation experiments

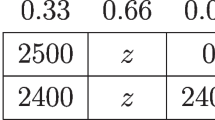
Time preference embeds risk preference. In a seminal paper, Andersen et al. (2008) jointly estimate risk and time preference by using two multiple price lists, which are displayed below. Subjects are asked to make choices, A or B, for every row in both tables.

Table 3 Time preference elicitation experimental design in Andersen et al. (2008)

We denote Option A and B in Row $i (i=1,\ldots ,10)$ in Table 3I as $IA_i$ and $IB_i$, and Option A and B in Row $i (i=1,\ldots ,10)$ in Table 3II as $IIA_i$ and $IIB_i$.

In Table 3I, we want subjects to make comparisons between $IA_i$ and $IB_i$. On the other hand, $IA_{10}>^{FOSD}IA_9>^{FOSD}\cdots >^{FOSD} IA_1$ and $IB_{10}>^{FOSD}IB_9>^{FOSD}\cdots >^{FOSD} IB_1$. We can apply ABC in the way similar to Experiment I in this paper: Without knowing future options, at Round 1, subjects face $IA_1$ and $IB_1$. If they choose $IA_1$, then at Round 2, they face $IA_1$ and $IA_2$; if they choose $IB_1$, then at Round 2, they face $IB_1$ and $IB_2$. As long as subjects follow first-order stochastic dominance, they should choose $IA_2$ or $IB_2$ in Round 2. For either case, at Round 3, they face $IA_2$ and $IB_2$, and so on and so forth. First-order stochastic dominance leads subjects to complete all the comparisons between $IA_i$ and $IB_i (i=1,\ldots ,10)$, and subjects meet all 20 lotteries in the table.

In Table 3II, subjects are supposed to stick with A or B or switch from A to B once and never switch back to A. We also see that $IIA_1=IIA_2=\cdots =IIA_{10}$, and we call it IIA. On the other hand, $IIB_{10}\succ IIB_9\succ \cdots \succ IIA$ for all non-satiated preferences. With ABC, at Round 1, subjects face IIA and $IIB_1$. The accessible options in Round $i (i=2,\ldots ,10)$ are subject’s choice from preceding round and $IIB_i$. Therefore, if subjects choose IIA over $IIB_i$ in Round i, then they compare the carried-over IIA and the added $IIB_{i+1}$, which are in Row $i+1$ of Table 3II. If subjects ever choose $IIB_i$ at some round, the remaining tasks are obvious since IIB gets better going down the table, and they will not want to switch back to IIA.

Notice that if we want subjects to complete both tables, we need to connect the two tasks, too. For example, to make subjects transition from Table 3II to 3I, we may need to change the payoff scale in Table 3I. Let us set the scale, say, 2.5. Then, $IA_1$ becomes (5000, 0.1; 4000, 0.9). Thus, no matter what option subjects end up choosing in Table 3II, IIA or $IIB_{10}$, their carry-over choice is strictly worse than the adjusted $IA_1$. That motivates subjects to move from the last choice in one table to the first choice in the other. Eventually, subjects get paid for their last choice in Table 3I.

Compared with RLIS, which can elicit unbiased risk attitude modeled by payoff transformation only, the adoption of ABC allows both payoff and probability transformation. Since only the former, not the latter, affects decisions in Table 3II, ABC can lead us to a better estimate than RLIS by not confounding probability transformation with payoff transformation in risk preferences elicited from Table 3I.

6.2 Application 2: ABC with generalized axiom of revealed preference (GARP) testing experiments

Generalized Axiom of Revealed Preference (GARP) is a necessary and sufficient condition for choice to support the utility maximization hypothesis (Varian 1982). Various experimental studies test whether individual behavior violates GARP by changing the incomes and the prices of goods. Here is an example of testing GARP with ABC¹⁵: suppose there are three budget lines with different relative prices (different slopes): a (flattest), b, and e(steepest). As in Fig. 2a, $A_1, A_2$ are on a; $B_1, B_2$ are on b; $E_1, E_2$ are on e. $A_1, B_1, E_1$ have the same amount of Good X, and $E_1$ has more Good Y than $B_1$, and $B_1$ more than $A_1$. A similar pattern applies to $E_2, B_2, A_2$, as shown in the figure. Pairwise violations of GARP are: (1) $A_1$ and $E_2$; (2) $B_1$ and $E_2$; (3) $A_1$ and $B_2$.

Fig. 2

Experiments to test GARP

The conventional way to do the experiment is through a three-round task with $\{A_1, A_2\}, \{B_1, B_2\}, \{E_1, E_2\}$. The conventional payoff mechanisms are paying all choices or RLIS, paying one choice randomly. The issue of paying all is the portfolio incentive provided; the issue of RLIS is that the independence axiom presumed confounds GARP: if we detect the GARP violation behavior, maybe it is because people violate independence. Either way, we test the joint hypothesis instead of merely GARP.

We can apply a design with ABC as follows (illustrated in Fig. 2b): Without knowing the future options, at Round 1, subjects face $\{A_1, E_2\}$ to make a choice. If $c_1=A_1$, at Round 2, they will face $\{A_1, B_1\}$ (the left path); if $c_1=E_2$, at Round 2, they will choose between $\{E_2, B_2\}$(the right path). Given that preferences are non-satiated, subjects should choose $B_1$ on the left path or $B_2$ on the right path. In Round 3, on the left path, the new option is $B_2$, and $B_1$ on the right path. In Round 4, the path diverges: the new added option being $E_1$ or $A_2$, depends on subject’s choice in Round 3. In Round 5, the path converges again due to the non-satiated preferences. Up to Round 5, regardless of choices, each subject meets the same six bundles $A_1, A_2, B_1, B_2, E_1, E_2$. Round 6 is added to complete the test for all pairwise violations of GARP.¹⁶ GARP is violated if we observe subjects choosing the pairs of $\{A_1{\text { in Round 1}}, E_2{\text { in Round 6}}\}$, or $\{E_2{\text { in Round 1}}, A_1{\text { in Round 6}}\}$, or $\{B_2{\text { in Round 3}}, A_1{\text { in Round 6}}\}$, or $\{B_1{\text { in Round 3}}, E_2{\text { in Round 6}}\}$.¹⁷ ABC provides a direct test of GARP which avoids confounds from the payoff mechanism.