Optimistic irrationality and overbidding in private value auctions

Abstract

Bidding one’s value in a second-price, private-value auction is a weakly dominant solution (Vickrey in J Finance 16(1):8–37, 1961), but repeated experimental studies find more overbidding than underbidding. We propose a model of optimistically irrational bidders who understand that there are possible gains and losses associated with higher bids but who may overestimate the additional probability of winning and/or underestimate the potential losses when bidding above value. These bidders may fail to discover the dominant strategy—despite the fact that the dominant strategy only requires rationality from bidders—but respond in a common sense way to out-of-equilibrium outcomes. By varying the monetary consequences of losing money in experimental auctions we observe more overbidding when the cost to losing money is low, and less overbidding when the cost is high. Our findings lend themselves to models in which less than fully rational bidders respond systematically to out-of-equilibrium incentives, and we find that our model better fits the effects of our manipulations than most of the existing models we consider.

1 Introduction

In a sealed-bid second-price auction (SPA) with private valuations, where the highest bidder wins and pays the second highest bid, bidding one’s value is a weakly dominant strategy (WDS, Vickrey 1961). This strategy requires only that each bidder behave rationally and it is unaffected by the number of rivals or their valuations, a bidder’s risk preferences, or beliefs regarding rationality of rivals. Repeated experimental studies have found that subjects deviate from the WDS by overbidding much more than underbidding, resulting in overbidding on average (e.g., Kagel et al. 1987; Kagel and Levin 1993). By contrast, experimental evidence from the strategically equivalent ascending English auction demonstrates almost immediate convergence to the dominant strategy (e.g. Kagel et al. 1987; Kagel and Levin 1993; Kagel 1995).¹ While overbidding relative to the risk-neutral, Nash equilibrium (RNNE) has also been frequently found in first-price auctions (FPA, e.g., Kagel 1995; Kagel and Levin 1993), the “usual suspects,”—risk aversion, beliefs about others’ play, biases in perceptions of probabilities—that may explain overbidding in FPAs are of no avail in SPAs.

The contrast between SPAs and English auctions suggests that subjects discover the WDS in the English auction but not in the SPA; why is this the case? The cognitive process that leads to the discovery of the WDS in an SPA is far from trivial and an experimental subject may be unable to recognize it without experience or training. In an English auction, on the other hand, a subject needs to answer a simple question for herself: “Am I ‘in’ or ‘out’?” Answering this question leads a bidder to drop out at his value.

Subjects who do not bid their value in SPAs are nevertheless still motivated by common sense economic incentives, such as expected payoffs, though imperfectly. Kagel et al. (1987) conjectured that subjects are aware that higher bidding increases the probability of winning the auctions but underestimate the additional cost associated with it. Instead of looking for dominant strategies, we suggest that optimistically irrational bidders are guided by a desire to maximize their profits combined with an inability to fully grasp the intricacies of the auction environment that allows them to view the consequences of their actions more favorably. We do this by modeling reasonable bidders who recognize (i) a higher bid increases the probability of winning, and (ii) the bidder may understate negative payoffs to higher bids. These behaviorally plausible assumptions about bidders are the building blocks of our simple model of how out-of-equilibrium incentives might affect behavior in SPAs.

We test our model in SPAs in which we introduce a parameter that changes the expected payoff as a function of one’s bid but does not affect the WDS. The parameter multiplies realized losses by some amount $\beta$, where $\beta =1$ is the standard case. Consistent with previous results we find that when $0<\beta \le 1$, overbidding is pervasive. In contrast, when we change $\beta$ to 20, overbidding is significantly reduced and underbidding is more prevalent. Overbidding when $0<\beta \le 1$ results in very few and fairly small losses (5.8% of auctions; median loss of $0.10). This is a product of our design: the domain of bidders’ private values is quite large relative to the number of bidders, so the second highest bid is almost always below the highest value, even with overbidding. This allows us to rule out a “hot stove” type of learning whereby losses reduce overbidding in subsequent auctions.² Instead, it appears that the dramatic reduction in overbidding occurs when $\beta$ is exogenously and publicly increased and can be attributed to changes in expected out-of-equilibrium payoffs.

While explanations for overbidding in various auction formats abound, and we compare the fit of our model to several of them in Sect. 5, the contribution of our model lies in its focus on the dominant strategy, adding to the recent theoretical interest in how dominant strategies influence decision calculus in games (e.g., obvious strategy-proofness, Li 2016). Our strong findings suggest that incentives outside equilibrium affect behavior in predictable ways in the laboratory, and probably in the field as well, even when equilibrium analysis predicts otherwise. Goeree et al. (2002) show a similar result in a FPAs, but in FPAs, as in many other games where Nash equilibrium is the solution concept, best responding requires “cardinal” computations. Since such computations often involve a high degree of complexity and a heavy mental cost, we do not expect that the outcome in FPAs will exactly reflect the point prediction of Nash equilibrium. It is much less surprising to find that the subjects’ calculations, possibly involving heuristics, approximations and simplification rules, will be affected by a change in the incentives, even if these ought to have no effect on Nash equilibrium. This complexity motivates many models that predict overbidding by allowing bidders to make, and learn from, mistakes (e.g., QRE). In an SPA with private values, however, the dominant strategy can be reached with just “ordinal logic” of dominance, without even a need for common knowledge of rationality.³ Thus, one would expect the solution norm—bid your value—to have its best chance for success in this environment. Our study shows that behavior is still guided by some degree of conscious profit maximization, but subjects’ decision processes fail to recognize a characteristic that is very seldom present outside the lab: the dominant strategy. Errors in recognizing a dominant strategy require a new perspective on the cognitive processes underlying bidding behavior of the sort provided by optimistic irrationality to try to explain “errors” made by bidders that are as much a function of the simplicity of a dominant strategy as the complexity of the environment.

2 Optimistically irrational bidders

The overlooked availability of a WDS must be the starting point of any explanation to overbidding in SPA. We formalize the intuition behind the conjecture laid out in Kagel et al. (1987) by modeling an “optimistically irrational” bidder who understands that there are possible gains and losses associated with higher bids but who may overstate the additional probability of winning due to higher bidding and/or understate the losses associated with it.⁴

Let there be n risk-neutral bidders, each of whom privately observes her value $x_{i},$ $i=1,\ldots ,n$. It is common knowledge that the $x_{i}$’s are i.i.d draws from a distribution with a cumulative density function F(t), where $F^{\prime }(t)=f(t)>0$ on [0, 1], $F(0)=0,$ and $F(1)=1$. For our purposes, we assume that the $x_{i}$’s are drawn from a generalized uniform distribution, $F(t)=t^{{\widehat{\alpha }}}$ and ${\widehat{\alpha }} \ge 1$, where ${\widehat{\alpha }}=1$ corresponds to the uniform distribution used in almost all laboratory SPAs and FPAs. We first make four assumptions:

Assumption 1

Symmetry

Assumption 2

Upon winning, a bidder’s gross payoff is x.

Assumption 3

Bidders believe values are i.i.d from a c.d.f. $F(t)=t^{\alpha }$ with $\alpha \ge {\widehat{\alpha }}$.

Assumption 4

A bidder with a value x who bids $b>x$ and wins at a price $p\in (x,b)$ believes that the expected payment is $\gamma (x)\frac{b+x}{2},$ with $0<\gamma (x)\le 1$, i.e., expected losses are $x-\gamma (x)\frac{b+x}{2}$.

The first two assumptions simply mean that each bidder believes that all other bidders use the same, strictly monotonic bidding function, and that they receive their full value if they win the auction. Assumption 3 implies that a bidder potentially overstates the impact of bidding past his value because he believes values are closer together than they actually are. That is, he believes the increase in the probability of winning corresponding to an increase in his bid is greater than it actually is. This assumption finds support in other studies of auctions. For example, Cooper and Fang (2008) found that subjects who perceive their rivals to have values similar to their own are more likely to overbid in experimental SPAs, while Breitmoser (2015) uses “projection,” the tendency to believe that rivals have value or beliefs similar to one’s own, to explain the winner’s curse.⁵ Finally, Assumption 4 captures the notion that a bidder in an SPA may understate possible losses when he bids above his value and wins.

These assumptions allow us to make two important observations about an optimistically irrational bidder’s maximization problem.

Proposition 1

Sincere bidding, i.e., $b(x)=x$ for all x, occurs if and only if for all x, $\gamma (x)=1$.

Proof

See “Appendix”. $\square$

Proposition 1 means that an optimistically irrational bidder may still bid his value when $\alpha ={\widehat{\alpha }}$ and $\gamma (x)=1$. This does not require that the bidder recognizes the availability of the WDS. In fact, sincere bidding only requires $\gamma (x)=1$ but allows $\alpha >{\widehat{\alpha }}$.⁶

Remark

There is a linear solution to the maximization problem with $b(x; \alpha , \gamma , n)=\delta (\alpha , \gamma , n)x$.⁷

Put more simply, the bid will be a multiple of the value. The exact multiple will be a function of the number of competitors, how “close” a bidder believes those competitors’ values are to his value, and the extent to which he understates the losses from overbidding. In the next section we make use of the fact that there is a linear solution to the maximization problem to inform our experimental design.

2.1 Experimental test of the model

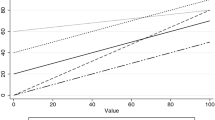
Optimistically irrational bidders need not recognize the WDS but can be influenced by “out-of-equilibrium” payoffs. Several authors have argued that, in English or first-price auctions with private values, the exact shape of the expected payoff functions matters (e.g., Harrison 1989; Goeree et al. 2002; Georganas 2011; Georganas and Nagel 2011).⁸ Similarly, Noussair et al. (2004) compare value revelation using the Becker–DeGroot–Marschak (BDM) method and SPAs and find that the shape of the expected payoff function may influence behavior. They find that the shape of the expected payoff function in the SPAs means that the probability of winning increases faster in overbids than it decreases in underbidding, which drives bidders who start out below the WDS towards the WDS, while overbidding is also more costly in the SPA than in the BDM with three or more bidders. Taken together, these observations about the shape of the expected payoff function seem to reflect the assumptions we make in our model. As a simple test of optimistically irrational bidders, we implement standard second-price, sealed-bid auctions for one unit of an indivisible good in the laboratory. The WDS predicts that players bid their values in equilibrium. We introduce a factor $\beta$ by which we multiply eventual negative profits of the bidders. $\beta$ does not affect the equilibrium if bidders are bidding sincerely because no bidder earns negative profits in equilibrium. However, the bidders’ expected payoff functions do change, given that their opponents follow the equilibrium strategies; in Fig. 1 we plot, for different values of $\beta$, the expected payoff function for a bidder whose rivals bid their values.

Given the remark in the previous section, we can determine how our experimental treatments will affect the bidding of optimistically irrational bidders. Applying the theory to our experimental treatments, when a bidder wins with $b>x$ and loses, his expected payment is $\beta [x-\gamma _{\beta }\frac{b+x}{2}]$. A standard SPA corresponds to the situation where $\beta =1$, such that the expected losses are $1\times [x-\gamma _{1}\frac{b+x}{2}].$ This allows us to define $\gamma _{\beta }$ as a function of $\gamma$ in a standard auction, i.e., $\gamma _{1}$, which we do by setting $[x-\gamma _{1}\frac{b+x}{2}]=\beta [x-\gamma _{\beta }\frac{b+x}{2}]$, and solving for $\gamma _{\beta }.$ Doing this, we get

$$\begin{aligned} \gamma _{\beta }=\frac{\beta -1}{\beta }\frac{2x}{b+x}+\frac{\gamma _{1}}{\beta } \end{aligned}$$

(1)

We can substitute $b(x)=\delta x$ into Eq. (1) to obtain

$$\begin{aligned} \gamma _{\beta }=\frac{1}{\beta }\left[ \frac{2(\beta -1)}{\delta +1}+\gamma _{1}\right] \end{aligned}$$

(2)

Plugging Eq. (2) into the linear solution, we solve the problem numerically.⁹ The results can be found in Table 1. Assuming $\alpha =1.1$ and $\gamma _{1}=0.95$, i.e., a bidder slightly overstates the increase in his probability of winning associated with a higher bid and slightly understates his expected loss, the model predicts that $\delta ^{*}$ increases monotonically in $\beta$ and bidding above value that ranges from 9.7% above value for a $\beta =0.1$ to 0.5% above value for a $\beta =20$. These numerical estimates yield three testable hypotheses:

Hypothesis 1

Subjects will overbid on average.

Hypothesis 2

Subjects will overbid by more on average when $\beta <1$ than when $\beta =1$.

Hypothesis 3

Subjects will overbid by less on average when $\beta >1$ than when $\beta =1$.

3 Experimental details

The data come from nine experimental sessions conducted at Ohio State University. Students were recruited via e-mail and sessions took place in the Experimental Economics Lab. The experiment was programmed and conducted with the software z-Tree (Fishbacher 2007). In every session, subjects participated in 62 second-price, sealed-bid auctions—2 trial auctions followed by 60 paying auctions—with either three or six bidders per auction. Subjects were randomly and anonymously re-matched between auction periods.¹⁰ At the beginning of each auction, subjects privately observed their own independent private values denominated in an experimental currency unit (ECU), but they did not observe the values of others. All values were drawn from a uniform distribution on the interval [0, 100], which was common knowledge. At the end of each period the bidder who obtained the item was informed of the price and his profit, while bidders who did not obtain the item received no information about the price or the bids of others. The instructions can be found in the “Appendix”.

We multiplied negative profits by a parameter, $\beta$, which took on three values in every session: 1, 0.1, and 20. Beta took on one of these values for periods 1–19, another for periods 20–39, and the final value for periods 40–60. Subjects knew the value of $\beta$, that it is the same for all bidders, and that they would be made aware when it changed; subjects did not know when $\beta$ would change, how many times it would change, or what its magnitude would be. All subjects were given starting balances of 150 ECUs to cover the possibility of losses. Profits and losses were added to this balance and the balance was paid at the end of each session. We ran two sessions with 3 bidder auctions and a $\beta$ order of 1, 0.1, 20 ($\beta _{1/0.1/20}^{3}$), two sessions with 6 bidder auctions and a $\beta$ order of 1, 0.1, 20 ($\beta _{1/0.1/20}^{6}$), two sessions with 3 bidder auctions and a $\beta$ order of 1, 20, 0.1 ($\beta _{1/20/0.1}^{3}$), and three sessions with 3 bidder auctions and a $\beta$ order of 20, 1, 0.1 ($\beta _{20/1/0.1}^{3}$). In sessions with three bidder auctions, the exchange rate was $1 = 20 ECU, while the exchange rate in sessions with six bidder auctions was $1 = 14 ECU. The exchange rates were different in order to equalize the expected payoff between sessions with different group sizes. In the event that a player went bankrupt, they were no longer permitted to bid and were paid a participation fee of $8. Due to the uneven numbers after a bankruptcy, at the beginning of every period after a bankruptcy two subjects were randomly assigned to sit out that period in 3 bidder auctions, while five subjects were chosen to sit out in 6 bidder auctions. In the six sessions that started with $\beta =1$, there were two bankruptcies; in the three sessions that started with $\beta =20$ there were 10 bankruptcies, with all but one occurring in the first 10 periods. Complete session details can be found in Table 2.

4 Results

Average differences between values and bids can be found in Table 3, and Figs. 2, 3, 4, 5 and Figure 6 of Supplementary material compare subjects’ bids and their values. Consistent previous research, we see overbidding on average in every treatment for every value of $\beta$. To test whether or not this overbidding is significantly different from 0, we calculated the mean difference between bid and private value for each session within a $\beta$ regime, i.e., the block of periods during which $\beta$ remained the same. Using these means as our measure of overbidding, average overbidding is significantly greater than 0 at the 5% level in every case except for $\beta =20$ for $\beta _{1/0.1/20}^{3}$ (t test $p=0.174$) and $\beta _{1/0.1/20}^{6}$ (t test $p=0.129$).

Observation 1

Consistent with Hypothesis 1, subjects overbid on average for all values of $\beta$.

The effects of changes in $\beta$ are visible and drastic, in contrast to the standard theoretical prediction of no change at all. For example, when we reduce the punishment for negative outcomes from $\beta =1$ to $\beta =0.1$ in period 20 of $\beta _{1/0.1/20}^{3}$, there is an immediate effect as the average difference between bid and value more than doubles from approximately 2.8 to 7.5—an increase equal to approximately 5% of the support of values. When $\beta$ rises to 20 in period 40 and punishment for negative outcomes is severe, the overbidding largely disappears, with average overbids falling from 7.5 to 1.1. Similar patterns emerge in all treatments, and the differences in overbidding across $\beta$ regimes are significant.¹¹ $^{,}$ ¹²

Observation 2

Consistent with Hypotheses 2 and 3, overbidding varies significantly across different values of $\beta$, with higher levels of $\beta$ leading to less overbidding.

Our specific design allows for an additional important and interesting observation about learning. There is significant overbidding in the first 40 periods with $\beta =1$ and $\beta =0.1$ in $\beta _{1/0.1/20}^{3}$ and $\beta _{1/0.1/20}^{6}$, and we do not observe learning in the direction of value bidding in these periods.¹³ Nonetheless, there is a drastic reduction of overbidding in period 40. One possible explanation for the decline in overbidding in period 40 is that subjects who have overbid in earlier periods are chastened by losing money, a sort of “hot stove” learning. The evidence in Table 4 does not support this explanation. Before $\beta$ increases to 20, few auctions result in realized losses. They range from a minimum of 4.3% of auctions for the case with six bidders when $\beta =1$, to 9.3% with three bidders and $\beta =0.1$. The average loss is also quite small, ranging from 1.1 ECUs with six bidders and $\beta =0.1$, to 10.8 ECUs with six bidders and $\beta =1$. Moreover, this small and infrequent negative feedback for the first two levels of $\beta$ appears to have no effect on those who experience it. Of the 31 bidders who lose money when $\beta =1$, 29 also lose money when $\beta =0.1$. Of the six bidders who lost money when $\beta =20$, 5 lost money at all three levels of $\beta$ and the sixth lost money when $\beta =0.1$.

Observation 3

Reductions in overbidding when $\beta$ is increased are not caused by learning due to previous losses.

In order to move beyond unconditional means and investigate the effects of $\beta$ while allowing for individual heterogeneity, we estimate a random effects Tobit model, regressing the difference between subject i’s bid and his value in auction j on dummies for each $\beta$ regime.¹⁴

The results in columns 1–4 of Table 5 are similar to the means in Table 3. In every treatment bids are significantly higher when $\beta =0.1$ than when $\beta =1$; similarly, bidding is significantly lower in every treatment when $\beta =20$ than when $\beta =1$. We do, however, see some differences across treatments, and we reject the null hypothesis that the marginal effects of $D_{\beta =0.1}$ and $D_{\beta =20}$ are jointly equal across all treatments (Wald test, $p=0.000$ for both).

Although learning due to negative reinforcement is unlikely in $\beta _{1/0.1/20}^{3}$ and $\beta _{1/0.1/20}^{6}$, one possible explanation for the differences across treatments we observe may be some other sort of learning or experience. To address this possibility, we augment the model in columns 5–8 with a linear time trend and its interaction with the $\beta$ regime. We observe small, but statistically significant increases in bids over time in the first 20 periods in treatments $\beta _{1/0.1/20}^{6}$, $\beta _{1/20/0.1}^{3}$, and $\beta _{20/1/0.1}^{3}$, where bids increase by roughly 0.12–0.18 ECUs per period; we see no significant changes over time in subsequent periods. With the inclusion of the time trend, the same pattern emerges: greater overbidding when $\beta =0.1$ and less overbidding when $\beta =20$, though the treatment effects are no longer significant in $\beta _{1/20/0.1}^{3}$. Allowing for changes to bidding behavior over time, we cannot reject the null hypothesis that the marginal effects of $D_{\beta =0.1}$ and $D_{\beta =20}$ are the same across all treatments (Wald tests, $p=0.551$ and $p=0.318$, respectively); we find no significant differences at conventional levels across treatments in pair-wise comparisons of $D_{\beta =0.1}$ and $D_{\beta =20}$.¹⁵ $^{,}$ ¹⁶

Observation 4

The effects of changes in $\beta$ are robust to controls for individual differences and learning over time.

The linear trend presupposes that the effect of all periods is the same within a $\beta$ regime, however Fig. 2 suggests that the first few periods in a session might be slightly different.¹⁷ In columns 9–12 we estimate the same model as in columns 5–8 but exclude the first 3 periods in each session. After excluding the first three periods, there is no significant learning over time for any value of $\beta$ in any treatment.

Observation 5

Bidding behavior evolves substantially in the first few periods of a session, but little thereafter.

5 Alternative models

One important test of our model of optimistically irrational bidders is how well it fits the data relative to existing models. Among our candidate models, we begin by considering a symmetric Nash equilibrium (SNE) with normally distributed errors, given that without errors the SNE fails completely to predict the change in bidding when we shift $\beta$. Models that take all payoffs into account, even if they are not on the equilibrium path, are good candidates to explain our results. Perhaps the simplest way to consider all payoffs is to use the Nash model but assume that subjects’ errors depend on the expected utility of each action in a systematic way. We do this by considering an SNE with a logistic error structure, as in Crawford and Iriberri (2007). Finally, we consider is quantal response equilibrium (QRE), which also makes explicit use of the payoff function shapes, by positing that players choose an action with a probability proportional to its expected payoff.¹⁸ In preliminary comparisons, we find that the SNE+normal model outperforms the other two models in all but one $\beta$-number of bidder combinations.¹⁹ The reason is that, under a logit error structure, a high frequency of underbidding is predicted for intermediate private values, since the expected payoffs are quite flat to the left of the maximum (as seen in Fig. 1); yet we see far more overbidding than underbidding in all cases.²⁰ QRE improves on the Nash model with logistic errors, but still performs worse than the Nash model with normal errors.

One way to account for the fact that we observe much more overbidding than underbidding is to allow bidders to experience joy-of-winning (JOW). JOW can be incorporated by adding an extra fixed utility, $U_{i},$ to the payoff of subject i, conditional on winning the auction.²¹ It is easy to show that with such modification a new dominant solution emerges, with $b_{i} (x_{i})=\frac{U_{i}}{\beta }+x_{i}$.²² This implication helps as it predicts that players who enjoy winning will overbid with respect to the Nash equilibrium and the amount of overbidding will depend inversely on $\beta .$ The JOW parameter j is found to be positive and yields a significantly higher likelihood in every case. Nonetheless, SNE with normal errors still provides the best fit among JOW models.

To evaluate its broad applicability, in Table 6 we examine how well the SNE models with normal errors, both with and without JOW, fare against our model of optimistically irrational (MI) bidders in SPAs, English auctions, and FPAs, by comparing estimated log-likelihoods.²³ $^{,}$ ²⁴ We find that our model fares better than the SNE with just normal errors (but no JOW) in all auctions. On the other hand, the SNE with normal errors and JOW outperforms our model in every auction. The SNE with normal errors and JOW may have slight advantages by the measure of Table 6, but these advantages do not reveal the full story. In Table 7 we break out the fit by the number of bidders and values of $\beta$. In this case, the SNE fares better than MI in six of the nine $\beta$-number of bidder combinations. In Table 8, we compare the the predicted mean overbidding by optimistically irrational bidders and the SNE with JOW to the observed mean overbidding. In 4 out of the 7 cases, the magnitude of overbids by MI bidders is closer to the predicted overbidding than SNE bidders who experience JOW. While on a strictly econometric basis, SNE+JOW seems to be performing slightly better than MI, MI outperforms SNE+JOW in several instances.²⁵ Moreover, there are good qualitative reasons not to be satisfied with JOW, chief among them its failure to explain why JOW occurs in SPAs but not in the strategically analogous English auction. Ultimately, further work and additional data will be needed to completely analyze the relative strengths of the two models.

6 Conclusions

Experiments consistently find that in second-price, sealed-bid auctions with private values—a mechanism with incomplete information where bidding one’s value is a WDS—subjects deviate significantly from the WDS. The availability of a “dominant” action that is best irrespective of the other features of the decision is rare in games with incomplete information and in strategic situations outside the lab. The behavior of a bidder in a second-price auction who fails to recognize or discover such an available strategy is still likely to be guided by rules that are useful in a wide range of situations, such as cost-benefit analysis. Subjects in our SPAs provide support for this characterization of bidders: their bidding is reasonable if not optimal. Subjects overbid on average but their overbidding is influenced by manipulations which affect expected payoffs out of equilibrium but not the dominant strategy. In accordance with lessons learned in more familiar settings, as we vary the magnitude of the penalty for losses, a natural reaction is to hedge and bid lower when the penalty is relatively larger and to be more aggressive when the penalty is relatively lower. The behavioral changes may not be optimal in a second-price auction, yet they are sensible when viewed through the lens of their applicability in richer environments.

We propose a model of optimistically irrational bidders who fail to recognize the availability of a dominant strategy. Bidders in this model understand that raising their bid increases the probability of winning but may either overstate the increase in the likelihood of winning and/or fail to appreciate the costs associated with increasing their bids. We fit several existing models designed to explain overbidding using our data, but we find that most of these models perform poorly even when they consider out-of-equilibrium payoffs that would be affected by our experimental manipulation, and none of the models outperform ours consistently.

Our results build on the cautiously optimistic findings in Cooper and Fang (2008). They find that bounded rationality—more than non-standard preferences like spite and JOW—contributes to overbidding in SPAs. Subjects in their experiment could purchase costly and noisy information about rivals’ values, information which does not affect the WDS. Subjects who purchase the information were significantly more likely to overbid, but the behavior of those subjects who did not purchase information was consistent with theoretical predictions. They conclude by noting that this heterogeneity may be of less significance outside the lab where selection might weed out the irrational bidders, leaving only rational bidders. Our finding of large and theoretically unpredicted responses to our treatments can inform mechanism designers, theorists and practitioners who are concerned that such selection may be insufficient or too slow: even in cases with a dominant strategy, the nature of incentives outside equilibrium can influence behavior. In instances where the common sense implications of manipulating out-of-equilibrium incentives can steer behavior toward the desired norm, such as in SPAs, designers may be able to use these incentives to design more stable and efficient mechanisms.²⁶

Fig. 1

Expected payoff functions in a second price auction with 3 bidders, for the three different values of $\beta .$ There are 5 curves in every panel which represent expected utility, depending on one’s bid for a private value $v = 0$, 25, 50, 75 and 100

Fig. 2

Mean difference between bids and private values over time in all treatments

Fig. 3

Scatter plot of values versus bids in all treatments when $\beta =1$

Fig. 4

Scatter plot of values versus bids in all treatments when $\beta =0.1$

Fig. 5

Scatter plot of values versus bids in all treatments when $\beta =20$

Table 1 Numerical estimates of parameters for optimistically irrational bidders in auctions with 3 bidders

Table 2 Summary of sessions

Table 3 Mean difference between bid and value by treatment

Table 4 Subjects experiencing losses with $\beta$ order 1, 0.1, 20

Table 5 Estimated coefficients from a random effects Tobit model of the effect of $\beta$ on bids

Table 6 Comparing estimated log likelihoods across models and auction formats

Table 7 Comparing estimated log likelihoods across models, auction formats, values of $\beta$, and number of bidders

Table 8 Comparing predicted mean overbidding to observed mean overbidding

Appendix

1.1 Second price auctions

The maximization problem of an optimistically irrational bidder in an SPA in our model is:

$$\begin{aligned}&\underset{b\ge 0}{\max }[\sigma (b)]^{\alpha (n-1)}\left\{ x-\left[ \frac{[\sigma (x)]^{\alpha (n-1)}}{[\sigma (b)]^{\alpha (n-1)}}\right] {\theta }_{n}{(x)}\right. \\&\left. +\left. \left[ \frac{[\sigma (b)]^{\alpha (n-1)}-[\sigma (x)]^{\alpha (n-1)}}{[\sigma (b)]^{\alpha (n-1)}}\right] \gamma (x)\frac{b+x}{2} \right] \right\} , \end{aligned}$$

where ${ \theta }_{n}{(x)}$ denotes the expected price if a bidder wins at a price below his value and $\sigma (b)$ denotes the inverse bidding function.

The first-order condition (FOC) for the maximization problem is:

$$\begin{aligned}&2x\alpha (n-1)[\sigma (b)]^{\alpha (n-1)-1}\sigma ^{\prime }(b)-\gamma (x)\alpha (n-1)[\sigma (b)]^{\alpha (n-1)-1}\sigma ^{\prime }(b)(b+x) \nonumber \\&\quad -\gamma (x)[[\sigma (b)]^{\alpha (n-1)}-[\sigma (x)]^{\alpha (n-1)}]=0 \end{aligned}$$

After simplifying we have:

$$\begin{aligned}&2x\alpha (n-1)[\sigma (b)]^{\alpha (n-1)-1}[1-\gamma (x)]\sigma ^{\prime }(b)-\gamma (x)\alpha (n-1)[\sigma (b)]^{\alpha (n-1)-1}(b-x)\sigma ^{\prime }(b) \nonumber \\&\quad -\gamma (x)[[\sigma (b)]^{\alpha (n-1)}-[\sigma (x)]^{\alpha (n-1)}]=0 \end{aligned}$$

(3)

Proof of Proposition 1

Proof

Assume that $\forall x\in [0,1],$ $b(x)=x.$ In such a case Eq. (3) becomes

$$\begin{aligned} 2x\alpha (n-1)[\sigma (b)]^{\alpha (n-1)-1}(1-\gamma (x))=0 \end{aligned}$$

implying $\gamma (x)=1,$ for all $x>0,$ as $\sigma ^{\prime }(b)=1$ with $b(x):=x.$

Assume that $\forall x\in [0,1]$, $\gamma (x):=1.$ In such a case Eq. (3) becomes

$$\begin{aligned} -\{[\alpha (n-1)\sigma (b)]^{\alpha (n-1)-1}(b-x)\sigma ^{\prime }(b)+[[\sigma (b)]^{\alpha (n-1)}-[\sigma (x)]^{\alpha (n-1)}]\}\lesseqgtr 0 \quad \text {as} \quad b(x)\gtreqqless x. \end{aligned}$$

$\square$

Derivation of remark 1

Consider the FOC in Eq. (3). Recognizing that at the solution $\sigma (b)=x$ and $\sigma ^{\prime }(b)=\frac{1}{b^{\prime }(x)}$, and simplifying, we can rewrite (3) as

$$\begin{aligned} 2\alpha (n-1)[1-\gamma (x)]-\gamma (x)\alpha (n-1)\left( \frac{b}{x} -1\right) -\gamma (x)b^{\prime }(x) \left[ 1-\left( \frac{\sigma (x)}{x}\right) ^{^{\alpha (n-1)}}\right] =0. \end{aligned}$$

(4)

Assume that $\forall x\in [0,1],\gamma (x)=\gamma <1$ and $b(x)=\delta x,$ with $\delta \ge 1$. Equation (4) can be written as:

$$\begin{aligned} 2\alpha (n-1)[1-\gamma ]-\gamma \alpha (n-1)(\delta -1)-\gamma \delta \left[ 1-\left( \frac{1}{\delta }\right) ^{^{\alpha (n-1)}}\right] =0 \end{aligned}$$

(5)

When $\delta =1$ then (5) becomes $2\alpha (n-1)[1-\gamma ]>0$ when $\gamma <1$, which is the case for overbidding.

By inspecting (5), it is clear that the LHS is strictly declining in $\delta$, so that there is a unique $\delta ^{*}$ that solves

$$\begin{aligned} 2\alpha (n-1)[1-\gamma ]-\gamma \alpha (n-1)(\delta ^{*}-1)-\gamma \delta ^{*}\left[ 1-\left( \frac{1}{\delta ^{*}} \right) ^{^{\alpha (n-1)}}\right] =0 \end{aligned}$$

(6)

1.2 First price auctions

The maximization problem of an optimistically irrational bidder in an FPA:

$$\begin{aligned} \underset{B\ge 0}{\max }[\sigma (B)]^{\alpha (n-1)}[x-B] \end{aligned}$$

(7)

Denote the solution to (7) by $B(x;\alpha )$ and the risk-neutral Nash equilibrium by $B(x;{\widehat{\alpha }}).$ It is well known that the solution to (5) is given by,

$$\begin{aligned} B(x;\alpha )=x-\frac{\int _{0}^{x}t^{\alpha (n-1)}dt}{x^{\alpha (n-1)}}=x-\frac{x}{\alpha (n-1)+1}=\frac{\alpha (n-1)}{\alpha (n-1)+1}x \end{aligned}$$

Proposition 2

$B(x;\alpha )\ge B(x;{\widehat{\alpha }})$ as $\alpha \ge {\widehat{\alpha }}.$

Proof

The proof is immediate.$\square$

Thus, optimistically irrational bidders will bid above the RNNE but below their value.

1.3 Joy of winning

Lemma 3

In a second price auction where negative payoffs are multiplied times $\beta$ and bidders have a heterogeneous joy of winning $U_{i}$, the dominant strategy equilibrium is $b_{i}(x_{i})=\frac{U_{i}}{\beta }+x_{i}$.

Proof

Expected profits in the auctions are $\Pi _{i}=prob\{b_{i}>\max (b_{-i} )\}(x_{i}+U_{i}-E[\max (b_{-i})|b_{i}>\max (b_{-i})])$, and subjects choose a $b_{i}(x_{i})$ to maximize $\Pi _{i}$. Consider bidding $b_{0}<b_{i} (x_{i})=\frac{U_{i}}{\beta }+x_{i},$ when it matters i.e. you win with $b_{i}(x_{i})$ but lose with $b_{0}.$ It also means that the price the winner pays is $p\in [b_{0},b_{i}(x_{i})]$. If $\ p>x_{i}$, winning earns $U_{i}-\beta (p-x_{i})\ge U_{i}-\beta ((\frac{U_{i}}{\beta }+x_{i})-x_{i})=0.$ When $p\le x_{i},$ strict positive payoffs are assured. With a similar step we show that bidding $b_{i}(x_{i}),$ weakly dominates bidding $b_{0} >b_{i}(x_{i}).$ $\square$

Table 9 Model fit in all treatments with $\beta$ order 1, 0.1, 20