On a Temporal Investigation of Hurricane Strength and Frequency

Abstract

Hurricanes originating in the West Atlantic often have devastating consequences on the cities in the US east coast, both monetary and otherwise, and hence pose a source of considerable concern to several authorities. The possibility of a connection between global warming in general and an increased frequency of these strong hurricanes is well researched, but is still actively debated. The present work tries to promote the use of a smoothing statistic termed empirical recurrence rates and to advocate the use of another, termed empirical recurrence rates ratio in a bid to better understand the rich history of these storms on one hand and to make appropriate inferences on the other, so that some light can be shed on the acceptability of conjectures held by renowned climate scientists. The methods introduced are intuitive and simple to implement and should find wide applications in diverse disciplines.

1 Introduction

As one nears the end of the current decade, strong hurricanes and tropical storms originating from the Atlantic Ocean continue to pose a relentless threat, especially to the east coast of the USA and researchers believe that in the absence of a sophisticated forecasting tool and a better understanding of the cyclone dynamics, the years to come shall witness an unprecedented loss of human lives and property. In 1926, a category 4 hurricane lashed out at Miami and a report published by the Times estimates that if such a hurricane should hit the same place today (which now has a population in excess of 2.5 million), the estimated monetary damage would easily surpass $180 billion. Hurricane Sandy struck the east coast in October 2012 and inflicted a $20 billion damage in New York City alone. Simulation-based research (Emanuel [7]) published by leading atmospheric scientist Dr. Kerry Emanuel based at Massachusetts Institute of Technology paints a grim picture: the frequency of tropical cyclones will increase by 10 to 40% by 2100 and the intensity of these storms should increase by 45% by the end of the century.

There is no dearth of climate literature that hint at a connection between the increased restlessness of these devastating storms and other controllable factors, notably climate change: Hansen et al. [12] have identified ocean heat content and water vapor as significant factors contributing to more intense tropical cyclones and have described how they have increased considerably over the past several decades, primarily due to human activities such as burning of fossil fuels and massive deforestation—an inevitable consequence of which is an increased concentration of carbon dioxide in the atmosphere—which in turn, acts as an envelope over the ocean, thereby preventing its heat content to escape. Trenberth and Shea’s [34] and Trenberth’s [33] study probed into the causes of an abnormal increase in ocean temperature with specific emphasis on North Atlantic and concluded that about 0.3 °C of the increase was due to ocean oscillations, 0.2 °C came from natural weather variation, but alarmingly enough, global warming accounted for the most—0.45 °C. Hoyos et al. [14] and Santer et al. [28] voice similar concerns: over the period of 1970 onwards, warmer sea surface temperature is the most significant player behind the increased frequency of strong hurricanes. Sriver and Huber [31] have found that a 0.25 °C increase in the average annual tropical sea surface temperature can lead to a 60% increase in a hurricane’s potential destructiveness.

Awareness about the harmful consequences of climate change is on the rise over the last few years: Delegates met in Peru to try and agree on a negotiating text for a new global climate deal to be signed at the end of 2015 (http://www.bbc.co.uk/news/science-environment-30225511), Australia pledged A$200 m (£106 m; $166 m) to help poor nations mitigate the impact of global warming (http://www.bbc.co.uk/news/world-australia-30408036), while there are skeptics who believe that schemes to tackle climate change could prove disastrous for billions of people, but might still be required for the good of the planet (http://www.bbc.co.uk/news/science-environment-30197085). Following Hurricane Sandy, Mayor Michael Bloomberg came up with a voluminous 430-page report detailing a $19.5 billion plan to shield New York from climate change-related hazards. But as Dr. Emanuel [6,7,8] points out, this connection portraying climate change as a pivotal cause behind frequent hurricanes is still at the level of a probable hypothesis and the possibility of a vehement confirmation would need to wait for a few more years and for more reliable data.

The principal purpose of the present statistical endeavor is neither to challenge nor to support this cause-effect hypothesis that relates global warming and strong hurricanes, but to promote the use of a smoothing empirical recurrence rates (ERR) statistic developed by Ho [15, 16] and used by Tan, Bhaduri, and Ho [32] and Ho and Bhaduri [17], as an aid to better understand the recent trends in strong hurricane frequency and also to check whether some of the conjectures held by leading environmentalists, oceanographers, and atmospheric scientists that relate to the frequency and incidence of these strong hurricanes are tenable enough. The methods employed will essentially be nonparametric and the development of a new statistic termed as empirical recurrence rates ratio (ERRR) will facilitate arguments even further. These two statistics are intended to serve rather different purposes: as will be evidenced later, ERR tracks the history of the maximum likelihood estimate of the intensity of the single time series it is generated from, while ERRR, defined as a ratio of two ERRs, will elucidate the evolution of the mutual interplay between two competing processes. As a welcome corollary, one will also be able to shed some light on the previously mentioned suspicion. The latter quantity has recently been introduced and profitably used by Ho et al. [18] in the financial industry to analyze the interaction structure between the size of a bank and its likelihood of failure. Success in such competitive and adversarial a field as banking, where the intricacies of interaction is undoubtedly comparable to weather science, should go a long way in convincing skeptics about the versatility of the technique.

One must hasten to add that methods exist in literature to assess risks for extreme hydrological hazards, but most of them are forbiddingly technical to be of use to scientists working outside the realm of weather science. Sisson et al. [30], for instance, uses Bayesian technologies for inference from annual maxima and peaks over threshold models, in the context of assessing the long-term risks of rainfall and flooding in the Caribbean. They explain how standard Gumbel hazard analyses assign almost zero probabilities to extremely intense and rare events. While methods such as these are novel and implementable in the present context, the computational difficulties involved (for instance sampling from posterior densities) might pose a considerable hindrance to applied practitioners. On the other extreme, works carried out by Elsner et al. [5], for instance, concentrates on quantifying the fluctuations of North Atlantic hurricane frequencies using frequency domain spectral analyses for the period 1886–1996. In the present work, however, one opts for a time domain analyses (in view of its ready interpretability) and is encouraged to reach similar conclusions. Considering the different categories of hurricanes possible (Table 1), based on their maximum wind speeds, the current work delivers a stronger message. Another breed of studies looks into the forecasting aspects of hurricane tracks. Lin et al. [23], for example, uses generalized linear models and probabilistic clustering technique to classify the best tracks of typhoons around Taiwan during 1951–2009. General reliability studies concerning oceanic hazards are also available: for instance, a generalized version of the Poisson reliability model that we are going to employ has been used by Zhang and Lam [38] for reliability modeling of offshore structures.

Table 1 Major hurricane categories

The paper is organized as follows: Section 2 lays down the basic definitions and tools that will be used frequently from a general viewpoint. Section 3 will talk about the data collection method, the observation domain both with respect to space and time, and the rationale behind such a choice. Sections 4 and 5 detail the analyses using different categories of hurricanes and two different ocean basins with the statistics introduced previously. Section 6 summarizes key findings.

2 Theory and Methodology

2.1 Empirical Recurrence Rate

Let t₁, . . ,t_n be the time of the n ordered events during an observation period [0, T] from the first occurrence to the last occurrence. Then a discrete time series {Z_l} is generated sequentially at equidistant time intervals h, 2h, . . , lh, …Nh(=T). If 0 is adopted as the time-origin and h as the time step, then one regards z_l as the observation at timet = lh. A time series of the empirical recurrence rates (Ho [16]) is developed as

$$ {z}_l={n}_l/ lh, $$

(1)

where n_l is the total number of observations in [0, lh) and l = 1, 2,…, N. Note that Z_l evolves over time and is simply the maximum likelihood estimator (MLE) of the mean unit rate, λ, if the underlying process observed in [0, lh) is a homogeneous Poisson process (HPP). The ERR curve should be approximately flat for a typical HPP, where the correlation function for z_j and z_j + kz_j + k is

$$ {p}_{j,j+k}={\left[j/\left(j+k\right)\right]}^{1/2},\mathrm{for}\;j=1,2,...,N-1,k=0,1,...,N-j. $$

2.2 ERR Plot

The very definition of the ERR statistic helps one realize its inherent advantage over an ordinary time series in that it is able to “recall” past events: If {X_t} represents the underlying ordinary time series counting the number of events at time t, then the numerator of the ERR statistic is given by n_l = ∑_{t ∈ [0, lh)}x_t and this cumulative effect imparts greater inertia to the z_l series, which sometimes is extremely desirable. Since a simple time series forgets the past, it is very easy for a small random shock to destabilize the series considerably. However, a process needs to behave sufficiently abnormally to induce a significant change in the ERR series since small increments are smothered by a deterministic increase in t, especially for large t. Such a property, building upon a more reliable description, should be of immense help to exercises such as change point identification.

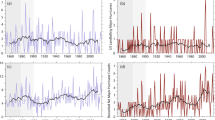
The following graph (Fig. 1) will help clarify this point even further in terms of a concrete example: The ordinary time series that is depicted through the dotted line will ultimately count the number of H5 category (the strongest) hurricanes in the West Atlantic basin over the period of 1923–2013, later in the paper and its corresponding ERR series is plotted as well.

Fig. 1

Simultaneous behavior of ERR and original time series

As can be seen, although the original time series fluctuates quite often, the ERR series is rather stable, especially after the initial noise dies down and the ERR series jumps up significantly only when there is a corresponding abnormal increase in the original time series, specifically at t = 11, 83. So, an unnecessarily complex and immensely sensitive algorithm might generate more than one change point if the original series is fed into it, but such a danger can be largely avoided by the use of ERR.

This smoothing property can best be described using the fact that under the assumption of a homogeneous Poisson process, the random variable n_t has a Poisson distribution with parameter λt. Consequently,

$$ E\left({z}_t\right)=E\left(\frac{n_t}{t}\right)=\frac{\lambda t}{t}=\lambda $$

which proves the unbiasedness of the ERR statistic, irrespective of the sample size. In view of the fact that it also serves as the maximum likelihood estimate, this fact is particularly interesting since there are occasions when these two cannot be achieved simultaneously for small samples (for instance, while estimating variance). Regarding smoothing and the reduction of variance, we can observe:

$$ \mathrm{Var}\left({z}_t\right)=\mathrm{Var}\left(\frac{n_t}{t}\right)=\frac{1}{t^2}\lambda t=\lambda /t\to 0\kern0.24em \mathrm{as}\kern0.24em t\to \infty $$

Although the ERR statistic is endowed with nice smoothing power, it cannot describe more than one series at the same time. Thus to address the interesting issue of interaction between two possibly correlated series, the following ERRR statistic is proposed, using similar ideas.

2.3 Empirical Recurrence Rates Ratio

Let X₁ and X₂ be independent observations from Poisson (λ₁) and Poisson (λ₂) distributions, respectively. A well-known method of testing the difference of two Poisson means is the conditional test (Przyborowski and Wilenski [25]) and is referred to as the C-test. It is based on the fact that the sum S = X₁ + X₂ follows a Poisson distribution with rate parameter, λ₁ + λ₂, and the conditional distribution of X₁ given S = s is distributed as binomial (s,p₁₂), where p₁₂ = λ₁/(λ₁ + λ₂) = ω₁₂ with ω₁₂ = λ₁/λ₂. Thus, for the C-test, testing H₀ : λ₁ = λ₂ vs H_a : λ₁ ≠ λ₂ is equivalent to testing H₀ : ω₁₂ = 1 vs H_a : ω₁₂ ≠ 1, which is also equivalent to testing H₀ : p₁₂ = 0.5 vs H_a : p₁₂ ≠ 0.5. Motivated by the simplicity of the C-test and the smoothing power of the empirical recurrence rate (Ho [15, 16]), the following empirical recurrence rates ratio time series, to be referred to as ERRR, is introduced, to measure the event rates ratio between two processes: K and M.

First as before, we partition the observation period (0, T) into N equidistant time intervals h, 2h, . . , lh, …Nh(=T) for a given time step, h. The ERRR, R_{KM, l}, at time t = lh is then generated as follows:

$$ {\displaystyle \begin{array}{l}{R}_{KM.l}=\frac{n_{Kl}}{n_{Kl}+{n}_{Ml}} for\ {n}_{Kl}+{n}_{Ml}>0, where\\ {}{n}_{Kl}= Total\ number\ of\ events\ for\ the\ K\ series\ in\ \left(0, lh\right);\\ {}{n}_{Ml}= Total\ number\ of\ events\ for\ the\ M\ series\ in\left(0, lh\right);\\ {} and\ l=1,2,...,N.\end{array}} $$

(2)

If 0 is adopted as the time-origin, then we regard R_{KM, l} as the observation at time, t = lh, discarding the burn-in period where n_Kl + n_Ml = 0. Also, if both of the targeted processes are homogeneous Poisson processes, then at every time step, the ERRR updates the MLE of p_ij, the binomial success probabilities defined previously, which can be used to find the MLE of ω_ij = λ_i/λ_j using the invariance property of the MLE. The ERRRs are unconventionally created to be cumulative to offset the potential of creating a time series with a lot of detrimental but seasonal zero values through a discretization process. It can accommodate the complexity of the data. For instance, point processes that characterize small recurrence rates or, in particular, exhibit seasonality with a lot of off-season zero counts such as sand-dust storms and hurricane data, are recorded as well. Numerous time series that attempt to model rare events are frequently plagued with such annoying zeroes which pose considerable problems to researchers. Apart from its inherent capability of generating pseudo data over such barren periods of time, ERRR is endowed with other nice properties that appeal to intuition. For instance, the nature and strength of the two processes involved are coded into this statistic. While sheltered by the versatility provided by the time step parameter, data analysis with a counter-intuitive time step should be supported by a rigorous sensitivity analysis.

2.4 ERRR Plots

Intuitively, every ERRR_KM (= R_KM) is simply the (absolute) frequency of events from K, normalized by the total number of events from both groups, a relative frequency cumulated at each time-point. Mathematically, ERRR_KM = ERR_K/(ERR_K + ERR_M). Therefore, any information accrued from comparing any pair of ERR curves is reproduced and displayed by a single ERRR time series plot (ERRR plot). Set M as the baseline group for the pairwise comparison. R_KM = 0.5 means that there are same numbers of events for both the series up to that time-point. If R_KM < 0.5, there are more events from M, while R_KM > 0.5 indicates that, so far, the K series is more frequent. Therefore, a reference line at R_KM = 0.5 is added in Fig. 2. Deviation from this reference line in either direction indicates departure from an ideal independence and raises suspicion that the two series might be correlated.

Fig. 2

ERRR comparisons for the artificially constructed series

For instance, with a pair of equal size ratio series defined as

$$ {\displaystyle \begin{array}{l}K=1,0,0,2,4,2,2,4,2,0,0,0,0,0,0,2,4,2,2,4,2,0,0,0,0,0,0,2,4,2,2,4,2,0,0,...\\ {}M=2,4,2,1,0,0,0,0,0,2,4,2,2,4,2,0,0,0,0,0,0,2,4,2,2,4,2,0,0,0,0,0,0,2,4,...\end{array}} $$

and with a pair of different size ratio series defined as

$$ {\displaystyle \begin{array}{l}K=1,0,0,2,4,2,2,4,2,0,0,0,0,0,0,2,4,2,2,4,2,0,0,0,0,0,0,2,4,2,2,4,2,0,0,...\\ {}M=1,2,1,1,0,0,0,0,0,1,2,1,1,2,1,0,0,0,0,0,0,1,2,1,1,2,1,0,0,0,0,0,0,1,2,1,1,...,\end{array}} $$

one has the first panel of the following graph.

It is expected that the ERRR series from two sequences that are directly correlated should exhibit a significant and consistent trend (either upwards or downwards), while the one from two inversely related sequences should show a wavy pattern. To check this, a pair of sequences counting the imaginary number of events in 1 year can be created: one direct, given by:

$$ {\displaystyle \begin{array}{l}K=n\\ {}M=n-2\end{array}}\Big\} for\ n=1,2,...\mathrm{20} $$

and one inverse, given by:

$$ {\displaystyle \begin{array}{l}K=2,3,4,3,2,0,1,0,0,0,2,3,4,3,2,0,0,1,0,0\\ {}M=0,0,1,0,0,2,3,4,3,3,0,0,0,1,0,2,3,4,3,2.\end{array}} $$

The ERRR curves shown (Fig. 2) confirm the expected patterns.

In addition to simply helping one understand the nature of the dependence (if any), these curves can also be used profitably to quantify the strength of the dependence through usual quantities like the slope, namely, the steeper the slope, the stronger the dependence.

3 Data

The term “tropical cyclone” is generic and embraces all types of closed atmospheric circulation that forms over a tropical or subtropical ocean. If the maximum sustained wind speed exceeds 74 miles per hour, these storms are called hurricanes in the Atlantic Ocean, typhoons in the Pacific, and cyclones elsewhere. The National Oceanic and Atmospheric Administration (NOAA) is a government organization under the United States Department of Commerce and their Historical Hurricane Tracks webpage at http://coast.noaa.gov/hurricanes/?redirect=301ocm# records most of the recent storms that occur globally. Based on geographical criteria, the water mass of the earth has been partitioned into several basins such as West Atlantic, North Pacific, Gulf of Mexico, Southern Indian, and Eastern Australian and data are available on the speeds, dates, and duration of storms originating in each of these basins. Additionally, based on the strength of the storms judged by the maximum sustained wind speeds (MSW), one has six major categories: and some of the records date back to 1851. But the earlier records are mostly based on eyewitness’s accounts and other less reliable methods and, hence, after consultation with experts well versed with the data collection method, 1923–2013 was finalized as the observation period. Preliminary analyses have been done on storms originating in the West Atlantic basin, mainly because of its proximity to the US east coast which has to face the wrath of these natural calamities almost every year and often with grave consequences, but also because of the fact that this basin is well studied by oceanographers and climatologists and hence would render one a chance to compare the findings to their beliefs. Similar analyses can, of course, be done on other basins as well.

4 Data Analysis on West Atlantic Basin

Emanuel [6,7,8] believes that it is the category 3, 4, and 5 hurricanes that cause the most damage and so, entirely for the sake of a simplified analysis, one may define these as the “strong” group of hurricanes. H2 and H1 constitute the “weak” class of hurricanes and the “Tropical” category is reserved for the final class. It may be found that over the period under consideration, there has been 32 H5 storms, 84 H4 storms, 87 H3 storms, 93 H2 storms, 150 H1 storms, 271 tropical, and 24 subtropical storms. In this section, one uses (1) to create the ERR series for each of the three major categories and agrees to follow the following convention: while comparing two categories of hurricanes through ERRR, say category i and category j (denoted by an i − j population), the i population will serve as the numerator in (2).

It is worth noticing the views of Emanuel once again. From a candid interview with the Discovery Channel (http://news.discovery.com/earth/global-warming/does-climate-change-mean-more-or-stronger-hurricanes-120907.htm), one knows that he is of the opinion that with a continually warming climate, it is increasingly difficult to start a devastating hurricane due to a hike in saturation deficit which works against its creation, but if it gets started somehow, it has the potential to become more intense. Thus, the total number of storms should decline globally, but the proportion of hurricanes which are intense should rise. The gradual decline in the number of strong hurricanes is confirmed by the above ERR plot (Fig. 3), at least over a considerable range of time and the conjecture of an increase in the proportion of strong hurricanes in recent years is accepted by the above ERRR curve (Fig. 3), especially on the strong-weak population.

Fig. 3

ERR and pairwise ERRR comparison among different West Atlantic hurricane categories

Interestingly enough, the three curves in both the diagrams seem to meet at roughly t = 47, which corresponds to the year 1970 (= 1923 + 47). Global warming tightened its grip at about the same time which brings to the fore the troubling realization that perhaps changes in the hurricane behavior pattern, at least over the West Atlantic, might be a rueful consequence of this preventable scourge. Knutson et al. [22] point out that sea surface temperatures (SST) in regions where cyclones and hurricanes typically originate from have increased by several tenths of a degree Celsius over the past several decades. Although this variability makes trend analyses complex, they conclude that substantial proportions of the increased sea surface temperature over the Atlantic and Pacific is due to greenhouse warming. Others such as Ke [20] study the zonal asymmetry of the Antarctic oscillations and finds that this measure for the Western Hemisphere is directly correlated with the number of hurricanes in the Atlantic. This has been done through an examination of the main contributors for hurricane formation such as vertical wind shear, convergence and divergence conditions, and low-level atmospheric pressure. Evan et al. [9] speculate that the increased restlessness could in part be a consequence of increased dust transport over the Tropical Atlantic.

4.1 Modeling ERR and ERRR Series for Strong West Atlantic Hurricanes

The descriptive statistical analyses on both ERR and ERRR generate encouraging results. So to understand whether such a pattern will continue in the near future and also to make the generated process inherit the rich structure of such established domains such as time series, one may take recourse to fitting efficient seasonal autoregressive integrated moving average (SARIMA) models to both the ERR and ERRR series. A detailed sensitivity analysis with respect to the time step h did not generate alarming results and so, for the sake of simplicity and also for generating a sufficiently large number of data points, the time step can be fixed at h = 1 year. The ERR (treated now as a time series e_t) modeling is described in detail here, the analysis for ERRR can be carried out on a similar vein.

To ensure reliable modeling results, one treats the first 10 ERR and ERRR observations as belonging to a burn-in period, when the series are expected to fluctuate widely. Also to understand the predictive ability of the fitted model, one reserves the final 10 observations as a prediction set. The residual set is the training sample and these observations may be used to search for a good model.

Established procedures for model selection, for instance, the ones detailed in Shumway and Stoffer [29], have been followed here. The initial autocorrelation function (ACF) and partial autocorrelation function (PACF) graphs are shown below (Fig. 4) which clearly show a steady cyclical pattern, but a very slow decrease.

Fig. 4

Time series analysis results

Then, to capture a possible seasonality pattern, one takes the first order differenced series ∇e_t = e_t − e_t − 1 and plot the corresponding ACF and PACF curves (Fig. 4):

Significant peaks can be seen at 1s, 2s, 3s, 4s, …, where s = 5 (approximately) with relatively slow decay indicating the need for seasonal differencing. The ACF and PACF curves for the new series

$$ {\nabla}_5\nabla {e}_t=\left(1-{B}^5\right)\left(1-B\right){e}_t $$

tend to show a strong peak at 1s and relatively smaller peaks at 2s, 3s, and 4s. So it appears that either

• (i) The ACF is cutting off after lag 1s and the PACF is tailing off in the seasonal lags.

• (ii) The ACF is cutting off after lag 2s and the PACF is tailing off at the seasonal lags.

• (iii) They are both tailing off in the seasonal lags.

These suggest either (i) a seasonal moving average (SMA) of order Q = 1, (ii) an SMA of order Q = 2, or (iii) a seasonal autoregressive moving average (SARMA) of order P = 2 or 3 (due to 2 or 3 significant peaks in the final PACF) and Q = 1.

Next, to identify the non-seasonal parameters, one focuses on the within season lags and it seems that either

• (i) Both ACF and PACF are tailing off.

• (ii) ACF and PACF are tailing off at lags 2 or 3.

These suggest either (i) p = q = 1 or (ii) p = 2 or 3, q = 2 or 3.

Narrowing down the search domain this way, one now chooses the best from these competing “nearby” models according to the minimum AIC criterion. The best parsimonious model found was a seasonal autoregressive integrated moving average (SARIMA) with these parameters: p = 2, d = 1, q = 1 and P = 2, D = 1, Q = 1, s = 5 with the AIC value of − 237.84. Thus, the final model is the following SARIMA(2, 1, 1) × (2, 1, 1)₅:

$$ {\varPhi}_2\left({B}^5\right)\phi (B){\nabla}_5^1{\nabla}^1{e}_t={\varTheta}_1\left({B}^5\right)\theta (B){w}_t $$

(3)

where φ, Φ₂, θ, and Θ₁ are polynomials of orders 1, 2, 1, and 1 respectively, B is the backward shift operator, and w_t represents a purely random process. The parameter estimates and the summary statistics are shown in Table 2.

Table 2 Parameter estimates and summary statistics

Next, one subjects this model to the usual diagnostic tests and the findings are detailed in the next few figures (Fig. 5). The standardized residuals from the fit can be found to be well within acceptable limits, ACF of the residuals are negligible, and the Ljung-Box tests have significantly high p values (close to 0.9), thereby failing to reject the independence hypothesis of the residuals. The Q-Q plot obtained from these residuals also seems to support the normality assumption on the residuals.

Fig. 5

Model diagnostic plots

Model (3) does quite well from a prediction point of view as is evidenced by Fig. 6 above and so, one eventually pools the training and prediction set together to form the observed data set to be fed into this SARIMA model. Next, 10-year forecasts are extracted and the findings are recorded in Fig. 7. A constant and an upward trend is generally observed in the forecasts for the ERR and the ERRR cases respectively, which tend to support the hypothesis that if similar climatic conditions prevail in the near future, the proportion of strong Atlantic hurricanes will significantly go up, although their actual number might not increase drastically.

Fig. 6

ERR and ERRR modeling for strong West Atlantic hurricanes

Fig. 7

ERR and ERRR forecasts

In a wonderfully crafted review article, Knutson et al. [22] reach similar conclusions and note that using existing modeling techniques and observations, the mean number of cyclone frequency will either remain unaffected or will decrease due to the greenhouse effect. The global decrease should range somewhere between 6 and 34%. Following their argument, one can attribute this phenomenon to the weakening of oceanic circulation, together with a decrease in the upward mass flux accompanying deep convection and an increase in the saturation deficit of the middle troposphere. We note that ARMA models (or its several generalizations such as ARIMA or SARIMA) suffer from stifling assumptions on the residuals (such as their independently and identically distributed-ness (Hamilton, [11]) or normality (Damsleth and El-Shaarawi [4]), and thus, one may inquire about their applicability to study bounded quantities like ERRRs. We note, however, that in this specific hurricane instance, as evidenced by the residual diagnostic plots (Fig. 5), the assumptions seem to be satisfied. Any departure from these constraints, possibly due to the boundedness of these variables, would have been signaled by considerable deviations of the sample quantiles from the theoretical ones in the Q-Q plot, or by significant spikes in the autocorrelation function curve. One has to admit that this might not be true in every situation, and to model bounded variables from a general time series framework, one may use transformations as proposed by Wallis [36] in an economic context, or beta regression, proposed by Guolo and Varin [10] using Gaussian copula.

The modeling exercise conducted here aimed to track the evolution of the ERR and ERRR series in the immediate future. Aided by insights from experts, the modeling and the forecasts may be fine-tuned by including other climatic variables such as sea temperature, oceanic currents, and atmospheric pressure. Such an attempt would require SARIMA modeling with exogenous variables (SARIMAX models), along lines similar to Xie et al. [37], and while possible in principle, we refrain from treading that route immediately, since issues such as variable selection, among others, could prove distracting to the central theme of the present work.

5 Comparisons Between Atlantic and Pacific Basins

Scholars are of the opinion that the West Atlantic basin is one of the most well studied areas and it would be interesting to explore the possibility of its interaction with other basins, especially the East Pacific. Thus, as a final analysis, one pools together all the different hurricane categories over each of the Atlantic and Pacific basins and construct the following ERRR series, based on annual data over the same period: 1923–2013:

$$ {\displaystyle \begin{array}{c}{R}_{KM.l}=\frac{n_{Kl}}{n_{Kl}+{n}_{Ml}}\kern0.24em {\mathrm{for}}_{Kl}+{n}_{Ml}>0,\mathrm{where}\\ {}{n}_{Kl}=\mathrm{Total}\ \mathrm{number}\ \mathrm{of}\ \mathrm{hurricanes}\ \mathrm{in}\ \mathrm{the}\ \mathrm{Atlantic}\ \mathrm{basin}\ \mathrm{in}\ \left(0, lh\right);\\ {}{n}_{Ml}=\mathrm{Total}\ \mathrm{number}\ \mathrm{of}\ \mathrm{hurricanes}\ \mathrm{in}\ \mathrm{the}\ \mathrm{Pacific}\ \mathrm{basin}\ \mathrm{in}\ \left(0, lh\right);\\ {}\mathrm{and}\ l=1,2,\dots, N.\end{array}} $$

The definition of ERRR has been so constructed that it is extremely susceptible to identifying abrupt movements in the progression of both the processes under consideration. Thus, it serves as a reliable tool to capture the simultaneous dynamics, by locating the change points for the two series together on a single graph. Forecasts from an efficient model such as (3) can describe the future interplay with a reasonable degree of confidence. For instance, an abrupt increase in the intensity pattern for the Pacific basin should necessitate a downward trend in the ERRR series and, similarly, an upward trend should result from an increased activity in the Atlantic basin.

Figure 8 confirms this hypothesis. Modern statistical literature on change point detection houses several competing methodologies, each thriving on such assumptions as a possible retrospective or prospective analysis (Ross [27]) or a parametric or distribution-free approach (Ross [26], Pettitt [24]). In the present context of handing discrete counts, a Poisson-based likelihood ratio test was believed to be the most apt. With {N_i} representing a sequence of independent Poisson variables with rates {λ_i}, i = 1, 2, …, c, the change point detection under this framework boils down to choosing one of the following:

$$ {\displaystyle \begin{array}{l}{H}_0:{\lambda}_1={\lambda}_2=\cdots ={\lambda}_c=\lambda \\ {}{H}_1:{\lambda}_1={\lambda}_2=\cdots ={\lambda}_k=\lambda \ne {\lambda}_{k+1}={\lambda}_{k+2}=\cdots ={\lambda}_c={\lambda}^{\prime }.\end{array}} $$

Fig. 8

Peaks and troughs of ERRR series help to locate possible change points

The null likelihood

$$ {L}_0\left(\lambda \right)=\prod \limits_{i=1}^c\frac{e^{-\lambda }{\lambda}^{n_i}}{n_i!} $$

and the alternate likelihood

$$ {L}_1\left(\lambda, {\lambda}^{\prime}\right)=\prod \limits_{i=1}^k\frac{e^{-\lambda }{\lambda}^{n_i}}{n_i!}\prod \limits_{i=k+1}^c\frac{e^{-\lambda \hbox{'}}\lambda {\prime}^{n_i}}{n_i!} $$

enables one to construct a likelihood ratio statistic

$$ {L}_k=-2\log \frac{L_0\left(\widehat{\lambda}\right)}{L_1\left(\widehat{\lambda},\widehat{\lambda^{\prime }}\right)} $$

where the hats represent the maximum likelihood estimates of the rate parameters. The optimum change point position is given by the value of k that maximizes L_k, say $\widehat{k}$, and the null assumption is rejected if ${L}_{\widehat{k}}<C$, where C is appropriately chosen to satisfy the level condition. Information on the null distribution of max_kL_k can be obtained from Chen and Gupta [3]. Generalized versions of these likelihood ratio based tests may be implemented using the “changepoint” package in R, created by Killick and Eckley [21], where one may control the type of change desired (mean, variance, both, etc.), the number of change points, the penalty function, etc.

Such routine parametric change point analysis (on the statistical software R) indicates a change point at around t = 24 for the Pacific and one at around t = 43 for the Atlantic basin, both showing instances of increased activity thereafter. From the first panel, one observes that these are extremely close to the peak and trough of the generated ERRR series. At t = 24, the peak is clearly visible, while at t = 43, the rapid rate of descent is somewhat arrested, giving the impression of a “change of inflection” point. The proximity of these peaks and troughs can be taken as a measure that quantifies the extent of the suspected inverse relationship, with the strength being negatively correlated to the period length. Finally, a general wavy pattern of the ERRR series indicates that the two basins are inversely related, the justification for which must be left to the able hands of specialists. For instance, Knutson et al. [22] argue that Atlantic Ocean SST has increased at a pace faster than tropical mean SST over the last three decades, which is coincident with the positive trend in the Atlantic power dissipation index over this period. This differential warming of the Atlantic can be affected by natural multidecadal variability, as well as by aerosol forcing, but not strongly by greenhouse gas forcing as various climate models seem to suggest. If the relationship between Atlantic power dissipation and this differential warming is causal, then a substantial part of the increase in Atlantic power dissipation since 1950 is likely due to factors other than greenhouse gas-induced warming. On the other hand, the case for the importance of local SSTs would be strengthened by observations of an increase in power dissipation in other basins, in which local warming in recent decades does not exceed the tropical mean warming. Emanuel [8] finds a statistical correlation between low-frequency variability of power dissipation and local SSTs for the northwest Pacific. But this correlation is considerably weaker than for the Atlantic Ocean, and other key measures of storm activity in the northwest Pacific, such as the number of category 4 and 5 typhoons, do not show a significant correlation with SST.

6 Conclusions

Formulation of theories to understand and quantify the nature and strength of dependence between two stochastic processes in general and time series, in particular, has attracted the attention of researchers since quite some time. Methods exist in the literature that often address this issue, but most are too technical to be appraised by non-specialists in applied areas. The present work endeavored to propose and popularize a simple smoothing statistic termed as empirical recurrence rates ratio (ERRR) which is endowed with properties that appeal to intuition, but at the same time, preserves the necessary statistical rigor.

In addition to resolving the fundamental question related to the dependence strength, it can also simultaneously identify the possible change points of the two series involved with remarkable precision. In general, statistical methods differ while analyzing discrete data from continuous ones: for instance, the theory of Poisson count regression is different from the standard normality based methods and modelers will have to be conscious of the nature of the underlying data structure. ERRR, however, is versatile enough to handle both types at the same time owing to properties such as under independence, the quantity

$$ \frac{N_1(t)}{N_1(t)+{N}_2(t)} $$

follows a beta distribution if the individual components follow gamma laws. Due to properties like this, one can effortlessly extend the analyses carried out in this work to a dependence study context where the quantities being measured are not discrete like counts, but are continuous such as volume or area affected. Another way to claim the novelty of this approach could be by arguing that there exist a close connection between a time series and a point process and each area can learn significantly from the other. A relation such as this has been sparsely conjectured in literature: Brillinger [2] for instance, tries to find unifying characteristics embracing time series, point processes, marked point processes and hybrids through the introduction of a “stationary increment process” and examination of second- and third-order autocovariances where he talks about converting a linear point process to a binary time series, but refrains from forecasts and inferences. Henschel et al. [13] make a casual remark about converting a point process to a time series but does not explicitly show how. As is thus evidenced, although there are separate tools designed for the specific tasks of forming bridges between time series and point processes, detecting change points, or handling count data and non-count data separately, to the best of the authors’ knowledge, there exists no statistic that combines all of these properties and remains easily amenable. ERR and ERRR are bright exceptions in this regard.

One would also like to emphasize the fact that ERR would be an invaluable weapon in every modeler’s arsenal, especially while dealing with events which are sparse or rare or both. Figure 5 depicts a slowly decaying ACF curve, a classic signature of a long memory process and interested researchers might explore the possibility of fitting fractionally differenced time series models in this situation. Here, following the principle of parsimony, the authors have refrained from creating a model which is unnecessarily complex. It goes without saying that a relentless search for a better model would invariably bring in more advanced technical ideas, but it is our firm conviction that as long as the underlying structure remains ERR or ERRR, better forecasts can be achieved without paying a hefty price in terms of model complexity.

The purpose of the present work was twofold: On one hand and on a lesser extent, one attempted to address the issue of a suspected cause-effect relationship between global warming and hurricane intensity from a rigorous statistical perspective—the absence of which created a void too wide to ignore. On the other hand and to a much larger extent, one intended to formulate and popularize a smoothing statistic which should be able to understand the nature (both direct and inverse) and extent (strong or weak) of the dependence between two time series and which, at the same time, should have a simple construction and should preferably provide useful insights into the dynamics of the process: identify change points, for instance. ERRR provided a nice solution to both and the authors are confident that owing to its simplicity and strong intuitive properties, it should find wide applications in applied areas such as geology, volcanology, medical science, and meteorology. Encouraging evidence of its growing popularity may be garnered from Ho and Bhaduri [19] and Bhaduri and Zhan [1]. Once the acceptability of the proposed simple method is established, one can extend these to more complex Bayesian hierarchical spatio-temporal or co-regional models along lines described by Vanem [35], for instance.

Modern literature is thriving on new and evolving techniques and each day, one is bombarded with batteries of complex statistical tests and estimates and it is easy to lose sight of the fact that simplicity is a virtue one can never afford to overlook, especially if it can provide results that are in considerable agreement with the ones generated by established methods. It is believed that both ERR and ERRR are excellent examples in this regard.