1 Introduction

The modern progress in tissue engineering design and ensuing applications calls for the definition of new sophisticated constitutive modeling of soft materials, which rely on robust tools of computational mechanics [1]. In terms of constitutive difficulties, fibrous bio-tissues can be considered among the most challenging materials, since the need of finding patient-specific solutions requires modeling the microstructural complexity and variability typical of such tissues [2, 3]. Under several biological working conditions, biomaterials manifest reversible behaviors, suggesting the use of hyperelastic models, where the multiscale microstructure of the material can be embedded, in a continuum sense, within an appropriate strain energy density. Hyperelasticity facilitates the achievement of microstructurally consistent material models to be used in predictive numerical applications [4,5,6,7].

In a more general framework, fiber-reinforced composite materials characterized by two or more sets of fibers are modeled often by assuming the mechanical superposition of distinct contributions of the material constituents. In particular, the strain energy describing a homogeneous and isotropic matrix is usually combined with an anisotropic strain energy density term for each fiber family considered in the model. These models apply very well to composites, where the distinct fiber components are disposed in an ordered manner and with a homogeneous strong alignment. Most soft biological tissues, by the way of contrast, are multiphasic materials [7] characterized by a position-dependent fiber arrangement and by a random orientation of the reinforcement [8]. Biological fiber-reinforced media represent one important example of study encompassing the well-established mechanical theory of continua with large deformations with the less explored statistical characterization of anisotropic materials with microstructural features. The geometrical and topological complexity demands adopting a statistical approach in the description of the fiber arrangement. Stochastic approaches are based on the introduction of a probability distribution function (PDF) to express the probability of finding a fiber oriented in a given direction [9].

The description of statistical distributions of fibers in a material model was introduced by Lanir [10]. Experimental evidence has been prompting towards the characterization of fiber distributions by means of von Mises PDF (see, e.g., [11]), although Bingham orientation density functions built on microsphere models have also been considered [12]. For the sake of computational convenience, however, material models for bio-tissues have been formulated in terms of invariant-based hyperelastic strain energy densities [13,14,15,16]. Such models, i.e., account for the presence of distributed fibers by introducing first- and second-order statistics of the pseudo-invariant \({\mathrm{I}_4}\) associated to the structure tensor of the main orientation of the fibers [11, 17, 18]. Note that the non-Italic symbol \({\mathrm{I}_4}\) stands for the aleatoric variable in opposition to the deterministic variable \(I_4\). Although such approximations introduce a theoretical limitation in the material model, nevertheless several efficient numerical implementations based on experimental evidence [8] have been proposed in the literature; see [9] and [19] for an extended review.

In the present study, we propose a generalization of the stochastic description of fiber distributed tissues approximated through the pseudo-invariant \({\mathrm{I}_4}\) statistics at the first order [11] and at the second order [18], thus extending the approach described in [19]. In particular, we characterize the non-uniform orientation of the fiber arrangement by generalizing the three-dimensional (3D) PDF in the composition of two independent PDFs. We begin from a well-established theoretical framework [20] and assume the tridimensional distribution of the reinforcement to be described by means of a PDF dependent on the first spherical angle (\(\Theta \)) and a PDF dependent on the second spherical angle (\(\Phi \)). We demonstrate the ability of the present formulation to recover the typical mechanical behavior of isotropic, transversely isotropic, fully anisotropic, and planar distributions [9] by tuning only two material parameters. We characterize a complete set of parameter combinations for the superposition of the two PDFs. Furthermore, we illustrate the mechanical meaning of the proposed formulation in terms of averaged integral constants and highlight the relevance of the approach in numerical modeling of fiber-reinforced tissues and the feasibility to introduce a switch for the exclusion of the compressed portion of fibers [21].

The paper is organized as follows. In Sect. 2, we provide a brief summary of the material model for distributed fibers and introduce the statistical definition of our generalized spatial PDF superposition. In Sect. 3, we present a quantitative characterization of the fiber distribution identifying the limit cases and the potential three-dimensional configurations implicitly included in the model. We further provide a quantitative analysis of the generalized integral constants that characterize the model. Finally, in Sect. 5 we discuss model reliability and limitations, thus presenting future perspectives.

2 Generalized fiber distributed material model

In the following discussion, we consider only the anisotropic part of the strain energy density of a fibrous material, which is the only part affected by the presence of the fibers, and assume a rather standard exponential form that possesses good mathematical properties. In the following, we assume tacitly that the material is incompressible, i.e., \(J=1\).

2.1 Anisotropic directional strain energy density

We comply with the usual definitions in finite kinematics and denote with \({\mathbf {F}}\) the deformation gradient, with \(J = \det {\mathbf {F}}\) the Jacobian or determinant of \({\mathbf {F}}\), with \(\overline{{\mathbf {F}}}= J^{-1/3}{\mathbf {F}}\) the isochoric deformation gradient, with \({\overline{{\mathbf {C}}}}=\overline{{\mathbf {F}}}^\mathrm{{T}} \overline{{\mathbf {F}}}\) the isochoric right Cauchy–Green deformation tensor, and with \({\mathbf {A}}= {\mathbf {a}}\otimes {\mathbf {a}}\) the structure tensor associated to a specific orientation \({\mathbf {a}}\). The fourth isochoric pseudo-invariant \({\overline{I}_4}= {\mathbf {A}}: {\overline{{\mathbf {C}}}}\) accounts for the global effects of a deformation over the fiber reinforcement [13]. We remark that the theoretical formulation proposed in the present work can be readily adopted with the classical anisotropic invariants in the case of compressible materials avoiding non-physical computational issues [22, 23]. The anisotropic strain energy density associated to the orientation \({\mathbf {a}}\) has the form:

$$\begin{aligned} {\Psi }({\overline{I}_4})=\frac{k_1}{2k_2} \exp \left[ k_2\left( {\overline{I}_4}- 1 \right) ^2\right] - \frac{k_1}{2k_2}\, , \end{aligned}$$
(1)

where \(k_1\) (a stiffness-like parameter) and \(k_2\) (a dimensionless rigidity parameter) control the mechanical response at low and high strains, respectively.

Fig. 1
figure 1

Generalized anisotropic probability distribution density functions, describing fiber orientation, mapping the directions \({\mathbf {a}}\) within the unit sphere into real numbers that measure the density. Surface plots are defined by the vector \(\rho ({\mathbf {a}}){\mathbf {a}}\) with \({\rho _{\Theta }(\theta )}\), \({\rho _{\Phi }(\phi )}\) based on von Mises distributions (4), (5). The limit case of \({b_\Theta }={b_\Phi }=0\) describes full isotropy. The limit case \({b_\Theta }\rightarrow \infty \) with \({b_\Phi }=0\) describes fibers all aligned in the polar direction (deterministic transverse isotropy). The limit case \({b_\Phi }\rightarrow \infty \) with \({b_\Theta }=0\) describes a two-dimensional fiber arrangement (deterministic planar isotropy). The inset describes the Euler angles associated with the generic direction \({\mathbf {a}}\), when it does not coincide with any of the Cartesian basis vectors

Full size image

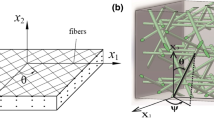
We identify a specific orientation stemming from a material point of a fibrous solid in a unit sphere \(\Omega \) with the unit vector in spherical coordinates (see the inset in Fig. 1):

$$\begin{aligned} {\mathbf {a}}= \sin {\Theta }\cos {\Phi } \, {\mathbf {e}}_1 + \sin {\Theta }\sin {\Phi } \, {\mathbf {e}}_2 + \cos {\Theta } \, {\mathbf {e}}_3 \, , \end{aligned}$$
(2)

defined in the orthogonal basis \(({\mathbf {e}}_1,{\mathbf {e}}_2,{\mathbf {e}}_3)\), where \(\Theta \) and \(\Phi \) are the Euler angles in the reference configuration. Fibers in \(\Omega \) are spatially oriented according to a normalized PDF, \(\rho ({\mathbf {a}})\equiv \rho (-{\mathbf {a}})\), which quantifies the fraction of fibers in the direction \({\mathbf {a}}\). We regard \(\Theta \) and \(\Phi \) as aleatoric variables varying in the ranges \([0,\pi ]\) and \([0,\pi ]\), respectively. As customary in statistical descriptions, we indicate with capital letter X the aleatoric variable and with small letter x its occurrence, i.e., its deterministic value.

2.2 Generalized distributed fibers

In the following, we generalize the formulation proposed by Petsche and Pinsky [24] and assume that the tridimensional distribution of the reinforcement decomposes into the product of two independent PDFs, each of which is a function of one Eulerian angle, i.e.,

$$\begin{aligned} \rho ({\mathbf {a}}) \equiv { {N_{\Theta ,\Phi }}} \, {\rho _{\Theta ,\Phi }(\theta ,\phi )}= { {N_\Theta }{N_\Phi }} \, {\rho _{\Theta }(\theta )}\, {\rho _{\Phi }(\phi )}\, . \end{aligned}$$
(3)

As customary for collagen reinforcement in biological tissues [8], we assume a von Mises type PDF for the angle \(\Theta \). Additionally, we assume a von Mises type distribution centered in \(\phi =\pi /2\) for the PDF of \(\Phi \). Expression (3) is chosen relying on recent experimental findings concerning the tridimensional distribution of the orientation of collagen fibers in biological tissues [25], where a different physiological spreading of collagen fibers is observed in the two orthogonal directions. To construct the sought PDF, we make use of the following observation: (i) since the two PDFs are statistically independent, they can be normalized through two distinct coefficients \({N_\Theta }={N_\Theta }({b_\Theta })\) and \({N_\Phi }={N_\Phi }({b_\Phi })\), respectively; (ii) the necessity of describing, in a general manner, all the location-dependent changes observed in the fiber arrangement requires the introduction of two distinct and in general different concentration parameters, \({b_\Theta }\), \({b_\Phi }\), one for each PDF; (iii) the character of the resulting distribution is fully tridimensional and it will generalize the transversely isotropic model originally proposed in [11]; (iv) the formulation recovers, as a limiting case, the planar distribution of the fibers. Thus, we write

$$\begin{aligned} {\rho _{\Theta }(\theta )}&= \exp {\left[ {b_\Theta }\cos {2\theta } \right] }, \end{aligned}$$
(4)
$$\begin{aligned} {\rho _{\Phi }(\phi )}&= \exp {\left[ {b_\Phi }\cos (\phi - \pi /2) \right] }, \end{aligned}$$
(5)

where \({b_\Theta }\) and \({b_\Phi }\) define the concentration parameters of the two independent PDFs, respectively.

We comply with the normalization condition in the half sphere

$$\begin{aligned} \dfrac{1}{2\pi } \int _0^\pi \int _0^\pi \rho ({\mathbf {a}}) \sin \theta \, \mathrm{d}\theta \, \mathrm{d}\phi \equiv {N_{\Theta ,\Phi }}\int _0^\pi \int _0^\pi {\rho _{\Theta ,\Phi }(\theta ,\phi )}\sin \theta \, \mathrm{d}\theta \, \mathrm{d}\phi = 1 \, , \end{aligned}$$
(6)

and define the normalization coefficients

$$\begin{aligned} {N_\Theta }= \dfrac{1}{\int _0^\pi {\rho _{\Theta }(\theta )}\, \sin \theta \, \mathrm{d}\theta },\qquad {N_\Phi }= \dfrac{1}{\int _0^\pi {\rho _{\Phi }(\phi )}\, \mathrm{d}\phi }, \end{aligned}$$
(7)

such that, given (3) and (6), the following relation is obtained:

$$\begin{aligned} {N_{\Theta ,\Phi }}={N_\Theta }{N_\Phi }\equiv \dfrac{1}{2\pi } \,. \end{aligned}$$
(8)

Here we note that \({N_\Phi }\) in (7)\(_2\) corresponds to the correct normalization of \({\rho _{\Phi }(\phi )}\), while \({N_\Theta }\) in (7)\(_1\) does not fulfill such a condition due to the presence of \(\sin \theta \). However, \({N_\Theta }\) can be expressed as a function of \({N_{\Theta ,\Phi }}\) and \({N_\Phi }\) resulting very useful in what follows.

The structure tensor approach requires introducing the average operator [18]

$$\begin{aligned} \langle \cdot \rangle = \int _\omega \rho ({\mathbf {a}}) (\cdot ) \, \mathrm{d}\omega , \end{aligned}$$
(9)

where the infinitesimal solid angle is \(\mathrm{d}\omega =\sin \theta \, \mathrm{d}\theta \, \mathrm{d}\phi \) in polar coordinates. In particular, the average and variance of the fourth pseudo-invariant are computed in terms of the generalized averaged structure tensors \({\mathbf {H}}=\langle {\mathbf {A}}\rangle \) and \({{\mathbb {H}}}=\langle {\mathbf {A}}\otimes {\mathbf {A}}\rangle \), i.e.,

$$\begin{aligned} {I^*_4}&\equiv \langle {\overline{I}_4}\rangle = {\mathbf {H}}: {\overline{{\mathbf {C}}}}, \end{aligned}$$
(10)
$$\begin{aligned} {\sigma ^2_{I_4}}&\equiv \langle ({\overline{I}_4}- {I^*_4})^2\rangle = {\overline{{\mathbf {C}}}}: {{\mathbb {H}}}: {\overline{{\mathbf {C}}}}- ({\mathbf {H}}: {\overline{{\mathbf {C}}}})^2 \, . \end{aligned}$$
(11)

In keeping with the theoretical tensor notation adopted in the mechanics of fiber composites [9, 26,27,28], the two generalized structure tensors \({\mathbf {H}}\), \({{\mathbb {H}}}\) are characterized by symmetries that reflect the symmetries of the material behavior. In particular, the average second-order tensor \({\mathbf {H}}\) has a diagonal representation

$$\begin{aligned}{}[H]=\left[ \begin{array}{ccc} {\kappa }_\theta \, {\kappa }_\phi &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {\kappa }_\theta (1-{\kappa }_\phi ) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1-{\kappa }_\theta \\ \end{array} \right] , \end{aligned}$$
(12)

and the average fourth-order tensor \({{\mathbb {H}}}\) has non-vanishing terms

$$\begin{aligned} \begin{array}{l} H_{1111} = \hat{\kappa }_\theta \, \hat{\kappa }_\phi , \\ H_{2222} = \hat{\kappa }_\theta \, (1 - 2 {\kappa }_\phi + \hat{\kappa }_\phi ), \\ H_{3333} = 1 - 2 {\kappa }_\theta + \hat{\kappa }_\theta , \\ H_{1122} = H_{2211} = H_{1212} = H_{2121} = H_{1221} = H_{2112} = \hat{\kappa }_\theta \, ({\kappa }_\phi - \hat{\kappa }_\phi ), \\ H_{1133} = H_{3311} = H_{3131} = H_{1313} = H_{3113} = H_{1331} = {\kappa }_\phi \, ({\kappa }_\theta - \hat{\kappa }_\theta ), \\ H_{2233} = H_{3322} = H_{2323} = H_{3232} = H_{2332} = H_{3223} = ({\kappa }_\theta - \hat{\kappa }_\theta ) (1 - {\kappa }_\phi ) \, , \\ \end{array} \end{aligned}$$
(13)

where the coefficients are

$$\begin{aligned} {\kappa }_\theta&= { {N_\Theta }}\int _0^\pi {\rho _{\Theta }(\theta )}\,\sin ^3\theta \, \mathrm{d}\theta , \quad \hat{\kappa }_\theta = { {N_\Theta }} \int _0^\pi {{\rho _{\Theta }(\theta )}\,\sin ^5{\theta } \, \mathrm{d}\theta } \, , \end{aligned}$$
(14)
$$\begin{aligned} {\kappa }_\phi&= { {N_\Phi }} \int _0^\pi {{\rho _{\Phi }(\phi )}\,\cos ^2{\phi } \, \mathrm{d}\phi } \, , \quad \hat{\kappa }_\phi = { {N_\Phi }} \int _0^\pi {{\rho _{\Phi }(\phi )}\,\cos ^4{\phi } \, \mathrm{d}\phi } \, . \end{aligned}$$
(15)

In the integrals (14) and (15) expressing the coefficients, note that the exponents relative to \(\Phi \) are one unit smaller than those relative to \(\Theta \).

Remark

In the limiting case of uniform distribution of the set of fibers over the range of the angle \(\Phi \), the non-vanishing coefficients of \({\mathbf {H}}\) and \({{\mathbb {H}}}\) converge to the ones originally derived by Gasser et al. [11] and Pandolfi and Vasta [18] (see Appendix A).

Remark

The statistical independence of the two PDFs allows us to relate the new integral coefficients \({\kappa }_\theta , \hat{\kappa }_\theta , {\kappa }_\phi , \hat{\kappa }_\phi \) with those previously derived in [11, 18, 20] (see Appendix B).

2.3 Second-order approximation of strain energy density

According to the second-order or variance approach introduced in [18], the strain energy density \({\Psi }\) is approximated with a Taylor expansion up to the second-order terms about the expected average value of the fourth pseudo-invariant, \({I^*_4}\), i.e.,

$$\begin{aligned} \langle {\Psi }\rangle = {{{\Psi }^{*}}}+ \frac{1}{2} \, {{{\Psi }^{''}}^*}\, {\sigma ^2_{I_4}}\, , \end{aligned}$$
(16)

where \({{{\Psi }^{*}}}= \Psi ({I^*_4})\) and the prime stands for the derivative with respect to \(\overline{\mathrm{I}}_4\). The closed form expression of the average second Piola–Kirchhoff stress tensor is derived then as

$$\begin{aligned} \langle {\overline{{\mathbf {S}}}}\rangle = 2 \, \frac{\partial \langle {\Psi }\rangle }{\partial {\overline{{\mathbf {C}}}}} = f\left( {I^*_4}, {\sigma ^2_{I_4}}\right) \, {\mathbf {H}}\, + \, g\left( {I^*_4}, {\sigma ^2_{I_4}}\right) \, {{\mathbb {H}}}:{\overline{{\mathbf {C}}}}\, , \end{aligned}$$
(17)

where the coefficients f and g depend upon the statistics of \(\overline{\mathrm{I}}_4\) as

$$\begin{aligned} f\left( {I^*_4}, {\sigma ^2_{I_4}}\right) = {{{\Psi }^{*}}}\sum _j^{0...3} a_{j} \, {I^*_4}^j \, , \qquad g\left( {I^*_4}, {\sigma ^2_{I_4}}\right) = {{{\Psi }^{*}}}\sum _j^{0...2} b_{j} \, {I^*_4}^j \, , \end{aligned}$$

with

$$\begin{aligned} \begin{array}{ll} a_0 = -4k_2 - 8 {\sigma ^2_{I_4}}k_2^3 - 12 {\sigma ^2_{I_4}}k_2^2, &{} \quad b_0 = 4k_2 + 8k_2^2, \\ a_1 = 24 {\sigma ^2_{I_4}}k_2^3 + 12{\sigma ^2_{I_4}}k_2^2 - 8k_2^2, &{} \quad b_1 = -16k_2^2, \\ a_2 = 16k_2^2 - 24 {\sigma ^2_{I_4}}k_2^3, &{} \quad b_2 = 8k_2^2, \\ a_3 = 8 {\sigma ^2_{I_4}}k_2^3 - 8k_2^2\,. \end{array} \end{aligned}$$

For details about the derivation, we refer to the original works [18, 20, 29] where also the corresponding tangent stiffness is provided.

3 Distribution characterization

In this section, we illustrate with diagrams and 3D plots the geometrical significance of the proposed generalized approach, which clarifies the mechanical consequences on the behavior of the material.

3.1 Generalized fiber distributions

We begin with the sequence of surface plots presented in Fig. 1. For selected combinations of the concentration parameters \({b_\Theta }\), \({b_\Phi }\), each surface plot maps on the unit sphere the weighted density \(\rho ({\mathbf {a}})\) in the direction \({\mathbf {a}}\). Starting from the isotropic case (\({b_\Theta }={b_\Phi }=0\), center), by increasing only the \(\Theta \) concentration coefficient the transverse isotropic limit case is reached, for \({b_\Theta }\rightarrow \infty \) and \({b_\Phi }=0\) (on the right). By increasing only the \(\Phi \) concentration coefficient, the planar isotropic limit case is reached for \({b_\Phi }\rightarrow \infty \) and \({b_\Theta }=0\) (on the left).

We note that there is a close correspondence between the sequence and the two limit conditions here described and the ones previously presented in [9], obtained by altering of the nature of the PDF, and in [30], obtained by including negative values of the concentration parameter b. In particular, when \({b_\Phi }=0\), the standard von Mises distribution is retrieved and, for \({b_\Theta }>0\), the results are the same as in the right-hand side of the plot in Figure 1 of the paper by Federico and Gasser [9]. In contrast, for \({b_\Phi }\ne 0\), the distribution used in the present work gives results that the traditional von Mises distribution cannot achieve, by construction, in agreement with Holzapfel et al. [19]. Accordingly, when \({b_\Phi }\rightarrow \infty \) we recover planar symmetry over the plane aligned to the symmetry axis of the standard von Mises distribution. Contrariwise, the approach in [9] recovers axial symmetry for both limiting conditions. Moreover, the present approach uses a unified theoretical description that allows to model with two distinct concentration parameters a continuous variety of PDF combinations, including different forms of fiber-dependent anisotropy.

The present model represents an enrichment and extension of previous formulations and allows to describe with higher accuracy the microstructure of complex fibrous materials.

Figure 2 visualizes representative examples of surface plots, for different combinations of the concentration parameters. The surface representation of the PDF considers only half spherical domain \([\Theta ,\Phi ]\in [0,\pi ]\) and each image compares three different combinations of the concentration parameters. The selected cases highlight the modularity of the approach in reproducing experimental based biological tissue anisotropies that result highly diversified by definition [25].

Fig. 2
figure 2

Surface plots defined by the vector \(\rho ({\mathbf {a}}){\mathbf {a}}\) in the half range \(\Theta \in [0,\pi ]\), \(\Phi \in [0,\pi ]\). Representative examples of multiple combinations of the concentration parameters \({b_\Theta },{b_\Phi }\) (legend provided)

Full size image

Figure 2a, b represents typical planar configurations (green) of the fiber arrangement in which a smooth transition from isotropy or little anisotropy (yellow) is shown. In these cases, the intermediate configurations, required for a continuum location-dependent material assignment, are represented by the red surfaces. Figure 2c, d shows how a uniform anisotropic case (yellow) can be modified in different flattened three-dimensional distributions (green) where, again, the red surface indicates a possible root for the transition. Finally, Fig. 2e, f shows typical representations of planar anisotropic distributions. In particular, Fig. 2e shows a smooth continuous transition from yellow to green, while Fig. 2f compares a purely uniform transverse isotropic case (red) with two alternative planar transverse isotropic cases (yellow, green). This is a key feature of our generalized formulation that allows for fine modeling of planar anisotropic fiber arrangements not included in previous works.

In Fig. 3, we provide the surface plots disposed in a matrix format according to different values of the concentration parameters. By properly selecting the two concentration parameters \({b_\Theta }\), \({b_\Phi }\) it is possible to investigate several different spatial distributions of the fibers and their mechanical implications [25].

Fig. 3
figure 3

Surface plots \(\rho ({\mathbf {a}}){\mathbf {a}}\) resulting from the combination of \({b_\Theta },{b_\Phi }\in [0,0.225,1,2,8]\)

Full size image
Fig. 4
figure 4

Dependence of the different integral constants \(\kappa \) and \({\hat{\kappa }}\) on the corresponding concentration parameters, for different types of PDF. a \(\kappa \), \({\hat{\kappa }}\) as provided in Eq. (25), versus the concentration parameter b. b \({\kappa }_\theta \), \(\hat{\kappa }_\theta \) as provided in Eq. (14), versus the concentration parameter \({b_\Theta }\). c \({\kappa }_\phi \), \(\hat{\kappa }_\phi \) as provided in Eq. (15), versus the concentration parameter \({b_\Phi }\). d Uniaxial loading (correct integration domain) with \(\lambda =1.2\): \(\kappa \), \({\hat{\kappa }}\) as provided in Eq. (25), versus the concentration parameter b. e Uniaxial loading with \(\lambda =1.2\): \({\kappa }_\theta \), \(\hat{\kappa }_\theta \) as provided in Eq. (14), versus the concentration parameter \({b_\Theta }\). f Uniaxial loading with \(\lambda =1.2\): \({\kappa }_\phi \), \(\hat{\kappa }_\phi \) as provided in Eq. (15), versus the concentration parameter \({b_\Phi }\). The plot coincides with (c), since the fourth pseudo-invariant does not depend on the \(\Phi \) angle under uniaxial loading

Full size image

3.2 Integral constants and integration domain

In order to visualize the differences of the distribution of the fibers between previous approaches and the present formulation, in Fig. 4 we plot the constants that characterize the structure tensors \({\mathbf {H}}\) and \({{\mathbb {H}}}\) versus the concentration parameters. The figure shows and compares the variability of the integral constants \(\kappa \), \({\hat{\kappa }}\), \({\kappa }_\theta \), \(\hat{\kappa }_\theta \), \({\kappa }_\phi \), and \(\hat{\kappa }_\phi \) defined in Eqs. (14), (15), and (25), respectively, as a function of the corresponding concentration parameters b, \({b_\Theta }\), and \({b_\Phi }\). Figure 4 shows the progressive reduction of the value of the integral constants with the increase of the concentration parameters. This trend is in strong agreement with the expected variation of the PDF of von Mises type [11, 18]. The values of the generalized integral constants \({\kappa }_\theta \), \(\hat{\kappa }_\theta \), \({\kappa }_\phi \), \(\hat{\kappa }_\phi \) assume the same order of magnitude as of \(\kappa ,\hat{\kappa }\), underlying a similar mechanical contribution to the averaged second- and fourth-order tensors \({\mathbf {H}}\) in Eq. (12) and \({{\mathbb {H}}}\) in (13), respectively.

Plots in Fig. 4d–f illustrate the non-linear behavior of the same integral constants when the material is undergoing uniaxial loading. In order to exclude non-physical conditions of compressed fibers, in the plots the reduced integration domain \(\overline{\mathrm{I}}_4>1\) is considered, cf. [29]. In fact, under uniaxial loading conditions, the directional fourth invariant depends only on the angle \(\Theta \) according to the following relation:

$$\begin{aligned} \overline{\mathrm{I}}_4 = \dfrac{1}{\lambda } + \dfrac{\lambda ^3 - 1}{\lambda } \cos ^2\Theta \, . \end{aligned}$$

Fibers in extension, thus contributing to the mechanical response, fall between the following limits dependent on the stretch \(\lambda \) [29]:

$$\begin{aligned} \arccos \dfrac{1}{\sqrt{1+\lambda +\lambda ^2}} \le&\,\, \Theta \le \pi -\arccos \dfrac{1}{\sqrt{1+\lambda +\lambda ^2}} \quad \text {if}\,\,\lambda \le 1, \end{aligned}$$
(18)
$$\begin{aligned} 0 \le \Theta \le \arccos \dfrac{1}{\sqrt{1+\lambda +\lambda ^2}} \quad&\, \cup \quad -\arccos \dfrac{1}{\sqrt{1+\lambda +\lambda ^2}} \le \Theta \le \pi \quad \text {if}\,\,\lambda \ge 1 \,. \end{aligned}$$
(19)

Contrariwise, there is no variation of the integration domain for the angle \(\Phi \), which remains in \([0,\pi ]\). According to the limitation in (18) and (19), the constants \(\kappa \), \(\hat{\kappa }\), \({\kappa }_\theta \), and \(\hat{\kappa }_\theta \) assume reduced values; see Fig. 4d, f.

The same procedure can be applied for multiaxial loading patterns, but in such cases multiple inequalities will arise [29], which renders the evaluation of the constants rather complex. A detailed analysis of the tension–compression problem for the generalized statistical formulation is left to a forthcoming contribution.

4 Examples of mechanical response

By way of example, we present for the proposed model numerical stress–strain curves obtained by uniaxial and biaxial loading conducted at the constitutive level. In order to compare the present results with the those reported in [18], we make the following simplifying assumptions: (i) compressed fibers are not excluded from the calculations and they will contribute to the mechanical response, and (ii) only the contribution of the anisotropic part of the strain energy density is considered. In the present calculations, the main direction of the fibers is assumed to coincide with axis 3, while the planar condition is reached in the plane normal to axis 2, cf. Fig. 5.

Fig. 5
figure 5

Orientation of fiber distribution. Axis 3 defines the main direction of the fibers. The planar distribution lies on the 1–3 plane

Full size image
Table 1 Values of the model coefficients according to the dispersion parameters
Full size table

We investigate the performance of the model by considering material properties in the deformation and stress range of interest of soft biological material, such as the cornea [2], but without addressing a particular material. In the following calculations, thus, the two rigidity parameters \(k_1\) and \(k_2\) are set to 0.15 MPa and 1, respectively. The parameters \(\kappa _\Theta \), \(\hat{\kappa }_\Theta \), \(\kappa _\Phi \), and \(\hat{\kappa }_\Phi \) vary according to the values of the dispersion parameters \(b_\Theta \) and \(b_\Phi \); see Table 1.

To assess the anisotropic response of the material, uniaxial tests are performed in three directions of loading. As shown in Fig. 5, the first loading direction is parallel to the mean orientation of the fibers (direction 3), the second within the plane of the fibers (direction 1), and the third coincides with axis 2.

Figure 6 shows the response of the model undergoing uniaxial loading. Curves plot the Cauchy normal stress \(\sigma _{ii}\) in the loading direction versus the corresponding logarithmic strain \(e_{ii}\). The response is shown for different combinations of the dispersion parameters \(b_\Theta \) and \(b_\Phi \). In particular, Fig. 6a–e shows the cases with equal values of the two dispersion parameters, while Fig. 6b–f visualizes the effect of varying one of the two dispersion parameters.

For uniaxial loading in the direction of the fibers, shown in Fig. 6a, b, the dominant dispersion parameter is \(b_\Theta \). For \(b_\Theta = 8\), the uniaxial response is almost the same, independently of the value of \(b_\Phi \). When the dispersion of the fibers increases (i.e., the value of \({b_\Theta }\) decreases), curves differentiate, more markedly for low values of the dispersion parameters (isotropic case). For uniaxial loading in the plane of the planar distribution of the fibers, normal to the main direction of the fibers, it can be observed from Fig. 6c, d that the dominant dispersion parameter is still \(b_\Theta \), but \(b_\Phi \) contributes to the differentiation of the response. Note that the values of the stress are one order of magnitude lower than that in the previous case. For the case of loading in the direction normal to the plane of fibers, it can be observed from Fig. 6e, f that when fibers are aligned well the stress is substantially null. The uniaxial behavior is in line with the assumptions of the model.

Equi-biaxial tests are performed considering two cases of loading. In the first loading case, load is applied to the directions 1 and 3. In the second case, load is applied to the directions 1 and 2.

Fig. 6
figure 6

Uniaxial response of the proposed model for loading acting a, b in the direction of the fibers, c, d in the direction normal to the plane of fibers, and e, f in the plane of the fibers, normal to the main direction. Figures compare the dimensionless uniaxial response for different values of the dispersion parameters \(b_\Theta \) and \(b_\Phi \). Curves are combined to show the effect of a–e equal values of the dispersion parameters for the two distributions and b–f different values of the dispersion parameters for the two distributions. Note that the stress axis scales are different. Stress in MPa. a Main fiber direction, b main fiber direction, c normal to the fiber plane, d normal to the fiber plane, e in the fiber plane, f in the fiber plane

Full size image
Fig. 7
figure 7

Biaxial response of the proposed model for loading acting a, b in the plane of the fibers, c, d in the direction of the fibers and in the normal direction in the plane of the fibers. The figures show the comparison of the biaxial response for different values of the dispersion parameters \(b_\Theta \) and \(b_\Phi \). Curves are combined to show the effect of different values of the dispersion parameters for the two distributions. Note that the stress axis scales are different. Stress in MPa. a Main fiber direction, b in the fiber plane, c main fiber direction, d normal to the fiber plane

Full size image

Results of equi-biaxial tests are shown in Fig. 7. Curves show the normal components of the Cauchy stress versus the normal components of the logarithmic strain. The response is shown for different combinations of the dispersion parameters \(b_\Theta \) and \(b_\Phi \). Note that the stresses \(\sigma _{11}\) and \(\sigma _{22}\) are negative, due to the imposed isochoric condition. The incompressibility condition is responsible also for slightly higher stresses in the direction normal to the plane of the fibers. For equi-biaxial loading, a fully dispersed material (\(b_\Theta = b_\Phi = 0\)) provides very low stresses in both directions of loading. The more concentrated the fiber orientation, the higher the biaxial response.

5 Discussion

We presented a generalized statistical formulation of the constitutive behavior of fiber-reinforced anisotropic tissues characterized by a distributed arrangement of fibers. We began our discussion from a consolidated theoretical hyperelastic framework [20], based on the definition of structure tensors [31] that are introduced to characterize the microstructural properties of the fibrous tissue by means of directional fourth pseudo-invariants. With the generalized formulation, we extend the recent suggestion appeared in [19, 24] by introducing two independent probability distribution functions of von Mises type, one for each Eulerian angle \(\Theta \), \(\Phi \) that identifies the generic spatial orientation. In doing so, we characterize the non-uniform spatial orientation of fiber distribution by means of two parameters that represent the concentration coefficients of the two von Mises distributions. The approach allows to recover previous formulations available in the literature as a limiting case, when a uniform distribution of the PDF of \(\Phi \) is considered. As an additional feature, important configurations of the fiber distributions are recovered for specific values of the concentration parameters, e.g., isotropic, transversely isotropic, and planar isotropic configurations [9] characterized by planar symmetry rather than axial symmetry.

Our approach is well suited for computational applications when soft hyperelastic materials with dispersed fibers are involved [32, 33]. We presented examples of the mechanical response of the model, for various values of the dispersion parameters, in uniaxial and biaxial loading under isochoric conditions.

We highlighted that the proposed formulation allows for the direct implementation of the tension–compression switch procedure [21, 29, 34], in which fibers under compression are excluded, within a statistical description of the tissue.

Limitations of the present approach are related to the assumption of statistical independence of the two von Mises PDF. However, notable examples of fiber disorganization [25] can easily be modeled via the proposed approach in a location-dependent fashion as well as failure mode prediction [35,36,37], non-local elasticity [38], multiscale [39, 40], and multiphysics problems [41,42,43,44,45].