Introduction

Accurate and reliable precipitation data are essential for modeling studies in hydrology. Precipitation is one of the most important components of the hydrological cycle and cannot be ignored in hydrological modeling (Pascale et al., 2015). For hydro-meteorological analysis in many regions, long-term data sets for rain gauge observations are unavailable (Salman et al., 2018). Remote sensing satellite-based precipitation can provide homogeneous, continuous information in space and time over a region (Roca, 2019). At present, various gridded data sets like ground- and satellite-based data sets are increasingly used in hydrological studies. Even though many data sources for precipitation are available, these data sets may not be consistent due to different sources and estimation procedures (Tapiador et al., 2017). Hence, it is very imperative to evaluate the suitability of these time series data for hydrological modeling studies. Few studies have been carried out recently that compare various gridded data sources (Beck et al., 2017; Cattani et al., 2016; Hu et al., 2016; Prakash et al., 2016a, 2016b; Salman et al., 2018; Sharannya et al., 2020; Sireesha et al., 2020; Sun et al., 2018). These methods can be classified under two groups, namely (1) comparison of the statistical indices using a reference data set and (2) evaluation of its use for a specific application.

Sharannya et al. (2020) performed analysis of gridded precipitation data, specifically Tropical Rainfall Measuring Mission (TRMM) and the Climate Hazards Group Infra-Red Station Precipitation (CHIRPS) data sets, for the an Indian river catchment named Gurupura. They have used Soil and Water Assessment Tool (SWAT) in order to simulate stream flows and compare them with flows generated by the India Meteorological Department (IMD). The TRMM outperformed CHIRPS in terms of rainfall estimation, based on the statistical results. Sireesha et al. (2020) evaluated the performance of gridded precipitation data sets, namely, Global Precipitation Climatology Centre (GPCC), TRMM, and Modern-Era Retrospective Analysis for Research and Applications (MERRA) in the Sina basin, India. The statistical indicators, percentage bias (PBias), normalized root-mean-square error (NRMSE), Nash–Sutcliffe efficiency (NSE), modified index of agreement (MD), and volumetric efficiency (VE) were used to check the suitability of the gridded data sets. The selected gridded precipitation data sets were ranked using compromise programming (CP). TRMM occupies the first position, followed by MERRA.

In the present study, three gridded data sets, namely India Meteorological Department gridded data (IMD gridded), TRMM, and MERRA were used. Among these data sets, IMD gridded data are prepared using Shepard’s interpolation using the daily precipitation data from 6995 observed stations over India after controlling the quality of observed station data (Pai et al., 2014). TRMM data are based on remote sensing, while MERRA data are based on reanalysis. In India, recently, many studies have been carried out by taking IMD gridded data as the standard data for evaluation of satellite-based data and many other hydrological studies (Sharannya et al., 2020; Venkatesh et al., 2020). There are only limited studies on the assessment of IMD gridded rainfall for its suitability in hydrological applications (Chowdhury et al., 2021; Subash et al., 2020). Subash et al. (2020) carried out a study to assess the error characteristics of gauge-only gridded product (IMD gridded data) and multi-satellite gridded precipitation data (TRMM-TMPA-3B42). As the reference data set, rain gauge observation data from the Kabini drainage basin in southern India were selected. Multiple visual and statistical metrics were used for evaluating the gridded data set. The results show that IMD gridded data outperforms the multi-satellite precipitation product. Chowdhury et al. (2021) analyzed the various gridded precipitation data of the Satluj River basin in India using compromise programming. The Technique for Order Preference by Similarity to an Ideal Solution in Fuzzy Field (f-TOPSIS) was applied to get the weight of the selected performance indicators. The APHRODITE (Asian Precipitation-Highly-Resolved Observational Data Integration towards Evaluation) got the highest rank, followed by IMD gridded data and ERA interim.

Few studies have ranked global climate models (GCMs) using multi-criteria decision-making (MCDM) techniques. Raju et al. (2017) ranked thirty-six GCMs based on the simulations of maximum and minimum temperatures of India across 40 grid data points. The correlation coefficient, skill score, and normalized root mean square error are used as performance indicators for assessing GCMs. The entropy method was adopted to compute the indicator weights, and the compromise programming technique is adopted for GCM ranking. Raju and Kumar (2014) adopted MCDM for evaluating 11 GCM data sets in India based on precipitation data. Raju and Kumar (2014) used Preference Ranking Organization Method (PROMETHEE II) to rank eleven GCMs for the climate variable precipitation based on five performance indicators, considering equal and varying weights. To calculate the weights, they employed the entropy method.

The precipitation data sets have to be checked for homogeneities because measurement techniques and observational procedures are different for different data sources; environment characteristics may be different. In the case of gauge-based measurements, the location of stations may be different. For the detection of non-homogeneities in data series, there are various methods. The absolute homogeneity tests are a combination of the Pettitt test, standard normal homogeneity test (SNHT), Buishand range test (BR), and von Neumann ratio (VNR) test (Che Ros et al., 2016). In these tests, the results are classified into homogeneous, doubtful, and change point (suspect) based on the number of tests accepting the alternative hypothesis.

The precipitation concentration index (PCI) is an essential index for understanding the temporal variation of rainfall and for evaluating changes in the seasonal rainfall pattern (Ghorbani et al., 2021; Zhang et al., 2019). PCI is a valuable indicator for predicting hydrological risks like droughts and floods (Gocic et al., 2016).

The present study focuses on the Kallada River basin, Kerala, India, originating from the Western Ghats Mountains. Even though a few studies have already been carried out related to the adequacy of gridded data sets, there are only limited studies on the ranking of precipitation data sources. In addition, these techniques have not been applied to the Kerala basin. In the present study, the main objectives are (a) to examine and to assess the suitability of gridded precipitation data sets using multi-criteria decision-making methods such as the compromise programming technique and PROMETHEE II, (b) to examine the homogeneity of data sets, and (c) to rectify the top-ranked data for inconsistency, if present, and to evaluate the temporal variability in precipitation using the precipitation concentration index.

Materials and methods

Study area

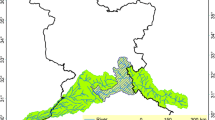
The Western Ghats, also known as the Sahyadri, is a mountain range that extends 1600 km along the western coast of Peninsular India and passes through Tamil Nadu, Kerala, Karnataka, Maharashtra, and Gujarat. These mountains forms Kerala’s most crucial topographic feature, significantly affecting the state’s climate, vegetation, and river hydrology. In Kerala, there are 44 rivers, out of which 41 are west flowing with the origin from the Western Ghats and flows westwards towards the Arabian Sea or into the Backwaters of Kerala. The Kallada River basin was chosen as the study area, with its origin in Kulathupuzha at 1750 m. It passes through Punalur, Pathanapuram, Kunnathur, Puthoor, and Kallada for 121 km until it reaches Ashtamudi Lake. The catchment area of the river basin is 1699 km2. The Kallada River is significant to south Kerala as a source of irrigation, electricity generation, and aquaculture (Satya narayana reddy et al., 2021). Kallada River is positioned between 8° 49′–9° 17′ north latitudes and 76° 24′–77° 16′ east longitudes (Fig. 1). This river is the confluence of three major rivers, named Kulathupuzha, Shenduary, and Kalthuruthi, which join near Parappar in Thenmala. Major rain gauge stations are located at Punalur, Kollam, and Aryankavu. The landscape is classified into four physiographic zones: lowland (0–30 m), midland (30–200 m), foothill zones (200–600 m), and highland (above 600 m) (GSI, 2005).

Fig. 1
figure 1

Study area

Full size image

The climate of the Kallada River is generally tropical with marked warm and humid seasons and seasonal precipitation. In summer and winter, maximum and minimum temperatures of 34 °C and 21 °C were recorded. The mean yearly precipitation is 2600 mm. Moisture is about 90% in the wet season. The catchment receives precipitation from two types of monsoon, i.e., one is southwest (June to September) and the other is northeast (October to November) with 51.8% and 24% of yearly precipitation, respectively. The remaining 24.2% of precipitation is received during the non-monsoon season.

Data sets

Monthly observed rainfall data for Punalur station in the Kallada basin and ground-based gridded data with 0.25° × 0.25° resolution is obtained from IMD Pune. The observed precipitation data and the ground-based gridded data of IMD were available from 1981 to 2013. The satellite-based gridded precipitation data TRMM is a joint mission between Japan Aerospace Exploration Agency (JAXA) and the National Aeronautics and Space Administration (NASA). Monthly TRMM 3B43, version 7 product with a spatial resolution of 0.25° × 0.25° during the years 1998–2013 were downloaded from the GES DISC-NASA website in NetCDF format. MERRA-2 is a global atmospheric reanalysis data developed by the NASA Global Modeling and Assimilation Office (GMAO). It supplies a regularly gridded and homogeneous data set, with 0.5° × 0.625° spatial resolution for 1981–2013. MERRA data are generally classified as modern reanalysis systems with a higher spatial resolution that applies advanced numerical models and assimilation schemes to combine observations from multiple sources. Table 1 provides the details of the data.

Table 1 Precipitation data set information
Full size table

Methodology

The inverse distance interpolation technique is used to resample the three gridded precipitation data sets to the position of the observed data point. Statistical parameters are utilized as performance indicators to compare the different gridded data with the observed data. The entropy method is adopted to determine indicator weights. Ranking of selected data sources was done using MCDM techniques, namely compromise programming (CP) and PROMETHEE II. A homogeneity test was also performed for all the data sets. The highest-ranked data set is corrected based on double mass curve analysis. The corrected data set is examined for the variability of precipitation rate using PCI. The step-by-step adopted procedure is shown in Fig. 2.

Fig. 2
figure 2

Methodology flowchart

Full size image

Statistical indices

The statistical indices, namely correlation coefficient (R), normalized root mean square error (NRMSE), Nash–Sutcliffe efficiency (NSE), modified index of agreement (MD), and volumetric efficiency (VE), are determined in comparison with IMD observed station data. The statistical indices were normalized before analysis.

Correlation coefficient (R)

It is used to find how robust a relationship exists between different sets of data. If the value of R = 1, there is a positive correlation; if R =  −1, then there is a negative correlation; and if R = 0, then there is no correlation between the data sets. It is evaluated as:

$$R=\frac{n(\sum pq)-(\sum p)(\sum q)}{\sqrt{[n\sum {p}^{2}-\left({\sum p)}^{2}\right][n\sum {q}^{2}-({\sum q)}^{2}]}}$$
(1)

Normalized root mean square error (NRMSE)

NRMSE of 0 value means a perfect fit for the data. NRMSE is calculated as:

$$NRMSE=\frac{{\left[\frac{1}{n}{ \sum_{i=1}^{n}({X}_{sim i} - {X}_{obs i })}^{2}\right]}^\frac{1}{2}}{\frac{1}{n}\sum_{i=1}^{n}{ X}_{obs i}}$$
(2)

Nash-Sutcliffe efficiency (NSE)

This index is a normalized static measure and is calculated as:

$$NSE=1-\frac{\sum_{i=1}^{n}({{X}_{obs i}- {X}_{sim i })}^{2}}{{\sum_{i=1}^{n}\left({X}_{obs i }- {\overline{X} }_{obs i}\right)}^{2}}$$
(3)

A positive value shows that the estimation is good, a negative value shows that the estimation ability is poor, and 1 indicates the best model.

Modified index of agreement (MD)

MD varies between 0 and 1. A value of 1 means perfect agreement.

MD is calculated as:

$$MD=1-\frac{{\sum }_{i=1}^{n}|{X}_{sim}-{X}_{obs}|}{{\sum }_{i=1}^{n}(\left|{X}_{obs}-{\overline{X} }_{obs}\right|+\left|{X}_{sim}-{\overline{X} }_{obs}\right|)}$$
(4)

Volumetric efficiency (VE)

It measures the ratio between observed and model precipitation volumes over a period of time. A value of 1 indicates the ideal condition.

VE is calculated as:

$$VE=1-\frac{\sum_{i=1}^{n}({X}_{sim i}-{X}_{obs i})}{\sum_{i=1}^{n}{X}_{obs i}}$$
(5)

Here, \({X}_{obs}\) = observed precipitation, \({X}_{sim}\) = gridded precipitation, and \({\overline{X} }_{obs}\) = mean observed precipitation.

Ranking of gridded data sets

Determination of weights of indicators using the entropy method

Various indicators’ weights are determined by employing the entropy method (Raju and Kumar 2014). The weight of indicators for each gridded data set was assessed using a formulated payoff matrix (Pomerol and Romero 2000). The weights for each indicator are determined without decision maker intervention, which is the main advantage of this method, which eliminates the excessive bias against the indicator. The indicator weights can be computed as follows:

For the given normalized payoff matrix \({P}_{ij}\), the entropy \({E}_{j}\) for the indicators j for the set of gridded precipitation data sets are computed as follows:

$$E_j=-\frac{1}{\mathrm{ln}\left({P}_{ij}\right)}{\sum }_{i=1}^{N}{P}_{ij}\mathrm{ln}\left({P}_{ij}\right)\ for\ j=1\dots \dots , J$$
(6)

where i = 1, …….., N is the number of gridded precipitation data sets and j is the number of indicators.

The degree of diversification, \({D}_{j}\), for the information given by outcomes of indicator j is

$${D}_{j}=1-{E}_{j}\ for\ j=1\dots .., J$$
(7)

Normalized indicator weights are estimated as

$${W}_{j}=\frac{{D}_{j}}{{\sum }_{i=1}^{J}{D}_{j}}$$
(8)

Compromise programming

Compromise programming is a multi-criteria approach to decision-making, based on the principle that a solution to an acceptable “distance” solution is as “similar” as possible (Raju et al., 2017; Zeleny, 2011). The Lp metric family is used as a distance measure for CP and expressed as

$${{L}_{p}\left(a\right)=\left[\sum\nolimits_{j=1}^{J}{{W}_{J}}^{P}{\left|{{f}_{j}}^{*}-{f}_{j}(a)\right|}^{p}\right]}^\frac{1}{p}$$
(9)

where \(a\) represents a particular precipitation data set; \(j\) is the performance indicator, \(j\) = 1, 2, …, n; \({W}_{j}\) is the weight of each indicator; \({f}_{j}^{*}\) is the normalized ideal value for indicator \(j\); \({f}_{j}(a)\) is the normalized value of the indicator \(j\) for the precipitation data \(a\); and \(p\) is the metric parameter (\(p=1\) for linear measure and \(p=2\) for Euclidian squared distance measure). The precipitation data set having the least \({L}_{p}\) metric value is considered the best.

PROMETHEE II

PROMETHEE II, a multi-criteria decision-making approach (MCDM), is formulated according to the preference function approach (Brans, et al., 1986). The preference function \({P}_{j}(x,y)\) represents the degree of preference of a particular precipitation data set “x” with regard to precipitation data set “y,” for a given performance indicator \(j\) and generalized criterion function. Different types of criterion functions are available, but the usual criterion was adopted in the present study, in which the preference function depends on a small positive difference \({d}_{j}\left(x,y\right)\).

The definition of preference function is as follows:

$${P}_{j}\left(x,y\right)=\left[\begin{array}{cc}0& \mathrm{if }{d}_{j}(x,y)\le 0\\ 1& \mathrm{if }{d}_{j}(x,y)>0\end{array}\right]$$
(10)

Then, the multi-criteria preference index \(\pi \left(x,y\right)\) is the weighted average of preference function \({P}_{j}\left(x,y\right)\) defined as:

$$\pi \left(x,y\right)=\frac{\sum_{j=1}^{J}{W}_{j}{P}_{j}(x, y)}{\sum_{j=1}^{J}{W}_{j}}$$
(11)

Here, \({W}_{j}\) is the weight that is assigned for each indicator, based on the entropy method. J is the performance indicator.

$${\phi }^{+}\left(x\right)=\frac{\sum_{n}\pi \left(x,y\right)}{n-1}$$
(12)
$${\phi }^{-}\left(x\right)=\frac{\sum_{n}\pi \left(y,x\right)}{n-1}$$
(13)
$$\phi \left(x\right)={\phi }^{+}\left(x\right)-{\phi }^{-}\left(x\right)$$
(14)

Here, \({\phi }^{+}\left(x\right)\) and \({\phi }^{-}\left(x\right)\) are the outranking index of the gridded precipitation data set “x” in the total data set “n,” and \(\phi \left(x\right)\) is the overall ranking of the gridded data set “x.” The gridded data set having the highest \(\phi \left(x\right)\) value is considered to be the most suitable precipitation data set.

Homogeneity tests

The homogeneity test was used to check whether the given data is homogeneous over time. In other words, if there exists any significant change point in a time series, then it is classified as non-homogeneous. This test is used to identify and adjust the variation of non-climatic parameters caused due to the differences in observation procedures, time, and relocation of the gauging site (Peterson, et al., 1998). This inhomogeneity in the historical data has a high impact on the outcome of data analysis and forecast. Data homogeneity is an integral part of historical data archival. There are several methods and tools available for testing homogeneity. The most common types of these tests are the Pettitt test, standard normal homogeneity test (SNHT), Buishand test, and von Neumann ratio (VNR) test. The combination of all four tests together is called as absolute homogeneity test.

Pettitt test

It is a non-parametric ranking method widely used for continuous climate series or hydrological series data to capture a single point of change. The steps for non-parametric statistic are as follows (Pettitt, 1979):

  1. 1.

    Ranking of the observations (x) in increasing order (i.e., \({x}_{1,}\) \({x}_{2}\) ……….\({x}_{n}).\)

  2. 2.

    The estimation of \({V}_{i,n}\) is as follows:

    $${V}_{i}=n+1-2{r}_{i}\ for\ i=\ {1,2},3, \dots \dots .n$$
    (15)

Here, \({r}_{i}\) is the rank of \({x}_{i}\).

  1. 3.

    The estimation of \({U}_{i}\) is as follows:

    $${U}_{i}={U}_{i-1}+{V}_{i}$$
    (16)
  2. 4.

    The value of \({K}_{n}\) is obtained from:

    $${K}_{n}={\mathrm{max}}_{1\le i\le n}\left|{U}_{i}\right|$$
    (17)
  3. 5.

    Finally, the estimation of \(P\) is as follows:

    $$P={2e}^{\left(-\frac{6{{K}^{2}}_{n}}{{n}^{3}+{n}^{2}}\right)}$$
    (18)

The null hypothesis rejects if the \(P\) value is smaller than “α,” whereas “α” is the level of significance.

Buishand test

This test is a parametric test that is more susceptible to deviations in the center of the data set (Costa & Soares, 2009). This test is based on the adjusted partial sum with the total deviation from the average value.

Calculation of adjusted partial sum is as follows:

$${S}_{0}^{*}=0; {S}_{k}^{*}={\sum }_{i=1}^{k}({X}_{i}-\overline{X })\ {for\ }k=\mathrm{1,2},\dots.N$$
(19)

Here,\(\overline{X }\) is the average of the observations in a data set (\({X}_{1,}\) \({X}_{2}\)………. \({X}_{N}\)) and \(k\) is the observation number where the change point has occurred.

The rescaled adjusted partial sum is calculated as:

$${S}_{k}^{**}=\frac{{S}_{k}^{*}}{{D}_{X}} \ {for\ }k=1, 2,\dots \dots .N$$
(20)
$${D}_{X}=\sqrt{\frac{\sum_{i=1}^{N}{\left({x}_{i}-{x}_{n}\right)}^{2}}{N}}$$
(21)

The statistic \(Q\) used to test homogeneity is given by:

$$Q={\mathrm{max}}_{0\le k\le N}\left|{S}_{k}^{**}\right|$$
(22)

The null hypothesis will be accepted if the \(\frac{Q}{\sqrt{N}}\) value is less than the standard critical values.

Standard normal homogeneity test

In the study of climatic variations, SNHT is the most widespread homogeneity tests. SNHT is more susceptible to detecting the change points at the start and end of the series.

The statistic \(T\left(k\right)\) is computed as:

$$T\left(k\right)=k{\overline{z} }_{1}^{2}+\left(n-k\right){\overline{z} }_{2}^{2}$$
(23)
$${\overline{z} }_{1}=\frac{1}{k}\frac{\sum_{i=1}^{k}\left({Y}_{i}-\overline{Y }\right)}{s}$$
(24)
$${\overline{z} }_{2}=\frac{1}{n-k}\frac{\sum_{i=k+1}^{n}\left({Y}_{i}-\overline{Y }\right)}{s}$$
(25)

If there exists a change point in the data set, \(T(k)\) hits the peak value during the kth year. Then, \({T}_{0}\) is computed as:

$${T}_{0}=\mathrm{max}\left(T\left(k\right)\right)\mathrm{ for }1 \le k \le n$$
(26)

Von Neumann ratio (VNR) test

This test detects the change point according to the statistics of N (von Neumann, 1941), which is given by:

$$N=\frac{\sum_{i=1}^{n-1}{\left({Y}_{i}-{Y}_{i+1}\right)}^{2}}{\sum_{i=1}^{n}{\left({Y}_{i}-\overline{Y }\right)}^{2}}$$
(27)

If the value of N = 2, it states that the data set is a homogeneous series, whereas if there is a change point in the data set, then the value of N ˂ 2 (Buishand, 1982). The critical values of N are taken from Buishand (1982).

Precipitation concentration index (PCI)

This index is helpful to assess the variation of precipitation in annual, seasonal, and supra-seasonal scales (Michiels et al., 1992; Oliver, 1980). Based on PCI, the classification of precipitation distribution is shown in Table 2 (EE et al., 2017). The PCI at annual scale is calculated as follows:

Table 2 Significance of PCI values
Full size table
$${PCI}_{annual}=\frac{\sum_{i=1}^{12}{P}_{i}^{2}}{{(\sum_{i=1}^{12}{p}_{i})}^{2}}\times 100$$
(28)

\({P}_{i}\)= annual rainfall in an ith month.

Seasonal PCIs for winter (December–February), summer (Mar–May), SW monsoon (June–September), and NE monsoon (October–Nov) and supra-seasonal PCI for dry season (December–May) and wet season (June–November) are as follows:

$${PCI}_{winter,summer}=\frac{\sum_{i=1}^{3}{P}_{i}^{2}}{{\left(\sum_{i=1}^{3}{p}_{i}\right)}^{2}}\times 25; {PCI}_{SW monsoon}=\frac{\sum_{i=1}^{4}{P}_{i}^{2}}{{\left(\sum_{i=1}^{4}{p}_{i}\right)}^{2}}\times 33; {PCI}_{NE monsoon}=\frac{\sum_{i=1}^{2}{P}_{i}^{2}}{{\left(\sum_{i=1}^{2}{p}_{i}\right)}^{2}}\times 17$$
(29)
$${PCI}_{supra-seasonal} =\frac{\sum_{i=1}^{6}{P}_{i}^{2}}{{(\sum_{i=1}^{6}{p}_{i})}^{2}}\times 50$$
(30)

PCI values theoretically lie between 8.3 (uniform) and 100 (extreme) distributions. Based on the values of Table 2, the type of precipitation distribution is classified.

Results and discussion

In this study, the three gridded data sets, namely IMD gridded data, TRMM, and MERRA data, are evaluated on a monthly scale with reference to the observed rain gauge data. The gridded precipitation data were resampled to the observation data point using inverse distance interpolation. The statistical indices obtained by comparing different gridded data sets with the observed data are given in Table 3. From the present study, it was observed that TRMM is showing the best performance based on the indices R and NRMSE. These results agree with the finding of Sireesha et al. (2020). Prakash et al. (2015) stated that most satellite data have difficulties in representing rainfall over orographic regions including the Western Ghats Mountains, Northeast India, and the Himalayan foothills. In terms of NSE and MD, IMD performs better. MERRA is the best based on VE. Thus, it is evident that one cannot finalize the performance of the gridded data sets purely based on these statistical indices alone.

Table 3 Statistical parameters
Full size table

The visual comparison is also carried out using the Taylor diagram, box plots, cumulative distribution function, time series plots, and scatter plots. The TRMM shows a higher correlation and less standard deviation (Fig. 3). The interquartile range of TRMM is small compared to those of the other gridded data sets for the annual series (Fig. 4). This tallies with the study of Subash et al. (2020). This is true during the northeast monsoon season also (Fig. 5). The monthly average values of IMD gridded, TRMM, and MERRA were 193 mm, 166 mm, and 258 mm, respectively, against 221 mm for the observed data. The cumulative distribution plot of IMD gridded data compares well with the station rain gauge data (Fig. 6). Based on these figures, it is clear that the gridded IMD data are very close to the observed data; however, the MERRA data is overestimated, and the TRMM data is underestimated. Almeida et al. (2020) stated that for a river basin in Brazil, TRMM satellite data overestimated precipitation during the wet season while it was underestimated during the dry season. Prakash et al. (2016a, 2016b) also stated that TRMM (TMPA-3B42RT) overestimates over most part of India during monsoon season. In this study, it was found that during all the months, the TRMM data is underestimated. The gridded IMD data set underestimates during the initial period, which is evident from the time series plot (Fig. 7). From the scatter plot, it is clear that TRMM is more diagonally oriented than MERRA and IMD gridded data sets (Figs. 8, 9, and 10).

Fig. 3
figure 3

Taylor diagram of gridded precipitation data sets

Full size image
Fig. 4
figure 4

Box plot of annual gridded precipitation data sets

Full size image
Fig. 5
figure 5

Box plot of monthly gridded precipitation data sets

Full size image
Fig. 6
figure 6

Comparison of the non-exceedance probability of data sources

Full size image
Fig. 7
figure 7

Monthly rainfall time series of Punalur station and gridded data

Full size image
Fig. 8
figure 8

Observed precipitation vs IMD gridded data set scatter plot

Full size image
Fig. 9
figure 9

Observed precipitation vs TRMM gridded data set scatter plot

Full size image
Fig. 10
figure 10

Observed precipitation vs MERRA gridded data set scatter plot

Full size image

Ranking of gridded data sets

Compromise programming and PROMETHEE II are applied to rank the three gridded data sets. Before applying these techniques to rank the data sets, the indicator weights are found using the entropy method. Because the performance of the gridded data set was different based on different indices, all the statistical indices were normalized before applying the entropy method. Table 4 presents the total entropy \({E}_{j}\), degree of diversification \({D}_{j}\), and normalized weights of indicators \({W}_{j}\). These are computed using Eqs. (6), (7), and (8), respectively. Among all five indicators, NSE appears to have a higher significance value of 41%, indicating that its impact on the ranking of the precipitation data set is significant, whereas R, VE, and MD’s total contribution is less than 20%, and NRMSE contributes 26%.

Table 4 Weights of indices obtained from entropy method
Full size table

Ranking using compromise programming

The CP technique is used to rank data sets, which calculates the deviation between ideal and data values (Sireesha et al., 2020; Ghorbani et al., 2021). For R, NSE, VE, and MD, the highest value are taken as the ideal, whereas for NRMSE, the lowest value is taken. The ideal values of statistical indicators, namely R, NRMSE, NSE, VE, and MD, are found to be 0.24, 0.15, 0.17, 0.26, and 0.24. The Lp metric was calculated using Eq. (9) and is given in Table 5. The \({L}_{p}\) metric of IMD gridded data is the lowest value out of the three data sets of gridded precipitation. So IMD gridded is ranked 1, followed by TRMM and MERRA.

Table 5 Compromise programming results
Full size table

Ranking using PROMETHEE II

The function of the usual criterion of Brans et al. (1986) was considered in this study. According to this function, the preference of elements is either 0 or 1. In Table 4, the difference between the correlation coefficient values of IMD and TRMM is 0.22 −0.24 =  −0.02, and so the equivalent value of preference function is 0 as per Eq. (10) (as −0.02 < 0) (Raju & Kumar, 2014). Likewise, the difference between the correlation coefficient values of TRMM and IMD for R is 0.02, and the equivalent value of preference function is 1 as per Eq. (10) (as 0.02 > 0). Likewise, all the indicator difference function of the pairs of gridded precipitation is estimated. The preference function weightage is calculated using the weights estimated by the entropy method, i.e., the multi-criteria preference index using Eq. (12), and is given in Table 6. \({\phi }^{+}\), \({\phi }^{-}\), and \(\phi\) values and ranking corresponding to each data set are given in Table 7. The values in Table 7 are computed based on Eqs. (12), (13), and (14). In the case of IMD, the sum of all elements in the row from Table 6 / (number of elements − 1) = (0 + 0.53 + 0.62) / (3 − 1) = 0.58 \(({\phi }^{+})\) (Eq. (12)). Similarly, the summation of the elements in the column / (no. of elements − 1) = (0 + 0.13 + 0.38) / (3 − 1) = 0.26 (\({\phi }^{-})\) (Eq. (13)). The \(\phi\) value according to Eq. (14) is 0.32 for IMD. The gridded data set having the highest value of \(\phi\) is considered the best. Table 7 shows that, based on the \(\phi\) value, the IMD gridded data are rated as the best data set (rank 1), and the TRMM is rated as the second-best (rank 2), followed by MERRA (rank 3) with 0.32, −0.08, and −0.24, respectively.

Table 6 Multi-criteria preference index values
Full size table
Table 7 Values of \({\phi }^{+}\), \({\phi }^{-}\), and \(\phi\) ranks of gridded precipitation data sets
Full size table

Homogeneity test

The four available precipitation monthly data sets at the Punalur location are tested for homogeneity using Pettitt, SNHT, Buishand, and von Neumann ratio tests. Test results are tested at 5% significant level. The data set is rated as non-homogeneous when the P-value is less than 5% significant level. The results are tabulated in Table 8, and the results show that all data excluding IMD gridded precipitation were homogeneous for Pettitt, SNHT, and Buishand tests, whereas for all data sets, the VNR test showed inhomogeneity characteristics. Pettitt and Buishand tests show that the IMD gridded data sets are homogeneous, while SNHT and VNR tests show that the data series is inhomogeneous. The rainfall data sets are classified into homogeneous, doubtful, and existence of change point (suspect) based on the absolute homogeneity test. The data set is graded to be homogeneous when it rejects one or none null hypothesis, doubtful when it rejects two tests out of the four tests, and is said to be suspect when it rejects three or all tests under 5% significant level. Based on this, the results are shown in Table 8. Except for IMD gridded data set, all the data were found to be valid.

Table 8 Homogeneity test results
Full size table

The SNHT test result graph and a double mass curve are drawn for IMD gridded data set and are given in Figs. 11 and 12. During the period 1985–1990, there exists an inconsistency, which is evident from the figures. The IMD gridded data is corrected based on the slope of the double mass curve and is given in Fig. 13.

Fig. 11
figure 11

SNHT test for IMD gridded data during the period of 1981–2013

Full size image
Fig. 12
figure 12

Double mass curve during the period of 1981–2013

Full size image
Fig. 13
figure 13

Comparison of observed data with corrected IMD gridded data set

Full size image

Assessment of IMD gridded precipitation data set using PCI

The IMD gridded precipitation data set after correction is analyzed for the variation of the precipitation rate on a temporal scale. The estimation of PCI uses Eq. (28) for annual, Eq. (29) for seasonal, and Eq. (30) for supra-seasonal. The results are tabulated in Table 9 based on the significance criteria of PCI values. The annual PCI of the precipitation data set ranges from 9.80 (2011) to 20.96 (1999). Further analysis of annual PCI shows that 81.82% falls under the zone of moderate precipitation, whereas 12.12% in the zone of irregular precipitation, 3.03% in the zone of the strong irregularity of precipitation, and 3.03% in the zone of uniform precipitation distribution out of 33 years of available data. The graphical representation of the yearly annual PCI showed in Fig. 14a.

Table 9 PCI results of IMD gridded data set for the period 1981–2013
Full size table
Fig. 14
figure 14

Yearly PCI of IMD gridded data: a annual; b seasonal; c supra-seasonal

Full size image

Similarly, on a seasonal basis, PCI was calculated for winter, summer, and SW (southwest) and NE (northeast) monsoon seasons. In Fig. 14b, the graphical plot of calculated values is shown for seasonal variation. From Table 9, it is clear that the mean values of seasonal PCI show that the type distribution is strong irregular (winter) and uniform (summer, SW and NE monsoons). On the supra-seasonal basis, i.e., dry and wet seasons, PCI is calculated and represented in Fig. 14c. From Table 9, it is clear that for the dry season, 60.61% falls under the zone of moderate precipitation, and for the wet season, 66.67% falls under the zone of uniform precipitation.

Conclusions

Accurate precipitation data has a significant role to play in river basin level planning and management. In the present study, a suitable data source was selected from IMD, TRMM, and MERRA gridded precipitation data sets by comparing with the IMD observed data. Multi-criteria decision-making techniques, namely compromise programming and PROMETHEE II, were employed to select the best data set. The data set ranked 1 is selected and corrected for inconsistency. The PCI was estimated for the corrected data set to characterize the temporal patterns of precipitation in the catchment area. One of the critical findings from the present study is that the gridded data set, whether it is gauge-based/satellite-based data set, should not be directly used for hydrological studies. A suitable correction has to be applied before its use.

The key findings are as follows:

  • Based on CP and PROMETHEE II, IMD gridded data set ranked 1, followed by TRMM and MERRA.

  • Gridded IMD precipitation data fails the homogeneity test. The homogeneity test and the double mass curve show that gridded IMD data have inconsistency during the periods 1985 and 1990. The gridded IMD data is corrected for inconsistency.

  • The PCI average values of corrected gridded IMD data set for the period 1981–2013 state that the location falls in the zone of moderate for annual precipitation and uniform for summer, SW monsoon, and NE monsoon.