Abstract
A unified treatment of slip and twinning in Bravais lattices is given, focussing on the case of cubic symmetry, and using the Ericksen energy well formulation, so that interfaces correspond to rank-one connections between the infinitely many crystallographically equivalent energy wells. Twins are defined to be such rank-one connections involving a nontrivial reflection of the lattice across some plane. The slips and twins minimizing shear magnitude for cubic lattices are rigorously calculated, and the conjugates of these and other slips analyzed. It is observed that all rank-one connections between the energy wells for the dual of a Bravais lattice can be obtained explicitly from those for the original lattice, so that in particular the rank-one connections for fcc can be obtained explicitly from those for bcc.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
This paper gives a unified treatment of slip and twinning in Bravais lattices, focussing on the case of cubic symmetry, and using the Ericksen energy well formulation, so that interfaces correspond to rank-one connections between the infinitely many crystallographically equivalent energy wells. Inevitably there is a considerable overlap with other such treatments, most notably with that of Pitteri and Zanzotto [28] (especially Chap. 8).
A main contribution is that we calculate rigorously the slips and Type 1/Type 2 twins \({\mathbf {F}}={\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) that minimize the shear magnitude \(|{\mathbf {a}}|\) for cubic lattices, these corresponding to well-known statements in the materials science literature. This reduces to the minimization of products \(G({\mathbf {p}})H({\mathbf {q}})\) of quadratic forms, where \({\mathbf {p}},{\mathbf {q}}\in {\mathbb{Z}}^{3}\) are such that \({\mathbf {p}}\cdot {\mathbf {q}}=0\) for slip and \({\mathbf {p}}\cdot {\mathbf {q}}=2\) for Type 1/Type 2 twins. The principle of minimizing \(|{\mathbf {a}}|\) as a means of selecting preferred slips and twins has been proposed for slips by Chalmers and Martius [8] and for twins by Kiho [25, 26] and Jaswon and Dove [20]. In fact the Type 1/Type 2 twins minimize the shear magnitude among all rank-one connections between the energy wells. We also calculate the conjugates to the minimizing slips, together with certain other slips for bcc, showing that they are all twins. Further, we determine all the slips for cubic lattices whose conjugates are also slips.
An apparently new observation is that all rank-one connections for the dual of a Bravais lattice can be obtained explicitly from those for the original lattice. In particular the rank-one connections for fcc lattices can be obtained explicitly in terms of those for bcc lattices (and vice versa).
The plan of the paper is as follows. In Sect. 2 we review standard material on Bravais lattices. Here and throughout the paper we use a matrix formulation, so that the lattice vectors \({\mathbf {b}}_{1}\), \({\mathbf {b}}_{2}\), \({\mathbf {b}}_{3}\) are written as the columns of a matrix \({\mathbf {B}}\); at least for the author this makes calculations easier to follow. We define lattice planes and the dual lattice, largely following Ashcroft and Mermin [1]. Then in Sect. 3 we recall the Ericksen energy-well picture, whereby the macroscopic free-energy density inherits an infinite family of crystallographically equivalent energy wells from those of the lattice free-energy via the Cauchy–Born rule.
In Sect. 4 we review standard results for the existence of rank-one connections as well as establishing (Theorem 3) the correspondence between rank-one connections for Bravais lattices and their duals. In Sect. 5 we give a characterization of slip systems in terms of rank-one connections not involving lattice rotation (Theorem 4), and determine the slips that minimize the shear magnitude (Theorem 5) for the simple cubic, bcc and fcc lattices. In Sect. 6 we give a definition of twins in terms of interfaces separating nontrivially reflected lattices, and determine (Theorem 6) the Type 1/Type 2 twins minimizing the shear magnitude for the simple cubic, bcc and fcc lattices. In Sect. 7 we address the problem of determining general rank-one connections of minimum shear magnitude, showing in particular (Corollary 3) that the twins in Theorem 6 minimize the shear amplitude among all rank-one connections. Finally in Sect. 8 we determine (Theorem 9) all slips for cubic lattices whose conjugates are also slips, and show (Theorems 10, 11) that the conjugates of all the specific slips discussed in Sect. 5 are twins of various types.
This paper focusses on cubic Bravais lattices, but extensions of the results to noncubic lattices, multilattices and crystals undergoing martensitic phase transformations would be valuable.
2 Bravais Lattices
2.1 Definitions and Basic Properties
Denote by \({\mathbf {e}}_{i}\) the unit vector in the \(i\)th coordinate direction of \(\mathbb{R}^{3}\). A Bravais lattice is an infinite lattice of points in \(\mathbb{R}^{3}\) generated by linear combinations with integer coefficients of three linearly independent basis vectors \({\mathbf {b}}_{1}\), \({\mathbf {b}}_{2}\), \({\mathbf {b}}_{3}\). Representing these basis vectors with respect to the orthonormal basis \(\{{\mathbf {e}}_{i}\}\), and letting \({\mathbf {B}}=({\mathbf {b}}_{1},{\mathbf {b}}_{2},{\mathbf {b}}_{3})\) be the matrix with columns \({\mathbf {b}}_{i}\), so that \(B_{ij}={\mathbf {b}}_{j}\cdot {\mathbf {e}}_{i}\), we write the corresponding Bravais lattice as
where ℤ denotes the set of integers. All lattice sites \({\mathbf {p}}\in{\mathcal {L}}({\mathbf {B}})\) are equivalent, i.e.
We denote by \(\mathbb{R}^{3\times 3}\) the space of real \(3\times 3\) matrices, by \({\mathbb{Z}}^{3\times 3}\) the set of \(3\times 3\) matrices with integer entries, and
For \({\mathbf {F}}\in \mathbb{R}^{3\times 3}\) we denote the Euclidean norm of \({\mathbf {F}}\) by \(|{\mathbf {F}}|:=(\operatorname {tr}{\mathbf {F}}^{T}{\mathbf {F}})^{\frac {1}{2}}\).
The following standard theorem (see, for example, [14], [28, Proposition 3.1]) characterizes the sets of basis vectors that are equivalent in the sense that they generate the same Bravais lattice.
Theorem 1
\({\mathcal {L}}({\mathbf {B}})={\mathcal {L}}(\mathbf {C})\) if and only if
Proof
Let \({\mathbf {B}}=({\mathbf {b}}_{1},{\mathbf {b}}_{2},{\mathbf {b}}_{3})\), \(\mathbf {C}=({\mathbf {c}}_{1},{\mathbf {c}}_{2},{\mathbf {c}}_{3})\). If \({\mathcal {L}}({\mathbf {B}})={\mathcal {L}}({\mathbf{C}})\) then \({\mathbf {b}}_{i}=\mu _{ji}{\mathbf{c}}_{j}\) for some \(\boldsymbol {\mu}=(\mu _{ij})\in {\mathbb{Z}}^{3\times 3}\), so that \({\mathbf {B}}={\mathbf{C}}{\boldsymbol {\mu}}\). Similarly \({\mathbf{C}}={\mathbf {B}}{\boldsymbol {\mu}}'\) for some \({\boldsymbol {\mu}}'\in{\mathbb{Z}}^{3\times 3}\). So \({\boldsymbol{\mu}}'={\boldsymbol{\mu}}^{-1}\) and \(\boldsymbol{\mu}\in GL(3,{\mathbb{Z}})\).
Conversely, if \({\mathbf {B}}={\mathbf{C}}{\boldsymbol{\mu}}\) then \({\mathbf {b}}_{i}={\mu}_{ji}{\mathbf{c}}_{j}\) and so \({\mathcal {L}}({\mathbf {B}})\subset{\mathcal {L}}(\mathbf{C)}\). Similarly \({\mathcal {L}}(\mathbf{C)}\subset\mathbf{{\mathcal {L}}({\mathbf {B}})}\). □
Corollary 1
If \({\mathbf{F}}\in GL(3,\mathbb{R})\), then \({\mathcal {L}}({\mathbf{F}}{\mathbf {B}})={\mathcal {L}}({\mathbf {B}})\) if and only if
The point group \(P({\mathbf {B}})\) is
2.2 Lattice Planes and the Dual Lattice
A lattice plane is a plane \(\varPi ({\mathbf {n}})=\{{\mathbf {x}}\in \mathbb{R}^{3}:{\mathbf {x}}\cdot {\mathbf {n}}=k\}\) with unit normal \({\mathbf {n}}\) such that \(\varPi ({\mathbf {n}})\cap{\mathcal {L}}({\mathbf {B}})\) contains 3 non-collinear points. Equivalently, \(\varPi ({\mathbf {n}})\cap{\mathcal {L}}({\mathbf {B}})\) is a translate of a 2D Bravais lattice of the form
where \({\mathbf {m}}_{1},{\mathbf {m}}_{2}\in {\mathcal {L}}({\mathbf {B}})\) and \({\mathbf {m}}_{1}\), \({\mathbf {m}}_{2}\) are linearly independent. (Taking without loss of generality \(k=0\) this can be proved by first choosing \({\mathbf {m}}_{1}\) to be a nonzero vector in \(\varPi ({\mathbf {n}})\cap{\mathcal {L}}({\mathbf {B}})\) of minimum length, and then \({\mathbf {m}}_{2}\) a nonzero vector in \(\varPi ({\mathbf {n}})\cap{\mathcal {L}}({\mathbf {B}})\) not parallel to \({\mathbf {m}}_{1}\) and of minimum length.)
Then, following Ashcroft and Mermin [1], there exists \({\mathbf {p}}\in{\mathcal {L}}({\mathbf {B}})\) with \({\mathbf {p}}\cdot {\mathbf {n}}>0\) such that
so that \({\mathcal {L}}({\mathbf {B}})\) is the union of its intersection with a family of planes parallel to \(\varPi ({\mathbf {n}})\) with interplane spacing \(d={\mathbf {p}}\cdot {\mathbf {n}}\).
The dual (or reciprocal) lattice of \({\mathcal {L}}({\mathbf {B}})\) is the set
The vector \({\mathbf {k}}\) belongs to the dual lattice if and only if \({\mathbf {k}}\cdot {\mathbf {B}}{\mathbf {e}}_{i}\in {\mathbb{Z}}\) for each \(i\), which holds if and only if \({\mathbf {k}}=\sum _{i=1}^{3}r_{i}{\mathbf {B}}^{-T}{\mathbf {e}}_{i}\) for \({\mathbf {r}}\in{\mathbb{Z}}^{3}\). Hence the dual lattice is the Bravais lattice \(\mathcal {L}({\mathbf {B}}^{-T})\).
Theorem 2
see [1, p. 90]
\(\varPi ({\mathbf {n}})=\{{\mathbf {x}}:{\mathbf {x}}\cdot {\mathbf {n}}=0\}\) is a lattice plane if and only if there exists \({\mathbf {k}}\in {\mathcal {L}}({\mathbf {B}}^{-T})\setminus \{0\}\) with \({\mathbf {k}}\) parallel to \({\mathbf {n}}\), and then \(d^{-1}\) is the minimum length of such a vector \({\mathbf {k}}\).
Proof
We give a slightly different proof to that in [1] for the convenience of the reader. If \(\varPi ({\mathbf {n}})\) is a lattice plane then \(d^{-1}{\mathbf {n}}\cdot {\mathbf {b}}\in {\mathbb{Z}}\) for all \({\mathbf {b}}\in {\mathcal {L}}({\mathbf {B}})\), so that \(d^{-1}{\mathbf {n}}\in {\mathcal {L}}({\mathbf {B}}^{-T})\), and there is no shorter such dual lattice vector.
Conversely, if \({\mathbf {k}}\in {\mathcal {L}}({\mathbf {B}}^{-T})\setminus \{{\mathbf {0}}\}\) with \({\mathbf {k}}\) parallel to \({\mathbf {n}}\) then \({\mathbf {k}}\cdot {\mathbf {B}}{\mathbf {e}}_{i}=n_{i}\in {\mathbb{Z}}\) for each \(i\), and hence \({\mathbf {B}}^{T}{\mathbf {k}}=\sum _{i=1}^{3}n_{i}{\mathbf {e}}_{i}:={\mathbf {n}}\in {\mathbb{Z}}^{3}\). Pick \({\mathbf {m}},{\mathbf {m}}'\in {\mathbb{Z}}^{3}\setminus \{{\mathbf {0}}\}\) with \({\mathbf {m}}\cdot {\mathbf {n}}={\mathbf {m}}'\cdot {\mathbf {n}}=0\) and \({\mathbf {m}}\), \({\mathbf {m}}'\) linearly independent, which is possible because the vectors \({\mathbf {n}}\wedge {\mathbf {e}}_{i}\) are not all parallel. Then \({\mathbf {B}}^{T}{\mathbf {k}}\cdot {\mathbf {m}}={\mathbf {B}}^{T}{\mathbf {k}}\cdot {\mathbf {m}}'=0\), so that \({\mathbf {k}}\cdot {\mathbf {B}}{\mathbf {m}}={\mathbf {k}}\cdot {\mathbf {B}}{\mathbf {m}}'=0\) and \(\varPi ({\mathbf {n}})\) is a lattice plane. □
Remark 1
Suppose \({\mathbf {k}}={\mathbf {B}}^{-T}{\mathbf {q}}\) is parallel to \({\mathbf {n}}\), where \({\mathbf {q}}=(q_{1},q_{2},q_{3})\in {\mathbb{Z}}^{3}\setminus \{{\mathbf {0}}\}\). Then the formula for \(d\) can be rewritten as
where \(\text{gcd}(q_{1},q_{2},q_{3})\) is the greatest common divisor of the \(q_{i}\). Indeed
and the \(\bar{q}_{i}\) have no common factor. If \(\hat {{\mathbf {q}}}\in {\mathbb{Z}}^{3}\) is parallel to \({\mathbf {q}}\) we have that \(n\hat {{\mathbf {q}}}=m\bar {{\mathbf {q}}}\) for coprime integers \(n\geqslant 1\) and \(m\). Thus \(n=1\) and so \(|\bar{{\mathbf {q}}}|\leqslant |\hat{{\mathbf {q}}}|\) and thus \(|{\mathbf {B}}^{-T}\hat{{\mathbf {q}}}|\geqslant |{\mathbf {B}}^{-T}\bar{{\mathbf {q}}}|\).
2.3 Cubic Lattices
As examples we consider:
(i) The simple cubic lattice, for which \({\mathbf {B}}={\mathbf {B}}_{\mathrm{c}}\), where
Equivalently
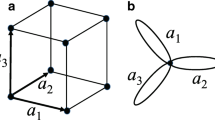
(ii) The face-centred cubic (fcc) lattice (see Fig. 1(a)) with the indicated basis vectors, for which \({\mathbf {B}}={\mathbf {B}}_{\mathrm{fcc}}\), where
Equivalently
(iii) The body-centred cubic (bcc) lattice (see Fig. 1(b)), for which one could take the basis vectors \(\hat{{\mathbf {b}}}_{i}\) shown, but the usual choice is \({\mathbf {B}}={\mathbf {B}}_{\mathrm{bcc}}\), where
for which
Below we always take \({\mathbf {Q}}={\mathbf {1}}\) for these lattices.
Remark 2
It follows from Theorem 1 that for fcc or bcc lattices it is not possible to choose lattice vectors such that \({\mathbf {B}}\in {\mathbb{Z}}^{3\times 3}\). Taking the case of fcc, for example, this would imply that
for some \(\boldsymbol {\mu }\in GL(3,{\mathbb{Z}})\), so that \(\frac {1}{2}\mu _{3j}\in {\mathbb{Z}}\) for each \(j\), and hence \(\mu _{3j}\) is even, implying that \(\det \boldsymbol {\mu }\) is even, a contradiction.
Remark 3
We have that \({\mathbf {B}}_{\mathrm{fcc}}^{T}{\mathbf {B}}_{\mathrm{bcc}}=\frac {1}{2}{\boldsymbol {\omega}}^{-1}\), where
Hence \({\mathbf {B}}_{\mathrm{fcc}}^{-T}=2{\mathbf {B}}_{\mathrm{bcc}}\boldsymbol {\omega}\), proving the well-known result that the dual lattice to fcc is 2bcc.
The simple cubic, bcc and fcc lattices all have the same point group \(P^{48}\) consisting of the 48 matrices \({\mathbf {Q}}\in \mathrm {O} (3)\) mapping \({\mathbb{Z}}^{3}\) to itself (equivalently the matrices with a single entry \(\pm 1\) in each row and column). We write
for the 24 such matrices \({\mathbf {Q}}\) with \(\det {\mathbf {Q}}=1\).
3 The Ericksen Energy Well Picture
Suppose that the free energy per unit volume of a crystalline material with atoms at the points of the Bravais lattice \(\mathcal {L}(\mathbf {C})\), where \(\mathbf {C}\in GL^{+}(3,\mathbb{R})\), is given by \(\varphi (\mathbf {C})\geqslant 0\). For simplicity we assume that the temperature is constant, so that there are no phase transformations.
Natural requirements on \(\varphi \) are
-
(i)
(frame-indifference)
$$ \varphi ({\mathbf {Q}}\mathbf {C})=\varphi (\mathbf {C})\text{ for all }{\mathbf {Q}}\in \operatorname {SO}(3), $$ -
(ii)
(invariance with respect to equivalent lattices)
$$ \varphi (\mathbf {C}{\boldsymbol{\boldsymbol {\mu }}})=\varphi (\mathbf {C}) \text{ for all } {\boldsymbol{\boldsymbol {\mu }}}\in GL^{+}(3, \mathbb{Z}). $$
We assume further that \(\varphi (\mathbf {C})=0\) iff \(\mathbf {C}={\mathbf {Q}}{\mathbf {B}}\boldsymbol {\mu }\) for \({\mathbf {Q}}\in \operatorname {SO}(3)\), \(\boldsymbol {\mu }\in GL^{+}(3,\mathbb{Z})\), so that the minimum value zero is attained only for the unstrained lattice.
As is standard, we use the Cauchy–Born rule to relate the macroscopic free-energy density \(\psi \) to \(\varphi \), thus defining an elastic free energy
for a deformation \({\mathbf {y}}:\Omega \to \mathbb{R}^{3}\), where \(\Omega \subset \mathbb{R}^{3}\) is an open reference domain.
Choosing a reference configuration in which the crystal lattice is \(\mathcal {L}({\mathbf {B}})\), where \({\mathbf {B}}\in GL^{+}(3,\mathbb{R})\), we assume that
Thus \(\psi \geqslant 0\) inherits from \(\varphi \) the invariances
-
(i)
\(\psi ({\mathbf {Q}}{\mathbf {A}})=\psi ({\mathbf {A}})\) for all \({\mathbf {Q}}\in \operatorname {SO}(3)\),
-
(ii)
\(\psi ({\mathbf {A}}{\mathbf {B}}{\boldsymbol {\mu}} {\mathbf {B}}^{-1})=\psi ({\mathbf {A}})\) for all \({\boldsymbol{\mu}}\in GL^{+}(3,{\mathbb{Z}})\),
and \(\psi \) has zero set
The energy wells \(\operatorname {SO}(3){\mathbf {B}}\boldsymbol {\mu }{\mathbf {B}}^{-1}\) are not all distinct, because \(\operatorname {SO}(3){\mathbf {B}}\boldsymbol {\mu }{\mathbf {B}}^{-1} = \operatorname {SO}(3){\mathbf {B}}\tilde{\boldsymbol {\mu }}{\mathbf {B}}^{-1}\) iff
But since \(P({\mathbf {B}})\) is finite and \(GL^{+}(3,\mathbb{Z})\) is infinite, there are infinitely many distinct energy wells.
4 Interfaces
4.1 Rank-One Connections
We are interested in possible planar interfaces between distinct constant gradients on the energy wells, that is in pairs of distinct matrices \({\mathbf {F}},{\mathbf {G}}\in \psi ^{-1}(0)\) with
We can assume that \({\mathbf {G}}={\mathbf {1}}\), so that we are interested in the \(\boldsymbol {\mu }\in GL^{+}(3,\mathbb{Z})\) with \({\mathbf {M}}={\mathbf {B}}\boldsymbol {\mu }{\mathbf {B}}^{-1}\notin \operatorname {SO}(3)\) such that
Note that since \({\mathbf {M}}\) is independent of the scale of \({\mathcal {L}}({\mathbf {B}})\) (that is it is the same for \({\mathcal {L}}(t{\mathbf {B}})\) for any \(t\neq 0\)) the rank-one connections are also independent of scale. If (14) holds then since \(\det {\mathbf {M}}=1\) we have that
and thus
We denote by \(0<\lambda _{1}\leqslant \lambda _{2}\leqslant \lambda _{3}\) the eigenvalues of the positive definite symmetric matrix \({\mathbf {M}}^{T}{\mathbf {M}}\), which satisfy \(\lambda _{1}\lambda _{2}\lambda _{3}=1\), and by \(\hat{{\mathbf {e}}}_{i}\) the corresponding orthonormal eigenvectors, so that \({\mathbf {M}}^{T}{\mathbf {M}}\) has spectral decomposition
A necessary and sufficient condition for (14) to hold (see e.g. [4, Prop. 4], [2, Theorem 2.1], [24], [3, Lemma 1]) is that \(\lambda _{2}=1\), or (since \({\mathbf {M}}^{T}{\mathbf {M}}\neq {\mathbf {1}}\)) that \({\mathbf {M}}^{T}{\mathbf {M}}\) has an eigenvalue equal to one. Then \(0<\lambda _{1}<1=\lambda _{2}<\lambda _{3}=\lambda _{1}^{-1}\). An equivalent condition is that
which follows from the identity
(This implies in particular, as observed in [28, Remark 8.4], that there is a rank-one connection to \(\operatorname {SO}(3){\mathbf {M}}\) iff there is a rank-one connection to \(\operatorname {SO}(3){\mathbf {M}}^{-1}\), which can be verified directly.)
There are then exactly two distinct such conjugate (or reciprocal) rank-one connections
These can be calculated explicitly by comparing the spectral decomposition (17) with the relation
that follows from (14) (see e.g. [4, Prop. 4]). A straightforward calculation then shows that (up to a change of sign)
From (16) or (21) we have that \(|{\mathbf {a}}_{+}|=|{\mathbf {a}}_{-}|\). Also \({\mathbf {n}}_{+}\cdot {\mathbf {n}}_{-}= \frac{1-\lambda _{1}}{1+\lambda _{1}}\), so that the planes corresponding to the two rank-one connections are never orthogonal.
It also follows from (21) that if we know one rank-one connection \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}={\mathbf {R}}{\mathbf {M}}\) then the conjugate rank-one connection \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}=\tilde{{\mathbf {R}}}{\mathbf {M}}\) is given by
From (22) we have that
from which, recalling from (15), (16) that \({\mathbf {a}}\cdot {\mathbf {n}}=0\) and \(|\tilde{{\mathbf {a}}}|^{2}=|{\mathbf {a}}|^{2}\), we deduce that
Hence we obtain the relations
where (26) is obtained from (25) by interchanging \({\mathbf {a}}\), \({\mathbf {n}}\) and \(\tilde{{\mathbf {a}}}\), \(\tilde{{\mathbf {n}}}\). Thus \(\tilde{{\mathbf {R}}}{\mathbf {R}}^{T}\) can be expressed as the product of two \(180^{\circ}\) rotations in the two ways
We will see that there are always \(\boldsymbol {\mu }\) such that \({\mathbf {M}}^{T}{\mathbf {M}}\) has an eigenvalue one. However this is not true for general \(\boldsymbol {\mu }\).
4.2 Correspondence Between Rank-One Connections for Bravais Lattices and Their Duals
It turns out that the rank-one connections for the dual of a Bravais lattice can be obtained explicitly in terms of the rank-one connections for the original lattice (and vice versa). On account of Remark 3 this implies that the rank-one connections for fcc can be obtained explicitly in terms of those for bcc, which are a bit easier to calculate due to the more symmetric form of the matrix \({\mathbf {B}}_{\mathrm{bcc}}\).
Note that the energy wells for the dual lattice \({\mathcal {L}}({\mathbf {B}}^{-T})\) of the Bravais lattice \({\mathcal {L}}({\mathbf {B}})\) are given by \(\operatorname {SO}(3){\mathbf {B}}^{-T}\boldsymbol {\mu }^{T}{\mathbf {B}}^{T}\) for \(\boldsymbol {\mu }\in GL^{+}(3,{\mathbb{Z}})\).
Theorem 3
The rank-one connection
for \({\mathbf {R}}\in {\mathrm{SO}}(3)\) and \(\boldsymbol {\mu }\in GL^{+}(3,{\mathbb{Z}})\) holds iff
Furthermore, if \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}\) is the conjugate of \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) then \({\mathbf {1}}+{\mathbf {R}}^{T}\tilde{{\mathbf {n}}}\otimes {\mathbf {R}}^{T}\tilde{{\mathbf {a}}}\) is the conjugate of \({\mathbf {1}}+{\mathbf {R}}^{T}{\mathbf {n}}\otimes {\mathbf {R}}^{T}{\mathbf {a}}\).
Proof
Taking the transpose of (28) and pre- and post-multiplying by \({\mathbf {R}}^{T}\) and \({\mathbf {R}}\) respectively, we see that (28) and (29) are equivalent.
The statement about the conjugates follows from (22), or more directly by noting that
where \({\mathbf {R}}\neq {\mathbf {1}}\), implies that
as required. □
From Remark 3 we thus obtain
Corollary 2
The rank-one connection
for \({\mathbf {R}}\in \operatorname {SO}(3)\) and \(\boldsymbol {\mu }\in GL^{+}(3,{\mathbb{Z}})\) holds iff
where \(\tilde{\boldsymbol {\mu }}=\boldsymbol {\omega }\boldsymbol {\mu }^{T}\boldsymbol {\omega }^{-1}\) and \(\boldsymbol {\omega }\) is given by (10).
5 Slip
5.1 Slip Systems and Lattice Invariant Shears
A slip system \((\varPi ({\mathbf {n}}),{\mathbf {b}})\) consists of a lattice plane \(\varPi ({\mathbf {n}})\) with unit normal \({\mathbf {n}}\) and interplane spacing \(d\), and a nonzero lattice vector \({\mathbf {b}}\in{\mathcal {L}}({\mathbf {B}})\) (the Burgers vector) with \({\mathbf {b}}\cdot {\mathbf {n}}=0\). If \((\varPi ({\mathbf {n}}),{\mathbf {b}})\) is a slip system so is \((\varPi ({\mathbf {n}}),-{\mathbf {b}})\), which corresponds to an opposite direction of shear on the same lattice plane, and when counting slip systems we identify \((\varPi ({\mathbf {n}}),{\mathbf {b}})\) with \((\varPi ({\mathbf {n}}),-{\mathbf {b}})\).
Equivalently
so that if the part of \({\mathcal {L}}({\mathbf {B}})\) in the half-space \(\{{\mathbf {x}}\cdot {\mathbf {n}}>0\}\) is rigidly displaced by \({\mathbf {b}}\) then \({\mathcal {L}}({\mathbf {B}})\) is restored.
Theorem 4
The following are equivalent:
-
(i)
\({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}={\mathbf {B}}\boldsymbol {\mu }{\mathbf {B}}^{-1}\), where \({\mathbf {a}},{\mathbf {n}}\in \mathbb{R}^{3}\), \(|{\mathbf {n}}|=1\), and \(\boldsymbol {\mu }\in GL^{+}(3,{\mathbb{Z}})\).
-
(ii)
\(\boldsymbol {\mu }={\mathbf {1}}+{\mathbf {p}}\otimes {\mathbf {q}}\), where \({\mathbf {p}},{\mathbf {q}}\in {\mathbb{Z}}^{3}\setminus \{{\mathbf {0}}\}\), \({\mathbf {p}}\cdot {\mathbf {q}}=0\), and
$$\begin{aligned} {\mathbf {n}}=\tau \frac{{\mathbf {B}}^{-T}{\mathbf {q}}}{|{\mathbf {B}}^{-T}{\mathbf {q}}|},\qquad {\mathbf {a}}=\tau {\mathbf {B}}{\mathbf {p}}|{\mathbf {B}}^{-T} {\mathbf {q}}|, \end{aligned}$$(34)where \(\tau =\pm 1\).
-
(iii)
\((\varPi ({\mathbf {n}}),{\mathbf {b}})\) is a slip system with interplane spacing \(d\) and Burgers vector \({\mathbf {b}}=d{\mathbf {a}}\).
The proof uses the following lemma.
Lemma 1
The matrix \({\mathbf {c}}\otimes {\mathbf {d}}\in {\mathbb{Z}}^{3\times 3}\) for some \({\mathbf {c}},{\mathbf {d}}\in \mathbb{R}^{3}\) if and only if \({\mathbf {c}}\otimes {\mathbf {d}}={\mathbf {p}}\otimes {\mathbf {q}}\) for some \({\mathbf {p}},{\mathbf {q}}\in {\mathbb{Z}}^{3}\).
Proof
We only have to prove the necessity, and may assume \({\mathbf {c}}\otimes {\mathbf {d}}\) is a nonzero matrix of integers. Thus some \(c_{i}\neq 0\) and \(c_{i}d_{1}\), \(c_{i}d_{2}\), \(c_{i}d_{3}\) are integers, so that \({\mathbf {d}}=\frac{1}{c_{i}}{\mathbf {m}}\) for some \({\mathbf {m}}\in {\mathbb{Z}}^{3}\). Similarly \({\mathbf {c}}=\frac{1}{d_{j}}{\mathbf {r}}\) for some \(j\) and \({\mathbf {r}}\in {\mathbb{Z}}^{3}\). Hence \({\mathbf {c}}\otimes {\mathbf {d}}=\frac{1}{c_{i}d_{j}}{\mathbf {r}}\otimes {\mathbf {m}}\). We can write \({\mathbf {r}}=k{\mathbf {r}}'\), \({\mathbf {m}}=l{\mathbf {m}}'\), where \(k\), \(l\) are integers and neither \((r_{1}',r_{2}',r_{3}')\) nor \((m_{1}',m_{2}',m_{3}')\) have common factors. Thus
where \(\frac{r}{s}\) is a rational number expressed in its lowest terms. Suppose \(s\neq \pm 1\), so that \(s\) has a prime factor \(S\). For some \(r_{i}'\), \(S\) does not divide \(r_{i}'\). Hence \(S\) divides \(m_{j}'\) for all \(j\), a contradiction. Hence \(s=\pm 1\), giving the result. □
Proof of Theorem 4
(i)⇒(ii). (i) implies that \({\mathbf {1}}+{\mathbf {B}}^{-1}{\mathbf {a}}\otimes {\mathbf {B}}^{T}{\mathbf {n}}=\boldsymbol {\mu }\). Hence, by Lemma 1, \({\mathbf {a}}\otimes {\mathbf {n}}={\mathbf {B}}{\mathbf {p}}\otimes {\mathbf {B}}^{-T}{\mathbf {q}}\) for \({\mathbf {p}},{\mathbf {q}}\in {\mathbb{Z}}^{3}\), and \({\mathbf {a}}\cdot {\mathbf {n}}={\mathbf {p}}\cdot {\mathbf {q}}=0\), giving (ii).
(ii)⇒(iii). We can suppose that the \(q_{i}\) have no common factor, so that by Remark 1, \({\mathbf {n}}=\tau {{\mathbf {B}}^{-T}{\mathbf {q}}}/{|{\mathbf {B}}^{-T}{\mathbf {q}}|}\) is the normal to a lattice plane \(\varPi ({\mathbf {n}})\) with interplane spacing \(d={1}/{|{\mathbf {B}}^{-T}{\mathbf {q}}|}\). Also \({\mathbf {b}}=\tau {\mathbf {B}}{\mathbf {p}}\in {\mathcal {L}}({\mathbf {B}})\) with \({\mathbf {b}}\cdot {\mathbf {n}}=0\), and so \({\mathbf {b}}=d{\mathbf {a}}\), giving (iii).
(iii)⇒(i). By Theorem 2 and Remark 1 we know that \({\mathbf {n}}={{\mathbf {B}}^{-T}{\mathbf {q}}}/{|{\mathbf {B}}^{-T}{\mathbf {q}}|}\), \(d= {1}/{|{\mathbf {B}}^{-T}{\mathbf {q}}|}\), for some \({\mathbf {q}}\in {\mathbb{Z}}^{3}\setminus \{{\mathbf {0}}\}\). Also \({\mathbf {b}}={\mathbf {B}}{\mathbf {p}}\) for some \({\mathbf {p}}\in {\mathbb{Z}}^{3}\setminus \{{\mathbf {0}}\}\), where \({\mathbf {b}}\cdot {\mathbf {n}}=d{\mathbf {B}}{\mathbf {p}}\cdot {\mathbf {B}}^{-T}{\mathbf {q}}=d{\mathbf {p}}\cdot {\mathbf {q}}=0\). Then
giving (i). □
Thus a slip system corresponds to a lattice invariant shear giving a rank-one connection between \(\operatorname {SO}(3)\) and \(\operatorname {SO}(3){\mathbf {B}}\boldsymbol {\mu }{\mathbf {B}}^{-1}\) without lattice rotation. The shear can correspond to a shear band, or in the case of rigid slip to a ‘microshear’ over just one pair of adjacent lattice planes. Note that Theorem 4 shows that the slip systems for any Bravais lattice are in 1-1 correspondence with those for the simple cubic lattice (having deformation gradient \({\mathbf {1}}+{\mathbf {p}}\otimes {\mathbf {q}}\)). For the use of such rank-one connections in continuum theories of plasticity see e.g. Ortiz and Repetto [27].
5.2 Slips of Minimum Shear Magnitude
Since if \(\boldsymbol {\mu }={\mathbf {1}}+{\mathbf {p}}\otimes {\mathbf {q}}\),
we have that \(|{\mathbf {a}}|^{2}=d^{-2}|{\mathbf {b}}|^{2}=|{\mathbf {B}}{\mathbf {p}}|^{2}|{\mathbf {B}}^{-T}{\mathbf {q}}|^{2}\). Hence, to minimize the shear magnitude \(|{\mathbf {a}}|\) we need to minimize \(|{\mathbf {B}}{\mathbf {p}}|^{2}|{\mathbf {B}}^{-T}{\mathbf {q}}|^{2}\) subject to \({\mathbf {p}},{\mathbf {q}}\in{\mathbb{Z}}^{3}\setminus \{0\}\) with \({\mathbf {p}}\cdot {\mathbf {q}}=0\).
Minimizing the shear magnitude is the criterion proposed by Chalmers and Martius [8], who give a heuristic justification in terms of energetics, pointing out that the criterion of minimizing the magnitude of the Burgers vector \({\mathbf {b}}\) does not determine the preferred slip planes. A review of different possible criteria is given in [13].
In the following theorem we give the slips of minimum shear magnitude for the simple cubic, bcc and fcc lattices, reproducing in our framework classical results for the slip systems for these lattices (see, for example, [17]). See below for further comments.
Theorem 5
The slips \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) minimizing \(|{\mathbf {a}}|\) are given by:
-
(a)
Simple cubic: \({\mathbf {a}}\otimes {\mathbf {n}}=\pm {\mathbf {e}}_{i}\otimes {\mathbf {e}}_{j}\), where \(i\neq j\), for which \(|{\mathbf {a}}|^{2}= 1\).
-
(b)
bcc:
$$\begin{aligned} {\mathbf {a}}\otimes {\mathbf {n}}&=\frac {1}{2}({\mathbf {e}}_{1}+{\mathbf {e}}_{2}+{\mathbf {e}}_{3})\otimes ({\mathbf {e}}_{j}-{\mathbf {e}}_{k}), \\ {\mathbf {a}}\otimes {\mathbf {n}}&=\frac {1}{2}({\mathbf {e}}_{j}+{\mathbf {e}}_{k}-{\mathbf {e}}_{i})\otimes ({\mathbf {e}}_{j}-{\mathbf {e}}_{k}), \\ {\mathbf {a}}\otimes {\mathbf {n}}&=\pm \frac {1}{2}({\mathbf {e}}_{j}+{\mathbf {e}}_{k}-{\mathbf {e}}_{i})\otimes ({\mathbf {e}}_{i}+ {\mathbf {e}}_{k}), \end{aligned}$$where \(i,j,k\in \{1,2,3\}\) are distinct, for which \(|{\mathbf {a}}|^{2}=\frac{3}{2}\).
-
(c)
fcc:
$$\begin{aligned} {\mathbf {a}}\otimes {\mathbf {n}}&=\frac {1}{2}({\mathbf {e}}_{j}-{\mathbf {e}}_{k})\otimes ({\mathbf {e}}_{1}+{\mathbf {e}}_{2}+{\mathbf {e}}_{3}), \\ {\mathbf {a}}\otimes {\mathbf {n}}&=\frac {1}{2}({\mathbf {e}}_{j}-{\mathbf {e}}_{k})\otimes ({\mathbf {e}}_{j}+{\mathbf {e}}_{k}-{\mathbf {e}}_{i}), \\ {\mathbf {a}}\otimes {\mathbf {n}}&=\pm \frac {1}{2}({\mathbf {e}}_{i}+{\mathbf {e}}_{k})\otimes ({\mathbf {e}}_{j}+{\mathbf {e}}_{k}- {\mathbf {e}}_{i}), \end{aligned}$$where \(i,j,k\in \{1,2,3\}\) are distinct, for which \(|{\mathbf {a}}|^{2}=\frac{3}{2}\).
Remark 4
Without loss of generality we may take for simple cubic \({\mathbf {a}}\otimes {\mathbf {n}}={\mathbf {e}}_{1}\otimes {\mathbf {e}}_{2}\), for bcc \({\mathbf {a}}\otimes {\mathbf {n}}=\frac {1}{2}({\mathbf {e}}_{1}+{\mathbf {e}}_{2}+{\mathbf {e}}_{3})\otimes ({\mathbf {e}}_{1}-{\mathbf {e}}_{2})\), and for fcc \({\mathbf {a}}\otimes {\mathbf {n}}=\frac {1}{2}({\mathbf {e}}_{1}-{\mathbf {e}}_{2})\otimes ({\mathbf {e}}_{1}+{\mathbf {e}}_{2}+{\mathbf {e}}_{3})\), since all the other cases are given by \({\mathbf {P}}{\mathbf {a}}\otimes {\mathbf {n}}{\mathbf {P}}^{-1}\) for suitable \({\mathbf {P}}\in P^{24}\), where \(P^{24}\) is defined in (11).
Proof
(a) Since \({\mathbf {B}}_{\mathrm{c}}={\mathbf {1}}\) we have \(|{\mathbf {a}}|^{2}=|{\mathbf {p}}|^{2}|{\mathbf {q}}|^{2}\geqslant 1\), and \(|{\mathbf {a}}|^{2}=1\) for \(|{\mathbf {p}}|^{2}=|{\mathbf {q}}|^{2}=1\), giving the result.
(b) For bcc
and we have to minimize \(\frac{1}{4}G({\mathbf {p}})H({\mathbf {q}})\), subject to \({\mathbf {p}},{\mathbf {q}}\in{\mathbb{Z}}^{3}\setminus \{0\}\) and \({\mathbf {p}}\cdot {\mathbf {q}}=0\), where
The minimum value of \(H({\mathbf {q}})\) is 2, with minimizers \({\mathbf {q}}=\pm {\mathbf {e}}_{i}\) and \({\mathbf {q}}={\mathbf {e}}_{i}-{\mathbf {e}}_{j}\), \(i\neq j\), while the minimum value of \(G({\mathbf {p}})\) is 3, with minimizers \({\mathbf {p}}=\pm {\mathbf {e}}_{i}\) and \({\mathbf {p}}=\pm ({\mathbf {e}}_{1}+{\mathbf {e}}_{2}+{\mathbf {e}}_{3})\). Hence the minimizers of \(\frac{1}{4}G({\mathbf {p}})H({\mathbf {q}})\), subject to \({\mathbf {p}},{\mathbf {q}}\in{\mathbb{Z}}^{3}\setminus \{0\}\) and \({\mathbf {p}}\cdot {\mathbf {q}}=0\) are given by
Calculating \({\mathbf {B}}_{\mathrm{bcc}}{\mathbf {p}}\otimes {\mathbf {B}}_{\mathrm{bcc}}^{-T}{\mathbf {q}}\) for these possibilities gives the slip systems in the theorem.
(c) For fcc it suffices to note that by Corollary 2 the slips minimizing \(|{\mathbf {a}}|\) are given by \({\mathbf {1}}+{\mathbf {n}}\otimes {\mathbf {a}}\), where \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) are the slips for bcc minimizing \(|{\mathbf {a}}|\). □
For bcc metals the experimental determination of slip planes is not straightforward. One can ask what the slips are that give the next lowest value of \(|{\mathbf {a}}|^{2}\), and whether such slips are observed. Since \(H({\mathbf {q}})\) is even, the next lowest value of \(G({\mathbf {p}})H({\mathbf {q}})\) is greater than or equal to 8, for which \(|{\mathbf {a}}|^{2}=2\), and the value 8 is achieved with \(G({\mathbf {p}})=4\), \(H({\mathbf {q}})=2\) and
giving the slips
These slips are consistent with those described by Chalmers and Martius [8], who noted that they had not been reported experimentally; in a more recent survey Weinberger, Boyce and Bataille [31] appear to confirm this, stating that “It is clear from numerous experiments that slip occurs in the closest packed \(\langle 111\rangle \) direction and the Burgers vector is \(\frac {1}{2}\langle 111\rangle \)”. The slips in (35) have Burgers vector magnitude \(|{\mathbf {b}}|^{2}=1\), whereas those in Theorem 5(b) have \(|{\mathbf {b}}|^{2}=\frac{3}{4}\).
It is often stated (see, for example, [17]) that there are up to 48 slip systems for bcc, consisting of the 12 systems given in Theorem 5 (identifying \(\pm {\mathbf {a}}\otimes {\mathbf {n}}\)) together with 12 having \((112)\) slip planes given by
with \(|{\mathbf {a}}|^{2}=\frac{9}{2}\), and 24 having \((123)\) slip planes, given by
with \(|{\mathbf {a}}|^{2}=\frac{21}{2}\). That these are slips can be checked by verifying that \({\mathbf {a}}\cdot {\mathbf {n}}=0\) and \({\mathbf {B}}^{-1}{\mathbf {a}}\otimes {\mathbf {B}}^{T}{\mathbf {n}}\in {\mathbb{Z}}^{3}\otimes {\mathbb{Z}}^{3}\). These extra slip systems have the same Burgers vector magnitude \(|{\mathbf {b}}|^{2}=\frac{3}{4}\) as those in Theorem 5(b), but considerably higher values of shear magnitude.
For further discussion of the Chalmers and Martius criterion for bcc crystals see [9].
6 Twinning
6.1 Twins
In this paper we define \({\mathbf {F}}={\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) to be a (mechanical) twin if the lattices \({\mathcal {L}}({\mathbf {B}})\) and \({\mathbf {F}}{\mathcal {L}}({\mathbf {B}})\) on either side of the interface are non-trivially reflected with respect to each other, so that \({\mathbf {F}}={\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) is not a slip and satisfies for some unit vector \({\mathbf {m}}\)
where for the second equality we have used \({\mathcal {L}}({\mathbf {B}})={\mathcal {L}}(-{\mathbf {B}})\). (Note that if \({\mathbf {F}}\) is a slip then (38) holds for any \(180^{\circ}\) rotation \(-{\mathbf {1}}+2{\mathbf {m}}\otimes {\mathbf {m}}\in P({\mathbf {B}})\).) By Corollary 1, (38) holds iff
for some \(\boldsymbol {\mu }\in GL^{+}(3,{\mathbb{Z}})\).
The definition given above of twins corresponds to that given by Christian [11, p. 51], except that we require that \({\mathbf {F}}\) is not a slip, and grew out of a discussion with R.D. James [18]. It covers the cases of Type 1 and Type 2 twins in the next section, but other possibilities too; on the other hand it is less general than that used e.g. by Pitteri and Zanzotto [28], who give (pp 28,29) references to various different definitions. According to their terminology ‘nonconventional twins’ correspond to rank-one connections which are neither Type 1 nor Type 2 twins. In Sect. 8 we give different examples of such ‘nonconventional twins’ which are, and which are not, twins as defined in this paper. For a related discussion see [10].
6.2 Type 1, Type 2 and Compound Twins
We shall be interested in Type 1 twins, for which \({\mathbf {m}}={\mathbf {n}}\), so that the lattices are non-trivially reflected with respect to the twin plane, and thus
for some \(\boldsymbol {\mu }\in GL^{+}(3,{\mathbb{Z}})\), and in Type 2 twins, for which \({\mathbf {F}}\) satisfies (39) with \({\mathbf {m}}=\frac{{\mathbf {a}}}{|{\mathbf {a}}|}\). From (25) it follows that if \({\mathbf {F}}={\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) is a Type 1 twin, then its conjugate \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}\) satisfies
and so (see [28, p. 254]) is a Type 2 twin (unless it is a slip, which can happen — see Theorem 6(a)). Conversely the conjugate to a Type 2 twin, unless it is a slip, is a Type 1 twin. \({\mathbf {F}}\) is a compound twin if it is both a Type 1 and Type 2 twin, so that
for some \(\boldsymbol {\nu }\in GL^{+}(3,{\mathbb{Z}})\). This holds iff
or equivalently iff
We will use (44) to check for compound twins; other criteria are given in [28, Proposition 8.7], [15]. Obviously the conjugate of a compound twin is either a slip or a compound twin.
From (40), to find the Type 1 twins (and hence their conjugate Type 2 twins) we need to find \(\boldsymbol {\mu }\), \({\mathbf {a}}\), \({\mathbf {n}}\) such that \({\mathbf {B}}\boldsymbol {\mu }{\mathbf {B}}^{-1}\notin SO(3)\) and
Equivalently \(\boldsymbol {\mu }=-{\mathbf {1}}+{\mathbf {B}}^{-1}(2{\mathbf {n}}-{\mathbf {a}})\otimes {\mathbf {B}}^{T}{\mathbf {n}}\), and hence, by Lemma 1,
for some \({\mathbf {p}},{\mathbf {q}}\in \mathbb{Z}^{3}\), and \({\mathbf {p}}\cdot {\mathbf {q}}=2\). Thus we can suppose that
so that
It follows from (22), (47), (48) that the conjugate Type 2 twin is given by
6.3 Twins of Minimum Shear Magnitude
From (48), in order to minimize \(|{\mathbf {a}}|^{2}\) we have to minimize \(|{\mathbf {B}}{\mathbf {p}}|^{2}|{\mathbf {B}}^{-T}{\mathbf {q}}|^{2}\) among \({\mathbf {p}},{\mathbf {q}}\in{\mathbb{Z}}^{3}\) with \({\mathbf {p}}\cdot {\mathbf {q}}=2\) and \(|{\mathbf {B}}{\mathbf {p}}|^{2}|{\mathbf {B}}^{-T}{\mathbf {q}}|^{2}>4\). In the following theorem we give the Type 1/Type 2 twins minimizing the shear magnitude for the simple cubic, bcc and fcc lattices. Note that by Theorem 3 and Corollary 2 the Type 1 (respectively Type 2) twins for fcc are given by \({\mathbf {1}}-{\mathbf {n}}\otimes {\mathbf {a}}\), where \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) are the Type 2 (respectively Type 1) twins for bcc. The twins identified, and their shear magnitude, correspond to those given in Christian and Mahajan [12, Table 1], which summarizes earlier work of Jaswon and Dove [19–21], Bilby and Crocker [7], Bevis and Crocker [5, 6].
Theorem 6
The Type 1 and Type 2 twins \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) minimizing \(|{\mathbf {a}}|\) are given by:
-
(a)
Simple cubic: the compound twins
$$\begin{aligned} {\mathbf {a}}\otimes {\mathbf {n}}&=\frac{1}{5}(2{\mathbf {e}}_{j}-\kappa {\mathbf {e}}_{i})\otimes (2 \kappa {\mathbf {e}}_{i}+{\mathbf {e}}_{j}), \end{aligned}$$where \(i\neq j\), \(\kappa =\pm 1\), whose conjugates are the slips \(\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}= \kappa {\mathbf {e}}_{i}\otimes {\mathbf {e}}_{j}\) in Theorem 5(a), for which \(|{\mathbf {a}}|^{2}=1\).
-
(b)
bcc: the conjugate pairs
$$\begin{aligned} {\mathbf {a}}\otimes {\mathbf {n}}&=\frac{1}{6}({\mathbf {e}}_{j}-{\mathbf {e}}_{k}+{\mathbf {e}}_{i})\otimes (2{\mathbf {e}}_{j}+ {\mathbf {e}}_{k}-{\mathbf {e}}_{i}), \\ \tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}&=\frac{1}{6}({\mathbf {e}}_{j}+{\mathbf {e}}_{k}-{\mathbf {e}}_{i}) \otimes (2{\mathbf {e}}_{j}+{\mathbf {e}}_{i}-{\mathbf {e}}_{k}), \end{aligned}$$and
$$\begin{aligned} {\mathbf {a}}\otimes {\mathbf {n}}&=\frac{1}{6}({\mathbf {e}}_{1}+{\mathbf {e}}_{2}+{\mathbf {e}}_{3})\otimes (2{\mathbf {e}}_{i}- {\mathbf {e}}_{j}-{\mathbf {e}}_{k}), \\ \tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}&=\frac{1}{6}({\mathbf {e}}_{i}-{\mathbf {e}}_{j}-{\mathbf {e}}_{k}) \otimes (2{\mathbf {e}}_{i}+{\mathbf {e}}_{j}+{\mathbf {e}}_{k}), \end{aligned}$$where \(i\), \(j\), \(k\) are distinct, which are all compound twins, and for which \(|{\mathbf {a}}|^{2}=\frac {1}{2}\).
-
(c)
fcc: the conjugate pairs
$$\begin{aligned} {\mathbf {a}}\otimes {\mathbf {n}}&=\frac{1}{6}(-2{\mathbf {e}}_{j}-{\mathbf {e}}_{k}+{\mathbf {e}}_{i})\otimes ({\mathbf {e}}_{j}- {\mathbf {e}}_{k}+{\mathbf {e}}_{i}), \\ \tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}&= \frac{1}{6}(-2{\mathbf {e}}_{j}-{\mathbf {e}}_{i}+{\mathbf {e}}_{k}) \otimes ({\mathbf {e}}_{j}+{\mathbf {e}}_{k}-{\mathbf {e}}_{i}), \end{aligned}$$and
$$\begin{aligned} {\mathbf {a}}\otimes {\mathbf {n}}&=\frac{1}{6}(-2{\mathbf {e}}_{i}+{\mathbf {e}}_{j}+{\mathbf {e}}_{k})\otimes ({\mathbf {e}}_{1}+ {\mathbf {e}}_{2}+{\mathbf {e}}_{3}), \\ \tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}&=\frac{1}{6}(2{\mathbf {e}}_{i}+{\mathbf {e}}_{j}+{\mathbf {e}}_{k}) \otimes ({\mathbf {e}}_{j}+{\mathbf {e}}_{k}-{\mathbf {e}}_{i}), \end{aligned}$$where \(i\), \(j\), \(k\) are distinct, which are all compound twins, and for which \(|{\mathbf {a}}|^{2}=\frac {1}{2}\).
Proof
(a) Since \({\mathbf {B}}={\mathbf {1}}\) we have to minimize \(|{\mathbf {p}}|^{2}|{\mathbf {q}}|^{2}\) among \({\mathbf {p}},{\mathbf {q}}\in {\mathbb{Z}}^{3}\) subject to \({\mathbf {p}}\cdot {\mathbf {q}}=2\) and \(|{\mathbf {p}}|^{2}|{\mathbf {q}}|^{2}>4\), since \(|{\mathbf {p}}|^{2}|{\mathbf {q}}|^{2}=4\) implies \({\mathbf {a}}=0\). The minimum is given by \(|{\mathbf {p}}|^{2}|{\mathbf {q}}|^{2}=5\) with minimizers
From (47) we have that
which together with (22) gives the conjugate pairs in the statement. Note that \({\mathbf {a}}\otimes {\mathbf {n}}=\frac{1}{5}(2{\mathbf {e}}_{j}-\kappa {\mathbf {e}}_{i})\otimes (2 \kappa {\mathbf {e}}_{i}+{\mathbf {e}}_{j})\) is not a slip because it does not belong to \({\mathbb{Z}}^{3\times 3}\), and is a compound twin by the criterion (44), since \(2({\mathbf {e}}_{j}\otimes {\mathbf {e}}_{j}+{\mathbf {e}}_{i}\otimes {\mathbf {e}}_{i})\in {\mathbb{Z}}^{3\times 3}\).
(b) For bcc (see the proof of Theorem 5(b)) we have to minimize \(G({\mathbf {p}})H({\mathbf {q}})\) subject to \({\mathbf {p}}\cdot {\mathbf {q}}=2\) and \(G({\mathbf {p}})H({\mathbf {q}})>16\), where
Since \(H({\mathbf {q}})\) is even the minimum value is \(\geqslant 18\) and we show that the value 18 is attained. Also \(G({\mathbf {p}})\geqslant 3\), so that the possibilities are \(G({\mathbf {p}})=9\), \(H({\mathbf {q}})=2\), \(G({\mathbf {p}})=3\), \(H({\mathbf {q}})=6\). But \(G({\mathbf {p}})=9\) implies either (i) that \(p_{i}+p_{j}-p_{k}=\pm 3\), \(p_{i}+p_{k}-p_{j}=p_{j}+p_{k}-p_{i}=0\) for \(i\), \(j\), \(k\) distinct, so that \(p_{k}=0\) and \(2p_{i}=\pm 3\), which is impossible, or (ii) that \(p_{i}+p_{j}-p_{k}=2\kappa \), \(p_{k}+p_{i}-p_{j}=2\kappa '\), \(p_{j}+p_{k}-p_{i}=\kappa ''\) for \(i\), \(j\), \(k\) distinct and \(\kappa ,\kappa ',\kappa ''=\pm 1\), giving \(2p_{k}=2\kappa '+\kappa ''\), again impossible. Hence we need only consider the case \(G({\mathbf {p}})=3\), \(H({\mathbf {q}})=6\).
It is easy to check that \(G({\mathbf {p}})=3=1^{2}+1^{2}+1^{2}\) iff
and that \(H({\mathbf {q}})=6=2^{2}+1^{2}+1^{2}\) iff
From (50), (51) we find that \({\mathbf {p}}\cdot {\mathbf {q}}=2\) iff
Calculating \({\mathbf {a}}\otimes {\mathbf {n}}\) from (47) for these \({\mathbf {p}}\otimes {\mathbf {q}}\) and using (22) we obtain the conjugate pairs in the statement, none of which belong to \({\mathbb{Z}}^{3\times 3}\) and so are not slips.
To show that the twins are compound we note that from (47) and the relations \(|{\mathbf {a}}|=\frac {1}{2}\), \(|{\mathbf {B}}_{\mathrm{bcc}}^{-T}{\mathbf {q}}|^{2}=6\), \(|{\mathbf {B}}_{\mathrm{bcc}}{\mathbf {p}}|^{2}=\frac{3}{4}\) that
where \({\mathbf {G}}={\mathbf {B}}_{\mathrm{bcc}}^{T}{\mathbf {B}}_{\mathrm{bcc}}\). Since \({\mathbf {G}}^{-1}, 4{\mathbf {G}}\in {\mathbb{Z}}^{3\times 3}\), the twins are compound by (44).
(c) The twins for fcc are obtained from those for bcc using Theorem 3 and Corollary 2 as described above, which also imply that the twins are compound. □
Remark 5
For the cubic lattices we consider it is not in general true that Type 1 and Type 2 twins are compound. For example, we can take \({\mathbf {p}}=2{\mathbf {e}}_{1}-{\mathbf {e}}_{3}\), \({\mathbf {q}}=2{\mathbf {e}}_{1}+{\mathbf {e}}_{2}+2{\mathbf {e}}_{3}\), so that for the simple cubic lattice we obtain from (47)
with conjugate
Then none of
belong to \({\mathbb{Z}}^{3\times 3}\) so that, by (44), \(1+{\mathbf {a}}\otimes {\mathbf {n}}\), \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}\) are a pair of Type 1/Type 2 twins that are not compound. For the same \({\mathbf {p}}\), \({\mathbf {q}}\) it can be checked that the corresponding pair of conjugate bcc Type 1/Type 2 twins given by
are also not compound.
7 General Rank-One Connections Minimizing Shear Magnitude
We ask what the rank-one connections \({\mathbf {F}}={\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) are between \({\mathbf {1}}\) and \(\psi ^{-1}(0)=\bigcup _{\boldsymbol {\mu }\in GL^{+}(3,\mathbb{Z})}\operatorname {SO}(3){\mathbf {B}}\boldsymbol {\mu }{\mathbf {B}}^{-1}\) that minimize \(|{\mathbf {a}}|^{2}\). For the simple cubic lattice we have a complete answer.
Theorem 7
For the simple cubic lattice the rank-one connections \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}={\mathbf {R}}\boldsymbol {\mu }\), \({\mathbf {R}}\in \operatorname {SO}(3)\), \(\boldsymbol {\mu }\in GL^{+}(3,\mathbb{Z})\setminus \operatorname {SO}(3)\) that minimize \(|{\mathbf {a}}|\) are given by the slips in Theorem 5(a) and the twins in Theorem 6(a), with the minimum value \(|{\mathbf {a}}|^{2}=1\).
Proof
If \(\boldsymbol {\mu }\in GL^{+}(3,{\mathbb{Z}})\) then \(|\boldsymbol {\mu }|^{2}\geqslant 3\) with \(|\boldsymbol {\mu }|^{2}=3\) iff \(\boldsymbol {\mu }\in \operatorname {SO}(3)\) (this follows either by noting that each row and column must contain a nonzero entry, and that if there is a single entry \(=\pm 1\) then \(\boldsymbol {\mu }\) is a rotation, or by use of the AM⩾GM inequality applied to the squares of the singular values of \(\boldsymbol {\mu }\)). Since \(|\boldsymbol {\mu }|^{2}=3+|{\mathbf {a}}|^{2}\) is an integer, the minimum value of \(|{\mathbf {a}}|^{2}\) for a rank-one connection is \(\geqslant 1\), and so by Theorems 5, 6 the minimum value is \(|{\mathbf {a}}|^{2}=1\), with \(|\boldsymbol {\mu }|^{2}=4\).
But \(|\boldsymbol {\mu }|^{2}=4\) implies that each row and column of \(\boldsymbol {\mu }\) contains an entry \(\pm 1\) and that there is a single additional entry \(\pm 1\). Thus
for some \({\mathbf {Q}}\in P^{48}\) with \(Q_{kj}=0\) and \(\kappa =\pm 1\). Hence
where \({\mathbf {e}}_{i}=\kappa \kappa '{\mathbf {Q}}^{T}{\mathbf {e}}_{k}\), \(\kappa '=\pm 1\), and thus \({\mathbf {e}}_{i}\cdot {\mathbf {e}}_{j}=0\), from which it follows that \(\det {\mathbf {Q}}=1\) and hence \({\mathbf {Q}}\in \operatorname {SO}(3)\). The corresponding rank-one connections are then given by \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}={\mathbf {R}}{\mathbf {Q}}({\mathbf {1}}+\kappa '{\mathbf {e}}_{i}\otimes {\mathbf {e}}_{j})\) and are thus those in Theorems 5, 6. □
For bcc and fcc we have the following result.
Theorem 8
For bcc and fcc the squared magnitude \(|{\mathbf {a}}|^{2}\) for any rank-one connection \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}={\mathbf {R}}{\mathbf {B}}\boldsymbol {\mu }{\mathbf {B}}^{-1}\notin \operatorname {SO}(3)\), \(\boldsymbol {\mu }\in GL^{+}(3,\mathbb{Z})\) is given by \(|{\mathbf {a}}|^{2}=\frac{m}{2}\), where \(m\) is a positive integer.
Proof
By Theorem 3 it suffices to prove the result for bcc, for which we can write
Then, setting \({\mathbf {M}}={\mathbf {B}}_{\mathrm{bcc}}\boldsymbol {\mu }{\mathbf {B}}_{\mathrm{bcc}}^{-1}\), \({\mathbf {G}}={\mathbf {B}}_{\mathrm{bcc}}^{T}{\mathbf {B}}_{\mathrm{bcc}}={\mathbf {1}}-\frac{1}{4}{\mathbf {v}}\otimes {\mathbf {v}}\), and noting that \({\mathbf {G}}^{-1}={\mathbf {1}}+{\mathbf {v}}\otimes {\mathbf {v}}\), we calculate
We now note that
where \(c_{i}\) denotes the sum of the entries in the \(i^{\mathrm{th}}\) column of \(\boldsymbol {\mu }\). Since \(\boldsymbol {\mu }\in {\mathbb{Z}}^{3\times 3}\), \({\mathbf {v}}\in {\mathbb{Z}}^{3}\), and \(|{\mathbf {a}}|^{2}=|{\mathbf {M}}|^{2}-3\), the result follows from (56), (57). □
Corollary 3
For bcc and fcc the twins in Theorem 6(b), (c) minimize \(|{\mathbf {a}}|^{2}\).
Proof
The twins satisfy \(|{\mathbf {a}}|^{2}=\frac {1}{2}\), the least possible value. □
Remark 6
Corollary 3 leaves unresolved the possibility that some other rank-one connection for bcc or fcc also gives the value \(|{\mathbf {a}}|^{2}=\frac {1}{2}\). This could be decided computationally, since there are only finitely many possibilities for \(\boldsymbol {\mu }\), for each of which the existence of rank-one connections could be checked. Indeed, if \(|{\mathbf {M}}|^{2}=3+\frac {1}{2}=\frac{7}{2}\) then \(|\boldsymbol {\mu }|^{2}\leqslant |{\mathbf {B}}_{\mathrm{bcc}}^{-1}|^{2}|{\mathbf {M}}|^{2}|{\mathbf {B}}_{\mathrm{bcc}}|^{2}=47.25\) so that \(|\boldsymbol {\mu }|^{2}\leqslant 47\). However we can get a better estimate by noting that (56) can be rewritten as
Since \(\boldsymbol {\mu }\) is nonsingular we have that \(|\boldsymbol {\mu }{\mathbf {v}}|^{2}\geqslant 1\). Also \(\boldsymbol {\mu }^{T}\) is not a rank-one matrix, so that \(|3\boldsymbol {\mu }^{T}-\boldsymbol {\mu }^{T}{\mathbf {v}}\otimes {\mathbf {v}}|^{2}\geqslant 1\). Hence \(|\boldsymbol {\mu }|^{2}\leqslant 13-\frac{1}{3}\) and so \(|\boldsymbol {\mu }|^{2}\leqslant 12\).
8 Conjugates of Slips
We first ask when the conjugate of a slip is a slip.
Theorem 9
For simple cubic, bcc and fcc the only slips whose conjugates are slips are given by the conjugate pairs
with \(i\neq j\) and \(\kappa =\pm 1\), for which \(|{\mathbf {a}}|^{2}=4\).
Proof
We need to find the slips \({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}}\) such that
where we have used (22) and \(({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}})^{-1}={\mathbf {1}}-{\mathbf {a}}\otimes {\mathbf {n}}\).
For this to be the case we need that
so that \(|{\mathbf {a}}|^{2}= 4\left (\frac{3-m}{1+m}\right )\), giving the possibilities \(m=0,1\) or 2.
The case \(m=2\) is impossible since no \({\mathbf {Q}}\in P^{24}\) has \(\operatorname {tr}{\mathbf {Q}}=2\). The case \(m=0\) gives \(|{\mathbf {a}}|^{2}=12\) and
where \(\boldsymbol {\nu }= \frac{{\mathbf {a}}}{|{\mathbf {a}}|}\). But this is a rotation about \(\boldsymbol {\nu }\wedge {\mathbf {n}}\) through an angle \(\pm \frac{\pi}{3}\), and there are no such elements of \(P^{24}\).
Thus we only have to consider the case \(m=1\), for which \(|{\mathbf {a}}|^{2}=4\) and
This is a rotation through an angle \(\pm \pi /2\) about \(\boldsymbol {\nu }\wedge {\mathbf {n}}\), and the only such rotations in \(P^{24}\) are those with axes \({\mathbf {e}}_{i}\), so that without loss of generality we can suppose that
where \(\kappa =\pm 1\), and \({\mathbf {n}}=\cos \theta \,{\mathbf {e}}_{1}+\sin \theta \,{\mathbf {e}}_{2}\), \(\boldsymbol {\nu }=\kappa (\sin \theta \,{\mathbf {e}}_{1}-\cos \theta \,{\mathbf {e}}_{2})\). For the simple cubic case we then require that
which holds iff \(2\theta =k\frac{\pi}{2}\), giving the possibilities in the statement. Similarly, for bcc we require that \({\mathbf {B}}^{-1}{\mathbf {a}}\otimes {\mathbf {B}}^{T}{\mathbf {n}}\in {\mathbb{Z}}^{3\times 3}\), which again holds iff \(2\theta =k\frac{\pi}{2}\). □
It is interesting to calculate the conjugates to the slips in Theorem 5 and (35)-(37). For the simple cubic case we have already seen (Theorem 6(a)) that the rank-one connections conjugate to the slips in Theorem 5(a) are compound twins. For bcc and fcc we can without loss of generality (using Theorem 3) take the case of bcc, when we have the following result.
Theorem 10
The conjugates of the slips in Theorem 5(b) are twins which are neither Type 1 nor Type 2.
Proof
By Remark 4 we need only consider the case
which by (22) has conjugate
and is not a slip by Theorem 9, since \(|{\mathbf {a}}|^{2}\neq 4\). Then the rotation (see (27)) \({\mathbf {Q}}=\tilde{{\mathbf {R}}}{\mathbf {R}}^{T}=({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}})({\mathbf {1}}+{\mathbf {a}}\otimes {\mathbf {n}})^{-1}\) is given by
and setting \({\mathbf {m}}=\frac{1}{\sqrt{22}}(3{\mathbf {e}}_{1}+2{\mathbf {e}}_{2}-3{\mathbf {e}}_{3})\) we find that
so that \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}\) is a twin by (39). It is not a Type 1 or Type 2 twin because by computation neither \((-{\mathbf {1}}+2\tilde{{\mathbf {n}}}\otimes \tilde{{\mathbf {n}}}){\mathbf {Q}}\) nor \(\left (-{\mathbf {1}}+2 {\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {a}}}}/{|\tilde{{\mathbf {a}}}|^{2}}\right ){\mathbf {Q}}\) belong to \(P^{24}\). □
Next we look at the conjugates of the slips for bcc mentioned in (35)–(37).
Theorem 11
-
(i)
The conjugates of the slips for bcc with
$$\begin{aligned} {\mathbf {a}}\otimes {\mathbf {n}}\in \{\pm {\mathbf {e}}_{k}\otimes ({\mathbf {e}}_{i}+{\mathbf {e}}_{j}), {\mathbf {e}}_{k} \otimes ({\mathbf {e}}_{i}-{\mathbf {e}}_{j}), i,j,k\textit{ distinct}\} \end{aligned}$$(68)are Type 2 twins.
-
(ii)
The conjugates of the slips (36), (37) for bcc with \((112)\) and \((123)\) slip planes are twins that are neither Type 1 nor Type 2.
Proof
(i) As in Remark 4 it suffices to consider the case \({\mathbf {a}}\otimes {\mathbf {n}}={\mathbf {e}}_{3}\otimes ({\mathbf {e}}_{1}+{\mathbf {e}}_{2})\), for which
and
Then \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}\) is not a slip by Theorem 9, and
so that \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}\) is a Type 2 twin.
(ii) For the \((112)\) slips it suffices to consider the case
for which
and
Then \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}\) is not a slip by Theorem 9, and to show that it is a twin we let \({\mathbf {m}}=\frac{1}{34}(3{\mathbf {e}}_{1}+3{\mathbf {e}}_{2}-4{\mathbf {e}}_{3})\), so that
It is not a Type 1 or Type 2 twin because by computation neither \((-{\mathbf {1}}+2\tilde{{\mathbf {n}}}\otimes \tilde{{\mathbf {n}}}){\mathbf {Q}}\) nor \(\left (-{\mathbf {1}}+2 {\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {a}}}}/{|\tilde{{\mathbf {a}}}|^{2}}\right ){\mathbf {Q}}\) belong to \(P^{24}\).
For the \((123)\) slips it suffices to consider the case
for which
and
Letting \({\mathbf {m}}=\frac{1}{\sqrt{29}}(3{\mathbf {e}}_{1}-4{\mathbf {e}}_{2}-2{\mathbf {e}}_{3})\) we find that
so that \({\mathbf {1}}+\tilde{{\mathbf {a}}}\otimes \tilde{{\mathbf {n}}}\) is a twin, and as for the \((112)\) case one can check that it is not of Type 1 or Type 2. □
Remark 7
It is not in general true that the conjugate of a slip is a twin or a slip. For example we can take
which is a slip for both bcc and simple cubic, albeit for a high value of \(|{\mathbf {a}}|^{2}\). A calculation then shows that
and \({\mathbf {Q}}{\mathbf {P}}\) cannot equal \(-{\mathbf {1}}+2{\mathbf {m}}\otimes {\mathbf {m}}\) for any \({\mathbf {m}}\) because the absolute values of the entries of \({\mathbf {Q}}\) are all different, and the action of multiplying on the right by \({\mathbf {P}}\) permutes the columns of \({\mathbf {Q}}\) with possible changes of sign.
This shows in particular that there are rank-one connections which are neither twins nor slips. Such rank-one connections without mirror symmetry across the interface are observed for martensitic phase transformations, e.g. for \({\mathrm{LaNbO}}_{4}\) (Jian and Wayman [23], Jian and James [22]) and for NiMnGa (Seiner et al. [29]).
Conjugates of slips are observed in ‘kink deformations’; see Inamura [16], and for earlier work Starkey [30].
References
Ashcroft, N.W., Mermin, N.D.: Solid State Physics. Holt, Rinehart & Winston, New York (1976)
Ball, J.M.: Mathematical models of martensitic microstructure. Mater. Sci. Eng. A 78(1–2), 61–69 (2004)
Ball, J.M., Carstensen, C.: Interaction of martensitic microstructures in adjacent grains. In: Proceedings of International Conference on Martensitic Transformations, Chicago. TMS. Springer, Cham (2017). arXiv:1708.03286
Ball, J.M., James, R.D.: Fine phase mixtures as minimizers of energy. Arch. Ration. Mech. Anal. 100, 13–52 (1987)
Bevis, M., Crocker, A.G.: Twinning shears in lattices. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 304(1476), 123–134 (1968)
Bevis, M., Crocker, A.G.: Twinning modes in lattices. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 313(1515), 509–529 (1969)
Bilby, B.A., Crocker, A.G.: The theory of the crystallography of deformation twinning. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 288(1413), 240–255 (1965)
Chalmers, B., Martius, U.M.: Slip planes and the energy of dislocations. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 213(1113), 175–185 (1952)
Chen, N.K., Maddin, R.: Slip planes and the energy of dislocations in a bodycentered cubic structure. Acta Metall. 2(1), 49–51 (1954)
Chen, X., Srivastava, V., Dabade, V., James, R.D.: Study of the cofactor conditions: conditions of supercompatibility between phases. J. Mech. Phys. Solids 61(12), 2566–2587 (2013). https://doi.org/10.1016/j.jmps.2013.08.004. https://www.sciencedirect.com/science/article/pii/S002250961300149X
Christian, J.W.: The Theory of Transformation in Metals and Alloys Pergamon. Elsevier, New York (2002)
Christian, J.W., Mahajan, S.: Deformation twinning. Prog. Mater. Sci. 39(1–2), 1–157 (1995)
Cordier, P.: Dislocations and slip systems of mantle minerals. Rev. Mineral. Geochem. 51(1), 137–179 (2002)
Ericksen, J.L.: Special topics in elastostatics. In: Yih, C.S. (ed.) Advances in Applied Mechanics, vol. 17, pp. 189–244. Academic Press, San Diego (1977)
Forclaz, A.: A simple criterion for the existence of rank-one connections between martensitic wells. J. Elast. 57, 281–305 (1999)
Inamura, T.: Geometry of kink microstructure analysed by rank-1 connection. Acta Mater. 173, 270–280 (2019). https://doi.org/10.1016/j.actamat.2019.05.023. https://www.sciencedirect.com/science/article/pii/S1359645419303052
Jackson, A.G.: Handbook of Crystallography: For Electron Microscopists and Others. Springer, Berlin (2012)
James, R.D.: Private communication
Jaswon, M.A., Dove, D.B.: Twinning properties of lattice planes. Acta Crystallogr. 9(8), 621–626 (1956)
Jaswon, M.A., Dove, D.B.: The prediction of twinning modes in metal crystals. Acta Crystallogr. 10(1), 14–18 (1957)
Jaswon, M.A., Dove, D.B.: The crystallography of deformation twinning. Acta Crystallogr. 13(3), 232–240 (1960)
Jian, L., James, R.: Prediction of microstructure in monoclinic LaNbO4 by energy minimization. Acta Mater. 45(10), 4271–4281 (1997). https://doi.org/10.1016/S1359-6454(97)00080-3
Jian, L., Wayman, C.M.: Electron back scattering study of domain structure in monoclinic phase of a rare-Earth orthoniobate LaNbO4. Acta Metall. Mater. 43(10), 3893–3901 (1995)
Khachaturyan, A.G.: Theory of Structural Transformations in Solids. Wiley, New York (1983)
Kihô, H.: The crystallographic aspect of the mechanical twinning in metals. J. Phys. Soc. Jpn. 9(5), 739–747 (1954). https://doi.org/10.1143/JPSJ.9.739
Kihô, H.: The crystallographic aspect of the mechanical twinning in Ti and \(\alpha \)-U. J. Phys. Soc. Jpn. 13(3), 269–272 (1958). https://doi.org/10.1143/JPSJ.13.269
Ortiz, M., Repetto, E.A.: Nonconvex energy minimization and dislocation structures in ductile single crystals. J. Mech. Phys. Solids 47(2), 397–462 (1999)
Pitteri, M., Zanzotto, G.: Continuum Models for Phase Transitions and Twinning in Crystals. Chapman & Hall/CRC, Boca Raton (2003)
Seiner, H., Chulist, R., Maziarz, W., Sozinov, A., Heczko, O., Straka, L.: Non-conventional twins in five-layer modulated Ni-Mn-Ga martensite. Scr. Mater. 162, 497–502 (2019). https://doi.org/10.1016/j.scriptamat.2018.12.020. https://www.sciencedirect.com/science/article/pii/S1359646218307553
Starkey, J.: The geometry of kink bands in crystals—a simple model. Contrib. Mineral. Petrol. 19(2), 133–141 (1968)
Weinberger, C.R., Boyce, B.L., Battaile, C.C.: Slip planes in bcc transition metals. Int. Mater. Rev. 58(5), 296–314 (2013). https://doi.org/10.1179/1743280412Y.0000000015
Acknowledgements
I am grateful to Sergio Conti, Duvan Henao, Tomonari Inamura, Dick James, Kostas Koumatos, Michael Ortiz, Hanuš Seiner and Dave Srolowitz for their interest and helpful suggestions, and to the referees for careful reading which led to improvements in presentation.
Funding
This paper grew out of an invitation to give the 2019 Leçons Jacques-Louis Lions at Sorbonne Université Paris, and was developed during visits to the Hong Kong Institute for Advanced Study and the Hausdorff Institute of Mathematics (funded by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy – EXC-2047/1 – 390685813). The research forms part of the project Mathematical theory of polycrystalline materials supported by the EPSRC grant EP/V00204X.
Author information
Authors and Affiliations
Contributions
John Ball wrote the entire paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
In memoriam Jerry Ericksen, from whom I learnt so much
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ball, J.M. Slip and Twinning in Bravais Lattices. J Elast 155, 763–785 (2024). https://doi.org/10.1007/s10659-023-10034-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-023-10034-9