Abstract
We consider a recently introduced geometrically nonlinear elastic Cosserat shell model incorporating effects up to order \(O(h^{5})\) in the shell thickness \(h\). We develop the corresponding geometrically nonlinear constrained Cosserat shell model, we show the existence of minimizers for the \(O(h^{5})\) and \(O(h^{3})\) case and we draw some connections to existing models and classical shell strain measures. Notably, the role of the appearing new bending tensor is highlighted and investigated with respect to an invariance condition of Acharya (Int. J. Solids Struct. 37(39):5517–5528, 2000) which will be further strengthened.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Recently [20] we have established a novel geometrically nonlinear Cosserat shell model including terms up to order \(O(h^{5})\) in the shell-thickness \(h\), by extending the techniques from [30–33, 44]. The dimensional descent was obtained starting with a 3D-parent Cosserat model and assuming an appropriate 8-parameter ansatz for the shell-deformation through the thickness. This is the derivation approach and it has allowed us to arrive at specific novel strain and curvature measures. See also [7] for an alternative derivation of a \(O(h^{3})\) Cosserat shell model. In this way, we obtain a kinematical model which is similar, but it does not coincide, with the kinematical model of 6-parameter shells. The theory of 6-parameter shells was developed for shell-like bodies made of Cauchy materials, see the monographs [12, 27] or the papers [19, 37]. We have remarked that even if we restrict our model to order \(O(h^{3})\), the obtained minimization problem is not the same as that previously considered in the literature, since the influence of the curved initial shell configuration appears explicitly in the expression of the coefficients of the energies for the reduced two-dimensional variational problem and additional bending-curvature and curvature terms are present.
In order to improve our understanding of the new Cosserat shell model, it is useful to consider certain extreme limit cases. The investigated limit case considered in this paper, i.e., letting the Cosserat couple modulus \(\mu _{\mathrm{c}}\to \infty \), is similar to that considered in the case of the Cosserat plate model [30] and is naturally suggested by the situation for the three dimensional Cosserat model, which will now be explained.
The underlying nonlinear elastic 3D-problem is the two-field Cosserat variational problem
where

Here, \(\Omega _{\xi }\subset \mathbb{R}^{3}\) is a three-dimensional domain, see Fig. 1. The elastic material constituting the body is assumed to be homogeneous and isotropic and the reference configuration \(\Omega _{\xi }\) is assumed to be a natural state. All the body configurations are referred to a fixed right Cartesian coordinate frame with unit vectors \(e_{i}\) along the axes \(Ox_{i}\). A generic point of \(\Omega _{\xi }\) will be denoted by \((\xi _{1},\xi _{2},\xi _{3})\). The deformation of the body occupying the domain \(\Omega _{\xi }\) is described by a vector map \(\varphi _{\xi }:\Omega _{\xi }\subset \mathbb{R}^{3}\rightarrow \mathbb{R}^{3}\) (called deformation) and by a microrotation tensor  attached at each point. We denote the current configuration (deformed configuration) by \(\Omega _{c}:= \varphi _{\xi }(\Omega _{\xi })\subset \mathbb{R}^{3}\). Moreover, \(\mu >0\) denotes the shear modulus, \(\kappa >0\) is the bulk modulus and \(\mu _{\mathrm{c}}\geq 0\) is the Cosserat couple modulus.
attached at each point. We denote the current configuration (deformed configuration) by \(\Omega _{c}:= \varphi _{\xi }(\Omega _{\xi })\subset \mathbb{R}^{3}\). Moreover, \(\mu >0\) denotes the shear modulus, \(\kappa >0\) is the bulk modulus and \(\mu _{\mathrm{c}}\geq 0\) is the Cosserat couple modulus.
For Cosserat couple modulus \(\mu _{\mathrm{c}}\to \infty \) and characteristic length  the previous Cosserat model approximates the classical (Cauchy-elastic) Biot variational problem
the previous Cosserat model approximates the classical (Cauchy-elastic) Biot variational problem
where

Now, we consider \(\Omega _{\xi }\subset \mathbb{R}^{3}\) to be a three-dimensional curved shell-like thin domain, see Fig. 1. We take the fictitious Cartesian (planar) configuration of the body \(\Omega _{h} \). This parameter domain \(\Omega _{h}\subset \mathbb{R}^{3}\) is a right cylinder of the form
where \(\omega \subset \mathbb{R}^{2}\) is a bounded domain with Lipschitz boundary \(\partial \omega \) and the constant length \(h>0\) is the thickness of the shell. For shell–like bodies we consider the domain \(\Omega _{h} \) to be thin, i.e., the thickness \(h\) is small. The diffeomorphism \(\Theta :\mathbb{R}^{3}\rightarrow \mathbb{R}^{3}\) describing the reference configuration (i.e., the curved surface of the shell), will be chosen in the specific form
where \(y_{0}:\omega \to \mathbb{R}^{3}\) is a function of class \(C^{2}(\omega )\). If not otherwise indicated, by \(\nabla \Theta \) we denote \(\nabla \Theta (x_{1},x_{2},0)\), so that \(\nabla \Theta =(\nabla y_{0}\,|\,n_{0})\). We use the polar decomposition [35] of \(\nabla \Theta \) and write

Further, let us define the map \(\varphi :\Omega _{h}\rightarrow \Omega _{c},\ \varphi (x_{1},x_{2},x_{3})= \varphi _{\xi }( \Theta (x_{1},x_{2},x_{3}))\). We view \(\varphi \) as a function which maps the fictitious planar reference configuration \(\Omega _{h}\) into the deformed configuration \(\Omega _{c}\). We also consider the elastic microrotation \(\overline{Q}_{e,s}:\Omega _{h}\rightarrow {\mathrm{SO}}(3),\ \overline{Q}_{e,s}(x_{1},x_{2},x_{3}):= \overline{R}_{\xi }( \Theta (x_{1},x_{2},x_{3}))\). In [20], by assuming that the elastic microrotation is constant through the thickness, i.e., \(\overline{Q}_{e,s}(x_{1},x_{2},x_{3})=\overline{Q}_{e,s}(x_{1},x_{2})\), and considering an 8-parameter quadratic ansatz in the thickness direction for the reconstructed total deformation \(\varphi _{s}:\Omega _{h}\subset \mathbb{R}^{3}\rightarrow \mathbb{R}^{3}\) of the shell-like body, i.e.,
where \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) represents the total deformation of the midsurface, \(\varrho _{m},\,\varrho _{b}:\omega \subset \mathbb{R}^{2}\to \mathbb{R}\) allow in principal for symmetric thickness stretch (\(\varrho _{m}\neq 1\)) and asymmetric thickness stretch (\(\varrho _{b} \neq 0\)) about the midsurfaceFootnote 1

we have obtained a completely two-dimensional minimization problem, see Fig. 2, in which the energy density is expressed in terms of the following tensor fields (the same strain measures are also considered in [8, 9, 12, 19, 27] but with different motivations) on the surface \(\omega \)

Kinematics of the 2D-constrained Cosserat shell model (\({\boldsymbol{\mu _{\mathrm{c}}\to \infty }}\)). Here, \({Q}_{ \infty } \) is the elastic rotation field, \({Q}_{0}\) is the initial rotation from the fictitious planar Cartesian reference \(\omega \) configuration to the initial configuration \(\omega _{\xi }\), and \(R_{\infty }\) is the total rotation field from the fictitious planar Cartesian reference configuration \(\omega \) to the deformed configuration \(\omega _{c}\)
In the constrained Cosserat shell model, i.e., letting \(\mu _{\mathrm{c}}\to \infty \), the elastic microrotation \(\overline{Q}_{e,s}\) is not any more an independent tensor field (trièdre caché, Cosserat [18]). A direct consequence of the assumption \(\mu _{\mathrm{c}}\to \infty \) is that the elastic microrotation \(\overline{Q}_{e,s}\) is coupled to the midsurface displacement vector field \(m\), through

Considering Fig. 3, in this paper we determine the precise form of the Koiter-type limit problem appearing for \(\mu _{\mathrm{c}}\to \infty \). We recall that (see Appendix A.2), in the absence of external loads, in matrix format and for a nonlinear elastic shell, the variational problem for the classical isotropic Koiter shell model is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing:
Here \(\mathrm{I}_{m}:= [{\nabla m}]^{T}\,{\nabla m}\in \mathbb{R}^{2 \times 2}\) and \(\mathrm{II}_{m}:= \,-[{\nabla m}]^{T}\,{\nabla n}\in \mathbb{R}^{2 \times 2}\) are the matrix representations of the first fundamental form (metric) and the second fundamental form on \(m(\omega )\), respectively, \(n\,=\,\displaystyle \frac{\partial _{x_{1}}m\times \partial _{x_{2}}m}{\lVert \partial _{x_{1}}m\times \partial _{x_{2}}m\rVert } \), and with \(\mathrm{L}_{m}\) we identify the Weingarten map (or shape operator) on \(m(\omega )\) with its associated matrix defined by \(\mathrm{L}_{m}\,=\, \mathrm{I}_{m}^{-1} {\mathrm{II}}_{m}\in \mathbb{R}^{2 \times 2} \), with similar definitions for \(\mathrm{I}_{y_{0}}\), \(\mathrm{II}_{y_{0}}\), \({n_{0}}\) and \(\mathrm{L}_{y_{0}}\) on the surface \(y_{0}(\omega )\), see Sect. 2 for further notations.
A schematic representation of the appearing models. Here, \(\varphi =x+u(x)\) is the 3D-deformation, \(u\) is the three-dimensional displacement, \(F=\nabla \varphi \) is the deformation gradient, \(\overline{R}\in {\mathrm{SO}}(3)\) represents the Cosserat microrotation, \(m=y_{0}+v(x)\) is the midsurface deformation, \(v\) is the midsurface displacement, \(\overline{A}_{\vartheta }\in \mathfrak{so}(3)\) is the infinitesimal microrotation, \(\mathrm{I}_{m}:= [{\nabla m}]^{T}\,{\nabla m}\in \mathbb{R}^{2 \times 2}\) and \(\mathrm{II}_{m}:= \,-[{\nabla m}]^{T}\,{\nabla n}\in \mathbb{R}^{2 \times 2}\) are the matrix representations of the first fundamental form (metric) and the second fundamental form on \(m(\omega )\), respectively, \(n\,=\,\displaystyle \frac{\partial _{x_{1}}m\times \partial _{x_{2}}m}{\lVert \partial _{x_{1}}m\times \partial _{x_{2}}m\rVert } \), and with \(\mathrm{L}_{m}\) we identify the Weingarten map (or shape operator) on \(m(\omega )\) with its associated matrix defined by \(\mathrm{L}_{m}\,=\, \mathrm{I}_{m}^{-1} {\mathrm{II}}_{m}\in \mathbb{R}^{2 \times 2} \), with similar definitions for \(\mathrm{I}_{y_{0}}\), \(\mathrm{II}_{y_{0}}\), \({n_{0}}\) and \(\mathrm{L}_{y_{0}}\) on the surface \(y_{0}(\omega )\). The tensor \(\mathcal{G}_{\mathrm{{Koiter}}}^{\mathrm{{lin}}} = \frac{1}{2}[{\mathrm{I}}_{m} - \mathrm{I}_{y_{0}}]^{\mathrm{{lin}}} = \mathrm{sym} [ (\nabla y_{0})^{T}(\nabla v)]\) represents the infinitesimal change of metric, \(\mathcal{R}_{\mathrm{{Koiter}}}^{\mathrm{{lin}}}=[{\mathrm{II}}_{m} - \mathrm{II}_{y_{0}} ]^{\mathrm{{lin}}} \) is the infinitesimal change of curvature, and we have used the linear approximation of the normal \(n=n_{0}+\delta n+\mathrm{h.o.t.}\), where \(\delta n=\frac{1}{\sqrt{\det {\mathrm{I}}_{y_{0}}}}\left (\partial _{x_{1}} y_{0}\times \partial _{x_{2}} v+\partial _{x_{1}} v\times \partial _{x_{2}} y_{0}\right ) -\mathrm{tr}(\mathrm{I}_{y_{0}}^{-1}\, \mathrm{sym}((\nabla y_{0})^{T} \nabla v) )\,n_{0}\) is the increment of the normal when \(y_{0}\to y_{0}+v(x)\). The dimensional reduction is undertaken in the sense of an engineering ansatz and \(\kappa \) denotes a typical principal curvature. The relations concerning the third column of this table will be made explicit in [22]
In comparison with this nonlinear Koiter model, in the obtained new constrained elastic Cosserat shell model, the pure membrane energy is expressed in terms of the difference
and not in terms of

as it is the case in the classical Koiter shell model. This is a consequence of the fact that in the parent three-dimensional energy, we are starting from the non-symmetric Biot-type stretch tensor (similar to the right stretch tensor \(U=\sqrt{F^{T}F}\)), while the Koiter shell model is typically constructed considering a quadratic form in terms of the right Cauchy-Green deformation tensor \(C=U^{2}=F^{T}F\). We notice that in our constrained Cosserat shell model there does not exist a pure bending energy, the bending terms (those involving the second fundamental form) are always coupled with membrane terms (those involving the first fundamental form). The presence of energies depending on the difference of the square roots of the first fundamental forms is consistent with new estimates of the distance between two surfaces [16, 17] obtained in [28]. There, it is shown that the difference \(v=m-y_{0}\) is completely controlled by
and
The sum of the two expressions appears in the constrained Cosserat plate model ( ), too, see Eq. (3.69), while an additional term is present in our membrane-bending energy which has a format that cannot be guessed: it is a quadratic form in terms of the change of curvature tensor
), too, see Eq. (3.69), while an additional term is present in our membrane-bending energy which has a format that cannot be guessed: it is a quadratic form in terms of the change of curvature tensor

Therefore, our particular cases follow the recent trends of considering new shell models which are similar (but not equivalent) to the Koiter shell model with the aim to lead to improved modelling results, especially for not so thin shells. Of course, for in-extensional deformations \(\mathrm{I}_{m}=\mathrm{I}_{y_{0}}\) (pure bending mode, flexure), our change of curvature tensor (1.16) turns into

and coincides with the curvature tensor considered in the Koiter shell model (1.11), cf. [28].
In a forthcoming paper [22] we will see that the linearization of the strain measures of our constrained Cosserat shell model naturally leads to the same strain measures that are preferred in the later works by Sanders and Budiansky [10, 11] and by Koiter and Simmonds [24], who called the resulting theory the “best first-order linear elastic shell theory”.
In [20] the geometrically nonlinear constrained Cosserat shell model including terms up to order \(O(h^{5})\) is constructed under the assumption
where \(\kappa _{1},\kappa _{2}\) are the principal curvatures. Condition (1.17) guarantees that \(\det \nabla \Theta (x_{3})=1-2\,\mathrm{H}\, x_{3}+\mathrm{K}\, x_{3}^{2} \neq 0 \ \text{ for all} \ x_{3}\in \left [-\frac{h}{2},\frac{h}{2} \right ]\), i.e., it excludes self-intersection of the initially curved shell parametrized by \(\Theta \), see [20, Proposition A.2.]. However, condition (1.17) can be weakened since the classical condition (1.18)
is necessary and sufficient (see the Appendix A.3.1) to assure that \(\det \nabla \Theta (x_{3})=1-2\,\mathrm{H}\, x_{3}+\mathrm{K}\, x_{3}^{2} \neq 0 \ \text{ for all} \ x_{3}\in \left [-\frac{h}{2},\frac{h}{2} \right ]\). Therefore, without further remarks and computations, the model presented in [20] is valid under weakened conditions (1.18) on the thickness \(h\). Clearly, in terms of the principal radii of curvature \(R_{1}=\frac{1}{{|\kappa _{1}|}}\), \(R_{2}=\frac{1}{{|\kappa _{2}|}}\), see Fig. 4, the condition (1.18) is equivalent to
(and not \(\displaystyle h\ll 2\,\min \{\inf _{(x_{1},x_{2})\in {\omega }} R_{1}, \inf _{(x_{1},x_{2})\in {\omega }} R_{2}\}\) as is the modelling thin shell assumption for the classical Koiter model). For models which coincide to leading order with the classical Koiter model for small enough thickness [4, 5], the existence of the solution is proven under the conditions (1.19).
For the geometrically nonlinear Cosserat shell model including terms up to order \(O(h^{5})\) [20], we have shown the existence of the solution [21] for the theory including \(O(h^{5})\) terms, as well as the existence of the solution for the theory including terms up to order \(O(h^{3})\). In Appendix A.3.1 we show that condition (1.17) on the thickness, under which the existence result presented in [21] was shown, can be weakened, but the new condition still remains more restrictive than (1.18), i.e., the following existence result holds true
Theorem 1.1
Existence result for the theory including terms up to order \(O(h^{5})\)
Assume that the external loads satisfy the conditions
and the boundary data satisfy the conditions
Assume that the following conditions concerning the initial configuration are satisfied: \(y_{0}:\omega \subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}\) is a continuous injective mapping and

where \(a_{0}\) is a constant. Then, for sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients such that \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\), the minimization problem (2.4)–(2.8) admits at least one minimizing solution pair \((m,\overline{Q}_{e,s})\in \mathcal{A}\), where the admissible set \(\mathcal{A}\) of solutions is defined by
and the boundary conditions are to be understood in the sense of traces.
We noted that, in order to prove the existence of the solution, while in the theory including \(O(h^{5})\) the condition on the thickness \(h\) is similar to that originally considered in the modelling process, in the sense that it is independent of the constitutive parameters, in the \(O(h^{3})\)-case the coercivity is proven under more restrictive conditions on the thickness \(h\) which are depending on the constitutive parameters. This remains also true when the problem of the existence of solution in the nonlinear constrained Cosserat shell model is considered, as we show in Sects. 3.3 and 3.4.
Even if the condition (1.17) suggest that the existence of the solution is still valid for \(L_{c}\to 0\), this turns out to be false, since the presence of the extra Cosserat curvature energy, i.e., the condition \(L_{c}>0\), is essential in our proof. The missing extra curvature energy, which in classical shell models is not present, is responsible for the typical non-well-posedness of the classical models in the nonlinear case. Note that this also applies to Naghdi-type shell models with one independent director.
This paper is now structured as follows. After fixing our notation we briefly recapitulate the unconstrained Cosserat shell model. Then in Sect. 3 we turn our attention to the constraint Cosserat shell model which introduces several symmetry constraints in the model. These symmetry constraints are put into perspective with the underlying modeling of the three-dimensional problem. We prove conditional existence results since after all the problem may now be over-constrained. This motivates to introduce a modified model in Sect. 4, in which certain symmetry requirements are waived. Unconditional existence theorems are then presented. In Sect. 5 we express the strain measures in the Cosserat shell model in terms of classical quantities and finally in Sect. 6 we discuss the new invariance condition for bending tensors.
2 The Geometrically Nonlinear Cosserat Shell Model up to \(O(h^{5})\)
2.1 Notation
In this paper, for \(a,b\in \mathbb{R}^{n}\) we let \(\bigl \langle {a},{b} \bigr \rangle _{\mathbb{R}^{n}}\) denote the scalar product on \(\mathbb{R}^{n}\) with associated (squared) vector norm \(\lVert a\rVert _{\mathbb{R}^{n}}^{2}=\bigl \langle {a},{a} \bigr \rangle _{\mathbb{R}^{n}}\). The standard Euclidean scalar product on the set of real \(n\times {m}\) second order tensors \(\mathbb{R}^{n\times {m}}\) is given by \(\bigl \langle {X},{Y} \bigr \rangle _{\mathbb{R}^{n\times {m}}}=\mathrm{tr}(X \, Y^{T})\), and thus the (squared) Frobenius tensor norm is \(\lVert {X}\rVert ^{2}_{\mathbb{R}^{n\times {m}}}=\bigl \langle {X},{X} \bigr \rangle _{\mathbb{R}^{n\times {m}}}\). The identity tensor on \(\mathbb{R}^{n \times n}\) will be denoted by  , so that
, so that  , and the zero matrix is denoted by \(0_{n}\). We let \(\mathrm{Sym}(n)\) and \(\mathrm{Sym}^{+}(n)\) denote the symmetric and positive definite symmetric tensors, respectively. We adopt the usual abbreviations of Lie-group theory, i.e., \(\mathrm{GL}(n)=\{X\in \mathbb{R}^{n\times n}\;|\det ({X})\neq 0\}\) the general linear group,
, and the zero matrix is denoted by \(0_{n}\). We let \(\mathrm{Sym}(n)\) and \(\mathrm{Sym}^{+}(n)\) denote the symmetric and positive definite symmetric tensors, respectively. We adopt the usual abbreviations of Lie-group theory, i.e., \(\mathrm{GL}(n)=\{X\in \mathbb{R}^{n\times n}\;|\det ({X})\neq 0\}\) the general linear group,  with corresponding Lie-algebras \(\mathfrak{so}(n)=\{X\in \mathbb{R}^{n\times n}\;|X^{T}=-X\}\) of skew symmetric tensors and \(\mathfrak{sl}(n)=\{X\in \mathbb{R}^{n\times n}\;| \,\mathrm{tr}({X})=0 \}\) of traceless tensors. For all \(X\in \mathbb{R}^{n\times n}\) we set \(\mathrm{sym}\, X\,=\frac{1}{2}(X^{T}+X)\in {\mathrm{Sym}}(n)\), \(\mathrm{skew}\,X\,=\frac{1}{2}(X-X^{T})\in \mathfrak{so}(n)\) and the deviatoric part
with corresponding Lie-algebras \(\mathfrak{so}(n)=\{X\in \mathbb{R}^{n\times n}\;|X^{T}=-X\}\) of skew symmetric tensors and \(\mathfrak{sl}(n)=\{X\in \mathbb{R}^{n\times n}\;| \,\mathrm{tr}({X})=0 \}\) of traceless tensors. For all \(X\in \mathbb{R}^{n\times n}\) we set \(\mathrm{sym}\, X\,=\frac{1}{2}(X^{T}+X)\in {\mathrm{Sym}}(n)\), \(\mathrm{skew}\,X\,=\frac{1}{2}(X-X^{T})\in \mathfrak{so}(n)\) and the deviatoric part  and we have the orthogonal Cartan-decomposition of the Lie-algebra
and we have the orthogonal Cartan-decomposition of the Lie-algebra  ,
,  . For vectors \(\xi ,\eta \in \mathbb{R}^{n}\), we have the tensor product \((\xi \otimes \eta )_{ij}=\xi _{i}\,\eta _{j}\). A matrix having the three column vectors \(A_{1},A_{2}, A_{3}\) will be written as \((A_{1}\,|\, A_{2}\,|\,A_{3})\). For a given matrix \(M\in \mathbb{R}^{2\times 2}\) we define the 3D-lifted quantities
. For vectors \(\xi ,\eta \in \mathbb{R}^{n}\), we have the tensor product \((\xi \otimes \eta )_{ij}=\xi _{i}\,\eta _{j}\). A matrix having the three column vectors \(A_{1},A_{2}, A_{3}\) will be written as \((A_{1}\,|\, A_{2}\,|\,A_{3})\). For a given matrix \(M\in \mathbb{R}^{2\times 2}\) we define the 3D-lifted quantities

We make use of the operator \(\mathrm{axl}: \mathfrak{so}(3)\to \mathbb{R}^{3}\) associating with a skew-symmetric matrix \(A\in \mathfrak{so}(3)\) the vector \(\mathrm{axl}({A}):= (-A_{23},A_{13},-A_{12})^{T}\). The corresponding inverse operator will be denoted by \(\mathrm{Anti}: \mathbb{R}^{3}\to \mathfrak{so}(3)\).
For an open domain \(\Omega \subseteq \mathbb{R}^{3}\), the usual Lebesgue spaces of square integrable functions, vector or tensor fields on \(\Omega \) with values in ℝ, \(\mathbb{R}^{3}\), \(\mathbb{R}^{3\times 3}\) or \(\mathrm{SO}(3)\), respectively will be denoted by \(\mathrm{L}^{2}(\Omega ;\mathbb{R})\), \(\mathrm{L}^{2}(\Omega ;\mathbb{R}^{3})\), \(\mathrm{L}^{2}(\Omega ; \mathbb{R}^{3\times 3})\) and \(\mathrm{L}^{2}(\Omega ; \mathrm{SO}(3))\), respectively. Moreover, we use the standard Sobolev spaces \(\mathrm{H}^{1}(\Omega ; \mathbb{R})\) [2, 23, 26] of functions \(u\). For vector fields \(u=\left ( u_{1}, u_{2}, u_{3}\right )^{T}\) with \(u_{i}\in {\mathrm{H}}^{1}(\Omega )\), \(i=1,2,3\), we define \(\nabla \,u:= \left ( \nabla \, u_{1}\,|\, \nabla \, u_{2}\,| \, \nabla \, u_{3} \right )^{T}\). The corresponding Sobolev-space will be denoted by \(\mathrm{H}^{1}(\Omega ; \mathbb{R}^{3})\). A tensor \(Q:\Omega \to {\mathrm{SO}}(3)\) having the components in \(\mathrm{H}^{1}(\Omega ; \mathbb{R})\) belongs to \(\mathrm{H}^{1}(\Omega ; \mathrm{SO}(3))\). For tensor fields \(P\) with rows in \(\mathrm{H}(\mathrm{curl}\,; \Omega )\), i.e., \(P= \begin{footnotesize} \begin{pmatrix} P^{T}.e_{1}\,|\, P^{T}.e_{2}\,|\, P^{T}.e_{3} \end{pmatrix} \end{footnotesize} ^{T}\) with \((P^{T}.e_{i})^{T}\in {\mathrm{H}}(\mathrm{curl}\,; \Omega )\), \(i=1,2,3\), we define \(\mathrm{Curl}\,P:= \begin{footnotesize} \begin{pmatrix} {\mathrm{curl}}\, (P^{T}.e_{1})^{T}\,|\, \mathrm{curl}\, (P^{T}.e_{2})^{T}\,| \, \mathrm{curl}\, (P^{T}.e_{3})^{T} \end{pmatrix} \end{footnotesize} ^{T} \). The corresponding Sobolev-space will be denoted by \(\mathrm{H}(\mathrm{Curl};\Omega )\).
In writing the norm in the corresponding Sobolev-space we will specify the space. The space will be omitted only when the Frobenius norm or scalar product is considered. In the formulation of the minimization problem we have considered the Weingarten map (or shape operator) on \(y_{0}(\omega )\) defined by its associated matrix \(\mathrm{L}_{y_{0}}\,=\, \mathrm{I}_{y_{0}}^{-1} {\mathrm{II}}_{y_{0}}\in \mathbb{R}^{2\times 2}\), where \(\mathrm{I}_{y_{0}}:= [{\nabla y_{0}}]^{T}\,{\nabla y_{0}}\in \mathbb{R}^{2\times 2}\) and \(\mathrm{II}_{y_{0}}:= \,-[{\nabla y_{0}}]^{T}\,{\nabla n_{0}} \in \mathbb{R}^{2\times 2}\) are the matrix representations of the first fundamental form (metric) and the second fundamental form of the surface \(y_{0}(\omega )\), respectively. Then, the Gauß curvature \(\mathrm{K}\) of the surface \(y_{0}(\omega )\) is determined by \(\mathrm{K} := \,\mathrm{det}{(\mathrm{L}_{y_{0}})}\) and the mean curvature \(\mathrm{H}\) through \(2\,\mathrm{H}\, := {\mathrm{tr}}({\mathrm{L}_{y_{0}}})\). We have also used the tensors defined by
and the so-called alternator tensor \(\mathrm{C}_{y_{0}}\) of the surface [45]
2.2 The Unconstrained Cosserat Shell Model
In [20], we have obtained the following two-dimensional minimization problem for the deformation of the midsurface \(m:\omega \,{\to }\, \mathbb{R}^{3}\) and the microrotation of the shell \(\overline{Q}_{e,s}:\omega \,{\to }\, \textrm{SO}(3)\) solving on \(\omega \,\subset \mathbb{R}^{2} \): minimize with respect to \((m,\overline{Q}_{e,s}) \) the functional
where the membrane part \(W_{\mathrm{memb}}\big ( \mathcal{E}_{m,s} \big )\), the membrane–bending part \(W_{\mathrm{memb,bend}}\big ( \mathcal{E}_{m,s} ,\, \mathcal{K}_{e,s} \big ) \) and the bending–curvature part \(W_{\mathrm{bend,curv}}\big ( \mathcal{K}_{e,s} \big )\) of the shell energy density are given by

with

Contrary to other 6-parameter theory of shells [12, 13, 19, 36] the membrane-bending energy is expressed in terms of the specific tensor \(\mathcal{E}_{m,s} \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{e,s}\). This tensor represents a nonlinear change of curvature tensor, since in the linear constrained Cosserat model [22] it reduces to the change of curvature tensor considered by Anicic and Léger [6] and more recently by Šilhavỳ [39].
The parameters \(\mu \) and \(\lambda \) are the Lamé constants of classical isotropic elasticity, \(\kappa =\frac{2\,\mu +3\,\lambda }{3}\) is the infinitesimal bulk modulus, \(b_{1}, b_{2}, b_{3}\) are non-dimensional constitutive curvature coefficients (weights), \(\mu _{\mathrm{c}}\geq 0\) is called the Cosserat couple modulus and \({L}_{\mathrm{c}}>0\) introduces an internal length which is characteristic for the material, e.g., related to the grain size in a polycrystal. The internal length \({L}_{\mathrm{c}}>0\) is responsible for size effects in the sense that thinner samples are relatively stiffer than thicker samples. If not stated otherwise, we assume that \(\mu >0\), \(\kappa >0\), \(\mu _{\mathrm{c}}>0\), \(b_{1}>0\), \(b_{2}>0\), \(b_{3}> 0\). All the constitutive coefficients are now deduced from the three-dimensional formulation, without using any a posteriori fitting of some two-dimensional constitutive coefficients.
The potential of applied external loads \(\overline{\Pi }(m,\overline{Q}_{e,s}) \) appearing in (2.4) is expressed by
where \(u(x_{1},x_{2}) \,=\, m(x_{1},x_{2})-y_{0}(x_{1},x_{2}) \) is the displacement vector of the midsurface, \(\Pi _{\omega }(m,\overline{Q}_{e,s})\) is the potential of the external surface loads \(f\), while \(\Pi _{\gamma _{t}}(m,\overline{Q}_{e,s})\) is the potential of the external boundary loads \(t\). The functions \(\Lambda _{\omega }\,, \Lambda _{\gamma _{t}} : \mathrm{L}^{2} (\omega , \textrm{SO}(3))\rightarrow \mathbb{R} \) are expressed in terms of the loads from the three-dimensional parental variational problem [20] and they are assumed to be continuous and bounded operators. Here, \(\gamma _{t} \) and \(\gamma _{d} \) are measurable nonempty subsets of the boundary of \(\omega \) such that \(\gamma _{t} \cup \gamma _{d}= \partial \omega \) and \(\gamma _{t} \cap \gamma _{d}= \emptyset \). On \(\gamma _{t} \) we have considered traction boundary conditions, while on \(\gamma _{d} \) we have the Dirichlet-type boundary conditions:
where the boundary conditions are to be understood in the sense of traces.
In our model the total energy is not simply the sum of energies coupling the pure membrane and the pure bending effect, respectively. Two mixed coupling energies are still present after the dimensional reduction of the variational problem from the geometrically nonlinear three-dimensional Cosserat elasticity.
Considering materials for which \(\mu _{\mathrm{c}}>0\) and the Poisson ratio \(\nu =\frac{\lambda }{2(\lambda +\mu )}\) and Young’s modulus \(E=\frac{\mu (3\,\lambda +2\,\mu )}{\lambda +\mu }\) are such thatFootnote 2\(-\frac{1}{2}<\nu <\frac{1}{2}\) and \(E>0\) the Cosserat shell model admits global minimizers [21]. Under these assumptions on the constitutive coefficients, together with the positivity of \(\mu \), \(\mu _{\mathrm{c}}\), \(b_{1}\), \(b_{2}\) and \(b_{3}\), and the orthogonal Cartan-decomposition of the Lie-algebra \(\mathfrak{gl}(3)\) and with the definition

it follows that there exists positive constants \(c_{1}^{+}, c_{2}^{+}, C_{1}^{+}\) and \(C_{2}^{+}\) such that for all \(X\in \mathbb{R}^{3\times 3}\) the following inequalities hold
Here, \(c_{1}^{+}\) and \(C_{1}^{+}\) denote the smallest and the largest eigenvalues, respectively, of the quadratic form \({W}_{\mathrm{shell}}^{\infty }( X)\). Hence, they are independent of \(\mu _{\mathrm{c}}\).
3 The Limit Problem for Infinite Cosserat Couple Modulus \(\mu _{\mathrm{c}}\to \infty \)
In this section we consider the case \(\mu _{c}\rightarrow \infty \), since then the constraint \(\overline{R}_{\xi }=\mathrm{polar}(F_{\xi })\) is enforced in the starting three-dimensional variational problem. In that case, the parental three-dimensional model turns into the Toupin couple stress model [42, Eq. 11.8].
3.1 Constrained Elastic Cosserat Shell Models
Let us see what is happening to the dimensionally reduced model under the same circumstances. The following lemma gives us information on the constitutive restrictions under which the energy density remains bounded.
Lemma 3.1
For sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients satisfying \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\), the energy density
satisfies the estimate

Proof
The proof is similar to the proof of Theorem 4.1 from [21] and the proof given in Appendix A.3.2. □
In the remainder of this paper, the strain tensors corresponding to the constrained elastic Cosserat shell models will be denoted with the subscript \(\cdot _{ \infty }\), i.e., \({Q}_{ \infty }\), \(\mathcal{E}_{ \infty }\), \(\mathcal{K}_{ \infty }\) etc.
Therefore, since the membrane energy and the membrane-bending energy have to remain finite when \(\mu _{c}\rightarrow \infty \), in view of Lemma A.2 and (2.10) we have to impose [42, 43] that
We notice that the constraints (3.4) will imply that \(Q_{\infty }\) and \(m\) are not independent variables. Therefore, we need to take into account all the compatibility conditions between \({Q}_{ \infty }\Big |_{\gamma _{d}}\) and the values of \(m\) on \({\gamma _{d}}\) imposed by the limit case \(\mu _{\mathrm{c}}\to \infty \). More precisely, anticipating the implications of the constraints (3.4), we assume in the limit case \(\mu _{\mathrm{c}}\to \infty \) that a solution \((m,{Q}_{ \infty })\in {\mathrm{H}}^{1}(\omega , \mathbb{R}^{3})\times \mathrm{H}^{1}( \omega , \mathrm{SO}(3))\) has to satisfy the following compatibility conditions (in the sense of traces) on the boundary
The assumption \(\mathcal{E}_{ \infty }\in {\mathrm{Sym}}(3)\) and the above compatibility condition imply that \({Q}_{ \infty }=\mathrm{polar}\big [(\nabla m|n) [\nabla \Theta ]^{-1} \big ]\in \textrm{SO}(3)\), where \(n= \frac{\partial _{x_{1}} m\times \partial _{x_{2}} m}{\lVert \partial _{x_{1}} m\times \partial _{x_{2}} m\rVert }\) is the unit normal vector to the deformed midsurface, and \(\mathrm{polar}(X)\in \textrm{SO}(3)\) denotes the orthogonal part of the invertible matrix \(X\in {\mathrm{GL}}^{+}(3)\) in the polar decomposition [35], i.e., \(X=\mathrm{polar}(X)\, U\) with \(U\in {\mathrm{Sym}}^{+}(3)\). Indeed, we have
Thus, the vector \({Q}_{ \infty }Q_{0}.e_{3}\) is collinear with \(n\). Moreover, since \({Q}_{ \infty }Q_{0}\in {\mathrm{SO}}(3)\) and due to the compatibility conditions (3.5), we have \({Q}_{ \infty }Q_{0}.e_{3}=n\).
Hence,  implies \({Q}_{ \infty }^{T}(\nabla m|n)[\nabla \Theta ]^{-1}\in {\mathrm{Sym}}(3)\), and therefore
implies \({Q}_{ \infty }^{T}(\nabla m|n)[\nabla \Theta ]^{-1}\in {\mathrm{Sym}}(3)\), and therefore
where \(\widetilde{U}\in {\mathrm{Sym}}^{+}(3)\) is defined by
The constraint \({Q}_{ \infty }=\mathrm{polar}\big ((\nabla m|n) [\nabla \Theta ]^{-1} \big )\) not only adjusts the “trièdre mobile” [18] to be tangential to the surface (equivalent to \({Q}_{ \infty } Q_{0}.e_{3}=n\), Kirchhoff-Love normality assumption), see Fig. 5 such that the third column coincides with the normal to the surface, but also chooses a specific in-plane drill rotation, coming from the planar polar decomposition.
Using \(\widetilde{U}^{2}=\widetilde{U}^{T}\, \widetilde{U}=\big ((\nabla m|n)[ \nabla \Theta ]^{-1}\big )^{T} (\nabla m|n)[\nabla \Theta ]^{-1} =[ \nabla \Theta ]^{-T}\,\widehat{\mathrm{I}}_{m}\,[\nabla \Theta ]^{-1}\), we deduce
with the lifted quantity \(\widehat{\mathrm{I}}_{m} \in \mathbb{R}^{3\times 3}\) given by \(\widehat{\mathrm{I}}_{m}:= ({\nabla m}|n)^{T}({\nabla m}|n)\). Moreover, since \({Q}_{ \infty }\nabla \Theta .e_{3}={Q}_{ \infty }Q_{0}.e_{3}=n\), the latter identity leads to

An alternative expression of \(\mathcal{E}_{ \infty }\) containing only classical quantities can be obtained using Remark A.1 from Appendix A.1, i.e.,  which impliesFootnote 3
which impliesFootnote 3
Indeed, we obtain
In the following, we proceed to compute \(\mathcal{E}_{ \infty } \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{ \infty }\) which is appearing in the expression of the membrane-bending energy. From Remark A.1 we note the identity

which, together with the other identities from Remark A.1, leads to

Because \(\sqrt{[\nabla \Theta ]^{-T}\,\widehat{\mathrm{I}}_{m}\,[\nabla \Theta ]^{-1} \,[\nabla \Theta ]\,\widehat{\mathrm{I}}_{m}^{-1}[\nabla \Theta ]^{T}}=\, \sqrt{[\nabla \Theta ]\,\widehat{\mathrm{I}}_{m}^{-1}[\nabla \Theta ]^{T} \,[\nabla \Theta ]^{-T}\,\widehat{\mathrm{I}}_{m}\,[\nabla \Theta ]^{-1}}\), it follows \(\sqrt{[\nabla \Theta ]^{-T}\,\widehat{\mathrm{I}}_{m}\,[\nabla \Theta ]^{-1}} \,[\nabla \Theta ]\,\widehat{\mathrm{I}}_{m}^{-1}[\nabla \Theta ]^{T}= \sqrt{[\nabla \Theta ]\,\widehat{\mathrm{I}}_{m}^{-1}[\nabla \Theta ]^{T}}\). Using also the two formulae \(\widehat{\mathrm{I}}_{y_{0}}^{-1}{\mathrm{II}}_{y_{0}}^{\flat }=\mathrm{L}_{y_{0}}^{\flat }\),\(\widehat{\mathrm{I}}_{m}^{-1}{\mathrm{II}}_{m}^{\flat }=\mathrm{L}_{m}^{\flat }\), we may write

In view of the identity  , the quantity \(\mathcal{E}_{ \infty } \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{ \infty }\) can equivalently be written in the alternative form
, the quantity \(\mathcal{E}_{ \infty } \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{ \infty }\) can equivalently be written in the alternative form
and therefore we see how both pairs \(\widehat{\mathrm{I}}_{y_{0}}, \mathrm{L}_{y_{0}}^{\flat }\) and \(\widehat{\mathrm{I}}_{m}, \mathrm{L}_{m}^{\flat }\), together, influence the constitutive quantity \(\mathcal{E}_{ \infty } \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{ \infty }\). Since \((\mathcal{E}_{ \infty } \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{ \infty })\mathrm{B}_{y_{0}}\) is also an argument of an energy term defining the membrane-bending energy, i.e., \(W_{\mathrm{shell}} \big (( \mathcal{E}_{ \infty } \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{ \infty } ) \mathrm{B}_{y_{0}} \,\big )\), we have to compute as well

Note that for \({Q}_{ \infty }=\mathrm{polar}\big ((\nabla m|n) [\nabla \Theta ]^{-1} \big )\), which is a consequence of the limit \(\mu _{\mathrm{c}}\to \infty \), it follows that \(\mathcal{E}_{ \infty }\in {\mathrm{Sym}}(3)\), while the other two requirements (3.4)2,3, which are also implied by the limit \(\mu _{\mathrm{c}}\to \infty \) are not automatically satisfied. The remaining additional constraints in the minimization problem are
and
If \(L_{c}>0\) is finite and non-vanishing, the bending-curvature energy is still present in the minimization problem. The latter energy is expressed in terms of \(\mathcal{K}_{ \infty }\), which for \(\mu _{\mathrm{c}}\to \infty \) turns into
In view of the constitutive restrictions imposed by the limit case \(\mu _{\mathrm{c}}\to \infty \), the variational problem for the constrained Cosserat \(O(h^{5})\)-shell model is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \):

such that
where
3.2 3D Versus 2D Symmetry Requirements for \(\mu _{\mathrm{c}}\to \infty \)
As already mentioned in Sect. 3.1, in the starting three-dimensional variational problem (1.1), the limit \(\mu _{c}\rightarrow \infty \) leads to the constraint

and the parental three-dimensional model turns into the Toupin couple stress model [42, Eq. 11.8].
Motivated by modelling arguments, after obtaining a suitable form of the relevant coefficients \(\varrho _{m},\,\varrho _{b}\), in [20] we have based the expansion of the three-dimensional elastic Cosserat energy on a further simplified expression for the (reconstructed) deformation gradient \(F_{\xi }\), namely
Corresponding to this ansatz of the deformation gradient, the tensor  is approximated by
is approximated by

which admits the following expression with the help of the usual strain measures in the nonlinear 6-parameter shell theory
We substitute the expansion of the factor \(\dfrac{1}{\det \nabla \Theta (x_{3})}\) in the form
and get
If we multiply out all terms and use the relation \(\mathrm{B}_{y_{0}}^{2} = 2\,\mathrm{H}\,\mathrm{B}_{y_{0}} - \mathrm{K}\, \mathrm{A}_{y_{0}} \), then we obtain
Since \(\{1,x_{3},x_{3}^{2}\}\) are linear independent, from the last relation we see that the symmetry constraint \(\widetilde{\mathcal{E}}_{\xi }\approx \mathcal{E}_{s}\in {\mathrm{Sym}}(3)\) imposed by the limit case \(\mu _{\mathrm{c}}\to \infty \) implies the symmetry constraints on the tensors \(\mathcal{E}_{m,s} \), \((\mathcal{E}_{m,s} \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{e,s}) \) and \(( \mathcal{E}_{m,s} \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{e,s} ) \mathrm{B}_{y_{0}} \), i.e.,

This fact has in essence the following physical significance:

The terms of order \(O(x_{3}^{3}) \) are not relevant here, since we have taken a quadratic ansatz for the deformation.
Since  , this condition is equivalent to: the Biot-type stretch tensor \(\overline{{U}}_{e,s}=\overline{Q}_{e,s}^{T}\, \widetilde{F}_{e,s}\) for the 3D shell is symmetric. In conclusion, from (3.30) we see that the tensor \((\mathcal{E}_{m,s} \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{e,s}) \) can be viewed as a bending tensor for shells in the sense of Anicic and Léger [6] and Šilhavỳ [39].
, this condition is equivalent to: the Biot-type stretch tensor \(\overline{{U}}_{e,s}=\overline{Q}_{e,s}^{T}\, \widetilde{F}_{e,s}\) for the 3D shell is symmetric. In conclusion, from (3.30) we see that the tensor \((\mathcal{E}_{m,s} \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{e,s}) \) can be viewed as a bending tensor for shells in the sense of Anicic and Léger [6] and Šilhavỳ [39].
3.3 Conditional Existence for the \(O(h^{5})\)-Constrained Elastic Cosserat Shell Model
In this subsection we give a conditional existence result regarding the \(O(h^{5})\)-constrained elastic Cosserat shell model. First, it is important to define the appropriate admissible set of solutions, since \({Q}_{ \infty }\) and \(m\) are not any more independent: \({Q}_{ \infty }\) is determined by \({Q}_{ \infty }=\mathrm{polar}[(\nabla m|n)[\nabla \Theta ]^{-1}]\), once \(m\in {\mathrm{H}}^{1}(\omega , \mathbb{R}^{3})\) is known. However, \({Q}_{ \infty }=\mathrm{polar}[(\nabla m|n)[\nabla \Theta ]^{-1}]\) has to belong to \(\mathrm{H}^{1}(\omega , \mathrm{SO}(3))\), which does not directly follow from \(m\in {\mathrm{H}}^{1}(\omega , \mathbb{R}^{3})\). Hence, since the existence result of the solution for the unconstrained elastic Cosserat shell model assures the desired regularity for \({Q}_{ \infty }\), we follow the same method as in [21]. We notice that the existence result presented in [21] is valid in the case of no boundary conditions upon \({Q}_{ \infty }\), too.Footnote 4 In the definition of the admissible set of solution, we need to take into account all the compatibility conditions between \({Q}_{ \infty }\Big |_{\gamma _{d}}\) and the values of \(m\) on \({\gamma _{d}}\) imposed by the limit case \(\mu _{\mathrm{c}}\to \infty \). The set \(\mathcal{A}\) of admissible functions is therefore defined by

which incorporates a weak reformulation of the symmetry constraint in (3.22), in the sense that all the derivatives are considered now in the sense of distributions, and the boundary conditions are to be understood in the sense of traces. However, a priori it is not clear if the set \(\mathcal{A}\) is non-empty. In view of (3.22), we note that if \(m\in {\mathrm{H}}^{2}(\omega ,\mathbb{R}^{3})\) is such that \(\mathrm{L}_{y_{0}}=\mathrm{L}_{m}\) and \(m\big |_{ \gamma _{d}}=m^{*}\), then by choosing  we obtain \((m,{Q}_{ \infty })\in \mathcal{A}\). In general, \(\mathcal{A}\) may be empty. Therefore we propose:
we obtain \((m,{Q}_{ \infty })\in \mathcal{A}\). In general, \(\mathcal{A}\) may be empty. Therefore we propose:
Theorem 3.2
Conditional existence result for the theory including terms up to order \(O(h^{5})\)
Assume that the admissible set \(\mathcal{A}\) is non-empty and the external loads satisfy the conditions \({f}\in \mathrm{L}^{2}(\omega ,\mathbb{R}^{3})\), \(t\in \mathrm{L}^{2}(\gamma _{t},\mathbb{R}^{3})\), and the boundary data satisfy the conditions \({m}^{*}\in {\mathrm{H}}^{1}(\omega ,\mathbb{R}^{3})\) and \(\mathrm{polar}(\nabla {m}^{*}\,|\,n^{*}) \in {\mathrm{H}}^{1}(\omega , \mathrm{SO}(3))\). Assume that the following conditions concerning the initial configuration are satisfied:Footnote 5\(y_{0}:\omega \subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}\) is a continuous injective mapping and

where \(a_{0}\) is a positive constant. Then, for sufficiently small values of the thickness \(h\) satisfying
and for constitutive coefficients such that \(\mu >0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\), \(b_{3}>0\) and \(L_{\mathrm{c}}>0\), the minimization problem (3.21) admits at least one minimizing solution \(m\) such that \((m,{Q}_{ \infty })\in \mathcal{A}\).
Proof
The proof follows similar steps as in [21] for the proof of the existence of solution for the unconstrained \(O(h^{5})\) elastic Cosserat shell model and is similar to the proof of Proposition A.2 from Appendix A.3.1. Here, we provide only certain milestones, to guide the reader and explain those details that differ in comparison to [21]. First, it follows that for sufficiently small values of the thickness \(h\) such that (3.34) is satisfied and for constitutive coefficients satisfying \(\mu >0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\), the energy density
is coercive, where \(W_{\mathrm{memb}}^{\infty }\) and \(W_{\mathrm{memb,bend}}^{\infty }\) are the membrane energy and the membrane-bending energy corresponding to the limit case \(\mu _{\mathrm{c}}\to \infty \). This means that there exists a constant \(a_{1}^{+}>0\) such that
where \(a_{1}^{+}\) depends on the constitutive coefficients (but not on the Cosserat couple modulus \(\mu _{\mathrm{c}}\)). Indeed, all the steps used in the proof of Proposition A.2 from Appendix A.3.1 remain valid by considering \(\mu _{\mathrm{c}}\to \infty \) since for all \((m,{Q}_{ \infty })\in \mathcal{A}\) it follows that \(\mathcal{E}_{ \infty }\in {\mathrm{Sym}}(3)\) and \(\mathcal{E}_{ \infty }{\mathrm{B}}_{y_{0}}+\mathrm{C}_{y_{0}}\, \mathcal{K}_{ \infty }\in {\mathrm{Sym}}(3)\).
Moreover, under the same hypothesis and using the same arguments as above, it follows that for \(\mu _{\mathrm{c}}\to \infty \), too, the energy density \(W^{\infty }(\mathcal{E}_{ \infty }, \mathcal{K}_{ \infty }) \) is uniformly convex in \((\mathcal{E}_{ \infty }, \mathcal{K}_{ \infty })\) for all \((m,{Q}_{ \infty })\in \mathcal{A}\), i.e., there exists a constant \(a_{1}^{+}>0\) such that
The assumptions on the external loads and the boundedness of \(\Pi _{S^{0}}\) and \(\Pi _{\partial S^{0}_{f}}\) imply that there exists a constant \(c>0\) such thatFootnote 6
Considering
we write
Using this expression for \(\mathcal{E}_{ \infty }\) we obtain
where \(\lambda _{0}\) is the smallest eigenvalue of the positive definite matrix \(\widehat{\mathrm{I}}^{-1}_{y_{0}}\) and \({c}_{1}>0\), \({c}_{2}>0\) are some positive constants. Similarly, we deduce that
In view of the coercivity of the internal energy and (3.33), (3.38) and (3.41), and after using the Poincaré–inequality we deduce that the functional \(I(m,{Q}_{ \infty })\) is bounded from below on \(\mathcal{A}\), i.e.,

where \(c_{1}>0\) and \(c {_{2}}\in \mathbb{R}\). Hence, there exists an infimizing sequence \(\big \{(m_{k},\overline{Q}_{k})\big \}_{k=1}^{\infty }\) in \(\mathcal{A}\), such that
Since we have \(I(m^{*},{Q}_{ \infty }^{*})<\infty \), in view of the conditions on the boundary data, the infimizing sequence \(\big \{(m_{k},\overline{Q}_{k})\big \}_{k=1}^{\infty }\) can be chosen such that
Using (3.43) and (3.45) we remark that the sequence \(\big \{m_{k} \big \}_{k=1}^{\infty }\) is bounded in \(\mathrm{H}^{1}(\omega ,\mathbb{R}^{3})\). Hence, we can consider a subsequence of \(\big \{m_{k} \big \}_{k=1}^{\infty }\) (not relabeled) which converges weakly in \(\mathrm{H}^{1}(\omega ,\mathbb{R}^{3})\). According to Rellich’s selection principle, it converges strongly in \(\mathrm{L}^{2}(\omega ,\mathbb{R}^{3})\), i.e., there exists an element \(\widehat{m}\in {\mathrm{H}}^{1}(\omega ,\mathbb{R}^{3})\) such that
We skip further details, since they mimic the proof of existence theorem from [21], and we use only the fact that there exists a subsequence of  (not relabeled) and an element \(\widehat{\overline{Q}}_{ \infty }\in {\mathrm{H}}^{1}(\omega ,\mathrm{SO}(3))\) with
(not relabeled) and an element \(\widehat{\overline{Q}}_{ \infty }\in {\mathrm{H}}^{1}(\omega ,\mathrm{SO}(3))\) with
Let us next construct the limit strain and curvature measures

Note that using
and the identity \(\mathrm{axl}(Q\, A\, Q^{T})\,=\,Q\,\mathrm{axl}( A)\) for all \(Q\in {\mathrm{SO}}(3)\) and for all \(A\in \mathfrak{so}(3)\), we obtain
In the next steps of the proof, all the arguments from [21] hold true and we conclude that
in \(\mathrm{L}^{2}(\omega ,\mathbb{R}^{3\times 3})\), where \(\widehat{\overline{R}}_{k}(x_{1},x_{2}) := \widehat{\overline{Q}}_{k}(x_{1},x_{2})\,Q_{0}(x_{1},x_{2},0)\in {\mathrm{SO}}(3)\), as well as
in \(\mathrm{L}^{2}(\omega ,\mathbb{R}^{3\times 3})\). The admissible set \(\mathcal{A}\) defined by (3.32) is closed under weak convergence. Indeed, since the set of symmetric matrices is closed under weak convergence, we find

whenever the sequence \(\big \{(m_{k},\overline{Q}_{k})\big \}_{k=1}^{\infty }\subseteq \mathcal{A}\) is weakly convergent to \((\widehat{{m}},\widehat{\overline{Q}}_{ \infty })\in {\mathrm{H}}^{1}( \omega , \mathbb{R}^{3})\times \mathrm{H}^{1}(\omega , \mathrm{SO}(3))\). Moreover, by virtue of the relations \((m_{k},\overline{Q}_{k})\in \mathcal{A}\) and (3.46), (3.47), we derive that \(\widehat{m}={m}^{*}\) and \(\widehat{\overline{Q}}_{ \infty }Q_{0}.e_{3}=\,\displaystyle \frac{\partial _{x_{1}}m^{*}\times \partial _{x_{2}}m^{*}}{\lVert \partial _{x_{1}}m^{*}\times \partial _{x_{2}}m^{*}\rVert }\) on \(\gamma _{d}\) in the sense of traces. The second boundary condition is satisfied, since a similar procedure with that used in (3.5)–(3.7) shows that (3.53) and the compatibility of the boundary conditions imply that \(\widehat{\overline{Q}}_{ \infty }Q_{0}.e_{3}=\widehat{n}:= \displaystyle \frac{\partial _{x_{1}}\widehat{m}\times \partial _{x_{2}}\widehat{m}}{\lVert \partial _{x_{1}}\widehat{m}\times \partial _{x_{2}}\widehat{m}\rVert }\) and \(\widehat{\overline{Q}}_{ \infty }=\mathrm{polar}[(\nabla \widehat{m}| \widehat{n})[\nabla \Theta ]^{-1}]\). Hence, we obtain that the limit pair satisfies \((\widehat{m},\widehat{\overline{Q}}_{ \infty })\in \mathcal{A}\) and, in view of convexity in the chosen strain and curvature measures (3.51), (3.52) and (3.53), we also have
Taking into account the assumptions on the external loads, the continuity of the load potential functions, and the convergence relations (3.46)2 and (3.47)2, we deduce
Finally, the relations (3.44) and (3.56) show that \(I(\widehat{{m}},\widehat{\overline{Q}}_{ \infty })\,=\, \,\inf \, \big \{I({m},{Q}_{ \infty })\, \big |\, ({m},{Q}_{ \infty })\in \mathcal{A}\big \}\). Since \((\widehat{{m}},\widehat{\overline{Q}}_{ \infty })\in \mathcal{A}\), we conclude that \((\widehat{{m}},\widehat{\overline{Q}}_{ \infty })\) is a minimizing solution pair of our minimization problem, in which \(\widehat{\overline{Q}}_{ \infty }=\mathrm{polar}\big ((\nabla \widehat{{m}}|\widehat{{n}}) [\nabla \Theta ]^{-1}\big )\), \(\widehat{\mathcal{E}}_{ \infty } \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \widehat{\mathcal{K}}_{ \infty }\in {\mathrm{Sym}}(3)\) and \((\widehat{\mathcal{E}}_{ \infty } \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \widehat{\mathcal{K}}_{ \infty })\mathrm{B}_{y_{0}} \in {\mathrm{Sym}}(3)\). □
3.4 Conditional Existence for the \(O(h^{3})\)-Constrained Elastic Cosserat Shell Model
In the \(O(h^{5})\)-shell model and for \(\mu _{\mathrm{c}}\to \infty \) the assumptions
are not sufficient to ensure that the energy density is finite, we need to require additionally
This condition is necessary since the energy term \(\frac{h^{5}}{80}\,\frac{1}{6} W_{\mathrm{shell}} \big (( \mathcal{E}_{m,s} \, \mathrm{B}_{y_{0}} + \mathrm{C}_{y_{0}} \mathcal{K}_{e,s} ) \mathrm{B}_{y_{0}} \,\big )\) must remain finite for \(\mu _{\mathrm{c}}\to \infty \). However, in the \(O(h^{3})\)-shell model the latter energy term is not anymore present and there is no need to impose the extra symmetry condition (3.58). Indeed, if we restrict our model to order \(O(h^{3})\), then the internal energy density reads

which, under the restrictions (3.57), can be expressed as

and which remains finite for \(\mu _{\mathrm{c}}\to \infty \).
In view of the above constitutive restrictions (3.57) imposed by the limit case, the variational problem for the constrained Cosserat \(O(h^{3})\)-shell model is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \):

such that
where
We consider the admissible set \(\mathcal{A}_{(h^{3})}\) of solutions to be defined by
where the boundary conditions are to be understood in the sense of traces. As in the case of the constrained Cosserat shell model up to \(O(h^{5})\), the set \(\mathcal{A}_{(h^{3})}\) may be empty. In [21] and Appendix A.3.3 we have shown that if the constitutive coefficients are such that \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\), \(b_{3}>0\) and \(L_{\mathrm{c}}>0\) and if the thickness \(h\) satisfies at least one of the following conditions:
-
(i)
\(h\max \{\sup _{x\in \omega }|\kappa _{1}|, \sup _{x\in \omega }| \kappa _{2}|\}<\alpha \) and \(h^{2}<\frac{(5-2\sqrt{6})(\alpha ^{2}-12)^{2}}{4\, \alpha ^{2}} \frac{ {c_{2}^{+}}}{\max \{C_{1}^{+},\mu _{c}\}}\) with \(\quad 0<\alpha <2\sqrt{3}\);
-
(ii)
\(h\max \{\sup _{x\in \omega }|\kappa _{1}|, \sup _{x\in \omega }| \kappa _{2}|\}<\frac{1}{a}\) and \(a>\max \Big \{1 + \frac{\sqrt{2}}{2}, \frac{1+\sqrt{1+3\frac{\max \{C_{1}^{+},\mu _{c}\}}{\min \{c_{1}^{+},\mu _{c}\}}}}{2} \Big \}\),
where \(c_{1}^{+}\) and \(C_{1}^{+}\) denote the smallest and the largest eigenvalues, respectively, of the quadratic form \({W}_{\mathrm{shell}}^{\infty }( X)\), then the energy density

is coercive. However, this result is not suitable for the limit case \(\mu _{\mathrm{c}}\to \infty \) since the above conditions imposed upon the thickness would imply \(h\to 0\) for \(\mu _{\mathrm{c}}\to \infty \). We circumvent the problem by proving the following result.
Proposition 3.3
Coercivity in the theory including terms up to order \(O(h^{3})\)
Assume that the constitutive coefficients are such that \(\mu >0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\), \(b_{3}>0\) and \(L_{\mathrm{c}}>0\) and let \(c_{2}^{+}\) denote the smallest eigenvalue of \(W_{\mathrm{curv}}( S )\), and \(c_{1}^{+}\) and \(C_{1}^{+}>0\) denote the smallest and the largest eigenvalues of the quadratic form \(W_{\mathrm{shell}}^{\infty }( S)\). If the thickness \(h\) satisfies one of the following conditions:
-
(i)
\(h\max \{\sup _{x\in \omega }|\kappa _{1}|, \sup _{x\in \omega }| \kappa _{2}|\}<\alpha \) and \(h^{2}<\frac{(5-2\sqrt{6})(\alpha ^{2}-12)^{2}}{4\, \alpha ^{2}} \frac{ {c_{2}^{+}}}{C_{1}^{+}}\) with \(\quad 0<\alpha <2\sqrt{3}\);
-
(ii)
\(h\max \{\sup _{x\in \omega }|\kappa _{1}|, \sup _{x\in \omega }| \kappa _{2}|\}<\frac{1}{a}\) and \(a>\max \Big \{1 + \frac{\sqrt{2}}{2}, \frac{1+\sqrt{1+3\frac{C_{1}^{+}}{c_{1}^{+}}}}{2}\Big \}\),
then the internal energy density

is coercive on \(\mathcal{A}_{(h^{3})}\), in the sense that there exists a constant \(a_{1}^{+}>0\) such that
where \(a_{1}^{+}\) depends on the constitutive coefficients but is independent of the Cosserat couple modulus \(\mu _{\mathrm{c}}\).
Proof
The proof is similar with the proof of Proposition 4.1 from [21] and Proposition A.3 from the appendix, the only difference consists in using \(\lVert X\rVert \geq \lVert {\mathrm{sym}}\,X\rVert \), \(\forall X\in \mathbb{R}^{3\times 3}\) and the positive definiteness conditions (2.10). □
Once the coercivity is proven, the following existence result follows easily:
Theorem 3.4
Conditional existence result for the constrained theory including terms up to order \(O(h^{3})\)
Assume that the admissible set \(\mathcal{A}_{(h^{3})}\) is non-empty and the external loads satisfy the conditions \({f}\in \mathrm{L}^{2}(\omega ,\mathbb{R}^{3})\), \(t\in \mathrm{L}^{2}(\gamma _{t},\mathbb{R}^{3})\), the boundary data satisfy the conditions \({m}^{*}\in {\mathrm{H}}^{1}(\omega ,\mathbb{R}^{3})\) and \(\mathrm{polar}(\nabla {m}^{*}\,|\,n^{*})\in {\mathrm{H}}^{1}(\omega , \mathrm{SO}(3))\), and that the following conditions concerning the initial configuration are fulfilled: \(y_{0}:\omega \subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}\) is a continuous injective mapping and

where \(a_{0}\) is a positive constant. Assume that the constitutive coefficients are such that \(\mu >0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\), \(b_{3}>0\) and \(L_{\mathrm{c}}>0\). Then, if the thickness \(h\) satisfies at least one of the following conditions:
-
(i)
\(h\max \{\sup _{x\in \omega }|\kappa _{1}|, \sup _{x\in \omega }| \kappa _{2}|\}<\alpha \) and \(h^{2}<\frac{(5-2\sqrt{6})(\alpha ^{2}-12)^{2}}{4\, \alpha ^{2}} \frac{ {c_{2}^{+}}}{C_{1}^{+}}\) with \(\quad 0<\alpha <2\sqrt{3}\);
-
(ii)
\(h\max \{\sup _{x\in \omega }|\kappa _{1}|, \sup _{x\in \omega }| \kappa _{2}|\}<\frac{1}{a}\) and \(a>\max \Big \{1 + \frac{\sqrt{2}}{2}, \frac{1+\sqrt{1+3\frac{C_{1}^{+}}{c_{1}^{+}}}}{2}\Big \}\),
where \(c_{2}^{+}\) denotes the smallest eigenvalue of \(W_{\mathrm{curv}}( S )\), and \(c_{1}^{+}\) and \(C_{1}^{+}>0\) denote the smallest and the biggest eigenvalues of the quadratic form \(W_{\mathrm{shell}}^{\infty }( S)\), the minimization problem corresponding to the energy density defined by (3.61) admits at least one minimizing solution \(m\) such that the pair \((m,{Q}_{ \infty })\in \mathcal{A}_{(h^{3})}\).
3.5 The Constrained Elastic Cosserat Plate Model
In the case of Cosserat plates (planar shell) there is no initial curvature and we have \(\Theta (x_{1},x_{2},x_{3})\,=\,(x_{1},x_{2},x_{3})\) together with

Therefore, all \(O(h^{5})\)-terms of our constrained elastic Cosserat shell model given in Sect. 3.3 as well as all the mixed terms are automatically vanishing and we obtain that the variational problem of the constrained Cosserat plate model is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \):

such that
where
We already observe that the bending tensor \(\displaystyle \sqrt{\widehat{\mathrm{I}}_{m}^{-1}} {\mathrm{II}}_{m}^{\flat }\) is invariant under \(m\to \alpha \, m\), \(\alpha >0\) (cf. the discussion in Sect. 6.1). Note that the scaling \(m\to \alpha \, m\), \(\alpha >0\) is certainly not connected to a bending type deformation. Therefore, it does make sense that \(\sqrt{\widehat{\mathrm{I}}_{m}^{-1}} {\mathrm{II}}_{m}^{\flat }\) remains invariant.
The existence of minimizers for this problem was already discussed in [30]. The considered admissible set \(\mathcal{A}_{\mathrm{plate}}\) of solutions is [30]
where the boundary conditions are to be understood in the sense of traces. The restriction \(\mathfrak{K}_{\mathrm{1}}:= {Q}_{ \infty }^{T}(\nabla n|0) \stackrel{!}{\in } {\mathrm{L^{2}}}(\omega , \mathrm{Sym}(3))\ \Leftrightarrow \ \sqrt{\widehat{\mathrm{I}}_{m}^{-1}} {\mathrm{II}}_{m}^{\flat }\stackrel{!}{\in }{\mathrm{Sym}}(3)\) is not automatically satisfied, in general. However, it is satisfied for pure bending, i.e., when no change of metric is present \((\nabla m|n)\in {\mathrm{SO}}(3)\ \Leftrightarrow \ \mathrm{I}_{m}=\mathrm{I}_{y_{0}}\), situation when \(\mathcal{G}_{\infty }^{\flat }=0\), \(\mathcal{R}_{\infty }^{\flat }=\mathrm{II}_{m}^{\flat }\in {\mathrm{Sym}}(3)\). Therefore, if there exists a solution of the pure bending problem, i.e., the situation \((\nabla m|n)\in {\mathrm{SO}}(3)\), when \(U \in {\mathrm{diag}}\) and \(\mathrm{II}_{m}\in {\mathrm{diag}}\), such that \(\mathrm{I}_{m}=\mathrm{I}_{y_{0}}\), then the set \(\mathcal{A}_{\mathrm{plate}}\) is not empty.
In the constrained planar case, the change of metric tensor is given by  , the bending strain tensor becomes \(\mathcal{R}_{\infty }^{\flat }=\sqrt{\widehat{\mathrm{I}}_{m}^{-1}} {\mathrm{II}}_{m}^{\flat }\stackrel{!}{\in } {\mathrm{Sym}}(3)\) (which is not automatically satisfied if \({Q}_{ \infty }=\mathrm{polar}(\nabla m|n)\)), the transverse shear deformation vector vanishes \(\mathcal{T}_{\infty }=(0,0) \) and the vector of drilling bending reads \(\mathcal{N}_{\infty } := e_{3}^{T}\, \big (\mbox{axl}({Q}_{ \infty }^{T}\partial _{x_{1}}{Q}_{ \infty })\,| \, \mbox{axl}({Q}_{ \infty }^{T}\partial _{x_{2}}{Q}_{ \infty }) \big )\).
, the bending strain tensor becomes \(\mathcal{R}_{\infty }^{\flat }=\sqrt{\widehat{\mathrm{I}}_{m}^{-1}} {\mathrm{II}}_{m}^{\flat }\stackrel{!}{\in } {\mathrm{Sym}}(3)\) (which is not automatically satisfied if \({Q}_{ \infty }=\mathrm{polar}(\nabla m|n)\)), the transverse shear deformation vector vanishes \(\mathcal{T}_{\infty }=(0,0) \) and the vector of drilling bending reads \(\mathcal{N}_{\infty } := e_{3}^{T}\, \big (\mbox{axl}({Q}_{ \infty }^{T}\partial _{x_{1}}{Q}_{ \infty })\,| \, \mbox{axl}({Q}_{ \infty }^{T}\partial _{x_{2}}{Q}_{ \infty }) \big )\).
4 Modified Constrained Cosserat Shell Models
4.1 A Modified \(O(h^{5})\)-Constrained Cosserat Shell Model. Unconditional Existence
As we have seen in Sect. 3.2, the symmetry restrictions

assure that the (through the thickness reconstructed) strain tensor \(\widetilde{\mathcal{E}}_{s} \) for the 3D-shell is symmetric. However, the (reconstructed) strain tensor \(\widetilde{\mathcal{E}}_{s} \) for the 3D shell represents in itself only an approximation of the true tensor  in the limit case \(\mu _{\mathrm{c}}\to \infty \), too.
in the limit case \(\mu _{\mathrm{c}}\to \infty \), too.
The considered ansatz for the (reconstructed) deformation gradient \(F_{\xi }\) given by \(\widetilde{F}_{e,s}\) in (3.25) does not assure, in the absence of the other two symmetry conditions, that \(\mathcal{E}_{m,s} \in {\mathrm{Sym}}(3) \) implies that the (reconstructed) strain tensor \(\widetilde{\mathcal{E}}_{s} \) for the 3D-shell is symmetric. This is not surprising because in the general Cosserat model the strain tensor  is not symmetric anyway, so the choice of an ansatz for the (reconstructed) deformation gradient \(\widetilde{F}_{e,s}\) which would lead to a symmetric strain tensor was not our purpose.
is not symmetric anyway, so the choice of an ansatz for the (reconstructed) deformation gradient \(\widetilde{F}_{e,s}\) which would lead to a symmetric strain tensor was not our purpose.
In the existence proof we have seen that the admissible set may be empty for general boundary conditions. Therefore, the existence Theorem 3.2 is only conditional. With this motivation, we want to modify the resulting constrained Cosserat shell model such that the new constrained model allows for an unconditional existence proof. In order to do so, we relax the symmetry conditions and further on impose only the first symmetry condition
In addition, looking back at (3.18), (3.19) and (3.21), we assume that the energy density depends only on the (symmetric parts)
instead of

For the (reconstructed) strain tensor \(\widetilde{\mathcal{E}}_{s} \) for the 3D shell we would then propose the modified ansatzFootnote 7
which is symmetric once \(\mathcal{E}_{m,s}\) is symmetric.
Therefore, taking into account the modified constitutive restrictions imposed by the limit \(\mu _{\mathrm{c}}\to \infty \), the variational problem for the constrained Cosserat \(O(h^{5})\)-shell model is now to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \):

where
The set \(\mathcal{A}^{\mathrm{mod}}\) of admissible functions is accordingly defined by
which incorporates a weak reformulation of the imposed symmetry constraint \(\mathcal{E}_{m,s} \in {\mathrm{Sym}}(3)\).
Theorem 4.1
Unconditional existence result for the modified theory including terms up to order \(O(h^{5})\)
Assume that the external loads satisfy the conditions \({f}\in \mathrm{L}^{2}(\omega ,\mathbb{R}^{3})\), \(t\in \mathrm{L}^{2}(\gamma _{t},\mathbb{R}^{3})\), and the boundary data satisfy the conditions \({m}^{*}\in {\mathrm{H}}^{1}(\omega ,\mathbb{R}^{3})\) and \(\mathrm{polar}(\nabla {m}^{*}\,| \,n^{*}) \in {\mathrm{H}}^{1}(\omega , \mathrm{SO}(3))\). Assume that the following conditions concerning the initial configuration are satisfied:Footnote 8\(y_{0}:\omega \subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}\) is a continuous injective mapping and

where \(a_{0}\) is a positive constant. Then, for sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients such that \(\mu >0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\), \(b_{3}>0\) and \(L_{\mathrm{c}}>0\), the minimization problem (4.6) admits at least one minimizing solution \(m\) such that \((m,{Q}_{ \infty })\in \mathcal{A}^{\mathrm{mod}}\).
Proof
The proof is similar to the proof of Theorem 3.2, excluding the discussion of the other two symmetry constraints appearing in the definition of the admissible set in Theorem 3.2. The essential difference is that the admissible set \(\mathcal{A}^{\mathrm{mod}}\) is not empty since, e.g., for \(m\in {\mathrm{H}}^{2}(\omega ,\mathbb{R}^{3})\) and \({Q}_{ \infty }=\mathrm{polar} [(\nabla m|n)[\nabla \Theta ]^{-1}]\) we have \((m,{Q}_{ \infty })\in \mathcal{A}^{\mathrm{mod}}\). □
4.2 A Modified \(O(h^{3})\)-Constrained Cosserat Shell Model. Unconditional Existence
Another particularity of the new modified constrained Cosserat shell model is that the admissible set is the same for both the modified constrained theory including terms up to order \(O(h^{5})\) and the modified constrained theory including terms up to order \(O(h^{3})\).
Indeed, by considering the new variational problem for the constrained Cosserat \(O(h^{3})\)-shell model, i.e., to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \):

where
the following existence results holds:
Theorem 4.2
Unconditional existence result for the modified theory including terms up to order \(O(h^{3})\)
Assume that the external loads satisfy the conditions \({f}\in \mathrm{L}^{2}(\omega ,\mathbb{R}^{3})\), \(t\in \mathrm{L}^{2}(\gamma _{t},\mathbb{R}^{3})\), the boundary data satisfy the conditions \({m}^{*}\in {\mathrm{H}}^{1}(\omega ,\mathbb{R}^{3})\) and \(\mathrm{polar}(\nabla {m}^{*}\,|\,n^{*})\in {\mathrm{H}}^{1}(\omega , \mathrm{SO}(3))\), and that the following conditions concerning the initial configuration are fulfilled: \(y_{0}:\omega \subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}\) is a continuous injective mapping and

where \(a_{0}\) is a positive constant. Assume that the constitutive coefficients are such that \(\mu >0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\), \(b_{3}>0\) and \(L_{\mathrm{c}}>0\). Then, if the thickness \(h\) satisfies at least one of the following conditions:
-
(i)
\(h\max \{\sup _{x\in \omega }|\kappa _{1}|, \sup _{x\in \omega }| \kappa _{2}|\}<\alpha \) and \(h^{2}<\frac{(5-2\sqrt{6})(\alpha ^{2}-12)^{2}}{4\, \alpha ^{2}} \frac{ {c_{2}^{+}}}{C_{1}^{+}}\) with \(\quad 0<\alpha <2\sqrt{3}\);
-
(ii)
\(h\max \{\sup _{x\in \omega }|\kappa _{1}|, \sup _{x\in \omega }| \kappa _{2}|\}<\frac{1}{a}\) and \(a>\max \Big \{1 + \frac{\sqrt{2}}{2}, \frac{1+\sqrt{1+3\frac{C_{1}^{+}}{c_{1}^{+}}}}{2}\Big \}\),
where \(c_{2}^{+}\) denotes the smallest eigenvalue of \(W_{\mathrm{curv}}( S )\), and \(c_{1}^{+}\) and \(C_{1}^{+}>0\) denote the smallest and the biggest eigenvalues of the quadratic form \(W_{\mathrm{shell}}^{\infty }( S)\), the minimization problem corresponding to the energy density defined by (4.10) admits at least one minimizing solution \(m\) such that the pair \((m,{Q}_{ \infty })\in \mathcal{A}^{\mathrm{mod}}\).
4.3 A Modified Constrained Cosserat Plate Model. Unconditional Existence
In the case of the Cosserat plate theory, the modified constrained model is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \):

where
The admissible set is now
which is non-empty.
Theorem 4.3
Unconditional existence result for the modified constrained Cosserat plate theory
Assume that the external loads satisfy the conditions \({f}\in \mathrm{L}^{2}(\omega ,\mathbb{R}^{3})\), \(t\in \mathrm{L}^{2}(\gamma _{t},\mathbb{R}^{3})\), the boundary data satisfy the conditions \({m}^{*}\in {\mathrm{H}}^{1}(\omega ,\mathbb{R}^{3})\) and \(\mathrm{polar}(\nabla {m}^{*}\,|\,n^{*})\in {\mathrm{H}}^{1}(\omega , \mathrm{SO}(3))\). Assume that the constitutive coefficients are such that \(\mu >0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\), \(b_{3}>0\) and \(L_{\mathrm{c}}>0\). Then, the minimization problem corresponding to the energy density defined by (4.13) admits at least one minimizing solution \(m\) such that the pair \((m,{Q}_{ \infty })\in \mathcal{A}^{\mathrm{mod}}_{\mathrm{plate}}\).
5 Strain Measures in the Cosserat Shell Model
Using the Remark (A.27), we can express the strain tensors of the unconstrained Cosserat shell model using the (referential) fundamental forms \(\mathrm{I}_{y_{0}} \), \(\mathrm{II}_{y_{0}}\), \(\mathrm{III}_{y_{0}} \) and \(\mathrm{L}_{y_{0}} \) (instead of using the matrices \(\mathrm{A}_{y_{0}}\), \(\mathrm{B}_{y_{0}}\) and \(\mathrm{C}_{y_{0}}\)), i.e.,
where
The definition of \(\mathcal{G}\) is related to the classical change of metric tensor in the Koiter model

while the bending strain tensor may be compared with the classical bending strain tensor in the Koiter shell model and the Naghdi-shell model [29, p. 11] with one independent director field \(d:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\)

Since, in our constrained Cosserat shell model
using its alternative expression, see (A.30),
we deduce that in the constrained Cosserat shell model it follows that the change of metric tensor (in-plane deformation) must also be symmetric
the transverse shear deformation vector
is zero, while the bending strain tensor reads
and which remains non-symmetric, even if in the minimization problem the extra constraints (coming from \(\mu _{\mathrm{c}}\to \infty \) and bounded energy)
are imposed.Footnote 9 Hence, in the constrained Cosserat shell model, we have the following consequences of the imposed assumptions when \(\mu _{\mathrm{c}}\to \infty \):
It is clear that \(\bigl \langle {Q}_{ \infty } n_{0}, \partial _{x_{\alpha }} m \bigr \rangle =({Q}_{ \infty } n_{0})^{T} \partial _{x_{\alpha }} m =0\) and \(\bigl \langle n, \partial _{x_{\alpha }} m\bigr \rangle =0\) imply that \({Q}_{ \infty } n_{0}\) is collinear with \(n\). Since \({Q}_{ \infty } \in {\mathrm{SO}}(3)\) and due to the compatibility (3.5) with the boundary conditions, we obtain \({Q}_{ \infty } n_{0}=n\). The above restrictions (5.12) are natural in the constrained nonlinear Cosserat shell model, they are also the underlying hypotheses of the classical Koiter model. Moreover, the conditions \(\mathcal{G}_{\infty }\in {\mathrm{Sym}}(2)\) and \(\mathcal{T}_{\infty }=(0,0)\), i.e., (5.12), coincide with the conditions imposed by TambačaFootnote 10 [41, page 4, Definition of the set \(\mathcal {A}^{K}\)].
Due to the equality
we find the expression of the change of metric tensor considered in the constrained Cosserat shell model, in terms of the first fundamental form
As we may see from (2.5), (3.21) and (A.30), in the constrained Cosserat shell model the energy is expressed in terms of three strain measures: the change of metric tensor \(\mathcal{G}_{\infty }\in {\mathrm{Sym}}(2)\), the nonsymmetric quantity \(\mathcal{G}_{\infty }\,\mathrm{L}_{y_{0}}- \mathcal{R}_{\infty }\) which represents the change of curvature tensor and the elastic shell bending–curvature tensor
where
The choice of the name the change of curvature for the nonsymmetric quantity \(\mathcal{G}_{\infty }\,\mathrm{L}_{y_{0}}- \mathcal{R}_{\infty }\) will be justified in a forthcoming paper [22], in the framework of the linearized theory. The bending strain tensor \(\mathcal{R}_{\infty }\) generalizes the linear Koiter-Sanders-Budiansky bending measure [11, 24] which vanishes in infinitesimal pure stretch deformation of a quadrant of a cylindrical surface [1], while the classical bending strain tensor tensor in the Koiter model does not have this property (cf. the invariance discussion in Sect. 6.2).
For the bending-curvature energy density \(W_{\mathrm{bend,curv}} \) we can write its tensor argument \(\mathcal{K}_{\infty }\) in terms of the tensor \(\mathrm{C}_{y_{0}}\, \mathcal{K}_{\infty }\) and the vector \(\mathcal{K}_{\infty }^{T}\,n_{0}\), using Remark A.1 and according to the decomposition
We can express \(\mathrm{C}_{y_{0}} \mathcal{K}_{\infty }\) in terms of the bending strain tensor \(\mathcal{R}_{\infty } \), see (A.29) and (3.14)
From here, we find that in the constrained Cosserat shell model, the non-symmetric bending strain tensor has the following expression in terms of the first and second fundamental form
Moreover, for in-extensional deformations \(\mathrm{I}_{m}=\mathrm{I}_{y_{0}}\) (pure flexure), the bending strain tensor turns into
Here, the bending strain tensor is incorporated into both the membrane-bending energy

and the bending-curvature energy

The remaining part \(\mathcal{K}_{\infty }^{T}\,n_{0}\) from (5.16) is completely characterized by the (row) vector
which is called the vector of drilling bendings [38]. The vector of drilling bendings \(\mathcal{N}_{\infty }\) does not vanish in general and it is present only due to the bending-curvature energy.
The membrane-bending energy is expressed in terms of \(\mathcal{G}_{\infty }\), \((\mathcal{R}_{\infty }-2\,\mathcal{G}_{\infty } \,\mathrm{L}_{y_{0}})^{\flat }\) and  and the non-modified constrained variational problem imposes the following additional symmetry conditions, see (3.22) and (A.30):
and the non-modified constrained variational problem imposes the following additional symmetry conditions, see (3.22) and (A.30):

In the modified constrained Cosserat shell model presented in Sect. 4.1 these constraints are excluded from the variational formulation, since the energy density is then expressed in terms of \(\mathrm{sym}(\mathcal{R}_{\infty } -\mathcal{G}_{\infty } \,\mathrm{L}_{y_{0}}) \in {\mathrm{Sym}}(2)\) and \(\mathrm{sym}[(\mathcal{R}_{\infty } -\mathcal{G}_{\infty } \,\mathrm{L}_{y_{0}}) \,\mathrm{L}_{y_{0}}]\in {\mathrm{Sym}}(2)\). It is clear that using the properties of the occurring quadratic forms, we may rewrite the membrane-bending energy only as quadratic energies having \(\mathcal{G}_{\infty }\) and \(\mathcal{R}_{\infty } \) as arguments, while the bending-curvature energy may be written in terms of \(\mathcal{R}_{\infty } \) and \(\mathcal{N}_{\infty }\). However, the coercivity estimate of the total energy
i.e.,

or equivalently
indicates that the total energy is controlled by the values of \(\mathcal{G}_{ \infty }\), \((\mathcal{R}_{ \infty }-2\,\mathcal{G}_{ \infty } \,\mathrm{L}_{y_{0}})\) and \(\mathcal{K}_{ \infty }\) individually. We have not been able to identify a similar coercivity inequality showing that the total energy is controlled by the values of \(\mathcal{G}_{ \infty }\), \(\mathcal{R}_{ \infty }\) and \(\mathcal{K}_{ \infty }\) alone. Moreover, the assumptions which follow from considering \(\mu _{\mathrm{c}}\to \infty \) are also expressed naturally in terms of \(\mathcal{R}_{ \infty }-2\,\mathcal{G}_{ \infty } \,\mathrm{L}_{y_{0}}\), i.e., the conditions \(\mathcal{R}_{ \infty }-2\,\mathcal{G}_{ \infty } \,\mathrm{L}_{y_{0}} \stackrel{!}{\in }{\mathrm{Sym}}(3)\) and \((\mathcal{R}_{ \infty }-2\,\mathcal{G}_{ \infty } \,\mathrm{L}_{y_{0}}) \,\mathrm{L}_{y_{0}}\stackrel{!}{\in }{\mathrm{Sym}}(3)\), see estimate (3.66) and Sect. 3.2.
This line of thought, beside some other arguments presented in the linearised framework by Anicic and Léger [6], see also [3], and more recently by Šilhavỳ [39], suggest that the triple \(\mathcal{G}_{ \infty }\), \(\mathcal{R}_{ \infty }-2\,\mathcal{G}_{ \infty } \,\mathrm{L}_{y_{0}}\) and \(\mathcal{K}_{ \infty }\) are appropriate measures to express the change of metric and of the curvatures \(\mathrm{H}\) and \(\mathrm{K}\), while the bending and drilling effects are both additionally incorporated in the bending-curvature energy through the elastic shell bending-curvature tensor \(\mathcal{K}_{\infty }\).
In order to make connections with existing works in the literature on 6-parameter shell models [12, 13, 19], see also [20, Sect. 6], we conclude that the membrane-bending energy \(W_{\mathrm{memb,bend}}^{\infty }\big ( \mathcal{E}_{\infty },\, \mathcal{K}_{\infty }\big )\) defined by (5.19), i.e., the influence of the change of curvature tensor \(\mathcal{R}_{ \infty }-2\,\mathcal{G}_{ \infty } \,\mathrm{L}_{y_{0}}\), is omitted if a constrained Cosserat shell model would be derived from other available simpler 6-parameter shell models [12, 13, 19], even if the bending strain tensor \(\mathcal{R}_{ \infty }\) is present (through the presence of the curvature energy).
6 Scaling Invariance of Bending Tensors
6.1 Revisiting Acharya’s Invariance Requirements for a Bending Strain Tensor
This brings us to the question of how to model the physical notion of bending: a clear understanding of bending measures will certainly lead to a clear definition of its work conjugate pair when the equilibrium equations are established. Alongside, it helps to have a proper formulation of the traction boundary conditions, when needed. In this context, Acharya [1, page 5519] has proposed a set of modelling requirements for a bending strain tensor in any first order nonlinear shell theory:
- AR1:
-
“Being a strain measure, it should be a tensor that vanishes in rigid deformations”.
- AR2:
-
“It should be based on a proper tensorial comparison of the deformed and underformed curvature fields [\(\mathrm{II}_{m}\) and \(\mathrm{II}_{y_{0}}\)]”.
- AR3:
-
“A vanishing bending strain at a point should be associated with any deformation that leaves the orientation of the unit normal field locally unaltered around that point.”
The first two requirements AR1 and AR2 are satisfied by all considered nonlinear bending tensors in the literature and both are physically intuitive, while the third requirement AR3 suggests that a nonzero bending tensor should only be associated with a change of the orientation of tangent planes and that, for instance, a radial expansion of a cylinder (see Fig. 6) should give a zero bending strain measure, since it produces no further bending deformation of the shell (but changes the curvature).
A radial expansion of a cylinder preserves the tangent planes and therefore it should produce a zero bending strain tensor. However, the metric of the surface is changed, the curvature changes (the principal radius of curvature is changed), but the normal is conserved. The radial expansion occurs rather because of in-plane stretch
It is easy to see that \(\mathcal{R}_{\mathrm{{Koiter}}}=\mathrm{II}_{m}-\mathrm{II}_{y_{0}}\) satisfies AR2 and AR1, since rigid deformations keep the second fundamental form. But the latter is in general not the case for deformations which leave the normal field unaltered, so that \(\mathcal{R}_{\mathrm{{Koiter}}}\) does not satisfy AR3, for calculations, see (6.24).
In [1, Eq. (8) and (10)] Acharya has proposed a bending strain tensor \(\mathcal{R}_{\mathrm{Acharya}}\) for a first-order nonlinear elastic shell theory which in our notation reads (see Appendix A.4)

Acharya’s bending tensors are similar to but do not coincide with the bending tensor appearing in our nonlinear constrained Cosserat-shell model which reads
Interestingly, it is possible to express \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) through our nonlinear bending tensor \(\mathcal{R}_{\infty }^{\flat }\). It holds (see Appendix A.4)
From (6.3), we might believe that \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) vanishes when \(\mathcal{R}_{\infty }^{\flat }\) vanishes, while the reverse might not be true. However, since

we have

and we deduce
and Acharya’s bending tensor admits the alternative form
Therefore,
The nonlinear bending strain tensor \(\mathcal{R}_{\mathrm{Acharya}}\) would satisfy all three requirements AR1 - AR3 “if locally pure stretch deformations are the only ones that leaves the orientation of tangent planes unaltered locally under deformation.” Incidentally, the tensor (6.1)2 introduced by Acharya reduces, after linearization as well to the Koiter-Sanders-Budiansky “best” bending measure, see [22] for details. According to Acharya, his nonlinear bending measure should only be seen as a mathematical “better alternative” for modelling the physical bending process since “the set of deformations that leave the orientation of tangent planes unaltered locally can be divided into two classes - deformations that have a pure stretch deformation gradient locally, and those that have their local rotation tensor field consisting of either [in-plane] drill rotations or the identity tensor.” Acharya has shown that his nonlinear bending strain measure vanishes in pure stretch deformations that leave the normal unaltered, while the other classical bending strain measures fail to do so, but \(\mathcal{R}_{\mathrm{Acharya}}\) does not necessarily vanish for deformations whose rotation tensor is a “drill” rotation. Thus, \(\mathcal{R}_{\mathrm{Acharya}}\) does not satisfy AR3 in general. While physically appealing, condition AR3 may, therefore, be too strict to be applicable in general. Hence we will introduce and investigate in the following a weaker invariance requirement. To this end let us introduce
Definition 6.1
Let \(m\) be a deformation of the midsurface \(y_{0}\). Denoting by \(n\) and \(n_{0}\) normal fields on the surface \(m\) and \(y_{0}\), respectively, we say that the midsurface deformation \(m\) is obtained from a pure elastic stretch (see Fig. 7) provided that \(\mathrm{U_{e}} := (\nabla m \,|\, n)\,(\nabla y_{0}\,|\,n_{0})^{-1} = ( \nabla m \,|\, n)\,[\nabla \Theta ]^{-1}\) is symmetric and positive-definite, i.e., belongs to \(\operatorname{Sym}^{+}(3)\).
[Multiplicative view] The initial curved midsurface \(y_{0}(\omega )\) and deformed midsurface \(m(\omega )\), connected by a pure elastic stretch \(\mathrm{U_{e}}\in {\mathrm{Sym}}^{+}(3)\). It leaves the normal unaltered if \(\mathrm{U_{e}}\,(\nabla y_{0}\,|\,n_{0})= (\nabla m \,|\, n_{0})\), i.e., \(n= \frac{\partial _{x_{1}}m\times \partial _{x_{2}}m}{\|\partial _{x_{1}}m\times \partial _{x_{2}}m\|}=n_{0}\)
Remark 6.2
\(\mathrm{U_{e}}\) is invertible by definition.
With this definition, Acharya’s essential invariance requirement can be stated as
- AR3∗:
-
A vanishing bending strain at a point should be associated with any deformation obtained from a pure elastic stretch that leaves the orientation of the unit normal field locally unaltered around that point.
Example 6.1
Of special interest for us are deformations, which leave the unit normal field locally unaltered in a point. So, introducing locally orthogonal coordinates on the given curved initial configuration (which is always possible, cf. e.g., [25])
the partial derivatives of \(m\) must be linear combinations
(in order to leave the unit normal field invariant), where we require additionally
The first condition (6.10b)1 appears in the calculation of \(\partial _{x_{1}}m \times \partial _{x_{2}}m\) and guarantees the existence and the orientation preservation of the normal, whereas the second condition (6.10b)2 implies \((\nabla m\,|\,0) [\nabla \Theta \,]^{-1}\) is symmetric and positive-definite so that it is exactly the desired condition for the class of pure elastic stretches (in particular, \((\nabla m)^{T}\nabla y_{0}\) is symmetric). Indeed, we get (using orthogonal coordinates) for the inverse of \(\nabla \Theta = (\nabla y_{0} \,|\,n_{0})\)
Recall, that for vectors \(a,b,c,d,e,f\in \mathbb{R}^{3}\) it holds
so that we obtain
which is symmetric provided that \(a\,\delta = \beta \,\gamma \), cf. (6.10b)2 and (6.11), since
Furthermore, \(\mathrm{U_{e}}\) is positive-definite because

is a sum of four positive (semi-)definite matrices since we required \(\alpha \ge \beta \ge 0\) and \(\ b \ge a\ge 0\). Acharya’s examples [1, Sect. 6] satisfy both conditions (6.10b).Footnote 11
6.2 Investigation of the Invariance Requirement for a Bending Tensor
Using (6.12) we have always (not only in orthogonal coordinates)

since \(e_{3}^{T} [\nabla \Theta ]^{-1}=n_{0}^{T}\) because \([\nabla \Theta ]^{-1}= \begin{pmatrix} \cdots \\ \cdots \\ n_{0}^{T} \end{pmatrix} \) where \(\nabla \Theta = (\nabla y_{0} \, | \, n_{0})\).
We now show, that both tensors \(\mathcal{R}_{\mathrm{Acharya}}\) and \(\mathcal{R}_{\infty }^{\flat }\) satisfy the three requirements AR1, AR2 and AR3∗. Due to (6.7), it is sufficient to prove this property only for one of these tensors. In this subsection, we show that \(\mathcal{R}_{\mathrm{Acharya}}\) satisfy the three requirements AR1, AR2 and AR3∗, while a direct proof corresponding to these properties of \(\mathcal{R}_{\infty }^{\flat }\) is presented, only for completeness, in Appendix A.5.
The expressions of both tensors (6.1) and (6.2) fulfill condition AR2. Moreover, for a rigid deformation \(y_{0}\to m =\widehat{Q}y_{0}\), \(\widehat{Q}\in \operatorname{SO}(3)\) the fundamental forms coincide,  , due to the identities \(\nabla m=\widehat{Q} \nabla y_{0}, \ \nabla n=\nabla (\widehat{Q}\, n_{0})= \widehat{Q}\,\nabla \, n_{0}\). Hence, for a rigid deformation, we obtain
, due to the identities \(\nabla m=\widehat{Q} \nabla y_{0}, \ \nabla n=\nabla (\widehat{Q}\, n_{0})= \widehat{Q}\,\nabla \, n_{0}\). Hence, for a rigid deformation, we obtain

since  is positive semi-definite because
is positive semi-definite because  for all \(\xi \in \mathbb{R}^{3}\). Keeping in mind that \([\nabla \Theta \,]^{-1} n_{0} = e_{3}\) it follows that for a rigid deformation we have
for all \(\xi \in \mathbb{R}^{3}\). Keeping in mind that \([\nabla \Theta \,]^{-1} n_{0} = e_{3}\) it follows that for a rigid deformation we have

Thus, using also (6.7), we have shown, that both tensors vanish for rigid deformations, so that both satisfy AR1.
It remains to check AR3∗ for \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) and \(\mathcal{R}_{\infty }^{\flat }\) for pure elastic stretches that in addition leave the unit normal field unaltered in a point, i.e., we have
where ➀ requires that the unit normal field is left unaltered and ➁ requires \(m\) to be obtained from a pure elastic stretch. Thus,
and, since the matrix \(\mathrm{U_{e}}\) is invertible, also \(\mathrm{U}^{-1}_{\mathrm{e}}\,n_{0}=n_{0}\). With \(\mathrm{I}_{m}^{\flat }=(\nabla m |0)^{T}(\nabla m | 0)\) we obtain
since \(\mathrm{U_{e}}\) is symmetric (by requirement (6.19)). Moreover, the positive definite square root of \(\mathrm{U_{e}}\) fulfills also \(\sqrt{\mathrm{U_{e}}}\,n_{0}=n_{0} \), thus \((\sqrt{\mathrm{U_{e}}}-n_{0}\otimes n_{0})^{2}=(\sqrt{ \mathrm{U_{e}}}-n_{0}\otimes n_{0})(\sqrt{\mathrm{U_{e}}}-n_{0} \otimes n_{0})^{T}=\mathrm{U_{e}}-n_{0}\otimes n_{0}\) is positive semi-definite and we conclude

Using (6.19) and (6.22) in the expression (6.1) it now follows that Acharya’s bending tensor vanishes for pure elastic stretches that in addition leave the unit normal field unaltered. Indeed, having \(\mathrm{II}_{m}^{\flat }=-(\nabla m|0)^{T}(\nabla n|0) = -(\nabla m|0)^{T}( \nabla n_{0}|0)\), so that again using the symmetry of \(\mathrm{U_{e}}\) we obtain
all in all, we have shown, that \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) satisfies AR1, AR2 and AR3∗.
Continuing, our derived bending tensor \(\mathcal{R}_{\infty }^{\flat }\) has the same properties as Acharya’s bending tensor \(\mathcal{R}_{\mathrm{Acharya}}\), due to (6.7).
We have already shown, that \(\mathcal{R}_{\mathrm{Koiter}}= \mathrm{II}_{m}-\mathrm{II}_{y_{0}}\) satisfies AR1, AR2 but it does not satisfy AR3∗ as we show presently. Consider \([\nabla \Theta ]^{-T}\,(\mathrm{II}_{m}^{\flat }-\mathrm{II}_{y_{0}}^{\flat }) \,[\nabla \Theta ]^{-1}\). Indeed, the latter expression does not satisfy AR3∗ since

does not generally vanish for deformations obtained from a pure elastic stretch that leave the normal field unaltered. From (6.24) it follows that  under the same circumstances.
under the same circumstances.
Finally, let us strengthen further the additional invariance requirements on the bending tensor by postulating
- \(\mathbf{AR3}^{*}_{\mathrm{plate}}\):
-
For a planar reference geometry \((\mathrm{II}_{y_{0}}\equiv 0_{2})\) the bending tensor should be invariant under the scaling \(m\to \alpha \, m\), \(\alpha >0\).
It is clear that the simple scaling \(m\to \alpha \, m\), \(\alpha >0\) corresponds to an additional in-plane stretch, while there is no additional bending involved. Therefore, \(\mathbf{AR3}^{*}_{\mathrm{plate}}\) should be adopted as a suitable requirement for a true bending tensor expression. Furthermore, the new condition \(\mathbf{AR3}^{*}_{\mathrm{plate}}\) allows to differentiate between Acharya’s ad hoc bending tensors \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) and \({\mathcal{R}}_{\mathrm{Acharya}}\) and our derived bending tensor \(\mathcal{R}_{\infty }^{\flat }\). Indeed,
Remark 6.3
The bending tensor \(\mathcal{R}_{\infty }^{\flat }\) satisfies \(\mathbf{AR3}^{*}_{\mathrm{plate}}\) while \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) and \({\mathcal{R}}_{\mathrm{Acharya}}\) do not have this invariance property, since in the planar referential configuration ( ,
,  , \(\mathrm{II}_{\mathrm{id}}=0_{2}\)) Acharya’s bending tensors reduce to \(-\mathrm{II}_{m}^{\flat }\), which violate \(\mathbf{AR3}^{*}_{\mathrm{plate}}\). Both \(\mathcal{R}_{\infty }^{\flat }\) and \({\mathcal{R}}_{\mathrm{Acharya}}\) reduce after linearisation [22] to the Sanders and Budiansky bending tensor of the [10, 11, 24] “best first-order linear elastic shell theory”.
, \(\mathrm{II}_{\mathrm{id}}=0_{2}\)) Acharya’s bending tensors reduce to \(-\mathrm{II}_{m}^{\flat }\), which violate \(\mathbf{AR3}^{*}_{\mathrm{plate}}\). Both \(\mathcal{R}_{\infty }^{\flat }\) and \({\mathcal{R}}_{\mathrm{Acharya}}\) reduce after linearisation [22] to the Sanders and Budiansky bending tensor of the [10, 11, 24] “best first-order linear elastic shell theory”.
Remark 6.4
Let us mention the explicit dependence of the bending tensors on the two configurations \(y_{0}\) and \(m\) such as \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}(m(x_{1},x_{2}),y_{0}(x_{1},x_{2}))\). Since the scaling \(\alpha \,y_{0}\), \(\alpha >0\), leaves the normals invariant we have of course \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}(\alpha \, y_{0},y_{0})\equiv 0_{3}\) and \(\mathcal{R}_{\infty }(\alpha \, y_{0},y_{0})\equiv 0_{3}\). Now, for a planar reference configuration  we obtain the scaling
we obtain the scaling
but we have the scaling invariance
7 Conclusion
We have thoroughly investigated a recently introduced isotropic nonlinear Cosserat shell model. We focussed on what happens when the independent Cosserat rotation is made to coincide with the continuum rotation. This case can be steered in the model under consideration by sending the Cosserat couple modulus \(\mu _{\mathrm{c}}\to \infty \). In this way we obtained a constrained Cosserat shell, which incorporates strong symmetry requirements on the appearing strain and bending-curvature tensors. For such a class of constrained models we proposed conditional existence theorems for the resulting minimization problem: conditional, since we cannot exclude that the admissible set is empty. This led us to consider a modified shell model in which certain symmetry requirements are waived. Then unconditional existence follows easily. A conceptual advantage of the constrained Cosserat shell model is that it can be entirely expressed in “classical” quantities from differential geometry (first and second fundamental forms of the initial and deformed surface, respectively). We have provided the necessary calculations for this identification which allowed us to compare the resulting model with other classical models, like the Koiter shell model. While the membrane part of the constrained model incorporates only the respective first fundamental forms it turns out that our constrained model incorporates a bending tensor which always couples bending and membrane effects. This was neither expected nor aimed at originally. To our great surprise, the new bending tensor satisfies a generalized invariance condition, previously introduced by Acharya, while the Koiter bending tensor does not. We added a new invariance condition in the same spirit which allows us to differentiate further between existing proposals for bending tensors. By identifying a true bending tensor validated by the novel invariance requirements AR3∗ and \(\mathbf{AR3}^{*}_{\mathrm{plate}}\) we observe a clear advantage of the constrained Cosserat shell model compared to more classical approaches: the obtained bending tensor measures really only bending (change in normals) and the additional Cosserat curvature tensor measures the remaining total curvature. Classical shell approaches do not have the possibility to incorporate a curvature tensor and their proposed bending tensors are not invariant under scaling. We also expect manifest differences in predicting the small-scale wrinkling behaviors between a theory that shows scaling invariance of the bending tensor versus a theory that does not. Since in the development of the model we took great care to approximate the shell as exact as possible it seems to be the simplifying assumptions in the classical Koiter shell model that destroy the mentioned, physically appealing invariance condition. In this respect more research seems to be necessary to generally ascertain the invariance condition in any first order nonlinear shell model. In a follow up paper [22], we will linearize the model and compare it to available linear shell models. The obtained clear and consistent structure of the Cosserat model together with the sound invariance conditions which are automatically satisfied make us confident that the new Cosserat shell model will find its place when isotropic thin shell theory need to be actually applied in a FEM-context. In that case, however, it will rather be the unconstrained Cosserat shell model that will be implemented in order to obtain second order equilibrium equations.
Notes
They may be written in terms of the Poisson ratio of the isotropic and homogeneous material \(\nu =\frac{\lambda }{2\,(\lambda +\mu )} \).
These conditions are equivalent to \(\mu >0\) and \(2\,\lambda +\mu > 0\), which assure the positive definiteness of the quadratic form \(W_{\mathrm{shell}}( X) = \mu \,\lVert \mathrm{sym}\,X\rVert ^{2} + \mu _{\mathrm{c}}\lVert \mathrm{skew}\,X\rVert ^{2} + \dfrac{\lambda \,\mu }{\lambda +2\,\mu }\,\big [ \mathrm{tr} (X)\big ]^{2} = \mu \, \lVert \mathrm{ dev \,sym} \,X\rVert ^{2} + \mu _{\mathrm{c}} \lVert \mathrm{skew} \,X\rVert ^{2} +\, \dfrac{2\,\mu \,(2\,\lambda +\mu )}{3(\lambda +2\,\mu )}\,[ \mathrm{tr} (X)]^{2}\).
In our assertion, the square root of a positive semidefinite matrix \(X\) is the unique positive semidefinite matrix \(Y\), denoted by \(\sqrt{X}\), such that \(Y^{2}=X\). If \(X\) is positive definite, then its square root is also positive definite. For an idempotent positive semidefinite matrix \(A\), meaning \(A^{2}=A\), by the definition, its square root is the matrix itself \(\sqrt{A}=A\).
Since \(\mathrm{SO}(3)\) is compact, a property that does not transfer to the linearized problem.
For shells with little initial regularity. Classical shell models typically need to assume that \(y_{0}\in {\mathrm{C}}^{3}(\overline{\omega },\mathbb{R}^{3})\).
By \(c\) and \(c_{i}\), \(i\in \mathbb{N}\), we will denote (positive) constants that may vary from estimate to estimate but will remain independent of \(m\), \(\nabla m\) and \({Q}_{ \infty }\).
It does add nothing to the shell model itself.
For shells with little initial regularity. Classical shell models typically need to assume that \(y_{0}\in {\mathrm{C}}^{3}(\overline{\omega },\mathbb{R}^{3})\).
However, in the modified constrained Cosserat shell model presented in Sect. 4.1 the energy density is expressed in terms of
$$\begin{aligned} {\mathrm{sym}}(\mathcal{R}_{\infty } -\mathcal{G}_{\infty } \,\mathrm{L}_{y_{0}}) \in {\mathrm{Sym}}(2)\qquad \text{and}\qquad \mathrm{sym}[(\mathcal{R}_{\infty } -\mathcal{G}_{\infty } \,\mathrm{L}_{y_{0}})\,\mathrm{L}_{y_{0}}]\in {\mathrm{Sym}}(2). \end{aligned}$$(5.11)Tambača [41, page 4, Definition of the set \(\mathcal {A}^{f}\)] also requires \({Q}_{ \infty } \nabla y_{0}=\nabla m\), in order to arrive at the pure bending shell model. In this case \(\mathcal{G}_{\infty }=0\) and
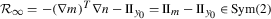 .
.Indeed, the biaxial stretching of a cylinder [1, Sect. 6.2] satisfies (6.10b) with \(a=\beta =0\) (see [1, Eq. (34)]) and for the uniform normal deflection [1, Sect. 6.1] we have \(m=y_{0}+ c\, n_{0}\) where \(c\in \mathbb{R}\) is a fixed factor. Hence,
$$ \partial _{x_{1}}m=\partial _{x_{1}}y_{0}+c\,\partial _{x_{1}}n_{0} \quad \text{and}\quad \partial _{x_{2}}m=\partial _{x_{2}}y_{0}+c\, \partial _{x_{2}}n_{0}. $$So that, \(a\,\|\partial _{x_{1}}y_{0}\|^{2} \overset{\text{(6.10a)}}{=} \langle \partial _{x_{2}}m, \partial _{x_{1}}y_{0}\rangle = c\,\langle \partial _{x_{2}}n_{0}, \partial _{x_{1}}y_{0}\rangle \overset{(\ast )}{=} c\,\langle \partial _{x_{1}}n_{0},\partial _{x_{2}}y_{0}\rangle = \langle \partial _{x_{1}}m,\partial _{x_{2}}y_{0}\rangle \overset{\text{(6.10a)}}{=}\beta \,\|\partial _{x_{2}}y_{0}\|^{2}\) where in \((\ast )\) we made use of the symmetry of the second fundamental form. Furthermore, since \(\|n_{0}\|^{2}=1\) implies that \(\langle \partial _{x_{i}}n_{0},n_{0}\rangle =0\) we have \(\partial _{x_{1}}n_{0}=\theta _{1}\ \partial _{x_{1}}y_{0}+\theta _{2} \ \partial _{x_{2}}y_{0}\) and \(\partial _{x_{2}}n_{0}=\vartheta _{1}\ \partial _{x_{1}}y_{0}+ \vartheta _{2}\ \partial _{x_{2}}y_{0}\) so that \(\partial _{x_{1}}m\times \partial _{x_{2}}m=((1+c\,\theta _{1})(1+c \,\vartheta _{2})-c^{2}\,\theta _{2}\vartheta _{1})\,\partial _{x_{1}}y_{0} \times \partial _{x_{2}}y_{0} \), implying that the range of the fixed value \(c\) should be adjusted in such a way that the prefactor is positive and \(1+c\,\theta _{1}\ge c\,\theta _{2}\ge 0\) as well as \(1+c\,\vartheta _{2}\ge c\,\vartheta _{1}\ge 0\), which are exactly the requirements for the positive-definiteness improved in (6.10b).
References
Acharya, A.: A nonlinear generalization of the Koiter–Sanders–Budiansky bending strain measure. Int. J. Solids Struct. 37(39), 5517–5528 (2000)
Adams, R.A.: Sobolev Spaces, 1st edn. Pure and Applied Mathematics, vol. 65. Academic Press, London (1975)
Anicic, S.: Du modèle de Kirchhoff-Love exact à un modèle de coque mince et á un modèle de coque pliée. PhD thesis, Université Joseph Fourier (Grenoble 1) (2001)
Anicic, S.: Polyconvexity and existence theorem for nonlinearly elastic shells. J. Elast. 132(1), 161–173 (2018)
Anicic, S.: Existence theorem for a first-order Koiter nonlinear shell model. Discrete Contin. Dyn. Syst., Ser. S 12(6), 1535–1545 (2019)
Anicic, S., Léger, A.: Formulation bidimensionnelle exacte du modèle de coque 3D de Kirchhoff-Love. C. R. Acad. Sci. Paris, Ser. Math. 329(8), 741–746 (1999)
Bîrsan, M.: Derivation of a refined 6-parameter shell model: Descent from the three-dimensional Cosserat elasticity using a method of classical shell theory. Math. Mech. Solids 25(6), 1318–1339 (2020)
Bîrsan, M., Neff, P.: Existence of minimizers in the geometrically non-linear 6-parameter resultant shell theory with drilling rotations. Math. Mech. Solids 19(4), 376–397 (2014)
Bîrsan, M., Neff, P.: Shells without drilling rotations: A representation theorem in the framework of the geometrically nonlinear 6-parameter resultant shell theory. Int. J. Eng. Sci. 80, 32–42 (2014)
Budiansky, B., Sanders, J.L. Jr.: On the “best” first-order linear shell theory. Tech. Rept. No. 14, Contract No. 1886(02), Division of Engineering and Applied Physics, Harvard University (1962)
Budiansky, B., Sanders, J.L. Jr.: On the “best” first-order linear shell theory. In: Progress in Applied Mechanics, the Prager Anniversary Volume (1963)
Chróścielewski, J., Makowski, J., Pietraszkiewicz, W.: Statics and Dynamics of Multifold Shells: Nonlinear Theory and Finite Element Method. Wydawnictwo IPPT PAN, Warsaw (2004) (in Polish)
Chróścielewski, J., Pietraszkiewicz, W., Witkowski, W.: On shear correction factors in the non-linear theory of elastic shells. Int. J. Solids Struct. 47, 3537–3545 (2010)
Ciarlet, Ph.G.: Mathematical Elasticity, Vol. III: Theory of Shells, 1st edn. North-Holland, Amsterdam (2000)
Ciarlet, Ph.G.: An Introduction to Differential Geometry with Applications to Elasticity. Springer, Berlin (2005)
Ciarlet, Ph.G., Mardare, C.: Nonlinear Korn inequalities. J. Math. Pures Appl. 104(6), 1119–1134 (2015)
Ciarlet, Ph.G., Mǎlin, M., Mardare, C.: New estimates of the distance between two surfaces in terms of the distance between their fundamental forms. Anal. Appl. 17(03), 363–392 (2019)
Cosserat, E., Cosserat, F.: Théorie des corps déformables. Hermann et Fils, Paris (1909) (reprint 2009)
Eremeyev, V.A., Pietraszkiewicz, W.: Local symmetry group in the general theory of elastic shells. J. Elast. 85, 125–152 (2006)
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: The isotropic Cosserat shell model including terms up to \({O}(h^{5})\). Part I: Derivation in matrix notation. J. Elast. 142, 201–262 (2020). https://doi.org/10.1007/s10659-020-09796-3. arXiv:2003.00549
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: The isotropic elastic Cosserat shell model including terms up to order \(O(h^{5})\) in the shell thickness. Part II: Existence of minimizers. J. Elast. 142, 263–290 (2020). https://doi.org/10.1007/s10659-020-09795-4. arXiv:2003.08594
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: Linear Cosserat-shell models including terms up to \({O}(h^{5})\). In preparation
Girault, V., Raviart, P.A.: Finite Element Approximation of the Navier-Stokes Equations. Lect. Notes Math., vol. 749. Springer, Heidelberg (1979)
Koiter, W.T., Simmonds, J.G.: Foundations of shell theory. In: Theoretical and Applied Mechanics, pp. 150–176. Springer, Berlin (1973)
Korn, A.: Zwei Anwendungen der Methode der sukzessiven Annäherungen. In: Carathéodory, C., Hessenberg, G., Landau, E., Lichtenstein, L. (eds.) Mathematische Abhandlungen Hermann Amandus Schwarz, pp. 215–229. Springer, Berlin (1914)
Leis, R.: Initial Boundary Value Problems in Mathematical Physics. Teubner, Stuttgart (1986)
Libai, A., Simmonds, J.G.: The Nonlinear Theory of Elastic Shells, 2nd edn. Cambridge University Press, Cambridge (1998)
Malin, M., Mardare, C.: Nonlinear Korn inequalities on a hypersurface. Chin. Ann. Math., Ser. B 39(3), 513–534 (2018)
Mardare, C.: On the derivation of nonlinear shell models from three-dimensional elasticity. Rev. Roum. Math. Pures Appl. 53, 499–522 (2008), hal-00392028
Neff, P.: A geometrically exact Cosserat-shell model including size effects, avoiding degeneracy in the thin shell limit. Part I: Formal dimensional reduction for elastic plates and existence of minimizers for positive Cosserat couple modulus. Contin. Mech. Thermodyn. 16, 577–628 (2004)
Neff, P.: A geometrically exact viscoplastic membrane-shell with viscoelastic transverse shear resistance avoiding degeneracy in the thin-shell limit. Part I: The viscoelastic membrane-plate. Z. Angew. Math. Phys. 56(1), 148–182 (2005)
Neff, P.: Local existence and uniqueness for a geometrically exact membrane-plate with viscoelastic transverse shear resistance. Math. Methods Appl. Sci. 28, 1031–1060 (2005)
Neff, P.: A geometrically exact planar Cosserat shell-model with microstructure: Existence of minimizers for zero Cosserat couple modulus. Math. Models Methods Appl. Sci. 17, 363–392 (2007)
Neff, P., Münch, I.: Curl bounds Grad on \(\mathrm{SO}(3)\). ESAIM Control Optim. Calc. Var. 14, 148–159 (2008)
Neff, P., Lankeit, J., Madeo, A.: On Grioli’s minimum property and its relation to Cauchy’s polar decomposition. Int. J. Eng. Sci. 80, 207–217 (2014)
Pietraszkiewicz, W.: Consistent second approximation to the elastic strain energy of a shell. Z. Angew. Math. Mech. 59, 206–208 (1979)
Pietraszkiewicz, W.: Refined resultant thermomechanics of shells. Int. J. Eng. Sci. 49, 1112–1124 (2011)
Pietraszkiewicz, W., Konopińska, V.: Drilling couples and refined constitutive equations in the resultant geometrically non-linear theory of elastic shells. Int. J. Solids Struct. 51, 2133–2143 (2014)
Šilhavỳ, M.: Curvature measures in linear shell theories. Preprint No. 22-2020, Institute of Mathematics, The Czech Academy of Sciences (2020)
Steigmann, D.J.: Koiter’s shell theory from the perspective of three-dimensional nonlinear elasticity. J. Elast. 111, 91–107 (2013)
Ljulj, M., Tambača, J.: A Naghdi type nonlinear model for shells with little regularity. J. Elast. 142, 447–494 (2020). https://doi.org/10.1007/s10659-020-09802-8
Toupin, R.A.: Elastic materials with couple stresses. Arch. Ration. Mech. Anal. 11, 385–413 (1962)
Toupin, R.A.: Theories of elasticity with couple-stresses. Arch. Ration. Mech. Anal. 17, 85–112 (1964)
Weinberg, K., Neff, P.: A geometrically exact thin membrane model-investigation of large deformations and wrinkling. Int. J. Numer. Methods Eng. 74(6), 871–893 (2008)
Zhilin, P.A.: Applied Mechanics – Foundations of Shell Theory. State Polytechnical University Publisher, Sankt Petersburg (2006) (in Russian)
Acknowledgements
The work of I.D. Ghiba was supported by a grant of the Romanian Ministry of Research and Innovation, CNCS–UEFISCDI, Project no. PN-III-P1-1.1-TE-2019-0348, Contract No. TE 8/2020, within PNCDI III. This research has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project no. 415894848 (M. Bîrsan, P. Lewintan and P. Neff).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 A.1 Useful Identities
We provide some properties of the tensors in the variational formulation of the shell models from [20, 21]:
Remark A.1
The following identities are satisfied:
-
(i)
\(\mathrm{tr}[{\mathrm{A}}_{y_{0}}]\,=\,2\), \({\det }[{\mathrm{A}}_{y_{0}}]\,=\,0;\quad \) \(\mathrm{tr}[{\mathrm{B}}_{y_{0}}]\,=\,2\,\mathrm{H}\), \({\det }[{\mathrm{B}}_{y_{0}}]\,=\,0\),
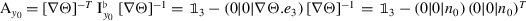 ,
,\(\mathrm{B}_{y_{0}} = [\nabla \Theta ]^{-T}\; \mathrm{II}_{y_{0}}^{\flat }\; [ \nabla \Theta ]^{-1}\)
-
(ii)
\(\mathrm{B}_{y_{0}}\) satisfies the equation of Cayley-Hamilton type \(\mathrm{B}_{y_{0}}^{2}-2\,\mathrm{H}\, \mathrm{B}_{y_{0}}+\mathrm{K}\, \mathrm{A}_{y_{0}} \,=\,0_{3}\);
-
(iii)
\(\mathrm{A}_{y_{0}}{\mathrm{B}}_{y_{0}}\,=\,\mathrm{B}_{y_{0}}{\mathrm{A}}_{y_{0}}\,= \,\mathrm{B}_{y_{0}}\), \(\mathrm{A}_{y_{0}}^{2}\,=\,\mathrm{A}_{y_{0}}\), \(\mathrm{C}_{y_{0}}\in \mathfrak{so}(3)\), \(\quad \mathrm{C}_{y_{0}}^{2}\,=\,-\mathrm{A}_{y_{0}}\), \(\lVert {\mathrm{C}}_{y_{0}}\rVert ^{2}=2\);
-
(iv)
 ;
; -
(v)
\(\mathrm{C}_{y_{0}} \mathcal{K}_{e,s} {\mathrm{A}}_{y_{0}}\,\,=\,\,\mathrm{C}_{y_{0}} \mathcal{K}_{e,s} \), \(\mathcal{E}_{m,s} {\mathrm{A}}_{y_{0}}\,\,=\,\,\mathcal{E}_{m,s} \).
Further, in view of \(\mathrm{I}_{y_{0}}^{-1} {\mathrm{II}}_{y_{0}}= \mathrm{L}_{y_{0}} \) and considering also the third fundamental form defined by \(\mathrm{III}_{y_{0}}= \mathrm{II}_{y_{0}} {\mathrm{L}}_{y_{0}}\), we note the relations
1.2 A.2 The Classical Nonlinear Koiter Shell Model in Cartesian Matrix Notation
In this subsection, we consider the variational problem for the geometrically nonlinear Koiter energy for a nonlinear elastic shell [15, page 147] and we rewrite it in matrix format. The problem written in tensor format [15, page 147], [40, Eq. (1) and Eq. (101)] is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \):

where the fourth order constitutive tensor \(\mathbb{C}_{\mathrm{shell}}^{\mathrm{iso}}:\mathrm{Sym}(2)\to {\mathrm{Sym}}(2)\) for isotropic elastic shells in the Koiter model is given by [14]
Since our model is completely written in matrix format, we also transform the above classical minimization problem in matrix format. To this aim, let us remark that in (A.2), for a second order symmetric tensor \(X \,=\,X_{\alpha \beta } e _{\alpha }\otimes e _{\beta }\), we have
A little calculation shows
where \(P\,=\, \nabla \Theta \), and similarly
If we substitute (A.5) and (A.6) into (A.4), we obtain
which holds for any symmetric tensor \(X \,=\,X_{\alpha \beta } e _{\alpha }\otimes e _{\beta }\).
Writing the equation (A.7) for the symmetric matrix \(X\,=\, \frac{1}{2}(\mathrm{I}_{m}-\mathrm{I}_{y_{0}})\) and respectively the matrix \(X\,=\, \mathrm{II}_{m}-\mathrm{II}_{y_{0}}\), then we obtain the following relations

Hence, putting all together, in matrix format and for a nonlinear elastic shell, the variational problem for the Koiter energy is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \)
The main feature of the classical Koiter model is that it is just the sum of the correctly identified membrane term and bending terms (under inextensional deformation).
1.3 A.3 Thickness Versus Invertibility and Coercivity
1.3.1 A.3.1 Invertibility Conditions for the Parametrized Initial Surface \(\Theta \)
We note that \(\det \nabla \Theta (x_{3})= 1-2\, H\,x_{3}+K\, x_{3}^{2}=(1-\kappa _{1} \,x_{3})(1-\kappa _{2}\, x_{3})>0\)  if and only if \(1-\kappa _{1}\,x_{3}\) and \(1-\kappa _{2}\, x_{3}\) have the same sign. However, \(1-\kappa _{1}\,x_{3}\) cannot be negative, since for \(\kappa _{1}<0\) this will imply that \(1<\kappa _{1}\,x_{3}\)
if and only if \(1-\kappa _{1}\,x_{3}\) and \(1-\kappa _{2}\, x_{3}\) have the same sign. However, \(1-\kappa _{1}\,x_{3}\) cannot be negative, since for \(\kappa _{1}<0\) this will imply that \(1<\kappa _{1}\,x_{3}\)  which is not true if \(x_{3}>0\), while for \(\kappa _{1}\geq 0\) this will imply that \(1<\kappa _{1}\,x_{3}\)
which is not true if \(x_{3}>0\), while for \(\kappa _{1}\geq 0\) this will imply that \(1<\kappa _{1}\,x_{3}\)  which is not true if \(x_{3}<0\). Therefore, \(1-2\, H\,x_{3}+K\, x_{3}^{2}>0\)
which is not true if \(x_{3}<0\). Therefore, \(1-2\, H\,x_{3}+K\, x_{3}^{2}>0\)  if and only if \(1>\kappa _{1}\,x_{3}\) and \(1>\kappa _{2}\, x_{3}\)
if and only if \(1>\kappa _{1}\,x_{3}\) and \(1>\kappa _{2}\, x_{3}\)  . These conditions are equivalent with
. These conditions are equivalent with  and
and  , i.e., equivalent with (1.18).
, i.e., equivalent with (1.18).
1.3.2 A.3.2 Coercivity for the \(O(h^{5})\) Model
The decisive point in the proof of the existence where the condition on the thickness is used is only in the proof of the coercivity of the internal energy density. Therefore, in this appendix, we extend the result regarding the coercivity of the internal energy to the following result:
Proposition A.2
Coercivity in the theory including terms up to order \(O(h^{5})\)
For sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients satisfying \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\), the energy density
is coercive in the sense that there exists a constant \(a_{1}^{+}>0\) such that \(W(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\,\geq \, a_{1}^{+}\, \big ( \lVert \mathcal{E}_{m,s}\rVert ^{2} + \lVert \mathcal{K}_{e,s}\rVert ^{2} \,\big )\), where \(a_{1}^{+}\) depends on the constitutive coefficients.
Proof
From the assumptions \(h\, |\kappa _{1}|<\alpha \), \(\ h\, |\kappa _{2}|<\alpha \), it follows that
Therefore, for \(\alpha <\sqrt{\frac{20}{3}}\) it follows \(h-\mathrm{K}\,\frac{h^{3}}{12}> h-\,\frac{h}{12}\alpha ^{2}>0 \ \ \textrm{and} \ \ \frac{h^{3}}{12}\,-\frac{h^{3}}{80}\alpha ^{2}>0\). On the other hand, from [21, Proposition 3.1.] we have
Using the inequalities (A.12), we deduce
Let us remark for \(0<\alpha <\sqrt{\frac{20}{3}}\), if there exist \(\delta >\frac{20}{3}\) and \(\varepsilon >\frac{40\, \alpha }{20-3\, \alpha ^{2}}\) such that
then \(\alpha <\sqrt{\frac{2}{3}(29-\sqrt{761})}\simeq 0.97083\). Since the map \((\delta , \varepsilon )\mapsto \delta + 2\,\varepsilon \,\alpha \) is linear, it increases in gradient direction and hence, the condition \(\alpha <\sqrt{\frac{2}{3}(29-\sqrt{761})}\simeq 0.97083\) is also sufficient for the existence of \(\delta >\frac{20}{3}\) and \(\varepsilon >\frac{40\, \alpha }{20-3\, \alpha ^{2}}\) such that (A.15) is satisfied.

In view of (A.14) and (2.10), we see that there exist positive constants \(b_{1}^{+}, b_{2}^{+},b_{3}^{+}>0\) such that

The desired constant \(a_{1}^{+}\) from the conclusion can be chosen as \(a_{1}^{+}\,{=}\,\min \big \{\dfrac{h}{12}\,b_{1}^{+}\, \min \{c_{1}^{+}, \mu _{\mathrm{c}}\}, \dfrac{h}{12}\,b_{2}^{+}\,\min \{c_{1}^{+},\mu _{\mathrm{c}} \}, h\,b_{3}^{+}\, { c_{2}^{+}} \big \}\). □
1.3.3 A.3.3 Coercivity for the \(O(h^{3})\) Model
In this subsection we investigate if the conditions which assure the existence of the solution may be relaxed in the Cosserat shell model up to \(O(h^{3})\), too. In fact, as in the previous subsection, it is enough to prove some new coercivity results under weakened conditions on the thickness. We recall that in the Cosserat shell model up to \(O(h^{3})\) the shell energy density \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\) is given by (3.65).
Proposition A.3
The first coercivity result in the theory including terms up to order \(O(h^{3})\)
For sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients satisfying the constitutive coefficients are such that \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\) and where \(c_{2}^{+}\) denotes the smallest eigenvalue of \(W_{\mathrm{curv}}( S )\), and \(C_{1}^{+}>0\) denotes the largest eigenvalues of the quadratic form \(W_{\mathrm{shell}}^{\infty }( S)\), the total energy density \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\) is coercive, in the sense that there exists a constant \(a_{1}^{+}>0\) such that \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\,\geq \, a_{1}^{+} \, \big ( \lVert \mathcal{E}_{m,s}\rVert ^{2} + \lVert \mathcal{K}_{e,s} \rVert ^{2}\,\big ) \), where \(a_{1}^{+}\) depends on the constitutive coefficients.
Proof
Similarly as in the proof presented in [21, Proposition 4.1], we obtain the estimate

which after imposing the conditions \(-h^{2} |K|>-\alpha ^{2}\) and \(-h\, |H|>-\alpha \), using (A.12), (2.10) and since the Frobenius norm is sub-multiplicative and \(\lVert C_{y_{0}}\rVert ^{2}=2 \), leads to

for all \(\alpha , \delta , \varepsilon >0\) such that \(12-\alpha ^{2}- \varepsilon -2\,\alpha \, \delta >0\) and \(12-\alpha ^{2}>0\). Since \(\lVert B_{y_{0}}\rVert ^{2}=4\, \mathrm{H}^{2}-2\,\mathrm{K}\), it follows
Using again that \(h\) is small, we obtain \(-h^{2}\,(4\, \mathrm{H}^{2}-2\,\mathrm{K})\geq -h^{2}\,(4\, \mathrm{H}^{2}+2 \,|{\mathrm{K}}|)\geq -6\,\alpha ^{2} \) and
We consider \(\delta =\gamma \, \varepsilon \) and we choose \(\epsilon >0\) and \(\gamma >0\) such that
This choice of the variable \(\varepsilon >0\) is possible if and only if \(\frac{(12-\alpha ^{2})^{2}\gamma }{4\,(a+2\,\alpha \gamma )\,(\alpha +3\, \alpha ^{2}\gamma )}> \frac{h^{2}\,\max \{C_{1}^{+},\mu _{\mathrm{c}}\} }{c_{2}^{+}}\). At this point we use that
and this maximum value is attained for \(\gamma =\frac{1}{\sqrt{6}\,a}\). Hence, we arrive at the following condition on the thickness \(h\):
which proves the coercivity if the condition from the hypothesis is satisfied. □
The condition (A.18) on the thickness does not represent a relaxation of the condition imposed in [21, Proposition 4.1], i.e., not in the sense of the relaxed condition (A.10) which is found for the \(O(h^{5})\) Cosserat shell model. Indeed, since the map \(\alpha \mapsto \frac{(5-2\sqrt{6})(\alpha ^{2}-12)^{2}}{4\, \alpha ^{2}} \frac{ {c_{2}^{+}}}{\max \{C_{1}^{+},\mu _{\mathrm{c}}\} }\) is monotone decreasing on \([0,2]\) (the interval of the values of the parameter \(\alpha \) for which the construction of the model has sense), a large value for \(\alpha \) will relax the first condition (A.18)1 while the other condition (A.18)2 on the thickness will become more restrictive. Since the second condition (A.18)2 is expressed in terms of all constitutive parameters, through \(c_{2}^{+}\) and \(\max \{C_{1}^{+},\mu _{\mathrm{c}}\} \), while the first condition (A.18)1 depends on the curvatures of the referential configuration, the largest value of the parameter \(\alpha \) in the coercivity result would be chosen as the best compromise between the conditions (A.18)1 and (A.18)2. In conclusion, in comparison to the conditions imposed in [21, Proposition 4.1], for a specific material and a specific referential configuration the new condition (A.18) would offer a largest interval of values for the upper bound of the thickness.
We also note that in [21, Proposition 4.1], because the condition of the form (A.18)2 from the hypothesis of Proposition A.3 depends on the length scale \(L_{c}\), we have proved another coercivity result which avoids this aspect:
Proposition A.4
The second coercivity result in the theory including terms up to order \(O(h^{3})\)
For sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients satisfying the constitutive coefficients are such that \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\) and let \(c_{1}^{+}\) and \(\max \{C_{1}^{+},\mu _{\mathrm{c}}\} >0\) denote the smallest and the largest eigenvalues of the quadratic form \(W_{\mathrm{shell}}^{\infty }( S)\), the total energy density \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\) is coercive, in the sense that there exists a constant \(a_{1}^{+}>0\) such that \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\,\geq \, a_{1}^{+} \, \big ( \lVert \mathcal{E}_{m,s}\rVert ^{2} + \lVert \mathcal{K}_{e,s} \rVert ^{2}\,\big )\), where \(a_{1}^{+}\) depends on the constitutive coefficients.
1.4 A.4 Acharya’s Bending Tensor in Cartesian Matrix Notation
For comparison purpose, let us mark all the vectors and tensors defined by Acharya [1, Page 5520] with the subscript \(A\) (e.g., \(\boldsymbol{f}_{A} \), \(\boldsymbol{b}^{*}_{A} \), \((\boldsymbol{E}_{\alpha })_{A} \)). We express them using our notations as follows:
Let us denote by \([ \boldsymbol{T}_{A}] \) the \(3\times 3 \) matrix of the components in the basis \(\{ e_{i}\otimes e_{j}\} \) for any tensor \(\boldsymbol{T} \) defined by Acharya [1, Page 5519]. Then, we have
and
so that
Furthermore, we have
and using (A.41) we get
By virtue of (A.28) and (A.29), the classical bending strain measure can be written as [1, Eq. 3]
For the tensor \(\boldsymbol{U}_{A} \) we obtain using equation (A.28) the expression
Thus, the bending tensor defined by Acharya [1, Eq. 8] is given by
Inserting here the relations (A.28), (A.29) and (A.31), we obtain that the bending tensor \(\widetilde{\boldsymbol{K}}_{A} \) defined in the paper by Acharya [1, Eq. 7 and 8] can be written in our matrix notation as follows:

Since  and
and  , the following relation between the nonlinear bending tensor \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) introduced by Acharya and our nonlinear bending tensor \(\mathcal{R}_{\infty }^{\flat }\) holds
, the following relation between the nonlinear bending tensor \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) introduced by Acharya and our nonlinear bending tensor \(\mathcal{R}_{\infty }^{\flat }\) holds

where we have used  and (6.2).
and (6.2).
1.5 A.5 A Direct Proof of the Fact That \(\mathcal{R}_{\infty }^{\flat }\) Satisfies AR1, AR2 and AR3 ∗
It is obvious that the tensor (6.1) satisfies condition AR2, see Sect. 6.2. Moreover, using similar calculations as in Sect. 6.2, for a rigid deformation, we have

so that we conclude

which means that \(\mathcal{R}_{\infty }^{\flat }\) satisfies AR1.
In order to show that \(\mathcal{R}_{\infty }^{\flat }\) satisfies AR3∗, using
we deduce that

where we have used that \(\mathrm{U_{e}}\) is positive-definite. Together with the definition of the symmetric matrix \(\mathrm{U_{e}}\) we get

Again, using the intermediate steps (6.16) and (A.38) in the expression (6.2) we obtain \(\mathcal{R}_{\infty }^{\flat }=0_{3}\) since

so that also \(\mathcal{R}_{\infty }^{\flat }\) satisfies AR1, AR2 and AR3∗.
1.6 A.6 Alternative Representation of Energy in Terms of the New Strain Tensors
We present in the following an alternative formulation of the unconstrained Cosserat-shell model from (3.21). In this section, for a matrix of the form \(X\,=\,(X^{S}\, |\, 0)\; [\nabla \Theta \,]^{-1}\in \mathbb{R}^{3 \times 3}\), we consider the matrix \(X^{C} \,=\, [\nabla \Theta \,]^{T} X^{S}\in \mathbb{R}^{3\times 2}\), i.e.,
For the bilinear form \(W_{\mathrm{shell}}( X, Y) \) given in (2.6) we have then the transformations
where, e.g.,
We note that the last relation can be written using the first fundamental form \(\mathrm{I}_{y_{0}} \) and its square root in the following alternative ways:
Moreover, if we decompose the matrix \(X^{C} \in \mathbb{R}^{3\times 2}\) in two block matrices (the matrix  and the matrix \(e_{3}^{T}\, X^{C} \in \mathbb{R}^{1\times 2}\)), then we can write the bilinear form as
and the matrix \(e_{3}^{T}\, X^{C} \in \mathbb{R}^{1\times 2}\)), then we can write the bilinear form as

where we define for any \(X, Y\in \mathbb{R}^{2\times 2} \) the bilinear form
Analogous results hold for the quadratic form \(W_{\mathrm{curv}}( X, X) \).
We can decompose the \(3\times 2 \) matrices in two block matrices (\(2 \times 2 \) and \(1\times 2 \)) and express the strain energy densities \(W_{\mathrm{memb}} \) and \(W_{\mathrm{memb,bend}}\) as functions of the matrices \(\mathcal{G}_{\infty }\) and \(\mathcal{R}_{\infty }\) (we have used that \(\mathcal{T}_{\infty }\) vanishes) in the following form
where  , \(W_{\mathrm{inplane}} \) is given by (A.45) and we have denoted
, \(W_{\mathrm{inplane}} \) is given by (A.45) and we have denoted
We can see in the expression (A.46) the different parts of the energy corresponding to in-plane deformation, transverse shear, or coupling terms with bending.
Finally, the bending-curvature energy density \(W_{\mathrm{bend,curv}} \) can be written as function of \(\mathcal{R}_{\infty }\) and \(\mathcal{N}_{\infty }\) as follows
where we have denoted for any \(2\times 2 \) matrix \(X \) the quadratic form (positive definite)

Thus, the model can be expressed entirely in terms of the change of metric tensor \(\mathcal{G}_{\infty }\), the bending strain tensor \(\mathcal{R}_{\infty }\) and the vector of drilling bendings \(\mathcal{N}_{\infty }\), through the relations (A.46) and (A.48).
Rights and permissions
About this article
Cite this article
Ghiba, ID., Bîrsan, M., Lewintan, P. et al. A Constrained Cosserat Shell Model up to Order \(O(h^{5})\): Modelling, Existence of Minimizers, Relations to Classical Shell Models and Scaling Invariance of the Bending Tensor. J Elast 146, 83–141 (2021). https://doi.org/10.1007/s10659-021-09851-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-021-09851-7
Keywords
- Geometrically nonlinear Cosserat shell
- 6-parameter resultant shell
- In-plane drill rotations
- Constrained Cosserat elasticity
- Isotropy
- Existence of minimizers
- Scaling invariance
- Bending tensor


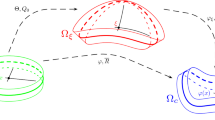








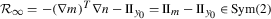 .
.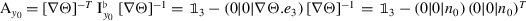 ,
, ;
;