Need the Uniform Stress Field Inside Multiple Interacting Inclusions Be Hydrostatic?

Abstract

Since the pioneering work of Eshelby on a single ellipsoidal inclusion embedded in an infinite space, much attention has been devoted in the literature to the question of the uniformity of the stress field inside inclusions surrounded by an elastic matrix. Over the last decade or so, researchers have established the existence of multiple (interacting) inclusions enclosing uniform internal stress distributions when embedded in an infinite elastic matrix subjected to a uniform far-field loading and identified a variety of shapes of such inclusions. In the design of multiple inclusions with uniform internal stresses, it is customary to assume that the uniform stress field inside each inclusion (each with different shear modulus distinct from that of the matrix) is hydrostatic. In this paper, we examine whether this assumption is actually necessary to ensure the required existence of multiple inclusions enclosing uniform stresses. By establishing several theorems in the theory of functions of a complex variable, we prove rigorously that for any collection of multiple inclusions enclosing uniform stresses in an infinite isotropic plane subjected to uniform remote in-plane loading, the internal uniform stress field must indeed be hydrostatic if the corresponding inclusion’s shear modulus is distinct from that of the matrix.

1 Introduction

In his seminal work on elastic inclusions, Eshelby [1] studied the deformation of a single ellipsoidal inclusion embedded in an elastic matrix and showed that the stress field inside the inclusion is always uniform for any uniform remote loading applied to the matrix. Over the last decade or so, researchers have turned their attention to the question of uniformity of the stress distribution inside multiple interacting inclusions in an elastic matrix subjected to uniform remote loading. The conventional approach is to examine the case when the shapes of the inclusions are given a priori. In our present analysis, we consider the inverse problem which seeks to identify shapes of interacting inclusions which admit internal uniform stresses despite the interaction between them. This is entirely different from the aforementioned conventional approach (in which the shapes of the interacting inclusions are given beforehand) since, when considering inclusions of general shape (including ellipsoidal shapes), the interaction between them means that there is no guarantee of uniformity of the internal stress field. Consequently, most of the effective techniques (for example, those in [2,3,4,5]) used in solving the conventional problem of multiple interacting inclusions of given shape may not be suitable in the case of the inverse problem. In fact, only a few relevant papers can be found in the literature, most likely as a result of certain formidable mathematical challenges. For example, Liu [6] demonstrated the existence of multiple inclusions with uniform stresses in two- and three-dimensions based on a variational inequality; Kang et al. [7] used the Weierstrass zeta function and Schwarz–Christoffel formula to identify, for two-dimensional deformations, a pair of inclusions enclosing uniform stresses; Wang [8] introduced a specific fractional conformal mapping and derived explicit formulae describing the shapes of some two-dimensional inclusion pairs enclosing uniform stresses; Dai et al. [9, 10] found a series of multiple inclusions with uniform stresses and geometric symmetry in anti-plane and plane elasticity by making use of the Faber series. Some specific shapes of multiple inclusions enveloping uniform stresses for plane deformation are illustrated in Fig. 1.

Fig. 1

Multiple rationally symmetric inclusions with uniform hydrostatic stresses in an infinite elastic plane under plane strain deformation for a uniform remote equal-biaxial tension/compression ($G$ and $\nu$ are the shear modulus and Poisson’s ratio of the matrix, while $G_{j}$ and $\nu _{j}$ denote those of the corresponding inclusion)

In the case of a single ellipsoidal (three-dimensional) or elliptical (two-dimensional) inclusion, the corresponding uniform stress field need not necessarily be hydrostatic. For example, when the remote loading imposed on the matrix takes the form of a uniform pure shear loading, the ellipsoidal or elliptical inclusion must undergo a certain shear deformation leading to an internal non-hydrostatic (uniform) stress field. When it comes to multiple interacting inclusions in either three-dimensional or plane deformations, however, it would seem that the stress field inside each inclusion must be hydrostatic to ensure uniformity whenever the shear modulus of the inclusion differs from that of the matrix. For example, in the design of multiple inclusions with uniform stresses in plane deformation, the authors consistently treat the uniform stresses inside each inclusion (of shear modulus distinct from that of the matrix) as being hydrostatic [7,8,9]. We are not aware of a contribution to the literature which identifies shapes of multiple (interacting) inclusions (of shear moduli different from that of the matrix) which admit uniform but non-hydrostatic internal stress distributions in the case of either three-dimensional or plane deformations. In this paper, we aim to address this question and whether it is possible to construct multiple interacting inclusions (of shear moduli distinct from that of the surrounding matrix) enclosing uniform yet non-hydrostatic stresses in plane deformation.

The paper is subsequently organized as follows. In Sect. 2, we present (and prove) several important theorems from the theory of functions of a complex variable. In Sect. 3, we consider the plane deformation of a system consisting of multiple elastic inclusions embedded in an infinite elastic plane subjected to a uniform far-field loading and use the theorems introduced in Sect. 2 to prove the necessity of the ‘hydrostatic property’ in establishing the uniformity of the internal stress field inside the inclusions. Finally, in Sect. 4, we summarize our main conclusions and make some additional remarks.

2 Preliminaries

In this section, we present and prove several theorems for use in subsequent sections. In particular, throughout the paper, the analytic functions involved are functions of a complex variable whose real and imaginary parts correspond to the coordinates of a Cartesian system, and which are always assumed to be analytic in a connected domain and continuously extendable to the boundary of the domain.

Theorem 1

If two functions are analytic in a connected domain and coincide on a certain continuous arc of the boundary of the domain, then they are equal in the entire domain.

The proof of this theorem follows directly from the Identity Theorem in complex analysis.

Theorem 2

Consider a function $f(z)$ analytic in an infinite multiply-connected domain $S$ with $n$ non-overlapping holes each bounded by a simple smooth closed curve $L_{i}$ ($i=1,\dots ,n$). If the boundary value of $f$ on $L_{i}$ ($i=1,\dots ,n$) takes the form

$$ f(t) = \alpha _{i}t + \beta _{i}\bar{t} + \gamma _{i}, \quad t \in L_{i} \ (i = 1,\ldots,n), $$

(1)

where $\alpha _{i}$, $\beta _{i}$ and $\gamma _{i}$ are certain constants, then $\beta _{i}$ ($i=1,\dots ,n$) are either all zero or all non-zero.

Proof 2

To prove Theorem 2, it is sufficient to show that if $\beta _{i} = 0$ for a certain value of $i$, then $\beta _{j} = 0$ for all $j$. In fact, without loss of generality, assuming $\beta _{1} = 0$, from Eq. (1) we have that

$$ f(t) = \alpha _{1}t + \gamma _{1}, \quad t \in L_{1}. $$

(2)

Using Theorem 1, we determine $f(z)$ in the entire domain $S$ as

$$ f(z) = \alpha _{1}z + \gamma _{1}, \quad \forall z \in S. $$

(3)

Combining Eqs. (1) and (3) leads to

$$ (\alpha _{j} - \alpha _{1})t + \beta _{j}\bar{t} + (\gamma _{j} - \gamma _{1}) = 0, \quad \forall t \in L_{j}\ (j = 2,\ldots,n). $$

(4)

Here, since $L_{j}$ ($j=2,\dots ,n$) are simple closed curves, it follows from Eq. (4) that

$$ \alpha _{j} = \alpha _{1},\qquad \beta _{j} = 0,\qquad \gamma _{j} = \gamma _{1} \quad (j = 2,\ldots,n), $$

(5)

which completes the proof. □

Theorem 3

In the complex plane, if for a simple smooth closed curve $L$ we have

$$ At + B\bar{t} + C + \left ( Dt + E\bar{t} + F \right )\frac{d\bar{t}}{dt} = 0,\quad \forall t \in L, $$

(6)

where $A$, $B$, $C$, $D$, $E$ and $F$ are certain constants, then the curve is an ellipse, otherwise $A$, $B$, $C$, $D$, $E$ and $F$ must all vanish.

Proof 3

The contour integral of Eq. (6) with respect to $t$ over $L$ gives

$$ B\oint _{L} \bar{t}dt + D\oint _{L} td\bar{t} = 0. $$

(7)

Noting that

$$ \oint _{L} \bar{t}dt = 2\chi \cdot \mathrm{I},\qquad \oint _{L} td\bar{t} = - 2\chi \cdot \mathrm{I}, $$

(8)

where I is the imaginary unit and $\chi$ is the area of the region enclosed by $L$, it readily follows from Eq. (7) that

$$ B = D. $$

(9)

Using Eq. (9), the indefinite integration of Eq. (6) with respect to $t$ results in

$$ At^{2} + 2Bt \cdot \bar{t} + E\bar{t}^{2} + 2Ct + 2F\bar{t} = H, \quad \forall t \in L, $$

(10)

where $H$ is a certain constant.

When $A$, $B$ and $E$ do not all vanish, Eq. (10) is the equation of a conic section and then $L$ must be an ellipse since it is closed. In the case when $A$, $B$ and $E$ all vanish, Eq. (10) cannot correspond to a simple closed curve $L$ unless $C$ and $F$ both become zero. This completes the proof. □

Theorem 4

Consider in the complex $z$-plane an infinite multiply-connected domain $S$ with $n$ non-overlapping holes ($n \ge 2$) each bounded by a simple smooth closed curve $L_{i}$ ($i=1,\dots ,n$). It has been verified that the (infinite) exterior of each curve $L_{i}$ in the $z$-plane can be transformed into that of the unit circle in an imaginary plane via a polynomial conformal mapping [11]. If the conformal mapping for a certain curve $L_{j}$ contains only finite terms, then there is no function $h(z)$ analytic in $S$ that

$$ \lim _{\left | z \right | \to \infty } h(z) = 0, $$

(11)

$$ h(t) = a_{i}t + b_{i}\bar{t} + c_{i},\quad b_{i} \ne 0, \ t \in L_{i}\ (i = 1,\ldots,n), $$

(12)

where $a_{i}$, $b_{i}$ and $c_{i}$ are certain constants.

Proof 4

We denote the (infinite) exterior of the curve $L_{i}$ in the $z$-plane by $T_{i}$. Let $T_{i}$ be transformed into the (infinite) exterior of the unit circle in the imaginary $\xi _{i}$-plane by the conformal mapping [11]

$$ z = \omega _{i}(\xi _{i}),\quad z \in T_{i}, \ \left | \xi _{i} \right | > 1. $$

(13)

In particular, when $\xi _{i}$ tends towards the unit circle, Eq. (13) becomes

$$ t \in L_{i}: t = \omega _{i}(\sigma _{i}), \quad \sigma _{i} = e^{\mathrm{I}\theta _{i}} \ (0 \le \theta _{i} < 2\pi ). $$

(14)

In the context of the mapping (13), since $S \subset T_{i}$, $S$ must correspond to a multiply-connected domain $\Upsilon _{i}$ in the $\xi _{i}$-plane which contains also $n$ non-overlapping holes, and the $n$ internal boundaries (denoted by $L_{ik}$ ($k=1,\dots ,n$)) of $\Upsilon _{i}$ in the $\xi _{i}$-plane correspond to the curves $L_{k}$ ($k=1,\dots ,n$) in the $z$-plane, respectively. We note in particular that $L_{ii}$ is the unit circle in the $\xi _{i}$-plane. Consequently, it is sufficient to rewrite Eq. (13) for our purposes as

$$ z = \omega _{i}(\xi _{i}), \quad z \in S,\quad \xi _{i} \in \Upsilon _{i}. $$

(15)

We prove Theorem 4 by contradiction. We assume that there exists in $S$ an analytic function $h(z)$ satisfying Eqs. (11) and (12) and that the conformal mapping for $i=1$ is of finite-series form. Specifically, Eqs. (15) and (14) corresponding to $i=1$ are given as [11]

$$ z = \omega _{1}(\xi _{1}) = z_{01} + R_{1}\left ( \xi _{1} + \sum _{j = 1}^{N} m_{1j}\xi _{1}^{ - j} \right ),\quad z \in S,\ \xi _{1} \in \Upsilon _{1}, $$

(16)

$$ t \in L_{1}: t = \omega _{1}(\sigma _{1}) = z_{01} + R_{1}\left ( \sigma _{1} + \sum _{j = 1}^{N} m_{1j}\sigma _{1}^{ - j} \right ), $$

(17)

where $z_{01}$ is a certain point inside the region enclosed by $L_{1}$ in the $z$-plane, while $R_{1}$ ($R_{1} \ne 0$) and $m_{1j}$ are constants characterizing the size and shape of $L_{1}$ in the $z$-plane.

In the context of the conformal mapping (15), $h[\omega _{i}(\xi _{i})]$ is analytic in $\Upsilon _{i}$. For $h[\omega _{1}(\xi _{1})]$, we obtain from Eqs. (12) and (17) its boundary value $h[\omega _{1}(\sigma _{1})]$ on $L_{11}$ in the $\xi _{1}$-plane as

$$ h\left [ \omega _{1}(\sigma _{1}) \right ] = \left \{ \textstyle\begin{array}{l} a_{1}\left [ z_{01} + R_{1}\left ( \sigma _{1} + \sum _{j = 1}^{N} m_{1j}\sigma _{1}^{ - j} \right ) \right ] \\ {}+ b_{1}\left [ \bar{z}_{01} + \bar{R}_{1}\left ( \sigma _{1}^{ - 1} + \sum _{j = 1}^{N} \bar{m}_{1j}\sigma _{1}^{j} \right ) \right ] + c_{1} \end{array}\displaystyle \right \} ,\quad \text{on}\ L_{11}. $$

(18)

Using Eq. (18) and Theorem 1, we may immediately derive $h[\omega _{1}(\xi _{1})]$ in the entire $\Upsilon _{1}$ as

$$ h[\omega _{1}(\xi _{1})] = \left \{ \textstyle\begin{array}{l} a_{1}\left [ z_{01} + R_{1}\left ( \xi _{1} + \sum _{j = 1}^{N} m_{1j}\xi _{1}^{ - j} \right ) \right ] \\ {}+ b_{1}\left [ \bar{z}_{01} + \bar{R}_{1}\left ( \xi _{1}^{ - 1} + \sum _{j = 1}^{N} \bar{m}_{1j}\xi _{1}^{j} \right ) \right ] + c_{1} \end{array}\displaystyle \right \} ,\quad \xi _{1} \in \Upsilon _{1}. $$

(19)

Noting Eq. (11) and

$$ \left | \xi _{1} \right | \to \infty \quad \text{when}\ \left | z \right | \to \infty , $$

(20)

we require in Eq. (19) that

$$ a_{1}z_{01} + b_{1}\bar{z}_{01} + c_{1} = 0,\qquad a_{1}R_{1} + b_{1}\bar{R}_{1}\bar{m}_{11} = 0,\qquad m_{1j} = 0\quad (2 \le j \le N). $$

(21)

Substituting Eq. (21) into Eqs. (16) and (19) leads to

$$ z = z_{01} + R_{1}\left ( \xi _{1} + m_{11}\xi _{1}^{ - 1} \right ),\quad z \in S,\ \xi _{1} \in \Upsilon _{1}, $$

(22)

$$ h(z) \equiv h[\omega _{1}(\xi _{1})] = b_{1}\bar{R}_{1}\left ( 1 - \left | m_{11} \right |^{2} \right )\xi _{1}^{ - 1}, \quad z \in S,\ \xi _{1} \in \Upsilon _{1}. $$

(23)

It is worth noting that $\left | m_{11} \right | \ne 1$ otherwise $L_{1}$ described by Eq. (22) becomes a straight line in the $z$-plane violating the stipulation of ‘simple closed curve’.

Consider the boundary value $h(t)$ on $L_{k}$ ($k \ne 1$) in the $z$-plane by using Eqs. (12) and (23). We then see that

$$ a_{k}t + b_{k}\bar{t} + c_{k} = b_{1}\bar{R}_{1}\left ( 1 - \left | m_{11} \right |^{2} \right )\xi _{1}^{ - 1},\quad t \in L_{k},\ \xi _{1} \in L_{1k}. $$

(24)

It follows from Eq. (22) that

$$ t = z_{01} + R_{1}\left ( \xi _{1} + m_{11}\xi _{1}^{ - 1} \right ),\quad t \in L_{k},\ \xi _{1} \in L_{1k}. $$

(25)

From Eqs. (24) and (25) we extract an algebraic equation describing the configuration of $L_{k}$ as

$$\begin{aligned} & \beta a_{k}t^{2} - m_{11}\frac{b_{k}^{2}}{\alpha } \bar{t}^{2} + \left ( \beta b_{k} - m_{11}\frac{a_{k}b_{k}}{\alpha } \right )t\bar{t} \\ &\quad {}+ \left ( \beta c_{k} - \gamma a_{k} \right )t - \left ( \gamma b_{k} + m_{11}\frac{b_{k}c_{k}}{\alpha } \right )\bar{t} - \gamma c_{k} - \alpha = 0,\quad t \in L_{k}, \end{aligned}$$

(26)

where

$$ \alpha = b_{1}\bar{R}_{1}\left ( 1 - \left | m_{11} \right |^{2} \right ),\qquad \beta = \frac{1}{R_{1}} - m_{11}\frac{a_{k}}{\alpha },\qquad \gamma = \frac{z_{01}}{R_{1}} + m_{11}\frac{c_{k}}{\alpha }. $$

(27)

Since $R_{1} \ne 0$ and $b_{k} \ne 0$, the coefficients of $t^{2}$, $\bar{t}^{2}$ and $t\bar{t}$ in Eq. (26) cannot be zero simultaneously so that Eq. (26) is always an equation describing a conic section. Consequently, the closed curve $L_{k}$ in the $z$-plane must be an ellipse, resulting in the conformal mapping of $L_{k}$ as

$$ z = \omega _{k}(\xi _{k}) = z_{0k} + R_{k}\left ( \xi _{k} + m_{k1}\xi _{k}^{ - 1} \right ),\quad z \in S,\ \xi _{k} \in \Upsilon _{k}, $$

(28)

$$ t \in L_{k}: t = \omega _{k}(\sigma _{k}) = z_{0k} + R_{k}\left ( \sigma _{k} + m_{k1}\sigma _{k}^{ - 1} \right ), $$

(29)

where $z_{0k}$ represents the center of the elliptical region bounded by $L_{k}$, while $R_{k}$ and $m_{k1}$ characterize the size, aspect ratio and orientation of $L_{k}$ in the $z$-plane. In particular, $\left | m_{k1} \right | \ne 1$ otherwise $L_{k}$ becomes a straight line in the $z$-plane.

We note that the procedure used in the derivation between Eqs. (18) and (23) is also applicable to $h[\omega _{k}(\xi _{k})]$ with Eqs. (28) and (29). Consequently, we can readily see that

$$ h(z) \equiv h[\omega _{k}(\xi _{k})] = b_{k}\bar{R}_{k}\left ( 1 - \left | m_{k1} \right |^{2} \right )\xi _{k}^{ - 1},\quad z \in S,\ \xi _{k} \in \Upsilon _{k}. $$

(30)

Equating Eqs. (23) and (30) leads to

$$ \xi _{k} = \lambda \xi _{1}\quad (\xi _{1} \in \Upsilon _{1}, \xi _{k} \in \Upsilon _{k}), $$

(31)

where

$$ \lambda = \frac{b_{k}\bar{R}_{k}\left ( 1 - \left | m_{k1} \right |^{2} \right )}{b_{1}\bar{R}_{1}\left ( 1 - \left | m_{11} \right |^{2} \right )}. $$

(32)

From another perspective that $\xi _{1}$ and $\xi _{k}$ always correspond to the same point $z$ in the $z$-plane, we obtain by combining Eqs. (22) and (28) that

$$ z_{01} + R_{1}\left ( \xi _{1} + m_{11}\xi _{1}^{ - 1} \right ) = z_{0k} + R_{k}\left ( \xi _{k} + m_{k1}\xi _{k}^{ - 1} \right ),\quad \xi _{1} \in \Upsilon _{1}, \xi _{k} \in \Upsilon _{k}. $$

(33)

Substituting Eq. (31) into Eq. (33) yields

$$ z_{01} + R_{1}\left ( \xi _{1} + m_{11}\xi _{1}^{ - 1} \right ) = z_{0k} + R_{k}\left ( \lambda \xi _{1} + m_{k1}\lambda ^{ - 1}\xi _{1}^{ - 1} \right ),\quad \forall \xi _{1} \in \Upsilon _{1}. $$

(34)

If Eq. (34) holds everywhere in $\Upsilon _{1}$, then we have to require $z_{01} = z_{0k}$ which is however contradictory to the original stipulation that the region enclosed by $L_{1}$ does not overlap with that enclosed by $L_{k}$. The proof is completed. □

Theorem 5

Consider an infinite multiply-connected domain $S$ with $n$ non-overlapping holes ($n \ge 2$) each bounded by a simple smooth closed curve $L_{i}$ ($i=1,2,\dots ,n$) and a function $p(t)$ defined on the curves $L_{i}$ ($i=1,2,\dots ,n$) as

$$ p(t) = at + b\bar{t} + c, b \ne 0, \quad t \in L_{i}\ (i = 1,\ldots,n), $$

(35)

for some constants $a$, $b$ and $c$. Then there exists no analytic function in $S$ that vanishes at infinity and converges to $p(t)$ on $L_{i}$ ($i=1,\dots ,n$).

Proof 5

We present the proof of Theorem 5 by contradiction. We assume that there exists a certain function analytic in $S$ which vanishes at infinity and whose boundary value on $L_{i}$ ($i=1,\dots ,n$) is identical to $p(t)$. Consequently, based on the Sokhotski–Plemelj theorem, $p(t)$ should satisfy

$$ \sum _{j = 1}^{n} \oint _{L_{j}} \frac{p(t)}{t - z}dt = 0, \quad \forall z \in S_{i}\ (i = 1,\ldots,n), $$

(36)

where $S_{i}$ is the finite simply-connected domain bounded by $L_{i}$. In particular, according to Theorem 4, $L_{i}$ ($i=1,\dots ,n$) must not be ellipses since any ellipse corresponds to a conformal mapping with finite terms [11].

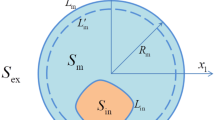
As shown in Fig. 2, we construct a new simply-connected domain $S_{0}$ containing all the $S_{i}$ ($i=1,\dots ,n$) by bridging $S_{i}$ and $S_{i + 1}$ ($i=1,\dots ,n$-1) using a group of narrow channels. The entire boundary of $S_{0}$ is denoted by $L_{0}$, that of each channel is denoted by $C_{i(i + 1)}$ ($i=1,\dots , n$-1), and the intersection of $L_{0}$ and each of $L_{i}$ ($i=1,\dots ,n$) is denoted by $L'_{i}$ ($i=1,\dots ,n$). In particular, $\varepsilon$ is used to represent the width of the narrow channels. We define a function $q(t)$ on $L_{0}$ as

$$ q(t) = at + b\bar{t} + c,\quad t \in L_{0}, $$

(37)

where $a$, $b$ and $c$ are the same constants as those introduced in $p(t)$, and introduce an analytic function $F(z)$ in $S_{0}$ as

$$ F(z) = \oint _{L_{0}} \frac{q(t)}{t - z}dt,\quad z \in S_{0}. $$

(38)

Fig. 2

Bridged simply-connected domain

Since $L_{0}$ is a simple closed curve, one may always introduce a conformal mapping (in the form of infinite series) to describe the configuration of its (infinite) exterior $T$. The mapping is defined by [11]

$$ z \in T: z = \omega (\xi ) = z_{0} + R\left ( \xi + \sum _{j = 1}^{\infty } m_{j}\xi ^{ - j} \right ),\quad \left | \xi \right | > 1, $$

(39)

where $z_{0}$ is a certain point within $S_{0}$, while the constants $R$ and $m_{j}$ determine the size and shape of $S_{0}$ (or $L_{0}$). Here, Eq. (39) connects $T$ in the $z$-plane to the exterior of the unit circle in the imaginary $\xi$-plane, and it converges to

$$ t \in L_{0}: t = \omega (\sigma ) = z_{0} + R\left ( \sigma + \sum _{j = 1}^{\infty } m_{j}\sigma ^{ - j} \right ),\quad \sigma = e^{\mathrm{I}\theta }\ (0 \le \theta < 2\pi ), $$

(40)

when $\xi$ tends towards the unit circle in the imaginary plane. Noting that $F(z)$ is analytic in $S_{0}$, it may be expanded in Faber series as

$$ F(z) = \sum _{j = 0}^{\infty } d_{j}P_{j}(z),\quad z \in S_{0}, $$

(41)

where $d_{j}$ are constant coefficients and $P_{j}(z)$ are the Faber polynomials of $S_{0}$. Specific expressions for the Faber polynomials depend on the configuration of $S_{0}$ and can be established via the following recurrence relation as [12]

$$ P_{j + 1}(z) = P_{1}(z)P_{j}(z) - \sum _{k = 1}^{j - 1} m_{k}P_{j - k}(z) - (j + 1)m_{j}, \quad j = 1,2,3,\ldots $$

(42)

with

$$ P_{0}(z) = 1,\qquad P_{1}(z) = \frac{z - z_{0}}{R}. $$

(43)

Here, it is seen from Eqs. (42) and (43) that the Faber polynomial $P_{j}(z)$ is no more than a $j$-th order polynomial in $z$ with the leading term $(z - z_{0})^{j} / R^{j}$. In particular, the coefficients of the Faber series for a given analytic function in $S_{0}$ are always unique. For $F(z)$ defined in Eq. (38), the corresponding coefficients $d_{j}$ ($j=0,1,2,\dots$) may be determined from [12] as

$$ d_{j} = \oint _{\mathrm{unit} \mathrm{circle}} q(\omega (\sigma ))\sigma ^{ - j - 1}d\sigma ,\quad j = 0,1,2,\ldots $$

(44)

Substituting Eqs. (37) and (40) into Eq. (44) we obtain the explicit expressions of $d_{j}$ ($j=0,1,2,\dots$) as

$$ d_{j} = \left \{ \textstyle\begin{array}{l@{\quad }l} 2\pi \mathrm{I}(Az_{0} + B\bar{z}_{0} + C), & j = 0, \\ 2\pi \mathrm{I}(AR + B\bar{R}\bar{m}_{1}),& j = 1, \\ 2\pi \mathrm{I} \cdot B\bar{R}\bar{m}_{j},& j \ge 2. \end{array}\displaystyle \right . $$

(45)

Let us now consider $F(z)$ from another perspective. Noting that

$$ L_{0} = \bigcup _{i = 1}^{n} L'_{i} \cup \bigcup _{i = 1}^{n - 1} C_{i(i + 1)}, $$

(46)

$$ q(t) = p(t),\quad t \in L'_{i}\ (i = 1,\ldots,n), $$

(47)

one may rewrite $F(z)$ as

$$ F(z) = \sum _{j = 1}^{n} \int _{L'_{j}} \frac{p(t)}{t - z}dt + \sum _{j = 1}^{n - 1} \int _{C_{j(j + 1)}} \frac{q(t)}{t - z}dt,\quad z \in S_{0}. $$

(48)

When the width $\varepsilon$ of the channels tends towards zero, $L'_{i}$ converges towards $L_{i}$ ($i=1,\dots ,n$) while the left and right boundaries of the channel $C_{i(i + 1)}$ tend to coincide, resulting in

$$ \lim _{\varepsilon \to 0}\sum _{j = 1}^{n} \int _{L'_{j}} \frac{p(t)}{t - z}dt = \sum _{j = 1}^{n} \int _{L_{j}} \frac{p(t)}{t - z}dt, \quad \forall z \in S_{i} \ (i = 1,\ldots,n), $$

(49)

$$ \lim _{\varepsilon \to 0}\sum _{j = 1}^{n - 1} \int _{C_{j(j + 1)}} \frac{q(t)}{t - z}dt = 0,\quad \forall z \in S_{i}\ (i = 1,\ldots,n). $$

(50)

Imposing Eqs. (36), (49) and (50) on Eq. (48) leads to

$$ \lim _{\varepsilon \to 0}F(z) = 0,\quad \forall z \in S_{i}\ (i = 1,\ldots,n). $$

(51)

Substituting Eqs. (41) and (45) into Eq. (51) and noting that each of $S_{i}$ ($i=1,\dots ,n$) is a connected subdomain of $S_{0}$, we immediately see that

$$ \lim _{\varepsilon \to 0}m_{j} = \left \{ \textstyle\begin{array}{l@{\quad }l} - (\bar{A}\bar{R}) / (\bar{B}R),& j = 1, \\ 0,& j \ge 2. \end{array}\displaystyle \right . $$

(52)

Here, it is indicated from Eq. (52) that $L_{0}$ converges to an ellipse as the width $\varepsilon$ of the channels tends towards zero. This is, however, contradictory to the original inference (see the first paragraph of the proof) that none of the $L_{i}$ ($i=1,\dots ,n$) could be elliptical in shape. The proof is thus complete. □

3 Multiple Interacting Inclusions with Uniform Stresses

Consider the plane deformation of $n$ non-overlapping inclusions ($n \ge 2$) surrounded by an infinite isotropic elastic matrix undergoing a uniform far-field in-plane loading. Each of the inclusions is bounded by a simple smooth closed curve $L_{i}$ ($i=1,\dots ,n$), and the infinite multiply-connected domain occupied by the matrix is denoted by $S$.

As shown in [9], the sufficient and necessary condition for the each of the inclusions to achieve a uniform internal stress field is that there exist two analytic functions $\varphi (z)$ and $\psi (z)$ in $S$ such that

$$ \lim _{\left | z \right | \to \infty } \varphi (z) = \lim _{\left | z \right | \to \infty } \psi (z) = 0, $$

(53)

$$ \varphi (t) = A_{i}t + B_{i}\bar{t} + C_{i},\quad t \in L_{i}\ (i = 1,\ldots,n), $$

(54)

$$ \psi (t) = D_{i}t + E_{i}\bar{t} - B_{i}\bar{t}\frac{d\bar{t}}{dt} + F_{i}, \quad t \in L_{i}\ (i = 1,\ldots,n), $$

(55)

where $A_{i}$, $B_{i}$, $D_{i}$ and $E_{i}$ are constants determined by the uniform far-field loading, the elastic constants of the matrix and each inclusion and specific uniform stress field inside each inclusion, while $C_{i}$ and $F_{i}$ are some constants. In particular, $B_{i} = 0$ only when the corresponding inclusion has either the same shear modulus as that of the matrix or a uniform (in-plane) hydrostatic stress field (see Eq. (2.8) in [9]).

Since Eq. (54) puts the limitation on both the real and imaginary parts of the boundary value of $\varphi (z)$ on $L_{i}$ ($i=1,\dots ,n$), the desired function $\varphi (z)$ may exist only when the configuration of $L_{i}$ ($i=1,\dots ,n$) is very specific. Similarly, as indicated from Eq. (55), the existence of the desired $\psi (z)$ requires a group of $L_{i}$ ($i=1,\dots ,n$) with specific configuration. In the design of multiple interacting inclusions achieving uniform internal stresses, however, one obstacle concerns how to specify the uniform stress field inside each inclusion (yielding appropriate constants $A_{i}$, $B_{i}$, $D_{i}$ and $E_{i}$) to ensure that the shapes of $L_{i}$ ($i=1,\dots ,n$) related to the existence of $\varphi (z)$ are consistent with those related to the existence of $\psi (z)$. A simple way to deal with this problem is to assume that the uniform stress field inside each inclusion (each with a shear modulus different from that of the matrix) is hydrostatic leading to $B_{i} = 0$ ($i=1,\dots ,n$), which was adopted in all of the related research [7,8,9]. Here, our purpose is to examine whether it is possible to solve the above-mentioned problem when $B_{i} \ne 0$ ($i=1,\dots ,n$).

We assume that there exist in $S$ two certain analytic functions $\varphi (z)$ and $\psi (z)$ satisfying Eqs. (53)–(55) with $B_{i} \ne 0$ ($i=1,\dots ,n$). According to Theorem 2 (see Eq. (54)), if $B_{i} \ne 0$ for a certain $i$, then $B_{i} \ne 0$ for all $i$. Consequently, we only need to consider the case in which none of $B_{i}$ ($i=1,\dots ,n$) is zero.

It follows from Eq. (54) that

$$ t \in L_{1}: \bar{t} = \frac{\varphi (t) - A_{1}t - C_{1}}{B_{1}}, $$

(56)

whose derivative with respect to $t$ is

$$ t \in L_{1}: \frac{d\bar{t}}{dt} = \frac{\varphi '(t) - A_{1}}{B_{1}}, $$

(57)

where $\varphi '(t)$ denotes the boundary value of $\varphi '(z)$. Substituting Eqs. (56) and (57) into Eq. (55) we obtain

$$ \psi (t) = D_{1}t + \frac{E_{1}\left ( \varphi (t) - A_{1}t - C_{1} \right )}{B_{1}} - \frac{\left ( \varphi (t) - A_{1}t - C_{1} \right )\left ( \varphi '(t) - A_{1} \right )}{B_{1}} + F_{1},\quad t \in L_{1}. $$

(58)

Based on Theorem 1, one may determine $\psi (z)$ in the entire $S$, from its boundary value (58) on $L_{1}$, as

$$ \psi (z) = D_{1}z + \frac{E_{1}\left ( \varphi (z) - A_{1}z - C_{1} \right )}{B_{1}} - \frac{\left ( \varphi (z) - A_{1}z - C_{1} \right )\left ( \varphi '(z) - A_{1} \right )}{B_{1}} + F_{1}, \quad z \in S. $$

(59)

Letting $z$ in Eq. (59) tend towards a certain boundary $L_{j}$ ($j \ne 1$), one obtains the boundary value $\psi (t)$ on $L_{j}$ as

$$ \psi (t) = D_{1}t + \frac{E_{1}\left ( \varphi (t) - A_{1}t - C_{1} \right )}{B_{1}} - \frac{\left ( \varphi (t) - A_{1}t - C_{1} \right )\left ( \varphi '(t) - A_{1} \right )}{B_{1}} + F_{1},\quad t \in L_{j}. $$

(60)

Using Eq. (54) one has

$$ \left . \textstyle\begin{array}{c} \varphi (t) = A_{j}t + B_{j}\bar{t} + C_{j}, \\ \varphi '(t) = A_{j} + B_{j}\frac{d\bar{t}}{dt}, \end{array}\displaystyle \right \} t \in L_{j}. $$

(61)

Substituting Eq. (61) into Eq. (60) yields

$$\begin{aligned} \psi (t) &= \left [ D_{1} + \frac{(A_{j} - A_{1})\left [ E_{1} - (A_{j} - A_{1}) \right ]}{B_{1}} \right ]t + \frac{B_{j}\left [ E_{1} - (A_{j} - A_{1}) \right ]}{B_{1}}\bar{t} \\ &\quad {}- \frac{B_{j}(C_{j} - C_{1})}{B_{1}}\frac{d\bar{t}}{dt} - \frac{B_{j}(A_{j} - A_{1})}{B_{1}}t\frac{d\bar{t}}{dt} - \frac{B_{j}^{2}}{B_{1}}\bar{t}\frac{d\bar{t}}{dt} \\ &\quad {}+ \frac{(C_{j} - C_{1})\left [ E_{1} - (A_{j} - A_{1}) \right ]}{B_{1}} + F_{1}, \quad t \in L_{j}. \end{aligned}$$

(62)

Comparing Eq. (62) with Eq. (55) we obtain an algebraic equation with respect to $t$ on $L_{j}$ as

$$\begin{aligned} &\left \{ D_{1} - D_{j} + \frac{(A_{j} - A_{1})\left [ E_{1} - (A_{j} - A_{1}) \right ]}{B_{1}} \right \} t + \left \{ \frac{B_{j}\left [ E_{1} - (A_{j} - A_{1}) \right ]}{B_{1}} - E_{j} \right \} \bar{t} \\ &\quad {}+ \frac{(C_{j} - C_{1})\left [ E_{1} - (A_{j} - A_{1}) \right ]}{B_{1}} + F_{1} - F_{j} \\ &\quad {}- \left [ \frac{B_{j}(A_{j} - A_{1})}{B_{1}}t + \left ( \frac{B_{j}^{2}}{B_{1}} - B_{j} \right )\bar{t} + \frac{B_{j}(C_{j} - C_{1})}{B_{1}} \right ]\frac{d\bar{t}}{dt} = 0, \quad t \in L_{j}. \end{aligned}$$

(63)

Since $L_{j}$ is a simple closed curve, we apply Theorem 3 to Eq. (63) and arrive at two cases. In the first case, $L_{j}$ is an ellipse, while in the second case, there is no specific limitation on the geometry of $L_{j}$ but $A_{j} = A_{1}$, $B_{j} = B_{1}$, $C_{j} = C_{1}$, $D_{j} = D_{1}$, $E_{j} = E_{1}$ and $F_{j} = F_{1}$.

For the first case, since the elliptical $L_{j}$ corresponds to a conformal mapping with finite terms, then, according to Theorem 4, there exists in $S$ no analytic function that meets the remote condition (53) and the boundary condition (54). This is however contradictory to the original assumption that $\varphi (z)$ exists.

For the second case, since $L_{j}$ is not fixed to a specific boundary curve, one has

$$ \left . \textstyle\begin{array}{c} A_{j} = A_{1}, B_{j} = B_{1}, C_{j} = C_{1} \\ D_{j} = D_{1}, E_{j} = E_{1}, F_{j} = F_{1} \end{array}\displaystyle \right \}, \quad j = 2,\ldots,n. $$

(64)

Consequently, Eq. (54) may be rewritten as

$$ \varphi (t) = A_{1}t + B_{1}\bar{t} + C_{1},\quad t \in L_{i}\ (i = 1,\ldots,n). $$

(65)

Here, as stated in Theorem 5, there does not exist any analytic function in $S$ that complies with Eqs. (53) and (65). This is contradictory to the original assumption that $\varphi (z)$ exists.

Up to this point, we have shown by contradiction that if $B_{i} \ne 0$ ($i=1,\dots ,n$), there do not exist analytic functions $\varphi (z)$ and $\psi (z)$ in $S$ that meet Eqs. (53)–(55). Consequently, in the design of multiple interacting inclusions achieving uniform stresses in an elastic plane under plane deformation, one must require $B_{i} = 0$ ($i=1,\dots ,n$) indicating that the uniform stress field inside each inclusion (of different shear modulus from that of the matrix) is necessarily hydrostatic.

4 Concluding Remarks

In the design of multiple (interacting) inclusions with uniform stresses in an elastic matrix, a general procedure is to first specify the uniform stress field inside each inclusion and then determine the shapes of the inclusions. In this paper we consider the problem of multiple inclusions enclosing uniform stresses in an infinite elastic plane under plane deformation for a uniform in-plane loading applied remotely. We establish a necessary criterion in specifying the uniform stress field inside each of the multiple inclusions that the uniform stress field should be hydrostatic if the inclusion has a shear modulus different from that of the matrix. We prove strictly that any system of multiple inclusions with uniform stresses does not exist if not complying with this criterion. The proof is based mainly on two theorems involving certain characteristics of the boundary values of a complex analytic function defined in an infinite multiply-connected domain. It is anticipated that the theorems and ideas presented in this paper may contribute to the further study of more challenging problems of multiple inclusions with uniform stresses (for example, those associated with an isotropic half-plane or an anisotropic whole plane).