On the Bending and Twisting of Rods with Misfit

Abstract

We derive a one-dimensional variational problem representing the elastic energy of a rod with misfit, starting from a nonlinear, three-dimensional elastic energy with nontrivial preferred strain. Our approach to dimension reduction is to find a Gamma-limit as the thickness of the rod tends to 0. The limiting energy is a quadratic function of the rates at which the rod bends and twists, and we give explicit expressions for the preferred curvature and twist in the special case of isotropic elastic moduli.

1 Introduction

There are many examples of rods in nature that deform due to misfit.¹ The best-known of these is a metallic bilayer, which bends when heated [35]. Recently, it has been proposed that misfit causes many rod-like or ribbon-like objects to twist or form helices; examples include some crystals [34] and plant tendrils such as Erodium awns [2]. We give a systematic discussion of the deformation of a rod due to misfit.

A rigorous treatment of rod theory as a $\varGamma$-limit of three-dimensional elasticity was given by Mora and Müller [27] and independently by Pantz [31]. The present work uses the same tools: we identify the elastic energy of a rod with misfit (Eq. (4)) by taking the $\varGamma$-limit of the elastic energy of a three-dimensional rod (Eq. (2)) as its thickness tends to 0. The resulting one-dimensional rod energy depends on the rod’s configuration through the rates at which it bends and twists. There is, in general, a non-zero preferred curvature and twist, which we express in terms of certain integrals over the two-dimensional cross section. We also find symmetry conditions which guarantee that the rod will not prefer to bend or twist.

We hope that this work is interesting and accessible to audiences in both applied mechanics and the calculus of variations. To that end, we include a brief orientation. Read linearly, this paper motivates the rod theory in Sects. 1.1 and 1.2, then precisely states the dimension reduction result (Theorem 1) and necessary definitions in Sects. 1.4–1.6. Section 2 continues with an informal derivation of the rod energy (Eq. (4)). The remainder of this paper, except for Sect. 7, analyzes the rod energy and provides examples. A theoretically-minded reader could instead read Sects. 1.4–2.1, and perhaps 1.3 and 2.2, then turn to the proof of Theorem 1 in Sect. 7. A practically-minded reader might instead focus on the examples, starting with a quick characterization of the limiting rod theory through Eq. (4) and Theorems 2 (the general case) and 3 (a more explicit version for materials with isotropic Hooke’s law).

1.1 Examples

We begin with a few examples of rods with misfit. Several of the experiments mentioned in this section deal with ribbons rather than rods, but find results that are present in rod theory. See Sect. 5.1 for some comments on the distinction between ribbons and rods.

The isotropic bilayer: We start with a well-known example. Consider a rod made of two different layers, bonded as shown in Fig. 1. Both layers prefer to expand isotropically when heated, but by different amounts. The two layers cannot assume their stress-free deformation because they must meet on the boundary, but one layer can expand more than the other if the rod bends. Of course, each cross section will deform slightly, and that there can be boundary effects. It is well known, both theoretically and experimentally, that the rod bends.

Fig. 1

The isotropic bilayer

Motivated by the application to bimetallic thermometers, Timoshenko calculated the preferred curvature of the isotropic bilayer using linear elasticity [35]. We reproduce this classical result in Sect. 6.1 using the framework of this paper, except that unlike Timoshenko we assume that the elastic moduli are the same in both layers. This example leads to a restricted class of deformations in that the bilayer bends, but it does not twist. This is a general pattern; Theorem 3 implies that a rod made out of an isotropic material will never twist in response to isotropic misfit.

The diagonally prestrained bilayer: In view of the previous example, it is natural to ask whether misfit can also give rise to twist. The answer is yes. We outline a simple example of twist caused by misfit, and defer a systematic treatment to Sect. 6.2. Several groups performed closely related experiments, motivated by the study of crystals [37], the opening of seed pods [3], and tunable helical ribbons [6].

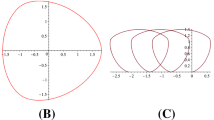
Consider two elastic sheets, stretched in orthogonal directions and glued together. Now suppose that a rod is cut from the sheets along an angle $\theta$ to the principal stretches, as shown in Fig. 2. For generic $\theta$ the rod twists and bends uniformly (Fig. 3b). If $\theta =0$ or $\theta =\pi /2$ then it bends without twisting (Fig. 3c), and if $\theta =\pi /4$ it twists without bending (Fig. 3a).

Fig. 2

The construction of the anisotropic bilayer

Fig. 3

Configurations of the anisotropic bilayer

Plant tendrils: Many plants have long, thin helical tendrils. It has been conjectured that these deform due to swelling or contraction in parts of the tendril. Aharoni et al. correctly predicted the shape of long, thin cells in Erodium awns using a theory closely related to this work [2].

Quartz: ² Crystals are sometimes thin in one or two dimensions. Remarkably, although the crystal lattice seems to prefer polyhedra, crystalline rods sometimes spontaneously twist [34]. We focus on naturally occurring $\alpha$-quartz, and on the question of whether its intrinsic twist can be explained by modeling the crystal as a linearly elastic body with misfit. The dimension reduction discussed in the present work challenges this idea: there should be no intrinsic twist or curvature for a rod with the misfit and elastic stiffness tensor typical of quartz. See Sect. 6.5 for details.

Quartz is far from the only crystal that can resemble a twisted rod, and our description of quartz relies crucially on two conditions: that the crystal lattice has twofold rotational symmetry about the long axis of the crystal, and that the misfit is caused by variations in the preferred lattice lengths.

1.2 An Overview of the Problem

Classically, one would find the energy required to twist or bend an elastic rod by minimizing the linear elastic energy of a cylinder within an appropriate ansatz [4, 24]. The resulting energy, in the simplest setting, is of the form

$$ E_{\mathrm{rod}}= \int_{0}^{L}c_{1}\omega^{2}(x_{1}) + c_{2}\kappa _{2}^{2}(x_{1}) + c_{3} \kappa_{3}^{2}(x_{1}) dx_{1}, $$

(1)

where the rates of twisting and bending at position $x_{1}$ are denoted by $\omega (x_{1})$ and $\kappa_{j}(x_{1})$, $j=2, 3$. The purpose of the linearly elastic energy minimizations mentioned above is to identify the constants $c_{j}$, which requires knowledge of how the cross sections warp in response to curvature or twist. This approach gives an algorithm to compute the energy, but it is unsatisfying if viewed as a justification of Eq. (1): it describes locally how each cross section should deform, but it does not exhibit an ansatz and does not explicitly use the fact that the thickness is assumed to be small. Even using linear elasticity is questionable: the strains are small but the displacements large.

One approach is to define a warping function separately for each cross section via the linear elastic energy minimization mentioned above, then combine these to get a full ansatz. One can then use Taylor’s Theorem to estimate the nonlinear elastic energy in terms of only the linear strain, which takes advantage of the assumption that the thickness is small. Of course, for this to be meaningful the ansatz must be chosen correctly. A more modern approach, called $\varGamma$-convergence, asks also that we show that the ansatz achieves the minimum energy to leading order in thickness. We use $\varGamma$-convergence.

One feature of this framework is that it requires that we be precise about what we mean by “the limit as the thickness vanishes”. We mean that we consider an elastic cylinder with length parameterized by $z_{1}\in (0,L)$ and cross section parameterized by ${\boldsymbol{z}} _{\mathrm{cs}}= (z_{2}, z_{3})\in hS$. Here $h$, which represents the thickness, has units of length. We send $h$ to 0, holding fixed the curvature and twist, so in order to apply the present rod theory one should have $h \ll 1/\kappa$ and $h \ll 1/\omega$.

In order to get a consistent theory we must also scale the linear elastic misfit, denoted here by $\boldsymbol{{m}}^{(h)}( \boldsymbol{z})$, with the thickness. Heuristically, we expect that bending the centerline with curvature $\kappa$ should result in strains of $O(h\kappa )$, so $\boldsymbol{{m}}^{(h)}$ should scale like $h$. We allow the misfit to depend on $z_{1}$ (i.e. to vary along the length of the rod), but it must vary slowly. Precisely, we consider misfit of the form

$$\boldsymbol{{m}}^{(h)}(z_{1}, {\boldsymbol{z}}_{\mathrm{cs}}) = h \boldsymbol{{m}}(z_{1}, {\boldsymbol{z}}_{\mathrm{cs}}/h) \quad\mbox{for } z_{1}\in (0,L), {\boldsymbol{z}}_{\mathrm{cs}}\in hS. $$

With slight abuse of notation we refer to $\boldsymbol{{m}}$ as the as the misfit. Notice however, that it has units of length inverse, whereas the physical misfit is a strain and therefore dimensionless. We consider the limit $h\to 0$, so the physical misfit must be small.

1.3 Methods and Related Results

We are not aware of any prior derivation, rigorous or otherwise, of a rod theory with general misfit.³ The one presented here is variational in character: we show that a one-dimensional rod energy with non-zero preferred curvature and twist arises as the $\varGamma$-limit [9] of a three-dimensional elastic energy with misfit.⁴ $\varGamma$-convergence is a familiar tool in dimension reduction, and has been used to justify a rich class of one-dimensional [1, 27, 28] and two-dimensional [14, 15, 20] energies for thin elastic structures. The direct analogue of the present work without misfit was given independently by Mora and Müller [27] and Pantz [31].

We hasten to add that there is some general work on thin structures with misfit. Kupferman and Solomon used a modified $\varGamma$-limit to identify the elastic energy of an $m$-dimensional manifold with a non-Euclidean metric [19], which is specialized to rods in [2]. Their metric and our misfit play similar roles, but in the context of rods our discussion is more general. In fact (as we show in Sect. 5.2), the Kupferman-Solomon theory, when specialized to rods, is equivalent to our theory with a misfit that depends linearly on the cross-sectional variables.

Plates with misfit have received additional attention. Schmidt showed that multilayers—plates with piecewise constant misfit depending only on the thin variable—can be modeled with an energy similar to that of an inextensible plate, but with non-zero preferred second fundamental form [33]. Assuming instead that the misfit does not depend on the thin direction there are analogues to both Kirchhoff [23] and von Kármán [21, 22] plate theories.

Classically, rod theories have often been justified using force-balance. Saint-Venant found a twelve-dimensional set of solutions to the equations of force balance for an infinite, linearly elastic prism,⁵ which he called the reference solutions. He conjectured that the displacement of a long but finite prism approaches the reference solutions far from the ends. Mielke used center manifold theory in a Banach space to prove Saint-Venant’s conjecture in the setting of nonlinear elasticity [25, 26], assuming only that the strains are uniformly small. This was motivated in part by Ericksen’s observation [11] that, in linear elasticity, Saint-Venant’s reference solutions are precisely the solutions with bounded strain.

It is natural to ask how dimension reduction via $\varGamma$-convergence is related to the work of Mielke. $\varGamma$-convergence, together with a compactness condition, implies that minima of the three-dimensional energy converge to minima of the limiting energy, which makes it useful when studying energy minimization. The critical points of an energy functional represent force-balance, and in general $\varGamma$-convergence does not imply that critical points converge. However, Mora and Müller [29] and Davoli and Mora [10] showed that critical points indeed converge for a hierarchy of rod energies without misfit. That partially closed the gap between force-balance and energy minimization.

After this paper was completed, we learned about simultaneous and independent work by Cicalese, Ruf, and Solombrino on essentially the same problem [8]. Our work and theirs overlap: in particular, a version of Theorem 1 is found in [8] as well, and we both study in some detail the case of the bilayer. However, there are also significant differences. We show additional properties of the reduced energy, and compare our results with different parts of the literature. The paper [8] covers local as well as global minimizers, a topic that we do not address.

1.4 Notation

In this work we will use the convention that $(\nabla \boldsymbol{y})_{ij} = \partial_{j} y_{i}$. Matrices will sometimes be written in block notation; if so the blocks will be separated by solid lines.

It will be useful to distinguish between the coordinate $x_{1}$ along the rod and the coordinates ${\boldsymbol{x}}_{\mathrm{cs}} = (x_{2}, x_{3})$ in the cross section. We extend this notation in various self-explanatory ways, for example by using ${\boldsymbol{\beta }} _{\mathrm{cs}}= (\boldsymbol{\beta }_{2}, \boldsymbol{\beta }_{3})$ for other vectors (typically representing linearly elastic displacements of the cross section) and ${\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} = ( \partial_{2}\boldsymbol{\beta }, \partial_{3} \boldsymbol{\beta } )$. Similarly, for matrices $\boldsymbol{{m}}\in \mathbb{R}^{3\times 3}$ we will use $\boldsymbol{{m}}_{\mathrm{cs},\mathrm{cs}}$ to denote the lower right 2-by-2 block and $\boldsymbol{m}_{\mathrm{cs},1}= (m_{21}, m_{31})$.

1.5 The Three-Dimensional Energy

We start with a generic elastic energy with misfit, defined on a cylindrical reference domain $\varOmega_{h} = (0,L)\times hS$. We will take the limit as the thickness $h$ tends towards 0. The cross section $S$ is an open, bounded, connected subset of $\mathbb{R}^{2}$ with Lipschitz boundary. By translating the reference domain we may assume that $S$ is centered at the origin: $\int_{S} {\boldsymbol{x}}_{ \mathrm{cs}} d{\boldsymbol{x}}_{\mathrm{cs}} = 0$. The energy is defined for $y\in W^{1,2}(\varOmega_{h},\mathbb{R}^{3})$ by

$$E^{(h)} (\boldsymbol{y}) = \frac{1}{h^{4}} \int_{\varOmega_{h}} W \bigl( \nabla \boldsymbol{y}(\boldsymbol{z}) \boldsymbol{{M}}_{h}^{-1}(z_{1}, z_{2}/h, z_{3}/h) \bigr) d\boldsymbol{z}. $$

By rescaling $\boldsymbol{x}= (z_{1}, z_{2}/h, z_{3}/h)$ we write the energy as

$$ E^{(h)} (\boldsymbol{y}) = \frac{1}{h^{2}} \int_{\varOmega } W \bigl( \nabla_{h} \boldsymbol{y}( \boldsymbol{x}) \boldsymbol{{M}}_{h}^{-1} ( \boldsymbol{x} ) \bigr) $$

(2)

with the notation $\nabla_{h} \boldsymbol{f} = ( \partial_{1} \boldsymbol{f}| \frac{1}{h}\partial_{2} \boldsymbol{f}| \frac{1}{h}\partial_{3} \boldsymbol{f} )$ and $\varOmega = \varOmega _{1}$.

The elastic energy density $W\in C^{0}(\mathbb{R}^{3\times 3}, [0, \infty ])$ satisfies the standard conditions:

• 1. Frame indifference: $W(\boldsymbol{{R}}\boldsymbol{{F}}) = W( \boldsymbol{{F}})$ for all $\boldsymbol{{F}}\in \mathbb{R}^{3\times 3}$ and $\boldsymbol{{R}}\in \operatorname{SO}(3)$.

• 2. Stress-free: $W = 0$ on $\operatorname{SO}(3)$.

• 3. Coerciveness: $W(\boldsymbol{{F}}) \geq \operatorname{dist}^{2}( \boldsymbol{{F}},\operatorname{SO}(3))$.

• 4. Regularity: $W\in C^{2}$ in a neighborhood of $\operatorname{SO}(3)$.

We use $\mathcal{Q}_{3}$ to denote the associated linear elastic energy density: $\mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) } = \frac{1}{2}W''(\operatorname{Id})(\boldsymbol{{F}},\boldsymbol{{F}})$.

We assume that the preferred strain is of the form $\boldsymbol{{M}} _{h}(\boldsymbol{x}) = \operatorname{Id}+ h\boldsymbol{{m}}( \boldsymbol{x})$ for $\boldsymbol{{m}}\in L^{\infty }(\mathrm{Sym}(3))$. As mentioned in Sect. 1.2, the scaling of $\boldsymbol{{M}}_{h}(\boldsymbol{x})$ is chosen such that it produces $O(1)$ bend or twist in the limit as $h\to 0$.

1.6 The One-Dimensional Energy

In the limit $h\to 0$, we will find an energy for an inextensible rod depending only on the curvature and twist. It is not enough to know the position of the midline $\tilde{\boldsymbol{y}}$, which must be a unit speed curve from $(0,L)$ to $\mathbb{R}^{3}$ (the rod is indexed by the long variable $x_{1}$). In order to define the twist we also need to know the orientation of each cross section. The energy depends on the material frame (Fig. 4), a function $\boldsymbol{{R}}:(0,L)\to \operatorname{SO}(3)$ such that the first column is the tangent to the midline: $\boldsymbol{r}_{1}(x_{1}) = \frac{d \tilde{\boldsymbol{y}}}{dx_{1}}(x_{1})$. The second and third columns, which represent the orientation of the cross section, are normal to $\boldsymbol{r}_{1}$.

Fig. 4

A sketch of the material frame. The midline $\tilde{\boldsymbol{y}}$ is in solid black. The columns of $\boldsymbol{{R}}$, controlling the orientation of the cross section, are drawn with thick blue arrows for several values of $x_{1}$ (Color figure online)

The skew-symmetric matrix $\boldsymbol{{A}}= \boldsymbol{{R}}^{T} \partial_{1} \boldsymbol{{R}}$ controls the bending (in the $x_{2}$ and $x_{3}$ directions) of the rod as well as the twist. The one-dimensional energy derived here is a function of $\boldsymbol{{A}}$ alone. We will sometimes write $\boldsymbol{{A}}$ in terms of the twist $\omega$ and bending $\boldsymbol{\kappa }= ( \kappa_{2}, \kappa_{3})$:

$$ \boldsymbol{{A}}(\omega ,\boldsymbol{\kappa }) = \left(\textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & -\kappa_{2} & -\kappa_{3} \\ \kappa_{2} & 0 & -\omega \\ \kappa_{3} & \omega & 0 \end{array}\displaystyle \right) . $$

(3)

The limiting energy involves the following quantities, defined in Sect. 2.1:

• ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}\in L^{2}((0,L), \operatorname{Skew}(3))$ measures the preferred bending and twisting at each cross section. We will sometimes use the notation $\boldsymbol{{A}}({\omega }^{\boldsymbol{{m}}},{\boldsymbol{\kappa }} ^{\boldsymbol{{m}}}) = {\boldsymbol{{A}}}^{\boldsymbol{{m}}}$.

• $\mathcal{Q}_{1}: \operatorname{Skew}(3)\to \mathbb{R}$ is a positive definite quadratic form.

• $E_{0}\in \mathbb{R}$, $E_{0}\ge 0$ is a constant measuring the incompatibility of the misfit with strains.

Section 3 gives more computationally useful characterizations of $\mathcal{Q}_{1}$ and ${\boldsymbol{{A}}}^{ \boldsymbol{{m}}}$ in Theorem 2 (the general case) and Theorem 3 (isotropic rods).

Definition 1

(Limiting Energy Functional)

We define $E: W^{1,2}(\varOmega ,\mathbb{R} ^{3\times 3})\to [0,\infty ]$ by

$$ E(\boldsymbol{{R}}) = \textstyle\begin{cases} E_{0}+ \int_{0}^{L} \mathcal{Q}_{1}{ ( \boldsymbol{{R}}^{T} \partial_{1} \boldsymbol{{R}}(x_{1})-{\boldsymbol{{A}}}^{ \boldsymbol{{m}}}(x_{1}) ) } dx_{1} &\mbox{if }\boldsymbol{{R}}\mbox{ is admissible,} \\ \infty &\mbox{otherwise,} \end{cases} $$

(4)

where $\boldsymbol{{R}}\in W^{1,2}(\varOmega ,\mathbb{R}^{3\times 3})$ is admissible if and only if $\boldsymbol{{R}}(\boldsymbol{x})\in \operatorname{SO}(3)$ and $\boldsymbol{{R}}(\boldsymbol{x})$ depends only on $x_{1}$.

Section 2 gives an informal derivation of the one-dimensional energy via minimization within an ansatz. Theorem 1 rigorously derives the one-dimensional energy equation (4) from the three-dimensional energy equation (2) in the small-thickness limit.

Theorem 1

($\varGamma$-Convergence)

The functionals $E^{(h)}$ $\varGamma$-converge to the functional $E$ as $h\to 0$ in the following sense:

• 1. (liminf inequality) For any positive sequence $h_{j}\to 0$ and corresponding deformations $\boldsymbol{y}^{(h_{j})}$ in $W^{1,2}( \varOmega ,\mathbb{R}^{3})$ such that $\nabla_{h} \boldsymbol{y}^{(h_{j})} \to \boldsymbol{{R}}$ strongly in $L^{2}$,

  $$E(\boldsymbol{{R}}) \leq \liminf_{j\to \infty } E^{(h_{j})}\bigl( \boldsymbol{y}^{(h_{j})}\bigr). $$

• 2. (limsup inequality) For any positive sequence $h_{j}\to 0$ and for every $\boldsymbol{{R}}\in L^{2}(\varOmega ,\mathbb{R}^{3\times 3})$ there exists a sequence $\boldsymbol{y}^{(h_{j})}$ in $W^{1,2}(\varOmega ,\mathbb{R} ^{3})$ such that $\nabla_{h} \boldsymbol{y}^{(h_{j})} \to \boldsymbol{{R}}$ strongly in $L^{2}$,

  $$E(\boldsymbol{{R}}) \geq \limsup_{j\to \infty } E^{(h_{j})}\bigl( \boldsymbol{y}^{(h_{j})}\bigr). $$

The proof is deferred to Sect. 7.

2 Minimization Within an Ansatz

2.1 Definitions

The one-dimensional energy $E$ (Eq. (4)) depends on several quantities, which we now define. These definitions are geared towards a formal ansatz (Sect. 2.2) that achieves the correct energy. Theorem 2 gives computationally explicit definitions of $\mathcal{Q}_{1}$ and ${\boldsymbol{{A}}}^{ \boldsymbol{{m}}}$. Equations (8) and (9) of Sect. 2.2 give a concise but more opaque definition of $E$.

Definition 2

(Admissible Strains)

For $\boldsymbol{{A}}\in \operatorname{Skew}(3)$, we define the set

$$\mathcal{E}(\boldsymbol{{A}}) =\left. \left\{ \operatorname{sym} \left( \xi \boldsymbol{{e}}_{1} + \boldsymbol{{A}} \left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| { \nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} \right) : \xi \in \mathbb{R}, \boldsymbol{\beta }\in W^{1,2}\bigl(S,\mathbb{R}^{3}\bigr) \right\} $$

and the vector space $\mathcal{E}= \cup_{\boldsymbol{{A}}\in \operatorname{Skew}(3)}\mathcal{E}( \boldsymbol{{A}})$. We associate to $L^{2}(S,\mathrm{Sym}(3))$ the inner product $\langle \boldsymbol{{F}},\boldsymbol{{G}} \rangle _{W''(\operatorname{Id})} = \int_{S} \langle \boldsymbol{{F}}, W''( \operatorname{Id})\boldsymbol{{G}}\rangle d{\boldsymbol{x}}_{ \mathrm{cs}}$ with the inherited norm $\lVert \cdot \rVert _{W''(\operatorname{Id})}$. Note that ℰ is a closed subspace of $L^{2}(S,\mathrm{Sym}(3))$ with respect to this norm.

Remark 1

(Uniqueness of $\boldsymbol{{A}}$, $\boldsymbol{\beta }$ and $\xi$)

Notice that a strain $\boldsymbol{{F}}\in \mathcal{E}$ does not correspond to a unique $\boldsymbol{\beta }$. However, it does correspond to a unique skew-symmetric matrix $\boldsymbol{{A}}$. To see this more clearly, we write out $\boldsymbol{{F}}$ in block form:

$$\boldsymbol{{F}}= \left ( \renewcommand{\arraystretch}{1.5} \textstyle\begin{array}{c|c} \xi - \boldsymbol{\kappa }\cdot {\boldsymbol{x}}_{\mathrm{cs}} & \frac{1}{2}(\omega {\boldsymbol{x}}_{\mathrm{cs}}^{\perp }+ {\nabla } _{\mathrm{cs}}{\beta_{1}}) \\ \hline \frac{1}{2}(\omega {\boldsymbol{x}}_{\mathrm{cs}}^{\perp }+ {\nabla }_{\mathrm{cs}}{\beta_{1}}) & \operatorname{sym}{\nabla }_{ \mathrm{cs}}{{\boldsymbol{\beta }}_{\mathrm{cs}}} \end{array}\displaystyle \renewcommand{\arraystretch}{1} \right ) . $$

• 1. $\xi$, $\boldsymbol{\kappa }$ and $\omega$ are uniquely associated to $\boldsymbol{{F}}\in \mathcal{E}$.

• 2. $\beta_{1}$ is unique up to an additive constant.

• 3. $\boldsymbol{{F}}$ involves ${\boldsymbol{\beta }}_{\mathrm{cs}}= ( \boldsymbol{\beta }_{2},\boldsymbol{\beta }_{3})$ only through $\operatorname{sym}{\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }}_{ \mathrm{cs}}$. Therefore ${\boldsymbol{\beta }}_{\mathrm{cs}}$ is uniquely defined modulo infinitesimal rigid motions.

Definition 3

(Decomposition of $\boldsymbol{{m}}$)

In this definition we hold $x_{1}$ fixed. By orthogonally projecting $\boldsymbol{{m}}$ onto ℰ, we see that there exist ${A}^{\boldsymbol{{m}}}(x_{1})$, ${\xi }^{\boldsymbol{{m}}}(x_{1})$ and ${\boldsymbol{\beta }}^{\boldsymbol{{m}}}(\boldsymbol{x})$ such that

$$ \boldsymbol{{m}}(\boldsymbol{x}) = \boldsymbol{{m}}_{\mathcal{E}}( \boldsymbol{x}) + \boldsymbol{{m}}_{\perp }(\boldsymbol{x}) = \operatorname{sym} \left( {\xi }^{\boldsymbol{{m}}} \boldsymbol{{e}} _{1} + {\boldsymbol{{A}}}^{\boldsymbol{{m}}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{{\boldsymbol{\beta }}^{ \boldsymbol{{m}}}} \right) + \boldsymbol{{m}}_{\perp }(\boldsymbol{x}) $$

and $\langle \boldsymbol{{m}}_{\perp }(x_{1}, {\boldsymbol{x}} _{\mathrm{cs}} ),\boldsymbol{{F}} \rangle _{W''( \operatorname{Id})} = 0$ for all $\boldsymbol{{F}}\in \mathcal{E}$ and a.e. $x_{1}$. ${A}^{\boldsymbol{{m}}}$, ${\xi }^{\boldsymbol{{m}}}$ and ${\boldsymbol{\beta }}^{\boldsymbol{{m}}}$ are in $L^{2}$ (by boundedness of the projection operator). By Remark 1, we can also insist that $\int_{S} {\boldsymbol{\beta }}^{\boldsymbol{{m}}}(x_{1},{\boldsymbol{x}} _{\mathrm{cs}} ) d{\boldsymbol{x}}_{\mathrm{cs}} = 0$ and $\int_{S} \operatorname{skew}{\nabla }_{\mathrm{cs}}{{\boldsymbol{\beta }}_{ \mathrm{cs}}}^{\boldsymbol{{m}}}(x_{1},{\boldsymbol{x}}_{\mathrm{cs}} )d{\boldsymbol{x}}_{\mathrm{cs}} = 0$. With these conditions, ${\boldsymbol{\beta }}^{\boldsymbol{{m}}}$ is uniquely defined.

Let $\mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) } = \frac{1}{2}W''( \operatorname{Id})(\boldsymbol{{F}},\boldsymbol{{F}})$ denote the three-dimensional linear elastic energy density. We define a corresponding one-dimensional energy density $\mathcal{Q}_{1}$ and the limiting energy functional.

Definition 4

(The One-Dimensional Energy Density)

Let $\mathcal{Q}_{1}: \operatorname{Skew}(3)\to \mathbb{R}$ be defined by

$$ \mathcal{Q}_{1}(\boldsymbol{{A}}) = \min_{\boldsymbol{{F}}\in \mathcal{E}(\boldsymbol{{A}})} \int_{S} \mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) } d{ \boldsymbol{x}} _{\mathrm{cs}} , $$

(5)

and define $E_{0}= \int_{\varOmega }\mathcal{Q}_{3}{ ( \boldsymbol{{m}}_{\perp } ) } d\boldsymbol{\boldsymbol{x}}$.

In the following remark we check that $\mathcal{Q}_{1}$ agrees with the one-dimensional energy density for a rod without misfit, which was found in [27]. This amounts to showing that the minimal $\boldsymbol{{F}}$ in Definition 4 satisfies $\xi =0$. The Euler-Lagrange equations associated to $\mathcal{Q}_{1}$ are explicitly written in [27] Remark 3.4, and specialized in Remarks 3.5 (isotropic rods) and 3.6 (circular cross sections).

Remark 2

(Some Properties of the Optimal $\boldsymbol{{F}}$ in the Definition of $\mathcal{Q}_{1}$)

Let $\boldsymbol{F}$ minimize $\int_{S} \mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) }d{\boldsymbol{x}}_{\mathrm{cs}}$ among $\mathcal{E}(\boldsymbol{{A}})$ as in Eq. (5). We write

$$\boldsymbol{{F}}= \operatorname{sym} \left( \xi \boldsymbol{{e}}_{1} + \boldsymbol{{A}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{ \boldsymbol{\beta }} \right) . $$

Then $\boldsymbol{{F}}$ has $\xi = 0$ and $\int_{S}{\nabla }_{ \mathrm{cs}}\boldsymbol{\beta }d{\boldsymbol{x}}_{\mathrm{cs}} = 0$.

Proof

The first variation of $\int_{S}\mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) } d{\boldsymbol{x}}_{\mathrm{cs}}$ with respect to $\xi$ and $\boldsymbol{\beta }$ must vanish. This condition reads

$$0 = \int_{S} \left\langle \operatorname{sym} \left({\xi}\boldsymbol{e}_{1} + {\boldsymbol{A}} \left.\left(\textstyle\begin{array}{c} 0\\ x_{2}\\ x_{3} \end{array}\displaystyle \right)\right| {\nabla}_{\mathrm{cs}}{\boldsymbol{\beta}}(\boldsymbol{x}_{\mathrm{cs}}) \right), W''(\operatorname{Id}) \operatorname{sym}\bigl(\zeta\boldsymbol{e}_{1} \big| {\nabla}_{\mathrm{cs}}\eta(\boldsymbol{x}_{\mathrm{cs}})\bigr) \right\rangle d \boldsymbol{x}_{\mathrm{cs}} $$

for any $\eta\in W^{1,2}(S,\mathbb{R}^{3})$ and $\zeta \in \mathbb{R}$. By considering $\eta$ linear, we see that for any matrix $\boldsymbol{{G}}\in \mathrm{Sym}(3)$,

$$0 = \biggl\langle \int_{S}\operatorname{sym} ( {\xi } \boldsymbol{{e}}_{1} + {\boldsymbol{{A}}} {\boldsymbol{x}}_{ \mathrm{cs}} | {\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} ) d{\boldsymbol{x}}_{\mathrm{cs}} , W''(\operatorname{Id}) \boldsymbol{{G}} \biggr\rangle . $$

The elastic stiffness tensor $W''(\operatorname{Id})$ maps $\mathrm{Sym}(3)$ onto itself, so $W''(\operatorname{Id}) \boldsymbol{{G}}$ is an arbitrary matrix in $\mathrm{Sym}(3)$. Thus the integrand must vanish. Using our convention that $\int_{S} {\boldsymbol{x}} _{\mathrm{cs}} d{\boldsymbol{x}}_{\mathrm{cs}} = 0$, we get

$$0 = \int_{S}\operatorname{sym} \left( \xi \boldsymbol{{e}}_{1} + \boldsymbol{{A}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{ \boldsymbol{\beta }} \right) d{\boldsymbol{x}} _{\mathrm{cs}} = \operatorname{sym} \biggl( |S|\xi \boldsymbol{{e}}_{1} \bigg| \int_{S}{\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }}d{ \boldsymbol{x}} _{\mathrm{cs}} \biggr) . $$

By considering the 11 component of this matrix it follows that $\xi = 0$. The other components show that $\int_{S} \operatorname{sym} ( 0|{\nabla }_{\mathrm{cs}} \boldsymbol{\beta } ) d{\boldsymbol{x}}_{\mathrm{cs}} = 0$. The condition that $\int_{S} \operatorname{skew}{\nabla }_{\mathrm{cs}} {\boldsymbol{\beta }}_{\mathrm{cs}}d{\boldsymbol{x}}_{\mathrm{cs}} = 0$ completes the proof. □

This technique can be used to compute the preferred extension ${\xi }^{\boldsymbol{{m}}}$, along with a few other projections of $\boldsymbol{{m}}_{\mathcal{E}}$.

Remark 3

(Some Properties of $\boldsymbol{{m}}_{\mathcal{E}}$)

The following equations hold a.e. in $x_{1}$:

• ${\xi }^{\boldsymbol{{m}}}(x_{1}) = \frac{1}{|S|}\int_{S} m_{11}( \boldsymbol{x}) d{\boldsymbol{x}}_{\mathrm{cs}}$,

• $\int_{S} {\nabla }_{\mathrm{cs}}\boldsymbol{\beta }_{\mathrm{cs}} ^{\boldsymbol{{m}}}(\boldsymbol{x}) d{\boldsymbol{x}}_{\mathrm{cs}} = \int_{S} \boldsymbol{{m}}_{\mathrm{cs},\mathrm{cs}}(\boldsymbol{x}) d {\boldsymbol{x}}_{\mathrm{cs}}$, and

• $\int_{S} {\nabla }_{\mathrm{cs}}\beta_{1}^{\boldsymbol{{m}}}( \boldsymbol{x}) d{\boldsymbol{x}}_{\mathrm{cs}} = 2\int_{S} \boldsymbol{m}_{\mathrm{cs},1}(\boldsymbol{x}) d{\boldsymbol{x}}_{ \mathrm{cs}}$.

The proof is essentially identical to that of Remark 2, and is therefore omitted.

2.2 The Ansatz

The proof of the main result, Theorem 1, is deferred to Sect. 7. Here we present a formal ansatz which, ignoring regularity issues, gives the correct limiting energy.

Given a frame $\boldsymbol{{R}}(x_{1})\in \operatorname{SO}(3)$ we define

$$ \boldsymbol{y}^{(h)}(\boldsymbol{x}) = \tilde{ \boldsymbol{y}}(x_{1}) + h\bigl(\boldsymbol{t}(x_{1}) + x_{2} \boldsymbol{r}_{2}(x_{1}) + x_{3} \boldsymbol{r}_{3}(x_{1})\bigr) + h^{2} \boldsymbol{{R}}\boldsymbol{\beta }( \boldsymbol{x}). $$

(6)

Here $\boldsymbol{t}(x_{1})$ and $\boldsymbol{\beta }(\boldsymbol{x})$ are $\mathbb{R}^{3}$-valued functions to be determined, and $\tilde{\boldsymbol{y}}(x_{1}) = \int_{0}^{x_{1}} \boldsymbol{r}_{1}(s)ds$. Let $\boldsymbol{{A}}=\boldsymbol{{R}}^{T} \partial_{1} \boldsymbol{{R}}$. As previously mentioned, the entries of $\boldsymbol{{A}}$ control the bending and twist of the rod as one moves along the midline (see Eq. (3)). $\xi \boldsymbol{{e}}_{1}=\boldsymbol{{R}}^{T}\partial_{1} \boldsymbol{t}$ measures the infinitesimal stretching, and $\boldsymbol{\beta }$ controls the slight deformation of the cross section. We compute the gradient:

$$ \boldsymbol{{R}}^{T}\nabla_{h} \boldsymbol{y}^{(h)}(\boldsymbol{x}) = \operatorname{Id}+ h \left( \xi \boldsymbol{{e}}_{1} + \boldsymbol{{A}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| { \nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} \right) + O\bigl(h ^{2} \bigr). $$

(7)

Therefore the energy is, at least formally, given to leading order in $h$ by

$$ E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} (\boldsymbol{{A}}, \boldsymbol{ \beta },\xi ) = E^{(h)} \bigl(\boldsymbol{y}^{(h)}\bigr) = \int_{\varOmega }\mathcal{Q}_{3}{ \left( \operatorname{sym} \left( \xi \boldsymbol{{e}}_{1} + \boldsymbol{{A}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} \right) - \boldsymbol{{m}}(\boldsymbol{x}) \right) } d \boldsymbol{\boldsymbol{x}}, $$

(8)

where $\mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) } = \frac{1}{2}W''( \operatorname{Id})(\boldsymbol{{F}},\boldsymbol{{F}})$ is the linear elastic energy density associated with $W$.

The energy $E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} (\boldsymbol{{A}}, \boldsymbol{\beta },\xi )$ is closely connected to our final energy $E(\boldsymbol{{R}})$. Notice in particular that

$$ E(\boldsymbol{{R}}) = \min_{\boldsymbol{\beta },\xi } E^{\mathrm{ansatz}} _{\boldsymbol{{m}}} \bigl( \boldsymbol{{R}}^{T} \partial_{1} \boldsymbol{{R}}, \boldsymbol{\beta }, \xi \bigr) , $$

(9)

and that $E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} (\boldsymbol{{A}}, \boldsymbol{\beta },\xi )$ is minimized by $({\boldsymbol{{A}}}^{ \boldsymbol{{m}}}, {\boldsymbol{\beta }}^{\boldsymbol{{m}}}, {\xi } ^{\boldsymbol{{m}}})$. To make this explicit, we plug in $\boldsymbol{{m}}= \boldsymbol{{m}}_{\mathcal{E}}+ \boldsymbol{{m}} _{\perp }$ and minimize over $\boldsymbol{\beta }$ and $\xi$.

Using $\tilde{\xi } = \xi -{\xi }^{\boldsymbol{{m}}}$, and similarly for $\tilde{\boldsymbol{{A}}}$ and $\tilde{\boldsymbol{\beta }}$, the energy is

$$\begin{aligned} \lim_{h\to 0}E^{(h)} \bigl(\boldsymbol{y}^{(h)} \bigr) =& \int_{\varOmega } \mathcal{Q}_{3}{ \left( \operatorname{sym} \left( \tilde{\xi } \boldsymbol{\psi }+ \tilde{\boldsymbol{{A}}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{\tilde{\boldsymbol{\beta }}} \right) - \boldsymbol{{m}}_{\perp }(\boldsymbol{x}) \right) } d \boldsymbol{\boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{ \left( \operatorname{sym} \left( \tilde{\xi }\boldsymbol{{e}}_{1} + \tilde{\boldsymbol{{A}}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{\tilde{\boldsymbol{\beta }}} \right) \right) } + \mathcal{Q}_{3}{ ( \boldsymbol{{m}}_{\perp } ) } d\boldsymbol{\boldsymbol{x}}. \end{aligned}$$

By choosing $\boldsymbol{\beta }$ and $\xi$ optimally and choosing $E_{0}= \int_{\varOmega }\mathcal{Q}_{3}{ ( \boldsymbol{{m}}_{\perp } ) } d\boldsymbol{\boldsymbol{x}}$, we get that

$$\lim_{h\to 0}E^{(h)} \bigl(\boldsymbol{y}^{(h)} \bigr) = E_{0}+ \int_{0}^{L} \mathcal{Q}_{1} \bigl( \boldsymbol{{A}}(x_{1})-{\boldsymbol{{A}}}^{ \boldsymbol{{m}}}(x_{1}) \bigr) dx_{1}. $$

3 Explicit Computation of $\mathcal{Q}_{1}$ and ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$

The one-dimensional energy

$$E(\boldsymbol{y}) = E_{0}+ \int_{0}^{L}\mathcal{Q}_{1}{ \bigl( \boldsymbol{{R}}(x_{1})^{T}\partial_{1} \boldsymbol{{R}}(x_{1}) - {\boldsymbol{{A}}}^{\boldsymbol{{m}}}(x_{1}) \bigr) }dx_{1} $$

is defined in Sect. 2.1. The definition of ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$ is computationally cumbersome: $({\boldsymbol{{A}}}^{\boldsymbol{{m}}},{\boldsymbol{\beta }}^{ \boldsymbol{{m}}},{\xi }^{\boldsymbol{{m}}})$ minimize a quadratic energy $E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} (\boldsymbol{{A}}, \boldsymbol{\beta },\xi )$. The bulk of the work goes into computing ${\boldsymbol{\beta }}^{\boldsymbol{{m}}}$, which does not appear in the reduced energy. This amounts to solving a partial differential equation in each cross section. Computing ${\boldsymbol{{A}}}^{ \boldsymbol{{m}}}$ ought to be easier than that; we project $\boldsymbol{{m}}$ onto a three-dimensional space, which by the Riesz representation theorem only requires computing three integrals. In this section we write down those integrals.

We start the task of identifying ${\boldsymbol{{A}}}^{ \boldsymbol{{m}}}$. Elements of ℰ are determined by a scalar $\xi \in \mathbb{R}$ controlling extension, a matrix $\boldsymbol{{A}}\in \operatorname{Skew}(3)$ controlling bending and twist, and a function $\boldsymbol{\beta }$ controlling the warping of the cross section. The energy is the minimum of $E^{\mathrm{ansatz}}_{ \boldsymbol{{m}}} (\boldsymbol{{A}},\boldsymbol{\beta },\xi )$ over $\boldsymbol{\beta }$ and $\xi$. To find this, we write down the optimal warping of the cross section $\boldsymbol{\psi }^{(j)}$ associated to stretching ($j=0$), twist ($j=1$) or bending ($j=2,3$). The optimal $\boldsymbol{\beta }$ is a linear combination of $\boldsymbol{\psi }^{(j)}$.⁶

It is useful to consider the response of the rod to unit twist, unit bending in each direction, and also stretching by an amount $h$ per unit length. We define

$$\begin{aligned} I^{(0)}(\boldsymbol{\psi }) =& \int_{\varOmega }\mathcal{Q}_{3}{ \bigl( \operatorname{sym} ( \boldsymbol{{e}}_{1}| {\nabla }_{ \mathrm{cs}}{\boldsymbol{\psi }} ) \bigr) }d \boldsymbol{\boldsymbol{x}}, \\ I^{(1)}(\boldsymbol{\psi }) =& \int_{\varOmega }\mathcal{Q}_{3}{ \bigl( \operatorname{sym} ( -x_{3}\boldsymbol{{e}}_{2} + x_{2} \boldsymbol{{e}}_{3}| {\nabla }_{\mathrm{cs}}{\boldsymbol{\psi }} ) \bigr) }d \boldsymbol{\boldsymbol{x}}, \\ I^{(j)}(\boldsymbol{\psi }) =& \int_{\varOmega }\mathcal{Q}_{3}{ \bigl( \operatorname{sym} ( x_{j}\boldsymbol{{e}}_{1}| {\nabla } _{\mathrm{cs}}{\boldsymbol{\psi }} ) \bigr) } d\boldsymbol{ \boldsymbol{x}}. \end{aligned}$$

Notice that these are closely related to the energy of our ansatz with no misfit (see Eq. (8)). For example, $I^{(0)}(\boldsymbol{\psi }) = E^{\mathrm{ansatz}}_{0} (0, \boldsymbol{\psi },1)$ is the energy of a rod stretched by $h$ per unit length with a cross section warped by an amount $\boldsymbol{\psi }$. We let $\boldsymbol{\psi }^{(j)}$ be the minimizer of $I^{(j)}$, then define the associated strains by:

$$ \begin{aligned} \boldsymbol{{F}}^{(0)} &= \operatorname{sym} ( \boldsymbol{{e}} _{1}|{\nabla }_{\mathrm{cs}}{\boldsymbol{\psi }^{(0)}} ), \\ \boldsymbol{{F}}^{(1)} &= \operatorname{sym} ( -x_{3} \boldsymbol{{e}}_{2} + x_{2}\boldsymbol{{e}}_{3}|{\nabla }_{ \mathrm{cs}}{\boldsymbol{\psi }^{(1)}} ), \\ \boldsymbol{{F}}^{(j)} &= \operatorname{sym} ( x_{j} \boldsymbol{{e}}_{1}|{\nabla }_{\mathrm{cs}}{\boldsymbol{\psi } ^{(j)}} ) \quad\mbox{for } j=2,3. \end{aligned} $$

(10)

Theorem 2

($\mathcal{Q}_{1}$ and $\boldsymbol{{A}}$ for a General Rod)

Let $\tilde{\boldsymbol{{m}}} = \boldsymbol{{m}}- \frac{ \boldsymbol{{e}}_{1}\otimes \boldsymbol{{e}}_{1}}{|S|}\int_{S} m_{11}( {\boldsymbol{x}}_{\mathrm{cs}} )d{\boldsymbol{x}}_{\mathrm{cs}}$. For a.e. $x_{1}$ the preferred twist ${\omega }^{\boldsymbol{{m}}}$ and bending ${\boldsymbol{\kappa }}^{\boldsymbol{{m}}}$ solve the following three-by-three linear system:

$$ \bigl\langle \tilde{\boldsymbol{{m}}},\boldsymbol{{F}}^{(j)} \bigr\rangle _{W''(\operatorname{Id})} = {\omega }^{\boldsymbol{{m}}} \bigl\langle \boldsymbol{{F}} ^{(1)},\boldsymbol{{F}}^{(j)} \bigr\rangle _{W''(\operatorname{Id})} + \sum_{i=2,3}{\kappa }^{\boldsymbol{{m}}}_{i} \bigl\langle \boldsymbol{{F}} ^{(i)},\boldsymbol{{F}}^{(j)} \bigr\rangle _{W''(\operatorname{Id})} $$

(11)

for $j\in \{1, 2, 3\}$. The one-dimensional energy density is given by

$$ \mathcal{Q}_{1}(\omega ,\boldsymbol{\kappa }) = \int_{S} \mathcal{Q} _{3}{ \bigl( \omega \boldsymbol{{F}}^{(1)} + \kappa_{2} \boldsymbol{{F}}^{(2)} + \kappa_{3} \boldsymbol{{F}}^{(3)} \bigr) } d { \boldsymbol{x}}_{\mathrm{cs}} . $$

(12)

Proof

To simplify notation we will write $\kappa_{1} = \omega$ for the duration of this proof. The symmetrized gradient with respect to cross-sectional variables only is denoted by ${\operatorname{e}}_{ \mathrm{cs}}(\boldsymbol{\alpha }) = \operatorname{sym} ( 0|{\nabla }_{\mathrm{cs}}\boldsymbol{\alpha } )$ for $\boldsymbol{\alpha }\in W^{1,2}(\varOmega , \mathbb{R}^{3})$.

Notice that the strains $\boldsymbol{{F}}^{(j)}$ are all orthogonal to the cross-sectional symmetrized gradients: for any $\boldsymbol{\alpha }\in W^{1,2}(\varOmega ,\mathbb{R}^{3})$,

$$ \delta I^{(j)}\bigl(\boldsymbol{\psi }^{(j)}\bigr)[ \boldsymbol{\alpha }] = \bigl\langle \boldsymbol{{F}}^{(j)},{ \operatorname{e}}_{\mathrm{cs}}( \boldsymbol{\alpha }) \bigr\rangle _{W''(\operatorname{Id})} = 0. $$

By projecting $\boldsymbol{{m}}$ onto ℰ, we have

$$ \boldsymbol{{m}}= \bigl( {\xi }^{\boldsymbol{{m}}}\boldsymbol{{F}} ^{(0)} + {\omega }^{\boldsymbol{{m}}}\boldsymbol{{F}}^{(1)} + {\kappa }^{\boldsymbol{{m}}}_{2}\boldsymbol{{F}}^{(2)} + {\kappa }^{ \boldsymbol{{m}}}_{3}\boldsymbol{{F}}^{(3)} \bigr) + { \operatorname{e}} _{\mathrm{cs}}\bigl({\boldsymbol{\alpha }}^{\boldsymbol{{m}}} \bigr)+ \boldsymbol{{m}}_{\perp } $$

(13)

for some ${\boldsymbol{\alpha }}^{\boldsymbol{{m}}}$, where $\boldsymbol{{m}}_{\perp }$ is orthogonal to each of the other terms in the sense of $\langle \cdot ,\cdot \rangle _{W''( \operatorname{Id})}$. Recall that, according to Remark 3, ${\xi }^{\boldsymbol{{m}}}= \frac{1}{|S|}\int_{S} m_{11}({\boldsymbol{x}} _{\mathrm{cs}} )d{\boldsymbol{x}}_{\mathrm{cs}}$. Taking the inner product of each side with $\boldsymbol{{F}}^{(j)}$, $j\in \{1, 2, 3\}$ yields

$$\biggl\langle \boldsymbol{{m}}-\frac{\boldsymbol{{F}}^{(0)}}{|S|} \int _{S} m_{11}({\boldsymbol{x}}_{\mathrm{cs}} )d{ \boldsymbol{x}}_{ \mathrm{cs}} ,\boldsymbol{{F}}^{(j)} \biggr\rangle _{W''( \operatorname{Id})} = \sum_{i=1}^{3}{\kappa }^{\boldsymbol{{m}}}_{i} \bigl\langle \boldsymbol{{F}}^{(i)}, \boldsymbol{{F}}^{(j)} \bigr\rangle _{W''(\operatorname{Id})}. $$

The orthogonality of $\boldsymbol{{F}}^{(j)}$ with symmetrized gradients implies that $\langle \boldsymbol{{F}}^{(j)},\boldsymbol{{e}} _{1}\otimes \boldsymbol{{e}}_{1} \rangle _{W''(\operatorname{Id})} = \langle \boldsymbol{{F}}^{(j)},\boldsymbol{{F}}^{(0)} \rangle _{W''(\operatorname{Id})}$, which shows Eq. (11).

Recalling $E^{\mathrm{ansatz}}_{\boldsymbol{{m}}}$ from Eq. (8), the one-dimensional energy is given by

$$\begin{aligned} E(\boldsymbol{{R}}) =& \min_{\xi ,\boldsymbol{\beta }} E^{\mathrm{ansatz}} _{\boldsymbol{{m}}} \bigl( \boldsymbol{{R}}^{T}\partial_{1} \boldsymbol{{R}},\boldsymbol{\beta },\xi \bigr) \\ =& \min_{\xi ,\boldsymbol{\beta }} \int_{\varOmega }\mathcal{Q}_{3} { \left( \operatorname{sym} \left( \xi \boldsymbol{{e}}_{1} + \boldsymbol{{A}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right|{\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} \right) - \boldsymbol{{m}} \right) }d\boldsymbol{\boldsymbol{x}} \\ =& \min_{\xi ,\boldsymbol{\alpha }} \int_{\varOmega }\mathcal{Q}_{3} { ( \boldsymbol{{m}}_{\perp } ) } + \mathcal{Q}_{3}{ \bigl( {\operatorname{e}}_{\mathrm{cs}}\bigl( \boldsymbol{\alpha }-{\boldsymbol{\alpha }} ^{\boldsymbol{{m}}}\bigr) \bigr) } \\ & \quad\quad\ \ \,{}+ \mathcal{Q}_{3}{ \Biggl( \bigl(\xi -{\xi }^{\boldsymbol{{m}}}\bigr) \boldsymbol{{F}}^{(0)} + \sum_{j=1}^{3} \bigl(\kappa_{j}-{\kappa }^{ \boldsymbol{{m}}}_{j}\bigr) \boldsymbol{{F}}^{(j)} \Biggr) }d \boldsymbol{\boldsymbol{x}}\\ =& E_{0} + \int_{\varOmega }\mathcal{Q}_{3}{ \Biggl( \sum _{j=1}^{3}\bigl(\kappa _{j}-{\kappa }^{\boldsymbol{{m}}}_{j}\bigr) \boldsymbol{{F}}^{(j)} \Biggr) }d \boldsymbol{\boldsymbol{x}}. \end{aligned}$$

The third line used orthogonality. The fourth used the definition of $E_{0} = \int_{\varOmega }\mathcal{Q}_{3}{ ( \boldsymbol{{m}}_{ \perp } ) }$, and the fact that the minimum is achieved when $\xi = {\xi }^{\boldsymbol{{m}}}$ (Remark 2). This implies Eq. (12). □

Corollary 1

(The Quadratic Nature of $\mathcal{Q}_{1}$)

$\mathcal{Q}_{1}:\operatorname{Skew}(3)\to \mathbb{R}$ is a positive definite quadratic form.

Proof

This follows immediately from Eq. (12). □

Notice that finding the energy density $\mathcal{Q}_{1}$ requires finding the strains $\boldsymbol{{F}}^{(j)}$, $j\in \{1, 2, 3\}$. Given those strains, one can compute ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$ by taking several integrals and solving a linear system. If one considers a rod with misfit that depends on the cross section (i.e., $\boldsymbol{{m}}(\boldsymbol{x})$ depends on $x_{1}$) then the above theorem simplifies the computation immensely.

We can make Theorem 2 more explicit when the material is isotropic: $W''(\operatorname{Id})(\boldsymbol{{F}}) = 2 \mu \boldsymbol{{F}}+ \lambda \operatorname{tr}(\boldsymbol{{F}}) \operatorname{Id}$ where $\mu > 0$ and $\lambda + \mu > 0$. ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$ depends on one parameter, $\nu = \frac{\lambda }{2(\mu +\lambda )}$ (Poisson’s ratio).

Remark 4

(Strain of an Isotropic Rod)

Let the elastic stiffness tensor be isotropic with Poisson’s ratio $\nu$. Define $\phi ({\boldsymbol{x}} _{\mathrm{cs}} )$ (called the torsion function) to be the solution to

$$ \textstyle\begin{cases} \Delta \phi ({\boldsymbol{x}}_{\mathrm{cs}} ) = 0 &\mbox{for }{\boldsymbol{x}} _{\mathrm{cs}} \in S, \\ \partial_{n} \phi ({\boldsymbol{x}}_{\mathrm{cs}} ) = (-x_{3},x_{2}) \cdot n &\mbox{for }{\boldsymbol{x}}_{\mathrm{cs}} \in \partial S. \end{cases} $$

The strains $\boldsymbol{{F}}^{(j)}$ are given by

$$ \begin{aligned} \boldsymbol{{F}}^{(0)} &= \left(\textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 & -\nu & 0 \\ 0 & 0 & -\nu \end{array}\displaystyle \right), \\ \boldsymbol{{F}}^{(1)} &= \left(\textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 &\frac{1}{2}(\partial_{2}\phi - x_{3})& \frac{1}{2}(\partial_{3} \phi + x_{2}) \\ \frac{1}{2}(\partial_{2}\phi - x_{3})& 0 & 0 \\ \frac{1}{2}(\partial_{3}\phi + x_{2}) & 0 & 0 \end{array}\displaystyle \right), \\ \boldsymbol{{F}}^{(j)} &= x_{j} \left(\textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 &-\nu & 0 \\ 0 & 0 & -\nu \end{array}\displaystyle \right)\quad \mbox{for } j=2,3. \end{aligned} $$

(14)

The proof follows directly from the Euler-Lagrange Equations of $I^{(j)}$. For $j \neq 0$ this observation was also in [27].

Theorem 3

($\mathcal{Q}_{1}$ and $\boldsymbol{{A}}$ for an Isotropic Rod)

Let $W''(\operatorname{Id})$ be isotropic, and assume that $\int_{S} x _{2} x_{3} d{\boldsymbol{x}}_{\mathrm{cs}} = 0$. Then

• 1. the quadratic form $\mathcal{Q}_{1}$ is diagonal in $\omega$, $\kappa_{2}$, $\kappa_{3}$:

  $$ \mathcal{Q}_{1}\bigl(\boldsymbol{{A}}(\omega ,\boldsymbol{\kappa }) \bigr) = \int _{S} \omega^{2} \mathcal{Q}_{3}{ \bigl( \boldsymbol{{F}}^{(1)} \bigr) } + \kappa_{2}^{2} \mathcal{Q}_{3}{ \bigl( \boldsymbol{{F}}^{(2)} \bigr) } + \kappa_{3}^{2} \mathcal{Q}_{3}{ \bigl( \boldsymbol{{F}}^{(3)} \bigr) }d{\boldsymbol{x}}_{\mathrm{cs}} ; $$

  (15)

• 2. moreover, ${\omega }^{\boldsymbol{{m}}}$, ${\kappa }^{ \boldsymbol{{m}}}_{j}$ have the simple formulas:

  $$ {\omega }^{\boldsymbol{{m}}} = \frac{ \langle \boldsymbol{{F}} ^{(1)},\boldsymbol{{m}} \rangle _{W''(\operatorname{Id})} }{ \lVert \boldsymbol{{F}}^{(1)} \rVert _{W''( \operatorname{Id})}^{2} } , {\kappa }^{\boldsymbol{{m}}}_{j} = \frac{ \int_{S} x_{j}m_{11}(\boldsymbol{x})d{\boldsymbol{x}}_{\mathrm{cs}} }{ \int_{S} x_{j}^{2} d{\boldsymbol{x}}_{\mathrm{cs}} }\textit{ for }j=2, 3. $$

  (16)

Proof

The key observation is that $\{ \boldsymbol{{F}}^{(j)} \} _{j=0}^{3}$ are mutually orthogonal with respect to $\langle \cdot , \cdot \rangle _{W''(\operatorname{Id})}$. Equation (15) follows immediately from this and the analogous statement for general rods, Eq. (12) of Theorem 2. The orthogonality of $\boldsymbol{{F}}^{(j)}$, together with Eq. (11), shows that

$$ {\omega }^{\boldsymbol{{m}}} = \frac{ \langle \boldsymbol{{F}} ^{(1)},\boldsymbol{{m}} \rangle _{W''(\operatorname{Id})} }{ \lVert \boldsymbol{{F}}^{(1)} \rVert _{W''( \operatorname{Id})}^{2} } , \quad\quad {\kappa }^{\boldsymbol{{m}}}_{2} = \frac{ \langle \boldsymbol{{F}}^{(2)},\boldsymbol{{m}} \rangle _{W''(\operatorname{Id})} }{ \lVert \boldsymbol{{F}}^{(2)} \rVert _{W''(\operatorname{Id})}^{2} } , \quad\quad {\kappa }^{\boldsymbol{{m}}} _{3} = \frac{ \langle \boldsymbol{{F}}^{(3)},\boldsymbol{{m}} \rangle _{W''(\operatorname{Id})} }{ \lVert \boldsymbol{{F}}^{(3)} \rVert _{W''(\operatorname{Id})}^{2} }. $$

Elementary manipulations reduce this to Eq. (16). □

Remark 5

(The Geometric Effect of Poisson’s Ratio)

It is remarkable that the preferred bending and twist do not depend on $\nu$, although this is well known in the special case of the bimetallic rod. In general (for anisotropic materials), ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$ depends on $W''(\operatorname{Id})$.

Remark 6

(Conditions on $\boldsymbol{{m}}$ That Produce no Bending or Twist)

For isotropic rods, we see that the preference to bend is driven by a propensity to stretch in the long direction, and the preference to twist is driven by a propensity that cross sections prefer to shear. Specifically, if $m_{11} = 0$ then ${\boldsymbol{\kappa }}^{ \boldsymbol{{m}}} = 0$ and if $m_{12} = m_{13} = 0$ then ${\omega } ^{\boldsymbol{{m}}} = 0$. It follows in particular that isotropic misfit will never make a rod twist. This explains why the well-known bimetallic strip bends but does not twist, and suggests how we might create a rod that prefers to twist. See Sects. 6.1 and 6.2 for examples related to these remarks.

4 Properties of the One-Dimensional Energy

This section discusses how properties of the three-dimensional energy have consequences for the limiting, one-dimensional rod theory. In particular, we show in Sect. 4.1 how symmetries can force the preferred twist ${\omega }^{\boldsymbol{{m}}}$ or preferred bending ${\boldsymbol{\kappa }}^{\boldsymbol{{m}}}$ to vanish, and we discuss in Sect. 4.2 the circumstances in which $E_{0}= 0$.

4.1 Symmetries of the Rod

Finding ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$ typically requires computing several integrals. However, symmetries in the three-dimensional energy can imply that certain entries in ${\boldsymbol{{A}}} ^{\boldsymbol{{m}}}$ are 0. Consider the following concrete example: suppose that the three-dimensional energy has a rotational symmetry ${\boldsymbol{{Q}}}_{\mathrm{cs}}$ in the cross section. Rotating the cross section (in reference coordinates) by a matrix ${\boldsymbol{{Q}}} _{\mathrm{cs}}\in \operatorname{SO}(2)$ rotates the curvature vector $\boldsymbol{\kappa }= (\kappa_{2}, \kappa_{3})$ by the same matrix ${\boldsymbol{{Q}}}_{\mathrm{cs}}$. The energy is minimized by some unique $\boldsymbol{\kappa }= {\boldsymbol{\kappa }}^{ \boldsymbol{{m}}}$, so ${\boldsymbol{\kappa }}^{\boldsymbol{{m}}} = {\boldsymbol{{Q}}}_{\mathrm{cs}}{\boldsymbol{\kappa }}^{ \boldsymbol{{m}}}$. This implies that ${\boldsymbol{\kappa }}^{ \boldsymbol{{m}}} = 0$. A symmetry can also imply that ${\omega }^{ \boldsymbol{{m}}}=0$: if the rod is symmetric with respect to a reflection, then because reflections change orientation the energy cannot distinguish between left-handed and right-handed twist. The following theorem generalizes and makes rigorous these ideas.

Theorem 4

(Symmetries of a Rod)

Let $\boldsymbol{{Q}}\in \operatorname{O}(3)$ be of the following form:

$$ \boldsymbol{{Q}}= \left(\textstyle\begin{array}{c@{\quad}c@{\quad}c} q_{11} & 0 & 0 \\ 0 & q_{22} & q_{23} \\ 0 & q_{32} & q_{33} \end{array}\displaystyle \right), $$

and let ${\boldsymbol{{Q}}}_{\mathrm{cs}}$ be the lower right two-by-two block of $\boldsymbol{{Q}}$. Assume also that:

• 1. (Symmetry of the elastic stiffness tensor). For any $\boldsymbol{{F}}\in \mathrm{Sym}(3)$,

  $$W''(\operatorname{Id}) \bigl(\boldsymbol{{Q}}^{T} \boldsymbol{{F}} \boldsymbol{{Q}}\bigr) = \boldsymbol{{Q}}^{T} \bigl(W''(\operatorname{Id}) \boldsymbol{{F}}\bigr) \boldsymbol{{Q}}. $$

• 2. (Symmetry of the cross section). If ${\boldsymbol{x}}_{ \mathrm{cs}} \in S$ then ${\boldsymbol{{Q}}}_{\mathrm{cs}}{\boldsymbol{x}} _{\mathrm{cs}} \in S$.

• 3. (Symmetry of the misfit). For a.e. $\boldsymbol{x}\in \varOmega$, $\boldsymbol{{Q}}^{T} \boldsymbol{{m}}(\boldsymbol{x}) \boldsymbol{{Q}}= \boldsymbol{{m}}(x_{1}, {\boldsymbol{{Q}}}_{ \mathrm{cs}}{\boldsymbol{x}}_{\mathrm{cs}} )$.

Then the preferred bending ${\boldsymbol{\kappa }}^{\boldsymbol{{m}}}$ and twist ${\omega }^{\boldsymbol{{m}}}$ satisfy the following conditions:

• If $\det (\boldsymbol{{Q}}) = -1$ then ${\omega }^{\boldsymbol{{m}}}=0$.

• ${\boldsymbol{{Q}}}_{\mathrm{cs}}{\boldsymbol{\kappa }}^{ \boldsymbol{{m}}} = {\boldsymbol{\kappa }}^{\boldsymbol{{m}}}$. In particular, if ${\boldsymbol{{Q}}}_{\mathrm{cs}}\in \operatorname{SO}(2)$ and ${\boldsymbol{{Q}}}_{\mathrm{cs}}\ne \operatorname{Id}$ then ${\boldsymbol{\kappa }}^{\boldsymbol{{m}}} = 0$.

The above conditions mean that the rod is symmetric with respect to the rigid motion given by $\boldsymbol{{Q}}$. The first special case outlined above corresponds to $q_{11} = 1$, ${\boldsymbol{{Q}}}_{ \mathrm{cs}}\in \operatorname{SO}(2)$.

Remark 7

(Symmetry of the Misfit with $q_{11} = -1$)

Notice that the third condition is not $\boldsymbol{{Q}}^{T} \boldsymbol{{m}}( \boldsymbol{x}) \boldsymbol{{Q}}= \boldsymbol{{m}}(\boldsymbol{{Q}} \boldsymbol{x})$, which would relate the misfit in two different cross sections. Our conditions 2 and 3, by contrast, involve symmetries of the cross section obtained by fixing $x_{1}$.

Proof

Let $\tilde{\boldsymbol{x}}_{1} = x_{1}$, ${\tilde{\boldsymbol{x}}} _{\mathrm{cs}} = {\boldsymbol{{Q}}}_{\mathrm{cs}}{\boldsymbol{x}}_{ \mathrm{cs}}$ and suppose that $E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} ( \boldsymbol{{A}}, \boldsymbol{\beta }, \xi )$ is minimized at $\boldsymbol{{A}}({\omega }^{\boldsymbol{{m}}},{\boldsymbol{\kappa }} ^{\boldsymbol{{m}}})$, ${\boldsymbol{\beta}}^{\boldsymbol{{m}}}$, and ${\xi }^{\boldsymbol{{m}}}$. We will show that the energy is invariant under the transformation at $\tilde{\omega } = (\det \boldsymbol{{Q}}) \omega$, $\tilde{\boldsymbol{\kappa }} = {\boldsymbol{{Q}}}_{ \mathrm{cs}}\boldsymbol{\kappa }$ and $\tilde{\boldsymbol{\beta }} = \boldsymbol{{Q}}\boldsymbol{\beta }$. By strict convexity of the energy (Corollary 1), the minimizers ${\boldsymbol{\kappa }} ^{\boldsymbol{{m}}}$ and ${\omega }^{\boldsymbol{{m}}}$ are unique so in fact ${\boldsymbol{\kappa }}^{\boldsymbol{{m}}} = {\boldsymbol{{Q}}} _{\mathrm{cs}}{\boldsymbol{\kappa }}^{\boldsymbol{{m}}}$ and ${\omega }^{\boldsymbol{{m}}} = (\det {\boldsymbol{{Q}}}){\omega } ^{\boldsymbol{{m}}}$.

$$\begin{aligned} E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} =& \int_{\varOmega }\mathcal{Q}_{3} { \left( \operatorname{sym} \left( \xi \boldsymbol{{e}}_{1} + \boldsymbol{{A}}(\omega ,\boldsymbol{ \kappa }) \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} \right) - \boldsymbol{{m}}(\boldsymbol{x}) \right) } d \boldsymbol{ \boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{ \left( \boldsymbol{{Q}}^{T} \left( \operatorname{sym} \left( \xi \boldsymbol{{e}}_{1} + \boldsymbol{{A}}( \omega ,\boldsymbol{\kappa }) \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} \right) - \boldsymbol{{m}}(\boldsymbol{x}) \right) \boldsymbol{{Q}} \right) } d \boldsymbol{\boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{\left ( \boldsymbol{{Q}}^{T}\left ( \renewcommand{\arraystretch}{1.5} \textstyle\begin{array}{c|c} \xi - \boldsymbol{\kappa }\cdot {\boldsymbol{x}}_{\mathrm{cs}} & \frac{1}{2}(\omega {\boldsymbol{x}}_{\mathrm{cs}}^{\perp }+ {\nabla } _{\mathrm{cs}}\beta_{1}) \\ \hline \frac{1}{2}(\omega {\boldsymbol{x}}_{\mathrm{cs}}^{\perp }+ {\nabla }_{\mathrm{cs}}\beta_{1}) & \operatorname{sym}{\nabla }_{ \mathrm{cs}}{\boldsymbol{\beta }}_{\mathrm{cs}} \end{array}\displaystyle \renewcommand{\arraystretch}{1} \right ) \boldsymbol{{Q}}- \boldsymbol{{m}}(x_{1},{\boldsymbol{{Q}}} _{\mathrm{cs}}{ \boldsymbol{x}}_{\mathrm{cs}} ) \right ) } d \boldsymbol{\boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{\left ( \left ( \renewcommand{\arraystretch}{1.5} \textstyle\begin{array}{c|c} \xi - \boldsymbol{\kappa }\cdot {\boldsymbol{x}}_{\mathrm{cs}} & \frac{1}{2}(\omega {\boldsymbol{x}}_{\mathrm{cs}}^{\perp }+ {\nabla } _{\mathrm{cs}}\beta_{1}){\boldsymbol{{Q}}}_{\mathrm{cs}} \\ \hline \frac{1}{2}{\boldsymbol{{Q}}}_{\mathrm{cs}}^{T}(\omega {\boldsymbol{x}} _{\mathrm{cs}}^{\perp }+ {\nabla }_{\mathrm{cs}}\beta_{1}) & {\boldsymbol{{Q}}} _{\mathrm{cs}}^{T}\operatorname{sym}{\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} _{\mathrm{cs}}{\boldsymbol{{Q}}}_{\mathrm{cs}} \end{array}\displaystyle \renewcommand{\arraystretch}{1} \right ) - \boldsymbol{{m}}(x_{1}, {\boldsymbol{{Q}}}_{\mathrm{cs}} { \boldsymbol{x}}_{\mathrm{cs}} ) \right ) } d \boldsymbol{\boldsymbol{x}}. \end{aligned}$$

To derive the second line we used symmetry of the elastic stiffness tensor, and to find the third we used the symmetry of the misfit. We write the energy in terms of $\tilde{\boldsymbol{x}}$:

$$\begin{aligned} E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} =& \int_{\varOmega }\mathcal{Q}_{3} {\left ( \left ( \renewcommand{\arraystretch}{1.5} \textstyle\begin{array}{c|c} \xi - \tilde{\boldsymbol{\kappa }}\cdot {\tilde{\boldsymbol{x}}}_{ \mathrm{cs}} & \frac{1}{2}(\tilde{\omega }{\tilde{\boldsymbol{x}}} _{\mathrm{cs}}^{\perp } + {\nabla }_{\mathrm{cs}}\tilde{\beta }_{1}) \\ \hline \frac{1}{2}(\tilde{\omega }{\tilde{\boldsymbol{x}}}_{ \mathrm{cs}}^{\perp } + {\nabla }_{\mathrm{cs}}\tilde{\beta }_{1}) & \operatorname{sym}{\nabla }_{\mathrm{cs}}{\tilde{\boldsymbol{\beta }}} _{\mathrm{cs}} \end{array}\displaystyle \renewcommand{\arraystretch}{1} \right ) - \boldsymbol{{m}}(\tilde{\boldsymbol{x}}) \right ) } d \tilde{ \boldsymbol{x}} \\ =& E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} (\tilde{\omega }, \tilde{\boldsymbol{\kappa }}; \tilde{\boldsymbol{\beta }},\xi ). \end{aligned}$$

In finding the off-diagonal components we used the fact that, if ${\boldsymbol{{Q}}}_{\mathrm{cs}}$ is a rotation, $({\boldsymbol{{Q}}} _{\mathrm{cs}}{\tilde{\boldsymbol{x}}}_{\mathrm{cs}})^{\perp }= {\boldsymbol{{Q}}} _{\mathrm{cs}}{\tilde{\boldsymbol{x}}}_{\mathrm{cs}}^{\perp }$ because rotations commute in two dimensions. If ${\boldsymbol{{Q}}}_{ \mathrm{cs}}$ is a reflection then by direct computation we see that $({\boldsymbol{{Q}}}_{\mathrm{cs}}{\tilde{\boldsymbol{x}}}_{ \mathrm{cs}})^{\perp }= -{\boldsymbol{{Q}}}_{\mathrm{cs}}{\tilde{\boldsymbol{x}}} _{\mathrm{cs}}^{\perp }$. Thus,

$$q_{11} \bigl( {\boldsymbol{{Q}}}_{\mathrm{cs}}^{T} { \tilde{\boldsymbol{x}}} _{\mathrm{cs}} \bigr) ^{\perp }= q_{11} ( \det {\boldsymbol{{Q}}} _{\mathrm{cs}} ) {\boldsymbol{{Q}}}_{\mathrm{cs}}^{T}{ \tilde{\boldsymbol{x}}} _{\mathrm{cs}}^{\perp } = (\det \boldsymbol{{Q}}){ \boldsymbol{{Q}}} _{\mathrm{cs}}^{T}{\tilde{\boldsymbol{x}}}_{\mathrm{cs}}^{\perp }. $$

We conclude that, for any $\omega$ and $\boldsymbol{\kappa }$,

$$E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} (\omega , \boldsymbol{\kappa }; \boldsymbol{ \beta }, \xi ) = E^{\mathrm{ansatz}}_{\boldsymbol{{m}}} \bigl( (\det \boldsymbol{{Q}}) \omega , {\boldsymbol{{Q}}}_{\mathrm{cs}} \boldsymbol{\kappa }; \tilde{ \boldsymbol{\beta }}, \xi \bigr) . $$

The theorem follows from the fact that minimizers of $E^{\mathrm{ansatz}} _{\boldsymbol{{m}}}$ exist and are unique. □

4.2 Condition for Vanishing $E_{0}$

We present a test to determine whether the minimum energy $E_{0}$ is 0. This is equivalent to $\boldsymbol{{m}}\in \mathcal{E}$, which we interpret as the statement that $\boldsymbol{{m}}$ is a linear strain admissible achievable by a suitable combination of bending, twist, extension, and warping of the cross section.

Theorem 5

(Conditions for $E_{0}= 0$)

Note that $E_{0}= 0$ if and only if $\boldsymbol{{m}}(x_{1},{\boldsymbol{x}}_{\mathrm{cs}} )\in \mathcal{E}$ for a.e. $x_{1}$. For rods with simply connected cross section $S$, this is equivalent to the following conditions a.e. in $\boldsymbol{x}$. Derivatives are meant in the distributional sense.

• 1. $m_{11}$ is affine in ${\boldsymbol{x}}_{\mathrm{cs}}$, and

• 2. $\partial_{2} m_{13} - \partial_{3} m_{12}$ is constant in ${\boldsymbol{x}} _{\mathrm{cs}}$, and

• 3. $\partial_{22}m_{33} + \partial_{33}m_{22} - 2\partial_{23}m_{23} = 0$.

Proof

First assume that $\boldsymbol{{m}}({\boldsymbol{x}}_{\mathrm{cs}} ) \in \mathcal{E}$ for a.e. $x_{1}$, i.e. that

$$\begin{aligned} \boldsymbol{{m}}({\boldsymbol{x}}_{\mathrm{cs}} ) =& \operatorname{sym} \left( {\xi }^{\boldsymbol{{m}}} \boldsymbol{{e}} _{1} + {\boldsymbol{{A}}}^{\boldsymbol{{m}}} \left.\left(\textstyle\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}\displaystyle \right) \right| {\nabla }_{\mathrm{cs}}{{\boldsymbol{\beta }}^{ \boldsymbol{{m}}}} \right) \\ =& \operatorname{sym} \left ( \renewcommand{\arraystretch}{1.5} \textstyle\begin{array}{c|c} {\xi }^{\boldsymbol{{m}}}- {\boldsymbol{\kappa }}^{\boldsymbol{{m}}} \cdot {\boldsymbol{x}}_{\mathrm{cs}} & \frac{1}{2}({\omega }^{ \boldsymbol{{m}}} {\boldsymbol{x}}_{\mathrm{cs}}^{\perp }+ {\nabla } _{\mathrm{cs}}{\beta_{1}^{\boldsymbol{{m}}}}) \\ \hline \frac{1}{2}({\omega }^{\boldsymbol{{m}}} {\boldsymbol{x}}_{ \mathrm{cs}}^{\perp }+ {\nabla }_{\mathrm{cs}}{\beta_{1}^{ \boldsymbol{{m}}}}) & \operatorname{sym}{\nabla }_{\mathrm{cs}}{\boldsymbol{\beta } _{\mathrm{cs}}^{\boldsymbol{{m}}}} \end{array}\displaystyle \renewcommand{\arraystretch}{1} \right ) . \end{aligned}$$

(17)

The first condition, that $m_{11}$ be affine in ${\boldsymbol{x}}_{ \mathrm{cs}}$, is obvious. The second condition is obtained by commuting derivatives:

$$ \partial_{2} m_{13} - \partial_{3} m_{12} = \frac{1}{2} \bigl( {\omega }^{\boldsymbol{{m}}} + \partial_{23}\beta_{1}^{\boldsymbol{{m}}} \bigr) - \frac{1}{2} \bigl( -{\omega }^{\boldsymbol{{m}}} + \partial_{32}\beta _{1}^{\boldsymbol{{m}}} \bigr) = {\omega }^{\boldsymbol{{m}}}. $$

(18)

The third condition follows from the compatibility condition for linear strains (see e.g., [7]).

We show the converse: if $\boldsymbol{{m}}$ satisfies conditions 1–3 then $\boldsymbol{{m}}\in \mathcal{E}$. It suffices to find ${\xi }^{\boldsymbol{{m}}}$, ${\boldsymbol{\kappa }}^{ \boldsymbol{{m}}}$, ${\omega }^{\boldsymbol{{m}}}$ and ${\boldsymbol{\beta }} ^{\boldsymbol{{m}}}$ such that Eq. (17) holds. Finding ${\boldsymbol{\kappa }}^{\boldsymbol{{m}}}$ and ${\xi }^{ \boldsymbol{{m}}}$ is simple: by condition 1, we can define $m_{11} = {\xi }^{\boldsymbol{{m}}}+ {\boldsymbol{\kappa }}^{ \boldsymbol{{m}}}\cdot {\boldsymbol{x}}_{\mathrm{cs}}$.

The second condition tells us that $\partial_{2} m_{13} - \partial _{3} m_{12}$ is a constant, so in order to match Eq. (18) we call this constant ${\omega } ^{\boldsymbol{{m}}}$. Condition 2 shows that $\boldsymbol{m}_{ \mathrm{cs},1}- \frac{1}{2}{\omega }^{\boldsymbol{{m}}} {\boldsymbol{x}} _{\mathrm{cs}}^{\perp }$ has curl 0. The domain $S$ is simply connected, so there is some $\beta_{1}^{\boldsymbol{{m}}}$ such that ${\nabla }_{\mathrm{cs}}\beta_{1}^{\boldsymbol{{m}}}= \boldsymbol{m} _{\mathrm{cs},1}- \frac{1}{2}{\omega }^{\boldsymbol{{m}}} {\boldsymbol{x}} _{\mathrm{cs}}^{\perp }$.

By the compatibility condition for linear strains [7] the third condition implies that $\boldsymbol{{m}}_{\mathrm{cs},\mathrm{cs}}= \operatorname{e}( \boldsymbol{\beta }_{\mathrm{cs}}^{\boldsymbol{{m}}})$ for some function $\boldsymbol{\beta }_{\mathrm{cs}}^{\boldsymbol{{m}}}$. □

Remark 8

In general, ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$ depends on both $W''(\operatorname{Id})$ and $\boldsymbol{{m}}$. If $\boldsymbol{{m}} \in \mathcal{E}$ then this is not the case; ${\boldsymbol{{A}}}^{ \boldsymbol{{m}}}$ depends only on $\boldsymbol{{m}}$.

5 Related Energy Functionals

5.1 Comparison Between Rods and Ribbons

There has been much recent interest in ribbons (informally, elastic bodies with three length scales $t \ll w \ll L$) with misfit, motivated by diverse applications in physics [6], biology [3] and chemistry [34]. In principle Theorem 1 makes no assumptions about the eccentricity of the cross section, and so one might use this (or other rod theories) to study ribbons. We urge caution. The bounds in Theorem 1 hold for any cross section $S$, but they do not hold uniformly over all $S$. Audoly and Pomeau suggest [4] that a narrow enough ribbon can be modeled as a rod; specifically they require that $w \ll \sqrt{tL}$.⁷

Alternatively, one could model a ribbon as a narrow sheet. The Sadowsky functional [32, 36], which was recently justified via $\varGamma$-convergence [12, 17], gives an elastic energy functional for an inextensible ribbon (without misfit) depending only on the configuration of the ribbon’s midline.⁸ In the present context it is natural to ask whether something similar can be done for ribbons with misfit. The answer is yes, but the theory is not yet complete. One reasonable analogue [19] of an inextensible plate with misfit is of the form

$$E(\boldsymbol{y}) = \textstyle\begin{cases} \int_{\mathcal{S}} Q{ ( \operatorname{II}_{\boldsymbol{y}}- \operatorname{II}^{0} ) } &\mbox{if } \nabla \boldsymbol{y}^{T} \nabla \boldsymbol{y}= g \\ \infty &\mbox{otherwise} \end{cases} $$

where $\operatorname{II}_{\boldsymbol{y}}$ denotes the second fundamental form of $\boldsymbol{y}$, $\operatorname{II}^{0}$ the preferred second fundamental form and $g$ the preferred metric. Both $\operatorname{II}^{0}$ and $g$ are determined by the misfit, which is defined on a thin, three-dimensional sheet $\mathcal{S}\times (- \epsilon ,\epsilon )$. Freddi et al. derived an analogue of the Sadowsky functional assuming that $g$ is the Euclidean metric, which is true for multilayers [33]. We expect that extending this result to arbitrary $g$ is non-trivial: the set of immersions with some prescribed metric is not well understood.

The rod-like and Sadowsky energies appear to be very different, so given that they model similar physical systems it is natural to ask how they are related. We are not aware of a general answer, but an enlightening example due to Armon et al. [3] compares the narrow and wide regimes for a ribbon with misfit similar to the anisotropic bilayer of Sect. 1.1.⁹ In the narrow ribbon limit $w \ll \sqrt{tL}$ the bending energy dominates, which gives rise to a rod-like theory similar to Eq. (4). If $w \gg \sqrt{tL}$ then the membrane energy dominates, so Armon et al. minimize the bending energy (modified due to misfit) among isometries. This matches the assumptions used in [13] to derive a Sadowski-like functional. The resulting elastic energy functional illustrates a significant difference between rods and ribbons: even with free boundary conditions it may have two local minima, which is impossible for a quadratic functional such as Eq. (4).

5.2 Comparison to the Theory of Kupferman and Solomon

In Sect. 1.3 we mentioned a general theory of dimension reduction due to Kupferman and Solomon [19]. We briefly outline their results, specialized to rods [2], and show that in that case the present theory is more general: in our language, [19] uses $W''(\operatorname{Id})\boldsymbol{{F}}=\operatorname{sym} \boldsymbol{{F}}$ and assumes that $\boldsymbol{{m}}(\boldsymbol{x})$ is linear in ${\boldsymbol{x}}_{\mathrm{cs}}$. Of course, the main strength of the work of Kupferman and Solomon is that it is not restricted to rods, but instead deals with arbitrary manifolds.

The starting point of [19] is an energy of the form¹⁰

$$ E^{\mathrm{KS}}_{h}\bigl(\boldsymbol{y}^{(h)} \bigr) = \frac{C}{h^{4}} \int_{\varOmega _{h}} \operatorname{dist}^{2}\bigl(d \boldsymbol{y}^{(h)}(\boldsymbol{z}), \operatorname{SO}(3)\bigr) d \mathrm{vol}_{g}(\boldsymbol{z}), $$

(19)

where $d\boldsymbol{y}^{(h)}$ is a derivative in the sense of some smooth metric $g$ defined on $\varOmega_{1}$. For the sake of simplicity we take $g(x_{1}, 0, 0) = \operatorname{Id}$. Equation (19) closely resembles the energy $E^{(h)} (\boldsymbol{y}^{(h)})$ (Eq. (2)), where $\boldsymbol{{M}}_{h}^{2}$ is the preferred value of $(\nabla_{h} \boldsymbol{y}^{(h)})^{T}\nabla_{h}\boldsymbol{y}^{(h)}$ and therefore naturally thought of as a metric. A key difference is that $g$ does not depend on $h$. If we set $\boldsymbol{{M}}_{h}^{2}(\boldsymbol{x}) = g(x _{1}, h{\boldsymbol{x}}_{\mathrm{cs}} ) + O(h^{2})$ and take a power series expansion in $h$ we see that $\boldsymbol{{m}}(\boldsymbol{x})$ must be linear in ${\boldsymbol{x}}_{\mathrm{cs}}$.

Kupferman and Solomon study the limit of $E^{\mathrm{KS}}_{h}$ in the sense of reduced-convergence (Eq. 2.3 and 2.4 of [19]), which is closely related the $\varGamma$-convergence. The limiting energy is

$$ E^{\mathrm{KS}}_{\mathrm{rod}}= \int_{0}^{L}C_{1} \bigl( \omega - \omega^{ \mathrm{KS}} \bigr) ^{2} + C_{2} \bigl( \kappa - \kappa^{\mathrm{KS}}_{2} \bigr) ^{2} + C_{3} \bigl( \kappa - \kappa^{\mathrm{KS}}_{3} \bigr) ^{2}, $$

where $\omega$ and $\kappa_{j}$ are defined as in this work, and

$$ \kappa^{\mathrm{KS}}_{j} = \frac{1}{2} \partial_{j} \tilde{g}_{11} \mbox{ and } \omega^{\mathrm{KS}} = \frac{1}{2}(\partial_{2} \tilde{g}_{13} - \partial _{3}\tilde{g}_{12}) $$

(20)

are the preferred curvatures. For notational convenience, in this section alone we use $\partial_{j} \tilde{g} = \partial_{j} g(x_{1}, 0, 0)$. Here we assumed that $\int_{S} x_{2} x_{3} d{\boldsymbol{x}}_{ \mathrm{cs}} = 0$.

We show that, should their theory and ours both apply, the limiting energies prefer the same bend and twist. Let $\boldsymbol{{m}}( \boldsymbol{x}) = \frac{1}{2} ( x_{2} \partial_{2}\tilde{g} + x _{3} \partial_{3}\tilde{g} )$ and $W(\boldsymbol{{F}}) = \operatorname{dist}^{2}(\boldsymbol{{F}},\operatorname{SO}(3))$. The misfit $\boldsymbol{{m}}$ as defined above is exactly achievable: $m_{11} = \frac{1}{2}(x_{2}\partial_{2}\tilde{g}_{11} + x_{3} \partial _{3}\tilde{g}_{11})$ so the preferred curvatures are ${\kappa }^{ \boldsymbol{{m}}}_{j} = \frac{1}{2}\partial_{j}\tilde{g}_{11}= \kappa^{\mathrm{KS}}_{j}$. The preferred twist is slightly more complicated: we set $\beta_{1}^{\boldsymbol{{m}}}= \frac{x_{2} x_{3}}{2}(\partial _{3}\tilde{g}_{12} + \partial_{2}\tilde{g}_{13})$ and ${\omega }^{ \boldsymbol{{m}}} =\omega^{\mathrm{KS}}$. Then

$$ m_{12} = \frac{1}{2}\bigl(-{\omega }^{\boldsymbol{{m}}} x_{3} + \partial _{2}\beta_{1}^{\boldsymbol{{m}}} \bigr) \mbox{ and } m_{13} = \frac{1}{2}\bigl( {\omega }^{\boldsymbol{{m}}} x_{2} + \partial_{3}\beta_{1}^{ \boldsymbol{{m}}} \bigr). $$

(21)

Lastly, we note that the lower two-by-two block of $\boldsymbol{{m}}$ is affine and therefore equal to $\operatorname{e}({\boldsymbol{\beta }} _{\mathrm{cs}})$ for some function ${\boldsymbol{\beta }}_{ \mathrm{cs}}\in W^{1,2}(S, \mathbb{R}^{2})$. It follows that $\kappa^{\mathrm{KS}}_{j}$ and $\omega^{\mathrm{KS}}$ are the preferred values given by both theories.

Notice that, in the rod theory of Kupferman and Solomon, the minimum energy is always 0 and the preferred bend and twist do not depend on the elastic moduli [2].

6 Examples

We make several of the examples from Sect. 1.1 precise.

6.1 The Isotropic Bilayer

We return to the classical example of the bimetallic strip. Consider a square cross section $S = [-1,1]^{2}$ and piecewise constant misfit $\boldsymbol{{m}}(\boldsymbol{x}) = \operatorname{sgn}(x_{3}) \operatorname{Id}$. Suppose that the linear elastic tensor is isotropic:¹¹ $[W''(\operatorname{Id})] \boldsymbol{{F}}= 2\mu \boldsymbol{{F}}+ \lambda \operatorname{tr}( \boldsymbol{{F}}) \operatorname{Id}$ for $\mu > 0$ and $\lambda + \mu > 0$.

Our goal is to find ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$, which gives us the preferred bending and twist. To find the full energy we would also have to compute $\mathcal{Q}_{1}$ (the energy density, which does not depend on the misfit) and the minimum energy $E_{0}$. Theorem 3 reduces this to the evaluation of several integrals. It is clear that ${\omega }^{\boldsymbol{{m}}} = {\kappa }^{\boldsymbol{{m}}}_{2} = 0$. We calculate $\kappa_{3}$.

According to Theorem 3,

$${\kappa }^{\boldsymbol{{m}}}_{3} =\frac{\int_{S} x_{3} m_{11}( \boldsymbol{x})d{\boldsymbol{x}}_{\mathrm{cs}} }{\int_{S} x_{3}^{2} d {\boldsymbol{x}}_{\mathrm{cs}} } = \frac{\int_{-1}^{1} |x_{3}| d \boldsymbol{\boldsymbol{x}}_{3}}{\int_{-1}^{1} x_{3}^{2} d \boldsymbol{\boldsymbol{x}}_{3}} = \frac{3}{2}. $$

This agrees exactly with the result found in [35] (Eq. 6).

We can alternatively invoke Theorem 4 to show that ${\omega }^{\boldsymbol{{m}}} = {\kappa }^{\boldsymbol{{m}}}_{2} = 0$. The relevant symmetry $\boldsymbol{{Q}}$ is given by $q_{11} = 1$ and ${\boldsymbol{{Q}}}_{\mathrm{cs}}{\boldsymbol{x}}_{\mathrm{cs}} = (-x _{2}, x_{3})$.

6.2 The Diagonally Prestrained Bilayer

We return to the diagonally prestrained bilayer of Sect. 1.1. The description of the diagonally prestrained bilayer is based on experiments conducted independently by Armon et al. [3] and Ye et al. [37]. Both experiments dealt with ribbons rather than rods.

It is worth asking why diagonal prestrains (i.e. $\boldsymbol{{m}}$ that have an eigenvector neither in the cross section nor perpendicular to it) are associated with twist. Notice that $\boldsymbol{{F}}^{(1)}$, which measures the strain of a twisted rod, has eigenvectors $(\pm c, \partial_{2}\phi - x_{3}, \partial_{3}\phi + x_{2})$ for $c = |{\nabla }_{\mathrm{cs}}\phi + {\boldsymbol{x}}_{\mathrm{cs}} ^{\perp }|$, which make an angle of $45^{\circ }$ with the long axis. These have eigenvalues $\pm c$.¹² Geometrically, this means that twisting a rod clockwise stretches helices that wrap clockwise around the centerline. Helices wrapping in the opposite direction are instead compressed. It is intuitive that, if ${\omega }^{\boldsymbol{{m}}} \neq 0$, then $\boldsymbol{{m}}$ must favor extension or compression of helices. For isotropic materials this cannot be accomplished with either preferred expansion along the length of the rod or in the cross section. This can be readily seen from the formula for ${\omega }^{\boldsymbol{{m}}}$ in Theorem 3: if $\boldsymbol{{e}}_{1}$ is an eigenvector of $\boldsymbol{{m}}(\boldsymbol{x})$ then $\langle \boldsymbol{{F}} ^{(1)}(\boldsymbol{x}),W''(\operatorname{Id})\boldsymbol{{m}}( \boldsymbol{x}) \rangle =0$.

We again use an isotropic material with square cross section. The misfit is piecewise constant, but rather than being isotropic the two sides prefer the same magnitude of stretching but in two different directions. Making this precise: let $\boldsymbol{u}= (\cos (\theta ), \sin ( \theta ), 0)$ and $\boldsymbol{u}_{\perp }= (-\sin (\theta ), \cos ( \theta ), 0)$. We define the misfit:

$$\boldsymbol{{m}}(\boldsymbol{x}) = \textstyle\begin{cases} \boldsymbol{u}\otimes \boldsymbol{u} &\mbox{if } x_{3} > 0 \\ \boldsymbol{u}_{\perp }\otimes \boldsymbol{u}_{\perp } &\mbox{if } x _{3} < 0. \end{cases} $$

We can also write $\boldsymbol{{m}}$ in the form

$$\boldsymbol{{m}}(\boldsymbol{x}) = \frac{1}{2}\operatorname{Id}+ \frac{ \operatorname{sgn}(x_{3})}{2} \left(\textstyle\begin{array}{c@{\quad}c@{\quad}c} \cos (2\theta ) & \sin (2\theta ) & 0 \\ \sin (2\theta ) & -\cos (2\theta ) & 0 \\ 0 & 0& 0 \end{array}\displaystyle \right) . $$

We observe that $\int_{S} x_{2} m_{11}(\boldsymbol{x}) d{\boldsymbol{x}} _{\mathrm{cs}} = 0$, so ${\kappa }^{\boldsymbol{{m}}}_{2} = 0$. Following Theorem 3 we compute:

$${\kappa }^{\boldsymbol{{m}}}_{3} = \frac{ \int_{S} x_{3} m_{11}( \boldsymbol{x}) d{\boldsymbol{x}}_{\mathrm{cs}} }{ \int_{S} x_{3}^{2} d{\boldsymbol{x}}_{\mathrm{cs}} } = \frac{3}{4} \int_{S} \frac{|x_{3}|}{2} \cos (2\theta )d{ \boldsymbol{x}}_{\mathrm{cs}} = \frac{3}{4}\cos (2\theta ). $$

The preferred twist is given by

$${\omega }^{\boldsymbol{{m}}} = \frac{ \langle \boldsymbol{{F}} ^{(1)},\boldsymbol{{m}} \rangle _{W''(\operatorname{Id})} }{ \lVert \boldsymbol{{F}}^{(1)} \rVert _{W''( \operatorname{Id})}^{2} } = 2\sin (2\theta ) \frac{\int_{S} (\partial _{2}\phi -x_{3})\operatorname{sgn}(x_{3})d{\boldsymbol{x}}_{ \mathrm{cs}} }{\int_{S}|{\nabla }_{\mathrm{cs}}\phi + {\boldsymbol{x}} _{\mathrm{cs}}^{\perp }|^{2}d{\boldsymbol{x}}_{\mathrm{cs}} }. $$

Armon et al. [3] analyzed this system using plate theory of Kupferman and Solomon [19], which requires that the misfit be linear in the thin direction. Our analysis has two principal differences: we work with rods rather than ribbons, and we choose piecewise constant misfit. We unsurprisingly fail to reproduce their results for wide ribbons, but up to a multiplicative constant our results agree with those of Armon et al. in the narrow regime. See Sect. 5.1 for further comments on the distinction between wide and narrow strips.

6.3 Rods with Surface Stress

We turn to a model meant to approximate rods with surface stress using a thin layer with misfit. Chen et al. [6] reported an experiment in which strained latex membranes were glued to thicker rubber sheets. Ribbons were cut out of the composite sheet. Depending on the angle between the long axis of the ribbon and the direction in which the latex was stretched, the ribbon can bend, twist or form a helix. As before, we use rods whereas the experiment used ribbons. The principal difference between this experiment and [37] or [3] is that one layer is much thinner than the other.

We again use an isotropic material and a square cross section $S = [-1,1]^{2}$. Let $\epsilon > 0$, which will be the non-dimensional thickness of the (thin) latex sheet. The direction in which the latex was stretched is given by the unit vector $\boldsymbol{u}= (\cos ( \theta ), \sin (\theta ), 0)$. The misfit $\boldsymbol{{m}}$ is

$$\boldsymbol{{m}}(\boldsymbol{x}) = \textstyle\begin{cases} \frac{1}{\epsilon }\boldsymbol{u}\otimes \boldsymbol{u} &\mbox{if } x _{3} > 1-\epsilon \\ 0 &\mbox{otherwise.} \end{cases} $$

We compute ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$. We use Theorem 3 to compute the other two components of ${\boldsymbol{{A}}}^{\boldsymbol{{m}}}$. As in the last example, it is immediately clear that ${\kappa }^{\boldsymbol{{m}}}_{2} = 0$.

$$\begin{aligned} {\kappa }^{\boldsymbol{{m}}}_{3} =& \frac{ \int_{S} x_{3}m_{11} d {\boldsymbol{x}}_{\mathrm{cs}} }{ \int_{S} x_{3}^{2} d{\boldsymbol{x}} _{\mathrm{cs}} } = \frac{3}{4}(2-\epsilon )\cos^{2}\theta \\ {\omega }^{\boldsymbol{{m}}} =& \sin 2\theta \frac{\frac{1}{\epsilon }\int_{1-\epsilon }^{1}\int_{-1}^{1} (\partial_{2}\phi - x_{3}) d \boldsymbol{\boldsymbol{x}}_{2} d\boldsymbol{\boldsymbol{x}}_{3}}{\int _{S} |{\nabla }_{\mathrm{cs}}\phi + {\boldsymbol{x}}_{\mathrm{cs}} ^{\perp }|^{2} d{\boldsymbol{x}}_{\mathrm{cs}} }. \end{aligned}$$

We are especially interested in the behavior when $\epsilon$ is small, so we note that

$$\lim_{\epsilon \to 0}{\omega }^{\boldsymbol{{m}}} = \sin 2\theta \frac{ \int_{-1}^{1} (\partial_{2}\phi (x_{2},1) - 1) d \boldsymbol{\boldsymbol{x}}_{2} }{\int_{S} |{\nabla }_{\mathrm{cs}} \phi + {\boldsymbol{x}}_{\mathrm{cs}}^{\perp }|^{2} d{\boldsymbol{x}} _{\mathrm{cs}} }. $$

Chen et al. [6] found an explicit minimizer to a linear elastic energy with surface stress in a three-dimensional body. The body is thin in only one direction, and therefore the solution resembles a plate more than a rod. For this reason their analysis does not match this example exactly, but it is qualitatively similar. In particular, our results and theirs agree that the rod forms a part of a circle if $\theta =0$, and in general the centerline forms a helix.

6.4 The Trilayer

We turn to an example in which thin rods behave very differently from thin ribbons. This is not motivated by any particular experiment, though kelp blades are somewhat similar [18].

Consider a rod comprised of three layers, as shown in Fig. 5. The outer two layers are identical, and the misfit favors isotropic expansion relative to the inner layer. For definiteness, we consider the following problem. Let $S = [- \epsilon ,\epsilon ]\times [-1,1]$ and with isotropic elastic stiffness tensor.

$$\boldsymbol{{m}}(\boldsymbol{x}) = \textstyle\begin{cases} \operatorname{Id} &\mbox{if } |x_{3}| > \frac{1}{3} \\ 0 &\mbox{otherwise.} \end{cases} $$

Fig. 5

A schematic of the isotropic trilayer. The misfit prefers expansion in the outer layers

It is natural to guess that the rod should twist, because twist makes lines along the outside of the rod expand without changing the midline. This logic is, however, incorrect: due to mirror symmetry, the preferred twist must be 0 (Theorem 4 with $q_{11} = -1$, ${\boldsymbol{{Q}}}_{\mathrm{cs}}= \operatorname{Id}$). The key error is that we ignored strains due to shear which are $O(h\omega )$, whereas the change in length scales as $h^{2}\omega ^{2}$. Shear dominates in the thin-rod limit. In Remark 6 we noticed that, in an isotropic rod, twist is caused by misfit $\boldsymbol{{m}}$ that prefers shear.

The geometric reasoning that suggested twist was not completely wrong. Ribbons with similar misfit can prefer twist, as studied in [5] (Example 2 of Sect. 1.4). Formally, the shear should scale as $h\omega \epsilon$ while the membrane effect is order $h^{2}\omega^{2}$. In a ribbon both $h$ and $\epsilon$ are small, but treating this is a rod takes the $h\to 0$ limit first, leaving $\epsilon$ fixed, then sends $\epsilon$ to 0. Theorem 1 applies for any $\epsilon$, but it does not apply uniformly for all $\epsilon > 0$. We could instead consider the opposite distinguished limit: first we $\epsilon \to 0$, then $h\to 0$. This approach treats the ribbon as a narrow two-dimensional sheet.¹³

6.5 Quartz

As mentioned in Sect. 1.1, naturally occurring $\alpha$-quartz sometimes resembles a twisted macroscopic rod. It has been proposed, for an example by Shtukenberg et al. in [34] Sect. 5.7, that the twist is caused by slight variations in the preferred lengths of the crystalline lattice. Attempting to capture this idea within the framework of the present study, it seems natural to model a quartz crystal as a rod with misfit. Alas, the attempt seems to fail: Proposition 1 shows that under some (reasonable, in our view) hypotheses based on the symmetries of quartz, the associated rod should have no preferred twist. This is of course a highly idealized picture of quartz, as we briefly discuss at the end of this subsection.

To get started, we begin by reviewing the physical origin of the misfit. A quartz crystal may be long and thin because the growth processes on distinct (not symmetry related) faces are different. In particular, some faces grow much faster than others. The differences in the growth processes also cause slight impurities,¹⁴ which give rise to variations in $\boldsymbol{{m}}$. Although we will not use this, it is natural to assume that $\boldsymbol{{m}}$ is constant on polyhedral zones: each point $\boldsymbol{x}$ in the crystal is included because some face grew through it, which partitions the crystal. Two different points in the same zone grew through the same process, and so likely have similar misfit.

We turn to a discussion of symmetry, which is essential in our proof of Proposition 1. The crystal lattice of quartz has three axes of twofold rotational symmetry (called $a$ axes), which are perpendicular to a threefold axis of symmetry (the $c$ axis). The crystal, should it resemble a rod, advances along an $a$ axis [34]. The results in this section only use the symmetry of the crystal lattice under the rotation matrix

$$\boldsymbol{{Q}}= \left(\textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{array}\displaystyle \right) $$

representing the twofold symmetry around the long axis. As in Theorem 4, ${\boldsymbol{{Q}}}_{\mathrm{cs}}= - \operatorname{Id}_{\mathbb{R}^{2}}$ denotes the lower right two-by-two block of $\boldsymbol{{Q}}$. We assume that the three-dimensional elastic energy inherits the symmetry $\boldsymbol{{Q}}$ of the crystal lattice in the sense of Conditions 1–3 of Proposition 1 below, and that the misfit respects this symmetry in the sense of Condition 4.¹⁵

Proposition 1

Assume that $W''(\operatorname{Id})$, $S$ and $\boldsymbol{{m}}$ satisfy the following conditions for $\boldsymbol{{Q}}$ defined above.

• 1. (Symmetry of the Hooke’s Law) For any $\boldsymbol{{F}}\in \mathrm{Sym}(3)$, $W''(\operatorname{Id})(\boldsymbol{{Q}}^{T} \boldsymbol{{F}}\boldsymbol{{Q}}) = \boldsymbol{{Q}}^{T} (W''( \operatorname{Id})\boldsymbol{{F}}) \boldsymbol{{Q}}$, and

• 2. (Symmetry of the cross section) If ${\boldsymbol{x}}_{ \mathrm{cs}} \in S$ then ${\boldsymbol{{Q}}}_{\mathrm{cs}}{\boldsymbol{x}} _{\mathrm{cs}} \in S$, and

• 3. (Symmetry of the misfit) For a.e. $\boldsymbol{x}\in \varOmega$, $\boldsymbol{{Q}}^{T} \boldsymbol{{m}}(\boldsymbol{x}) \boldsymbol{{Q}}= \boldsymbol{{m}}(\boldsymbol{{Q}}\boldsymbol{x})$, and

• 4. (Misfit due to lattice parameters) For a.e. $\boldsymbol{x} \in \varOmega$, $\boldsymbol{{Q}}^{T} \boldsymbol{{m}}(\boldsymbol{x}) \boldsymbol{{Q}}= \boldsymbol{{m}}(\boldsymbol{x})$.

It follows that ${\boldsymbol{{A}}}^{\boldsymbol{{m}}} = 0$.

Proof

We first check that ${\boldsymbol{\kappa }}^{\boldsymbol{{m}}}=0$. Noting that $q_{11} = 1$, we see that the first three conditions above are precisely the assumptions of Theorem 4. $\boldsymbol{{Q}}$ is a rotation matrix, so ${\boldsymbol{\kappa }} ^{\boldsymbol{{m}}} = 0$.

We again invoke Theorem 4, but this time with respect to $-\boldsymbol{{Q}}$ rather than $\boldsymbol{{Q}}$. Because $\det (-\boldsymbol{{Q}}) = -1$, in order to conclude ${\omega }^{ \boldsymbol{{m}}}=0$ it suffices to check that the minimization problem is symmetric under $-\boldsymbol{{Q}}$:

• 1. (Symmetry of the Hooke’s Law with respect to $-\boldsymbol{{Q}}$ ) For any $\boldsymbol{{F}}\in \mathrm{Sym}(3)$,

  $$W''(\operatorname{Id}) \bigl( (-\boldsymbol{{Q}})^{T} \boldsymbol{{F}}(- \boldsymbol{{Q}}) \bigr) = (-\boldsymbol{{Q}})^{T} \bigl(W''( \operatorname{Id})\boldsymbol{{F}}\bigr) (- \boldsymbol{{Q}}). $$

• 2. (Symmetry of the cross section with respect to $- \boldsymbol{{Q}}$ ) If ${\boldsymbol{x}}_{\mathrm{cs}} \in S$ then $-{\boldsymbol{{Q}}}_{\mathrm{cs}}{\boldsymbol{x}}_{\mathrm{cs}} \in S$.

• 3. (Symmetry of the misfit with respect to $-\boldsymbol{{Q}}$ ) For a.e. $\boldsymbol{x}\in S$, $(-\boldsymbol{{Q}})^{T} \boldsymbol{{m}}(\boldsymbol{x}) (-\boldsymbol{{Q}}) = \boldsymbol{{m}}(x_{1}, -{\boldsymbol{{Q}}}_{\mathrm{cs}}{\boldsymbol{x}} _{\mathrm{cs}} )$.

The condition for symmetry of the Hooke’s Law is quadratic in $\boldsymbol{{Q}}$, so it holds for $-\boldsymbol{{Q}}$ as well. The symmetry of the cross section is trivial because $-{\boldsymbol{{Q}}} _{\mathrm{cs}}= \operatorname{Id}$. The symmetry of the misfit with respect to $-\boldsymbol{{Q}}$ follows from the assumption that $\boldsymbol{{Q}}^{T} \boldsymbol{{m}}(\boldsymbol{x}) \boldsymbol{{Q}}= \boldsymbol{{m}}(\boldsymbol{x})$. □

We briefly comment on the differences between our model and real quartz. The most significant is that quartz is likely highly inelastic, except perhaps in a thin newly-accreted layer. Alternatively, perhaps it is also possible that our assumptions on the form of $\boldsymbol{{m}}$ are mistaken: although we have a plausible explanation why we might expect misfit of this form, there might be similar explanations for different types of misfit. Finally, real quartz should be narrow near the tip compared to the base, although the thickness changes slowly. The present rod theory deals only with cylindrical bodies: the misfit can depend on $x_{1}$, but the shape of the cross section cannot.

7 $\varGamma$-Convergence

Although we think of a rod as a one-dimensional object, it is really a thin, three-dimensional object governed by three-dimensional elasticity theory. We would like to rigorously reduce this to a one-dimensional theory in the limit as thickness tends towards 0. We will show that the three-dimensional energy functional $E^{(h)}$ (Eq. (2)) $\varGamma$-converges to the one-dimensional energy $E$ (Eq. (4)) in the sense of Theorem 1. The analogous theorem for rods without misfit, which has a similar proof, was done independently in [31] and [27].

Whenever we study $\varGamma$-convergence it is useful to identify compact sets in the corresponding topology. The compactness result for rods without misfit, stated and proved in [27] and [31], also applies here and is restated below in Theorem 6.

Theorem 6

(Compactness)

Let $\boldsymbol{y}^{(h)}$ be a sequence in $W^{1,2}(\varOmega , \mathbb{R}^{3})$ such that

$$\limsup_{h\to 0}\frac{1}{h^{2}} \int_{\varOmega }\operatorname{dist}^{2} \bigl( \nabla_{h}\boldsymbol{y}^{(h)},\operatorname{SO}(3) \bigr) d \boldsymbol{\boldsymbol{x}}< \infty . $$

• 1. There exists a subsequence (not relabeled) such that $\nabla_{h} \boldsymbol{y}^{(h)}\to \boldsymbol{{R}}$ strongly in $L^{2}(\varOmega )$. Furthermore, $\boldsymbol{{R}}\in W^{1,2}(\varOmega \to \operatorname{SO}(3))$ depends only on $x_{1}$.

• 2. Given some $\boldsymbol{{R}}^{(h)}$ (rotations approximating $\nabla_{h}\boldsymbol{y}^{(h)}$) define $\boldsymbol{{G}}^{(h)}$ (infinitesimal displacement) by

  $$\bigl(\boldsymbol{{R}}^{(h)}\bigr)^{T} \nabla_{h} \boldsymbol{y}^{(h)}( \boldsymbol{x}) = \operatorname{Id}+ h \boldsymbol{{G}}^{(h)}( \boldsymbol{x}). $$

  For some well-chosen sequence of rotations $\boldsymbol{{R}}^{(h)}$. $\boldsymbol{{G}}^{(h)}$ converges weakly in $L^{2}$ to a matrix $\boldsymbol{{G}}\in L^{2} ( \varOmega ,\mathbb{R}^{3} )$ with $\boldsymbol{{G}}(x_{1},\cdot ,\cdot ) \in \mathcal{E} ( \boldsymbol{{R}}^{T}\partial_{1} \boldsymbol{{R}} )$ almost everywhere.

The first part is Theorem 2.2 of [27], and the second part is embedded in the proof of Theorem 3.1 of the same paper. Theorem 6 is closely related to Theorem 3.1 of [31].

Notice that any sequence with $E^{(h)} (\boldsymbol{y}^{(h)}) \le C < \infty$ satisfies the hypotheses of Theorem 6 by the triangle inequality and the coerciveness of $W$:

$$\begin{aligned} C \ge & \frac{1}{h^{2}} \int_{\varOmega } \operatorname{dist}^{2} \bigl( \nabla_{h} \boldsymbol{y}(\boldsymbol{x}),\operatorname{SO}(3) \boldsymbol{{M}}_{h}^{-1} \bigr) d\boldsymbol{\boldsymbol{x}} \\ =& \frac{1}{h^{2}} \int_{\varOmega } \operatorname{dist}^{2} \bigl( \nabla _{h} \boldsymbol{y}(\boldsymbol{x}),\boldsymbol{{R}}(\boldsymbol{x}) \boldsymbol{{M}}_{h}^{-1} \bigr) d\boldsymbol{\boldsymbol{x}} \mbox{ for some }\boldsymbol{{R}}\in \operatorname{SO}(3) \\ \gtrsim & \frac{1}{h^{2}} \int_{\varOmega } \bigl( \operatorname{dist} ^{2} \bigl( \nabla_{h} \boldsymbol{y}(\boldsymbol{x}),\boldsymbol{{R}} \bigr) - \operatorname{dist}^{2}\bigl(\boldsymbol{{R}},\boldsymbol{{R}} \boldsymbol{{M}}_{h}^{-1}\bigr) \bigr) d\boldsymbol{ \boldsymbol{x}} \\ \geq & \frac{1}{h^{2}} \int_{\varOmega } \operatorname{dist}^{2} \bigl( \nabla_{h} \boldsymbol{y}(\boldsymbol{x}),\operatorname{SO}(3) \bigr) d \boldsymbol{\boldsymbol{x}}- \int_{\varOmega }\bigl\vert \boldsymbol{{m}}( \boldsymbol{x})\bigr\vert ^{2} d\boldsymbol{\boldsymbol{x}}. \end{aligned}$$

We recall Theorem 1. This theorem has two parts; the first bounds the energy from below (called the lim inf inequality) and the second provides an ansatz achieving the lower bound (called the lim sup inequality). The proof is similar to that of [27] Theorem 3.1 and [31] Propositions 4.1 and 5.1. The key ideas in the ansatz are found in Sect. 2.2, assuming enough regularity to use Taylor’s Theorem.

Proof of Theorem 1

We omit the subscripts on $h$, and we do not relabel subsequences.

Lim inf inequality. Assume that $\liminf E^{(h)} ( \boldsymbol{y}^{(h)}) < \infty$ (if not, the inequality is trivial). By the compactness lemma, there exists rotations $\boldsymbol{{R}} ^{(h)}$ and deformations $\boldsymbol{{G}}^{(h)}$, related by $\nabla_{h}\boldsymbol{y}^{(h)}= \boldsymbol{{R}}^{(h)}( \operatorname{Id}+ h\boldsymbol{{G}}^{(h)})$ such that up to a subsequence $\boldsymbol{{G}}^{(h)}\to \boldsymbol{{G}}$ weakly in $L^{2}$, with $\boldsymbol{{G}}(x_{1})\in \mathcal{E}$. By frame indifference of $W$,

$$ E^{(h)} \bigl(\boldsymbol{y}^{(h)}\bigr) = \frac{1}{h^{2}} \int_{\varOmega }W \bigl( \bigl(\operatorname{Id}+ h \boldsymbol{{G}}^{(h)}\bigr) (\operatorname{Id}- h \boldsymbol{{m}}) \bigr) d\boldsymbol{\boldsymbol{x}}. $$

Let $\rho (\boldsymbol{{F}})\in o(|\boldsymbol{{F}}|^{2})$ be the Taylor Series remainder such that $W(\operatorname{Id}+ \boldsymbol{{F}}) = \operatorname{Id}+ \mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) } + \rho (\boldsymbol{{F}})$, and let $\bar{\rho }(t) = \sup_{|\boldsymbol{{F}}| \leq t} \rho (\boldsymbol{{F}})$. We also define

$$\chi_{h}(\boldsymbol{x}) = \textstyle\begin{cases} 1 &\mbox{if }|\boldsymbol{{G}}^{(h)}(\boldsymbol{x})| < h^{-1/2} \\ 0 &\mbox{otherwise.} \end{cases} $$

This goes to 1 in measure because $\boldsymbol{{G}}^{(h)}$ is bounded in $L^{2}$. It follows that $\tilde{\boldsymbol{{G}}}^{(h)} := ( \boldsymbol{{G}}^{(h)} - \boldsymbol{{m}}- h\boldsymbol{{G}}^{(h)} \boldsymbol{{m}})\chi_{h}\to \boldsymbol{{G}}-\boldsymbol{{m}}$ weakly in $L^{2}$.

Returning to the computation of $E^{(h)}$:

$$\begin{aligned} E^{(h)} \bigl(\boldsymbol{y}^{(h)}\bigr) \geq & \frac{1}{h^{2}} \int_{\varOmega }W \bigl( \bigl(\operatorname{Id}+ h \boldsymbol{{G}}^{(h)}\bigr) (\operatorname{Id}- h\boldsymbol{{m}}) \bigr) \chi_{h} d\boldsymbol{\boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{ \bigl( \tilde{ \boldsymbol{{G}}}^{(h)} \bigr) } + \frac{1}{h^{2}}\rho \bigl( h \tilde{ \boldsymbol{{G}}}^{(h)} \bigr) \chi_{h} d \boldsymbol{ \boldsymbol{x}} \\ \geq & \int_{\varOmega }\mathcal{Q}_{3}{ \bigl( \tilde{ \boldsymbol{{G}}} ^{(h)} \bigr) } - \bigl\vert \tilde{ \boldsymbol{{G}}}^{(h)}\bigr\vert ^{2}\frac{\bar{ \rho } ( h\vert \tilde{\boldsymbol{{G}}}^{(h)}\vert ) }{h ^{2}|\tilde{\boldsymbol{{G}}}^{(h)}|^{2}} \chi_{h} d \boldsymbol{\boldsymbol{x}}. \end{aligned}$$

By using weak lower semicontinuity of the first term, boundedness of $\Vert \tilde{\boldsymbol{{G}}}^{(h)}\Vert _{L^{2}(\varOmega )}$ and that $\bar{\rho }(t) \in o(t^{2})$ we conclude that

$$\begin{aligned} \liminf_{h\to 0} E^{(h)} \bigl(\boldsymbol{y}^{(h)} \bigr) \geq & \int_{\varOmega }\mathcal{Q}_{3}{ ( \boldsymbol{{G}}- \boldsymbol{{m}} ) }d \boldsymbol{\boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{ ( \boldsymbol{{G}}- \boldsymbol{{m}}_{\mathcal{E}}- \boldsymbol{{m}}_{\perp } ) }d \boldsymbol{ \boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{ ( \boldsymbol{{G}}- \boldsymbol{{m}}_{\mathcal{E}} ) } + \bigl\langle \boldsymbol{{G}}- \boldsymbol{{m}}_{\mathcal{E}}, W''(\operatorname{Id}) \boldsymbol{{m}}_{\perp }\bigr\rangle + \mathcal{Q}_{3}{ ( \boldsymbol{{m}}_{\perp } ) } d\boldsymbol{\boldsymbol{x}} \\ =& E_{0}+ \int_{\varOmega }\mathcal{Q}_{3}{ ( \boldsymbol{{G}}- \boldsymbol{{m}}_{\mathcal{E}} ) }d\boldsymbol{\boldsymbol{x}} \\ \geq & E_{0}+ \int_{0}^{L} \min_{\boldsymbol{{F}}\in \mathcal{E}(\boldsymbol{{R}}^{T} \partial _{1} \boldsymbol{{R}}-{\boldsymbol{{A}}}^{\boldsymbol{{m}}})} \int_{S} \mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) } d{ \boldsymbol{x}} _{\mathrm{cs}} dx_{1} \\ =& E_{0}+ \int_{0}^{L}\mathcal{Q}_{1}{ \bigl( \boldsymbol{{R}}^{T} \partial_{1} \boldsymbol{{R}}- { \boldsymbol{{A}}}^{\boldsymbol{{m}}} \bigr) }dx_{1} \\ =& E(\boldsymbol{{R}}). \end{aligned}$$

The third line uses the orthogonality of $\boldsymbol{{m}}_{\perp }$ and ℰ. The fifth line notices that $G-\boldsymbol{{m}}_{ \mathcal{E}}\in \mathcal{E}(\boldsymbol{{R}}^{T}\partial_{1} \boldsymbol{{R}}-{\boldsymbol{{A}}}^{\boldsymbol{{m}}})$. This concludes the proof of the $\varGamma$-lim inf inequality.

Lim sup inequality. Let $\boldsymbol{{R}}\in W^{1,2}(\varOmega , \operatorname{SO}(3))$ depending only on $x_{1}$. We construct a sequence $\boldsymbol{y}^{(h)}$ such that $\nabla_{h}\boldsymbol{y} ^{(h)}\to \boldsymbol{{R}}$ in $L^{2}$ and

$$E(\boldsymbol{{R}}) \geq \limsup_{h\to 0} E^{(h)} \bigl( \nabla_{h} \boldsymbol{y}^{(h)}\bigr). $$

As before, we use $\boldsymbol{{A}}= \boldsymbol{{R}}^{T}\partial_{1} \boldsymbol{{R}}$ to encode the bending and torsion given by the frame $\boldsymbol{{R}}$. Recall also the definitions from Sect. 2.1. In particular, we can extract ${\boldsymbol{{A}}} ^{\boldsymbol{{m}}}$ from the misfit $\boldsymbol{{m}}$, which gives the preferred bending and torsion. The displacement of the cross section $\boldsymbol{\beta }$ will also be important. The minimization problem in Eq. (5) associates to $\boldsymbol{{A}}$ a minimizer¹⁶ $\operatorname{sym} ( \boldsymbol{{A}}{\boldsymbol{x}}_{\mathrm{cs}} |{\nabla }_{\mathrm{cs}}{\boldsymbol{\beta }} )$, which defines $\boldsymbol{\beta }$. The misfit also gives a preferred displacement ${\boldsymbol{\beta }}^{\boldsymbol{{m}}}$ and a small stretching ${\xi }^{\boldsymbol{{m}}}$.

The core of this argument is found in Sect. 2.2. We make that section rigorous by mollifying the functions involved so that we can use Taylor’s theorem. Because the functions depend on $\boldsymbol{{A}}-{\boldsymbol{{A}}} ^{\boldsymbol{{m}}}$, we mollify $\boldsymbol{{A}}-{\boldsymbol{{A}}} ^{\boldsymbol{{m}}}$ and $\boldsymbol{\beta }-{\boldsymbol{\beta }} ^{\boldsymbol{{m}}}$. We use these to pick $\nabla_{h}\boldsymbol{y} ^{(h)}$ to leading order in $h$, which allows us to define $\boldsymbol{y}^{(h)}$ by integrating. The paper [27] uses a slightly different proof; it instead mollifies $\boldsymbol{y} ^{(h)}$ and then projects $\nabla_{h}\boldsymbol{y}^{(h)}$ onto $\operatorname{SO}(3)$.

We will pick

$$\boldsymbol{y}^{(\delta ,h)}(\boldsymbol{x}) = \tilde{\boldsymbol{y}} ^{(\delta )}(x_{1}) + h \bigl( \boldsymbol{t}^{(\delta )}(x_{1}) + x _{2} \boldsymbol{r}^{(\delta )}_{2}(x_{1}) + x_{3} \boldsymbol{r}_{3} ^{(\delta )}(x_{1}) \bigr) + h^{2}\boldsymbol{{R}}^{(\delta )}(x_{1}) \boldsymbol{\beta }^{(\delta )}(\boldsymbol{x}) $$

where $\tilde{\boldsymbol{y}}^{(\delta )}\in W^{1,2}([0,l],\mathbb{R} ^{3})$ controls the midline, $\boldsymbol{t}^{(\delta )}\in W^{1,2}([0,l], \mathbb{R}^{3})$ controls the infinitesimal stretching and shear, and $\boldsymbol{\beta }^{(\delta )}(\boldsymbol{x})$ is the next-order deformation of the cross section induced by the curvature and torsion of the rod in addition to the misfit. All of these depend on a small parameter $\delta$, which will be used to smooth out $\boldsymbol{{R}}$.

Consider a family of mollifiers $\psi_{\delta }(\boldsymbol{x}) = \frac{1}{ \delta^{3}}\psi { ( \frac{\boldsymbol{x}}{\delta } ) }$ with the standard properties $\psi \in C^{1}_{0}(\mathbb{R}^{3}, [0,\infty ))$ and $\int \psi (\boldsymbol{x}) d\boldsymbol{\boldsymbol{x}}= 1$. It follows that $\lVert \nabla \psi_{\delta }\rVert_{L^{2}} \lesssim \delta^{-5/2}$.

Using the fact that $\varOmega$ has Lipschitz boundary, we extend $\boldsymbol{{A}}$ and $\boldsymbol{\beta }$ in a $W^{1,2}$-bounded fashion to some open, bounded superset of $\bar{\varOmega }$. Let $\boldsymbol{{A}}^{(\delta )}= {\boldsymbol{{A}}}^{\boldsymbol{{m}}} + ( \boldsymbol{{R}}^{T}\partial_{1} \boldsymbol{{R}}- {\boldsymbol{{A}}} ^{\boldsymbol{{m}}} ) *\psi_{\delta }$ and $\boldsymbol{\beta } ^{(\delta )} = {\boldsymbol{\beta }}^{\boldsymbol{{m}}} + ( \boldsymbol{\beta }- {\boldsymbol{\beta }}^{\boldsymbol{{m}}} ) * \psi_{\delta }$, where $\boldsymbol{\beta }(x_{1},\cdot )$ minimizes $\int_{S} \mathcal{Q}_{3}{ ( \operatorname{sym} ( \boldsymbol{{A}}{\boldsymbol{x}}_{\mathrm{cs}} |{\nabla }_{ \mathrm{cs}}\boldsymbol{\beta } ) ) }d{\boldsymbol{x}}_{ \mathrm{cs}}$. We define $\boldsymbol{{R}}^{(\delta )}$ by the differential equation $\partial_{1}\boldsymbol{{R}}^{(\delta )}= \boldsymbol{{A}}^{(\delta )}\boldsymbol{{R}}^{(\delta )}$ with $\boldsymbol{{R}}^{(\delta )}(0) = \boldsymbol{{R}}(0)$. The midline is given by $\tilde{\boldsymbol{y}}^{(\delta )}(x_{1}) = \int_{0}^{x_{1}} \boldsymbol{r}^{(\delta )}_{1}(s)ds$, and the infinitesimal stretching by $\partial_{1} \boldsymbol{t}(x_{1}) = r(x_{1}){\xi }^{ \boldsymbol{{m}}}$.

We must check that $\boldsymbol{y}^{(\delta ,h)}$ converges in the right sense to $\boldsymbol{y}$ as $(h,\delta )\to 0$, $h \le \delta^{5/2}$. First, we note that $\boldsymbol{{A}}^{(\delta )}\to \boldsymbol{{A}}$ in $L^{2}$ and $\boldsymbol{\beta }^{(\delta )}\to \boldsymbol{\beta }$ in $W^{1,2}$. By continuous dependence of the differential equation defining $\boldsymbol{{R}}^{(\delta )}$ on $\boldsymbol{{A}}^{(\delta )}$ it follows that $\boldsymbol{{R}}^{( \delta )}\to \boldsymbol{{R}}$ in $W^{1,2}$. We compute the gradient to conclude that $\nabla \boldsymbol{y}^{(\delta ,h)}\to \boldsymbol{{R}}$ in $L^{2}$.

$$\begin{aligned} \nabla_{h} \boldsymbol{y}^{(\delta ,h)}(\boldsymbol{x}) =& \boldsymbol{{R}}^{(\delta )}+ h \bigl( \partial_{1} \boldsymbol{t}+ x _{2} \partial_{1} \boldsymbol{r}_{2}^{(\delta )} + x_{3} \partial_{1} \boldsymbol{r}_{3}^{(\delta )} | {\nabla }_{\mathrm{cs}} \bigl( \boldsymbol{{R}}^{(\delta )} \boldsymbol{\beta }^{(\delta )} \bigr) \bigr) \\ &{}+ h^{2}\partial_{1} \bigl( \boldsymbol{{R}}^{(\delta )} \boldsymbol{\beta }^{(\delta )} \bigr) \otimes \boldsymbol{{e}}_{1}. \end{aligned}$$

The first term converges to $\boldsymbol{{R}}$ as $\delta \to 0$. The second term is bounded in $L^{2}$ uniformly in $\delta$ and is small in $h$, so it vanishes as $(h,\delta )\to 0$. We note that the final term is bounded in $L^{2}$ by $h^{2}\delta^{-5/2}$ due to the bounds on $\lVert \partial_{1}\psi \rVert_{L^{2}}$. Thus this vanishes in the limit $(h,\delta )\to 0$ and $h \le \delta^{5/2}$. By taking a subsequence, we can also assume that $\boldsymbol{{R}}^{(\delta )}$, $\partial_{1} \boldsymbol{{R}}^{(\delta )}$, $\boldsymbol{\beta }^{( \delta )}$ and ${\nabla }_{\mathrm{cs}}\boldsymbol{\beta }^{(\delta )}$ converge almost everywhere.

We now show that the recovery sequence gives the right energy. The proof has two steps. First, we hold $\delta$ fixed and let $h\to 0$. We then pick a dependence of $\delta$ on $h$ to find the recovery sequence.

We expand $(\boldsymbol{{R}}^{(\delta )})^{T}\nabla_{h} \boldsymbol{y}^{(\delta ,h)}(\boldsymbol{x})\boldsymbol{{M}}_{h}^{-1}( {\boldsymbol{x}}_{\mathrm{cs}} )$ in $h$ to estimate the energy:

$$\begin{aligned} \bigl(\boldsymbol{{R}}^{(\delta )}\bigr)^{T}\nabla_{h} \boldsymbol{y}^{(\delta ,h)}(\boldsymbol{x})\boldsymbol{{M}}_{h}^{-1}( \boldsymbol{x}) =& \bigl( \operatorname{Id}+ h\boldsymbol{{B}}^{(\delta )}+ h^{2} \boldsymbol{{C}}^{(\delta )} \bigr) \bigl(\operatorname{Id}- h \boldsymbol{{m}}+ O\bigl(h^{2}\bigr)\bigr) \\ =&\operatorname{Id}+ h\bigl(\boldsymbol{{B}}^{(\delta )}-\boldsymbol{{m}} \bigr) + O\bigl(h^{2}\bigr), \end{aligned}$$

where the $O(h^{2})$ terms are uniform in $\boldsymbol{x}$ because $m\in L^{\infty }$ and

$$\begin{aligned} \boldsymbol{{B}}^{(\delta )} =& \bigl( s + \boldsymbol{{A}}^{(\delta )}{ \boldsymbol{x}}_{\mathrm{cs}} \big| {\nabla }_{\mathrm{cs}} {\boldsymbol{ \beta }^{(\delta )}} \bigr), \\ \boldsymbol{{C}}^{(\delta )} =& \bigl(\boldsymbol{{A}}^{(\delta )} \boldsymbol{\beta }^{(\delta )} + \partial_{1}\boldsymbol{\beta }^{( \delta )}\bigr)\otimes \boldsymbol{{e}}_{1}. \end{aligned}$$

Expanding $\boldsymbol{{m}}= \boldsymbol{{m}}_{\mathcal{E}}+ \boldsymbol{{m}}_{\perp }$ as before,

$$\boldsymbol{{B}}^{(\delta )}-\boldsymbol{{m}}= \bigl( \bigl( \boldsymbol{{A}}^{(\delta )}-{\boldsymbol{{A}}}^{\boldsymbol{{m}}}\bigr) { \boldsymbol{x}}_{\mathrm{cs}} \big| {\nabla }_{\mathrm{cs}}{\bigl( \boldsymbol{\beta }^{(\delta )}-{\boldsymbol{\beta }}^{ \boldsymbol{{m}}}\bigr)} \bigr) - \boldsymbol{{m}}_{\perp }({\boldsymbol{x}} _{\mathrm{cs}} ). $$

The next step is to apply Taylor’s Theorem to the energy. In the sequel $c_{j}$ denotes constants possibly depending on $\delta$ but not $\boldsymbol{x}$ or $h$. We first notice that

$$\operatorname{dist} \bigl( \nabla_{h} \boldsymbol{y}^{(\delta ,h)} \boldsymbol{{M}}_{h}^{-1},\operatorname{SO}(3) \bigr) < c_{1} h. $$

By the facts that $W = 0$ on $\operatorname{SO}(3)$ and that $W$ is $C^{2}$ near $\operatorname{SO}(3)$ we conclude that

$$\frac{1}{h^{2}} W \bigl( \nabla_{h} \boldsymbol{y}^{(\delta ,h)} \boldsymbol{{M}}_{h}^{-1} \bigr) < c_{2} $$

for all sufficiently small $h$. Thus the bounded convergence theorem shows that:

$$\begin{aligned} \lim_{h \to 0} E^{(h)} \bigl(\nabla_{h} \boldsymbol{y}^{(\delta ,h)}\bigr) =& \lim_{h \to 0} \frac{1}{h^{2}} \int_{\varOmega }W \bigl( \operatorname{Id}+ h\bigl( \boldsymbol{{B}}^{(\delta )}-\boldsymbol{{m}}\bigr) + O\bigl(h^{2} \bigr) \bigr) d \boldsymbol{\boldsymbol{x}} \\ =& \int_{\varOmega }\lim_{h \to 0}\frac{1}{h^{2}} W \bigl( \operatorname{Id}+ h\bigl(\boldsymbol{{B}}^{(\delta )}-\boldsymbol{{m}} \bigr) + O\bigl(h^{2}\bigr) \bigr) d\boldsymbol{\boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{ \bigl( \boldsymbol{{B}}^{(\delta )}- \boldsymbol{{m}} \bigr) } d\boldsymbol{ \boldsymbol{x}} \\ =& \int_{\varOmega }\mathcal{Q}_{3}{ \bigl( \boldsymbol{{B}}^{(\delta )}- \boldsymbol{{m}}_{\mathcal{E}} \bigr) } + \mathcal{Q}_{3}{ ( \boldsymbol{{m}}_{\perp } ) } d\boldsymbol{ \boldsymbol{x}}, \end{aligned}$$

which is equal to

$$ E_{0}+ \int_{\varOmega }\mathcal{Q}_{3}{ \Bigl( \bigl(\bigl( \boldsymbol{{A}}-{\boldsymbol{{A}}} ^{\boldsymbol{{m}}}\bigr)*\psi_{\delta } \bigr){\boldsymbol{x}}_{\mathrm{cs}} \big| {\nabla }_{\mathrm{cs}}{\bigl( \bigl(\boldsymbol{\beta }-{\boldsymbol{\beta }} ^{\boldsymbol{{m}}}\bigr)* \psi_{\delta }\bigr)} \Bigr) } d \boldsymbol{\boldsymbol{x}}. $$

(22)

We now vary $\delta$. The energy $\int \mathcal{Q}_{3}{ ( \boldsymbol{{F}} ) } d\boldsymbol{\boldsymbol{x}}$ is continuous with respect to the strong $L^{2}$ topology, so for any $j\in \mathbb{N}$ there exists $\delta_{j}$ such that

$$\int_{\varOmega }\mathcal{Q}_{3}{ \Bigl( \bigl(\bigl( \boldsymbol{{A}}-{\boldsymbol{{A}}} ^{\boldsymbol{{m}}}\bigr)*\psi_{\delta_{j}}\bigr) {\boldsymbol{x}}_{\mathrm{cs}} \big| {\nabla }_{\mathrm{cs}}{\bigl(\bigl( \boldsymbol{\beta }-{\boldsymbol{\beta }} ^{\boldsymbol{{m}}}\bigr)* \psi_{\delta_{j}}\bigr)} \Bigr) } d \boldsymbol{\boldsymbol{x}}< \int_{\varOmega }\mathcal{Q}_{1}{ \bigl( \boldsymbol{{A}}- { \boldsymbol{{A}}}^{\boldsymbol{{m}}} \bigr) } dx _{1}+ \frac{1}{j}. $$

By Eq. (22), we can pick $h_{j} < \delta_{j}$ such that

$$\begin{aligned} E^{(h_{j})}\bigl(\nabla_{h_{j}} \boldsymbol{y}^{(h_{j},\delta_{j})}\bigr) < & E _{0}+ \int_{\varOmega }\mathcal{Q}_{3}{ \Bigl( \bigl(\bigl( \boldsymbol{{A}}-{\boldsymbol{{A}}} ^{\boldsymbol{{m}}}\bigr)*\psi_{\delta_{j}} \bigr){\boldsymbol{x}}_{\mathrm{cs}} \big| {\nabla }_{\mathrm{cs}}{\bigl( \bigl(\boldsymbol{\beta }-{\boldsymbol{\beta }} ^{\boldsymbol{{m}}}\bigr)* \psi_{\delta_{j}}\bigr)} \Bigr) } d \boldsymbol{\boldsymbol{x}}+ \frac{1}{j} \\ < & E_{0}+ \int_{\varOmega }\mathcal{Q}_{1}\bigl(\boldsymbol{{A}}- { \boldsymbol{{A}}} ^{\boldsymbol{{m}}}\bigr) dx_{1}+ \frac{2}{j} \\ < & E(\boldsymbol{{R}}) + \frac{2}{j}. \end{aligned}$$

We conclude that $\lim_{j\to \infty } E^{(h)} (\nabla_{h_{j}} \boldsymbol{y}^{(h_{j},\delta_{j})}) \leq E(\boldsymbol{{R}})$. This concludes the proof of the lim sup inequality. □