On the Decay Rates of Porous Elastic Systems

Abstract

In this paper we analyze the porous elastic system. We show that viscoelasticity is not strong enough to make the solutions decay in an exponential way, independently of any relationship between the coefficients of wave propagation speed. However, it decays polynomially with optimal rate. When the porous damping is coupled with microtemperatures, we give an explicit characterization on the decay rate that can be exponential or polynomial type, depending on the relation between the coefficients of wave propagation speed. Numerical experiments using finite differences are given to confirm our analytical results. It is worth noting that the result obtained here is different from all existing in the literature for porous elastic materials, where the sum of the two slow decay processes determine a process that decay exponentially.

1 Introduction

In recent years, elastic materials with voids, which have nice physical properties, are used widely in engineering, such as vehicles, aeroplanes, large space structures and so on. Due to their extensive applications, the elasticity problems of these kinds of materials have become hot issues which attract the attention of many researchers.

Since elastic solids with voids is one of the simple extensions of the theory of the classical elasticity, it allows the treatment of porous solids in which the matrix material is elastic and the interstices are void of material (see Goodman and Cowin [17] and Nunziato and Cowin [13] for details). It is worth noting that in the last decades, research on porous elastic systems has been made considering various types of dissipative mechanisms.

So let us consider the evolution equations for one-dimensional theories of porous materials with temperature and microtemperature given by

$$\begin{aligned} \left \{ \textstyle\begin{array}{l} \rho u_{tt}=T_{x},\qquad J \phi_{tt}=H_{x}+G,\\ \rho\eta_{t}=q_{x},\qquad \rho E_{t}=P_{x}+q-Q. \end{array}\displaystyle \right . \end{aligned}$$

(1.1)

Here $T$ is the stress, $H$ is the equilibrated stress, $G$ is the equilibrated body force, $q$ is the heat flux, $\eta$ is the entropy, $P$ is the first heat flux moment, $Q$ is the mean heat flux and $E$ is the first moment of energy. The variables $u$ and $\phi$ are, respectively, the displacement of the solid elastic material and the volume fraction. The constitutive equations are

$$\begin{aligned} \left \{ \textstyle\begin{array}{l} T=\mu u_{x}+b \phi+\gamma u_{tx}-\beta\theta,\qquad H=\delta\phi_{x}-dw,\\ G=-bu_{x}-\xi\phi+m \theta-\tau\phi_{t},\qquad \rho\eta=\beta u_{x}+c\theta+m\phi,\\ q=\kappa\theta_{x}+\kappa_{1}w,\qquad P=-\kappa_{2}w_{x},\\ Q=\kappa_{3}w+\kappa_{4}\theta_{x},\qquad \rho E=-\alpha w-d \phi_{x}. \end{array}\displaystyle \right . \end{aligned}$$

(1.2)

Here $\rho$, $J$, $\mu$, $b$, $\gamma$, $\delta$, $d$, $\xi$, $m$, $\tau$, $\beta$, $c$, $\kappa$, $\kappa_{1}$, $\kappa_{2}$, $\kappa_{3}$, $\kappa_{4}$ and $\alpha$ are the constitutive coefficients whose physical meaning is well known. It is worth noting that $\theta$ and $w$ are the temperature and microtemperatures, respectively.

The constitutive coefficients, in one-dimensional case, satisfies

$$\begin{aligned} \xi>0,\qquad\delta>0,\qquad\mu>0,\qquad\rho>0,\qquad J>0,\quad \mbox{and}\quad\mu\xi\geq b^{2}. \end{aligned}$$

(1.3)

As coupling is considered, $b$ must be different from 0, but its sign does not matter in the analysis. On the other hand, when thermal effects are considered, we assume that the thermal capacity $c$ and the thermal conductivity $\kappa$ are strictly positive. Analogously, if microtemperatures are present, parameters $\alpha$, $\kappa_{2}$ and $\kappa$ are positive.

It is worth noting that $\gamma$ and $\tau$ are nonnegative. If $\gamma >0$ viscoelastic dissipation is assumed in the system, and if $\tau>0$ porous dissipation is present.

In this paper we analyze two problems. All of them are particular cases of the above system.

The paper is organized as follows. In Sect. 2, we study existence and uniqueness of solutions associated with porous elastic system where we are neglecting the thermal and microthermal effects. Also, we prove that the system lacks exponential decay independent of any relationship between the propagation speed coefficient. However, we prove that it decays polynomially as $\frac{1}{\sqrt{t}}$, with optimal rate. We also present numerical evidence of analytical results. In Sect. 3, we study the porous elastic system in the presence of porous viscosity but not elastic dissipation, and we combine it with microtemperatures. We prove that it is exponentially stable if and only if $\frac{\rho}{\mu}-\frac{J}{\delta}=0$. But, if $\frac{\rho}{\mu }-\frac{J}{\delta}\neq0$ we prove that it decays polynomially as $\frac {1}{\sqrt{t}}$, with optimal rate. Section 4 will be dedicated to present other types of dissipation that can be considered the porous elastic system for consideration by the interested reader.

2 Porous-Elasticity with Elastic Dissipation

Our analysis begins with the question: is there optimal rate of asymptotic behavior of the solutions of the porous elasticity problem if elastic dissipation is taken into account? We will show that viscoelasticity is not strong enough to make the solutions decay in an exponential way. In addition we will show that it decays polynomially with optimal rate.

Thus, if we introduce the constitutive equations into the evolution equations, but neglecting the thermal and microthermal effects, we obtain the system

$$\begin{aligned} \left \{ \textstyle\begin{array}{l@{\quad}l} \rho u_{tt}-\mu u_{xx}-b\phi_{x}-\gamma u_{txx}=0 & \mbox{in } (0,L) \times(0,\infty),\\ J \phi_{tt}-\delta\phi_{xx}+bu_{x}+\xi\phi=0 &\mbox{in } (0,L) \times(0,\infty). \end{array}\displaystyle \right . \end{aligned}$$

(2.1)

We added to system (2.1) the initial conditions given by

$$\begin{aligned} \left \{ \textstyle\begin{array}{l@{\quad}l} (u(x,0),\phi(x,0))=(u_{0}(x),\phi_{0}(x)),&\mbox{in }(0,L),\\ (u_{t}(x,0),\phi_{t}(x,0))=(u_{1}(x),\phi_{1}(x)),&\mbox{in }(0,L), \end{array}\displaystyle \right . \end{aligned}$$

(2.2)

and Dirichlet-Neumann boundary conditions

$$\begin{aligned} u(0,t)=u(L,t)=\phi_{x}(0,t)=\phi_{x}(L,t)=0, \quad t>0. \end{aligned}$$

(2.3)

It is worth mentioning that system (2.1)–(2.3) has been studied by A. Magaña and R. Quintanilla in [5]. There, the authors used the Routh–Hurwitz Theorem to prove the lack of exponential decay. In another paper, J.M. Rivera and R. Quintanilla [9] proved that the energy of system (2.1)–(2.3) is controlled by a rate decay of type $\frac{1}{t}$. Moreover, using a result due to Prüss [12] they improved the polynomial rate of decay by taking more regular initial data.

Remark 2.1

In this section, we will show that viscoelasticity is not strong enough to make the solutions decay in an exponential way, independently of any relationship between the coefficients of wave propagation speed. However, it decays polynomially with optimal rate.

2.1 Preliminary

We begin with the issue of wellposedness of solutions corresponding to the system (2.1)–(2.3). To this, let us consider the Hilbert space

$$\mathcal{H}=H^{1}_{0}(0,L)\times L^{2}(0,L)\times H^{1}_{*}(0,L)\times L^{2}_{*}(0,L), $$

where

$$H^{1}_{*}(0,L)=H^{1}(0,L)\cap L^{2}_{*}(0,L),\quad \mbox{where } L^{2}_{*}(0,L)=\biggl\{ z\in L^{2}(0,L): \int^{L}_{0}z(x)\,dx=0\biggr\} $$

with inner product given by

$$\begin{aligned} \langle U,V\rangle_{\mathcal{H}}:= \int^{L}_{0} \bigl(\rho\varphi\overline {\varPhi}+\mu u_{x}\overline{v}_{x}+J\psi\overline{\varPsi}+ \delta \phi_{x}\overline{\zeta}_{x}+\xi\phi\overline{ \zeta}+b(u_{x}\overline {\zeta}+\overline{v}_{x}\phi) \bigr) \,dx, \end{aligned}$$

(2.4)

for $U=(u,\varphi,\phi,\psi)'$, $V=(v,\varPhi,\zeta,\varPsi)'$. Hereafter a superposed bar denotes the conjugate complex number. By hypothesis, we have $\mu\xi\geq b^{2}$. Take $\xi_{1} \in(0,\xi]$ such that $\mu\xi _{1}-b^{2}=0$. Then, we obtain

$$\begin{aligned} \langle U,U\rangle_{\mathcal{H}} \geq&\rho \int^{L}_{0}\varphi^{2}\,dx+J \int ^{L}_{0}\psi^{2}\,dx +\delta \int^{L}_{0}\phi_{x}^{2}\,dx+ \int^{L}_{0}\bigl\vert \mu^{\frac{1}{2}}u_{x}- \xi ^{\frac{1}{2}}_{1}\phi\bigr\vert ^{2}\,dx \\ &{}+(\xi-\xi_{1}) \int^{L}_{0}\phi^{2}\,dx. \end{aligned}$$

(2.5)

This enables us to see clearly that the above $\langle U,V\rangle _{\mathcal{H}}$ defines an inner product on ℋ, and the associated norm $\|\cdot\|_{\mathcal{H}}$ is equivalent to the usual one. If we denote $\varPsi=\{u,u_{t},\phi,\phi_{t}\}$ and $\varPsi_{0}=\{ u_{0},u_{1},\phi_{0},\phi_{1}\}$ then the system (2.1)–(2.3) can be rewritten as follows

$$ \left \{ \textstyle\begin{array}{l} \frac{d\varPsi}{dt}=\mathcal{A}\varPsi,\quad \hbox{for } t>0,\\ \varPsi(0)=\varPsi_{0}, \end{array}\displaystyle \right . $$

(2.6)

where the operator $\mathcal{A}$ is given by

$$\begin{aligned} \mathcal{A}\{u,\varphi,\phi,\psi\}=\biggl\{ \varphi,\frac{1}{\rho}(\mu u_{x}+\gamma u_{tx})_{x}+\frac{b}{\rho} \phi_{x},\psi,\frac{1}{J}\delta\phi _{xx}- \frac{b}{J}u_{x} -\frac{\xi}{J}\phi\biggr\} , \end{aligned}$$

for $(u,\varphi,\phi,\psi)'\in\mathcal{D}(\mathcal{A})$, where

$$\begin{aligned} \mathcal{D}(\mathcal{A})=\bigl\{ &(u,\varphi,\phi,\psi)\in\mathcal{H}:\mu u+ \gamma\varphi\in H^{2}(0,L),\ \phi\in H^{2}(0,L),\ \varphi\in H^{1}_{0}(0,L), \\ &\psi\in H^{1}_{*}(0,L) \mbox{ and } \phi_{x}, \psi_{x} \in H^{1}_{0}(0,L)\bigr\} . \end{aligned}$$

It is easy to see that the operator $\mathcal{A}$ is dissipative in the energy space ℋ, then we have the following results concerning existence and uniqueness of solution of system (2.1)–(2.3) (see [7] for details).

Theorem 2.1

The operator ${\mathcal{A}}$ generates a $\mathrm{C}_{0}$-semigroup $S(t)$ of contraction on ℋ. Thus, for any initial data $U_{0}\in{\mathcal{H}}$, the system (2.1)–(2.3) has a unique weak solution $U\in C^{0}([0,\infty[;\,{\mathcal{H}})$. Moreover, if $U_{0}\in\mathcal{D}({\mathcal{A}})$, then $U$ is strong solution of (2.1)–(2.3), that is $U\in C^{0}([0,\infty[;\, \mathcal{D}({\mathcal{A}}))\cap C^{1}([0,\infty[;\,{\mathcal{H}})$.

2.2 Lack of Exponential Decay

In this section we will prove that the system (2.1)–(2.3) has lack of exponential decay. To do this, we use the following result due to Gearhart [15] (also see [12]).

Theorem 2.2

Let $S(t)=e^{\mathcal{A}t}$ be a $\mathrm{C}_{0}$-semigroup of contractions in ℋ. Then $S(t)$ is exponentially stable if and only if

$$\begin{aligned} i \mathbb {R}\equiv\{i\beta:\beta\in \mathbb {R}\} \subset\rho({\mathcal{A}}) \quad\textit{and}\quad \overline{\lim_{|\beta| \rightarrow\infty}} \bigl\| (i \beta I-\mathcal{A})^{-1}\bigr\| _{\mathcal{L}(\mathcal{H})}< \infty. \end{aligned}$$

(2.7)

The main result of this section is given by the following theorem.

Theorem 2.3

The $\mathrm{C}_{0}$-semigroup $S(t)=e^{\mathcal{A}t}$ on the Hilbert space ℋ is not exponentially stable, independent of any relationship between of the wave speed coefficients $\rho$, $\mu$, $J$ and  $\delta$.

Proof

We will prove that there exists a sequence of imaginary number $\lambda _{n}$ and functions $F_{n}=(f^{1},f^{2},f^{3},f^{4})'\in{\mathcal {H}}$, with $\| F_{n}\|_{\mathcal{H}}\leq1$ such that

$$\bigl\| (\lambda_{n} I-{\mathcal {A}})^{-1}F_{n} \bigr\| _{\mathcal{H}}\rightarrow\infty, $$

where

$$\begin{aligned} \lambda_{n}U_{n}-\mathcal{A}U_{n}=F_{n}, \end{aligned}$$

(2.8)

with $U_{n}=(u,\varphi,\phi,\psi)'$ not bounded. Rewrite the spectral equation (2.8) in term of its components, we have

$$\begin{aligned} i\lambda u-\varphi =&f^{1}, \end{aligned}$$

(2.9)

$$\begin{aligned} i\lambda\rho\varphi-\mu u_{xx}-\gamma \varphi_{xx}-b\phi_{x} =&\rho f^{2}, \end{aligned}$$

(2.10)

$$\begin{aligned} i\lambda\phi-\psi =&f^{3}, \end{aligned}$$

(2.11)

$$\begin{aligned} i\lambda J \psi-\delta\phi_{xx}+bu_{x}+\xi \phi =&Jf^{4}. \end{aligned}$$

(2.12)

Here we take $\lambda_{n}=i\lambda$. With this in mind, we choose $F\equiv F_{n}$ and $F=(0,0,0,\frac{1}{J}\cos(nx))'$. Then, we have

$$\varphi=i\lambda u \quad\mbox{and}\quad\psi=i\lambda\phi, $$

and consequently,

$$\begin{aligned} -\lambda^{2} \rho u-\mu u_{xx}-\gamma \varphi_{xx}-b\phi_{x} =&0, \end{aligned}$$

(2.13)

$$\begin{aligned} -\lambda^{2} J \phi-\delta\phi_{xx}+bu_{x}+ \xi\phi =&\cos(nx). \end{aligned}$$

(2.14)

Because of the boundary conditions we can take solution of type

$$u=A\sin(nx)\quad\mbox{and}\quad\phi=B\cos(nx). $$

Then, Eqs. (2.13) and (2.14) can be rewritten as

$$\begin{aligned} \bigl(-\rho\lambda^{2}+\mu n^{2}+\gamma\lambda n^{2}\bigr)A+bnB =&0, \\ bnA+\bigl(-J\lambda^{2}+\delta n^{2}+\xi\bigr)B =&1. \end{aligned}$$

Taking $\lambda$ such that $\lambda=\sqrt{\frac{1}{J}(\delta n^{2}+\xi )}$, we have

$$A:=A_{n}=\frac{1}{bn}\quad\mbox{and}\quad B:=B_{n}= \frac{- [ (\mu -\frac{\rho\delta}{J} )+\gamma\sqrt{\frac{1}{J}(\delta n^{2}+\xi )} ]n^{2}+\frac{\rho\xi}{J}}{(bn)^{2}}. $$

Therefore,

$$A_{n}\rightarrow0 \quad\mbox{and}\quad B:=B_{n}\approx O(n). $$

Choosing $L=\pi$, we have

$$\|U_{n}\|^{2}_{\mathcal{H}}\geq J \int^{\pi}_{0}|\psi|^{2}\,dx=J\lambda ^{2}_{n}B^{2}_{n} \int^{\pi}_{0}\bigl|\cos(nx)\bigr|^{2}\,dx\approx O \bigl(n^{4}\bigr), $$

from where it follows that

$$\|U_{n}\|_{\mathcal{H}}\geq\sqrt{\frac{J\pi}{2}} \lambda_{n}B_{n}\approx O\bigl(n^{2}\bigr) \rightarrow\infty,\quad \mbox{as } n\rightarrow\infty. $$

Therefore, follows from Theorem 2.2 the lack of exponential stability. □

2.3 Optimal Polynomial Decay Rate

In this section we will show that the system (2.1)–(2.3) goes to zero polynomially as $\frac{1}{\sqrt{t}}$. Moreover, we show that this rate is optimal. Our main result is based on the following theorem (see [1], Theorem 2.4).

Theorem 2.4

Let $S(t)=e^{\mathcal{A}t}$ be a bounded $\mathrm{C}_{0}$-semigroup on a Hilbert space ℋ with generator $\mathcal{A}$ such that $i \mathbb {R}\subset\rho(\mathcal{A})$. Then for any $\alpha>0$ and $x \in\mathcal{H}$, we have

$$\begin{aligned} \bigl\| R(\lambda,\mathcal{A})\bigr\| = O\bigl(|\lambda|^{\alpha}\bigr),\quad |\lambda|\rightarrow\infty\Longleftrightarrow \bigl\| S(t)\mathcal {A}^{-1}x\bigr\| _{\mathcal{H}}=o \bigl(t^{-\frac{1}{\alpha}}\bigr),\ t\rightarrow \infty. \end{aligned}$$

(2.15)

Let us take $(u,\varphi,\phi,\psi)'\in\mathcal{D}(\mathcal{A})$ and $F=(f^{1},f^{2},f^{3},f^{4})'\in\mathcal{H}$, and we consider the resolvent equation

$$\begin{aligned} i\lambda U-\mathcal{A}U=F. \end{aligned}$$

(2.16)

Taking the inner product in ℋ from resolvent equation with $U$, we have

$$i\lambda\|U\|^{2}_{\mathcal{H}}-\langle\mathcal{A}U,U \rangle_{{\mathcal {H}}}=\langle F,U\rangle_{{\mathcal{H}}}. $$

Taking the real part in the above equality, we obtain

$$\gamma \int^{L}_{0}|\varphi_{x}|^{2} \,dx=-\mathcal{R}e\langle\mathcal {A}U,U\rangle_{{\mathcal{H}}}=\langle F,U \rangle_{{\mathcal{H}}}. $$

Thus,

$$\begin{aligned} \gamma \int^{L}_{0}|\varphi_{x}|^{2} \,dx\leq\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}. \end{aligned}$$

(2.17)

Using Poincaré inequality, we get

$$\begin{aligned} \int^{L}_{0}|\varphi|^{2}\,dx\leq C \|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}, \end{aligned}$$

(2.18)

where $C$ is a positive constant. Now, the resolvent equation in terms of its components is given by

$$\begin{aligned} i\lambda u-\varphi =&f^{1}, \end{aligned}$$

(2.19)

$$\begin{aligned} i\lambda\rho\varphi-\mu u_{xx}-\gamma \varphi_{xx}-b\phi_{x} =&\rho f^{2}, \end{aligned}$$

(2.20)

$$\begin{aligned} i\lambda\phi-\psi =&f^{3}, \end{aligned}$$

(2.21)

$$\begin{aligned} i\lambda J \psi-\delta\phi_{xx}+bu_{x}+\xi \phi =&Jf^{4}. \end{aligned}$$

(2.22)

Lemma 2.1

Under the above notations, we have

$$i\mathbb{R}\subset\rho(\mathcal{A}). $$

The proof can be done using the same ideas as in [7, 16], for this reason we omit it here.

Lemma 2.2

The solution $(u,\varphi,\phi,\psi)'$ of system (2.1)–(2.3), satisfies

$$\begin{aligned} \biggl(1-\frac{1}{|\lambda|} \biggr) \int^{L}_{0}|u_{x}|^{2}\,dx\leq \frac {C}{|\lambda|}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}} \end{aligned}$$

for $|\lambda|$ large enough and $C$ a positive constant.

Proof

From Eq. (2.19), we have

$$\begin{aligned} \int^{L}_{0}|u_{x}|^{2}\,dx\leq \frac{1}{|\lambda|} \int^{L}_{0}|\varphi_{x}| |u_{x}|\, dx+\frac{1}{|\lambda|}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}, \end{aligned}$$

from where one has that

$$\begin{aligned} \biggl(1-\frac{1}{|\lambda|} \biggr) \int^{L}_{0}|u_{x}|^{2}\,dx\leq \frac {1}{|\lambda|} \int^{L}_{0}|\varphi_{x}|^{2} \,dx+\frac{1}{|\lambda|} \|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}, \end{aligned}$$

for $|\lambda|$ large enough. Using the inequality (2.17) follows the conclusion of the lemma. □

Theorem 2.5

The semigroup associated with the system (2.1)–(2.3) satisfies

$$\bigl\| e^{\mathcal{A}t}U_{0}\bigr\| _{\mathcal{H}}\leq\frac{1}{\sqrt {t}}\|U_{0}\|_{\mathcal{D}{(\mathcal{A})}}. $$

Moreover, this rate is optimal.

Proof

We multiply Eq. (2.20) by $\overline{\phi}_{x}$. Performing integration by parts on $(0,L)$ and using the Young inequality, and Eq. (2.22), we have

$$\begin{aligned} b \int^{L}_{0}|\phi_{x}|^{2}\,dx \leq&C|\lambda|^{2} \int^{L}_{0}|\varphi|^{2}\,dx+ \frac {1}{\delta} \int^{L}_{0}(\mu u_{x}+\gamma \varphi_{x}) \bigl(-iJ\lambda\overline{\psi }+b\overline{u}_{x}+ \xi\overline{\phi}-J\overline{f^{4}}\bigr)\,dx \\ &{}+\epsilon\|U\|^{2}_{\mathcal{H}}+C\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}, \end{aligned}$$

where $\epsilon$ is a small positive constant and $C_{\epsilon}$ is a positive constant. From inequality (2.17) and Lemma 2.2, we get

$$\begin{aligned} b \int^{L}_{0}|\phi_{x}|^{2}\,dx \leq&C|\lambda|^{2}\|U\|_{\mathcal {H}}\|F\|_{\mathcal{H}}+C_{\epsilon}| \lambda|^{2}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}} \\ &{}+\epsilon J \int^{L}_{0}|\psi|^{2}\,dx+C\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}+ \epsilon\|U\|^{2}_{\mathcal{H}}. \end{aligned}$$

(2.23)

Now, multiply Eqs. (2.19) and (2.22) by $\overline{u}$ and $\overline{\phi}$, respectively, and integrate by parts on $(0,L)$. Summing up the product results, and taking into account the inequalities (2.17), (2.18), (2.23) and Lemma 2.2, we arrive at

$$\begin{aligned} &J(1-\delta\epsilon) \int^{L}_{0}|\psi|^{2}\,dx+b \int^{L}_{0}(u_{x}\overline{\phi }+ \overline{u}_{x}\phi)\,dx+\xi \int^{L}_{0}|\phi|^{2}\,dx \\ &\quad{}\leq C|\lambda |^{2}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}} \\ &\qquad{}+C_{\epsilon}|\lambda|^{2}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}+ \frac {C}{|\lambda|}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}+C\|U\|_{\mathcal {H}}\|F\|_{\mathcal{H}}. \end{aligned}$$

(2.24)

Finally, combining the inequalities (2.17), (2.23), (2.24) and Lemma 2.2, choosing $\epsilon>0$ small enough and $|\lambda|$ large enough, one has that

$$\begin{aligned} \|U\|_{\mathcal{H}}\leq C|\lambda|^{2}\|F\|_{\mathcal{H}}, \quad\forall U\in\mathcal{D}(\mathcal{A}), \end{aligned}$$

(2.25)

which is equivalent to

$$\bigl\| R(\lambda,{\mathcal{A}})\bigr\| \leq O\bigl(|\lambda|^{2}\bigr)\quad \mbox{as } |\lambda|\rightarrow\infty. $$

Then using Theorem 2.4 (see Theorem 2.4 in [1]), our conclusion follows. Now, in order to prove the inverse inequality we use contradiction arguments. Suppose that $O(|\lambda|^{2})$ is not optimal. This means that there exists $\varepsilon>0$ such that

$$\begin{aligned} \bigl\| R(\lambda,{\mathcal{A}})\bigr\| \leq O\bigl(|\lambda|^{2-\varepsilon} \bigr),\quad \mbox{as } |\lambda|\rightarrow\infty, \end{aligned}$$

(2.26)

which implies that, for all $F\in{\mathcal{H}}$, there exists $c>0$ such that

$$\frac{1}{|\lambda|^{2-\varepsilon}}\|U\|_{{\mathcal{H}}}\leq c \|F\|_{{\mathcal{H}}},\quad\forall \lambda\in i \mathbb {R},\ \lambda\neq0, $$

where $U\in{\mathcal{H}}$ is the solution of the resolvent equation $i\lambda U-{\mathcal{A}}U=F$ in ℋ. This is a contradiction because, taking advantage of Theorem 2.3 we can construct sequences

$$(\lambda_{n} )_{n \in \mathbb {N}}\subset i \mathbb {R},\quad (U_{n} )_{n \in \mathbb {N}}\subset\mathcal{D}({\mathcal{A}})\quad \mbox{and}\quad (F_{n} )_{n \in \mathbb {N}}\subset{\mathcal{H}}, $$

such that

$$\|U_{n}\|^{2}_{{\mathcal{H}}}\geq c|\lambda_{n}|^{2}\|F_{n}\|^{2}_{{\mathcal {H}}}, \quad\bigl(\mbox{see inequality (2.25)}\bigr) $$

which implies that

$$\frac{1}{|\lambda_{n}|^{2-\varepsilon}} \bigl\| R(\lambda_{n},{\mathcal{A}})\bigr\| \geq c| \lambda_{n}|^{\varepsilon}\rightarrow\infty\quad(\mbox{as } n \rightarrow\infty), $$

contradicting (2.26). The proof of theorem is complete. □

Remark 2.2

It is important to mention the case $\mu=\xi=b$. In this case, (2.1) can be seen as a system of Timoshenko type, where the variables $u$ and $\phi$ represent, respectively, the transverse displacement of a beam and the rotation angle of a filament. With the above considerations, the system (2.1) becomes the Timoshenko system with viscoelastic damping

$$\begin{aligned} \left \{ \textstyle\begin{array}{l} \rho u_{tt}-\mu(u_{x}+\phi)_{x}-\gamma u_{xxt}=0 \quad\mbox{in }(0,L) \times(0,\infty),\\ J \phi_{tt}-\delta\phi_{xx}+\mu(u_{x}+\phi)=0 \quad\mbox{in } (0,L) \times(0,\infty),\\ u(0,t)=u(L,t)=\phi_{x}(0,t)=\phi_{x}(L,t)=0\quad t>0, \\ (u(x,0),\phi(x,0))=(u_{0}(x),\phi_{0}(x)),\quad\mbox{in } (0,L),\\ (u_{t}(x,0),\phi_{t}(x,0))=(u_{1}(x),\phi_{1}(x)), \quad \mbox{in } (0,L). \end{array}\displaystyle \right . \end{aligned}$$

(2.27)

If we denote $\varPsi=\{u,u_{t},\phi,\phi_{t}\}$ and $\varPsi_{0}=\{u_{0},u_{1},\phi _{0},\phi_{1}\}$ then the system (2.27) can be rewritten as follows

$$ \left \{ \textstyle\begin{array}{l} \frac{d\varPsi}{dt}=\mathcal{B}\varPsi,\quad \hbox{for } t>0,\\ \varPsi(0)=\varPsi_{0}, \end{array}\displaystyle \right . $$

(2.28)

where the operator ℬ is given by $\mathcal{B}\{u,\varphi ,\phi,\psi\}=\{\varphi,\frac{\mu}{\rho}( u_{x}+\phi)_{x}+\frac{\gamma }{\rho}u_{xxt},\psi,\frac{\delta}{J} \phi_{xx}-\frac{\mu}{J}(u_{x} +\phi)\}$, for $(u,\varphi,\phi,\psi)'\in\mathcal{D}(\mathcal {B})=\mathcal{D}(\mathcal{A})$. In ℋ, let us consider the inner product

$$\begin{aligned} \langle U,V\rangle_{\mathcal{H}}:= \int^{L}_{0} \bigl(\rho\varphi\overline {\varPhi}+ \mu(u_{x}+\phi) (\overline{v}_{x}+\overline{w})+J\psi \overline{\varPsi}+ \delta\phi_{x}\overline{w}_{x} \bigr) \,dx, \end{aligned}$$

(2.29)

for $U=(u,\varphi,\phi,\psi)',\ V=(v,\varPhi,w,\varPsi)'\in\mathcal{H}$. It is easy to see that the operator ℬ is dissipative in the energy space ℋ, then existence and uniqueness of solution of the problem (2.28) is analogous as in Theorem 2.1 (see [7] for details).

Theorem 2.6

The semigroup associated with the system (2.27) has lack of exponential decay independent of any relationship between of the wave speed coefficients $\rho$, $\mu$, $J$ and $\delta$ and it decays as

$$\bigl\| e^{\mathcal{B}t}U_{0}\bigr\| _{\mathcal{H}}\leq\frac{1}{\sqrt {t}}\|U_{0}\|_{\mathcal{D}{(\mathcal{B})}}. $$

Moreover, this rate is optimal.

The proof follows the same steps as in the proof of Theorems 2.3 and 2.5, so we omitted it here.

2.4 Numerical Simulations

In this section, we focus on the numerical scheme (2.1)–(2.3) and its energy $E^{n}$ to illustrate by means of the numerical experiments the analytical results established in previous sections. We emphasize that we are not concerned with issues of numerical convergence between exact solution and numerical solution and the respective rate of convergence. However, given the accuracy of the scheme used, we believe strongly that it preserves qualitatively the analytical results.

We consider a numerical scheme using finite difference and we reproduce numerically the analytical results established on lack of exponential decay. Thus, given $K,N\in \mathbb {N}$ we set $\Delta x=\frac {L}{K+1}$ and $\Delta t=\frac{T}{N+1}$, and we introduce the grids

$$ \begin{aligned} x_{0}={}&0< x_{1}=\Delta x< \cdots< x_{K}=K\Delta x< x_{K+1}=(K+1)\Delta x=L,\\ t_{0}={}&0< t_{1}=\Delta t< \cdots< t_{N}=N\Delta t< t_{N+1}=(N+1)\Delta t=T, \end{aligned} $$

(2.30)

with $x_{k}=k\Delta x$ and $t_{n}=n\Delta t$ for $k=0,1,\ldots,K+1$, and $n=0,1,\ldots,N+1$. We then introduce the following explicit scheme using finite difference of (2.1)–(2.3)

$$\begin{aligned} \rho\frac{u_{k}^{n+1}-2u_{k}^{n}+u_{k}^{n-1}}{\Delta t^{2}} =&\mu\frac{u_{k+1}^{n}-2u_{k}^{n}+u_{k-1}^{n}}{\Delta x^{2}} +b \frac{\phi_{k+1}^{n}-\phi_{k-1}^{n}}{2\Delta x} +\gamma\frac{u_{k+1}^{n}-2u_{k}^{n}+u_{k-1}^{n}}{\Delta t\Delta x^{2}} \\ &{}-\gamma\frac{u_{k+1}^{n-1}-2u_{k}^{n-1}+u_{k-1}^{n-1}}{\Delta t\Delta x^{2}}, \end{aligned}$$

(2.31)

$$\begin{aligned} J\frac{\phi_{k}^{n+1}-2\phi_{k}^{n}+\phi_{k}^{n-1}}{\Delta t^{2}} =&\delta\frac{\phi_{k+1}^{n}-2\phi_{k}^{n}+\phi_{k-1}^{n}}{\Delta x^{2}} -b \frac{u_{k+1}^{n}-u_{k-1}^{n}}{2\Delta x} \\ &{}-\xi\frac{\phi_{k+1}^{n}+2\phi_{k}^{n}+\phi_{k-1}^{n}}{4}, \end{aligned}$$

(2.32)

for all $k=1,\dots, K$ and $n=1,\dots, N$. To simplicity our numerical calculations, we consider the homogeneous boundary conditions given by

$$\begin{aligned} u_{0}^{n}=u_{K+1}^{n}=0, \qquad\phi_{0}^{n}=\phi_{K+1}^{n}=0,\quad \forall n=1,2,\dots,N, \end{aligned}$$

(2.33)

and initial conditions given by

$$ \begin{aligned} &u_{k}^{0}=u(x_{k},0),\qquad u_{k}^{1}=u_{k}^{0}+\Delta tu_{t}(x_{k},0),\quad\forall k=1,\dots,K,\\ &\phi_{k}^{0}=\phi(x_{k},0),\qquad \phi_{k}^{1}=\phi_{k}^{0}+\Delta t\phi_{t}(x_{k},0),\quad\forall k=1,\dots,K. \end{aligned} $$

(2.34)

Here, we are denoting by $u_{k}^{n}$ and $\phi_{k}^{n}$ the numerical approximations to the exact solutions $u$ and $\phi$ respectively, evaluated on the mesh. More precisely, we have $u_{k}^{n}\approx u(x_{k},t_{n})$ and $\phi_{k}^{n}\approx\phi(x_{k},t_{n})$. It is worth mentioning the discretization adopted for term $\phi$ on the second equation on (2.1), as we can see on (2.32), we used the following approximation

$$\begin{aligned} \phi(x_{k},t_{n})\approx\frac{\phi_{k+1}^{n}+2\phi_{k}^{n}+\phi_{k-1}^{n}}{4}. \end{aligned}$$

(2.35)

Numerical discretization like (2.35) has been used to avoid a numerical anomaly known as locking phenomenon on shear force. That happens mainly for elastic structures such Timoshenko beams and Reissner-Mindlin-Timoshenko plates [2, 8, 10, 11].

The numerical scheme presented here is explicit and its computational implementation requires knowledge of the approximations at time level ${t_{n}}$ and $t_{n-1}$ in order to approximate the numerical solutions at time level $t_{n+1}$. The totally discrete equations are all consistent with the problem under studied and of order $\mathcal{O}(\Delta x^{2},\Delta t^{2})$. For issues related to stability criterion, we have to make a more elaborate analysis based on references by Wright [10, 11]. However, we will show in Sect. 2.4.1 that discrete energy $E^{n}$ is positive since that $\Delta t\leq\min \{\Delta x\sqrt {\frac{J}{\delta}},2\sqrt{\frac{J}{\xi}},\Delta x\sqrt{\frac{2\rho}{\mu }} \}$. Therefore, this restriction for $\Delta t$ is a candidate to be the stability criterion of system (2.31)–(2.34) (see reference [18]).

The discrete energy at the time step $t_{n}$ of system (2.31)–(2.34) will be computed using the expression

$$\begin{aligned} E^{n} :=&\frac{\Delta x}{2}\sum _{k=0}^{K} \biggl[ \rho \biggl(\frac{u_{k}^{n+1}-u_{k}^{n}}{\Delta t} \biggr)^{2} +J \biggl(\frac{\phi_{k}^{n+1}-\phi_{k}^{n}}{\Delta t} \biggr)^{2} +\delta \biggl(\frac{\phi_{k+1}^{n+1}-\phi_{k}^{n+1}}{\Delta x} \biggr) \biggl(\frac{\phi_{k+1}^{n}-\phi_{k}^{n}}{\Delta x} \biggr) \\ &{}+\mu \biggl(\frac{u_{k+1}^{n+1}-u_{k}^{n+1}}{\Delta x} \biggr) \biggl(\frac{u_{k+1}^{n}-u_{k}^{n}}{\Delta x} \biggr) +\xi \biggl(\frac{\phi_{k+1}^{n+1}+\phi_{k}^{n+1}}{2} \biggr) \biggl(\frac{\phi_{k+1}^{n}+\phi_{k}^{n}}{2} \biggr) \\ &{}+b \biggl(\frac{u_{k+1}^{n+1}-u_{k}^{n+1}}{\Delta x} \biggr) \biggl(\frac{\phi_{k+1}^{n}+\phi_{k}^{n}}{2} \biggr) +b \biggl(\frac{\phi_{k+1}^{n+1}+\phi_{k}^{n+1}}{2} \biggr) \biggl(\frac{u_{k+1}^{n}-u_{k}^{n}}{\Delta x} \biggr) \biggr], \end{aligned}$$

(2.36)

which is a discretization of the continuous energy. Furthermore, we have the following dissipation law in the numerical context analogous to continuous case

$$\begin{aligned} \frac{E^{n}-E^{n-1}}{\Delta t} =&-\gamma\frac{\Delta x}{2}\sum _{k=0}^{K} \biggl(\frac{u_{k+1}^{n+1}-u_{k}^{n+1}-u_{k+1}^{n-1}+u_{k}^{n-1}}{\Delta t\Delta x} \biggr) \\ &{}\times\biggl(\frac{u_{k+1}^{n}-u^{n}_{k}-u^{n-1}_{k+1}+ u_{k}^{n-1}}{\Delta t\Delta x} \biggr), \end{aligned}$$

(2.37)

for all $n=1,\dots,N,N+1$. As in the continuous case, the technical procedure for obtaining the energy $E^{n}$ is analogous to the continuous case, we multiply equation (2.31) by ${\frac {u_{k}^{n+1}-u_{k}^{n-1}}{2\Delta t}}$ and we organize the results in order to make up the difference $E^{n}-E^{n-1}$. The proof is too long and we omitted in this work.

For numerical example, we consider $L=1$, $T=2$, $\rho=7.85$, $J=4.088\times10^{-4}$, $\delta=1.093\times10^{-2}$, $\xi=67.829$, $b=17$ and take in account that $\mu\xi\geq b^{2}$. For cases in which the speeds of wave propagation are equal we consider $\rho=\frac{J\mu }{\delta}$. In the initial conditions we assume that

$$\begin{aligned} &u(x_{k},0)=\phi(x_{k},0)=0, \\ &u_{t}(x_{k},0)=\sin \biggl(\nu\frac{\pi x_{k}}{L} \biggr), \qquad \phi_{t}(x_{k},0)=\sin \biggl(\nu\frac{\pi x_{k}}{L} \biggr),\quad\nu\in \mathbb {N}. \end{aligned}$$

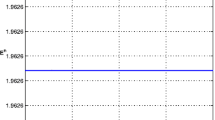
The accuracy of the numerical scheme (2.31)–(2.34) can be seen through of the energy conservation law. Indeed, taking $\gamma = 0$ in (2.37) we obtain that $E^{n} = E^{0}$, $n = 1,2,\dots, N + 1$, as we can see in Fig. 1 below

Fig. 1

Conservative case

In Fig. 2, we can see that numerical experiments are in qualitative agreement with the analytical results established in Theorem 2.3. That is to say, the system (2.1)–(2.3) is not exponentially stable, independent of any relation between the constants of the system, which is a different result from the one obtained in the next section where the condition $\frac{\rho}{\mu}=\frac {J}{\delta}$ is sufficient and necessary to obtain exponential stability. Here, in both cases, we take $E^{n}=E^{n}/E^{0}$.

Fig. 2

As we can see, when taking $\rho=J\mu/\delta$ then the energy $E^{n}$ decay faster over time. However, in these graphics, we can still see the lack of exponential decay according to exponential curve, that is, the decay is slow, like a decreasing straight line

As mentioned on Remark 2.2, when we have $\mu=\xi=b$ then the system (2.1) becomes a system of Timoshenko with viscoelastic damping given by (2.27). In Fig. 3, we can see numerical simulations for (2.27) system, where we take $\mu=\xi =b$ on (2.31)–(2.32).

Fig. 3

As we can see, numerically, the energy of systems solutions of (2.27) behaved in a manner similar to (2.1) system, that is, the curve shown decreases slowly and that can be characterized as a typical polynomial decay behavior. At this point, it is important to emphasize that the lack of exponential decay also occurs independent of any relationship between the wave speed coefficients

As we see in Fig. 3, the energy behavior is analogous to that obtained in Fig. 2, that is, we have a lack of exponential decay independent of relation between coefficients of system. This result disagree from the case in which it has a frictional damping [6], in that case, the authors showed that the system is exponentially stable if and only if $\frac{\rho}{\mu}=\frac{J}{\delta}$.

2.4.1 Positivity of energy $E^{n}$

Theorem 2.7

If $\Delta t\leq\min \{\Delta x\sqrt{\frac{J}{\delta}},2\sqrt{\frac {J}{\xi}},\Delta x\sqrt{\frac{2\rho}{\mu}} \}$, then for all non-trivial solutions of the discrete system (2.31)–(2.32) ($\gamma=0$) more homogeneous boundary conditions (2.33) it holds

$$\begin{aligned} &{E^{n}}\geq\frac{1}{2} \biggl(\frac{\rho}{\Delta t^{2}}- \frac{\mu}{2\Delta x^{2}} \biggr){\Delta x}\sum_{k=0}^{K} \bigl({u_{k}^{n+1}-u_{k}^{n}} \bigr)^{2} +\frac{1}{4} \biggl(\frac{J}{\Delta t^{2}}- \frac{\xi}{4} \biggr){\Delta x}\sum_{k=0}^{K} \bigl({\phi_{k}^{n+1}-\phi_{k}^{n}} \bigr)^{2} \\ &\phantom{{E^{n}}\geq\,}+ \biggl(\frac{\delta}{8\Delta x^{2}} \biggr){\Delta x}\sum_{k=0}^{K} \bigl[ \bigl(\phi_{k}^{n+1}-\phi_{k+1}^{n} \bigr)^{2} + \bigl(\phi_{k+1}^{n+1}- \phi_{k}^{n} \bigr)^{2} \bigr]\geq0, \\ &\quad\forall n=1,2,\dots,N. \end{aligned}$$

(2.38)

Proof

In order to prove the statement, we use the following identities for Dirichlet boundary conditions

$$\begin{aligned} \begin{aligned} &\sum_{k=0}^{K}u_{k+1}^{n+1}u_{k+1}^{n}=\sum_{k=0}^{K}u_{k}^{n+1}u_{k}^{n}, \qquad \sum_{k=0}^{K} \bigl(u_{k}^{n+1}\bigr)^{2} =\sum_{k=0}^{K}\bigl(u_{k+1}^{n+1} \bigr)^{2}, \\ &\sum_{k=0}^{K} \bigl(u_{k}^{n}\bigr)^{2} =\sum_{k=0}^{K}\bigl(u_{k+1}^{n} \bigr)^{2}. \end{aligned} \end{aligned}$$

(2.39)

with analogous identities for $\phi_{k}^{n}$. From the energy $E^{n}$, we have

$$\begin{aligned} \frac{E^{n}}{\Delta x} \geq&\frac{\rho}{2}\sum _{k=0}^{K} \biggl(\frac{u_{k}^{n+1}-u_{k}^{n}}{\Delta t} \biggr)^{2} +\frac{J}{2}\sum_{k=0}^{K} \biggl(\frac{\phi_{k}^{n+1}-\phi _{k}^{n}}{\Delta t} \biggr)^{2} +\frac{\delta}{2}\sum _{k=0}^{K}\frac{\phi_{k+1}^{n+1}-\phi _{k}^{n+1}}{\Delta x} \frac{\phi_{k+1}^{n}-\phi_{k}^{n}}{\Delta x} \\ &{}+\varepsilon\frac{\mu}{2}\sum_{k=0}^{K} \frac {u_{k+1}^{n+1}-u_{k}^{n+1}}{\Delta x} \frac{u_{k+1}^{n}-u_{k}^{n}}{\Delta x} +\varepsilon\frac{\xi}{2}\sum _{k=0}^{K}\frac{\phi_{k+1}^{n+1}+\phi_{k}^{n+1}}{2} \frac{\phi_{k+1}^{n}+\phi_{k}^{n}}{2} \\ &{}+\varepsilon\frac{b}{2}\sum_{k=0}^{K} \frac {u_{k+1}^{n+1}-u_{k}^{n+1}}{\Delta x} \frac{\phi_{k+1}^{n}+\phi_{k}^{n}}{2} +\varepsilon\frac{b}{2}\sum _{k=0}^{K}\frac{\phi_{k+1}^{n+1}+\phi_{k}^{n+1}}{2} \frac{u_{k+1}^{n}-u_{k}^{n}}{\Delta x}, \end{aligned}$$

(2.40)

for $\varepsilon\in(0,1/2)$. The last four summations we denote by $\mathcal{S}_{k}^{n}$. Then, using the inequality $xy\geq-x^{2}/2\epsilon -y^{2}\epsilon/2$, for all $x,y$ and $\epsilon>0$, we obtain

$$\begin{aligned} \mathcal{S}^{n}_{k} \geq&\frac{\mu}{2}\sum _{k=0}^{K}\frac {u_{k+1}^{n+1}-u_{k}^{n+1}}{\Delta x} \frac{u_{k+1}^{n}-u_{k}^{n}}{\Delta x} - \frac{b^{2}}{4\epsilon}\sum_{k=0}^{K} \biggl( \frac {u_{k+1}^{n+1}-u_{k}^{n+1}}{\Delta x} \biggr)^{2} -\frac{b^{2}}{4\epsilon}\sum _{k=0}^{K} \biggl(\frac {u_{k+1}^{n}-u_{k}^{n}}{\Delta x} \biggr)^{2} \\ &{}+\frac{\xi}{2}\sum_{k=0}^{K} \frac{\phi_{k+1}^{n+1}+\phi_{k}^{n+1}}{2} \frac{\phi_{k+1}^{n}+\phi_{k}^{n}}{2} -\frac{\epsilon}{4}\sum _{k=0}^{K} \biggl(\frac{\phi_{k+1}^{n}+\phi _{k}^{n}}{2} \biggr)^{2} -\frac{\epsilon}{4}\sum_{k=0}^{K} \biggl(\frac{\phi_{k+1}^{n+1}+\phi _{k}^{n+1}}{2} \biggr)^{2}. \end{aligned}$$

Choosing $\epsilon=\xi$ and taking in account that $\mu\xi\geq b^{2}$, we obtain

$$\begin{aligned} \mathcal{S}^{n}_{k} \geq& -\frac{\mu}{4}\sum _{k=0}^{K} \biggl(\frac {u_{k+1}^{n+1}-u_{k}^{n+1}}{\Delta x}- \frac {u_{k+1}^{n}-u_{k}^{n}}{\Delta x} \biggr)^{2} -\frac{\xi}{4}\sum _{k=0}^{K} \biggl(\frac{\phi_{k+1}^{n+1}+\phi_{k}^{n+1}}{2} - \frac{\phi_{k+1}^{n}+\phi_{k}^{n}}{2} \biggr)^{2} \\ =&-\frac{\mu}{4}\sum_{k=0}^{K} \biggl(\frac {u_{k+1}^{n+1}-u_{k+1}^{n}}{\Delta x}-\frac {u_{k}^{n+1}-u_{k}^{n}}{\Delta x} \biggr)^{2} - \frac{\xi}{4}\sum_{k=0}^{K} \biggl( \frac{\phi_{k+1}^{n+1}-\phi_{k+1}^{n}}{2} +\frac{\phi_{k}^{n+1}-\phi_{k}^{n}}{2} \biggr)^{2}, \end{aligned}$$

from where it follows that

$$\begin{aligned} \mathcal{S}^{n}_{k} \geq& -\frac{\mu}{2} \sum_{k=0}^{K} \biggl(\frac {u_{k+1}^{n+1}-u_{k+1}^{n}}{\Delta x} \biggr)^{2} -\frac{\mu}{2}\sum_{k=0}^{K} \biggl(\frac{u_{k}^{n+1}-u_{k}^{n}}{\Delta x} \biggr)^{2} -\frac{\xi}{2}\sum _{k=0}^{K} \biggl(\frac{\phi_{k+1}^{n+1}-\phi_{k+1}^{n}}{2} \biggr)^{2} \\ &{}-\frac{\xi}{2}\sum_{k=0}^{K} \biggl( \frac{\phi_{k}^{n+1}-\phi _{k}^{n}}{2} \biggr)^{2}. \end{aligned}$$

(2.41)

From identities (2.39), we obtain

$$\begin{aligned} \sum_{k=0}^{K} \biggl(\frac{u_{k+1}^{n+1}-u_{k+1}^{n}}{\Delta x} \biggr)^{2} =\sum_{k=0}^{K} \biggl(\frac{u_{k}^{n+1}-u_{k}^{n}}{\Delta x} \biggr)^{2}, \qquad\sum _{k=0}^{K} \biggl(\frac{\phi_{k+1}^{n+1}-\phi_{k+1}^{n}}{2} \biggr)^{2}= \sum_{k=0}^{K} \biggl(\frac{\phi_{k}^{n+1}-\phi_{k}^{n}}{2} \biggr)^{2}. \end{aligned}$$

Thus, we can rewrite (2.41) as

$$\begin{aligned} \mathcal{S}^{n}_{k}&\geq -{\mu}\sum _{k=0}^{K} \biggl(\frac{u_{k}^{n+1}-u_{k}^{n}}{\Delta x} \biggr)^{2} -{\xi}\sum_{k=0}^{K} \biggl(\frac{\phi_{k}^{n+1}-\phi_{k}^{n}}{2} \biggr)^{2}. \end{aligned}$$

Substituting $\mathcal{S}^{n}_{k}$ into (2.40) and rearranging some appropriated terms we get

$$\begin{aligned} \frac{E^{n}}{\Delta x} \geq& \biggl(\frac{\rho}{2\Delta t^{2}}-\varepsilon\frac {\mu}{\Delta x^{2}} \biggr)\sum_{k=0}^{K} \bigl({u_{k}^{n+1}-u_{k}^{n}} \bigr)^{2} +\frac{1}{4} \biggl(\frac{J}{\Delta t^{2}}-\varepsilon{ \xi} \biggr)\sum_{k=0}^{K} \bigl({ \phi_{k}^{n+1}-\phi_{k}^{n}} \bigr)^{2} \\ &{}+\frac{J}{4\Delta t^{2}}\sum_{k=0}^{K} \bigl({ \phi_{k}^{n+1}-\phi _{k}^{n}} \bigr)^{2} +\frac{\delta}{2\Delta x^{2}}\sum_{k=0}^{K} \bigl({\phi_{k+1}^{n+1}-\phi _{k}^{n+1}} \bigr) \bigl({\phi_{k+1}^{n}-\phi_{k}^{n}} \bigr). \end{aligned}$$

Since that $\Delta t^{2}\leq\frac{J}{\delta}\Delta x^{2}$, it follows that

$$\begin{aligned} \mathcal{S}_{k1}^{n}&\geq\frac{\delta}{4\Delta x^{2}} \Biggl[\sum _{k=0}^{K} \bigl({\phi_{k}^{n+1}- \phi_{k}^{n}} \bigr)^{2} +\sum _{k=0}^{K} \bigl({\phi_{k+1}^{n+1}- \phi_{k}^{n+1}} \bigr) \bigl({\phi_{k+1}^{n}- \phi_{k}^{n}} \bigr) \Biggr] \\ &=\frac{\delta}{4\Delta x^{2}}\sum_{k=0}^{K} \bigl[ \bigl(\phi_{k}^{n+1} \bigr)^{2}+ \bigl( \phi_{k}^{n} \bigr)^{2} -\phi_{k+1}^{n+1} \phi_{k}^{n}-\phi_{k}^{n+1} \phi_{k+1}^{n} \bigr] \\ &=\frac{\delta}{8\Delta x^{2}}\sum_{k=0}^{K} \bigl[ \bigl(\phi_{k}^{n+1} \bigr)^{2} + \bigl( \phi_{k+1}^{n} \bigr)^{2}-2\phi_{k}^{n+1} \phi_{k+1}^{n} + \bigl(\phi_{k+1}^{n+1} \bigr)^{2} + \bigl(\phi_{k}^{n} \bigr)^{2} -2\phi_{k+1}^{n+1}\phi_{k}^{n} \bigr] \\ &=\frac{\delta}{8\Delta x^{2}}\sum_{k=0}^{K} \bigl[ \bigl(\phi_{k}^{n+1}-\phi_{k+1}^{n} \bigr)^{2} + \bigl(\phi_{k+1}^{n+1}- \phi_{k}^{n} \bigr)^{2} \bigr]\geq0, \end{aligned}$$

finally, we arrive at

$$\begin{aligned} \frac{E^{n}}{\Delta x} \geq& \biggl(\frac{\rho}{2\Delta t^{2}}-\varepsilon\frac {\mu}{\Delta x^{2}} \biggr)\sum_{k=0}^{K} \bigl({u_{k}^{n+1}-u_{k}^{n}} \bigr)^{2} +\frac{1}{4} \biggl(\frac{J}{\Delta t^{2}}-\varepsilon{ \xi} \biggr)\sum_{k=0}^{K} \bigl({ \phi_{k}^{n+1}-\phi_{k}^{n}} \bigr)^{2} \\ &{}+\frac{\delta}{8\Delta x^{2}}\sum_{k=0}^{K} \bigl[ \bigl(\phi_{k}^{n+1}-\phi_{k+1}^{n} \bigr)^{2} + \bigl(\phi_{k+1}^{n+1}- \phi_{k}^{n} \bigr)^{2} \bigr], \end{aligned}$$

then, choosing $\varepsilon=\frac{1}{4}$ we conclude the proof. □

The stability criterion of system (2.31)–(2.32) is not known, because of that, in our numerical simulations, we take $\Delta t$ sufficiently smaller than $\Delta x$ to make it convergent. However, in the case where $\mu=\xi=b$ the stability criterion to the explicit finite difference scheme obeys restrictions similar to those obtained (see [11, 22]). Therefore, as we said before it is reasonable to expect that the restrictions obtained for $\Delta t$ in Theorem 2.7 establish a stability criterion for scheme (2.31)–(2.32).

3 Elasticity, Viscoporosity and Microtemperatures

In this section, we raise the question whether porous dissipation coupled with microtemperature lead the system to be exponentially or polynomially stable, depending on a relation between the coefficients of wave propagation speed.

Since the pioneering work of A. Soufyane to Timoshenko systems [3], where a single damping on rotation angle leads the system to decay exponentially depending on a relationship between the wave propagation coefficients, many researches have been made in order to obtain the minimum dissipation to stabilize the Timoshenko system (see [4, 14, 16] for details).

In this way, here we are considering the presence of porous dissipation but not elastic dissipation, and we are combining it with microtemperatures. The obtained system is

$$\begin{aligned} \left \{ \textstyle\begin{array}{l} \rho u_{tt}-\mu u_{xx}-b\phi_{x}=0 \quad\mbox{in }(0,L) \times(0,\infty),\\ J \phi_{tt}-\delta\phi_{xx}+bu_{x}+dw_{x}+\xi\phi+\tau\phi_{t}=0 \quad \mbox{in } (0,L) \times(0,\infty),\\ \alpha w_{t}-\kappa_{2}w_{xx}+d\phi_{tx}+\kappa_{3}w=0\quad\mbox{in } (0,L) \times(0,\infty),\\ u(0,t)=u(L,t)=\phi_{x}(0,t)=\phi_{x}(L,t)=w(0,t)=w(L,t)=0,\quad t>0,\\ (u(x,0),\phi(x,0),w(0,t))=(u_{0}(x),\phi_{0}(x),w_{0}(x)),\quad\mbox{in }(0,L)\\ (u_{t}(x,0),\phi_{t}(x,0))=(u_{1}(x),\phi_{1}(x)), \quad \mbox{in }(0,L). \end{array}\displaystyle \right . \end{aligned}$$

(3.1)

It is worth mentioning that system (3.1) has been studied by A. Magaña and R. Quintanilla in [5]. There, the authors used the Routh–Hurwitz Theorem to prove the lack of exponential decay if $\frac{\rho}{\mu}\neq\frac{J}{\delta}$.

The natural question now is whether there exist or not a polynomial rate of decay of the solution of system (3.1) in some appropriate norms when $\frac{\rho}{\mu}\neq\frac{J}{\delta}$. In addition, to show that this polynomial decay rate is optimal. Another question is to know what type of decay occurs when $\frac{\rho}{\mu }=\frac{J}{\delta}$.

From what was said above, the main goal here is to show that the system (3.1) decays exponentially if and only if $\frac{\rho}{\mu }=\frac{J}{\delta}$. On the contrary, to prove that the system (3.1) decays polynomially as $\frac{1}{\sqrt{t}}$ if $\frac{\rho }{\mu}\neq\frac{J}{\delta}$. Moreover, to prove that this rate is optimal. We emphasize here that the issues raised for the porous elastic system is new and has not been addressed in the literature for these models.

To do this, we note that the solutions of this problem can be generated by means of a semigroup of contractions. In fact, this semigroup is defined in

$$\mathcal{H}=\bigl\{ (u,\varphi,\phi,\psi,w)\in H^{1}_{0}(0,L) \times L^{2}(0,L)\times H^{1}_{*}(0,L)\times L^{2}_{*}(0,L)\times H^{1}_{0}(0,L)\bigr\} , $$

by the operator

$$\begin{aligned} \mathcal{A}\{u,\varphi,\phi,\psi,w\}=\biggl\{ &\varphi,\frac{\mu}{\rho }u_{xx}+ \frac{b}{\rho}\phi_{x},\psi,\frac{1}{J}\delta \phi_{xx}-\frac{b}{J}u_{x} -\frac{d}{\rho}w_{x}- \frac{\xi}{J}\phi,\\ &\frac{\kappa_{2}}{\alpha}w_{xx}-\frac {d}{\alpha} \phi_{tx}-\kappa_{3}w\biggr\} . \end{aligned}$$

Now, we recall an inner product in ℋ given by

$$\begin{aligned} \langle U,V\rangle_{\mathcal{H}} :=& \int^{L}_{0} \bigl(\rho\varphi\overline {\varPhi}+\mu u_{x}\overline{v}_{x}+J\psi\overline{\varPsi}+ \delta \phi_{x}\overline{\zeta}_{x} \\ &{}+\xi\phi\overline{\zeta}+\alpha w\overline{W}+b(u_{x}\overline{\zeta}+\overline{v}_{x}\phi) \bigr)\,dx, \end{aligned}$$

(3.2)

for $U=(u,\varphi,\phi,\psi,w)'$, $V=(v,\varPhi,\zeta,\varPsi,W)'$. It is worth recalling that this product is equivalent to the usual product in the Hilbert space ℋ.

The domain of $\mathcal{A}$ is

$$\begin{aligned} \mathcal{D}(\mathcal{A})=\bigl\{ &(u,\varphi,\phi,\psi,w)\in\mathcal {H}:u\in H^{2}(0,L),\varphi\in H^{1}_{0}(0,L),\phi\in H^{2}(0,L), \\ &\psi\in H^{1}_{*}(0,L),w\in H^{2}(0,L) \mbox{ and } \phi_{x},\psi_{x}\in H^{1}_{0}(0,L)\bigr\} . \end{aligned}$$

Then the initial-boundary value problem (3.1) is equivalent to

$$ \left \{ \textstyle\begin{array}{l} \frac{d\varPsi}{dt}=\mathcal{A}\varPsi,\quad\hbox{for } t>0,\\ \varPsi(0)=\varPsi_{0}, \end{array}\displaystyle \right . $$

(3.3)

where $\varPsi_{0}=(u_{0},u_{1},\phi_{0},\phi_{1},w_{0})$. Simple calculations give us

$$\begin{aligned} \langle\mathcal{A}U,U\rangle_{\mathcal{H}}=-\kappa_{2} \int^{L}_{0}|w_{x}|^{2}\, dx- \kappa_{3} \int^{L}_{0}|w|^{2}\,dx-\tau \int^{L}_{0}|\psi|^{2}\,dx\leq0, \end{aligned}$$

(3.4)

from where it follows that $\mathcal{A}$ is a dissipative operator. So, using the same procedure as in [7], we conclude that $\mathcal{A}$ is the generator of a $\mathrm{C}_{0}$ semigroup of contractions on Hilbert space ℋ.

3.1 Lack of Exponential Decay

This section will be devoted to the study of the lack of exponential decay. To do this we will use the Gearhart Theorem [15]. To start, let us consider the resolvent equation

$$\begin{aligned} i\lambda U-\mathcal{A}U=F, \end{aligned}$$

(3.5)

where $\lambda\in\mathbb{R}$, $U=(u,\varphi,\phi,\psi,w)'\in\mathcal {D}(\mathcal{A})$ and $F=(f^{1},f^{2},f^{3},f^{4},f^{5})'\in\mathcal{H}$. In terms of its components de above equation becomes

$$\begin{aligned} i\lambda u-\varphi =&f^{1}, \end{aligned}$$

(3.6)

$$\begin{aligned} i\lambda\rho\varphi-\mu u_{xx}-b\phi_{x} =& \rho f^{2}, \end{aligned}$$

(3.7)

$$\begin{aligned} i\lambda\phi-\psi =&f^{3}, \end{aligned}$$

(3.8)

$$\begin{aligned} i\lambda J\psi-\delta\phi_{xx}+bu_{x}+dw_{x}+ \xi\phi+\tau\psi =&Jf^{4}, \end{aligned}$$

(3.9)

$$\begin{aligned} i\lambda\alpha w-\kappa_{2} w_{xx}+d \psi_{x}+\kappa_{3} w =&\alpha f^{5}. \end{aligned}$$

(3.10)

Choosing $f^{1}=f^{3}=f^{4}=f^{5}=0$, we have

$$\begin{aligned} -\lambda^{2} \rho u-\mu u_{xx}-b \phi_{x} =&\rho f^{2}, \end{aligned}$$

(3.11)

$$\begin{aligned} -\lambda^{2} J\phi-\delta\phi_{xx}+bu_{x}+dw_{x}+ \xi\phi+\tau\psi =&0, \end{aligned}$$

(3.12)

$$\begin{aligned} i\lambda\alpha w-\kappa_{2} w_{xx}+d \psi_{x}+\kappa_{3} w =&0. \end{aligned}$$

(3.13)

Theorem 3.1

The $\mathrm{C}_{0}$-semigroup $T(t)=e^{\mathcal{A}t}$ associated with system (3.1) on the Hilbert space ℋ is not exponentially stable if $\frac{\rho}{\mu}\neq\frac{J}{\delta}$.

Proof

Choosing

$$\begin{aligned} &u=A\sin \biggl(\frac{n\pi}{L}x \biggr),\qquad \psi=B\cos \biggl( \frac{n\pi}{L}x \biggr),\\ &w=C\sin \biggl(\frac{n\pi}{L}x \biggr) \quad\mbox{and}\quad f^{2}=\frac{1}{\rho}\sin \biggl( \frac{n\pi}{L}x \biggr), \end{aligned}$$

and using the same procedure as in the proof of Theorem 2.3, one has the conclusion of the theorem. □

3.2 Exponential Decay

This section will be devoted to the study of exponential stability of the system (3.1). To start, we take the inner product in ℋ of equation (3.5) with $U$. This results in

$$i\lambda\|U\|^{2}_{\mathcal{H}}-\langle\mathcal{A}U,U \rangle_{\mathcal {H}}=\langle F,U\rangle_{\mathcal{H}}. $$

Taking the real parts and with the help of equation (3.4), we get

$$\begin{aligned} \kappa_{2} \int^{L}_{0}|w_{x}|^{2}\,dx+ \kappa_{3} \int^{L}_{0}|w|^{2}\,dx+\tau \int^{L}_{0}|\psi |^{2}\,dx \leq\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}. \end{aligned}$$

(3.14)

Lemma 3.1

Under the above notations, we have

$$i\mathbb{R}\subset\rho(\mathcal{A}). $$

The proof can be done using the same ideas as in [7, 16], for this reason we omit it here.

Lemma 3.2

The solution $U=(u,\varphi,\phi,\psi,w)'$ of system (3.1) satisfies

$$ \int^{L}_{0}|\phi|^{2}\,dx\leq \frac{C}{|\lambda|} \bigl(\|U\|^{2}_{\mathcal {H}}+\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}} \bigr), $$

(3.15)

and

$$\begin{aligned} &\delta\int^{L}_{0}|\phi_{x}|^{2}\,dx+b \int^{L}_{0}u_{x}\overline{\phi}\,dx+\xi \int ^{L}_{0}|\phi|^{2}\,dx \\ &\quad{}\leq C\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}+\epsilon\|U\|^{2}_{\mathcal {H}}+C_{\epsilon}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}, \end{aligned}$$

(3.16)

where $\epsilon$ and $C$ are positive constant, $C_{\epsilon}$ is a positive constant that depend on $\epsilon$ and $\lambda$ is such that $|\lambda|$ is large enough.

Proof

Multiply Eq. (3.8) by $\overline{\phi}$ and the result integrate on $(0,L)$. Then, applying the Poincaré inequality, one has the conclusion of inequality (3.15).

To prove the inequality (3.16), multiply Eq. (3.9) by $\overline{\phi}$ and the result integrate by parts on $(0,L)$. Then, with the help of Eq. (3.8), we get

$$\begin{aligned} &\delta \int^{L}_{0}|\phi_{x}|^{2}\,dx+b \int^{L}_{0}u_{x}\overline{\phi}\,dx+\xi \int ^{L}_{0}|\phi|^{2}\,dx\\ &\quad{}=J \int^{L}_{0}|\psi|^{2}\,dx-d \int^{L}_{0}w_{x}\overline{\phi}\, dx -\tau \int^{L}_{0}\psi\overline{\phi}\,dx+J \int^{L}_{0}\bigl(\psi\overline {f^{3}}+f^{4} \overline{\phi}\bigr)\,dx. \end{aligned}$$

Using the inequality (3.14) we can conclude that para any $\epsilon>0$ there exist a constant $C_{\epsilon}>0$ such that

$$\begin{aligned} &\delta \int^{L}_{0}|\phi_{x}|^{2}\,dx+b \int^{L}_{0}u_{x}\overline{\phi}\,dx+\xi \int ^{L}_{0}|\phi|^{2}\,dx\\ &\quad{}\leq C\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}+\epsilon\|U\|^{2}_{\mathcal {H}}+C_{\epsilon}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}. \end{aligned}$$

From where we get the second inequality of lemma. □

Lemma 3.3

For any $\epsilon>0$ there exist a constant $C_{\epsilon}>0$ such that

$$\begin{aligned} &\mu \int^{L}_{0}|u_{x}|^{2}\,dx+b \int^{L}_{0}\overline{u}_{x}\phi\,dx+ \frac{\xi\mu }{b} \int^{L}_{0}|\phi|^{2}\,dx + \biggl( \frac{\delta\mu}{b}-\delta \biggr) \int^{L}_{0}|\phi_{x}|^{2}\, dx \\ &\quad{}\leq|\lambda|\frac{\delta\mu}{|b|}\biggl\vert \frac{\rho}{\mu}- \frac {J}{\delta}\biggr\vert \int^{L}_{0}|\psi| |u_{x}|\,dx +C\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}+\epsilon\|U\|^{2}_{\mathcal {H}}+C_{\epsilon}\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}} \\ &\qquad{}+\frac{C}{|\lambda|} \bigl(\|U\|^{2}_{\mathcal{H}}+\|U\|_{\mathcal {H}}\|F\|_{\mathcal{H}} \bigr) \end{aligned}$$

where $C$ is a positive constant and $\lambda$ is such that $|\lambda|$ is large enough.

Proof

Multiply Eq. (3.9) by $\frac{\mu}{b}(\overline {u}_{x}+\overline{\phi})$ and the result integrate by parts on $(0,L)$. Thus, we have

$$\begin{aligned} &\mu \int^{L}_{0}|u_{x}|^{2}\,dx+ \frac{\xi\mu}{b} \int^{L}_{0}\overline{u}_{x}\phi\, dx+ \frac{\xi\mu}{b} \int^{L}_{0}|\phi|^{2}\,dx\\ &\quad{}=-i\lambda \frac{J\mu}{b} \int ^{L}_{0}\psi\overline{u}_{x}\,dx -i \lambda\frac{J\mu}{b} \int^{L}_{0}\psi\overline{\phi}\,dx \\ &\qquad{}-\underbrace{\frac{\delta\mu}{b} \int^{L}_{0}\phi_{x} \overline{u}_{xx} \,dx}_{:=I_{1}} -\frac{\delta\mu}{b} \int^{L}_{0}|\phi_{x}|^{2}\,dx- \mu \int^{L}_{0}u_{x}\overline {\phi}\,dx- \frac{d\mu}{b} \int^{L}_{0}w_{x}\overline{u}_{x} \,dx \\ &\qquad{}-\frac{d\mu}{b} \int^{L}_{0}w_{x}\overline{\phi}\,dx- \frac{\tau\mu}{b} \int ^{L}_{0}\psi\overline{u}_{x}\,dx- \frac{\tau\mu}{b} \int^{L}_{0}\psi\overline{\phi }\,dx+ \frac{J\mu}{b} \int^{L}_{0}f^{4}(\overline{u}_{x}+ \overline{\phi})\,dx. \end{aligned}$$

The substitution of term $-\mu\overline{u}_{xx}$ given by (3.7) into $I_{1}$ give us

$$\begin{aligned} &\mu\int^{L}_{0}|u_{x}|^{2}\,dx+ \frac{\xi\mu}{b} \int^{L}_{0}\overline{u}_{x}\phi\, dx+ \frac{\xi\mu}{b} \int^{L}_{0}|\phi|^{2}\,dx \\ &\quad{}=-i\lambda \frac{J\mu}{b} \int ^{L}_{0}\psi\overline{u}_{x}\,dx -\underbrace{i\lambda\frac{J\mu}{b} \int^{L}_{0}\psi\overline{\phi}\,dx}_{:=I_{2}} + \underbrace{i\lambda\frac{\delta\rho}{b} \int^{L}_{0}\phi_{x} \overline {\varphi} \,dx}_{:=I_{3}} \\ &\qquad{}+\delta \int^{L}_{0}|\phi_{x}|^{2}\,dx + \frac{\delta\rho}{b} \int^{L}_{0}\phi_{x}\overline{f^{2}} \,dx -\frac{\delta\mu}{b} \int^{L}_{0}|\phi_{x}|^{2}\,dx \\ &\qquad{}-\mu \int^{L}_{0}u_{x}\overline{\phi}\,dx- \frac{d\mu}{b} \int ^{L}_{0}w_{x}\overline{u}_{x} \,dx -\frac{d\mu}{b} \int^{L}_{0}w_{x}\overline{\phi}\,dx- \frac{\tau\mu}{b} \int ^{L}_{0}\psi\overline{u}_{x}\,dx \\ &\qquad{}-\frac{\tau\mu}{b} \int^{L}_{0}\psi\overline{\phi}\,dx+ \frac{J\mu}{b} \int ^{L}_{0}f^{4}(\overline{u}_{x}+ \overline{\phi})\,dx. \end{aligned}$$

(3.17)

From Eq. (3.8), we get

$$\begin{aligned} I_{2}=\frac{J\mu}{b} \int^{L}_{0}|\psi|^{2}\,dx+ \frac{\rho J\mu}{b} \int^{L}_{0}\psi \overline{f^{3}}\,dx. \end{aligned}$$

(3.18)

Now, from Eqs. (3.8) and (3.6) we get

$$\begin{aligned} I_{3}=i\lambda\frac{\delta\rho}{b} \int^{L}_{0}\psi\overline{u}_{x}\,dx- \frac {\delta\rho}{b} \int^{L}_{0}\psi_{x}\overline{f^{1}} \,dx +\frac{\delta\rho}{b} \int^{L}_{0}f^{3}_{x}\overline{ \varphi}\,dx. \end{aligned}$$

(3.19)

The replacement of $I_{2}$ and $I_{3}$ into (3.17) give us

$$\begin{aligned} &\mu \int^{L}_{0}|u_{x}|^{2}\,dx+ \frac{\xi\mu}{b} \int^{L}_{0}\overline{u}_{x}\phi\, dx+ \frac{\xi\mu}{b} \int^{L}_{0}|\phi|^{2}\,dx + \biggl( \frac{\delta\mu}{b}-\delta \biggr) \int^{L}_{0}|\phi_{x}|^{2}\, dx \\ &\quad{}=i\lambda\frac{\delta\mu}{b} \biggl(\frac{\rho}{\mu}-\frac{J}{\delta } \biggr) \int^{L}_{0}\psi\overline{u}_{x}\,dx + \frac{J\mu}{b} \int^{L}_{0}|\psi|^{2}\,dx+ \frac{\rho J\mu}{b} \int^{L}_{0}\psi \overline{f^{3}}\,dx \\ &\qquad{} + \frac{\delta\rho}{b} \int^{L}_{0}\phi_{x}\overline{f^{2}} \,dx -\mu \int^{L}_{0}u_{x}\overline{\phi}\,dx - \frac{d\mu}{b} \int^{L}_{0}w_{x}\overline{u}_{x} \,dx -\frac{d\mu}{b} \int^{L}_{0}w_{x}\overline{\phi}\,dx \\ &\qquad{}- \frac{\tau\mu}{b} \int ^{L}_{0}\psi\overline{u}_{x}\,dx- \frac{\delta\rho}{b} \int^{L}_{0}\phi_{x} \overline {f^{1}}\,dx -\frac{\tau\mu}{b} \int^{L}_{0}\psi\overline{\phi}\,dx \\ &\qquad{}+ \frac{J\mu}{b} \int ^{L}_{0}f^{4}(\overline{u}_{x}+ \overline{\phi})\,dx+\frac{\delta\rho}{b} \int ^{L}_{0}f^{3}_{x}\overline{ \varphi}\,dx. \end{aligned}$$

(3.20)

Since $\mu\xi\geq b^{2}$, then with the help of the inequalities (3.14) and (3.15) one has the conclusion of lemma. □

Theorem 3.2

The semigroup $T(t)=e^{{\mathcal{A}}t}$ associated with the system (3.1) is exponentially stable if only if

$$\frac{\rho}{\mu}=\frac{J}{\delta}. $$

Proof

From Lemmas 3.2, 3.3 and inequality (3.14), we have

$$\begin{aligned} &\mu \int^{L}_{0}|u_{x}|^{2}\,dx+b \int^{L}_{0}(\overline{u}_{x} \phi+u_{x}\overline{\phi })\,dx+\frac{\delta\mu}{b} \int^{L}_{0}|\phi_{x}|^{2}\,dx + \xi \int^{L}_{0}|\phi|^{2}\,dx \\ &\qquad{}+J \int^{L}_{0}|\psi|^{2}\,dx+\alpha \int^{L}_{0}|w|^{2}\,dx \leq\delta \int^{L}_{0}|\phi_{x}|^{2}\,dx+b \int^{L}_{0}u_{x}\overline{\phi}\, dx \\ &\qquad{}+\xi \int^{L}_{0}|\phi|^{2}\,dx+\mu \int^{L}_{0}|u_{x}|^{2}\,dx+b \int^{L}_{0}\overline {u}_{x}\phi\,dx+J \int^{L}_{0}|\psi|^{2}\,dx \\ &\qquad{}+\frac{\xi\mu}{b} \int^{L}_{0}|\phi|^{2}\,dx + \biggl( \frac{\delta\mu}{b}-\delta \biggr) \int^{L}_{0}|\phi_{x}|^{2}\,dx+ \alpha \int^{L}_{0}|w|^{2}\,dx \\ &\quad{}\leq C\|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}+\epsilon \|U\|^{2}_{\mathcal{H}}+C_{\epsilon}\|U\|_{\mathcal{H}}\|F\|_{\mathcal {H}} \\ &\qquad{}+\frac{C}{|\lambda|} \bigl(\|U\|^{2}_{\mathcal{H}}+\|U\|_{\mathcal {H}}\|F\|_{\mathcal{H}} \bigr). \end{aligned}$$

(3.21)

Now, multiply the equality (3.7) by $\overline{u}$ and integrate by parts on $(0,L)$. The result is

$$\rho \int^{L}_{0}|\varphi|^{2}\,dx=\mu \int^{L}_{0}|u_{x}|^{2}\,dx-b \int^{L}_{0}\phi \overline{u}_{x}\,dx+\rho \int^{L}_{0}\bigl(\varphi\overline{f^{1}}+f^{2} \overline {u}\bigr)\,dx, $$

from where it follows that

$$\begin{aligned} \rho \int^{L}_{0}|\varphi|^{2}\,dx \leq&C\|U\|_{\mathcal{H}}\|F\|_{\mathcal {H}}+\epsilon\|U\|^{2}_{\mathcal{H}}+C_{\epsilon}\|U\|_{\mathcal {H}}\|F\|_{\mathcal{H}} \\ &{}+\frac{C}{|\lambda|} \bigl(\|U\|^{2}_{\mathcal{H}}+\|U\|_{\mathcal {H}}\|F\|_{\mathcal{H}} \bigr). \end{aligned}$$

(3.22)

Combining the above estimate with the inequality (3.21) and choosing $\epsilon>0$ small enough and $|\lambda|$ large enough, we can conclude that there exist a positive constant $M$ such that

$$\|U\|_{\mathcal{H}}\leq M \|F\|_{\mathcal{H}},\quad\forall U\in \mathcal{D}( \mathcal{A}). $$

Using Gearhart’s result [15] the conclusion of the theorem follows. □

3.3 Polynomial Decay and Optimal Rate

This section will be devoted to show that in general the $\mathrm{C}_{0}$-semigroup $T(t)=e^{{\mathcal{A}}t}$ associated with the system (3.1) goes to zero polynomially as $\frac{1}{\sqrt{t}}$. In addition, we will prove that this rate is optimal.

Theorem 3.3

If $\frac{\rho}{\mu}\neq\frac{J}{\delta}$, then the semigroup associated with system (3.1) satisfies

$$\bigl\| e^{{\mathcal{A}}t}U_{0}\bigr\| _{{\mathcal{H}}}\leq\frac{c}{\sqrt {t}}\|U_{0}\|_{\mathcal{D}{({\mathcal{A}})}}. $$

Moreover, this rate is optimal.

Proof

Since $\psi=i\lambda\phi-f^{3}$, then from Lemma 3.3 we get

$$\begin{aligned} &\mu \int^{L}_{0}|u_{x}|^{2}\,dx+b \int^{L}_{0}\overline{u}_{x}\phi\,dx+ \frac{\xi\mu }{b} \int^{L}_{0}|\phi|^{2}\,dx + \biggl( \frac{\delta\mu}{b}-\delta \biggr) \int^{L}_{0}|\phi_{x}|^{2}\, dx \\ &\quad{}\leq|\lambda|^{2}\frac{\delta\mu}{|b|}\biggl\vert \frac{\rho}{\mu}- \frac {J}{\delta}\biggr\vert \int^{L}_{0}|\phi| |u_{x}|\,dx +C|\lambda| \|U\|_{\mathcal{H}}\|F\|_{\mathcal{H}}+\epsilon \|U\|^{2}_{\mathcal{H}}+C_{\epsilon}\|U\|_{\mathcal{H}}\|F\|_{\mathcal {H}} \\ &\qquad{}+\frac{C}{|\lambda|} \bigl(\|U\|^{2}_{\mathcal{H}}+\|U\|_{\mathcal {H}}\|F\|_{\mathcal{H}} \bigr). \end{aligned}$$

Consequently, combining the above inequality with Lemma 3.2 and inequalities (3.14) and (3.22), we can conclude for $\epsilon>0$ small enough there exist a positive constant $M$ such that

$$\|U\|_{\mathcal{H}}\leq M |\lambda|^{2}\|F\|_{\mathcal{H}}, \quad \forall U\in\mathcal{D}(\mathcal{A}), $$

which is equivalent to

$$\bigl\| R(\lambda,{\mathcal{A}})\bigr\| \leq O\bigl(|\lambda|^{2}\bigr)\quad \mbox{as } |\lambda|\rightarrow\infty. $$

Then using Theorem 2.4 (see Theorem 2.4 in [1]), one gets the first conclusion of theorem.

To prove that the rate is optimal we use the same ideas as in the proof of Theorem 2.5. So it will be omitted here. The proof is now complete. □

4 Final Comment

This section will be dedicated to present other types of dissipation that can be considered to the porous-elastic system for consideration by the interested reader. To start, let us consider the system obtained for the variables $u$, $\phi$ and $\theta$ when we assume viscoelasticity $(\gamma>0)$, but we do not assume porousviscosity $(\tau=0)$ and microtemperature. Thus, by combining (1.1)–(1.2) we obtain a system that has been studied by A. Magaña and R. Quintanilla [23]. In that paper, they proved that the system lacks exponential decay. However, the authors do not showed any type of decay rate. However, in the present paper, we believe that with the help of Theorem 2.3, we can show that the system has lack of exponential decay independent of any relationship between of the wave speed coefficient $\rho$, $\mu$, $J$ and $\delta$. Finally, with the assistance of Theorem 2.5 we can prove that the obtained system is polynomially stable, and it decay as $\frac{1}{\sqrt{t}}$. Moreover, this rate is optimal.

Now, we will consider the system obtained for the variables $u$, $\phi$ and $\theta$ when we do not assume viscoelasticity $(\gamma=0)$ and microtemperature, but we assume porousviscosity $(\tau>0)$. Again, by combining (1.1)–(1.2) we obtain a system that has been studied by Casas and Quintanilla [19]. In that paper, they discussed the asymptotic behavior of obtained system and proved the exponential stability based on the methods developed by Liu and Zheng [24]. It is worth noting that, in this case, the sum of two slow decay processes determine a process that decay exponentially.

In turn, when in the equations (1.1)–(1.2) we do not assume viscoelasticity, porousviscosity ($\gamma=0$ and $\tau=0$) and microtemperature, we obtain a problem determined by the system porous elastic where the only dissipation mechanism is the heat conduction given by the Fourier law. This system has been studied by Jaime Muñoz Rivera and Ramón Quintanilla [9]. They proved the polynomial decay of solutions of the system whenever $m(\beta b-m\mu)>0$ (also see [20, 21] for details). However, the authors believe that with the aid of Theorem 3.1 and quite designed calculations lead us to conclude that this system lacks exponential stability when $\frac{\rho}{\mu}\neq\frac{J}{\delta }$. An interesting open problem is to prove that the energy associated with this system is controlled by a polynomial when $\frac{\rho}{\mu }\neq\frac{J}{\delta}$ and controlled by a negative exponential in the case of $\frac{\rho}{\mu}=\frac{J}{\delta}$. Also, it is interesting to note that when $\tau=0$, we get a system where the damping term is only the microtemperature. Then from Theorem 3.1, simple calculations lead us to conclude that this system lacks exponential stability when $\frac{\rho}{\mu}\neq\frac{J}{\delta}$. An interesting open problem is to prove that the energy associated with the system is controlled by a polynomial when $\frac{\rho}{\mu}\neq\frac{J}{\delta}$ and controlled by a negative exponential in the case of $\frac{\rho}{\mu }=\frac{J}{\delta}$.

5 Conclusion

We show here that the porous-elastic system with different damping term, can be reduced to an evolution equation. We present a series of results on the operator which is the generator for an evolution semigroup. This semigroup is dissipative, and also we give an explicit characterization on the decay rate that can be exponential or polynomial type, depending or not on a relation between the coefficients of the speeds of wave propagation. It is worth noting that the result obtained here is different from all existing in the literature for porous elastic materials, where the sum of the two slow decay processes determine a process that decay exponentially (see [19]). Therefore, the analysis conducted in the paper gave us complete information on the asymptotic stability of porous-elastic system with the minimum of dissipation. Thus, the results of this paper imply a new contribution to these models, showing that they have the same behavior as the Timoshenko system. In this sense we can say that the results presented here generalize the results obtained for Timoshenko system.