1 Introduction

One of the most important relationships for a river engineer is the stage-discharge relationship, which is essential for designing hydraulic structures, flood risk mapping, and flood management purposes. Investigating the effect of roughness on the stage-discharge relationship and flow characteristics is important [1,2,3,4,5]. Several methods have been developed for computing the stage-discharge relationship for the main river channel with floodplains in straight compound channels, such as a 1-D and a 2-D model based on an analytical solution of the depth-averaged Navier–Stokes equations [7,8,9,10,11].

Multi-roughness channels are not uncommon in-field applications of open-channel flow hydraulics. Due to the different roughnesses of the wetted perimeter, the overall roughness of the channel is given by composite roughness [6, 13,14,15,16]. Seventeen different equations based on several assumptions, along with six other techniques to subdivide the channel cross-section, were given by numerous investigators, and are summarized by Chen and Yen [12]. The credibility of these equations will be assessed by employing experimental data. An effective methodology has been proposed to evaluate the optimal design of a cross-sectional area of a channel having composite roughness using Manning's roughness equation. The composite flow resistance coefficient of a smooth compound channel is found to increase with overbank depth. However, in the case of a compound channel with a floodplain, the values first increase with overbank flow depth and then decrease. This is due to the momentum-transfer effect and different roughnesses associated with the floodplain and the main channel [2, 15, 17,18,19,20,21].

The stage-discharge relationships and hydrodynamics of rough-bed flows have been extensively studied for the last 2–3 decades. However, many unsolved problems still need clarification for compound channels with different roughness. Still, a more experimental study on flow resistance parameters, stage-discharge relationships, and the determination of rating curves with composite roughness is required to model flows in compound channels. The present study used three different channel roughnesses, i.e., rough, smooth and heterogeneous. The influence of channel roughness on depth-averaged velocity and boundary shear stress distribution is discussed and analyzed. An expression for the composite roughness, non-dimensional coefficient and integration constants was derived from an appropriate boundary condition used in the present study. The models were applied to different data sets. In order to check the strength and weaknesses of different models, error analysis is also discussed.

2 Analytical solutions

2.1 Stage-discharge relationship

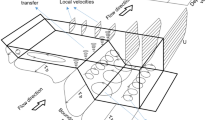
Consider a half-symmetric compound channel having different channel roughnesses with a water body length of \({\text{dx}}\), water body width of \({\text{dy}}\), water depth of H and acting shear forces on the channel beds and walls, as shown in Fig. 1.

Fig. 1
figure 1

Sketch of a half-symmetric compound channel with shear forces acting on the channel beds and walls with different channel roughness

Full size image

From Fig. 1b is half of the main channel width, B is the semiwidth of the main channel with floodplain, h is bank full height, 0 is the centre line, x, y, and z are streamwise, lateral and vertical directions, respectively, W is the velocity component in the z-direction, \({{\text{n}}}_{1}\) is the main channel roughness, \({{\text{n}}}_{2}\) is the main channel wall roughness, \({{\text{n}}}_{3}\) is a floodplain bed roughness and \({{\text{n}}}_{4}\) is a floodplain wall roughness.

The present study investigates the stage-discharge relationships and the percentage of flow carried by the main channel and floodplains with different channel roughnesses. The stage-discharge relationship may be obtained using the power function given by Eq. (1) for test configurations.

$${\text{H}}={{\text{aQ}}}^{{\text{b}}}$$
(1)

Here, a and b are constants, which can be determined from the curve fitting process, and Q is the discharge in m3/s. By using the continuity equation, the discharge may be written as

$${\text{Q}}={\text{AV}},$$
(2)

where A is the cross-sectional area in m2, and V is the cross-sectional mean velocity in m/s.

In the present study, the measured and predicted discharge match better when using Ud instead of V in Eq. (2), where Ud is the depth-averaged velocity. Considering the shear forces acting on the channel, as shown in Fig. 1, then the streamwise depth-averaged momentum equation for steady uniform flow gives

$$\left[\rho {\overline{\varepsilon }}_{yx}\frac{{\partial U}_{d}}{\partial y}+ \frac{\partial }{\partial y}\left(\rho {\overline{\varepsilon }}_{yx}\frac{{\partial U}_{d}}{\partial y}\right)dy\right]Hdx-\rho {\overline{\varepsilon }}_{yx}\frac{{\partial U}_{d}}{\partial y}Hdx- {\tau }_{b}dydx+ \rho g{S}_{o}Hdydx= \frac{\partial }{\partial y}\left[H{\left(\rho UV\right)}_{d}\right]dydx,$$
(3)

where U, V are longitudinal and lateral velocity components, respectively, subscript d is the depth-averaged value, \({\overline{\varepsilon }}_{yx}\) is depth-averaged eddy viscosity, So is channel-bed slope, and the right-hand side terms represent the secondary flow term (Γ), respectively.

$$ \overline{\varepsilon }_{yx} = \lambda HU_{*} ;\; U_{*} = \left( {\frac{{\tau_{b} }}{\rho }} \right)^{1/2} ;\;\; \Gamma= \frac{\partial }{\partial y}\left[ {H\left( {\rho UV} \right)_{d} } \right]dydx $$
(4)

Here, \({U}_{*}\) is the shear velocity, g is the gravitational acceleration, ρ is the water density, λ is the dimensionless eddy viscosity, and \({\uptau }_{{\text{b}}}\) is the boundary shear stress.

According to the present experimental results of relative depth, Dr = 0.45, as shown in Fig. 2, the term (ρUV)d decreases approximately linearly on either side of the interface between the main channel and its floodplain. The lateral distribution of \({(\mathrm{\rho UV})}_{{\text{d}}}\) is more or less linear and similar for different relative depths, and it is more reasonable to assume linear variation for \({(\mathrm{\rho UV})}_{{\text{d}}}\) rather than \({\text{H}}{(\mathrm{\rho UV})}_{{\text{d}}}\). It is apparent from Fig. 2 that the variation is similar in both situations. However, based on the linear variation of \({(\mathrm{\rho UV})}_{{\text{d}}}\), the problem is significantly simplified.

Fig. 2
figure 2

Lateral distribution of \({({\varvec{\uprho}}\mathbf{U}\mathbf{V})}_{\mathbf{d}}\) and \(\mathbf{H}{({\varvec{\uprho}}\mathbf{U}\mathbf{V})}_{\mathbf{d}}\)

Full size image

It implies that, \(\frac{\partial }{\partial {\text{y}}}[{(\mathrm{\rho UV})}_{{\text{d}}}]\) defined as ϕ, may be considered a constant in view of the linear variation of \({(\mathrm{\rho UV})}_{{\text{d}}}\); but, having a different value in the main channel and floodplains. Thus, as ϕ is constant and has the same dimension of \(\mathrm{\rho g}{{\text{S}}}_{{\text{o}}}\), it may be expressed as

$$\upphi =\upbeta \left(\mathrm{\rho g}{{\text{S}}}_{{\text{o}}}\right)$$
(5)

where β is a non-dimensional coefficient that can take on different values in the main channel compared to the floodplains. Then, for a constant water depth (H) domain, the secondary flow term may be expressed as

$$ \Gamma = \frac{\partial }{{\partial {\text{y}}}}\left[ {{\text{H}}\left( {\uprho {\text{UV}}} \right)_{{\text{d}}} } \right] = \upbeta \uprho {\text{gHS}}_{{\text{o}}} . $$
(6)

According to the Darcy equation, the boundary shear stress \({\uptau }_{{\text{b}}}\) maybe expressed as

$${\uptau }_{{\text{b}}}= \frac{{\text{f}}}{8}\uprho {{{\text{U}}}_{{\text{d}}}}^{2}.$$
(7)

Here, f is the friction factor.

Then, by substituting Eqs. (6), and (7) into Eq. (3) gives

$$\frac{1}{2}{{\lambda H}^{2}\left(\frac{8}{f}\right)}^{1/2}\frac{{\partial }^{2}{{U}_{d}}^{2}}{{\partial y}^{2}}-{{U}_{d}}^{2}+\frac{8g{HS}_{o}}{f}\left(1-\beta \right)=0$$
(8)

Thus, in the present study, an expression for the non-dimensional coefficient β is derived as follows.

$$\beta =0.17{\lambda H\left(f\right)}^{1/2}\frac{{\partial }^{2}{{U}_{d}}^{2}}{{\partial y}^{2}}-\frac{{\tau }_{b}}{\rho gH{S}_{o}}+1$$
(9)

The other main objective of the current study is to model laterally varying β, which was a fixed coefficient regardless of spatial locations in the Shiono and Knight method. β is a coefficient for considering the influence of the lateral bed slope on boundary shear stress.

Therefore, the analytical solution to Eq. (8) for a region with a constant flow depth maybe then expressed as

$${{\text{U}}}_{{\text{d}}}= {\left[{{\text{A}}}_{1}{{\text{e}}}^{\mathrm{\gamma y}}+{{\text{A}}}_{2}{{\text{e}}}^{-\mathrm{\gamma y}}+\left(1-\upbeta \right)\frac{8{{\text{gHS}}}_{{\text{o}}}}{{\text{f}}}\right]}^{1/2}.$$
(10)

Thus, Eq. (10) is the analytical solution derived in the present study to determine the depth-averaged velocity distribution. The present analytical solution is different from Shiono and Knight [21] due to the dealing approach on β.

Then, substituting the present analytical solution Eq. (10) to Eq. (2), the discharge may be written as

$${\text{Q}}={\text{A}}{\left[{{\text{A}}}_{1}{{\text{e}}}^{\mathrm{\gamma y}}+{{\text{A}}}_{2}{{\text{e}}}^{-\mathrm{\gamma y}}+\left(1-\upbeta \right)\frac{8{{\text{gHS}}}_{{\text{o}}}}{{\text{f}}}\right]}^{1/2}.$$
(11)

Thus, Eq. (11) is an analytical solution derived in the present study to determine discharge. The present analytical solution is different from Shiono and Knight [21] due to the dealing approach on β.

By substituting Eq. (11) for Eq. (1), then, the stage-discharge relationships maybe then expressed as

$${\text{H}}=\mathrm{ a}{\left({\text{A}}{\left[{{\text{A}}}_{1}{{\text{e}}}^{\mathrm{\gamma y}}+{{\text{A}}}_{2}{{\text{e}}}^{-\mathrm{\gamma y}}+\left(1-\upbeta \right)\frac{8{{\text{gHS}}}_{{\text{o}}}}{{\text{f}}}\right]}^{1/2}\right)}^{{\text{b}}}$$
(12)

Thus, Eq. (12) is the analytical solution derived in the present study to determine the stage-discharge relationships.

The present study also discusses the percentage of flow carried by the main channel and floodplains with different channel roughness. The percentage of the total flow in the main channel and floodplains for Rough, Heterogeneous and Smooth bed roughness is determined from the following equations.

$$\mathrm{\% }{{\text{Q}}}_{{\text{mc}}}=\left\{{{\text{bH}}\left[{{\text{A}}}_{1}{{\text{e}}}^{\mathrm{\gamma y}}+{{\text{A}}}_{2}{{\text{e}}}^{-\mathrm{\gamma y}}+\left(1-{\upbeta }_{1}\right)\frac{8{{\text{gHS}}}_{{\text{o}}}}{{{\text{f}}}_{1}}\right]}^{1/2}\right\}100$$
(13)
$$\mathrm{\% }{{\text{Q}}}_{{\text{fp}}}=2\left\{({{\text{B}}-{\text{b}})({\text{H}}-{\text{h}})\left[{{\text{A}}}_{1}{{\text{e}}}^{\mathrm{\gamma y}}+{{\text{A}}}_{2}{{\text{e}}}^{-\mathrm{\gamma y}}+\left(1-{\upbeta }_{2}\right)\frac{8{\text{g}}{({\text{H}}-{\text{h}}){\text{S}}}_{{\text{o}}}}{{{\text{f}}}_{2}}\right]}^{1/2}\right\}100$$
(14)
$${{\text{Q}}}_{{\text{t}}}={{\text{Q}}}_{{\text{mc}}}+{{\text{Q}}}_{{\text{fp}}}$$
(15)
$${{\text{Q}}}_{{\text{mc}}}={{\text{bH}}\left[{{\text{A}}}_{1}{{\text{e}}}^{\mathrm{\gamma y}}+{{\text{A}}}_{2}{{\text{e}}}^{-\mathrm{\gamma y}}+\left(1-{\upbeta }_{1}\right)\frac{8{{\text{gHS}}}_{{\text{o}}}}{{{\text{f}}}_{1}}\right]}^{1/2}$$
(16)
$${{\text{Q}}}_{{\text{fp}}}=({{\text{B}}-{\text{b}})({\text{H}}-{\text{h}})\left[{{\text{A}}}_{1}{{\text{e}}}^{\mathrm{\gamma y}}+{{\text{A}}}_{2}{{\text{e}}}^{-\mathrm{\gamma y}}+\left(1-{\upbeta }_{2}\right)\frac{8{\text{g}}{({\text{H}}-{\text{h}}){\text{S}}}_{{\text{o}}}}{{{\text{f}}}_{2}}\right]}^{1/2}$$
(17)

In the above equatins, Qmc is the main channel discharge, Qfp is floodplains discharge, Qt is total discharge, β1 and f1 are the main channel's non-dimensional coefficients and friction factors, and β2 and f2 are the non-dimensional coefficient and friction factor in the floodplains, respectively.

2.2 Boundary conditions

Consider a two-stage symmetric rectangular channel, as shown in Fig. 1, with each section having a different constant water depth and f, λ, Г, k and β. Then, four boundary conditions were used in the present study, as presented below.

$${\left({\frac{\partial {{\text{U}}}_{{\text{d}}}}{\partial {\text{y}}}}^{(1)}\right)}_{\mathrm{y }= 0}=0$$
(18)
$${\left({{{\text{U}}}_{{\text{d}}}}^{(2)}\right)}_{\mathrm{y }=\mathrm{ B}}=0$$
(19)
$${{\left({{\text{U}}}_{{\text{d}}}\right)}^{(1)}}_{\mathrm{y }=\mathrm{ b }}={{\left({{\text{U}}}_{{\text{d}}}\right)}^{(2)}}_{\mathrm{y }={\text{b}}}$$
(20)
$${\left({\frac{\partial {{\text{U}}}_{{\text{d}}}}{\partial {\text{y}}}}^{(1)}\right)}_{\mathrm{y }=\mathrm{ b }}={\left({\frac{\partial {{\text{U}}}_{{\text{d}}}}{\partial {\text{y}}}}^{(2)}\right)}_{\mathrm{y }={\text{b}}}$$
(21)

2.3 Integration constants A1 and A2

In the present study, after applying the selected boundary conditions to Eq. (10), the integration constants A1 and A2 were derived as follows.

$${{\text{A}}}_{1}={{\text{A}}}_{2}=\frac{{\upgamma }_{2}\left({{{\text{A}}}_{3}{\text{e}}}^{{\upgamma }_{2}{\text{b}}/2}-{{\text{A}}}_{4}{{\text{e}}}^{{-\upgamma }_{2}{\text{b}}/2}\right)}{2{\upgamma }_{1}{\text{sinh}}({\upgamma }_{1}{\text{b}}/2)}$$
(22)
$${{\text{A}}}_{3}=-{{\text{C}}}_{2}{{\text{e}}}^{{-\upgamma }_{2}{\text{B}}}-{{\text{A}}}_{4}{{\text{e}}}^{-2{\upgamma }_{2}{\text{B}}}$$
(23)
$${{\text{A}}}_{4}=\frac{{{\text{C}}}_{2}-{{\text{C}}}_{1}+\frac{\left[{{\upgamma }_{2}{{\text{C}}}_{2}{\text{e}}}^{{\upgamma }_{2}\left({\text{b}}/2-{\text{B}}\right)}\right]}{\left[{\upgamma }_{1}{\text{tanh}}\left({\upgamma }_{1}{\text{b}}/2\right)\right]}-{{\text{C}}}_{2}{\text{e}}{\upgamma }_{2}\left({\text{b}}/2-{\text{B}}\right)}{{{\text{e}}}^{{\upgamma }_{2}(2{\text{b}}/2-{\text{B}})}-{{\text{e}}}^{{-\upgamma }_{2}{\text{b}}}-\frac{\left[{{\upgamma }_{2}{\text{e}}}^{{\upgamma }_{2}\left({\text{b}}/2-2{\text{B}}\right)}\right]}{\left[{\upgamma }_{1}{\text{tanh}}\left({\upgamma }_{1}{\text{b}}/2\right)\right]}-\left({{\upgamma }_{2}{\text{e}}}^{{-\upgamma }_{2}{\text{b}}/2}\right)/\left[{\upgamma }_{1}{\text{tanh}}\left({\upgamma }_{1}{\text{b}}/2\right)\right]}$$
(24)

Then, the depth-averaged velocity distributions in the main channel and floodplains can be determined from

$${{{\text{U}}}_{{\text{d}}}}^{(1)}={\left[2{{\text{A}}}_{1}{\text{cosh}}\left({\upgamma }_{1}{{\text{b}}}_{2}/2\right)+{{\text{C}}}_{1}\right]}^{1/2}$$
(25)
$${{{\text{U}}}_{{\text{d}}}}^{(2)}={\left[{{{\text{A}}}_{3}{{\text{e}}}^{{\upgamma }_{2}{{\text{b}}}_{2}/2}+{{\text{A}}}_{4}{{\text{e}}}^{{-\upgamma }_{2}{{\text{b}}}_{2}/2}+\mathrm{ C}}_{2}\right]}^{1/2}$$
(26)

Thus, boundary shear stress distributions in the main channel and floodplains can be

$${{\uptau }_{{\text{b}}}}^{(1)}=\left(\frac{{{\text{f}}}_{1}}{8}\right)\uprho \left[2{{\text{A}}}_{1}{\text{cosh}}\left({\upgamma }_{1}{{\text{b}}}_{2}/2\right)+{{\text{C}}}_{1}\right]$$
(27)
$${{\uptau }_{{\text{b}}}}^{(2)}=\left(\frac{{{\text{f}}}_{2}}{8}\right)\uprho \left[{{{\text{A}}}_{3}{{\text{e}}}^{{\upgamma }_{2}{{\text{b}}}_{2}/2}+{{\text{A}}}_{4}{{\text{e}}}^{{-\upgamma }_{2}{{\text{b}}}_{2}/2}+\mathrm{ C}}_{2}\right],$$
(28)

where the C1 and C2 represent the secondary flow coefficient and can be expressed as

$${{\text{C}}}_{1}=\frac{8{{\text{gHS}}}_{{\text{o}}}}{{{\text{f}}}_{1}}\left(1-{\upbeta }_{1}\right), {{\text{C}}}_{2}=\frac{8{\text{g}}{({\text{H}}-{\text{h}}){\text{S}}}_{{\text{o}}}}{{{\text{f}}}_{2}}\left(1-{\upbeta }_{2}\right)$$
(29)
$${\upgamma }_{1}={\left(\frac{2}{{\uplambda }_{1}}\right)}^{1/2}{\left(\frac{{{\text{f}}}_{1}}{8}\right)}^{1/2}\left(\frac{1}{{\text{H}}}\right),{\upgamma }_{2}={\left(\frac{2}{{\uplambda }_{2}}\right)}^\frac{1}{2}{\left(\frac{{{\text{f}}}_{2}}{8}\right)}^{1/2}\left(\frac{1}{{\text{H}}-{\text{h}}}\right).$$
(30)

In the present study, we used a value of dimensionless eddy viscosity λ1 = 0.07 for the main channel, and the floodplain dimensionless eddy viscosity λ2 was determined from\({\lambda }_{2}= {\lambda }_{1}\left(-0.2+1.2{{D}_{r}}^{1.44}\right)\), where Dr is the relative depth given as \({D}_{r}\)=\(\frac{(H-h)}{H}\).

2.4 Composite roughness

Determining the composite roughness for a compound channel having different roughnesses is necessary. In the present study, three different channels having different roughness were used. Thus, the analytical solution is developed to determine composite roughness as follows. By considering a compound channel having different channel roughnesses, as shown in Fig. 1, Manning's flow equation may be written as

$${\text{Q}}=\frac{1}{{{\text{n}}}_{{\text{c}}}}{{\text{AR}}}^{2/3}{{{\text{S}}}_{{\text{o}}}}^{1/2}.$$
(31)

By substituting Eq. (31) with Eq. (2), the composite roughness may be written as

$${{\text{n}}}_{{\text{c}}}=\frac{1}{{{\text{U}}}_{{\text{d}}}}{{\text{R}}}^{2/3}{{{\text{S}}}_{{\text{o}}}}^{1/2}.$$
(32)

Then, by substituting the present analytical solution for depth-averaged velocity Eq. (10) to Eq. (32) then, the composite roughness may be expressed as

$${{\text{n}}}_{{\text{c}}}=\frac{{{{\text{R}}}_{{\text{i}}}}^{2/3}{{{\text{S}}}_{{\text{o}}}}^{1/2}}{{\left[{{\text{A}}}_{1}{{\text{e}}}^{\mathrm{\gamma y}}+{{\text{A}}}_{2}{{\text{e}}}^{-\mathrm{\gamma y}}+\left(1-{\upbeta }_{{\text{i}}}\right)\frac{8{{\text{gHS}}}_{{\text{o}}}}{{{\text{f}}}_{{\text{i}}}}\right]}^{1/2}},$$
(33)

where nc is composite roughness, and Ri is the hydraulic radius of the subsection.

3 Applications of the model to rectangular compound channels

3.1 Description of the experiments

The present experiments were conducted in 18 m long and 1.20 m wide straight compound channels with different channel roughnesses. Performing sieve analysis is required to find the particle size of the channel bed that will be channel the bed materials used to create the artificial bed roughness. Three different grain sizes, d50 = 12 mm, d50 = 8 mm, and 2 mm lined concrete, are selected to form Rough, Heterogeneous and Smooth bed configurations, respectively, as shown in Fig. 3.

Fig. 3
figure 3

Present experimental channel roughness configurations

Full size image

The flow depth was controlled downstream of the flume by adjusting the tailgate to achieve uniform flow. After uniform flow was achieved, when the streamwise gradient of the water depth and the velocity is constant, the depth-averaged velocity measurements were made using an acoustic doppler velocimetry (ADV) probe at a 14 m distance from the inlet. The measurements were taken at 0.4 H from the bed for the main channel and 0.40(H–h) for the floodplains with 10 mm intervals vertically and 25 mm laterally. ADV measures velocities where sound waves bounce off a moving object with their frequency shifted by the objects. The Nortek Vectrino probe automatically measures the water temperature, the user's sample length, and the instrument's sample rate. The Nortek Vectrino ADV can sample up to 200 measurements per second (200 Hz) at several rates. The boundary shear stress was measured at the same measurement section of velocity by using a Preston tube. The specific characteristics of ADV and Preston tube are shown in Fig. 4.

Fig. 4
figure 4

Specific characteristics of a ADV and b Preston tube used in the present experiments

Full size image

The present experimental channel geometry and hydraulic parameters are presented in Table 1.

Table 1 Experimental channel geometry and parameters used in the present study
Full size table

3.2 Application of the model to the present experiments

The analytical depth-averaged velocity distributions in the main channel and floodplains were determined from Eqs. (25) and (26), respectively, while the ADV measured the velocity distribution. The Preston tube was used to measure the local boundary shear stress in the main channel and floodplains, and the analytical boundary shear stress distributions can be determined from Eqs. (27 and 28). A comparison between analytical and experimental Ud and τb distribution for the present experiments is shown in Fig. 5.

Fig. 5
figure 5

A comparison between analytically calculated and measured Ud and \({\uptau }_{{\text{b}}}\) from the present experiments with different roughnesses

Full size image

As shown in Fig. 5, the results indicate that the variations of the flow resistance with lateral distance are different for the main channel and floodplains. The lateral depth-averaged velocity distributions and boundary shear stress in the main channel are approximately constant for a smooth bed, while it increases suddenly as the lateral distance and roughness increase on the floodplain due to the roughness increasing from the main channel towards the floodplains. This indicates the influence of channel roughness on depth-averaged velocity distributions and boundary shear stress.

The computed lateral distribution of roughness from the present experiments is shown in Fig. 6.

Fig. 6
figure 6

Computed lateral variation of roughness from the present experiments with different roughnesses

Full size image

As shown in Fig. 6, the variations of the flow resistance with lateral distance are different for the main channel and floodplains. The lateral channel roughness in the main channel is approximately constant at 0.009, while it increases suddenly as the lateral distance and roughness increase on the floodplain. Thus, the roughness increases from the main channel towards the floodplain. The result shows that the lateral roughness in the rough bed, with ranges from 0.016 to 0.024 in the floodplain, is higher than the smooth bed, with ranges between 0.012 to 0.018 and the heterogeneous bed, with ranges from 0.014 to 0.021. It indicates that the composite roughness increases in the floodplains as the channel bed roughness increases.

The stage-discharge relationship using the power function provided by Eq. (12) for the test configurations is shown in Fig. 7.

Fig. 7
figure 7

Stage-discharge relationships from the present experiment with Rough, Heterogeneous and Smooth roughness

Full size image

As shown in Fig. 7, the stage-discharge relationships can be influenced by channel roughness. The discharge is higher for smooth beds compared to rough and heterogeneous overbank flows.

The percentage of the total flow in the main channel and in the floodplains with different channel roughnesses is determined from Eqs. (13 and 14), as shown in Fig. 8.

Fig. 8
figure 8

Comparison of the percentage of total flow in the main channel and floodplains for different bed roughnesses for the present experiments

Full size image

As shown in Fig. 8, the percentage of the total flow in the floodplains is higher for smooth channels compared to the rough and heterogeneous channel beds. This indicates that channel roughness can influence the percentage of the total flow in the main channel and floodplains.

3.3 Application to Atabay [22] and Rezaei [23] experiments

Further details of the experimental data may be found in Atabay [22] and Rezaei [23]. The channel geometry and hydraulic parameters used in in Atabay [22] and Rezaei [23] experiments are presented in Table 2.

Table 2 Experimental channel geometry and parameters used by Atabay [22] and Rezaei [23]
Full size table

The lateral depth-averaged velocity distribution from the in Atabay [22] and Rezaei [23] experiments is shown in Fig. 9.

Fig. 9
figure 9

A comparison between the analytical and measured Ud and τb from the Atabay [22] and Rezaei [23] experiments with smooth roughness

Full size image

As shown in Fig. 9, the lateral depth-averaged velocity distributions and boundary shear stress increase suddenly as the lateral distance and roughness increase on the floodplain due to the roughness increasing from the main channel towards the floodplains. This indicates the influence of channel roughness on depth-averaged velocity distributions and boundary shear stress.

The computed distribution of roughness from the Atabay and Rezaei experiments is shown in Fig. 10.

Fig. 10
figure 10

Lateral variation of roughness from Atabay and Rezaei experiments with smooth roughness

Full size image

As shown in Fig. 10, the variations of the channel roughness with lateral distance are different for the main channel and the floodplains. The lateral channel roughness in the main channel is approximately constant at 0.004, while it increases suddenly as the lateral distance and roughness increase on the floodplains.

The stage-discharge relationship using the power function provided by Eq. (12) for test configurations of the Atabay and Rezaei experiments is shown in Fig. 11, respectively.

Fig. 11
figure 11

Stage-discharge relationships from a Atabay [22] and b Rezaei [23] experiments

Full size image

4 Discussion on modeling results

4.1 Non-dimensional coefficient

The non-dimensional coefficient β is one of the key parameters of the present model. It may be considered constant for each panel but different in the main channel and floodplain and can be expressed as

$${\upbeta }_{1}=0.17{{\uplambda }_{1}H\left({{\text{f}}}_{1}\right)}^{1/2}\frac{{\partial }^{2}{{U}_{d}}^{2}}{{\partial y}^{2}}-\frac{{{\tau }_{b}}_{1}}{\rho gH{S}_{o}}+1 {\upbeta }_{2}=0.17{{\uplambda }_{2}H\left({{\text{f}}}_{2}\right)}^\frac{1}{2}\frac{{\partial }^{2}{{U}_{d}}^{2}}{{\partial y}^{2}}-\frac{{{\tau }_{b}}_{2}}{\rho g(H{-h)S}_{o}}+1.$$
(34)

Thus, the determined non-dimensional coefficient β from the present, Atabay [22] and Rezaei [23] experiments with different roughness are shown in Fig. 12, respectively.

Fig. 12
figure 12

The computed non-dimensional coefficient from a the present experiments and b the Atabay [22] and Rezaei [23] experiments

Full size image

As shown in Fig. 12, the non-dimensional coefficient increases from the centre of the main channel to the interfaces and suddenly decreases toward the floodplains. The value is high at the interface between the main channel and floodplains due to momentum transfer and velocity differences. The non-dimensional value is higher for rough channels compared to smooth, as shown in Fig. 12. Thus, the non-dimensional coefficient plays an important role in predicting depth-averaged velocity distributions that influence the composite roughness and stage discharges relationships.

4.2 Composite roughness estimation methods

Investigations into the effect of composite roughness on flow characteristics and its estimation method are required. Among many composite roughness methods, we selected (1) the Einstein and Banks Method, (2) the Lotter Method, (3) the Cox Method, (4) the Yen method, and (5) the present model.

4.2.1 Einstein and banks method

Einstein and Banks [13] assumed that the total cross-sectional mean velocity is equal to the subarea mean velocity. Based on this assumption, they proposed a composite roughness expression as

$${{\text{n}}}_{{\text{c}}}={\left[\sum \frac{{{{\text{n}}}_{{\text{i}}}}^{3/2}{{\text{p}}}_{{\text{i}}}}{{\text{P}}}\right]}^{2/3},$$
(35)

where nc is Composite roughness, P is the total wetted perimeter, ni and pi are Manning's coefficient and wetted perimeter of the subsections, respectively.

4.2.2 Lotter method

Lotter [24] assumed that the total discharge equals the sum of the constituent discharges. Thus, based on this assumption, Lotter proposed a composite roughness expression as

$${{\text{n}}}_{{\text{c}}}=\frac{{{\text{PR}}}^{5/3}}{\sum \left(\frac{{{\text{p}}}_{{\text{i}}}{{\text{R}}}_{{\text{i}}}}{{{\text{n}}}_{{\text{i}}}}\right)},$$
(36)

where R is the total hydraulic radius, and Ri is the hydraulic radius of the subsections.

4.2.3 Cox method

Cox [25]assumed that the total shear force equals the sum of the constituent subsection shear force. Thus, based on this assumption, Cox proposed a composite roughness expression as

$${{\text{n}}}_{{\text{c}}}=\frac{\sum {{\text{A}}}_{{\text{i}}}{{\text{n}}}_{{\text{i}}}}{{\text{A}}},$$
(37)

where A is the total cross-sectional area, and Ai is the area of the subsections.

4.2.4 Yen method

Yen [26] assumed that the total shear velocity is a weighted sum of subarea shear velocity. Thus, based on this assumption, Yen proposed a composite roughness expression as

$${{\text{n}}}_{{\text{c}}}=\frac{\sum {{\text{n}}}_{{\text{i}}}{{\text{p}}}_{{\text{i}}}}{{\text{P}}}.$$
(38)

4.2.5 The present model

The composite roughness of the present and other experiments was estimated by using Eq. (33). Thus, we used Eq. (33) as a model to estimate composite roughness. A comparison of predicted and actual roughness using different methods from the present and other experiments is shown in Fig. 13.

Fig. 13
figure 13

Comparison of predicted and actual roughness using a different approach from the present experiments a Rough, b Heterogeneous and c Smooth roughness, d Smooth roughness for Atabay [22], and e smooth roughness for Rezaei [23] experiments

Full size image

4.3 Error analysis

In order to check the strengths and weaknesses of the models, an error analysis was conducted and analyzed in terms of mean absolute error (MAE), mean absolute percentage error (MAPE), root mean square error (RMSE) and Nash–Sutcliffe efficiency (E) as follows.

4.3.1 Mean absolute error (MAE)

$$MAE=\frac{1}{n}\sum_{i}^{n}\frac{{P}_{i}-{O}_{i}}{{O}_{i}},$$
(39)

where Pi is the predicted, and Oi is the observed value. MAE measures the degree to which the Pi differs from the Oi. Thus, the best results are the least deviation of the Pi from Oi.

4.3.2 Mean absolute percentage error (MAPE)

$${\text{MAPE}}=\frac{1}{{\text{n}}}\sum_{{\text{i}}}^{{\text{n}}}\frac{\left|{{\text{P}}}_{{\text{i}}}-{{\text{O}}}_{{\text{i}}}\right|}{{{\text{O}}}_{{\text{i}}}}*100$$
(40)

MAPE is also known as percentage deviation. If the MAPE of Pi from Oi is within 10%, the model is considered a good prediction model [8, 10].

4.3.3 Root mean square error (RMSE)

$${\text{RMSE}}=\sqrt{\frac{1}{{\text{n}}}\sum_{{\text{i}}}^{{\text{n}}}{\left({{\text{P}}}_{{\text{i}}}-{{\text{O}}}_{{\text{i}}}\right)}^{2}}$$
(41)

RMSE is also a measure of the difference between the predicted and observed value and measures how far the error is from zero on average.

4.3.4 Nash–Sutcliffe efficiency (E)

$${\text{E}}=1-\frac{\sum_{{\text{i}}}^{{\text{n}}}{\left({{\text{O}}}_{{\text{i}}}-{{\text{P}}}_{{\text{i}}}\right)}^{2}}{\sum_{{\text{i}}}^{{\text{n}}}{\left({{\text{O}}}_{{\text{i}}}-{\overline{{\text{O}}} }_{{\text{i}}}\right)}^{2}}$$
(42)

where \(\overline{{\text{O}} }\) is the mean of the observed values. An efficiency of E = 1 indicates a perfect match of the predicted to the observed data. In contrast, an efficiency less than zero occurs when the observed mean is a better predictor than the model. Thus, the closer the model efficiency is to 1, the more accurate the model is.

The summary of error analysis using a different approach from the present experiments with three different roughness and from Atabay [22] and Rezaei [23] with smooth roughness is presented in Tables 3, 4, 5, 6 and 7 respectively.

Table 3 Error statistics from the present experiments with a rough floodplain
Full size table
Table 4 Error statistics from the present experiments with a Heterogeneous floodplain
Full size table
Table 5 Error statistics from the present experiments with a Smooth floodplain
Full size table
Table 6 Error statistics from Atabay (2001) experiment with a smooth floodplain
Full size table
Table 7 Errors from Rezaei (2006) experiment with smooth floodplain
Full size table

The detailed error analysis results from the different methods are presented in Tables 3, 4, 5, 6 and 7. It indicated that the present model error is the least in the present and Atabay and Rezaei experiments. Thus, the present model can predict composite roughness in a compound channel having different roughness.

5 Conclusions

The present study discusses and analyses the flow resistance parameters and stage-discharge relationships in compound channels having different roughnesses. An analytical solution is presented. The model was applied to the present experiments with three different channels of roughnesses, i.e., rough, heterogeneous and smooth bed and two other experiments with a smooth channel bed. The model application to different data sets discusses the key model parameters of composite roughness and the non-dimensional coefficient. The influence of the flow resistance parameters on stage-discharge relationships and flow characteristics was analyzed.

The present study examines the depth-averaged and boundary shear stress distributions in compound channels with different roughnesses. The key model parameter, a non-dimensional coefficient that makes the present analytical solution different from Shiono and Knight [21], plays an important role in predicting the depth-averaged velocity distributions. This parameter depends on the boundary shear stress, and can influence the flow characteristics and stage-discharge relationships. As shown in Fig. 12, the non-dimensional coefficient increases from the centre of the main channel to the interfaces and suddenly decreases toward the floodplains. The value is high at the interface between the main channel and floodplains due to momentum transfer and velocity differences. The non-dimensional value is higher for the rough channel than the smooth one, as shown in Fig. 10. Thus, the non-dimensional coefficient plays an important role in predicting depth-averaged velocity distributions that influences the composite roughness and stage discharges relationships.

The present study investigates the stage-discharge relationships and the percentage of flow carried by the main channel and floodplains with different channel roughness. From the stage-discharge Fig. 7, the stage-discharge rating curve increases as roughness decreases. It indicated that the smooth channel discharge increases significantly compared to rough channels because the flow resistance is less for a smooth bed. This shows that channel roughness influences stage-discharge relationships.

The present experiments indicate that the variations of the flow resistance with lateral distance are different for the main channel and the floodplains. The lateral channel roughness in the main channel is approximately constant at 0.009, while it increases suddenly as the lateral distance and roughness increase on the floodplain. Thus, the roughness increases from the main channel towards the floodplain. The results show that the rough channel lateral roughness is higher than the smooth bed. It indicates that the composite roughness increases in the floodplains as the channel bed roughness increases.

The present study compared different roughness estimation methods from the literature with the present model. An error analysis was conducted by evaluating different error metrics for the different roughness estimation methods, and the present model produced the least error. This indicates that the present model can predict the composite roughness for compound channels having different channel roughness.

The application of the present model can be a powerful tool for fluid mechanics, sediment analysis, river engineering, and flood control structures, modelling flows in complex channels, and designing and planning water resource structures that may benefit from expanding the proposed model. More investigation on this application is recommended. Investigations with more complex flow conditions and the extension of the proposed model are recommended as the subject of further investigations.