1 Introduction

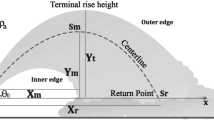
In some practical cases, pollutant could be denser than the receiving fluid, i.e., brine from desalination or geothermal plants, wastes from mining and dredging operations as well as industrial discharges [1]. In an inclined dense jet, due to the initial momentum and negative buoyancy, the jet ascends to a maximum rise height and then descends to the source level. Afterwards, it spreads as a density current. Inclination causes a longer trajectory and higher dilution and makes the flow not to fall back directly onto itself [2]. Reverse osmosis (RO) desalination plants discharge the effluents as submerged negatively buoyant jets. One of the important aspects of designing the outfall of a RO desalination plant is to optimize the configuration of its own outfall system. Figure 1 illustrates a schematic view of an inclined negatively buoyant jet and its environmentally important parameters.

Fig. 1
figure 1

Schematic view of an inclined dense jet and its parameters

Full size image

Experimental investigations in this field can be divided into two main categories:

First, the optimization of nozzle angle of single-port negatively buoyant jets. It was shown that the mixing of the saline effluent is improved at an angle of \(60^\circ \) to the horizontal, and it is recommended for releasing in coastal regions with steep slopes [3]. Apart from the pioneering investigation of Zeitoun et al. [4], in recent years, Kikkert et al. [5] used Laser Induced Fluorescence (LIF) technique to produce images and profiles of cross-sectional tracer concentration. They emphasized that the outer edge of the jet is sharp and definable in contrast to the blur inner edge. Additionally, they pointed out the deficiency of their integral model to capture the additional mixing due to buoyancy-induced instability. Shao and Law [6] used a combination of Particle Image Velocimetry (PIV) and Planar Laser Induced Fluorescence (PLIF) technique to resolve the velocity and concentration distribution profiles. They deduced that although the existence of buoyancy-induced instability is evident, the task of its modeling is still an open question. Lai and Lee [7] conducted a comprehensive investigation for inclinations of \(15^\circ \), \(30^\circ \), \(38^\circ \), \(45^\circ \), \(52^\circ \), and \(60^\circ \). They concluded that for inclinations between \(38^\circ \) and \(60^\circ \) impact dilution is not sensitive to the jet angle. Oliver et al. [8] performed a set of experiments relying on removing the boundary influences on the geometrical and mixing parameters. They covered inclinations ranging from \(15^\circ \) to \(75^\circ \). They reported that effect of the buoyancy-induced instability is more crucial at the return point compared to centerline peak. Other than these studies, several investigations have been reported in this subject [1, 2, 9,10,11,12,13,14,15].

Second, several studies examined the depth at which the waste discharge system is employed [3, 16,17,18,19].

In spite of the experimental investigations, numerical models employing Computational Fluid Dynamics (CFD) are less noticed. Vafeiadou et al. [20] performed a 3-D numerical simulation of negatively buoyant jets in a quiescent ambient using CFX package as a CFD toolbox. They employed Shear Stress Transport (SST) turbulence model. Oliver et al. [21] conducted a series of simulations using CFX package to adjust the turbulent Schmidt number in tracer transport equation using the standard k–\(\epsilon \) model. However, they made a comparison between the results of \(Sc_t=0.9\) and \(Sc_t=0.6\) through the standard and calibrated k–\(\epsilon \) model focusing only on the centerline peak integrated dilution and geometrical parameters of this point. Kheirkhah Gildeh et al. [22, 23] performed CFD simulations of \(30^\circ \) and \(45^\circ \) inclinations. Employing OpenFOAM,Footnote 1 they used k–\(\epsilon \) family, nonlinear k–\(\epsilon \), LRR,Footnote 2 and Launder–Gibson as turbulence models. They also employed \(Sc_t=1.0\) reporting no special difference between the results of cases with different values of \(Sc_t\) (0.6–1.0). Zhang et al. [24] performed a Large Eddy Simulation (LES) of \(45^\circ \) inclined dense jets with both Smagorinsky and Dynamic Smagorinsky sub-grid scale (SGS) for turbulence modeling. They considered \(Sc_t=0.7\) as a constant value in their simulation without any report on the effects of this number. Zhang et al. [25] used large eddy simulation to simulate \(45^\circ \) and \(60^\circ \) inclinations with body impact. Similar to [24], they found that adequacy of the model is promising only in prediction of the geometrical parameters. Again, turbulent Schmidt number was not of the concern to their study. They also performed a k–\(\epsilon \) simualtion to make the comparison more comprehensive. Ardalan and Vafaei [3] performed a CFD modeling using realizable k–\(\epsilon \) model to simulate thermal-saline \(45^\circ \) buoyant jets regarding \(Sc_t=1.0\). However, they didn’t report mixing parameters for purely saline scenarios of their simulations. Jiang et al. [26] performed both experimental and numerical (LES) investigations of \(45^\circ \) inclination. A constant \(Sc_t=0.7\) was considered in their LES simulation. They provided an energy spectrum along trajectory at different locations. Compared to the experimental data, the LES result showed good performance in lower frequencies. However, poor performance of the LES far from the nozzle (after centerline peak) and in cases of lower Froude number was observed.

Regarding experimental and numerical investigations, several key points are traceable in the literature:

First of all, there are huge discrepancies among the dilution ratio reports specifically at return point in experimental studies, which reaches up to about 50% (e.g. reported numbers by [7] and [27] for \(30^\circ \) inclined dense jets). Additionally, underestimation of dilution ratio in nearly all numerical models is observable. The range of this underestimation varies between more than 50\(\%\) in some commercial codes with integral modeling approach [28] and 20\(\%\) in the LES modeling of \(45^\circ \) inclined dens jets [24, 25]. However, it should be noted that using the modified reduced buoyancy flux (RBF) approach, Crowe et al. [29] addressed the flux conservative approach’s shortcomings. By employing the modified RBF model, they reported an improved performance over some previous integral modeling approaches. Moreover, both the experimental (e.g. [5, 6, 8]) and numerical (e.g. [26]) modelings stressed the importance of the buoyancy-induced instability leading to a poor prediction of mixing parameters in inclined negatively buoyant jets. Finally, although there are several reports and studies devoted to the role of turbulent Schmidt number in environmental fluid mechanics involving both water and air systems [30], there is no detailed study in earlier numerical simulations directly related to the effects of this factor on all parameters of inclined negatively buoyant jets.

Based on previous numerical and experimental modelings and their outcomes, the objective of this paper is to investigate the effects of turbulent Schmidt number on the environmentally important parameters such as dilution ratios and trajectory parameters in inclined negatively buoyant jets employing the realizable k–\(\epsilon \) model and OpenFOAM with two approaches. Within the first approach, seven different \(Sc_t\) values ranging from 0.4 to 1.0 were taken into account to make a plausible discussion about the range of influence of \(Sc_t\) on numerical results. Regarding the results of the first approach, a Regional Turbulent Schmidt Number (RTSN) methodology was introduced as a new numerical technique to mitigate the under-prediction of mixing parameters based on the different regional behavior of the flow. Among different inclinations used in numerical and experimental investigations, \(45^\circ \) is one of the most prevailing and was employed in this study.

2 Computational methodology and model setup

2.1 Governing equations

Using the Reynolds decomposition method, which results in Reynolds-Averaged Navier–Stokes (RANS) equations, the equations can be used for describing turbulent flows. With RANS approach, the governing equations for three-dimensional unsteady incompressible fluid flows can be shown as follows:

$$\begin{aligned}&\frac{\partial U_i}{\partial x_i}=0 \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial U_i}{\partial t}+\frac{\partial (U_i U_j)}{\partial x_j}= \frac{-1}{\rho _r}\frac{\partial P}{\partial x_i}+\frac{\partial \tau _{ij}}{\partial x_j}-\frac{\partial \overline{u'_i u'_j}}{\partial x_j}+g_i \frac{\varDelta \rho }{\rho _r} \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial \varPhi }{\partial t}+\frac{\partial {(\varPhi U_j)}}{\partial x_j}= \frac{\partial }{\partial x_j}\left( \varGamma \frac{\partial \varPhi }{\partial x_j}\right) -\frac{\partial \overline{u'_j \phi '}}{\partial x_j} +S_\varPhi \end{aligned}$$
(3)

where

$$\begin{aligned}&\tau _{ij}=\nu \left( \frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right) -\frac{2}{3}\nu \delta {ij}\left( \frac{\partial U_k}{\partial x_k}\right) \end{aligned}$$
(4)
$$\begin{aligned}&-\overline{u'_i u'_j}=\nu _t \left( \frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right) -\frac{2}{3}\delta {ij}k \end{aligned}$$
(5)
$$\begin{aligned}&-\overline{u'_j \phi '}=\frac{\nu _t}{\sigma _t}\frac{\partial \varPhi }{\partial x_j} \end{aligned}$$
(6)

where \(\rho _r\) is the reference fluid density (\(=\rho _a\)), \(S_\varPhi \) is a source term and \(\sigma _t\) is turbulent Schmidt/Prandtl number. \(\varPhi \) is a scalar quantity, which can be represented by concentration (salinity), temperature, turbulent kinetic energy (k), and its dissipation rate (\(\epsilon \)). Equations (5) and (6) already demonstrate the Boussinesq approximation. Density variation is assumed to be a function of concentration and temperature using the equation of state [31]:

$$\begin{aligned} \rho = \rho _t +AS+BS^\frac{3}{2}+CS^2 \end{aligned}$$
(7)

where \(\rho _t\), A, and B contain the variation of T (temperature), S represents concentration, and C is a constant value.

2.2 Turbulence modeling

Solving RANS closure needs extra equations to estimate the Reynolds stress tensor (\(-\overline{u'_i u'_j}\)) and turbulent scalar flux (\( -\overline{u'_j \phi '}\)). Boussinesq approximation results in prediction of Reynolds stresses by Eq. (5) and turbulent scalar fluxes by Eq. (6). In this manner, the only unknown parameter will be eddy viscosity (\(\nu _t\)). In this study, realizable k–\(\epsilon \) model was used as a Boussinesq approximation based turbulence model. The governing transport equations of realizable k–\(\epsilon \) model for incompressible flow consisting of buoyancy terms using Eq. (3) can be described as follows:

$$\begin{aligned}&\frac{\partial k}{\partial t}+\frac{\partial {(U_j k)}}{\partial x_j}=\frac{\partial }{\partial x_j}\left( \frac{\nu _t}{\sigma _k}\frac{\partial k}{\partial x_j}\right) +P+G-\epsilon \end{aligned}$$
(8)
$$\begin{aligned}&\frac{\partial \epsilon }{\partial t}+\frac{\partial {(U_j \epsilon )}}{\partial x_j}=\frac{\partial }{\partial x_j}\left( \frac{\nu _t}{\sigma _\epsilon }\frac{\partial \epsilon }{\partial x_j}\right) +C_{1\epsilon }S\epsilon -C_{2\epsilon } \frac{\epsilon ^2}{k+\sqrt{\epsilon \nu }} +C_{1\epsilon }C_{3\epsilon }\frac{\epsilon }{k}G \end{aligned}$$
(9)

where P and G are turbulent kinetic energy production due to shear and buoyancy, respectively. Other constant and variables in Eqs. (8) and (9) can be found in [32]. Prediction of k and \(\epsilon \) will result in \(\nu _t=C_\mu \frac{k^2}{\epsilon }\). Buoyancy augmentation is associated with different types of source-term in right hand side of Eq. (9). There are several proposals for buoyancy implementation specifically in fire and thermal applications [33]. In this study, the proposal of Heindel et al. [34] (\(C_{3\epsilon } = tanh\frac{v}{u}\). where v and u are vertical and horizontal components of velocity, respectively) was implemented for \(C_{3\epsilon }\). Estimation of buoyancy production (G) depends on how to model \(\overline{u'_j \phi '}\). Using the Standard Gradient Diffusion Hypothesis (SGDH) leads to:

$$\begin{aligned} G=-\beta \overline{u'_j \phi '}g_j=\beta \frac{\nu _t}{Sc_t}\frac{\partial C}{\partial x_j}g_j \end{aligned}$$
(10)

There are other non-Boussinesq approximation based suggestions to model G similar to the proposal of Daly and Harlow [35], Generalized Gradient Diffusion Hypothesis (GGDH), which contains an algebraic model for turbulent diffusivity to take the effects of turbulence anisotropy into account. Nevertheless, it seems more reasonable to stay restricted in Boussinesq approximation when the employed turbulence model is a Boussinesq approximation based model. Thus, the SGDH approach was employed here. In thermal applications, \(\beta \) is thermal expansion coefficient. For a saline domain it can be defined as saline (or haline) contraction coefficient (\(\beta =\frac{1}{\rho }\frac{\partial \rho }{\partial C}\)) [36].

2.3 Turbulent Schmidt number

The turbulent Schmidt number in Eq. (3) (\(\varGamma _{total}=\frac{\nu }{Sc}+\frac{\nu _t}{Sc_t}\) ) and (10), is defined as the ratio of momentum diffusivity to mass diffusivity in a turbulent flow:

$$\begin{aligned} Sc_t=\frac{\nu _t}{D_t} \end{aligned}$$
(11)

where \(D_t(=\varGamma _t)\) is turbulent diffusion rate. Presence of \(Sc_t\) in Eq. (3) directly affects the distribution of concentration values in a domain, which in turn affects the variation of density in equation of state (Eq. (7)). As a result, the momentum (Eq. (2)) and turbulence equations (Eqs. (8), (9)) will be affected, and the whole flow pattern will experience the results of changed turbulent Schmidt number. Figure 2 shows a part of solution’s loop regarding the presence of \(Sc_t\) in equations. However, \(\nu _t\) is another factor which affects the \(D_t\). Accordingly, a combination of both of these factors, \(Sc_t\) and \(\nu _t\), determines the distribution of the scalar field. The turbulent scalar flux (\(\overline{u'\phi '}\)) is another key parameter and restricted to SGDH approach here. Hiring a global constant \(Sc_t\), several reports show a broad range for this parameter. For instances, a ranging from 0.1 to 2.2 in combustion modeling [37, 38], urban diffusion [39], and jet in crossflow [40] can be seen in the literature. In earlier studies, Reynolds [41] introduced a formula accounting for dependency of \(Sc_t\) on turbulent intensity and laminar (molecular) Schmidt number (Sc). In more recent and related studies to the scope of the dense jets, Shao and Law [42] made an experimental study on turbulent characteristics of horizontal dense jets. They calculated \(Sc_t\) along and across the jet and reported the values ranging from 0.4 to 1.0. Xu and Chen [43] showed the importance of variation of turbulent Schmidt number in horizontal stratified jets reporting the variation of \(\sigma _t\) from 0.6 to more than unity. Shi et al. [44] introduced a linear formulation for predicting turbulent Schmidt number’s variation through experiments to calibrate the formula constants in horizontal stratified jets. As mentioned earlier, with regard to the importance of \(Sc_t\) on the whole flow pattern and mixing parameters, results and discussions are presented within two approaches:

Approach one: assigning a constant turbulent Schmidt number to the whole domain.

Approach two: Introducing a regional turbulent Schmidt number (RTSN).

Fig. 2
figure 2

Part of the solution’s loop regarding presence of \(Sc_t\)

Full size image

2.4 Initial conditions and geometry

To investigate the first approach, inclined \(45^\circ \) turbulent jets with two different initial conditions were modeled to compare the results of seven scenarios (14 cases) associated with seven values for turbulent Schmidt number, Table 1. Regarding the symmetrical nature of the flow, symmetric tanks with \(1.8Fr_d D\) width, \(6Fr_d D\) length, and \(2Fr_d D\) height (Fig. 3) were created. Length, width, and height of the domains were determined based on the criteria introduced by Zhang et al. [24]. Nozzle tap height (\(H_0\)) was considered above the bottom based on the findings of Shao and Law [6] (\(\frac{H_0}{lm}\ge 0.05\)) to avoid boundary influence. Initial tests were also performed to reach mesh independence based on 2% difference in dilution ratio at return point and centerline peak in every pair of geometries with different number of grids. Except for the symmetry plain, back, inlet, and bottom, other boundaries were considered as zero-gradient boundaries. Wall boundary condition was assigned to the back and bottom sides. Crank–Nicolson scheme was used for temporal discretization. To minimize the numerical diffusion, a second order Total Variation Diminishing (TVD) scheme was employed for divergence terms and a fourth-order cubic scheme for Laplacian terms. Computations for all cases were continued until they reach the steady state condition, which usually happened between 20 and 50 s. All of the required modifications and implementations for thr solver (pimpleFoam) and turbulence model (realizableKE) were accomplished in OpenFOAM.

Fig. 3
figure 3

One of the computational domains. a: symmetry plane of the domain and b: isometric view

Full size image
Table 1 Initial conditions and parameters of simulations within different scenarios
Full size table

3 Results and discussion

3.1 Approach one-flow characteristics and trajectory

Figure 4 shows the non-dimensional concentration (\(\frac{C}{C_0}\)) field of S2 (\(Sc_t=0.5\)), S4 (\(Sc_t=0.7\)), and S7 (\(Sc_t=1.0\)) on the symmetry plane. In comparison to the outer (upper) edge, the inner edge (lower) is blurred. A visual centerline is hard to define due to the detrainment of flow destroying the axis-symmetrical nature of the jet [7]. Additional mixing occurs in the inner half of the flow makes it extended where the unstable density gradients exist. On the other hand, stable density gradients in the outer side result in a rather unaffected region [8]. As can be seen from the figure, S7 with \(Sc_t=1.0\) is less diffused (more conservative) in comparison with S2, which is conducted with \(Sc_t=0.5\). S4 with \(Sc_t=0.7\) lies between S2 and S7. As discussed earlier, presence of \(Sc_t\) in turbulent diffusion rate at the right hand side of Eq. (3) directly affects the distribution of mean scalar field. Figure 5 is a representation of cases presented in Fig. 4 using superimposition for S2 and S7. From the figure, for the both Froude numbers, S7 reveals a more conservative performance where each contour of it is more squeezed and elongated than S2.

Fig. 4
figure 4

Non-dimensional concentration fields of a, d S2, b, e S4, and c, f S7 on the symmetry plane

Full size image
Fig. 5
figure 5

Super imposition of four contours of (\(\frac{C}{C_0}\)) in S2 and S7 for a \(Fr_d=12\) and b \(Fr_d=20\)

Full size image

Different patterns of scalar contours shown in Figs. 4 and  5 can be observed quantitatively using the jet growth or jet spread definition. To compare the results with the experimental data, analogous to the procedure hired by Shao and Law [6], Gaussian fitting and using \(e^{-1}\) ratio of the maximum concentration for each selected point along the jet centerline were used here. Figure 6 shows the result of both the upper and lower \(b_c\) (\(b_c\) is a radial distance defined by where \(C/C_m=1/e\)) from the present simulation in comparison with the experimental data. It can be observed that the scenario with lower turbulent Schmidt number value (S2, \(Sc_t=0.5\)) shows a better performance compared to the other one with \(Sc_t=1.0\) behaving conservative specifically in terms of lower \(b_c\). The most difference between the results occurs at the lower half of the flow where the jet is under the effect of unstable density gradients. The better performance of the scenarios with lower turbulent Schmidt number implies the effects of this parameter on numerical results.

Fig. 6
figure 6

Variation of upper and lower \(b_c\)

Full size image

The jet centerline, or trajectory, is one of the most important features of the inclined dense jet. The jet centerline could be built as the consecutive locus of the maximum velocity or concentration at various cross-sections. Figure 7 shows the normalized jet centerlines (concentration centerline) derived from the present simulation in comparison with each other and other numerical and experimental data in the past. From the figure, increasing the \(Sc_t\) results in more elongated trajectories with higher centerlines’ peaks and further return point’s locations. As discussed earlier, it was anticipated to see the effect of turbulent Schmidt number variation on the whole flow pattern, and this expectation was met in deflections of the jet trajectories. As it noticeable, the present results lie under the LES predictions [25]. Regarding the similar value for \(Sc_t\), it can be seen that the realizable k–\(\epsilon \) with \(Sc_t=0.7\) shows a superior performance compared with the standard k–\(\epsilon \) from Zhang et al. [25] which make the realizable k–\(\epsilon \) the best version among k-e family. This finding was confirmed by Kheirkhah Gildeh et al. [23] as well. It is worth noting that since velocity and concentration centerlines are not exactly the same, taking velocity centeline as the jet trajectory changes the geometrical and mixing parameters. This difference between the concentration and velocity centerlines is discussed by Shao and Law [6] and documented by Kheirkhah Gildeh et al. [22] in their CFD simulations. Thus, in order to make the results more clear and comprehensive, both of the trajectoies are provided here (Table 2).

Fig. 7
figure 7

Trajectories from a present study only and b together with other data

Full size image

It is important to note that Froude numbers with which the present study was conducted were selected based on simulating cases with initial turbulent Reynolds number close to the critical value (\(Fr_d=12, Re \sim 2800\)) and above that (\(Fr_d=20, Re \sim 3600\)) for a full turbulent jet flow to capture the differences between them. Some experiments discussed the effect of Froude number range on the dynamics of the jet and its trajectory. Roberts and Toms [45] declared that \(Fr_d > 20\) is needed to cancel out the effects of initial volume flux. Lai and Lee [7] paid attention to the relation between dimensionless constants and the hired range for \(Fr_d\). Based on their results, dimensionless dilution ratios at the return point tend to collapse onto a constant for \(Fr_d > 20\). Also, they reported that the dimensionless terminal rise height has an additional reliance on \(Fr_d\) for small \(Fr_d\), and come close to a constant when \(Fr_d \ge 25\). For CFD modelings, Kheirkhah Gildeh et al. [23] reported 5% difference in centerline dilution ratios for Froude numbers ranging from 50 to 100. In consistence with the experimental reports, this study’s results confirmed the effect of Froude number on the mixing and trajectory parameters, i.e, dimensionless constants are not the same for both of the hired Froude numbers. Regrading trajectory parameters, dimensionless return point distance (\(\frac{X_r}{DFr_d}\)) and terminal rise height (\(\frac{Y_t}{DFr_d}\)) show \(\sim 10\%\) and \(\sim 7\%\) differences, respectively. Generally, Results of cases with \(Fr_d=20\) had a better agreement with the experimental data. Thus, provided numbers in Table 2, cover the results of the hired values for \(Fr_d\) using ± sign. In each Scenario, the highest value addresses the \(Fr_d=20\). Therefore, this Froude number (\(Fr_d=20\)) was selected for more investigation within approach two.

To continue with mixing parameters under the influence of turbulent Schmidt number, variation of concentration along jet centerline (concentration decay) would be a good indicator to evaluate the results. Figure 8 shows a comparison between present study and experimental investigations by Papanicolaou and List [46] and Shao [16]. In this figure, \(S=C/C0\), s is the streamwise distance along the jet centerline, Q is the initial volume flux, and M is the initial momentum flux. Although the experiment by [46] was conducted for vertical buoyant jets, valuable insight into the dynamics of the flow is provided. From Fig. 8a, before the \(\frac{s}{lm}\sim 1\) (where \(l_m\) is the momentum length scale) the scatter of the numerical results are more than the case where the jet leaves this region (known as jet-like region) and enters the transition and plume-like regions. This difference between the results in the jet-like region could be attributed to the initial difference in Froude numbers (i.e. initial momentum and turbulent Reynolds number) characterizing the flow at initial stages. After this region, numerical data collapse onto two different regimes governed by turbulent Schmidt number. Results with lower turbulent Schmidt number values are more close to experimental data. It can be interpreted from the results that after jet passes jet-like region, the flow behavior changes dramatically, and concentration field could be manipulated by turbulent Schmidt number.

Concentration decay compared to the experimental results of [16] also confirms the effect of \(Sc_t\) on the results. As can be seen in Fig. 8b, reducing the turbulent Schmidt number led to a closer agreement with experimental data specifically in downstream of the flow where the jet enters the transition and plume-like regions.

Fig. 8
figure 8

Concentration decay and dilution along jet centerline compared to a [46] and b [16]

Full size image

3.2 Approach one-quantitative results: geometrical and mixing parameters

In order to examine the environmental effects of the brine discharge, the assessment should find out the geometrical parameters consisting of terminal rise height, return point location, and dilution at different locations [24].

Table 2 is presented to provide a comprehensive report from this simulation accompanied by previous experimental and numerical studies. From Table2, following deductions can be remarked:

Table 2 Summarized comparison of dimensionless geometrical and mixing parameters
Full size table

  • Reducing \(Sc_t\) up to 60% led to about 60% improvement in return point dilution ratio. This drastic variation shows that the effects of \(Sc_t\) on simulations is undeniable. Kheirkhah Gildeh et al. [22, 23] reported the insensitivity of their results to the variation (0.6–1.0) of the turbulent Prandtl number (\(Pr_t\)), which is not surprising for temperature equation due to the negligible temperature difference between the inclined negatively buoyant jet and the receiving ambient water where the concentration difference is the main source of buoyancy. In contrast to the approach employed in this study, it appears that they did not include the effects of turbulent Schmidt number as the main effective mixing parameter in the transport equation of concentration using the SGDH approach. Moreover, they only applied the effects of turbulent Prandtl (Schmidt) number in the buoyancy production term of their employed turbulence model. As can be seen in Fig. 2, in the present study, the turbulent Schmidt number is appropriately included in two levels in the equations, i.e. the scalar transport equation (Eq. (3)) and buoyancy augmentation in turbulence model (Eqs. (8), (9), and (10)), to capture the mixing process in inclined negatively buoyant jets.

  • Both of the present study and the LES prediction [25] underestimated the dilution ratio at the return point. The LES results, which were derived based on using \(Sc_t=0.7\), are close to the results of the present study using \(Sc_t=0.5, 0.4\). Thus, it can be noticed that the effects of \(Sc_t\) would hold a different level of significance using different turbulence modeling approaches.

  • Average values of five Scenarios (from \(Sc_t=0.4\) to \(Sc_t=0.8\)) derived from the present simulation stood \(35\%\) above the numerical results from the integral models used by Palomar et al. [28] (not shown here) at the return point.

  • Reducing \(Sc_t\) up to 50% led to about 10% aggravation in trajectory parameters. Regarding the experimental data, geometrical parameters of this simulation were under-predicted. On the contrary, the LES prediction overestimated these parameters.

  • For numerical simulations, to predict mixing and trajectory parameters of \(45^\circ \) inclined negatively buoyant jets employing the realizable k–\(\epsilon \) model, \(0.5 \le Sc_t \le 0.6\) is recommended. However, it results in a poor prediction of geometrical parameters.

3.3 Approach one-concentration profiles

Figure 9 reveals transverse distribution of non-dimensional concentration (\(C/C_m\)) against dimensionless normal coordinate (\(r/b_c\)). One should note that \(C_m\) is the local concentration value at each cross-section’s center. From Fig. 9, S2 with \(Sc_t=0.5\) is more transversely diffused in comparison with S7 (\(Sc_t=1.0\)) moving from upstream toward downstream of the flow. The general pattern for both scenarios reveals the effect of buoyancy instability on the lower half of the flow, which results in asymmetry. Reducing \(Sc_t\) led to intensified widening of the profiles in the lower half of the flow indicating the effect of this parameter associated with buoyancy-induced distortion. Figure 10 shows the performance of cases with \(Sc_t=0.5, 1.0\) along with the experimental results of Oliver et al. [8] at centerline peak and return point. From the figure, S2 predicts the experimental data at the centerline peak (\(X_m\)) better than S7. Performance of the both revealed cases in this figure and other scenarios (not shown here) indicated that values of \(Sc_t \le 0.7\) are closer to experimental data.

Fig. 9
figure 9

Non-dimensional cross-sectional distributions of normalized concentration at various sections for a S2, b S7. \(Fr_d=20\)

Full size image
Fig. 10
figure 10

Comparison of cross-sectional distributions of non-dimensional concentration at centeline peak and return point with experimental data

Full size image

3.4 Approach two-regional turbulent Schmidt number (RTSN)

It was shown in the previous section that reducing turbulent Schmidt number can successfully improve the mixing parameters. Nevertheless, this improvement is aligned with an aggravation in geometrical parameters and cross sectional distributions. Such partial improvements in numerical predictions can be seen in different studies. for instance, He et al. [40] reported that \(Sc_t=0.2\) is the best constant value to simulate jet in crossflow. However, the predicted turbulent intensity around the jet was underestimated using \(Sc_t=0.2\). Riddle et al. [47] reported similar underestimation of turbulent kinetic energy along with improved ground level concentrations by reducing \(Sc_t\) from 0.7 to 0.3 in numerical stimulation of pollutant dispersion. Inadequacy of the first approach (constant \(Sc_t\) in the whole domain) of the present study in accurate prediction of the both mixing and trajectory parameters could be attributed to the ignorance of the regional behavior of the flow. This regional behavior is discussed within the following sections.

Experimental results proved that buoyancy-induced instability at the inner half of the jet, which accounts for additional vertical mixing in this region, considerably changes the concentration profiles and results in higher integrated dilution along flow centerline [48]. Some other researchers [7, 8, 21, 24, 29] independently emphasized on importance of the additional mixing or buoyant instability taking place in the lower half of the jet due to unstable density gradients. Jiang et al. [26] reported that the difference between LES simulation and experimental results in terms of turbulent kinetic energy spectrum was intensified after centerline peak where the flow is under the influence of turbulent kinetic energy production due to buoyancy. Regardless of the grid number deficiency that they addressed as the main source of the LES inaccuracy, it can be interpreted from their results that buoyancy-induced instability (in the inner half of the flow) was not captured very well in the LES simulation.

Figure 11 graphically shows that why inner half of the jet is associated with the induced-driven instability and the outer half with stable density gradients. In the outer half, every fluid particle tends to act in agreement with density stratification, which results in stable density gradients in this region. On the contrary, in the inner half, some of the fluid particles tend to peel off from the jet to make detrainment process and produce unstable density gradients creating additional mixing zone [7].

Fig. 11
figure 11

Schematic view of stable and unstable density gradients and additional mixing zone

Full size image
Fig. 12
figure 12

Distribution of buoyancy production (G) in a case with \(Sc_t=0.7\) (S4)

Full size image

Stable and unstable density gradients and their different attributes can be quantitatively characterized using production of shear (P) and buoyancy (G) of turbulence. Figure  12 demonstrates distribution of G in a case with \(Sc_t=0.7\). In the outer half (stable density gradients), turbulence is damped due to negative values of G (as a result of stable density gradients), which leads to reduction of k (see Eq. (8)). On the contrary, the process is reversed in the lower half. Hence, turbulence will be enhanced (G is positive) in this region due to unstable density gradients [43, 49]. From this point of view, G is directly related to the enhancing and damping mechanisms of turbulence due to buoyancy in the stable and unstable density gradients. Therefore, the accuracy of modeling of G is a determining factor, which is restricted to Boussinesq approximation here (see Eq. (10)). Flux Richardson number (\(R_f\)) is another key parameter to understand the different behavior of inner and outer halves of the flow. \(R_f\) is generally defined as [49]:

$$\begin{aligned} R_f=\frac{-G}{P} \end{aligned}$$
(12)

Wherever \(\mid G \mid \ll P\) (\(\mid R_f \mid \ll 1\)) buoyancy is negligible in comparison with momentum. Distribution of \(R_f\) along sections A–A and B–B (Fig. 12) shown in Fig. 13a confirms the complete dominance of momentum in the jet-like region, and the strong effect of buoyancy after centerline peak, respectively. Figure 13b also shows the distribution of G along the section B–B for a case with \(Sc_t=0.7\). From the figure, the lower values of G at the inner half could be as an indication for underestimation of turbulent kinetic energy. With regards to the results of the approach one, the most critical deficiency of turbulence modeling occurs in this region (inner half) where the jet is under the influence of buoyancy instability and can not capture the additional mixing zone properly, and thereby, the dilution would be underestimated.

The mixing process not only is influenced by the advective (momentum) transport but also mainly by the diffusive transport process (scalar transport equation, i.e., Eq. (3)). To predict the mixing process in jet in crossflow, Galeazzo et al. [50] reported that different values of turbulent Schmidt/Prantdle number should be used in the core of the jet and its boundaries. The core and boundaries of the flow directly address different advective and diffusive mixing behaviors. To take into account the effect of variable turbulent Schmidt number on inclined negatively buoyant jets, a rigorous approach can be defined as a formulation for \(Sc_t\) similar to what was accomplished by Shi et al. [44] for horizontal stratified jets. However, lack of experimental data consisting of measured Reynolds stresses and turbulent scalar fluxes impedes developing such a dynamically variable formulation. Being restricted to Boussinesq approximation (Eq. (6) and the turbulence model), which simplifies the effect of Reynolds stresses and turbulence anisotropy, adjusting the turbulent Schmidt number according to the flow structure should handle the deficiencies of this simplification.

Fig. 13
figure 13

Distribution of \(R_f\) and G along a sections A–A/B–B and b section B–B

Full size image

Based on the experimental and numerical evidences, the RTSN approach was introduced to capture the different behavior of jet-like, plume-like, inner/outer regions and the additional mixing taking place in the inner half of the flow. To achieve this goal, the following values for \(Sc_t\) are assigned in different regions of a computational domain (see Fig. 14):

$$\begin{aligned} Sc_t= {\left\{ \begin{array}{ll} 0.8, &{} \quad{\text {almost jet-like region and outer half of the flow}}\\ 0.4, &{} \quad{\text {additional mixing zone }}\\ 1.0, &{}\quad {\text {absence of density stratification}} \end{array}\right. } \end{aligned}$$
(13)

Isolating these regions in the code (OpenFOAM) was accomplished by using negative/positive values of G and vertical components of velocity vectors. The boundary between regions marked with \(Sc_t=0.8\) and \(Sc_t=1.0\) was defined based on using \(R_f=0\) (\(G \simeq 0\)). \(Sc_t=1.0\) was established by assigning \(Sc_t=Sc_0\), where \(Sc_0\) is the turbulent Schmidt number in regions without density stratification [51]. Finally, \(Sc_t=0.4\) and \(Sc_t=0.8\) were determined from numerical experiments and with general idea of using a lower turbulent Schmidt number for the additional mixing zone and a higher one for the outer half and jet-like region. This can be justified by regarding the damping effect of stable density gradients in the outer half. It should be noted that the maximum and minimum of the hired range are relatively consistent with the measurement of \(Sc_t\) in horizontal dens jets through the experiments conducted by Shao and Law [42] where they reported this range between 0.4 to 1.0.

Fig. 14
figure 14

Distribution of \(Sc_t\) along and across a test case with \(Fr_d\)=20 on the symmetry plain using RTSN approach

Full size image

Figure 15 shows the distribution of turbulent eddy viscosity and diffusivity in cases with constant turbulent Schmidt number (\(Sc_t=0.7\)) and the RTSN approach, respectively. From the figure, reducing turbulent Schmidt number increases the turbulent diffusivity (\(\varGamma _t=D_t=\frac{\nu _t}{Sc_t}\)), which results in higher dilution ratios. It can be observed that in the first approach, (Fig. 15a, b) both the \(\nu _t\) and \(D_t\) have the same pattern due to assigning a constant \(Sc_t\) to the whole domain. There is an increase in turbulent viscosity moving form the nozzle towards the return point. This pattern is consistent with the experimental observations of Shaw and Law [42] and Jiang et al. [26] reporting a similar trend for turbulence intensity along the jet centerline of horizontal and inclined dense jets, respectively. Differences between the distribution of turbulent diffusivity and viscosity are evident in Fig. 15c, d as a result of using the RTSN approach. Effects of the RTSN on distribution of \(D_t\) is consistent with the report of Gualtieri et al. [30] where they emphasized the more sensitivity of mass diffusivity (\(D_t\)) to the stratification (i.e., stable and unstable density gradients) than the momentum diffusivity (\(\nu _t\)).

The intensified turbulent diffusivity can be seen in Fig. 16a where the inner half of the flow in a point close to the return point location of a case with RTSN approach is characterized with higher values of \(D_t\) compared to the case with \(Sc_t=0.7\). This local (regional) change in turbulent Schmidt number compensates for the flaws of Boussinesq simplification. The figure shows that the maximum value of \(\nu _t\) (and \(D_t\)) occurs in the outer half of the flow, which is consistent with observations of Oliver et al. [8]. They reported the concentration fluctuations at the centerline peak and return point with peak values and steeper decay of the fluctuations at the outer half. Figure 16b represents the redistribution of G after using the RTSN approach. It can be observed that how RTSN increases the buoyancy production (G) at the inner half, and therefore, enhancing the mixing process in this region.

Figure 17 shows the non-dimensional field of concentration after using the RTSN approach along with cases with constant \(Sc_t\) for \(Fr_d=20\). Compared to the simulations conducted with constant turbulent Schmidt number, concentration fields are very close to test cases with \(Sc_t=0.7\). However, quantitative results show the superior performance of the RTSN approach (Table 3).

Fig. 15
figure 15

Distribution of \(\nu _t\) and \(D_t\) in cases with a, b \(Sc_t=0.7\) and c, d RTSN approach. \(Fr_d=20\)

Full size image
Fig. 16
figure 16

profiles of a \(\nu _t\) / \(D_t\) and b G in cases with \(Sc_t=0.7\) and RTSN approach. \(Fr_d=20\)

Full size image
Fig. 17
figure 17

Non-dimensional concentration fields of a, b, c cases with constant \(Sc_t\) together with d the case with the RTSN approach

Full size image

Using the RTSN approach successfully improved the mixing parameters along with keeping the accuracy of trajectory parameters nearly unchanged in comparison with using any other constant \(Sc_t\) for the whole domain (see Table 3). Figure 18 shows non-dimensioanl concentration profiles of cases with the RTSN approach and \(Sc_t=0.7\). From the figure, results of the RTSN stand close to their counterparts of a case with \(Sc_t=0.7\) and the experimental data from [8].

A glimpse to the quantitative results of mixing and trajectory parameters for two cases with \(Sc_t=0.7\) and the RTSN approach is provided in Table 3. The last row provides the range of errors for RTSN compared to the average values of the experimental data. From the table, the RTSN had an underestimation of \(14\%\) on \(\frac{S_r}{Fr_d}\) compared to the average of experiments. Regarding the results of standard and realizable k–\(\epsilon \), RTSN shows a superior performance. It is also can be seen that for both of the geometrical and mixing parameters the RTSN approach under-predicted the experimental data with \(\sim 10\%\) error in average making it a beneficial choice for simulations with lower economic costs compared to the LES modeling using up to 16 million of grids (e.g. [26]).

Fig. 18
figure 18

Cross-sectional distributions of non-dimensional concentration at return point using RTSN approach. \(Fr_d=20\)

Full size image
Table 3 Comparison of dimensionless geometrical and mixing parameters regarding RTSN approach
Full size table

4 Conclusions

In this investigation, \(45^\circ \) inclined dense jets were simulated using realizable k–\(\epsilon \) model with buoyancy corrections and different values of turbulent Schmidt number within two approaches. In the first one, seven scenarios with different values of \(Sc_t\) were simulated. In the second approach, a regional turbulent Schmidt number configuration was introduced based on the different behavior of the dense jet in jet-like, plume-like, and inner/outer regions. Following points can be remarked as the conclusions of this study:

  • This study showed that changing the turbulent Schmidt number has significant consequences for mixing and geometrical parameters. Reducing \(Sc_t\) from 1.0 to 0.4 led to more than \(\sim 60\%\) and \(\sim 40\%\) improvement in dilution ratio at return point and centerline peak, respectively. However, this change adversely affected geometrical parameters and cross-sectional distribution of concentration. The results of dilution ratio at centerline peak in comparison with return point were in a better agreement with the experimental data. This is an indication of complexity of the flow behavior under the influence of buoyancy-induced instability (additional mixing), which occurs almost beyond the centerline peak in the descending zone of the flow.

  • This study led to the under-prediction of mixing parameters comparable to some other previous numerical studies (e.g. [24, 25]). However, it was shown that \(Sc_t\) plays a manipulating role in distribution of the scalar field in simulation domain for an inclined negatively buoyant jet.

  • In consistence with the experimental reports, this study’s results confirmed the effect of Froude number on the mixing and trajectory parameters, i.e, dimensionless constants are not the same for both of the hired Froude numbers. Regrading the trajectory parameters, the dimensionless return point distance (\(\frac{X_r}{DFr_d}\)) and terminal rise height (\(\frac{Y_t}{DFr_d}\)) show \(\sim 10\%\) and \(\sim 7\%\) differences, respectively.

  • For numerical simulations, to predict the mixing and trajectory parameters of \(45^\circ \) inclined negatively buoyant jets employing realizable k–\(\epsilon \) model, \(0.5 \le Sc_t \le 0.6\) is recommended. However, this recommendation is based on using a constant value of \(Sc_t\) for the whole domain, which results in a poor prediction of geometrical parameters.

  • Using RTSN approach successfully improved the mixing parameters along with keeping nearly unchanged the accuracy of geometrical parameters. That was the case, specifically at the return point in comparison with using any other constant \(Sc_t\) for the whole domain (first approach) .Based on the results of this study and previous investigations, using dynamically variable turbulent Schmidt number formulation in negatively buoyant jets could be regarded more vigorously, which is under investigation by the authors.

  • Effects of \(Sc_t\) as a compensatory factor for deficiencies of the realizable k–\(\epsilon \) model (as a Boussinesq approximation based model) was highlighted in this investigation. It can be concluded that this effect of \(Sc_t\) would hold a different level of significance using different eddy viscosity turbulence models, which remains as an open room for future investigations.

  • Comparing to the previous LES results [24,25,26], the RTSN approach combined with the realizable k–\(\epsilon \) model stands as an economically superior solution employing much lower grid numbers for engineering applications.