1 Introduction

Effluents that have a density heavier than the ambient environment are often discharged directly into coastal waters using submerged outfalls, and the effluent discharges thus behave as dense jets. Typical examples include brine discharges from desalination plants and de-cooling water discharges from liquefied natural gas (LNG) plants. These effluent discharges can have an adverse influence on the local waterborne ecosystem [1, 2]. In order to mitigate the potential environmental impact, it is essential to design the outfall in an optimal manner to achieve a rapid mixing of the brine effluent with the ambient waters. Hence, a good prediction of the outfall performance is important for design purpose.

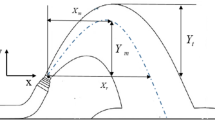
A submerged inclined outfall configuration is typically adopted for brine discharges in coastal waters, as the inclined dense jet exhibits a longer curvilinear trajectory before impacting the sea bed and hence the configuration can achieve a higher dilution. Figure 1 illustrates the schematic side view of the inclined dense jet in stagnant ambient, where z t is the terminal rise height, x r is the return point location, x m and z m are the horizontal and vertical locations of the centerline peak, respectively. Upon discharging from the bottom, the inclined dense jet first rises due to the initial momentum. After reaching the peak height, it then falls and impacts onto the seabed due to the negative buoyancy.

Fig. 1
figure 1

Schematic side view of an inclined negatively buoyant jet in stagnant ambient

Full size image

Many analytical and experimental studies had been conducted on inclined dense jets. Zeitoun et al. [3] performed a pioneering experimental study with various inclinations, and suggested an inclination of 60° (relative to the horizontal) to achieve the maximum dilution. The 60° inclination was then investigated in many subsequent experimental investigations [4–6], where both the jet geometrical and dilution characteristics were determined. Pincince and List [4] compared their experimental results with integral modelling predictions, and concluded that the integral model was able to predict the flow trajectories with reasonable accuracy while significantly underestimated the dilution. More recently, several studies [7–9] extended the investigations of negatively buoyant discharges to smaller inclinations of 30° and 45°, which are more feasible for outfalls in coastal regions where the near-shore bathymetry is relatively shallow. Their studies characterized the jet geometrical features, including the maximum rise height and the impact/return point distances, as well as the dilution characteristics. Generally, these earlier analytical and experimental investigations indicated a dependence of the mixing characteristics with the discharge densimetric Froude number, which is defined as:

$$ Fr = \frac{{U_{0} }}{{\sqrt {\frac{{\rho_{b} - \rho_{a} }}{{\rho_{a} }}gD} }} $$

where U 0 is the jet exit velocity, \( \rho_{a} \) and \( \rho_{b} \) are ambient and brine densities, respectively, g is the gravitational acceleration, D is the diameter of the discharge nozzle.

Numerical studies on negatively buoyant jets had also been performed in recent years. These studies mostly focused on vertical fountains [10–12]. The fountain is inherently different from the inclined dense jet because it re-entrains the negatively buoyant fluid which falls back around the vertical discharge. Vafeiadou et al. [13] was the first to report a numerical study on inclined dense jets. They employed the software CFX with the Reynolds Averaged Navier–Stokes (RANS) approach and k–ε turbulence closure for the simulations. Oliver et al. [14] conducted a more detailed numerical investigation also using the RANS approach with k–ε turbulence closure. They compared their numerical results with those obtained from previous integral models and experimental observations, and concluded that the k–ε predictions provided a more accurate representation of the mixing processes compared to the integral models. More recently, Palomar et al. [15] reported an overview of the performances of some widely-used integral models, including CORMIX, VISUAL PLUMES and VISJET, on the analysis of inclined dense jets. Their study revealed significant discrepancies in the dilution predictions by these integral models for brine discharge modeling.

In the present study, we employ the large eddy simulation (LES) approach to simulate the submerged inclined dense jet with a 45° inclination. LES is anticipated to provide a better prediction of the mixing behavior due to improved accuracy in resolving the large coherent eddies than the RANS approach. The objective is to evaluate the performance of LES on the predictions of both the kinematic and mixing behavior of the inclined dense jet in the near field. Experimental measurements are also performed for the validation of the LES predictions. In the following, we shall first introduce the computational methodology. The numerical and experimental results are then presented and compared to the available data in the literature.

2 Computational methodology

2.1 Governing equations

In the LES approach, eddies are filtered into large and small sizes based on the local grid spacing. Large eddies are then computed directly by solving the instantaneous Navier–Stokes equations, while small eddies are modelled based on assumptions such as the Boussinesq hypothesis. The filtered continuity, momentum and concentration transport equations in Cartesian coordinates for LES are as follows [16]:

$$ \frac{{\partial \overline{\rho } }}{\partial t} + \frac{\partial }{{\partial x_{j} }}(\overline{\rho } \widetilde{{u_{j} }}) = 0 $$
(1)
$$ \frac{{\partial (\overline{\rho } \widetilde{{u_{i} }})}}{\partial t} + \frac{\partial }{{\partial x_{j} }}(\overline{\rho } \widetilde{{u_{i} }}\widetilde{{u_{j} }}) = - \frac{{\partial \overline{p} }}{{\partial x_{j} }} + \overline{\rho } g_{i} + \frac{{\partial^{2} }}{{\partial x_{j}^{2} }}(\mu \widetilde{{u_{i} }}) - \frac{{\partial \tau_{ij} }}{{\partial x_{j} }} $$
(2)
$$ \frac{{\partial (\overline{\rho } \widetilde{\phi })}}{\partial t} + \frac{\partial }{{\partial x_{j} }}(\overline{\rho } \widetilde{\phi }\widetilde{{u_{j} }}) = \frac{{\partial^{2} }}{{\partial x_{j}^{2} }}(\varGamma \widetilde{\phi }) - \frac{{\partial Q_{j} }}{{\partial x_{j} }} $$
(3)

where u i , u j are the velocity in i, j direction, respectively; ρ is the fluid density, p is the pressure, t is the time, g is the gravity acceleration, μ is the fluid viscosity, \( \varGamma \) is the scalar diffusivity, \( \phi \) is the scalar concentration; the overbar indicates time averaged variables and the tilde indicates spatially filtered variables; \( \tau_{ij} = \overline{\rho } \widetilde{{u_{i} u_{j} }} - \overline{\rho } \widetilde{{u_{i} }}\widetilde{{u_{j} }} \) are the SGS Reynolds stresses and \( Q_{j} = \overline{\rho } \widetilde{{\phi u_{j} }} - \overline{\rho } \widetilde{\phi }\widetilde{{u_{j} }} \) are the SGS scalar flux.

The effect of unresolved small scale eddies on the resolved flow can be represented by a sub-grid scale (SGS) model. The Smagorinsky SGS model is arguably the most commonly used among existing SGS models [17, 18] and is also adopted here. The SGS stress tensor and the SGS turbulent concentration flux in the Smagorinsky model are modelled by

$$ \tau_{ij} - \frac{1}{3}\tau_{kk} \delta_{ij} = - 2\mu_{t} \widetilde{S}_{ij} $$
(4)
$$ Q_{j} = - \frac{{\mu_{t} }}{{Sc_{t} }}\frac{{\partial \widetilde{\phi }}}{{\partial x_{j} }} $$
(5)

where \( \tau_{kk} \) is the isotropic part of SGS stress which usually can be neglected for incompressible flows, \( Sc_{t} = 0.7 \) [19, 20] is the SGS turbulent Schmidt number and \( \widetilde{S}_{ij} = \frac{1}{2}\left( {\frac{{\partial \widetilde{u}_{i} }}{{\partial u_{j} }} + \frac{{\partial \widetilde{u}_{j} }}{{\partial u_{i} }}} \right) \) is the rate of strain tensor for the resolved scale. The remaining undetermined variable SGS eddy viscosity, μ t , is controlled by the following equations involving \( \widetilde{S}_{ij} \) proposed by Smagorinsky [21] and Lilly [22]:

$$ \mu_{t} = \rho \left( {C_{S} \Delta } \right)^{2} \left| {\widetilde{S}} \right| $$
(6)
$$ \left| {\widetilde{S}} \right| = \sqrt {2\widetilde{S}_{ij} \widetilde{S}_{ij} } $$
(7)

where ∆ is the LES filter width which is defined by the grid spacing and C s is the Smagorinsky constant set to 0.17 herein.

Here, it should be noted that the coefficient C s may not always be a constant, and in fact can be better determined by a localized dynamic procedure proposed by Germano et al. [23] and further modified by Lilly [24] as follow:

$$ C_{S}^{2} = \frac{{\left\langle {L_{ij} M_{ij} } \right\rangle }}{{2\left\langle {M_{ij} M_{ij} } \right\rangle }} $$
(8)
$$ L_{ij} = \widehat{{\widetilde{u}_{i} \widetilde{u}_{j} }} - \widehat{{\widetilde{u}}}_{i} \widehat{{\widetilde{u}}}_{j} $$
(9)
$$ M_{ij} = \Delta^{2} \widehat{{\left| {\widetilde{S}} \right|\widetilde{S}_{ij} }} - \widehat{\Delta }^{2} \left| {\widehat{{\widetilde{S}}}} \right|\widehat{{\widetilde{S}_{ij} }} $$
(10)

where the angular brackets indicate a spatial averaging procedure over directions of statistical homogeneity, and the caret indicates a spatial filtered quantity on the test-filter. This procedure can be further developed to include the scalar transport as [24]

$$ Sc_{t} = \frac{{C_{S}^{2} }}{{C_{\phi }^{2} }} $$
(11)
$$ C_{\phi }^{2} = \frac{{\left\langle {\varepsilon_{j} R_{j} } \right\rangle }}{{\left\langle {R_{j} R_{j} } \right\rangle }} $$
(12)
$$ \varepsilon_{j} = \widehat{{\widetilde{u}_{j} \widetilde{\phi }}} - \widehat{{\widetilde{u}}}_{j} \widehat{{\widetilde{\phi }}} $$
(13)
$$ R_{j} = \Delta^{2} \widehat{{\left| {\widetilde{S}} \right|\frac{{\partial \widetilde{\phi }}}{{\partial x_{j} }}}} - \widehat{\Delta }^{2} \left| {\widehat{{\widetilde{S}}}} \right|\frac{{\partial \widehat{{\widetilde{\phi }}}}}{{\partial x_{j} }} $$
(14)

Equations (8) to (14) constitute what is now called the Dynamic Smagorinsky SGS model.

In the present study, the equations were discretized using the finite volume method and the simulations were performed with an open source code OpenFOAM [25]. Specifically, the implementation in OpenFOAM was performed with the turbulence solver twoLiquidMixingFoam and with both the Smagorinsky and Dynamic Smagorinsky SGS models, respectively. The twoLiquidMixingFoam is a solver for the mixture flow of two incompressible fluids, and it has been used and validated in many studies [26, 27].

2.2 Flow configuration and computational setup

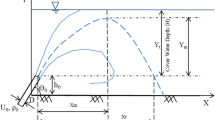
The simulation domain was configured based on a fully submerged inclined jet with an inclination of 45°. As shown in Fig. 2, the origin of Cartesian coordinates was set at the center of the discharge nozzle, the diameter of which was D. The distances from the nozzle center to the back (L b ), front (L f ), left and right sides (W), surface (H s ) and bottom (H d ) boundaries were equal to or larger than 0.7 DFr, 6 DFr, 1.8 DFr, 2 DFr, 1 DFr, respectively. Particular attention was paid to the nozzle’s cover water depth (H s ) to avoid the surface contact of the inclined dense jet [28]. In the present study, all the cases satisfied the criteria for fully submerged 45° inclined dense jets (H s  > 1.6 DFr).

Fig. 2
figure 2

Schematic diagram of the computational domain

Full size image

The computational domain was discretized with a stretched and structured mesh with increasing grid spacing from the center of the nozzle to the boundaries, as shown in Fig. 3a. A double refinement was performed within a region that covered the core of the jet. The grids attached to the nozzle tube were generated by a tool of OpenFOAM, namely snappyHexMesh, which can divide a base cell into several sub-cells and then snap the sub-cell boundaries onto the surface of the nozzle tube, as shown in Fig. 3b. The fluid viscosity and diffusivity were 10−6 kg m−1s−1 and 10−9 m2/s, respectively. The other parameters for each case and their corresponding meshes are summarized in Table 1.

Fig. 3
figure 3

a A structured mesh of the domain; b detailed grids near the nozzle at the center plane

Full size image
Table 1 Parameters and mesh sizes
Full size table

To examine the grid convergence, the method of Grid Convergence Index (GCI) [29] was used for the estimation of uncertainty in the CFD simulations. With GCI, the uncertainty is determined by a formula incorporating the results of two additional simulations of which a coarser mesh and a finer mesh are used individually. Figure 4 shows the dilution (represented in a line) and its uncertainty (represented in vertical bars) near the return point (at ~3.6 FrD) in case S1. C and C 0 are the local and initial concentrations, respectively. From the figure, the uncertainty near the return point can be observed to be relatively small.

Fig. 4
figure 4

Dilution at the nozzle height level near the return point

Full size image

The boundary condition at the top surface was set to free slip, while a zero gradient open boundary was used for the other five outer boundaries. The nozzle surface was set as a velocity inlet with a uniform discharge velocity at a turbulence intensity of 10 %. The corresponding dense fluid density was specified in Table 1. The other surfaces of the discharge tube were taken to be wall boundaries. A second order implicit backward scheme was used for the discretization of the temporal term. An upwind and a linear scheme were chosen to compute the divergence term and the Laplacian term, respectively. The convergence criterion of 10−6 was set for the continuity, velocities as well as scalar concentrations. The time step interval was adjusted to ensure that the Courant number was less than 1.0. The computations were performed using parallel processors in the High Performance Computing centre of the Nanyang Technological University. As an example, for case S2, the flow was computed up to 50 s, with a real-time computing duration exceeding 7 days with four nodes (each node having 16 cores).

2.3 Experimental measurements

In addition to the numerical simulations, the velocity and concentration distributions of the 45° inclined dense jet were also experimentally determined in the present study using the laser imaging techniques of particle image velocimetry (PIV) and planar laser-induced fluorescence (PLIF), respectively. The experiments were performed in a glass test tank at the Nanyang Technological University, Singapore. The methodology and experimental setup adopted were very similar to those in Jiang et al. [28]. In the present experiments, the nozzle had an inner diameter of 5.8 mm, and the center of the nozzle was set at 50 mm above the perspex bottom to avoid the influence of the bottom boundary.

3 Results and discussion

In the following discussion, the LES predictions were compared with the experimental results obtained in the present study as well as previous experimental and numerical studies [7–9, 14, 15, 30–33], including the jet trajectories, geometrical and dilution parameters, and turbulence characteristics. Except for the eddy structures shown in Fig. 17, all the results were time-averaged over the period starting from 15 or 120 s (for simulation and experimental measurements, respectively), and lasting for approximately 60 to 80 s.

Crowe [34] examined the possible influence of the bottom wall boundary in the mixing characteristics of the inclined dense jet. Based on his results, for the 45° inclined dense jet, the minimum nozzle height (H d ) necessary to avoid the boundary effect is ~0.6 DFr. The previous studies with and without a bottom boundary were included for a comprehensive comparison herein, and the potential boundary effect has been clearly indicated for those with a bottom boundary.

3.1 Jet trajectory and overall flow characteristics

Figure 5 shows the mean velocity magnitude and normalized concentration contours (C/C 0) of case S1 at the centerline plane. From the velocity contours, the inclined dense jet first rises due to the initial discharge momentum until it reaches the peak height as shown in Fig. 5. The concentration contours also show a similar pattern. Subsequently, the negative buoyancy becomes dominant, and the inclined dense jet sinks downwards. The following jet characteristics, including the jet trajectory, geometrical and dilution characteristics, cross-sectional profiles and jet spread widths, can be obtained from the velocity magnitude and concentration contours at the center plane.

Fig. 5
figure 5

Non-dimensional mean a velocity (m/s) and b concentration contours at the center plane for case S1

Full size image

The jet centerline, also known as the trajectory, is a main geometrical feature of the inclined dense jet. The jet centerline can be defined as the locus of the maximum velocity or concentration at various cross sections from the respective velocity or concentration contour maps shown in Fig. 5. Figure 6 presents the normalized jet concentration and velocity centerlines, with different Fr obtained from the LES predictions (with both Smagorinsky and Dynamic Smagorinsky models) and experimental measurements, where \( L_{M} = \left( {{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}} \right)^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} DFr \) is the jet characteristic length scale. The experimental results from Kikkert et al. [8] and Oliver et al. [30] as well as the integral modelling predictions from Palomar et al. [15] are also included for comparison. From the figure, the normalized LES predictions with different Fr were similar to each other with slight divergences towards the downstream direction. The predictions with the Dynamic Smagorinsky model (D1) were almost identical to the Smagorinsky model (S1) for the jet trajectory. Compared with the present experimental results and those from previous studies, the LES predictions coincided with them near the nozzle and then diverged after the peak height, which was somewhat over-predicted. However, the divergence between the LES and experimental results was relatively smaller compared with the integral modeling predictions from Palomar et al. [15]. It is noted that both the velocity (solid line) and concentration centerlines (dotted line) almost coincided with each other, which had also been noted in previous experimental studies [9]. In the following discussion, the centerline refers to the concentration centerline if not indicated otherwise.

Fig. 6
figure 6

Comparison of normalized centerline trajectories

Full size image

3.2 Geometrical and mixing features

To assess the environmental impact of the brine discharge, the analysis must include the determination of the geometrical features of the inclined dense jet, including the terminal rise height, return point location as well as dilution at different locations. As discussed earlier, previous studies had verified that the various normalized geometrical and mixing quantities of the inclined dense jet for a specific nozzle inclination are proportional to Fr. The various geometrical and mixing quantities predicted by LES are summarized in Table 2 together with the experimental results from the present and previous studies, with S m and S r being the dilution at the centerline peak height and return point, respectively.

Table 2 Comparison of coefficients
Full size table

In Table 2, the coefficients of the LES results are average values from the simulation runs shown in Table 1. The maximum variations of the coefficients from the Smagorinsky LES results are also indicated in the table. Based on the simulations, the variations were within around 10 % and most of them were approximately within 5 %. The trend lines of the Smagorinsky LES results are also plotted for comparison based on these average coefficients in Figs. 7–10.

Fig. 7
figure 7

Comparison of normalized terminal rise height

Full size image
Fig. 8
figure 8

Comparison of normalized centerline peak: a horizontal and b vertical locations

Full size image
Fig. 9
figure 9

Comparison of normalized return point location

Full size image
Fig. 10
figure 10

Comparison of normalized dilution at the return point

Full size image

3.2.1 Terminal rise and centerline peak

The terminal rise height, z t, is crucial to the assessment of the environmental impact of the brine discharge. The criteria to determine the terminal rise height were different among the previous studies. Herein, the terminal rise height is defined as the peak height at the location where the concentration drops to 5 % of the centerline peak concentration. This definition was also used in Jiang et al. [28]. Figure 7 presents the terminal rise height derived from the mean concentration fields at the centerline plane. The previous experimental and numerical results are included for comparison. It should be noted that the results of Oliver et al. [30] are represented by a trend line based on the averaged coefficient. From the figure, the LES predictions with the Smagorinsky and Dynamic Smagorinsky models coincided with each other, and they were close to the experimental results from Oliver et al. [30], Cipollina et al. [7], Kikkert et al. [8]. The trend line based on the LES predictions (with the Smagorinsky SGS model) is plotted in the figure as well. The LES trend line was obviously closer to the experimental trend line from Oliver et al. [30] than the prediction of integral models presented by Palomar et al. [15].

Once the centerline was determined, the horizontal and vertical locations of the centerline peak, x m and z m , can be derived which are plotted against Fr in Fig. 8. From the figure, it can be observed that the LES predictions agreed well with the present experimental results as well as the results from previous studies. The normalized horizontal location x m/D and vertical location z m/D increased linearly with increasing Fr. The trend lines based on the averaged coefficients of the LES are also plotted in the respective figures. The scattering of the LES data points from the trend lines was relatively small, which demonstrated the consistency and accuracy of the predictions.

3.2.2 Return point location

Upon reaching the peak height, the inclined dense jet falls back onto the bottom due to its negative buoyancy. The location of the impact point, where the downward flow impinges onto the bottom, as well as the associated dilution is important parameters for the environmental impact analysis. The impact location can be dependent on the site conditions, including the source height and bed slope [35, 36]. Here, the bottom effect was not considered, and the return point position (where the downward flow returns to the source height), is examined instead. The LES predictions were compared with corresponding experimental measurements from the literature.

Figure 9 shows the normalized horizontal location of the return point against Fr. The trend line based on the averaged LES coefficient is plotted in the figure as well. The differences between the two SGS models were small. It can be observed that the LES predictions were close to the experimental data especially from Kikkert et al. [8] but with slight over-predictions.

3.2.3 Dilution

The dilution at a specific location is defined as the initial concentration at the source over the local concentration, C 0/C. In the present study, the dilution at the return point is normalized and plotted against Fr in Fig. 10. It can be observed that the results of previous studies deviated from each other, which may be due to their various bottom conditions as suggested by Oliver et al. [30]. Seen from the figure, the LES predictions were close to the results from Oliver et al. [30] but slightly lower. The LES averaged trend line based on the Smagorinsky results is also plotted in the figure. In comparison, the LES trend line still somewhat under-predicted the experimental results, but the agreement was much better compared to the integral modeling predictions from Palomar et al. [15].

3.3 Cross sectional profiles

Figure 11 shows the normalized velocity and concentration profiles at different cross sections along the respective jet trajectories based on the Smagorinsky model. The cross sections began at s = 0.1 FrD, where s is the distance from the nozzle center along the jet centerline, and the interval between the sections was 0.3 FrD. As can be observed from the profiles, the flow pattern can be divided into the inner (or lower) and outer (or upper) halves in the regions below and above the trajectories of velocity or concentration maxima, respectively. Both the velocity and concentration profiles showed symmetry with respect to the centerline trajectory in the initial stage (s < 1.0 FrD). After s ≈ 1.0 FrD, asymmetry developed and the velocity or concentration profiles in the inner half were now wider than the outer half. Further downstream, the distributions became even more flattened.

Fig. 11
figure 11

Cross-sectional profiles of a velocity and b concentration fields (case S1)

Full size image

In Fig. 12, the non-dimensional cross-sectional profiles of the concentration C/C c from case S1 are plotted against r/b c , where r is the radial distance (negative represents upper half), b c is the concentration spread width and C c is the centerline concentration. A Gaussian profile is also plotted here for comparison. The results from previous studies are included by re-normalizing s/D into s/FrD. In the near-nozzle region, the cross-sectional profiles obtained by LES showed self-similarity and distributed in the Gaussian manner. In the downstream region, the inner half began to deviate from the Gaussian profile, and the distortion increased with the distance from the nozzle within the range of the investigation in the present study. This phenomenon was also noted in previous experimental studies [8, 9, 33] and numerical study [14], which can be attributed to the additional spreading by the buoyancy induced instability.

Fig. 12
figure 12

Non-dimensional cross-sectional distributions of normalized concentration at a s/DFr = 0.5–1.2 and b s/DFr = 1.2–2.5

Full size image

3.4 Jet spread

In the present study, the jet spread widths are characterized based on the distance from the centerline to the 5 % value of the centerline maximum. Figure 13 presents the velocity and concentration spread widths along the centerline trajectory. As seen from the figure, the LES predictions were nearly identical between the Smagorinsky and Dynamic Smagorinsky models, and the spread widths of the LES predictions in the upper region were closer to the experimental data. However, the LES spread width was smaller in the inner region. Clearly, the enhanced inner spreading due to the buoyancy-induced instability was again not sufficiently captured by LES.

Fig. 13
figure 13

Comparison of the jet velocity and concentration spread widths

Full size image

The variation of the jet spread width along the trajectory is further examined in Fig. 14. In the figure, the upper and lower spread widths of the LES predictions with both the Smagorinsky and Dynamic Smagorinsky SGS models are extracted from Fig. 13, and re-plotted against normalized s. Consistent with Fig. 13, the differences between the Smagorinsky and Dynamic Smagorinsky models were small as shown in Fig. 14a. Starting from the nozzle, the upper and lower spread widths of the LES predictions increased almost linearly in the beginning matching closely the experiment results, and then the rate of increase began to decline after s ≈ 2.0 FrD where the centerline peak was located. Around the peak region, the vertical momentum of the inclined dense jet became weak physically, while the buoyancy-induced instability at the bottom became prominent and drove the centerlines significantly lower, resulting wider spread widths in the experimental results. From the figure, the LES predictions were not able to fully capture this phenomenon due to the inadequacy of the SGS models with the adopted grid spacing. Subsequently, the spread widths resumed its increase at s ≈ 2.7 FrD in the downward plume region.

Fig. 14
figure 14

Variation of a upper and b lower jet spread widths along the trajectory

Full size image

3.5 Turbulence characteristics and eddy structures

In Fig. 15, the concentration turbulence intensity of the LES predictions at the centerline peak is computed and compared with the experimental data from Oliver et al. [30] and Papakonstantis et al. [32]. From the figure, the LES and experimental results showed similar distributions, having a peak value at r/b c  ≈ −0.7 in the outer region. Compared to Oliver et al. [30], LES under-predicted the turbulence intensity in the inner region where the buoyancy-induced momentum and instability were present.

Fig. 15
figure 15

Concentration turbulence intensity at the centerline peak in the a vertical and b lateral directions

Full size image

The concentration turbulence intensity in the lateral direction was also extracted at the concentration peak and compared with the experimental data from Papakonstantis et al. [32] and Lai and Lee [33]. It is noted, however, that both Papakonstantis et al. [32] and Lai and Lee [33] performed their experiments with the bottom boundary, while the present simulations were conducted without the boundary. The predictions of the Smagorinsky and Dynamic Smagorinsky models were comparably similar to the experimental data from Lai and Lee [34], but generally lower than Papakonstantis et al. [32], with twin peaks at \( {r \mathord{\left/ {\vphantom {r {b_{c} }}} \right. \kern-0pt} {b_{c} }} \approx \pm 0.5 \).

Figure 16 shows the concentration turbulence intensity at the return point. In Fig. 16a, the azimuthal (normal to the jet centerline) distribution of the LES turbulence intensity is compared to Oliver et al. [30]. Similar to the centerline peak, the turbulence intensity at the return point also had a peak value at r/b c  ≈ −0.7. However, the turbulence intensity at the return point preserved the linear decline in the inner region. Compared to the experimental data, the LES predictions somewhat over-predicted the turbulence intensity. The lateral turbulence intensity at the return point is also plotted in Fig. 16b. Unlike in Fig. 15b, the turbulence intensity at the return point did not show the twin peaks in Fig. 16b, and the Smagorinsky model predicted higher turbulence intensity in general.

Fig. 16
figure 16

Concentration turbulence intensity at the return point in the a azimuthal and b lateral directions

Full size image

The coherent structure of the inclined dense jet is important to the understanding the flow development, and can aid in the analysis of the mixing characteristics as well as the turbulence intensity. The LES eddy structures from case S1, visualized by plotting the concentration contours in a diverging color map at the center plane, are compared with the present experimental PLIF images in a time sequence of 0.5 s interval as shown in Fig. 17. From the figure, the LES predictions had similar length scales to the experimental images in terms of the size of the coherent large eddies. Particularly, a series of similar-size vortex rings can be observed in the lower region below the centerline in the LES images. In contrast, the experimental images showed a fuller spectrum of large eddy sizes in the lower region. This discrepancy of the eddy sizes explained the lower turbulence intensity of the LES predictions in Fig. 15, and also revealed the weakness of the SGS models with the adopted grid spacing in resolving the convective mixing by buoyancy-induced instability in the lower region.

Fig. 17
figure 17

Eddy structures at the central plane: (Left) experimental images; (Right) LES predictions (case S1)

Full size image

4 Conclusions

In the present study, the 45° inclined dense jet was simulated numerically using LES with both the Smagorinsky and Dynamic Smagorinsky SGS models, and the simulation results were compared with the experimental measurements performed in the present study as well as from previous studies in the literature. The comparison covered the geometrical and dilution characteristics, the spread width characteristics and the eddy structures at the center plane.

In summary, both the standard Smagorinsky and the dynamic Smagorinsky LES predicted the geometrical characteristics reasonably well, including the return point location, horizontal and vertical location of the centerline peak, with a slight over-prediction of ~10 % compared with the experimental data. Hence, the LES approach performed much better than the existing integral models in terms of the geometrical characteristics. LES is also much superior to the integral models in predicting the dilution at the return point. For dilution, the LES results had an under-prediction of ~20 % compared with the experimental data, while the comparison with integral modeling results in Palomer et al. [15] yielded ~50 % under-predictions. Note, however, that the recent improvements in integral modelling approach such as reduced buoyancy flux (RBF) model from Oliver et al. [37] and escaping mass approach (EMA) from Yannopoulos and Bloutsos [38] had achieved better results. In terms of the jet spread widths, the LES predictions were in reasonable agreement with the experimental measurements near the nozzle region, but beyond the centerline peak the under-prediction became prominent. The predicted turbulence intensity was satisfactory in the upper half but not the inner half. Together with the comparison of the eddy structures, it is obvious that, with the currently used mesh sizes, both the Smagorinsky and Dynamic Smagorinsky SGS models are not fully able to capture the convective turbulence under the influence of buoyancy. Improvement of the SGS model is therefore necessary in this direction, and it is being pursed in a further study.