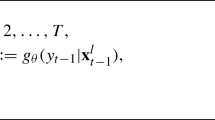Switching state-space models for modeling penguin population dynamics

Abstract

Tracking individual animals through time using mark-recapture methods is the gold standard for understanding how environmental conditions influence demographic rates, but applying such tags is often infeasible due to the difficulty of catching animals or attaching marks/tags without influencing behavior or survival. Due to the logistical challenges and emerging ethical concerns with flipper banding penguins, relatively little is known about spatial variation in demographic rates, spatial variation in demographic stochasticity, or the role that stochasticity may play in penguin population dynamics. Here we describe how adaptive importance sampling can be used to fit age-structured population models to time series of point counts. While some demographic parameters are difficult to learn through point counts alone, others can be estimated, even in the face of missing data. Here we demonstrate the application of adaptive importance sampling using two case studies, one in which we permit immigration and another permitting regime switching in reproductive success. We apply these methods to extract demographic information from several time series of observed abundance in gentoo and Adélie penguins in Antarctica. Our method is broadly applicable to time series of abundance and provides a feasible means of fitting age-structured models without marking individuals.

1 Introduction

Understanding the survival and reproduction of organisms has traditionally required the tracking of individuals through time, usually through bands, tags, or the addition of distinguishing marks that persist through time (e.g., marks on turtle scutes) (Lebreton et al. 1992; Williams et al. 2002). Mark-recapture methods are often challenging or infeasible, either because capturing animals is difficult or because the marks themselves negatively impact fitness. Methods that allow for the estimation of demographic parameters, such as age-structured survival and reproduction, without the need to mark (or track by any means) individual animals would greatly expand our capacity to understand the population biology of many organisms. Point count data (e.g., abundance) of key life stages (e.g., adults, chicks/pups) are often available over large spatial scales and can be collected more cheaply than mark-recapture data. This has led to a growing interest in using this kind of data to extract more detailed demographic information.

Adélie (Pygoscelis adeliae) and gentoo (P. papua) penguins breed throughout the Antarctic continent and associated sub-Antarctic islands. Despite their remoteness, Adélie and gentoo penguins are among the world’s most well-studied seabirds (see Borboroglu and Boersma 2013 and references therein), and researchers have studied their population dynamics, behavior, foraging, breeding success, as well as the impacts of tourism and other human activities, fishing and climate change. Despite this intense focus over the last 40 years, our understanding of age-structured survival and reproduction is unavoidably limited to a small number of locations where long-term banding or tagging has been permitted (e.g., Lescroël et al. 2009 and Dugger et al. 2010). Mark-recapture data are extraordinarily valuable and provide the basis for much of our understanding of penguin life history, but the intense logistics required for banding, combined with concerns that flipper bands increase drag and thus decrease survival (Culik et al. 1993; Putman 1995; Dugger et al. 2010; Dann et al. 2014), have sharply limited its use.

On the other hand, time series of abundance are widely available. Penguin biologists have been recording abundance data since the earliest days of Antarctic exploration, and compilations of such data (e.g., (Croxall and Kirkwood 1979; Woehler and Croxall 1997; Lynch et al. 2013) have been critical to our current understanding of how populations have changed over time. Abundance can now be estimated indirectly from satellite imagery of penguin guano stains (Lynch et al. 2012b; LaRue et al. 2014) and directly from unmanned aerial drones (Shah et al. 2020). Such abundance data are relatively inexpensive to obtain and compilations of count data can be assembled from multiple research teams working independently across the continent (Humphries et al. 2017). Here we report on a method to infer age- or stage-structured demographic rates from time series of abundance, a method illustrated here in the context of Antarctic penguins but widely applicable to other animals with annual reproduction.

One way to model state-structured penguin abundance is to use a state-space model (SSM) (Patterson et al. 2008). SSMs represent the relationship between time-varying latent states (e.g., true abundance) and observed time-series (e.g., collected point count data). SSMs can be described using probability distributions and are parameterized by a set of model parameters representing demographic rates. In an inference task involving SSMs, the goal is to jointly infer the unknown latent states and the parameters of the model (see Kantas et al. 2015 for a survey of approaches). Among the set of available approaches, particle Markov chain Monte Carlo (PMCMC) sampling is one that can be used for the Bayesian learning of the unknowns in an SSM (Andrieu et al. 2010), which involves inferring the joint posterior distribution of the latent states and model parameters. In this work, our focus will be on Bayesian learning for SSMs using importance sampling (IS)-based methods (Tokdar and Kass 2010; Robert and Casella 2013) for the purposes of identifying those demographic rates that can be successfully learned from time series of abundance.

Our inverse modeling efforts are similar in spirit to the efforts by Gonzales et al. (2016) to jointly estimate the size structure and abundance of a population without individual-level demographic information. Whereas Gonzales et al. (2016) considered a population structured by size (a continuous variable) and assumed prior information on the size structure of the population, here we focus on estimating demographic rates in a discrete age-structured population with no auxiliary information on the population age structure. We explore two case studies to illustrate the approach, one involving immigration and the other involving regime switching in reproductive success, in order to evaluate which demographic parameters are strongly informed by data (rather than the prior) and the sensitivity of these estimates to the amount of missing data in each time series.

2 Methods

2.1 State-space models (SSMs)

SSMs describe how a latent state $\mathbf{x}_t\in \mathbb {R}^{d_x}$ is related to an observation $\mathbf{y}_t\in \mathbb {R}^{d_y}$ at a time instant t over a fixed time horizon T. More specifically, SSMs are described by a set of probability distributions,

$$\begin{aligned} \mathbf{x}_0&\sim p(\mathbf{x}_0) \end{aligned}$$

(1)

$$\begin{aligned} \mathbf{x}_t&\sim p(\mathbf{x}_t|\mathbf{x}_{t-1}, \varvec{\theta }),&\quad t=1,\ldots ,T, \end{aligned}$$

(2)

$$\begin{aligned} \mathbf{y}_t&\sim p(\mathbf{y}_t|\mathbf{x}_t, \varvec{\theta }),&\quad t=1,\ldots , T, \end{aligned}$$

(3)

where $p(\mathbf{x}_0)$ is the distribution of the initial state $\mathbf{x}_0$, $p(\mathbf{x}_t|\mathbf{x}_{t-1}, \varvec{\theta })$ is the state transition distribution describing how the latent states evolve from one time instant to the next, $p(\mathbf{y}_t|\mathbf{x}_t,\varvec{\theta })$ is the observation distribution describing how observations $\mathbf{y}_t$ are distributed with respect to the true abundance $\mathbf{x}_t$, and $\varvec{\theta }\in \mathbb {R}^{d_\theta }$ is a vector of model parameters that parameterize both the state transition distribution and the observation distribution. The goal is to infer the unknown states $\mathbf{x}_{0:T}=\{\mathbf{x}_0, \mathbf{x}_1,\ldots ,\mathbf{x}_T\}$ and the model parameters $\varvec{\theta }$ of the SSM using the observations $\mathbf{y}_{1:T}=\{\mathbf{y}_1,\ldots ,\mathbf{y}_T\}$ under the Bayesian paradigm. In other words, we aim to estimate $p(\mathbf{x}_{0:T},\varvec{\theta }|\mathbf{y}_{1:T})$, the posterior distribution of $\mathbf{x}_{0:T}$ and $\varvec{\theta }$ given $\mathbf{y}_{1:T}$.

This joint distribution can be written as the following product:

$$\begin{aligned} p(\mathbf{x}_{0:T},\varvec{\theta }|\mathbf{y}_{1:T}) = p(\mathbf{x}_{0:T}|\mathbf{y}_{1:T}, \varvec{\theta })p(\varvec{\theta }|\mathbf{y}_{1:T}), \end{aligned}$$

(4)

where $p(\mathbf{x}_{0:T}|\mathbf{y}_{1:T}, \varvec{\theta })$ is the conditional posterior of the latent states given the model parameters, and $p(\varvec{\theta }|\mathbf{y}_{1:T})$ is the marginal posterior of the model parameters.

Under the assumption that the model parameters are known, the conditional posterior distribution of the states $\mathbf{x}_{0:T}$ given $\mathbf{y}_{1:T}$ and $\varvec{\theta }$ can be determined by Bayes’ theorem as

$$\begin{aligned} p(\mathbf{x}_{0:T}|\mathbf{y}_{1:T},\varvec{\theta })=\frac{p(\mathbf{x}_{0:T},\mathbf{y}_{1:T}|\varvec{\theta })}{p(\mathbf{y}_{1:T}|\varvec{\theta })}\propto p(\mathbf{x}_{0:T}, \mathbf{y}_{1:T}|\varvec{\theta }). \end{aligned}$$

(5)

The structure of SSMs allows us to easily obtain an expression for the joint distribution $p(\mathbf{x}_{0:T}, \mathbf{y}_{1:T}|\varvec{\theta })$

$$\begin{aligned} p(\mathbf{x}_{0:T}, \mathbf{y}_{1:T}|\varvec{\theta }) = p(\mathbf{x}_0)\prod _{t=1}^T p(\mathbf{y}_t|\mathbf{x}_t,\varvec{\theta })p(\mathbf{x}_t|\mathbf{x}_{t-1},\varvec{\theta }). \end{aligned}$$

(6)

Furthermore, the marginal likelihood $p(\mathbf{y}_{1:T}|\varvec{\theta })$ can be obtained by integrating out the states from the joint distribution

$$\begin{aligned} p(\mathbf{y}_{1:T}|\varvec{\theta })=\int \cdots \int \left( p(\mathbf{x}_0)\prod _{t=1}^T p(\mathbf{y}_t|\mathbf{x}_t,\varvec{\theta })p(\mathbf{x}_t|\mathbf{x}_{t-1},\varvec{\theta })\right) d\mathbf{x}_0\cdots d\mathbf{x}_T. \end{aligned}$$

(7)

If the interest is solely in the parameters of the SSM, then the goal is to obtain the marginal posterior distribution of $\varvec{\theta }$ given $\mathbf{y}_{1:T}$. This can also be determined by applying Bayes’ rule:

$$\begin{aligned} p(\varvec{\theta }|\mathbf{y}_{1:T}) = \frac{p(\mathbf{y}_{1:T}|\varvec{\theta })p(\varvec{\theta })}{p(\mathbf{y}_{1:T})}. \end{aligned}$$

(8)

Unfortunately, a tractable solution to (7) only exists for certain classes of SSMs (e.g., linear and Gaussian SSMs Carter and Kohn 1994) and hence, the conditional posterior $p(\mathbf{x}_{0:T}|\mathbf{y}_{1:T},\varvec{\theta })$ and the marginal posterior $p(\varvec{\theta }|\mathbf{y}_{1:T})$ cannot generally be analytically computed. In the following, we discuss a class of numerical integration techniques that use importance sampling (IS) (Robert and Casella 2013) to obtain a sample-based approximation to the posterior distribution of interest.

2.2 Importance sampling

Under the assumption that the likelihood can be analytically computed (e.g., linear Gaussian case), IS techniques are sufficient for approximation of the marginal posterior $\varphi (\varvec{\theta })\triangleq p(\varvec{\theta }|\mathbf{y}_{1:T})$, also called the target distribution. IS is a Monte Carlo sampling method that can be used to approximate expectation values with respect to the distribution $\varphi (\varvec{\theta })$, i.e.,

$$\begin{aligned} \mathbb {E}_\varphi [f(\varvec{\theta })] = \int \varphi (\varvec{\theta })f(\varvec{\theta })d\varvec{\theta }\end{aligned}$$

(9)

without the need to draw samples from $\varphi (\varvec{\theta })$ directly. In IS, samples $\{\varvec{\theta }^{(m)}\}_{m=1}^M$ are drawn from a proposal distribution $q(\varvec{\theta }; \varvec{\lambda })$, where $\varvec{\lambda }$ denotes the parameters of that proposal. Samples are then weighted according to

$$\begin{aligned} \tilde{w}^{(m)} = \frac{\tilde{\varphi }(\varvec{\theta }^{(m)})}{q(\varvec{\theta }^{(m)};\varvec{\lambda })}, \quad m=1,\ldots ,M, \end{aligned}$$

(10)

where $\tilde{\varphi }(\varvec{\theta })\triangleq p(\mathbf{y}_{1:T}|\varvec{\theta })p(\varvec{\theta })$. The collection of samples and importance weights can be used to obtain a numerical approximation to integrals of the form in (9) as

$$\begin{aligned} \mathbb {E}_\varphi \left[ f(\varvec{\theta })\right] \approx \sum _{m=1}^M w^{(m)}f(\varvec{\theta }^{(m)}), \end{aligned}$$

(11)

where $w^{(m)}$ denotes the normalized weight of the mth sample $\varvec{\theta }^{(m)}$ determined as

$$\begin{aligned} w^{(m)} = \frac{\tilde{w}^{(m)}}{\sum _{j=1}^M \tilde{w}^{(j)}}. \end{aligned}$$

(12)

A nice property of the estimator in Eq. (11) is that it converges to the true value of $\mathbb {E}_\varphi \left[ f(\varvec{\theta })\right]$ as the number of samples M tends to infinity (Tokdar and Kass 2010). The variance of the estimator depends on how “close” the proposal distribution is to the target distribution, and so a poorly chosen proposal (far from the target) can lead to high variance estimators (Owen and Zhou 2000). When the dimension of $\varvec{\theta }$ is large, it is difficult to choose the proposal parameters $\varvec{\lambda }$ to obtain a good fit to the target. In these scenarios, it is often beneficial to use adaptive IS (AIS) methods (see Bugallo et al. (2017) for a review), which can iteratively adapt the proposal parameters to construct a better fit to the target distribution $\varphi (\varvec{\theta })$. At the ith iteration of an AIS method, samples are drawn from a proposal $q(\varvec{\theta }; \varvec{\lambda }_i)$, i.e.,

$$\begin{aligned} \varvec{\theta }_i^{(m)} \sim q(\varvec{\theta }; \varvec{\lambda }_i), \quad m=1,\ldots ,M, \end{aligned}$$

(13)

which are then weighted accordingly

$$\begin{aligned} \tilde{w}_i^{(m)} = \frac{\tilde{\varphi }(\varvec{\theta }_i^{(m)})}{q(\varvec{\theta }_i^{(m)}; \varvec{\lambda }_i)}, \quad m=1,\ldots ,M. \end{aligned}$$

(14)

After the samples are drawn and weighted, the proposal parameter $\varvec{\lambda }_i$ are adapted using some rule. For example, if the proposal parameters $\varvec{\lambda }_i$ refer to the mean vector $\varvec{\mu }_i$ and the covariance matrix $\varvec{\Sigma }_i$ of the proposal, then one possible method for updating $\varvec{\mu }_i$ and $\varvec{\Sigma }_i$ is to use the following rule:

$$\begin{aligned} \varvec{\mu }_{i+1}&= \eta _{1, i}\varvec{\mu }_i + (1-\eta _{1,i})\sum _{m=1}^M w_i^{(m)}\varvec{\theta }_i^{(m)}, \end{aligned}$$

(15)

$$\begin{aligned} \varvec{\Sigma }_{i+1}&= \eta _{2, i}\varvec{\Sigma }_i + (1-\eta _{2, i})\sum _{m=1}^M w_i^{(m)}(\varvec{\theta }_i^{(m)}-\varvec{\mu }_{i+1})(\varvec{\theta }_i^{(m)}-\varvec{\mu }_{i+1})^\top , \end{aligned}$$

(16)

where $0< \eta _{1,i}, \eta _{2, i} < 1$ and $w_i^{(m)}$ denotes the normalized importance weight of the mth sample drawn in the ith iteration.

2.3 Particle adaptive importance sampling

If the marginal likelihood in Eq. (7) cannot computed analytically, then it is impossible to evaluate the importance weights in an AIS scheme, and the use of standard AIS techniques to approximate the marginal posterior $p(\varvec{\theta }|\mathbf{y}_{1:T})$ becomes impractical. Alternatively, one can consider using unbiased estimates of the marginal likelihood obtained through some numerical approach. For SSMs, a straightforward way to obtain an unbiased estimate of Eq. (7) is to use particle filtering (PF) methods (Djuric et al. 2003), which are sometimes more generally referred to as sequential Monte Carlo (SMC) methods (Doucet et al. 2001). With PF methods, one can obtain an IS-based approximation to $p(\mathbf{x}_{0:T}|\mathbf{y}_{1:T}, \varvec{\theta })$ in a recursive manner. Given this approximation of $p(\mathbf{x}_{0:T}|\mathbf{y}_{1:T},\varvec{\theta })$, one can use the collected importance weights to obtain an unbiased estimator of the marginal likelihood as (Doucet and Johansen 2009):

$$\begin{aligned} p(\mathbf{y}_{1:T}|\varvec{\theta }) \approx \hat{Z} = \prod _{t=1}^T\left( \frac{1}{N}\sum _{n=1}^N \tilde{v}_t^{(n)}\right) , \end{aligned}$$

(17)

where $\tilde{v}_t^{(n)}$ is the unnormalized importance weight of the nth sampled particle stream and N is total number of samples in the PF algorithm. Furthermore, one can obtain a sample of the trajectory $\mathbf{x}_{0:T}$ from the conditional posterior distribution $p(\mathbf{x}_{0:T}|\mathbf{y}_{1:T},\varvec{\theta })$ using PF, i.e.,

$$\begin{aligned} \mathbf{x}_{0:T, i}^{(m)} \sim \hat{p}(\mathbf{x}_{0:T}|\mathbf{y}_{1:T}, \varvec{\theta }_i^{(m)}), \end{aligned}$$

(18)

Additional details on the PF method, how the marginal likelihood estimator is derived, and how latent state trajectories are sampled are provided in the Supplementary Materials.

Algorithm 1 shows a general implementation of the particle AIS (PAIS) method used in this work to estimate the joint posterior distribution of the unknown states $\mathbf{x}_{0:T}$ and the model parameters $\varvec{\theta }$. The main differences between Algorithm 1 and a standard AIS algorithm are in the sampling and weighting steps. In the sampling step, M model parameters $\{\varvec{\theta }_i^{(m)}\}_{m=1}^M$ are drawn from a proposal distribution $q(\varvec{\theta }; \varvec{\lambda }_i)$. Then, for each of the sampled model parameters $\varvec{\theta }_i^{(m)}$, a PF scheme is employed to sample a corresponding state trajectory $\mathbf{x}_{0:T, i}^{(m)}$ and obtain an unbiased estimate of the marginal likelihood $Z_i^{(m)}$. In the weighting step, instead of evaluating $\tilde{\varphi }(\varvec{\theta }_i^{(m)})$, one uses an unbiased approximation of $\tilde{\varphi }(\varvec{\theta }_i^{(m)})$ given by $\gamma _i^{(m)} = \hat{Z}_i^{(m)} p(\varvec{\theta }_i^{(m)})$, where $\hat{Z}_i^{(m)}$ is the unbiased marginal likelihood estimate obtained from running a PF scheme conditioned on $\varvec{\theta }_i^{(m)}$. Indeed, since $\mathbb {E}[\hat{Z}_i^{(m)}]=p(\mathbf{y}_{1:T}|\varvec{\theta }_i^{(m)})$, then

$$\begin{aligned} \mathbb {E}[\gamma _i^{(m)}]&= \mathbb {E}[\hat{Z}_i^{(m)}p(\varvec{\theta }_i^{(m)})] \\&= \mathbb {E}[\hat{Z}_i^{(m)}]p(\varvec{\theta }_i^{(m)}) \\&= p(\mathbf{y}_{1:T}|\varvec{\theta }_i^{(m)})p(\varvec{\theta }_i^{(m)}) \\&= \tilde{\varphi }(\varvec{\theta }_i^{(m)}). \end{aligned}$$

A flow diagram summarizing the basic steps of a PAIS method is shown in Fig. 1.

Fig. 1

Schematic of particle adaptive importance sampling

2.3.1 Computational complexity

Here, we briefly discuss the computational complexity of Algorithm 1. At each iteration of the algorithm, M samples are drawn from the proposal distribution. For each of these samples, a particle filter is run to compute the marginal likelihood, where for simplicity we assume N particles are used in each particle filter. For each run of the particle filters, N particles are drawn at each time step for $(T+1)$ total time steps. This sampling process is repeated for I iterations of the algorithm. In summary, the number of samples drawn in the algorithm is $M_\mathrm{total}=MN(T+1)I$. Given the per-sample complexity of the AIS method and the PF method (which varies by method), we can get a sense of the total computational complexity of the overall PAIS algorithm. A more complete discussion of the computational complexity of AIS and PF methods may be found in Bugallo et al. (2017) and Doucet and Johansen (2009), respectively.

Depending on the chosen AIS and PF schemes, PAIS can become too computationally expensive to run in practice. To address this, we exploit the embarrassingly parallel nature of the PF step of the algorithm. At each PAIS iteration, since the M runs of the PF scheme are independent of one another, one can easily parallelize this process across computing resources. To that end, we utilize a computational cluster to efficiently sample the states, which allows the algorithm to become practically feasible.

2.4 Population data

We apply our model to data on gentoo and Adélie penguin population dynamics (Humphries et al. 2017; original data plotted in Supplementary Materials Figures 1 and 2). These time series include counts on the number of nests (equivalent to the number of breeding pairs) and chicks at nine breeding colonies spread across Antarctica. The available time series are highly patchy, and there are relatively few instances in which both a nest count and a chick count are available in the same year. In many years, there is no information on either nests or chicks. While observation error for each count is often estimated by the researchers collecting the data, we found that using this information made model convergence more difficult (see Discussion) and so we assumed a 20% observation error for all nests and chick counts.

Fig. 2

Basic life cycle diagram with $J=5$ stages, excluding any immigration. There are two non-breeding stages before penguins mature into the $S_{3}$ stage, and penguins are assumed to follow a juvenile survival rate ($\psi _{juv}$) in the first year and an adult survival rate ($\psi _{adu}$) in all following years. Breeding success $p_r$ is allowed to vary by stage. Counts of abundance are agnostic to the age of breeders and therefore counts of nests represent the sum of $S_{3}$ through $S_{5}$ (lower blue box) and counts of chicks represent the sum of $C_{3}$ through $C_{5}$ (upper blue box)

2.4.1 Gentoo population dynamics with immigration

At each breeding population in year t, the observations $\mathbf{y}_t$ reflect the total number of adult breeding penguins and chicks, denoted $\tilde{S}_{b,t}$ and $\tilde{C}_t$, respectively. To illustrate the estimation of demographic rates in a realistic scenario, we fit the model described in Fig. 2 with the addition of immigration to the $S_{3}$ stage. This model tracks female breeders only and therefore we divide the total number of chicks in year $t-1$ by 2 to calculate the number of $S_{1}$ females in year t (Eq. 19). We assume that immigration in year t is a function of the total number of breeding females in year $t-1$ (Eq. 21) and that immigrants arrive at the $S_{3}$ stage and are therefore added to the number of individuals aging into the $S_{3}$ stage from the local population (Eq. 22). We assume that reproductive success is related to penguin age (Eq. 25), consistent with observation, and that each breeding female lays two eggs and therefore has an upper bound of two chicks (Eq. 26). We assume that the year-specific observation error for both nests and chicks is Normally distributed with the standard deviation being some fraction of the counted abundance (Eq. 27, 28). While, in principle, the observation error could be fit as an additional free parameter, here we constrain observation error to ±20%. The model is described by the following equations

$$\begin{aligned} S_{1,t}&\sim \text {Binomial}\left( \frac{C_{t-1}}{2},\psi _{juv}\right) , \end{aligned}$$

(19)

$$\begin{aligned} S_{2,t}&\sim \text {Binomial}\left( S_{1 ,t-1},\psi _{adu}\right) , \end{aligned}$$

(20)

$$\begin{aligned} S_\mathrm{im, t}&\sim \mathrm{Poisson}(\alpha _{im} + \beta _{im} \times S_{t-1})\ ,\end{aligned}$$

(21)

$$\begin{aligned} S_{3,t}&=\bar{S}_{3,t}+S_{im, t},\quad \bar{S}_{3,t}\sim \text {Binomial}\left( S_{2,t-1}, \psi _{adu}\right) , \end{aligned}$$

(22)

$$\begin{aligned} S_{j,t}&\sim \text {Binomial}\left( S_{j-1,t-1},\psi _{adu}\right) , \quad j=4, \ldots ,J-1 \end{aligned}$$

(23)

$$\begin{aligned} S_{J,t}&\sim \text {Binomial}\left( S_{J-1,t-1}+S_{J,t-1},\psi _{adu}\right) , \end{aligned}$$

(24)

$$\begin{aligned} p_{r,j}&= \mathrm{InvLogit}(\alpha _{rs} + \beta _{rs}\times j), \quad j=1,\ldots , J-2, \end{aligned}$$

(25)

$$\begin{aligned} C_{j,t}&\sim \text {Binomial}\left( 2S_{j+2,t},p_{r, j}\right) , \quad j=1,\ldots , J-2,\end{aligned}$$

(26)

$$\begin{aligned} \tilde{S}_{t}&\sim \mathcal {N}\left( S_{t},(\sigma _{s, t} S_{t})^2\right) , \quad S_{t}=\sum _{j=3}^{J} S_{j,t}, \end{aligned}$$

(27)

$$\begin{aligned} \tilde{C}_t&\sim \mathcal {N}\left( C_t,(\sigma _{c, t} C_t)^2\right) , \quad C_{t}=\sum _{j=1}^{J-2} C_{j,t}, \end{aligned}$$

(28)

where the latent states are $\mathbf{x}_t=[S_{im, t}, S_{1,t},\ldots ,S_{J,t}, C_{1,t},\ldots , C_{J-2,t}]^\intercal$. $S_{j,t}$ denotes the number of stage j female penguins, $C_{j,t}$ the number of chicks from stage $j+2$ female penguins, $S_{im, t}$ denotes the number of females immigrating into the third stage, and J denotes the total number of non-chick age classes (here $J=5$). The unknown model parameters are $\varvec{\theta }=[\psi _{juv}, \psi _{adu}, \alpha _{im}, \beta _{im}, \alpha _{rs}, \beta _{rs}]^\intercal$, where $\psi _{juv}$ denotes the juvenile survivorship, $\psi _{adu}$ denotes the adult survivorship, $\alpha _{im}$ and $\beta _{im}$ denote the intercept and slope of a linear model for the number of immigrants, respectively, and $\alpha _{rs}$ and $\beta _{rs}$ denote the slope and intercept of a logistic model for the stage-structured reproductive success, respectively. We note that the stage-structured reproductive rates $p_{r, j}$ can be extracted from the model using the inverse logit (i.e., sigmoid) transformation.

2.4.2 Adélie population dynamics with regime switching

As a second illustration of these methods, we expand our basic (no immigration) model (Fig. 2) to permit switching between two regimes. This represents one manifestation of regime-switching state-space models (RS-SSM) that have been explored in other contexts (Ghahramani and Hinton 1996; Kim and Nelson 1999). RS-SSMs augment a discrete-valued latent state (called a regime) to an SSM and allows for parameters to switch from one time-instant to another depending on the regime state. In the Adélie model, the intercept of the reproductive rate ($\alpha _{rs}$) switches between two values, depending on the state of the regime in year t ($r_{t}$) as follows:

$$\begin{aligned} r_t&\sim \mathrm{Bernoulli}(1-\gamma ), \quad r_t\in \{0, 1\},\end{aligned}$$

(29)

$$\begin{aligned} p_{rs,j, t}&= \mathrm{InvLogit}(\alpha _{rs, r_t} + \beta _{rs}\times j), \quad j=1,\ldots , J-2 \end{aligned}$$

(30)

where the parameter $\gamma =\mathbb {P}(r_t=0)$ denotes the probability of being in the $r_t=0$ regime governed by intercept $\alpha _{rs,0}$.

2.4.3 Model priors and prior-posterior overlap

Prior distributions for model parameters are summarized in Table 1. For switching reproductive success parameters in the Adélie model ($\alpha _{rs, 0}$ and $\alpha _{rs, 1}$), we define the prior of the smaller reproductive rate $\alpha _{rs, 0}$ and the difference between the larger one and the smaller one as $\phi =\alpha _{rs, 1}-\alpha _{rs, 0}$. This parameterization, along with the choice of prior on $\phi$restricting it to positive values, adds a monotonicity constraint in the reproductive success parameters and ensures that the parameters are identifiable.

Table 1 Prior distributions for each unknown parameter in the gentoo and Adélie models

To assess how much the parameter posteriors are informed by the data (as opposed to simply reflecting the prior), we use a metric called the prior-posterior overlap (PPO), which reflects the percentage of overlap between the prior and posterior distributions for each parameter (Gimenez et al. 2009). If the PPO is large (close to 1), then the posterior is nearly identical to the prior and the parameter is considered uninformed by the data (either because the parameter is structurally unidentifiable or because the data are insufficient). If the PPO is small, then the posterior is very different from the prior and we consider the parameter ‘learnable’.

3 Results

Table 2 Posterior means, credible intervals, and prior-posterior overlaps for the gentoo datasets. For the synthetic dataset, the true values of the parameters were $\psi _{juv}=0.43$, $\psi _{adu}=0.82$, $\alpha _{rs}=0.5$, $\beta _{rs}=0.5$, $\alpha _{im}=20$, and $\beta _{im}=0.02$

Table 3 Posterior means, credible intervals, and prior-posterior overlaps for the Adélie datasets. For the synthetic dataset, the true values of the parameters were $\psi _{juv}=0.45$, $\psi _{adu}=0.85$, $\alpha _{rs, 0}=-0.5$, $\phi =1.5$, $\beta _{rs}=0.5$, and $\gamma =0.2$

For the gentoo time-series, the PPO is generally larger for the survivorship parameters and the slope of reproductive success (Table 2). Indeed, strong priors based on Ainley (2002) and Hinke (2012) were assumed for both juvenile and adult survivorship, and the PPO was larger than 0.90 for each dataset run (including the synthetic data). In contrast, the PPOs for the immigration-related parameters ($\alpha _{im}$ and $\beta _{im}$) were quite small, implying that they can be learned even with such short and patchy time-series. The intercept of reproductive success was also a learnable parameter in the model and, unsurprisingly, its estimation is sensitive to the amount of chick data available. For example, there was only a single chick count at Vernadsky Station and since this chick count was quite low (relative to the number of nests), our estimate of average reproductive success was also low. While this could reflect increased risk of egg and chick predation at smaller colonies, more chick data would allow us to estimate reproductive success with more confidence.

Unlike the gentoo model, the PPO for the survivorship parameters in the Adélie model are quite small (Table 3). Because this model does not include immigration, fluctuations in the nest time-series are more informative of survivorship. The intercept of reproductive success (for regime $r_t=0$) is also a learnable parameter, as the PPO for that parameter was small $(<0.3)$ for all sites. We also can extract some information about the difference between the reproductive success of the two regimes (i.e., $\phi =\alpha _{rs, 1}-\alpha _{rs, 0}$), as we obtain moderate values for PPO for that site. Litchfield Island’s small PPO may reflect the comprehensiveness of the time series available. Similar to the gentoo model, the slope of reproductive success had high PPO ($>0.9$) for all sites, meaning that inference on that parameter heavily relies on prior information. Regarding the regime-switching probability $\gamma$, the PPO is quite large for that parameter, especially when there is a lot of missing chick data (e.g., Port Charcot, which has 78% missing chick data). In contrast, sites with a lot of chick data, such as Litchfield Island, Cormorant Island, and Bechervaise Island, which have a moderate amounts of chick data, have a smaller PPO for $\gamma$.

We provide additional results for both the gentoo and Adélie models in the Supplementary Material, including results regarding the predictive performance of each model, the estimated average reproductive success for each site, and posterior histograms for a subset of the parameters. We also provide results on the stochasitic sensitivity of the PAIS algorithm over multiple realizations.

4 Discussion

Despite the challenge of estimating demographic parameters from point counts of total abundance, especially in the face of missing data, several demographic parameters were informed by the data. The immigration component of the gentoo penguin time series was estimable from the data but the addition of immigration made it difficult to estimate either juvenile or adult survival. In contrast, with no assumption of immigration, the model for Adélie penguins did permit an estimation of both juvenile and adult survival even with the inclusion of two reproductive regimes. As would be expected for a long-lived seabird like the Adélie, our estimates suggest greater variation among sites for juvenile survival than for adult survival. Bechervaise Island had the highest estimated juvenile survival among the sites included in the study. In this context, its worth noting that Bechervaise Island specifically (and the surrounding region of Eastern Antarctica more generally) has an increasing Adélie population in contrast to the other sites, all located on the Antarctic Peninsula, where persistent population declines are well documented (Lynch et al. 2012a).

Regarding the sampler, we encountered several challenges. In particular, the convergence of the sampling algorithm was sensitive to the initial values of the latent states (i.e., the penguin abundances). This was not an issue for modeling gentoo penguins, since those time series involved increasing populations starting from a very small numbers of penguins. For the Adélie time series, initial values needed to be well-calibrated for the algorithm to converge. This is especially difficult for sites with large populations, as there was a correspondingly large range of possible initial values. In order to overcome this issue, we opted to calibrate the initial values using the data in the first year. In particular, under the assumption that the relative distribution of abundance (across stages) is known a priori, one can use the observations of total abundance in the first year (i.e., $\tilde{S}_1$ and $\tilde{C}_1$) to select appropriate priors for the initial latent states. To clarify this procedure, let us consider an example. If it is known that the ratio between stage 4 penguins and all breeding penguins is 1:10, then one can approximate an initial value as $\hat{S}_{4, 0}=0.1\tilde{S}_1$ and add some noise to it before feeding it to the PF algorithm. In our implementation, we added noise that perturbed the approximated initial value up to 10% using a uniform distribution, i.e., each particle for stage 4 penguins would be initialized as,

$$\begin{aligned} S_{4, 0}^{(n)} \sim \mathrm{Uniform}(0.9\hat{S}_{4, 0}, 1.1 \hat{S}_{4, 0}), \quad n=1,\ldots ,N. \end{aligned}$$

(31)

Therefore, for initial value calibration, one needs to rely on domain expert knowledge of stage distribution, which can be assumed prior to running the analysis. Model convergence required a larger uncertainty in the observations (20% error in both the nest and chick counts) than was recorded alongside the initial abundance counts, because more precise abundance estimates led to an insufficient number of particles with non-trivial weight. Model convergence was assessed using the Pareto smoothed importance sampling (PSIS) diagnostic (Vehtari et al. 2021). The PSIS diagnostic provides a means to assess the degeneracy in the importance sampling weights by fitting them to the shape parameter of a generalized Pareto distribution. Theoretical findings in Vehtari et al. (2021) suggest that if the PSIS diagnostic is less than 0.7, then the importance sampling algorithm produces reliable estimates. In the case of our experiments, we were only able to achieve PSIS diagnostics less than 0.7 if we assumed the observation error was at least $20\%$, which is larger (in almost all cases) than the nominal observation error.

The time series used for this analysis were relatively short and the missing data, while an unavoidable feature of many Antarctic time series, had a major impact on our ability to estimate our model’s parameters. Additional data collected over time will generate longer time series from which even more precise estimates of demographic parameters can be extracted, and efforts to estimate abundance using archived satellite imagery may reduce the amount of missing data in the existing time series. One of the advantages of using this approach is that it permits the inclusion of environmental conditions (e.g., sea ice concentration) as covariates on specific demographic transitions, which will allow for a more direct and biologically-interpretable approach than linking environmental conditions to changes in population growth rates. Moreover, this approach provides a natural link to Integrated Population Models and the explicit inclusion of auxiliary data on demographic parameters such as reproductive success (Besbeas et al. 2002).

While aggregated point count data have been used to infer regional patterns of population change (e.g., Che-Castaldo et al. 2017), such data have not been used to estimate demographic rates such as survivorship and reproduction. The use of advanced computational methods allow us to learn something about the underlying demographic rates using simple point counts of breeding animals and, in doing so, greatly expand our capacity for linking environmental conditions to population dynamics in a way that is both highly cost-effective and scalable.