1 Introduction

In the present time, a special consideration is given to find new probability models in probability theory to facilitate the practitioners and applied researchers for model specification and investigation of the real-life data sets. This urge implies that there is a powerful desire for presenting suitable probability models for better data exploration. Due to high-level computational facilities’ availability, the methods in defining probability models are different from the previous models depicted before 1997 (see Tahir and Cordeiro 2016; Hussain et al. 2018). The main focus in developing probability models is to fulfill various requirements arising from diverse fields such as environmental sciences, medical sciences, engineering sciences, and many more.

In order to circumvent the inadaptability and inadequacy for some of the very well-known probability models such as Rayleigh, Weibull, exponential gamma, Lindley, among others, several authors have investigated the problem of finding new distributions. For instance, we cite the distribution of Kumaraswamy introduced by Kumaraswamy and Krishnamurthy (1980) as an alternative to the Beta distribution with more important advantages. The latter is usually used to model several phenomena such as atmospheric temperature or daily rainfall, daily streamflow in hydrological data. In theory as well as in practice, this distribution has received a lot of attention; see, for instance, Sundar and Subbiah (1989), Fletcher and Ponnambalam (1996), Seifi et al. (2000), Ponnambalam et al. (2001)), and Ganji et al. (2006) for previous works and Jones (2009), Golizadeh et al. (2011), Sindhu et al. (2013) and Sharaf EL-Deen et al. (2014) for recent advances and references. We refer to Lemonte et al. (2013) for the exponentiated Kumaraswamy (EK) distribution and its log-transform. They proved some mathematical properties of both distributions as well as the maximum likelihood estimators of theirs parameters. More recently, Shawki and Elgarhy (2017) presented a new class of distribution called Kumaraswamy Sushila distribution, and they stated the theoretical properties, but they have not applied it to any real data. Although these distributions have some interest in dealing with real data applications, authors have been focused more on the notion of weighted distribution introduced by Fisher (1934). Since this pioneering work, the weighted distribution has been the subject of many works in the probability and statistical literature. For instance, Rao (1965) gave a general formula for this concept of weighted distribution, which can be used to analyze statistical data when the standard distributions are failed. We cite Zelen (1974) for the length-biased sample’s modelization using weighted distributions ideas. From a practical perspective, weighted distributions are usually used to model data from the reliability domain (materials strength data), bio-medicine, or ecology and branching processes. We refer to Patil and Rao (1978), Gupta and Keating (1986), Gupta and Kirmani (1990), Oluyede (1999), among others) for some real data examples. Castillo and Pérez-Casany (1998) defined new exponential families based on the notion of the weighted distribution, and Priyadarshani (2011) introduced the weighted distribution of the generalized gamma distribution. In contrast, Abd El-Monsef and Ghoneim (2015) studied the weighted Kumaraswamy distribution. Later, Abd AL-Fattah et al. (2017) introduced the inverted Kumaraswamy distribution (IKD), studied some of its properties, and showed its performance on real data.

In this paper, we use the weighted technique to develop a new model to measure the strength of materials strength data, mainly modeling the strength of Carbon fiber data. The newly developed probability model constitutes the weighted version of the inverted Kumaraswamy distribution obtained by Abd AL-Fattah et al. (2017). We will use WIKD as an abbreviation for this new distribution, i.e., Weighted Inverted Kumaraswamy Distribution. The constructed distribution plays a vital role to fit the fiber strength, which is very important in the industries allowing to guarantee the safety of material used in the aero industry and construction of bridges. To the best of our knowledge, our proposed model has not been studied theoretically or dealt with it in a practice way. On the other hand, the statistical analysis of the variability in the strength of the composite is promoter subject in the micromechanical area. At this stage, the WIKD model is significantly more efficient than the classical probability models. The superiority of the WIKD model was confirmed by the different measures of goodness of fit, including AIC, CAIC, BIC rules.

The current paper is organized as follows. We devote Sect. 2 to the methodology. Section 3 derives in detail the statistical properties of the WIKD such as the probability density function, the cumulative distribution function, reliability measures including survival, hazard, the reverse hazard, Mills ratio rate functions, and mean residual. For completeness, we also present some further properties, include the moments and related measures (such as harmonic mean, moment generating function and characteristic function), stochastic ordering, order statistics, measures of skewness and kurtosis and information-theoretic measures. Section 4 gives statistical inferences and deals with the parameter estimation methods of the WIKD. Simulation studies and applications of the WIKD and discussions are given in Sect. 5. This section contains two parts. The first part considers the simulation studies to investigate the efficiency of both the maximum likelihood and the moment estimators of the WIKD. Then, we present the performance and comparison of the WIKD model with the existing models. Second, a strength of carbon fiber data is shown and modeled by the proposed model. Also, the performance and comparison of the WIKD model with the existing sub-models are discussed based on the given real data sets. Finally, we conclude our study in Sect. 6.

2 Method

As discussed in the first section, our main purpose is to study the WIKD distribution and its statistical properties. From a theoretical point of view, the present contribution completes previous studies in Kumaraswamy distribution. Motivated by its flexibility to fit some natural phenomena whose outcomes are bounded from both sides, namely, the climatological data and daily hydrological data of rainfall, the family of Kumaraswamy distribution has received growing interest. For example, Abd AL-Fattah et al. (2017) have studied by inverted Kumaraswamy distribution. The latter is built as the transformation of the Kumaraswamy distribution using the function \(\displaystyle \frac{1}{x}-1\). This transformation is defined analogously to the inverted beta distribution. It allows to explicit the probability density of the Inverted Kumaraswamy Distribution (IKD) by

$$\begin{aligned} f_{IKD}(x,\alpha ,\beta )=\alpha \beta (1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1}, x>0,\alpha ,\beta >0. \end{aligned}$$
(1)

Unlike the classical Kumaraswamy distribution, the (IKD) has a large domain that is in \((0, +\infty )\). For the statistical properties of the IKD distribution, we may refer the readers to Mansour et al. (2018), who estimated the unknown parameters of IKD. In particular, they studied the maximum likelihood and Bayesian estimators. The applicability of the constructed estimators under censoring is illustrated in simulated data. We return to Zafar et al. (2017) for the Generalized IKD distribution (GIKD). The latter is constructed by using the power transformation \(x^\gamma \). Therefore, the probability density function of the GIKD is

$$\begin{aligned} f_{GIKD}(x,\alpha ,\beta ,\gamma )=\alpha \beta \gamma x^{\gamma -1}(1+x^\gamma )^{-(\alpha +1)}\left[ 1-(1+x^\gamma )^{-\alpha }\right] ^{\beta -1}, \end{aligned}$$

where \(x>0,\alpha ,\beta>,\gamma >0\).

The novelty of this paper is to study another version of the IKD distribution that is the weighted version. We focus on its statistical properties such as cumulative distribution, moments, mean residual life, reversed residual life functions, moment generating function, characteristic function, harmonic mean, and geometric mean. The maximum likelihood and the moment estimators of the parameters are determined. Numerical studies are carried out to investigate and illustrate the theoretical results of both estimators. From a practical point of view, we also applied this distribution to Carbon fiber data. The material scientist constantly searches for the most suitable model that could fit the sample data better and can be mathematically improved and recognized.

3 Results

We study and derive the mathematical and statistical properties of WIKD.

3.1 The density function of WIKD

In the following, we suppose that X is a random variable (r.v.) and takes non-negative values, follows IKD (Abd AL-Fattah et al. 2017). The weighted probability density function (pdf) of (1) is determined by

$$\begin{aligned} f_w(x)=\frac{W(X)f(x)}{{\mathbb {E}}(W(X))}=\frac{W(X)f(x)}{\int _{-\infty }^{\infty }W(X)f(x)dx}. \end{aligned}$$
(2)

In (2), assume that \(W(X)=x^k\), \(k>0\) is the weight of the distribution. Then use (2) to get

$$\begin{aligned} {\mathbb {E}}(W(X))=&\int _0^{\infty }x^kf(x)dx \nonumber \\ =&\alpha \beta \int _0^{\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1}dx \end{aligned}$$
(3)

Using the variable change

$$\begin{aligned} z=(1+x)^{-\alpha }\, \Rightarrow dz= -\alpha (1+x)^{-(\alpha +1)} dt\qquad \text{ and } \quad x=z^{-1/\alpha }-1, \end{aligned}$$

We obtain

$$\begin{aligned} \begin{array}{ll} {\mathbb {E}}(W(X)) &{}\displaystyle =-\beta \int _1^{0} (z^{-1/\alpha }-1)^k (1-z)^{\beta -1}dz \\ &{}\displaystyle =\beta \int _{0}^1 \sum _{i=0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i}z^{-(k-i)1/\alpha } (1-z)^{\beta -1}dz\\ &{}\displaystyle = \beta \sum _{i=0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i} \int _{0}^1z^{-(k-i)/\alpha } (1-z)^{\beta -1}dz\\ &{}\displaystyle = \beta \sum _{i=0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i} B \left( \frac{\alpha -k+i}{\alpha },\beta \right) .\\ \end{array} \end{aligned}$$

Here, the B(., .) represents Beta-function. Hence, the pdf of WIKD is explicitly given by

$$\begin{aligned} f_{WIKD}(x)= \frac{\alpha }{W(\alpha ,\beta , k)} x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \end{aligned}$$
(4)

with

$$\begin{aligned} W(\alpha ,\beta , k)=\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^i B \left( \frac{\alpha -k+i}{\alpha },\beta \right) , \text{ for } \, \alpha>k>0 \ \beta >0. \end{aligned}$$

It is clear that

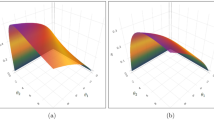
$$\begin{aligned} \lim _{x\rightarrow 0} f_{WIKD}(x,\alpha ,\beta ,k)=0 \qquad \text{ and } \qquad \lim _{x\rightarrow \infty } f_{WIKD}(x,\alpha ,\beta ,k)=0 \end{aligned}$$

The latter is obtained as the ratio of two polynomial functions. It appears clearly that this limits and the integrability of \(f_{WIKD}\) require \(\alpha>k>0\). Graphically, the shapes of this density are varied with respect to the values of \((\alpha , k,\beta )\); see plots in Fig. 1. Note that if \(k=1\), we get size-biased WIKD. if \(k=2\), we get area biased WIKD.

Fig. 1
figure 1

Some examples of WIKD densities

Full size image

3.2 Cumulative distribution function of WIKD

Now, consider a random variable X which follows WIKD with parameters \(\alpha \), \(\beta \) and k. The cumulative distribution function is derived as follows.

$$\begin{aligned} \begin{array}{ll} G(x)&{}=\displaystyle \int _0^x f_{WIK}(t,\alpha ,\beta ) dt \\ &{} \displaystyle =\frac{\alpha }{\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i} B\left( \frac{\alpha -k+i}{\alpha },\beta \right) }\int _0^x t^k (1+t)^{-(\alpha +1)}(1-(1+t)^{-\alpha })^{\beta -1}dt\\ \end{array} \end{aligned}$$

Then, use the same previous variables change to write that

where \(\nu =(1+x)^{-\alpha }\). It follows that, the corresponding cumulative distribution function (cdf) is defined by:

$$\begin{aligned} G(x)=&1-\frac{1 }{\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i} B\left( \frac{\alpha -k+i}{\alpha },\beta \right) }\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i}B\left( \frac{\alpha -k+i}{\alpha },\beta \right) \nonumber \\&\times {\mathbb {B}} \left( (1+x)^{-\alpha },\frac{\alpha -k+i}{\alpha },\beta \right) . \end{aligned}$$
(5)

where \({\mathbb {B}} (x,a,b)\) is the incomplete beta function. Fig. 2 shows various plots for the cdf.

Fig. 2
figure 2

Some examples of the cumulative function of WIKD

Full size image

3.3 Reliability measures

In the current section, we study the reliability characteristics of the WIKD, including the functions of reliability, hazard, and reversed hazard. Also, we derive the central tendency, dispersion measures, graphical and order statistics for such distribution.

3.3.1 Reliability function

Suppose that X is an r.v. follows WIKD with parameters \(\alpha \), \(\beta \) and k. The distribution survival function is determined by

$$\begin{aligned} S(x)=1-G(x) \end{aligned}$$

Thus, from (5) we get

$$\begin{aligned} S(x)=&\frac{1}{\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^i \beta \left( \frac{\alpha -k+i}{\alpha },\beta \right) }\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^i B\left( \frac{\alpha -k+i}{\alpha },\beta \right) \nonumber \\&\times {\mathbb {B}}\left( (1+x)^{-\alpha },\frac{\alpha -k+i}{\alpha },\beta \right) . \end{aligned}$$
(6)

3.3.2 Hazard, reversed hazard and mills ratio rate functions

Recall that the hazard function is expressed by

$$\begin{aligned} H_1(x)=\frac{f(x)}{S(x)}. \end{aligned}$$

Therefore, having that the X follows WIKD, the hazard function is deduced by combining (4) and (6) to get the expression

$$\begin{aligned} H_1(x)=\frac{\alpha x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1}}{\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^i B\left( \frac{\alpha -k+i}{\alpha },\beta \right) {\mathbb {B}}\left( (1+x)^{-\alpha },\frac{\alpha -k+i}{\alpha },\beta \right) }. \end{aligned}$$

The reversed hazard function is defined by

$$\begin{aligned} H_2(x)=\frac{f(x)}{F(x)}. \end{aligned}$$

Now, by (4) and (5) we get

Both functions \(H_1(x)\) and \(H_2(x)\) are graphically shown in Fig. 3.

Fig. 3
figure 3

Some examples of WIKD Hazard functions

Full size image

On the other hand, we express the Mills ratio function, which is denoted by m(t) where

$$\begin{aligned} m(t)=\frac{1}{H_1(t)} . \end{aligned}$$

It suffices to replace \(H_1(t)\) by its expression to prove that the WIKD has a Mills ratio function defined by

$$\begin{aligned} m(t)=\frac{\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^i B(\frac{\alpha -k+i}{\alpha },\beta ) {\mathbb {B}} ((1+x)^{-\alpha },\frac{\alpha -k+i}{\alpha },\beta )}{\alpha x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1}} \end{aligned}$$

3.3.3 Mean residual life (MRL)

The MRL function is defined by

$$\begin{aligned} M(x)=E\left[ (X-x|X>x\right] =\frac{\int _x^\infty y f(y)dy}{S(x)}-x. \end{aligned}$$

Now, having that the X follows WIKD, we obtain by some analytical arguments, used on the determination of \(f_{WIKD}\), G and S, the MRL of WIKD. Thus, the MRL can be expressed by

$$\begin{aligned} M(x)=\frac{\sum _{i=0}^{k+1}\left( {\begin{array}{c}k+1\\ i\end{array}}\right) (-1)^i {\mathbb {B}} ((1+x)^{-\alpha },\frac{\alpha -k+i}{\alpha },\beta )}{{\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^i B\left( \frac{\alpha -k+i}{\alpha },\beta \right) {\mathbb {B}} ((1+x)^{-\alpha },\frac{\alpha -k+i}{\alpha },\beta )}}-x. \end{aligned}$$

3.4 Stochastic ordering

Assume that the corresponding distributions to the random variables X and Y are \(F_X(x)\) and \(F_Y(y)\) respectively. Then, if \(F_Y(x)\le F_X(x)\), we say that X is stochastically larger than Y. We use st to represent the stochastic relationship between variables. In our case, we write that \(X\ge _{st} Y\) if \(F_X(x) \ge F_Y(x)\). This stochastic property can also be held if we compare the two random variables in terms of hazard rate order and mean residual life order. In terms of likelihood ratio order, we can say that \((Y\le _{lr} X)\) if \(\frac{f_X(x)}{f_Y(x)}\) is an increasing function of X.

Theorem 1

If X and Y are independent r.v.s and follow WIKD where their distributions parameters are \((\alpha _1, \beta _1, k_1)\) and \((\alpha _2, \beta _2, k_2)\), respectively, then, \(Y\le _{lr}X\) if \(k_1>k_2\),  \(\alpha _2>\alpha _1\), \(\beta _1>\beta _2\) and \(\alpha _1\, \alpha _2,\, \beta _1, \beta _2>1\).

Proof

Let \(X\sim WIKD(k_1,\alpha _1,\beta _1)\) and \(Y\sim WIKD(k_2,\alpha _2,\beta _2)\). Denote by \(\phi (x)\) the likelihood ratio where

$$\begin{aligned} \phi (x)=\frac{f_X(x)}{f_Y(x)}. \end{aligned}$$
(7)

The \(f_X(x)\) and \(f_Y(x)\) are:

$$\begin{aligned} f_X(x)&=\frac{\alpha _1}{W(\alpha _1,\beta _1,k_1)}x^{k_1}(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha _1}\right] ^{\beta _1-1}\\ f_Y(x)&=\frac{\alpha _2}{W(\alpha _2,\beta _2,k_2)}x^{k_2}(1+x)^{-(\alpha _2+1)}\left[ 1-(1+x)^{-\alpha _2}\right] ^{\beta _2-1} \end{aligned}$$

Rewrite (7) as

$$\begin{aligned} \phi (x)&=R\,x^{k_1-k_2}(1+x)^{(\alpha _2+1)-(\alpha +1)}\frac{\left[ 1-(1+x)^{-\alpha _1}\right] ^{\beta _1-1}}{\left[ 1-(1+x)^{-\alpha _2}\right] ^{\beta _2-1}}, \end{aligned}$$

where

$$\begin{aligned} R=\frac{\alpha _1 W(\alpha _2,\beta _2,k_2)}{\alpha _2 W(\alpha _1,\beta _1,k_1)}. \end{aligned}$$

Take the logarithm to get

$$\begin{aligned} \log \phi (x)&=\log R + (k_1-k_2)\log x +(\alpha _2+1)\log (1+x) +(\beta _1-1)\\&\times \log \left[ 1-(1+x)^{-\alpha _1}\right] b+(\beta _2-1)\log \left[ 1-(1+x)^{-\alpha _2}\right] . \end{aligned}$$

Now, \((Y\le _{lr} X)\) if \(\frac{d}{dx}\log \phi (x)>0\). Then, differentiate \(\log \phi (x)\) to get

$$\begin{aligned} \frac{d}{dx}\log \phi (x)=\frac{k_1-k_2}{x}+\frac{\alpha _2-\alpha _1}{1+x}+\frac{(\beta _1-1)\alpha _1}{(1+x)^{\alpha _1+1}-(1+x)}-\frac{(\beta _2-1)\alpha _2}{(1{+}x)^{\alpha _2{+}1}-(1{+}x)} \end{aligned}$$

It is clearly that \( \frac{d}{dx}\log \phi (x)>0\) if \(k_1<k_2\),  \(\alpha _2>\alpha _1\), \(\beta _1>\beta _2\) and \(\alpha _1\, \alpha _2,\, \beta _1, \beta _2>1\). Hence, for \(k_1<k_2\),  \(\alpha _2>\alpha _1\), \(\beta _1>\beta _2\) and \(\alpha _1\, \alpha _2,\, \beta _1, \beta _2>1\), Shaked and Shanthikumar (1994) showed stochastic ordering implications of a distribution as: \(Y\le _{lr}X \rightarrow Y\le _{hr}X \rightarrow Y\le _{mrl}X\) or \(Y\le _{lr}X \rightarrow Y\le _{st}X \rightarrow Y\le _{mrl}X\).

3.5 Order statistics

Consider the sample \(X_1, X_2,\ldots X_n\) of a random variable X which follows the WIKD. It is well known that the cumulative function of the \(l^{th}\) order statistics, denoted by \(X_{(l)}\) (such that \((X_{(1)}< X_{(2)}<X_{(l)}<X_{(l+1)}\ldots < X_{(n)}) \)), is determined by

$$\begin{aligned} F_{X_{(l)}}(t)=\sum _{j=l}^n \left( {\begin{array}{c}n\\ j\end{array}}\right) \left( 1-F_X(t)\right) ^{n-j}F_X^j(t). \end{aligned}$$

It follows that the density of \(X_{(l)}\) is expressed by

$$\begin{aligned} f_{X{(l)}}(t)=n \left( {\begin{array}{c}n-1\\ l-1\end{array}}\right) \left( 1-F_X(t)\right) ^{n-l}F_X^{j-1}(t)f_X(t). \end{aligned}$$

Thus, the expression for the pdf of \(X_{(l)}\) is

$$\begin{aligned} f_{X_{(l)}}(t)&=\frac{\alpha \, n \left( {\begin{array}{c}n-1\\ l-1\end{array}}\right) }{(W(\alpha ,\beta , k))^2}\left( \sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i}B\left( \frac{\alpha -k+i}{\alpha },\beta \right) {\mathbb {B}} \left( (1+t)^{-\alpha },\frac{\alpha -k+i}{\alpha },\beta \right) \right) ^{n-l}\\&\quad \left( 1-\sum _{i=0}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i}B\left( \frac{\alpha -k+i}{\alpha },\beta \right) {\mathbb {B}} \left( (1+t)^{-\alpha },\frac{\alpha -k+i}{\alpha },\beta \right) \right) ^{j-1} \\&\quad \times t^k(1+t)^{-(\alpha +1)}\left[ 1-(1+t)^{-\alpha }\right] ^{\beta -1} \end{aligned}$$

3.5.1 Shannon entropy

Assume that X is a non-negative continuous r.v. with the f(x) as a pdf. The uncertainty classical measure for the r.v. X is the derivative of entropy; this also gives the well known Shannon entropy (see Shannon 1948) and is determined by

$$\begin{aligned} H_{Shan}(X)=-E[log (f(x))]=\int _{-\infty }^{+\infty } f(x)\log [f(x)]\,dx. \end{aligned}$$

Hence, the \(H_{Shan}\) is derived as follows.

$$\begin{aligned} H_{Shan}(X)&= \displaystyle - \int _0^{+\infty }\left( f_{WIK}(x,\alpha ,\beta )\right) \log \left( f_{WIK}(x,\alpha ,\beta )\right) dx \\&\displaystyle =-\frac{\alpha }{W(\alpha ,\beta , k)} \int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \\&\displaystyle \quad \left( k\log (x) -(\alpha +1) \log (1+x)+(\beta -1)\log \left( 1-(1+x)^{-\alpha }\right) \right) dx\\&\displaystyle =-\frac{\alpha }{W(\alpha ,\beta , k)} \left( k\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \log (x)dx\right. \\&\quad \left. -\,(\alpha +1)\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \log (1+x)dx\right. \\&\quad \left. \displaystyle +\, (\beta -1)\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1}\log \left( 1-(1+x)^{-\alpha }\right) \right) dx\\&\displaystyle =-\frac{\alpha }{W(\alpha ,\beta , k)} \left( k\frac{\partial }{\partial k}\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} dx\right. \\&\quad \left. +\, (\alpha +1)\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \log (1+x)dx\right. \\&\quad \left. -\, (\beta -1)\frac{\partial }{\partial \beta }\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1}\right) dx\\&\displaystyle =-\frac{1}{W(\alpha ,\beta , k)} \left( k\frac{\partial }{\partial k}W(\alpha ,\beta , k) \right) +\frac{1}{W(\alpha ,\beta , k)}\\&\quad \times \left( (\alpha +1)\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \log (1+x)\right) dx \\&\quad \displaystyle -\left( (\beta -1)\frac{1}{W(\alpha ,\beta , k)}\frac{\partial }{\partial \beta } W(\alpha ,\beta , k)\right) \\&\displaystyle =-k\frac{\partial }{\partial k}\log \left( W(\alpha ,\beta , k) \right) - \displaystyle (\beta -1)\frac{\partial }{\partial \beta } log( W(\alpha ,\beta , k)) \displaystyle +\frac{\alpha }{W(\alpha ,\beta , k)}\\&\quad \times \left( (\alpha +1)\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \log (1+x)\right) dx. \end{aligned}$$

Now, we treat

$$\begin{aligned} I=\frac{\alpha }{W(\alpha ,\beta , k)} \left( (\alpha +1)\int _0^{+\infty } x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \log (1+x)\right) \,\nonumber \\ \end{aligned}$$
(8)

by using the same variable change, as in the determination of \(f_{WIKD}\), as follows.

$$\begin{aligned} I&\displaystyle =\frac{(\alpha +1)}{\alpha W(\alpha ,\beta , k)}\int _1^{0} (z^{-1/\alpha }-1)^k (1-z)^{\beta -1} \log (z)dz\\&\displaystyle =\frac{(\alpha +1)}{\alpha W(\alpha ,\beta , k)}\int _{0}^1 \sum _{i=0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i}z^{-(k-i)/\alpha } (1-z)^{\beta -1}\log (z)dz\\&\displaystyle = \frac{(\alpha +1)}{\alpha W(\alpha ,\beta , k)}\sum _{i=0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i} \int _{0}^1z^{-(k-i)/\alpha } (1-z)^{\beta -1}\log (z)\\&\displaystyle =- \frac{(\alpha +1)}{W(\alpha ,\beta , k)}\left( \sum _{i=0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i} \frac{\partial }{\partial k}B\left( \frac{\alpha -k+i}{\alpha },\beta \right) \right) . \end{aligned}$$

Thus,

$$\begin{aligned}&H_{Shan}(X)=-k\frac{\partial }{\partial k}\log \left( W(\alpha ,\beta , k) \right) - \displaystyle (\beta -1)\frac{\partial }{\partial \beta } log( W(\alpha ,\beta , k)) \\&\quad -\frac{(\alpha +1)}{W(\alpha ,\beta , k)}\left( \sum _{i=0}^k \left( {\begin{array}{c}k\\ i\end{array}}\right) (-1)^{i} \frac{\partial }{\partial k}B\left( \frac{\alpha -k+i}{\alpha },\beta \right) \right) . \end{aligned}$$

3.6 Renyi entropy

The Renyi Entropy is defined by

$$\begin{aligned} H_a(X)=\frac{1}{a-1}\log \left[ \int _0^{+\infty }\left( f_{WIK}(x,\alpha ,\beta )\right) ^a\right] \end{aligned}$$

Firstly, we calculate

$$\begin{aligned} \int _0^{+\infty }\left( f_{WIK}(x,\alpha ,\beta )\right) ^a&=\int _0^{+\infty }\left( f_{WIK}(x,\alpha ,\beta )\right) ^adx \\&\displaystyle =\frac{\alpha ^a}{W^a(\alpha ,\beta , k)} \int _0^{+\infty } x^{ak}(1+x)^{-a(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{a(\beta -1)}\\&\displaystyle =\frac{\alpha ^a}{W^a(\alpha ,\beta , k)} \int _0^{+\infty } x^{ak}(1+x)^{-(a\alpha -a)}\left[ 1-(1+x)^{-\alpha }\right] ^{(a\beta -a)} \end{aligned}$$

Use the same variables changes, as in the prove of (2), to prove that

$$\begin{aligned}&\int _0^{+\infty } x^{ak}(1+x)^{-(a\alpha -a)}\left[ 1-(1+x)^{-\alpha }\right] ^{(a\beta -a)}\\&\qquad =\int _1^{0} (z^{-1/\alpha }-1)^{ak} z^{-((1-a)(\alpha +1))/\alpha }(1-z)^{\beta -1} dz\\&\qquad = \int _{0}^1 \sum _{i=0}^{ak} \left( {\begin{array}{c}ak\\ i\end{array}}\right) (-1)^{i}z^{-((ak-i)+((1-a)(\alpha +1)))/\alpha } (1-z)^{\beta -1}dz\\&\qquad =\sum _{i=0}^{ak} \left( {\begin{array}{c}ak\\ i\end{array}}\right) (-1)^{i} B\left( \frac{\alpha -(ak-i)-((1-a)(\alpha +1)))}{\alpha },\beta \right) \end{aligned}$$

Finally,

4 Statistical inferences

We devote this section to the estimation of the parameters of WIKD. We construct two estimators in which the maximum likelihood obtains the first one and the second one is constructed by the moment methods. All estimators can be obtained by a numerical procedure.

4.1 Maximum likelihood estimators

Consider a size n, \(X_1,\ldots X_n\), a random sample drawn from a r.v. X with the pdf

$$\begin{aligned}f_{WIKD}(x,\alpha ,\beta ,k)= \frac{\alpha }{W(\alpha ,\beta , k)} x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \end{aligned}$$

Based on the above pdf, the function of the likelihood is determined by

$$\begin{aligned} L(x_1,\ldots x_n, \alpha ,\beta , k)&= \left( \frac{\alpha }{W(\alpha ,\beta , k)}\right) ^n \left( \prod _{i=1}^n x_i\right) ^k \left( \prod _{i=1}^n (1+x_i)^{-(\alpha +1)}\right) \\&\quad \times \;\left( \prod _{i=1}^n \left( 1-(1+x_i)^{-(\alpha +1)}\right) \right) ^{\beta -1}, \end{aligned}$$

and the corresponding log-likelihood is determined by

$$\begin{aligned} \log L(x_1,\ldots x_n, \alpha ,\beta , k)&= -n\log (W(\alpha ,\beta , k)) +n log(\alpha )+k \sum _{i=1}^n \log (x_i)-(\alpha +1) \\&\quad \times \sum _{i=1}^n \log (1+x_i) + (\beta -1)\sum _{i=1}^n \log \left( 1-(1+x_i)^{-(\alpha +1)}\right) . \end{aligned}$$

It follows that the estimates \({\hat{\alpha }}\), \({\hat{\beta }}\) and \({{\hat{k}}}\) are the maximum likelihood estimators (MLE) which are the solutions of the following set equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} -n\frac{\partial }{\partial \alpha } \log (W(\alpha ,\beta , k))+ n\alpha ^{-1}-\sum _{i=1}^n\log (1+x_i) \\ &{} -(\beta -1)\sum _{i=1}^n \log (1+x_i)\frac{(1+x_i)^{-(\alpha +1)}}{(1-(1+x_i)^{-(\alpha +1)})}=0 \\ &{}-n\frac{\partial }{\partial \beta }\log (W(\alpha ,\beta , k))+\sum _{i=1}^n \log \left( 1-(1+x_i)^{-(\alpha +1)}\right) =0. \\ &{} -n\frac{\partial }{\partial k} \log \left( W(\alpha ,\beta , k)\right) +\sum _{i=1}^n \log (x_i)=0 \end{array}\right. } \end{aligned}$$

The estimators are computed by using the code-routine goodness.fit of the R-package AdequacyMode. The latter is based on the Particle Swarm Optimization (PSO) algorithm, which provides greater control of the optimization process, allowing to overcome the effects of the presence of flat regions or the independence to the choice of the initial values. The initial values are automatically chosen. Of course, the solution of these equations require the positive-definite of the Hussein matrix on the solution \(({\hat{\alpha }}, {\hat{\beta }},{{\hat{k}}})\). The Hussein matrix is defined by

$$\begin{aligned} \sum (\alpha , \beta ,k)= \left( \begin{array}{ccc} I_{11}&{}I_{12}&{}I_{13}\\ I_{21}&{}I_{22}&{}I_{23}\\ I_{31}&{}I_{32}&{}I_{33} \end{array} \right) ^{-1}, \end{aligned}$$

where

$$\begin{aligned} I_{23}&=\displaystyle -n\frac{\partial ^2}{\partial \beta \partial k} \log (W(\alpha ,\beta , k)), \qquad I_{31}=\displaystyle -n\frac{\partial ^2}{\partial k\partial \alpha } \log (W(\alpha ,\beta , k)), \\ I_{32}&=\displaystyle -n\frac{\partial ^2}{\partial k\partial \beta } \log (W(\alpha ,\beta , k)),\qquad I_{33}=\displaystyle -n\frac{\partial ^2}{\partial k^2} \log (W(\alpha ,\beta , k)). \end{aligned}$$

The matrix \(\sum \) is used to evaluate the asymptotic variance-covariance matrix of maximum likelihood estimators (MLE). The latter is the inverse of the observed Fisher information matrix. Empirically, by the maximum likelihood method and the fisher information given by \(\sum \) , it suffices to replace \((\alpha ,\beta , k)\) by \({\hat{\alpha }}, {\hat{\beta }},{{\hat{k}}}\) to get the variance asymptotic of the maximum likelihood estimator.

Table 1 Simulation studies: parameter estimates for WIKD based on maximum likelihood and moment methods
Full size table

4.2 Estimation by the moments’ method

Now, we construct the Moment Method Estimator (MME) of the parameters \((\alpha ,\beta , k)\). To do that, we consider a size n, \(X_1,\ldots X_n\), of a random sample drawn from a r.v. X with the pdf

$$\begin{aligned}f_{WIKD}(x,\alpha ,\beta ,k)= \frac{\alpha }{W(\alpha ,\beta , k)} x^k(1+x)^{-(\alpha +1)}\left[ 1-(1+x)^{-\alpha }\right] ^{\beta -1} \end{aligned}$$

Then, the estimates \({\tilde{\alpha }}, {\tilde{\beta }},{\tilde{k}}\) are the solutions of the below set of equations:

$$\begin{aligned} \left\{ \begin{array}{c} \displaystyle W(\alpha ,\beta , k+1) - W(\alpha ,\beta , k) n^{-1}\sum X_i=0\\ \displaystyle W(\alpha ,\beta , k+2) - W(\alpha ,\beta , k) n^{-1}\sum X_i^2=0\\ W(\alpha ,\beta , k+3) - W(\alpha ,\beta , k) n^{-1}\sum X_i^3=0\\ \end{array} \right. \end{aligned}$$

The solution is obtained by using the R-code nleqslv with the initial values (10, 5, 6).

5 Performance and discussion

In this section, we test the performance of our introduced model using simulation studies and real data and discuss its superiority by comparing it to the comparative models.

5.1 Simulation studies

In the first illustration, a comparative study between both estimation methods is developed to show both estimators’ applicability (MLE and MME). For this purpose, we generate n random variables from the weighted inverted Kumaraswamy distribution by inverting the cumulative distribution function over the uniform distribution, using the R-code inverse. The simulation experiment is performed over two cases \((\alpha , k,\beta ) =(2,1,3)\) and \((\alpha , k,\beta ) =(10,9,10)\). The bias and the mean square errors (MSE) are summarized in Table 1. The bias for an estimator is calculated as the difference between the expected and the true values. The MSE is non-negative and is used to measure the estimator quality; a better estimator is that with an MSE value closer to zero.

Comparing the results of MLE and MME of the first case to the second case of the experiment, based on the bias values, we see that the precision for the MLE is very high for a very small sample size. But, when the sample size is increased, there are some differences between both methods. In addition, and based on the MSE values, we see that for each n, the MSE values for the MLE method are smaller than those for the MME method. In what follows, we will carry our analysis and investigation based on the MLE method.

In the second illustration, we use Monte Carlo data to test the efficiency of the proposed probability model compared to the known model that is the Kumaraswamy Sushila distribution (KSD) (Shawki and Elgarhy 2017). To do that, we consider two simulated models that are very close to realistic situations. Precisely, we use some observations drawn by the absolute variable of the Laplace Distribution (\(Laplace(\mu ,b)\)) which cover the nonhomogeneous data, and the second one is constructed from the absolute variable of the mixture model \(\rho N(0,.1)+(1-\rho )N(0,1)\). Recall that our main aim in this second illustration is to test the quality of WIKD over these usual models. In fact, there are many measures for the model selection and the goodness of fit in probability theory. The AIC and BIC are two of the most used measures. These criteria permit the quantification of the information loss in this simulated data. Indeed, the best model is the model with smaller values of the AIC and BIC. The Monte Carlo study is carried out over several values of the parameters \(\mu \), b, \(\rho \), m, and p. Table 2 displays the results.

Table 2 Comparison of the information loss between WIKD, IKD and KSD over simulated data
Full size table

It apparats clearly that the WIKD is significantly better than the IKD and KSD. Of course, this gain is varied with respect to the generated data and the choice of the parameters. In particular, the best result of the WIKD corresponds to the Laplace distribution with \(\mu =0\) and \(b=0.5\). Meanwhile, for the IKD and KSD, there is a significant loss of information, mainly when using the BIC measure. The border range for IKD (respectively for KSD) is between 175.61 and 507.42 (respectively, 504.98 and 618.78) versus 91.82 and 450.93 for the WIKD.

5.2 A real life application

Two real data sets of Carbon fiber data are used to compare the efficiency and flexibility of the WIKD with existing sub-models. Carbon fibers distinct lightness and strength make it a viable, versatile, and useful commercial product for a wide variety of markets. Carbon fiber is commonly used to reinforce composite materials to make them strong and reliable. It is typically two times stronger, six times harder, and half time heavier than fiberglass. Accurate and reliable modeling of this important material is of great importance in a variety of fields. Noting that, in survival analysis, practitioners are usually interested in choosing the distribution providing the best fit for the underlying data. This is the principal motivation to build new distributions. For this purpose, we highlight the feasibility of the WIKD using the two data sets evaluating the strength of carbon fiber. The first one contains \((n = 63)\) observations. Such data is frequently used in this kind of study. It was initially reported and studied by Badar and Priest (1982) and then by Mead et al. (2017) as an application for the beta exponential Frechet distribution. The data is measured in GPA and represents the strength of single carbon fibers and impregnated 1000-carbon fiber tows. More examples of this kind of data are available in the R-package AdequacyMode. In the first part of this computational study, we use the following observations:

1.901, 2.132, 2.203, 2.228, 2.257, 2.350, 2.361, 2.396, 2.397, 2.445, 2.454, 2.474, 2.518, 2.522, 2.525, 2.532, 2.575, 2.614, 2.616, 2.618, 2.624, 2.659, 2.675, 2.738, 2.740, 2.856, 2.917, 2.928, 2.937, 2.937, 2.977, 2.996, 3.030, 3.125, 3.139, 3.145, 3.220, 3.223, 3.235, 3.243, 3.264, 3.272, 3.294, 3.332, 3.346, 3.377, 3.408, 3.435, 3.493, 3.501, 3.537, 3.554, 3.562, 3.628, 3.852, 3.871, 3.886, 3.971, 4.024, 4.027, 4.225, 4.395, 5.020.

This data is fitted using three models; WIKD and its sub-models, i.e., IKD and KSD. Recall that the fit of this data is performed by R-code goodness.fit based on the PSO algorithm. As we mentioned before, this algorithm provides greater control of the optimization process and overcomes the effects of flat regions or the independence to the choice of the initial values.

For comparing the WIKD with its sub-models, criteria such as the AIC, BIC, and the corrected Akaike information criterion (AICC) are used. A distribution with smaller AIC, AICC, and BIC values is judged to be the best fit compared with its existing models. The estimation of the parameters of the WIKD and its sub-models are achieved with the help of R-code goodness.fit; Table 3 displays the results.

Table 3 Performance of distributions for the Dataset I: WIKD, IKD and KSD
Full size table

It is evident from Table 3 that the WIKD gives a superior fit when contrasted with other sub-models since it has the most minimal estimations of AIC, AICC, and BIC.

The second illustration also concerns another example of carbon fiber data. Recall that this data’s popularity is motivated by the fact that carbon fiber is essential to measure the benefit of a material in strength and stiffness. In particular, obtaining carbon fiber materials with high stiffness and strength is possible through specialized heat treatment processes with very expansive and costs much higher values. In this sense, the devolvement of new distributions allowing to fit these characteristics is extremely important. To confirm the superiority of the WIKD over its competitive models, we evaluate its performance over other celebrated data that represent the tensile strength of carbon fibers. The considered data was initially reported and studied by Badar and Priest (1982) and then by Shanker et al. (2016) as an application for weighted Lindley distribution. It contains \((n = 69)\) observations. It gives the GPA measures of the tensile strength of carbon fibers. The data observations are:

1.312, 1.314, 1.479, 1.552, 1.700, 1.803, 1.861, 1.865, 1.944, 1.958, 1.966, 1.997, 2.006, 2.021, 2.027, 2.055, 2.063, 2.098, 2.14, 2.179, 2.224, 2.240, 2.253,2.270, 2.272, 2.274, 2.301, 2.301, 2.359, 2.382, 2.382, 2.426, 2.434, 2.435, 2.478, 2.490, 2.511,2.514, 2.535, 2.554, 2.566, 2.57, 2.586, 2.629, 2.633, 2.642, 2.648, 2.684, 2.697, 2.726, 2.770,2.773, 2.800, 2.809, 2.818, 2.821, 2.848, 2.88, 2.954, 3.012, 3.067, 3.084, 3.090, 3.096, 3.128,3.233, 3.433, 3.585, 3.585.

The WIKD estimates and its sub-models parameters, AIC, AICC and BIC for dataset II, are also obtained with the help of R-code goodness.fit; Table 4 displays the results.

Table 4 Performance of distributions for the Dataset II: WIKD, IKD and KSD
Full size table

From Table 4, it is again apparent that the WIKD gives a superior fit when contrasted with other sub-models since it has the lowest estimations of AIC, AICC, and BIC.

6 Conclusion

Materials of high strength are always necessary to ensure the safety of human lives and infrastructures to elude the significant obligations linked with the provisions of non-compliant products. In this paper, we introduced the weighted inverted Kumaraswamy distribution. We provide explicit expressions for the model properties: the moments, mgf, hazard rate function, mean residual function, stochastic ordering, and measure of uncertainty for WIKD. Parameters of the proposed model are achieved using the maximum likelihood and moments method. Also, comparative studies of both methods based on simulation studies are conducted to show the applicability of both estimators and test the performance of WIKD over that KSD. The results show that the WIKD performance better than KSD. Finally, we present an illustration that endorses the applicability of the WIKD for modeling real-life data over their existing sub-models. Two real carbon fiber data are used, and again the results show the superiority of the WIKD in fitting the data better than IKD and KSD.