A new probability model with application to heavy-tailed hydrological data

Abstract

Because of the dramatic changes that are being observed in the climatic conditions of the world, such as excess of rains, drought and huge floods, we introduce a versatile hydrologic probability model with three parameters. The proposed model is a combination of the Lomax and generalized Weibull distributions based on an exponent odd function. Main properties of the distribution are obtained, such as shapes of the probability density and hazard rate functions, quantile function, asymptotic distribution, information matrix and characterization via hazard rate function. Parameters are estimated via the maximum likelihood estimation method. Four data sets are used to compare the proposed model with a number of well-known hydrologic models. The proposed model is found to be suitable and representative for heavy-tailed hydrological data sets, with least loss of information attitude and a realistic return period.

1 Introduction with the proposed model

Frequency of heavy precipitation or proportion of total rainfall from heavy falls will increase in the 21st century over many areas on the globe, this will increase the likelihood of floods and devastation of infrastructures (Intergovernmental Panel on Climate Change IPCC 2012). These upcoming future devastating effects have certainly opened the hidden corner for accurate modeling of the flood/precipitation/earth quake data which will not only produce good fit but also yield realistic return periods. Such requisition for modeling the hydrologic phenomenon needs to assess the tail behavior which is the only realistic knowledge regarding the behavior of the distribution beyond the range of the sample (Markovich 2007). Such tail behavior has its own significance in its relative discipline. For example, light tail distributions (kurtosis less or equal to 3) can effectively be used in the analysis of global warming in terms of extreme warm and cold temperature (Loikith and Neelin 2015) and rainfall data analysis (Papalexiou et al. 2013), while the heavy-tailed distributions are used to model the service time and input in queuing models, flood levels of rivers, major insurance claims, wave heights during a storm, and low and high temperatures (Markovich 2007). These heavy-tailed distributions include the Pareto, the lognormal, the Weibull with shape parameter less than 1, the Cauchy, the Burr and the Fréchet, while the light-tailed distributions include the exponential, the gamma, the Weibull with shape parameter greater than 1, and the normal distributions.

In this regard, the conventional frequency analysis (CFA) is used for modeling these extreme events via heavy-tailed distributions which include the the Log-Pearson type III (LP(3)) defined by Bobee (1975), the three parameter log-normal distribution (LN(3)) as stated by Krige (1960), the generalized Pareto (GP) distribution used by Hosking and Wallis (1987) and Dargahi-Noubary (1989), the generalized logistic (GLO) distribution studied by Dyrrdal (2012) and Balakrishnan and Leung (1988), Gumbel distribution known as the generalized extreme value type I (GEV-I) distribution investigated by Mujere (2011), the three parameter Kappa distribution studied by Junior and Johnson (1973), the gamma distribution, the generalized exponentiated exponential Lindley (GEEL) proposed by Hussain et al. (2018) and the Fréchet distribution discussed by Ramos et al. (2018).

Moreover, the domain of attractions for maxima–minima, of the LP(3), LN(3), GP, GLO and GEEL distributions belong to the Gumbel–Weibull, the Gumbel–Gumbel, the Fréchet-Weibull, the Gumbel–Gumbel and the Gumbel–Fréchet distributions, respectively. However, the Gumbel distribution is not considered an appropriate model for the analysis of extreme events because its right tail is light. Furthermore, in extreme events analysis, researchers generally prefer the positive skewness coupled with the heavy-tailed phenomena instead of light or intermediate tails distributions (Hussain et al. 2018).

Here, we study a phenomenal procedure designed for modeling heavy-tailed environmental data sets, based on flexible parametric modeling by adding shape, location or scale parameters, while constraining the number of parameters to be at most equal to four. However, three is a recommended number of parameters to draw valid conclusions (Mudholkar et al. 1996, Johnson et al. 2005), which provides a broader range of hazard shapes and allow an assessment of each competing model relative to a more comprehensive one (Mudholkar et al. 1996). Also, such addition of extra parameter is useful in exploring tail behavior which not only improves the goodness of fit of the proposed models but also provides lower information criteria. Moreover, the exploration of tails usually reflects the importance of extreme and intermediate order statistics or exceedances over high thresholds. Focusing our attention on tails may advantageously inspire the introduction of new parametric statistical models.

The first motivational ground of modeling the extreme events and heavy-tailed phenomenon is based on the selection of Pareto Type II distribution, which was first proposed by Lomax (1987). It is effectively used in reliability modelling, life testing, income, wealth, business failure, firm size, queuing problems, biological sciences, modeling the distribution of the sizes of computer files on servers and as an alternative to the exponential distribution when the data are heavy-tailed data. The Lomax distribution is defined as follows.

Definition 1

A random variable T has the Lomax distribution with shape parameter $\beta >0$ if its cumulative distribution function (cdf) is given by

$$\begin{aligned} \pi (t)=1-(1+t)^{-\beta }, \quad t> 0, \, \beta > 0, \end{aligned}$$

and its corresponding probability density function (pdf) is expressed as

$$\begin{aligned} \ell (t)=\beta (1+t)^{-\beta -1}, \quad t> 0, \, \beta > 0. \end{aligned}$$

The second motivational ground is to handle the shortcomings of Weibull distribution (an asymptotic version of one of the three heavy-tailed phenomena) which is frequently used in statistical analysis of many practical data, however it is inappropriate when the failure rate is indicated to be unimodal and bathtub shaped as well as when data exhibit high kurtosis usually greater (or equal) twenty. The third motivation is the selection of two parameter generalized Weibull (GW); possessing a bathtub hazard rate, simple structure and heavy-tailed behavior, defined by Mudholkar et al. (1996) as a baseline distribution whose cdf defined on the interval $(0,\infty )$ as $G(x)=1-\left( 1-\lambda x^{\theta }\right) ^{\frac{1}{\lambda }}$ with the pdf $g(x)=\theta x^{\theta -1}\left( 1-\lambda x^{\theta }\right) ^{\frac{1}{\lambda }-1}$ for $x > 0, \lambda \le 0$. The fourth motivational aspect is the choice of an appropriate link function, with its help we can overcome the scaling issues of environmental data sets $D(.):[a,b]\rightarrow [0,\infty ]$ which satisfies the next conditions: (i) D(.) is differentiable and monotonically non-decreasing (ii) $D(x) \rightarrow a$ as $x \rightarrow 0$ and $D(x) \rightarrow b$ as $x \rightarrow \infty$, and can be considered as exponent odd function $D(x)=(e^{\theta \frac{G(x)}{1-G(x)}}-1)/(e^{\theta }-1)$, $\theta > 0;$  where $\theta$ and $e^{\theta }-1$ and behave as scale parameters which usually help to overcome the scaling issues of the environmental data sets. Now on the basis of above four motivational aspects, we define the cdf of Lomax D-GW abbreviated as LDGW distribution as follows.

Definition 2

If X is a continuous random variable, then the cdf of the LDGW distribution with parameters $\lambda ,\theta , \beta$ is defined as

$$\begin{aligned} {F}_{{LDGW}}(x|\lambda , \theta ,\beta )&= \int _{0}^{D(x)}\ell (t)dt=1-\left( 1+ \dfrac{e^{-\theta +\theta \left( 1- \lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) ^{-\beta }, \end{aligned}$$

(1)

where $\beta > 0$, $\theta > 0$, $\lambda \le 0$ and $x > 0$.

The corresponding probability density function (pdf) of the LDGW distribution is expressed as

$$\begin{aligned}&f_{{LDGW}}(x|\lambda , \theta , \beta )\nonumber \\&\quad = \beta \theta ^{2} \left( 1+ \dfrac{e^{-\theta +\theta \left( 1- \lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) ^{-\beta -1} \dfrac{e^{-\theta +\theta \left( 1- \lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}} x^{\theta -1}\left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }-1}}{e^{\theta }-1}. \nonumber \\ \end{aligned}$$

(2)

Similarly the survival function (sf) of the LDGW distribution is

$$\begin{aligned} {S}_{{LDGW}}(x|\lambda , \theta ,\beta )=\left( 1+ \dfrac{e^{-\theta +\theta \left( 1- \lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) ^{-\beta } \end{aligned}$$

(3)

and the hazard rate function (hrf) of the LDGW distribution is given by

$$\begin{aligned} {h}_{{LDGW}}(x|\lambda , \theta ,\beta )=\frac{\beta \theta ^2 e^{-\theta +\theta \left( 1- \lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}} x^{-1+\theta } \left( 1- \lambda x^{\theta } \right) ^{-1-\frac{1}{\lambda }}}{e^{-\theta +\theta \left( 1- \lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}}+ e^{\theta }-2}. \end{aligned}$$

(4)

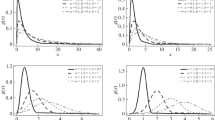
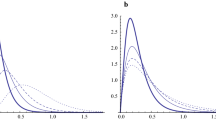
In addition, we have observed that $\lim _{x\rightarrow \infty }e^{\alpha x}{S}_{{LDGW}}(x|\lambda , \theta ,\beta )= \infty$, for all $\alpha > 0$ and $\theta < -\lambda$. Furthermore, $\lim _{x\rightarrow \infty }{h}_{{LDGW}}(x|\lambda , \theta ,\beta ) = 0$ for $\theta < -\lambda$. Hence, the LDGW distribution has a heavy tail when $\theta < -\lambda$ (Foss et al. 2011). This behavior of such distribution adapts hydrological data with heavy tails in the application portion of this paper. Other motivational factors include the handling of floods devastation effects, generally, floods are caused by the heavy concentrated rainfall, which are sometimes augmented by snowmelt flows in rivers. Such floods usually become the causes of financial loss, destruction of infrastructure and spreadness distance issue. In order to cope with the above mentioned causes our proposed model is desired which not only addresses flood and precipitation data at a site or a region but also produces a realistic return period, see real life application of the four data sets as mentioned in the application portion of this paper. Moreover, the proposed model exhibits not only increasing but also upside down bathtub shapes, see Figs. 1 and 2. In addition to, the proposed model exhibits, positive skewness, symmetry and negative skewness coupled with leptokurtic, mesokurtic and plattykurtic behavior (see Figs. 3, 4 and 5). Last but not the least, the asymptomatic distribution of both maxima and minima lies in the Weibull domain of attraction which rarely exists in the literature.

Fig. 1

LDGW hrf graphs for the indicated values

Fig. 2

LDGW hrf graphs for the indicated values

Fig. 3

LDGW pdf graphs for the indicated values

Fig. 4

LDGW pdf graphs for the indicated values

The contents in the rest of this article are arranged as follows. Section 2 deals with some statistical properties of the LDGW distribution, such as quantile function, asymptotic distributions of largest and smallest order statistics and characterization issues via the hazard function. Parameters estimation by maximum likelihood is studied in Sect. 3 as well as hydrological applications are explored and comparison is made with reputed hydrological probability models. Concluding remarks, findings and recommendation are given in Sect. 4.

2 Some properties of the model

Here, we shall discuss some properties of the LDGW distribution.

2.1 Quantile function

If X is an absolutely continuous random variable having the pdf defined in (2), then its quantile function, say $Q_{p}$ (quantile of order p), is defined as ${F}_{{LDGW}}(Q_{p}|\lambda , \theta ,\beta )=p$, where $0<p<1$. Quantile function gives a number $Q_{p}$ in such a way that area to the left of $Q_{p}$ is p, i.e., it is the root of the function

$$\begin{aligned} Q_p=\lambda ^{-\frac{1}{\theta }}\left( 1-\left( \dfrac{ \theta +\ln \left\{ 2-e^{\theta }-(1-e^{\theta })(1-p)^ {-\frac{1}{\beta }}\right\} }{\theta }\right) ^{-\lambda }\right) ^ {\frac{1}{\theta }}. \end{aligned}$$

(5)

Equation (5) can be used to simulate LDGW random variables.

Now by using (5) we can find the median, skewness and kurtosis of LDGW as Median $= Q_{0.5}$, when $p = 0.5$,

$$\begin{aligned} {Sk.}= & {} \frac{Q_{\frac{3}{4}}-2 Q_{\frac{1}{2}}+Q_{\frac{1}{4}}}{Q_{\frac{3}{4}}-Q_{\frac{1}{4}}}, \end{aligned}$$

(6)

$$\begin{aligned} {Ku.}= & {} \frac{Q_{\frac{7}{8}}- Q_{\frac{5}{8}} +Q_{\frac{3}{8}}-Q_{\frac{1}{8}}}{Q_{\frac{6}{8}} -Q_{\frac{2}{8}}}. \end{aligned}$$

(7)

Equation (7) indicates that: As kurtosis increases, the tail of the distribution becomes heavier. These measures are less sensitive to outliers and they exist even for distributions without moments (Cakmakyapan and Ozel 2016). Figure 5 gives the plots of skewness and kurtosis for the LDGW distribution. From this figure, the distribution is leptokurtic and mesokurtic as well as platykurtic attitudes. From this, it is evident the distribution reflects light and heavy tail behavior.  Moreover, it is also observed that kurtosis and skewness decrease as $\beta$ increases.

Fig. 5

Skewness and Kurtosis of the LDGW distribution for the indicated values

2.2 Asymptotic distribution

Here, we present the asymptotic distributions of $W_{n}=X_{n:n}$ and $w_{n}=X_{1:n}$ that are the largest and smallest observations, respectively, from the random sample of n observations. For this purpose we take the cdf and pdf of the LDGW distribution. Then, when $\theta < -\lambda$, the distribution of maxima is

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1-{F}_{{LDGW}}(t+x|\lambda , \theta , \beta )}{1-{F}_{{LDGW}} (t|\lambda , \theta , \beta )}=\lim _{t\rightarrow \infty }\frac{{S}_{{LDGW}}(t+x|\lambda , \theta , \beta )}{{S}_{{LDGW}} (t|\lambda , \theta , \beta )}=1. \end{aligned}$$

Hence, the tail of $F_{LDGW}(.)$ is of slow variation. Also, the distributions with slowly varying tails are shown to be of valuable use in practice (Alves et al. 2009). So, the standardized form of distribution of maxima is Weibull (type -III). Now, the distribution of minima for all values of $\lambda$, after using L’Hôpital’s rule, is

$$\begin{aligned} \lim _{t\rightarrow 0}\frac{{F}_{{LDGW}} (tx|\lambda , \theta , \beta )}{{F}_{{LDGW}} (t|\lambda , \theta , \beta )}=\lim _{t\rightarrow 0} \frac{x f_{{LDGW}}(tx|\lambda , \theta , \beta )}{f_{{LDGW}}(t|\lambda , \theta , \beta )}=x^{\theta }, \end{aligned}$$

and its standardized form is Weibull (type -III), i.e., $1-e^{-x^{\theta }}$. According to (Leadbetter et al. 1987, Theorem 1.6.2) of norming constants $a_{n}>0,b_{n}>0,c_{n}>0$ and $d_{n}>0$, we obtain

$$\begin{aligned} P\left\{ a_{n}(W_{n}-b_{n})\le x\right\} \rightarrow e^{-1}, \quad P\left\{ c_{n}(w_{n}-d_{n})\le x\right\} \rightarrow 1-e^{-x^{\theta }}, \end{aligned}$$

as $n\rightarrow \infty .$ From this, it is clear that the asymptotic distribution of sample maxima and sample minima is in the domain of attraction of Weibull distribution.

2.3 Characterization based on the hazard rate function

Characterization usually helps the researchers for determining the exact probability distribution. The hrf is twice differentiable and usually satisfies the first order differential equation

$$\begin{aligned} \dfrac{f'(x)}{f(x)}=\dfrac{h'_{f}(x)}{h_{f}(x)}-h_{f}(x), \end{aligned}$$

where $h_{f}(x)=\dfrac{f(x)}{1-F(x)}$ is the hrf. The following characterization establishes a non-trivial characterization for the LDGW distribution in terms of the hazard rate function.

Theorem 1

Let $X : \Omega \rightarrow (0, \infty )$ be an absolutely continuous random variable possessing sf ${S}_{{F}}(x) {and} \, f(x)$. Then it is said to have pdf as defined in Eq. (2) iff it satisfies the expression

$$\begin{aligned} \frac{(\ln h(x))^{\prime }}{h(x)}&=\bigg \lbrace \theta ^{2}x^{\theta -1}(1-\lambda x^{\theta })^{-\frac{1}{\lambda }-1}+\frac{\theta -1}{x}+\frac{\lambda \theta x^{\theta -1}(1-\lambda x^{\theta })^{-1}(1+\lambda )}{\lambda }\nonumber \\&\quad -\frac{(\beta +1)\theta ^{2}x^{\theta -1}(1-\lambda x^{\theta })^{-\frac{1}{\lambda }-1}e^{-\theta +\theta (1-\lambda x^{\theta })^{-\frac{1}{\lambda }}}}{e^{-\theta +\theta (1-\lambda x^{\theta })^{-\frac{1}{\lambda }}}+e^{\theta }-2}\bigg \rbrace h(x) + 1, \end{aligned}$$

(8)

for $\beta > 0$, $\theta > 0$, $\lambda \le 0$ and $x > 0$.

The proof is postponed in “Appendix-A”.

3 Maximum likelihood estimation and hydrological applications

3.1 Maximum likelihood estimation

Let $X_{1}, X_{2}, \ldots , X_{n}$ be a random sample from the distribution characterized by (2) with parameter vector ${\varvec{\Theta }}=(\lambda ,\beta ,\theta )$ and $x_{1}, x_{2}, \ldots ,x_{n}$ are the corresponding observed values, then its log-likelihood is expressed as

$$\begin{aligned} \ell (\Theta )&=\ln [{L}(x_{1},x_{2},\ldots x_{n}|\Theta )]=(\theta -1)\sum _{i=1}^n \ln (x_i)-n \ln (e^{\theta }-1)\nonumber \\&\quad -n \theta +\theta \sum _{i=1}^n \left( 1- \lambda x_{i}^{\theta } \right) {}^{-\frac{1}{\lambda }}\nonumber \\&\quad + n \ln (\beta )+2 n \ln (\theta )-\left( 1+\frac{1}{\lambda }\right) \sum _{i=1}^n \ln (1- \lambda x_{i}^{\theta }) \nonumber \\&\quad -(\beta +1)\sum _{i=1}^n \ln \left[ 1+\frac{-1+e^{-\theta +\theta \left( 1-\lambda x_i^{\theta } \right) {}^{-\frac{1}{\lambda }}}}{e^{\theta }-1}\right] . \end{aligned}$$

(9)

The maximum-likelihood estimators (MLEs) of $\lambda$, $\theta$ and $\beta$ are obtained by solving numerically the nonlinear system of equations $\frac{\partial \ell (\Theta )}{\partial \theta }=0, \frac{\partial \ell (\Theta )}{\partial \lambda }=0$ and $\frac{\partial \ell (\Theta )}{\partial \beta }=0$. Those partial derivatives are given in “Appendix-B”. Moreover, for determining the variance co-variance matrix and the confidence interval for the distribution parameters, one requires information matrix which can be generated by the taking the expectation of the second order derivative. In this regard the second order derivatives of the equations above can be provided on demand.

3.2 Evaluation tests

In order to demonstrate the proposed methodology, we consider four different real-world data sets, and compare ten distributions which are too much popular in hydrologic data analysis including, the Weibull, generalized Pareto (3), log-normal (3), log Pearson Type 3, Kappa(3), extreme value, Fréchet, generalized logistic generalized exponentiated exponential Lindley (GEEL) and generalized Weibull distributions, for probability density functions of these distributions readers referred to Hussain et al. (2018). The statistics: Akaike information criterion (AIC), corrected Akaike information criterion (AICc), Hannan–Quinn information criterion (HQIC) and consistent Akaike information criterion (CAIC) along with Vuong test are used to select the best model among several models. The definitions of AIC, AICc, HQIC and CAIC are given as:

$$\begin{aligned} {AIC}= & {} 2 k -2\ell ({\hat{\Theta }}), \qquad {AICc}={AIC}+\frac{2k(k+1)}{n-k-1},\\ {HQIC}= & {} -2 \ell ({\hat{\Theta }})+2k \ln (\ln (n)), \qquad {CAIC}=-2 \ell ({\hat{\Theta }} )+\frac{2 k n}{n-k-1}. \end{aligned}$$

Moreover, perfection of competing models is also tested via the Kolmogrov$-$ Simnorov(K-S), the Anderson–Darling ($A_{0}^{*}$) and the Cramer Von Misses ($\hbox {W}_{0}^{*}$) statistics. The mathematical expressions for the statistics above are given by

$$\begin{aligned} {KS}= & {} \max \left\{ \frac{i}{m}-z_{i},z_{i}-\frac{i-1}{m}\right\} ,\chi ^{2}=\sum _{i=1}^m \frac{(o_{i}-e_{i})^{2}}{e_{i}},\\ A_{0}^{*}= & {} \left( \frac{2.25}{m^{2}}+\frac{0.75}{m}+1\right) \left\{ -m- \frac{1}{m}\sum _{i=1}^{m}(2i-1)\ln (z_{i}(1-z_{m-i+1})) \right\} ,\\ W_{0}^{*}= & {} \sum _{i=1}^{m}\left( z_{i}-\frac{2i-1}{2m}\right) ^{2} +\frac{1}{12m}, \end{aligned}$$

where k denotes the number of parameters, n denotes the number of observations, m denotes the number of classes, $z_{i}={\mathfrak {Q}}(x_{i})$, the $x_{i}$’s are the ordered observations, $o_{i}$ and $e_{i}$ are the observed and expected frequencies of the ith class, respectively.

Whereas the Vuong test with its concerning procedure is outlined as follows.

Vuong test Chi-square approximation in the regard of the likelihood ratio test statistic is valid only for testing restrictions on the parameters of a statistical model (i.e., ${\mathbf {H}}_{0}$ and ${\mathbf {H}}_{1}$ are nested hypotheses). However when models are non-nested, we can not use the likelihood ratio tests for model comparison. In this scenario, the AIC AICc, CAIC and HQIC as well as the Vuong test for non-nested models are useful. Vuong (1989) proposed a likelihood ratio-based statistic for testing the null hypothesis that the competing models are equally close to the true data generating process against the alternative that one model is closer. Let us consider two statistical models based on the probability density functions $f_{A}(x;\xi )=F_{A}(b)- F_{A}(a)$ and $f_{B}(x;\varrho )=F_{B}(b)-F_{B}(a)$ possess equal or unequal number of parameters. Now, we define the likelihood ratio statistic for the model $f_{1}(x;\xi )$ against $f_{2}(x;\varrho )$ as

$$\begin{aligned} {{\mathfrak {L}}}{{\mathfrak {R}}}(\hat{\xi _{n}},\hat{\varrho _{n}})=\sum _{k=0}^{k_{max}} f_{k} ln \left( \frac{f_{A}(x;\hat{\xi _{n}})}{f_{B}(x;\hat{\varrho _{n}})}\right) , \end{aligned}$$

where $\hat{\xi _{n}}$ and $\hat{\varrho _{n}}$ are the MLEs in each model based on the sample $k_{1}, k_{2},\ldots k_{n}$ and $f_{k}$ denotes the observed frequency (Denuit et al. 2007). If both models are strictly non-nested, then under ${\mathbf {H}}_{0}$ we have the test statistic ${\mathbf {Z}} = \frac{{{\mathfrak {L}}}{{\mathfrak {R}}}(\hat{\xi _{n}}, \hat{\varrho _{n}})}{\sqrt{n}\hat{\omega _{n}}}$, having the ${\mathcal {N}}(0,1)$ distribution as approximated distribution when n is large, where

$$\begin{aligned} \hat{\omega _{n}}=\frac{1}{n}\sum _{i=1}^{n} \left( ln \frac{f_{A}(x_{i}; \hat{\xi _{n}})}{f_{B}(x_{i};\hat{\varrho _{n}})} \right) ^{2}- \left( \frac{1}{n}\sum _{i=1}^{n} ln \frac{f_{A}(x_{i}; \hat{\xi _{n}})}{f_{B}(x_{i};\hat{\varrho _{n}})} \right) ^{2}. \end{aligned}$$

In order to select an appropriate model we usually construct the following hypothesis

$$\begin{aligned} {\mathbf {H}}_{0}:{{\mathfrak {K}}}{{\mathfrak {L}}}(f_{A}(x;\xi ))={{\mathfrak {K}}}{{\mathfrak {L}}}(f_{B}(x;\varrho )), \end{aligned}$$

that is, the model A is defined to be better than model B if model A’s ${{\mathfrak {K}}}{{\mathfrak {L}}}$ distance to the truth is smaller than the model B,

$$\begin{aligned} {\mathbf {H}}_{1A}:{{\mathfrak {K}}}{{\mathfrak {L}}}(f_{A}(x;\xi ))<{{\mathfrak {K}}}{{\mathfrak {L}}}(f_{B}(x;\varrho )), \end{aligned}$$

with corresponding critical value, i.e., we reject ${\mathbf {H}}_{0}$ when ${\mathbf {Z}} > {\mathbf {Z}}_{\gamma }$  in favor of A. Similarly, model B is defined to be better than model A if model B’s ${{\mathfrak {K}}}{{\mathfrak {L}}}$ distance to the truth is smaller than the model A,

$$\begin{aligned} {\mathbf {H}}_{1B}:{{\mathfrak {K}}}{{\mathfrak {L}}} (f_{A}(x;\xi ))>{{\mathfrak {K}}}{{\mathfrak {L}}}(f_{B}(x;\varrho )), \end{aligned}$$

with the corresponding critical region, i.e., we reject ${\mathbf {H}}_{0}$ when ${\mathbf {Z}} < - {\mathbf {Z}}_{\gamma }$ in favor of B otherwise decision can not be made, where ${{\mathfrak {K}}}{{\mathfrak {L}}}$ denotes the Kullback–Leibler distance measure and $\gamma$ denotes the level of significance. Therefore, if the value of the test statistic is higher than ${\mathbf {Z}}_{\gamma }$ then one can reject the null hypothesis that the models are equivalent in favor of $f_{A}(x;\xi )$ being better than $f_{B}(x;\varrho )$,  and if the test statistic is smaller than $- {\mathbf {Z}}_{\gamma }$ then one rejects the null hypothesis in favor of $f_{B}(x;\varrho )$ being better than $f_{A}(x;\xi )$ else decision can not be made. The comparisons of the competing models are displayed in the Table 17 for the four data sets.

Example 1

The first data set (I) is the annual flood discharge rates of the Floyd River data flood discharge ($ft^3/s$) during 1935–1973, and it was first reported by Pickands (1975) and later on by Akinsete et al. (2008). The data consist of the following values: 1460, 4050, 3570, 2060, 1300, 1390, 1720, 6280, 1360, 7440, 5320, 1400, 3240, 2710, 4520, 4840, 8320, 13900, 71500, 6250, 2260, 318, 1330, 970, 1920, 15100, 2870, 20600, 3810, 726, 7500, 7170, 2000, 829, 17300, 4740, 13400, 2940, 5660.

Table 1 Descriptive statistics for data set I

Table 2 Some theoretical measures for data set I from LDGW

Analysis of data set I: It is evident from Table 1 that the data behave as positively skewed with high kurtosis in such a way that skewness to kurtosis ratio is 0.1791. Furthermore, Bowley skewness to Bowley kurtosis ratio based on quantiles is also worth noting which is 0.1400. So, such description of the data demands a model which can work very well in positively skewed and leptokurtic distributions. Moreover, Table 2 also affirms the above statement. To draw a valid conclusion we have converted the ungrouped data into grouped data by using the command bins of R computational package (Tables 3 and 4). For this purpose we have created different classes, such as, $[318, 1.37\times 10^{3}]$, $(1.37\times 10^{3}, 2.04\times 10^{3}]$, $(2.04\times 10^{3}, 3.57\times 10^{3}]$, $(5.43\times 10^{3}, 8.05\times 10^{3}]$, $(8.05\times 10^{3}, 7.15\times 10^{4}]$,  $(7.15\times 10^{4}, \infty )$ with observed frequencies of each class, which are 7, 6, 7, 6, 6, 7 respectively. So in this regard Tables 3 and 4 portray the comparison of the compared distributions which are highly recommended in heavy-tailed behavior. From this table, it is evident that our proposed model is the most suitable one, with least values for all statistics and highest p value for $\chi ^{2}$ statistics. Thus showing that there is a close association between the data and the proposed model.

Table 3 Maximum likelihood estimators and goodness of fit statistics of data set I

Table 4 Log likelihood (l)and information criterion for data set I

Example 2

The second data set (II) is the Wabash River Flows at Mt. Carmel (Threshold = 50,000 cfs). The data cover a period of 65 years (1928–1992) with 281 peaks that exceed 50,000 cfs with an average annual number of peaks $281/65= 4.32308$ . This data set was reported by (Rao and Hameed 2000, page 297).

Analysis of data set II: As Table 5 portrays that the data are positively skewed with high kurtosis. We have fitted all of the probability distributions by using the MLEs. The descriptive statistics are as displayed in Table 5 and the corresponding theoretical ones in Table 6.The skewness to kurtosis ratio is 0.1452. Among the competitive models the proposed model exhibits smaller values for all of the above defined statistics. For obtaining the $\chi ^{2}$ statistics we have created 10 classes via ${\mathbf {R}}$ computational package (R Core Team 2013). The created classes are $[1.26 \times 10^4, 5.48 \times 10^4$,$(5.48 \times 10^4, 6.07 \times 10^4]$,$(6.07 \times 10^4, 6.98 \times 10^4]$,$(6.98 \times 10^4, 7.87 \times 10^4 ]$,$(7.87 \times 10^4, 8.67 \times 10^4 ]$,$(8.67 \times 10^4, 1 \times 10^5 ]$,$(1\times 10^5, 1.14 \times 10^5 ]$,$(1.14 \times 10^4, 1.34 \times 10^5 ]$,$(1.34 \times 10^5, 1.60 \times 10^5 ]$,$(1.60 \times 10^5, 5.50 \times 10^5 ]$ while observed frequencies are 30, 27, 28, 28, 28, 28, 28, 31, 25, 28,  respectively. The calculated $\chi ^{2}$ for the proposed model is the least with highest p value thus indicating that the proposed model is the suitable one for such data set (Tables 7 and 8).

Table 5 Descriptive statistics for wabash river flows at Mt. Carmel

Table 6 Some theoretical measures for wabash river flows at Mt. Carmel from LDGW

Table 7 Maximum likelihood estimators and goodness of fit statistics for data set II

Furthermore, information criteria also exhibit least lost of information attitude. This indicates that proposed model use each value of the data set in an efficient manner which is not observed in other competing models.

Table 8 Log likelihood (l)and information criterion for data set II

Example 3

The third data set (III) is the maximum amount of rain in mm of Pakistani city Kalat. The data covers a period of 30 years (1981–2010) with 30 values of maximum rain fall, it was reported by Ahmad et al. (1988). The data are as follows: 32.77, 58.65, 60.71, 64.01, 42.6, 75.8, 88.6, 90.1, 97.9, 105.6, 73.1, 76.6, 78.5, 58.3, 122.5, 57.8, 546, 125.8, 50.5, 45.9, 21.7, 45.5, 38, 75.4, 168.2, 72.9, 95.8, 133.4, 71.9, 28.

Table 9 Descriptive statistics for maximum amount of rain in mm of Pakistani city Kalat

Table 10 Some theoretical measures for maximum amount of rain in mm of Pakistani city Kalat from LDGW

Analysis of data set III: Tables 9 and 10 depict that the data consist of 30 observations of rain fall data set of Pakistani city Kalat, indicating a positive skewness coupled with high kurtosis. All of the competing probability distributions are fitted by using the MLEs. The descriptive statistics are displayed in Table 9 and the corresponding theoretical ones in Table 10.The skewness to kurtosis ratio is 0.1969. The comparison as given in Table 11 indicates that the proposed model as good as the Kappa(3). Moreover, we calculate the the $\chi ^{2}$ statistics by creating 6 classes via ${\mathbf {R}}$ computational package (R Core Team 2013). The created classes are (21.7, 45], (45, 58.65] ,(58.65, 73] , (73, 81.9],(81.9, 108], (108, 546] while observed frequencies are 5, 5, 5, 5, 5, 5,  respectively.

Table 11 Maximum likelihood estimators and goodness of fit statistics for data set III

In addition to, the information criteria also suggest the proposed model exhibits the least loss of information behavior. Moreover, the Vuong test indicates that the proposed model and Dagum as well as Kappa distributions are the strong candidates for this data set. However, information criteria indicate that proposed model uses each value of the data set in an efficient manner which is not observed in other competing models (Table 12).

Table 12 Log likelihood (l)and information criterion for data set III

Example 4

The fourth data set (IV) is the annual maximum flow (in m$^{3}$/s) recorded at Kinrara, Spey for the period 1952–1982 and the number of records is 31. The data were reported by Ahmad et al. (1988). The data are as follows: 89.8, 109.1, 202.2, 146.3, 212.3, 116.7, 109.1, 80.7, 127.4, 138.8, 283.5, 85.6, 105.5, 118.0, 387.8, 80.7, 165.7, 111.6, 134.4, 131.5, 102.0, 104.3, 242.5, 214.8, 144.6, 114.2, 98.3, 102.8, 104.3, 196.2, 143.7.

Table 13 Descriptive statistics for annual maximum flow (in $m^{3}/s$) recorded at Kinrara, Spey

Table 14 Some theoretical measures for annual maximum flow (in $m^{3}/s$) recorded at Kinrara, Spey from LDGW

Analysis of data set IV: The descriptive statistics as displayed in Table 13 and the corresponding theoretical ones in Table 14. The skewness to kurtosis ratio is 0.2256, also the data having positive skewness coupled with high kurtosis. The comparison as given in Tables 15 and 16 indicates that the proposed model is the most recommended model with minimum $\chi ^{2}$ and highest p value. The $\chi ^{2}$ statistic is compiled by creating 5 classes via ${\mathbf {R}}$ computational package (R Core Team 2013). The created classes (80.7, 102], (102, 109], (109, 118] , (118, 144], (144, 202], (202, 388] along with the observed frequencies are 6, 6, 4, 5, 5, 5 respectively.

Table 15 Maximum likelihood estimators and goodness of fit statistics for data set IV

Table 16 Log likelihood (l)and information criterion for data set IV

The proposed model gives least loss of information criteria by depicting minimum values of AIC, AICC, HQIC and AICc. Moreover, the $\chi ^{2}$ indicates that the proposed model is the best one, also it can be seen again this result by looking up for the information criteria of this model.

Comparison via Vuong Test The Vuong test summary is portrayed in Table 17. In this table we have compared the competing distributions with the proposed model at 5 percent level of significance, i.e., Reject $H_{o}$ if ${Z}_{{Calculated}} \ge Z_{0.05} =1.645$ in favor of model A or Reject $H_{o}$ if ${Z}_{{Calculated}} \le Z_{0.05} =-1.645$ in favor of model B else decision cannot be made. This table indicates that the proposed model is also a reasonable choice for such data sets by portraying higher Vuong test statistic values, however it also indicates that the GP and LN3 for data set-I and the Kappa3 for data set-III are also reasonable competitor. However, an encouraging aspect of the proposed model is having least loss of information statistics and highest p value which makes it reasonable competitor of the existing models.

Table 17 Comparison via Vuong test with $Z_{{Calculated}}$

For the four data sets, we get the elements of the variance-covariance matrices of the MLES of the LDGW distribution, see Table 18. Using this table, we get the confidence intervals of the parameters of the LDGW distribution for all the data sets, see Tables 19, 20, 21 and 22. Tables 18, 19, 20, 21 and 22 are given in the “Appendix C”.

3.3 Hydrological parameters

After observing the suitability of the proposed model, we see that the LDGW distribution is the most appropriate model for analysis of the considered hydrologic data. based on this observation, we further explored some characteristics of the hydrology data, which are mentioned below.

3.3.1 Return period

Flood peaks/Heavy rain fall/High temperature do not occur with any fixed pattern in time or magnitude. Time intervals between floods vary. The definition of return period is the average of these inter-event times between flood events (Rao and Hameed 2000). This implies that large floods/Heavy rain falls/High temperatures naturally have large return periods and vice versa. Such definition of the return periods may not involve any reference to probability. However, a relationship between the probability of occurrence of a flood and its return period can be justified. A given flood $x_{T}$ with a return period T may be exceeded once in T years. Hence the probability of exceedance is ${P}({X}>x_{T})=\frac{1}{T}$. Now, a return level with a return period of $T=1/p$ is a high threshold $x_{T}$ (e.g., annual peak flow of a river) whose probability of exceedance is p. For this purpose the return level $x_{T}$ of the LDGW distribution is given by

Fig. 6

Return periods of the competing models for data set-I and II

Fig. 7

Return periods of the competing models for data set-III and IV

$$\begin{aligned} x_{T}=\left( \left\{ 1-\left( \dfrac{\theta +\ln \left\{ (1-e^{\theta })\left( 1+\dfrac{1}{1-e^{\theta }} -p^{-\frac{1}{\beta }}\right) \right\} }{\theta }\right) ^ {-\lambda }\right\} /\lambda \right) ^{\frac{1}{\theta }}, \end{aligned}$$

where $x_{T}>0$ and $T\ge 1$. Table 23 provides estimates of the return level $x_{T}$ for the data sets I, II, III and IV, respectively, for the return periods $T=2,$  5,    $10,\, 25,\,50,\, 100, \, 200 \,$ years. Moreover, the return periods for some largest values of all the data sets are reported in Tables 24 and 25 and computed using $T=\dfrac{1}{P(x_{T})}$, where $P(x_{T})=S(x_{T})$ is the survival function of the LDGW distribution given by

$$\begin{aligned} {S}_{{LDGW}}(x|\lambda , \theta ,\beta )= \left( 1+\dfrac{e^{-\theta +\theta \left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) ^{-\beta }, \end{aligned}$$

where ${\hat{\theta }}$, ${\hat{\lambda }}$ and ${\hat{\beta }}$ denote the MLEs of the LDGW distribution for the corresponding data set. Tables 23, 24 and 25 are given in the “Appendix C”. Moreover, comparison on the basis of return period is also depicted in Figs. 6 and 7 for the above mentioned data sets. On the basis of this comparison, we can conclude that the LDGW distribution shows a significant larger and realistic (neither too large nor too short) return period as compared to competing models.

4 Conclusion

We have developed and studied a new hydrologic probability model known as the LDGW distribution, which can effectively be used in modeling the higher kurtosis data sets, and also generates realistic return return periods for all types of environmental data irrespective of any region. It can also be used in modeling the data with bathtub or upside down bathtub or increasing hazard rate shapes. Furthermore, some properties of the proposed model are studied. Finally, the hydrological applications of the proposed model to real-life data sets demonstrate its competence, usefulness and applicability for future use. Finally, we recommend this model for data having much larger kurtosis typically greater than 20 and skewness to kurtosis ratio less than 0.29.

Appendices

Appendix-A

Proof

Necessity:

If $X\sim LDGW(\lambda ,\theta ,\beta )$, with a cdf defined by Equation (1), then its hrf can be expressed as

$$\begin{aligned} h(x)=h_{{LDGW}}(x|\lambda , \theta , \beta )=\frac{e^{-\theta +\theta \left( 1-\lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}} x^{-1+\theta } \beta \theta ^2 \left( 1-x^{\theta } \lambda \right) ^{-1-\frac{1}{\lambda }}}{ \left( e^{\theta }-1\right) \left( 1+\frac{e^{-\theta +\theta \left( 1-\lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) }, \end{aligned}$$

where $x>0$, $\lambda \le 0$, $\alpha >0$ and $\beta >0$.

Now, differentiating the logarithmic form of the hrf with respect to x, we get

$$\begin{aligned}&\frac{d \ln h(x)}{dx} =\frac{\theta -1}{x}+\theta ^{2}x^{\theta -1}\left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }-1} +\left( \frac{1}{\lambda }+1\right) \frac{\lambda \theta x^{\theta -1}}{1-\lambda x^{\theta }}\\&\qquad -\frac{e^{-\theta +\theta \left( 1-\lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}} x^{-1+\theta } \beta \theta ^2 \left( 1- \lambda x^{\theta } \right) ^{-1-\frac{1}{\lambda }}}{ \left( e^{\theta }-1\right) \left( 1+\frac{e^{-\theta +\theta \left( 1-\lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) }, \frac{h^{\prime }(x)}{h(x)}-\left( \frac{1}{\lambda }+1\right) \frac{\lambda \theta x^{\theta -1}}{1-\lambda x^{\theta }}\\&\quad =\frac{\theta -1}{x}+\theta ^{2}x^{\theta -1}(1-\lambda x^{\theta })^{-\frac{1}{\lambda }-1} -\frac{e^{-\theta +\theta \left( 1-\lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}} x^{-1+\theta } \beta \theta ^2 \left( 1-\lambda x^{\theta } \right) ^{-1-\frac{1}{\lambda }}}{ \left( e^{\theta }-1\right) \left( 1+\frac{e^{-\theta +\theta \left( 1-\lambda x^{\theta } \right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) }, \end{aligned}$$

which after some algebraic manipulations we get Equation(8).

Sufficiency:

Suppose Equation(8) holds, then it may be re-written as

$$\begin{aligned}&\frac{h^{\prime }(x)}{(h(x))^{2}} =\frac{\left( 1+\dfrac{e^{-\theta +\theta \left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) ^{-\beta }}{\left[ \beta \theta ^{2} \left( 1+\dfrac{e^{-\theta +\theta \left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) ^{-\beta -1} \dfrac{e^{-\theta +\theta \left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }}} x^{\theta -1}\left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }-1}}{e^{\theta }-1}\right] ^{2}} \\&\qquad \times \frac{d\left\{ \beta \theta ^{2} \left( 1+\dfrac{e^{-\theta +\theta \left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) ^{-\beta -1} \dfrac{e^{\theta -\theta \left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }}} x^{\theta -1}\left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }-1}}{e^{\theta }-1}\right\} }{dx}+1. \end{aligned}$$

From the above differential equation, we have

$$\begin{aligned} h(u)=\frac{e^{-\theta +\theta \left( 1-\lambda u^{\theta }\right) ^{-\frac{1}{\lambda }}} u^{-1+\theta } \beta \theta ^2 \left( 1-\lambda u^{\theta } \right) ^{-1-\frac{1}{\lambda }}}{ \left( e^{\theta }-1\right) \left( 1+\frac{e^{-\theta +\theta \left( 1-\lambda u^{\theta }\right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) }. \end{aligned}$$

(10)

Integrating the Equation (10) from 0 to x we get

$$\begin{aligned} -\ln (1-F_{{LDGW}}(x|\lambda , \theta , \beta ))=-\ln \left( \left( 1+\dfrac{e^{-\theta +\theta \left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1} \right) ^{-\beta }\right) , \end{aligned}$$

which after simplification yields

$$\begin{aligned} F_{{LDGW}}(x|\lambda , \theta , \beta )=1-\left( 1+\dfrac{e^{-\theta +\theta \left( 1-\lambda x^{\theta }\right) ^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) ^{-\beta }. \end{aligned}$$

This completes the proof. $\square$

Appendix-B

$$\begin{aligned}&\frac{\partial \ell (\Theta )}{\partial \theta } =-n-\frac{e^{\theta } n}{e^{\theta }-1}+\frac{2 n}{\theta }+\sum _{i=1}^n \ln (x_i)+\left( 1+\frac{1}{\lambda }\right) \sum _{i=1}^n \frac{\lambda \ln (x_i) x_i^{\theta }}{1-\lambda x_i^{\theta }}\\&\qquad \qquad \quad +\theta \sum _{i=1}^n \ln (x_i) x_i^{\theta } \left( 1-\lambda x_i^{\theta }\right) {}^{-1-\frac{1}{\lambda }}+\sum _{i=1}^n \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }}-(1+\beta )\\&\qquad \quad \times \sum _{i=1}^n \frac{-\frac{e^{\theta } \left( -1+e^{-\theta +\theta \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }}}\right) }{\left( -1+e^{\theta }\right) ^2}+\frac{e^{-\theta +\theta \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }}} \left( -1+\theta \ln (x_i) x_i^{\theta } \left( 1-\lambda x_i^{\theta }\right) {}^{-1-\frac{1}{\lambda }}-\left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }}\right) }{-1+e^{\theta }}}{1+\frac{e^{-\theta +\theta \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}}=0,\\&\frac{\partial \ell (\Theta )}{\partial \lambda } =\frac{1}{\lambda ^2}\sum _{i=1}^n \ln (1-\lambda x_i^{\theta })+\left( 1+\frac{1}{\lambda }\right) \sum _{i=1}^n \frac{x_i^{\theta }}{1-\lambda x_i^{\theta }}\\&\qquad \qquad + \theta \sum _{i=1}^n \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }} \left( \frac{\ln (1-\lambda x_i^{\theta })}{\lambda ^2}+\frac{x_i^{\theta }}{\lambda \left( 1-\lambda x_i^{\theta }\right) }\right) \\&\qquad \qquad -(1+\beta ) \sum _{i=1}^n -\frac{e^{-\theta +\theta \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }}} \theta \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }} \left( \frac{\ln (1-\lambda x_i^{\theta })}{\lambda ^2}+\frac{x_i^{\theta }}{\lambda \left( 1-\lambda x_i^{\theta }\right) }\right) }{\left( e^{\theta }-1\right) \left( 1+\frac{e^{-\theta +\theta \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right) }=0 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial \ell (\Theta )}{\partial \beta }=\frac{n}{\beta }-\sum _{i=1}^n \ln \left[ 1+\frac{e^{-\theta +\theta \left( 1-\lambda x_i^{\theta }\right) {}^{-\frac{1}{\lambda }}}-1}{e^{\theta }-1}\right] =0. \end{aligned}$$

Appendix-C

See Tables 18,19, 20, 21, 22, 23, 24 and 25.

Table 18 Variances and co-variances of MLEs for data set-I to IV

Table 19 Confidence interval with level of significance $\alpha$ for data set-I

Table 20 Confidence interval with level of significance $\alpha$ for data set-II

Table 21 Confidence interval with level of significance $\alpha$ for data set-III

Table 22 Confidence interval with level of significance $\alpha$ for data set-IV

Table 23 Return level estimates $\hat{x_T}$ for T of data set-I to IV

Table 24 Return periods for some largest values of data set-I and II

Table 25 Return periods for some largest values of data set-III and IV