Harvesting in a Fishery with Stochastic Growth and a Mean-Reverting Price

Abstract

We analyze a continuous, nonlinear bioeconomic model to demonstrate how stochasticity in the growth of fish stocks affects the optimal exploitation policy when prices are stochastic, mean-reverting and possibly harvest dependent. Optimal exploitation has nonlinear responses to the price signal and should be conservative at low levels of biological stochasticity and aggressive at high levels. Price stochasticity induces conservative exploitation with little or no biological uncertainty, but has no strong effect when the biological uncertainty is larger. We further observe that resource exploitation should be conservative when the price reverts slowly to the mean. Simulations show that, in the long run, both the stock level and the exploitation rate are lower than in the deterministic solution. With a harvest-dependent price, the long-run price is higher in the stochastic system. The price mean reversion rate has no influence on the long-run solutions.

1 Introduction

Resource management decisions made in a deterministic environment are suboptimal for resources that are inherently stochastic in nature, even after assuming risk neutrality and constant prices (Hannesson 1987). In particular, fishery management decisions are fraught with uncertainty, originating in both the biological and economic systems. We aim to advance the insight into management under multiple sources of uncertainty by providing a unified analysis of management decisions when the stock growth and the market price are stochastic. Stochastic terms that govern the behavior of both state variables are introduced into the dynamic equations. To capture likely nonlinearities in net benefits from the resource exploitation, we impose a quadratic objective function. While the setup with multiple uncertainties is of interest in itself, the price dynamics are of particular interest because relatively little attention has been devoted to rational responses to price fluctuations in the fisheries economics literature. In contrast, a comprehensive literature deals with dynamics and stochasticity in the biology.

Optimal fisheries management under multiple sources of uncertainty has attracted attention in recent decades. Reed (1979) and Clark and Kirkwood (1986) lay down the foundations for subsequent work, studying single sources of uncertainty. Roughgarden and Smith (1996) discuss multiple sources of uncertainty and their potential role in the collapse of fisheries; the focus on collapse has become a staple of later work. More recent articles of particular relevance are Sethi et al. (2005), Nøstbakken (2006), Sarkar (2009), and Poudel et al. (2013). Sethi et al. (2005) study optimal escapement levels in a model that includes uncertainty in growth, stock measurement and policy implementation. In their model, growth and implementation uncertainty have only small effects when compared with the deterministic solution. Measurement uncertainty has larger effects. One interesting result is that optimal escapement increases with the measured stock level, resembling the solution from a nonlinear model. The result contrasts with the constant escapement level in the deterministic model. Nøstbakken (2006) analyzes policy switching curves in the price–stock space under price and stock uncertainty. When policy switching is costly, entry and exit curves will differ. The difference is driven in part by the uncertainty and in part by the switching cost.

Both Sethi et al. (2005) and Nøstbakken (2006) assume a linear objective function. Sarkar (2009), on the other hand, studies a nonlinear objective function and his study is thereby more similar to ours. In a real option framework, he finds that the optimal policy has traits similar to pulse fishing regimes that typically arise from linear models. He calculates the optimal harvest trigger (the stock level where it is optimal to exercise the option to harvest); not unlike the entry curve in Nøstbakken (2006). Sarkar (2009) also calculates the optimal harvest size that implicitly defines an exit point in the state space; not unlike the exit curve in Nøstbakken (2006). The findings in Sarkar (2009) align with the analysis in Nøstbakken (2006), but the latter extends to uncertainty in price and is therefore the prominent work of comparison for our analysis. (Sethi et al. 2005 study different types of uncertainty. While our framework applies to studies of the same types of uncertainty, it requires a different interpretation of the stochastic term and is beyond the scope of this article.)

In summary, our setup compares to Nøstbakken (2006) in terms of dimensionality, where both price and stock are stochastic and treated as state variables. However, in contrast to Nøstbakken (2006), who studies a linear objective function when price follows a geometric Brownian motion, we analyze a nonlinear objective function when the price process is mean-reverting and harvest dependent. In terms of nonlinearity, our setup compares to Sarkar (2009). While we use a different functional form than him, the conceptual frameworks are similar and, as we discuss further below, relate to work by Boyce (1995), Grafton et al. (2006) and others. Thus, however incrementally, we aim to advance the complexity of cutting-edge fisheries economics models toward arguably more realistic models subject to a unified analysis of multiple sources of uncertainty.

Our arguably more realistic model produces results that require careful consideration of the inherent economic intuition. For example, the effect of increasing stochasticity in the Sarkar (2009) model leads to an increase in the harvest trigger and a decrease in the harvest size; the responses are motivated by caution and are found to be consistent with real-option theory. In our model, small levels of stochasticity lead to moderation in the harvest rule while higher levels lead to an aggressive and shortsighted harvest rule. Both effects are consistent with economic intuition; when transitioning from no uncertainty to a low level of uncertainty, moderation motivated by caution seems reasonable; when transitioning further to high levels of uncertainty, moderation, which essentially is investment, no longer pays off and the best course of action is shortsighted, aggressive harvesting. The important point is that there is not necessarily a unidirectional best response to a given change in the setup (such as increasing stochasticity). Alas, there are no simple rules-of-thumb when dealing with realistically complex systems. And, of course, we admit that our model contains a number of simplifications that require significant leaps of faith in order to apply to real-world fisheries management; the right mix and balance between simplifications and realism in fisheries management models will keep scientists and economists busy for years to come. Nevertheless, from our study, it becomes clear that once we leave the simple models behind, each particular system requires individual study, which suggests that a more positive focus would be in order. What we provide is a step towards a unified and robust framework for the study of fisheries management problems that encompass nonlinearities and multiple sources of uncertainty.

In terms of method, we apply dynamic optimization to a nonlinear, continuous time model with two stochastic state variables, where the objective function is nonlinear in the control variable. Further, the control variable is present in the dynamic equations such that the differential equation governing the value function is nonlinear, and the control variable cannot in general be treated as a constant. This last point is crucial and demarcate our work from the typical approach in real options. In real options, one usually considers impulse controls that are governed by trigger levels (see Sarkar (2009) and Marten and Moore (2011) for relevant examples). The methodological advantage of impulse controls is that they can be treated as constants in the dynamic equations, and the corresponding differential equations that govern the value function take the form of linear differential equations, for example of the Euler type that has known closed form solutions. Impulse controls have a conceptual disadvantage, however, in that how they translate into real-world fisheries policy is unclear, and the inherent dynamics, where changes to the system occur as shifts in the state variables when impulses are triggered, is unrealistic in for example fisheries models.

Several articles from the resource economics literature, in addition to those discussed above, are methodologically related to our work. For example, Mason (2012) provide a formal analysis of equilibrium in non-renewable resource markets with stochastic prices. While the analysis features a two-dimensional problem, there is only a single stochastic driver in the model. Poudel et al. (2013) study a fisheries fleet investment problem with two stochastic drivers, one related to the biology and one related to the economy. Notably, both Mason (2012) and Poudel et al. (2013) are formulations in continuous time.

There are a number of studies of optimization problems in discrete time formulations; in what follows, we can only mention a few of them. Discrete time formulations are subject to a related, but different methodological framework. Costello and Polasky (2008) analyzes the optimal harvest of a resource distributed in patches. Their special model setup leads to constant escapement policies where harvest increase linearly with stock size over a given threshold. Also the optimization problem in the aforementioned Sethi et al. (2005) is formulated in discrete time. The analysis of the social cost of climate change by Cai et al. (2013) feature a high-dimensional problem with two stochastic drivers that is solved by iterating backwards from an artificial finite time horizon. Another climate-related study in discrete time is Crost and Traeger (2013), who study a problem with deterministic dynamics, but where the objective function is subject to uncertainty.

2 The Bioeconomic Model

We employ a surplus production model in continuous time. The continuous framework is not as common as the discrete formulation in fisheries models, but both Nøstbakken (2006) and Sarkar (2009) use continuous time. Stochastic fish stock dynamics can be obtained by adding a volatility (or stochastic) term in the incremental description of the stock dynamics (Sandal and Steinshamn 1997a):

$$\begin{aligned} dx=\left( {f\left( x \right) -h} \right) \,dt+\sigma _x \left( x \right) \textit{dB}_x \end{aligned}$$

(1)

where $x$ is the fish stock and $h$ is the nonnegative harvest rate. $f(x)$ is the drift component of the natural growth function for the fish stock $x$ and is a generalized logistic growth function that is quasi-concave with roots in zero and $x=k$. $k$ is the carrying capacity of the environment. (Note that with the stochastic formulation, stock levels above the carrying capacity may occur but will not persist.) The term $\sigma _x \left( x \right) \textit{dB}_x$ represents the incremental stochastic part of the stock–growth relationship. We apply the functional form $\sigma _x \left( x \right) =\sigma _{0x}\,x$, with $\sigma _{0x}$ being a constant volatility coefficient. The term $dt$ is the time increment and $\textit{dB}_x$ represents the incremental Brownian motion that is independent and identically distributed with mean zero and variance $dt$.

The incremental, additive noise formulation is a general Wiener process description and contains the multiplicative case, as can be seen from the following. Let $\varepsilon$ be standard white noise, that is $dB_1 =\varepsilon dt$. It follows that:

$$\begin{aligned} dx=\left[ {\left\{ {r\left( x \right) +v\left( x \right) \varepsilon } \right\} g\left( x \right) -h} \right] dt+\sigma _0 \left( x \right) \textit{dB}_0 \equiv \left[ {f\left( x \right) -h} \right] dt+\sigma \left( x \right) \textit{dB} \end{aligned}$$

and

$$\begin{aligned} f\left( x \right)&\equiv r\left( x \right) g\left( x \right) \\ \sigma \left( x \right) \textit{dB}&\equiv v\left( x \right) g\left( x \right) \varepsilon dt+\sigma _0 \left( x \right) \textit{dB}_0 \equiv \sigma _0 \left( x \right) \textit{dB}_0 +\sigma _1 \left( x \right) \textit{dB}_1 \end{aligned}$$

The transformation holds even for a completely general nonautonomous Wiener process. Thus, if noise is multiplicative as in the example above, we can rewrite the system such that the noise is additive and generally our approach applies.

When the volatility $\sigma _x (x)$ is increasing in $x$, we have what we call a downward drag in the growth, that is, in the expected drift. In our case, where $\sigma _x \left( x \right) =\sigma _{0x} x$, we can transform Eq. (1) with $z=\ln x$ and obtain the following dynamic equation:

$$\begin{aligned} dz=\left( {\frac{f\left( x \right) -h}{x}-\frac{1}{2}\sigma _{0x} ^{2}} \right) dt+\sigma _{0x} \textit{dB} \end{aligned}$$

where the drift expression has a negative term that increases in the volatility coefficient $\sigma _{0x}$. Downward drag makes intuitive sense: after a negative stochastic movement, recovery requires a less likely stochastic movement than the movement required to recover the initial state after a positive stochastic movement. One consequence of the downward drag that will be of importance is that more paths have lower growth than the expected surplus growth as the volatility coefficient increases. Lund (2002) provides further analysis and discussion of downward drag and other stochastic effects in natural resource management models.

Let $y$ be the spot price of fish at the time of decision making and let $p(h)$ be an underlying, long-run expected price that may depend on the harvest level $h$. Further, let the spot price evolve as a mean-reverting stochastic process with reversion toward $p\left( h \right)$. When compared with the typical geometric Brownian motion model, a mean-reverting price better reflect basic, microeconomic ideas about supply behavior (see Insley 2002 and references therein). The setup allows us, in the simplest way we can think of, to combine noise into the relationship between quantity and price, while maintaining a typical tendency of demand behavior that is often empirically observed.

We can model our setup by the following process:

$$\begin{aligned} dy=-\alpha \,\left( {y-p(h)} \right) \,dt+\sigma _y \left( y \right) \textit{dB}_y \end{aligned}$$

(2)

The parameter $\alpha$ is the rate of reversion. The drift term $-\alpha \left( {y-p(h)} \right)$ consists of the distance between the current price $y$ and the possibly harvest-dependent reversion price $p(h)$, multiplied by the reversion rate $\alpha$. Thus, the stochastic spot price drifts towards the long-run expected price, which may change with the harvest level. The spot price is as such drifting towards a possibly moving target. The drift term will be positive if $y<p(h)$, resulting in an expected upward movement in price $y$. If $y>p(h)$, the drift term is negative, resulting in an expected downward movement in price $y$. The term $\sigma _y \left( y \right) \textit{dB}_y$ in (2), with $\sigma _y \left( y \right) =\sigma _{0y} y$, is the stochastic part of the price evolution; $\sigma _{0y}$ is a constant volatility coefficient.

We assume that the two Brownian noise drivers $(B_x ,B_y )$ in the system (1–2) are uncorrelated. We find the assumption reasonable because one driver represents biological noise and the other represents noise from the economy. The price process (2) is a generalization of the Orstein–Uhlenbeck process, where we replace the constant volatility with the level-dependent volatility. In comparison, Nøstbakken (2006) invokes the standard geometric Brownian motion as the price process. We apply the generalized Orstein–Uhlenbeck process because it lets us include the price–quantity relationship in $p(h)$ and because, in probability, the process has limited support in infinite time, something geometric Brownian motion has not.

Note that the mean (or long-term) price $p(h)$ may depend upon the harvest level, but in a noisy fashion, see (2). We have two main reasons for using the model above. First, it yields a more adaptive framework that applies to a wider range of real-world situations, where prices and harvest levels have empirical relationships; see, for example, Arnason et al. (2004). In situations with an exogenous price, $p(h)$ can simply be set to a constant and our general approach still applies. (As discussed below, key results also holds.) Second, the model likely better reflects the scenario faced by many high-level fishery management bodies, such as regional fishery management organizations, that primarily undertake fisheries management with the general biology and the economy of the direct users in mind (Grainger and Parker 2013). Further, the demand schedule $p(h)$ contributes to a nonlinear model (we find pulse fishing, which usually arises in linear models, undesirable) and, as highlighted by Grafton et al. (2000), the actual specification of functional forms is not as important as their ability to model the world.

The standard assumption is that the sole owner seeks to maximize the expected net present value from the fishery over an infinite time horizon, subject to the dynamic constraints in (1) and (2). We can then formulate the economic part of the dynamic optimal control problem through the expected present value given by:

$$\begin{aligned} J\left( {h,x_0 ,y_0 } \right)&= \hbox {E}\left[ {\mathop \int \nolimits _0^\infty e^{-\delta t}\,\pi \left( {h,x,y} \right) dt} \right] \nonumber \\ x\left( {t=0} \right)&= x_0 ,\,y\left( {t=0} \right) =y_0 \end{aligned}$$

(3)

The function $\pi \left( {h,x,y} \right)$ is the current payoff rate function from the harvest of fish that depends on the stock, harvest and price. $\hbox {E}$ is the expectation operator and the nonnegative parameter ${\updelta }$ is the discount rate. The dynamic optimization problem can be written as:

$$\begin{aligned} V\left( {x,y} \right) =\mathop {\max }\limits _{h\ge 0} J(h,x,y) \end{aligned}$$

(4)

subject to (1) and (2). The optimal harvest is found by solving the Hamilton–Jacobi–Bellman (HJB) equation for the given optimal control problem (4). The current value formulation of the HJB equation is given by:

$$\begin{aligned} \delta V&= \mathop {\max }\limits _{h\ge 0} \bigg \{ \pi \left( {h,x,y} \right) +\left( {f\left( x \right) -h} \right) V_x +\left( {-\alpha \,(y-p(h)} \right) V_y\nonumber \\&\quad +\,\frac{1}{2}\,\sigma _{0x} ^{2}\,x^{2}\,V_{xx} +\frac{1}{2}\,\sigma _{0y} ^{2}\,y^{2}\,V_{yy}\bigg \} \end{aligned}$$

(5)

The subscripts of $V$ denote partial derivatives. The formal (closed form) solution of the HJB equation for the multidimensional and stochastic problem is elusive, and we resort to a numerical approximation.

The model above poses the fisheries management problem in a two-dimensional state space, and thus represents a unified approach to multiple sources of stochasticity. The dimensionality make the analysis more demanding, but has merit because intuitions established in lower dimensional models may not hold in higher dimensions. The point is illustrated by Sandal and Steinshamn (2010), who show that the two-dimensional harvest rate in a predator–prey model is highly nonlinear and has surprising features. For example, in parts of the state space, the optimal harvest rate declines as the biomass of the target specie increases.

2.1 The Numerical Approximation

We have a two-dimensional nonlinear model with two state variables (stock and price) and one control variable (harvest) in continuous time. Explicit solutions do in general not exist. In practice, a numerical approximation is the only viable alternative. The Markov chain approximation approach is an effective and relatively simple method (Song 2008), is based on probability theory, and requires that the HJB Eq. (5) can be approximated by an appropriate controlled Markov chain approach. Kushner and Dupuis (2001) provide numerical algorithms for stochastic optimal control problems. They deal with the convergence of numerical methods and show that the value function to which the approximation converges is the optimal value function.

The numerical technique entails discretizing the state space for the HJB control problem (5), constructing transition probabilities for the controlled Markov chain by applying a finite difference technique, and then iterating on the HJB equation with an initial guess $V_0$ for the value function. In the two-dimensional state space, we establish a uniform grid consisting of 10,000 grid points. The optimal stochastic interpolation time is proportional to the size of the steps in the grid (Kushner and Dupuis 2001) and is notably not a free parameter. The transition probabilities describe the likelihood of the stochastic process jumping between neighboring nodes in the grid and reflect the underlying stochastic processes. The iterations in policy and value functions are carried out until the value function converges to the optimal value function. We assume the system has converged when the maximum residual numerical error is smaller than $1\,e^{-16}$ in absolute value for a given grid. It implies that the value function and harvest policy are correct for the particular finite-state discrete problem. In the base case, convergence requires approximately 20,000 iterations. We tested convergence by putting a test run through 500,000 iterations. The results from the test run were indistinguishable from the base case (the test run results lay within the residual error of the base case). In the iteration procedure, we exploit that we can derive the inner optimum of the HJB equation with respect to the control variable (see appendix); the inner solution is compared to boundary solutions.

Our numerical approach is conceptually similar to that of Sethi et al. (2005), who go into some further detail. In the interest of space, and because the approach is well known, we refrain from reiterating further details of the numerical scheme. Kushner and Dupuis (2001) provide expressions for transition probabilities and detailed discussions of the convergence scheme.

2.2 Parameters and Functional Forms

Up until now, our treatment has been general, and has basically presented a framework of analysis. Apart from the introduction of the Orstein–Uhlenbeck—inspired price process and the note on the generality of the additive noise formulation, our setup is standard in the fisheries economics literature. In order to apply the numerical approximation and solve the HJB equation, however, it is necessary to specify functional forms and parameter values. For the sake of simplicity, we base our parameter values and functional forms on empirical work. As noted by Zhang and Smith (2011), a unified approach is necessary to ensure consistency of the full model and we do not suggest that our specific results apply directly to any fishery. Our results serve merely to demonstrate the viability of the approach and the potential outcomes from a complex and nonlinear, but still relatively simple, model. Notwithstanding, when we base parameters and functional forms on existing, empirical work, it increases the likelihood that our parameterized model sits in a relevant part of the parameter space.

For convenience, we look at the Barents Sea cod and base functional forms and parameter values on the study by Arnason et al. (2004). (Agnarsson et al. (2008) extended the study to include stochastic effects.) The natural growth function in (1) takes the form $f\left( x \right) =rx^{2}(1-x/k)$, which is a modified logistic growth function with noncritical depensation. The modified logistic growth function observes what is known as the Allee effect (Stephens et al. 1999), which in our simple model means that the population growth is weakened at low population levels (a supplemental appendix, available from the authors, provides some further discussion of the biological motivation). $r$ is an intrinsic growth rate and $k$ is the environmental carrying capacity. The long-run expected price that goes into (2) is given by $p\left( h \right) =p_0 -\gamma _2 h$. The stream of profits in (3) is modeled as $\pi \left( {x,h} \right) =yh-c(x,h)$, where costs are given by $c\left( {x,h} \right) =c_1 h/x+\gamma _1 h^{2}$. Nonlinearities in both the long-run price and harvest costs make the problem nonlinear in the control variable (the harvest rate). Similar nonlinearities arise in a range of different fisheries models (Boyce 1995; Liski et al. 2001; Grafton et al. 2006; Sarkar 2009). Motivations for nonlinearities differ, with examples including fixed costs (Sarkar 2009) and market conditions (Boyce 1995; Grafton et al. 2006). The particular nonlinearities in our model are not as important as our demonstration of how they do not impede our ability to solve and analyze the model. To demonstrate robustness across functional forms, we solve the model under different functional forms and parameter values in the supplemental appendix. In particular, we solve the model with pure (unmodified) logistic growth and with no harvest dependence in $p(h)$. Notably, all main features of the results persist under the alternative specifications.

Table 1 lists parameter values. Relevant estimates of the volatility coefficients $\sigma _i$ and the price reversion parameter $\alpha$ are not readily available. We explore a range of possible values for the volatility coefficients. For the price reversion speed, we have a rough estimate (for a standard mean-reverting price process) based upon data from the International Council for the Exploration of the Sea. (Regressing price changes on the previous period price yields the coefficient $-0.5835$, standard error 0.2673, and $R^{2}=0.3461$, which implies a reversion speed of 0.5835.)

Table 1 Parameter values

3 Results and Discussion

First, we describe the optimal harvest rate in our model, in both the deterministic and stochastic settings. The optimal harvest rate is a surface in the stock–price state space and is of classical feedback type because of the autonomous model. To shed further light on the properties of the optimal harvest rate and to make the comparison of solutions for different levels of stochasticity as straightforward as possible, we present contour plots of the harvest rate in different scenarios. Further, we study the optimal solution with either stochastic elements active (that is, with one volatility coefficient non-zero) and with both stochastic elements active (both volatility coefficients non-zero). We study different combinations of values for the volatility coefficients in both cross sections of the optimal solution and in plots of the zero contour. Our study of all these different aspects of the optimal harvest rate yields insights into the general behavior of the solution and allows us to identify technical and economic intuitions for the observed behavior. To strengthen our analysis, we also analyze how sensitive the solution is to variations in some key parameters.

Further, we find it of interest to describe the dynamic behavior of the system in time. The optimal harvest rate tells us the best course of action at any given stock level and spot price, but how the system will evolve in time cannot be fully understood from the harvest rate alone, as the dynamic behavior involves both the state dependent harvest rate and the dynamic equations in the model. We provide some statistics on how the system settles at the end of a long simulation horizon; we also draw some simulated paths through time and study paths in a phase diagram. Finally, we study the sensitivity of the long-term behavior to changes in parameter values.

3.1 The Optimal Solution

Before we consider solutions to the stochastic problem in Eq. (5), we find it instructive to study the solution to the deterministic problem (where the stochastic diffusion terms are set to zero; $\sigma _{0x} =\sigma _{0y} =0)$. Figure 1 shows the optimal harvest rate for the deterministic model. The figure shows the harvest surface as a feedback solution in the stock–price state space, with stock size along the right axis, the spot price along the left axis and the optimal harvest rate along the vertical axis. At small stock levels (smaller than approximately one million tons), the harvest rate is zero for any spot price; density-dependent harvest costs make it very costly to harvest at low stock levels, but the zero harvest rate at low stock levels also depends on further nonlinear properties discussed below. At high stock levels (larger than two million tons), the harvest rate increases approximately linearly with the spot price. At intermediate stock levels, the solution is more complex, and we will explore this territory further below. For all spot price levels, the harvest rate has the familiar concave shape (once it turns positive) as a function of the stock level; see, for example, Sandal and Steinshamn (1997a) for similar solutions in a model with a similar objective function. In most cases, a higher price yields a higher optimal harvest rate, and for small price levels, the stock level has to be very large to make any harvest viable. Contours of the optimal harvest rate are similar in shape to the entry and exit curves in Nøstbakken (2006). In Nøstbakken (2006), the shape is driven by the density-dependent costs; in our model, the shape is driven in part by density-dependent costs and in part by other, nonlinear effects that we will delve into below. On another note, the solution in Fig. 1 leads to a gradual and adaptive (feedback) fishing process, while both Nøstbakken (2006) and Sarkar (2009) predict pulse fishing.

Fig. 1

Deterministic optimal harvest rate as a feedback policy in price–stock state space

Figure 2a shows a contour plot of the solution in Fig. 1. The white curve is the zero contour, that is, where the harvest rate switches from zero to a positive rate. Further, the harvest rate increases with 75 thousand tonnes per year between each contour. The contour plot shows that, at low price levels, an increase in price yields a higher harvest rate, but the effect does not necessarily occur at higher price levels. At price levels higher than approximately 13 (that is, approximately $p_0 )$ and at intermediate stock levels, the optimal harvest rate decreases in price. We call this effect backward folding, as the contours seem to fold backward. A technical explanation of backward folding is that while the gradient of the harvest rate in the price dimension ($\partial h/\partial y)$ is positive at low spot prices, it turns negative at higher spot prices, and it only occurs in parts of the state space (at moderate stock levels). Less technically, backward folding means that, in parts of the state space, the optimal response in the harvest rate to an increasing spot price is to reduce harvest. We find that backward folding does not conform to our common intuition (we expected that the harvest rate would increase with an increasing price, as it does in most of the state space) and that it is of interest to investigate further. First, we discuss our technical understanding of backward folding before discussing its economic intuition.

Fig. 2

The effect of stochasticity on the optimal harvest rate: a deterministic model $({\upsigma }_{0x} ={\upsigma }_{0y} =0)$, b stochastic model $({\upsigma }_{0x} ={\upsigma }_{0y} =0.5)$, c stochastic model $({\upsigma }_{0x} ={\upsigma }_{0y} =0.9)$, and d stochastic model $({\upsigma }_{0x} ={\upsigma }_{0y} =1.5)$

To understand the technical or mathematical intuition of backward folding, it is instructive to consider the optimal harvest rate in the limit where the spot price goes to infinity. In the limit, the nonlinearity of the objective function disappears as the first term dominates the second. That is, in the limit, the objective function is linear in the harvest rate, and the optimal harvest rate is the bang–bang policy. The critical stock level where the harvest rate would switch from the minimum to the maximum viable rate is possible to derive. We refrain from carrying out the derivation; suffice it to say that it is larger than the maximum sustainable yield stock level because of the density-dependent costs (Sandal and Steinshamn 1997b). Thus, in the limit, the optimal harvest rate is zero for all stock levels below the maximum sustainable yield level and, as the spot price increases, the harvest rate must approach the limit solution. Therefore, we explain backward folding as a consequence of the weakening or breakdown of the nonlinear structure in the objective function when the spot price increases.

We note that backward folding does not depend on the mean-reverting price property and, consequently, backward folding should be observable in similar nonlinear models where the nonlinear feature degenerates as the price increases. Indeed, we have solved our model under alternative specifications and parameterizations, and backward folding persist across the different models. The results are reported in the supplemental appendix. Backward folding will not appear in the Nøstbakken (2006) model because her model is linear. On the other hand, backward folding could occur in the Sarkar (2009) model if it was extended to the price dimension.

Backward folding, the fall in the optimal harvest rate as the spot price increases, has two positive effects on the economy in our model. First, a lower harvest rate conserves the fish stock and thereby reduces future harvest costs because harvest costs are density dependent. This temporal trade-off makes backward folding sensitive to the discount rate and the effect will vanish at high discount rates. Indeed, the myopic solution ($h_m )$ has no backward folding, a result that is straightforward from the solution formula that has level curves which are proportional to $1/x$:

$$\begin{aligned} h_m =\max \left( {\frac{y-{c_1 }/x}{2\gamma _1 },0} \right) \end{aligned}$$

Second, a lower harvest rate curbs the downward drift in the spot price. This effect is readily seen from inserting the expression for $p\left( h \right) =p_0 -\gamma _2 h$ in Eq. (2) and observing that the drift is negatively linear in harvest. Both effects improve the profitability of the future fishery at the expense of a lower, immediate return. According to our numerical analysis, the two positive effects overwhelm the negative effect of reducing the current flow of profits at high prices and intermediate stock levels. In the appendix, we derive a sufficient criterion on the curvature of the value function for backward folding to occur. We further show numerically that the criterion holds in the part of the state space where backward folding occurs.

The remaining panels in Fig. 2b–d, show the effect of stochasticity on the optimal solution. In the panels, the volatility coefficients ${\upsigma }_{0x}$ and ${\upsigma }_{0y}$ are increased successively and in tandem. At the moderate levels of stochasticity in panel (b), the contours are pushed away from the origin, and the solution is more conservative than the deterministic solution in panel (a). A more conservative harvest rate reduces the possibility of stock extinction as it yields a higher and less vulnerable stock level. Sarkar (2009) finds that the harvest trigger (the point of entry in the Nøstbakken (2006) terminology) increases in the volatility level and rationalizes it as cautious behavior in response to extinction risk. Another effect is that the stochasticity leads to a downward drag in the growth, which in turn leads to a reduced harvest rate; Sarkar (2009) did not consider downward drag as a potential driver in his results.

At the higher levels of stochasticity in Fig. 2c, d, the harvest contours move closer to the origin and the optimal harvest rate is thereby more aggressive. In other words, there is a reversal in the response to increasing stochasticity. Interestingly, Sarkar (2009) does not observe the reversal. (Saphores (2003), work that Sarkar (2009) builds upon, observes reversal in a linear model. But, according to Sarkar (2009, p. 281) and references therein, there could be a problem with the model. It is beyond our scope to delve into those details here.) Nevertheless, aggressive harvesting in highly stochastic settings relies on a strong, economic intuition. With high levels of stochasticity, the present state holds little information about future states and the optimal harvest rate moves toward the myopic solution (infinite discounting and maximization of present profits) at low stock levels. At high stock levels, the optimal harvest rate is still lower than in the deterministic solution because of the downward drag (the expected surplus growth is lower). That is, at high stock levels, moderation, which essentially is investment in future stock levels, is valuable at higher stochastic levels. This last result is difficult to discern in the contour plots, but Fig. 3a shows a cross-section of the solutions in Fig. 2a, b, d. The cross section runs parallel to the stock axis and shows the optimal harvest rate as a function of the stock level for a given price ($y=p_0 )$. From the cross sections in Fig. 3a, it is clear that the stochastic solution is lower than the deterministic solution at high stock levels.

Fig. 3

Cross-sections of the optimal harvest rate at $y=p_{0}$. a Effect of both price and stock stochasticity, b effect of stock stochasticity with deterministic price, and c effect of price stochasticity with deterministic stock growth

To disentangle the effects from the two sources of stochasticity we look at further cross sections of the optimal harvest rate. Figure 3 displays cross sections from three different scenarios: in panel (a), the volatility coefficients increase from 0 to 1.5, in tandem (as in Fig. 2); in panel (b), the price volatility coefficient is zero while the growth volatility coefficient increases from 0 to 1.5; and in panel (c), the growth volatility coefficient is zero while the price volatility coefficient increases, also from 0 to 1.5. The panels also show the myopic solution that is identical in all cases. The cross sections in the three panels in Fig. 3 suggest that the main driver behind the behavior of the solutions in Fig. 2 is the growth volatility. The results in panel (b) of Fig. 3, with volatility only in growth, are almost identical to those in panel (a), with volatility in both price and growth. Panel (c) shows that the effect from price volatility is relatively small and leads to some moderation of the harvest rate for the range of volatility rates we explore. In the related work, neither Nøstbakken (2006) nor Sarkar (2009) arrive at similar conclusions. The former does not focus on analyzing how the different sources of uncertainty affect the harvest rule; the latter only considers uncertainty in the biological dimension.

The two stochastic elements in our model are of rather different natures, where one relates to the biological stock and the other to the spot price, and, therefore, comparing their size directly ($\sigma _{0x}$ vs. $\sigma _{0y} )$ is not necessarily meaningful. However, when we use the form $\sigma _z \left( z \right) =\sigma _{0z} z$, where $z$ denotes the state variable, the volatility coefficient $\sigma _{0z}$ becomes a relative factor. Thus, while the relative volatility coefficients cannot be compared directly either, because the degree of stochasticity must be considered relative to the drift, which differs, we are at least confident that a volatility of 1.5 times the level of the state variable must nevertheless be considered large in any sense of the word. That is, we cannot compare the volatility coefficients in the different cases in Fig. 3, but we can consider the volatility levels as unanimously large, and we are thereby confident in our conclusion that growth volatility is the main stochastic driver.

The harvest rate cross-sections in Fig. 3 consider a given price level; to study how uncertainty affects the optimal harvest rate at different price levels, we draw the zero contour of the harvest rate (that is, the moratorium level) in the state space under different combinations of the volatility coefficients. (Figures and further details are presented in the supplemental appendix.) From the results, we conclude that growth dynamics (and its uncertainty) dictates the optimal harvest rate at high price levels, while the price (the price uncertainty can be mostly ignored) dictates the optimal harvest rate at low price levels.

The last part of the parameter space to investigate is that of the mean-reversion rate $\alpha$ in the equation of price dynamics (2). At low reversion rates, the price process is dominated by the noise term (when the reversion rate is zero, the price is pure noise). From our previous results, we expect moderate volatility levels to lead to moderation in the harvest rate, whereas higher volatility levels should move the harvest rate toward the myopic solution. At high reversion rates, the price reverts quickly to $p(h)$ and the drift dominates. As in Fig. 3, we study cross sections of the harvest rate, parallel to the stock axis, at $y=p_0$. Figure 4 shows the cross sections together with the (deterministic) growth curve and the cross section of the myopic solution. In total, the figure holds eight curves. In addition to the growth curve and the myopic cross-section, there are six cross-sections of the harvest rate—three with zero volatility coefficients and three with positive volatility coefficients. The reversion rate varies from a low level (0.3), to the base case (0.59), to a high level (1.0). Cases where only the reversion rate differs are close together; varying it has little influence. The optimal harvest rate increases and becomes more aggressive for a higher reversion rate, whereas it decreases and becomes more moderate for a lower reversion rate. In other words, the behavior agrees with our intuition. The effect of the reversion rate diminishes at high stock levels. The intuition is the same as earlier: a high stock level increases the probability that an investment in the fish stock via a moderate harvest rate pays off.

Fig. 4

Cross-sections of the optimal harvest rate at different levels of ${\upalpha }$ at spot price $y=p_0$

3.2 Dynamic Behavior

To study the behavior of the fishery and the optimal solution in time, we simulated the system forward in time from a range of initial conditions in the state space. For each initial condition, 1,000 different realizations were simulated for 500 years. We simulated both the deterministic and the stochastic system. At the end of the simulation horizon, the deterministic system had settled at the equilibrium for all initial positions. While there is no equilibrium in the stochastic setting, all simulated paths reached a stable, or stationary, region. We call this region the long-term sustainable optimal (LSO) region (Poudel et al. 2013); Smith (1986) calls it the optimal stochastic steady state.

The real interest in reporting steady state values is in how they relate to key parameters such as the carrying capacity. Therefore, we report them in terms of the relative variables $\tilde{x}$ (the stock level relative to carrying capacity, $x/k), \tilde{y}$ (the price level relative to the maximum price, $y/p_0 )$ and $\tilde{h}$ (the harvest level relative to the maximum sustainable yield, $h/h_{MSY} )$. In the deterministic setting, the equilibrium (denoted by asterisks) is characterized by the following values:

$$\begin{aligned} \tilde{x} ^{*}=0.896,\quad \tilde{y} ^{*}=0.775,\quad \tilde{h} ^{*}=0.560 \end{aligned}$$

It is beyond our scope to fully describe the distribution of the simulated paths at the simulation horizon in the stochastic case (a full description requires resolution of the Fokker–Planck equation). However, means and standard deviations of all simulated paths do give a rough idea of how the paths are situated and distributed at the simulation horizon. Below, we report means (and standard deviations in parentheses) of the simulated paths at the end of the simulation horizon in the stochastic case with $\sigma _{0x} =\sigma _{0y} =0.3$:

$$\begin{aligned} \tilde{x} ^{*}=0.815\,\left( {0.191} \right) ,\quad \tilde{y} ^{*}=0.802\,\left( {0.200} \right) ,\quad \tilde{h}^{*}=0.485\,(0.195) \end{aligned}$$

The stochastic LSO stock level has a mean lower than the deterministic steady state, but the mean is still substantially higher than the deterministic maximum sustainable yield level at $\tilde{x} _{MSY} =0.666$ (around 1,600 thousand tonnes, see Fig. 4). The LSO mean harvest level is still smaller than the harvest level in the deterministic equilibrium, which demonstrates the significant effect of the downward drag on the natural growth induced by the stochasticity. With a lower LSO mean stock level, the LSO mean price level becomes higher because of the price–quantity relationship in (2).

Given our simplifications of the functional forms, we should be careful when discussing our results about the long-term steady state in relation to the cod fishery in the Barents Sea. If our results are compared with the historical catch levels reported in Arnason et al. (2004), the optimal steady state harvest level is lower than most recorded annual landings. We see two possible reasons for the high historic catches. One is that the real discount rate is higher than the one we use here. Another is that maximum sustainable yield has been a historic target for the fishery management.

Figures 5 and 6 display how the stock and price levels evolve in time under the optimal harvest rate. Panels (a) in both figures display deterministic time paths, whereas panels (b) display stochastic time paths, with $\sigma _{0x} =\sigma _{0y} =0.3$. Each path is drawn from different initial positions in the stock–price space, such that some paths have an equal initial stock level, but different initial price levels while other paths have equal initial price levels but different initial stock levels. In the stochastic setting, each plotted path is the mean of 1,000 realized paths from the same initial condition and thereby approximates how the expected system behaves.

Fig. 5

Optimal evolution of the stock level over time for different initial stock and price levels: a deterministic model, b stochastic model with $\sigma _{0x} =\sigma _{0y} =0.3$

Fig. 6

Evolution of price to LSO over time for different initial stock levels: a deterministic model and b stochastic model

The general impression from Fig. 5 is that it takes more time to reach the stationary state (the equilibrium or the LSO region) from below than from above. From below, the natural growth constrains the drift, whereas from above, the harvest rate, which is practically unconstrained, constrains the drift. That the stock reaches the stationary state faster from above is thus no surprise. From very low initial stock levels, growth is slow for a number of years because of the depensation of the growth curve (see Fig. 4). Some overshooting occurs (where the stock level grows past the stationary state before it converges) when the initial price is low and exploitation is deferred to let the price revert toward its mean. Finally, it takes more time on average to reach the stationary state in the stochastic setting because of the stochastically induced downward drag on the growth. Also, for small initial stock levels, a significant number of the simulated paths remain trapped in a collapsed state and depreciate the mean path.

The behavior of the price dynamics in Fig. 6 are more difficult to rationalize. A number of paths first stabilize at a high level ($y=p_0 )$ before regressing to the long run stationary state. All of these paths relate to very low initial stock levels that dictate a zero harvest rate for a long period with slow natural growth. As long as the harvest rate is zero, the price will drift toward and stay at $p_0$. For the remaining paths, the price moves to the stationary state relatively quickly. For some cases with high initial price levels and low initial stock levels, more time is required to reach the stationary price. For yet other cases with low initial price levels and low initial stock levels, overshooting occurs while the stock grows to a level where a nonzero harvest rate is optimal. Again, when the optimal harvest rate is zero (see Fig. 2), the price will regress toward $p_0$, whereas when the optimal harvest rate is nonzero, the price will regress toward $p(h)$. As in Fig. 5, it takes more time on average to reach the stationary state in the stochastic setting; as long as the stock level, and hence the harvest rate, are out of the stationary state, the price will also be out of the stationary state.

To complete our description of the behavior of the dynamic system in time, we show how the time paths in Figs. 5 and 6 evolve in the state space. In Fig. 7, panel (a) displays how the deterministic system evolves; panel (b) displays how the average stochastic system evolves. Figure 7 demonstrates the contrast between the equilibrium state in the deterministic setting, which is a single, well-defined point in the state space, and the LSO region in the stochastic setting, which is more like a cloud in the state space. The figure also demonstrates the difference in location of the stationary states. The stochastic LSO region is placed more or less symmetrically in the stock dimension along a stretch of the price schedule $p(h)$. In panel (a), we recognize the price development for cases with small initial stock levels from Fig. 6a, where all paths first stabilize at $y=p_0$, before moving approximately along $p(h)$ to the equilibrium. Also, in panel (a), overshooting in both price and stock is observable, whereas the average, stochastic system in panel (b) moves more directly toward the stationary state. Individual, stochastic realizations display considerable over- and undershooting, of course, depending on the realization of the stochastic process, but the averaging smooths out such idiosyncrasies. Figure 7 holds an important policy lesson: while the deterministic model dictates an extensive initial period of no harvest when the initial stock level is low, the stochastic model has a positive expected harvest rate early on.

Fig. 7

The optimal paths in the stock price state space at ${\upalpha } = 0.59$ and ${\updelta } = 0.05$: a deterministic model and b stochastic model

In the supplemental appendix, we analyze the sensitivity of the long-run solutions to changes in the volatility coefficients and the reversion speed. Both the LSO stock and harvest levels decrease with increasing volatility coefficients, as expected from the stochastic effect (downward drag) on natural growth. Reed (1979) comes to similar conclusions. The LSO price level changes in accordance with the price–quantity relationship. Further, the price volatility coefficient has only small effects. For the reversion speed, we also find only small effects, which is in line with our earlier results.

4 Concluding Remarks

We have analyzed the optimal exploitation of a fishery in a general framework that incorporates two sources of uncertainty: uncertainty in the stock–growth relationship and uncertainty in the price dimension. The primary novelty in our analysis is that the price follows a stochastic, mean-reverting process. Another important feature is that the decision variable (the harvest rate) is present in the stochastic processes and the system dynamics, see Eqs. (1) and (2), which in general poses a problem involving non-trivial probability distributions determined by the associated Fokker–Planck equation. At the conceptual level, we provide a unified analysis of a more realistically complex fisheries management problem that contain two-dimensional stochastic dynamics and an objective function that is nonlinear in the control variable.

With our type of models, closed form solutions are virtually impossible to establish; they amount to solving a nonlinear partial differential equation of elliptic type. We have developed a numerical scheme, based on dynamic programming, which solves for the optimal harvest rate. While the shape and general properties of the solution are robust to changes in functional forms and parameters, the solution depends critically upon the level of stochasticity. That stochasticity is a driving factor resounds throughout the literature (Sethi et al. 2005; Nøstbakken 2006; Sarkar 2009). Further, the volatility in the stock growth equation has a much stronger influence on the solution than the price volatility. Our analysis suggests that, in the type of models we look at, little is lost if price volatility is assumed away, particularly when the relative volatility coefficients ($\sigma _{0i} )$ are at similar levels or larger in the stock growth equation.

Our solution represents a nonlinear harvest rate in a two-dimensional state space and contrasts the solutions presented by Nøstbakken (2006) and Sarkar (2009). Both suggest solutions with pulse-fishing traits that typically arise from linear models. While Nøstbakken (2006) studies a linear model, Sarkar (2009) studies a nonlinear model that could potentially give rise to nonlinear solutions like ours. The pulse-fishing traits in the Sarkar (2009) analysis arise from the particular harvest dynamics that derives from his real-option framework. Nøstbakken (2006) presents harvest switching curves, where the harvest rate switches from zero to some upper bound, in a two-dimensional state space. The shape of the switching curves aligns to a large degree to the shape of the contours of the optimal harvest rate in our model. However, while Nøstbakken (2006) predicts that in the long run the fishery will be closed more than half the time, we predict a permanently open fishery that approaches a stable, stationary state.

The fishery problem is too complex for any one model to solve, and a word of caution is in order. While we have tested the sensitivity of our solutions to perturbations in key parameters and functional forms, and taken steps to put our base case in a relevant part of the parameter space, our results could still be specific to our choices of functional forms, parameter values and general approach. Notwithstanding, we demonstrate the viability of pursuing highly nonlinear models of renewable resource management in settings with multiple sources of uncertainty.

Appendix

We expand the Hamilton–Jacobi–Bellman Eq. (5) and write as follows:

$$\begin{aligned} \delta V&= \mathop {\max }\limits _{h\ge 0} \bigg \{ \left( {y-\frac{c_1 }{x}-\gamma _1 h} \right) h+\left( {f\left( x \right) -h} \right) V_x +\left( {-\alpha y+\alpha (p_0 -\gamma _2 h)} \right) V_y\nonumber \\&\quad +\,\frac{1}{2}\,\sigma _x ^{2}\,x^{2}\,V_{xx} +\frac{1}{2}\,\sigma _y ^{2}\,y^{2}\,V_{yy} \bigg \} \end{aligned}$$

(6)

If we let $L$ denote the object of the maximum operator, (6) is written as $\delta V=\mathop {\max }\nolimits _{h\ge 0} L$. $L$ is concave in $h$ and the inner optimum is given by:

$$\begin{aligned} \frac{\partial L}{\partial h}=y-\frac{c_1 }{x}-2\gamma _1 h-V_x -\alpha \,\gamma _2 V_y =0 \end{aligned}$$

(7)

from which we have:

$$\begin{aligned} h=\max \left\{ {0,\frac{y-\frac{c_1 }{x}-V_x -\alpha \,\gamma _2 V_y }{2\,\gamma _2 }} \right\} \end{aligned}$$

(8)

From (8), we can derive an expression for a contour of the inner solution. In particular, the zero contour is characterized by setting the numerator equal to zero. We have:

$$\begin{aligned} y-\frac{c_1 }{x}-V_x -\alpha \,\gamma _2 V_y =0 \end{aligned}$$

(9)

Total differentiation with respect to $y$ yields an expression for $dx/dy$ along the contour; that is, the derivative of the x-component of the contour as a function of $y$ is:

$$\begin{aligned} \frac{dx}{dy}=-\frac{1-V_{xy} -\alpha \,\gamma _2 V_{yy} }{\frac{c_1 }{x^{2}}-V_{xx} -\alpha \,\gamma _2 V_{xy}} \end{aligned}$$

(10)

When the expression in (10) is positive we have backward folding.

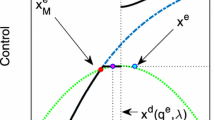
Figure 8 shows the zero contour of the right-hand side of (10) (the black curve), where the expression is positive above (north of) the contour. The figure also shows the unsmoothed zero contour of the harvest rate (the grey curve; identical to the white curve in Fig. 2a). Note that (10) changes behavior outside the zero harvest contour because the harvest rate has a kink along its zero contour. While we should be careful to interpret (10) in the $h=0$ region, Fig. 8 demonstrates that the right-hand side of (10) is positive along the part of the zero harvest contour where we observe backward folding.

Fig. 8

Zero contours of the right-hand side of (9) (black curve) and the harvest rate (grey curve) for the deterministic model