Design and verification of pipelined circuits with Timed Petri Nets

Abstract

A fundamental step in circuit design is the placement of pipeline stages, which can drastically increase the data throughput. Retiming allows optimizing the pipeline with regard to a criterion, for example the required number of registers. This article presents an extension of Timed Petri Net to model synchronous electronic circuits, in order to explore the design space of pipelines. The Timed Petri Nets “à la Ramchandani” with a maximal step firing rule, have notably been used for the modeling of electronic circuits. The RTPN extension, through the reset which model the pipeline stages, and through the delayable transitions which relax some temporal constraints, makes it possible to widen the design space of pipelined systems, and thus to deal with both the retiming and the verification. After a formal definition of this model, we present a method to explore pipelines verifying temporal properties. We apply our approach to a time-multiplexing property allowing the mutualization of operators while minimizing the number of registers.

1 Introduction

Timing constraints are a major problem in the design of synchronous logical circuits. To meet these constraints the pipeline is often inevitable, it allows increasing the operating frequency and thus the throughput. The circuit composed of atomic operators is sliced in several steps called stages. This slicing, physically implemented with memories (flip-flops), allows the concurrent execution of stages and the synchronization of their inputs/outputs. The automatic generation of a pipeline, i.e. the efficient placement of flip-flops (1-bit registers), aims not only at ensuring a target frequency but also minimizing the resources consumed by the pipeline.

1.1 Automatic pipeline generation

The automatic pipeline generation was initially formalized by Leiserson and Saxe (1991), using a model of graph. Their method is based on retiming, i.e. moving registers in the circuit without altering its behavior. Thanks to retiming they are able to build a pipeline guaranteeing a minimal throughput, while minimizing the resources consumed by the pipeline registers (Leiserson and Saxe 1991). They reformulate the problem with a minimum cost flow problem. But it turned out to be inefficient for large circuits, and therefore has been replaced in Hurst et al. (2007) by a reformulation into an iterative maximal flow problem. This solution is implemented at the logical synthesis level in the ABC tool (Brayton 2020), which is to our knowledge the current state of the art. However, these approaches are in practice hard to implement, and are mainly used by FPGA vendor tools at the logical synthesis level.

We propose a new approach able to solve this same problem, but also to verify by model checking temporal constraints. Moreover, this model, which preserves the structure of the circuit, is quite suitable for optimizations beyond the pipeline, such as the sharing of circuit parts.

1.2 Circuit design with Petri Nets

The authors of Leiserson and Saxe (1991) introduced an abstraction of circuits as weighted directed graphs. The intuition is actually that the model is a marked graph, which is a subclass of Petri Net (PN) where every place has exactly one input arc and one output arc. Because of their concurrent nature, the PNs have been widely employed to analyze and optimize temporal properties of synchronous and asynchronous circuits: Bufistov et al. (2007), Campos et al. (1992), Najibi and Beerel (2013), and Kim and Beerel (2006).

They proved to be very efficient for latency insensitive systems. Bufistov et al. (2007) extended the works of Leiserson and Saxe on latency insensitive systems, by combining retiming with recycling, i.e. insertion of bubbles (registers with no informative value), in order to reduce the total number of registers while ensuring a minimal throughput. More recently, Josipović et al. (2020) proposed a temporal optimization of circuits generated from an HLS (High Level Synthesis) description with control flow structures, by applying the approach of Bufistov et al. (2007) on extracted sub-circuits.

All those works share the same solving method: deduce temporal constraints from the structure of the PN, and reformulate with a linear optimization problem. In contrast, our approach makes use of the semantics of PNs and synthesizes directly the pipeline from the states of the model. The explicit exploration of the states offers a simple way to verify logical and temporal properties on the resulting pipelined circuit.

1.3 Model-checking

Model-checking was initially developed, among others, for the verification of electronic circuits (Kern and Greenstreet 1999). The expressive power of formal models like PN, allows modeling both the circuit and its environment, thus to verify a complete system. We can, for example, verify an FPGA working together with a microcontroler, and all connected to a set of sensors and actuators.

The temporal logics were first introduced by Pnueli (1977) as specification languages to describe the behavior of sequential and concurrent systems. The TCTL (Alur et al. 1993) and weighted CTL (Bouyer et al. 2008) logics extend respectively the temporal tree logic CTL, to time and to cost constraints.

We propose to illustrate a usage of those temporal logics for the model-checking of circuits with the example of time-multiplexing. It is a technique of resources sharing using time to sequence the access to a resource. This kind of property can be easily expressed and verified on a PN model.

1.4 Time-multiplexing

Time-multiplexing is especially interesting for applications with a low throughput with respect to the clock frequency. Such applications include, for example, signal processing applications implemented on FPGA, which require a very low sampling rate compared to the FPGA frequency (e.g. a 1 MHz signal processing algorithm onto a 100 MHz FPGA). In this kind of context, it is beneficial to implement only once, parts of the circuit which are used several times, and to schedule their access with the pipeline.

Many works have been carried out in this domain, notably through a problem called modulo scheduling. This problem aims for a minimal latency in a time-multiplexed circuit, given limited available resources (arithmetic or logic operators). The authors of Sittel et al. (2018) proposed an ILP (Integer Linear Programming) formulation which combines scheduling constraints, bounds on available resources, minimization of needed registers, and mutualization of registers when it is possible. More recently, a two-step process was demonstrated by Sittel et al. (2019): first the shareable configurations are detected, then each configuration is scheduled. This approach called folding allows sharing portions of the circuit in contrast with the previous approaches which were only able to share operators one by one.

1.5 Context of application

As part of a collaboration with Renault, the automotive company, we aim at optimizing VHDL synthesis for an FPGA target, from a Matlab/Simulink project. Specifically, the goal is to implement a synchronous circuit with a minimum resource consumption, both for logical units and flip-flops, while ensuring that the whole computation is done in a limited time-frame (the sampling period). A tool is under heavy development, in order to propose a complete chain for the hardware implementation of control laws directly in FPGA. This section briefly introduces the different parts considered in this tool.

The compiler is classically organized around an internal representation, independent of both the input (Simulink) and output (VHDL) representations. This internal model serves as a pivot for all the tools, with different optimizations. The general architecture of the tool is depicted in Fig. 1.

Fig. 1

Simulink-to-VHDL compiler dataflow diagram

The front-end consists in parsing the input file to transform it into this internal model. During this phase, some optimizations are directly performed, such as signal connections between the different modules. In the same way, the back-end (VHDL only at this date) allows generating the hardware description. These output files can be synthesized through the hardware vendor development chain.

Several steps are then performed, each time based on the same internal model and input and output. They allow refining the model. On the diagram presented in Fig. 1, only the 3 main steps are shown.

The first pass concerns the evaluation of the size of the signals and the associated encoding (fixpoint). It is currently done manually and is based on a labeling of the signals. This pass can be replaced by the internal tools of Matlab like the toolbox fixpoint designer. Eventually, the goal is to make this pass semi-automatic, using both interval arithmetic and affine arithmetic (Lee et al. 2006), as well as recent work for example for linear looped systems (Hilaire and Volkova 2017).

The evaluation of operator delays is required in modeling with Petri nets extensions defined in the paper. The level of abstraction of the operators in Simulink does not allow to calculate precisely these delays. The approach used, as for the FloPoco tool (de Dinechin and Pasca 2011), is to synthesize each operator to determine its critical path. The delay of each evaluated operator is then recorded in a database because this synthesis is computer intensive. This pass is automated through a script and is based on an experimental-only approach. The delay of the operators will necessarily vary during the synthesis of the final project (because of branching, internal optimizations, interconnections, …). It is only possible to validate that all deadlines are met after the final synthesis.

The last pass (in green in the figure) is the one that is presented in this article and is a synthesis and extension of the articles (Parrot et al. 2021b; 2021a), which introduce the model Timed Petri Net with reset and delayable transitions (RTPN in short) and present its usage for pipeline synthesis. Here, the focus is on the addition of temporal logic constraints to the generation of pipelines.

1.6 Outline

We first present in Section 2 a semantics of Timed Petri Nets “à la Ramchandani” (1974) with an atomic firing rule using maximal steps, i.e. without the three phases firing. Then, in Section 3, we present an extension of Timed Petri Nets (proposed in Parrot et al. 2021b) closer to real synchronous circuits, which embeds the impacts of registers on the delay of the circuit with a particular reset operation, and which allows relaxing some temporal constraints with delayable transitions.

Thanks to this accurate model of pipelined synchronous circuits, we present in Section 4 a design space exploration guided by a cost which stands for the number of needed registers (proposed in Parrot et al. 2021a). We extend this approach in Section 5 in order to build optimized pipelines (in terms of number of registers), while guaranteeing that a set of properties are verified by the synthesized circuit. We apply this approach to the time-multiplexing problem.

2 A synchronous model for the pipeline

The use of deterministic time in PN was first introduced by Ramchandani (1974), which led to a model called Timed Petri Net. Each transition is associated with a delay, representing the fact that actions take time to complete.

and are respectively the sets of integer and non-negative real numbers. For vectors of size n, the usual operators +,−,<,≤,>,≥ and = are used on vectors of and and are the point-wise extensions of their counterparts in and . As a reminder, for example the point-wise extension of the operator ≤ over is defined by , u ≤ v ⇔ ∀i ∈ [1..n], u(i) ≤ v(i). Let $\bar {0}$ be the null vector of size n.

2.1 The three-phases firing semantics

Ramchandani’s semantics is a three-phases firing semantic: delete the input tokens of the transition (consumption), wait until the firing time is reached (delay) and create the output tokens of the transition (production). Once initiated, this firing process cannot be interrupted or stopped. The consumption phase can therefore be seen as a reservation (in particular in case of conflict). Moreover, the transitions in the firing process are synchronized to a global clock. He furthermore prohibits zero-time firing, which prevents the same transition from being fired twice when other transitions are in conflict.

Popova proposed a semantics based on the same three-phases firing, but selecting beforehand a maximal step of transitions to fire in the same atomic action (Popova-Zeugmann 2013). In other words, instead of being reserved one after the other, the transitions are selected and then reserved all at the same time (consumption phase).

2.2 The maximal-step firing semantics

Classically the semantics of (timeless) PN is the interleaving semantics, in which transitions are fired one after the other. In the maximal-step semantics, a maximal set of fireable transitions is selected and are then fired all at once. In practice the maximal-step semantics avoids the interleaving, which is interesting for the modeling of synchronous systems. It imposes more constraints than the interleaving semantics, and thus increases the expressiveness and eliminates reachable markings.

Popova shows how a counter machine can be encoded and simulated by timeless PN with maximal-step firing, which then also applies to TPNs (Popova-Zeugmann 2013). In particular, she shows the modeling of the so-called zero-test, which is recalled in Fig. 2a. It means that Timeless as well as Timed PNs firing in maximal-step are Turing equivalent.

Fig. 2

Zero-test pattern

2.3 An atomic semantics for TPNs

We consider a TPNs atomic semantics (Parrot et al. 2021b) without any reservation: waiting is done while keeping the tokens in their place, then when at least one transition is fireable we select the maximal step and fire (consumption and production) all the transitions in one atomic action. The maximal step contains enabled transitions which have been enabled for a period of time equal to their delays.

Informally, a clock and a delay are associated with each transition of the Net. The clock measures the time elapsed since the transition has been enabled and the delay is interpreted as a firing condition: the transition may and must fire if the value of its clock is equal to the delay.

Formally:

Definition 1 (TPN)

A TPN is a tuple (P,T,^∙ (.),(.)^∙,δ,M₀) defined by:

• P = {p₁,p₂,…,p_m} is a non-empty set of places,

• T = {t₁,t₂,…,t_n} is a non-empty set of transitions,

• ^∙(.): is the backward incidence function,

• (.)^∙: is the forward incidence function,

• is the initial marking of the Petri Net,

• is the function giving the firing times (delays) of transitions.

A marking M is an element of such that ∀p ∈ P, M(p) is the number of tokens in place p. A marking M enables a transition t ∈ T if: M ≥^∙t. The set of transitions enabled by a marking M is enab(M) = {t ∈ T|M ≥^∙t}. A transition is fireable if it is enabled and its clock has reached its delay.

Fireable transitions are fired simultaneously according to the maximal-step firing rule. For a marked graph where every place has one incoming arc, and one outgoing arc, there can not be any conflict and the firing of a transition cannot disable another transition. In the general case, there can be conflict and, from a given state, there can be several maximal steps τ.

From a marking M, the simultaneous firing of a set τ of transitions leads to a marking $M^{\prime }=M+ {\Sigma }_{t \in \tau } (t^{\bullet }-^{\bullet }t)$.

A transition $t^{\prime }$ is said to be newly enabled by the firing of a set of transitions τ if M + Σ_t∈τ(t^∙−^∙t) enables $t^{\prime }$ and (M −Σ_t∈τ ^∙t) did not enable $t^{\prime }$. If t remains enabled after its firing then t is newly enabled. The set of transitions newly enabled by a set of transitions τ for a marking M is noted $\uparrow \!enab\left (M,\tau \right )$.

A state is a pair (M,v) where M is a marking and is a time valuation of the system (i.e. the value of the clocks). v(t) is the time elapsed since the transition t ∈ T has been newly enabled. $\bar {0}$ is the valuation assigning 0 to every transition.

Definition 2 (Maximal Step)

Let q = (M,v) be a state of the TPN (P,T,^∙(.),(.)^∙,δ,M₀), $\tau \subseteq T$ is a maximal step from q iff:

• 1. ∀t ∈ τ,v(t) = δ(t)

• 2. ${\sum }_{t \in \tau } ^{\bullet }t \leq M$

• 3. $\forall t^{\prime }\in T, (v(t^{\prime }) = \delta (t^{\prime })~ \text { and }~^{\bullet }t^{\prime } \leq M \text { and } t^{\prime } \not \in \tau ) \Rightarrow {\sum }_{t \in \tau } ^{\bullet }t +^{\bullet }t^{\prime }\not \leq M$

The set of maximal steps from q is noted maxStep(q)

The first condition ensures that the transitions are ready to fire, i.e. the clocks are equal to the delays. The second condition ensures that the transition are fireable, i.e. enabled and not in conflict with another transition of τ. The third condition disallows the existence of a proper superset of τ which fulfills the previous two conditions.

The semantics of TPN is defined as a Timed Transition System (TTS). Waiting in a marking is a delay transition of the TTS and firing a maximal step is a discrete transition of the TTS.

Definition 3 (Semantics of a TPN)

The semantics of a TPN is defined by the Timed Transition System $\mathcal {S}=(Q,q_{0},\to )$:

• is the set of states,

• $q_{0}=(M_{0},\bar {0})$ is the initial state,

• is the transition relation including a discrete transition and a delay transition.

  • The delay transition is defined by: $(M,v)\xrightarrow {d}(M,v^{\prime }) \ \text {iff} \begin {cases} v^{\prime }(t)= \begin {cases} v(t)+d &\text {if } t\in enab~\left (M\right )\\ v(t)&\text {otherwise} \end {cases}\\ \forall t \in enab~(M), v^{\prime }(t) \leq \delta (t) \end {cases}$

  • The discrete transition is defined ∀τ ∈ maxStep((M,v)) by: $(M,v)\xrightarrow {\tau }(M^{\prime },v^{\prime }) \text {iff} \begin {cases} M^{\prime } = M + {\sum }_{t \in \tau } (t^{\bullet }-^{\bullet }t)\\ v^{\prime }(t)= \begin {cases} 0 &\text {if } t\in \uparrow \!enab\left (M,\tau \right ) \text { or } t \not \in enab~(M^{\prime })\\ v(t)&\text {otherwise} \end {cases} \end {cases}$

A run in a TPN is a sequence $q_{0} \xrightarrow {\alpha _{1}} q_{1} \xrightarrow {\alpha _{2}} \dots$, such that for all i, $q_{i}\xrightarrow {\alpha _{i+1}}q_{i+1}$ is a transition in the semantics.

In the absence of conflict, the atomic semantics of Definition 3 is equivalent to the three-phases one of Ramchandani (extended with zero firing delay Popova-Zeugmann 2013): there exists only one run, there is no indeterminism. In case of conflict, it is possible to construct the three-phases firing in our semantics: just add a zero time transition before each transition, in order to simulate the reservation action (Parrot et al. 2021b).

2.4 Zero-test and model of the pipeline

Thanks to the maximal step firing, the TPN represented on Fig. 2a can perform the zero-test. The zero-test in the case of TPN is materialized by testing if a place is marked or not, here the place p. After firing the transition start, the transitions test and cancel are fired simultaneously if and only if the place p is marked. The next step will contain the transition is_zero iff p wasn’t marked, which leads to a token in p_zero. We will use this test several times in the following, thus we will replace it by the graphical shortcut of Fig. 2b for convenience.

Using this zero-test, it is directly possible to model the dataflow of a pipeline. The TPN of Fig. 3 models a D flip-flop, which is used for the synchronization of a signal between two pipeline stages. The marking of the place Q_i (or D_i) represents the presence of data (not its truth value).

Fig. 3

Model of pipeline dataflow with frequency $\frac {1}{N}$ (D flip-flop)

On the left of the zero-test, the generator models the oscillator by adding a token in the place clock every N time units. When the place clock is marked, the zero-test will put a token in Q_i (output) only if the place D_i (input) is marked. We thus model a D flip-flop (copy the input signal D_i to the output Q_i on a rising edge of the clock), which synchronizes the dataflow with clock.

Model-checking on pipeline is then possible. However, this model only allows the study of one pipeline (one placement of the D flip-flops in the circuit) at a time. Studying others pipeline requires to change completely the model by moving the flip-flop pattern.

3 TPN with reset and delayable transitions

We have proposed in Parrot et al. (2021b) an extension of TPN where transitions are separated in two groups: asap transitions (non-delayable) must fire as soon as possible, as in Definition 1, and delayable transitions can fire when their clock reaches their delay, or when their clock exceeds their delay and they are associated with another transition whose clock just reaches its delay. In addition, the clocks can be resetted (the corresponding action is called reset) and the delay between two consecutive reset s is fixed by an interval I_reset.

3.1 Definitions

Definition 4 (RTPN)

A RTPN $\mathcal {N}$ is a tuple $(P,T,T_{D},^{\bullet }(.),(.)^{\bullet },\delta ,{I}_{reset},M_{0})$ defined by:

• (P,T,^∙(.),(.)^∙,δ,M₀) is a TPN;

• $T_{D} \subseteq T$ is the set of delayable transitions;

• I_reset is the reset time interval with lower ($\underline {{I}_{reset}}$) and upper ($\overline {{I}_{reset}}$) bounds in .

From a state (M,v), a transition is fireable if it is enabled and its clock is greater or equal to its delay. As for the TPN, the clock of an asap transition t∉T_D cannot exceed δ(t). Consequently, v(t) ≤ δ(t) and t must fire when its clock is equal to its delay. A delayable transition t ∈ T_D may fire either when v(t) = δ(t) (not delayed in that case), or when v(t) > δ(t), but in this case t must be associated with at least one (or more) other fireable transition $t^{\prime }$ such that $v(t^{\prime })=\delta (t^{\prime })$.

The maximal step is then maximal only with regard to the asap transitions:

Definition 5 (Maximal Step w.r.t. T _D)

Let q = (M,v) be a state of $\mathcal {N}$. A set $\tau \subseteq T$ is a maximal step with regard to T_D from q iff:

• 1. ∀t ∈ τ,v(t) ≥ δ(t)

• 2. ∃t ∈ τ s.t. v(t) = δ(t)

• 3. ${\sum }_{t \in \tau } ^{\bullet }t \leq M$

• 4. $\forall t^{\prime }\in T\setminus T_{D}, (v(t^{\prime }) = \delta (t^{\prime })~ \text {and}~^{\bullet }t^{\prime } \leq M \text { and } t^{\prime } \not \in \tau ) \Rightarrow {\sum }_{t \in \tau } ^{\bullet }t +^{\bullet }{t^{\prime }}\not \leq M$

The set of maximal steps w.r.t. T_D from q is noted $maxStep_{\setminus T_{D}}(q)$.

A state is now a pair (M,v) such that is extended with a clock value for reset, evaluating the time elapsed since the last reset. The reset action resets all clocks of the net. It is possible only when its clock value belongs to the reset interval v(reset) ∈ I_reset.

The semantics of a RTPN is defined as a Timed Transition System (TTS). Waiting in a marking is a delay transition of the TTS, and firing a maximal step or the reset are discrete transitions of the TTS.

Definition 6 (Semantics of a RTPN)

The semantics of a RTPN $\mathcal {N}$ is defined by the Timed Transition System $\mathcal {S}_{\mathcal {N}}=(Q,q_{0},\to )$ with is the set of states; $q_{0}=(M_{0},\bar {0})$ is the initial state; and is the transition relation including a discrete transition and a delay transition:

• The delay transition is defined by: $(M,v)\xrightarrow {d}(M,v^{\prime }) \ \text {iff} \begin {cases} v^{\prime }(t)= \begin {cases} v(t)+d &\text {if } t\in enab~(M)\cup \{reset\}\\ v(t)&\text {otherwise} \end {cases}\\ v^{\prime }(reset)\leq \overline {{I}_{reset}} \\ \forall t \in enab~(M)\setminus T_{D} , v^{\prime }(t) \leq \delta (t) \end {cases}$

• The discrete transition is defined by:

  • $\forall \tau \in maxStep_{\setminus T_{D}}\big ((M,v)\big )$, ${}(M,v)\xrightarrow {\tau }(M^{\prime },v^{\prime }) \text {iff}\ \begin {cases} {}M^{\prime } = M + {\Sigma }_{t \in \tau } (t^{\bullet }-^{\bullet }t)\\ v^{\prime }(t)= \begin {cases} 0 &\text {if } t\in \uparrow \!enab\left (M,\tau \right ) \text { or } t \not \in enab\left (M^{\prime }\right )\\ v(t)&\text {otherwise} \end {cases} \end {cases}$

  • $(M,v)\xrightarrow {\{reset\}}(M,v^{\prime }) \text {iff} \begin {cases} v(reset)\in {I}_{reset} \\ v^{\prime }= \bar {0} \\ \end {cases}$

Definition 7 (Runs)

Let $\mathcal {N}$ be a RTPN and $\mathcal {S}_{\mathcal {N}}$ its semantics. A run of $\mathcal {N}$ from q is finite or infinite sequence $\rho = q \xrightarrow {d_{1}} q_{d_{1}} \xrightarrow {\tau _{1}} q_{\tau _{1}}{\dots } \xrightarrow {d_{n}} q_{d_{n}} \xrightarrow {\tau _{n}} q_{\tau _{n}}$ of alternating delay d_i (possibly null) and discrete transition τ_i where either $\tau _{i} \subseteq T$ or τ_i = {reset}. For all run ρ, there exists a discrete run $\rho _{\bar {d}} = q \xrightarrow {\tau _{1}} q_{\tau _{1}}{\dots } \xrightarrow {\tau _{n}} q_{\tau _{n}}$, in which only the discrete transitions are present.

3.2 Example

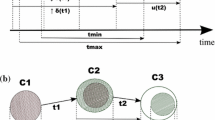
Let us consider the RTPN depicted in Fig. 4a. Figure 4b shows a part of its state graph, restricted to the first occurrence of a reset. States after a reset are framed in cyan. For more convenience, the markings are represented as the set of marked places. The initial state of the net is the state q₀ in the state graph.

Fig. 4

Example of RTPN and some of its possible runs. Delays are represented in red under the transitions, and delayable transitions are in gray (only t₀ in this example)

Note that the transition t₀ being delayable, it can fire either when it reaches its delay (edge between q₁ and q₂), or together with t₃ (edge between q₈ and q₉). Finally, it should be noted that not all the possible runs are represented here. It is for example possible to wait 7 time units from q₀ and then do a reset. Actually it exists infinitely many runs, as a result of the density of time.

3.3 Properties of RTPNs

Symbolic states

The RTPN semantics is a transition system in which each state consists of a marking and a valuation of the clocks. Note that there is (because we only consider bounded nets) only a finite number of markings, but there are an uncountable quantity of valuations because of the density of time (particularly for the states from which a reset is possible). For example, there is infinitely many states between q₈ and q₁₁ (in the Fig. 4b). These states correspond to the wait between 6 and 9 time units from the state q₀ which can be abstracted by v(t₀) = v(t₃) = v(reset) ∈ [6,9]. The state space can then easily be abstracted by a finite set of symbolic states (shown in Parrot et al. 2021b).

Definition 8 (Symbolic state)

A symbolic state is a pair (M,Z) where M is a marking, and the zone Z is a set of valuations v of T ∪{reset} defined by the conjunction of:

• rectangular constraints: $\left (v(x) \sim c \right )$ where x ∈ T ∪{reset}, $\sim \in \{\leq ,=,\geq \}$ and ,

• diagonal constraints: $\left (v({reset}) - v(t) = c \right )$ where $t\in enab\left (M\right )$ and .

It is then possible to build a symbolic state graph as defined in Parrot et al. (2021b), illustrated in the example in Fig. 5. Compared to the part of state graph of Fig. 4b, we can see that some states have been grouped into a single symbolic state.

Fig. 5

Part of the symbolic state graph of $\mathcal {N}$ (until the first reset s)

It is interesting to note that the zones have a particular shape: the diagonal constraints are equalities and compare all the clocks against v(reset). Thus, by simply setting a value of v(reset) we can “choose” a point of the zone. The discrete actions (other than reset) are then only done on integer points of the space and the symbolic state space preserves the language in addition to the reachability. Based on this abstraction it is possible to build a single clock automata that recognized the same language, as presented in Parrot et al. (2021b).

An abstraction preserving branching is readily accessible. Simply split the zone when a transition is no more fireable. For example the state s_a of Fig. 5 becomes the states presented in Fig. 6.

Fig. 6

Abstraction preserving the branching of state s_a of Fig. 5

Without going into details on symbolic state graphs, it should be noted that only few discrete runs are sufficient to describe all the behaviors. We will then only represent the relevant states in the following state graphs.

Decidability and complexity

Timeless PNs, with maximal-step firing, are as expressive as Turing Machines and are a subclass of RTPN for whom the reachability problem is then also not decidable. But if we consider bounded nets, we obtain the following results:

Theorem 1

Reachability and TCTL model checking for a bounded TPN, with or without reset and delayable transitions, are PSPACE-complete.

Proof

PSPACE-hardness comes from the PSPACE-completness of the reachability problem for a safe timeless PN with the classical interleaving semantics, which is a subclass of bounded TPN. Then the PSPACE-completness is obtained by applying the same procedure as in Alur et al. (1993) and Boucheneb et al. (2009) by checking TCTL formulae with an inductive algorithm for region graph exploration, which is polynomial in space. □

Theorem 2

For bounded RTPN, the universality and language inclusion problems are decidable for finite timed words.

Proof

It is a consequence of the translation preserving the timed bisimulation proposed in Parrot et al. (2021b) of bounded RTPNs to one clock timed automata, for which these problems are decidable (Ouaknine and Worrell 2004; Abdulla et al. 2008). □

4 Pipeline synthesis

The model presented in Section 3 can accurately represent pipelined synchronous circuits. The following will demonstrate how to use this model to build an optimized pipeline which ensures a minimal frequency while minimizing the required registers (and thus the material resource consumed).

In this modeling, transitions represent the operators and places represent the connections of the circuit. The PN is actually a Marked Graph, and there is no conflict. However, the state space still has an exponential size regarding the size of the RTPN. Some features are then used to limit the exploration according to an optimization objective.

The goal is to build the pipeline that minimizes the total number of flip-flops (1-bit registers). The RTPN model is then extended with a cost representing the number of flip-flops of a given pipeline. Note that the considered circuits are finite and with unfolded loops, so we focus on finite runs of RTPN: the accumulation of an increasing cost will not affect the termination.

This pipeline building problem that minimizes the number of registers while ensuring a minimal frequency was already solved by Leiserson and Saxe (1991). However, the proposed solution cannot be easily extended with additional constraints on the pipeline. The originality of the approach lies in the possibility to append a set of properties to check, to the pipeline synthesis. Those properties can, for example, permit sharing a portion of the circuit between several pipeline stages. The synthesis of pipeline allowing resource sharing will be addressed afterwards in Section 5.

4.1 RTPN with cost

The RTPN class is extended with a cost on each place, and a marking cost function.

Definition 9 (CRTPN)

A CRTPN is a tuple $(\mathcal {N},\mathcal {C},\omega )$ where $\mathcal {N}=(P,T,T_{D},^{\bullet }(.),(.)^{\bullet },$ δ,I_reset,M₀) is a RTPN and

• is the cost assigned to each place;

• is the marking cost function (recall that a marking is ).

A classical marking cost function is $\omega (M) ={\sum }_{p\in P} M(p)\cdot \mathcal {C}(p)$ which is the sum of the marking of each place weighted by its cost. This function is not necessarily linear, as we will see for the model of branching points.

Definition 10 (Cost of a run)

The cost Ω(ρ) of a run ρ is the accumulated marking cost of the states that immediately follow a reset in the run, starting by the cost of the initial marking.

It is defined inductively on a run $\rho _{n}=\rho _{n-1}\xrightarrow {\alpha _{n}} q_{n}$, with and q_n = (M_n,v_n) by:

• Ω(q₀) = ω(M₀)

• Ω(ρ_n) = { Ω(ρ_n− 1) + ω(M_n) if α_n = {reset} Ω(ρ_n− 1) otherwise

4.2 Modeling circuits

A set of rules to model a circuit with a CRTPN is defined in this section. Figure 7 shows an example of circuit, with the operators op_i connected by signals s_i. The size of each signal is noted between parentheses (in green). The propagation delay of each operator is noted under it (in red). Lastly the pipeline’s registers are represented by (blue) rectangles on the edges.

Fig. 7

An example of pipelined circuit and its corresponding model

In the following, a circuit is considered as a weighted graph (V,E,d,w), in which V = Op ⊎ B is the set of operators Op joint with the set of branching points B (⊎ is the disjoint union), and E is the set of signals. Additional signals following a branching point are defined, in order to match with the edges of the graph (on the example Fig. 7 the signal s₁ gives three signals s₁₁, s₁₂ and s₁₃ after the branching). Finally, the weights d and w represent respectively the propagation delay of the operators d(op) and the size of the signals w(s) (number of bits).

The CRTPN $((P,T,^{\bullet }(.),(.)^{\bullet },\delta ,{I}_{reset},M_{0}),\mathcal {C},\omega )$ built from the circuit Fig. 7a is represented on Fig. 7b, and is obtained thanks to 7 rules. The four first rules preserve the elements of the circuit and their connections:

rule 1::

∃ϕ_e: E↦P a bijection, with ∀s ∈ E, $\mathcal {C}(\phi _{e}(s))=w(s)$;

rule 2::

∃ϕ_v: V ↦T a bijection, with ∀op ∈ Op, δ(ϕ_v(op)) = d(op) and ∀b ∈ B, δ(ϕ_v(b)) = 0;

T = T_Op ⊎ T_B with T_Op = ϕ_v(Op) and T_B = ϕ_v(B).

rule 3::

If s ∈ E is an input signal of v ∈ V, then ^∙t(p) = 1 with t = ϕ_v(v) and p = ϕ_e(s);

rule 4::

If s ∈ E is an output signal of v ∈ V, then t^∙(p) = 1 with t = ϕ_v(v) and p = ϕ_e(s);

A place and its associated cost model respectively a signal and its size. A transition and its firing delay model respectively an operator and its propagation delay. Moreover, a transition with a null delay models each branching point (only b₁ in the example). Its purpose is to allow the placement of registers either before the branching (s₁), or on a particular output branch (s₁₁, s₁₂ or s₁₃). Rules 3 and 4 preserve the structure of the net.

All the input signals are considered synchronous, which is equivalent to have them all on the first pipeline stage. In the model, this corresponds to the initial marking M₀ defined by rule 5:

rule 5::

If s is an input signal (not outgoing from any operator), then M₀(p) = 1 with p = ϕ_e(s);

The reset action models the placement of a border of pipeline stage, and resets all the clocks of the CRTPN for the following stage. Rule 6 defines the upper bound of the reset interval:

rule 6::

$\overline {{I}_{reset}}=\frac {1}{f}$;

The time elapsed since the last reset is “stored” in v(reset). The semantics enforces a reset to happen only if v(reset) ∈ I_reset. Then, if the upper bound is fixed to $\frac {1}{f}$, the pipeline produced has at least a frequency f. Here $\frac {1}{f}$, and in the following $\frac {1}{2f}$, are supposed to be in , but they can be rational without altering the results (just apply a factor to all the delays of the model to come back to integer values).

The cost function gives the total number of flip-flops needed in the current pipeline stage:

rule 7::

We define P_Op = {p ∈ P∣∃t ∈ T_Op,^∙t(p) = 1} and $P_{B}(p)=\{p^{\prime } \in P \mid \exists t\in T_{B},^{\bullet }t(p)=1$ and $t^{\bullet }(p^{\prime })=1\}$. Then ∀M ∈{0,1}^P, $\omega (M)={\sum }_{p\in P_{Op}} \mathcal {C}(p)\cdot \max \limits (M(p), \max \limits _{p^{\prime }\in P_{B}(p)}(M(p^{\prime })) )$.

Indeed, the cost of a place matches the size of the signal, and consequently the number of flip-flops needed per register. The cost function manages specifically the branching points, where a mutualization of the registers on the output is possible. That explains why the cost of places after a transition modeling a branching point following a place p, is $\mathcal {C}(p) \cdot \max \limits _{p^{\prime } \in P_{B}(p)}(M(p^{\prime }))$.

These modeling rules are sufficient to fully define the circuit model with CRTPN. All possible pipelines can then be explored thanks to this model. In particular it is possible to find the optimal one, i.e. the one that minimizes the resource consumed while ensuring a minimal frequency. However, in practice we quickly face a combinatorial explosion during state space exploration. To avoid combinatorial explosion, the two heuristics proposed in Parrot et al. (2021a) lead to good pratical results by limiting the number of delayable transitions¹ and increasing the lower bound of the reset interval.

4.3 Pipeline synthesis from the model

Each reachable state of the model represents a pipeline stage that is possible on the real circuit. The reset operation sets the transition from a stage to the following one. The full pipeline is recovered by walking through a branch of the state graph, and accumulating the states following a reset.

A run ρ of the CRTPN of Fig. 7b, is represented on Fig. 8a. It is actually the best achievable run, i.e. the one minimizing the cost. The corresponding pipeline in the circuit is drawn on Fig. 8b.

Fig. 8

Example of pipeline synthesized from a run

Let q_i = (M_i,v_i) (0 ≤ i ≤ 14) be the states of this run ρ. The marking of each state after a reset gives the placement of the registers in the pipelined circuit, except for the signals after a branching point: if several are marked, then only one register is needed in the pipelined circuit (mutualization). For example, the marking M₄ = {s₁₁,s₁₂,s₁₃} leads to only one register on s₁.

The cost of this run is ${\Omega }(\rho )=\omega (M_{0})+\omega (M_{4})+\omega (M_{7})+\omega (M_{14}) = \mathcal {C}(s_{0}) + \mathcal {C}(s_{1}) + (\mathcal {C}(s_{1}) + \mathcal {C}(s_{2})) + (\mathcal {C}(s_{6}) + \mathcal {C}(s_{7}) + \mathcal {C}{s_{8}})= 61$. This cost matches the total number of flip-flops in the pipeline of Fig. 8b. On this example, a classical greedy “as-soon-as-possible” algorithm as implemented in FloPoCo (Istoan and de Dinechin 2017) (a generator of pipelined arithmetic operators for FPGA), produces the example of Fig. 7a, with a total of 94 flip-flops (54% more). The improvement of this approach over the classical greedy has been studied in Parrot et al. (2021a), on several arithmetic circuits.

5 Application to time-multiplexing

The RTPN model allows exploring many pipelines of a circuit with a frequency guaranteed in an interval. We can check temporal logic properties, such as ensuring that the time spent between the production and consumption of a data on a portion of the circuit is less than a bound. It is in fact possible to impose some specific constraints to the resulting pipelines.

In this section, we apply this approach to the time-multiplexing problem. As stated in the introduction, we focus here on circuits with a low throughput compared to the clock frequency, thus the whole computation is done in one sampling period.

5.1 Folding or time-multiplexing

With an ongoing concern of saving resources, a method called time-multiplexing (also called folding) has been developed. It aims at sharing the instantiation of operators or group of operators which are needed at several places of the circuit. The sharing is secured by sequential access to the instantiation.

Figure 9 shows an example of circuit that is suitable for resource sharing (based on an example of Sittel et al. 2017). Suppose that the operators op₁ (resp. op₂; op₃) and $op^{\prime }_{1}$ (resp. $op^{\prime }_{2}$; $op^{\prime }_{3}$) are two instances of the same operator. It is then possible to instantiate only once the portions of circuit in (orange) dotted frame, and to share the instantiation. Note that the signal sizes are willingly omitted for ease of understanding, but this approach is still valid with different signal sizes (as long as they are equal on the portions to be shared).

Fig. 9

Example of time-multiplexing

The sequencing of resources access is done with a particular pipeline. Identify this (or one of these) pipeline constitutes the modulo scheduling problem. A key step of modulo scheduling is to find the initiation interval: the delay between two introductions of new entries in the circuit. This periodical data introduction can be represented in a RTPN by a token generator on the input. However, as a first step, we will assume that a new data is introduced once the whole computation is done. This assumption is perfectly relevant in signal processing, where the initiation interval (the sampling period) is often significantly higher than the pipeline period (related to the FPGA frequency).

Our goal is to find a particular pipeline on the initial circuit containing all the instances, and afterwards to fold the instances (i.e. to merge them). The pipeline must then verify two properties:

• 1. The first is mutual exclusion. The resources must not be accessible at the same time by several clients.

• 2. The second concerns the register placement. The registers must be placed on the same locations in the portions of circuit to fold.

In the example in Fig. 9, the first constraint ensures that there is never some data at the same time on the twin signals: simultaneously in s₅ (resp. s₆) and in s₈ (resp. s₁₀). The second constraint means that there must be the same amount of registers in the pair of twin signals. That is why the pipeline of Fig. 9b doesn’t allow time-multiplexing, contrary to the one of Fig. 9a. Indeed, s₅ crosses no register whereas s₈ crosses one, which violates the second constraint.

It is possible to build these particular pipeline, using the approach presented in Section 4, by guiding the exploration with CTL properties. Thus, the exploration will be restricted to runs verifying those properties. Mutual exclusion can be simply expressed as a marking constraint verified by all states of the run. However, the CTL properties are expressed on markings, they do not allow observing the reset fired, which is required by the second constraint. As the reset is defined in the semantics of the model, it is not explicitly present in the net like the other transitions, it then cannot be connected to an observer place. Somehow the CTL must be extended with the ability to capture the reset s fired in each place.

5.2 Explicit reset

As explained in Section 3, due to the density of time the reset can fire from an infinite number of states with the same marking, but the successor state will always be the same. Therefore, the only relevant firing times either correspond to the bounds of the interval ($\underline {{I}_{reset}}$ and $\overline {{I}_{reset}}$) or are grouped together with a maximal step (in the semantics just after the maximal step firing). One can then consider the reset as a delayable transition with a temporal upper bound, and this preserves the discrete runs. Thus, for all RTPN, a TPN with delayable transitions that verifies the same CTL properties can be built.

Indeed, a reset can be explicitly expressed with the pattern drawn in Fig. 10. The place p_reset holds a token since the last firing of reset. The delayable transition with delay $\underline {{I}_{reset}}$ and the non-delayable transition with delay $\overline {{I}_{reset}}$ model the reset interval. For all places p_i of the net, the pattern in the dashed frame is added and connected to the transitions reset and end_reset. This pattern achieves the reset of the transitions enabled by the place p_i. It works in two steps: first the tokens in the place are drained and temporarily held in $p_{i}^{stock}$, then once the draining is finished all tokens are replaced in the place p_i. Each step is based on a zero-test with a loopback which simulates a while loop. In other words, the tokens are removed from p_i (resp. $p_{i}^{stock}$) while there are some left. Note that with a safe net, the pattern can be greatly simplified: only one zero-test that removes and sets back the token in p_i is enough.

Fig. 10

Pattern expressing the reset

In the pattern drawn in Fig. 10, the place $p_{i}^{obs}$ counts the total number of tokens which underwent a reset in p_i since the initial state. This observer place allows us to extend the temporal logic CTL for RTPN.

Definition 11

Let $\mathcal {N}$ be an RTPN, and q = (M,v) a state of $\mathcal {N}$. Let the property $\phi = (reset(p_{i})\sim n)$ with $\sim \in \{<,>,\leq ,\geq ,=,\neq \}$ and . The state q verifies the property ϕ if and only if q verifies the property $\psi = ((M(p_{i}^{obs}) \sim n)$.

5.3 Synthesis of a pipeline for the folding

With the RTPN approach and the CTL extension presented previously, it is possible to solve the modulo scheduling problem for the folding of circuits. More specifically, it is possible to build a pipeline allowing folding, while ensuring a minimal frequency and minimizing the number of flip-flops. This solution is applied to the example of circuit given in Section 5.1.

Our method for solving the folding problem is a reachability problem, where a CTL property define mutual exclusion. This property allows the state space exploration to be pruned on the fly. Thus, the synthesis is guided by the CTL property.

The RTPN model of the circuit of Fig. 9 is built using the modeling rules presented in Section 4. It is represented in Fig. 11a. Note that the transitions modeling the shared operators are delayable in order to relax the exploration, and so to satisfy the folding constraints. The places drawn in orange (s₅, s₆, s_6a, s_6b, s₈ and s₁₀) are subject to CTL constraints.

Fig. 11

Time-multiplexing with RTPN

A first atomic property guarantees the mutual exclusion of data in the twin places: ϕ_mutex = (M(s₅)+M(s₈) ≤ 1)∧(M(s₆)+M(s₁₀) ≤ 1)∧(M(s_6a)+M(s₁₀) ≤ 1)∧(M(s_6b)+M(s₁₀) ≤ 1). In fact, in the model, tokens represent both the placement of the future registers, and the data propagated when the circuit is pipelined (as soon as pipeline registers are in place). The property ϕ_mutex checks that the two signals s₅ (resp. s₆, s_6a, s_6b) and s₈ (resp. s₁₀) will never contain data simultaneously.

A second atomic property guarantees the consistency of registers placement in the twin places in a final state (state with the final marking): ϕ_consist = (M(s₁₁) = 1)∧(reset(s₅) = reset(s₈))∧(reset(s₆)+reset(s_6a) = reset(s₁₀))∧(reset(s₆)+reset(s_6b) = reset(s₁₀)). It checks that in a final state (M(s₁₁) = 1), the twin places have passed through the same number of reset s.

The final CTL property guarantees that ϕ_mutex holds until it is satisfied together with ϕ_consist (once a final state is reached): ϕ_fold = A(ϕ_mutexU(ϕ_mutex ∧ ϕ_consist)). The pruning during the state space exploration insures that each run satisfies the property ϕ_fold, as the one presented in Fig. 11b. The synthesized pipeline from this run is the one drawn in Fig. 9b.

5.4 Actually fold the circuit

The parts of shareable circuits are currently selected by hand. This problem has been addressed in the literature as automatic identification of isomorphic subgraphs, and some solutions have already been proposed (Sittel et al. 2017). In our case study, we benefit from the high-level abstraction of Matlab/Simulink and some parts of the evaluated models have fairly obvious redundancies to be determined. On the other hand, the use of libraries facilitates the identification of shareable parts.

Once the portions to be shared have been chosen, a minimum bound on the pipeline frequency f_p can be deduced from the desired minimum sampling rate f_s. Let n be the maximum number of times a circuit portion is shared, then the pipeline frequency must satisfy f_p ≥ n ⋅ f_s. This bound generalizes to the case of sharing nested parts, by multiplying the maximum number of occurrences between nested levels. However, this bound does not guarantee that the resulting folded circuit will have the minimum sampling rate f_s. A post-selection of the produced pipelines, based on their latency (which is the sampling period), is therefore necessary. In other words, the lower bound on the pipeline frequency f_p is only used to reduce the exploration to a few potential solutions.

Our pipeline synthesis approach for folding has been implemented in a prototype tool. The first tests are encouraging, and on the example presented, the tool produces the expected pipeline in a few milliseconds: 24ms on an Intel Core i7-6700HQ processor.

The last step is to generate the operators effectively folding the circuit. To do so, the shareable parts are merged, and multiplexers (MUX) are added in the circuit in place of their input/output registers. Figure 12 shows the folded circuit obtained from the pipelined circuit of Fig. 9a. Multiplexers (and de-multiplexers) are associated with a control signal produced by a sequencer (sel on the figure), that selects the input (output) signals. This part is under development since the code generation associated with the folding step is not yet implemented.

Fig. 12

Circuit defined in Fig. 9a after folding

6 Conclusion

We proposed a model for the pipeline of synchronous circuit based on TPN “à la Ramchandani”. Although it allows verification, this model is only able to study one pipeline at a time.

We then focused on the optimization of the pipeline in terms of resources. The RTPN model allows generating multiple pipelines with a target frequency, and to select one minimizing the resource consumption with regard to the size of registers and their eventual mutualization.

Using this result we then concentrated on handling together the optimization with the synthesis of pipeline following a specification expressed in temporal logic. In particular, we presented a solution to the time-multiplexing problem. It relies on the explicit expression of the reset in the RTPN model. This method produces a pipeline allowing time-multiplexing, ensuring a target frequency, and minimizing the number of flip-flops.

While these results are encouraging, their implementation may be slowed down by combinatorial explosion. We consider the possibility to combine them with an ILP approach in order to obtain both the computation speed and the possibilities offered by model-checking. We also think about exploiting further model-checking towards the interactions with the environment.