Resource-aware networked control systems under temporal logic specifications

Abstract

Temporal logics for control of dynamical systems have the potential to automatically synthesize controllers under complex goals expressed by temporal logic formulas. In this paper, we are interested in the situation, where a controller system that implements high and low level controllers is connected to a plant over a communication network. In such control architecture, it is known that the limited nature of computation and communication resources should be explicitly taken into account. In view of this, we jointly provide control and communication strategies, such that the resulting state trajectories satisfy the desired temporal logic formula, while at the same time the average communication rate is below a certain threshold. The proposed strategies are illustrated through numerical simulation examples.

1 Introduction

Temporal logic motion/task planning and control of dynamical systems have been receiving an increased attention in recent years (Kress-Gazit et al. 2018; Belta et al. 2007). In contrast to the standard control tasks that are formulated by well-known stability concepts or point-to-point navigations, temporal logics allow us to automatically synthesize controllers for more complicated specifications involving temporal constraints, such as “Survey the region A, B, C, D infinitely often, while making sure that the region E is always avoided until C is visited”. The availability of treating such temporal constraints has led to a wide variety of applications, including cooporative task planning of multi-robot systems (Guo et al. 2013; Guo and Dimarogonas 2015; Tumova and Dimarogonas 2016; Karimadini and Lin 2011), manufacturing systems (Heddy et al. 2015; Antoniotti et al. 1995; He et al. 2015; Morel et al. 2001), robot manipulation (Chinchali et al. 2012; Verginis and Dimarogonas 2017), motion planning of dynamic robots (Filippidis et al. 2016; Wongpiromsarn et al. 2012; Kloetzer and Belta 2008; Livingston and Murray 2013; Fainekos et al. 2009; Kress-Gazit 2009; Gol et al. 2015; Kress-Gazit et al. 2007), to name a few. In the temporal logic control framework, such temporal tasks are generally expressed by Linear Temporal Logic (LTL) or Computational Tree Logic (CTL) formulas. The basic control synthesis algorithm is given in a hierarchical manner, as briefly described below. First, we obtain a finite transition system that consists of symbolic states and corresponding transitions, which represents an abstracted behavior of the control system. The transition system may be obtained by decomposing the state-space into a finite number of polytopes, and the reachability for each pair of polytopes among them is analysed (Kloetzer and Belta 2008; Fainekos et al. 2009; Coogan et al. 2016). Once the transition system is obtained, a high level controller finds an accepting run to satisfy the desired specifications through an implementation of, e.g., automata-based model checking algorithms (Baier and Katoen 2008). If such accepting run is found, a low level controller implements a feedback control strategy, such that the generated state trajectory satisfies the desired specification.

In this paper, we are interested in the situation, where the plant aims at achieving desired goals expressed by temporal logic formulas, but the high and low level controllers need to be implemented over a communication network. In general, control systems whose plants and controllers are interacted over the communication network are referred to as Networked Control Systems (NCSs) (Hespanha et al. 2007). Introducing the NCSs in temporal logics are beneficial, especially when the plant has a limited capacity of memory and computational power, so that it needs to rely on the network to implement both high and low level controllers. Moreover, such situation can be met in emerging system architectures that are of great importance in current and future control technologies. Consider, for example, cloud robotics (Kehoe et al. 2015), where autonomous robots such as manufacturing robots or UAVs interact with the clouds for supporting various tasks involving their decision making and learning. In temporal logics, the temporal specification may be obtained by interacting with collaborators such as humans, robots, etc., as well as the remote operators that administrate the control system. The cloud computing can be responsible for implementing the high level controller to obtain robot motion planning, and the low level controller to compute and transmit control actions to operate the robot.

In NCSs, the increased popularity of integrating the communication network has brought new control design and implementation challenges. For example, network delays and packet losses are typically present while transmitting control signals or sensor data over a communication channel. In view of this, various results have been proposed to analyze the relation among network uncertainties, control performance, and stability (see e.g., Zhang et al. (2001) and Zhang et al. (2005)). Moreover, some approaches to obtain symbolic models for NCSs under shared communication resources, communication delays or packet dropouts have been provided in recent years (see, e.g., Borri et al. (2018), Pola et al. (2018), and Mazo et al. (2010)).

Another main challenge lies in the fact that NCSs are subject to a limited range of computation and communication resources, which will be the main focus of this paper. For example, in sensor networks, sensor and relay nodes are typically battery driven and are equipped with a frugal battery capacity. Therefore, designing appropriate controllers to save the energy consumption is a crucial problem that needs to be solved. Moreover, NCSs are typically dealing with resource-limited embedded micro processors, which means that the number of tasks that can be executed in real-time is limited. Hence, reducing the amount of communication tasks allows to assign other network tasks that are necessary to be executed in real time. Based on the above motivations, two resource-aware control schemes have been proposed in recent years, namely, event-triggered control and self-triggered control (Heemels et al. 2012). In both strategies, the objective is to reduce the communication frequency between the plant and the controller. Specifically, sensor data and control inputs are exchanged over a communication network only when they are needed based on the prescribed control performances, such as ${\mathcal L}_{2}$/${\mathcal L}_{\infty }$-gain stability (Wang and Lemmon 2009), so that communication is given aperiodically. Such aperiodic scheme can potentially lead to energy savings of battery powered devices, since the communication over the network is known to be one of the main energy consumers.

The main contribution of this paper is to provide novel control and communication strategies under temporal logic specifications, which is in particular inspired by the resource-aware control paradigm as described above. Specifically, given that the plant is described by a linear discrete-time system with additive disturbances, we jointly design control and communication strategies, such that: (i) the resulting state trajectory satisfies the LTL specification, and (ii) the average communication rate, which represents how often control packets are transmitted over the communication network, is below a given threshold. The latter requirement is useful in practical implementation, since it allows us to examine how much energy consumption is necessary for satisfying the LTL specifications. Moreover, it allows to examine the possibility to assign additional network tasks if necessary to be executed in real time. To achieve the goal of this paper, our control and communication synthesis framework has in particular the following technical contributions. First, we provide a reachability analysis based on Rapidly-Exploring Random Trees (RRT), which is adapted such that all state trajectories satisfy the requirements to achieve reachability (in the sense of satisfaction relation of the “trace” definition of the LTL formula), as well as that the corresponding communication strategy can be designed. To design the communication strategy, we revise the original RRT as follows: first, for each iterative step we draw a random sample in the free state-space and pick the closest node to the sample in the tree. Then, we pick the optimal pair of the control input and the inter-communication time steps, such that the corresponding state becomes the closest to the sample. As we will see later, such optimal node will be found by considering local reachability from the dynamics of the plant with different selections of inter-communication time steps. To deal with uncertainties due to initial states and disturbances, we also expand a tree of uncertainties together with states, which will be incorporated to check feasibility (collision avoidance to the obstacles). The approach proceeds by constructing a transition system based on the result of reachability analysis, and implementing both high and low level controllers. In particular, in the high-level controller part we generate a plan such that the LTL formula can be achieved and the average communication rate is below a given threshold. As will be seen later, this is achieved by assigning suitable (communication) costs for each edge of the transition system, and finding an accepting run such that certain conditions on the assigned weights are satisfied.

Related works

So far, a wide variety of controller synthesis algorithms under temporal logic specifications have been proposed; in particular, our approach is related to Livingston et al. (2015), Bhatia et al. (2010), Karaman and Frazzoli (2011a), and Karaman (2012), since the reachabiliy analysis is based on sampling-based techniques. For example, Livingston et al. (2015) proposed probabilistic sampling schemes to generate optimal state trajectories subject to LTL specifications. Moreover, Karaman (2012) proposed sampling-based algorithms under deterministic μ-calculus specifications for nonlinear control systems with the integration of RRT* algorithms. When limiting our scope to the reachability analysis, various sampling-based algorithms have been proposed; in particular, the approach is related to Luders et al. (2010), Pepy et al. (2009), Tedrake et al. (2010), Majumdar and Tedrake (2017), and Agha-mohammadi et al. (2014), in the sense that they handle uncertainties of the plant dynamics for the reachability analysis. For example, Tedrake et al. (2010) proposed a sampling-based motion planning scheme by designing both a local LQR feedback control law and level sets that guarantee the reachability towards the goal region. The main novelty of our approach with respect to the above previous results is that, we design not only a control strategy but also a communication strategy during the reachability analysis. As previously mentioned, this is achieved by extending the RRT algorithm, in which a tree of states is expanded with different selections of inter-communication time steps. Moreover, the approach is also novel in the sense that we provide a framework to design a communication strategy such that the average communication rate is guaranteed to be below a threshold.

The approach presented in this paper builds upon our previous work in Hashimoto et al. (2018). The approach presented in this paper is advantageous over this previous result in the following sense. In the previous approach, the communication strategy was designed in the low-level controller, which dynamically assigns the communication time steps during the online implementation. However, such approach makes it difficult to analyze the communication load; since the number of communication time steps is unknown apriori, it is also unknown how often control packets should be transmitted to satisfy the LTL specifications. On the other hand, the proposed approach in this paper preliminarily assigns the communication time steps during the reachability analysis (before the implementation). Thus, we can evaluate how much communication frequency is needed to satisfy the LTL specifications. As will be seen later, this allows us to design a communication strategy such that the average communication rate is below a threshold during high level controller implementation. The second drawback of the previous result is that the low-level controller needs to solve a finite horizon optimization (feasibility) problem and transmit a (potentially large) sequence of control inputs per each communication time. This formulation may not be suitable, since network delays as well as network congestions may arise due to the load of computing and transmitting control inputs to operate the plant. On the other hand, the proposed approach in this paper considers a simple stabilizing control law that does not rely on any optimization problem, and only one control sample is necessary to be transmitted for each communication time step.

The rest of the paper is organized as follows. We describe some preliminaries and the problem formulation in Sections 2 and 3, respectively. In Section 4, reachability analysis and an algorithm to obtain a finite transition system are given. In Section 5, we propose the implementation algorithm involving both high and low level strategies. In Section 6, a simulation example is given to validate the effectiveness of the proposed approach. We finally conclude in Section 7.

Notations

Let $\mathbb {R}$, $\mathbb {R}_{+}$, $\mathbb {N}$, $\mathbb {N}_{+}$, $\mathbb {N}_{a: b}$ be the non-negative real, positive real, non-negative integers, positive integers, and the set of integers in the interval [a,b], respectively. For given two sets ${\mathcal X}\subset {\mathbb {R}}^{n}$, ${\mathcal Y} \subset {\mathbb {R}}^{n}$, denote by ${\mathcal X} \oplus {\mathcal Y}$ the Minkowski sum: ${\mathcal X} \oplus {\mathcal Y} = \{ z \in {\mathbb {R}}^{n} \ |\ \exists x\in {\mathcal X}, y\in {\mathcal Y} : z = x + y \}$. Given ${A} \in \mathbb {R}^{n\times n}$ and ${\mathcal X} \subset \mathbb {R}^{n}$, let $A {\mathcal X} = \{A x \in \mathbb {R}^{n}\ |\ x \in {\mathcal X} \}$. Given $x\in \mathbb {R}^{n}$, we denote by ∥x∥ and $\| x\|_{\infty }$ the Euclidean norm and the infinity norm of x, respectively. For simplicity, we denote the collection of N sets ${\mathcal X}_{1},\ldots ,{\mathcal X}_{N} \subset {\mathbb {R}}^{n}$ as ${\mathcal X}_{1:N} = \{ {\mathcal X}_{1},\ldots ,{\mathcal X}_{N} \}$.

2 Preliminaries

In this section, we review several useful notions and established results for transition systems, Linear Temporal Logic (LTL) formula, and Büchi Automaton.

Transition System

A transition system is a tuple ${\mathcal T} = ({S}, s_{\text {init}}, \delta , {\Pi }, g, {\mathcal W})$, where S is a set of states, s_init ∈ S is an initial state, $\delta \subseteq S\times S$ is a transition relation, π is a set of atomic propositions, $g : S \rightarrow {\Pi }$ is a labeling function, and ${\mathcal W} : \delta \rightarrow \mathbb {R}$ is a weight function. A run of ${\mathcal T}$ is defined as an infinite sequence of states s_seq = s₀s₁⋯ such that s₀ = s_init, (s_i,s_i+ 1) ∈ δ, $\forall i\in \mathbb {N}$. We denote by $\text {Run} ({\mathcal T})$ the set of all runs of ${\mathcal T}$: $\text {Run} ({\mathcal T}) = \left \{ s_{\text {seq}} \ |\ s_{\text {seq}}\ \text {is\ a\ run\ of}\ {\mathcal T} \right \}$. A trace of a run s_seq = s₀s₁s₂⋯ is given by trace(s_seq) = g(s₀)g(s₁)g(s₂)⋯. $\text {Trace} ({\mathcal T})$ is defined as a set of all traces generated by the runs of ${\mathcal T}$; $\text {Trace} ({\mathcal T}) = \{ \text {trace} (s_{\text {seq}})\ |\ s_{\text {seq}} \in \text {Run} ({\mathcal T}) \}$.

(Linear Temporal Logic Formula)::

Throughout the paper, we consider that the specification ϕ is described by an LTL formula (see e.g., Chapter 5 in Baier and Katoen (2008)) over a set of atomic propositions π. LTL formulas are constructed according to the following grammars:

$$ \phi ::= \text{true}\ |\ \pi\ |\ \phi_{1} \wedge \phi_{2} \ |\ \neg \phi \ |\ \phi_{1} \mathsf{U} \phi_{2}, $$

(1)

where π ∈π is the atomic proposition, ∧ (conjunction), ¬ (negation) are Boolean connectives, and U (until) is the temporal operator. Other useful temporal operators such as $\Box$ (always), ♢ (eventually), R (release) can be expressed by combining the operators in (1) and how they are derived is omitted for brevity. Note that in contrast to standard LTL formulas, the operator ○ (next) is not defined in (1) and will not be used to express the specification ϕ in this paper. Such formulas are often called LTL_Xformulas (see, e.g., Kloetzer and Belta (2008)). The semantics of LTL formula is inductively defined over an infinite sequence of sets of atomic propositions π_seq = π₀π₁⋯ ∈ (2^π)^ω. Roughly speaking, an atomic proposition π ∈π is satisfied if π holds true at π₀. The formula ϕ₁ ∧ ϕ₂ is satisfied if both ϕ₁ and ϕ₂ hold true. The formula ϕ₁Uϕ₂ is satisfied if ϕ₁ is satisfied until ϕ₂ is satisfied. For a given π_seq = π₀π₁⋯ ∈ (2^π)^ω and an LTL formula ϕ, we denote by π_seq⊧ϕ if π_seq satisfies the formula ϕ. We further denote by Words(ϕ) the set of all words that satisfy the formula ϕ. That is,

$$ \text{Words}(\phi) = \{ {\pi}_{\text{seq}} \in (2^{\Pi})^{\omega} \ |\ {\pi}_{\text{seq}}\models \phi \}. $$

(2)

(Büchi Automaton)::

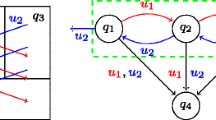
A Büchi Automaton is a tuple ${\mathcal B} = (Q , Q_{\text {init}} , {\Sigma }, \delta _{B}, F)$, where Q is a set of states; $Q_{\text {init}} \subseteq Q$ is a set of initial states; Σ is an input alphabet; $\delta _{B} \subseteq Q \times {\Sigma } \times Q$ is a non-deterministic transition relation; F is an acceptance set. A word is defined as σ_seq = σ₀σ₁⋯, with σ_i ∈Σ, $\forall i \in \mathbb {N}$. A run of ${\mathcal B}$ over a word σ_seq is defined as an infinite sequence of states q_seq = q₀q₁⋯ generated such that q₀ ∈ Q_init and (q_i,σ_i,q_i+ 1) ∈ δ_B, $\forall i \in \mathbb {N}$. A run q_seq is called accepting if there exists a word σ_seq such that F is intersected infinitely often. A word σ_seq is accepted by ${\mathcal B}$ if there exists an accepting run for σ_seq. A language$\text {Lang} ({\mathcal B})$ is defined as a set of all words accepted by ${\mathcal B}$. It is known that any LTL formula ϕ can be translated into the corresponding Büchi Automaton ${\mathcal B}$ with Σ = 2^π, such that $\text {Words}(\phi ) = \text {Lang} ({\mathcal B})$. Many off-the-shelf tools for this translation algorithm have been proposed and can be found online, e.g., LTL2BA (Oddoux and Gastin 2001).

3 Problem formulation

3.1 Plant dynamics

We consider a Networked Control System illustrated in Fig. 1, where the plant and the controller are connected over a communication network. The controller system is responsible for both implementing a high level controller that generates symbolic and communication plans for a given LTL specification ϕ, and a low level controller that generates (low level) control inputs to operate the plant. How these controllers are designed will be formally given later in this paper. Throughout the paper, we assume that the communication network is ideal; it induces neither packet dropouts nor any network delays. The dynamics of the plant is given by the following Linear-Time-Invariant (LTI) systems:

$$ \begin{array}{@{}rcl@{}} x_{k+1} = A x_{k} + B u_{k} + w_{k}, \end{array} $$

(3)

for $k\in \mathbb {N}$, where $x_{k} \in \mathbb {R}^{n}$ is the state, $u_{k} \in \mathbb {R}^{m}$ is the control input, and $w_{k} \in \mathbb {R}^{n}$ is the additive disturbance. We assume that the pair (A,B) is controllable, and that the disturbance is constrained as $w_{k} \in {\mathcal W}$, $\forall k \in \mathbb {N}$, where ${\mathcal W}$ is a given polytopic set. Regarding the state, we assume $x_{k} \in {\mathcal X}$, $\forall k \in \mathbb {N}$, where ${\mathcal X}$ is a polygonal set that can be either a convex or non-convex region. The set ${\mathcal X}$ represents the free space, in which the state is allowed to move. Inside ${\mathcal X}$, we assume that there exist in total N_I number of polytopic regions ${\mathcal R}_{1}, {\mathcal R}_{2}, \ldots , {\mathcal R}_{N_{I}} \subset {\mathcal X}$, which represent the regions of interest in ${\mathcal X}$. These regions are assumed to be disjoint, i.e., ${\mathcal R}_{i} \cap {\mathcal R}_{j} = \emptyset , \forall i, j \in \mathbb {N}_{1:N_{I}}$ with i≠j. Moreover, let ${x}_{\text {cent},i} \in {\mathcal R}_{i}$, $i \in \mathbb {N}_{1:N_{I}}$ denote the Chebyshev center (Borrelli et al. 2017) of the polytope ${\mathcal R}_{i}$. The Chebyshev center is the center of the maximum ball that is included in ${\mathcal R}_{i}$ and is obtained by solving a linear program (for details, see Section 5.4.5 in Borrelli et al. (2017)). In addition, the initial state is assumed to be given and is inside one of the regions of interest, i.e., $x_{0} \in {\mathcal R}_{\text {init}}$ where ${\mathcal R}_{\text {init}} \in {\mathcal R}_{1:N_{I}}$.

Fig. 1

Networked control system

Let π_i, $i \in \mathbb {N}_{1:N_{I}}$ be the atomic proposition assigned to the region ${\mathcal R}_{i}$. Namely, π_i holds true if and only if $x \in {\mathcal R}_{i}$. Also, denote by π₀ an atomic proposition associated to the regions of non-interest, i.e., π₀ holds true if and only if $x \in {\mathcal X} \backslash (\cup ^{N_{I}}_{i=1} {\mathcal R}_{i})$. The atomic proposition π₀ represents a dummy symbol, which will not be used to describe the specification. Let ${\Pi } = \{\pi _{1}, \pi _{2}, \ldots , \pi _{N_{I}}\}$ and ${h}_{X} : \mathbb {R}^{n} \rightarrow {\Pi }$ be the mapping from the state to the corresponding atomic proposition, i.e.,

where ${\mathcal X}_{\backslash {\mathcal R}} = {\mathcal X}\backslash (\cup ^{N_{I}}_{i=1} {\mathcal R}_{i})$.

3.2 Satisfaction relation over the state trajectory

Denote by mathx = x₀x₁x₂⋯ a state trajectory in accordance to (3), with $x_{k} \in {\mathcal X}$, $u_{k} \in \mathbb {R}^{m}$, $w_{k} \in {\mathcal W}$, $\forall k \in \mathbb {N}$. We next define the satisfaction relation of the formula ϕ by the state trajectory mathx. Let us first define the trajectory of interest as follows:

Definition 1

Given a state trajectory mathx = x₀x₁x₂⋯, the trajectory of interestmathx_I corresponding to mathx is defined as $math{{x}}_{I} = x_{\ell _{0}} x_{\ell _{1}} x_{\ell _{2}} {\cdots }$ with ℓ₀ = 0, ℓ_j < ℓ_j+ 1, $\forall j \in \mathbb {N}$, such that: $h_{X} (x_{\ell _{j}}) \in {\Pi }$, $\forall j \in \mathbb {N}$, and h_X(x_k) = π₀, ∀k ∈ (ℓ_j,ℓ_j+ 1), $\forall j \in \mathbb {N}$. ${\Box }$

Stated in words, the trajectory of interest is given by eliminating all states that belong to the regions of non-interest. The trace of the state trajectory is generated based on the trajectory of interest as defined next:

Definition 2

Given a state trajectory mathx = x₀x₁⋯, the trace of mathx is given by trace(mathx) = ρ₀ρ₁⋯, which is generated over the corresponding trajectory of interest $math{{x}}_{I} = x_{\ell _{0}} x_{\ell _{1}} x_{\ell _{2}} {\cdots }$, satisfying the following rules for all $L \in \mathbb {N}$, $i \in \mathbb {N}$:

• (i) $\rho _{0} = h_{X}(x_{\ell _{0}})$;

• (ii) If $\rho _{L} = h_{X} (x_{\ell _{i}})$ and there exists j > i such that $h_{X} (x_{\ell _{i}}) = h_{X} (x_{\ell _{i+1}}) = {\cdots } = h_{X} (x_{\ell _{j}})$, $h_{X} (x_{\ell _{j}}) \neq h_{X} (x_{\ell _{j+1}})$, then $\rho _{L +1} = h_{X} (x_{\ell _{j+1}})$;

• (iii) If $\rho _{L} = h_{X} (x_{\ell _{i}})$, and $h_{X} (x_{\ell _{j}}) = h_{X} (x_{\ell _{i}})$, ∀j ≥ i, then ρ_m = ρ_L, ∀m ≥ L.

For example, assume that $x_{k} \in {\mathcal R}_{1}$ for k = 0,1,2, $x_{k} \in {\mathcal X}_{\backslash {\mathcal R}}$ for k = 4,5 and $x_{k} \in {\mathcal R}_{2}$ for k = 6,7,8⋯. This means that the state initially starts from ${\mathcal R}_{1}$, leave ${\mathcal R}_{1}$ for entering ${\mathcal R}_{2}$, and remains there for all the time afterwards. The trajectory of interest is given by x₀x₁x₂x₆x₇x₈⋯. The trace of the trajectory according to Definition 2 is ρ = ρ₀ρ₁ρ₂⋯ with ρ₀ = h_X(x₀) = π₁ and ρ_L = π₂, ∀L ≥ 1.

Definition 3

Given a state trajectory mathx = x₀x₁x₂⋯, we say that mathx satisfies the formula ϕ if and only if the corresponding trace according to Definition 2 satisfies ϕ, i.e., π_seq = trace(mathx)⊧ϕ.

3.3 Communication strategy

To satisfy the formula ϕ, the plant interacts with the low level controller over the communication network for obtaining control inputs in real time. To indicate the communication times, let $k_{m}, m\in \mathbb {N}$ with $k_{m+1} > k_{m}, \forall m\in \mathbb {N}$ be the communication time steps between the plant and the controller. That is, for each k_m, $m\in \mathbb {N}$ the plant transmits the current state information $x_{k_{m}}$ to the controller, and the controller computes a suitable control input to be applied and transmit it back to the plant. We assume that the control input is given in a sample-and-hold implementation, i.e., $u_{k_{m}+\ell } = u_{k_{m}}$, $\forall \ell \in \mathbb {N}_{1 : k_{m+1}-k_{m}-1}$, $\forall m\in \mathbb {N}$. In what follows, we introduce the notion of average communication rate:

Definition 4

Given k_m, $m\in \mathbb {N}$, the average communication rateρ_ave ∈ [0,1] is given by

$$ \rho_{\text{ave}} =\lim\limits_{m \rightarrow \infty}\cfrac{m}{k_{m}} $$

(6)

Intuitively, the average communication rate is an asymptotic ratio between the number of communication time steps and the time steps. As we will see below, the communication time steps $k_{m}, m\in \mathbb {N}$ are designed, such that the state trajectory satisfies the LTL formula, as well as that a certain communication constraint on ρ_ave is satisfied.

Remark 1

Note that the actual number of communication time steps until k_m is m + 1, instead of m. However, since $k_{m} \rightarrow \infty$ as $m \rightarrow \infty$, we have $\lim _{m\rightarrow \infty } (m+1)/k_{m} = \lim _{m\rightarrow \infty } m/k_{m}$. Hence, the lack of “plus one” term does not affect our result provided in this paper.

3.4 Problem formulation

We now describe the main problem to be solved in this paper:

Problem 1

Given $x_{0} \in {\mathcal R}_{\text {init}} \in {\mathcal R}_{1:N_{I}}$, ϕ and $\bar {\rho } \in (0, 1]$, design both control and communication strategies in a sample-and-hold implementation (see Section 3.3), such that:

• (A.1) the resulting state trajectory satisfies ϕ;

• (A.2) the average communication rate is below $\bar {\rho }$, i.e., $\rho _{\text {ave}} < \bar {\rho }$.

That is, the goal of this paper is to design control and communication strategies, such that the resulting state trajectory satisfies the desired LTL formula ϕ, and the corresponding average communication rate is below a given threshold $\bar {\rho }$. In practice, $\bar {\rho }$ can be provided in terms of the limited communication resources that are present in NCSs, such as the lifetime of the battery powered devices, the number of network tasks that can be executed in real time, and so on. For example, if the relationship between the frequency of communication and the lifetime of the battery powered devices is known, we may select $\bar {\rho }$ in order to ensure that the battery powered devices can stay alive longer than the desired period. As another example, suppose that the embedded micro-processor is able to execute only one task for each k (i.e., there exists only one time slot that the micro-processor can assign the task for each k), and that in addition to the communication task, another network task should be executed within 60% of the total number of executions. In this case, we may select $\bar {\rho }$ as $\bar {\rho } = 1 -0.6 = 0.4$, so that the rate of executing the communication task is below 40%.

4 Constructing transition system

As a first step to solve Problem 1, we construct a finite transition system that represents an abstracted model to describe the behavior of the control systems in (3). Specifically, we aim at obtaining ${\mathcal T} = (S , s_{\text {init}} , \delta , {\Pi }, g, {\mathcal W}_{1}, {\mathcal W}_{2})$, where $S = \{ s_{1}, \ldots , s_{N_{I}} \}$ is a set of symbolic states, s_init ∈ S is an initial state, $\delta \subseteq S \times S$ is a transition relation, ${\Pi } = \{\pi _{1}, \ldots , \pi _{N_{I}}\}$ is a set of atomic propositions, $g : S \rightarrow {\Pi }$ is a labeling function, and ${\mathcal W}_{1}, {\mathcal W}_{2} : \delta \rightarrow \mathbb {N}$ are weight functions. Roughly speaking, each symbol s_i ∈ S indicates the region of interest ${\mathcal R}_{i}$ (i.e., the region having the same index i). To relate each symbol to the corresponding region of interest, let ${\Gamma } : S \rightarrow {\mathcal R}_{1:N_{I}}$ be the mapping given by

$$ {\Gamma} ({s}_{i}) = {\mathcal R}_{i}, \ \ \forall i \in \mathbb{N}_{1:N_{I}}. $$

(7)

Conversely, let ${\Gamma }^{-1}: {\mathcal R}_{1:N_{I}} \rightarrow S$ be the mapping from each region of interest to the corresponding symbolic state. The symbol s_init ∈ S represents the symbolic state associated with ${\mathcal R}_{\text {init}}$, i.e., $s_{\text {init}} = {\Gamma }^{-1} ({\mathcal R}_{\text {init}})$. The labeling function g outputs the atomic proposition assigned to ${\mathcal R}_{i}$, i.e., g(s_i) = π_i. The weight functions ${\mathcal W}_{1}, {\mathcal W}_{2}$ are defined to output, as we will see later, the number of communication time steps and the total number of time steps for each transition in δ, respectively. The transition relation (s_i,s_j) ∈ δ indicates that every $x\in {\mathcal R}_{i}$ can be steered to ${\mathcal R}_{j}$ in finite time. A more formal definition of δ is provided in the next subsection.

4.1 Definition of reachability

To characterize δ in the transition system, we next introduce the notion of reachability among the regions of interest. To this end, consider a pair $({\mathcal R}_{i}, {\mathcal R}_{j}) \in {\mathcal R}_{1:N_{I}} \times {\mathcal R}_{1:N_{I}}$ with i≠j. For notational simplicity, let ${\mathcal X}_{ij} \subset {\mathcal X}$ be given by

$$ {\mathcal X}_{ij} = {\mathcal X} \backslash \bigcup_{n\in \mathbb{N}_{\backslash ij}} {\mathcal R}_{n}, $$

(8)

where $\mathbb {N}_{\backslash ij} = \{1, \ldots , N_{I} \}\backslash \{i, j \}$. That is, ${\mathcal X}_{ij}$ represents the free space that we exclude all regions of interest other than ${\mathcal R}_{i}$ and ${\mathcal R}_{j}$. Note that ${\mathcal X}_{ij}$ is a polygonal set that can be a non-convex region. Whether the transition is allowed in ${\mathcal T}$, from $s_{i} = {\Gamma }^{-1} ({\mathcal R}_{i})$ to $s_{j} = {\Gamma }^{-1} ({\mathcal R}_{j})$ (i.e., (s_i,s_j) ∈ δ), is determined according to the following notion of reachability:

Definition 5 (Reachability)

We say that the reachability holds from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$ (i≠j), which we denote by (s_i,s_j) ∈ δ, if there exists $k_{F} \in \mathbb {N}_{+}$ such that the following holds: for any $x_{0} \in {\mathcal R}_{i}$ and the disturbance sequence $w_{0}, w_{1}, \ldots , w_{k_{F}-1} \in {\mathcal W}$, there exist $u_{0}, u_{1}, \ldots , u_{k_{F} - 1} \in \mathbb {R}^{m}$ such that the resulting state trajectory $x_{0}, x_{1}, \ldots , x_{k_{F}}$ in accordance with (3) satisfies

• (C.1) $x_{k_{F}}\in {\mathcal R}_{j}$,

• (C.2) $x_{k} \in {\mathcal X}_{ij}, \ \forall k \in \mathbb {N}_{0:k_{F}}$,

• (C.3) If $x_{k^{\prime }} \in {\mathcal R}_{j}$ for some $k^{\prime } \in \mathbb {N}_{1:k_{F}}$, then $x_{k} \notin {\mathcal R}_{i}$, $\forall k \in \mathbb {N}_{k^{\prime }:k_{F}}$.

Based on Definition 5, reachability holds from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$ if there exists a controller such that any state in ${\mathcal R}_{i}$ can be steered to ${\mathcal R}_{j}$ in finite time. Moreover, we require by (C.2) that the state needs to avoid any other region of interest apart from ${\mathcal R}_{i}$ and ${\mathcal R}_{j}$. Also, (C.3) implies that once the state enters ${\mathcal R}_{j}$ it must not enter ${\mathcal R}_{i}$ afterwards. The conditions (C.2), (C.3) are essentially required to guarantee that the trace of the state trajectory satisfies the following property:

Proposition 1

For every$x_{0} \in {\mathcal R}_{i}$, the trace of the state trajectoryx₀,x₁,…, $x_{k_{F}}$satisfying (C.1)–(C.3) isπ_iπ_j.

Proposition 1 implies that the trace of the state trajectory satisfying (C.1)–(C.3), which is generated according to the rules in Definition 2, is consistent with the trace for the transition from s_i to s_j (i.e., g(s_i)g(s_j)). As will be seen later, this leads to that the trace of ${\mathcal T}$ that satisfies ϕ implies that the corresponding trace of the actual state trajectory also satisfies ϕ.

4.2 Reachability analysis from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$

This section provides a way to analyze reachability from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$. The reachability analysis presented in this paper is based on the RRT algorithm (LaValle 2006), which is adapted such that the state trajectories satisfy all requirements to achieve reachability (i.e., the conditions (C.1)–(C.3)), as well as that the corresponding communication strategy can be designed. The overall algorithm is illustrated in Algorithm 1 and the details are described below. As the inputs to the algorithm, we give $N_{\max \limits } \in \mathbb {N}_{+}$ and $L_{\max \limits } \in \mathbb {N}_{+}$ as the user-defined parameters, which represent the total number of iterations for building a tree and the maximum inter-communication time steps, respectively. Moreover, we give a matrix $K \in \mathbb {R}^{m\times n}$, where A + BK is stable, which will be used to obtain (state feedback) control inputs and uncertainty propagations around the nominal state trajectory. The algorithm starts by initializing the set of nodes ${\mathcal V}$ and edges ${\mathcal E}$ as empty sets. In addition, we initialize the mapping ${\mathcal I} : {\mathcal X} \times {\mathcal X} \rightarrow \mathbb {N}_{+}$, which will be used to stack the inter-communication time steps required to steer the states in ${\mathcal X}$. As shown in the algorithm (Line 3), we stack the pair $(x_{\text {cent}, i}, {\mathcal R}_{i})$ in ${\mathcal V}$ as the initial node. Intuitively, the set ${\mathcal R}_{i}$ represents the uncertainty of the (actual) initial state, which is also stacked together with x_cent,i in ${\mathcal V}$.

The algorithm proceeds by expanding a tree of states (Line 4–Line 22). First, $\mathsf {Sample} ({\mathcal X}_{ij})$ draws a state randomly chosen from ${\mathcal X}_{ij}$. For given ${\mathcal V}$ and $x_{\text {samp}} \in {\mathcal X}_{ij}$, $\mathsf {FindNearest}({\mathcal V}, x_{\text {samp}})$ finds the closest node in ${\mathcal V}$ to x_samp, i.e.,

$$ \mathsf{FindNearest} ({\mathcal V}, x_{\text{samp}}) = \underset{(x, {\mathcal X} ) \in {\mathcal V}}{\arg\min} \| x - x_{\text{samp}}\|. $$

(9)

The function Steer(x_nearest,x_samp,L) finds a control input and the corresponding state by solving the following problem:

$$ \begin{array}{@{}rcl@{}} \underset{u \in \mathbb{R}^{m}}{{\min}} \ \left \|A^{L} x_{\text{nearest}} + \sum\limits^{L}_{\ell=1} A^{\ell -1} Bu - x_{\text{samp}} \right \|. \end{array} $$

(10)

In (10), the term $A^{L} x_{\text {nearest}} + {\sum }^{L}_{\ell =1} A^{\ell -1} Bu$ represents the nominal state from x_nearest by applying uconstantly for L time steps. Namely, the function finds an L-step constant control input such that the corresponding state is close to x_samp as much as possible from x_nearest. Since the control input is applied constantly for L time steps, we will utilize L as the inter-communication time steps to steer the state from x_nearest. Let $\hat {u}$ be an optimal control input by solving (10) and let $\hat {x}_{L} = A^{L} x_{\text {nearest}} + {\sum }^{L}_{\ell =1} A^{\ell -1} B\hat {u}$. Then, Steer returns $\hat {x}_{L}$ and $\hat {u}$, i.e.,

$$ \mathsf{Steer} (x_{\text{nearest}}, x_{\text{samp}}, L) = \left \{\hat{x}_{L}, \hat{u}\right \}. $$

(11)

The function $\mathsf {IfClose} (\hat {x}_{L}, \hat {x}_{\text {opt}}, x_{\text {samp}})$:

$$ \begin{array}{@{}rcl@{}} {\mathsf{IfClose} (\hat{x}_{L}, \hat{x}_{\text{opt}}, x_{\text{samp}}) = }\left\{\begin{array}{ll} \mathsf{True}, \ \ \ \text{if}\ \|\hat{x}_{L} - x_{\text{samp}}\| < \|\hat{x}_{\text{opt}} - x_{\text{samp}}\|\\ \ \ \ \ \ \ \ \ \ \ \ \ \text{or}\ \| \hat{x}_L - x_{\text{samp}} \| < \varepsilon, \\ \mathsf{False}, \ \ \text{otherwise}, \end{array}\right. \end{array} $$

(12)

where ε > 0 is a given threshold. That is, it examines if x_samp is closer to $\hat {x}_{L}$ than to $\hat {x}_{\text {opt}}$ or it is close enough tox_samp. If $\mathsf {IfClose} (\hat {x}_{L}, \hat {x}_{\text {opt}}, x_{\text {samp}}) =\mathsf {True}$, then $\hat {x}_{\text {opt}}$ is replaced by $\hat {x}_{L}$ (Line 11). Note that if $\| \hat {x}_{L} - x_{\text {samp}} \| < \varepsilon$ is satisfied for several values of L, then $\hat {x}_{L}$ with the largestL is chosen (since the algorithm computes IfClose starting with L = 1). The function GenTraj(x_nearest, $\hat {u}_{\text {opt}}, L_{\text {opt}} )$ is executed to obtain the nominal state trajectory by applying the optimal control input: $\mathsf {GenTraj}(x_{\text {nearest}}, \hat {u}_{\text {opt}}, L_{\text {opt}} ) = \hat {x}_{0:L_{\text {opt}}}$, where $\hat {x}_{0} = x_{\text {nearest}}$ and $\hat {x}_{\ell + 1} = A \hat {x}_{\ell } + B \hat {u}_{\text {opt}}$, $\forall \ell \in \mathbb {N}_{0:L_{\text {opt}} -1}$. Then, the function $\mathsf {UncertainSets}(\hat {x}_{0:L_{\text {opt}}}, \hat {u}_{\text {opt}})$ (Line 16) yields a sequence of polytopic sets as follows:

$$ \mathsf{UncertainSets} (\hat{x}_{0:L_{\text{opt}}}, \hat{u}_{\text{opt}}) = \{ {\mathcal X}_{0}, \ldots, {\mathcal X}_{L_{\text{opt}}} \}, $$

(13)

where $(\hat {x}_{0}, {\mathcal X}_{0}) \in {\mathcal V}$ and ${\mathcal X}_{1}, \ldots , {\mathcal X}_{L_{\text {opt}}}$ are given by

$$ \begin{array}{@{}rcl@{}} {\mathcal X}_{\ell} = \hat{x}_{\ell} \oplus \left (A^{\ell} + \sum\limits^{\ell}_{\ell^{\prime} =1} A^{\ell^{\prime} -1} B K \right) \left (- \hat{x}_{0} \oplus {\mathcal X}_{0} \right ) \oplus \sum\limits^{\ell-1}_{\ell^{\prime} =0} A^{\ell^{\prime}} {\mathcal W}, \end{array} $$

(14)

for all $\ell \in \mathbb {N}_{1 : L_{\text {opt}}}$. Intuitively, and as will be clearer later in this section (see in particular Lemma 1), the sets ${\mathcal X}_{0}, \ldots , {\mathcal X}_{L_{\text {opt}}}$ represent uncertainty propagations of the actual state trajectory around the nominal one $\hat {x}_{0}, \ldots , \hat {x}_{L_{\text {opt}}}$, starting from any initial state from ${\mathcal X}_{0}$ by applying a suitable control strategy. The function $\mathsf {IfFeasible}({\mathcal X}_{{0:L_{\text {opt}}}})$ (Line 17) examines if all ${\mathcal X}_{{0}}, \ldots , {\mathcal X}_{{L}_{\text {opt}}}$ are inside ${\mathcal X}_{ij}$, i.e.,

If the feasibility holds, the pair $(\hat {x}_{L_{\text {opt}}}, {\mathcal X}_{L_{\text {opt}}})$, and the triple $((\hat {x}_{0},$${\mathcal X}_{0}), \hat {u}_{\text {opt}}$, $(\hat {x}_{L_{\text {opt}}}, {\mathcal X}_{L_{\text {opt}}}))$ are stored in ${\mathcal V}$ and ${\mathcal E}$, respectively. Moreover, we assign the corresponding inter-communication time steps to the mapping ${\mathcal I}$ (Line 18–Line 22).

Once a set of nodes and edges $({\mathcal V}, {\mathcal E})$ are obtained, the function FindTraj is executed to find nominal states, inputs and the corresponding uncertain sets from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$ in the following way: if there exist $M \in \mathbb {N}_{+}$ and $\tilde {x}_{0:M}, \tilde {u}_{0:M-1}, \widetilde {{\mathcal X}}_{0:M}$, where $(\tilde {x}_{0}, \widetilde {{\mathcal X}}_{0}) = ({x}_{\text {cent},i}, {\mathcal R}_{i})$, and

$$ \begin{array}{@{}rcl@{}} && ((\tilde{x}_{m}, \widetilde{{\mathcal X}}_{m}), \tilde{u}_{m}, (\tilde{x}_{m+1}, \widetilde{{\mathcal X}}_{m+1})) \in {\mathcal E},\ \forall m \in \mathbb{N}_{0 : M-1 }, \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} &&\widetilde{{\mathcal X}}_{M}\subseteq {\mathcal R}_{j}, \end{array} $$

(18)

then we set $\mathsf {FindTraj} ({\mathcal V}, {\mathcal E}) = \{ \tilde {x}_{0:M}, \tilde {u}_{0:M-1}, \widetilde {{\mathcal X}}_{0:M} \}$. The illustration of the trajectory $\tilde {x}_{0:M}$ is shown in Fig. 2a. Roughly speaking, the condition in (18) indicates that the uncertainty around the terminal state (i.e., $\widetilde {{\mathcal X}}_{M}$) is small enough such that the actual state trajectory is guaranteed to enter ${\mathcal R}_{j}$. The above sequences can be found by implementing a graph search from the initial node $({x}_{\text {cent},i}, {\mathcal R}_{i})$ to some node in ${\mathcal V}$, whose state and the set are both inside ${\mathcal R}_{j}$. If multiple feasible sequences satisfying (17) and (18) are found, we select the one with the minimum value of the communication rate M/k_M. Note that to steer the state from $\tilde {x}_{m}$ to $\tilde {x}_{m+1}$ ($m \in \mathbb {N}_{0:M-1}$), $\tilde {u}_{m}$ needs to be applied constantly for ${\mathcal I} (\tilde {x}_{m}, \tilde {x}_{m+1})$ time steps, i.e., $\tilde {x}_{m+1} = A^{L_{m}} \tilde {x}_{m} + {\sum }^{L_{m}}_{\ell =1} A^{\ell -1} B\tilde {u}_{m}$, where $L_{m} = {\mathcal I} (\tilde {x}_{m}, \tilde {x}_{m+1})$.

The function UpdateTimes (Line 24) is defined as follows: $\mathsf {UpdateTimes}(\tilde {x}_{0:M}$, ${\mathcal I}) = \{k_{0}, k_{1}, \ldots , k_{M}\}$, where k₀ = 0 and

$$ k_{m} = k_{m-1} + {\mathcal I} (\tilde{x}_{m-1}, \tilde{x}_{m}),\ \forall m \in \mathbb{N}_{1:M}. $$

(19)

Intuitively, k₀,k₁,…,k_M− 1 indicate the time steps when control inputs are updated, which, as will be seen below, represent the communication time steps between the plant and the controller. In addition, k_M indicates the terminal time step when the state trajectory enters ${\mathcal X}_{j}$. The function GenAllTraj is defined to generate all nominal states, inputs and the corresponding uncertain sets including the ones during the inter-communication time steps: $\mathsf {GenAllTraj} (\tilde {x}_{0:M}, \tilde {u}_{0:M-1}, \widetilde {\mathcal X}_{0:M}, k_{0: M}) = \{\hat {u}_{0:k_{M}-1}, \hat {x}_{0:k_{M}}, {{\mathcal X}}_{0: k_{M}} \}$, where

$$ \begin{array}{@{}rcl@{}} \hat{u}_{k_{m}} &=& \tilde{u}_{m},\ \ \forall m\in\mathbb{N}_{0:M-1}, \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} \hat{u}_{k_{m} + \ell} & =& \hat{u}_{k_{m}},\ \forall \ell \in \mathbb{N}_{1:k_{m+1} - k_{m}-1}, \forall m\in\mathbb{N}_{0:M-1}, \end{array} $$

(21)

and

$$ \begin{array}{@{}rcl@{}} \hat{x}_{k+1} = A \hat{x}_{k} + B \hat{u}_{k},\ \forall k\in\mathbb{N}_{0:k_{M}-1}. \end{array} $$

(22)

An example of the trajectory $\hat {x}_{0}, \ldots , \hat {x}_{k_{M}}$ is illustrated in Fig. 2b. Note that from (20), (21) and (22), it follows that $\hat {x}_{k_{m}} = \tilde {x}_{m}$, $\forall m\in \mathbb {N}_{0:M}$. The sequence ${\mathcal X}_{0 : k_{M}}$ is given as follows: ${\mathcal X}_{0} = \widetilde {\mathcal X}_{0} (= {\mathcal R}_{i})$ and

$$ \begin{array}{@{}rcl@{}} {\mathcal X}_{k_{m} + \ell} = \hat{x}_{k_{m} + \ell} \oplus \left (A^{\ell} + \sum\limits^{\ell}_{\ell^{\prime} =1} A^{\ell^{\prime} -1} B K \right) (- \hat{x}_{k_{m}} \oplus {\mathcal X}_{k_{m}}) \oplus \sum\limits^{\ell-1}_{\ell^{\prime} =0} A^{\ell^{\prime}} {\mathcal W}, \end{array} $$

(23)

for all $\ell \in \mathbb {N}_{1:k_{m+1} - k_{m}}, m \in \mathbb {N}_{0:M-1}$. Note that from (23) and (14), it follows that ${\mathcal X}_{k_{m}} = \widetilde {\mathcal X}_{m}$, $\forall m \in \mathbb {N}_{0:M}$. Finally, the function IfReachable examines if the reachability holds from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$ in the following way: $\mathsf {IfReachable} ({\mathcal X}_{0:k_{M}}) = \mathsf {True}$ if the following holds:

$$ {\mathcal X}_{k^{\prime}} \cap {\mathcal R}_{j} \neq \emptyset,\ k^{\prime} \in \mathbb{N}_{0:k_{M}} \implies {\mathcal X}_{k} \cap {\mathcal R}_{i} = \emptyset,\ \forall k\in\mathbb{N}_{k^{\prime}:k_{M}}, $$

(24)

and $\mathsf {IfReachable} ({\mathcal X}_{0:k_{M}}) = \mathsf {False}$ otherwise. The condition in (24) indicates that once some uncertain set intersects ${\mathcal R}_{j}$, it does not intersect ${\mathcal R}_{i}$ afterwards, which aims at fulfilling the condition (C.3) in Definition 5. Finally, if IfReachable returns True, the algorithm returns the sequences k_0:M, $\hat {x}_{0:k_{M}}$, $\hat {u}_{0:k_{M}-1}$, ${{\mathcal X}}_{0: k_{M}}$.

Fig. 2

Illustration of $\tilde {x}_{0}, \ldots , \tilde {x}_{M}$ from (17) and (18) and $\hat {x}_{0}, \ldots , \hat {x}_{k_{M}}$ from (22)

The fact that the reachability holds based on the above is validated by the following result:

Lemma 1

Suppose that$\mathsf {IfReachable} ({\mathcal X}_{0:k_{M}}) = \mathsf {True}$and Algorithm 1 returns$k_{0:M}, \hat {x}_{0:k_{M}}, \hat {u}_{0:k_{M}-1}, {{\mathcal X}}_{0: k_{M}}$. Then, it follows that the reachability holds from${\mathcal R}_{i}$ to ${\mathcal R}_{j}$. ${\Box }$

Proof

: Suppose that $\mathsf {IfReachable} ({\mathcal X}_{0:k_{M}}) = \mathsf {True}$ and Algorithm 1 returns $k_{0:M}, \hat {x}_{0:k_{M}}, \hat {u}_{0:k_{M}-1}, {{\mathcal X}}_{0: k_{M}}$. For any $x_{0} \in {\mathcal R}_{i}$, let x_k, $k\in \mathbb {N}_{0:k_{M}}$ be the actual state trajectory by applying u_k, $k\in \mathbb {N}_{0:k_{M}-1}$, i.e., x_k+ 1 = Ax_k + Bu_k + w_k, $\forall k\in \mathbb {N}_{0:k_{M}-1}$, where

$$ \begin{array}{@{}rcl@{}} u_{k} &=& K (x_{k} - \hat{x}_{k}) + \hat{u}_{k},\ \ \text{if}\ k=k_{m}, m\in\mathbb{N}_{0:M-1} \end{array} $$

(25)

$$ \begin{array}{@{}rcl@{}} u_{k} &=& u_{k-1},\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{otherwise}. \end{array} $$

(26)

That is, the state feedback controller is utilized for the update times $k_{m}, m\in \mathbb {N}_{0:M-1}$, and the constant controller is utilized for all the other time steps. In the following, we first show by induction that $x_{k} \in {\mathcal X}_{k}$, $\forall k \in \mathbb {N}_{0: k_{M}}$. For the initial time step k = k₀ = 0, we have $x_{0} \in {\mathcal R}_{i} = {\mathcal X}_{0}$. Assume that $x_{k_{m}} \in {\mathcal X}_{k_{m}}$ for some $m\in \mathbb {N}_{0:M-1}$. Then the difference between the actual state and the nominal one for k_m + ℓ, $\ell \in \mathbb {N}_{1:k_{m+1} -k_{m}}$ is given by

$$ \begin{array}{@{}rcl@{}} x_{k_{m} + \ell} - \hat{x}_{k_{m} + \ell} &=& A^{\ell} x_{k_{m}} + \sum\limits^{\ell}_{\ell^{\prime} =1} A^{\ell^{\prime}-1} B \left( K (x_{k_{m}} - \hat{x}_{k_{m}}) + \hat{u}_{k_{m}}\right) \\&&+ \sum\limits^{\ell}_{\ell^{\prime} =1} A^{\ell^{\prime}-1} w_{k_{m} + \ell^{\prime}} - \left (A^{\ell} \hat{x}_{k_{m}} + \sum\limits^{\ell}_{\ell^{\prime} =1} A^{\ell^{\prime}-1} B \hat{u}_{k_{m}} \right ) \\ &= &\left (A^{\ell} + \sum\limits^{\ell}_{\ell^{\prime} =1} A^{\ell^{\prime} -1} B K\right ) (x_{k_{m}} - \hat{x}_{k_{m}}) + \sum\limits^{\ell-1}_{\ell^{\prime} =0} A^{\ell^{\prime}} w_{k_{m} + \ell^{\prime}}, \end{array} $$

for all $\ell \in \mathbb {N}_{1:k_{m+1} -k_{m}}$. Thus, from (23), it follows that $x_{k_{m} + \ell } \in {\mathcal X}_{k_{m} + \ell }$, $\forall \ell \in \mathbb {N}_{1:k_{m+1} -k_{m}}$. Therefore, we have $x_{k_{m}} \in {\mathcal X}_{k_{m}} \implies x_{k_{m} + \ell } \in {\mathcal X}_{k_{m} + \ell }, \forall \ell \in \mathbb {N}_{1:k_{m+1} -k_{m}}$, and it is inductively shown that $x_{k} \in {\mathcal X}_{k}$, $\forall k \in \mathbb {N}_{0: k_{M}}$. Moreover, from the feasibility condition in (15), it follows that ${\mathcal X}_{{k}} \subseteq {\mathcal X}_{ij}$, $\forall k\in \mathbb {N}_{0:k_{M}}$. Thus, we obtain $x_{k} \in {\mathcal X}_{ij}$, $\forall k\in \mathbb {N}_{0:k_{M}}$ and the condition (C.2) in Definition 5 holds. Moreover, from (18), it follows that $x_{k_{M}} \in {\mathcal X}_{k_{M}} = \widetilde {\mathcal X}_{M} \subseteq {\mathcal X}_{j}$. Hence, the condition (C.1) in Definition 5 holds. Finally, from the definition of IfReachable, it follows that

$$ x_{k^{\prime}} \in {\mathcal R}_{j},\ k^{\prime} \in \mathbb{N}_{1:k_{M}} \implies x_{k} \notin {\mathcal R}_{i},\ \forall k \in \mathbb{N}_{k^{\prime}:k_{M}}, $$

(27)

which directly shows that the condition (C.3) in Definition 5 holds. Therefore, it is shown that the reachability holds from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$. □

From Lemma 1, if IfReachable returns True there exists a control strategy, as shown in (25) and (26), such that the reachability holds from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$. Moreover, from (25) and (26), each $u_{k_{m}}$, $m\in \mathbb {N}_{0:M-1}$ is applied constantly for all [k_m,k_m+ 1), which means that the control inputs are updated at k₀,k₁,…,k_M− 1. In other words, the communication time steps when the plant needs to transmit the current state information to the controller are given by k₀,k₁,…,k_M− 1. For the notational use in the next section, let ${\mathcal L}_{x0}, {\mathcal L}_{x}$, ${\mathcal L}_{u}$, ${\mathcal L}_{I}$ be the mappings given by

$$ \begin{array}{@{}rcl@{}} &&{\mathcal L}_{x0} ({\mathcal R}_{i}, {\mathcal R}_{j}) = \hat{x}_{0:k_{M}}, \ \ {\mathcal L}_{x} ({\mathcal R}_{i}, {\mathcal R}_{j}) = \hat{x}_{1:k_{M}}, \end{array} $$

(28)

$$ \begin{array}{@{}rcl@{}} &&{\mathcal L}_{u} ({\mathcal R}_{i}, {\mathcal R}_{j}) =\hat{u}_{0:k_{M}-1},\ \ {\mathcal L}_{I} ({\mathcal R}_{i}, {\mathcal R}_{j}) = L_{0:M-1}, \end{array} $$

(29)

where L_m = k_m+ 1 − k_m, $\forall m\in \mathbb {N}_{0:M-1}$. That is, the above mappings yield the nominal state and control trajectories, and the inter-communication time steps to achieve the reachability from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$.

Some remarks on Algorithm 1 are in order as follows:

Remark 2

(On achieving the minimum communication frequency): In this paper, we employ an extended version of the RRT algorithm, so that the communication strategy can be designed while ensuring reachability. Note that the algorithm is not guaranteed to provide the optimal communication strategy, which means the resulting communication scheduling may not provide the minimum communication frequency. The minimum number of communication times may be achieved by solving an appropriate optimal control problem for the steering function and by employing the RRT* algorithm (Karaman 2011b) that integrates the rewiring procedure. Since we aim at reducing the number of control updates, one might attempt to solve the following optimization problem for the steering function:

$$ \begin{array}{@{}rcl@{}} &\underset{\hat{x}_{0:N}, u_{0:N-1}, N}{{\arg\min}} \ \sum\limits^{N-1}_{\ell =0} \|u_{\ell +1} - u_{\ell} \|_{0}, \\ & \text{s.t.}\ \hat{x}_{\ell+1} = A \hat{x}_{\ell} + B u_{\ell}, \ \forall \ell \in\mathbb{N}_{0:N-1} \\ &\ \ \ \ \ \ x_{0} = x_{\text{nearest}} \\ &\ \ \ \ \ \ x_{N} = x_{\text{sample}}, \end{array} $$

where ∥⋅∥₀ denotes the ℓ₀-norm that represents the number of non-zero components. In other words, we aim to find control inputs and the time step such that the number of control updates is minimized. Using the above problem for the steering function and by the rewiring procedure as in Karaman (2011b), one may obtain the reachable trajectory that minimizes the number of control updates (i.e., the communication frequency). However, the above optimization problem is a computationally expensive problem, as it involves the ℓ₀-norm cost function. Since the steering function would be utilized for both generating a new sample and the rewiring procedure, using the above problem is clearly unrealistic. Although one may relax the problem by using the ℓ₁-norm cost function, there is no guarantee how such relaxation results in reducing the number of control updates. Therefore, while Algorithm 1 may not minimize the communication frequency, it is more suitable for practical implementations than the above approach in terms of the computation load. ${\Box }$

Remark 3

(On the computational complexity of Algorithm 1) : The computational complexity of Algorithm 1 can be analyzed by looking at some primitive procedures in Algorithm 1. The complexity of drawing a sample (Sample) is constant. The complexity of finding the nearest neighbor FindNearest is O(N) (N denotes the iteration number as in Algorithm 1) by using a naive brute-force search, while other efficient but approximate solutions exist (see, e.g., Karaman (2011b)). The steering procedure (Steering) requires to solve a quadratic programming, in which the computational complexity is polynomial with the size of the variables (see, e.g., Monteiro and Adler (1989)), which is m in this case, i.e., the dimension of the control input. To analyze the complexity of $\mathsf {IfFeasible} ({\mathcal X}_{0:L})$, suppose that ${\mathcal X} = \overline {{\mathcal X}} \backslash {\mathcal O}_{1} \cup {\cdots } \cup {\mathcal O}_{N_{o}}$, where $\overline {{\mathcal X}} \subset \mathbb {R}^{n}$ denotes a polytopic set, ${\mathcal O}_{1}, {\ldots } {\mathcal O}_{N_{o}}$ are the polytopic obstacles to be avoided in $\widetilde {{\mathcal X}}$, and N_o is the number of the obstacles. For given inter-communitation time steps $L \in \mathbb {N}_{1:L_{\max \limits }}$, IfFeasible examines if L polytopic sets are all inside ${\mathcal X}_{ij}$, which can be done as follows: (i) compute the intersections between each ${\mathcal X}_{\ell }$, $\ell \in \mathbb {N}_{1:L}$ and each obstacle and check if these are all empty; (ii) compute the intersections between each ${\mathcal X}_{\ell }$, $\ell \in \mathbb {N}_{1:L}$ and each region of interest except ${\mathcal R}_{i}$, ${\mathcal R}_{j}$, and check if these are all empty. The complexity of computing the intersection between each pair $({\mathcal X}_{\ell }, {\mathcal O}_{n})$, $(\ell , n) \in \mathbb {N}_{1:L}\times \mathbb {N}_{1:N_{o}}$ (or each pair $({\mathcal X}_{\ell }, {\mathcal R}_{n})$, $(\ell , n) \in \mathbb {N}_{1:L}\times \mathbb {N}_{\backslash ij}$) is $O(N_{\text {ver}} \log N_{\text {ver}})$, where N_ver denotes the sum of the number of verticies of ${\mathcal X}_{\ell }$ and ${\mathcal O}_{n}$ (or ${\mathcal X}_{\ell }$ and ${\mathcal R}_{n})$, see, e.g., Monteiro and Adler (1989). Hence, the computational complexity of IfFeasible depends on the workspace environment, such as the number of obstacles in the state-space. ${\Box }$

4.3 Construction of ${\mathcal T}$

Let us now go back to the beginning of Section 4 and consider constructing the transition system ${\mathcal T}$. Suppose that reachability holds from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$ (i.e., $\mathsf {IfReachable} ({\mathcal X}_{0:k_{M}}) = \mathsf {True}$) and Algorithm 1 returns $k_{0:M}, \hat {x}_{0:k_{M}}, \hat {u}_{0:k_{M}-1}$, ${{\mathcal X}}_{0: k_{M}}$. Then, to construct the transition system ${\mathcal T}$, we set (s_i,s_j) ∈ δ and assign the values for the weight functions ${\mathcal W}_{1}, {\mathcal W}_{2}$ as follows:

$$ \begin{array}{@{}rcl@{}} {\mathcal W}_{1} (s_{i}, s_{j}) = M,\ \ {\mathcal W}_{2} (s_{i}, s_{j}) = k_{M}. \end{array} $$

(30)

That is, we assign for ${\mathcal W}_{1} (s_{i}, s_{j})$ and ${\mathcal W}_{2} (s_{i}, s_{j})$ the number of communication time steps and the total number of time steps to achieve reachability from ${\mathcal R}_{i}$ to ${\mathcal R}_{j}$, respectively. The weight functions ${\mathcal W}_{1}$ and ${\mathcal W}_{2}$ will be utilized to obtain the accepting run of ${\mathcal T}$, such that the corresponding average communication rate is below the threshold $\bar {\rho }$. Based on the above, by applying Algorithm 1 for every pair of the regions of interest, we can characterize both the transition relation δ and the functions ${\mathcal W}_{1}$, ${\mathcal W}_{2}$. As a consequence, the transition system ${\mathcal T}$ can be constructed as an abstraction of the control system (3).

5 Implementation

Based on the transition system ${\mathcal T}$ given in the previous section, we now present our control and communication strategies as a solution to Problem 1. Following the hierarchical-based approach, the proposed algorithm consists of high and low level controllers. The details of each implementation is described below.

5.1 High level controller

In the high level controller part, the controller produces an infinite sequence of the regions of interest that the state should follow to satisfy the formula ϕ, as well as that the average communication rate is below $\bar {\rho }$. Since the reachability among the regions of interest can be captured by the transition system ${\mathcal T}$, this can be done by finding a run s_seq = s₀s₁⋯ of ${\mathcal T}$, such that trace(s_seq)⊧ϕ holds. Although there exist several methodologies to achieve this, this paper adopts an automata-based model checking algorithm; we only describe the overview of the approach here and refer the reader to Chapter 5 in Baier and Katoen (2008) for a more detailed explanation. The approach relies on the idea that checking the existence of a run to satisfy ϕ is equivalent to checking the non-emptiness of $\text {Trace} ({\mathcal T}) \cap \text {Words} (\phi )$. Since $\text {Words} (\phi ) = \text {Lang} ({\mathcal B}_{\phi })$, where ${\mathcal B}_{\phi } = (Q , Q_{0} , 2^{\Pi }, \delta _{B}, {F})$ denotes the Büchi Automaton corresponding to the LTL formula ϕ, the above problem is also equivalent to checking the non-emptiness of $\text {Trace} ({\mathcal T}) \cap \text {Lang} ({\mathcal B}_{\phi })$, i.e., a language of the product automaton between ${\mathcal T}$ and ${\mathcal B}_{\phi }$, which is defined below:

Definition 6 (Product Automaton)

A product automaton between ${\mathcal T}= (S , s_{\text {init}} , \delta , {\Pi }, g, {\mathcal W}_{1}, {\mathcal W}_{2}),$ and ${\mathcal B}_{\phi }= (Q , Q_{\text {init}} , \delta _{B}, 2^{\Pi }, {F})$ is defined as a tuple ${\mathcal B}_{p} = {\mathcal T}\otimes {\mathcal B}_{\phi } = (Q_{p}, {Q}_{\text {init}, p}, \delta _{p}, {\Sigma }_{p}, F_{p})$, where

• Q_p = Q × S is a set of states;

• $Q_{\text {init}, p} = Q_{\text {init}} \times s_{\text {init}} \subseteq Q_{p}$ is a set of initial states;

• $\delta _{p} \subseteq Q_{p} \times Q_{p}$ is a transition relation, where $((q, s), (q^{\prime }, s^{\prime })) \in \delta _{p}$ iff $(s, s^{\prime }) \in \delta$ and $(q, g(s^{\prime }), q^{\prime } ) \in \delta _{B}$;

• Σ_p = 2^π is an input alphabet;

• F_p = F × S is a set of accepting states.

For a given word σ_seq = σ₀σ₁⋯ with σ_i ∈Σ_p, $\forall i\in \mathbb {N}$, a run of ${\mathcal B}_{p}$ over σ_seq is defined as an infinite sequence of states: (q_seq,s_seq) = (q₀,s₀) (q₁,s₁)⋯, such that (q₀,s₀) ∈ Q_init,p (i.e., s₀ = s_init,q₀ ∈ Q_init) and ((q_i,s_i),(q_i+ 1,s_i+ 1)) ∈ δ_B, $\forall i\in \mathbb {N}$. A run of ${\mathcal B}_{p}$ is called accepting if there exists a word σ_seq = σ₀σ₁⋯ such that F_p is intersected infinitely often. Let

$$ (q_{\text{seq}}, s_{\text{seq}}) = (q_{0}, s_{0})\ (q_{1}, s_{1})\ (q_{2}, s_{2}) \cdots $$

(31)

be one of the accepting runs of ${\mathcal B}_{p}$. It is known that any accepting run can be represented by a prefix-suffix structure, i.e., there exist $n_{1}, n_{2} \in \mathbb {N}$, such that

$$ \begin{array}{@{}rcl@{}} (q_{seq}, &s_{\text{seq}}) \\ &= \underbrace {(q_{0}, s_{0}) {\cdots} (q_{n_{1}-1}, s_{n_{1}-1})}_{\text{prefix\ part}} [ \underbrace {\left (q_{n_{1}}, s_{n_{1}}) {\cdots} (q_{n_{1}+n_{2}-1}, s_{n_{1}+n_{2}-1} \right)}_{\text{suffix \ part}} ]^{\omega}. \end{array} $$

(32)

As shown in (32), n₁, n₂ represent the length of the prefix and the suffix part, respectively. Based on (32) and the weight functions defined in (30), denote by ${\mathcal A} (s_{seq})$ the ratio between the total number of time steps and the communication time steps required for the suffix part of s_seq, i.e.,

$$ {\mathcal A} (s_{\text{seq}}) = \cfrac{\displaystyle \sum\limits^{n_{1} + n_{2}-1}_{n=n_{1}+1} {\mathcal W}_{1} (s_{n-1}, s_{n})}{ \displaystyle \sum\limits^{n_{1} + n_{2}-1}_{n=n_{1}+1} {\mathcal W}_{2} (s_{n-1}, s_{n})}. $$

(33)

Based on the above definitions, in this paper the high level controller finds an appropriate run of ${\mathcal B}_{p}$ in the following way. First, it finds a set of accepting runs:

$$ Q_{p, seq} = \{ (q_{\text{seq}}, s_{\text{seq}}) \ | \ (q_{\text{seq}}, s_{\text{seq}})\ \text{is}\ \text{an\ accepting\ run}\ \text{of}\ {\mathcal B}_{p}\}, $$

(34)

which can be obtained by finding strongly connected components through depth-search methods (see, e.g., Baier and Katoen (2008)). Then, we select the accepting run such that the average communication time step for the suffix part is minimized, i.e.,

$$ \begin{array}{@{}rcl@{}} (q^{*}_{\text{seq}}, s^{*}_{\text{seq}}) = \underset{{(q_{\text{seq}}, s_{\text{seq}}) \in Q_{p, seq}}}{\arg\min} {\mathcal A} (s_{\text{seq}}). \end{array} $$

(35)

Since $q^{*}_{p, \text {seq}} = (q^{*}_{\text {seq}}, s^{*}_{\text {seq}})$ is an accepting run of ${\mathcal B}_{p}$, it is shown that $\text {trace} (s^{*}_{\text {seq}}) \models \phi$ (see, e.g., Baier and Katoen (2008)) and we can obtain the corresponding sequence of regions of interest that is projected from $s^{*}_{\text {seq}}$, i.e.,

$$ {\mathcal R}^{*}_{\text{seq}} = R^{*}_{0} R^{*}_{1} R^{*}_{2} \cdots $$

(36)

where we denote $s^{*}_{\text {seq}} =s^{*}_{0} s^{*}_{1} \cdots$ and ${\mathcal R}^{*}_{i} = {\Gamma } (s^{*}_{i})$, $\forall i \in \mathbb {N}$. Note that since $s^{*}_{0} = s_{\text {init}}$, we have ${\mathcal R}^{*}_{0} = {\mathcal R}_{\text {init}}$. Namely, the sequence ${\mathcal R}^{*}_{\text {seq}}$ represents the infinite sequence of the regions of interest that the state trajectory should traverse to satisfy ϕ.

Remark 4 (On selecting the accepting run)

As shown in (35), in this paper we select the accepting run such that the average communication rate is minimized. However, we could consider several other criteria in order to select the accepting run. For example, one could select the accepting run according to the following:

$$ \begin{array}{@{}rcl@{}} (q^{*}_{\text{seq}}, s^{*}_{\text{seq}}) &= &\underset{{(q_{\text{seq}}, s_{\text{seq}}) \in Q_{p, seq}}}{\arg\min} \sum\limits^{n_{1} + n_{2}-1}_{n=n_{1} + 1} {\mathcal W}_{2} (s_{n-1}, s_{n}) \\ &&\text{s.t.}\ {\mathcal A} (s_{\text{seq}}) < \bar{\rho}. \end{array} $$

(37)

That is, among all accepting runs such that the average communication rate for the suffix is below $\bar {\rho }$, we select the one that minimizes the total time steps (in order to satisfy the formula ϕ “as soon as possible”). Here, the constraint ${\mathcal A} (s_{\text {seq}}) < \bar {\rho }$ is enforced in order to deduce that the average communication rate is indeed below the threshold $\bar {\rho }$; for details, see Theorem 1.

5.2 Low level controller

Based on the obtained sequence as in (36), the low-level controller iteratively implements the control and communication strategies, such that the resulting state trajectory satisfies ϕ as well as that the average communication rate is below $\bar {\rho }$. To this end, let $\hat {x}^{*}_{0} \hat {x}^{*}_{1} \hat {x}^{*}_{2}, \cdots$, $\hat {u}^{*}_{0} \hat {u}^{*}_{1} \hat {u}^{*}_{2} \cdots$, ${L}^{*}_{0} {L}^{*}_{1} {L}^{*}_{2} \cdots$ be an infinite sequence of nominal states, inputs, and inter-communication time steps that are generated based on ${\mathcal R}^{*}_{seq}$:

$$ \begin{array}{@{}rcl@{}} &\underbrace{{\mathcal L}_{{x}0} ({\mathcal R}^{*}_{0}, {\mathcal R}^{*}_{1})}_{\hat{x}^{*}_{0}\ {\cdots} \ \hat{x}^{*}_{k_{M_{1}}} }\ \underbrace{{\mathcal L}_{x} ({\mathcal R}^{*}_{1}, {\mathcal R}^{*}_{2})}_{\hat{x}^{*}_{k_{M_{1}}+1}\ {\cdots} \ \hat{x}^{*}_{k_{M_{2}}}}\ \underbrace{{\mathcal L}_{x} ({\mathcal R}^{*}_{2}, {\mathcal R}^{*}_{3})}_{\hat{x}^{*}_{k_{M_{2}}+1}\ {\cdots} \ \hat{x}^{*}_{k_{M_{3}}}} \cdots, \end{array} $$

(38)

$$ \begin{array}{@{}rcl@{}} &\underbrace{{\mathcal L}_{{u}} ({\mathcal R}^{*}_{0}, {\mathcal R}^{*}_{1})}_{\hat{u}^{*}_{0}\ {\cdots} \ \hat{u}^{*}_{k_{M_{1}}-1} }\ \underbrace{{\mathcal L}_{u} ({\mathcal R}^{*}_{1}, {\mathcal R}^{*}_{2})}_{\hat{u}^{*}_{k_{M_{1}}}\ {\cdots} \ \hat{u}^{*}_{k_{M_{2}}-1 }}\ \underbrace{{\mathcal L}_{u} ({\mathcal R}^{*}_{2}, {\mathcal R}^{*}_{3})}_{\hat{u}^{*}_{k_{M_{2}}}\ {\cdots} \ \hat{u}^{*}_{k_{M_{3}}-1}} \cdots, \end{array} $$

(39)

$$ \begin{array}{@{}rcl@{}} &\underbrace{{\mathcal L}_{I} ({\mathcal R}^{*}_{0}, {\mathcal R}^{*}_{1})}_{L^{*}_{0}\ {\cdots} \ L^{*}_{{M_{1}}-1} }\ \underbrace{{\mathcal L}_{I} ({\mathcal R}^{*}_{1}, {\mathcal R}^{*}_{2})}_{L^{*}_{{M_{1}}}\ {\cdots} \ L^{*}_{{M_{2}}-1 }}\ \underbrace{{\mathcal L}_{I} ({\mathcal R}^{*}_{2}, {\mathcal R}^{*}_{3})}_{L^{*}_{{M_{2}}}\ {\cdots} \ L^{*}_{{M_{3}}-1}} \cdots, \end{array} $$

(40)

where for the notational simplicity we let ${\mathcal L}_{{x}0} ({\mathcal R}^{*}_{0}, {\mathcal R}^{*}_{1}) = \hat {x}^{*}_{0}\ {\cdots } \ \hat {x}^{*}_{k_{M_{1}}}$ and

$$ \begin{array}{@{}rcl@{}} &&{\mathcal L}_{x} ({\mathcal R}^{*}_{i}, {\mathcal R}^{*}_{i+1}) = \hat{x}^{*}_{k_{M_{i}}+1}\ {\cdots} \ \hat{x}^{*}_{k_{M_{i+1}}}, \end{array} $$

(41)

$$ \begin{array}{@{}rcl@{}} &&{\mathcal L}_{u} ({\mathcal R}^{*}_{i}, {\mathcal R}^{*}_{i+1}) = \hat{u}^{*}_{k_{M_{i}}}\ {\cdots} \ \hat{u}^{*}_{k_{M_{i+1}}-1}, \end{array} $$

(42)

$$ \begin{array}{@{}rcl@{}} &&{\mathcal L}_{I} ({\mathcal R}^{*}_{i}, {\mathcal R}^{*}_{i+1}) = L^{*}_{{M_{i}}}\ {\cdots} \ L^{*}_{{M_{i+1}}-1}, \end{array} $$

(43)

with $M_{i}\in \mathbb {N}$, $i\in \mathbb {N}_{+}$ appropriately chosen to line up the sequences:

$$ \begin{array}{@{}rcl@{}} \hat{x}^{*}_{0} \hat{x}^{*}_{1} \hat{x}^{*}_{2} \hat{x}^{*}_{3} \cdots, \ \hat{u}^{*}_{0} \hat{u}^{*}_{1} \hat{u}^{*}_{2} \hat{u}^{*}_{3}\cdots,\ L^{*}_{0} L^{*}_{1} L^{*}_{2} L^{*}_{3} {\cdots} . \end{array} $$

(44)

Moreover, let $k^{*}_{m}$, $m\in \mathbb {N}$ be given by

$$ k^{*}_{0} = 0,\ k^{*}_{m+1} = k^{*}_{m} + L^{*}_{m},\ \forall m\in\mathbb{N}, $$

(45)

i.e., $k^{*}_{m}$, $m\in \mathbb {N}$ are the communication time steps between the plant and the controller. Based on the above, a complete algorithm of the low-level implementation is summarized in Algorithm 2. As shown in the algorithm, for each communication time step $k^{*}_{m}$ the plant transmits the current state information to the controller, based on which the controller updates the control input according to (25) and (26), and transmits it back to the plant. The main result of this paper is now given as a solution to Problem 1.

Theorem 1

Suppose that for given $x_{0} \in {\mathcal R}_{\text {init}}$, ϕ and $\bar {\rho }\in (0, 1]$, the high level controller finds an accepting run $q^{*}_{p, \text {seq}} = (q^{*}_{\text {seq}}, s^{*}_{\text {seq}})$ according to (35) and that we have ${\mathcal A} (s^{*}_{\text {seq}}) < \bar {\rho }$. Moreover, suppose that the low level controller (Algorithm 2) is implemented. Then, the resulting state trajectory satisfies ϕ for any $w_{k} \in {\mathcal W}$, $\forall k \in \mathbb {N}$. Moreover, the average communication rate is below $\bar {\rho }$, i.e., $\rho _{\text {ave}} < \bar {\rho }$.

Proof

: For a given $i\in \mathbb {N}$, suppose that $x_{k_{M_{i}}} \in {\mathcal R}^{*}_{i}$, where $k_{M_{i}}$ is defined in (38). Since the reachability holds from ${\mathcal R}^{*}_{i}$ to ${\mathcal R}^{*}_{i+1}$ and from the proof of Lemma 1, it follows that the state trajectory enters ${\mathcal R}^{*}_{i+1}$ (i.e., $x_{k_{M_{i+1}}} \in {\mathcal R}^{*}_{i+1}$) by applying a control strategy according to (25) and (26), and this holds for any disturbance sequence $w_{k} \in {\mathcal W}$, $k\in \mathbb {N}_{k_{M_{i}} : k_{M_{i+1}-1} }$. Hence, starting from $x_{0} \in {\mathcal R}^{*}_{0} = {\mathcal R}_{\text {init}}$, it is inductively shown that the state trajectory traverses all regions of interest ${\mathcal R}^{*}_{\text {seq}} = {\mathcal R}^{*}_{0} {\mathcal R}^{*}_{1} {\cdots }$ by applying Algorithm 2. Moreover, from the proof of Lemma 1 the state trajectory from ${\mathcal R}^{*}_{i}$ to ${\mathcal R}^{*}_{i+1}$ for each $i\in \mathbb {N}$ satisfies (C.1)–(C.3) in Definition 5. That is, the trace of the state trajectory while moving from ${\mathcal R}^{*}_{i}$ to ${\mathcal R}^{*}_{i+1}$ is $g(s^{*}_{i}) g(s^{*}_{i+1})$ for all $i \in \mathbb {N}$ (see Proposition 1), which leads to the fact that the trace of the overall state trajectory is given by $\text {trace} (math{x}) = g(s^{*}_{0}) g(s^{*}_{1}) g(s^{*}_{2}) \cdots$. Thus, we obtain $\text {trace} (math{x}) = \text {trace} (s^{*}_{\text {seq}}) \models \phi$ and so the satisfaction of ϕ is achieved.

Now, it remains to show that the communication rate is below $\bar {\rho }$. From Section 5.1, the sequences ${s}^{*}_{\text {seq}}$ and ${\mathcal R}^{*}_{\text {seq}}$ can be expressed by the following prefix-suffix structure:

$$ \begin{array}{@{}rcl@{}} {s}^{*}_{\text{seq}} &=& s^{*}_{0} s^{*}_{1} {\cdots} s^{*}_{n^{*}_{1}-1} \left (s^{*}_{n^{*}_{1}} {\cdots} s^{*}_{n^{*}_{1} + n^{*}_{2} -1} \right)^{\omega}, \end{array} $$

(47)

$$ \begin{array}{@{}rcl@{}} {\mathcal R}^{*}_{\text{seq}} &=& {\mathcal R}^{*}_{0} {\mathcal R}^{*}_{1} {\cdots} {\mathcal R}^{*}_{n^{*}_{1}-1} \left ({\mathcal R}^{*}_{n^{*}_{1}} {\cdots} {\mathcal R}^{*}_{n^{*}_{1} + n^{*}_{2} -1} \right)^{\omega}, \end{array} $$

(48)

where $n^{*}_{1}$, $n^{*}_{2}$ denote the length of the prefix and the suffix parts, respectively. Note that we have ${\mathcal A} (s^{*}_{\text {seq}}) < \bar {\rho }$. Let $M^{*}_{\text {pref}}, M^{*}_{\text {suf}}, K^{*}_{\text {pref}}, K^{*}_{\text {suf}} \in \mathbb {N}_{+}$ be given by

$$ \begin{array}{@{}rcl@{}} M^{*}_{\text{pref}} = \sum\limits^{n^{*}_{1}-1}_{n=1} {\mathcal W}_{1} (s^{*}_{n-1}, s^{*}_{n}),\ \ \ \ M^{*}_{\text{suf}} = \sum\limits^{n^{*}_{1} + n^{*}_{2}-1}_{n=n^{*}_{1}+1} {\mathcal W}_{1} (s^{*}_{n-1}, s^{*}_{n}), \end{array} $$

(49)

$$ \begin{array}{@{}rcl@{}} K^{*}_{\text{pref}} = \sum\limits^{n^{*}_{1}-1}_{n=1} {\mathcal W}_{2} (s^{*}_{n-1}, s^{*}_{n}),\ \ \ \ \ K^{*}_{\text{suf}} = \sum\limits^{n^{*}_{1} + n^{*}_{2}-1}_{n=n^{*}_{1}+1} {\mathcal W}_{2} (s^{*}_{n-1}, s^{*}_{n}). \end{array} $$

(50)

That is, $M^{*}_{\text {pref}}$ and $M^{*}_{\text {suf}}$ represent the number of communication time steps for the prefix and the suffix parts, respectively, and $K^{*}_{\text {pref}}$ and $K^{*}_{\text {suf}}$ represent the total number of time steps for the prefix and the suffix parts, respectively. Hence, the total number of time steps when the state trajectory traverses the prefix part (i.e., ${\mathcal R}^{*}_{0} {\mathcal R}^{*}_{1} {\cdots } {\mathcal R}^{*}_{n^{*}_{1}-1}$) and p-cycles of the suffix part (i.e., the p repetitions of ${\mathcal R}^{*}_{n^{*}_{1}} {\cdots } {\mathcal R}^{*}_{n^{*}_{1} + n^{*}_{2} -1}$) is given by $K^{*}_{\text {pref}} + p K^{*}_{\text {suf}}$. Similarly, the total number of communication time steps when the state trajectory traverses the prefix part and p-cycles of the suffix part is given by $M^{*}_{pref} + p M^{*}_{suf}$. Hence, the average communication rate is given by

$$ \begin{array}{@{}rcl@{}} \rho_{\text{ave}} &=& \lim\limits_{p \rightarrow \infty} \cfrac{M^{*}_{\text{pref}} + p M^{*}_{\text{suf}}}{K^{*}_{\text{pref}} + p K^{*}_{\text{suf}}}\ \\ &=& \lim\limits_{p \rightarrow \infty} \left (\cfrac{M^{*}_{\text{pref}}}{K^{*}_{\text{pref}} + p K^{*}_{\text{suf}}} + \cfrac{p M^{*}_{\text{suf}}}{K^{*}_{\text{pref}} + p K^{*}_{\text{suf}}} \right ) \\ & =& \cfrac{M^{*}_{\text{suf}}}{K^{*}_{\text{suf}}}. \end{array} $$

(51)

Thus, it follows that $\rho _{\text {ave}} < \bar {\rho }$ since ${\mathcal A} (s^{*}_{\text {seq}}) = {M^{*}_{\text {suf}}}/{K^{*}_{\text {suf}}} <\bar {\rho }$. Thus, the average communication rate is below $\bar {\rho }$. □

6 Illustrative examples

In this section we illustrate the effectiveness of the proposed approach. As a simulation example, we consider the motion planning problem of a vehicle moving in a given free space. Let $x = [x_{\text {pos}}; x_{\text {vel}}] \in \mathbb {R}^{4}$ denote the state of the vehicle, where $x_{\text {pos}} = [x_{\text {pos}1}; x_{\text {pos}2}] \in \mathbb {R}^{2}$ and $x_{\text {vel}} = [x_{\text {vel}1}; x_{\text {vel}2}] \in \mathbb {R}^{2}$ are the position and the velocity of the vehicle, respectively. The dynamics of the vehicle is given by the following double integrator:

$$ \dot{{x}} = \left [ \begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0& 0 \\ 0 & 0 & 0 & 0 \end{array} \right ] x + \left [ \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ 1& 0 \\ 0 & 1 \end{array} \right ] u + w, $$

(52)

where $u \in \mathbb {R}^{2}$ is the control input and $w \in \mathbb {R}^{4}$ is the disturbance. To obtain the discrete-time model, we discretize the system in (52) under zero-order hold controller with 0.5 sampling time interval. The disturbance set is given by ${\mathcal W} = \{ w \in \mathbb {R}^{4} : \|w\|_{\infty } \leq 0.1\}$. The position space of the vehicle, denoted as ${\mathcal X}_{\text {pos}} \subset \mathbb {R}^{2}$ is shown in Fig. 3a. In the figure, the white regions represent ${\mathcal X}_{\text {pos}}$ in which the state (vehicle) can move freely, and the black regions represent obstacles to be avoided. As shown in Fig. 3a there exist 4 regions of interest ${\mathcal R}_{1}, {\mathcal R}_{2}, {\mathcal R}_{3}, {\mathcal R}_{4}$, which are all 1 × 1 squares. The velocity space, denoted as ${\mathcal X}_{\text {vel}} \subset \mathbb {R}^{2}$, is given by ${\mathcal X}_{\text {vel}} = \{ x_{\text {vel}} \in \mathbb {R}^{2} : \| x_{\text {vel}} \|_{\infty } \leq 2.0 \}$. The (free) state space is thus given by ${\mathcal X} = {\mathcal X}_{\text {pos}} \times {\mathcal X}_{\text {vel}}$. Based on the above setting, we implement Algorithm 1 for each pair of the regions of interest. While implementing Algorithm 1, we assume $L_{\max \limits } = 20$, $N_{\max \limits } = 500$ and the matrix K is given by

$$ \begin{array}{@{}rcl@{}} K = \left [ \begin{array}{cccc} 0.004 & 0 & 0.139 & 0 \\ 0 & 0.004 & 0 & 0.139 \end{array} \right ] \end{array} $$

(53)

so that the matrix A + BK is stable. Figure 3b illustrates the nominal state trajectory $\hat {x}_{0:k_{M}}$ obtained by implementing Algorithm 1 for the pair $({\mathcal R}_{1}, {\mathcal R}_{3})$. In the figure, the red circles represent the instants when the communication is given (i.e., $\hat {x}_{k_{0}}, \hat {x}_{k_{1}}, {\ldots } \hat {x}_{k_{M-1}}$). The total number of communication time steps and the total number of time steps are given by M = 10 and k_M = 78, respectively. From the figure, it is shown that the nominal state trajectory reaches ${\mathcal R}_{3}$, while avoiding all the obstacles. Moreover, Fig. 3c illustrates 100 state trajectories by applying the control strategies in (25) and (26), starting from different initial states randomly selected from ${\mathcal R}_{1}$. It can be shown from the figure that all state trajectories satisfy (C.1)–(C.3) in Definition 5. Similarly, we analyze reachability for all the other pairs of the regions of interest and construct the transition system. The resulting transition system ${\mathcal T}$ contains 4 symbolic states and 16 transitions. The total time to construct ${\mathcal T}$ is 4398s on Windows 10, Intel(R) Core(TM) 2.40GHz, 8GB RAM. To compare with the previous result in Hashimoto et al. (2018), we illustrate in Table 1 the average execution time to compute a control input per each communication time step by employing the approach in this paper (i.e., (46)) and the one presented in our previous work (i.e., Eq.(24) and Eq.(25) in (Hashimoto et al. 2018)). The table shows that, the approach presented in this paper results in a significant reduction of the computation load, since it does not need to solve an optimal control problem. On the other hand, the table shows that the approach in this paper requires longer time steps than Hashimoto et al. (2018) to achieve the reachability, which may be due to the fact that only one control action can be applied during the inter-communication time steps (while different control actions can be used in the previous approach).

Fig. 3

Illustration of the position space ${\mathcal X}_{\text {pos}}$ and the results by applying Algorithm 1 for $({\mathcal R}_{1}, {\mathcal R}_{3})$

Table 1 The average execution time to compute a control input per each communication time step and the total number of time steps to achieve reachability from ${\mathcal R}_{1}$ to ${\mathcal R}_{3}$

To illustrate the proposal, we consider the following specification: $\phi = (\Diamond \pi _{1} \wedge \Diamond \pi _{2} \wedge \Diamond \pi _{3} \wedge \Diamond \pi _{4} ) \wedge \{ (\Box \Diamond \pi _{1} \wedge \Box \Diamond \pi _{2}) \vee (\Box \Diamond \pi _{1} \wedge \Box \Diamond \pi _{2} \wedge \Box \Diamond \pi _{3}) \}$. The specification means that, the vehicle should visit all regions of interest at least once, and visit ${\mathcal R}_{1}$, ${\mathcal R}_{2}$ or ${\mathcal R}_{1}$, ${\mathcal R}_{2}$, ${\mathcal R}_{3}$ infinitely often. Moreover, we assume that the threshold of the average communication rate is given by $\bar {\rho } = 0.1$. Based on the above problem setup, we implemented both high and low level controllers. Figure 4a illustrates the resulting state trajectory by implementing the low level controller (Algorithm 2) with $x_{0} = [8.3;\ -8.4;\ 0;\ 0] \in {\mathcal R}_{4}$. The figure shows that the state trajectories visit all the regions of interest, as well as that they visit ${\mathcal R}_{1}$, ${\mathcal R}_{2}$ infinitely often. Hence, the state trajectories are shown to satisfy the formula ϕ. In addition, Fig. 4b illustrates the corresponding sequence m/k_m, m = 1,2,…. The figure shows that the sequence m/k_m converges below $\bar {\rho } = 0.1$, which shows that that the average communication rate is indeed below $\bar {\rho }$.

Fig. 4

Resulting state trajectory by implementing the low level controller (Algorithm 2) and the corresponding sequence of m/k_m, m = 1,2,…

Note that the state trajectory could satisfy ϕ if the high level controller would select the run of ${\mathcal T}$ such that the state trajectory traverses ${\mathcal R}_{1}$, ${\mathcal R}_{2}$, ${\mathcal R}_{3}$ (instead of ${\mathcal R}_{1}$, ${\mathcal R}_{2}$) infinitely often. Figure 5 illustrates the sequence m/k_m, m = 1,2,… for the case when the state trajectory traverses ${\mathcal R}_{1}$, ${\mathcal R}_{2}$, ${\mathcal R}_{3}$ infinitely often. The figure illustrates that, the corresponding average communication rate cannot be below $\bar {\rho } = 0.1$. This means that, if the high level controller would select a run such that the state trajectory traverses ${\mathcal R}_{1}$, ${\mathcal R}_{2}$, ${\mathcal R}_{3}$, it would then violate the specification of the average communication rate (i.e., $\rho _{\text {ave}} > \bar {\rho }$). Hence, it is shown that the high level controller appropriately selected the accepting run, such that the average communication rate is below $\bar {\rho }$.

Fig. 5

The sequence of m/k_m, m = 1,2,… if the state trajectory would traverse ${\mathcal R}_{1}, {\mathcal R}_{2}, {\mathcal R}_{3}$ infinitely often

Finally, it is worth analyzing the execution time with respect to the number of regions of interest N_I as well as the state dimension n. Figure 6 plots of the execution time for constructing ${\mathcal T}$ (i.e., the total execution time of Algorithm 1 for all pairs of the regions of interest) against the state dimension n ≥ 5, with different selections of N_I = 2,4,6. Here, we fix the input dimension as m = 5 and the matrices A and B are randomly generated over the reals in the interval [0,1]. The state space is given by ${\mathcal X} = \{ x \in {\mathbb {R}}^{n} : \|x\|_{\infty } \leq 15 \}$, and we assume that the regions of interest are the full dimensional polytopes with n + 1 vertices, which are randomly generated from ${\mathcal X}$. The figure shows that, for fixed N_I, the execution time increases as n increases. This is due to some primitive procedures in Algorithm 1, such as IfFeasible, some vertex operations in (14), etc. In addition, for fixed n the execution time also increases as N_I increases. This is mainly due to the fact that the total number of combinations to select the pair of the regions of interest is N_I(N_I − 1)/2, implying that the execution time increases quadratically with N_I. Note that, thanks to the implementation of the sampling-based algorithm, the algorithm is tractable even for high-dimensional systems (e.g., n = 20), if the number of the regions of interest is small enough. This point may be an advantage over the previous discretization based approaches (e.g., Wongpiromsarn et al. 2012; Nilsson et al. 2012), in which the algorithm becomes intractable even with much lower state dimensions.

Fig. 6

Execution time against the state dimension n and N_I

7 Conclusions and future work

In this paper, we propose control and communication strategies, such that the state trajectories satisfy the LTL specification and the average communication rate is below a given threshold. We start by providing RRT-based reachability analysis, which is adapted such that the state trajectories satisfy the reachability specifications, as well as that the communication strategy can be designed. Then, we provide a high level controller that aims to find an accepting run of the transition system, and then provide a low level controller that aims to steer the state trajectories satisfying the desired specifications. Finally, we illustrate the benefits of the proposed approach through numerical simulations.

As previously stated in Remark 2, the reachability algorithm is not guaranteed to provide a communication strategy that minimizes the number of communication frequency. Hence, future work involves investigating the reachability algorithm that improves the optimality of the communication strategy. Moreover, the control synthesis that handles delays and packet dropouts explicitly for NCSs will be considered for our future work.