1 Introduction

Infinitesimal Perturbation Analysis (IPA) is a well-known gradient estimation technique that can be used in the general recursive Robbins-Monro stochastic approximation (SA) procedure to find the root of the gradient:

$$ \hat{\theta}_{n+1} = \hat{\theta}_{n} - a_{n}\hat{g}(\hat{\theta}_{n}) $$
(1)

where \(\hat {g}(\hat {\theta }_{n})\) is the noisy estimate of the gradient at the iterate \(\hat {\theta }_{n}\) and a n is the step size (or gain). Conditions that a n must satisfy include a n >0, \({\sum }^{\infty }_{n=1}{{a_{n}^{2}}}<\infty \) and \({\sum }^{\infty }_{n=1}{a_{n}}=\infty \). One sequence of gains that satisfies these conditions is a n =a 0 n −1.

IPA directly gleans all the data it needs to estimate the gradient of the performance function from a single arbitrary sample path (or simulation run); hence, there is no need for multiple replications at each value of the control parameter 𝜃. Additionally, IPA requires no knowledge of the underlying probability distributions governing the system and in the more simple cases, needs no knowledge of the traffic and service processes themselves (i.e., rates etc.). Therefore, while passively observing the system as it runs, IPA can simultaneously compute the gradient estimate using fairly simple counting processes, leading to an efficient “online” estimator.

Initial work on IPA gradient estimation used the traditional queueing paradigm, for which the enqueue and dequeue events for each “customer” were considered in the derivation and implementation of the gradient estimator. More recent work on IPA gradient estimation has shifted to the stochastic fluid model (SFM) paradigm. The time scale of the process is increased so that entities are aggregated into continuous flows that are characterised by random rates.

With regards to theoretical IPA work using stochastic fluid models (SFM), IPA gradient estimators have been derived for the expected loss rate and average queue length for the single-stage case with a simple threshold-based admission control, i.e., the control parameter is the buffer size (Cassandras et al. 2001). Also, for the single-stage case, IPA derivatives for the loss volume and cumulative queue workload were derived with respect to a service rate parameter and an inflow rate parameter (Wardi et al. 2002). Feedback was not considered. In Cassandras et al. (2003), the authors examined the single-stage in which two types of traffic were admitted: uncontrolled and threshold-based buffer controlled. Here, the queue was assumed to be infinite, and a “virtual” buffer size adjusted, such that when this limit was exceeded the controlled traffic was dropped, whereas the uncontrolled traffic was not. This work was generalized in Sun et al. (2004).

A number of works have also been generated for nodes in tandem. In Sun et al. (2003), the authors derived IPA gradient estimators for the loss volume and buffer workload with respect to only the first node’s buffer limit in a tandem of single-class nodes. (See also Sun et al. (2004)). The authors in Wardi and Riley (2002) examined the loss volume and buffer workload with respect to the buffer size of both nodes of a two-stage tandem. (See also Wardi and Melamed (2001)). The authors in Nosrati and Nikravesh (2004) examined tandem networks of two-class stochastic fluid models. In Panayiotou (2004) was examined the case when multiple buffers are served by a single server using non-idling scheduling polices, i.e., it addressed a resource allocation problem. The performance metrics of interest were the loss volume and the queue workload, and the control parameters were the buffer size as well as the bandwidth share for each buffer.

The notion of feedback in IPA-SFM work was first introduced by Yu and Cassandras (2003) and Yu and Cassandras (2004b). Here, the incoming rate to a single-stage network was decreased instantaneously and additively based on a function of the queue length. The control parameter was again buffer size and the performance measures were loss rate and average (queue) workload. The authors in Wardi and Riley (2004) then considered the IPA gradient estimator for loss volume in the case of retransmissions for the single-stage network and for which the control parameter was again the buffer size. Here, some notion of delay in the feedback path was examined. In Yu and Cassandras (2004c) and Yu and Cassandras (2004a), the authors dealt with multiplicative feedback on a single node SFM. In Yu and Cassandras (2004c) the input rate was decreased multiplicatively by a factor c (0<c≤1) if the queue length exceeded a certain threshold ϕ. They derived the IPA gradient estimators for the loss rate and average queue workload performance metrics with respect to the feedback gain parameter c instead of the usual buffer size. The authors in Yu and Cassandras (2004a) extended the work of Yu and Cassandras (2004c) by deriving the IPA gradient estimators for loss rate and throughput metrics with respect to the buffer threshold ϕ at which the multiplicative feedback will be invoked. They then used the IPA gradient estimators with respect to c and ϕ in a joint two-dimensional optimization procedure using SA to minimize a cost function of the weighted sum of loss rate and throughput. In Wardi et al. (2010) a unified approach for single-stage IPA-SFM was presented. A general framework for IPA of tandem networks in which there are delays was provided in Wardi and Riley (2010).

In Yao and Cassandras (2009), the authors derived IPA derivative estimators for a two-class system with each class having its own performance objectives. In this case the flow classes were differentiated in terms of service processes and flow content. In Yao and Cassandras (2011) they extended this work on multi-class systems by examining a class of stochastic non-cooperative games termed “resource contention games”. In either case, no feedback was considered.

In this paper we examine a single-stage stochastic fluid queue that is shared between two competing sources, one that employs additive loss-feedback congestion control and the other that employs no congestion-control (i.e., it is unresponsive). We derive the appropriate IPA gradient estimators, which are then used in the Robbins-Monro SA procedure to perform online stochastic optimization of the following objective function:

$$\begin{array}{@{}rcl@{}} J(\theta) & = & \omega_{L}L_{T}(\theta) + \omega_{Q}Q_{T}(\theta) \end{array} $$
(2)

where L T (𝜃) and Q T (𝜃) are the total loss volume and queue workload respectively, ω L and ω Q are their relative weights and 𝜃, the parameter for optimization, is chosen to be the buffer capacity b.

In Section 2, we analyze the system’s dynamics from which we determine the gradient estimators \(\frac {dL_{T}(\theta )}{d\theta }\) and \(\frac {dQ_{T}(\theta )}{d\theta }\). In Section 3, we perform some simulations to demonstrate the efficacy of the approach. We conclude in Section 4.

2 The gradient estimators

Consider the scenario depicted in Fig. 1. A non-responsive stochastic flow of rate σ 2(t) competes with that of a controlled source of rate σ 1(t). The loss-feedback constant is c, the buffer capacity, b, the buffer occupancy, x(𝜃;t), the service rate, β(t), the outflow rate, δ(𝜃;t) and the IPA time-horizon, the constant T such that T>0 and t∈[0,T]. It should be noted again that 𝜃, the optimization parameter, will be b. The total loss rate at the queue is denoted as γ(𝜃;t)=γ 1(𝜃;t)+γ 2(𝜃;t) where γ 1(𝜃;t) is the loss-rate of the IPA-controlled flow, and γ 2(𝜃;t) is that of the non-responsive flow.

Fig. 1
figure 1

Stochastic fluid model with instantaneous additive-loss feedback for the single stage case with a competing non-responsive flow

Full size image

The total loss volume, L T (𝜃), is given by

$$\begin{array}{@{}rcl@{}} L_{T}(\theta)& = & {{\int}^{T}_{0}}\gamma(\theta;t)\,dt \end{array} $$
(3)

and the cumulative queue workload, Q T (𝜃), is given by

$$\begin{array}{@{}rcl@{}} Q_{T}(\theta)& = & {{\int}^{T}_{0}}x(\theta;t)\,dt \end{array} $$
(4)

We define:

$$ A(\theta;t)=\sigma_{2}(t) + \alpha_{1}(\theta;t)-\beta(t) $$
(5)

So that the dynamics of the queue state, x(𝜃;t), can be expressed as follows:

$$ \frac{dx}{dt}= \left \{ \begin{array}{ll} 0 & \text{if \(x(\theta;t)=0\) and \(A(\theta;t)<0\)} \\ 0 & \text{if \(x(\theta;t)=b\) and \(A(\theta;t)>0\)} \\ A(\theta;t) & \text{otherwise} \end{array} \right. $$
(6)

Also:

$$ \gamma(\theta;t) = \left \{ \begin{array}{ll} A(\theta;t) & \text{if \(x(\theta;t)=b\)} \\ 0 & \text{otherwise} \end{array} \right. $$
(7)

Now:

$$ \begin{array}{lll} \alpha_{1}(\theta;t) & = & \sigma_{1}(t) - c\gamma_{1}(\theta;t) \end{array} $$
(8)

where

$$ \begin{array}{lll} \gamma_{1}(\theta;t) & = & \frac{\alpha_{1}(\theta;t)}{\alpha_{1}(\theta;t)+\sigma_{2}(t)}\gamma(\theta;t) \end{array} $$
(9)
$$ \begin{array}{lll} \Rightarrow \alpha_{1}(\theta;t) & = & \left \{ \begin{array}{ll} f(\sigma_{1}(t), \sigma_{2}(t), \beta(t), c) & \text{if \(x(\theta;t)=b\)} \\ \sigma_{1}(t) & \text{otherwise} \end{array} \right. \\ \Rightarrow A(\theta;t) & = & \left \{ \begin{array}{ll} \sigma_{2}(t) + f(\sigma_{1}(t), \sigma_{2}(t), \beta(t), c) - \beta(t) & \text{if \(x(\theta;t)=b\)} \\ \sigma_{2}(t) + \sigma_{1}(t) - \beta(t)& \text{otherwise} \end{array} \right. \end{array} $$
(10)

where

$$ \begin{array}{lll} f(\sigma_{1}(t), \sigma_{2}(t), \beta(t), c) & \equiv & -\frac{\sigma_{2}(t)}{2} + \frac{\sigma_{1}(t) + c\beta(t)}{2(1+c)} \\ \ & & + \sqrt{\left(\frac{\sigma_{2}(t)}{2} - \frac{\sigma_{1}(t) + c\beta(t)}{2(1+c)} \right)^{2} + \sigma_{1}(t)\sigma_{2}(t) } \end{array} $$
(11)

The derivation of Eq. 11 can be found in the Appendix (i.e., Section 1).

Using the relation in Eqs. 10, 6 and 7 can be rewritten as:

$$ \frac{dx}{dt}= \left \{ \begin{array}{ll} 0 & \text{if \(x(\theta;t)=0\)} \\ & \text{and \(\sigma_{2}(t) + \sigma_{1}(t) - \beta(t)<0\)} \\ 0 & \text{if \(x(\theta;t)=b\)} \\ & \text{and \(\sigma_{2}(t) + f(\sigma_{1}(t), \sigma_{2}(t), \beta(t), c) - \beta(t)>0\)} \\ \sigma_{2}(t) + \sigma_{1}(t) - \beta(t) & \text{otherwise} \end{array} \right. $$
(12)
$$ \gamma(\theta;t) = \left \{ \begin{array}{ll} \sigma_{2}(t) + f(\sigma_{1}(t), \sigma_{2}(t), \beta(t), c) - \beta(t) & \text{if \(x(\theta;t)=b\)} \\ 0 & \text{otherwise} \end{array} \right. $$
(13)

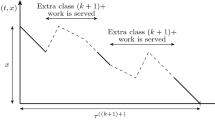
Consider the buffer-occupancy process in Fig. 2. Let τ i (𝜃) be the beginning of the i-th boundary period (BP) and let ς i (𝜃) be the end of the i-th BP, so that the i-th BP is denoted as B i =[τ i (𝜃),ς i (𝜃)] in the interval [0,T]. Let \(\mathcal {F} :=\{i:x(\theta ;t)=b\, \forall \,t\in B_{i}\}\) be the set of all indices of boundary periods that are full periods in the interval [0,T]. Then the total loss volume, denoted as L T (𝜃), is given by:

$$ L_{T}(\theta) = \sum\limits_{i\in\mathcal{F}}L_{i}(\theta) $$
(14)

where

$$ \begin{array}{lll} L_{i}(\theta) & = & {\int}^{\varsigma_{i}(\theta)}_{\tau_{i}(\theta)}\gamma(\theta;t)\, dt \\ & = &{\int}^{\varsigma_{i}(\theta)}_{\tau_{i}(\theta)}[\sigma_{2}(t) + f(\sigma_{1}(t), \sigma_{2}(t), \beta(t), c) - \beta(t)]\, dt \end{array} $$
(15)
Fig. 2
figure 2

Trajectory of buffer-occupancy for single-stage case with competing flow

Full size image

The loss derivative is then given by

$$ \frac{dL_{T}(\theta)}{d\theta} = \sum\limits_{i\in\mathcal{F}}\frac{dL_{i}(\theta)}{d\theta} $$
(16)

We define two types of events that are pertinent to this work: exogenous event and endogenous events. An exogenous event is a discontinuity in the defining processes σ(t) and β(t). Therefore, its time of occurrence, υ, is independent of the control parameter. Let υ be this time of occurrence, then \(\frac {d\upsilon }{d\theta }=0\).

On the other hand, an endogenous event is the beginning of an empty-period or full-period at the queue. However, we reiterate the formal definition for endogenous events as specified in Cassandras et al. (2010). An endogenous event occurs if there exists a continuously-differentiable function g(x,𝜃) such that at the time of its occurrence, υ(𝜃), g(x(𝜃,υ),𝜃)=0. At the beginning of an empty-period: υ(𝜃), g(x(𝜃,υ),𝜃)=x(𝜃,υ), and at the beginning of a full-period: g(x(𝜃,υ),𝜃)=x(𝜃,υ)−𝜃. It will be shown later, that \(\frac {d\upsilon }{d\theta }=\frac {1}{(\sigma _{2}(\tau _{i}(\theta )) + \sigma _{1}(\tau _{i}(\theta )) - \beta (\tau _{i}(\theta )))}\) when the queue becomes full after a cease-full event.

Now we will proceed to derive the loss derivative considering the case when the buffer capacity, b, is the control parameter.

$$ \begin{array}{lll} \frac{dL_{i}(\theta)}{d\theta} & = & \frac{d}{d\theta} \left[{\int}^{\varsigma_{i}(\theta)}_{\tau_{i}(\theta)}(\sigma_{2}(t) + f(\sigma_{1}(t), \sigma_{2}(t), \beta(t), c) - \beta(t))\, dt \right] \\ & = & {\int}^{\varsigma_{i}(\theta)}_{\tau_{i}(\theta)}\frac{d}{d\theta}[\sigma_{2}(t) + f(\sigma_{1}(t), \sigma_{2}(t), \beta(t), c) - \beta(t)]\, dt + \left(\sigma_{2}(\varsigma_{i}(\theta)^{-})\right. + \\ & & \left.f(\sigma_{1}(\varsigma_{i}(\theta)^{-}), \sigma_{2}(\varsigma_{i}(\theta)^{-}), \beta(\varsigma_{i}(\theta)^{-}), c) - \beta(\varsigma_{i}(\theta)^{-})\right)\frac{d\varsigma_{i}(\theta)}{d\theta} - \\ & & \left(\sigma_{2}(\tau_{i}(\theta)^{+}) + f(\sigma_{1}(\tau_{i}(\theta)^{+}), \sigma_{2}(\tau_{i}(\theta)^{+}), \beta(\tau_{i}(\theta)^{+}), c)\right. - \\ & & \left.\beta(\tau_{i}(\theta)^{+})\right)\frac{d\tau_{i}(\theta)}{d\theta} \end{array} $$
(17)

Since σ 1(t), σ 2(t) and β(t) are independent of 𝜃, then f(σ 1(t),σ 2(t),β(t),c) is also independent of 𝜃 within the interval (τ i (𝜃),ς i (𝜃)) so that \({\int }^{\varsigma _{i}(\theta )}_{\tau _{i}(\theta )}\frac {d}{d\theta }[\sigma _{2}(t) + f(\sigma _{1}(t), \sigma _{2}(t), \beta (t), c) - \beta (t)]\, dt = 0\)

Consider, t=ς i (𝜃), the time when the queue ceases to be full. For the discontinuous case, there is a jump in A(𝜃;t) i.e. A(𝜃;ς i (𝜃)−)>A(𝜃;ς i (𝜃)+). This implies that:

$$\begin{array}{@{}rcl@{}} & & \sigma_{2}(\varsigma_{i}(\theta)^{-}) + f(\sigma_{1}(\varsigma_{i}(\theta)^{-}), \sigma_{2}(\varsigma_{i}(\theta)^{-}), \beta(\varsigma_{i}(\theta)^{-}), c) - \beta(\varsigma_{i}(\theta)^{-}) \\ & > & \sigma_{2}(\varsigma_{i}(\theta)^{+}) + \sigma_{1}(\varsigma_{i}(\theta)^{+}) - \beta(\varsigma_{i}(\theta)^{+}) \end{array} $$
(18)

Suppose that there are no exogenous changes in the processes σ 1(t), σ 2(t) and β(t) at t=ς i (𝜃), then

$$\begin{array}{@{}rcl@{}} f(\sigma_{1}(\varsigma_{i}(\theta)),\sigma_{2}(\varsigma_{i}(\theta)),\beta(\varsigma_{i}(\theta)), c) & > & \sigma_{1}(\varsigma_{i}(\theta)) \end{array} $$
(19)

But this cannot be since for the same values of σ 1(t), σ 2(t) and β(t) at t=ς i (𝜃)

$$\begin{array}{@{}rcl@{}} \alpha_{1}(\varsigma_{i}(\theta)^{-}) & < & \alpha_{1}(\varsigma_{i}(\theta)^{+}) \\ & \Rightarrow & f(\sigma_{1}(\varsigma_{i}(\theta)), \sigma_{2}(\varsigma_{i}(\theta)), \beta(\varsigma_{i}(\theta)), c) < \sigma_{1}(\varsigma_{i}(\theta)) \end{array} $$
(20)

Therefore, for there to be a negative jump in A(𝜃;t), it must be due to an exogenous event in σ 1(t), σ 2(t) or β(t) at t=ς i (𝜃). As a result, \(\frac {d\varsigma _{i}(\theta )}{d\theta } = 0\).

In the continuous case, A(𝜃;t)=0 at t=ς i (𝜃) which implies that

$$ f(\sigma_{1}(\varsigma_{i}(\theta)), \sigma_{2}(\varsigma_{i}(\theta)), \beta(\varsigma_{i}(\theta)), c) = \sigma_{1}(\varsigma_{i}(\theta)) = \sigma_{2}(\varsigma_{i}(\theta)) - \beta(\varsigma_{i}(\theta)) $$
(21)

(which is possible) so that \(A(\theta ; \varsigma _{i}(\theta ))\frac {d\varsigma _{i}(\theta )}{d\theta } = 0\).

Equation 17 then becomes:

$$\begin{array}{@{}rcl@{}} \frac{dL_{i}(\theta)}{d\theta} & = & - \left(\sigma_{2}(\tau_{i}(\theta)^{+}) + f(\sigma_{1}(\tau_{i}(\theta)^{+}), \sigma_{2}(\tau_{i}(\theta)^{+}), \beta(\tau_{i}(\theta)^{+}), c)\right. \\ & & - \left. \beta(\tau_{i}(\theta)^{+})\right)\frac{d\tau_{i}(\theta)}{d\theta} \end{array} $$
(22)

We now attempt to determine an expression for the time-derivative, \(\frac {d\tau _{i}(\theta )}{d\theta }\), which corresponds to when the queue becomes full. To do this, we first consider the non-boundary period (NBP) that precedes the full-period. That NBP may have itself been preceded by an empty period (EF) or a full-period (FF).

$$ \begin{array}{lll} \left. x(\theta;t)\right|_{\varsigma_{i-1}(\theta)}^{\tau_{i}(\theta)} & = & x(\theta;\tau_{i}(\theta))-x(\theta;\varsigma_{i-1}(\theta)) = \left \{ \begin{array}{ll} \theta & \text{if preceding \textit{NBP} is \textit{EF}} \\ 0 & \text{if preceding \textit{NBP} is \textit{FF}} \\ \end{array} \right. \\ & = & {\int}_{\varsigma_{i-1}(\theta)}^{\tau_{i}(\theta)} \frac{dx(\theta,t)}{dt}\,dt \\ & = & {\int}_{\varsigma_{i-1}(\theta)}^{\tau_{i}(\theta)} (\sigma_{2}(t) + \sigma_{1}(t) - \beta(t))\,dt \end{array} $$
(23)

Taking derivatives of Eq. 23 with respect to 𝜃:

$$ (\sigma_{2}(\tau_{i}(\theta)^{-}) + \sigma_{1}(\tau_{i}(\theta)^{-}) - \beta(\tau_{i}(\theta)^{-}))\frac{d\tau_{i}(\theta)}{d\theta} = \left \{ \begin{array}{ll} 1 & \text{if preceding \textit{NBP} is \textit{EF}} \\ 0 & \text{if preceding \textit{NBP} is \textit{FF}} \\ \end{array} \right. $$
(24)

Because no exogenous event occurs at t=τ i (𝜃), then (σ 2(τ i (𝜃)−)+σ 1(τ i (𝜃)−)−β(τ i (𝜃)−))=(σ 2(τ i (𝜃)+)+σ 1(τ i (𝜃)+)−β(τ i (𝜃)+))=(σ 2(τ i (𝜃))+σ 1(τ i (𝜃))−β(τ i (𝜃))). Equation 24 then becomes:

$$ \begin{array}{lll} (\sigma_{2}(\tau_{i}(\theta)) + \sigma_{1}(\tau_{i}(\theta)) - \beta(\tau_{i}(\theta)))\frac{d\tau_{i}(\theta)}{d\theta} & = & \left \{ \begin{array}{cl} 1 & \text{if preceding \textit{NBP} is \textit{EF}} \\ 0 & \text{if preceding \textit{NBP} is \textit{FF}} \\ \end{array} \right. \end{array} $$
(25)

Substitute Eq. 25 into Eq. 22:

$$ \frac{dL_{i}(\theta)}{d\theta} = \left \{ \begin{array}{cl} -\frac{(\sigma_{2}(\tau_{i}(\theta)) + f(\sigma_{1}(\tau_{i}(\theta)), \sigma_{2}(\tau_{i}(\theta)), \beta(\tau_{i}(\theta)), c) - \beta(\tau_{i}(\theta)))}{(\sigma_{2}(\tau_{i}(\theta)) + \sigma_{1}(\tau_{i}(\theta)) - \beta(\tau_{i}(\theta)))} & \text{if preceding \textit{NBP}} \\ & \text{is \textit{EF}} \\ 0 & \text{if preceding \textit{NBP}} \\ & \text{is \textit{FF}} \\ \end{array} \right. $$
(26)

Because the loss-feedback is felt only when the queue is in a full-period, the IPA derivative for the queue workload is the same as that of the single-stage case with no loss-feedback as derived in Wardi et al. (2002). For ease of reference we repeat the result here. Denote the j-th non-empty period in which there is at least one full period as N E j . Let u j,1 be the beginning of the first full period in N E j . Let v j be the end of N E j . Then

$$ \frac{dQ_{T}(\theta)}{d\theta} = {\sum}^{M}_{j=1}v_{j}-u_{j,1} $$
(27)

where there are M such non-empty periods in the interval [0,T].

2.1 A note on unbiasedness

The IPA gradient estimators are said to be unbiased if the operations of integration and expectation can be interchanged so that:

$$\begin{array}{@{}rcl@{}} \frac{d}{d\theta}(E[J(\theta)]) & = & E\left[\frac{dJ}{d\theta} \right] \end{array} $$
(28)

When the following two conditions are both met, the IPA derivative estimators will be unbiased. Consider the IPA loss derivativeFootnote 1:

  • The sample derivative, \(\frac {dL(\theta )}{d\theta }\) exists for all 𝜃∈Θ where Θ is a closed and bounded set.

  • The sample function, L(𝜃;T) is Lipschitz continuous in 𝜃, and its Lipschitz constant has a finite first moment.

For the first condition to be satisfied, it is necessary that L(𝜃;T) should be continuous with respect to 𝜃 over the set 𝜃∈Θ. As can be seen from the previous section, the form of the loss derivative consists of the product of the net-inflow rate (A(𝜃;t)) and the derivative of an event-time with respect to the control parameter, 𝜃, i.e., \(\frac {dv}{d\theta }\). (See Eq. 25). Therefore the existence of the gradient estimator will depend on the behaviour of the net-inflow rate (A(𝜃;t)) with respect to 𝜃, as well as on the existence of the event-time derivatives.

For the event-times to be continuous in 𝜃 for all 𝜃∈Θ, small changes in 𝜃 should not alter the sequence of events. Therefore the following three assumptions must hold w.p.1:

Assumption 1

σ(t) and β(t) are piecewise continuously differentiable on the interval [0,T].

Assumption 2

No empty period or full period consists of a single point.

Assumption 3

Exogenous events cannot occur simultaneously with other exogenous events or with other endogenous events

In other words, no two events can occur at the same time unless one of them induces the other. Consider, as an example, the situation when the second assumption does not hold. It would mean that an endogenous and exogenous event would have occurred simultaneously. If the control parameter 𝜃 were to increase infinitesimally to 𝜃+Δ𝜃, then the exogenous event would have occurred before the endogenous event. And if the control parameter were to instead decrease infinitesimally to 𝜃−Δ𝜃, the opposite would be true. This can cause a discontinuity in the loss volume at 𝜃.

The assumption that follows constrains the behaviour of the net-inflow rate (A(𝜃;t)) with respect to 𝜃 so that it is continuous with respect to 𝜃, otherwise if this condition were not to hold, A(𝜃;t) would be discontinuous and so would be the gradient estimator dependent on it.

Assumption 4

During an open sub-interval of any boundary period it never occurs that A(𝜃;t)=0

If the following is true then the second condition is satisfied.

$$\begin{array}{@{}rcl@{}} \left\|L_{T}(\theta+{\Delta}\theta)-L_{T}(\theta)\right\|& < & K{\Delta}\theta \end{array} $$
(29)

where K>0 is a random variable with \(E[K]<\infty \). In other words, the maximum magnitude of the sample derivative over all 𝜃 should always be less than some constant, K, which is the Lipschitz constant and the mean of which is always finite.

In all, what remains to be done, is to determine the value of K for each sample-derivative we derived using IPA, to prove unbiasedness. In particular, for this single-stage case with instantaneous additive loss feedback and with buffer length being the control parameter of interest, we find that \(\left |\frac {dL}{d\theta }(\theta ) \right |<N_{T}\) where N T is the number of lossy busy-periods in the interval [0,T]. Within the interval [0,T], the independent processes, σ(t) and β(t), can have only a finite number of discontinuities, so that the number of sign changes in the net inflow-rate A(𝜃;t) is also finite. As a result, \(N_{T}>0, E[N_{T}]<\infty \). We can thus say that N T is the Lipschitz constant that we need, and that the IPA loss derivative is unbiased. The unbiasedness of the queue-workload derivative for this case was established in Wardi et al. (2002).

3 Simulations with buffer capacity, b, as the control variable 𝜃

Simulation results were obtained using a fluid model created in Matlab.

The service rate, β(t), is a random process, uniformly distributed between 6.75 Mbps and 11.25 Mbps. Its average service rate is 9 Mbps. The time interval between changes in the magnitude of β(t) is a constant at 75 ms. The IPA time-horizon, T=10 seconds. The average input-rate, λ=E[σ 1]+E[σ 2], into the first queue was held at 8.32 Mbps (taking into account packet-header adjustments). Let \(k \equiv \frac {E[\sigma _{2}]}{E[\sigma _{1}] + E[\sigma _{2}]}\). Also, let x=(1−k)×λ, and y=k×λ. For the controlled source, let p be the “HI-rat and q, the “LO-rate”. Therefore \(p=\frac {x}{d + (1-d)r}\) and q=r p, where d≡duty-cycle=0.5 and r≡ratio of off- to on-rate=0.25. The total (on- + off-)period on average was 200m s.

For the non-responsive source, let a be the “on-rate”, and b, the “off-rate”, so that \(a=\frac {y}{d}\) and b=0 where d≡duty-cycle=0.5. The total (on- + off-)period on average was 110m s.

In all, σ 1(t) switches between either of two levels, 13.31×(1−k) Mbps (“HI”-rate) and 3.32×(1−k) Mbps (”LO”-rate) every 100 ms or so. Its average is 8.32×(1−k) Mbps. σ 2(t) oscillates between 16.64×k Mbps and 0 Mbps every 55 ms or so, for an average of 8.32×k Mbps.

The loss-feedback constant, c is 0.3333. The packet size is 554 bytes (512 bytes for the payload, and 42 bytes for the header).

Three optimizations were carried out with different initial values for the buffer-limit, i.e., b=20,70,100. For each optimization, there were 120 independent iterations, with each iteration being a run of length 10s. The control variable 𝜃 (i.e. the buffer-limit) was adjusted after each run and was used as the new buffer-limit in the next run. The algorithm for the adjustment in 𝜃≡b is shown in Fig. 3 with Δ initialized to zero. The parameter values were chosen to be \(a_{i}=\frac {a_{0}}{i^{\rho }}, a_{0}=5, \rho =0.6,w_{L} = 10,w_{Q} = 83.5\), and \(\frac {dJ}{d\theta }= \frac {w_{L}}{T}\frac {dL_{T}}{d\theta }+ \frac {w_{Q}}{T}\frac {dQ_{T}}{d\theta }\).

Fig. 3
figure 3

Algorithm for the adjustment of the control parameter 𝜃

Full size image

With the optimization, each run is completely independent of each other. The results are shown for k=0.1 in Fig. 4. In spite of the noise, all three cases converge to b≈75packets. The corresponding cost function is shown in Fig. 5. It can be seen that the minimum value occurs at around b≈75packets.

Fig. 4
figure 4

Optimization for k=0.1, c=0.3333

Full size image
Fig. 5
figure 5

Cost function for k=0.1, c=0.3333

Full size image

Simulations were also conducted for the following cases:

  1. 1.

    c=0.25, k=0.1.

  2. 2.

    c=0.3333, k=0.5.

  3. 3.

    c=0.25, k=0.5.

The results for these cases, together with their corresponding cost functions are shown in Figs. 6, 7, 8, 9, 10 and 11.

Fig. 6
figure 6

Optimization for k=0.1, c=0.25

Full size image
Fig. 7
figure 7

Cost function for k=0.1, c=0.25

Full size image
Fig. 8
figure 8

Optimization for k=0.5, c=0.3333

Full size image
Fig. 9
figure 9

Cost function for k=0.5, c=0.3333

Full size image
Fig. 10
figure 10

Optimization for k=0.5, c=0.25

Full size image
Fig. 11
figure 11

Cost function for k=0.5, c=0.25

Full size image

In all cases presented the minima was found to occur within the range of 70 to 80 packets for the buffer limit. Based on the form of the cost function that was chosen and the relative sizes of the weights, it can be deduced that for low values of buffer limit, the loss-volume component of the cost function will dominate, and for higher values of the buffer limit, the queue workload will dominate. For all cases examined, the weight values were held constant. But it was found that when the proportion of traffic entering the queue due the competing, uncontrolled traffic increased from 10 % to 50 %, the contribution of the queue workload to the total cost seemed to have diminished considerably. This then led to the minimum cost being less pronounced. This in turn lead to a longer covergence time when the initial value of the buffer limit was greater than that of the minima. This behaviour may be attributed to the fact that the proportion of the total loss rate that is fedback to the controlled source would be less with k=50 % thereby diminishing the effect of the control function on the total loss volume. Hence the change in loss volume per unit-increase in buffer limit is greater for k=50 % than k=10 %. The queue workload derivative, however, being unaffected by the loss feedback, would not produce a comparable change in queue workload with buffer limit as that of the loss volume for the same change in k.

With k=10 %, a change in the feedback constant from c=0.3333 to c=0.25 led to an increase in the buffer-limit at minima from 75 packets to roughly 80 packets. This may be due to the less aggressive feedback policy (i.e., lower feedback constant) allowing the loss volume generated for a given buffer-limit to be greater. The impact of a change in loss feedback is less discernible when the proportion of traffic flow due to uncontrolled, competing traffic is greater. In the both cases: k=50 %,c=0.3333 and k=50 %,c=0.25, the buffer limit at the minimum cost was about 70 packets.

Therefore, for this optimization to be implemented in a real-world system, it may be necessary to dynamically adjust the weights of the cost function with changing traffic load.

4 Conclusion

We have derived the IPA gradient estimators for loss volume with respect to buffer capacity for a single-stage stochastic fluid queue that is shared between two competing sources, one that employs additive loss-feedback congestion control and the other that employs no congestion-control (i.e., it is unresponsive), a scenario that is applicable within the realm of computer communication networks particularly at bottleneck router queues where multiple and diverse flows compete for bandwidth. The IPA gradient estimators were then used to drive an online stochastic optimization so as to minimize a cost function which consisted of a weighted sum of loss volume and queue workload. There was convergence to the minima.

In this paper, only a single queue is considered with instantaneous loss feedback to the responsive source. In reality, however, a set of competing flows may traverse a tandem of queues connected by links that incur non-zero propagation delays. Additionally, there would be some non-zero delay in the feedback mechanism. Therefore, one suggested path of progression along this line of research would be to investigate and derive the IPA gradient estimators for the single-stage case with loss-feedback delay for a pair of responsive and non-responsive competing flows. The next step would be to extend these delayed-loss-feedback results to the tandem case with propagation delay.