Quantum attacks on some feistel block ciphers

Abstract

Post-quantum cryptography has attracted much attention from worldwide cryptologists. However, most research works are related to public-key cryptosystem due to Shor’s attack on RSA and ECC ciphers. At CRYPTO 2016, Kaplan et al. showed that many secret-key (symmetric) systems could be broken using a quantum period finding algorithm, which encouraged researchers to evaluate symmetric systems against quantum attackers. In this paper, we continue to study symmetric ciphers against quantum attackers. First, we convert the classical advanced slide attacks (introduced by Biryukov and Wagner) to a quantum one, that gains an exponential speed-up in time complexity. Thus, we could break 2/4K-Feistel and 2/4K-DES in polynomial time. Second, we give a new quantum key-recovery attack on full-round GOST, which is a Russian standard, with $2^{114.8}$ quantum queries of the encryption process, faster than a quantum brute-force search attack by a factor of $2^{13.2}$.

1 Introduction

Post-quantum cryptography is about the security of cryptographic systems against quantum attackers. In 1994, Peter Shor [35] invented the first notable and yet the most severe quantum attack, i.e., the Shor’s algorithm, that breaks the most currently used public-key systems, such as RSA cryptosystem [33] and elliptic curve cryptography. But since then quantum threats against secret-key (symmetric) systems are barely known, and it was the common belief that quantum attacks on symmetric primitives are of minor concern, as they mainly consist of employing Grover’s algorithm [16] to generically speed up search (sub-)problems. However, at CRYPTO 2016, Kaplan et al. [23] break a series of symmetric-key systems in polynomial time using quantum period finding algorithm, which stirs great interest of quantum cryptanalysis in symmetric-key cryptographic community.

According to the notions for PRF security in a quantum setting given by Zhandry [38], there are two different models for quantum cryptanalysis against symmetric ciphers:

• Standard security: a block cipher is standard secure against quantum adversaries if no efficient quantum algorithm can distinguish the block cipher from PRP (or a PRF) by making only classical queries (denoted as Q1 by Kaplan et al. [24]).

• Quantum security: a block cipher is quantum secure against quantum adversaries if no efficient quantum algorithm can distinguish the block cipher from PRP (or a PRF) even by making quantum queries (denoted as Q2 by Kaplan et al. [24]).

In Q1 model, the adversary collects data classically and processes them with quantum operations, while in Q2, the adversary can directly query the cryptographic oracle with a quantum superposition of classical inputs, and receives the superposition of the corresponding outputs. The adversary in Q1 model is more realistic, many cryptanalysis results [9, 18, 19] are based on this model. The adversary in Q2 model is much more powerful. Nevertheless, it is still meaningful to study ciphers in Q2 model, since it is possible to devise protocols secure against Q2 adversary, such as quantum-secure signatures from CRYPTO 2013 [6] and quantum-secure message authentication codes from EUROCRYPT 2013 [5], etc. Recently, the security of many specific symmetric ciphers in Q2 model has been evaluated, which includes the key-recovery attacks against Even-Mansour constructions [27], distinguishers against 3-round Feistel constructions [26], forgery attacks against block cipher based MACs [23], key recovery attacks against FX constructions [28], and so on. But more classical cryptographic schemes of greater importance are yet to be studied against quantum attackers. At Asiacrypt 2017, Moody [30] on behalf of NIST reports the ongoing competition for post-quantum cryptographic algorithms, including signatures, encryptions and key-establishment. The ship for post-quantum crypto has sailed, cryptographic communities must get ready to welcome the post-quantum age.

Feistel block ciphers [15] are observed to be important and constitute one of the extensively researched cryptographic schemes. Several standard block ciphers, such as DES, Triple-DES, MISTY1, Camellia, CAST-128 [20] and the Russian GOST [31], are based on the Feistel design. Classically, researchers only consider the security of Feistel block ciphers against attackers who are only equipped with classical computers. In the quantum age to come, the adversaries can be more powerful. There are some attacks on Feistel ciphers in quantum setting. Kuwakado and Morii [26] gave the first quantum distinguisher on 3-round Feistel in Q2 model. Later combining with Leander and May’s algorithm [28], Hosoyamada et al. [17] and Dong et al. [13, 14] introduced some key-recovery attacks in Q2 model by appending several rounds to the quantum distinguisher of Feistel construction. A meet-in-the-middle attack on Feistel cipher in Q1 model was also discussed by Hosoyamada et al. [17]. More recently, Ito et al. [22] introduce the first 4-round quantum distinguisher on Feistel cipher in the quantum chosen-ciphertext setting (Q2 model). In this paper, we only study some Feistel ciphers in Q2 model, that the adversaries could make quantum queries on some superposition quantum states of the relevant cryptosystem.

1.1 Our contributions

In this paper, we focus on the study of the symmetric ciphers against Q2 adversary. Combining with Simon’s algorithm [36], we convert the classical advanced slide attacks (introduced by Biryukov and Wagner [4]) to a quantum one, that gains an exponential speed-up of the time complexity. Thus, we could break 2K-/4K-Feistel block ciphers and 2K-/4K-DES block ciphers in polynomial time. Concretely, we turn the classical attacks on 2K-/4K-Feistel block ciphers with $2^{0.25n}$ encryptions into quantum attacks with about $n+2+2\sqrt{n/2+1}$ quantum queries of the encryption process using about $n+1$ qubits. We turn the classical attacks on 2K-/4K-DES block ciphers with $2^{33}$ encryptions into quantum attacks with 155 or 233 quantum queries of the encryption process with 65 qubits.

On the other hand, concerning the full-round GOST, a Russian block cipher standard, we give a new quantum key-recovery attack, that breaks GOST in $2^{114.8}$ quantum queries of the encryption process, which is faster than the quantum brute force search attack by a factor of $2^{13.2}$. The attack needs 224 qubits. The results are summarized in Table 1.

Table 1 Summary of key-recovery attacks on Feistel schemes in classical setting and Q2 model

1.2 Comparison with Bonnetain et al.’s work [7]

Shortly after our work is made public at ePrint in 24 May 2018 [12], there is a concurrent work on similar topic by Bonnetain et al. [7], which appears at ePrint in 2 Nov 2018. Now Bonnetain et al.’s work has been accepted to SAC 2019. Both of the two works include the quantum advanced slide attack. But we want to list the differences in our paper from Bonnetain et al.’s. In our paper, we not only give the attacks on 1K-/2K-/4K-Feistel ciphers (also given by Bonnetain et al.), but also give non-trivial applications on 1K-/2K-/4K-DES. In the attack on 1K-/2K-/4K-DES, we give a new reformulation of the DES-like ciphers e.g. Fig. 7 in Sect. 3.2.1 in order to construct a sound period function. After we derive the period, we have to deal with the irreversible property of DES’s s-box to recover the keys. The quantum circuits of the quantum advanced slide attacks are presented in our work, which is not given by Bonnetain et al. In addition, our paper also includes the new quantum key-recovery attacks on 30-/32-round GOST.

2 Preliminaries

2.1 Attack model

In this paper, we focus on the powerful Q2 model. In this model, the adversary is not only equipped with local quantum computation resource, but also granted an access with superposition inputs to the remote cryptographic oracle, and obtains the corresponding superposition of outputs. Concretely, suppose the encryption oracle is ${\mathcal {O}}_k: \{0,1\}^n\rightarrow \{0,1\}^n$, then the Q2 adversary can make quantum queries $|x\rangle |y\rangle \mapsto |x\rangle |{\mathcal {O}}_k(x)\oplus y\rangle$, where x and y are arbitrary n-bit strings and $|x\rangle$ and $|y\rangle$ are the corresponding n-qubit states expressed in the computation basis. Moreover, any superposition $\sum _{x,y}\lambda _{x,y} |x\rangle |y\rangle$ is a valid input to the quantum oracle, whose corresponding output is $\sum _{x,y}\lambda _{x,y} |x\rangle |y\oplus {\mathcal {O}}_k(x)\rangle$. In previous works, the Q2 model is also called superposition attacks [10], quantum chosen message attacks [6] or quantum security [38]. For symmetric cryptanalysis, Q2 model is important and rational to some extent, as we have already mentioned the protocol of Boneh and Zhandry [5] for MACs that remains secure against superposition attacks. Moreover, as stated by Ito et al. [22]: “the threat of this attack model becomes significant if an adversary has access to its white-box implementation. Because arbitrary classical circuit can be converted into quantum one, the adversary can construct a quantum circuit from the classical source code given by the white-box implementation.”

2.2 Quantum algorithms

Our quantum attacks are based on two of the most popular quantum algorithms, namely Simon’s algorithm [36] and Grover’s algorithm [16].

Black-box period finding: given a function, f :  $\{0,1\}^{n}\rightarrow \{0,1\}^{n}$, that is observed to be invariant under some n-bit XOR period a, find a. In other words, find $a\ne 0$ such that $x\oplus y=a \Rightarrow f(x)=f(y)$.

The optimal classical time to solve the problem is ${\mathcal {O}}(2^{n/2})$. However, Simon [36] presents a quantum algorithm that provides exponential speedup and requires only ${\mathcal {O}}(n)$ quantum queries to find a.

Simon’s Algorithm [36]: the algorithm includes five quantum steps that are as follows:

• I. Initialization of two n-bit quantum registers to state $|0\rangle ^{\otimes n}|0\rangle ^{\otimes n}$. Then apply the Hadamard transform to the first register to attain an equal superposition in the following manner:

  $$\begin{aligned} {H^{ \otimes n}}|0\rangle |0\rangle = \frac{1}{\sqrt{{2^n}}}\sum \limits _{x \in {{\{ 0,1\} }^n}} {|x\rangle |0\rangle }. \end{aligned}$$

  (1)

• II. A quantum query to the function f maps this to

  $$\begin{aligned} \frac{1}{{\sqrt{{2^n}} }}\sum \limits _{x \in {{\{ 0,1\} }^n}} {|x\rangle |f(x)\rangle }. \end{aligned}$$

• III. While measuring the second register, the first register collapses to the following state:

  $$\begin{aligned} \frac{1}{\sqrt{2}}(|z\rangle + |z\oplus a\rangle ). \end{aligned}$$

• IV. Applying the Hadamard transform to the first register, we obtain:

  $$\begin{aligned} \frac{1}{{\sqrt{2} }}\frac{1}{{\sqrt{{2^n}} }}\sum \limits _{y \in {{\{ 0,1\} }^n}} {{{( - 1)}^{y \cdot z}}(1 + {{( - 1)}^{y \cdot a}})|y\rangle }. \end{aligned}$$

• V. The vectors y, that $y\cdot a=1$, depict an amplitude of zero. Hence, measuring the state yields a value of y, which meets that $y\cdot a =0$.

Intuitively, after repeating the above algorithm n times, we may obtain a by solving a system of linear equations if the system is of rank $n-1$. However, Kaplan et al. [23] and Santoli [34] showed that in the cryptanalysis scenario, the period function f(x) constructed may have many so-called “unwanted collisions”, which means there might be other collisions in addition to those of the form $f(x)=f(x\oplus a)$. For example, there might exist a pair $(x',a')$, such that $f(x')=f(x'\oplus a')$, where $a'\ne a$. Hence, one may need more repetitions of the above algorithms to obtain a full rank linear system of equations to get a. At Asiacrypt 2017, Leander and May [28] assume that f(x) behaves as a random periodic function with period a, and show that any function value f(x) has only two preimages with probability at least $\frac{1}{2}$. Moreover, they show that $l=2(n+\sqrt{n})$ repetitions of the Simon’s algorithm are sufficient to compute a. The probability is greater than $\frac{4}{5}$ that it contains at least $n-1$ linearly independent vectors y that are orthogonal to a (Lemma 4, [28]). In this paper, we follow Leander and May’s assumption, that all the periodic functions used in our attacks behave as random periodic functions. Therefore we use Lemma 4 of [28] to evaluate the complexity of our attacks.

Simon’s algorithm has been used to attack many primitives, such as the key-recovery attacks against Even-Mansour constructions [27], distinguishers against 3-round Feistel constructions [26], forgery attacks against block cipher based MACs [23], key recovery attacks against FX constructions [28], and so on.

Quantum search: given an unordered set of $N=2^n$ items, quantum search problem is to find the unique element that satisfies some condition. In other words, given f(x), $f(x) = 0$ for all $0 \leqslant x < 2^n$ except $x_0$, for which $f(x_0) = 1$, find $x_0$. The best classical algorithm for a search over unordered data requires O(N) time, but Grover’s algorithm [16] performs the search on a quantum computer in only ${O}(\sqrt{N})$ operations, a quadratic speedup.

Grover’s Algorithm [16]: define a black box oracle ${\mathcal {O}}$ as ${\mathcal {O}}|x\rangle |q\rangle =|x\rangle |q\oplus f(x)\rangle$. The steps of the algorithm are as follows:

• 1. Initialization of an ($n+1$)-bit register $|0\rangle ^{\otimes n}|1\rangle$. Apply the Hadamard transform to attain an superposition that can be given as follows:

  $$\begin{aligned} {H^{ \otimes (n+1)}}|0\rangle ^{\otimes n}|1\rangle = \frac{1}{\sqrt{{2^n}}}\sum \limits _{x \in {{\{ 0,1\} }^n}} {|x\rangle [(|0\rangle -|1\rangle )/\sqrt{2}] = |\Phi \rangle }. \end{aligned}$$

  (2)

• 2. Define $|\varphi \rangle = \frac{1}{\sqrt{{2^n}}}\sum \limits _{x \in {{\{ 0,1\} }^n}} |x\rangle$ and define the Grover iteration as $(2|\varphi \rangle \langle \varphi | - I){\mathcal {O}}$, and apply it $R\approx \frac{\pi }{4}\sqrt{2^n}$ times to the state $|\Phi \rangle$:

  $$\begin{aligned} {\big [(2|\varphi \rangle \langle \varphi | - I){\mathcal {O}}]^R}|\Phi \rangle \approx |x_0 \rangle [(|0\rangle -|1\rangle )/\sqrt{2}\big ]. \end{aligned}$$

• 3. Measure the final state and return $x_0$.

We give some brief explanations on step 2, and for more details, we refer the readers to [37]. As shown in Fig. 1, Grover denotes $(2|\varphi \rangle \langle \varphi | - I)$ as diffusion transform. It includes two Hadamard transforms $H^{\otimes n}$ and a conditional phase shift operation, which is represented by the unitary operator $2|0\rangle \langle 0|-I$, and satisfies $(2|0\rangle \langle 0|-I)|0\rangle =|0\rangle$ and $(2|0\rangle \langle 0|-I)|x\rangle =-|x\rangle$, where $x\ne 0$. Therefore, the entire diffusion transform using the notation $|\varphi \rangle$ is:

$$\begin{aligned} H^{\otimes n}[2|0\rangle \langle 0|-I]H^{\otimes n}=2H^{\otimes n}|0\rangle \langle 0|H^{\otimes n}-I=2|\varphi \rangle \langle \varphi |-I. \end{aligned}$$

(3)

Hereafter, we get the Grover iteration: $(2|\varphi \rangle \langle \varphi | - I){\mathcal {O}}$.

For the oracle ${\mathcal {O}}$, when applying it to $|x\rangle [(|0\rangle -|1\rangle )/\sqrt{2}]$, we get ${\mathcal {O}}|x\rangle [(|0\rangle -|1\rangle )/\sqrt{2}]=\frac{1}{\sqrt{2}}(|x\rangle |0\oplus f(x)\rangle -|x\rangle |1\oplus f(x)\rangle )$. Since $f(x_0)=1$, then ${\mathcal {O}}|x_0\rangle [(|0\rangle -|1\rangle )/\sqrt{2}]=\frac{1}{\sqrt{2}}(|x_0\rangle |0\oplus 1\rangle -|x_0\rangle |1\oplus 1\rangle )=\frac{1}{\sqrt{2}}(|x_0\rangle |1\rangle -|x_0\rangle |0\rangle )= (-1)|x_0\rangle [(|0\rangle -|1\rangle )/\sqrt{2}]$. When $x\ne x_0$, ${\mathcal {O}}|x\rangle [(|0\rangle -|1\rangle )/\sqrt{2}]=\frac{1}{\sqrt{2}}(|x\rangle |0\oplus 0\rangle -|x\rangle |1\oplus 0\rangle )=\frac{1}{\sqrt{2}}(|x\rangle |0\rangle -|x\rangle |1\rangle )= |x\rangle [(|0\rangle -|1\rangle )/\sqrt{2}]$. So ${\mathcal {O}}|x\rangle [(|0\rangle -|1\rangle )/\sqrt{2}]= (-1)^{f(x)}| x\rangle [(|0\rangle -|1\rangle )/\sqrt{2}]$.

Fig. 1

Circuit diagram for Grover’s algorithm [1]

Further, Brassard et al. [8] generalized the Grover search as an amplitude amplification method.

Theorem 1

(Brassard et al. [8]). Let ${\mathcal {A}}$ be any quantum algorithm on q qubits that performs no measurement. Let ${\mathcal {B}}:{\mathbb {F}}_2^q\rightarrow \{0,1\}$ be a function that classifies the outcomes of ${\mathcal {A}}$ as either good or bad state. Let $p>0$ be the initial success probability that the measurement of ${\mathcal {A}}|0\rangle$ is good. Set $t=\lfloor \frac{\pi }{4\theta }\rfloor$, where $\theta$ is defined using $sin^2(\theta )=p$. Furthermore, define the unitary operator $Q=-{\mathcal {A}}S_0{\mathcal {A}}^{-1}S_{\mathcal {B}}$, where the operator $S_{\mathcal {B}}$ changes the sign of the good state,

$$\begin{aligned} \mathrm{{|}}x\rangle \mapsto \left\{ \begin{array}{l} - |x\rangle ~\text {if}~{\mathcal {B}}(x)=1,\\ ~~|x\rangle ~\text {if}~{\mathcal {B}}(x)=0. \end{array} \right. \end{aligned}$$

Further, $S_0$ changes the sign of the amplitude only in case of the zero state $|0\rangle$. Finally, after performing the computation of $Q^t{\mathcal {A}}|0\rangle$, the measurement yields a good state with probability at least max{1-p, p}.

Assume that $|\varphi \rangle = {\mathcal {A}}|0\rangle$ is the initial vector, whose projections on the good and the bad subspace are denoted by $|\varphi _1\rangle$ and $|\varphi _0\rangle$, respectively. The state $|\varphi \rangle = {\mathcal {A}}|0\rangle$ exhibits an $\theta$ with a bad subspace, where $sin^2(\theta )=p$. Each Q iteration increases the angle by $2\theta$. Hence, after $t\approx \frac{\pi }{4\theta }$, the angle is observed to be approximately equal to $\pi /2$. Therefore, the state after t iterations is almost orthogonal to that of the bad subspace. After measurement, it produces a good vector with high probability.

2.3 Hosoyamada and Sasaki’s method to truncate outputs of quantum oracles

At ISIT 2010, Kuwakado and Morii [26] introduced a quantum distinguish attack on 3-round Feistel scheme by using Simon’s algorithm. As shown in Fig. 2:

$$\begin{aligned} \begin{array}{rll} F:\{0,1\}\times \{0,1\}^{n/2} &{} \rightarrow &{} \{0,1\}^{n/2}\\ b,x &{} \mapsto &{} \alpha _b\oplus X_{3}, \hbox {where} (X_3,Y_3)=E_K(x,\alpha _b),\\ F(b,x) &{} = &{} f_1(k_1,f_0(k_0,\alpha _b)\oplus x).\\ \end{array} \end{aligned}$$

F is periodic function that $F(b,x)=F(b\oplus 1, x\oplus f_0(k_0,\alpha _0)\oplus f_0(k_0,\alpha _1))$, $\alpha _0$ and $\alpha _1$ are arbitrary constants. Then using Simon’s algorithm, one can get the period $s=1||f_0(k_0,\alpha _0)\oplus f_0(k_0,\alpha _1)$ in polynomial time.

Note that, in the above attack, one has to truncate the output n bits of $E_K$ to obtain the left half n/2 bits, namely $X_3$. However, Kaplan et al. [23] and Hosoyamada et al. [17] pointed out that in quantum setting it is not trivial to truncated the entangled n qubits to n/2 qubits, since the usual truncation destroys entanglements.

At SCN 2018, Hosoyamada and Sasaki [17] introduced a method to simulate truncation of outputs of quantum oracles without destroying quantum entanglements. Let ${\mathcal {O}}:|x\rangle |y\rangle |z\rangle |w\rangle \mapsto |x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle |w\oplus {\mathcal {O}}_R(x,y)\rangle$ be the encryption oracle $E_K$, where ${\mathcal {O}}_L$, ${\mathcal {O}}_R$ denote the left and right n/2 bits of the complete encryption, respectively. The goal is to simulate oracle ${\mathcal {O}}_L:|x\rangle |y\rangle |z\rangle \mapsto |x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle$ by using some ancilla qubits.

Let $|+\rangle :=H^{n/2}|0^{n/2}\rangle =\frac{1}{\sqrt{2^{n/2}}}\sum _w|w\rangle$, where $H^{n/2}$ is an n/2-qubit Hadamard gate. Then, ${\mathcal {O}}|x\rangle |y\rangle |z\rangle |+\rangle = {\mathcal {O}}(|x\rangle |y\rangle |z\rangle [\frac{1}{\sqrt{2^{n/2}}}\sum _w|w\rangle ]) = |x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle [\frac{1}{\sqrt{2^{n/2}}}\sum _w|w\oplus {\mathcal {O}}_R(x,y)\rangle ]$ holds. In addition, let $w'=w\oplus {\mathcal {O}}_R(x,y)$. Then, $|x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle [\frac{1}{\sqrt{2^{n/2}}}\sum _w|w\oplus {\mathcal {O}}_R(x,y)\rangle ] = |x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle [\frac{1}{\sqrt{2^{n/2}}}\sum _w|w'\rangle ]= |x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle [\frac{1}{\sqrt{2^{n/2}}}\sum _{w'}|w'\rangle ]=|x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle |+\rangle$ holds. Therefore, ${\mathcal {O}}|x\rangle |y\rangle |z\rangle |+\rangle =|x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle |+\rangle$ holds.

Based on this observation, Hosoyamada and Sasaki defined ${\mathcal {O}}'_L:=(I\otimes H^{n/2})\circ {\mathcal {O}} \circ (I\otimes H^{n/2})$. Since ${\mathcal {O}}'_L |x\rangle |y\rangle |z\rangle |0^{n/2}\rangle =|x\rangle |y\rangle |z\oplus {\mathcal {O}}_L(x,y)\rangle |0^{n/2}\rangle$ holds, $\mathcal {O'}_L$ completely simulates ${\mathcal {O}}_L$. Hence, ${\mathcal {O}}_L$ can be simulated given the complete encryption oracle ${\mathcal {O}}$ using ancilla qubits.

Fig. 2

3-round quantum distinguisher

3 New advanced quantum slide attacks

3.1 Slide attack and advanced slide attack

Slide attack and advanced slide attack were proposed by Biryukov and Wagner [3, 4]. They are a set of powerful cryptanalysis tools. Classically, slide attack and advanced slide attack are launched against block ciphers with exponential time complexity. At CRYPTO 2016, Kaplan et al. [23] converted the slide attack on iterated Even-Mansour cipher into a quantum one by applying the slide attack and Simon’s algorithm, shown in Fig. 3. They define $F: \{0,1\}^{n+1}\rightarrow \{0,1\}^{n}$ as

$$\begin{aligned} F(b\Vert x) = \left\{ \begin{array}{lc} P(E_k^P(x)) \oplus x &{}\quad \mathrm{{if}}~b=0,\\ E_k^P(P(x)) \oplus x &{}\quad \mathrm{{if}}~b=1, \end{array} \right. \end{aligned}$$

(4)

where $b\in \{0,1\}, x\in \{0,1\}^{n}$. For arbitrary $x\in \{0,1\}^{n}$, we have

$$\begin{aligned} F(0\Vert x)=P\big (E_k^P(x)\big ) \oplus x =E_k^P(P(x\oplus k)) \oplus (x\oplus k)=F(1\Vert (x\oplus k)). \end{aligned}$$

(5)

Thus, $s=1\Vert k$ is the period of F. Finally, they could retrieve the secret key by applying Simon’s algorithm with polynomial time complexity.

Fig. 3

Slide attack against iterated Even-Mansour cipher of which round keys are all the same

Feistel ciphers form an important special case for applying slide attacks. Kaplan et al.’s quantum slide attack against iterated Even-Mansour cipher could not be applied to Feistel ciphers trivially. Thus, we will give some new quantum attacks on some Feistel ciphers.

In this paper, we focus on the 1K-/2K-/4K-Feistel and 1K-/2K-/4K-DES block ciphers, which were introduced and studied by Biryukov and Wagner [3, 4]. They designed a novel advanced slide attack on these ciphers with exponential time complexities in classical computers. 2K-/4K-DES block ciphers are the modified DES examples which use two or four independent 48-bit keys and the key arrangements are the same as 2K-/4K-Feistel block ciphers. The total number of rounds of 2K-/4K-DES are 64 or more, thus they resist to the conventional differential [2] and linear attacks [29]. In this paper, we give some advanced quantum slide attacks on 1K-/2K-/4K-Feistel block ciphers and extend them to attacks on 1K-/2K-/4K-DES block ciphers by looking into the concrete round function of DES. Our attacks work on m-round 1K-Feistel/1K-DES block cipher, or on 2m-round 2K-Feistel/2K-DES block cipher, or 4m-round 4K-Feistel/4K-DES block cipher, where m is any positive integer. For simplicity, in the following sections, we only list example attacks on 4-round 1K-Feistel/1K-DES block cipher, 4-round 2K-Feistel/2K-DES block cipher and 8-round 4K-Feistel/4K-DES block cipher, respectively.

3.2 Advanced quantum slide attack on 1K-feistel

As shown in Fig. 4, 1K-Feistel block cipher adopts repeating round subkey and identical round function f.

Fig. 4

Quantum Attacks on 1K-Feistel Block Cipher

We first define the following function using given random constant $\alpha$:

$$\begin{aligned} \begin{array}{l} \begin{array}{*{20}{cl}} F:\{ 0,1\} \times {{\{ 0,1\} }^{n/2}} &{}\rightarrow {{\{ 0,1\} }^{n/2}}\\ b,x &{}\mapsto \left\{ \begin{array}{*{20}{ll}} {E_K}{{(x,\alpha )}_R}&{}\quad \mathrm{{if}}~b = 0,\\ {E_K}{{(\alpha ,f(\alpha ) \oplus x)}_L}&{}\quad \mathrm{{if}}~b = 1, \end{array} \right. \end{array} \end{array} \end{aligned}$$

(6)

where n is the block size of 1K-Feistel block cipher $E_K$, $E_K(\cdot )_L$ and $E_K(\cdot )_R$ are the left branch ($\frac{n}{2}$-bit) or right branch ($\frac{n}{2}$-bit) of $E_K(\cdot )$.

As shown in Fig. 4, ${E_K}(x,\alpha )_R=Y_4$, ${E_K}(X_1,Y_1)_L=X_5=Y_4$, $X_1=\alpha$ and $Y_1=f(k\oplus \alpha )\oplus x$ hold. Thus, from ${E_K}(x,\alpha )_R= {E_K}(X_1,Y_1)_L=Y_4$, we deduce

$$\begin{aligned} F(0,x)={E_K}(x,\alpha )_R=E_K(\alpha ,f(k\oplus \alpha )\oplus x)_L =F(1,x\oplus f(\alpha )\oplus f(k\oplus \alpha )). \end{aligned}$$

(7)

So F(b, x) is a function with period $s=1\Vert f(\alpha )\oplus f(k\oplus \alpha )$ and the period could be retrieved by applying Simon’s algorithm. According to Sect. 2.2, the time complexity is about $l=2(n/2+1+\sqrt{n/2+1})$ repetitions of Simon’s algorithm to recover s, which is equivalent to $l=2(n/2+1+\sqrt{n/2+1})$ quantum queries of the encryption process, using about $n+1$ qubits.

In order to simulate F(b, x), we have to truncate the output of $E_K$ to get the right half or left half n/2 bits. Thanks to Hosoyamada and Sasaki’s work [17] shown in Sect. 2.3, we can truncate outputs of quantum oracles with ease. The quantum circuit of F(b, x) is shown in Fig. 5. If f is reversible, such as GOST [31], Camellia [20] etc., it is easy to get k with the knowledge s. If f is irreversible, such as for DES and its variants, it is possible to recover the key by studying the detailed structure of their round function as shown in Sect. 3.2.1. Note that, the attack works for any number of rounds of 1K-Feistel, we only give a 4-round example attack in this section.

Fig. 5

A quantum circuit that computes the function F for the attack on 1K-Feistel. Please refer to [32] for the relevant quantum gates and circuit symbols

Fig. 6

DES Round Function

3.2.1 The application to 1K-DES

The round function of DES is shown in Fig. 6. We define that 1K-DES uses only one 48-bit key in every round. The 32-bit right branch, i.e., R branch word is expanded by EX function to 48-bit, then it is XORed by 48-bit k. The f function is applied to the 48-bit state, and outputs 32-bit word. The s-boxes map 6-bit input into 4-bit output. We only give $S_1$ s-box in Table 2 as an example.

Table 2 DES s-box: $S_1$

The quantum advanced slide attack on 1K-DES is shown in Fig. 7. The period function is therefore defined as follows:

$$\begin{aligned} \begin{array}{l} \begin{array}{*{20}{cl}} F:\{ 0,1\} \times {{\{ 0,1\} }^{n/2}} &{}\rightarrow {{\{ 0,1\} }^{n/2}}\\ b,x &{}\mapsto \left\{ \begin{array}{*{20}{ll}} {E_K}{{(x,\alpha )}_R}&{}\quad \mathrm{{if}}~b = 0,\\ {E_K}{{(\alpha ,f(EX(\alpha ) ) \oplus x)}_L}&{}\quad \mathrm{{if}}~b = 1, \end{array} \right. \end{array} \end{array} \end{aligned}$$

(8)

Then,

$$\begin{aligned} F(0,x)= & {} {E_K}(x,\alpha )_R=E_K(\alpha ,f(k\oplus EX(\alpha ))\oplus x)_L\nonumber \\= & {} F(1,x\oplus f(EX(\alpha ))\oplus f(k\oplus EX(\alpha ))). \end{aligned}$$

(9)

Fig. 7

Quantum Attack on 1K-DES Block Cipher

Thus, $s=1\Vert f(EX(\alpha ))\oplus f(k\oplus EX(\alpha ))$ is the period of F function. Suppose we have recovered s by Simon’s algorithm, and then $f(k\oplus EX(\alpha ))$ is known. Note that, $S_i (i=1,2,\ldots ,8)$ is mapping 6-bit input to 4-bit output. Thus, given a 4-bit output, we could recover 4 possible 6-bit inputs, then get four candidate 6-bit keys for each s-box. For example, suppose that the output of $S_1$ is 14, we could get four different 6-bit inputs as shown in Table 2.

Note that, we could use a different $\alpha$, to construct a different period function F. We select $\alpha$ so that in each s-box, the 6-bit inputs are different for each $\alpha$. For example, the 6-bit inputs of $S_1$ for all selected $\alpha$ should be different. Hence, we could get different $f(k\oplus EX(\alpha ))$ with different $\alpha$. It is expected that with 2 different $\alpha$, we could uniquely determine one correct 48-bit k by uniquely determining each 6-bit key separately for each s-box. According to Sect. 2.2, the time complexity is $2l=2\times 2\times (33+\sqrt{33})\approx 155$ repetitions of Simon’s algorithm, which is equivalent to 155 quantum queries of the encryption process, using 65 qubits.

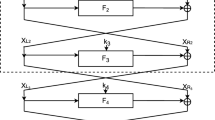
3.3 Quantum slide attack on 2K-feistel

As shown in Fig. 8, 2K-Feistel block cipher adopts round subkeys ($k_0,k_1$) iteratively and identical round function f.

Fig. 8

Quantum Attack on 2K-Feistel Block Cipher to Recover $k_0$

We first define the following function using given random constant $\alpha$:

$$\begin{aligned} \begin{array}{l} \begin{array}{*{20}{cl}} F:\{ 0,1\} \times {{\{ 0,1\} }^{n/2}} &{}\rightarrow {{\{ 0,1\} }^{n/2}}\\ b,x &{}\mapsto \left\{ \begin{array}{*{20}{ll}} {E_K}{{(x,\alpha )}_R}&{}\quad \mathrm{{if}}~b = 0,\\ {D_K}{{(f(\alpha ) \oplus x, \alpha )}_R}&{}\quad \mathrm{{if}}~b = 1. \end{array} \right. \end{array} \end{array} \end{aligned}$$

(10)

As shown in Fig. 8, $E_K(x,\alpha )_R=Y_4$, $D_K(Y_1,X_1)_R=X_5=Y_4$, $Y_1=f(k_0\oplus \alpha )\oplus x$, $X_1=\alpha$ hold. Thus, from $E_K(x,\alpha )_R=D_K(Y_1,X_1)_R=Y_4$, we deduce

$$\begin{aligned} F(0,x)={E_K}(x,\alpha )_R=D_K(f(k_0\oplus \alpha )\oplus x,\alpha )_R =F(1,x\oplus f(\alpha )\oplus f(k_0\oplus \alpha )). \end{aligned}$$

(11)

So F(b, x) is a function with period $s=1\Vert f(\alpha )\oplus f(k_0\oplus \alpha )$. According to Sect. 2.2, the time complexity is about $l=2(n/2+1+\sqrt{n/2+1})$ repetitions of Simon’s algorithm to recover s, which is equivalent to $l=2(n/2+1+\sqrt{n/2+1})$ quantum queries of the encryption process, using about $n+1$ qubits.

Fig. 9

A quantum circuit that computes the function F for 2K-Feistel. The X gate is the quantum equivalent of the NOT gate that flips the qubit $|0\rangle$ and $|1\rangle$

The quantum circuit of F(b, x) is shown in Fig. 9, and please refer to [32] for the relevant quantum gates and circuit symbols. If f is reversible, such as GOST [31], Camellia [20], etc., it is easy to get $k_0$ with s. If f is irreversible, such as 2K-DES, it is easy to recover $k_0$ with the same strategy as Sect. 3.2.1 and the same complexity. Note that, the attack works for any even number of rounds of 2K-Feistel, we only give a 4-round example attack in this section.

To get $k_1$, we design a similar quantum period function in Equation (12).

$$\begin{aligned} \begin{array}{l} \begin{array}{*{20}{cl}} F:\{ 0,1\} \times {{\{ 0,1\} }^{n/2}} &{}\rightarrow {{\{ 0,1\} }^{n/2}}\\ b,x &{}\mapsto \left\{ \begin{array}{*{20}{ll}} {D_K}{{(\alpha ,x)}_L}&{}{~~\mathrm {if}}~b = 0,\\ {E_K}{{(\alpha ,f(\alpha ) \oplus x)}_L}&{}{~~\mathrm {if}}~b = 1. \end{array} \right. \end{array} \end{array} \end{aligned}$$

(12)

As shown in Fig. 10, $D_K(\alpha ,x)_L=Y_4$, $E_K(X_1,Y_1)_L=X_5=Y_4$, $Y_1=f(k_1\oplus \alpha )\oplus x$, $X_1=\alpha$ hold. Thus, from $D_K(\alpha ,x)_L=E_K(X_1,Y_1)_L=Y_4$, we deduce

$$\begin{aligned} F(0,x)={D_K}(\alpha ,x)_L=E_K(\alpha ,f(k_1\oplus \alpha )\oplus x)_L =F(1,x\oplus f(\alpha )\oplus f(k_1\oplus \alpha )). \end{aligned}$$

(13)

So F(b, x) is a function with period $s=1\Vert f(\alpha )\oplus f(k_1\oplus \alpha )$, and $k_1$ is got consequently.

Fig. 10

Quantum Attacks on 2K-Feistel Block Cipher to Recover $k_1$

3.4 Quantum slide attack on 4K-feistel

As shown in Fig. 11, 4K-Feistel block cipher adopts round subkeys ($k_0,k_1,k_2,k_3$) iteratively and identical round function f. Given arbitrary constant $\alpha \in {\mathbb {F}}^{n/2}_2$, define:

$$\begin{aligned} \begin{array}{l} \begin{array}{*{20}{cl}} F: \{ 0,1\} \times {{\{ 0,1\} }^{n/2}} &{}\rightarrow {{\{ 0,1\} }^{n/2}}\\ b,x &{}\mapsto \left\{ \begin{array}{*{20}{ll}} {E_K}{{(x,\alpha )}_R}&{}\quad \mathrm{{if}}~b = 0,\\ {D_K}{{(f(\alpha )\oplus x, \alpha )}_R}&{}\quad \mathrm{{if}}~b = 1. \end{array} \right. \end{array} \end{array} \end{aligned}$$

(14)

As shown in Fig. 11, $E_K(x,\alpha )_R=Y_8$, $D_K(Y_1\oplus \varDelta ,X_1)_R=X_9=Y_8$, $Y_1=f(k_0\oplus \alpha )\oplus x$, $X_1=\alpha$ hold, where $\varDelta =k_1\oplus k_3$. Thus, from $E_K(x,\alpha )_R=D_K(Y_1\oplus \varDelta ,X_1)_R=Y_8$, we deduce

Fig. 11

Quantum Attacks on 4K-Feistel Block Cipher

$$\begin{aligned} F(0,x)= & {} {E_K}(x,\alpha )_R=D_K(f(k_0\oplus \alpha )\oplus x\oplus \varDelta ,\alpha )_R\nonumber \\= & {} F(1,x\oplus f(\alpha )\oplus f(k_0\oplus \alpha )\oplus \varDelta ). \end{aligned}$$

(15)

So, F(b, x) is a function with period $s=1\Vert f(\alpha )\oplus f(k_0\oplus \alpha )\oplus \varDelta$. According to Sect. 2.2, the time complexity is about $l=2(n/2+1+\sqrt{n/2+1})$ repetitions of Simon’s algorithm to recover s, which is equivalent to $l=2(n/2+1+\sqrt{n/2+1})$ quantum queries of the encryption process, using about $n+1$ qubits.

Similar to the attack on 2K-Feistel, we could also design a similar period function, with period $s'=1\Vert f(\alpha )\oplus f(k_3\oplus \alpha )\oplus \varDelta '$, where $\varDelta '=k_0\oplus k_2$. Note that, the attack works for any 4m-round 4K-Feistel, where m is any positive integer, we only give an 8-round example attack in this section.

We follow the the assumption made by the 2K-/4K-Feistel’s designers, i.e., Biryukov and Wagner, that the round function f is simple, just like the round function of GOST [31], Camellia [20], DES [20], etc. Hence, it is easy to get the secret keys by the knowledge of s and $s'$, when looking into the details of the round function. We give an example attack on 4K-DES in Sect. 3.4.1.

3.4.1 Application to 4K-DES

As shown in Fig. 12, 4K-DES block cipher adopts four 48-bit round subkeys ($k_0,k_1,k_2,k_3$) iteratively. Given arbitrary constant $\alpha \in {\mathbb {F}}^{n/2}_2$, the period function is defined as follows:

$$\begin{aligned} \begin{array}{l} \begin{array}{*{20}{cl}} F: \{ 0,1\} \times {{\{ 0,1\} }^{n/2}} &{}\rightarrow {{\{ 0,1\} }^{n/2}}\\ \\ b,x &{}\mapsto \left\{ \begin{array}{*{20}{ll}} {E_K}{{(x,\alpha )}_R}&{}\quad \mathrm{{if}}~b = 0,\\ {D_K}{{(f(EX(\alpha ))\oplus x, \alpha )}_R}&{}\quad \mathrm{{if}}~b = 1. \end{array} \right. \end{array} \end{array} \end{aligned}$$

(16)

As defined in Sect. 3.2.1, EX is the expand function. Let $\varDelta =EX^{-1}(k_1\oplus k_3)$, our attack works only when $EX(\varDelta )=k_1\oplus k_3$. Since $EX^{-1}$ maps 48-bit word $k_1\oplus k_3$ to a 32-bit word, $EX(\varDelta )=k_1\oplus k_3$ holds with probability $2^{-16}$. Thus, our attack on 4K-DES only works for $1/2^{16}$ of all keys, which is the same as Biryukov and Wagner’s attack [4].

Since $E_K(x,\alpha )_R=Y_4$, $D_K(Y_1\oplus \varDelta ,X_1)_R=X_5=Y_4$, $Y_1=f(k_0\oplus EX(\alpha ))\oplus x$, $X_1=\alpha$ hold, we could deduce the following equation from $E_K(x,\alpha )_R=D_K(Y_1\oplus \varDelta ,X_1)_R=Y_4$.

$$\begin{aligned} F(0,x)= & {} {E_K}(x,\alpha )_R=D_K(f(k_0\oplus EX(\alpha ))\oplus x\oplus \varDelta ,\alpha )_R\nonumber \\= & {} F(1,x\oplus f(EX(\alpha ))\oplus f(k_0\oplus EX(\alpha ))\oplus \varDelta ). \end{aligned}$$

(17)

Fig. 12

Quantum Attack on 4K-DES Block Cipher

So, F(b, x) is a function with period $s=1\Vert f(EX(\alpha ))\oplus f(k_0\oplus EX(\alpha ))\oplus \varDelta$. When given the value of $f(k_0\oplus EX(\alpha ))\oplus \varDelta$, we could look into the f function and study the s-box one by one in Fig. 6. For example, as shown in Fig. 13, if we use three different $\alpha$ to run Simon’s algorithm¹, we could get three valid input-output pairs of s-box $S_1$, i.e., $(in_1,out_1)$, $(in_2,out_2)$ and $(in_3,out_3)$. We guess the 6-bit $k_{in}$, we could get 3 candidate $k_{out}$ by the three pairs, which are equal with probability $2^{-8}$. Thus, at last only one ($k_{out}, k_{in}$) pair is expected to remain. After calculate ($k_{out}, k_{in}$) for each of the 8 s-boxes respectively, we find the right key ($k_0,EX^{-1}(k_1\oplus k_3)$). According to Lemma 4 of [28], the time complexity is $3l=3\times 2\times (33+\sqrt{33})\approx 233$ repetitions of Simon’s algorithm, which is equivalent to 233 quantum queries of the encryption process, using 65 qubits.

Fig. 13

Input and output of s-box $S_1$

4 Quantum key-recovery attack on GOST block cipher

4.1 GOST block cipher

GOST [31] is a block cipher designed during the 1970’s by the Soviet Union as an alternative to the American DES. Similar to DES, it has a 64-bit Feistel structure, employing 8 s-boxes and is intended for civilian use. Unlike DES, it has a significantly larger key (256 bits instead of just 56), more rounds (32 compared with DES’s 16), and uses different sets of s-boxes. After the USSR had been dissolved, GOST was accepted as a Russian standard.

Suppose the input state of i-th round function is $(X_{i-1},Y_{i-1})$, where $X_{i-1}$ and $Y_{i-1}$ are the left and right branches of the i-th round function for $i=1,2,\ldots ,32$. The first round of GOST is given in Fig. 14, the only difference for each round is the subkeys. The symbols used are

$+$:

modular addition,

−:

modular subtraction,

$\oplus$:

bitwise addition,

$\lll j$:

cyclic left rotation by j bits ,

$\ggg j$:

cyclic right rotation by j bits.

$X{[}i_1,\ldots ,i_{j}{]}$:

the $i_{1},\ldots ,i_{j}$th least significant bits of the 32-bit word X.

In the round function, the round key is (modular) added with 32-bit right branch; then the 32-bit state is substituted by S, which is composed of 8 $4\times 4$ s-boxes in parallel; then rotating left the 32-bit state by 11 bits. It has a simple key schedule: 256-bit key is divided into eight 32-bit words $k_0,k_1\cdots , k_7$ and the sequence of round keys is given as $k_0,\cdots , k_7,k_0,\cdots , k_7, k_0,\cdots , k_7,k_7,k_6,\cdots , k_1,k_0$.

Fig. 14

The first round of GOST block cipher

4.2 Quantum attack on 30-round GOST block cipher

We first give some properties of GOST.

Property 1

As shown in Fig. 15, for a two round GOST, if we know $(X_0,Y_0)$ and $(X_2,Y_2)$, then $k_0=S^{-1}((X_0\oplus X_2)\ggg 11)-Y_0$, $k_1=S^{-1}((Y_0\oplus Y_2)\ggg 11)-X_2$.

Fig. 15

2-round of GOST block cipher

Property 2

(Reflection Property[25]) If the input state of the 25th round meets condition $X_{24}=Y_{24}$, then the last 16-round of 32-round GOST acts as an identity by ignoring the last swap function, i.e., the input of 17th round is $(X_{16},Y_{16})$, and the output of 32th round is $(X_{32},Y_{32})=(Y_{16},X_{16})$.

Proof

As shown in Fig. 16, it is easy to see that, $X_{23}=f_{k_7}(Y_{23})\oplus Y_{24}$, $Y_{25}=f_{k_7}(Y_{24})\oplus X_{24}$. Since $X_{24}=Y_{24}$ and $Y_{23}=X_{24}$, we get $X_{23}=Y_{25}$. While $Y_{23}=X_{24}=X_{25}$ holds. Thus, we get ($X_{23},Y_{23}$)=($Y_{25},X_{25}$).

$X_{22}=f_{k_6}(Y_{22})\oplus Y_{23}$, $Y_{26}=f_{k_6}(Y_{25})\oplus X_{25}$. Since ($X_{23},Y_{23}$)=($Y_{25},X_{25}$) and $Y_{22}=X_{23}$, we get $X_{22}=Y_{26}$. While $Y_{22}=X_{23}=Y_{25}=X_{26}$ holds. Thus, we get ($X_{22},Y_{22}$)=($Y_{26},X_{26}$). Iterating the above procedures, finally, we get the conclusion of Property 2, i.e., $(X_{32},Y_{32})=(Y_{16},X_{16})$. $\square$

Fig. 16

Reflection Property of the last 16-rounds GOST block cipher

In this section, we only consider the last 30-round reduced GOST block cipher (from 3th to 32th round shown in Fig. 17), against quantum attackers from Q2 model. Since the key size of the 30-round GOST block cipher is 256-bit, if we trivially use quantum brute-force search (Grover’s algorithm [16]) to find the key, it needs $2^{128}$ Grover iterations. In the following, we combine the reflection property and Grover’s algorithm to attack 30-round GOST block cipher in $2^{112}$ Grover iterations.

Fig. 17

Attack on 30-round reduced GOST

Note that the input and output are $(X_2,Y_2)$ and $(X_{32},Y_{32})$. We first construct the following quantum algorithm ${\mathcal {A}}$: Preparing the initial ${32\times 7}$-bit register $|0\rangle ^{\otimes 224}$. Apply Hadamard transform ${H^{ \otimes 224}}$ to the register to attain an equal superposition (omitting the amplitudes):

$$\begin{aligned} \sum \limits _{X_2,k_2,k_3,\ldots ,k_7 \in {{\{ 0,1\} }^{32}}} {|X_2\rangle |k_2,k_3,\ldots ,k_7\rangle }=|\varphi \rangle , \end{aligned}$$

(18)

where $X_2$ is the left half of the input of the 30-round GOST; the right half $Y_2$ is a constant.

According to the Reflection Property 2, when $X_{24}=Y_{24}$, the last 16-round is an identical transformation by ignoring the last swap function. Thus, given $2^{32}$ inputs ($X_2,Y_2$), it is expected that there is one $(X_2,Y_2)$ pair that satisfies the condition $X_{24}=Y_{24}$, then $(X_{16}\Vert Y_{16})=(Y_{32}\Vert X_{32})$.

Once we get the right ($X_2,Y_2$) somehow, we guess $k_2,k_3,\ldots ,k_7$, then encrypt for round 3-8 to get the internal state $(X_8,Y_8)$, decrypt $(X_{16}\Vert Y_{16})$ for round 11-16 to get $(X_{10},Y_{10})$. According to Property 1, we could deduce $k_0$ and $k_1$ from $(X_8,Y_8)$ and $(X_{10},Y_{10})$.

Considering the superposition $|\varphi \rangle$, assume that we had a classifier ${\mathcal {B}}: \{0,1\}^{32\times 7}\rightarrow \{0,1\}$, which partitions $|\varphi \rangle$ into a good subspace and a bad subspace: $|\varphi \rangle =|\varphi _1\rangle +|\varphi _0\rangle$, where $|\varphi _1\rangle$ and $|\varphi _0\rangle$ denote the projection onto the good subspace and bad subspace, respectively. In the good subspace $|\varphi _1\rangle$, $(X_2,Y_2)$ meets the Reflection Property and $k_2,k_3,\ldots ,k_7$ are the right subkeys. For the good state $|x\rangle$, ${\mathcal {B}}(x)=1$.

We construct the quantum classifier ${\mathcal {B}}$. Define ${\mathcal {B}}:~\{0,1\}^{32\times 7}\rightarrow \{0,1\}$ that maps $(X_2,k_2,k_3,\ldots ,k_7)$ to 0 or 1:

• 1. For $(X_2,Y_2)$, derive $(X_{32},Y_{32})$ from the 30-round encryption oracle, note that $Y_2$ is a random given constant.

• 2. Use $(k_2,k_3,\ldots ,k_7)$, $(X_2,Y_2)$ and $(X_{32},Y_{32})$ to derive $k_0,k_1$ from Property 1.

• 3. Check the derived $(k_0,k_1,k_2,\ldots ,k_7)$ by 5 plaintext-ciphertext pairs using the 30-round encryption oracle. If the check is right, output 1. Else output 0.

We classify a state $|X_2\rangle |k_2,k_3,\ldots ,k_7\rangle$ is a good state if and only if ${\mathcal {B}}(X_2,k_2,k_3,\ldots ,k_7)=1$. The classifier ${\mathcal {B}}$ outputs good under two conditions:

• (a) Condition 1. $(X_2,Y_2)$ meets the Reflection Property. According to the above cryptanalysis, it is right with a probability of $2^{-32}$.

• (b) Condition 2. $k_2,k_3,\ldots ,k_7$ are the right subkeys. It is right with a probability $2^{-192}$.

If we measure $|\phi \rangle$, it produces the good state with probability p:

$$\begin{aligned} \begin{array}{ll} p &{}= \Pr [|X_2\rangle |k_2,k_3,\ldots ,k_7\rangle ~\texttt {is~good}] \\ &{}= \Pr [{\mathcal {B}}(X_2,k_2,k_3,\ldots ,k_7)=1] \\ &{}= \Pr [\texttt {Condition~1}]\cdot \Pr [\texttt {Condition~2}]\\ &{}\approx 2^{-32}\times 2^{-32\times 6}=2^{-224}. \end{array} \end{aligned}$$

(19)

Our classifier ${\mathcal {B}}$ defines a unitary operator $S_{{\mathcal {B}}}$ that conditionally change the sign of the quantum state $|X_2\rangle |k_2,k_3,\ldots ,k_7\rangle$:

$$\begin{aligned} \left\{ \begin{array}{ll} -&{}|X_2\rangle |k_2,\ldots ,k_7\rangle ~\texttt {if}~{\mathcal {B}}(X_2,k_2,\ldots ,k_7)=1\\ &{}|X_2\rangle |k_2,\ldots ,k_7\rangle ~\texttt {if}~{\mathcal {B}}(X_2,k_2,\ldots ,k_7)=0 \end{array} \right. \end{aligned}$$

(20)

The complete amplification process is realized by repeatedly for t times applying the unitary operator $Q=-{\mathcal {A}}S_0{\mathcal {A}}^{-1}S_{\mathcal {B}}$ to the state $|\varphi \rangle = {\mathcal {A}}|0\rangle$, i.e. $Q^t{\mathcal {A}}|0\rangle$.

Initially, the angle between $|\varphi \rangle = {\mathcal {A}}|0\rangle$ and the bad subspace $|\varphi _0\rangle$ is $\theta$, where $sin^2(\theta )=p=\langle \varphi _1|\varphi _1\rangle$. When p is smaller enough, $\theta \approx arcsin(\sqrt{p})\approx 2^{-\frac{224}{2}}$. According to Theorem 1, after $t=\lfloor \frac{\pi }{4\theta }\rfloor = \lfloor \frac{\pi }{4\times 2^{-\frac{224}{2}}}\rfloor \approx 2^{112}$ Grover iterations Q, the angle between resulting state and the bad subspace is roughly $\pi /2$. The probability $P_{good}$ that the measurement yields a good state is about $sin^2(\pi /2)=1$.

The whole attack needs 224 qubits and $2^{112}$ Grover iterations, where each Grover iteration needs about 6 quantum queries of 30-round GOST. Hence, it costs about $2^{114.6}$ quantum queries of the encryption process, which is more efficient than the trivial quantum search (256 qubits and $2^{128}$ Grover iterations).

4.3 Quantum attack on full-round GOST block cipher

Property 3

(Fixed Point Property[11]) As shown in Fig. 18, assume that when we encrypt a 64-bit plaintext $P=$($X_0,Y_0$), we obtain ($X_8,Y_8$)=($X_0,Y_0$) after 8 encryption rounds. Since rounds 9–16 and 17–24 are identical to rounds 1–8, we obtain P after 16 and 24 encryption rounds as well. In rounds 25–32, the round keys $k_0,\ldots ,k_7$ are applied in the reverse order, and we obtain some arbitrary ciphertext $C=(X_{32},Y_{32})$. The knowledge of P and C immediately gives us the two input-output pairs of the first 8-round, i.e., $(P, P)=(X_{0}\Vert Y_{0},X_{0}\Vert Y_{0})$ and $(\bar{C},\bar{P})=(Y_{32}\Vert X_{32},Y_{0}\Vert X_{0})$. The probability to get a fix point of the first 8 rounds is $2^{-64}$.

Proof

As shown in Fig. 18, once we get an input-output pair $(P, P)=(X_{0}\Vert Y_{0},X_{0}\Vert Y_{0})$ for the rounds 1–8, we get the input-output pair (P, C) for rounds 25-32. We focus on rounds 25–32 shown in Fig. 16, different from rounds 1–8, the subkeys are in inverse order. If we consider rounds 25–32 in inverse direction, i.e., from 32th round to 25th round, the only difference from rounds 1–8 is that there is an additional swap function in the first round but not in the last round. So, $(\bar{C},\bar{P})=(Y_{32}\Vert X_{32},Y_{0}\Vert X_{0})$ is also an input-output pair for rounds 1–8.

$\square$

Property 4

As shown in Fig. 19, if we know two valid input-output pairs of the 3-round GOST, i.e., $(X_5\Vert Y_5,X_8\Vert Y_8)$ and $(X'_5\Vert Y'_5,X'_8\Vert Y'_8)$, then we can easily determine the three subkeys $k_5,k_6,k_7$.

Proof

As shown in Fig. 19, we get

$$\begin{aligned} (S(Y_5+k_5)\lll 11)\oplus X_5= & {} (S(X_8+k_7)\lll 11)\oplus Y_8, \end{aligned}$$

(21)

$$\begin{aligned} (S(Y'_5+k_5)\lll 11)\oplus X'_5= & {} (S(X'_8+k_7)\lll 11)\oplus Y'_8. \end{aligned}$$

(22)

We rewrite Eq. (21), as $S(Y_5+k_5)\oplus S(X_8+k_7)=(X_5\oplus Y_8)\ggg 11$. Note that S is composed of 8 4$\times$4 s-boxes in parallel, we first guess the 4 least significant bits of $k_5$, i.e., $k_5[3,2,1,0]$, then compute $s_0(Y_5[3,\ldots ,0]+k_5[3,\ldots ,0])$, where $s_0$ is the s-box applied to the 4 least significant bits of $Y_5+k_5$, thus we could determine $X_8[3,\ldots ,0]+k_7[3,\ldots ,0]$ and get $k_7[3,\ldots ,0]$ by (modular $2^{4}$) subtracting $X_8[3,\ldots ,0]$. Similarly, by Eq. (22), we could also derive another value of $k_7[3,\ldots ,0]$, if they are not equal, then the guessing of $k_5[3,2,1,0]$ is wrong. After we determine a right candidate $k_5[3,2,1,0]$ and $k_7[3,2,1,0]$, we could continue to guess and determine $k_5[7,6,5,4]$ and $k_7[7,6,5,4]$ with the known carry bits of the previous nibbles. Finally, we are expected to get the right candidate $k_5,k_7$. Then we compute $Y_6=(S(Y_5+k_5)\lll 11)\oplus X_5$. Thus we get $k_6=S^{-1}((Y_5\oplus X_8)\ggg 11)-Y_6$. Totally, we only use $8 \times 2^4\times 2+2\times 8=272$s-boxes operations without any memory cost, which approximate one encryption of GOST (it needs $8\times 32=256$s-boxes operations).

$\square$

Fig. 18

Attack on the Full-round GOST

Fig. 19

3-round GOST

4.3.1 A classical attack:

Using Property 3 and 4, we could devise a classical attack without any memory complexity. We list the brief steps of the classical attack here:

• (1) For each of $2^{64}$ plaintexts, and for each of $2^{160}$ key guessing $k_0,k_1,\ldots ,k_4$:

  • (a) Construct two input-output pairs of rounds 1-8 according to Property 3, i.e., (P, P) and $(\bar{C}, \bar{P})$. Use Property 4 to compute $k_5,k_6,k_7$.

  • (b) Use 5 additional plaintext-ciphertext pairs to check $k_0,k_1,\ldots ,k_6,k_7$, if it is right, return the key.

The time complexity of the above classical attack is $2^{64+160}=2^{224}$. The data complexity is $2^{64}$, while the best previous attack only use $2^{32}$ data complexity with similar time complexity as shown in Table 1. However, our attack do not use any memory cost, which is very important to devise an efficient quantum algorithm. Since quantum memory is equivalent to the number of qubits in the circuit, which is very expensive.

4.3.2 The quantum attack:

In our quantum attack on full-round GOST, we first construct the following quantum algorithm ${\mathcal {A}}$: Preparing the initial ${32\times 7}$-bit register $|0\rangle ^{\otimes 224}$. Apply Hadamard transform ${H^{ \otimes 224}}$ to the register to attain an equal superposition (omitting the amplitudes):

$$\begin{aligned} \sum \limits _{X_0,Y_0,k_0,k_1,\ldots ,k_4 \in {{\{ 0,1\} }^{32}}} {|X_0,Y_0\rangle |k_0,k_1,\ldots ,k_4\rangle }=|\varphi \rangle . \end{aligned}$$

(23)

According to Property 3, once we get the right $P=$($X_0,Y_0$) that meets the fix point property, we get two input-output pairs of the first 8 rounds.

Considering the superposition $|\varphi \rangle$, assume that we had a classifier ${\mathcal {B}}: \{0,1\}^{32\times 7}\rightarrow \{0,1\}$, which partitions $|\varphi \rangle$ into a good subspace and a bad subspace: $|\varphi \rangle =|\varphi _1\rangle +|\varphi _0\rangle$, where $|\varphi _1\rangle$ and $|\varphi _0\rangle$ denotes the projection onto the good subspace and bad subspace, respectively. In the good subspace $|\varphi _1\rangle$, $P=(X_0,Y_0)$ meets the fixed point property and $k_0,k_1,\ldots ,k_4$ are the right subkeys. For the state $|x\rangle$ in the good subspace, ${\mathcal {B}}(x)=1$.

We construct the quantum classifier ${\mathcal {B}}$. Define ${\mathcal {B}}:~\{0,1\}^{32\times 7}\rightarrow \{0,1\}$ that maps $(X_0,Y_0,k_0,k_1,\ldots ,k_4)$ to 0 and 1:

• 1. For $(X_0,Y_0)$, derive $(X_{32},Y_{32})$ from the encryption oracle of GOST.

• 2. Suppose $(X_0,Y_0)$ meets the fix point property, use $(k_0,k_1,\ldots ,k_4)$ to derive $k_5,k_6,k_7$ from Property 4.

• 3. Check the derived $(k_0,k_1,k_2,\ldots ,k_7)$ by 5 plaintext-ciphertext pairs using the GOST encryption oracle. If the check is right, output 1. Else output 0.

We classify a state $|X_0,Y_0\rangle |k_0,k_1,\ldots ,k_4\rangle$ is a good if and only if ${\mathcal {B}}(X_0,Y_0,k_0,k_1,\ldots ,k_4)=1$. The classifier ${\mathcal {B}}$ outputs good under two conditions:

• (a) Condition 1. $(X_0,Y_0)$ meets the Property 3. It is right with a probability of $2^{-64}$.

• (b) Condition 2. $k_0,k_1,\ldots ,k_4$ are the right subkeys. It is right with a probability $2^{-160}$.

If we measure $|\phi \rangle$, it produces the good state with probability p:

$$\begin{aligned} \begin{array}{ll} p &{}= \Pr [|X_0,Y_0\rangle |k_0,k_1,\ldots ,k_4\rangle ~\texttt {is~good}] \\ &{}= \Pr [{\mathcal {B}}(X_0,Y_0,k_0,k_1,\ldots ,k_4)=1] \\ &{}= \Pr [\texttt {Condition~1}]\cdot \Pr [\texttt {Condition~2}]\\ &{}\approx 2^{-64}\times 2^{-32\times 5}=2^{-224}. \end{array} \end{aligned}$$

(24)

Our classifier ${\mathcal {B}}$ defines a unitary operator $S_{{\mathcal {B}}}$ that conditionally change the sign of the quantum state $|X_0,Y_0\rangle |k_0,k_1,\ldots ,k_4\rangle$:

$$\begin{aligned} \left\{ \begin{array}{l} -|X_0,Y_0\rangle |k_0,k_1,\ldots ,k_4\rangle ~\texttt {if}~{\mathcal {B}}(X_0,Y_0,k_0,k_1,\ldots ,k_4)=1\\ |X_0,Y_0\rangle |k_0,k_1,\ldots ,k_4\rangle ~\texttt {if}~{\mathcal {B}}(X_0,Y_0,k_0,k_1,\ldots ,k_4)=0 \end{array} \right. \end{aligned}$$

(25)

The complete amplification process is realized by repeatedly for t times applying the unitary operator $Q=-{\mathcal {A}}S_0{\mathcal {A}}^{-1}S_{\mathcal {B}}$ to the state $|\varphi \rangle = {\mathcal {A}}|0\rangle$, i.e. $Q^t{\mathcal {A}}|0\rangle$.

Initially, the angle between $|\varphi \rangle = {\mathcal {A}}|0\rangle$ and the bad subspace $|\varphi _0\rangle$ is $\theta$, where $sin^2(\theta )=p=\langle \varphi _1|\varphi _1\rangle$. When p is smaller enough, $\theta \approx arcsin(\sqrt{p})\approx 2^{-\frac{224}{2}}$. According to Theorem 1, after $t=\lfloor \frac{\pi }{4\theta }\rfloor = \lfloor \frac{\pi }{4\times 2^{-\frac{224}{2}}}\rfloor \approx 2^{112}$ Grover iterations Q, the angle between resulting state and the bad subspace is roughly $\pi /2$. The probability $P_{good}$ that the measurement yields a good state is about $sin^2(\pi /2)=1$. The whole attack needs 224 qubits and $2^{112}$ Grover iterations where each Grover iteration needs about 7 quantum queries of GOST encryption. Hence, it costs about $2^{114.8}$ quantum queries of the encryption process.

5 Conclusion

In this paper, we have studied several Feistel block ciphers against quantum attackers, including the attacks on 1K-/2K-/4K-Feistel and 1K-/2K-/4K-DES in polynomial time and the attacks on GOST which are faster than the quantum brute force search attack by a factor of $2^{13.2}$. Through this study, we believe that the communities should continue to deepen the understanding of quantum security of symmetric cryptographic schemes, as more plausible attacks might be found following quantum strategies.