Perfect contrast XOR-based visual cryptography schemes via linear algebra

Abstract

XOR-based visual cryptography scheme (XVCS) was proposed to solve the poor visual quality problem without darkening the background in the reconstructed secret image. However, investigations on XVCS are not sufficient. In this paper, we focus on the traditional model of VCS for general access structures and exploit some extended capabilities for XVCS. Our main contributions are: (1) we put forward constructions of perfect contrast XVCS using the linear algebraic technique without any assumptions such as participants may carry multiple shares or prior information about the shares are to be submitted during the secret reconstruction phase; (2) for some restricted access structures, we achieve perfect contrast and perfect pixel expansion, namely both 1, which is impossible for any OR-based visual cryptography scheme (OVCS); (3) for general access structures, we achieve perfect contrast with smaller pixel expansion compared with many of the results in the literature; (4) Theoretical analysis on the proposed constructions are provided, as well as extensive experimental results and comparisons for demonstrating the effectiveness and advantages of our constructions.

1 Introduction

Visual cryptography scheme (VCS) proposed by Naor and Shamir [18] is a special type of secret sharing scheme, where the secret is a black and white image. A (k, n)-VCS for a set of n participants, where $2\le k\le n$, is capable of encoding a secret image into n shadow images called shares, where each participant receives one share. One can reconstruct the secret image with any k or more than k shares; but, one cannot obtain any information of the secret image from fewer than k shares. The attractiveness of VCS is the stacking-to-see property by which the reconstruction requires neither knowledge of cryptography nor complex computation. Any k or more than k participants may photocopy their shares onto transparencies and stack them on an overhead projector to visually decode the secret image through the human visual system.

In some circumstances where the cost of computations may be not affordable, the decoding time should be instantly done in a constant time, or the recognition of the secret shape/pattern is sensitive or meaningful only to the human perception, VCS becomes very appropriate. For example, VCS can be applied to protect online transactions against manipulation like online money transfers by Trojans [19], realize visual voting while ensuring voter’s anonymity without counting process [10], design secure display screen with controllable visual area against malicious peep while avoiding the attacks of virus and electromagnetic leakage [15], and other application scenarios including print and scan [30] and bar codes [33].

Based on Naor and Shamir’s method [18], extensive researches on VCS were conducted [28]. VCS for general access structures including graph based access structures, which aims to design sophisticated sharing strategy, was proposed by Ateniese et al. [3], Adhikari [1] and Shyu and Chen [21] respectively. Constructions of VCS for encrypting grayscale/color images were studied in [5, 6, 12]. Approaches of generating meaningful shares were introduced in [27, 31]. Sharing multiple secrets in VCS was described in [22, 34]. Cheating prevention in VCS was proposed by Hu and Tzeng [13]. Furthermore, Arumugam et al. [2] introduced a VCS for a special type of threshold access structure. They called it (k, n)*-VCS, to address the scenario where one participant is “essential” and he needs the help of any $k-1$ parties other than him, to recover the secret image. Guo et al. [11] forwarded this idea to the concept of $t-(k,n)$*-VCS where t participants are essential. The mathematical operation that lies beneath the physical implementation of the above mentioned schemes is the Boolean OR operation. Thus, these schemes are also referred to as OR-based VCS (OVCS). However, OVCS suffers from the huge share size (reflected by pixel expansion) and very poor quality (reflected by contrast) of the recovered secret image. Several papers have tried to minimize the pixel expansion and maximize the contrast. One may refer to [4, 8, 20, 21, 25] for a detailed survey of these problems.

In the meantime, XOR-based VCS (XVCS) was studied to achieve advanced properties, such as good contrast and resolution. So far three ways have been found to realize the Boolean XOR operation physically: liquid crystal display [23], Mach–Zehnder Interferometer [14] and copy machine with the reversing function [26]. Due to the rapid advancement of technology these devices are becoming cheaper and easier to get. It is a reasonable expectation that XVCS will be implemented at the expense of utilizing these light-weight devices. Moreover, light weight computational devices such as cell phones and smart devices are popularly utilized in practical applications and the XOR operation can be done by such devices. In addition, some new technologies, such as google glass and flexible screen, may also provide new scenarios for the application of XVCS. Therefore, XVCS is possible to be widely used in the future.

In terms of constructing XVCS, Tuyls et al. [24] investigated the threshold XVCS and gave different constructions for (2, n) and (k, n) schemes. Yang and Wang [32] further analyzed the relation between OVCS and XVCS for threshold access structures, and they proved that the basis matrices of OVCS can be adopted to implement XVCS. The first XVCS for general access structures was proposed by Liu et al. [16]. They repeatedly used the share generation algorithm for a (2, 2)-XVCS to generate the shares of the participants for any access structure, and they reconstructed the secret image perfectly, where $\alpha =1$. Then Fu et al. [9] proposed a necessary condition for the optimality of pixel expansion in the traditional XVCS for general access structures, and they confirmed the existence of a perfect XVCS, namely, (n, n)-XVCS, where $m=1$ and $\alpha =1$. They also proved that no (k, n)-XVCS with $1<k<n$ can achieve perfect contrast $\alpha =1$ and perfect pixel expansion $m=1$ simultaneously. All the above mentioned schemes have considered the common property of non-monotonicity of the access structure, i.e., superset of the minimal qualified set may not get the secret back if all of them stack their shares. But, it does not prohibit us to define XVCS. For most of the practical scenarios, the access structure is generally a public information. That is, the participants have complete knowledge of the qualified sets and forbidden sets. Therefore if a qualified set of participants come together then any minimal qualified subset of it may produce the corresponding shares to reconstruct the secret image. Thus it is sufficient to restrict ourselves to the collection of all minimal qualified sets corresponding to the access structure. However, although perfect contrast is achieved by Liu et al.’s scheme [16], due to the presence of multiple shares (this makes their construction different from the traditional XVCS), at the time of revealing the secret, the participants have to know for which access structures they are going to submit which of their shares. Fu et al.’s findings [9] are based on the existence of basis matrices realizing an access structure. They have not given any construction method to produce the basis matrices capturing the access structure in the first place. Moreover, both Liu et al. [16] and Fu et al. [9] did not consider the question of classifying the access structures for which one can construct perfect XVCS.

At the same time, Wu and Sun [29] put forward a non-expansible $(m=1)$ XVCS for general access structures by random grids, where the secret image is correctly reconstructed with certain probability. But, their scheme suffers from the low visual quality of the reconstructed secret image. The above scheme is considered for monotone access structures, where the superset of the minimal qualified set reconstruct the secret if all of them stack their shares. Here, a question is raised: whether perfect contrast and perfect pixel expansion can be achieved at the same time if the access structure is non-monotone. More deeply, how to find and characterize such access structures needs to be solved.

1.1 Our contribution

In this paper, we focus on non-monotone access structures and exploit perfect contrast XVCS for general access structures. Motivated by analyzing the linear aspects of perfect contrast XVCS, we construct the schemes via linear algebra. The linear algebraic technique adopted in this paper, where we can take more than two equations simultaneously, is based on the new insight into Adhikari’s [1] linear algebraic construction of OVCS. With such technique, we prove perfect contrast and perfect pixel expansion can be achieved at the same time and conclude the sufficient and necessary conditions, a complete characterization of some restricted access structures including (n, n), the access structures with up to two minimal qualified sets, $(k-1)$-$(k, n)^{*}$, star graph and complete bipartite graph based access structures, for the existence of a perfect XVCS. Then we use the complete characterization to partition a general access structure into d parts and provide a region-by-region method to construct perfect contrast XVCS with pixel expansion equal to d. All the above XVCSs are proposed by distributing one share per participant and without the burden that each participant may carry multiple shares.

1.2 Organization of the paper

The rest of the paper is organized as follows. In Sect. 2, we discuss some terms and concepts that will be referenced in subsequent sections. In Sect. 3, after describing our motivation, new insight into linear algebraic technique to construct the basis matrices of OVCS is given. Then based on the new insight, we prove that the constructed basis matrices of OVCS can be adopted to implement perfect contrast XVCS and further conclude the sufficient and necessary conditions for the existence of a perfect XVCS, where the contrast and pixel expansion are both 1. Moreover, for some restricted access structures, such as (n, n), the access structures with up to two minimal qualified sets, $(k-1)$-$(k, n)^{*}$, star graph and complete bipartite graph based access structures, perfect XVCSs are given. For general access structures, we further put forward a region by region construction to achieve perfect contrast with small pixel expansion. Some experimental results and comparisons are presented in Sect. 4. Lastly we conclude the paper in Sect. 5.

2 Preliminaries

2.1 Access structure

In general, VCS is built on an access structure, which is a characterization of rights on participants. Let $P=\{1,2,\ldots ,n\}$ be a set of participants and $2^{P}$ denote the set of all subsets of P. Let $\varGamma _{{ Qual}}\subseteq 2^{P}$ and $\varGamma _{{ Forb}}\subseteq 2^{P}$, where $\varGamma _{{ Qual}}\cap \varGamma _{{ Forb}}=\emptyset$. Members of $\varGamma _{{ Qual}}$ are referred to as qualified sets and members of $\varGamma _{{ Forb}}$ are referred to as forbidden sets. The pair $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ is called an access structure on P. Define $\varGamma _{0}$ to consist of all the minimal qualified sets:

$$\begin{aligned} \varGamma _{0}=\{Q\in \ \varGamma _{{ Qual}}:Q'\notin \varGamma _{{ Qual}}~for~all~Q'\subset Q\} \end{aligned}$$

(1)

and $Z_{M}$ to consist of all the maximal forbidden sets:

$$\begin{aligned} Z_{M}=\{F\in \varGamma _{{ Forb}}:F\cup \{i\}\in \varGamma _{{ Qual}}~for~all~i\in P\setminus F\}. \end{aligned}$$

(2)

The monotone access structure is defined as follows.

Definition 1

An access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ on $P=\{1,2,\ldots ,n\}$ is said to be monotone if the following conditions are satisfied:

• 1. $\varGamma _{{ Qual}}$ is monotone increasing. Formally, for each $Q\in \varGamma _{{ Qual}}$ and $Q\subseteq Q'\subseteq P$, we have $Q'\in \varGamma _{{ Qual}}$.

• 2. $\varGamma _{{ Forb}}$ is monotone decreasing. Formally, for each $F\in \varGamma _{{ Forb}}$ and $F'\subseteq F\subseteq P$, we have $F'\in \varGamma _{{ Forb}}$.

• 3. $\varGamma _{{ Qual}}\cup \varGamma _{{ Forb}}=2^{P}$.

The non-monotone access structure considered in this paper is defined as follows.

Definition 2

An access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ on $P=\{1,2,\ldots ,n\}$ is said to be non-monotone if $\varGamma _{{ Qual}}=\varGamma _{0}$.

For non-monotone access structures, the monotonously increasing property of qualified set $\varGamma _{{ Qual}}$ is relaxed to $\varGamma _{{ Qual}}=\varGamma _{0}$. It is reasonable in practical applications since we can reconstruct the secret image from the minimal qualified set instead of the corresponding qualified set. Therefore, unless otherwise specified, in this paper we assume that a monotone access structure is denoted by $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ and its corresponding non-monotone access structure is denoted by $(\varGamma _{0},\varGamma _{{ Forb}})$. In addition, $\varGamma _{0}$ is termed a basis determining the corresponding monotone access structure completely since $\varGamma _{{ Qual}}=\{Q'\subseteq P: Q\subseteq Q'~for~some~Q \in \varGamma _{0}\}$ and $\varGamma _{{ Forb}}=2^{P}\setminus \varGamma _{{ Qual}}$. So when we discuss an access structure, we only need to give discussions based on $\varGamma _{0}$.

As a special access structure, a (k, n) threshold structure is an access structure $(\varGamma _{0},\varGamma _{{ Forb}})$ with the following constraints: $\varGamma _{0}=\{Q\subseteq P: |Q|=k\}$ and $\varGamma _{{ Forb}}=\{Q\subseteq P: |Q|\le k-1\}$. The (k, n)* threshold structure is defined by $\varGamma _{0}=\{Q\subseteq P: 1\in Q~and~|Q|=k\}$ and $\varGamma _{{ Forb}}=\{Q\subseteq P: |Q|\le k-1\}$, where the 1 is referred to as an essential participant. The $t-(k,n)$* threshold structure is defined by $\varGamma _{0}=\{Q\subseteq P: \{1,2,\ldots ,t\}\subseteq Q~and~|Q|=k\}$ and $\varGamma _{{ Forb}}=\{Q\subseteq P: |Q|\le k-1\}$, where the $1,2,\ldots ,t$, $t\le n$, are referred to as t essential participants. Note that the case when $t=0$ we have the scenario of a (k,n) threshold structure where no participant is essential. The case $t=1$ is the usual (k, n)* threshold structure while $t=n$ leads to the (n, n) threshold structure.

As another special access structure, a graph based access structure is depicted by a graph $G=(V(G),E(G))$, where the vertex set $V(G)=P$ and the edge set $E(G)=\varGamma _{0}$. Because some part of the paper deals with some special graph based access structures, we first recall some terminology from graph theory to clarify some notions. An independent set is a set of vertices in a graph, no two of which are connected. A complete graph is a graph, where each pair of vertices is connected by a unique edge. A complete bipartite graph is a graph, where all vertices are partitioned into two different independent sets and there is an edge between every pair of vertices from different independent sets.

2.2 Simplification of access structure

In this subsection, we discuss a technique, introduced in [16], to simplify and reduce a class of more complex access structure into a simpler one. For this we first define the notion of equivalent participants, which is presented as follows.

Definition 3

(adapted from [16]) For an access structure $(\varGamma _{0},\varGamma _{{ Forb}})$, participants i and j satisfy that, for all $F\in Z_{M}$, $i\in F$ if and only if $j\in F$, then participants i and j are called equivalent participants on $\varGamma _{0}$, denoted by $i\sim j$.

Table 1 Equivalent participants and simplified access structures with up to four participants

Then we can simplify the access structure $\varGamma _{0}$ based on the equivalent participants as follows.

Definition 4

(adapted from [16]) For an access structure $(\varGamma _{0},\varGamma _{{ Forb}})$ on a set of participants P, define $\widetilde{P}=\{\widetilde{p}:p\in P\}$ on the equivalence relation “$\sim$”. We call $\widetilde{\varGamma _{0}}=\{\{\widetilde{p}\in \widetilde{P}:p\in Q\}:Q\in \varGamma _{0}\}$ the simplified access structure on $\widetilde{P}$. If $\widetilde{\varGamma _{0}}=\varGamma _{0}$ then the access structure is called the most simplified access structure.

It is easy to see that no two participants are equivalent in a (k, n) threshold access structure. In other words, the (k, n) threshold access structure is already in the most simplified form. Furthermore, in order to explain the simplification clearly, we present different access structures with up to four participants and show the equivalent participants and the most simplified access structures in Table 1.

Given an access structure, we can first identify the equivalent participants according to Definition 3. In fact, equivalent participants are the parties who enjoy the same rights and hence they can be given identical shares without hampering the access structure of a VCS. Then we can reduce the access structure to a much simpler one according to Definition 4. One can treat the reduced access structure (which is simpler than the original one) as the given access structure and construct VCS for that.

2.3 The model

We assume that the secret image SI consists of a collection of black and white pixels. A white pixel is identified as 0 while a black pixel is identified as 1. Each pixel is shared separately. To understand the sharing process consider the case where the secret image consists of just a single black or white pixel. On sharing, this pixel appears in the n shares distributed to the participants. Generally, a secret pixel is encrypted into m subpixels in each share and thus the size of each share is m times the size of the secret image. This m is called the pixel expansion. We further assume that the subpixels are sufficiently small and close enough so that human visual system averages them to some shade of grey. In order that the recovered image is clearly discernible, it is important that the grey level of a black pixel be darker than that of a white pixel.

Notations Suppose $\varGamma _{0}=\{Q_{1},Q_{2},\ldots ,Q_{t}\}$. Let M be an $n\times m$ Boolean matrix and $X\subseteq P$. Then $M_{X}$ denotes the $|X|\times m$ submatrix obtained from M by considering its restriction to rows corresponding to the elements in X. $\star (M_{X})$ denotes the Boolean $\star$ operation to the rows of $M_{X}$. Here, the operation $\star$ can be either the Boolean OR operation “$\otimes$” or the Boolean XOR operation “$\oplus$”. $\omega (\star (M_{X}))$ denotes the Hamming weight of the row vector $\star (M_{X})$, which denotes the number of 1’s in the vector $\star (M_{X})$. For a $1\times n$ Boolean row vector $\mathbf{v }=\{v_{1},v_{2},\ldots ,v_{n}\}$, let $\mathfrak {R}_{\mathbf{v }}=\{j|v_{j}=1,j=1,2,\ldots ,n\}$. Given two Boolean row vectors $\mathbf{v }_{1}$ and $\mathbf{v }_{2}$, define $\mathfrak {R}_{\mathbf{v }_{1}}\oplus \mathfrak {R}_{\mathbf{v }_{2}}=\mathfrak {R}_{\mathbf{v }_{1}\oplus \mathbf{v }_{2}}$. Moreover, for $Q_{i}\in \varGamma _{0}$, $1\le i\le t$, $R^{\star }(Q_{i})$ denotes the Boolean $\star$ operation to the shares hold by all participants of $Q_{i}$. Denote $\varGamma _{0}^{odd}$ as the “$\oplus$”ed result of any odd number of elements of $\varGamma _{0}$ and $\varGamma _{0}^{even}$ as the “$\oplus$”ed result of any even number of elements of $\varGamma _{0}$.

The definition of VCS under the operations OR and XOR is given as follows.

Definition 5

(adapted from [3]) Let $(\varGamma _{{ Qual}}~(resp.~\varGamma _{0}),\varGamma _{{ Forb}})$ be an access structure on P. Two collections of $n\times m$ Boolean matrices $C_{0}$ and $C_{1}$ constitute a visual cryptography scheme $(\varGamma _{{ Qual}}~(resp.~\varGamma _{0}),\varGamma _{{ Forb}}, m)$-VCS if the following conditions are satisfied:

• 1. Any set $X=\{i_{1},i_{2},\ldots ,i_{p}\}\in \varGamma _{{ Qual}}~(resp.~\varGamma _{0})$ can recover the secret image. Formally, for any $M^{0}\in C_{0}$ and any $M^{1}\in C_{1}$, we have $\omega (\star (M^{1}_{X}))>\omega (\star (M^{0}_{X}))$.

• 2. Any set $X=\{i_{1},i_{2},\ldots ,i_{p}\}\in \varGamma _{{ Forb}}$ has no information on the shared image. Formally, the two collections of $p\times m$ matrices $D_{0}$ and $D_{1}$ obtained by restricting $C_{0}$ and $C_{1}$ to rows $i_{1},i_{2},\ldots ,i_{p}$, respectively, are distinguishable in the sense that they contain the same matrices with the same frequencies.

To share a secret pixel $b\in \{0,1\}$, the dealer randomly chooses a matrix from the Boolean matrix set $C_{b}$ and distributes its n rows to the n shares, respectively. Thus, the chosen matrix defines the m subpixels in each of the n shares. Actually, to construct a VCS, it is sufficient to construct the basis matrices corresponding to the black and white pixel. In the following, we formally define what is meant by basis matrices.

Definition 6

(adapted from [3]) Let $(\varGamma _{{ Qual}}~(resp.~\varGamma _{0}),\varGamma _{{ Forb}})$ be an access structure on P. Two $n\times m$ basis matrices $S^{0}$ and $S^{1}$ constitute a visual cryptography scheme $(\varGamma _{{ Qual}}~(resp.~\varGamma _{0}),\varGamma _{{ Forb}}, m)$-VCS if the following conditions are satisfied:

• 1. Any set $X=\{i_{1},i_{2},\ldots ,i_{p}\}\in \varGamma _{{ Qual}}~(resp.~\varGamma _{0})$ can recover the secret image. Formally, for $X\in \varGamma _{{ Qual}}~(resp.~\varGamma _{0})$, we have $\omega (\star (S^{1}_{X}))>\omega (\star (S^{0}_{X}))$.

• 2. Any set $X=\{i_{1},i_{2},\ldots ,i_{p}\}\in \varGamma _{{ Forb}}$ has no information on the shared image. Formally, for $X\in \varGamma _{{ Forb}}$, $S^{1}_{X}$ and $S^{0}_{X}$ are identical up to a column permutation.

The collections of matrices $C_{0}$ and $C_{1}$ are obtained by giving all possible column permutations to the basis matrices $S^{0}$ and $S^{1}$ respectively. As a result, the dealer only need to store the two matrices $S^{0}$ and $S^{1}$, making the scheme efficient space-wise. Notice that in Definition 5 we allow a matrix to appear more than once in $C_{0}$ (resp. $C_{1}$). Therefore the size of the collections $C_{0}$ and $C_{1}$ does not need to be the same. But, in Definition 6, the size of the collections $C_{0}$ and $C_{1}$ is the same.

The first property is related to the contrast of the reconstructed secret image. It states that when a (minimal) qualified set of participants stack their shares they can perceive the secret information due to the darkness difference. The definition of contrast for VCS is an interesting point of discussion and has been the subject of several papers [7, 8, 17, 18, 25]. Although these given contrast measurements have their own specific advantages, all of them favor a perfect contrast, namely 1. Therefore, we use the contrast measurement in the original model by Naor and Shamir [18], since we focus the attention on perfect contrast XVCS in this paper. The contrast is defined as follows:

$$\begin{aligned} \alpha =\frac{\omega (\star (M^{1}_{X}))-\omega (\star (M^{0}_{X}))}{m}~or~\frac{\omega (\star (S^{1}_{X}))-\omega (\star (S^{0}_{X}))}{m}, \end{aligned}$$

(3)

where $\alpha$ ($0\le \alpha \le 1$). To a certain extent, this measure determines how well human visual system can recognize the reconstructed secret image. It is lucid that for a valid VCS $\alpha =0$ if $X\in \varGamma _{{ Forb}}$; $\alpha >0$ where $X\in \varGamma _{{ Qual}}~(\varGamma _{0})$. From the point of view of the participants, the pixel expansion m is expected to be as small as possible, and the contrast $\alpha$ is expected to be as large as possible. The pixel expansion is called perfect when $m=1$ and the contrast is called perfect when $\alpha =1$. A VCS is perfect if its pixel expansion and contrast are both perfect.

The second property is called security, since it implies that, even by inspecting all their shares, a forbidden set of participants cannot gain any information in deciding whether the shared pixel was white or black.

3 Perfect contrast XVCS for general access structures via linear algebra

3.1 Our motivation

In a perfect contrast VCS where $\alpha =1$, every secret pixel is reconstructed in the correct color according to Eq. (3). In this case we can perceive the reconstructed secret image easily and clearly. Therefore, we are interested only in perfect contrast VCS in this paper.

So far most researches on VCS were dedicated to OR operation. The OR operation causes that the black subpixel in a share cannot be undone by the color of another subpixel laid over it. Therefore, the OVCS cannot obtain the perfect contrast (a white pixel cannot be represented by m white subpixels), while it may be achieved by XOR operation.

Due to the complementation property of XOR operation (note: $1\oplus 1=0$ and $0\oplus 1=1$), it is impossible to design perfect contrast XVCS for monotone access structures. However, it is possible to design perfect contrast XVCS for non-monotone access structures.

For a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}}, m)$-XVCS with basis matrices $S^{0}$ and $S^{1}$, where $\varGamma _{0}=\{Q_{1},Q_{2},\ldots ,Q_{t}\}$, if $X\in \varGamma _{0}$, $\omega (\oplus (S^{1}_{X}))=m$ means that the XOR-ed result of every column of $S^{1}_{X}$ is 1 and $\omega (\oplus (S^{0}_{X}))=0$ means that the XOR-ed result of every column of $S^{0}_{X}$ is 0. Seemingly, the construction of basis matrices can be associated with the establishment of linear equations over the binary field. For example, establish the following two systems of linear equations over the binary field: $A\mathbf{x } = \mathbf{0 }$ (its all possible solutions form $S^{0}$) and $A\mathbf{x } = \mathbf{1 }$ (its all possible solutions form $S^{1}$), where A is a $t\times n$ Boolean matrix of t rows $\mathbf{a }_{1},\mathbf{a }_{2},\ldots ,\mathbf{a }_{t}$ determined by the t minimal qualified sets $Q_{1},Q_{2},\ldots ,Q_{t}$ in such a way that $\mathfrak {R}_{\mathbf{a }_{i}}=Q_{i}$, $i=1,2,\ldots ,t$; x is an $n\times 1$ vector of unknowns; $\mathbf{0 }$ and $\mathbf{1 }$ are $t\times 1$ vectors of 0’s and 1’s respectively. If both systems are consistent, the question whether the above method can form the basis matrices of a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}}, m)$-XVCS needs to be solved.

Recently, Adhikari [1] utilized the similar linear algebraic technique to construct basis matrices and proved it is feasible. However, the basis matrices constitute OVCS for monotone access structures. At this point of time, a natural question may be asked: whether the basis matrices of OVCS can be used for capturing the corresponding non-monotone access structure in the XOR model. In [32], the authors theoretically proved that for threshold (k, n) access structures the basis matrices for a monotone OVCS can be used as the basis matrices for the corresponding non-monotone XVCS. The question whether the same is true or not for any non-monotone access structure remains open. Moreover, Adhikari’s method is confined to taking a system of two equations and cannot deal with more than two minimal qualified sets at a time.

Inspired by the above analysis, we are going to construct perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}}, m)$-XVCS via linear algebra. To understand how to do it, we will build our theory from the reverse direction in this paper. First, we will improve the linear algebraic technique to construct the basis matrices of monotone OVCS so that we are able to take a system of more than two equations simultaneously. Then we will prove that the constructed basis matrices can be used as the basis matrices of the corresponding non-monotone XVCS, and perfect contrast can be achieved at the same time. At last, we will exploit some extended capabilities for perfect contrast XVCS.

3.2 New insight into linear algebraic technique to construct OVCS

Similar to Adhikari’s method [1], we also start with the following two systems of linear equations over the binary field,

$$\begin{aligned} A\mathbf{x }= & {} \mathbf{0 } \end{aligned}$$

(4)

$$\begin{aligned} A\mathbf{x }= & {} \mathbf{1 } \end{aligned}$$

(5)

where, A is a $t\times n$ known Boolean matrix of rank r, $0<r\le t<n$; $\mathbf{x }$ is an $n\times 1$ vector of unknowns; $\mathbf{0 }$ and $\mathbf{1 }$ are $t\times 1$ vectors of 0’s and 1’s respectively; both the systems (4) and (5) are consistent. The difference from Adhikari’s systems [1] is the coefficient matrix A, which does not have to be of full row rank.

Let $S^{0}$ (resp. $S^{1}$) be an $n\times 2^{n-r}$ Boolean matrix whose columns are all possible solutions of the system (4) (resp. (5)). Then, to prove $S^{0}$ and $S^{1}$ can form the basis matrices of a $(\varGamma _{{ Qual}},\varGamma _{{ Forb}},m=2^{n-r})$-OVCS, the following lemma is first given immediately since the proof of Lemma 5 in Adhikari [1] also works for this lemma.

Lemma 1

Let $X=\{i_{1},i_{2},\ldots ,i_{p}\}\subseteq P=\{1,2,\ldots ,n\}$. Build a system of equations as follows:

$$\begin{aligned} \left( \begin{array}{c} A \\ B^{X} \end{array} \right) {\mathbf{x}}=\left( \begin{array}{c} {\mathbf{1}} \\ {\mathbf{0}} \end{array} \right) \end{aligned}$$

(6)

where $B^{X}$ is a column permutation of the $p\times n$ Boolean matrix $(\mathbf{I }_{p}|\mathbf{0 }_{p\times (n-p)})$ with unit vectors of the identity matrix $\mathbf{I }_{p}$, which is of order p, occupying columns indexed by $i_{1},i_{2},\ldots ,i_{p}$ in $B^{X}$. Then, for an access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$, $S^{0}$ and $S^{1}$ form the basis matrices of a $(\varGamma _{{ Qual}},\varGamma _{{ Forb}},m=2^{n-r})$-OVCS if the following conditions are satisfied:

• 1. For $X\in \varGamma _{{ Qual}}$, the system (6) is inconsistent;

• 2. For $X\in \varGamma _{{ Forb}}$, the system (6) is consistent.

Next we are going to explore the conditions for consistency or inconsistency of the system (6). Let rows of $A_{1}$ (resp. $A_{2}$) represent all possible sum of odd (resp. even) number of rows in A. Then we have the following lemma.

Lemma 2

For an access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$, $S^{0}$ and $S^{1}$ form the basis matrices of a $(\varGamma _{{ Qual}},\varGamma _{{ Forb}},m=2^{n-r})$-OVCS if the following conditions are satisfied:

• 1. For $X\in \varGamma _{{ Qual}}$, any row vector of $A_{1}$ belongs to the row space of $B^{X}$.

• 2. For $X\in \varGamma _{{ Forb}}$, A and $B^{X}$ are independent, or, any row vector of $A_{2}$ belongs to the row space of $B^{X}$.

Proof

In light of the system (6), there are two possibilities: the coefficient matrix A and $B^{X}$ are either linearly independent or linearly dependent.

If they are independent, since the system (5) is consistent and $B^{X}\mathbf{x }=\mathbf{0 }$ is consistent ($B^{X}$ is of full row rank), the system (6) is consistent.

If they are linearly dependent, then there exists a vector $\mathbf{u }=(\mathbf{u }_{1},\mathbf{u }_{2})\ne \mathbf{0 }$, where $\mathbf{u }_{1}$ and $\mathbf{u }_{2}$ are $1\times t$ and $1\times p$ vectors respectively, such that $\mathbf{u }\left( \begin{array}{c} A \\ B^{X} \end{array} \right)$ = 0 $\Leftrightarrow$ $\mathbf{u }_{1}A+\mathbf{u }_{2}B^{X}=\mathbf{0 }$. Note that $\mathbf{u }_{1}$ is nonzero, otherwise this will imply linear dependence of the rows of $B^{X}$. Now $\mathbf{u }_{1}A+\mathbf{u }_{2}B^{X}=\mathbf{0 }$ $\Leftrightarrow$ $\mathbf{u }_{1}A\in$ the row space of $B^{X}$. Also note that if $\mathbf{u }_{1}$ has an odd (resp. even) number of 1’s then $\mathbf{u }_{1}A$ will be a row of $A_{1}$ (resp. $A_{2}$). Then we have that any row of $A_{1}$ or $A_{2}$ belongs to the row space of $B^{X}$. On the right of the system (6), $\mathbf{u }\left( \begin{array}{c} \mathbf{1 } \\ \mathbf{0 } \end{array} \right) =\mathbf{u }_{1}\mathbf{1 }$. If $\mathbf{u }_{1}$ has an odd (resp. even) number of 1’s then the system (6) is inconsistent (resp. consistent).

Based on the above discussions and Lemma 1, this lemma is proved. $\square$

Lemma 2 shows that given a suitable binary matrix A and a suitable access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$, we can construct an OVCS by solving the two linear systems (4) and (5). Then, we are now in a position to give a concrete structure of the coefficient matrix A, together with which the access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ satisfies the conditions of Lemma 2. Towards this end, we prove the following lemma.

Lemma 3

For an access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ with $\varGamma _{0}=\{Q_{1},Q_{2},\ldots ,Q_{t}\}$, let $A=(\mathbf{v }_{1},\mathbf{v }_{2},\ldots ,\mathbf{v }_{t})^{T}$ of rank r and $\mathfrak {R}_{\mathbf{v }_{i}}=Q_{i}$, $i=1,2,\ldots ,t$. $S^{0}$ and $S^{1}$ form the basis matrices of a $(\varGamma _{{ Qual}},\varGamma _{{ Forb}},m=2^{n-r})$-OVCS if the following conditions are satisfied:

• 1. For any row v of $A_{1}$, $\mathfrak {R}_{\mathbf{v }}\in \varGamma _{{ Qual}}$;

• 2. For any row v of $A_{2}$, $\mathfrak {R}_{\mathbf{v }}=\emptyset$ or $\mathfrak {R}_{\mathbf{v }}\not \subseteq Q\in \varGamma _{0}$.

Proof

For $X\in \varGamma _{{ Qual}}$, because $\mathfrak {R}_{\mathbf{v }}\in \varGamma _{{ Qual}}$ for any row v of $A_{1}$, v obviously belongs to the row space of $B^{X}$.

For $X\in \varGamma _{{ Forb}}$, there are three cases to be considered:

Case 1 For any row v of $A_{1}$, $\mathfrak {R}_{\mathbf{v }}\in \varGamma _{{ Qual}}$; for any row v of $A_{2}$, $\mathfrak {R}_{\mathbf{v }}=\emptyset$.

In this case, any row vector of $A_{2}$ belongs to the row space of $B^{X}$ immediately.

Case 2 For any row v of $A_{1}$, $\mathfrak {R}_{\mathbf{v }}\in \varGamma _{{ Qual}}$; for any row v of $A_{2}$, $\mathfrak {R}_{\mathbf{v }}\not \subset Q\in \varGamma _{0}$ and $\mathfrak {R}_{\mathbf{v }}\in \varGamma _{{ Forb}}$.

In this case, any row vector of $A_{2}$ also belongs to the row space of $B^{X}$ immediately.

Case 3 For any row v of $A_{1}$, $\mathfrak {R}_{\mathbf{v }}\in \varGamma _{{ Qual}}$; for any row v of $A_{2}$, $\mathfrak {R}_{\mathbf{v }}\notin \varGamma _{0}$ and $\mathfrak {R}_{\mathbf{v }}\in \varGamma _{{ Qual}}$.

In this case, no row vector of $A_{1}$ and $A_{2}$ belongs to the row space of $B^{X}$, namely, A and $B^{X}$ are independent. $\square$

It should be noted that the sum operation “$+$” over the binary field is actually the Boolean XOR operation “$\oplus$”. Therefore, the sum of a number of row vectors, say $\mathbf{v }_{1},\cdots ,\mathbf{v }_{i}$, of the coefficient matrix A equals to $\mathbf{v }_{1}\oplus \cdots \oplus \mathbf{v }_{i}$. Since $Q_{i}=\mathfrak {R}_{\mathbf{v }_{i}}$, we have $\mathfrak {R}_{\mathbf{v }_{1}\oplus \cdots \oplus \mathbf{v }_{i}}=Q_{1}\oplus \cdots \oplus Q_{i}$. So, for clarity, we restate Lemma 3 as follows, and hence omit its proof.

Lemma 4

For an access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ with $\varGamma _{0}=\{Q_{1},Q_{2},\ldots ,Q_{t}\}$, if $\varGamma _{0}$ satisfies the following two conditions:

• 1. The “$\oplus$”ed result of any odd number of elements of $\varGamma _{0}$ is an element of $\varGamma _{{ Qual}}$. Formally, $\varGamma _{0}^{odd}\in \varGamma _{{ Qual}}$.

• 2. The “$\oplus$”ed result of any even number of elements of $\varGamma _{0}$ is an empty set, or not a subset of any element of $\varGamma _{0}$. Formally, $\varGamma _{0}^{even}=\emptyset$ or $\varGamma _{0}^{even}\not \subseteq Q\in \varGamma _{0}$.

Then the basis matrices $S^{0}$ and $S^{1}$ of a $(\varGamma _{{ Qual}},\varGamma _{{ Forb}},m=2^{n-r})$-OVCS are composed of all possible solutions of the systems (4) and (5) respectively, where $A=(\mathbf{v }_{1},\mathbf{v }_{2},\ldots ,\mathbf{v }_{t})^{T}$ of rank r and $\mathfrak {R}_{\mathbf{v }_{i}}=Q_{i}$, $i=1,2,\ldots ,t$.

Remark

Adhikari’s method [1] deals with the schemes obtained by taking at most two equations simultaneously. But, Lemma 4 shows that we can take t equations at a time to construct OVCS for some restricted access structures, which are characterized by the above two conditions. In fact, Adhikari’s method [1] can be viewed as a special case of our Lemma 4. This generalization will lead us to achieve the sufficient and necessary conditions for the existence of a perfect XVCS and smaller pixel expansions of perfect contrast XVCS for general access structures in the following subsections.

Let us try to illustrate the above theory through the following example.

Example 1

Let us consider the following access structure ($\varGamma _{{ Qual}},\varGamma _{{ Forb}}$) on a set of 4 participants having $\varGamma _{0}=\{\{1,2\},\{1,3\},\{1,4\}\}$. Obviously, this access structure satisfies the conditions of Lemma 4. Then solve the two systems of three linear equations over the binary field as follows:

$$\begin{aligned} \left\{ \begin{array}{l} x_{1}+x_{2}=0\\ x_{1}+x_{3}=0\\ x_{1}+x_{4}=0 \end{array} \right. \end{aligned}$$

(7)

and

$$\begin{aligned} \left\{ \begin{array}{l} x_{1}+x_{2}=1\\ x_{1}+x_{3}=1\\ x_{1}+x_{4}=1 \end{array} \right. \end{aligned}$$

(8)

Let $S^{0}$ and $S^{1}$ be the Boolean matrices whose columns are just all possible solutions of the above two systems of Eqs. (7) and (8) respectively. Thus, $S^{0}=\left[ \begin{array}{cc} 0 &{} 1\\ 0 &{} 1\\ 0 &{} 1\\ 0 &{} 1 \end{array} \right]$ and $S^{1}=\left[ \begin{array}{cc} 0 &{} 1\\ 1 &{} 0\\ 1 &{} 0\\ 1 &{} 0 \end{array} \right]$. According to Definition 6, $S^{0}$ and $S^{1}$ constitute a $(\varGamma _{{ Qual}},\varGamma _{{ Forb}}, 2)$-OVCS where $\varGamma _{0}=\{\{1,2\},\{1,3\},\{1,4\}\}$.

3.3 The sufficient and necessary conditions for the existence of a perfect XVCS

Based on the above improved linear algebraic technique, we are able to construct the basis matrices $S^{0}$ and $S^{1}$ of OVCS. In this subsection, we are going to prove that the constructed basis matrices $S^{0}$ and $S^{1}$ can be used for capturing perfect XVCS for the corresponding non-monotone access structures and the conditions of Lemma 4 are just the sufficient and necessary conditions for the existence of a perfect XVCS. To begin with, we prove the following lemma.

Lemma 5

For an access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ with $\varGamma _{0}=\{Q_{1},Q_{2},\ldots ,Q_{t}\}$, if $\varGamma _{0}$ satisfies the conditions of Lemma 4, then there exists a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},m)$-XVCS with basis matrices.

Proof

For an access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ with $\varGamma _{0}=\{Q_{1},Q_{2},\ldots ,Q_{t}\}$, if $\varGamma _{0}$ satisfies the conditions of Lemma 4, there exists a $(\varGamma _{{ Qual}},\varGamma _{{ Forb}},m)$-OVCS with basis matrices $S^{0}$ and $S^{1}$ by Lemma 4.

Note that $S^{0}$ and $S^{1}$ are made up of all possible solutions of the systems (4) and (5) respectively. For any row vector ${{\varvec{a}}}_{i}$ of the coefficient matrix A, we have ${{\varvec{a}}}_{i}S^{0}=\mathbf{0 }$ $({{\varvec{a}}}_{i}S^{1}=\mathbf{1 })$ by the system (4) (resp. (5)) over the binary field. Also note that $\varGamma _{0}$ determines the coefficient matrix $A=({{\varvec{a}}}_{1},{{\varvec{a}}}_{2},\ldots ,{{\varvec{a}}}_{t})^{T}$ by $\mathfrak {R}_{{{\varvec{a}}}_{i}}=Q_{i}$, $i=1,2,\ldots ,t$. Thus we have ${{\varvec{a}}}_{i}S^{0}=\oplus (S^{0}_{Q_{i}})$ and ${{\varvec{a}}}_{i}S^{1}=\oplus (S^{1}_{Q_{i}})$. In other words, for any $Q_{i}\in \varGamma _{0}$, we have $\omega (\oplus (S^{1}_{Q_{i}}))=m$ and $\omega (\oplus (S^{0}_{Q_{i}}))=0$. So the contrast condition of Definition 6 on $(\varGamma _{0},\varGamma _{{ Forb}})$ is met and the contrast is perfect according to Eq. (3).

For $X\in \varGamma _{{ Forb}}$, we have $S^{1}_{X}$ and $S^{0}_{X}$ are identical up to a column permutation by Definition 6 on $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$. Thus the security condition of Definition 6 on $(\varGamma _{0},\varGamma _{{ Forb}})$ is met. $\square$

Lemma 6

For a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},m)$-XVCS with basis matrices, there exists a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},1)$-XVCS.

Proof

For a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},m)$-XVCS with basis matrices $S^{0}$ and $S^{1}$, consider the collection of $n\times 1$ Boolean matrices $C_{0}$ (resp. $C_{1}$) consisting of all the columns of $S^{0}$ (resp. $S^{1}$).

For $X\in \varGamma _{0}$, since $\omega (\oplus (S^{1}_{X}))=m$, $\omega (\oplus (S^{0}_{X}))=0$, we have $\omega (\oplus (M^{1}_{X}))=1$ for any $M^{1}\in C_{1}$ and $\omega (\oplus (M^{0}_{X}))=0$ for any $M^{0}\in C_{0}$. Thus the contrast condition of Definition 5 on $(\varGamma _{0},\varGamma _{{ Forb}})$ is met and the contrast is perfect according to Eq. (3).

For $X\in \varGamma _{{ Forb}}$, we have $S^{1}_{X}$ and $S^{0}_{X}$ are identical up to a column permutation by Definition 6. Obviously, the security condition of Definition 5 is met.

So, the considered $C_{0}$ and $C_{1}$ constitute a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},1)$-XVCS. $\square$

Until now, we have already seen that the conditions of Lemma 4 lead to a non-monotone XVCS with perfect contrast and perfect pixel expansion. A relevant question in this regard would be: if the conditions of Lemma 4 are not satisfied, is there a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},1)$-XVCS? To answer this question, we prove the following theorem.

Theorem 1

For an access structure $(\varGamma _{{ Qual}},\varGamma _{{ Forb}})$ with $\varGamma _{0}=\{Q_{1},Q_{2},\ldots ,Q_{t}\}$, there exists a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},1)$-XVCS if and only if $\varGamma _{0}$ satisfies the conditions of Lemma 4.

Proof

If $\varGamma _{0}$ satisfies the conditions of Lemma 4, there exists a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},1)$-XVCS by Lemmas 5 and 6.

Conversely, if there exists a perfect XVCS where $R^{\oplus }(Q_{i})=SI,i=1,2,...,t$, it is easy to see that $R^{\oplus }(\varGamma _{0}^{odd})=SI$ and $R^{\oplus }(\varGamma _{0}^{even})=0$. According to $R^{\oplus }(\varGamma _{0}^{odd})=S$, we conclude $\varGamma _{0}^{odd}\notin \varGamma _{{ Forb}}$. Since $\varGamma _{{ Qual}}\cup \varGamma _{{ Forb}}=2^{P}$ and $\varGamma _{0}^{odd}\subseteq P$, we have $\varGamma _{0}^{odd}\in \varGamma _{{ Qual}}$. Thus the first condition of Lemma 4 is met. As for $R^{\oplus }(\varGamma _{0}^{even})=0$, the following two cases are considered:

• 1. $\varGamma _{0}^{even}=\emptyset$. In this case the second condition of Lemma 4 is met.

• 2. $\varGamma _{0}^{even}\ne \emptyset$ and $\varGamma _{0}^{even}\notin \varGamma _{0}$. Suppose there exists a minimal qualified set $Q\in \varGamma _{0}$ satisfying $\varGamma _{0}^{even}\subset Q$. Then we have $R^{\oplus }(Q)=R^{\oplus }(\varGamma _{0}^{even}\cup (Q-\varGamma _{0}^{even}))=R^{\oplus }(\varGamma _{0}^{even})\oplus R^{\oplus }(Q-\varGamma _{0}^{even})$. Because $R^{\oplus }(Q)=S$ and $R^{\oplus }(\varGamma _{0}^{even})=0$, we obtain $R^{\oplus }(Q-\varGamma _{0}^{even})=S$. Hence we have $Q-\varGamma _{0}^{even}\notin \varGamma _{{ Forb}}$, which contradicts the fact that $Q-\varGamma _{0}^{even}\in \varGamma _{{ Forb}}$. In summary, we conclude $\varGamma _{0}^{even}\not \subseteq Q\in \varGamma _{0}$, which meets the second condition of Lemma 4. $\square$

By Theorem 1, we have the following two corollaries immediately.

Corollary 1

For an (n, n) threshold access structure, there exists an (n, n)-XVCS having perfect contrast and perfect pixel expansion.

Corollary 2

For an access structure $(\varGamma _{0},\varGamma _{{ Forb}})$ with $|\varGamma _{0}|\le 2$, there exists a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},1)$-XVCS.

Before considering other access structures, the following lemma is first presented.

Lemma 7

Given an access structure $\varGamma _{0}$, the most simplified access structure $\widetilde{\varGamma _{0}}$ is obtained by simplification of $\varGamma _{0}$. A construction of XVCS for the $\widetilde{\varGamma _{0}}$ is also a construction of XVCS for $\varGamma _{0}$ and both XVCSs have the same parameters: contrast and pixel expansion.

Proof

Trivial: distribute the equivalent participants the same shares.

Then let us consider a $(k-1)$-(k, n)* threshold access structure having $k-1$ essential participants. Without loss of generality, we assume that the first $k-1$ participants are essential. Hence, the collection $\varGamma _{0}$ of all minimal qualified sets is $\{\{1,...,k-1,k\},\{1,...,k-1,k+1\},...,\{1,...,k-1,n-1\},\{1,...,k-1,n\}\}$. In this case, each maximal forbidden set is of the type $X\cup Y$ where X is a subset of the set of essential participants $\{1,...,k-1\}$ such that $|X|=k-2$ and $Y=\{k,...,n\}$. According to Definition 3, we have the participants in Y are equivalent. Then the access structure is now reduced to a (k, k) threshold access structure by Definition 4. In the light of Corollary 1 and Lemma 7, we have the following corollary without a proof.

Corollary 3

For a triplet $(k-1, k, n)$ where $k\ge 2$, there exists a non-monotone $(k-1)$-(k, n)*-XVCS having perfect contrast and perfect pixel expansion.

We have already seen from Corollary 3 that for any non-monotone 1-(2, n)*-XVCS both of the contrast and pixel expansion achieve their perfect values. It is not hard to realize that the access structure is nothing but a special type of complete bipartite graph namely, a star-graph. So let us consider the complete bipartite graph based access structure, and the following corollary is presented.

Corollary 4

There exists a complete bipartite graph based XVCS having perfect contrast and perfect pixel expansion.

Proof

Trivial: for a complete bipartite graph, because the participants in each of the two independent sets are equivalent, the scheme is reduced to a (2, 2)-XVCS. $\square$

3.4 Perfect contrast XVCS for general access structures

By Theorem 1, we have proved the sufficient and necessary conditions, a complete characterization of some access structures, for the existence of a perfect XVCS. However, those conditions are not always satisfied by any given access structure. Note that, any access structure $\varGamma _{0}$ can be always partitioned into several parts where each part is in such a complete characterization (the worst case: each part is one minimal qualified set), and hence we can construct a perfect XVCS for each part. But, if we distribute all the shares of these perfect XVCSs to the corresponding participants, this kind of construction, which has similar idea with [16], will deviates from the traditional VCS in the sense that,

• the participants may have to carry multiple shares;

• due to the presence of multiple shares, at the time of revealing the secret, the participants have to know for which access structures they are going to submit which of their shares.

Therefore, in order to avoid the above defects, we design a region-by-region construction of perfect contrast XVCS based on the partition of access structure in this subsection. However, to make our construction clearer, we first need to give a description of the structure of the share.

3.4.1 Share’s region-by-region structure

Suppose an access structure $\varGamma _{0}$ can be partitioned into d parts, where each part satisfies the conditions of Lemma 4. In the proposed region-by-region construction, a share is partitioned into d nonoverlapping regions, each of which has the same size as the secret image, and hence the size of the share is d times that of the secret image. The d regions, located one by one in the share, are corresponding to the d parts respectively.

Fig. 1

Region-by-region structure of a share for (2, 4) and (3, 6) threshold access structures

Take (2, 4) threshold access structure for example, we can partition $\varGamma _{0}=\{Q\subseteq P: |Q|=2\}$ into $d=2$ parts:

$$\begin{aligned} \varGamma ^{1}_{0}= & {} \{\{1,2\},\{1,3\},\{2,4\},\{3,4\}\}, \\ \varGamma ^{2}_{0}= & {} \{\{2,3\},\{1,4\}\}. \end{aligned}$$

So, we also partition each share into two nonoverlapping regions and the location of two regions is illustrated in Fig. 1(a). Furthermore, we can also arrange the regions in a rectangle or square. Take (3, 6) threshold access structure for example, we can partition $\varGamma _{0}=\{Q\subseteq P: |Q|=3\}$ into the following $d=4$ parts:

$$\begin{aligned} \varGamma ^{1}_{0}= & {} \{\{1,2,3\},\{1,2,4\},\{1,2,5\},\{1,3,6\},\{1,4,6\},\{1,5,6\}\}, \\ \varGamma ^{2}_{0}= & {} \{\{1,3,4\},\{2,3,4\},\{3,4,5\},\{3,4,6\}\}, \\ \varGamma ^{3}_{0}= & {} \{\{1,2,6\},\{2,4,6\},\{2,5,6\},\{2,3,6\}\}, \\ \varGamma ^{4}_{0}= & {} \{\{1,3,5\},\{1,4,5\},\{2,3,5\},\{2,4,5\},\{4,5,6\},\{3,5,6\}\}. \end{aligned}$$

So, we also partition each share into four regions and the location of these regions is illustrated in Fig. 1(b).

Fig. 2

Diagram of the proposed region-by-region construction

3.4.2 Region-by-region construction of perfect contrast XVCS

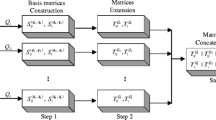
The region-by-region construction of perfect contrast XVCS for any $\varGamma _{0}$ is given based on the access structure simplifying technique and the partition of access structure. Diagram of the region-by-region construction is depicted in Fig. 2 and detailed information on the proposed construction is described as follows.

Region by Region Construction of Perfect Contrast XVCS.

• 1. Given an access structure $\varGamma _{0}$, simplify $\varGamma _{0}$ to $\widetilde{\varGamma _{0}}$ according to Definitions 3 and 4.

• 2. Partition the $\widetilde{\varGamma _{0}}$ into d parts $\widetilde{\varGamma ^{1}_{0}},\widetilde{\varGamma ^{2}_{0}},\ldots ,\widetilde{\varGamma ^{d}_{0}}$ with each part satisfying the conditions of Lemma 4.

• 3. For each $\widetilde{\varGamma ^{i}_{0}}, i=1,\ldots ,d$, generate shares by constructing a perfect contrast $(\widetilde{\varGamma ^{i}_{0}},\varGamma _{{ Forb}},1)$-XVCS according to Theorem 1, and distribute the shares to the corresponding participants as their initial shares, respectively.

• 4. In each $\widetilde{\varGamma ^{i}_{0}}, i=1,\ldots ,d$, for the participants, which are not involved in $\widetilde{\varGamma ^{i}_{0}}$, generate their initial shares with the size of the secret image by assigning 0 or 1 randomly.

• 5. Generate n blank shares with the region-by-region structure for all participants as their final shares, respectively.

• 6. For each participant, assign his d initial shares to the corresponding regions of his final share, respectively.

Remark

In the above construction, if the size of $\varGamma _{0}$ is large, it is hard for us to partition the access structure. To make the partition easier, Step 1 reduces, in some extent, the number of qualified sets in $\varGamma _{0}$ by simplification of access structure. In Steps 2 and 3, since each part of $\widetilde{\varGamma _{0}}$ satisfies the conditions of Lemma 4, this construction seems to terminate at Step 3 according to Theorem 1. However, in order to distribute one share per participant, in Steps 4, 5, and 6, the dealer need to further generate one final share for each participant with the initial shares. Note that, since each final share hold by each participant is d times the size of the secret image, the pixel expansion of our construction is d. Moreover, different partitions of the access structure in Step 2 will result in different values of pixel expansion.

Then we give the following lemma before proving the proposed construction generates a perfect contrast XVCS.

Lemma 8

For $P^{\prime }\subseteq P$, if there exists a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},1)$-XVCS on $P^{\prime }$, then there exists a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},1)$-XVCS on P.

Proof

Trivial: we generate the shares for the participants of $P-P^{\prime }$ by assigning 0 or 1 randomly. $\square$

Theorem 2

The proposed construction is a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},d)$-XVCS.

Proof

In the proposed region-by-region construction, there exists a perfect contrast XVCS with no pixel expansion for each part $\widetilde{\varGamma ^{i}_{0}}$ on $P^{i}\subseteq P$, where $i=1,\ldots ,d$, by Theorem 1. According to Step 4, the ith regions of the final shares hold by the participants of $P-P^{i}$ are assigned 0 or 1 randomly, respectively, so there exists a perfect contrast XVCS with no pixel expansion for each part $\widetilde{\varGamma ^{i}_{0}}$ on P by Lemma 8. In addition, since the d parts of $\widetilde{\varGamma _{0}}$ don’t include each other, the above d perfect contrast XVCSs with no pixel expansion have no influence on each other during recovering the secret. Therefore, the above d perfect contrast XVCSs together form a $(\widetilde{\varGamma _{0}},\varGamma _{{ Forb}},d)$-XVCS, where the secret image is recovered perfectly in one of the d regions of the reconstructed result of qualified shares. Finally, by Lemma 7, we conclude the proposed construction is a perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},d)$-XVCS. $\square$

3.4.3 Partition of access structure

In light of Corollary 2, in the proposed construction we can partition any given $\varGamma _{0}$ into $\lceil \frac{|\widetilde{\varGamma _{0}}|}{2}\rceil$ parts where each part consists of at most two elements of $\widetilde{\varGamma _{0}}$, and hence we state the following lemma without a proof.

Lemma 9

There exists a region-by-region construction of perfect contrast XVCS with the pixel expansion $d=\lceil \frac{|\widetilde{\varGamma _{0}}|}{2}\rceil$.

Then let us consider the $(n-1,n)$ threshold access structure having $\varGamma _{0}=\{Q_{1},Q_{2},\ldots ,Q_{t}\}$. Here, $t=\left( \begin{array}{c} n \\ n-1 \end{array} \right) =n$, $Q_{i}\subset P$ and $|Q_{i}|=n-1$. Then the following lemma is proved.

Lemma 10

For the $(n-1,n)$ threshold access structure having $\varGamma _{0}$, a collection of any three elements of $\varGamma _{0}$ does not satisfy the conditions of Lemma 4.

Proof

Without loss of generality, we assume that the collection is $\{Q_{1},Q_{2},Q_{3}\}$. Note that, any two elements of $\varGamma _{0}$ have a common part of $n-2$ participants. Hence, let $Q_{1}\oplus Q_{2}=\{i_{1},i_{21}\}$ and $Q_{2}\oplus Q_{3}=\{i_{22},i_{3}\}$, where $i_{1}\in Q_{1}$, $i_{21}, i_{22}\in Q_{2}$ and $i_{3}\in Q_{3}$. Since $i_{1},i_{3}\notin Q_{2}$, we have $i_{1}=i_{3}$. Assume $i_{21}=i_{22}$, then we obtain $Q_{1}=Q_{3}$, which contradicts the fact that $Q_{1}\ne Q_{3}$. Thus, we have $i_{21}\ne i_{22}$. Then $Q_{1}\oplus Q_{3}=\{i_{21},i_{22}\}\subseteq Q_{2}$, which does not satisfy the conditions of Lemma 4. $\square$

Based on Lemmas 9 and 10, the following theorem is immediate.

Theorem 3

The optimal pixel expansion of the proposed perfect contrast $(n-1,n)$-XVCS is $d=\lceil \frac{n}{2}\rceil$.

Until now, Lemma 9 gives a simple region-by-region construction of perfect contrast XVCS, even by this construction the optimal pixel expansion is achieved for the $(n-1,n)$ threshold access structure, but we can still reduce the pixel expansion for some other access structures. Hence, how to efficiently partition any given access structure into fewer parts (leading to less pixel expansion) deserves our further study. So, based on the conditions of Lemma 4, we give an efficient algorithm, Algorithm 1, to describe how to partition any given $\varGamma _{0}$ into fewer parts than Lemma 9. Note that, we assume the input $\varGamma _{0}$ is already in the most simplified form.

In Algorithm 1, a loop from Steps 3 to 9 generates one part of the partition. In the loop, based on Corollary 2, we first give Steps 3 and 4, which guarantees that the generated part consists of at least two elements of $\varGamma _{0}$ for $|\varGamma _{0}|\ge 2$. Then if there exists a collection of at least three elements of $\varGamma _{0}$ satisfying the conditions of Lemma 4, we give loops from Steps 5 to 8 to guarantee that the generated part consists of at least three elements of $\varGamma _{0}$ for $|\varGamma _{0}|\ge 3$. Moreover, in the loop from Steps 5 to 8, if the conditions of Lemma 4 are satisfied, we give Steps 6 and 8 to guarantee that we add elements to the generated part as quickly as possible in the next such loops. Based on the above discussions and Lemma 9, we give the following theorem immediately.

Theorem 4

By adopting Algorithm 1, the proposed construction of perfect contrast $(\varGamma _{0},\varGamma _{{ Forb}},d)$-XVCS achieves a pixel expansion $d\le \lceil \frac{|\widetilde{\varGamma _{0}}|}{2}\rceil$.

Table 2 A partition of (k, n) threshold access structures for $1<k<n<7$

In order to better illustrate this theorem, we present a partition, which are obtained by applying Algorithm 1 to (k, n) threshold access structures for $1<k<n<7$, in Table 2. Note that, elements are arbitrarily selected from $\varGamma _{0}$ in the Steps 3, 4 and 5 of Algorithm 1 and different selections may result in different partitions, so Table 2 just lists one case of the partitions.

4 Experiment and comparison

Extensive experimental results by the proposed XVCS are illustrated in this section. Moreover, some comparisons and further discussions among the proposed XVCS and related schemes are provided as well.

4.1 Experiment

To demonstrate the effectiveness of our XVCS, two experiments are conducted respectively.

An experiment of the proposed XVCS to demonstrate Theorem 1 is presented in Fig. 3, where $\varGamma _{0}=\{\{1,2\},\{1,3\},\{1,4\}\}$ and the set of forbidden sets is $\varGamma _{{ Forb}}=\{\{1\},\{2\},\{3\},\{4\},\{2,3\},\{2,4\},\{3,4\},\{2,3,4\}\}$. The secret image is shown in Fig. 3(a) and the generated four shares $T_{1},\ldots ,T_{4}$ are exhibited in Fig. 3(b–e). Obviously, the pixel expansion is 1, and the minimal qualified sets can recover the secret image perfectly while the forbidden sets cannot.

Fig. 3

An experiment by the proposed XVCS for $\varGamma _{0}=\{\{1,2\},\{1,3\},\{1,4\}\}$

Fig. 4

An experiment by the proposed XVCS for (2, 4) threshold access structure

Table 3 Comparison of functionality among the proposed XVCS and related schemes

An experiment of the proposed XVCS to demonstrate Theorem 2 is presented in Fig. 4, where the basis of (2, 4) threshold access structure is $\varGamma _{0}=\{\{1,2\},\{1,3\},\{1,4\},\{2,3\},\{2,4\},\{3,4\}\}$ and the set of forbidden sets is $\varGamma _{{ Forb}}=\{\{1\},\{2\},\{3\},\{4\}\}$. According to Table 2, The $\varGamma _{0}$ is partitioned two parts:$\varGamma ^{1}_{0}=\{\{1,2\},\{1,3\},\{2,4\},\{3,4\}\}$ and $\varGamma ^{2}_{0}=\{\{2,3\},\{1,4\}\}$. Then the share is also partitioned into two nonoverlapping regions, which are located vertically. The secret image is shown in Fig. 4(a) and the generated four shares $T_{1},\ldots ,T_{4}$ are exhibited in Fig. 4(b–e). The minimal qualified sets can recover the secret image perfectly in their corresponding regions while the forbidden sets cannot.

4.2 Comparison

Functionality comparisons among the proposed XVCS and related schemes are mainly demonstrated in Table 3, and major advantages of the proposed XVCS are

• Flexible sharing strategy. General access structure can be implemented by the proposed XVCS, more complicated sharing strategy in real world can be conducted. It is superior to the threshold schemes [2, 4, 8, 11, 20, 24, 25, 32].

• Perfect visual quality. The “XOR” operation causes that the black subpixel in a share can be undone by the color of another subpixel laid over it. In the proposed XVCS, the secret image can be perfectly recovered for all minimal qualified sets. It is more appealing in practical applications compared with [1–4, 8, 9, 11, 20, 21, 24, 25, 29, 32].

• The sufficient and necessary conditions for the existence of a perfect XVCS. If an access structure satisfies these conditions, then for the access structure, we can give an explicit construction of XVCS with the proposed linear algebraic technique, and achieve contrast and pixel expansion both equal to 1. Unlike the work of [9] which assumes the existence of XVCS over an access structure, our proof is constructive.

• Only one share for each participant. Different from [16], each participant does not have to carry multiple shares and is not required to know at the time of revealing the secret for which access structures he is going to submit which of his shares.

• Less storage and transmission bandwidth. Comparisons of pixel expansion are summarized in Tables 4 and 5, where the values in brackets, summarized from [20, 21, 24], are optimal for OVCS and XVCS to the best of our knowledge. According to Tables 4 and 5, our pixel expansion is close to that of Liu et al. [16]. Compared with the schemes [1–4, 8, 9, 11, 20, 21, 24, 25, 32], the proposed XVCS achieves no or smaller pixel expansion which will save the storage and transmission bandwidth.

• Efficient partitions of access structure. Unlike the work of [16] which adopted the hard and time-consuming computing search without consideration of some efficient partitions of access structure, we give efficient partitions of access structure based on the sufficient and necessary conditions, and approximate pixel expansions including the optimal value for $(n-1,n)$ threshold access structure are obtained.

Table 4 Comparison of pixel expansion for (k, n) threshold access structures with $2\le k\le n\le 6$

Table 5 Pixel expansions of the proposed non-monotone XVCS for access structures with up to four participants

5 Conclusion

In this paper, we have considered perfect contrast XVCS for general access structures from the theory of linear algebra and concluded the sufficient and necessary conditions, some constraints on the set $\varGamma _{0}$ of minimal qualified sets, for the existence of a perfect contrast XVCS with no pixel expansion. Then, for any given $\varGamma _{0}$, we have proposed a region by region construction to achieve perfect contrast with small pixel expansion. However, in Algorithm 1, we have claimed that different selections of elements from $\varGamma _{0}$ in the Steps 3, 4, and 5 may result in different partitions, and hence lead to different values of pixel expansion. Although we can find the minimum number of parts output by Algorithm 1 based on the exhaustive search strategy, whether the minimum number of parts is or not the optimal pixel expansion is unknown. Furthermore, the exhaustive search method is very hard and quite time-consuming. So, how to achieve the optimal pixel expansion efficiently remains as an open problem.