Improved indifferentiability security bound for the JH mode

Abstract

Indifferentiability security of a hash mode of operation guarantees the mode’s resistance against all generic attacks. It is also useful to establish the security of protocols that use hash functions as random functions. The JH hash function was one of the five finalists in the National Institute of Standards and Technology SHA-3 hash function competition. Despite several years of analysis, the indifferentiability security of the JH mode has remained remarkably low, only at $n/3$ bits, while the two finalist modes Keccak and Grøstl offer a security guarantee of $n/2$ bits. Note all these three modes operate with $n$-bit digest and $2n$-bit permutations. In this paper, we improve the indifferentiability security bound for the JH mode to $n/2$ bits (e.g. from approximately 171 to 256 bits when $n=512$). To put this into perspective, our result guarantees the absence of (non-trivial) attacks on both the JH-256 and JH-512 hash functions with time less than approximately $2^{256}$ computations of the underlying 1024-bit permutation, under the assumption that the underlying permutations can be modeled as an ideal permutation. Our bounds are optimal for JH-256, and the best known for JH-512. We obtain this improved bound by establishing an isomorphism of certain query-response graphs through a careful design of the simulators and bad events. Our experimental data strongly supports the theoretically obtained results.

1 Introduction

1.1 Generic attacks

In a generic attack, an adversary attempts to break a property of the target crypto-algorithm assuming that one or more of its smaller components are ideal objects, such as random oracles, ideal permutations, or ideal ciphers. For example, suppose that the target crypto-algorithm is a hash function $H:\{0,1\}*\rightarrow \{0,1\}^n$. Assume that for a given input $M\in \{0,1\}^{*}$, $H$ invokes an ideal object, say a random oracle $\mathsf{ro }:\{0,1\}^{m}\rightarrow \{0,1\}^{n}$, one or multiple times, to compute $H(M)$. Informally, a generic attack breaks a property of the hash function $H$ utilizing less resources than would be required to break the same property of the big random oracle $\mathsf{RO }:\{0,1\}^{*}\rightarrow \{0,1\}^{n}.$

Generic attacks against hash functions are plentiful in the literature. See, for example, Joux’s multi-collision attack [19], the Kelsey–Schneier expandable-message second pre-image attack¹ [21], and the Kelsey–Kohno herding attack [20], all on the popular Merkle–Damgård hash mode. Generic attacks have also been reported on hash modes other than the plain Merkle–Damgård mode. A few of these are the 2nd pre-image attacks on the dithered variants of the Merkle–Damgård construction [1], a pre-image attack on the JH mode [8], pre-image, second pre-image, and multi-collision attacks on the Sponge construction when the state-size is small [7], collision attacks on some concatenated hash functions [19], second pre-image, multi-collision and herding attacks on some hash functions based on checksums [13, 16], multi-collisions in iterated concatenated and expanded hash functions [18], and multi-collisions on some generalized sequential hash functions [24]. See also [14, 15, 17], which analyze generic attacks on randomized hashing (a variant of Merkle–Damgård).

In each of the above examples, a common assumption was that the underlying basic primitive of the hash function is an ideal object. Therefore, all of these attacks fit the definition of a generic attack. Generic attacks have changed the outlook on the security of a cryptographic hash function over the last few years. One naturally asks how to design a hash mode secure against all generic attacks.

1.2 Indifferentiability security

The indifferentiability security framework was introduced by Maurer et al. [23] in 2004, and was first applied to analyze hash modes of operation by Coron et al. [10] in 2005. A hash mode proven secure in this framework is able to resist all generic attacks. More technically, the indifferentiability framework measures the extent to which a hash function behaves as a random oracle under the assumption that the underlying small compression function is an ideal object. The class of indifferentiability attacks includes more attacks [4, 8, 9] than just useful generic attacks as above. Thus in some sense, an indifferentiable hash function can be viewed as eliminating potential future attacks. We note the security of many cryptographic protocols rely on the indifferentiability security of the underlying hash functions that the protocols use as random oracles. In such a case, security of the hash functions against selected specialized attacks—such as collision, pre-image attacks and second pre-image attacks—are inadequate to guarantee the security of the overlying protocol. The notion of indifferentiability security has also been applied to compression functions. See [5] for example. Some limitations of the indifferentiability framework have recently been discovered in [12] and [26]: the first paper shows how some hash modes can be attacked in the indifferentiability setting, even if they are “practically secure”; the second paper points out how a certain protocol allows for an attack by a multi-stage adversary when its underlying random oracle is replaced by an indifferentiable hash function. These limitations do not apply to the indifferentiability security of compression functions (i.e., [5]). Still, indifferentiability security has gradually become a de-facto requirement for the adoption of a hash mode as a standard because it guarantees security for hash function modes of operation against generic attacks.

1.3 Previous analysis of the JH mode

The JH hash function was one of the five finalist algorithms in the NIST SHA-3 hash function competition [25]. The hash function uses an iterative mode which is novel in the sense that it is based on a permutation [28]. Several popular hash functions—such as SHA-1 and SHA-2—are constructed instead using a block cipher. Since its publication in 2007, the JH mode of operation has undergone an extensive security analysis. The first published analysis of the JH mode was done by Bhattacharyya, Mandal and Nandi, who showed that the indifferentiability security of the basic version of the JH mode up to $n/3$ bits [8];² they have also shown a preimage attack on the JH-512 mode with approximately $2^{507}$ calls to the underlying permutation. A year later, in [22], it was shown that the JH mode achieves the optimal collision resistance of up to $n/2$ bits. Recently Andreeva, Mennink and Preneel have improved the first and second pre-image resistance of the JH mode from $n/3$ to $n/2$ bits [3]. However, the improvement of the indifferentiability security of the JH mode beyond $n/3$ bits has remained elusive. Table 1 gives an overview of the main results on the JH mode.

Table 1 The resistance of the JH mode against several attacks

1.4 Our contribution

The usage of an ideal permutation, instead of a random oracle, in the JH mode allows the adversary to use reverse queries in addition to forward queries. One of the main obstacles for an improved indifferentiability security analysis of the JH mode is how to handle these reverse queries. This additional privilege of the adversary makes challenging the construction of an efficient simulator able to withstand adversaries using up to (approximately) $2^{n/2}$ queries. It is important to note that these adversaries (working in the indifferentiability framework) are distinguishing adversaries telling apart the pair of the JH mode and the underlying permutation from the pair of a random oracle and a simulator. Since the framework involves two pairs of algorithms, the security guarantee obtained in this framework is at least as much as—and most likely even better than—the guarantee obtained in a framework that distinguishes output of one algorithm (e.g. JH mode) from that of the other (e.g random oracle) [23]. Another major challenge, which turns out to be quite hard, is to estimate the probability of the events when a current query submitted by an arbitrary adversary matches an old but unknown query. A somewhat easier task is to show that the probability of a node-collision on the graph constructed by an efficient simulator, is at most $\frac{\sigma ^2}{2^n}$, where $\sigma$ is the total number of submitted queries. We overcome these hurdles by carefully designing a set of bad events. Our construction is such that the absence of the bad events, (1) eliminates the possibility of a reverse query being attached to the simulator graph, (2) allows the graph to grow only linearly in the number of submitted queries, and most importantly (3) ensures the isomorphism of the simulator graphs in two different games. Using this isomorphism result and the linear bound on the number of nodes in the isomorphic graphs, we are able to improve the indifferentiability security bound of JH to $n/2$ bits. Another feature of our work, which may be of independent interest, is that the proof of our main theorem Theorem 1 requires only three games. The smaller number of games (in stark comparison with the usual practice of tackling such problems using a sequence of a large number of games) makes third-party verification of the proof a great deal easier and also allows the application of probabilistic tools to find practical security bounds [27] .

Our indifferentiability bound guarantees the absence of generic attacks on the JH hash function (using a $2n$-bit permutation) with work less than $2^{n/2}$. When the digest-size is $256$ or $512$ bits, the hash mode is resistant to all generic attacks up to (approximately) $2^{256}$ computations of the underlying 1024-bit permutation. This bound is optimal for JH-256 and the best known for JH-512. Furthermore, we have performed a series of experiments with the JH mode studying the effects of the bad events in our framework. Our experiments verify the theoretically obtained results, and also exhibit optimal adversarial strategies. See Sect. 6 for more on the experiments. We caution the reader that our result on the JH mode says nothing about the security of the underlying 1024-bit permutation, which is assumed to be free from all structural weaknesses throughout the paper.

1.5 Notation and convention

Throughout the paper we let $n$ be a fixed integer. We shall use the little-endian bit-ordering system. The symbol $|\cdot |$ is used for both length of a message and the cardinality of a set. For concatenation of fixed length strings $a$ and $b$, we use $a||b$, or just $ab$ if the meaning is clear. Let $S_X$ denote the sample space of the discrete random variable $X$. The relation $A\sim B$ is satisfied if and only if $\mathrm {Pr}\big [A=X\big ]=\mathrm {Pr}\big [B=X\big ]$ for all $X\in S$, where $S=S_A=S_B$. Let $T$ be an array or a table. Then $Dom(T)=\left\{ i \mid T[i]\ne \perp \right\}$ and $Rng(T)=\left\{ T[i] \mid T[i]\ne \perp \right\}$. We write ${\fancyscript{A}}^B\Rightarrow b$ to denote an algorithm ${\fancyscript{A}}$ with oracle access to $B$ outputting $b$. Finally, let $[c,d]$ be the set of integers between $c$ and $d$ inclusive, and $a[x,y]$ the bit-string between the $x$-th and $y$-th bit-positions of $a$. In algorithm descriptions, ‘$=$’ is used to denote the assignment operation.

2 Indifferentiability framework for JH

2.1 Description of the JH mode

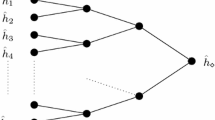
Suppose $n\ge 1$. Let $\pi :\{0,1\}^{2n}\rightarrow \{0,1\}^{2n}$ be a $2n$-bit ideal permutation used to build the JH hash function JH$^\pi :\{0,1\}^{*}\rightarrow \{0,1\}^{n}$. A pictorial description of the JH transform is given in Fig. 1. The semantics for the notation $M\mathop {\rightarrow }\limits ^{pad}m_1\cdots m_{k-1}m_k$ is as follows: Using an injective function $\mathsf{pad }: \{0,1\}^{*}\rightarrow \cup _{i\ge 1}\{0,1\}^{ni}$, $M$ is mapped into a string $m_1\cdots m_{k-1}m_k$ such that $k=\Big \lceil \frac{|M|}{n}\Big \rceil +1$, $|m_i|=n$ for $1\le i\le k$. The injective function $\mathsf{pad }(\cdot )$ ensures that distinct messages remain distinct after padding. In addition to the injectivity of $\mathsf{pad }(\cdot )$, we will also require that there exists a function $\mathsf{dePad }(\cdot )$ that can efficiently compute $M$, given pad $(M)$. Formally, the function $\mathsf{dePad }:\cup _{i\ge 1}\{0,1\}^{in}\rightarrow \{\perp \}\cup \{0,1\}^{*}$ is defined as follows: $\mathsf{dePad }(\mathsf{pad }(M))=M$, for all $M\in \{0,1\}^{*}$, and otherwise $\mathsf{dePad }(\cdot )$ returns a special symbol $\perp$ denoting that the padded message was not generated from a valid message. We note that the padding rules of all practical hash functions have the above properties. For more details, the reader is referred to the original specification written by the JH designer [28].

Fig. 1

Diagram for the JH mode. All rectangles denote the ideal permutation $\pi$ on $\{0,1\}^{2n}$. JH takes as input a message $M\in \{0,1\}^{*}$, and performs the following four steps: $M\mathop {\rightarrow }\limits ^{pad}m_1m_2\ldots m_{k-1}m_k$; $y_0=IV$, $y'_0=IV'$; $y_iy'_i=\pi \Big (y_{i-1}||(y'_{i-1}\oplus m_i)\Big )\oplus m_i||0$ for all $i\in \{1,2,\ldots k\}$; return $y_k$

2.2 Introduction to the indifferentiability framework

We will frequently refer to the use of a random oracle. A random oracle is a function $\mathsf{RO }: X\rightarrow Y$ chosen uniformly at random from the set of all $|Y|^{|X|}$ functions that map $X\rightarrow Y$. In other words, a function $\mathsf{RO }: X\rightarrow Y$ is a random oracle if and only if, for each $x\in X$, the value of $\mathsf{RO }(x)$ is chosen uniformly at random from $Y$.

We now define the indifferentiability security notion which is a slightly modified version of the original definition provided in [10, 23].

Indifferentiability security [10] An interactive Turing machine (ITM) $T$ with oracle access to an ideal primitive ${\fancyscript{F}}$ is said to be $(t_{\fancyscript{A}},t_S,q,\varepsilon )$-indifferentiable from an ideal primitive ${\fancyscript{G}}$ if there exists a simulator $S$ such that, for any distinguisher ${\fancyscript{A}}$, the following equation is satisfied:

$$\begin{aligned} |{\mathrm {Pr}}[{\fancyscript{A}}^{T,{\fancyscript{F}}}=1]-{\mathrm {Pr}}[{\fancyscript{A}}^{{\fancyscript{G}},S}=1]|\le \varepsilon . \end{aligned}$$

The simulator $S$ is an ITM which has oracle access to ${\fancyscript{G}}$ and runs in time at most $t_S$. The distinguisher ${\fancyscript{A}}$ – also known as an indifferentiability adversary—runs in time at most $t_{\fancyscript{A}}$. The number of queries used by ${\fancyscript{A}}$ is at most $q$. Here $\varepsilon$ is a real number in $(0,1)$.

Suppose, an ideal primitive ${\fancyscript{G}}$ (e.g. a variable-input-length random oracle) is indifferentiable from an algorithm $T$ based on another ideal primitive ${\fancyscript{F}}$ (e.g. a fixed-input-length random oracle). Then any cryptographic system ${\fancyscript{P}}$ based on ${\fancyscript{G}}$ is as secure as ${\fancyscript{P}}$ based on $T^{\fancyscript{F}}$ (i.e., ${\fancyscript{G}}$ replaces $T^{\fancyscript{F}}$ in ${\fancyscript{P}}$) [23]. For a more detailed explanation, we refer the reader to [23].

Pictorial description of indifferentiability security framework In Fig. 2, the five algorithms involved in the definition of indifferentiability security are shown: $T$, ${\fancyscript{F}}$, ${\fancyscript{G}}$ and $S$ have been replaced by a hash mode $H$, an ideal permutation $\pi /\pi ^{-1}$, a random oracle $\mathsf{RO }$, and a pair of simulators $S/S^{-1}$. For the purposes of our paper, $H$ is the JH hash mode based on the ideal permutation $\pi$. In this setting, the definition of indifferentiability addresses the degree to which any computationally bounded adversary is unable to distinguish between Option 1 and Option 2.

Fig. 2

Indifferentiability framework for a hash function based on an ideal permutation. An arrow indicates the direction in which a query is submitted

2.3 JH indifferentiability

To study the indifferentiability security of the JH mode, we use the ideal permutation $\pi /\pi ^{-1}: \{0,1\}^{2n}\rightarrow \{0,1\}^{2n}$ as the basic primitive of JH. To obtain the indifferentiability security bound, we follow the usual game-playing techniques [2, 6]. The schematic diagrams of the two games Option 1 and Option 2 (of Fig. 2) are Game(JH, $\pi$, $\pi ^{-1}$) and Game(RO, S, S $^{-1}$) as illustrated in Fig. 3. The other game $G1$ is an intermediate step, allowing us to more easily compare pairs of games. The pseudocode for all the games are provided in Sect. 3. One of the major challenges of the indifferentiability security analysis of JH is the construction of a simulator-pair $\mathsf{S }/\mathsf{S }^{-1}$ being able to withstand attacks by all adversaries limited by a total of $2^{n/2}$ queries to the underlying permutations. The construction techniques for designing such a simulator-pair and their effectiveness are described in detail in Sect. 3.

Fig. 3

Schematic diagrams of the security games used in the indifferentiability framework for JH. The arrows show the directions in which the queries are submitted

A necessary part of our analysis is determining equivalences between pairs of games. We define this notion formally.

Equivalence of games A game is a stateful probabilistic algorithm that takes an adversary-generated query as input, updates the current state, and produces an output to the adversary. Let $(x_i,y_i)$ denote the $i$-th query and response pair from the game $G$. The view of the game $G$ after $j$ queries (with respect to the adversary ${\fancyscript{A}}$), is the sequence $\{(x_1,y_1),\ldots ,(x_j,y_j)\}$.

Denote the views of the games $G1$ and $G2$ after $i$ queries by $V_1^i$ and $V_2^i$. The games $G1$ and $G2$ are said to be equivalent (with respect to the adversary ${\fancyscript{A}}$) if and only if $V_1^i\sim V_2^i$ for all $i>0$. Equivalence between the games $G1$ and $G2$ is denoted by $G_1\mathop {\equiv }\limits ^{\fancyscript{A}}\ G2$, or simply $G1\equiv \ G2$, when the adversary is clear from the context.

3 Description of the security games for JH

In this section, we elaborate on the games Game(JH, $\pi$, $\pi ^{-1}$), $G1$, and Game(RO, S, S $^{-1}$) that are schematically presented in Fig. 3. The pseudocode for all the games is given in Figs. 4 and 6.

Fig. 4

The main games Game(JH, $\pi$, $\pi ^{-1}$) and Game(RO, S, S $^{-1}$). (a) Game(JH, $\pi$, $\pi ^{-1}$): global variable is the table $D_\pi$ ; (b) Game(RO, S, S $^{-1}$): Global variables are the tables $D_l$ and $D_s$, and the graph $T_s$

JH, JH1, and RO are mappings from $\{0,1\}*$ to $\{0,1\}^{n}$. $\mathsf{S }$ is a mapping from $\{0,1\}^{2n}$ to $\{0,1\}^{2n}$. Also, $\pi$, $\pi ^{-1}$, $\mathsf{S1 }$, and $\mathsf{S1 }^{-1}$ are all permutations on $\{0,1\}^{2n}$, while $\mathsf{S }^{-1}$ is a mapping from $\{0,1\}^{2n}$ to $\{0,1\}^{2n}\cup \{\textsc {``INVALID''}\}$. The mapping $\mathsf{S }^{-1}$ returns a special string “INVALID” if it is not behaving like a permutation; more precisely, on input $r$, $\mathsf{S }^{-1}$ returns “INVALID” if there exist at least two distinct images $x_1$ and $x_2$ such that $\mathsf{S }(x_1)=\mathsf{S }(x_2)=r$. A query submitted to JH, or JH1, or RO is called an $l$-query, short for long query. Likewise, a query submitted to $\pi$ of Game(JH, $\pi$, $\pi ^{-1}$), or to S1 of $G1$, or to S of Game(RO, S, S $^{-1}$), is called an $s$-query. A query submitted to $\pi ^{-1}$ of Game(JH, $\pi$, $\pi ^{-1}$), or to S1$^{-1}$ of $G1$, or to S $^{-1}$ of Game(RO, S, S $^{-1}$), is called an $s^{-1}$-query. An $s$-, $s^{-1}$-, $\pi$-, or $\pi ^{-1}$-query is also called a short query.

The games will use several global and local variables. The global variables $D_l$ and $D_s$ are two tables used to store query-response pairs: $D_l$ for $l$-queries and responses, and $D_s$ for $s/s^{-1}$-queries and responses. The table $D_\pi$ contains all $\pi /\pi ^{-1}$-queries and responses. The tables $D_l$, $D_s$ and $D_\pi$, and all local variables are initialized with $\perp$. The graphs $T_\pi$ and $T_s$—built using elements of $D_\pi$ and $D_s$—are also global variables which initially contain only a root node $(IV,IV')$. The local variables are re-initialized every new invocation of the game, while the global data structures maintain their states across queries.

The queries can also be divided into types according to the time of submission and the location in the tables. The current query is the one that is submitted by the adversary at the current time. A current query can be of two types: it is an old query if already present in the query history; it is a fresh query if not present in the query history. Table 2 formally defines an old and a fresh query in the various security games.

Table 2 Definitions of old and fresh queries in various security games for JH

We assume that the adversary does not submit two identical $l$-queries, $s$-queries, or $s^{-1}$ queries. This implies that every current $l$-query is fresh in all the games; however, every current $s$-, $s^{-1}$-, $\pi$-, or $\pi ^{-1}$-query is not necessarily fresh in all games. For example, the current $s$-query in Game(JH, $\pi$, $\pi ^{-1}$) may accidentally match a query in $Dom(D_\pi )$ that was generated as an intermediate $\pi$-query from a previously submitted $l$-query. Later on, we shall collect these accidents as BAD events, and use them to bound the indifferentiability security of the JH mode (see Sects. 4 and 5).

Description of Game (JH, $\pi$, $\pi ^{-1}$) The pseudocode for this game is given in Fig. 4(a). Following the definition provided in Sect. 2.3, the game Game(JH, $\pi$, $\pi ^{-1}$) implements the JH hash function using the permutations $\pi$ and $\pi ^{-1}$. The ideal permutation $\pi /\pi ^{-1}$ has been implemented through lazy sampling. Lazy sampling is the postponement of sampling the random values until they are actually used for the first time. The query-response pairs for $\pi /\pi ^{-1}$ are stored in the table $D_\pi$.

Description of Game (${{\mathbf {\mathsf{{RO}}}}}, {{\mathbf {\mathsf{{S}}}}}, {{\mathbf {\mathsf{{S}}}}}^{-1}$) The pseudocode for this game is give in Fig. 4b. The functions $\mathsf{S }$ and $\mathsf{S }^{-1}$ are the simulators of the indifferentiability framework for JH. Construction of effective simulators is the most important part of the analysis of indifferentiability security for a hash mode of operation. The purpose of the simulator-pair $\mathsf{S }/\mathsf{S }^{-1}$ is two-fold: (1) to output values that are indistinguishable from the output from the ideal permutation $\pi /\pi ^{-1}$, and (2) to respond in such a way that $JH^{\pi }{(M)}$ and RO $(M)$ are identically distributed. It will easily follow that as long as the simulator-pair $\mathsf{S }/\mathsf{S }^{-1}$ is able to output values satisfying the above conditions, no adversary can distinguish between Game(JH, $\pi$, $\pi ^{-1}$) and Game(RO, S, S $^{-1}$).

Our design strategy for $\mathsf{S }/\mathsf{S }^{-1}$ is fairly intuitive and simple: $\mathsf{S }$ maintains a graph $T_s$ using $s$-queries and responses, such that every path in $T_s$ represents the execution of JH on some message. Correspondingly, any “JH-mode-compatible” message that can be reconstructed from the $s$-queries and responses is represented by some path on $T_s$. This helps S keep track of all “JH-mode-compatible” messages at all times. This is accomplished by a special subroutine FullGraph. The pictorial representation of $T_s$ is given in Fig. 5. In addition, whenever a new message $M$ is found on $T_s$, S makes a crucial adjustment using a subroutine MessageRecon, so that the distributions of $JH^{\pi }{(M)}$ and RO $(M)$ are close. The complete description of S/S $^{-1}$ is as follows.

Fig. 5

All arrows and dots are $n$ bits each. (i) The directed graph $T_s$ (or $T_\pi$) which is updated by the subroutine FullGraph of Game(RO, S, S $^{-1}$)(or PartialGraph of $G1$) (see Figs. 4b and 6). Example: The edge $(y_1y_1',m_2,y_2y_2')$ is composed of the head node $y_1y_1'$, the arrow $m_2$, and the tail node $y_2y_2'$. The left and right coordinates of a node $(y_ay'_a)$ is $y_a$ and $y'_a$. (ii) JH mode with $M\mathop {\rightarrow }\limits ^{pad}m_1m_2\cdots m_k$. The shaded region shows the generation of the edge $(y_1y_1',m_2,y_2y_2')$ in $T_s$ using $\mathsf{S }$ (or in $T_\pi$ using $\pi$);

Description of the simulator-pair ${\mathsf{\textit{S} }}/{\mathsf{\textit{S} }}^{-1}$ We first describe two important subroutines used by the simulator-pair.

• FullGraph This routine updates the graph $T_s$ using the elements in $D_s$ in such a way that each path originating from the root $(IV,IV')$ represents the execution of JH$^\mathsf{S }(\cdot )$ on a prefix of some message. Additionally and more importantly, the graph $T_s$ contains all possible paths derived from the elements in $D_s$; hence the name FullGraph. See Fig. 5 for the pictorial description of how several components of the graph $T_s$ are built. For example, suppose $M\mathop {\rightarrow }\limits ^{pad}m_1m_2M'$. Then the path $IVIV'\mathop {\rightarrow }\limits ^{m_1}y_1y_1'\mathop {\rightarrow }\limits ^{m_2}y_2y_2'$ represents the first two-block execution of JH$^\mathsf{S }(M)$ where, $y_1y_1'=\mathsf{S }(IV||IV'\oplus 0||m_1)\oplus m_1||0$ and $y_2y_2'=\mathsf{S }(y_1||y_1'\oplus 0||m_2)\oplus m_2||0$.

• MessageRecon $(x,T_s)$ The purpose of this routine is to reconstruct all messages $M$ such that the final input to $\mathsf{S }$ in JH$^\mathsf{S }(M)$ is the current $s$-query $x$. Hence JH$^\mathsf{S }(M)=\mathsf{S }(x)[0,n-1]\oplus z$, where $z$ is the final message-block of $M$ after padding. The subroutine uses $T_s$ to find all such $M$, by first calling the subroutine FindNode $(y=x[0,n-1])$ to check whether there exist nodes in $T_s$ with left-coordinate $y$. If present, then the subroutine FindBranch $(y)$ collects all paths between the root $(IV,IV')$ and the nodes $yz'$. A set ${\fancyscript{M}}$ is returned, containing all the sequences of arrows on those paths—denoted by $X$—concatenated with $z=z'\oplus x[n,2n-1]$. Notice that $\mathsf{dePad }(X||z)=M$. If no such $M\ne \perp$ is found, then the subroutine returns the empty set.

Using the above two subroutines, the simulator-pair $\mathsf{S }/\mathsf{S }^{-1}$ works as follows.

• For an $s$-query $x$, S assigns a uniformly sampled $2n$-bit value to $r$. The subroutine MessageRecon $(x,T_s)$ is then invoked, which returns a set of messages ${\fancyscript{M}}$. If $\vert {\fancyscript{M}}\vert =1$ then $r[0,n-1]$ is re-assigned the $n$-bit string $\mathsf{RO }(M)\oplus z$, where $M\in {\fancyscript{M}}$ and $M\mathop {\rightarrow }\limits ^{pad}m_1m_2\cdots m_k=X||z$. Finally, $D_s$ and $T_s$ are updated using FullGraph, and the value of $r$ is returned.

• For an $s^{-1}$-query $r$, if there exist $x_1\ne x_2$ such that $D_s[x_1]=D_s[x_2]=r$, then a special string “INVALID” is returned. If instead there exists a unique $x\in Dom(D_s)$ such that $D_s[x]=r$, then $x$ is returned. The last possible case is if $r\notin Rng(D_s)$, and then $x$ is assigned a $2n$-bit integer chosen according to the uniform distribution on $[0,2^{2n}-1]$. If $x\notin Dom(D_s)$ then $D_s[x]$ is assigned $r$. Finally $x$ is returned.

Description of RO The oracle RO works as follows. Given an $l$-query $M$, RO first checks whether $M$ has already been queried by $\mathsf{S }$. In such a case, $M$ already belongs to $Dom(D_l)$ and the RO returns $D_l[M]$. Otherwise, $D_l[M]$ is assigned a uniformly sampled $n$-bit value, which is eventually returned.

Description of G1 The pseudocode for this game is given in Fig. 6. The description of $G1$ apparently looks a bit artificial in the sense that it was constructed as a hybridization of the previous two games Game(JH, $\pi$, $\pi ^{-1}$) and Game(RO, S, S $^{-1}$). The purpose of this game is to be a transit point from Game(JH, $\pi$, $\pi ^{-1}$) to Game(RO, S, S $^{-1}$) so that their difference in execution can be understood.

Fig. 6

Game $G1$: Global variables are the tables $D_l$, $D_s$ and $D_\pi$, and the graphs $T_\pi$ and $T_s$

In the description of this game, we will ignore the bolded statements where the variable BAD is set, since they do not impact the output and the global data structures. The variable BAD is set when certain events occur in the global data structures. Those events will be discussed, when we compute $\big |\mathrm {Pr}\big [{\fancyscript{A}}^{G1}\Rightarrow 1\big ]-\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO }, \mathsf{S }, \mathsf{S }^{-1}}\Rightarrow 1\big ]\big |$ in Sect. 5.

Description of the simulator-pair ${\mathsf{\textit{S} }}1/{\mathsf{\textit{S} }}1^{-1}$ The intuition behind the design of this simulator-pair is similar to that of $\mathsf{S }/\mathsf{S }^{-1}$ of Game(RO, S, S $^{-1}$). The key difference is that rather than building a graph representing all “JH-compatible-messages”, the graph in this game contains a partial set of “JH-compatible-messages”. We will eventually see in Lemma 1, that if BAD events do not occur, then both the graphs are isomorphic. We now describe $\mathsf{S }1/\mathsf{S }1^{-1}$ in full detail using the following two subroutines.

• PartialGraph $(x,r)$ The subroutine builds the graph $T_\pi$ in such a way that each directed path originating from the root $(IV,IV')$ represents the execution of JH$^\pi (\cdot )$ on a prefix of some message (see Fig. 5). In constrast with FullGraph, rather than building all possible paths using the fresh pair $(x,r)$ and the old pairs in $D_\pi$, the PartialGraph augments the $T_\pi$ by only one level; hence the name PartialGraph. The details are as follows. First, the subroutine CreateCoset $(y_c=x[0,n-1])$ is invoked, which returns a set $\mathsf{Coset }$ containing all nodes in $T_\pi$ whose left-coordinate is $y_c$. The size of $\mathsf{Coset }$ determines the number of fresh nodes to be added to $T_\pi$ in the the current iteration. Using the members of $\mathsf{Coset }$ and the new pair $(x,r)$, new edges are constructed, stored in EdgeNew, and added to $T_\pi$ using the subroutine AddEdge.

• MessageRecon $(x,T_s)$. The current $s$-query is $x$, and the graph $T_s$ is the maximally connected subgraph (of $T_\pi$) with the root-node $(IV,IV')$, generated by the $s/s^{-1}$-queries and responses stored in $D_s$. This subroutine has been described already in game Game(RO, S, S $^{-1}$).

Using the above two subroutines, the simulator-pair $\mathsf{S }1/\mathsf{S }1^{-1}$ works as follows.

• For an $s$-query $x$, $r$ is assigned the value of $\pi (x)$. The ideal permutation $\pi$ is implemented through lazy sampling. MessageRecon is called with $(x, T_s)$, which returns a set of messages ${\fancyscript{M}}$. If $\vert {\fancyscript{M}}\vert =1$, and if $M\in {\fancyscript{M}}$ is not a previous $l$-query then $D_l[M]$ is re-assigned the value of $r[0,n-1]\oplus z$, where $M\mathop {\rightarrow }\limits ^{pad}Xz$. Then the table $D_s$ is updated. If $x$ is fresh then the routine PartialGraph is invoked on $(x,r)$ to update the graph $T_\pi$. Finally, $r$ is returned.

• For an $s^{-1}$ query $r$, $x$ is assigned the value of $\pi ^{-1}(r)$, $D_s[x]$ is updated, and $x$ is returned.

Description of JH1 If an $l$-query $M$ has already been queried by S1, then $D_l[M]$ is returned. Otherwise, JH1 mimics JH, in addition to updating the graph $T_s$ whenever a fresh intermediate input is generated. Afterwards, $D_l[M]$ is assigned the value of $r[0,n-1]\oplus m_k$. Finally, $D_l[M]$ is returned.

With the above description of the games at our disposal, now we are well equipped to state and prove an easy but important result.

Proposition 1

For any distinguishing adversary ${\fancyscript{A}}$, Game(JH, $\pi$, $\pi ^{-1}$) $\equiv G1$.

Proof

From the description of $\mathsf{S1 }$, and $\mathsf{S1 }^{-1}$, we observe that, for all $x\in \{0,1\}^{2n}$, $\mathsf{S1 }(x)=\pi (x)$, and $\mathsf{S1 }^{-1}(x)=\pi ^{-1}(x)$. Likewise, from the descriptions of JH1 and JH, for all $M\in \{0,1\}^{*}$, JH1$(M)=$ JH$(M)$. $\square$

A round of $G1$ and Game(RO, S, S $^{-1}$) A round is defined based on the type of the submitted query.

• s -query In the game $G1$, a round spans the lines 100 through 106 (Fig. 6). For the game Game(RO, S, S $^{-1}$), a round spans the lines 101 through 106 (Fig. 4b).

• s $^{-1}$ -query In the game $G1$, a round spans the lines 601 through 605. For Game(RO, S, S $^{-1}$) a round spans the lines 300 through 305.

• l -query Let $M\mathop {\rightarrow }\limits ^{pad}m_1m_2\cdots m_k$. For the game $G1$, the lines 004 through 007 form a round for the message-blocks $m_1$, $m_2$, $\ldots$ and $m_{k-1}$. For the last block, $m_k$, the round is between the lines 008 and 013. For the Game(RO, S, S $^{-1}$), it is not specified how the random oracle $\mathsf{RO }(\cdot )$ processes the individual message-blocks $m_j$ ($1\le j\le k$) internally. We assume that it processes the message-blocks sequentially and the time taken to process each block is equal.

Note that the sum of the numbers of message-blocks, $s$-queries and $s^{-1}$-queries before the $i+1$st round is $i$.

Time complexity of the simulator-pair S/S $^{-1}$ in Game(RO, S, S $^{-1}$) Since there are at most $i$ short queries and responses after $i$ rounds, the maximum number of distinct edges (or distinct nodes) in $T_s$ is $i^2$ after $i$ rounds. This follows because one edge (or one node) can be constructed from a pair of short queries (and responses), and that there are at most $i^2$ pairs of short queries. Therefore, to construct $T_s$ at the $i$-th round, the amount of time required is ${\fancyscript{O}}(i^4)$, since the maximum number of distinct edges in a path of $T_s$ is $i^2$ and the maximum number of distinct paths in $T_s$ is also $i^2$ (after $i$ rounds). Now, if the adversary submits $\sigma$ queries, then the time complexity to construct $T_s$ is ${\fancyscript{O}}(\sigma ^5)$, as $\sum _1^\sigma i^4={\fancyscript{O}}(\sigma ^5)$. Since the time to construct $T_s$ dominates over all the other steps, the simulator time complexity is also ${\fancyscript{O}}(\sigma ^5)$ in the worst case.

The events Type1, Type2, Type3, and Type4 of $G1$ are still not defined. These events are used to tell apart the game $G1$ from the game Game(RO, S, S $^{-1}$). We describe them in the next section.

4 Definition of the $\mathsf{BAD }$ events

Events GOOD $_i$ and BAD $_i$ $\mathsf{BAD }_i$ denotes the event when the variable $\mathsf{BAD }$ is set during round $i$ of $G1$. Let the symbol $\mathsf{GOOD }_i$ denote the event $\lnot \bigvee _{j=1}^{i}\mathsf{BAD }_i$. The symbol $\mathsf{GOOD }_0$ denotes the event when no queries are submitted.

From a high level, the intuition behind the construction of the $\mathsf{BAD }_{i}$ event is straight-forward: we will show that if $\mathsf{BAD }_{i}$ does not occur, and if $\mathsf{GOOD }_{i-1}$ did occur, then the views of $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ (after $i$ rounds) are identically distributed for any attacker ${\fancyscript{A}}$. Using the above facts, we will show

$$\begin{aligned} \Big |\mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\big ]-\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\big ]\Big | \le \sum _{i=1}^{\sigma }\mathrm {Pr}\big [\mathsf{BAD }_{{i}}\mid \mathsf{GOOD }_{i-1}\big ]. \end{aligned}$$

(1)

We will then establish a concrete upper bound for this inequality in Sect. 5. In the next few subsections, we define the Type1, Type2, Type3 and Type4 events of the game $G1$ (see Fig. 6).

4.1 Type1 events: collision on $T_\pi$

Let $(x,r)$ be a fresh pair of $\pi$-query and response generated at round $i$. Observe that such a fresh pair always invokes the subroutine PartialGraph. Type1 events—which are due to $\pi$-query and its response—are shown in Fig. 7. We divide this type into two subcases. Suppose $(y_cy_c', m, yy')$ is a new edge generated from a new $\pi$-query/response $(x,r)$.

• Event Type1-a (Fig. 7(Type1-a)) This event occurs if $y$ collides with the least-significant $n$ bits (or the left-coordinate) of a node already in $T_\pi$.

• Event Type1-b (Fig. 7(Type1-b)) This event occurs if $y$ collides with the least-significant $n$ bits of a query already in $D_\pi$.

• Event Type1-c (Fig. 7(Type1-c)) This event occurs, if the least-significant $n$ bits of output of a fresh $\pi ^{-1}$-query matches with the left-coordinate of a node already in $T_s$.

Fig. 7

Type1 events of game $G1$ defined in Fig. 6. All arrows are $n$ bits each. Red arrow denotes fresh $n$ bits of output from the ideal permutation $\pi /\pi ^{-1}$. The symbol “=” denotes $n$-bit equality (Color figure online)

4.2 Events Type2, 3 and 4: current short query is old

Before we define these events, we first classify all the query-response pairs stored in $D_\pi$ prior to the submission of the current query, according to their known and unknown parts. The known part of a query-response pair is the part that is present in the view of the game $G1$, while the unknown part is not present in the view. We observe that there are seven types of such a pair, and we denote them by Q0, Q1, Q2, Q3, Q4, Q5 and Q6 in Fig. 8a(i) and (ii); the head and tail nodes in each type denote the input and output, each of size 2$n$ bits. Down, up and two-sided arrows indicate $\pi$-query, $\pi ^{-1}$-query and any of the two, respectively. The red and green circles denote the unknown and the known parts of size $n$ bits each. The queries of type Q0 have no red circles, since they are $s/s^{-1}$ queries. The remaining six types are generated due to the intermediate $\pi$ calls during the processing of $l$-queries; these queries have at least one red circle. The Q5 type can be further divided into two subtypes Q5-1 and Q5-2 according to its position in the graph $T_\pi$. If all the query-response pairs preceding the Q5 query are of type Q0 then it is Q5-1, otherwise it is type Q5-2. We cannot have any other type beyond Q0, Q1, Q2, Q3, Q4, Q5, Q6 because in any given node we cannot have the leftmost $n$ bits of input or output be unknown while the rightmost $n$ bits are known; this fact is readily clear by observing the XOR operations between the message-blocks, queries and responses occurring in the JH mode. Note that the message-blocks are always known.

• Event Type2 (Fig. 8a) A Type2 event occurs when the current $s$-query is equal to an old query of type Q1, Q2, Q3, or Q4.

• Event Type3 (Fig.  8b(i)–(iii)) Let $M$ be the current $l$-query such that $M\mathop {\rightarrow }\limits ^{pad}{m_1m_2\cdots m_k}$ was already present as a branch in $T_\pi$, but not in $T_s$; such a branch is called a red branch since it has at least $n$ bits of unknown part. A Type3 event occurs if the current $\pi$-query is the final $\pi$-query of a red branch.

• Event Type4 (Fig. 8c) The Type4 event occurs, if the current $s^{-1}$-query is equal to an old query of type Q1, Q2, Q3, Q4, Q5, or Q6.

Fig. 8

Pictorial description of Type2, Type3 and Type4 events of the game $G1$ (Fig. 6). Green circle, or green arrow denotes $n$ bits of information present in the view of the game. Red circle or red arrow denotes $n$ bits of information not present in the view. Black arrow is not used to denote any information; it denotes the transition from input to output. The symbol “=” and “==” denote events representing $n$-bit and $2n$-bit equality respectively. (a) (i) and (ii): Q0, Q1, Q2, Q3, Q4, Q5 and Q6 denote seven types of $\pi /\pi ^{-1}$-query and response; Type Q5 has further been divided into Q5-1 and Q5-2. The corresponding Type2 events are also shown; (b) Different types of a branch in the graph $T_\pi$. (i)—(iii) are called red branches since they exist in $T_\pi$, but not in $T_s$; the corresponding Type3 events associated with red branches are described in Sect. 4.2. (iv) A green branch is a branch in the graph $T_s$. The final input to $\pi$ is denoted by $y_{k-1}y''_{k-1}$ in all cases; (c) Type4 events of game $G1$ (Color figure online)

4.3 Computational paradigm

To prove the inequality 1, we will need the following lemma.

Lemma 1

(Graph Isomorphism Lemma) Given GOOD $_{i}$ and $V^{i}_1=V^{i}_2$, the graphs $T_s$ for the games $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ are isomorphic after $i$ rounds.

Proof

For each fresh $\pi /\pi ^{-1}$-query, the graph $T_\pi$ for game $G1$ is augmented in one phase (see the subroutine PartialGraph of Fig. 6). In that phase, all possible nodes generated from a fresh $\pi$-query are added to the graph $T_\pi$. A straightforward analysis of the Type1-a, b and c events shows that if these events do not occur then no nodes can be added beyond this phase. In other words, if Type1-a , b and c events do not occur in $i$ rounds then the graph $T_\pi$ contains all possible paths generated from all elements stored in the table $D_\pi$ in $i$ rounds with root $(IV,IV')$. Note that the graph $T_s$ is the maximally connected subgraph of $T_\pi$ rooted at $(IV,IV')$, generated only by the $s$-queries and responses stored in $D_s$. Also recall that, due to absence of a Type-c event, no $s^{-1}$ query can be added to the graph $T_\pi$. This implies that the graph $T_s$ of the game $G1$ contains all paths generated from all $s/s^{-1}$-queries and responses with root $(IV,IV')$.

Observe that the graph $T_s$ for Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ also contains all paths generated from all $s/s^{-1}$-queries and responses with root $(IV,IV')$. Since $V_1^i=V_2^i$, the graphs $T_s$ for $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ are isomorphic after $i$ rounds. $\square$

With the help of the events described in Sects. 4.1 and 4.2 we are equipped to prove

Theorem 1

Let ${\fancyscript{A}}$ be an indifferentiability adversary interacting with the games $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$. If ${\fancyscript{A}}$ is limited by $\sigma$ queries, then

$$\begin{aligned} \Big |\mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\big ]&-\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\big ]\Big | \\&\le \sum _{i=1}^{\sigma }\mathrm {Pr}\big [\mathsf{BAD }_{{i}}\mid \mathsf{GOOD }_{i-1}\big ]. \end{aligned}$$

Proof

The event $\mathsf{GOOD }_{i-\frac{1}{2}}$ is defined as $\mathsf{GOOD }_{i-1}$ in addition to the $\mathsf{BAD }$ events Type2, Type3, and Type 4 having not occured in the $i$-th round. For brevity, $\mathsf{GOOD }_{(i+1)-\frac{1}{2}}$ will be denoted by $\mathsf{GOOD }_{i+\frac{1}{2}}$. We need to show two things:

$$\begin{aligned}&\Big |\mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\big ]-\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\big ]\Big |\le \mathrm {Pr}\big [\lnot \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ],\end{aligned}$$

(2)

$$\begin{aligned}&\mathrm {Pr}\big [\lnot \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ] \le \sum _{i=1}^{\sigma }\mathrm {Pr}\big [\mathsf{BAD }_{{i}}\mid \mathsf{GOOD }_{i-1}\big ]. \end{aligned}$$

(3)

The proof of 3 is straight-forward. To prove 2, we proceed in the following way. Observe

$$\begin{aligned}&\Big |\mathrm {Pr}\big [ {\fancyscript{A}}^{G_{1}}\Rightarrow 1\big ]-\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\big ]\Big |\nonumber \\&=\Big |\Big (\mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\mid \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]\nonumber \\&\quad -\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\mid \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]\Big )\cdot \mathrm {Pr}\big [\mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]\nonumber \\&\quad +\Big (\mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\mid \lnot \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]\nonumber \\&\quad -\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\mid \lnot \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]\Big )\cdot \mathrm {Pr}\big [\lnot \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]\Big |. \end{aligned}$$

(4)

If we can show that

$$\begin{aligned} \mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\mid \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]=\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\mid \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ], \end{aligned}$$

(5)

then 4 reduces to 2, since $\Big \vert \mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\mid \lnot \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]-\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\mid \lnot \mathsf{GOOD }_{\sigma -\frac{1}{2}}\big ]\Big \vert \le 1.$ As a result, we focus on establishing 5.

Let $V_1^i$ and $V_2^i$ denote the views of the games $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ respectively, after $i$ queries have been processed. To prove 5, it suffices to show that given $\mathsf{GOOD }_{\sigma -\frac{1}{2}}$, the views $V_1^\sigma$ and $V_2^\sigma$ are identically distributed. We do this by induction on the number of queries $i=\sigma$. When $i=0$, then no query has been made; therefore the views are identical. We now assume the induction hypothesis holds, where the hypothesis is: given $\mathsf{GOOD }_{i-\frac{1}{2}}$, then $V_1^i$ and $V_2^i$ are identically distributed. We have to show that if $\mathsf{GOOD }_{i+\frac{1}{2}}$ occurred, then $V_1^{i+1}$ and $V_2^{i+1}$ are identically distributed. We do so by examining all possible cases based on a set of conditions for the game $G1$. The details are quite technical, however the main idea is that if no BAD events have occurred, then the graphs $T_s$ in $G1$ and Game(RO, S, S $^{-1}$) are isomorphic, from the Graph Isomorphism Lemma 1. The identical distribution of the views is an easy consequence of the isomorphism.

Let $(I_1^{i+1}, O_1^{i+1})$ and $(I_2^{i+1}, O_2^{i+1})$ denote the input-output pairs for the games $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ respectively in the $i+1$st round.

Notice that if $V^i_1=V_2^i$, then the input views $I_1^{i+1}$ and $I_2^{i+1}$ are identically distributed. We also have Lemma 1 which shows that the graphs $T_s$ in two games are isomorphic.

A little reflection shows that proving the induction step is now equivalent to showing that if $I_1^{i+1}=I_2^{i+1}$ then the output-views $O_1^{i+1}$ and $O_2^{i+1}$ are identically distributed. Let $I^{i+1}$ denote the shared query input $I_1^{i+1}=I_2^{i+1}$.

We continue by considering all possible cases based on a set of conditions for the game $G1$ in the $i+1$st round; cases 1 through 9 consider when $I_{i+1}$ is an $s$-query, cases 10 and 11 consider $I_{i+1}$ to be an $s^{-1}$-query, while cases 12 through 17 consider when $I_{i+1}$ is part of an $l$-query. Our decision tree produced the above 17 cases, which have been derived from a sequence of questions (see Fig. 9). The reader is invited to verify that all cases are considered.

Case 1 $s$- query, $|{\fancyscript{M}}|=0$, and Fresh

Implication The condition implies that $O_1^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_\pi )$. (Fig. 6. Since the graphs $T_s$ are isomorphic in both games $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ by Lemma 1, $\vert {\fancyscript{M}}\vert =0$ for Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ (Fig. 4b). This implies that $O_2^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1]\setminus Rng(D_s)$ (Fig. 4b).

Case 2 $s$-query, $|{\fancyscript{M}}|=0$, not Fresh, and type Q6

Implication The event $\mathsf{GOOD }_{i+\frac{1}{2}}$ implies that Type2 event did not occur for $G1$ in the current $i+1$th round; therefore, since $\vert {\fancyscript{M}}\vert =0$, $O_1^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_\pi )$. As the graphs $T_s$ of the games $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ are isomorphic by Lemma 1, $\vert {\fancyscript{M}}\vert =0$ for Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$. This implies that $O_2^{i+1}=r$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_s)$.

Case 3 $s$-query, $|{\fancyscript{M}}|=0$, not Fresh, and type Q5-1

Implication This case is impossible since $\vert {\fancyscript{M}}\vert =0$ and $I^{i+1}$ being of type Q5-1 contradict each other.

Case 4 $s$-query, $|{\fancyscript{M}}|=0$, not Fresh, and type Q1, Q2, Q3, Q4, or Q5-2

Implication This case is impossible since $\mathsf{GOOD }_{i+\frac{1}{2}}$ implies that Type2 event did not occur for $G1$ in the current $i+1$st round. The given conditions create a Type2 event.

Case 5 $s$-query, $|{\fancyscript{M}}|>1$

Implication If $\vert {\fancyscript{M}}\vert >1$ then we would have a node-collision in $T_s$. However, this is impossible since $\mathsf{GOOD }_{i+\frac{1}{2}}$ ensures that a Type1 event did not occur for $G1$ in the previous $i$ rounds, and a node-collision in $T_s$ is a Type1 event.

Case 6 $s$-query, $|{\fancyscript{M}}|=1$, and Fresh

Implication Since $I^{i+1}$ is fresh, $O_1^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_\pi )$. Now, for $G1$, $M\in {\fancyscript{M}}$ implies that $M\notin Dom(D_l)$ in the first $i$ rounds, since the current $s$-query $I^{i+1}$ is fresh. Also note that, because $V^1_{i}=V^2_{i}$ and the $T_s$’s are isomorphic, we have that the $D_l$’s in both games are identical. Therefore, for Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$, $M\notin Dom(D_l)$ in the first $i$ rounds. This implies that $O_2^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_s)$.

Case 7 $s$-query, $|{\fancyscript{M}}|=1$, not Fresh, and type Q6

Implication The event $\mathsf{GOOD }_{i+\frac{1}{2}}$ implies that a Type2 event did not occur in the $i+1$st round of $G1$; therefore, $O_1^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_\pi )$. In $G1$, $M\in {\fancyscript{M}}$ implies that $M\notin Dom(D_l)$ in the first $i$ rounds, since the current $s$-query $I^{i+1}$ is either of type Q3 or Q4, while the final $\pi$-query of any $l$-query cannot be of type Q3 or Q4. As in the previous case, $V^1_{i}=V^2_{i}$ and the isomorphic $T_s$’s together imply that the $D_l$ in both games are identical. Therefore, for Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$, $M\notin Dom(D_l)$ in the first $i$ rounds. This implies that $O_2^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_s)$.

Case 8 $s$-query, $|{\fancyscript{M}}|=1$, not Fresh, and type Q5-1

Implication The event $\mathsf{GOOD }_{i+\frac{1}{2}}$ implies that Type2 event did not occur in the $i+1$st round of $G1$; therefore, $O_1^{i+1}[n,2n-1]$ follows the uniform distribution on $[0,2^n-1] \setminus Rng(D_\pi )$, and $O_1^{i+1}[0,n-1]$ is a fixed value. Now, for $G1$, $M\in {\fancyscript{M}}$ implies that $M\in Dom(D_l)$ after the first $i$ rounds, since the current $s$-query $I^{i+1}$ is of type Q5-1; also note that $O_1^{i+1}[0,n-1]=D_l[M]\oplus z$, where $z$ is final block of $M$ after padding. As in the previous case, $V^1_{i}=V^2_{i}$ and the isomorphism of $T_s$’s together imply that the $D_l$ are identical in both games. Therefore, $O_2^{i+1}[0,n-1]=D_l[M]\oplus z$ (line 103 of Fig. 4b); also note that $O_2^{i+1}[n,2n-1]$ follows the uniform distribution on $[0,2^n-1] \setminus Rng(D_s)$. In conclusion, $O_1^{i+1}$ and $O_2^{i+1}$ are identically distributed.

Case 9 $s$-query, $|{\fancyscript{M}}|=0$, not Fresh, and type Q1, Q2, Q3, Q4, or Q5-2

Implication This case is impossible since event Type2 did not occur in the current $i+1$st round, and, therefore, $I^{i+1}$ cannot be of type Q1, Q2, Q3, Q4.

Case 10 $s^{-1}$-query and Fresh

Implication The condition implies that $O_1^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_\pi )$. Because $V_1^{i}=V_2^{i+1}$, we have that the $s^{-1}$-query is also a fresh query for Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$. Also note that the tables $D_s$ of both games are an identical permutation.Therefore, $O_2^{i+1}$ follows the uniform distribution on $[0,2^{2n}-1] \setminus Rng(D_s)$.

Case 11 $s^{-1}$-query and not Fresh

Implication A Type4 event and the above condition contradict each other.

Case 12 $l$-query and not Final Block

Implication If $V^1_{i+1}=V^2_{i+1}$ then $O_1^{i+1}=O_2^{i+1}=\lambda$, where $\lambda$ is the empty string.

Case 13 $l$-query, Final Block, $l$-query not in $T_{\pi }$

Implication Let $M$ be the $l$-query in question. Since the event $\mathsf{GOOD }_{i+\frac{1}{2}}$ implies that a Type1 event did not occur in the previous $i$ rounds of $G1$, there are no node-collisions in the graph $T_\pi$. Therefore, the final $\pi$-query is fresh, and so $O_1^{i+1}$ follows the uniform distribution on $[0,2^n-1] \setminus Rng(D_\pi )$. Now notice, the tables $D_l$ in both games were identical when the $l$-query $M$ was submitted; therefore, at that time of submission, $M\notin Dom(D_l)$ for both games. This ensures that $O_2^{i+1}=\mathsf{RO }(M)$ follows the uniform distribution on $[0,2^n-1] \setminus Rng(D_s)$.

Case 14 $l$-query, Final Block, $l$-query in $T_{\pi }$, $l$-query in $T_s$

Implication The graphs $T_s$ in both games are isomorphic by Lemma 1. It follows that $O_1^{i+1}=O_2^{i+1}$.

Cases 15, 16 and 17 $l$-query, Final Block, $l$-query in $T_{\pi }$, $l$-query not in $T_s$ $I^{i+1}$ is the final message-block of the current $l$-query (denoted by $M$) which forms a red branch. Let the final $\pi$-query while processing the $l$-query $M$ be denoted by $y_{k-1}y''_{k-1}.$

Case 15 Final $\pi$-query is type Q1, Q2, or Q5

Implication The above condition implies the occurrence of Type3-1 event in the $i+1$st round; therefore, we arrive at a contradiction.

Case 16 Final $\pi$-query is type Q3, Q4, or Q6

Implication Since a Type3-2 event did not occur in the $i+1$st round, $O_1^{i+1}$ follows the uniform distribution on $[0,2^n-1] \setminus Rng(D_\pi )$. Also observe, for $G1$, the $l$-query $M$ did not belong to $Dom(D_l)$ (when $M$ was submitted), since the final $\pi$-query of any $l$-query cannot be of type Q3, Q4 or Q6. As the tables $D_l$ of both games are identical, then for Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$ we have that $M\notin Dom(D_l)$ (when $M$ was submitted). Therefore, $O_2^{i+1}=\mathsf{RO }(M)$, which follows the uniform distribution on $[0,2^n-1] \setminus Rng(D_s)$.

Case 17 Final $\pi$-query is type Q0 and an intermediate query is type Q1, Q2, Q3, Q4, Q5, or Q6

Implication This case is impossible since Type3-3 in the $i+1$st round did not occur.

In summary, for each of the 17 cases above we have shown that the outputs $O_1^{i+1}$ and $O_2^{i+1}$ are identically distributed if the variable $\mathsf{BAD }$ is not set. This completes the proof of the induction step of Theorem 1. $\square$

Fig. 9

The decision tree for the proof of the induction step of Theorem 1. The conditions for the game $G1$ are shown inside the diamonds of the decision tree. The text in each leaf-node shows the implications of the conditions to the outputs of games $G1$ and Game$(\mathsf{RO },\mathsf{S },\mathsf{S }^{-1})$, while the reasons for such implications are described in brief inside the bracket

5 Estimation of $\Big \vert \mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\big ]-\mathrm {Pr}\big [{\fancyscript{A}}^{\mathsf{RO },\mathsf{S },\mathsf{S }^{-1}}\Rightarrow 1\big ]\Big \vert$

We individually compute the probabilities of each of the events described in Sects. 4.1 and 4.2. We need the help of the following lemma to provide a rigorous analysis for the upper-bounds we compute in this section.

Lemma 2

(Correction factor) If the advantage of an indifferentiability adversary ${\fancyscript{A}}$ distinguishing between the games $G1$ and Game (RO,S), when limited by $\sigma$ queries, is bounded by $\varepsilon$, then

$$\begin{aligned} \mathrm {Pr}\big [\mathsf{GOOD }_i\big ]\ge \frac{1}{C} \end{aligned}$$

for some constant $C>0$, for all $0\le i\le \sigma$.

Proof

Since $\varepsilon <1$, $\mathrm {Pr}\big [{\fancyscript{A}}\text { sets }\mathsf{BAD }{\text { in }G1}\big ]\le \varepsilon \le 1-\frac{1}{C}$ for some constant $C>0$. Noting that $\mathrm {Pr}\big [\mathsf{GOOD }_i\big ]$ is a decreasing function in $i$, the result follows. $\square$

The Type1-a event guarantees that if $T_\pi$ is $\mathsf{GOOD }_{i-1}$, then it has at most $i$ nodes. Assuming $i \le 2^{n/2}$, from Fig. 7 we obtain,

$$\begin{aligned} \mathrm {Pr}\Big [\text {Type1}_{i}\mid \mathsf{GOOD }_{i-1}\Big ]&\le 3i/(2^n-i),\nonumber \\&=\frac{6Ci}{2^{n}}, \end{aligned}$$

(6)

since for $i\le 2^{n/2}$, then $(2^n-i) \ge \frac{1}{2}2^n$.

Using the definition of Type2, Type3, and Type4 events in Sect. 4, it is straightforward to deduce:

$$\begin{aligned}&\mathrm {Pr}\big [\text {Type2}_{i}\mid \mathsf{GOOD }_{i-1}\big ]\le \frac{2Ci}{2^{n}},\\&\mathrm {Pr}\big [\text {Type3}_{i}\mid \mathsf{GOOD }_{i-1}\big ] \le \frac{2Ci}{2^{n}},\\&\mathrm {Pr}\big [\text {Type4}_{i}\mid \mathsf{GOOD }_{i-1}\big ] \le \frac{2Ci}{2^{n}}. \end{aligned}$$

We conclude by combining the above bounds into the following inequality which holds for $1\le i\le \sigma$:

$$\begin{aligned} \mathrm {Pr}\big [\mathsf{BAD }_{i}\mid \mathsf{GOOD }_{i-1}\big ]&\le \mathrm {Pr}\big [\text {Type1}_{i}\mid \mathsf{GOOD }_{i-1}\big ]\nonumber \\&\quad +\mathrm {Pr}\big [\text {Type2}_{i}\mid \mathsf{GOOD }_{i-1}\big ]\nonumber \\&\quad +\mathrm {Pr}\big [\text {Type3}_{i}\mid \mathsf{GOOD }_{i-1}\big ]\nonumber \\&\quad +\mathrm {Pr}\big [\text {Type4}_{i}\mid \mathsf{GOOD }_{i-1}\big ]\nonumber \\&\le \frac{12Ci}{2^{n}}. \end{aligned}$$

(7)

Therefore, by Theorem 1, for all ${\fancyscript{A}}$,

$$\begin{aligned} \Big |\mathrm {Pr}\big [{\fancyscript{A}}^{G_{1}}\Rightarrow 1\big ]-\mathrm {Pr}\big [{\fancyscript{A}}^{\text {Game}(\mathsf{RO }, \mathsf{S }, \mathsf{S }^{-1}}\Rightarrow 1\big ]\Big |&\le \sum _{i=1}^{\sigma }\mathrm {Pr}\big [\mathsf{BAD }_{i}\mid \mathsf{GOOD }_{i-1}\big ]\nonumber \\&\le 12C\sum _{i=1}^{\sigma }\frac{i}{2^{n}}\nonumber \\&={\fancyscript{O}}\Big (\frac{\sigma ^2}{2^{n}}\Big ). \end{aligned}$$

(8)

Using 8 and that the advantage $\epsilon$ is less than 1, we see that the adversary must use at least $2^{n/2}$ queries to distinguish between the games $G1$ and Game(RO, S, S $^{-1}$) (or between the games Game(JH, $\pi$, $\pi ^{-1}$) and Game(RO, S, S $^{-1}$), since $G1\equiv$ Game(JH, $\pi$, $\pi ^{-1}$) by Proposition 1). This yields the indifferentiability bound of $n/2$ bits for the JH mode.

6 Experimental results

We performed a series of experiments verifying our theoretical framework. The motivation for doing experiments was three-fold: the first was to do a sanity check that the probability computed from experiments did not cross the theoretically obtained upper bound. Second, we wanted to identify the likely adversarial strategies that made our analysis tight. The final goal was to explore the possibility of the existence of a shorter proof for the bound obtained in Eq. 8. On all counts, we obtained useful results.

Our simple C implementation of the game $G1$ simulated the ideal permutation, $\pi$, with randomness supplied by cstdlib > rand(), by maintaining a database of input/output pairs, assuring that $\pi$ is a permutation. The experiments were performed allowing varying proportions of reverse queries to determine the optimal adversarial strategy.

For each of these experiments, we collected data providing accurate estimates for the values of the probabilities of Type1 events, $\mathrm {Pr}\big [\text {Type1}_{i}\mid \mathsf{GOOD }_{i-1}\big ]$, described in Sect. 4. Our experiments included as a parameter the proportion of reverse queries, $R$, allowed in the hopes that if an optimal adversarial strategy including reverse queries uses a positive proportion of reverse queries that we may discover a spike in performance near this proportion. Compiling these data we conclude that, as one would expect, when the proportion, $R$, approaches zero, the Type1-a event becomes dominant; whereas, when $R$ approaches 1, the Type1-c event dominates.

In addition to these event probabilities, we calculated security bounds for several values of $n$ and $R$. The computation was achieved by randomly generating a large number of graphs, $T_s$, and determining the number of queries, $\sigma$, required to cause $\sum _{i=1}^{\sigma }\mathrm {Pr}\big [\text {Type1}_{i}\mid \mathsf{GOOD }_{i-1}\big ]\ge 0.5$.

We did not consider the Type2, Type3, and Type4 events, since, their probabilities are bounded by that of the Type1 events, for any efficient adversary. We found that choosing the values at which to place the first query uniformly at random from among all possible nodes was the most advantageous strategy for an adversary.

The results of the experiments following this method are summarized in Fig. 10. The data support the theoretically obtained bound of $\sigma =\Omega (2^{n/2})$ (see 8). Some of the values in the graph are slightly lower than $1/2$, due to the effect of constants. We expect the data to asymptotically approach $1/2$.

Fig. 10

Plot of experimental data of value of $n$ versus the normalized logarithm of $\sigma$, $\log _2(\sigma )/n$, for the game $G1$ with various values of $R$, the proportion of reverse queries allowed

The data indicate that the optimal adversarial strategy does not include the use of reverse queries. For each fixed $R<1$, however, we observe that the data asymptotically approach $1/2$. Although it is the case that for $R=1$, $\sigma$ has an expected value of $2^{n-1}$, the data support our result that, for our definition of Type1 bad events and any fixed value of $R<1$, $\sigma =\Theta (2^{n/2})$.

Based on the experimental results, it seems likely that removing the Type2 to Type4 events, as well as the reverse queries from the JH indifferentiability framework may lead to the same upper bound. The only difference in such a case would be that the proof becomes much shorter. However, a theoretical argument to accomplish this is still an open problem.

7 Conclusion and open problems

The JH hash function was one of the finalist algorithms in the NIST SHA-3 hash function competition. In this paper we improve the indifferentiability security bound of the JH hash mode of operation from $n/3$ bits to $n/2$ bits, when it is used with a 2$n$-bit permutation. This bound is optimal for JH-256, and the best, so far, for JH-512. We believe that the bound could be further improved, likely closer to $n$ bits.

Our work leaves room for more research into the JH mode. It is somewhat remarkable that despite the absence of generic attacks with work-factor significantly lower than $n$ bits, the proven pre-image, second pre-image and indifferentiability bounds for the JH mode are only up to $n/2$ bits. In future work we plan to use the proof technique from this paper to narrow the exponential gap between the upper and lower bounds of JH’s indifferentiability security. It would be very interesting to find an attack that matches the indifferentiability bounds derived in this paper. Also, the complexity for the simulator could be improved.